PSO-Based Robust Control of SISO Systems with Application to a Hydraulic Inverted Pendulum
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Robust Tracking Controllers for Arbitrary Reference Signals—Preliminary Results
- (i)
- The elements of are continuous functions of the uncertainties;
- (ii)
- There exists —row submatrix of that is positive antisymmetric.
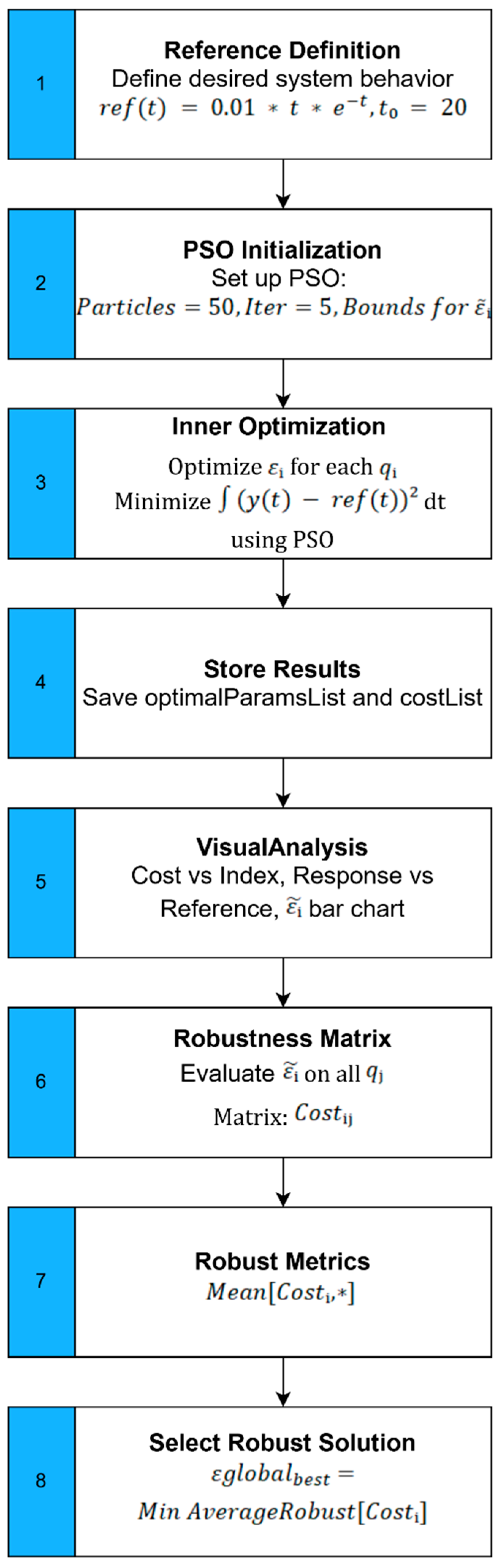
3.2. Robust Asymptotic Tracking Algorithms
| Algorithm 1: Computation of Hurwitz invariability regions | |
| Start | |
| Set the numbering indices and . | |
| Construct a sequence (maximum ) of positive up or down augmentation creating the matrix , starting from a positive Hurwitz core | |
| for | |
| ) | |
| Find stability region such that is Hurwitz invariant. | |
| End | |
| End | |
| Algorithm 2: Particle Swarm Optimization | |
| Start | |
| Initialize the swarm: Initialize particle’s position Initialize randomly particle’s velocity | |
| for | |
end end | |
| End | |
| End | |
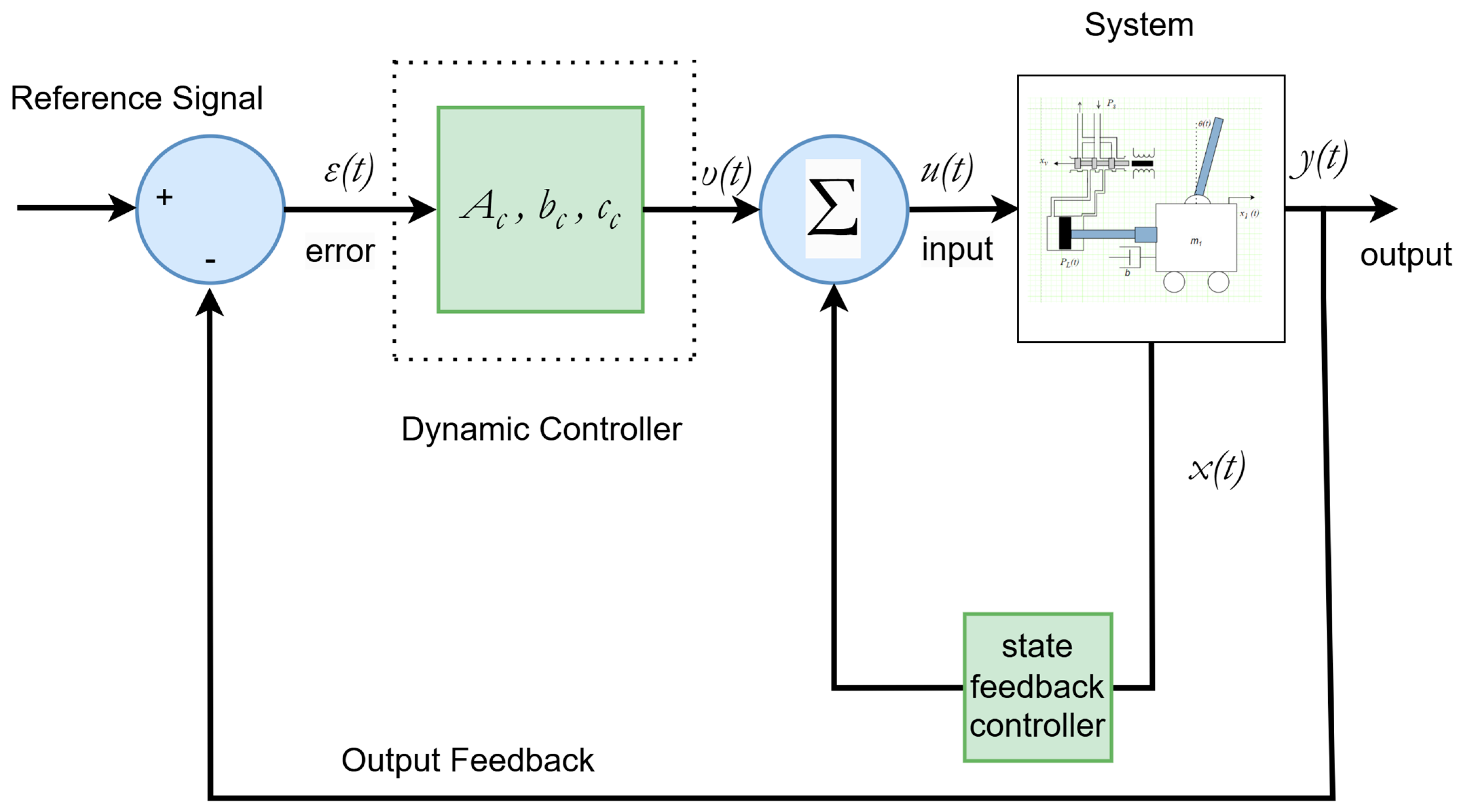
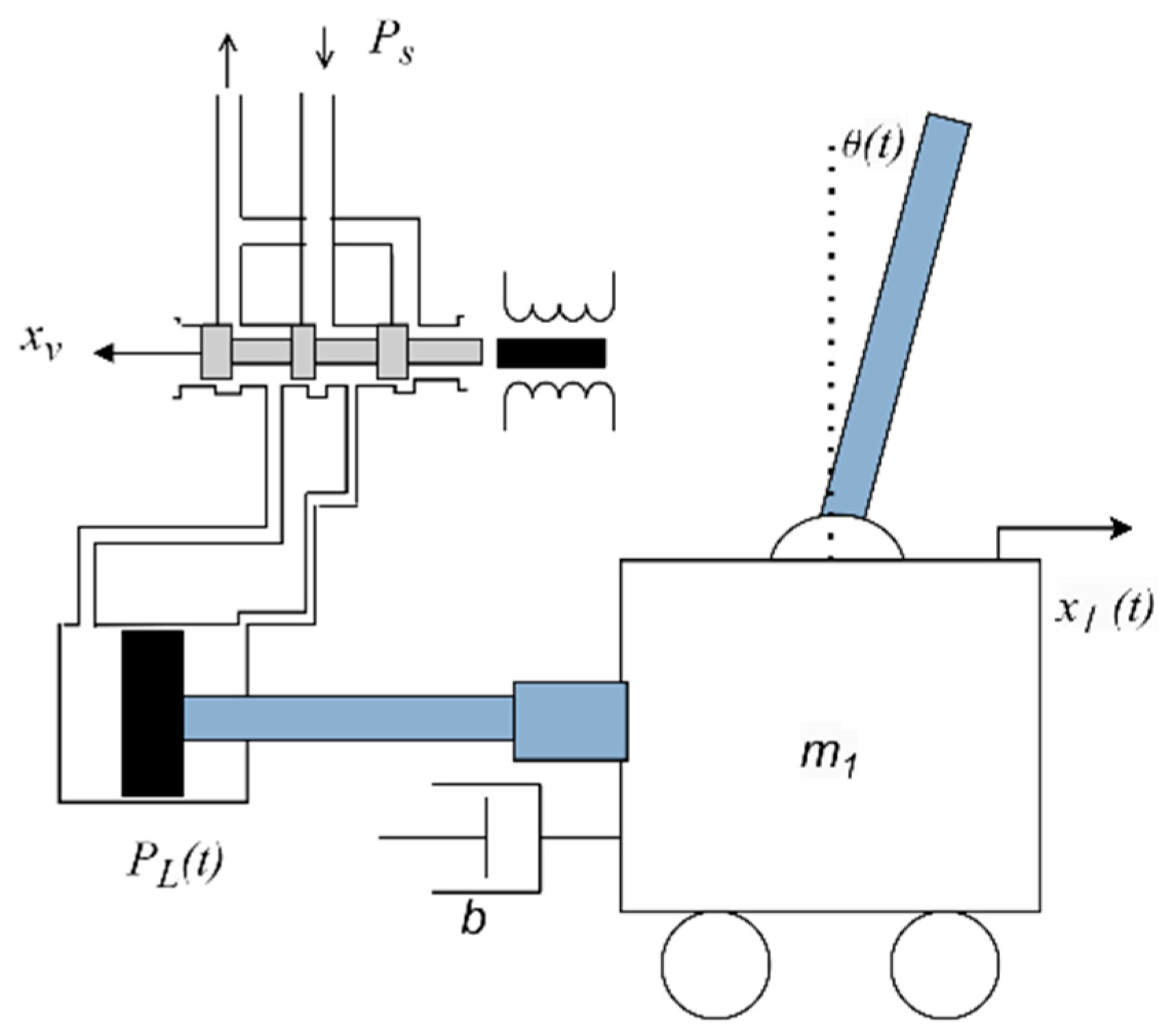
4. Robust Controller for a Hydraulic Actuator Driving a Cart with Inverted Pendulum
4.1. Linear Approximant
4.2. Solvability Conditions
4.3. Computation of the Robust Position Tracking Controller
4.4. Modification to the Initialization Bounds of the PSO Algorithm
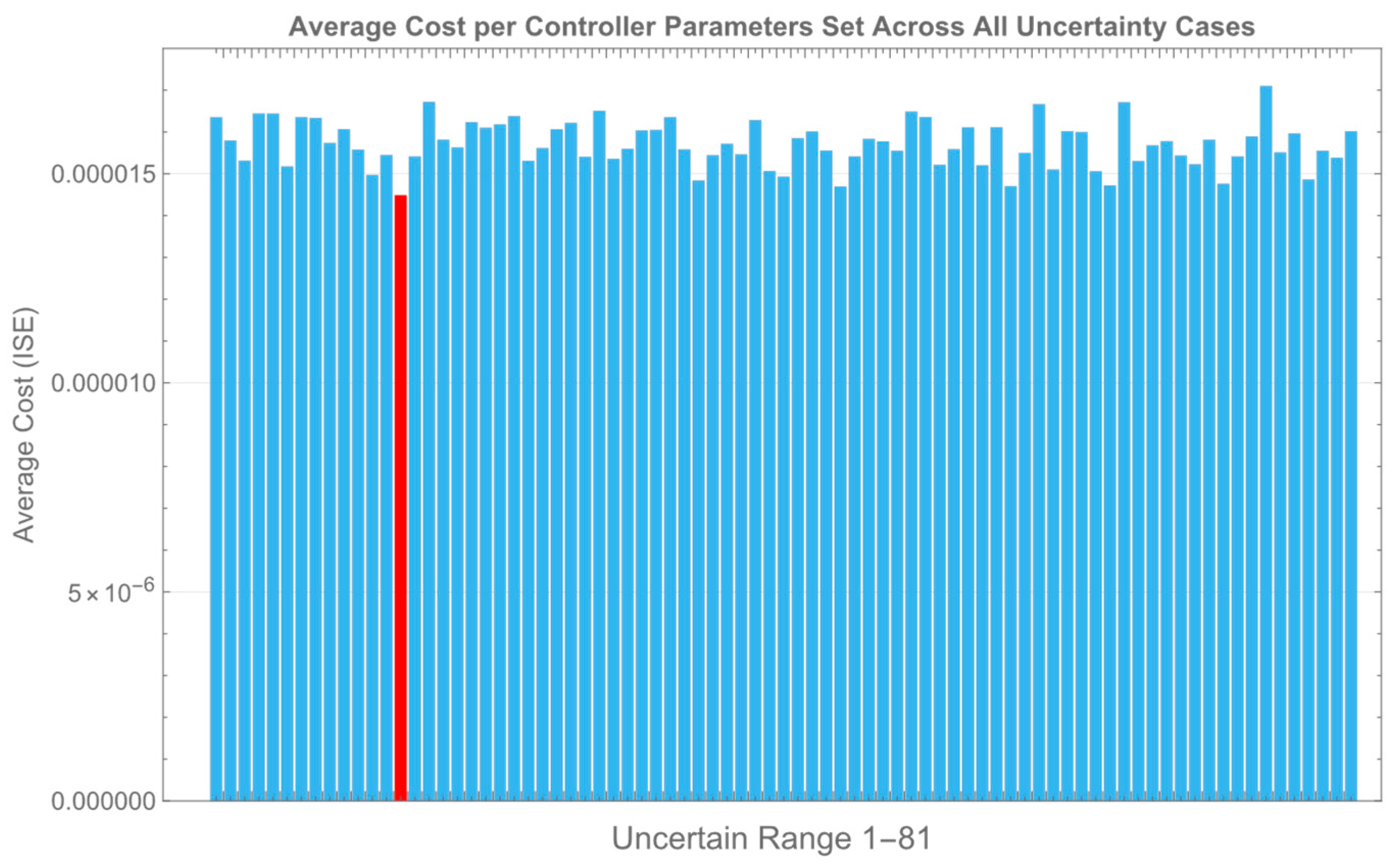
5. Simulation Results
6. Comparison Study
7. Conclusions and Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Skarpetis, M.G.; Koumboulis, F.N. Robust Controller Design for Uncertain Hydraulic Actuators Using Sine-Cosine Op-timization Algorithms. In Automatic Control of Hydraulic Systems; Nova Science Publishers: Hauppauge, NY, USA, 2023; ISBN 979-8-88697-619-9. [Google Scholar]
- Skarpetis, M.G.; Koumboulis, F.N.; Tzamtziou, K.A.; Michopoulos, P. A Robust Control Scheme for an Experimental Hydraulic System. In Proceedings of the 2021 International Conference on Engineering and Emerging Technologies (ICEET), Istanbul, Turkey, 27–28 October 2021; pp. 1–6. [Google Scholar]
- Skarpetis, M.G.; Koumboulis, F.N. Robust stabilizability algorithms with application to force control of a hydraulic actuator. In Proceedings of the 2015 6th International Conference on Modeling, Simulation, and Applied Optimization (ICMSAO), Istanbul, Turkey, 27–29 May 2015; pp. 1–6. [Google Scholar]
- Skarpetis, M.G.; Koumboulis, F.N.; Ntellis, A.S. A Heuristic Control Algorithm for Robust Internal Model Control with Arbitrary Reference Model. In Informatics in Control Automation and Robotics; Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2014; Volume 283. [Google Scholar]
- Skarpetis, M.G.; Koumboulis, F.N.; Ntellis, A.S. Robust Position Tracking for a Hydraulic Servo System. In Proceedings of the 22nd Mediterranean Conference on Control and Automation, Palermo, Italy, 16–19 June 2014; pp. 1553–1558. [Google Scholar] [CrossRef]
- Pesterev, A.V.; Morozov, Y.V. Stabilization of a Cart with Inverted Pendulum. Autom. Remote Control 2022, 83, 78–91. [Google Scholar] [CrossRef]
- Blondin, M.J.; Pardalos, P.M. A Holistic Optimization Approach for Inverted Cart-Pendulum Control Tuning. Soft Comput. 2020, 24, 4343–4359. [Google Scholar] [CrossRef]
- Maraslidis, G.S.; Kottas, T.L.; Tsipouras, M.G.; Fragulis, G.F. Design of a Fuzzy Logic Controller for the Double Pendulum Inverted on a Cart. Information 2022, 13, 379. [Google Scholar] [CrossRef]
- Chiasson, J. An Introduction to System Modeling and Control; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Rithirun, C.; Charean, A.; Sawaengsinkasikit, W. Comparison Between PID Control and Fuzzy PID Control on Invert Pendulum System. In Proceedings of the 2021 9th International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 10–12 March 2021; pp. 337–340. [Google Scholar]
- Hasan, M.; Saha, C.; Rahman, M.; Sarker, R.I.; Aditya, S.K. Balancing of an Inverted Pendulum Using PD Controller. Dhaka Univ. J. Sci. 2012, 60, 115–120. [Google Scholar] [CrossRef]
- Brumand-Poor, F.; Kauderer, L.; Matthiesen, G.; Schmitz, K. Application of Deep Reinforcement Learning Control of an Inverted Hydraulic Pendulum. Int. J. Fluid Power 2023, 24, 393–418. [Google Scholar] [CrossRef]
- White, W.N.; Fales, R.C. Control of a Double Inverted Pendulum with Hydraulic Actuation. In Proceedings of the 1999 American Control Conference, San Diego, CA, USA, 2–4 June 1999; IEEE: Piscataway, NJ, USA, 1999. [Google Scholar]
- Žilić, T.; Pavković, D.; Zorc, D. Modeling and Control of A Pneumatically Actuated Inverted Pendulum. ISA Trans. 2009, 48, 327–335. [Google Scholar] [CrossRef] [PubMed]
- Ding, G.; Bian, Y.; Yang, M. Design and Application of Hydraulic Inverted Pendulum. In Proceedings of the International Conference on Advances in Construction Machinery and Vehicle Engineering, Shanghai, China, 13–16 October 2023; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Cordasco, V.; Di Maggio, A. Modeling, Design, and Control of a Cart Inverted Pendulum with Electrical and Pneumatic Actuation. Master’s Thesis, Politecnico di Torino, Turin, Italy, 2020. [Google Scholar]
- Merritt, H.E. Hydraulic Control Systems; John Wiley & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- Karpenko, M.; Sepehri, N. Fault-tolerant control of a servohydraulic positioning system with crossport leakage. IEEE Trans. Control Syst. Technol. 2005, 13, 155–161. [Google Scholar] [CrossRef]
- Skarpetis, M.G.; Koumboulis, F.N. A Two-Step Design for Robust Input-Output Decoupling of a Class of Uncertain and Linear Parameter Dependent Systems. In Proceedings of the 2024 32nd Mediterranean Conference on Control and Automation (MED), Crete, Greece, 11–14 June 2024; pp. 884–890. [Google Scholar]
- Mohmmed, J.H.; Hassan, A.K.; Ali, M.; Kokz, S.A.; Mosa, M.H.; Kareem, A.; Zainulabdeen, A.A.; Feng, Z. Design of Uncertain Displacement Controlled Velocity Control System for Hydraulic Actuator. Heliyon 2024, 10, e26223. [Google Scholar] [CrossRef]
- Mohanty, A.; Yao, B. Indirect Adaptive Robust Control of Hydraulic Manipulators with Accurate Parameter Estimates. IEEE Trans. Control. Syst. Technol. 2010, 19, 567–575. [Google Scholar] [CrossRef]
- Hejrati, M.; Mattila, J. Impact-Resilient Orchestrated Robust Controller for Heavy-Duty Hydraulic Manipulators. IEEE/ASME Trans. Mechatron. 2025, 1–12. [Google Scholar] [CrossRef]
- Cheng, G.; Pan, S. Nonlinear Adaptive Robust Control of Single-Rod Electro-Hydraulic Actuator with Unknown Nonlinear Parameters Control Systems Technology. IEEE Trans. 2008, 16, 434–445. [Google Scholar]
- Niksefat, N.; Sepehri, N. Designing robust force control of hydraulic actuators despite system and environmental uncertainties. Control. Syst. Mag. IEEE 2001, 21, 66–77. [Google Scholar]
- Yao, B.; Bu, F.; Reedy, J.; Chiu, G.-C. Adaptive robust motion control of single-rod hydraulic actuators: Theory and experiments. IEEE/ASME Trans. Mechatronics 2000, 5, 79–91. [Google Scholar] [CrossRef]
- Jerouane, M.; Sepehri, N.; Lamnabhi-Lagarrigue, F.; Abou, S.C. Design and Experimental Evaluation of Robust Variable Structure Control for Hydraulic Actuators. In Proceedings of the 5th Asian Control Conference, Melbourne, Australia, 20–23 July 2004; Volume 3, pp. 1982–1990. [Google Scholar]
- Kliffken, M.G. Robust Sampled-Data Control of Hydraulic Flight Control Actuators. In Proceedings of the 5th Scandinavian International Conference on Fluid Power, Linköping, Sweden, 28–30 May 1997. [Google Scholar]
- Koumboulis, F.N.; Skarpetis, M.G.; Tzamtzi, M.P. Robust PI Controllers for Command Following with Application to an Electropneumatic Actuator. In Proceedings of the 2006 14th Mediterranean Conference on Control and Automation, Ancona, Spain, 28–30 June 2006; pp. 1–6. [Google Scholar]
- Koumboulis, F.N.; Skarpetis, M.G.; Mertzios, B.G. Robust Regional Stabilization of an Electropneumatic Actuator. IEEE Proc.-Control Theory Appl. 1998, 145, 226–230. [Google Scholar] [CrossRef]
- Skarpetis, M.G.; Koumboulis, F.N.; Ntellis, A.S.; Sarris, A. Robust controller design for active hydraulic suspension. In Proceedings of the 2007 IEEE Conference on Emerging Technologies & Factory Automation (EFTA 2007), Patras, Greece, 5–28 September 2007; pp. 1433–1436. [Google Scholar]
- Skarpetis, M.G.; Koumboulis, F.N.; Tzamtzi, M. Robust Control Techniques for Hydraulic Actuators. In Proceedings of the 15th Mediterranean Conference on Control and Automation, Athens, Greece, 27–29 July 2007; pp. 1–6. [Google Scholar]
- Wei, K.B.; Barmish, R. Making a polynomial Hurwitz invariant by choice of feedback gain. Int. J. Control 1989, 50, 1025–1038. [Google Scholar] [CrossRef]
- Wei, K. Stabilization of Linear Time-Invariant Interval Systems Via Constant State Feedback Control. IEEE Trans. Autom. Control 1994, 39, 22–32. [Google Scholar] [CrossRef]
- Koumboulis, F.; Skarpetis, M. Robust Triangular Decoupling with Application to 4ws Cars. IEEE Trans. Autom. Control 2000, 45, 344–352. [Google Scholar] [CrossRef]
- Koumboulis, F.; Skarpetis, M. Input-Output Decoupling for Linear Systems with Nonlinear Uncertain Structure. J. Frankl. Inst. 1996, 333, 593–624. [Google Scholar] [CrossRef]
- Koumboulis, F.N.; Skarpetis, M.G. Robust Disturbance Rejection for Left-Invertible Linear Systems With Nonlinear-Uncertain Structure. J. Dyn. Syst. Meas. Control 1999, 121, 218–225. [Google Scholar] [CrossRef]
- Skarpetis, M.G.; Koumboulis, F.N. Solving Robust Control Problems Using Robust Pole Placement in a Disk. In Proceedings of the 14th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Palma de Mallorca, Spain, 22–25 September 2009. [Google Scholar]
- Yang, S.; Yew-Soon, O.; Jin, Y. (Eds.) Evolutionary Computation in Dynamic and Uncertain Environments; Springer: Berlin/Heidelberg, Germany, 2007; Volume 51. [Google Scholar]
- Devarapalli, R.; Bhattacharyya, B.; Sinha, N.K. An Intelligent EGWO-SCA-CS Algorithm for PSS Parameter Tuning Under System Uncertainties. Int. J. Intell. Syst. 2020, 35, 1520–1569. [Google Scholar] [CrossRef]
- Geng, N.; Chen, Z.; Nguyen, Q.A.; Gong, D. Particle Swarm Optimization Algorithm For The Optimization Of Rescue Task Allocation With Uncertain Time Constraints. Complex Intell. Syst. 2021, 7, 873–890. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle Swarm Optimization. In Proceedings of IEEE International Conference on Neural Networks; IEEE Press: Piscataway, NJ, USA, 1995; pp. 1942–1948. [Google Scholar]
- Kim, T.-H.; Maruta, I.; Sugie, T. Robust PID Controller Tuning Based On The Constrained Particle Swarm Optimization. Automatica 2008, 44, 1104–1110. [Google Scholar] [CrossRef]
- Xu, G.; Yu, G. On Convergence Analysis of Particle Swarm Optimization Algorithm. J. Comput. Appl. Math. 2018, 343, 1–13. [Google Scholar]
- Poli, R.; Broomhead, D. Exact Analysis of The Sampling Distribution for the Canonical Particle Swarm Optimiser and its Convergence During Stagnation. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation (GECCO ‘07), London, UK, 7–11 July 2007; pp. 134–141. [Google Scholar]
- Erwin, K.; Engelbrecht, A. Control Parameter Sensitivity Analysis of the Multi-Guide Particle Swarm Optimization Algorithm. In Proceedings of the GECCO ‘19: Genetic and Evolutionary Computation Conference, Prague, Czechia, 13–17 July 2019; pp. 22–29. [Google Scholar]
- Cleghorn, C.W. Particle Swarm Optimization: Understanding Order-2 Stability Guarantees. In Applications of Evolutionary Computation; EvoApplications 2019; Kaufmann, P., Castillo, P., Eds.; Springer: Cham, Switzerland, 2019; Volume 11454, pp. 534–549, Lecture Notes in Computer Science. [Google Scholar]
- Clerc, M.; Kennedy, J. The Particle Swarm: Explosion, Stability, and Convergence in a Multi-Dimensional Complex Space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Nigatu, D.T.; Dinka, T.G.; Tilahun, S.L. Convergence Analysis Of Particle Swarm Optimization Algorithms For Different Constriction Factors. Front. Appl. Math. Stat. 2024, 10, 1304268. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiao, F.; Lu, J.; Wang, L.; Wu, Q. Performance Criteria Research on PSO-PID Control Systems. In Proceedings of the 2010 International Conference on Intelligent Computing and Cognitive Informatics, Kuala Lumpur, Malaysia, 22–23 June 2010; pp. 316–320. [Google Scholar]
- Hussein, A.M.; Alomari, S.A.; Almomani, M.H.; Abu Zitar, R.; Migdady, H.; Smerat, A.; Snasel, V.; Abualigah, L. A Hybrid PSO-GCRA Framework for Optimizing Control Systems Performance. Int. J. Robot. Control Syst. 2025, 5, 459–478. [Google Scholar] [CrossRef]
- Gade, S.; Shendage, S.B.; Mahadev, U. MATLAB Based Response of Systems Using Auto Tune PID Controller. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 157–162. [Google Scholar]
- Augustine, M.T. Model Predictive Control Using MATLAB. arXiv 2023, arXiv:2309.00293. [Google Scholar]
- Gahinet, P. Structured H-Infinity Synthesis in MATLAB. IFAC Proc. Vol. 2011, 18, 1435–1440. [Google Scholar] [CrossRef]
- Ravat, A.K.; Amit, D.; Manish, T. LMI and YALMIP: Modeling and Optimization Toolbox in MATLAB. In Advances in VLSI, Communication, and Signal Processing; David, H., Ed.; Springer: Singapore, 2021; pp. 507–515. [Google Scholar]
- Zhou, Y.; Helian, B.; Chen, Z.; Yao, B. Adaptive Robust Constrained Motion Control of an Independent Metering Electro-Hydraulic System Considering Kinematic and Dynamic Constraints. IEEE Trans. Ind. Inform. 2025, 1–11. [Google Scholar] [CrossRef]
- Hua, C.; Zhou, J.; Zhang, B.; Zhang, Y.; Luo, X. Prescribed Performance Tracking Control For Electro-Hydraulic Systems With Output Constraints And Valve Dynamics Compensation. Nonlinear Dyn. 2025, 113, 13211–13223. [Google Scholar] [CrossRef]
- Liao, L.; Sang, Y.; Chen, T.; Jiang, L.; Liu, J. Research on Position Tracking Control Of Electro-Hydraulic Actuator System Combining Feedforward Inverse Model Controller And Exponential Functional Link Network Adaptive Controller. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2025, 239, 643–658. [Google Scholar] [CrossRef]
- Chen, G.; Wu, W.; Yang, C.; Hu, H.; Zhang, J.; Shi, J.; Ma, Y. Practical Finite-Time Observ-er-Based Adaptive Backstepping Super-Twisting Sliding Mode Control for Deep-Sea Hydraulic Manipulator. IEEE Transac-Tions Ind. Electron. 2025. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Y.; Zhu, W.; Deng, W.; Zhao, X.; Yao, J. Adaptive Motion Control for Electro-hydraulic Servo Systems with Appointed-Time Performance. IEEE/ASME Trans. Mechatron. 2025, 1–10. [Google Scholar] [CrossRef]
- Yang, X.; Deng, W.; Yao, J. Neural Adaptive Dynamic Surface Asymptotic Tracking Control of Hydraulic Manipulators With Guaranteed Transient Performance. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 7339–7349. [Google Scholar] [CrossRef]
- Garanayak, C. Robust Adaptive Finite-Time Attitude Tracking with an unknown Inertia Matrix and Disturbance. In Proceedings of the 2024 IEEE 18th International Conference on Control & Automation (ICCA), Reykjavik, Iceland, 18–21 June 2024; pp. 270–275. [Google Scholar]
- Wu, X.; Ning, S.; Gao, Y.; Ma, J.; Qian, C.; Chen, Q. Prescribed Performance Asymptotic Tracking Control for Uncertain Non-Linear Systems With Full-State Constraints and Input Saturation. Int. J. Robust Nonlinear Control 2025, 35, 3028–3042. [Google Scholar] [CrossRef]
- Liu, C.; Yue, X.; Zhang, J.; Shi, K. Active Disturbance Rejection Control for Delayed Electromagnetic Docking of Spacecraft in Elliptical Orbits. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2257–2268. [Google Scholar] [CrossRef]
- Lyu, B.; Liu, C.; Yue, X. Integrated Predictor–Observer Feedback Control for Vibration Mitigation of Large-Scale Spacecraft With Unbounded Input Time Delay. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 4561–4572. [Google Scholar] [CrossRef]

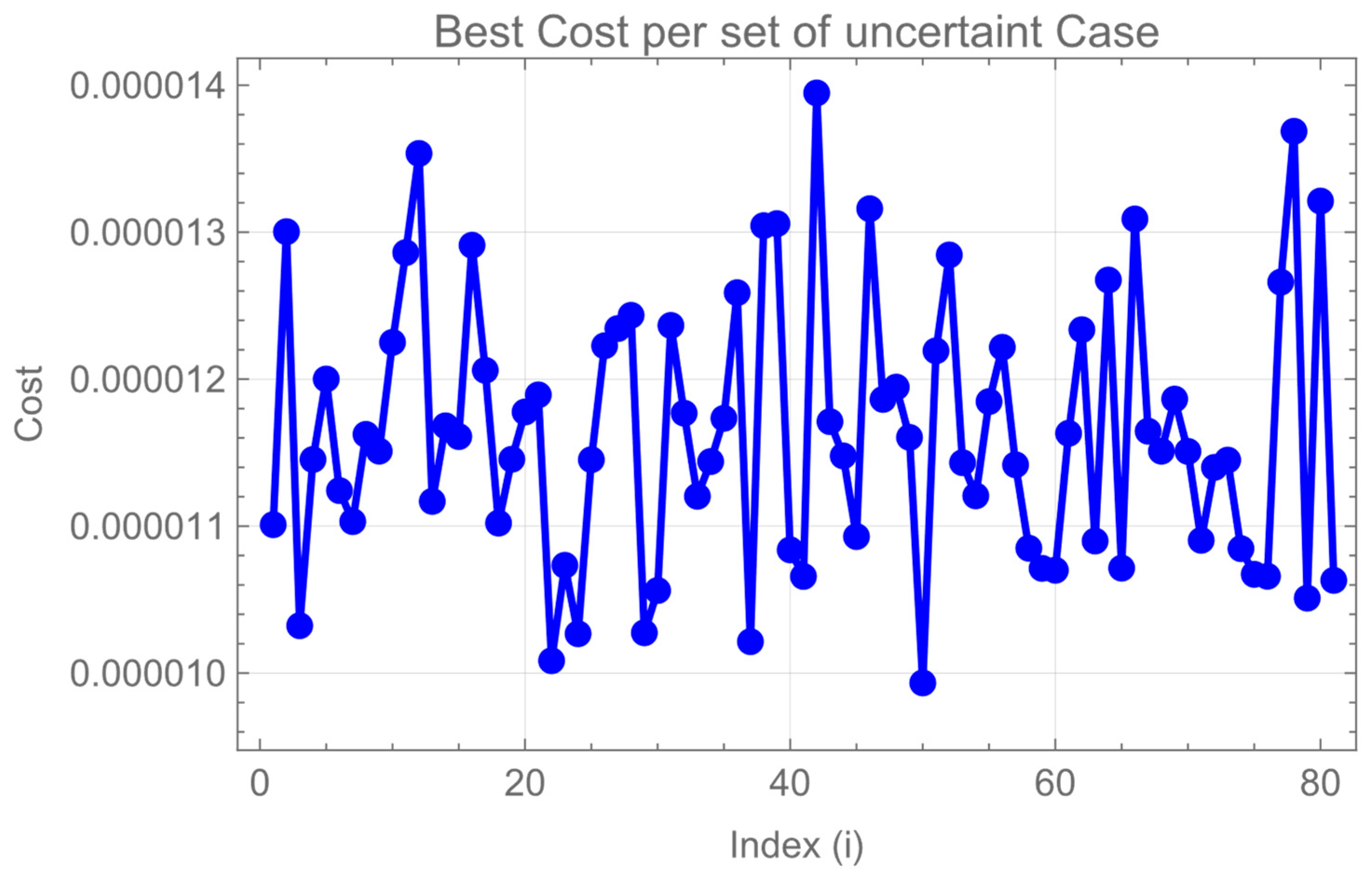
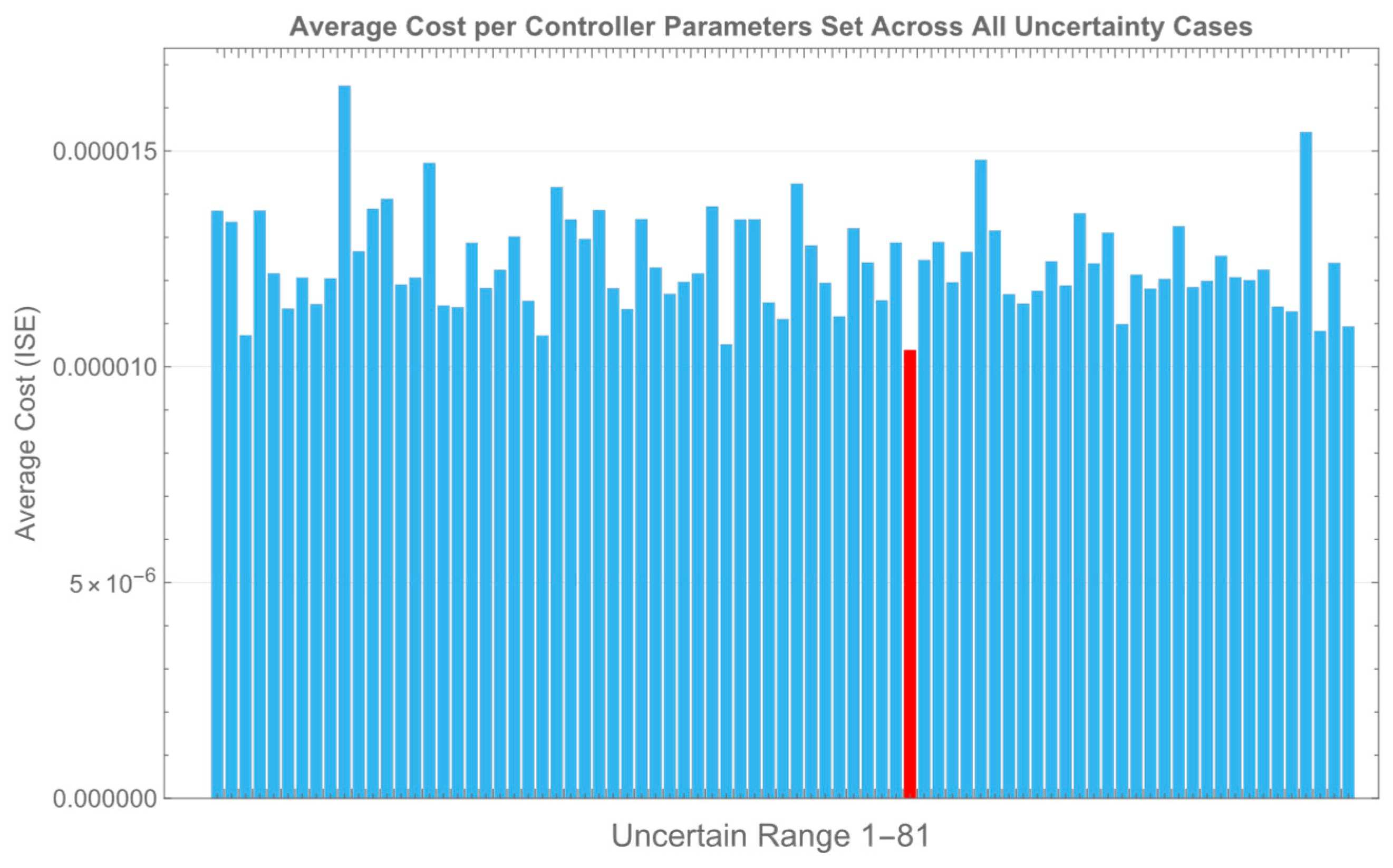
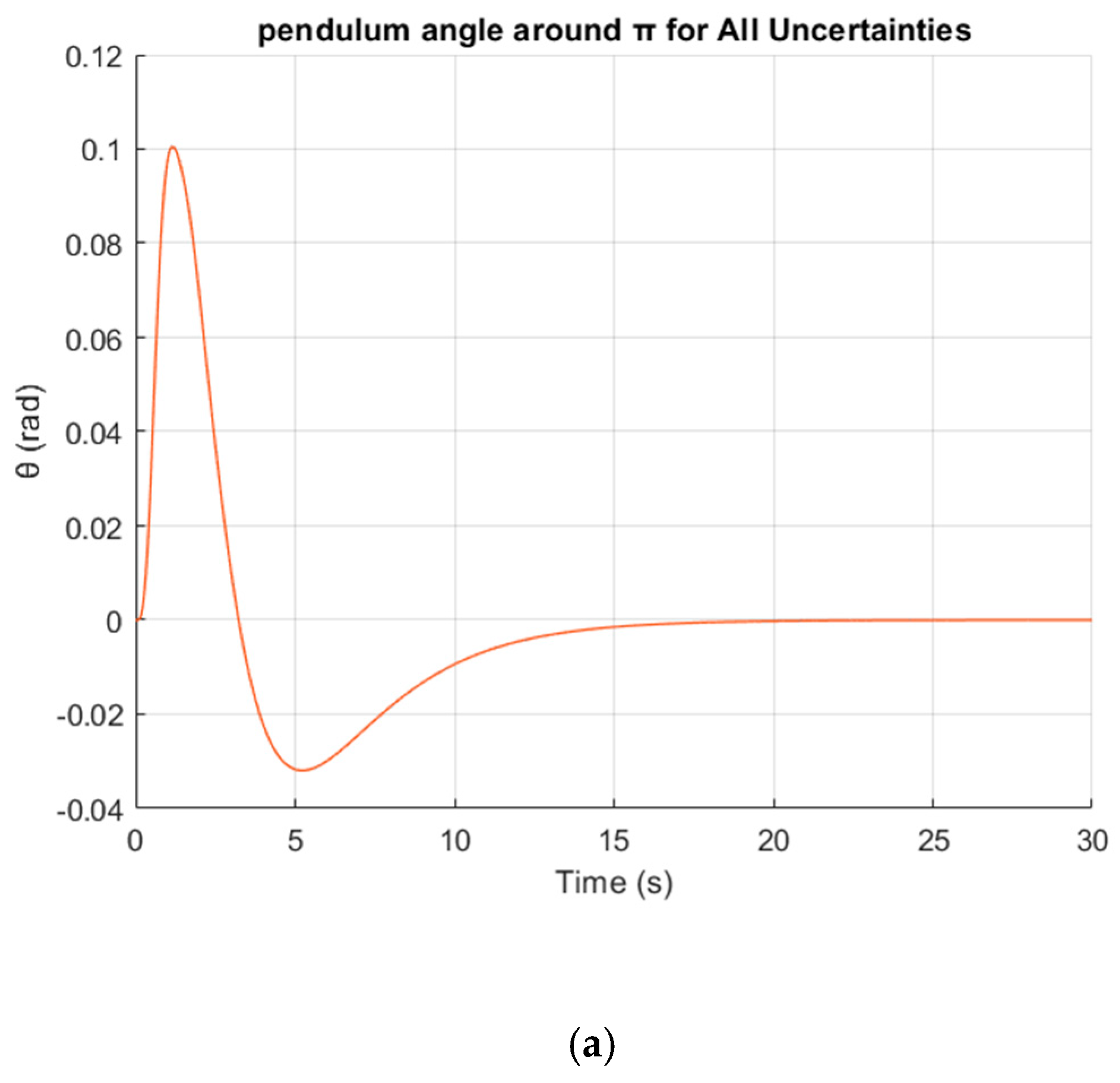

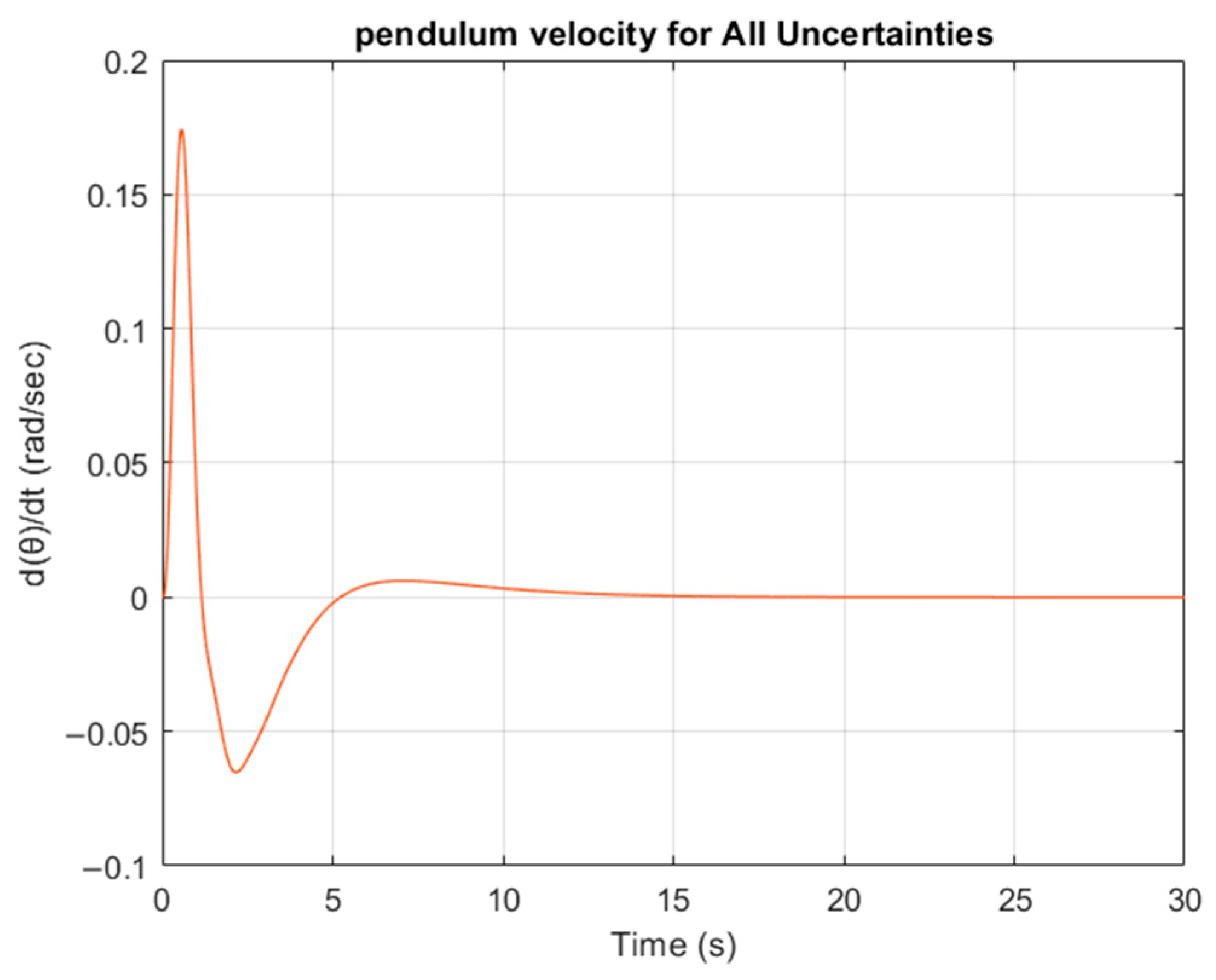
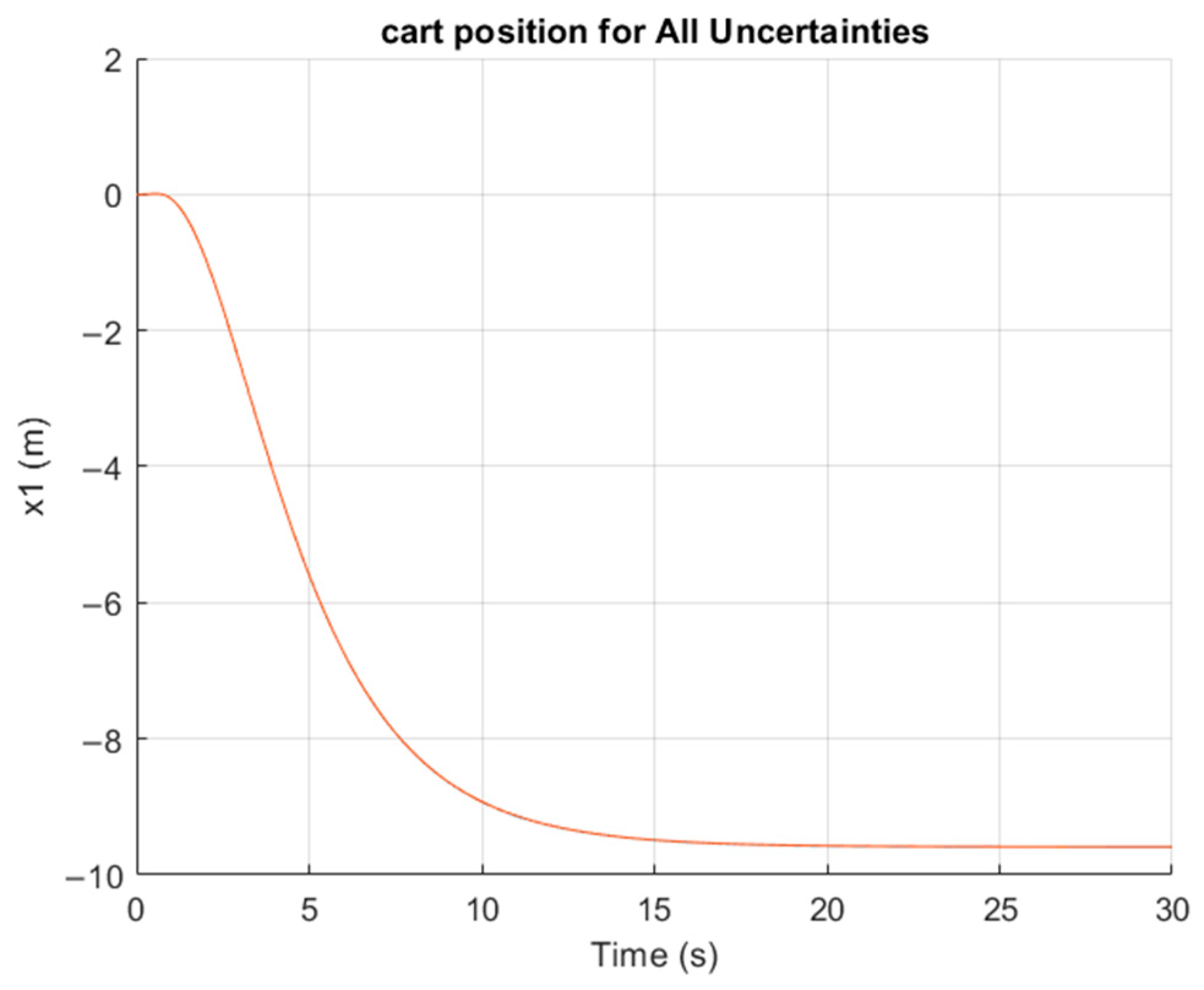
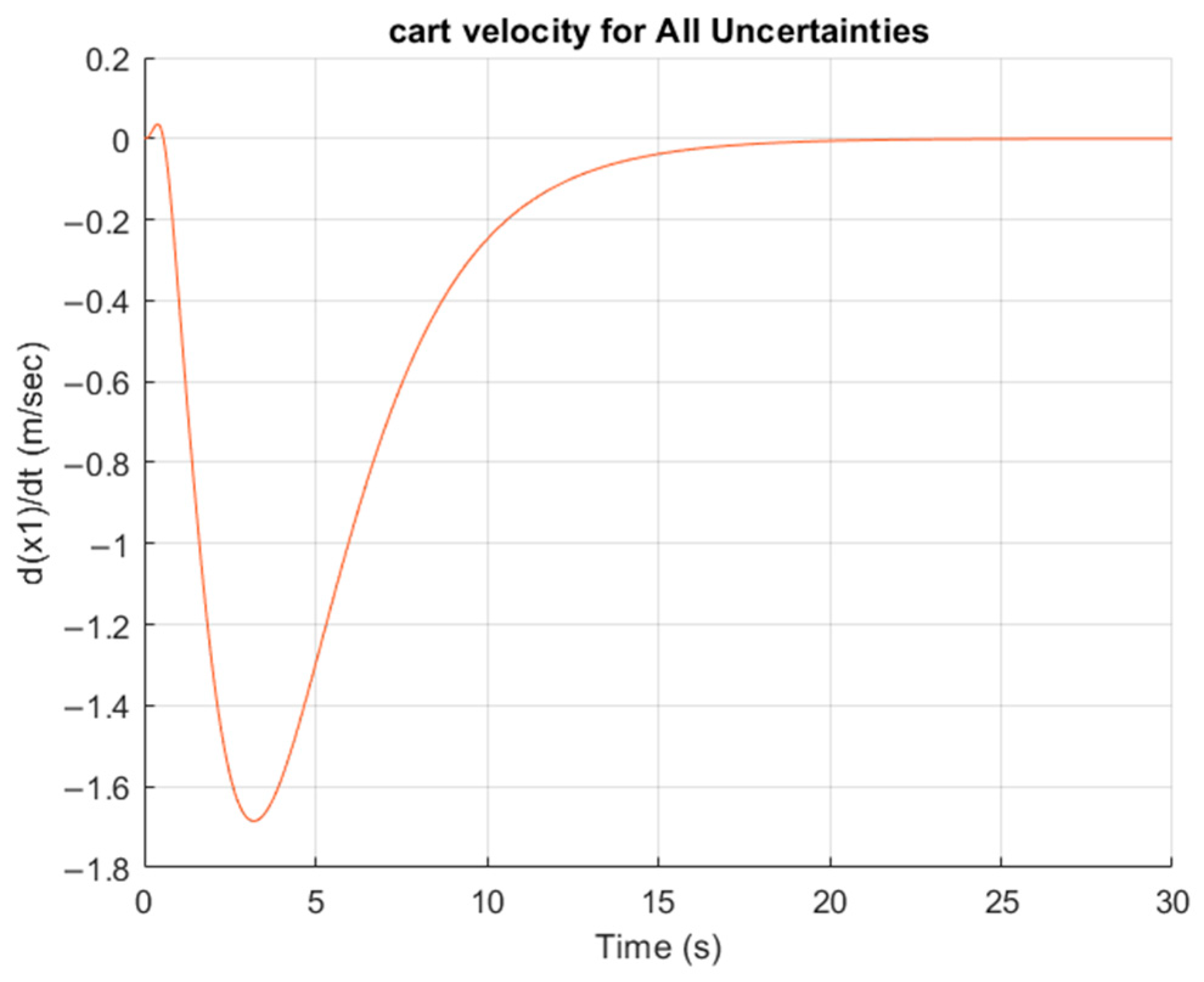
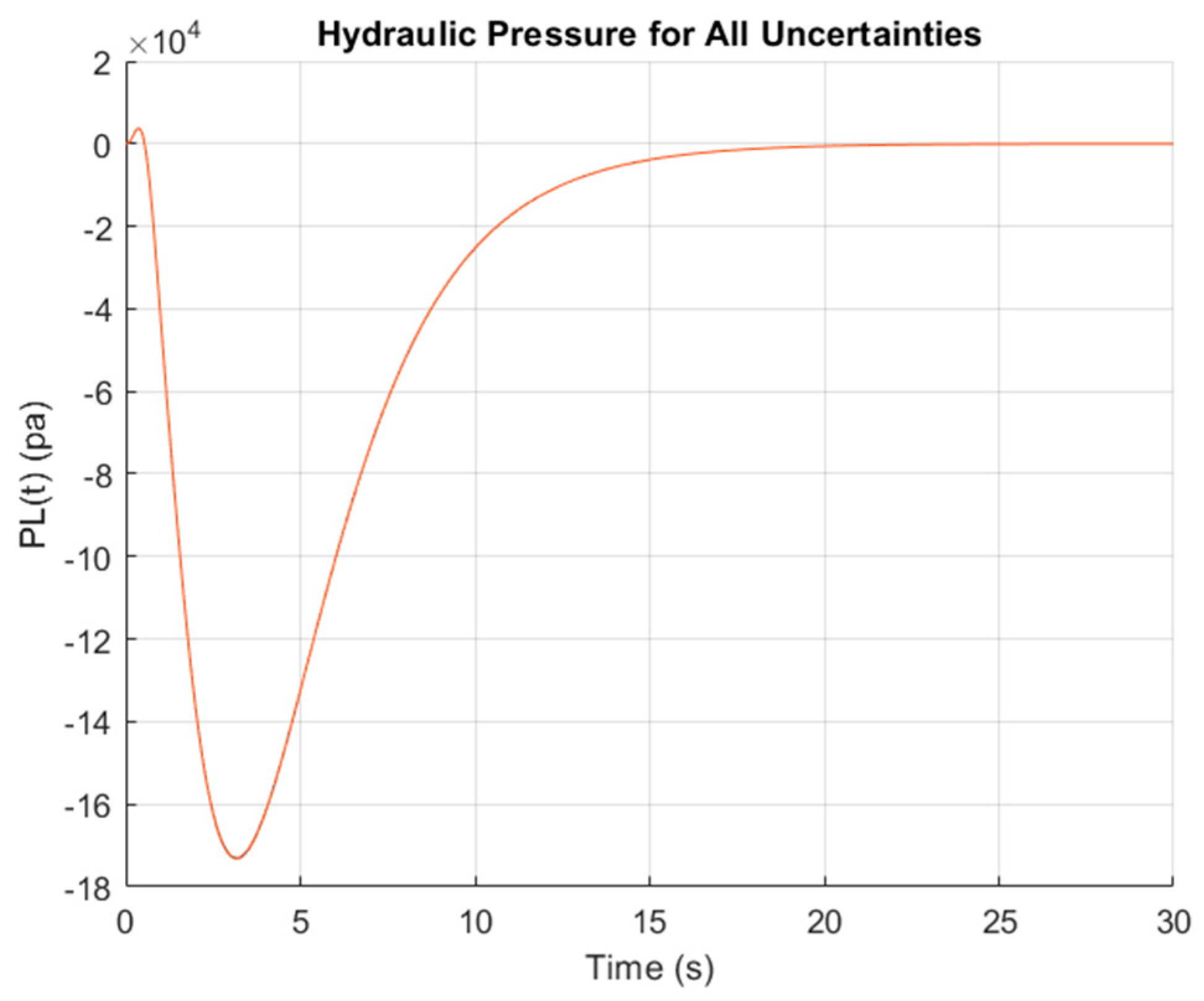
| Number of Particle | Cost Function Value | Execution Time (s) | Deviation | Squared Deviation |
|---|---|---|---|---|
| Methodology | Average Steady-State Error (Rad) | Average Time to Peak | Average Steady-State Time | Average Rise Time (10% to 90%) to Peak |
|---|---|---|---|---|
| Proposed controller | ||||
| MPC | 1 | |||
| PI | ||||
| state-feedback controller | ||||
| LMI-based state-feedback controller with integral axion |
| Methodology | Average Steady-State Error | Average Time to Peak | Average Steady-State Time | Average Rise Time (10% to 90%) to Peak |
|---|---|---|---|---|
| Proposed controller | ||||
| MPC | ||||
| PI | ||||
| state-feedback controller | ||||
| LMI-based state-feedback controller with integral axion |
| Methodology | Average Steady-State Error | Average Time to Peak | Average Steady-State Time | Average Rise Time (10% to 90%) to Peak |
|---|---|---|---|---|
| Proposed controller | ||||
| MPC | The controller does not provide robust performance across the full spectrum of system uncertainties. | |||
| PI | ||||
| state-feedback controller | ||||
| LMI-based state-feedback controller with integral axion | The controller does not provide robust performance across the full spectrum of system uncertainties. | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skarpetis, M.G.; Kouvakas, N.D.; Koumboulis, F.N.; Tsoukalas, M. PSO-Based Robust Control of SISO Systems with Application to a Hydraulic Inverted Pendulum. Eng 2025, 6, 146. https://doi.org/10.3390/eng6070146
Skarpetis MG, Kouvakas ND, Koumboulis FN, Tsoukalas M. PSO-Based Robust Control of SISO Systems with Application to a Hydraulic Inverted Pendulum. Eng. 2025; 6(7):146. https://doi.org/10.3390/eng6070146
Chicago/Turabian StyleSkarpetis, Michael G., Nikolaos D. Kouvakas, Fotis N. Koumboulis, and Marios Tsoukalas. 2025. "PSO-Based Robust Control of SISO Systems with Application to a Hydraulic Inverted Pendulum" Eng 6, no. 7: 146. https://doi.org/10.3390/eng6070146
APA StyleSkarpetis, M. G., Kouvakas, N. D., Koumboulis, F. N., & Tsoukalas, M. (2025). PSO-Based Robust Control of SISO Systems with Application to a Hydraulic Inverted Pendulum. Eng, 6(7), 146. https://doi.org/10.3390/eng6070146







