Prospects of Improving the Vibroacoustic Method for Locating Buried Non-Metallic Pipelines
Abstract
1. Introduction
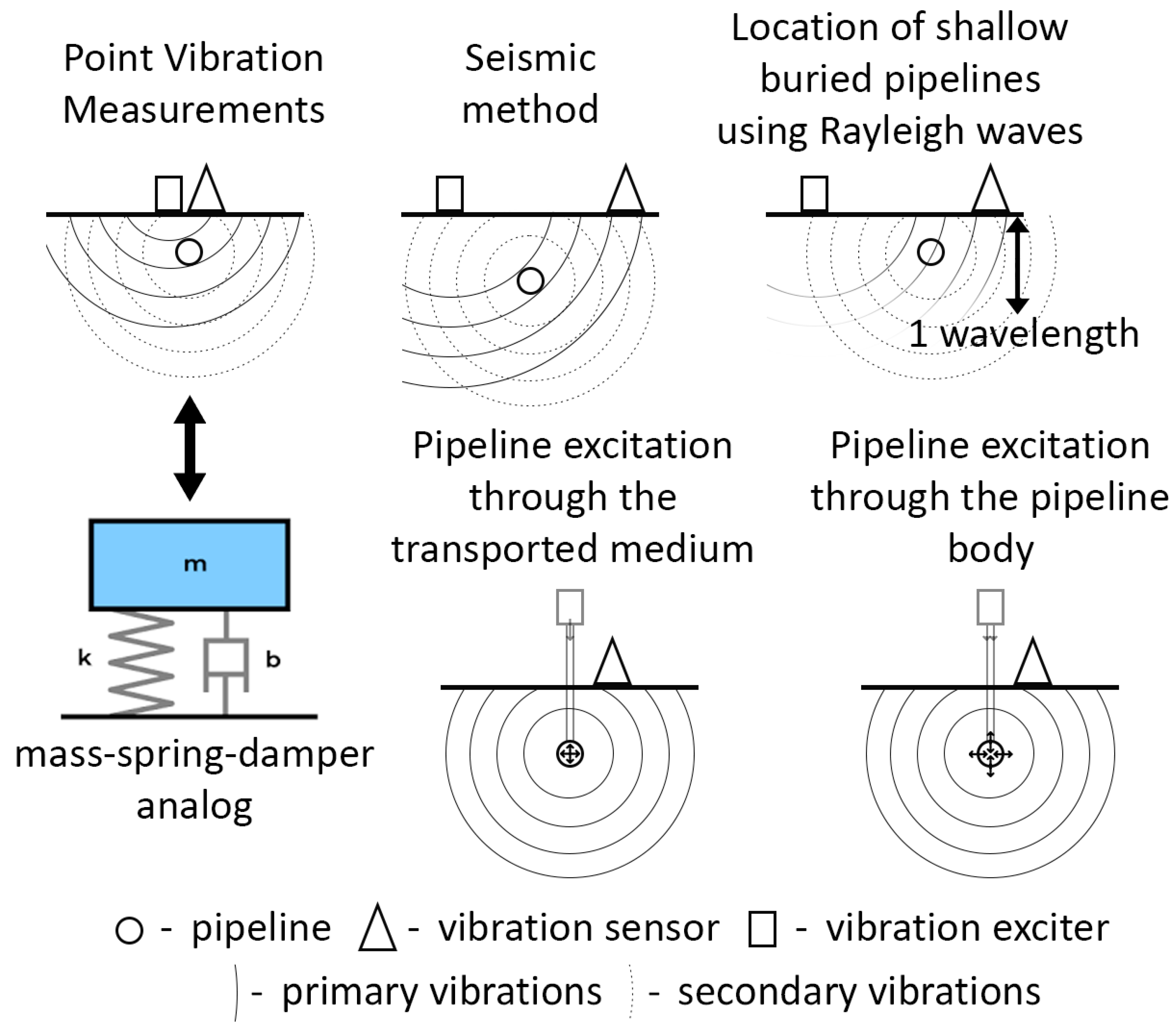
2. Acoustic Methods for Locating Buried Non-Metallic Pipelines
3. Challenges and Features of the Vibroacoustic Method for Locating Buried Non-Metallic Pipelines
- Axisymmetric wave with predominant propagation in the transported medium and some radial movement associated with the compliance of the pipe and soil (n = 0; s = 1);
- Axisymmetric wave with predominant propagation in the pipe body and some accompanying radial wall movement, influenced by Poisson’s ratio and the bulk modulus of the transported medium (n = 0; s = 2);
- Axisymmetric torsional wave, practically not accompanied by radial movement of the pipe wall (n = 0; s = 0).
4. Possible Approaches to Optimizing the Vibroacoustic Method to Increase the Operational Range for Locating Buried Non-Metallic Pipelines
5. Mechanisms of Acoustic Energy Attenuation in Pipes and Its Transmission into the Soil
6. Models Describing the Investigated Physical Process
- Narrow pipelines (viscothermal losses are significant across the entire cross-section);
- Wide pipelines (viscothermal losses are significant only in the layer adjacent to the pipe wall).
7. Results of Preliminary Modeling
8. Conclusions
- Increase in the amplitude of the transmitted signal and optimization of its characteristics;
- Optimization of measuring devices, signal filtering, and data processing;
- Variation in gas temperature, humidity, and pressure.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Semenova, T.; Martínez Santoyo, J.Y. Determining Priority Areas for the Technological Development of Oil Companies in Mexico. Resources 2025, 14, 18. [Google Scholar] [CrossRef]
- Perveitalov, O.G.; Nosov, V.V. An Approach to Evaluate the Fatigue Life of the Material of Liquefied Gases’ Vessels Based on the Time Dependence of Acoustic Emission Parameters: Part 1. Metals 2025, 15, 148. [Google Scholar] [CrossRef]
- Yamkin, A.V.; Yamkin, M.A.; Bubenchikov, M.A. Influence of convective amplification on aeroacoustics oscillations in main gas pipeline. Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2023, 334, 94–107. [Google Scholar] [CrossRef]
- Shammazov, I.; Dzhemilev, E.; Sidorkin, D. Improving the Method of Replacing the Defective Sections of Main Oil and Gas Pipelines Using Laser Scanning Data. Appl. Sci. 2022, 13, 48. [Google Scholar] [CrossRef]
- Liu, Y.; Habibi, D.; Chai, D.; Wang, X.; Chen, H.; Gao, Y.; Li, S. A Comprehensive Review of Acoustic Methods for Locating Underground Pipelines. Appl. Sci. 2020, 10, 1031. [Google Scholar] [CrossRef]
- Ge, L.; Zhang, C.; Tian, G.; Xiao, X.; Ahmed, J.; Wei, G.; Hu, Z.; Xiang, J.; Robinson, M. Current Trends and Perspectives of Detection and Location for Buried Non-Metallic Pipelines. Chin. J. Mech. Eng. 2021, 34, 97. [Google Scholar] [CrossRef]
- Tian, Y.; Palaev, A.; Goluntsov, A.; Liu, Z.; Shao, M.; Wang, B. Early assessment method for damage to polyethylene pipes based on linear directional waves. Mech. Adv. Mater. Struct. 2025, 1–21. [Google Scholar] [CrossRef]
- Zhang, A.; Zhong, D.; Xu, Z.; Zhang, H. Research on the positioning of buried polyethylene pipelines considering the acoustic attenuation characteristics. Sci. Rep. 2025, 15, 5826. [Google Scholar] [CrossRef]
- Muggleton, J.M.; Brennan, M.J.; Gao, Y. Determining the Location of Buried Plastic Water Pipes from Measurements of Ground Surface Vibration. J. Appl. Geophys. 2011, 75, 54–61. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Xu, Z.; Zhang, A.; Liu, X.; Sun, P.; Sun, X. Buried PE Pipeline Location Method Based on Double-Tree Complex Wavelet Cross-Correlation Delay. Sensors 2024, 24, 7310. [Google Scholar] [CrossRef]
- Palaev, A.G.; Fuming, Z.; Yifan, T. Method for Assessing Damage to Gas Distribution Network Pipelines Based on Nonlinear Guided Wave. Int. J. Eng. 2024, 37, 852–859. [Google Scholar] [CrossRef]
- Pshenin, V.V.; Komarovskiy, M.S.; Podlesniy, D.S.; Rozanova, L.R. Innovative technologies of subsurface utility engineering for non-metallic pipeline location. Transp. Storage Oil Prod. Hydrocarb. 2021, 5–6, 17–26. [Google Scholar] [CrossRef]
- Gogolinskiy, K.V.; Vinogradova, A.A.; Kopylova, T.N.; Povarov, V.G.; Vasilev, E.A.; Shchiptsova, E.K.; Rybkin, D.E.; Kolobov, D.S. Study of Physicochemical Properties of Polyethylene Gas Pipelines Material with a Prolonged Service Life. Int. J. Press. Vessel. Pip. 2022, 200, 104825. [Google Scholar] [CrossRef]
- Khokhlov, S.; Sokolov, S.; Vinogradov, Y.; Frenkel, I. Conducting Industrial Explosions near Gas Pipelines. J. Min. Inst. 2021, 247, 48–56. [Google Scholar] [CrossRef]
- Aleksandrov, P.N.; Krizsky, V.N. Direct and Inverse Problems of Seismic Exploration of Anisotropic and Dispersive Elastic Media on Volume Integral Equations. Math. Models Comput. Simul. 2023, 15, 976–986. [Google Scholar] [CrossRef]
- Ge, L.; Liu, Y.; Gao, Y.; Xiao, X.; Wu, J.; Hu, W. Improving acoustic localization using time delay estimation of wave reflection in buried pipelines. Measurement 2025, 242, 116157. [Google Scholar] [CrossRef]
- Cui, X.; Gao, Y.; Muggleton, J.; Liu, Y. Superimposed imaging of acoustic wave reflections for the detection of underground nonmetallic pipelines. Mech. Syst. Signal Process 2024, 209, 111127. [Google Scholar] [CrossRef]
- Muggleton, J.M.; Brennan, M.J.; Rogers, C.D.F. Point Vibration Measurements for the Detection of Shallow-Buried Objects. Tunn. Undergr. Space Technol. 2014, 39, 27–33. [Google Scholar] [CrossRef]
- Liu, Y.; Habibi, D.; Chai, D.; Wang, X.; Chen, H. A Numerical Study of Axisymmetric Wave Propagation in Buried Fluid-Filled Pipes for Optimizing the Vibro-Acoustic Technique When Locating Gas Pipelines. Energies 2019, 12, 3707. [Google Scholar] [CrossRef]
- Hooper, J.Z.; Kalkowski, M.; Muggleton, J.M. Improving Acoustic Methods of Pipeline Leak Location with Distributed Sensing. J. Phys. Conf. Ser. 2024, 2647, 192010. [Google Scholar] [CrossRef]
- Pinnington, R.J.; Briscoe, A.R. Externally Applied Sensor for Axisymmetric Waves in a Fluid Filled Pipe. J. Sound Vib. 1994, 173, 503–516. [Google Scholar] [CrossRef]
- Muggleton, J.M.; Yan, J. Wavenumber Prediction and Measurement of Axisymmetric Waves in Buried Fluid-Filled Pipes: Inclusion of Shear Coupling at a Lubricated Pipe/Soil Interface. J. Sound Vib. 2013, 332, 1216–1230. [Google Scholar] [CrossRef]
- Davis, R.B. A Simplified Approach for Predicting Interaction between Flexible Structures and Acoustic Enclosures. J. Fluids Struct. 2017, 70, 276–294. [Google Scholar] [CrossRef]
- Merkulov, V.N.; Prikhodko, V.I.; Tyutekin, V.V. Normal modes in a thin cylindrical elastic shell filled with fluid and driven by forces specified on its surfaces. Acoust. J. 1979, 25, 96–102. [Google Scholar]
- Merkulov, V.N.; Prikhodko, V.I.; Tyutekin, V.V. Excitation and propagation of normal modes in a thin cylindrical elastic shell filled with fluid. Acoust. J. 1978, 24, 723–730. [Google Scholar]
- Nie, R.; Li, T.; Zhu, X.; Zhang, C. Analysis of Free Vibration Characteristics of Cylindrical Shells with Finite Submerged Depth Based on Energy Variational Principle. Symmetry 2021, 13, 2162. [Google Scholar] [CrossRef]
- Norton, M.P.; Drew, S.J. VIBRATION GENERATED SOUND|Radiation by Flexural Elements. In Encyclopedia of Vibration; Elsevier: Amsterdam, The Netherlands, 2001; pp. 1456–1480. ISBN 978-0-12-227085-7. [Google Scholar]
- Silk, M.G.; Bainton, K.F. The Propagation in Metal Tubing of Ultrasonic Wave Modes Equivalent to Lamb Waves. Ultrasonics 1979, 17, 11–19. [Google Scholar] [CrossRef]
- Nishino, H.; Takashina, S.; Uchida, F.; Takemoto, M.; Ono, K. Modal Analysis of Hollow Cylindrical Guided Waves and Applications. Jpn. J. Appl. Phys. 2001, 40, 364. [Google Scholar] [CrossRef]
- Muggleton, J.M.; Kalkowski, M.; Gao, Y.; Rustighi, E. A Theoretical Study of the Fundamental Torsional Wave in Buried Pipes for Pipeline Condition Assessment and Monitoring. J. Sound Vib. 2016, 374, 155–171. [Google Scholar] [CrossRef]
- Dong, Y.; Lu, N. Dependencies of Shear Wave Velocity and Shear Modulus of Soil on Saturation. J. Eng. Mech. 2016, 142, 04016083. [Google Scholar] [CrossRef]
- Yu, Y.; Safari, A.; Niu, X.; Drinkwater, B.; Horoshenkov, K.V. Acoustic and Ultrasonic Techniques for Defect Detection and Condition Monitoring in Water and Sewerage Pipes: A Review. Appl. Acoust. 2021, 183, 108282. [Google Scholar] [CrossRef]
- Dutta, T.T.; Otsubo, M.; Kuwano, R. Stress Wave Transmission and Frequency-Domain Responses of Gap-Graded Cohesionless Soils. Soils Found. 2021, 61, 857–873. [Google Scholar] [CrossRef]
- Prasad, M.; Meissner, R. Attenuation Mechanisms in Sands: Laboratory versus Theoretical (Biot) Data. Geophysics 1992, 57, 710–719. [Google Scholar] [CrossRef]
- Lo, W.-C.; Yeh, C.-L.; Jan, C.-D. Effect of Soil Texture and Excitation Frequency on the Propagation and Attenuation of Acoustic Waves at Saturated Conditions. J. Hydrol. 2008, 357, 270–281. [Google Scholar] [CrossRef]
- Huang, S.; Lu, C.; Li, H.; He, J.; Wang, Q.; Cao, X.; Gao, Z.; Wang, Z.; Lin, H. Research on Acoustic Wave Attenuation from the Perspective of Soil Particle Movement Using the Discrete Element Method. Comput. Electron. Agric. 2023, 207, 107747. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, L.; Fu, M.; Ozevin, D.; Yuan, H. Study on Leak Localization for Buried Gas Pipelines Based on an Acoustic Method. Tunn. Undergr. Space Technol. 2022, 120, 104247. [Google Scholar] [CrossRef]
- Oelze, M.L.; O’Brien, W.D.; Darmody, R.G. Measurement of Attenuation and Speed of Sound in Soils. Soil Sci. Soc. Am. J. 2002, 66, 788–796. [Google Scholar] [CrossRef]
- Dain, Y.; Lueptow, R.M. Acoustic Attenuation in Three-Component Gas Mixtures—Theory. J. Acoust. Soc. Am. 2001, 109, 1955–1964. [Google Scholar] [CrossRef]
- Didmanidze, O.; Afanasev, A.; Khakimov, R. Natural gas methane number and its influence on the gas engine working process efficiency. J. Min. Inst. 2021, 251, 730–737. [Google Scholar] [CrossRef]
- Harris, C.M. Absorption of Sound in Air versus Humidity and Temperature. J. Acoust. Soc. Am. 1966, 40, 148–159. [Google Scholar] [CrossRef]
- Beranek, L.L.; Mellow, T.J. The Wave Equation and Solutions. In Acoustics: Sound Fields and Transducers; Elsevier: Amsterdam, The Netherlands, 2012; pp. 21–63. ISBN 978-0-12-391421-7. [Google Scholar]
- Lahiri, C.; Knobloch, K.; Bake, F.; Enghardt, L. Attenuation of Sound in Wide Ducts with Flow at Elevated Pressure and Temperature. J. Sound Vib. 2014, 333, 3440–3458. [Google Scholar] [CrossRef]
- Xerri, W.; Saracco, G.; Ribodetti, A.; Zomero, L.; Picon, P. Three-Dimensional Localization of Buried Polyethylene Pipes Using Acoustic Method. Sensors 2022, 22, 9433. [Google Scholar] [CrossRef] [PubMed]
- Rodarte, E.; Singh, G.; Miller, N.R.; Hrnjak, P. Sound Attenuation in Tubes due to Visco-Thermal Effects. J. Sound Vib. 2000, 231, 1221–1242. [Google Scholar] [CrossRef]
- Nikolaev, A.; Goluntsov, A.; Breff, A.T. Determination of the coefficient of hydraulic resistance when using anti-turbulence additives. Reliab. Theory Appl. 2024, 19, 107–124. [Google Scholar] [CrossRef]
- Andersen, P.R. Modelling of Acoustic Viscothermal Losses Using the Boundary Element Method: From Method to Optimization. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2018. [Google Scholar]
- Sharma, B.; Kumar, R. A brief introduction to bulk viscosity of fluids. arXiv 2023, arXiv:2303.08400. [Google Scholar] [CrossRef]
- Sharma, B.; Kumar, R.; Pareek, S. Bulk Viscosity of Dilute Gases and Their Mixtures. Fluids 2023, 8, 28. [Google Scholar] [CrossRef]
- Lin, J.; Scalo, C.; Hesselink, L. Bulk viscosity model for near-equilibrium acoustic wave attenuation. arXiv 2017, arXiv:1707.05876. [Google Scholar] [CrossRef]
- Cramer, M.S. Numerical Estimates for the Bulk Viscosity of Ideal Gases. Phys. Fluids 2012, 24, 066102. [Google Scholar] [CrossRef]
- Long, M. Environmental Noise. In Architectural Acoustics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 175–219. [Google Scholar]
- Richards, L.W.; Sigafoos, D.H. Vibrational Relaxation of Methane. J. Chem. Phys. 1965, 43, 492–497. [Google Scholar] [CrossRef]
- Franco, E.E.; Brizzotti, M.A.; Higuti, R.T.; Adamowski, J.C.; Buiochi, F. Acoustic transmission with mode conversion phenomenon. In Proceedings of the 18th International Congress of Mechanical Engineering, Ouro Preto, Brazil, 6–11 November 2005. [Google Scholar]
- Hu, W.-C.; Sari, S.K.; Hou, S.-S.; Lin, T.-H. Effects of Acoustic Modulation and Mixed Fuel on Flame Synthesis of Carbon Nanomaterials in an Atmospheric Environment. Materials 2016, 9, 939. [Google Scholar] [CrossRef]
- Razmi, A.R.; Hanif, A.R.; Shahbakhti, M. A comparative techno-economic assessment between solar-based hydrogen production by methane pyrolysis and water electrolysis methods. Renew. Energy 2025, 242, 122504. [Google Scholar] [CrossRef]
- Jordan, J.L.; Casem, D.T.; Bradley, J.M.; Dwivedi, A.K.; Brown, E.N.; Jordan, C.W. Mechanical Properties of Low Density Polyethylene. J. Dyn. Behav. Mater. 2016, 2, 411–420. [Google Scholar] [CrossRef]
- Jordan, J.L.; Rowland, R.L.; Greenhall, J.; Moss, E.K.; Huber, R.C.; Willis, E.C.; Hrubiak, R.; Kenney-Benson, C.; Bartram, B.; Sturtevant, B.T. Elastic Properties of Polyethylene from High Pressure Sound Speed Measurements. Polymer 2021, 212, 123164. [Google Scholar] [CrossRef]
- Press, F. Section 9: Seismic velocities. In Handbook of Physical Constants, Revised ed.; Clark, S.P., Jr., Ed.; Geological Society of America: New York, NY, USA, 1966; Volume 97, pp. 195–218. [Google Scholar] [CrossRef]
- Zimmer, M.A. Seismic Velocities in Unconsolidated Sands: Measurements of Pressure, Sorting, and Compaction Effects. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2004. [Google Scholar]
- P 01-72 Methodical Recommendations for Determination of Dynamic Properties of Soils, Rocks and Local Building Materials. Available online: https://meganorm.ru/Index2/1/4293769/4293769180.htm (accessed on 28 April 2025).
- Lee, Y.H.; Oh, T. The Measurement of P-, S-, and R-Wave Velocities to Evaluate the Condition of Reinforced and Prestressed Concrete Slabs. Adv. Mater. Sci. Eng. 2016, 2016, 1–14. [Google Scholar] [CrossRef]
- Park, J.Y.; Yoon, Y.G.; Oh, T.K. Prediction of Concrete Strength with P-, S-, R-Wave Velocities by Support Vector Machine (SVM) and Artificial Neural Network (ANN). Appl. Sci. 2019, 9, 4053. [Google Scholar] [CrossRef]
- Beltman, W. Viscothermal Wave Propagation, Including Acousto-Elastic Interaction. J. Acoust. Soc. Am. 1999, 116, 2542. [Google Scholar] [CrossRef]
- Weston, D.E. The Theory of the Propagation of Plane Sound Waves in Tubes. Proc. Phys. Soc. Sect. B 1953, 66, 695–709. [Google Scholar] [CrossRef]
- Nijhof, M.J.J. Viscothermal Wave Propagation. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2010. [Google Scholar] [CrossRef]
- Fuller, C.R.; Fahy, F.J. Characteristics of Wave Propagation and Energy Distributions in Cylindrical Elastic Shells Filled with Fluid. J. Sound Vib. 1982, 81, 501–518. [Google Scholar] [CrossRef]
- Muggleton, J.M.; Brennan, M.J.; Pinnington, R.J. Wavenumber Prediction of Waves in Buried Pipes for Water Leak Detection. J. Sound Vib. 2002, 249, 939–954. [Google Scholar] [CrossRef]
- Gao, Y.; Sui, F.; Muggleton, J.M.; Yang, J. Simplified Dispersion Relationships for Fluid-Dominated Axisymmetric Wave Motion in Buried Fluid-Filled Pipes. J. Sound Vib. 2016, 375, 386–402. [Google Scholar] [CrossRef]
- Gao, Y.; Muggleton, J.M.; Liu, Y.; Rustighi, E. An Analytical Model of Ground Surface Vibration Due to Axisymmetric Wave Motion in Buried Fluid-Filled Pipes. J. Sound Vib. 2017, 395, 142–159. [Google Scholar] [CrossRef]
- Farai, O.; Metje, N.; Anthony, C.; Chapman, D. Analysis of Acoustic Signal Propagation for Reliable Digital Communication along Exposed and Buried Water Pipes. Appl. Sci. 2023, 13, 4611. [Google Scholar] [CrossRef]
- Humberg, K.; Richter, M.; Trusler, J.P.; Span, R. Measurements and modelling of the viscosity of (methane + ethane) mixtures at temperatures from (253.15 to 473.15) K with pressures up to 2 MPa. J. Chem. Thermodyn. 2020, 147, 106104. [Google Scholar] [CrossRef]
- Krout, K.A.; Sohrab, S.H. On the Speed of Sound. Int. J. Thermodyn. 2016, 19, 29–34. [Google Scholar] [CrossRef]
- Trusler, J.P.M.; Zarari, M. The speed of sound and derived thermodynamic properties of methane at temperatures between 275 K and 375 K and pressures up to 10 MPa. J. Chem. Thermodyn. 1992, 24, 973–991. [Google Scholar] [CrossRef]
- Yan, B.; Tian, J.; Meng, X.; Zhang, Z. Vibration Characteristics and Location of Buried Gas Pipeline under the Action of Pulse Excitation. Processes 2023, 11, 2849. [Google Scholar] [CrossRef]






| Technology | Name of Commercial Device | Key Characteristics of the Device | Device Limitations |
|---|---|---|---|
| Excitation of oscillations in the transported gas | Gas Tracker 2, MADE S.A., La Farlède, France | The location accuracy is up to 15 cm from the pipeline route. Operating frequencies range from 400 to 500 Hz. The generator produces a sound pressure level of 110 dB. The oscillation sensor features various gain- and noise-filtering settings. The supplied software and hardware enable the device to be used “out-of-the-box”. | Requires connection to the pipeline system. Operation is possible without interrupting gas supply, but with reduced efficiency. Optimal performance is achieved within a pressure range of 0.021 to 4 bar. The effective location range is up to 200 m from the connection point. The device is not suitable for pipelines enclosed in casings and is susceptible to noise interference from road traffic and railway lines. The measuring device displays only the sought-after pipeline. Turns and tees significantly reduce the operational range of the device. The accuracy and location range of the pipeline are reduced in loose and heterogeneous soils. |
| Excitation of oscillations in the pipe body | The UM-112M impact mechanism as part of the Uspekh TPT-522N system, TECHNO-AC, Kolomna, Russian Federation | The location accuracy is within 20 cm of the pipeline route. The impact mechanism excites acoustic oscillations of the pipeline body at an adjustable frequency of 0.5, 1, or 2 strikes per second. The impact force is regulated by a voltage of 12/24 V. The acoustic sensor measures the received signal in the range of 0.09 to 2.2 kHz. The supplied software and hardware enable the device to be used “out-of-the-box”. | The maximum depth of the pipeline for location is up to 3 m. The method requires a connection to the surface of the pipe and is not applicable to pipes with a diameter of less than 50 mm. The effective location range extends up to 100 m from the connection point. The accuracy and location range of the pipeline are reduced in loose and heterogeneous soils. The measuring device displays only the sought pipeline. |
| Seismic method | Ultra-Trac APL, SENSIT Technologies, Valparaiso, IN, USA | The location accuracy is no less than 45 cm of the pipeline route. The device operates in two modes with frequencies of 500 and 900 Hz, depending on the estimated location depth of the target object and soil characteristics (such as the velocity of wave propagation within it). The supplied software and hardware enable the device to be used “out-of-the-box”. | The depth of the pipeline for location ranges from 30 cm to 250 cm, depending on the diameter. The device’s location efficiency decreases under conditions of heterogeneous and loose soils. Differentiation of the detected utilities is performed manually. The location range along the pipeline route is unlimited. |
| Point vibration measurements | Electromagnetic shaker system F4/Z820WA, Wilcoxon Sensing Technologies, Frederick, MD, USA | The location accuracy is within 20 cm of the pipeline route [18]. The device allows for determining the resonant frequency and amplitude of oscillations of soil at a specific point. The device requires proprietary software for data processing and interpretation but is supplied without it. | The maximum depth of the pipeline for location is up to 30 cm. The device requires a large number of point measurements and loses efficiency under heterogeneous soil conditions. Differentiation of the detected utilities is performed manually. The location range along the pipeline route is unlimited. |
| Potential Optimization Reserve | Description |
|---|---|
| Variation in gas temperature, humidity, and pressure | Adjusting these parameters changes the physical characteristics of the sound propagation medium without significantly deviating from the normal operational limits of the gas supply process, making it potentially acceptable for most gas distribution companies. However, the impact of these parameters on the efficiency of buried gas pipeline location is not yet sufficiently understood and requires further investigation. |
| Increase in the amplitude of the transmitted signal and optimization of its characteristics | The frequency of the signal introduced into the pipe directly affects the ratio between the energy transmitted by the gas to the surface and the energy propagated further through the gas inside the pipe. Higher frequencies result in larger soil oscillation amplitudes, which reduce the sound propagation distance along the pipeline route [19]. Conversely, lower frequencies exhibit the opposite effect. Therefore, during pipeline location, when the signal is lost, it may be advisable to perform repeated measurements at both higher and lower frequencies, as this could allow the signal to be re-detected due to changes in the balance between surface signal strength and its propagation distance. Special attention should also be paid to the resonant frequency of the pipeline–soil system, which enables a more efficient transmission of oscillations across the phase boundary with poor acoustic coupling. |
| Optimization of measuring devices, signal filtering, and data processing | The use of a greater number of highly sensitive devices and more advanced data processing algorithms will enable signal filtering and processing at lower signal-to-noise ratios. |
| Medium | Density, kg/m3 | Velocity of Elastic Wave Propagation, m/s | Characteristic Specific Acoustic Impedance (ρ ∙v), Pa·s/m | Source |
|---|---|---|---|---|
| Methane | 0.657 (at 25 °C and 1 atm) | 446 (at 25 °C and 1 atm) | 293 (at 25 °C and 1 atm) | [55,56] |
| HDPE | 941–965 | Longitudinal 2401–2493 Transverse 982–1024 | Longitudinal 2.26·106–2.41·106 Transverse 0.92·106–0.99·106 | [57,58] |
| LDPE | 910–930 | Longitudinal 2073–2142 Transverse 657–716 | Longitudinal 1.89·106–1.99·106 Transverse 0.6·106–0.66·106 | [57,58] |
| Dry sand | 1500–1750 | Longitudinal 350–600 Transverse 200–400 | Longitudinal 0.53·106–1.05·106 Transverse 0.30·106–0.70·106 | [59,60] |
| Saturated sand | 1900–2200 | Longitudinal 1750–2000 Transverse 175–250 | Longitudinal 3.33·106–4.40·106 Transverse 0.33·106–0.55·106 | [59,60] |
| Loose backfill soils | 1400–1700 | Longitudinal 100–300 Transverse 70–150 | Longitudinal 0.14·106–0.51·106 Transverse 0.10·106–0.26·106 | [61] |
| Loams | 1600–2100 | Longitudinal 300–1400 Transverse 140–700 | Longitudinal 0.48·106–2.94·106 Transverse 0.21·106–1.47·106 | [61] |
| Clay soils, moist, plastic | 1700–2200 | Longitudinal 500–2800 Transverse 130–1200 | Longitudinal 0.85·106–6.16·106 Transverse 0.22·106–2.64·106 | [61] |
| Clay soils, dense, semi-hard, and hard | 1900–2600 | Longitudinal 2000–3500 Transverse 1100–2000 | Longitudinal 3.80·106–9.10·106 Transverse 2.09·106–5.20·106 | [61] |
| Concrete | 2250–2400 | Longitudinal 3000–4600 Transverse 1750–2600 | Longitudinal 6.75·106–11.04·106 Transverse 3.93·106–6.24·106 | [62,63] |
| Parameter | Value |
|---|---|
| Material | CH4 (methane) [gas] |
| Bulk viscosity | 14·10−6 Pa·s at 1 atm, 25 °C calculated with [51]; 17.1·10−6 Pa·s at 1 atm, 75 °C calculated with [51]; 14.2·10−6 Pa·s at 10 atm, 25 °C estimated with [72]. |
| Ratio of specific heats | 1.31 under all simulation conditions |
| Speed of sound | 446 at 1 atm, 25 °C [55]; 485 at 1 atm, 75 °C calculated with [73]; 447 at 10 atm, 25 °C estimated with [74]. |
| Input boundary condition | Pressure = 6.3 Pa |
| Output boundary condition | Circular port |
| Varied Parameter | Relative Change in Attenuation |
|---|---|
| Increase in sound frequency to 1 kHz | +49.91% |
| Decrease in sound frequency to 100 Hz | −41.69% |
| Increase in pressure to 10 atm | +15.12% |
| Increase in temperature to 75 °C | +20.24% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pshenin, V.; Sleptsov, A.; Dukhnevich, L. Prospects of Improving the Vibroacoustic Method for Locating Buried Non-Metallic Pipelines. Eng 2025, 6, 121. https://doi.org/10.3390/eng6060121
Pshenin V, Sleptsov A, Dukhnevich L. Prospects of Improving the Vibroacoustic Method for Locating Buried Non-Metallic Pipelines. Eng. 2025; 6(6):121. https://doi.org/10.3390/eng6060121
Chicago/Turabian StylePshenin, Vladimir, Alexander Sleptsov, and Leonid Dukhnevich. 2025. "Prospects of Improving the Vibroacoustic Method for Locating Buried Non-Metallic Pipelines" Eng 6, no. 6: 121. https://doi.org/10.3390/eng6060121
APA StylePshenin, V., Sleptsov, A., & Dukhnevich, L. (2025). Prospects of Improving the Vibroacoustic Method for Locating Buried Non-Metallic Pipelines. Eng, 6(6), 121. https://doi.org/10.3390/eng6060121






