Investigation of the Hydrostatic Pressure Effect on the Formation of Hot Tearing in the AA6111 Alloy During Direct Chill Casting of Rectangular Ingots
Abstract
1. Introduction
1.1. The Direct Chill Casting Process
1.2. Hot Tearing in DC Casting
1.3. Mathematical Simulations of DC Casting
1.4. Study Intent
2. Experimental Section
2.1. Materials
2.2. Model Description
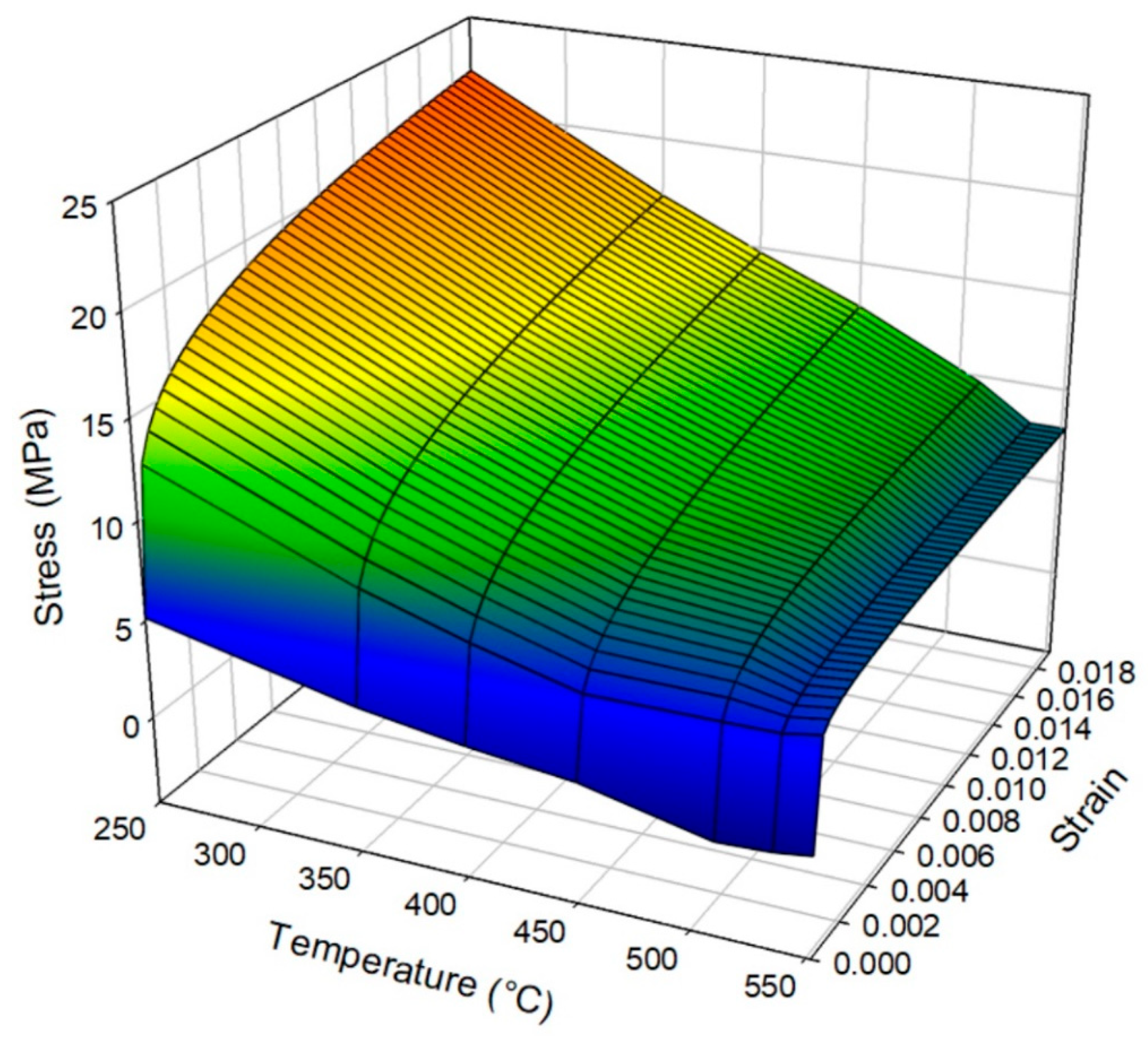
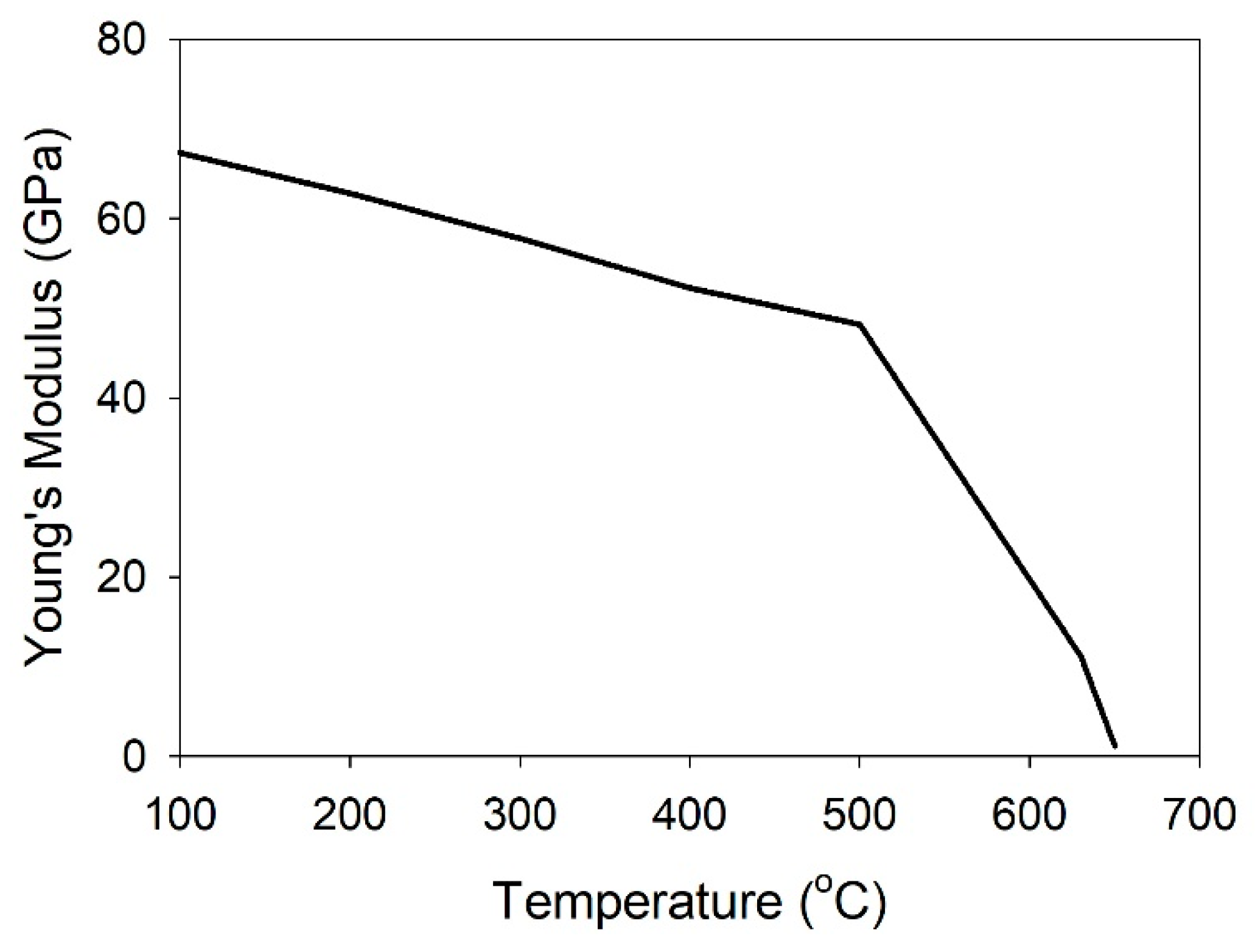
2.3. Material Properties
3. Results and Discussion
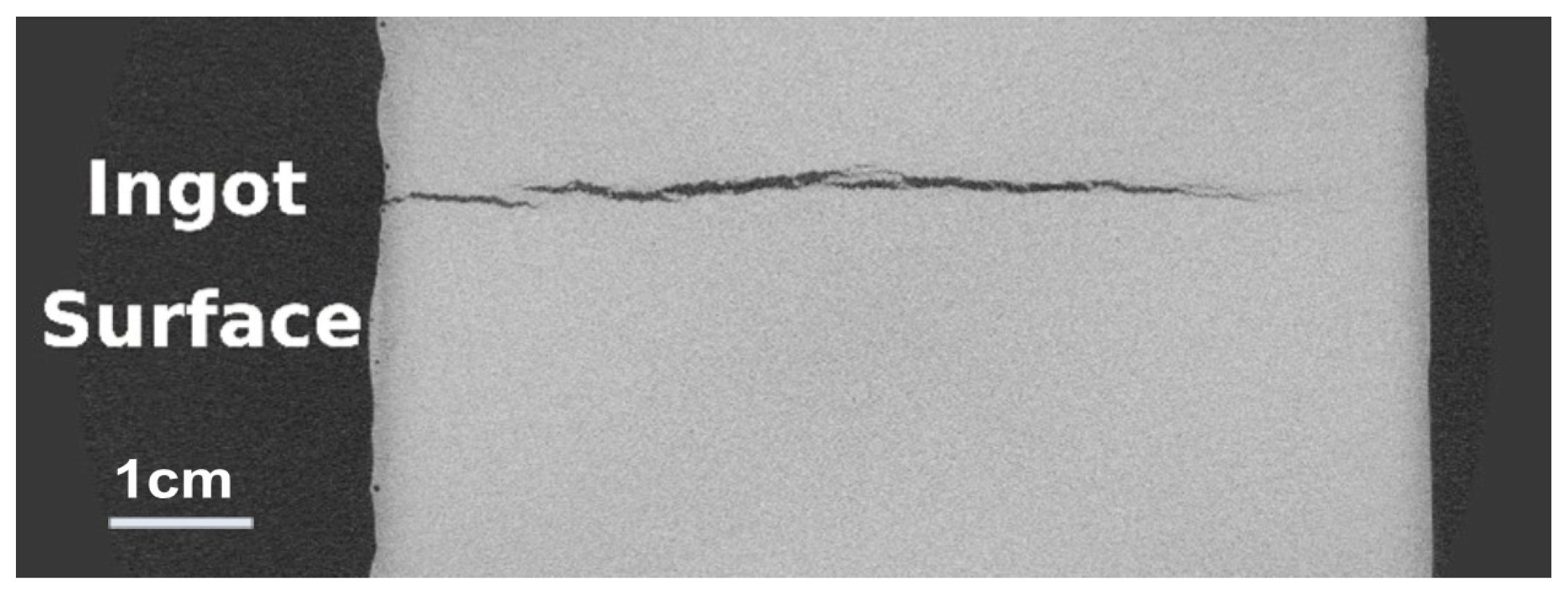
3.1. Macro Cracks in the Cast Ingots
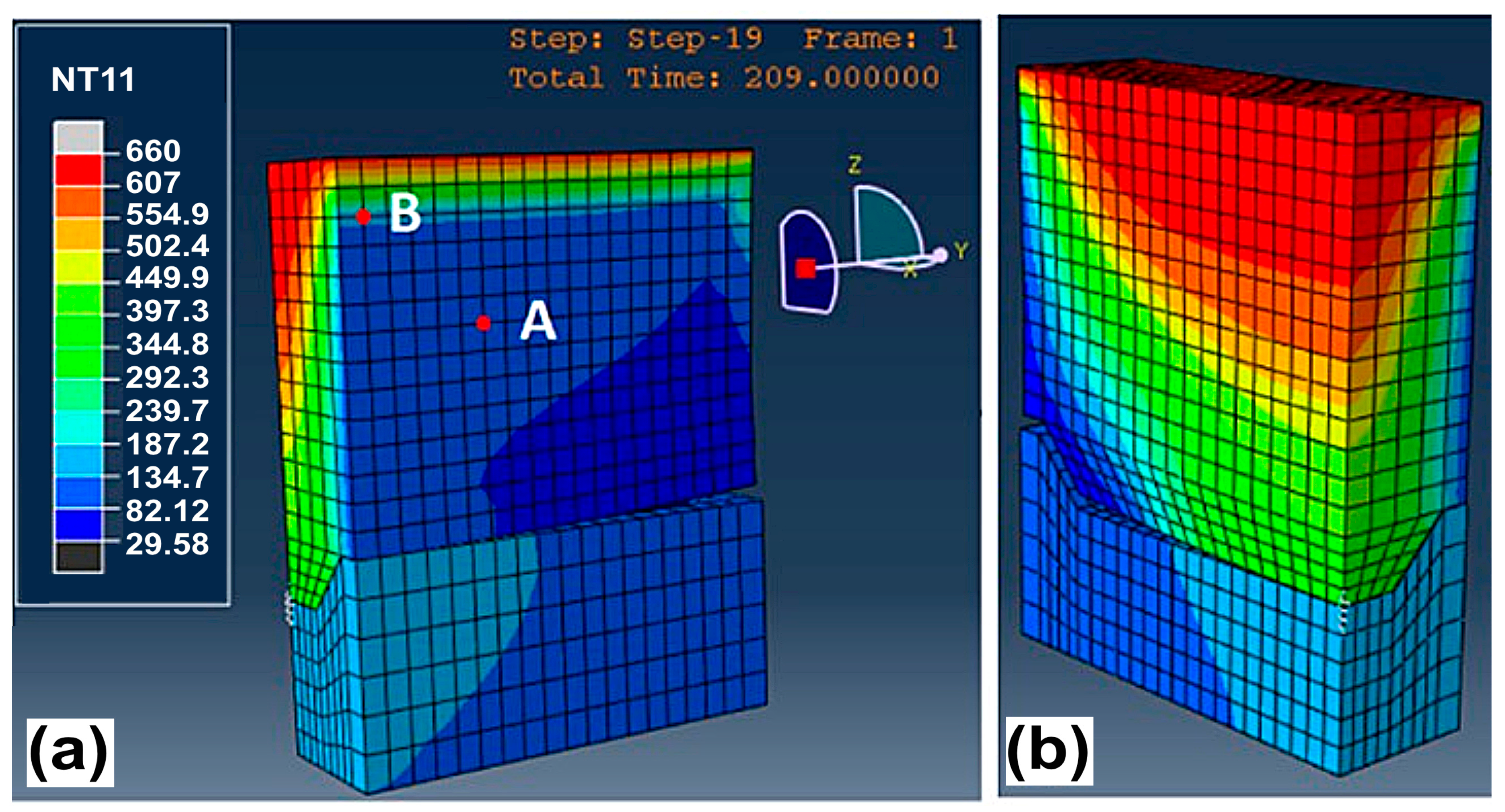
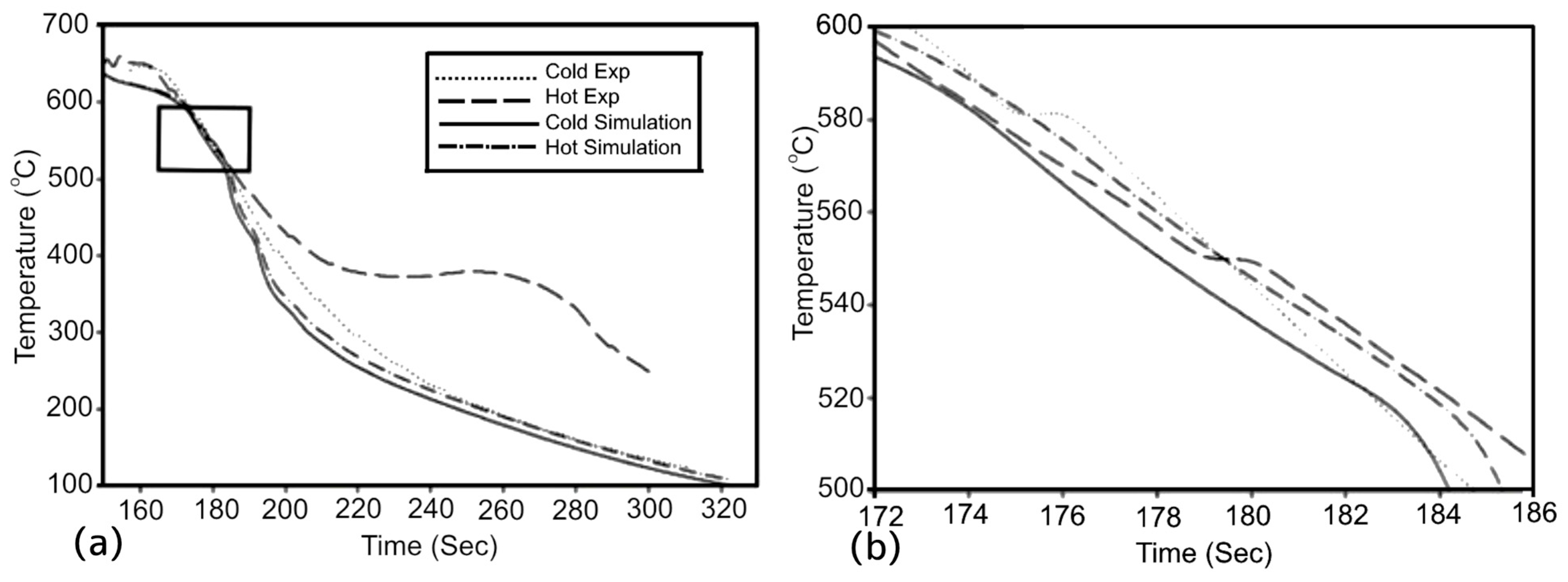
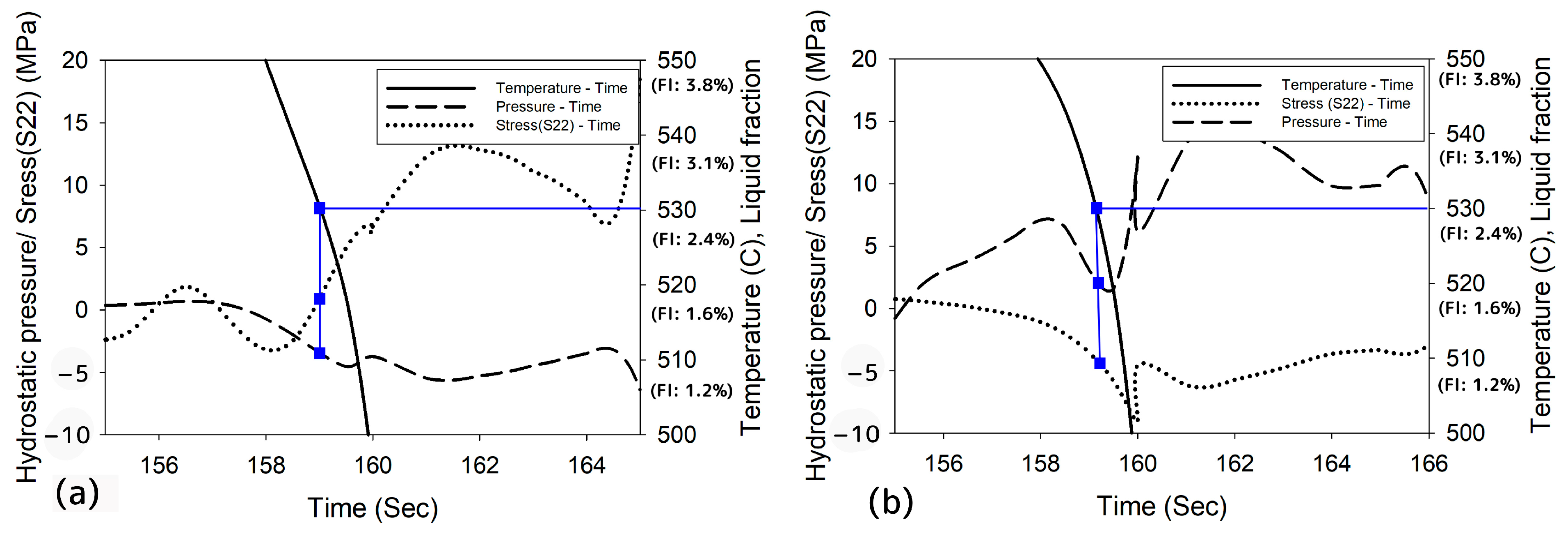
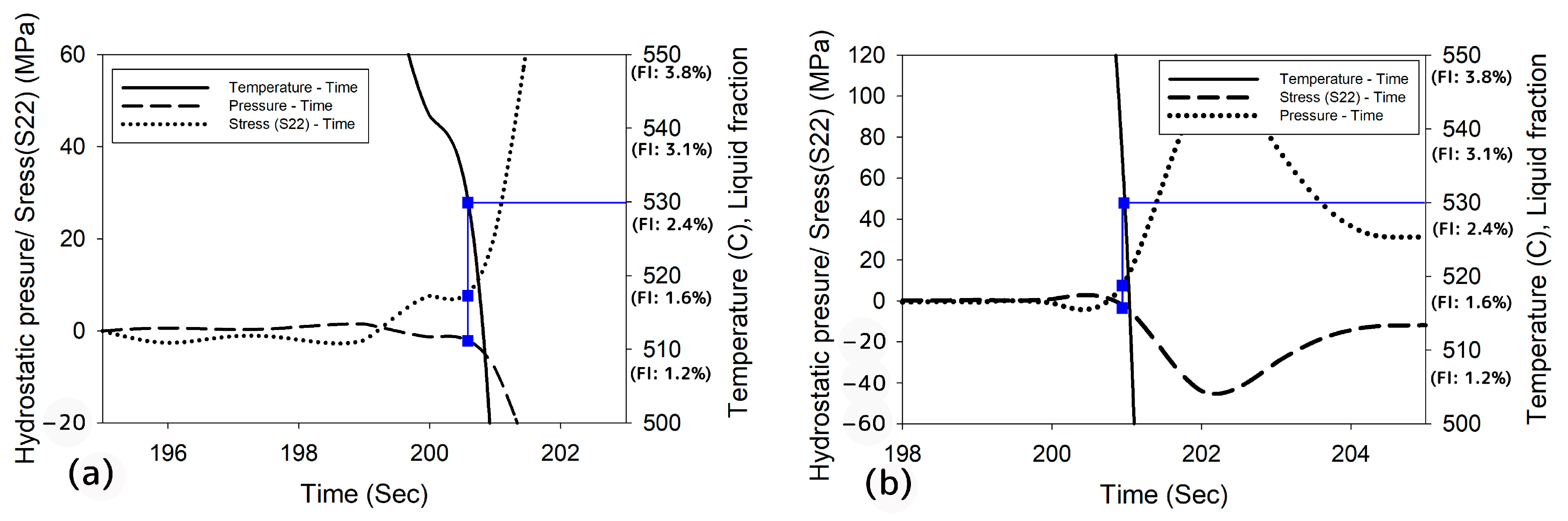
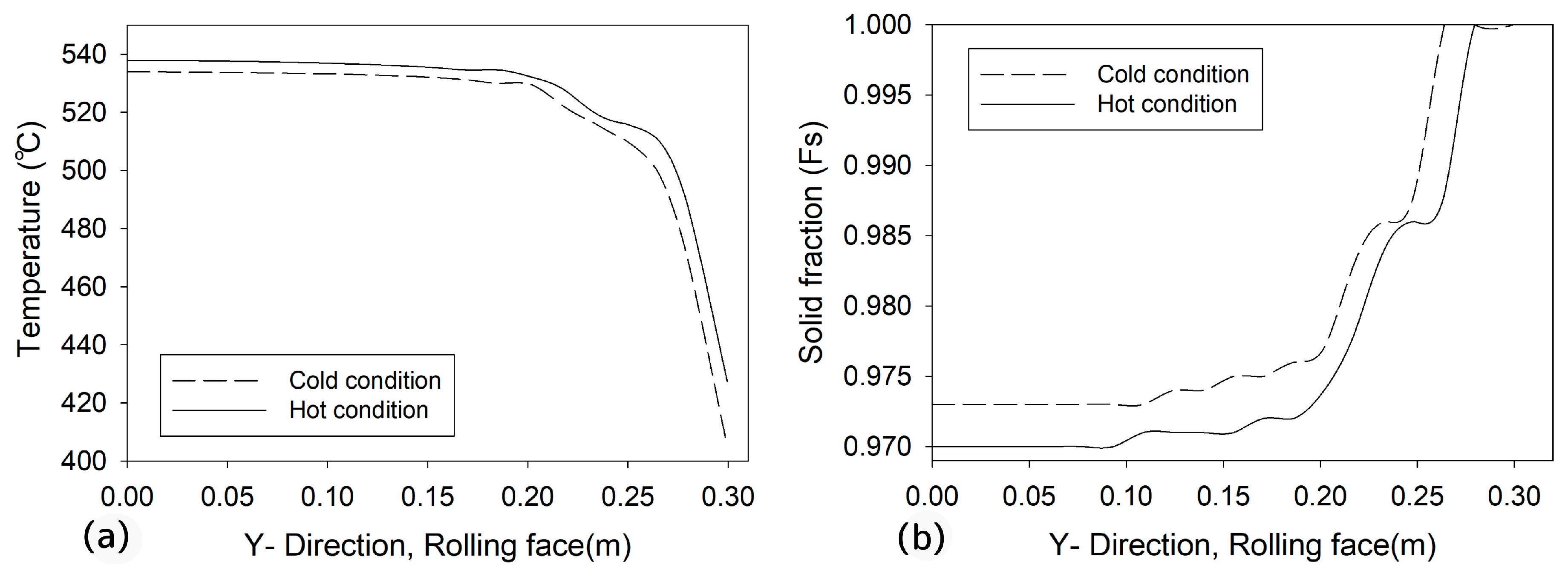
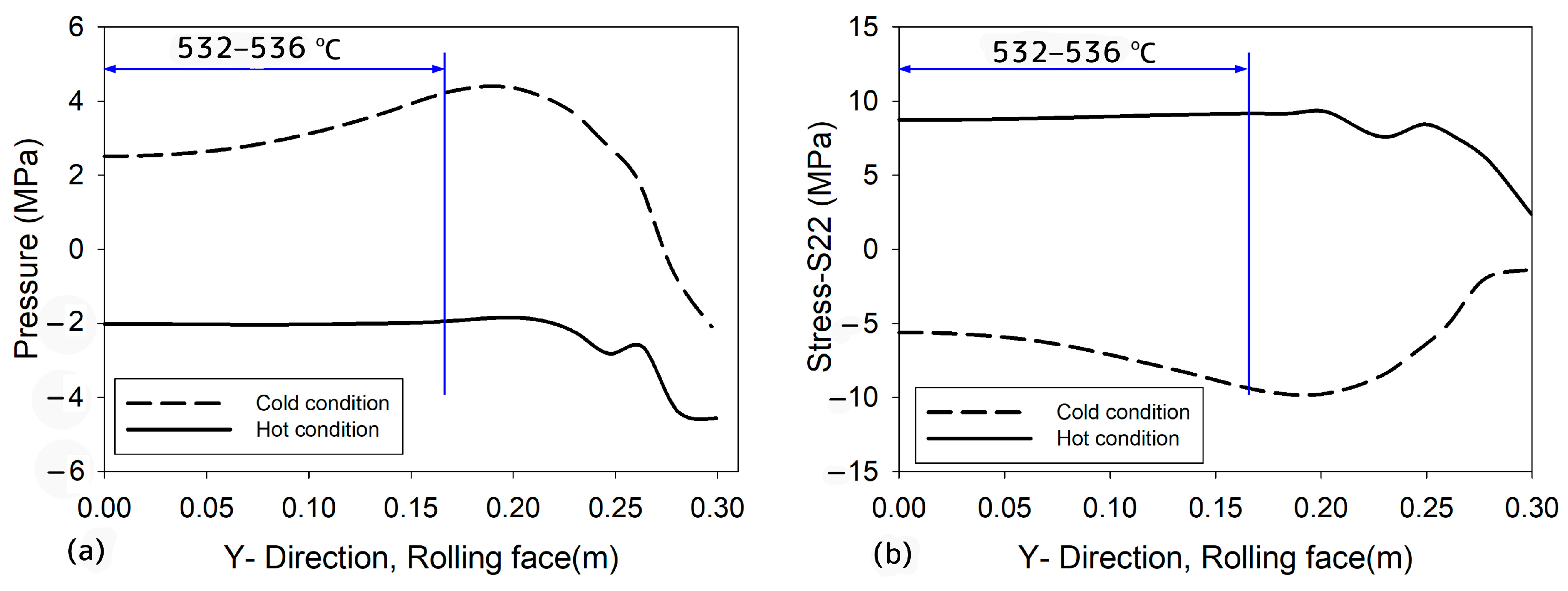
3.2. Modeling and Its Analysis
3.3. Crack Surfaces Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Li, H.; Katgerman, L.; Du, Q.; Zhang, J.; Zhuang, L. Recent advances in hot tearing during casting of aluminium alloys. Prog. Mater. Sci. 2021, 117, 100741. [Google Scholar] [CrossRef]
- Eskin, D. Physical Metallurgy of Direct Chill Casting of Aluminum Alloys; Taylor & Francis: London, UK, 2008; pp. 1–303. [Google Scholar]
- Jamaly, M.A.M.N. The Effects of Microstructural Features and Process Parameters on the Hot Tearing in Direct Chill Cast Aluminum Alloys. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2012. [Google Scholar]
- Suyitno. Hot Tearing and Deformation in Direct-Chill Casting of Aluminium Alloys; Delft University of Technology: Delft, The Netherlands, 2005. [Google Scholar]
- Boender, W.; Burghardt, A.; van Klaveren, E.P.; Rabenberg, J. Numerical Simulation of DC Casting; Interpreting the Results of a Thermo-Mechanical Model, Essential Readings in Light Metals; The Minerals, Metals, and Materials Society: Pittsburgh, PA, USA, 2016; pp. 933–938. [Google Scholar]
- Bolduc, S.; Kiss, L.I. Sensitivity study of the influence of the water boiling parameters on aluminum semi-continuous DC casting. Int. J. Therm. Sci. 2020, 151, 106276. [Google Scholar] [CrossRef]
- Begum, L.; Hasan, M. 3-D CFD simulation of a vertical direct chill slab caster with a submerged nozzle and a porous filter delivery system. Int. J. Heat Mass Transf. 2014, 73, 42–58. [Google Scholar] [CrossRef]
- Larouche, A.; Caron, Y.; Kocaefe, D. Impact of Water Heat Extraction and Casting Conditions on Ingot Thermal Response during DC Casting, in Essential Readings in Light Metals. In Essential Readings in Light Metals: Volume 3 Cast Shop for Aluminum Production; Springer International Publishing: Cham, Switzerland, 2013; pp. 690–695. [Google Scholar]
- Mukhopadhyay, P. Alloy Designation, Processing, and Use of AA6XXX Series Aluminium Alloys. Int. Sch. Res. Not. 2012, 2012, 165082. [Google Scholar] [CrossRef]
- Subroto, T.; Eskin, D.G.; Miroux, A.; Ellingsen, K.; M’hAmdi, M.; Katgerman, L. Semi-solid Constitutive Parameters and Failure Behavior of a Cast AA7050 Alloy. Metall. Mater. Trans. A 2021, 52, 871–888. [Google Scholar] [CrossRef]
- Rappaz, M.; Drezet, J.M.; Gremaud, M. A new hot-tearing criterion. Metall. Mater. Trans. A (USA) 1999, 30A, 449–455A. [Google Scholar] [CrossRef]
- Braccini, M.; Martin, C.L.; Suéry, M.; Bréchet, Y. Relation between mushy zone rheology and hot tearing phenomena in Al-Cu alloys. Model. Cast. Weld. Adv. Solidif. Process. IX 2000, 3, 18–24. [Google Scholar]
- Chen, D.-X.; Dou, R.-F.; Han, J.-Q.; Wang, J.-S. Prediction of hot tearing susceptibility of direct chill casting of AA6111 alloys via finite element simulations. Trans. Nonferrous Met. Soc. China 2020, 30, 3161–3172. [Google Scholar] [CrossRef]
- Suyitno; Eskin, D.G.; Savran, V.I.; Katgerman, L. Effect of casting speed on structure formation and hot tearing during direct-chill casting of AL-CU alloys. Metall. Mater. Trans. A 2004, 35A, 3551–3561. [Google Scholar] [CrossRef]
- Khodaei, N.; Phillion, A.B. A study on hot tearing in direct chill casting of Al-Mn-Mg alloys using a multi-scale approach. Metall. Mater. Trans. B 2021, 52, 1424–1435. [Google Scholar] [CrossRef]
- Nallathambi, A.K.; Penumakala, P.K.; Specht, E. Review of hot tearing studies in Al alloys during direct chill casting. In Proceedings of the 2013 International Symposium on Liquid Metal Processing & Casting, Austin, TX, USA, 22–25 September 2013; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Suyitno; Kool, W.H.; Katgerman, L. Hot tearing criteria evaluation for direct-chill casting of an Al-4.5 pct Cu alloy. Metall. Mater. Trans. A 2005, 36, 1537–1546. [Google Scholar] [CrossRef]
- Dou, R.; Phillion, A.B. Application of a Pore Fraction Hot Tearing Model to Directionally Solidified and Direct Chill Cast Aluminum Alloys. Metall. Mater. Trans. A 2016, 47, 4217–4225. [Google Scholar] [CrossRef]
- Nallathambi, A.K.; Tyagi, M.; Specht, E.; Bertram, A. Thermomechanical analysis of direct chill casting using finite element method. Trans. Indian Inst. Met. 2011, 64, 13. [Google Scholar] [CrossRef]
- Lalpoor, M.; Eskin, D.G.; Katgerman, L. Cold-Cracking Assessment in AA7050 Billets during Direct-Chill Casting by Thermomechanical Simulation of Residual Thermal Stresses and Application of Fracture Mechanics. Metall. Mater. Trans. A-Phys. Metall. Mater. Sci. 2009, 40A, 3304–3313. [Google Scholar] [CrossRef]
- Fjaer, H.G.; Mo, A. ALSPEN—A MATHEMATICAL-MODEL FOR THERMAL-STRESSES IN DIRECT CHILL CASTING OF ALUMINUM BILLETS. Metall. Trans. B-Process Metall. 1990, 21, 1049–1061. [Google Scholar]
- Han, Q.; Viswanathan, S.; Spainhower, D.L.; Das, S.K. The nature of surface cracking in direct chill cast aluminum alloy ingots. Metall. Mater. Trans. A 2001, 32, 2908–2910. [Google Scholar] [CrossRef]
- Sengupta, J.; Cockcroft, S.; Maijer, D.; Wells, M.; Larouche, A. The effect of water ejection and water incursion on the evolution of thermal field during the start-up phase of the direct chill casting process. J. Light Met. 2002, 2, 137–148. [Google Scholar] [CrossRef]
- Larouche, D.; Langlais, J.; Wu, W.; Bouchard, M. A constitutive model for the tensile deformation of a binary aluminum alloy at high fractions of solid. Metall. Mater. Trans. B 2006, 37, 431–443. [Google Scholar] [CrossRef]
- Jolly, M.; Katgerman, L. Modelling of defects in aluminium cast products. Prog. Mater. Sci. 2022, 123, 100824. [Google Scholar] [CrossRef]
- Guo, G.; Yao, T.; Liu, W.; Tang, S.; Xiao, D.; Huang, L.; Wu, L.; Feng, Z.; Gao, X. Numerical Simulation and Machine Learning Prediction of the Direct Chill Casting Process of Large-Scale Aluminum Ingots. Materials 2024, 17, 1409. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, J.; Cockcroft, S.L.; Maijer, D.M.; Wells, M.A.; Larouche, A. On the development of a three-dimensional transient thermal model to predict ingot cooling behavior during the start-up phase of the direct chill-casting process for an AA5182 aluminum alloy ingot. Metall. Mater. Trans. B 2004, 35, 523–540. [Google Scholar] [CrossRef]
- Larouche, D. Computation of solidification paths in multiphase alloys with back-diffusion. Calphad 2007, 31, 490–504. [Google Scholar] [CrossRef]
- Qassem, M.; Javidani, M.; Larouche, D.; Colbert, J.; Chen, X.-G. Effect of chemical composition on the semisolid tensile properties and hot tearing susceptibility of AA6111 DC cast alloys. J. Mater. Sci. 2022, 57, 21519–21536. [Google Scholar] [CrossRef]
- Wang, B.Z.; Huang, X.M.; Wang, C.; Wang, Z.Y.; Xing, C.; Ji, H.C. Constitutive equations of AA6111 aluminum alloy. Metalurgija 2019, 58, 267–271. [Google Scholar]
- Alankar, A.; Wells, M.A. Constitutive behavior of as-cast aluminum alloys AA3104, AA5182 and AA6111 at below solidus temperatures. Mater. Sci. Eng. A 2010, 527, 7812–7820. [Google Scholar] [CrossRef]
- Qassem, M.; Javidani, M.; Larouche, D.; Colbert, J.; Chen, X.-G. Temperature Dependence of Elastic Properties of Al-Mg-Si Direct-Chill-Cast AA6111 Alloy at Near-Solidus Temperatures. J. Mater. Eng. Perform. 2024, 33, 987–998. [Google Scholar] [CrossRef]
- Zhong, H.; Zhao, Y.; Lin, Z.; Li, T.; Guo, Q.; Li, L.; Zhai, Q.; Han, Q. Understanding the roles of interdendritic bridging on hot tearing formation during alloy solidification. J. Mater. Res. Technol. 2023, 27, 5368–5371. [Google Scholar] [CrossRef]
- Katgerman, L.; Van Haaften, W.; Kool, W. Constitutive behaviour and hot tearing during aluminium DC casting. Mater. Forum 2004, 28, 312–318. [Google Scholar]

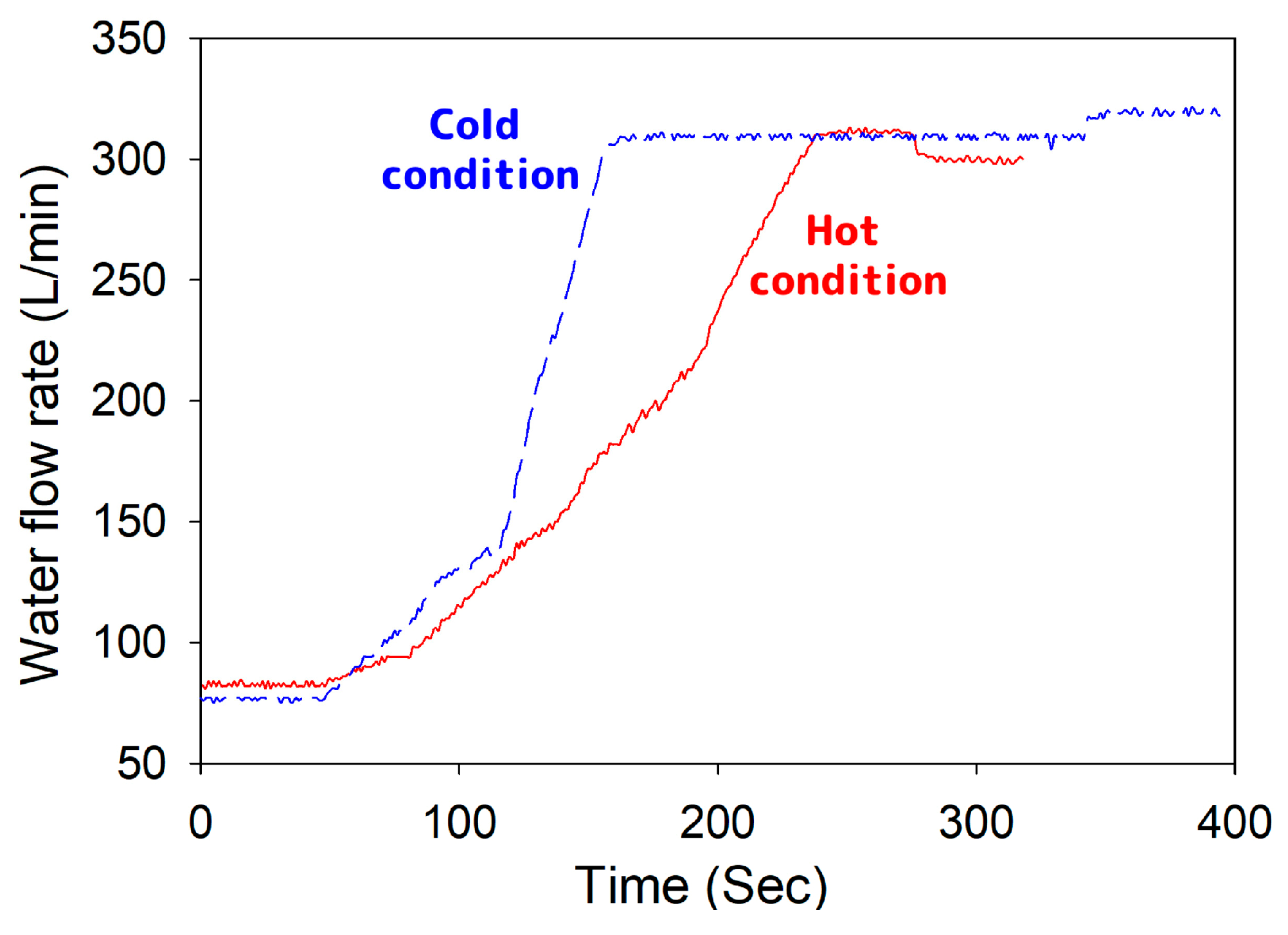
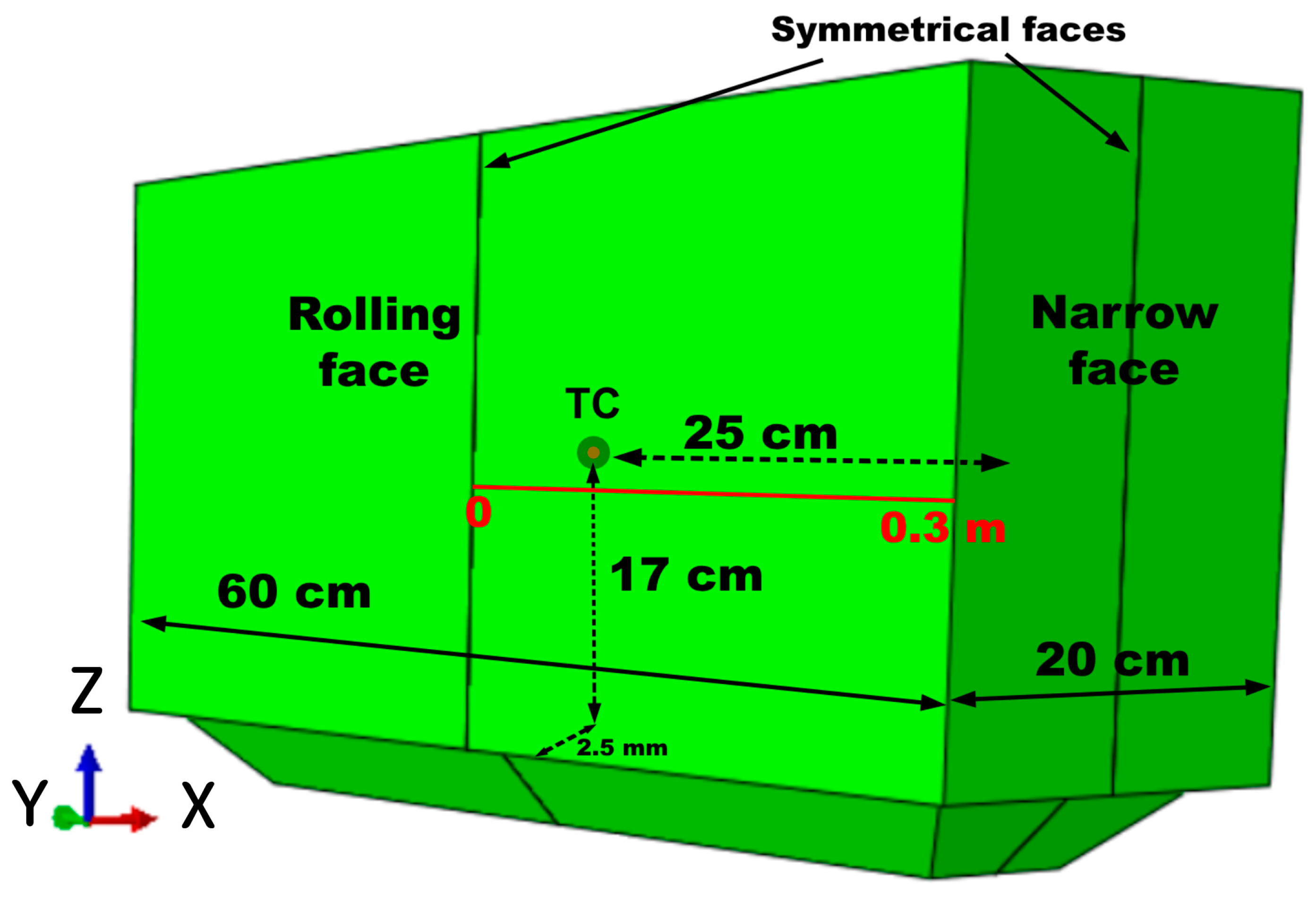

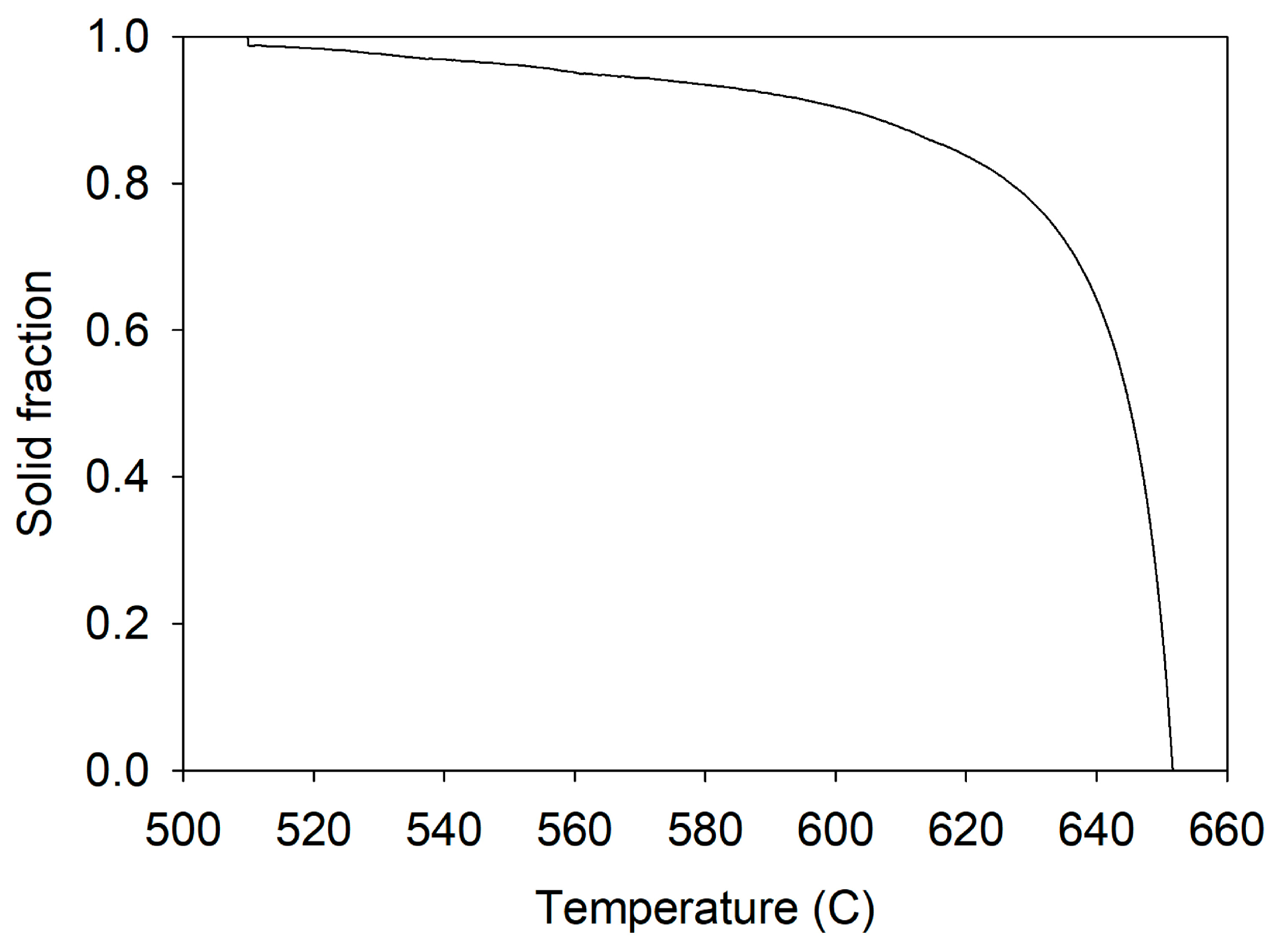
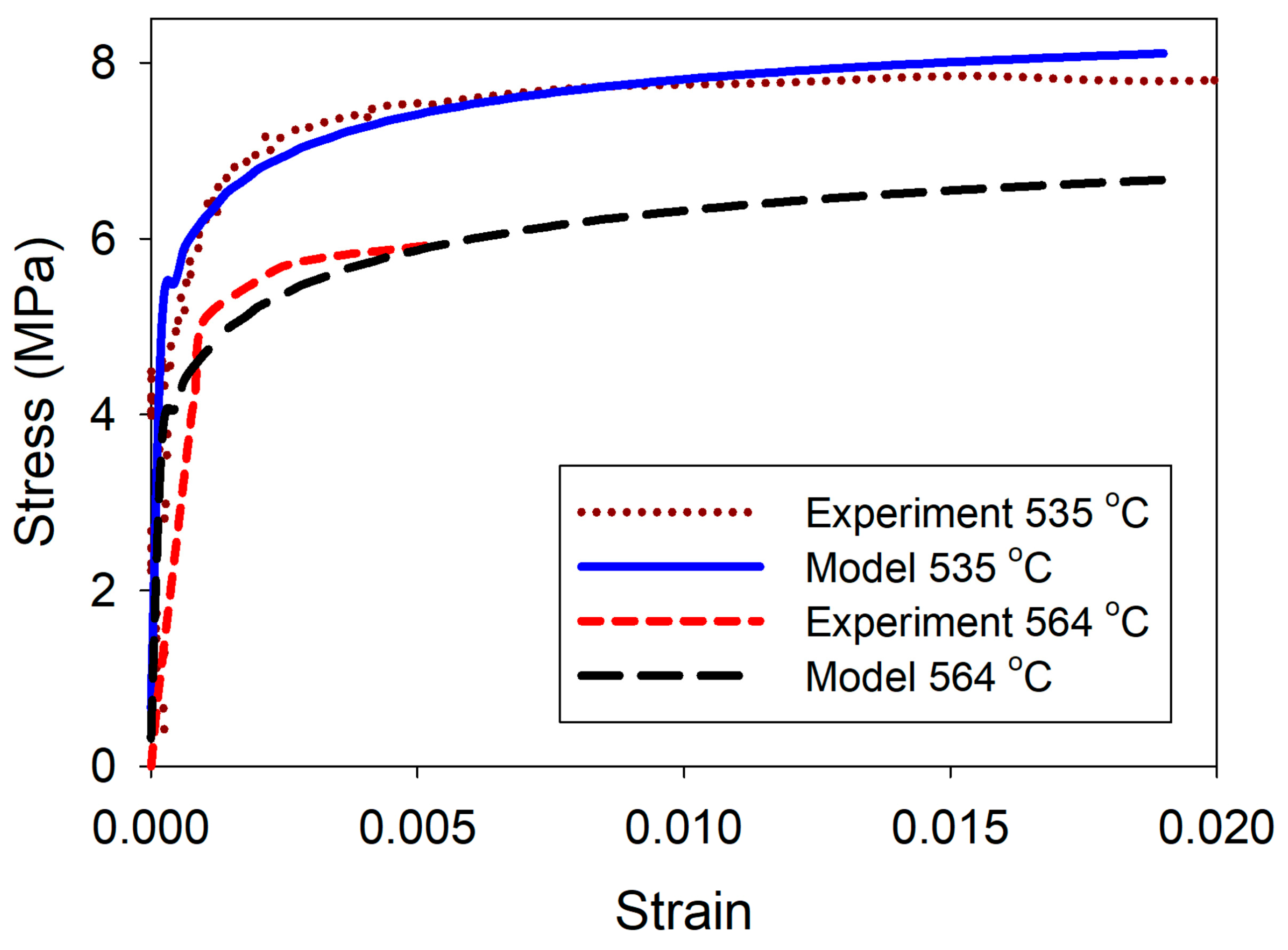





| Elements | Cu | Si | Mg | Mn | Fe | Al |
|---|---|---|---|---|---|---|
| 0.5 | 0.6 | 0.5 | 0.1 | 0.19 | Balance |
| Solidification Path | Temperature (°C) |
|---|---|
| 620 | |
| 581.25 | |
| 557 | |
| Phase (Al5Cu2Mg8Si6) | 541.75 |
| 514.5 |
| Temperature (°C) | Thermal Expansion Coefficient × 10−6 (K−1) [31] | Specific Heat Capacity (J.kg−1·K−1) [13] | Thermal Conductivity (W·m−1·K−1) [13] |
|---|---|---|---|
| 20 | 22.4147 | 909.2 | 196.8 |
| 100 | 23.1396 | 950.4 | 202.1 |
| 200 | 24.1860 | 999.6 | 204.6 |
| 300 | 25.2453 | 1044.8 | 204.1 |
| 400 | 26.3176 | 1090 | 201.7 |
| 500 | 27.4027 | 1135.2 | 198.1 |
| 510 | 27.5120 | 1170 | 197.6 |
| 550 | 29.4292 | 1217 | 190.1 |
| 600 | 32.4869 | 1112 | 177 |
| 630 | 38.9769 | 1023 | 151.5 |
| 660 | 67.8313 | 1003 | 88 |
| Constants | Value |
|---|---|
| m | 1/2 for a columnar structure |
| µ | 0.001 Pa·s |
| a | 100 µm |
| Q | 148,616 KJ/mol |
| Strain Rate (s−1) | Temp (°C) | Fraction Solid | κ | Yield Stress (MPa) | |
|---|---|---|---|---|---|
| 0.0001 | 510 | 0.988 | 7 | 0.5 | 5 |
| 535 | 0.971 | 17 | 0.65 | 5 | |
| 552 | 0.96 | 55 | 0.63 | 4 | |
| 564 | 0.947 | 27 | 0.75 | 4 | |
| 0.001 | 535 | 0.971 | 19 | 0.45 | 6 |
| 552 | 0.96 | 25 | 0.4 | 4 | |
| 564 | 0.947 | 15 | 0.45 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalilpoor, H.; Larouche, D.; Chen, X.G.; Phillion, A.; Colbert, J. Investigation of the Hydrostatic Pressure Effect on the Formation of Hot Tearing in the AA6111 Alloy During Direct Chill Casting of Rectangular Ingots. Appl. Mech. 2025, 6, 53. https://doi.org/10.3390/applmech6030053
Khalilpoor H, Larouche D, Chen XG, Phillion A, Colbert J. Investigation of the Hydrostatic Pressure Effect on the Formation of Hot Tearing in the AA6111 Alloy During Direct Chill Casting of Rectangular Ingots. Applied Mechanics. 2025; 6(3):53. https://doi.org/10.3390/applmech6030053
Chicago/Turabian StyleKhalilpoor, Hamid, Daniel Larouche, X. Grant Chen, André Phillion, and Josée Colbert. 2025. "Investigation of the Hydrostatic Pressure Effect on the Formation of Hot Tearing in the AA6111 Alloy During Direct Chill Casting of Rectangular Ingots" Applied Mechanics 6, no. 3: 53. https://doi.org/10.3390/applmech6030053
APA StyleKhalilpoor, H., Larouche, D., Chen, X. G., Phillion, A., & Colbert, J. (2025). Investigation of the Hydrostatic Pressure Effect on the Formation of Hot Tearing in the AA6111 Alloy During Direct Chill Casting of Rectangular Ingots. Applied Mechanics, 6(3), 53. https://doi.org/10.3390/applmech6030053





