Buckling Strength Assessment of Composite Patch Repair Used for the Rehabilitation of Corroded Marine Plates
Abstract
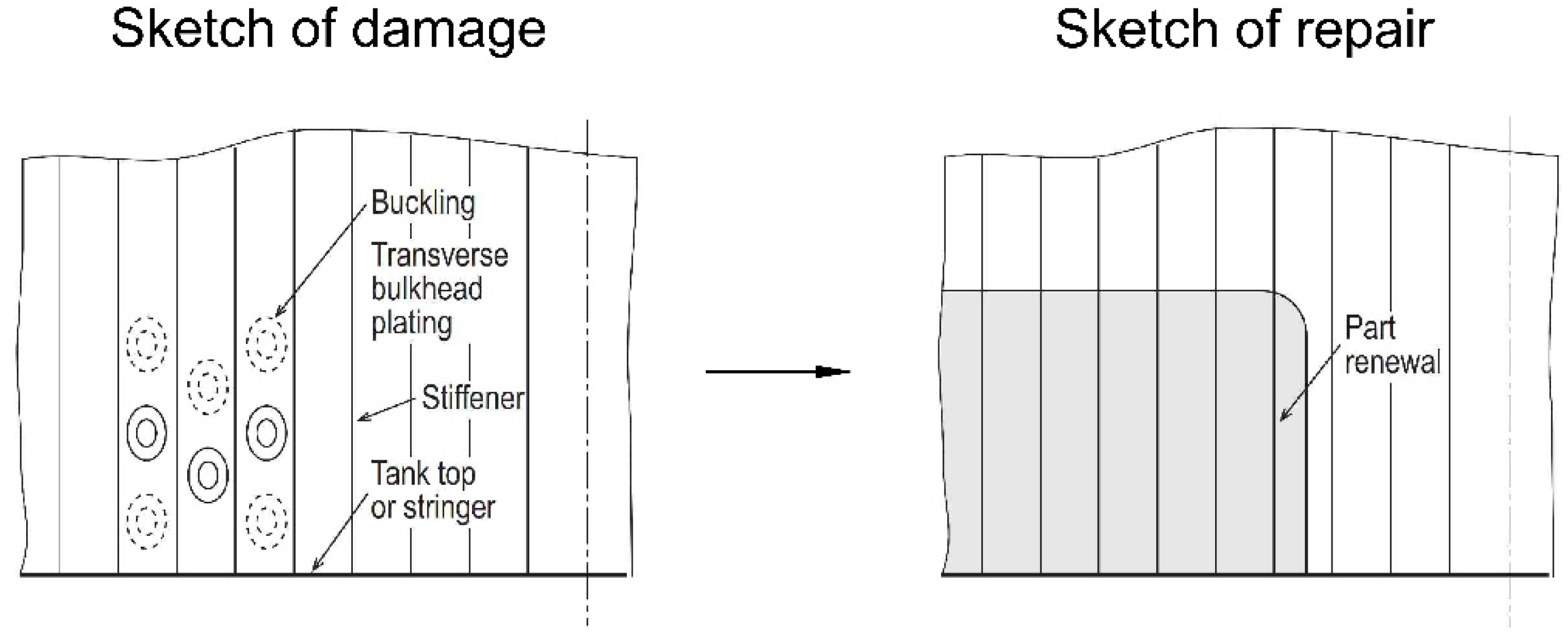
:1. Introduction
- Water, scale, dirt, or oil remainings due to poor drainage or design flaw.
- High stresses applied to the subject area.
- Coating breakdown usually caused by poor maintenance and the ship’s age.
- Operation in a corrosive enabling environment, such as near high-temperature regions (e.g., heated fuel tanks).
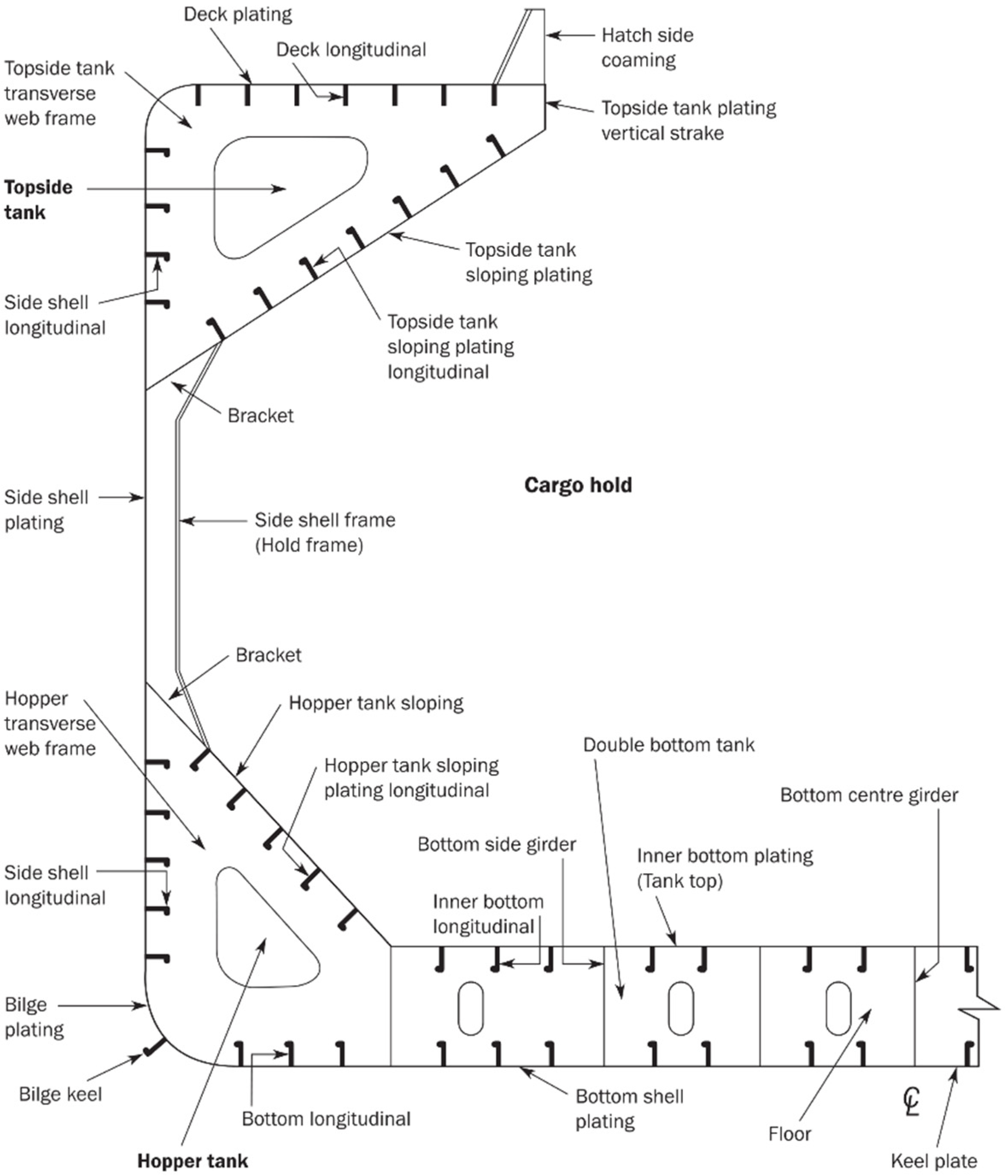
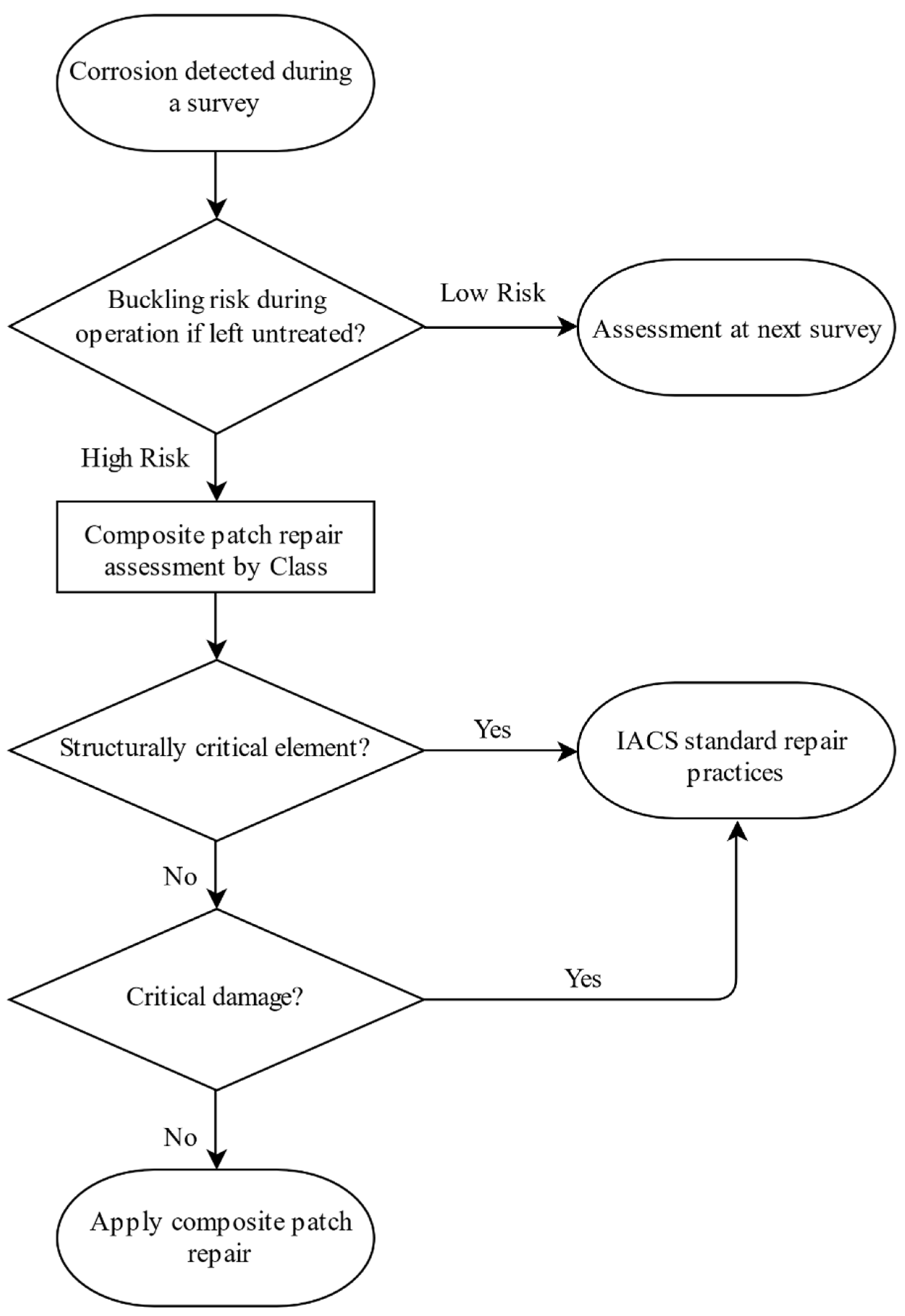
2. Design Basis
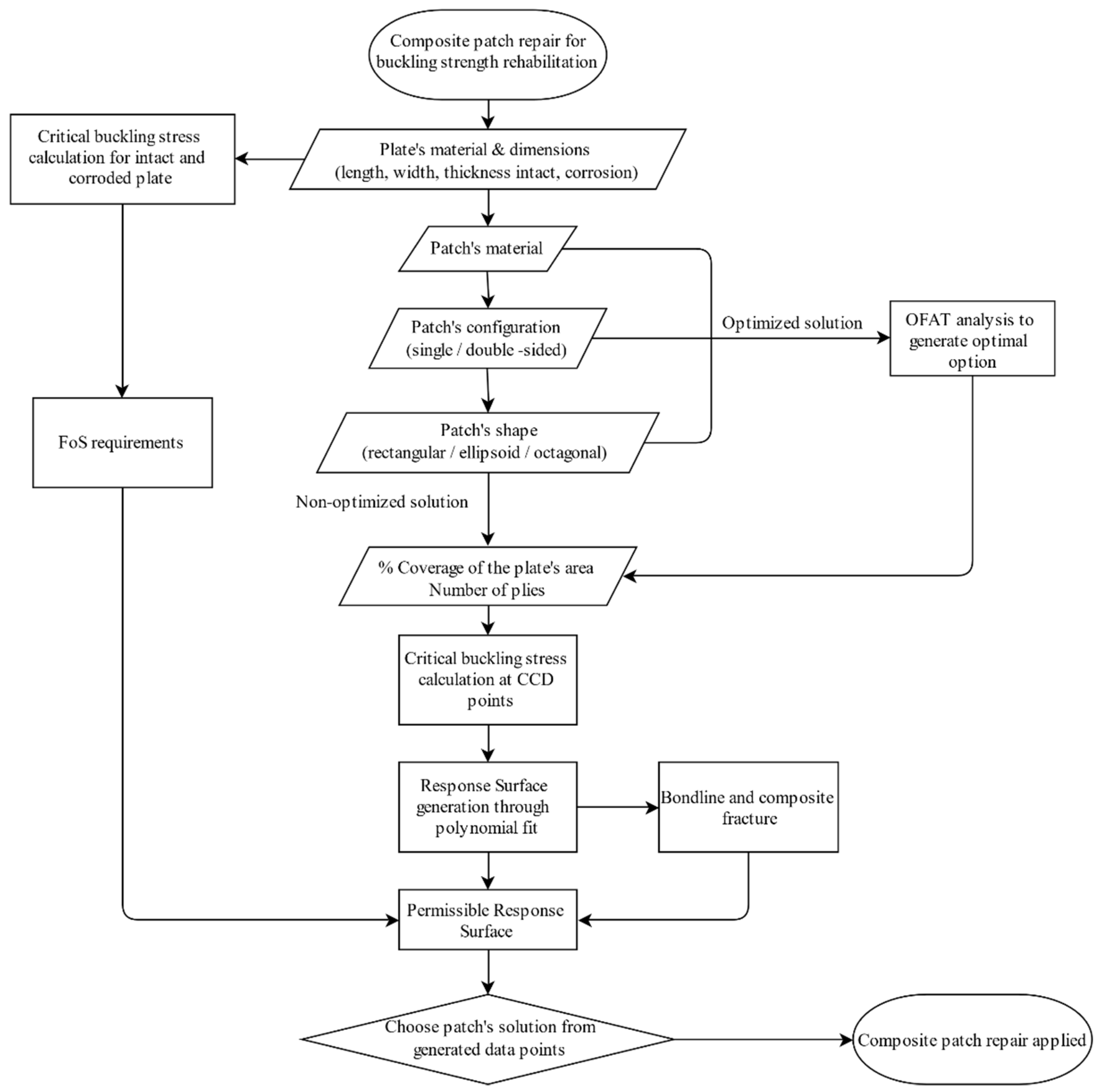
3. Optimal Design Method
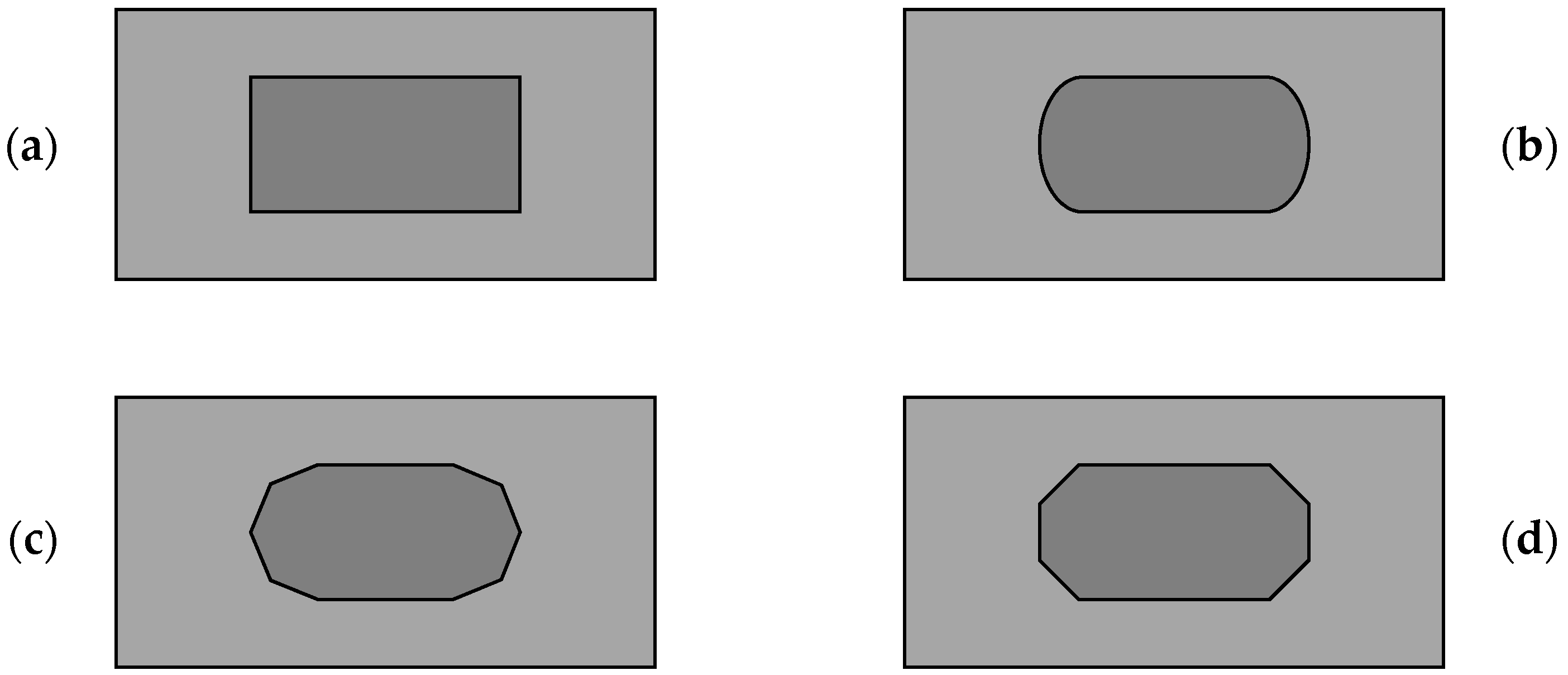
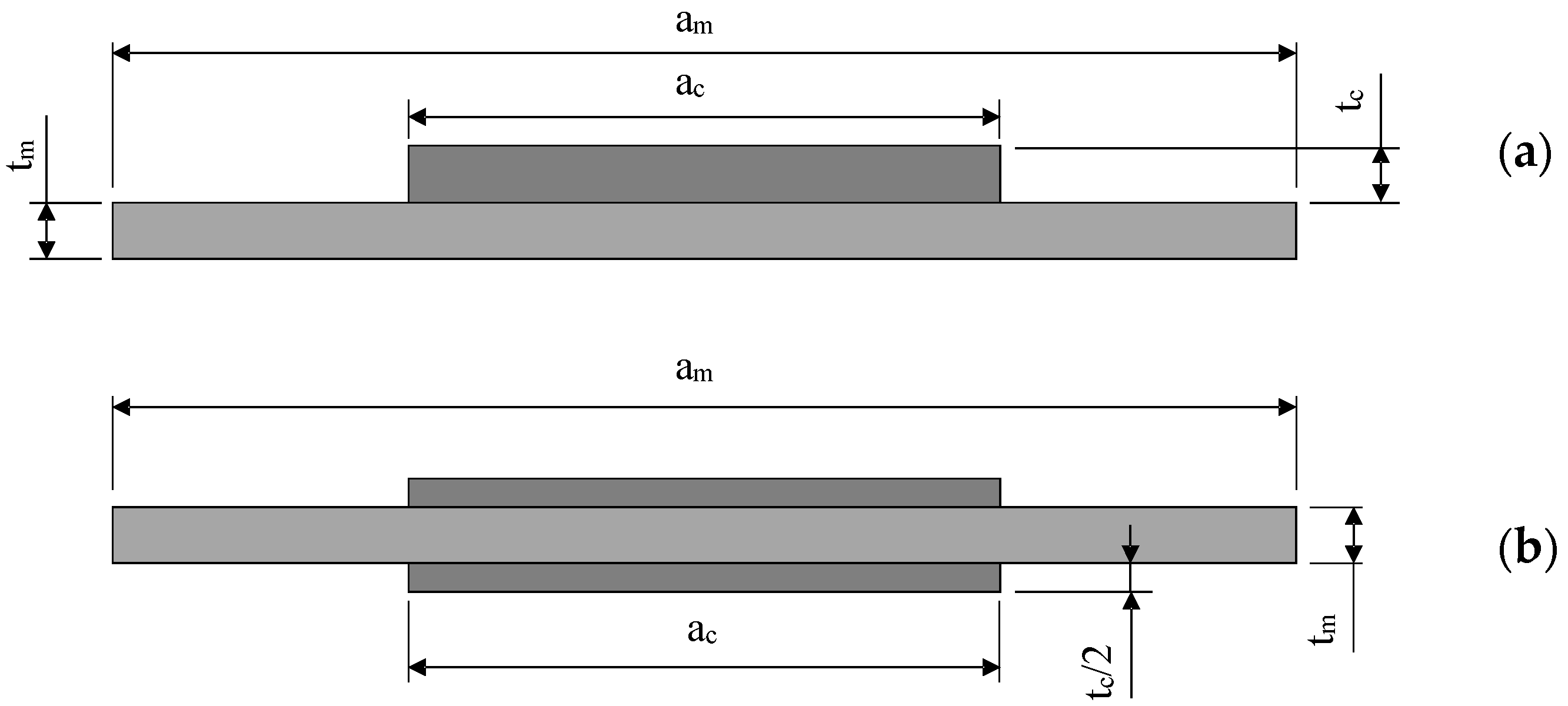
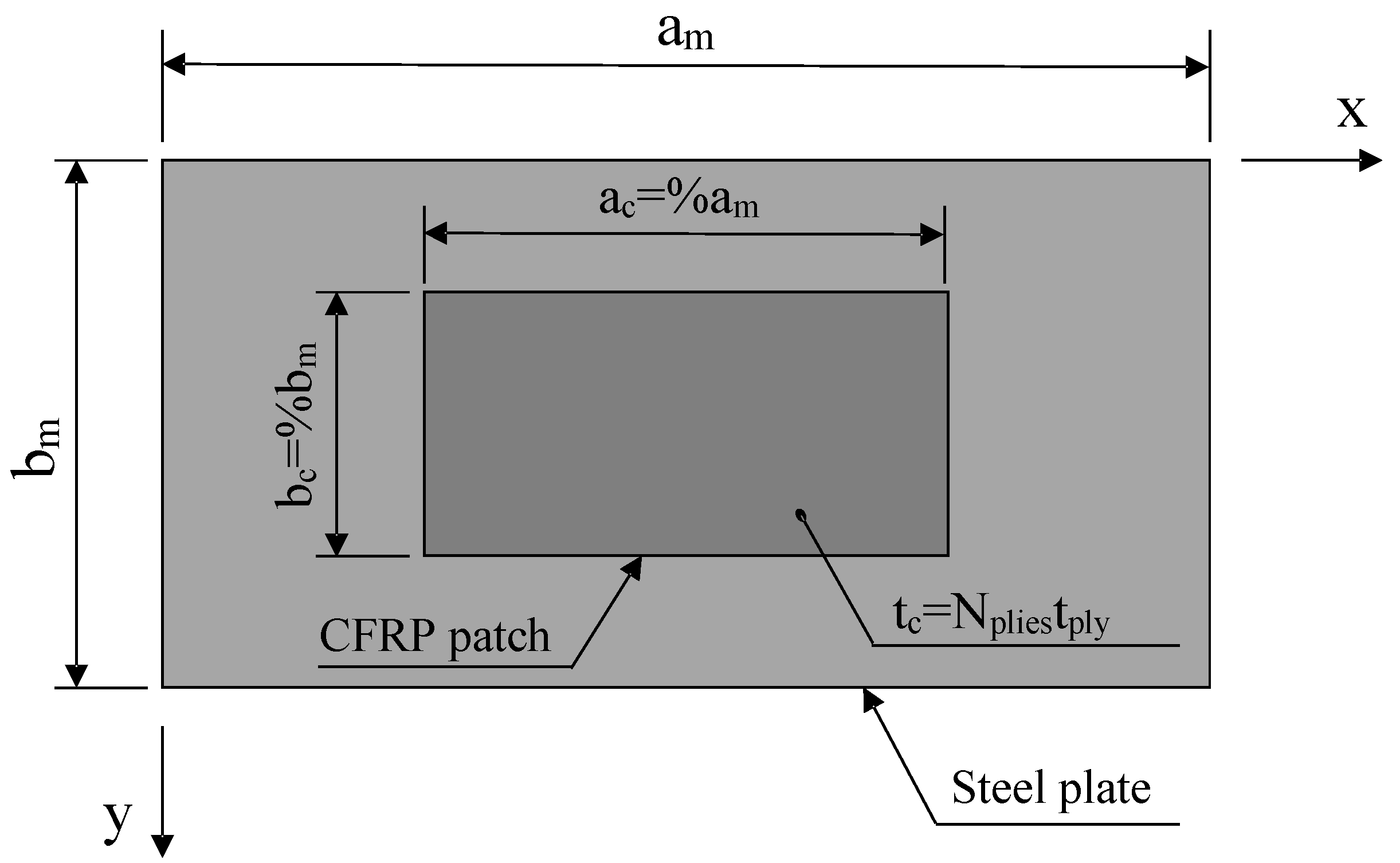
3.1. Design of the Repair
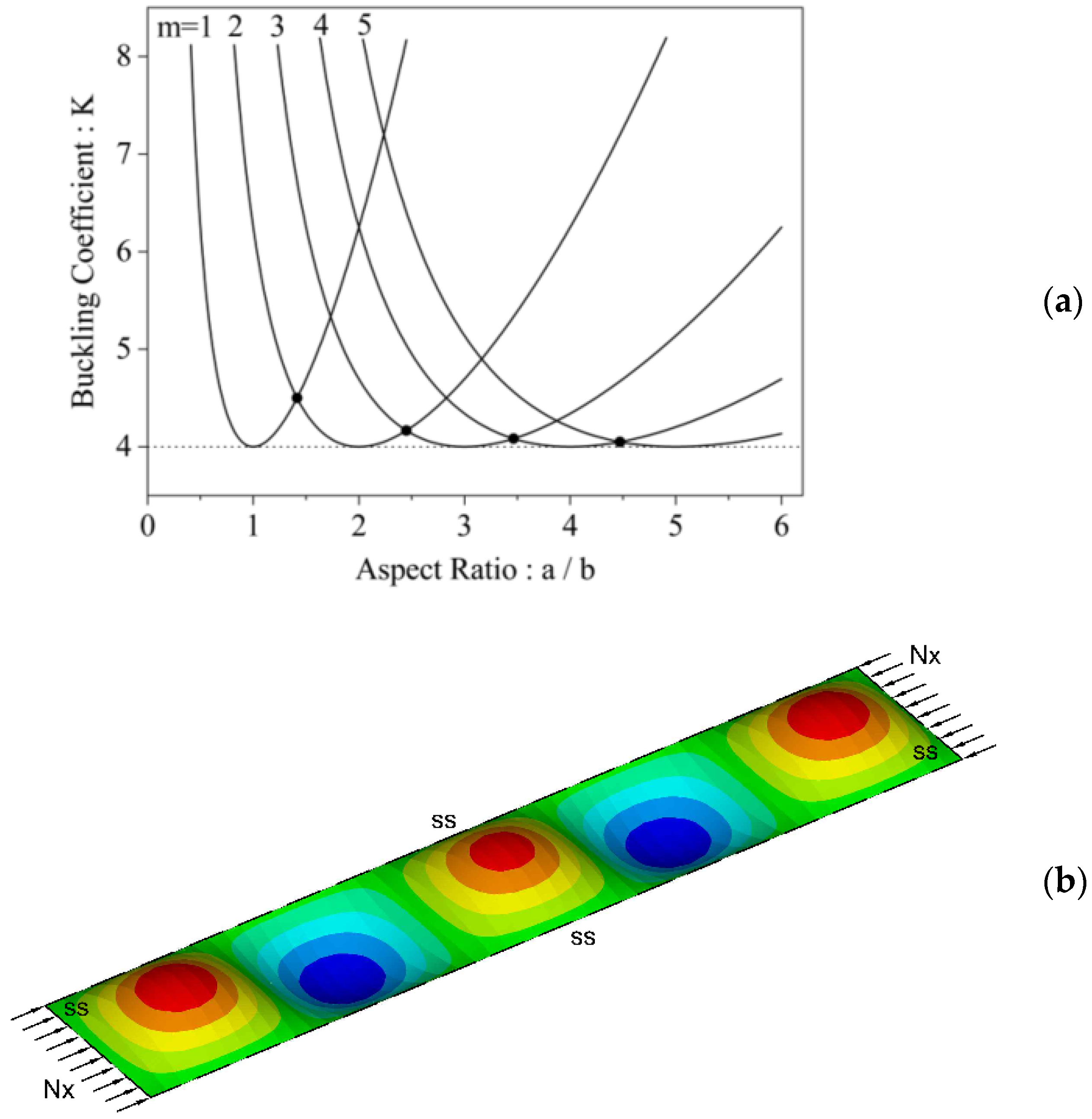
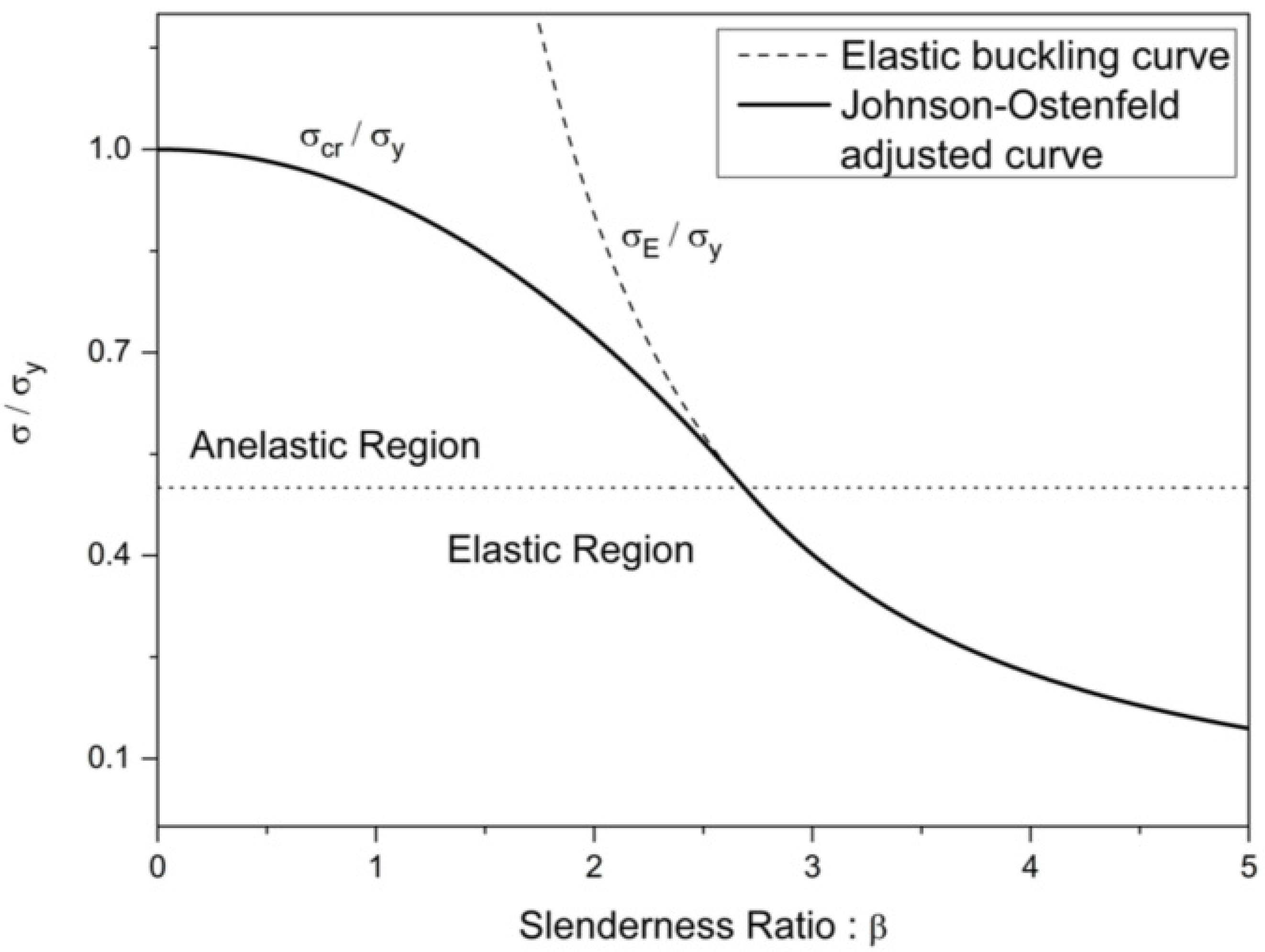
3.2. Theoretical Background
- P is the axial acting force.is the balance moment, with , and .
- and .
- and are the effective plane stress Young’s moduli of the composite and the plate respectively, while Ec and Em are their Young’s moduli of elasticity, and νc and νm their Poisson’s ratio.
4. Physics and Data-Based Models
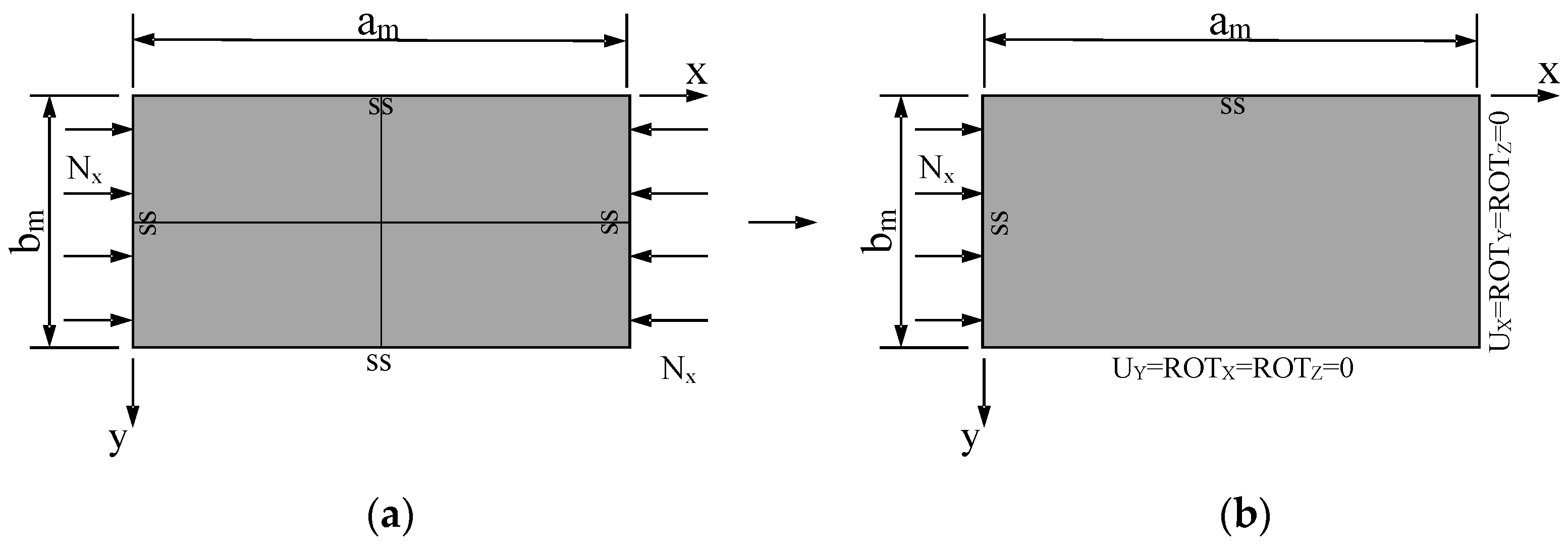
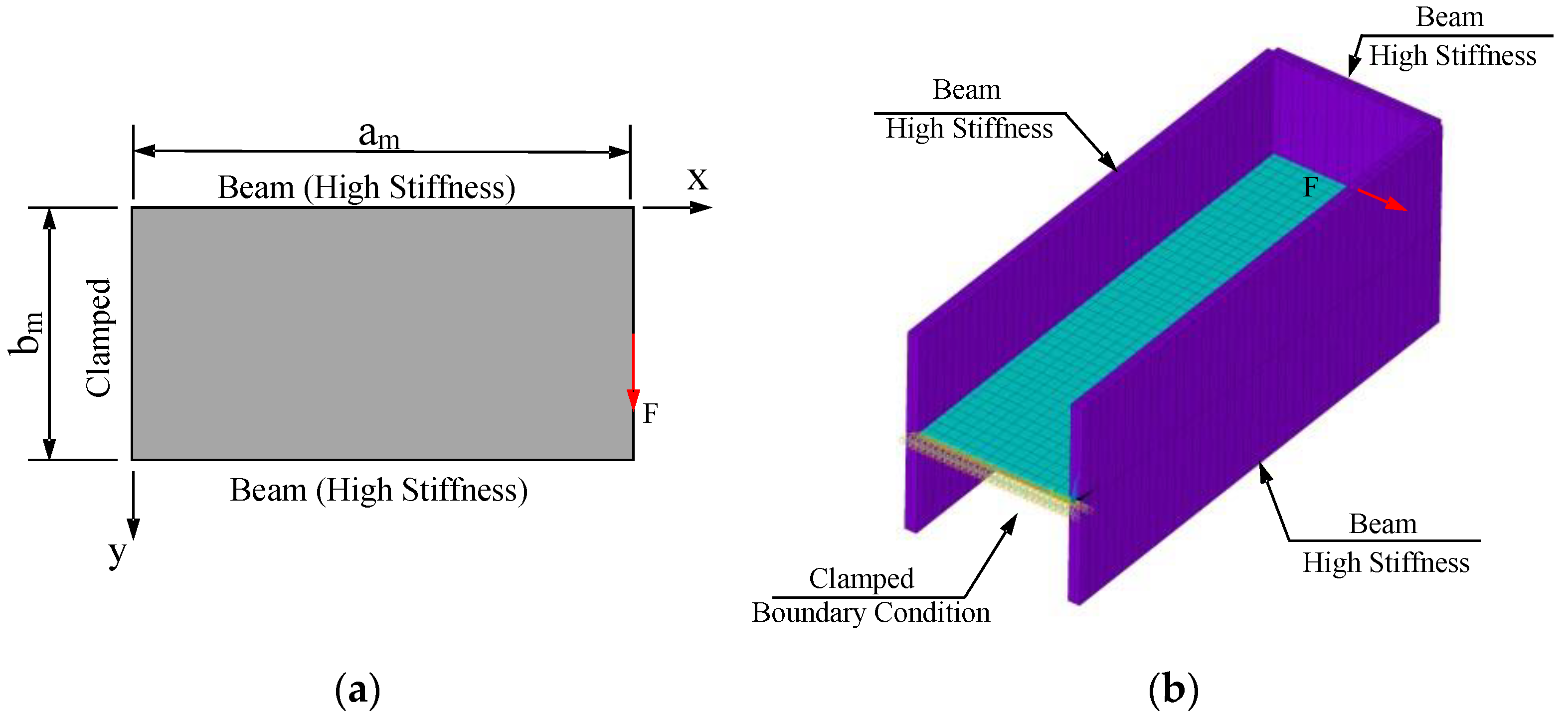
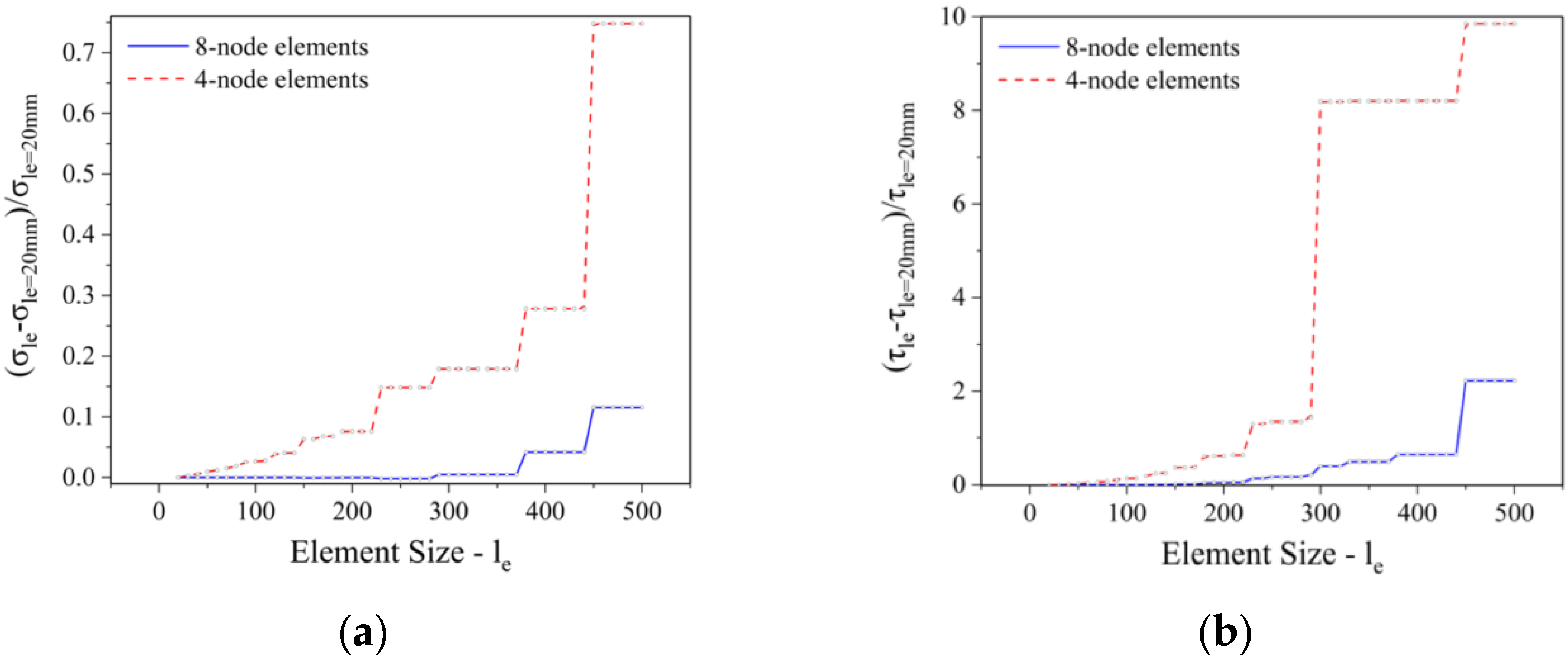
4.1. FEA Model
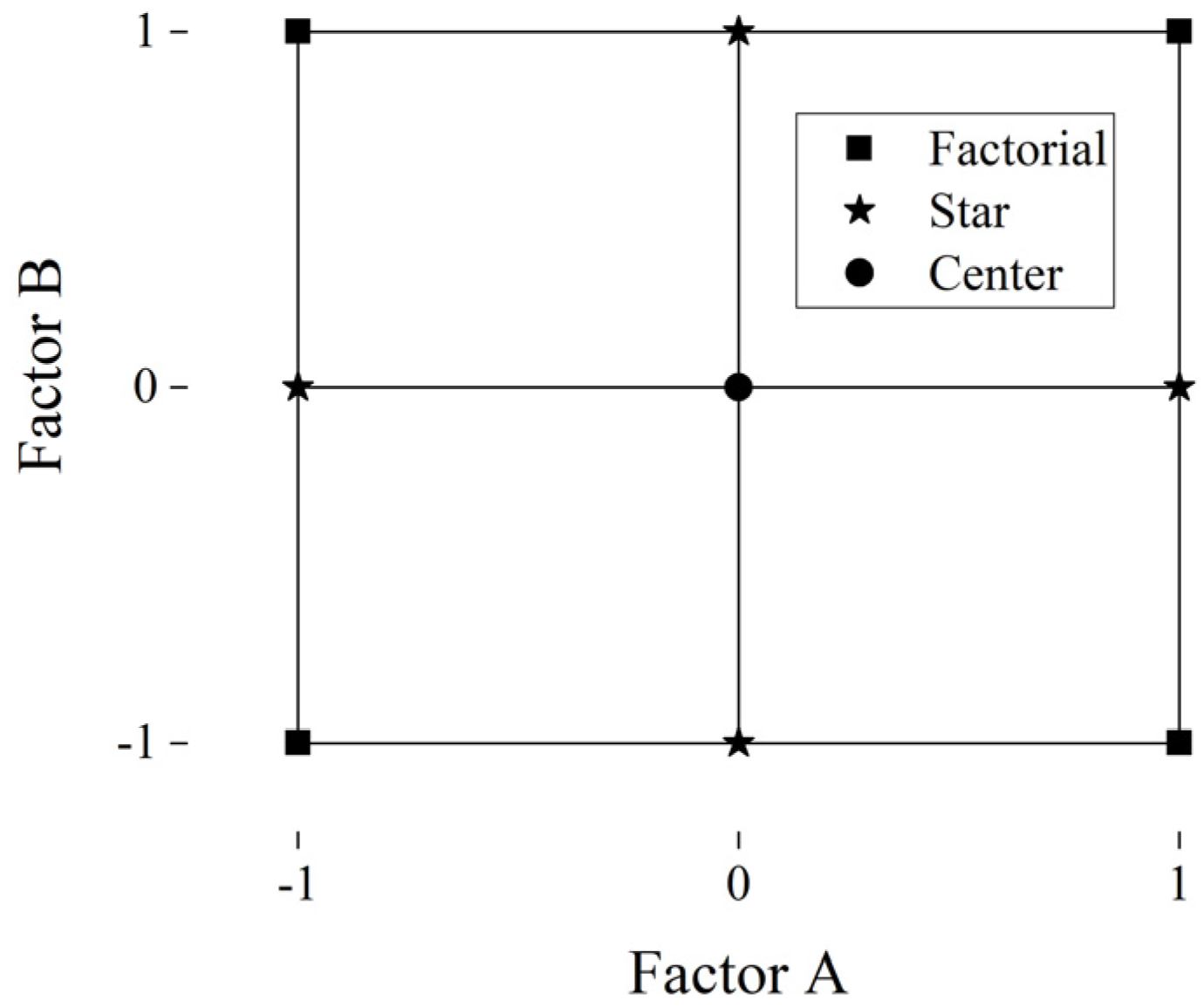
4.2. DoE Analysis
5. Case Study
5.1. Problem Set-Up
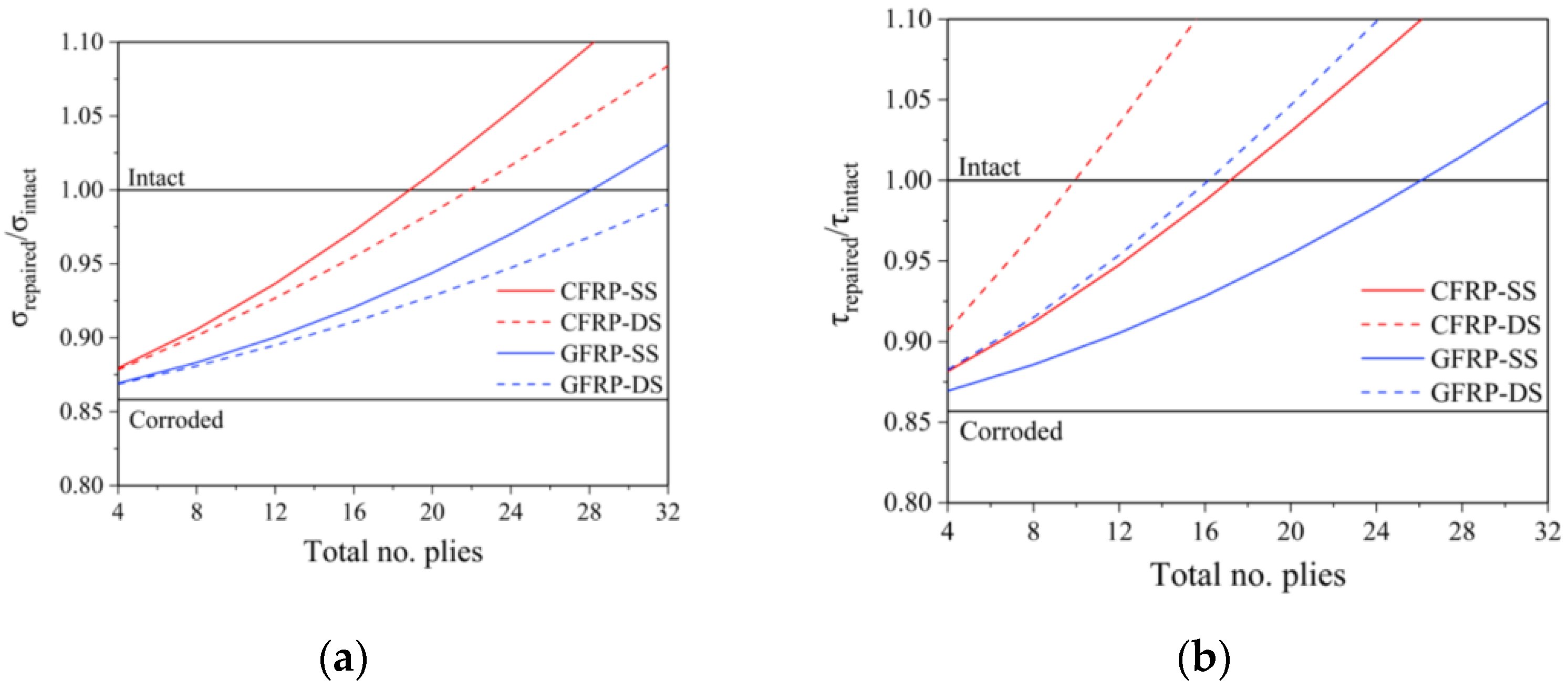
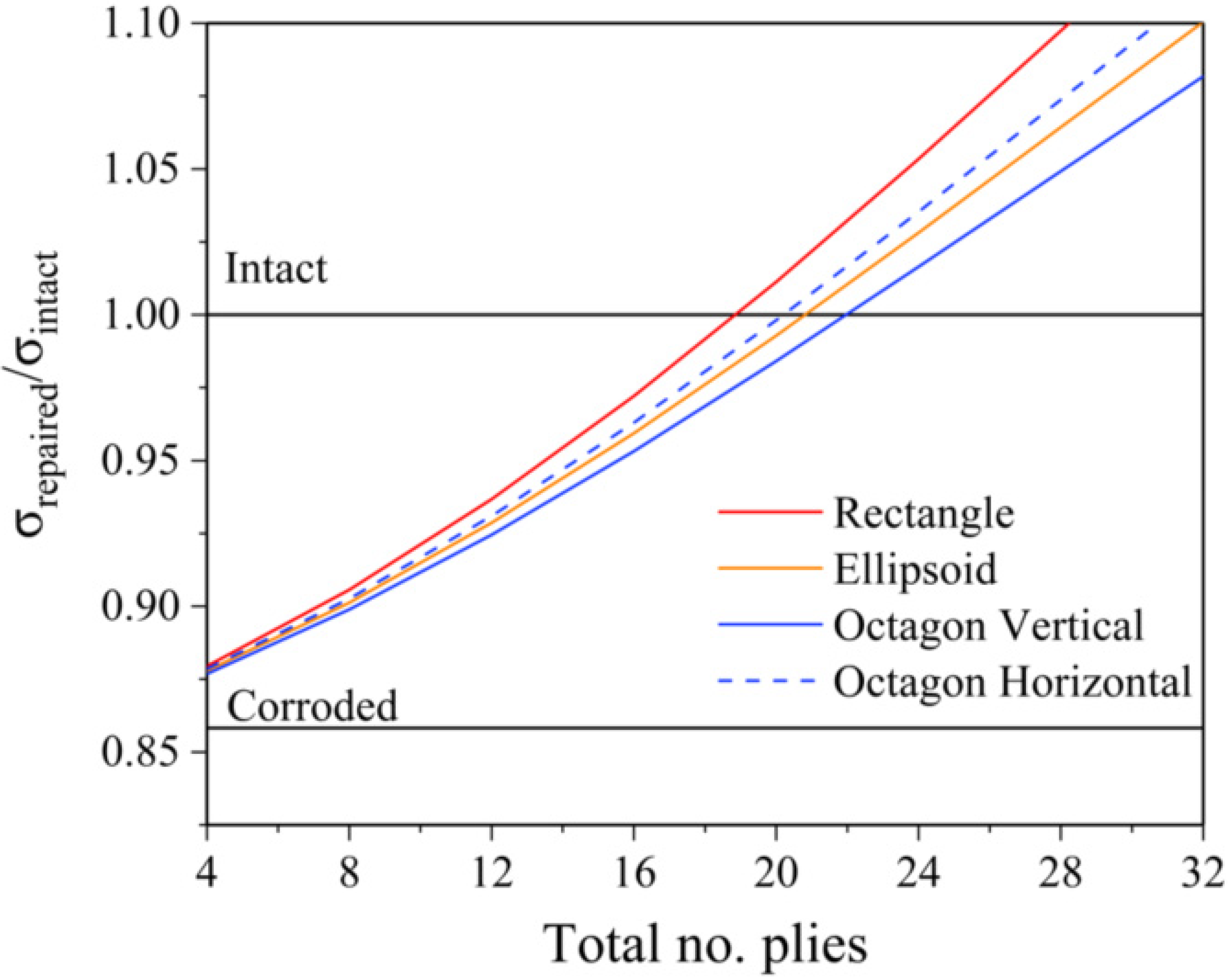
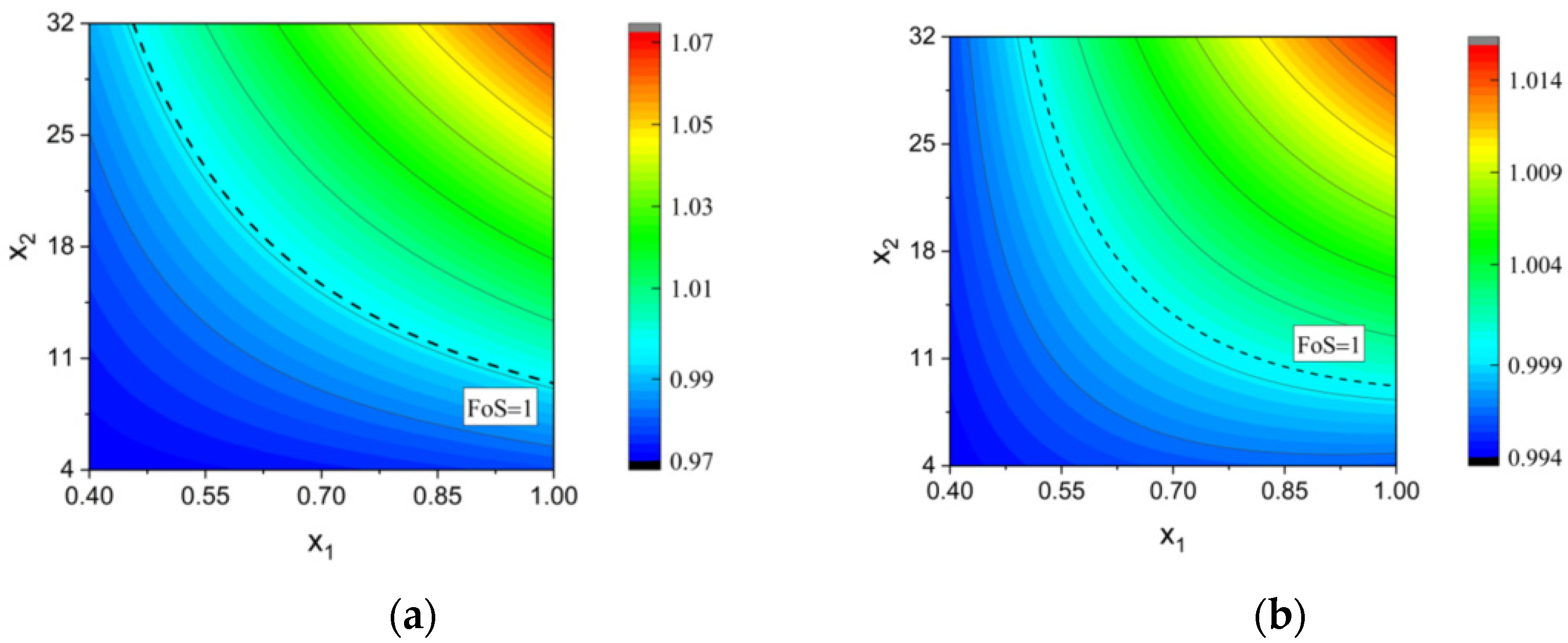
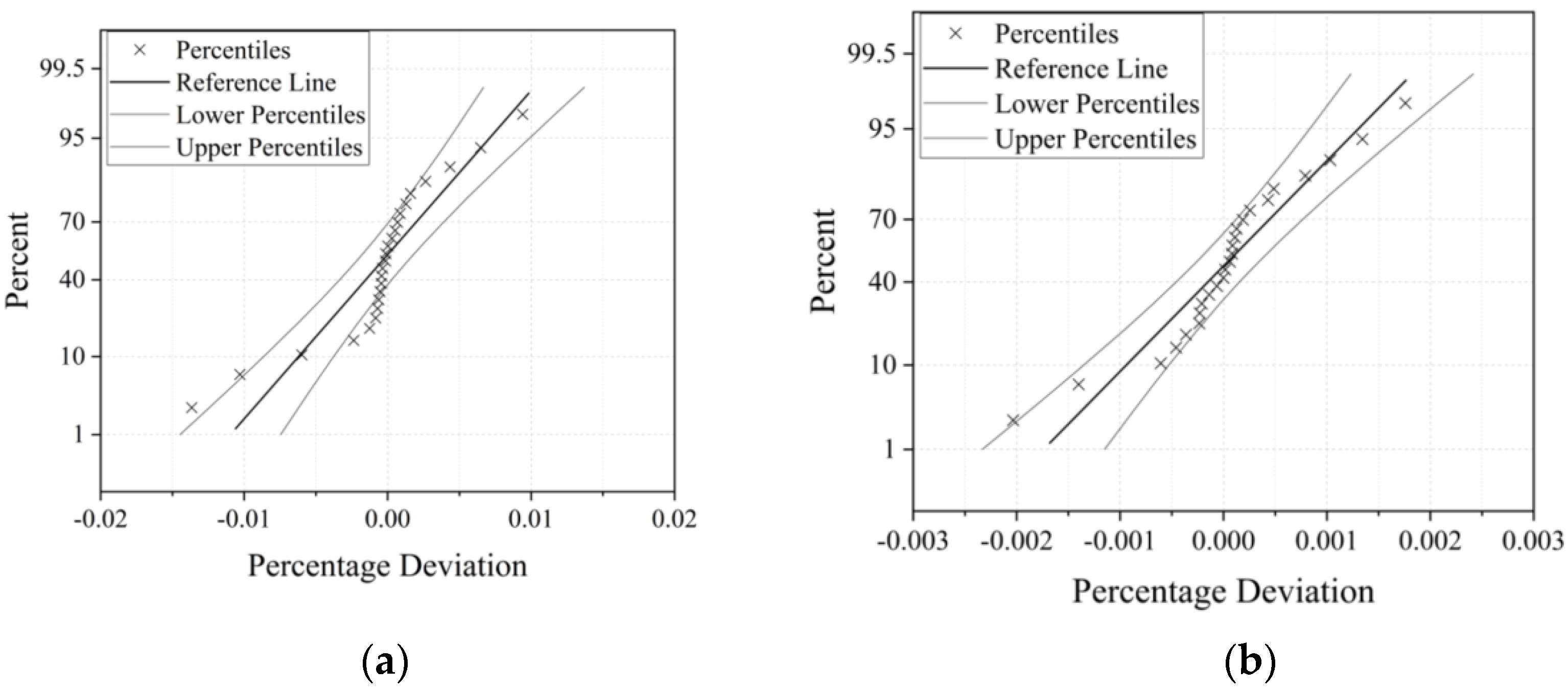
5.2. Analysis Results
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- IACS. Guidelines for Surveys, Assessment and Repair of Hull Structures—Container Ships, Rev.1; Witherbys Publishing: Livingstone, UK, 2018. [Google Scholar]
- Anyfantis, K.N. Preliminary design assessment of an alternative repair method for corroded shear panels in ship hull structures. Ocean Eng. 2019, 188, 106323. [Google Scholar] [CrossRef]
- Karatzas, V.A. Assessment and Design of Composite Patch Repairing in Marine Applications. Ph.D. Thesis, National Technical University of Athens, Athens, Greece, 2016. [Google Scholar]
- Karatzas, V.A.; Kotsidis, E.A.; Tsouvalis, N.G. Experimental fatigue study of composite patch repaired steel plates with cracks. Appl. Compos. Mater. 2015, 22, 507–523. [Google Scholar] [CrossRef]
- BV. Adhesive Joints and Patch Repair; Guidance Note NI613DTR00E; BV: Paris, France, 2015. [Google Scholar]
- DNV. Design, Fabrication, Operation and Qualification of Bonded Repair of Steel Structures; Recommended Practice DNVGL-RP-C301; DNV: Belum, Norwegen, 2015. [Google Scholar]
- ASME. Repair of Pressure Equipment and Piping; ASME PCC-2-2011; The American Society of Mechanical Engineers: New York, NY, USA, 2011. [Google Scholar]
- Hashim, S.; Berggreen, C.; Tsouvalis, N.; McGeorge, D.; Chirica, I.; Moore, P.; Boyd, S.; Nisar, J.; Anyfantis, K.; Misirlis, K.; et al. Fabrication, testing and analysis of steel/composite DLS adhesive joints. Ships Offshore Struct. 2011, 6, 115–126. [Google Scholar] [CrossRef]
- Aabid, A.; Hrairi, M.; Mohamed Ali, J.S. Optimization of composite patch repair for center-cracked rectangular plate using design of experiments method. Mater. Today Proc. 2020, 27, 1713–1719. [Google Scholar] [CrossRef]
- Turan, K. Buckling behavior of adhesively patch-repaired composite plates. J. Compos. Mater. 2013, 48, 3253–3261. [Google Scholar] [CrossRef]
- Lloyd’s Register. Rules and Regulations for the Classification of Ships; Lloyd’s Register: London, UK, 2016. [Google Scholar]
- Kollar, L.; Springer, G. Mechanics of Composite Structures; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Timoshenko, S.; Gere, J. Theory of elastic stability, International Student Edition, 2nd ed.; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Hughes, O.; Paik, J. Ship Structural Analysis and Design; SNAME: Jersey City, NJ, USA, 2010. [Google Scholar]
- Anyfantis, K.; Stavropoulos, P.; Chryssolouris, G. Fracture Mechanics Based Assessment of Manufacturing Defects Laying at the Edge of CFRP-Metal Bondlines; CrossMark: Plano, TX, USA, 2018. [Google Scholar]
- Zhang, S. A review and study on ultimate strength of steel plates and stiffened panels in axial compression. Ships Offshore Struct. 2016, 11, 81–91. [Google Scholar] [CrossRef]
- Lee, M.J.; Kim, W.S.; Jang, C.J.; Kim, K.H.; Cho, T.M.; Lee, B.C.; Lee, J.J. Analysis and Simulation of the Failure Characteristic of a Single Leg Bending Joint with a Micro-Patterned Surface. J. Adhes. 2011, 87, 826–841. [Google Scholar] [CrossRef]


| Property | Steel Grade ‘AH32′ 1 | CFRP 2,3 | GFRP 3 |
|---|---|---|---|
| Young’s modulus of elasticity | 206 GPa | 42.95 GPa | 213.4 GPa |
| Poisson’s ratio | 0.3 | 0.3 | 0.3 |
| Yield/Fracture Stress | 315 MPa | 352 MPa | 549 MPa |
| Plate’s Property | Symbol | Value | Unit |
|---|---|---|---|
| Material | - | Grade ‘AH32’ Steel | - |
| Length | am | 2250 | mm |
| Width | bm | 900 | mm |
| Intact thickness | tm,intact | 20 | mm |
| Corrosion | - | 5 | % |
| Corroded thickness | tm,corroded | 19 | mm |
| FoS requirement | FoSreq | 1.0 | - |
| Patch’s Property | Options | x | y |
|---|---|---|---|
| Material | CFRP/GFRP | No. Plies | FoS |
| Configuration | One-Sided/Two-Sided | ||
| Shape | Rectangular/Ellipsoid/Octagonal |
| Factor | Name | Low Level (−) | Center (0) | High Level (+) |
|---|---|---|---|---|
| x1 | Coverage (c) | 40% | 70% | 100% |
| x2 | No. Plies (Nplies) | 4 | 18 | 32 |
| Factor | Name | D + E 1 | E 2 | D + E 1 | E 2 | D + E 1 |
|---|---|---|---|---|---|---|
| x1 | Coverage (c) | 40% | 55% | 70% | 85% | 100% |
| x2 | No. Plies (Nplies) | 4 | 11 | 18 | 25 | 32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kallitsis, N.; Anyfantis, K.N. Buckling Strength Assessment of Composite Patch Repair Used for the Rehabilitation of Corroded Marine Plates. Appl. Mech. 2021, 2, 482-500. https://doi.org/10.3390/applmech2030027
Kallitsis N, Anyfantis KN. Buckling Strength Assessment of Composite Patch Repair Used for the Rehabilitation of Corroded Marine Plates. Applied Mechanics. 2021; 2(3):482-500. https://doi.org/10.3390/applmech2030027
Chicago/Turabian StyleKallitsis, Nikos, and Konstantinos N. Anyfantis. 2021. "Buckling Strength Assessment of Composite Patch Repair Used for the Rehabilitation of Corroded Marine Plates" Applied Mechanics 2, no. 3: 482-500. https://doi.org/10.3390/applmech2030027
APA StyleKallitsis, N., & Anyfantis, K. N. (2021). Buckling Strength Assessment of Composite Patch Repair Used for the Rehabilitation of Corroded Marine Plates. Applied Mechanics, 2(3), 482-500. https://doi.org/10.3390/applmech2030027





