Study of Influence of Width to Thickness Ratio in Sheet Metals on Bendability under Ambient and Superimposed Hydrostatic Pressure
Abstract
:1. Introduction
2. Constitutive Model
3. Problem Formulation and Method of Solution
4. Results and Discussion
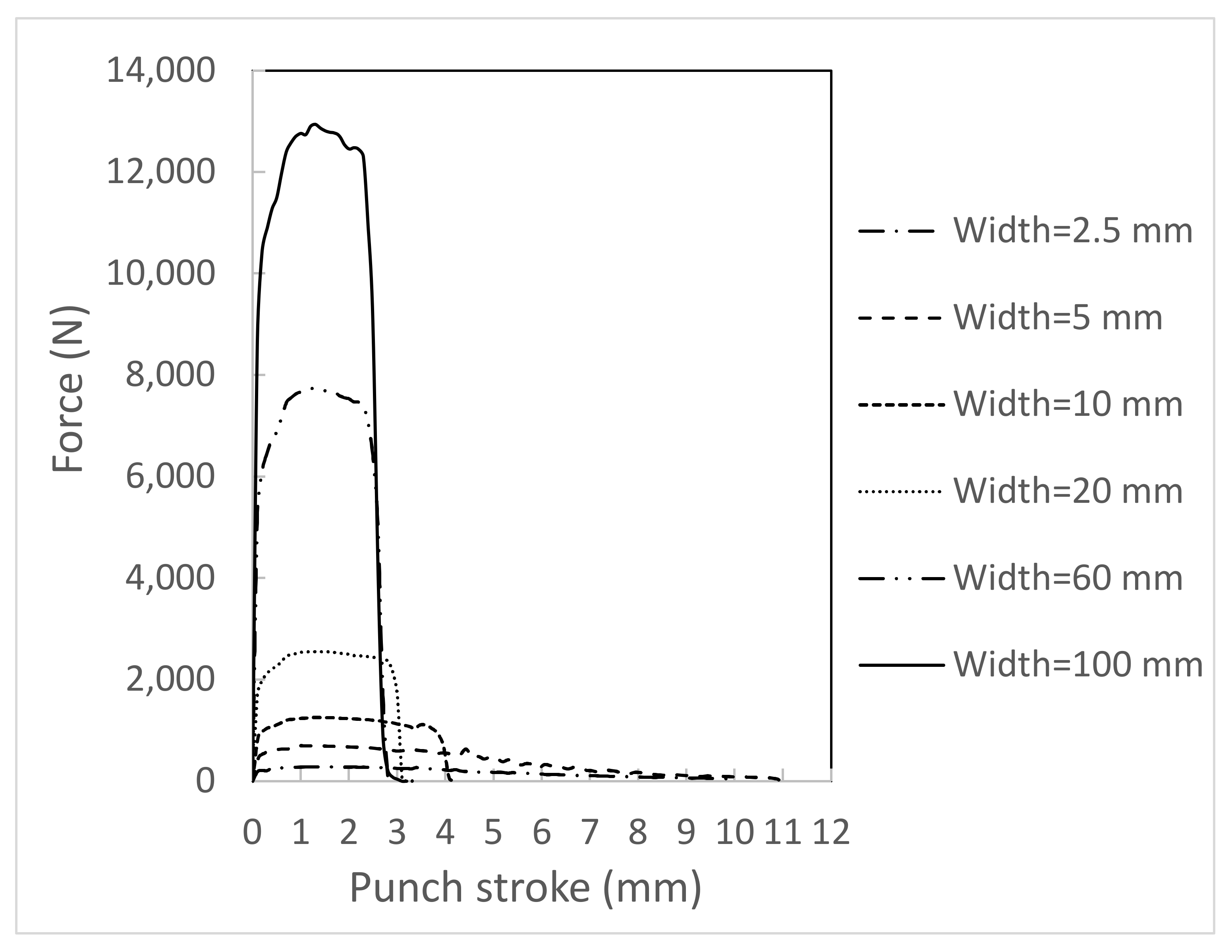
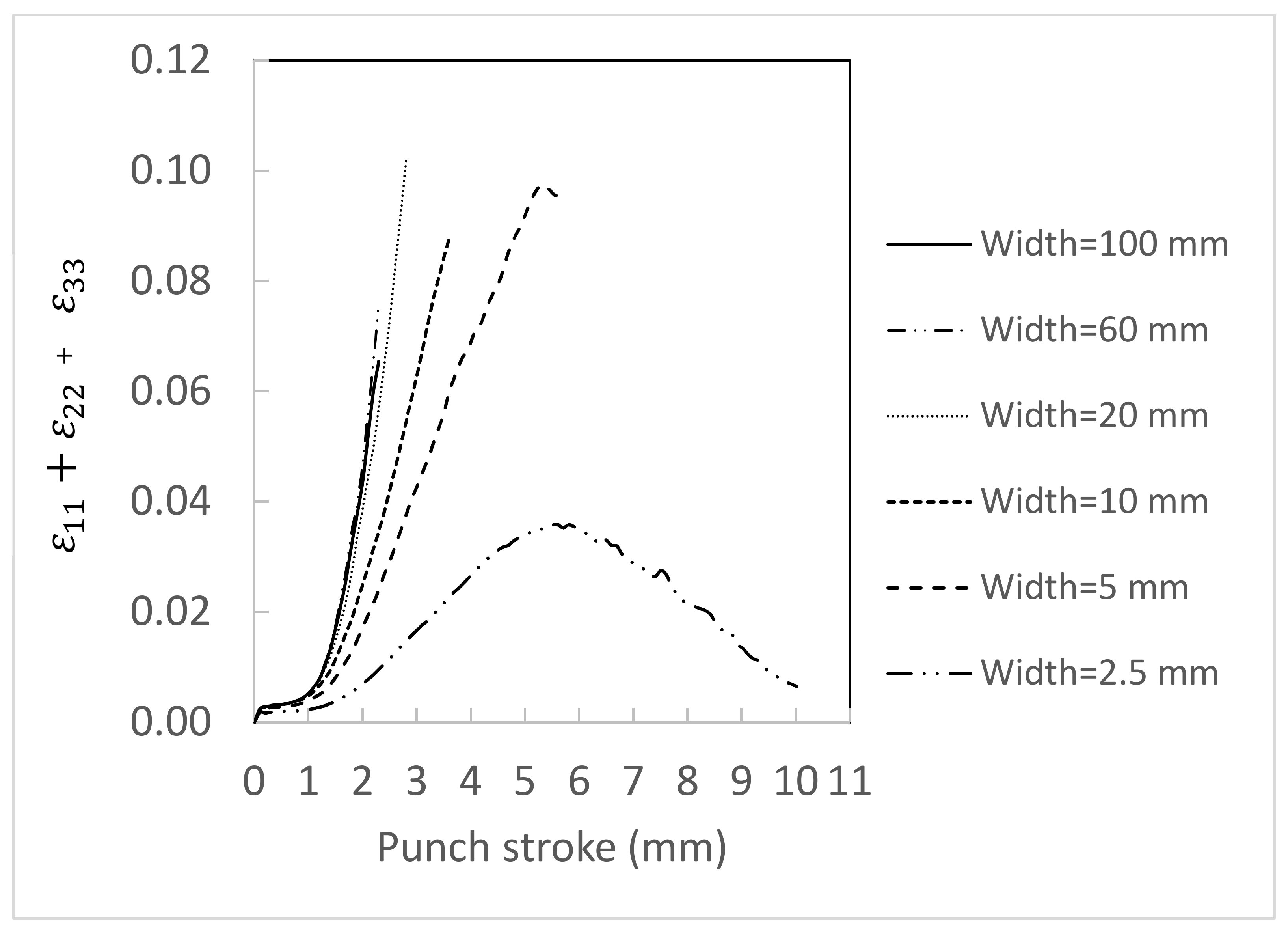
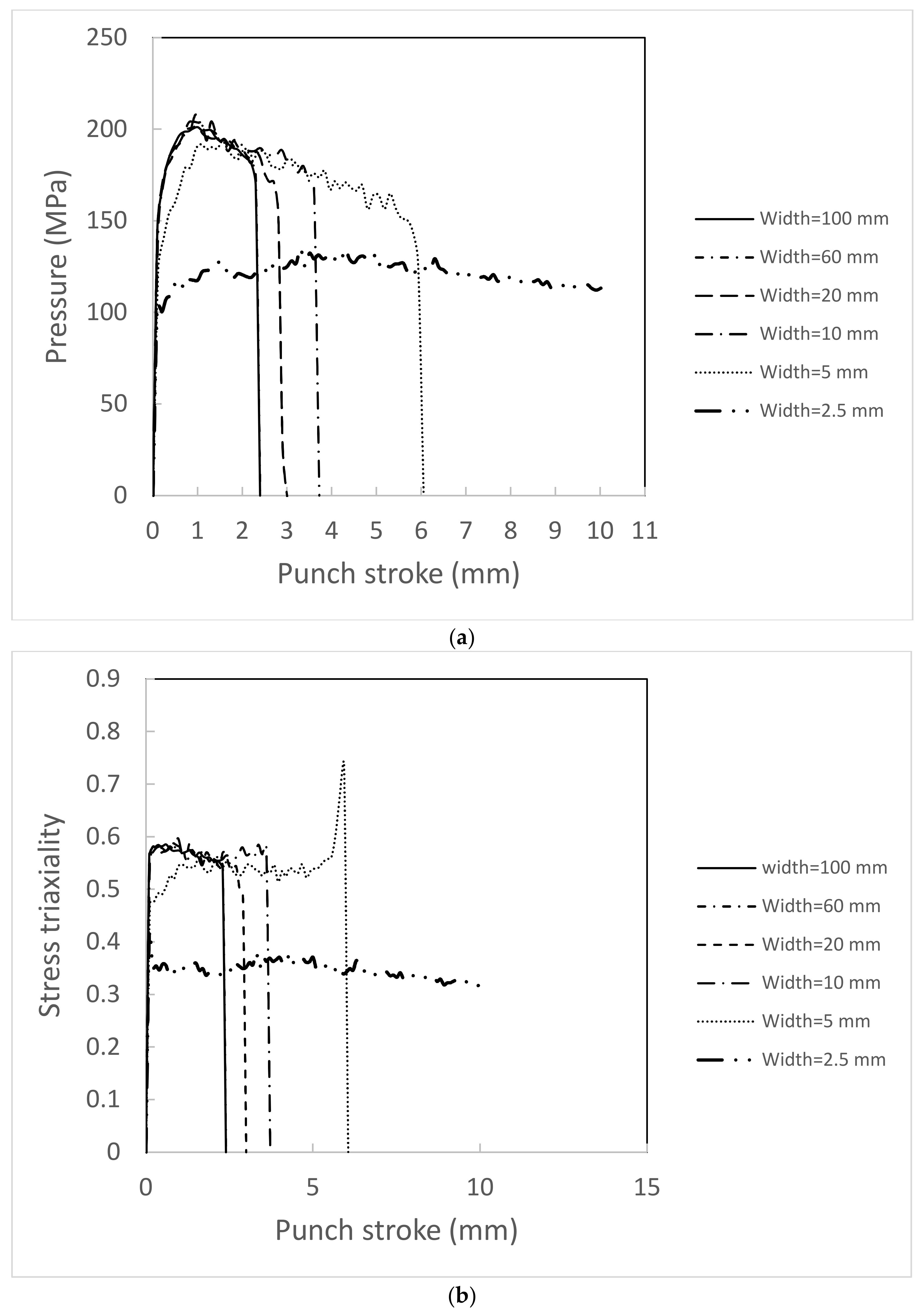
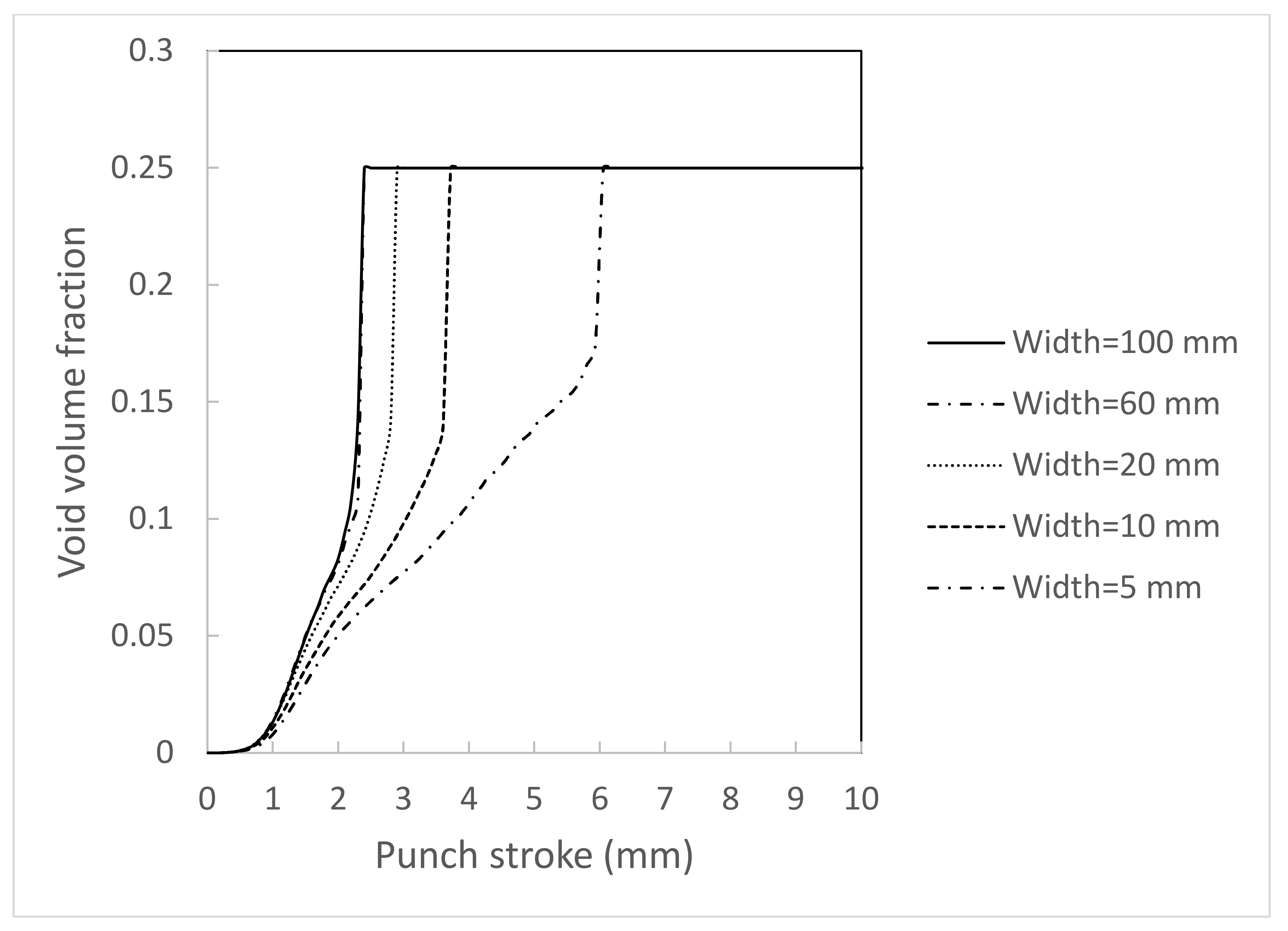
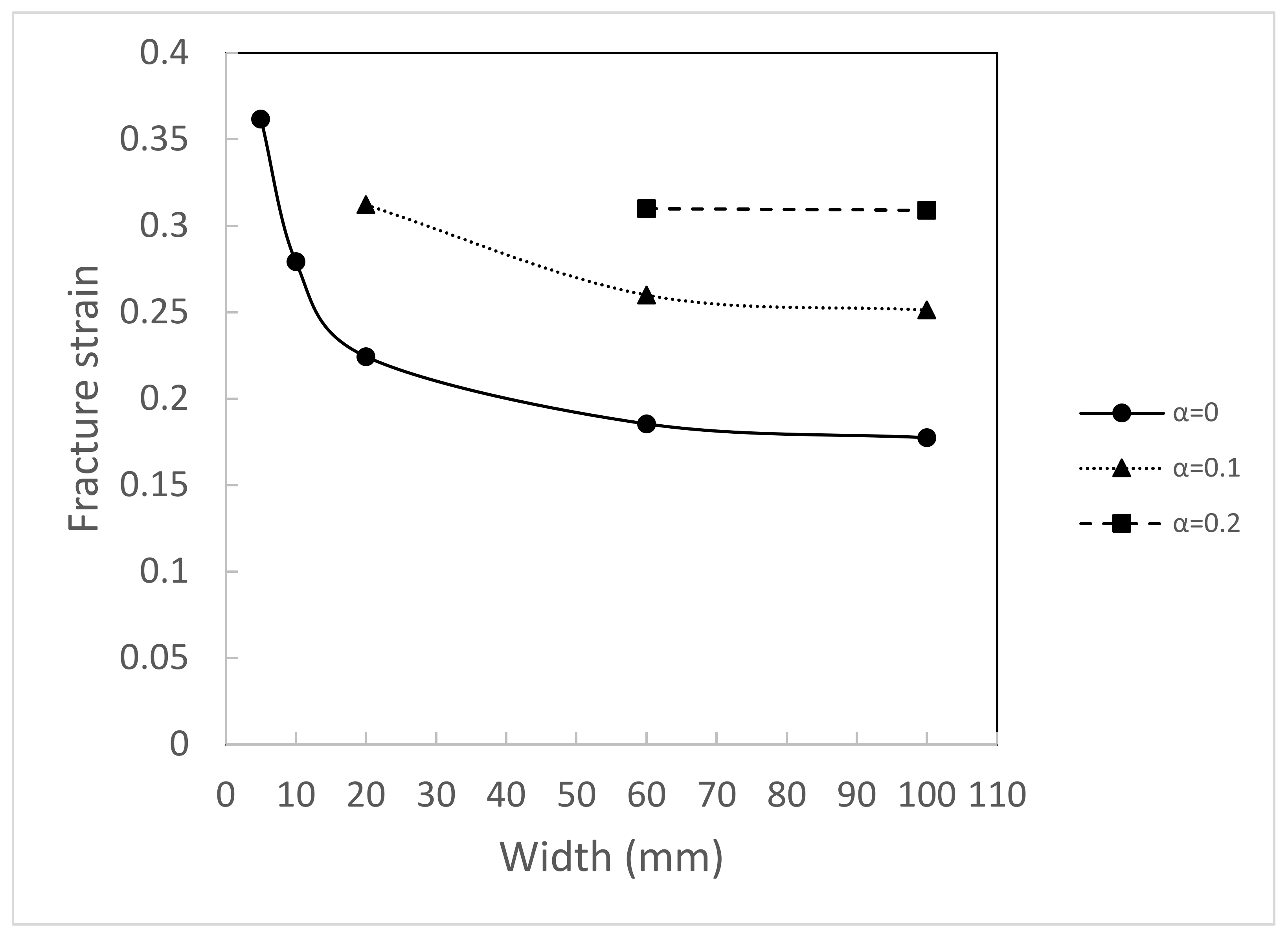
4.1. Effect of Width to Thickness Ratio on Bendability
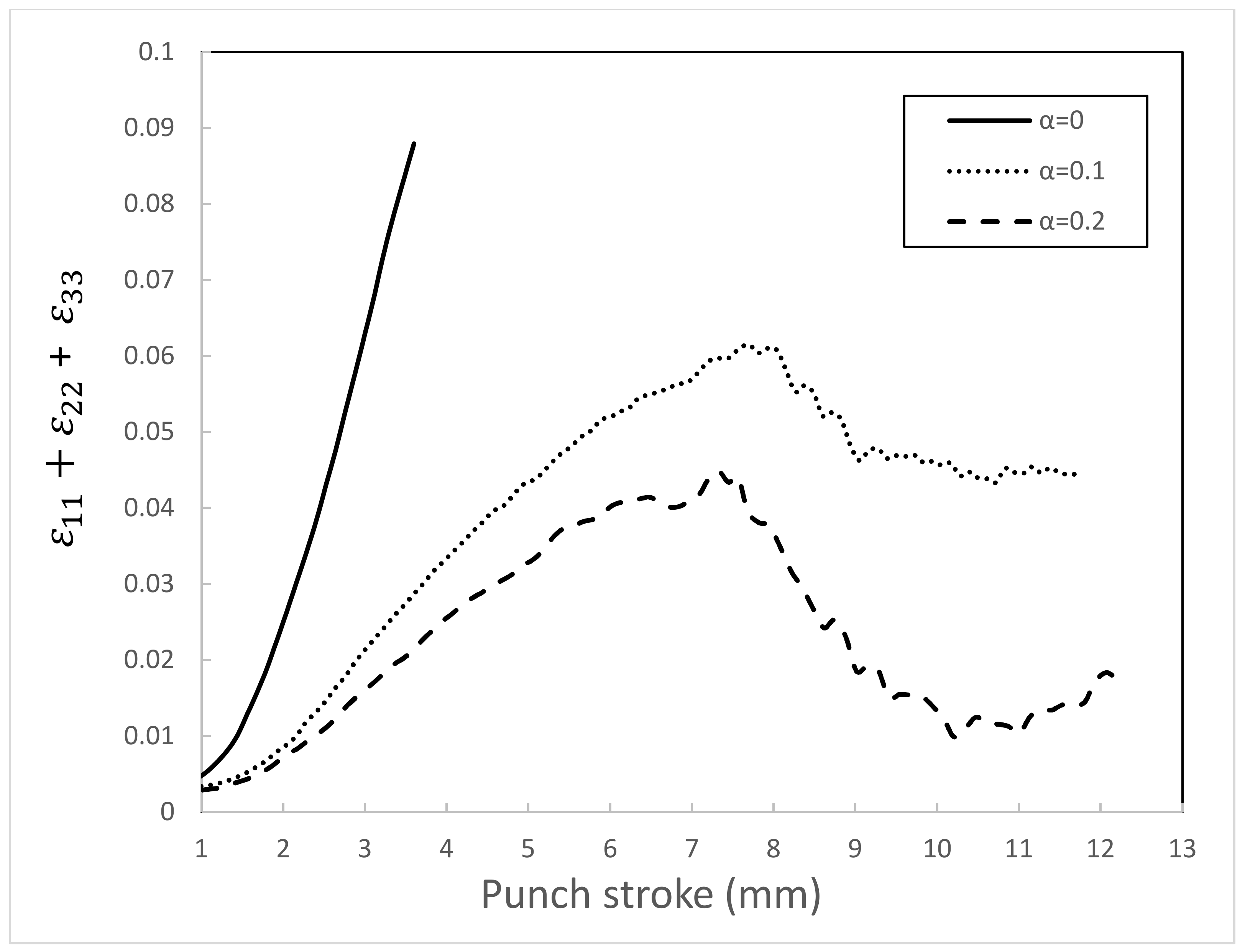
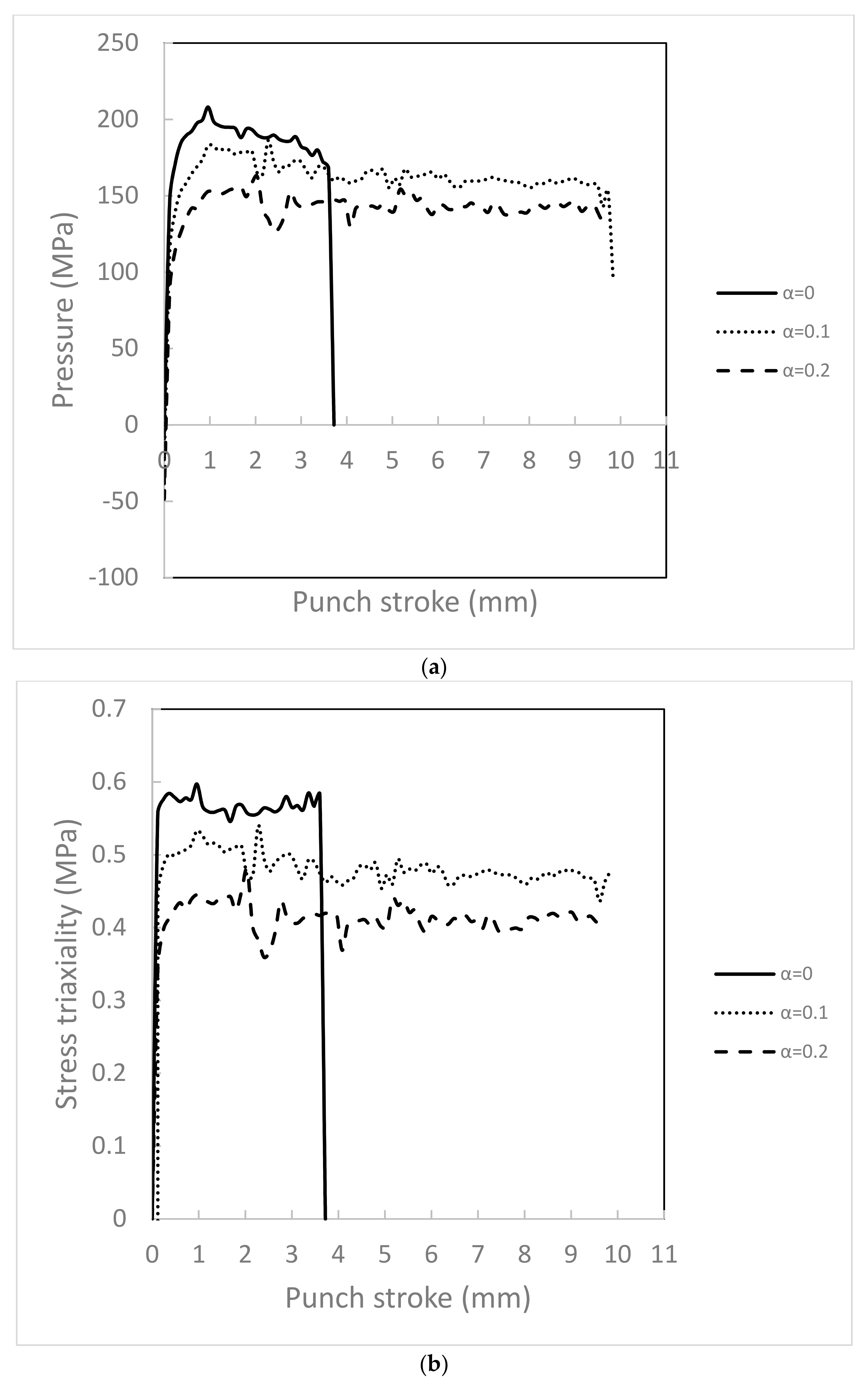
4.2. Effect of Pressure on Bendability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ragab, A.; Saleh, C.A. Evaluation of bendability of sheet metals using void coalescence models. Mater. Sci. Eng. A 2005, 395, 102–109. [Google Scholar] [CrossRef]
- Jin, Y.; Murata, M. Influence of pitch and cross-sectional ratio of strip of sheet metal on incremental in-plane bending. J. Mater. Process. Technol. 2004, 155, 1810–1814. [Google Scholar] [CrossRef]
- Lloyd, D.J.; Gallerneault, M.; Wagstaff, R.B. The deformation of clad aluminum sheet produced by direct chill casting. Metall. Mater. Trans. A 2010, 41, 2093–2103. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, P.Z.; Jin, H.; Wu, P.D.; Lloyd, D.J. Analysis of surface roughening in AA6111 automotive sheet under pure bending. Metall. Mater. Trans. A 2016, 47, 949–960. [Google Scholar] [CrossRef]
- Lloyd, D.J.; Evans, D.; Pelow, C.; Nolan, P. Bending in aluminium alloys AA 6111 and AA 5754 using the cantilever bend test. Mater. Sci. Technol. 2002, 18, 621–628. [Google Scholar] [CrossRef]
- Sarkar, J.; Kutty, T.R.G.; Conlon, K.T.; Wilkinson, D.S.; Embury, J.D.; Lloyd, D.J. Tensile and bending properties of AA5754 aluminum alloys. Mater. Sci. Eng. A 2001, 316, 52–59. [Google Scholar] [CrossRef]
- Sarkar, J.; Kutty, T.R.G.; Wilkinson, D.S.; Embury, J.D.; Lloyd, D.J. Tensile properties and bendability of T4 treated AA6111 aluminum alloys. Mater. Sci. Eng. A 2004, 369, 258–266. [Google Scholar] [CrossRef]
- Hou, P.; Zhao, H.; Ma, Z.; Zhang, S.; Li, J.; Dong, X.; Sun, Y.; Zhu, Z. Influence of punch radius on elastic modulus of three-point bending tests. Adv. Mech. Eng. 2016, 8, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Datsko, J.; Yang, C.T. Correlation of bendability of materials with their tensile properties. J. Manuf. Sci. Eng. 1960, 82, 309–313. [Google Scholar] [CrossRef]
- Shahzamanian, M.M.; Wu, D.J.L.P.D.; Xu, Z. Study of influence of superimposed hydrostatic pressure on bendability of sheet metals. Eur. J. Mech. A/Solids 2021, 85, 104132. [Google Scholar] [CrossRef]
- Shahzamanian, M.M.; Lloyd, D.; Wu, P.D. Enhanced bendability in sheet metal produced by cladding a ductile layer. Mater. Today Commun. 2020, 23, 100952. [Google Scholar] [CrossRef]
- Kao, A.S.; Kuhn, H.A.; Richmond, O.; Spitzig, W.A. Workability of 1045 spheroidized steel under superimposed hydrostatic pressure. Metall. Trans. A 1989, 20, 1735–1741. [Google Scholar]
- Kõrgesaar, M. The effect of low stress triaxialities and deformation paths on ductile fracture simulations of large shell structures. Mar. Struct. 2019, 63, 45–64. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Bao, Y.; Lee, Y.W.; Bai, Y. Calibration and evaluation of seven fracture models. Int. J. Mech. Sci. 2005, 47, 719–743. [Google Scholar] [CrossRef]
- Kao, A.S.; Kuhn, H.A.; Richmond, O.; Spitzig, W.A. Tensile fracture and fractographic analysis of 1045 spheroidized steel under hydrostatic pressure. J. Mater. Res. 1990, 5, 83–91. [Google Scholar] [CrossRef]
- Weinrich, P.; French, I. The influence of hydrostatic pressure on the fracture mechanisms of sheet tensile specimens of copper and brass. Acta Metall. 1976, 24, 317–322. [Google Scholar] [CrossRef]
- Ashby, M.F.; Embury, J.D.; Cooksley, S.H.; Teirlinck, D. Fracture maps with pressure as a variable. Scr. Metall. 1985, 19, 385–390. [Google Scholar] [CrossRef]
- French, I.E.; Weinrich, P.F. The influence of hydrostatic pressure on the tensile deformation and fracture of copper. Metall. Trans. A 1975, 6, 785. [Google Scholar] [CrossRef]
- French, I.; Weinrich, P.; Weaver, C. Tensile fracture of free machining brass as a function of hydrostatic pressure. Acta Metall. 1973, 21, 1045–1049. [Google Scholar] [CrossRef]
- Brownrigg, A.; Spitzig, W.A.; Richmond, O.; Teirlinck, D. The influence of hydrostatic pressure on the flow stress and ductility of a spherodized 1045 steel. Acta Metall. 1983, 31, 1141–1150. [Google Scholar] [CrossRef]
- Partovi, A.; Shahzamanian, M.M.; Wu, P.D. Study of Influence of Superimposed Hydrostatic Pressure on Ductility in Ring Compression Test. J. Mater. Eng. Perform. 2020, 29, 6581–6590. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Metall. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Tvergaard, V. Influence of voids on shear band instabilities under plane strain conditions. Int. J. Fract. 1981, 17, 389–407. [Google Scholar] [CrossRef]
- Tvergaard, V. On localization in ductile materials containing spherical voids. Int. J. Fract. 1982, 18, 237–252. [Google Scholar]
- Gurson, A.L. Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Shahzamanian, M.M.; Partovi, A.; Wu, P.D. Study of Pre-strain Effect on Bendability in Three-Point Bending Test. In Fracture Fatigue and Wear; Springer: Berlin/Heidelberg, Germany, 2020; pp. 261–268. [Google Scholar]
- Schowtjak, A.; Kusche, C.F.; Meya, R.; Korte-Kerzel, S.; Al-Samman, T.; Tekkaya, A.E.; Clausmeyer, T. Prediction of void evolution in sheet bending based on statistically representative microstructural data for the Gurson-Tvergaard-Needleman model. arXiv 2020, arXiv:2006.15973. [Google Scholar]
- Andersen, R.G.; Londono, J.G.; Woelke, P.B.; Nielsen, K.L. Fundamental differences between plane strain bending and far-field plane strain tension in ductile plate failure. J. Mech. Phys. Solids 2020, 141, 103960. [Google Scholar] [CrossRef]
- Achineethongkham, K.; Uthaisangsuk, V. Analysis of forming limit behaviour of high strength steels under non-linear strain paths using a micromechanics damage modelling. Int. J. Mech. Sci. 2020, 183, 105828. [Google Scholar] [CrossRef]
- Shahzamanian, M.M. Anisotropic Gurson-Tvergaard-Needleman plasticity and damage model for finite element analysis of elastic–plastic problems. Int. J. Numer. Methods Eng. 2018, 115, 1527–1551. [Google Scholar] [CrossRef]
- Malcher, L.; Pires, F.M.A.; de Sá, J.M.A.C. An extended GTN model for ductile fracture under high and low stress triaxiality. Int. J. Plast. 2014, 54, 193–228. [Google Scholar] [CrossRef]
- Bergo, S.; Morin, D.; Hopperstad, O.S. Numerical implementation of a non-local GTN model for explicit FE simulation of ductile damage and fracture. Int. J. Solids Struct. 2021, 219–220, 134–150. [Google Scholar] [CrossRef]
- He, Z.; Zhu, H.; Hu, Y. An improved shear modified GTN model for ductile fracture of aluminium alloys under different stress states and its parameters identification. Int. J. Mech. Sci. 2021, 192, 106081. [Google Scholar] [CrossRef]
- Li, X.; Chen, Z.; Dong, C. Size effect on the damage evolution of a modified GTN model under high/low stress triaxiality in meso-scaled plastic deformation. Mater. Today Commun. 2021, 26, 101782. [Google Scholar] [CrossRef]
- Chen, D.; Li, Y.; Yang, X.; Jiang, W.; Guan, L. Efficient parameters identification of a modified GTN model of ductile fracture using machine learning. Eng. Fract. Mech. 2021, 245, 107535. [Google Scholar] [CrossRef]
- Yildiz, R.A.; Yilmaz, S. Influence of heat treatments on the formability of the 6061 Al alloy sheets: Experiments and GTN damage model. Int. J. Adv. Manuf. Technol. 2021, 113, 2277–2299. [Google Scholar] [CrossRef]
- ABAQUS Inc. A.M.V.; Dassault Systèmes: Providence, RI, USA, 2014. [Google Scholar]
- Chu, C.; Needleman, A. Void nucleation effects in biaxially stretched sheets. J. Eng. Mater. Technol. 1980, 102, 249–256. [Google Scholar] [CrossRef]
- Wu, P.D.; Chen, X.X.; Lloyd, D.J.; Embury, J.D. Effects of superimposed hydrostatic pressure on fracture in sheet metals under tension. Int. J. Mech. Sci. 2010, 52, 236–244. [Google Scholar] [CrossRef]
- Chen, X.X.; Wu, P.D.; Lloyd, D.J.; Embury, J.D.; Huang, Y. Enhanced ductility in sheet metals produced by cladding a ductile layer. J. Appl. Mech. 2010, 77, 41015. [Google Scholar] [CrossRef]
- Peng, J.; Wu, P.D.; Huang, Y.; Chen, X.X.; Lloyd, D.J.; Embury, J.D.; Neale, K.W. Effects of superimposed hydrostatic pressure on fracture in round bars under tension. Int. J. Solids Struct. 2009, 46, 3741–3749. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.X.; Wu, P.D.; Embury, J.D.; Huang, Y. Enhanced ductility in round tensile bars produced by cladding a ductile ring. Model. Simul. Mater. Sci. Eng. 2010, 18, 25005. [Google Scholar] [CrossRef]

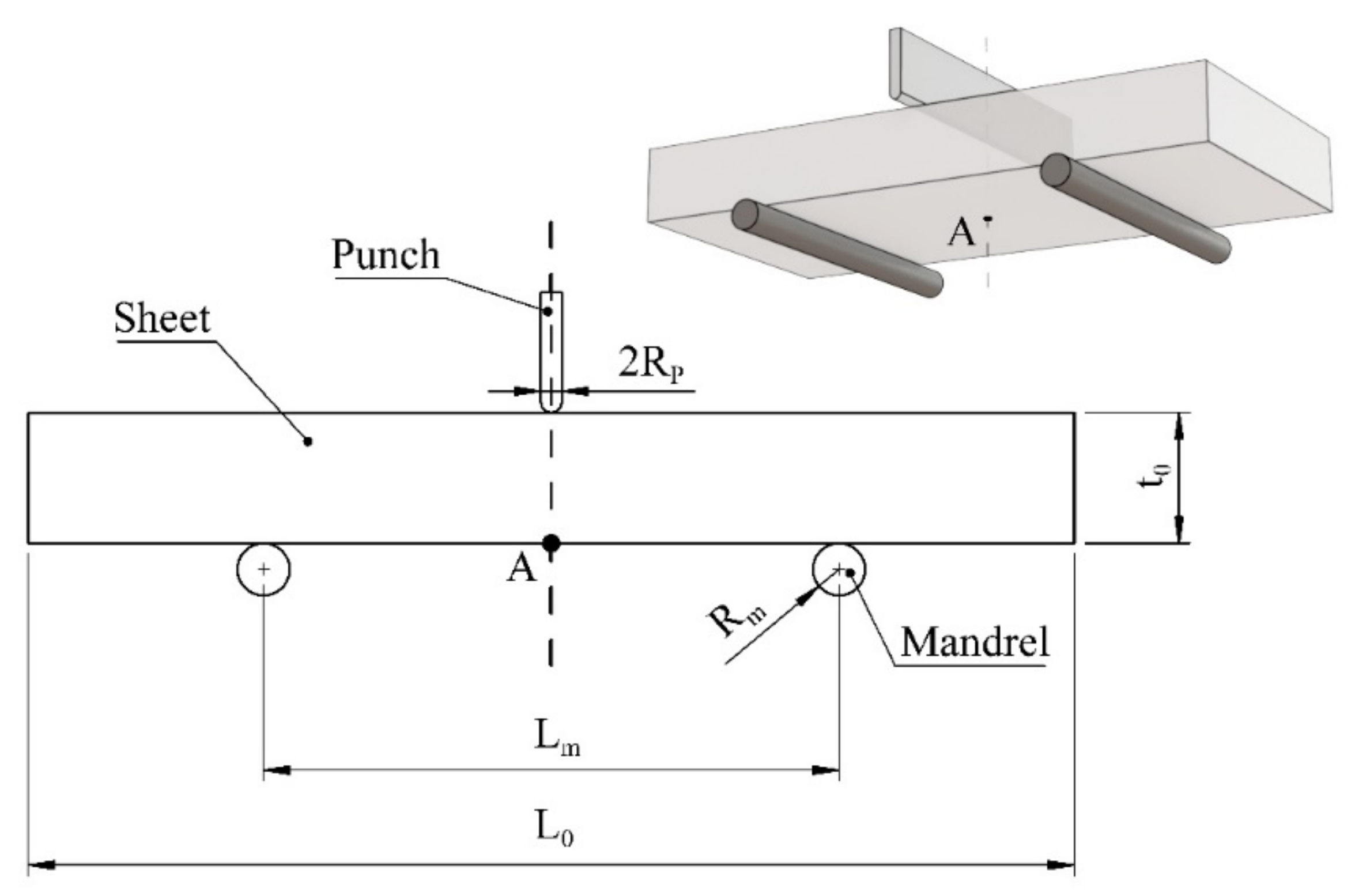
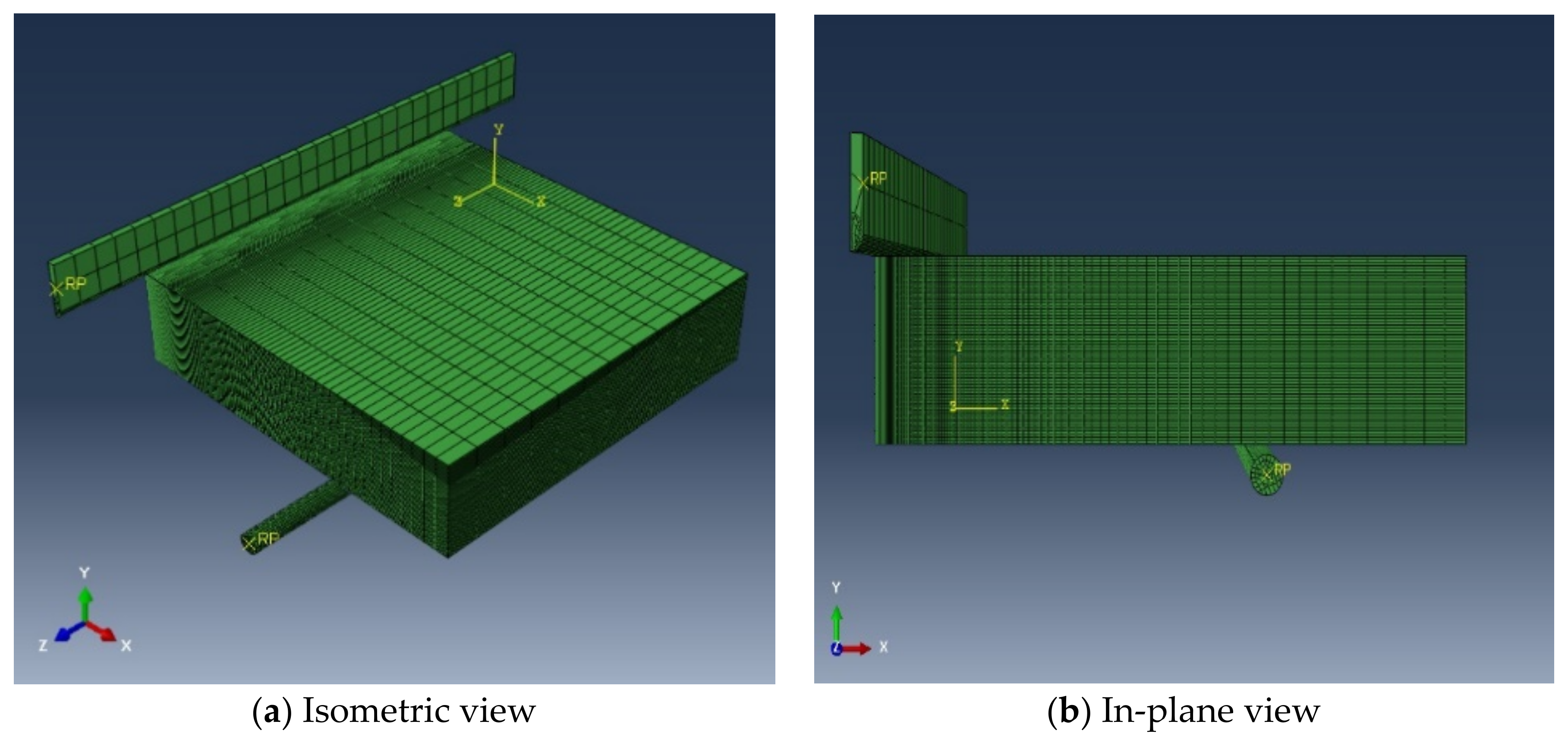
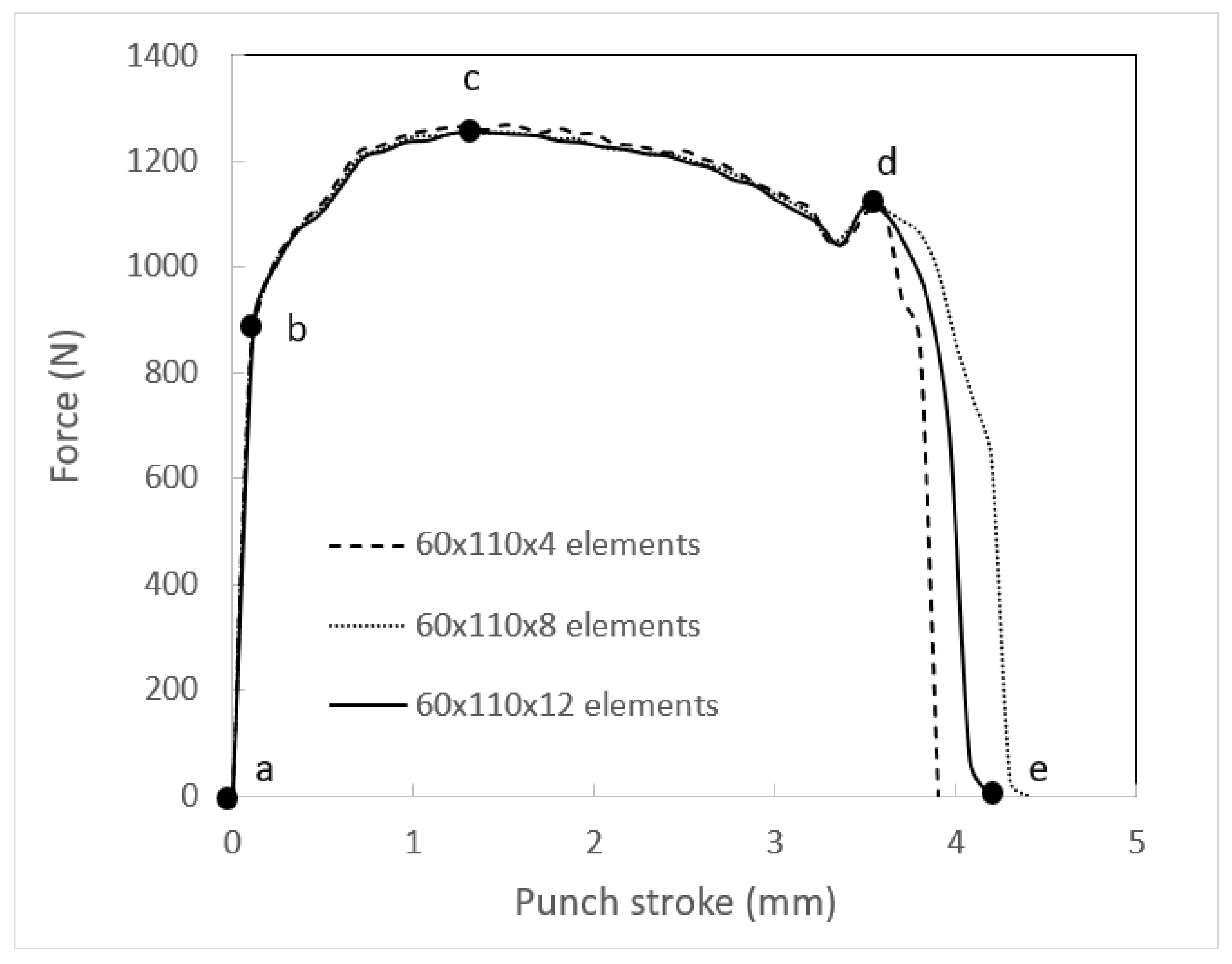


| Matrix material | 71 | 234.3 |
| Mesh distribution | |||
| Fracture strain | 0.279 | 0.288 | 0.283 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahzamanian, M.; Lloyd, D.; Partovi, A.; Wu, P. Study of Influence of Width to Thickness Ratio in Sheet Metals on Bendability under Ambient and Superimposed Hydrostatic Pressure. Appl. Mech. 2021, 2, 542-558. https://doi.org/10.3390/applmech2030030
Shahzamanian M, Lloyd D, Partovi A, Wu P. Study of Influence of Width to Thickness Ratio in Sheet Metals on Bendability under Ambient and Superimposed Hydrostatic Pressure. Applied Mechanics. 2021; 2(3):542-558. https://doi.org/10.3390/applmech2030030
Chicago/Turabian StyleShahzamanian, Mohammadmehdi, David Lloyd, Amir Partovi, and Peidong Wu. 2021. "Study of Influence of Width to Thickness Ratio in Sheet Metals on Bendability under Ambient and Superimposed Hydrostatic Pressure" Applied Mechanics 2, no. 3: 542-558. https://doi.org/10.3390/applmech2030030
APA StyleShahzamanian, M., Lloyd, D., Partovi, A., & Wu, P. (2021). Study of Influence of Width to Thickness Ratio in Sheet Metals on Bendability under Ambient and Superimposed Hydrostatic Pressure. Applied Mechanics, 2(3), 542-558. https://doi.org/10.3390/applmech2030030





