Abstract
Urban air mobility (UAM) is a revolutionary approach to transportation in densely populated cities. UAM involves using small, highly automated aircraft to transport passengers and goods at lower altitudes within urban and suburban areas, aiming to transform how people and parcels move within these environments. On average, UAM can reduce travel times by 30% to 40% for point-to-point journeys, with even greater reductions of 40% to 50% in major cities in the United States and China, compared to land transport. UAM includes advanced airborne transportation options like electric vertical takeoff and landing (eVTOL) aircraft and unmanned aerial vehicles (UAVs or drones). These technologies offer the potential to ease traffic congestion, decrease greenhouse gas emissions, and substantially cut travel times in urban areas. Studying the applications of eVTOLs and UAVs in parcel delivery and passenger transportation poses intricate challenges when examined through the lens of operations research (OR). By OR approaches, we mean mathematical programming, models, and solution methods addressing eVTOL- and UAV-aided parcel/people transportation problems. Despite the academic and practical importance, there is no review paper on eVTOL- and UAV-based optimization problems in the UAM sector. The present paper, applying a systematic literature review, develops a classification scheme for these problems, dividing them into routing and scheduling of eVTOLs and UAVs, infrastructure planning, safety and security, and the trade-off between efficiency and sustainability. The OR methodologies and the characteristics of the solution methods proposed for each problem are discussed. Finally, the study gaps and future research directions are presented alongside the concluding remarks.
1. Introduction
In the rapidly evolving urban transportation landscape, urban air mobility (UAM), a subset of advanced air mobility (AAM), has emerged as a transformative paradigm to redefine how we move within densely populated urban environments. UAM involves the utilization of “small, highly automated aircraft” to transport passengers or goods (parcels) at lower altitudes within urban and suburban regions [1]. Cities worldwide are facing unprecedented challenges related to congestion, pollution, and the limitations of traditional ground-based transportation systems. For instance, traffic congestion in the United States results in drivers wasting over three billion gallons of fuel and spending nearly seven billion additional hours stuck in their vehicles yearly [2]. UAM encompasses a spectrum of innovative aerial transportation solutions, including electric vertical takeoff and landing (eVTOL) aircraft and unmanned aerial vehicles (UAVs), also known as drones. These vehicles promise to alleviate the burden on congested roadways, reduce greenhouse gas emissions, and significantly reduce travel times within cities. Typically, UAM leads to a 30% to 40% reduction in travel times between origin and destination (O−D), and this reduction extends to 40% to 50% for major metropolitan areas or cities in the United States and China, respectively, compared to land transport [3].
UAM can handle the last-mile travel (LMT) for passengers and last-mile delivery (LMD) for parcels within urban or suburban areas. By the term “last mile”, we mean the last step of the journey of a person or parcel in urban logistics. For example, eVTOL aircraft, alternatively known as air taxis or flying taxis [4], can hover and fly, akin to helicopters, accommodate a passenger capacity ranging from two to six individuals, which may include a pilot, and transport them to their last destination [5]. Moreover, United Parcel Service (UPS), an “American multinational shipping & receiving and supply chain management company”, made a significant announcement on 7 April 2021, revealing its intent to acquire as many as 150 `ALIA-250’ eVTOL aircraft, employed for LMD and planned to be operated by taking off and landing directly at UPS facilities [6]. The expenses associated with LMD comprise a substantial portion of shipping costs, accounting for 53% of the overall expenses [7]. Also, efficient LMD does not just impact consumer buying choices; it plays a pivotal role in shaping urban development, sustainability initiatives, and transportation logistics [8]. Therefore, sustainable, innovative solutions, such as eVTOLs and UAVs, for last-mile transportation (e.g., LMT and LMD) can transform urban mobility logistics, reducing traffic congestion and pollution while improving efficiency and customer satisfaction.
The applications of UAM solutions like eVTOLs and UAVs in last-mile transportation present intricate challenges from the operations research (OR) perspective, specifically, mathematical programming models and heuristics. These complex optimization problems and models involve route planning, vehicle scheduling (e.g., drones), infrastructure planning, safety and security, and the trade-offs between efficiency (strategic, tactical, or operational costs) and sustainability (environmental or societal considerations). Classifying these problems and models through a structured framework indicates the differences and similarities between the problems and, therefore, shows the gaps and future research directions for OR community researchers interested in the applications of eVTOLs and UAVs in last-mile transportation. Also, a review paper on eVTOLs and UAVs in last-mile transportation from an OR perspective is essential in the urban mobility literature. This will be crucial in pinpointing deficiencies in the current knowledge base while suggesting potential directions for future multidisciplinary research endeavors.
Several review papers exist in the literature on UAM implementation challenges and the potential/prospects associated with technologies including VTOL, eVTOL, UAVs, and electric vehicles (EVs), as shown in Table 1. According to the literature, refs. [9,10,11,12] reviewed the passenger-and-parcel transportation within a UAM system. Also, refs. [13,14] investigated the challenges and mechanisms of both eVTOL and UAVs by comparing the different scenarios for passenger transportation. Despite the common focus area, our review work differs from these works by studying passenger and parcel (cargo) delivery with eVTOL and UAV technologies from the OR perspective (modeling and solution approaches). Therefore, the contributions of this work are presented as follows:

Table 1.
Comparison of the existing review works on UAM with the present paper.
- Presenting an OR-based classification framework by exploring the optimization problems (models) and solution methods in the literature of the applications of UAM solutions, e.g., eVTOLs and UAVs in last-mile transportation.
- Identifying the gaps in the existing knowledge and offering potential directions for future research by classifying the collected papers through a generic framework.
- Establishing a common understanding of the UAM system between various academic fields, including aerospace engineering, urban planning, and OR.
The paper is organized as follows: Section 2 explains this paper’s review methodology. Section 3 and Section 4 review the papers on eVTOLs and UAVs and the related problems and solution approaches, respectively. Section 5 highlights areas with room for further research and outlines potential future directions. Lastly, Section 6 contains concluding remarks.
2. Review Methodology
To carry out our systematic literature review, we adopted the methodology employed by [21], tailoring it to our specific research domain. The systematic literature review in our study comprises seven sequential steps, as presented in Figure 1. These steps are explained in more detail as follows:

Figure 1.
Overview of steps of the review methodology in the present paper.
- Formulating research questions (Section 2.1): we began by defining our research questions and establishing the foundation for our investigation.
- Determining scope (Section 2.2): we outlined the boundaries and scope of our study, delineating the specific areas and topics under examination.
- Database and keyword selection (Section 2.3): we identified the databases for sourcing the relevant literature and established a set of keywords and search terms to guide our information retrieval process.
- Establishing inclusion and exclusion criteria (Section 2.4): we laid out the criteria that would be used to include or exclude papers from our review, ensuring a structured and consistent selection process.
- Review and paper selection: we systematically reviewed the available literature and selected the most pertinent papers based on our established criteria.
- Defining a classification scheme (Section 2.5): we developed a classification framework to categorize the selected papers, facilitating a structured analysis of the research findings.
- Analysis, gap identification, and future research directions: finally, we conducted a thorough qualitative analysis (specifically, content and thematic analysis) of the selected papers according to the proposed classification scheme (previous step), identified research gaps, and proposed directions for future research, as outlined in Section 5.
Following these structured steps enabled us to conduct a comprehensive and systematic review of the literature in our research area.
2.1. Research Questions
It is important to craft research questions at the outset of a review study, as they lay the foundation for the research design and shape expectations regarding the outcomes. In the present review work, we articulate the research questions as follows:
- (RQ1) What are the primary problems and subproblems related to the applications of eVTOLs and UAVs (UAM technologies) in optimizing last-mile transportation from the OR perspective?
- (RQ2) What challenges and characteristics are associated with implementing the OR-based methodologies (like mathematical programming, models, and solution methods) in last-mile transportation optimization through applying the eVTOLs and UAVs?
- (RQ3) What research directions and gaps exist in utilizing UAM solutions for last-mile transportation from the OR perspective?
These research questions serve as a road map for our review study, guiding the exploration of challenges, methodologies, and future research prospects in last-mile transportation and UAM systems from the OR perspective. Answering the first research question leads to a classification scheme for the scope of this review paper. The second research question determines the mathematical models (including decision variables, objective functions, and constraints) and solution methods developed for each problem, addressing their challenges and characteristics. Finally, the third research question provides the research gaps and directions related to the scope of this paper.
2.2. Scope
This work focuses on employing novel UAM technologies (innovative solutions), including eVTOLs and UAVs in last-mile transportation from an OR perspective, and reviews the literature on this research area. As shown in Figure 2, UAM consists of three classes: first-, middle-, and last-mile transportation. First-mile transportation usually involves transporting raw materials or processed products to manufacturing sites or distribution centers (warehouses). Middle-mile transportation usually addresses the transportation of finished products from factories or distribution centers to retailers or stores. Last-mile transportation includes parcel delivery (LMD) and passenger transport (LMT), which transports parcels from stores to the end customer and people to their final destination. In the context of UAM, several technologies for vehicles, including electric and autonomous aircraft (e.g., eVTOLs and UAVs) and non-electric and traditional aircraft (like VTOLs and helicopters), exist. The applications of eVTOLs and UAVs in last-mile transportation can be studied through OR or non-OR (e.g., operations management) perspectives. This review paper focuses on the OR perspective, including mathematical programming, optimization models, and solution approaches (e.g., exact and heuristics methods).
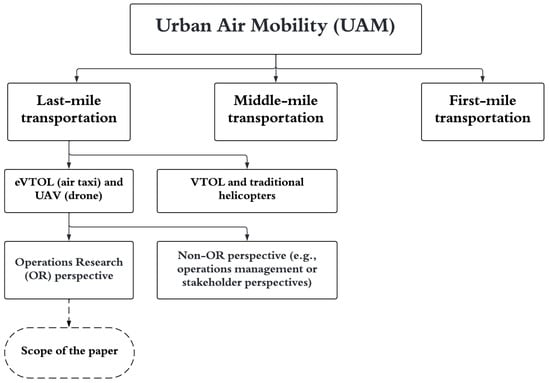
Figure 2.
Scope and focus area of the present review paper.
2.3. Database and Keywords Selection
The process of finding the relevant literature involved several steps. Initially, identification was based on the titles of papers. Subsequently, a more refined selection was made based on the abstracts, with an examination of critical sections within the papers when the abstracts alone did not provide adequate information to assess their alignment with the scope. The search engines and library databases were Google Scholar, SCOPUS, IEEE, PubMed, EBSCO, and ISI Web of Knowledge. The keywords were carefully selected and used to search the databases:
- “Last mile”; “parcel delivery”; “urban air mobility”; “eVTOL”; “sustainability”.
- “Last mile”; “parcel delivery”; “urban air mobility”; “air taxi”; “sustainability”.
- “Last mile”; “parcel delivery”; “urban air mobility”; “UAV”; “drone”; “sustainability”.
- “Last mile”; “passenger travel”; “urban air mobility”; “eVTOL”; “sustainability”.
- “Last mile”; “passenger travel”; “urban air mobility”; “air taxi”; “sustainability”.
- “Last mile”; “passenger travel”; “urban air mobility”; “UAV”; “drone”; “sustainability”.
Furthermore, the search was restricted to English journals in business and management, engineering, decision sciences, and social sciences. The initial search in the scientific databases resulted in 191 articles (including review works, preprints, conferences, and journal publications).
2.4. Criteria for Inclusion and Exclusion
The inclusion criteria to select the papers were electrified wingless UAM aircraft (e.g., eVTOLs, drones), papers with a focus on parcel delivery and passenger travel in last-mile transportation, peer-reviewed journal and conference papers published between 2010 and 2024, and papers with prescriptive analytic (optimization, mathematical programming, heuristics). Also, papers were excluded based on the following criteria: papers with focus on nonurban (e.g., regional, rural) air mobility, papers studying first- and middle-mile transportation, preprints or working papers, papers with a non-OR perspective (like policy, development, assessment, conceptual, control theory, pure case study, feasibility study), and papers with descriptive, predictive, or diagnostic analytic (data mining, machine learning, simulation, forecasting, and conceptual methods). After this step, 123 out of 191 papers were selected for deeper analysis and review: 23 papers on eVTOL optimization and 100 on UAV-based last-mile transportation problems.
2.5. Classification Scheme
This review classifies the collected papers based on the eVTOL and UAV technologies. Next, in each technology, the problems are described alongside the proposed solution techniques. Figure 3 shows an overview of the classification scheme. We divided the eVTOL’s application in last-mile transportation into eight primary problems: arrival sequencing and scheduling, charging sequencing and scheduling, passenger assignment, joint routing and charging scheduling, flight routing, infrastructure planning, safety and security, and trade-off between efficiency and sustainability. Also, the UAV-based problems are categorized into five classes: routing and scheduling of pure UAVs, routing and scheduling of truck-and-UAV, charging infrastructure planning, safety and security, and the trade-off between efficiency and sustainability. The papers related to each problem are discussed below.
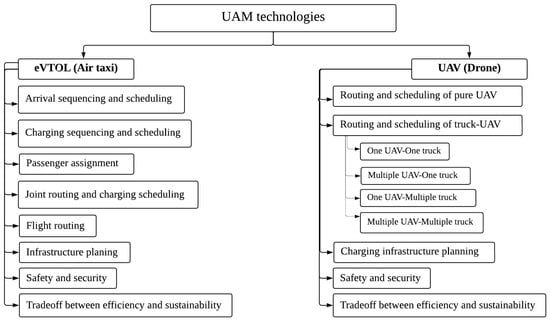
Figure 3.
Overview of the classification scheme for UAM optimization problems.
3. eVTOLs
3.1. Technological Background
eVTOL technology represents a significant advancement in aviation, combining electric propulsion with vertical take-off and landing capabilities [22]. This innovation is grounded in developments from the past decade, where improvements in battery energy density, electric motor efficiency, and lightweight composite materials have converged [11]. Companies like Joby Aviation, Lilium, and Volocopter are at the forefront of designing aircraft that operate quietly and efficiently within urban environments. Unlike traditional helicopters, eVTOLs leverage distributed electric propulsion systems, which provide redundancy and enhance safety [23]. These aircraft are designed to meet stringent UAM requirements, including minimal noise pollution and zero emissions, making them suitable for densely populated areas [24].
Implementing eVTOL technology in urban areas necessitates addressing several essential requirements and challenges. A primary requirement is the development of vertiports—specialized infrastructure for take-off, landing, and charging—which must be strategically located to optimize accessibility and integration with existing transportation networks [25]. Additionally, robust air traffic management systems are needed to ensure safe and efficient operation within the crowded urban airspace. Regulatory frameworks must be established and harmonized globally to address issues such as airspace permissions, noise levels, and safety standards [26]. Another significant challenge is public acceptance, which hinges on demonstrating the safety, reliability, and noise-reduction capabilities of eVTOLs [27]. Furthermore, technological hurdles, such as enhancing battery performance to extend flight range and duration and achieving cost-effective mass production, remain critical. Addressing these challenges requires a collaborative effort between aviation authorities, city planners, and technology developers to realize the full potential of eVTOLs in urban environments [28].
eVTOL technology holds substantial promise for revolutionizing parcel delivery services. As e-commerce grows, the demand for faster and more efficient delivery systems has surged [29]. eVTOLs can significantly reduce delivery times by bypassing congested road networks and directly accessing urban rooftops or designated vertiports [24]. This capability accelerates the logistics process and reduces the environmental impact by minimizing the reliance on fossil fuel-powered delivery trucks. Companies like Amazon and UPS are already exploring eVTOLs for LMD solutions to enhance operational efficiency and customer satisfaction [30]. Integrating eVTOLs into parcel delivery networks marks a pivotal step towards a more sustainable and responsive logistics infrastructure [31]. The optimization problems related to the applications of the eVTOL in last-mile transportation are explained below.
3.2. Arrival Sequencing and Scheduling Problem
To optimize the efficiency of eVTOLs, researchers have focused on energy-efficient trajectory planning during the arrival phase, which is critical due to high air traffic density and limited battery capacity. However, little research has been conducted on determining the optimal “required time of arrival (RTA)” for eVTOL aircraft. Ref. [32] discussed the “arrival sequencing and scheduling problem of eVTOL aircraft (ASSP-eVTOL)” in the context of UAM. The goal was to optimize the sequence and timing of mixed wingless and winged eVTOL landings at a single landing pad, aiming to minimize the time it takes for all eVTOLs to complete their landings, thus maximizing arrival throughput. In subsequent work, ref. [33] introduced a novel approach to calculate optimal RTAs, considering battery state and vertiport capacity, ensuring safe separation and minimal delays.
Furthermore, there is a pressing need for innovative operational management models to support service providers’ strategic and tactical decision making. This includes scheduling, dispatching, and fleet planning to optimize their desired objectives. Ref. [34] examined the three distinct service settings—on-demand service, scheduled service, and a combination of both (hybrid operations)— through comparative analysis, considering metrics such as the fraction of total demand met and profit. Ref. [35] extended their previous work [33] by exploring the capacity of a dual-landing-pad vertiport and proposing a new design for the vertiport terminal area airspace, along with an innovative rolling-horizon scheduling algorithm that includes route selection to determine the optimal arrival times for eVTOLs in a tactical manner.
Furthermore, ref. [36] addressed two critical challenges in the context of UAM. Firstly, it explored the complex issue of managing multi-vertiports in economically developed regions, where the conflict between UAM growth and limited operational resources is pronounced. Secondly, it focused on the unique operational characteristics and energy constraints of eVTOL aircraft, which can experience exhaustion risks and safety challenges during extended flights in terminal areas. The analysis revealed that flight density in the terminal area significantly impacts an “adaptive control system (ACS)” performance more than flight volume, with variations in the “terminal area of a multi-vertiport system (MVS-TA)” operating efficiency within a range of 10.3% when flight density remains below 120 flights/h. In addition, ref. [37] introduced two optimization models designed to schedule the arrival and departure of aircraft at various components of vertiports, including standard ground taxi routes (taxiways), gates, and “touchdown and lift-off (TLOF)” pads.
Solution approaches: To solve the ASSP-eVTOL, ref. [32] proposed a heuristic approach called “insertion and local search (ILS)” combined with either a mixed-integer linear programming (MILP) or a time-advance (TA) algorithm. They also conducted a sensitivity analysis to assess how the number of eVTOLs landing affects the computational times of both algorithms. Also, ref. [33] introduced a novel approach using a MILP to compute optimal RTAs while considering factors like battery state and vertiport capacity. They also proposed a framework for designing the airspace around vertiport terminals, incorporating existing trajectory optimization tools. Considering the unique operational constraints associated with UAM services, ref. [34] presented mathematical models for commercial transport service providers. These models helped determine the most suitable scheduling approach, fleet dispatching strategies, and operational schedules based on simulated market demand, ultimately maximizing profit. Also, ref. [35] acquired a collection of possible RTAs for incoming eVTOLs and introduced a rolling-horizon optimization model. This model arranged and coordinated a group of eVTOLs as they approached a vertiport to minimize the overall deviation in their estimated time of arrival (ETA).
Moreover, ref. [36] investigated an ACS for the MVS-TA. The ACS encompassed the design of the operational environment and an integrated scheduling model. Meanwhile, the integrated scheduling model, which considered power constraints and dynamic priorities, included path planning and distributed sequencing to address the cooperative scheduling of approach–departure flights. Also, two optimization models were presented in recent work by [37]. These models were specifically developed to plan and manage the arrival and departure of aircraft at different components within vertiports. The advanced air mobility considerations in the mathematical models included separation rules and blocking constraints. The primary goal of the initial model was to optimize the vertiport throughput, while the secondary model focused on reducing deviations from anticipated take-off and landing times. Two heuristic algorithms were introduced to address these scheduling challenges, which utilized scheduling rules to allocate and arrange aircraft at vertiport components.
3.3. Charging Sequencing and Scheduling Problem
Ref. [38] addressed a significant challenge in the implementation of large-scale UAM services, which was the limited flight range of eVTOLs by modeling it as an “eVTOL charging sequencing and scheduling problem (CSSP-eVTOL)”. The continuous and on-demand operation of eVTOLs required frequent recharging within tight time frames. This dual challenge necessitated advanced battery energy storage capabilities and fast charging infrastructure. Also, ref. [38] developed a MILP that models the eVTOL charging scheduling process. The primary objective was to minimize the total waiting time experienced by passengers. The proposed model can efficiently solve the scheduling problem, enabling real-time UAM service operations.
3.4. Passenger Assignment to Aerial Vehicles
The study by [39] focused on arranging the assignment of aerial vehicles (AVs) to customers to maximize the number of served customers while minimizing the energy consumption of AVs. The approach involved directing AVs to fly at the lowest feasible altitude. Furthermore, the study’s authors proposed an integer linear program (ILP) formulation that can be solved optimally in an offline setting for scheduling the allocation of AVs to customers. They also introduced an efficient near-optimal offline algorithm capable of solving the problem incrementally, addressing one AV at a time.
3.5. Joint Routing and Charging Scheduling Problem
Autonomous electric aerial vehicles (EAVs) are poised to change urban infrastructure and daily commuting patterns significantly. Presently, EAVs, which include delivery drones and eVTOL air taxis, face limitations in terms of battery endurance and vertiport capacity, making them unsuitable for long-range commutes. Ref. [40] introduced an “eVTOL joint routing and charging scheduling problem (RCSP-eVTOL)”, optimizing both routing and charging tasks for the EAV system. This approach considered the unique characteristics of on-demand EAVs and effectively allocated the system’s resources. The optimization problem was framed by incorporating charging considerations into the traditional “vehicle routing problem with time windows (VRP-TW)”. Similarly, ref. [41] delved into the “eVTOL aircraft recovery problem (eVTOL-ARP)”, which exists in scenarios like airport shuttles and intercity flights within UAM applications. What sets this problem apart is its flexibility regarding charging tasks, including the option to defer or cancel them.
Solution approaches: Ref. [40] introduced a joint scheduling methodology to optimize routing and charging tasks within the EAV system. To enhance solvability, the nonlinear problem was further transformed into a MILP. Also, ref. [41] devised an ILP model and proposed a branch-and-price algorithm to solve the eVTOL-ARP precisely. They also proposed a “tailored label-setting algorithm” that capitalized on the problem’s structural characteristics, particularly for the parallel pricing subproblems.
3.6. Flight Routing of eVTOLs
In a recent study, ref. [42] focused on optimizing flight routes within urban areas, considering multiple conflicting goals while navigating around restricted three-dimensional spaces. The study considered three main objectives: minimizing flight time, reducing energy consumption, and limiting additional noise. The research emphasized that minimizing added noise requires more search effort than the other objectives. Additionally, the study investigated urban flight route optimization using the nondominated sorting genetic algorithm II (NSGA-II), a technique for multiobjective optimization, to fine-tune three-dimensional flight paths. The study introduced a unique element in the optimization process that integrated geographical representations. Furthermore, it featured a seeding procedure to initialize flight routes and repair methods to address any invalid routes during optimization.
3.7. Infrastructure Planning
For readers interested in infrastructure planning for eVTOLs, ref. [12] provided a systematic review focused explicitly on vertiport characteristics. It seeks to compare various approaches and findings in the literature regarding vertiport location and capacity. The goal was to identify the key features influencing vertiport decisions and pinpoint research gaps that can inspire future studies.
Moreover, ref. [25] addressed the challenge of determining where to strategically place vertiports, which are essential facilities for eVTOL operations. To do this, they utilized census data products such as “LEHD Origin-Destination Employment Statistics (LODES) and the American Community Survey (AmCS)” to estimate daily commuting patterns, including the origins, destinations, and times of commuter journeys. Additionally, they delved into assessing the potential range requirements of eVTOL aircraft needed to facilitate daily commuting. Furthermore, ref. [43] explored the application of eVTOL aircraft originally designed for passenger operations in the context of transporting cargo. Specifically, they focused on a case study involving the delivery of small packages from a warehouse in Tracy, California, to vertiport hubs in the San Francisco Bay Area. This package transit involved two segments: an eVTOL flight from the warehouse to a vertiport near the recipient and a subsequent LMD from the vertiport to the end consumer using vehicles like cars, small unmanned aerial systems (UASs), or other modes of transportation. Moreover, ref. [44] envisioned a mature state of urban air taxi (UAT) operations where UAT operators offered “door-to-door, multi-modal, on-demand, and per-seat services." They introduced flexible meeting points, allowing passengers to choose UAT pads for boarding and deboarding. This flexibility enabled passengers to share aircraft, optimizing resource utilization.
Furthermore, ref. [45] discussed the difficulty of locating the best sites for vertiports while considering a range of factors, such as the limitations of UAM vehicles, desired operational approaches, and the potential for passenger journeys involving more than two vertiports. They framed the challenge of selecting vertiport locations as a modified single-allocation hub median location problem, integrating elements of subgraph isomorphism to establish structured networks that support public transit operations. Additionally, ref. [46] tackled optimizing different aspects of UAM systems, including the number, locations, and capacities of vertiports, while considering the intricate interconnections between strategic vertiport deployment, tactical operations, and passenger demand. These studies are significant as they blend manageable optimization techniques with nonconvex demand functions, rendering them valuable for academic exploration and practical application in UAM.
In addition, the research by [47] concentrated on identifying the best design for a vertiport to maximize its capacity and the net profit for the vertiport operator. They addressed the “vertiport design problem (VDP)”, which involves planning the arrangement and placement of different vertiport facilities within a potential site while complying with safety regulations for UAM operations. Also, ref. [48] centers on the planning of skyport infrastructure. Specifically, they focused on designing the locations of skyports to facilitate air taxis’ access to airports. They present the skyport location as a “modified single-allocation p-hub median location problem”, which considers the choice-constrained behavior of users selecting their transportation mode. Their approach revolves around two primary objectives: maximizing air taxi ridership and revenue. In recent work, ref. [49] adopted a holistic approach to UAM network optimization, recognizing the interrelated nature of these decisions. It employed a three-stage algorithm, including vertiport placement with vehicle sizing, infrastructure modeling, and feedback mechanism. It emphasized the importance of reducing waiting and loiter times to lower operational costs, with all optimal configurations resulting in waiting times below 5% of the total flight time. The study by [50] emphasized identifying infrastructure sites for air taxi operations in New York City (NYC) by applying prescriptive analytics. The primary goal was to strategically identify the most suitable locations for air taxi facilities, known as vertiports, to meet the anticipated air taxi demand in the city effectively.
Solution approaches: Ref. [25] optimized the vertiport placement using an ILP approach. The optimization objective was to maximize the cumulative potential time savings for the population when compared to traditional driving commutes. Ref. [43] studied the vertiport infrastructure planning by formulating and solving an optimization problem to select cargo vertiport locations. The objective was to maximize the number of package demands served while adhering to constraints on the number of vertiports that can be established. Also, ref. [44] formulated UAT fleet operation as a “capacitated location-allocation-routing problem with time windows”, presenting a MILP formulation, addressing request acceptance or rejection, allocating requests to flights, and routing and scheduling of aircraft.
In addition, ref. [45] devised five heuristic algorithms to identify potential solutions for vertiport location problems within reasonable computation times. These algorithms underwent testing and comparison with an optimal solution in three different regions of the United States. The most effective heuristic methods were found to be, on average, within 10% of the optimal solution. Furthermore, ref. [46] introduced an exact algorithm that approximated nonconvex functions using piece-wise constant segments for capacitated vertiport location problems. The algorithm operated by iteratively switching between a conservative model, ensuring a feasible solution, and a relaxed model, providing a solution guarantee. An adaptive discretization scheme was also introduced, enabling the algorithm to converge towards a global optimum, primarily due to the relaxed model. Also, ref. [47] formulated the VDP as an ILP model. The VDP likely included variables, constraints, and an objective function representing various aspects of vertiport design and operation, such as positioning of facilities, safety requirements, and capacity considerations. In addition to capacity, the net profit generated by the vertiport operator was another key objective. This would involve factors like operating costs, revenue from passenger fees, and possibly other financial considerations. The optimization model developed by [48] features two objectives. By including the mode choice as an objective coefficient, it becomes possible to formulate the skyport location problem as an ILP model and then utilize a Gurobi optimizer to solve it.
In addition, ref. [49] adopted a comprehensive approach to UAM network optimization by employing a three-stage algorithm. In the first stage, a linear vertiport placement model was developed, considering constraints related to vehicle sizing. This stage determined the optimal configuration of vertiports, considering the performance characteristics of eVTOL aircraft. The resulting vertiport configuration and vehicle sizing constraints were then integrated into an infrastructure model.
3.8. Safety and Security
In contrast to conventional transportation systems like cars or trains, which are constrained by terrestrial traffic conditions, flying vehicles such as UASs, drones, and air taxis cannot compete for space in transit. They possess spatial and temporal freedom, cover shorter distances, and entail less user stress. However, safety and security are primary concerns surrounding the widespread adoption of air taxis. Even a minor malfunction can result in significant losses, including damage to high-value assets, loss of the aircraft, and potential harm to human lives, including fatal accidents. The primary components of traffic regulation for eVTOLs include the following: (i) Air traffic management (ATM) systems: these systems will be crucial in monitoring and managing airspace usage, ensuring safe distances between flying vehicles, and preventing collisions. (ii) ACS and mathematical programming models: they manage the efficiency and safety of operations, especially in terminal areas with high traffic. (iii) Dynamic prioritization: UAM traffic management must account for dynamic prioritization of flights based on factors such as urgency, flight path, and weather conditions. (iv) Regulatory framework: government agencies, such as the Federal Aviation Administration (FAA) in the U.S., will establish regulations and guidelines for UAM operations, including certification standards, operational procedures, and safety protocols.
Despite considerable efforts, the literature on air taxi safety and security remains relatively scarce and specialized. Ref. [36] researched an ACS designed for the MVS-TA. The primary objective was to improve the efficiency and safety of operations within the terminal area, especially under high flight traffic conditions. This model accounted for power constraints and dynamic priorities. It focused on determining the most efficient path for approach and departure flights, considering factors like distance, altitude, and potential obstacles (safety measures).
Additionally, in a study conducted by [47], they devised an ILP model for the VDP. This model aimed to capture different facets of vertiport design and functioning. These aspects covered the placement of facilities, safety prerequisites, and the evaluation of capacity-related factors. Moreover, the primary objective of [51] was to conduct a comprehensive systematic literature review, spanning 2015 to January 2022, to compile the most noteworthy recent advancements in techniques, architectures, and global research endeavors related to UASs, drones, and air taxis. Additionally, the study identifies existing research gaps that could serve as valuable directions for future investigations. To the authors’ knowledge, no other research had undertaken such a focused review specifically centered on air taxi safety.
Moreover, first-aid provision in a UAM vehicle accident requires coordinated efforts between emergency services and air traffic control. Key measures may include the following: (i) Rapid response teams: specialized emergency response teams equipped to handle air incidents are deployed to accident sites quickly. (ii) Communication systems: robust communication systems ensure that emergency services are alerted immediately and provided with accurate information about the accident’s location and nature. (iii) First-aid facilities at vertiports: establishing first-aid facilities at vertiports and major UAM hubs provides immediate medical assistance to injured passengers or crew members.
3.9. Trade-off between Efficiency and Sustainability
Ref. [16] was inspired by a real-world case and was dedicated to creating a simulation algorithm that can aid same-day package delivery companies achieve instant customer service. The proposed recommender system was designed to identify the optimal solution based on three critical criteria: “cost-effectiveness, delivery time, and sustainability”. It considered variables such as travel time and cost parameters, adapting to changing conditions. Also, ref. [52] primarily focused on the future of urban air taxi services and introduced innovative methods and algorithms designed to facilitate the efficient operation of air taxis on a large scale. First, they adopted a passenger-centric perspective, which involved introducing different traveling classes and exchanging information between various transportation modes to enhance the quality of service. This approach aimed to facilitate seamless multimodal journeys, ultimately leading to higher passenger satisfaction. Second, they offered a flight routing and recharging solution that minimizes immediate operational costs and extends the long-term battery life by reducing energy-intensive recharging processes.
In recent work, ref. [53] introduced an innovative approach for conducting a cost–benefit analysis related to the bidirectional functionality of eVTOL aircraft charging. eVTOL aircraft represent an emerging segment of the aviation market, aiming to transform urban and intercity mobility by providing a passenger air transportation system characterized by safety, efficiency, and on-demand accessibility. The study employed an optimization technique based on a genetic algorithm (GA) to determine the number of eVTOL vehicles required to make vehicle-to-grid services financially viable for different electrical systems under consideration.
To summarize the models and solution methods developed for the applications of eVTOLs in last-mile transportation optimization problems, Figure 4 is presented. As observed, most of the optimization problems are modeled by MILP (nine papers) and ILP (six papers) and solved by (meta)heuristics (six papers). There is limited work on designing the exact solution approaches for optimizing last-mile transportation problems under eVTOL applications. Only a branch-and-price algorithm [41] and an adaptive discretization-based exact approach [46] were proposed, showing the need to design problem-tailored exact solution approaches for these problems.

Figure 4.
Overview of the models and solution methods developed for the application of eVTOLs in last-mile transportation with number of papers inside the parentheses.
4. UAVs
Using parcel delivery with drones, or UAVs, for sustainable LMD presents several challenges from the OR perspective. OR focuses on optimizing processes and decision making to achieve efficiency and effectiveness in the UAV delivery system.
4.1. Routing and Scheduling of Pure UAV Delivery System
Developing efficient routing and scheduling algorithms for pure UAV delivery is a complex problem. It involves determining the best routes for multiple UAVs to deliver packages while considering package size, weight, delivery locations, traffic, weather conditions, and airspace regulations. The classic VRPs were unsuitable for efficiently planning UAV deliveries due to two main issues. Firstly, the VRPs did not allow multiple trips to the depot, leading to solutions involving more UAVs than necessary. Secondly, they failed to consider the impact of battery and payload weight on energy consumption, resulting in costly or impractical routes. To address these challenges, ref. [54] proposed two “multitrip VRPs (MTVRP)” designed specifically for UAV delivery, called the “drone delivery problem (DPP)”, minimizing costs while adhering to a maximum delivery time, reducing the overall delivery time, and staying within a specified budget constraint. They formulated a MILP model based on the battery and payload weight decision variables. Also, they assumed that the UAV was recharged at the depot. The cost function was then applied in a simulated annealing (SA) heuristic to find near-optimal solutions for large (practical) cases. Moreover, ref. [55] focused on a distance-constrained mobile hierarchical “facility location problem (FLP)” to determine the optimal number and positions of UAV launching and recharging stations. Due to the limited flight endurance of UAVs, they might need to stop at one or more recharging stations before reaching their assigned destinations. To tackle this issue, the study suggested using heuristic algorithms.
While DDP has been the research subject, most existing models focus on single-objective optimization. However, practical drone delivery involves multiple objectives that shippers must fulfill. Ref. [56] designed a parcel delivery system using drones, covering strategic and operational planning aspects for a given region. The payload of the drones affected the “battery consumption rate (BCR)”, which could lead to delivery disruptions if not accurately estimated during planning or result in unnecessary expenses if overestimated. They proposed a reliable parcel delivery schedule that incorporated the BCR as a function of payload in the operational planning optimization. The strategic planning was modeled using a minimum set covering approach, while operational planning was formulated as a MILP. An apparent drawback of these works is their disregard for weather effects. For instance, flying with the wind could lead to lower energy consumption. Cold temperatures might negatively influence battery performance until they reach optimal operating conditions. Also, a routing and scheduling model for UAVs using network flow techniques and mathematical programming methods was presented by [57]. This model aimed to ensure that all advance delivery requests were fulfilled while respecting operational constraints, primarily minimizing overall operational costs. To address potentially intricate real-world scenarios, they proposed a relax-and-fix heuristic. They performed numerical tests to evaluate the practical applicability of the model combined with this heuristic algorithm.
An efficiently planned UAV delivery system reduces the impact of unpredictable weather conditions. When faced with uncertain wind factors, such as varying speeds and directions, the transit times of the UAVs to their destinations can be affected, resulting in delayed deliveries or potential service cancellations [58]. Developing strategies to adapt UAV routes and schedules during adverse weather is challenging for OR. According to the literature, ref. [59] investigated how weather data, specifically wind observations, can enhance scheduling decisions in UAV delivery systems. The system involved a fleet of homogeneous drones dispatched to serve geographically dispersed customers. Each drone can undertake multiple round trips, which consist of flights from the central depot to the customer’s location and then back to the depot for necessary preparations, such as loading a new payload or replacing a depleted battery. They introduced a two-period drone scheduling model designed to optimize the delivery schedule robustly. This approach allowed the system to adapt and make informed decisions based on the latest weather data, minimizing the impact of wind uncertainty on the overall delivery process. In addition, ref. [60] addressed the simultaneous location and routing problem for UAVs used in multiple missions under different weather conditions, focusing on air surveillance requirements for Turkish government public agencies. The problem was formulated as a two-stage stochastic ILP with recourse. An optimization-based heuristic with bounds based on the decomposition approach was also introduced.
UAV delivery systems must adhere to various regulations and airspace restrictions imposed by aviation authorities. Ref. [61] took an interdisciplinary perspective to address anticipated UAV-LMD operations comprehensively. They began by surveying the most significant societal and regulatory barriers currently facing UAV-LMD and those expected in the future. It provided insights into potential regulatory approaches that could limit UAV operations. They proposed and compared three competing routing models, highlighting the advantages of a heuristic-based routing approach.
4.2. Routing and Scheduling of Truck-UAV Delivery System
Implementing UAV delivery systems with existing trucks or vehicles requires seamless integration. In specific applications and resource scenarios, utilizing UAVs for every node visit may not be practical or efficient, especially when the primary goal is to minimize time. Such limitations can include deliveries that exceed the UAV’s capacity, restricted no-fly zones, the need for a mandatory signature upon parcel receipt, or unsafe landing territories. A mixed model that combines trucks and UAV routes may be more suitable to address these challenges and optimize the delivery process. While UAV deliveries can be faster and offer lower transportation costs, they are restricted by their battery life, operating range, and the size of parcels they can carry. Ground vehicles (GVs), on the other hand, can compensate for the weaknesses of UAVs by handling larger loads, overcoming longer distances, and adhering to traditional road networks.
4.3. One UAV–One Truck
Ref. [62] first introduced a unique variant of the classical “traveling salesman problem (TSP)”, which is considered a collaboration between a drone and a conventional delivery truck to distribute parcels. They called it the “flying sidekick TSP (FSTSP)”, which found an optimal route for a truck visiting a subset of customers and a route for a UAV, which launched from the truck and delivered products to the rest of the customers. Also, the UAV was required to depart from the truck to visit a customer and then return to the truck, ensuring that its flights did not exceed the battery capacity. They proposed MILP formulations for the problem and offered practical heuristic approaches to solve it efficiently. Several OR-based solution methods have been proposed for FSTSP and its variants as given in Table 2.

Table 2.
Optimization methodology proposed for FSTSP and its variants in the literature.
“TSP with drones (TSP-D)”, first introduced by [75], was an extension of FSTSP. However, UAV trips that start and end directly at the depot in the TSP-D are not allowed. This means that the UAV cannot make direct round trips from the depot; they must visit other locations before returning to the depot. Also, TSP-D is like FSTSP except for the objective function. Instead of focusing on the latest time for the vehicles’ return to the depot in the FSTSP, the TSP-D aims to minimize the travel cost incurred during deliveries. This variant emphasizes cost efficiency in utilizing truck and drone resources for timely and economical deliveries. Several models and methodologies have been proposed to solve TSP-D: local search and dynamic programming (DP) [75,76], branch-and-bound [77], branch-and-price [78], and greedy randomized adaptive search procedure (GRASP) [79]. Previous studies assumed battery swapping at the end of each drone flight, but [80] investigated a flexible recharging policy considering the remaining battery level. A new MILP formulation was developed, and a heuristic approach was proposed.
4.3.1. Multiple UAV–One Truck
Ref. [81] introduced a truck–drone system to address the flight range limitations by incorporating a drone station. This station housed drones and charging devices and was located away from the distribution center. To optimize routing, they developed a MILP model called the “TSP with a drone station (TSP-DS)”. The researchers showed that the model could be divided into separate traveling salesman and machine scheduling problems, and they suggested two solution methods for each. In their study, ref. [62] investigated the “parallel drone scheduling TSP (PDSTSP)”, which deals with a different issue than the previously discussed one. This problem does not require coordination between trucks and drones. Instead, a single truck delivers the parcels to customers far from the distribution center (DC). At the same time, drones are responsible for serving customers within their flight range around the DC. The truck and drones operate independently, with the truck handling distant deliveries and the drones concentrating on deliveries within their operational range around the DC.
Moreover, if in FSTSP multiple UAVs can launch from a truck and deliver products to the customers, it becomes “multiple-FSTSP (m-FSTSP)”. Several solution approaches have been proposed for m-FSTSP and its variants: a MILP model for m-FSTSP with heterogeneous UAVs [82], a three-phase algorithm for m-FSTSP with variable speed of UAV [83], and a four-index formulation [84]. The m-FSTSP makes two key assumptions. Firstly, it assumes that a UAV can transport just one package at a time. Secondly, it restricts the truck from deploying or retrieving only one UAV at any given moment. However, with recent technological progress, the relevance of the first assumption has diminished, as newer UAV models capable of carrying multiple consumer packages at once have been suggested and created.
In addition, if in TSP-D each truck could carry multiple UAVs serving the part of the customers, then it is called TSP-mD. Several researchers have proposed solution methods for TSP-mD, such as exact approaches [85] and TSP-mD with clusters [86]. In their research, ref. [87] investigated the optimization of the time required for a truck and multiple UAVs to collectively serve all customers in the “multivisit TSP with multiple drones (mTSP-mD)”. They highlighted the influence of flight time, drone weight, and total package weight on UAV energy consumption, which decreased as deliveries were made. The researchers proposed a MILP model and introduced a multistart TS algorithm with a customized neighborhood structure and a two-level solution evaluation method, encompassing a “UAV-level segment-based evaluation” and a “solution-level evaluation based on the critical path method” to address this issue. The coordination of a truck and multiple heterogeneous UAVs for LMD was addressed in a recent study by [88]. Unlike previous research that confined drone “launch and recovery operations (LARO)” to customer locations, they proposed a new approach that allows the truck to make stops at noncustomer locations, known as flexible sites, for drone LARO. To minimize the delivery completion time (makespan), they formulated a MILP model to optimize these decisions jointly. Additionally, they developed an optimization-enabled two-phase search algorithm that combines SA and variable neighborhood search (VNS).
4.3.2. One UAV–Multiple Truck
Ref. [89] formulated a mathematical model like the FSTSP for the capacitated multiple-truck scenario with time-constrained routes and a cost-minimization objective function. This problem was called “VRP with a single drone (VRPD)”. They also proposed an adaptive large neighborhood search (ALNS) metaheuristic to find near-optimal solutions. Also, ref. [90] studied the “VRPD with time windows (VRPD-TW)”. The drones could take off from their respective trucks at a given node, independently serving one or more customers within specified time windows and returning to the truck at another node along the truck’s route. They developed an enhanced branch-and-price-and-cut algorithm. Moreover, ref. [91] focused on scheduling the delivery to customers using drones, considering predetermined truck routes. They provided an analysis of computational complexity, introduced efficient MILP techniques, and compared all cases concerning their potential to reduce the delivery effort to the LMD. Furthermore, ref. [92] focused on optimizing an LMD system that involved multiple transportation modes. The problem revolved around delivering parcels to various customer points using a combination of road vehicles (trucks and vans) and a drone. The drone complemented the vans by serving customers who the vans could not reach. A discrete optimization model and a two-phase heuristic algorithm were presented to address this problem.
4.3.3. Multiple UAV–Multiple Truck
Ref. [93] introduced a new variant of TSP-D, where multiple trucks and UAVs were utilized for making deliveries. This problem was termed as “multiple TSP-D (m-TSP-D)”. The model was derived from the multiple TSP (m-TSP) [94] with the mathematical formulation adapted from the FSTSP model. They developed a new adaptive insertion heuristic (ADI) with three m-TSP heuristics. Also, ref. [95] introduced a new problem called the “multiple TSP with drone stations (mTSP-DS)”, which extended the classical m-TSP. The mTSP-DS involved a depot, a fleet of trucks, and several packet stations equipped with autonomous vehicles like drones or robots. The primary objective was to efficiently serve all customers using trucks or drones/robots while minimizing the makespan, i.e., the total time required for completion. The researchers expressed it as a MILP model. They suggested three methods: two versions of a decomposition-based metaheuristic and one that relies on populating a solution pool through multiple restarts of an ILS metaheuristic.
The VRP-D is an extension of the FSTSP that focuses on efficiently deploying UAVs and using multiple trucks for routing. In the VRP-D, a fleet of identical trucks is used, each equipped with different UAVs that can travel faster than the trucks. The trucks can move and deliver packages but must remain stationary when launching or retrieving UAVs at delivery locations or the central depot. VRP-D was introduced first time by [96]. They analyzed and calculated a range of worst-case scenarios. These worst-case results were contingent on two key factors: the number of UAVs allocated to each truck and the speed of these UAVs relative to the truck’s speed. Also, ref. [97] presented a review and expansion of several worst-case results. Several works have proposed OR-based models and solution methods for VRP-D and its variants as given in Table 3.

Table 3.
The OR methodologies proposed for VRP-D and its variants in the literature.
The issue known as the “truck-based drone delivery routing problem (TD-DRP)” concerned the coordination of several trucks and drones to meet the needs of a group of customers. Each truck was equipped with a specific number of drones, and the goal was to maximize delivery efficiency by optimizing routes and assignments. Research conducted by [119] delved into this problem and devised a MILP method capable of solving scenarios involving two trucks and ten customers. Several models and solution approaches have been proposed in the literature for TD-DRP and its variants: GRASP and VNS [120], GRASP [121], multiobjective ant colony optimization (ACO) and NSGA II [122], and with drone resupply [123].
Moreover, ref. [124] defined the “truck–drone routing problem with time windows (TDRP-TW)”. This problem encompassed several essential characteristics, including time windows for deliveries, synchronization of truck and drone routes, direct delivery from drones, the involvement of multiple trucks, and each truck carrying various drones. They proposed an efficient branch-and-price-and-cut and an ALNS to solve the problem. The case where multiple UAVs had varying characteristics, including speed and battery capacity, was examined by [125]. They aimed to minimize truck travel and waiting times for drones returning after deliveries. Their proposed model was termed “heterogeneous drone–truck routing problem (H-DTRP)”, and they provided a MILP formulation for the problem. They created an exact algorithm using the logic-based Benders decomposition approach, surpassing existing solvers.
In addition, the effective coordination of trucks and drones poses a significant challenge, especially when dealing with unpredictable traffic conditions and travel duration. In addressing this issue, ref. [126] introduced a resolution for the “truck–drone hybrid routing problem with time-dependent road travel time” (TDHRP-TDRTT), which was formulated as a cost-minimization problem with logistics demand-and-supply constraints. They devised an ILS algorithm incorporating “intrapair” and “interpair” customer exchanges to solve TDHRP-TDRTT efficiently. Additionally, ref. [127] examined the concept of same-day delivery utilizing a combination of vehicles and drones, referred to as “same-day delivery problems with vehicles and drones (SDDPVD)”. To enhance fleet utilization, they suggested a deep Q-learning approach, which learned the significance of assigning a new customer to either drones or vehicles and the option of not providing service at all.
The PDSTSP was further developed by [128] by adding two separate drone tasks: delivery and pickup. Following delivery, the drone could either return to the depot for another delivery or proceed directly to a customer for a pickup. The study also focused on optimizing the scheduling of multiple depots, each with its fleets of trucks and drones, to enhance operational efficiency. They formulated this complex scenario as an “unrelated parallel machine scheduling problem with sequence-dependent setups, precedence constraints, and reentrant flows”. To address these challenges, they proposed a constraint programming (CP) approach and validated it using various problem scenarios.
In addition, the study by [129] concentrated on addressing a “two-echelon cooperated routing problem involving a ground vehicle (GV) and an accompanying unmanned aerial vehicle (UAV) (2E-GU-RP)”. The GV operated on the road network, while the UAV was deployed to reach destinations situated beyond the road network, which were inaccessible to the GV. Unlike the traditional two-echelon routing problem, the UAV in this context was required to take off and land on the GV for battery swapping or recharging while traveling on the roads. The researchers developed a novel binary integer linear programming (ILP) model that accounted for spatial and temporal cooperation constraints between the routes of the GV and UAV. Additionally, they proposed two heuristic methods to solve the formulated model.
Additionally, a mathematical formulation and an efficient solution approach for the “hybrid vehicle–drone routing problem (HVDRP)” in the context of pick-up and delivery services was presented by [130]. The problem was defined as a MILP considering the interactions between vehicles and drone routing when dispatching and collecting drones. A new solution approach was developed by extending the traditional “Clarke and Wright algorithm”. In their work, ref. [131] presented an innovative routing model to facilitate coordinated truck–drone operations. This model enables multiple drones to take off from a truck, provide services to one or more customers, and then return to the same truck for battery replacement and package retrieval. They named this model “two-echelon VRP-D (2EVRPD)”. The researchers developed a MILP model and created two efficient heuristic algorithms called “drone truck route construction (DTRC)” and LNS. The 2EVRPD model expands on the FSTSP by allowing multiple drones and trucks to handle deliveries while considering the capacities of both types of vehicles. In a study by [132], a new version of the two-echelon routing problem was investigated, named the “two-echelon routing problem for the truck and drone (2E-RPTD)”. The truck served as a delivery vehicle and a movable base for the drone. The researchers presented a two-step model-based strategy to enhance the truck’s main route and the drone’s additional flight paths.
Furthermore, a study by [133] explored innovative variations of the “two-echelon VRP (2EVRP)” introduced by [134]. Termed “two-echelon VRP-D (2ER-TD)”, the problem involved a truck operating in the first echelon for parcel transportation, with a fleet of drones traveling to intermediate depots. In the second echelon, the drones delivered parcels from the intermediate depots to customers. The researchers developed MILP models and introduced a GRASP-based metaheuristic. There are two main differences between the 2ER-TD and the traditional 2EVRP. First, in the 2ER-TD, drone transportation is managed in the second echelon, unlike the 2EVRP, where trucks handle all transportation duties. Second, the objective function in the 2ER-TD is focused on minimizing the return time for the truck and drones to the depot. As a result, all the drones must return to the intermediate depots before the truck can proceed. Unlike in the 2ER-TD, in the 2EVRP, the trucks in the first echelon can continue without waiting for the trucks in the second echelon to return, as the main goal is to minimize the overall transportation cost of the entire system. Additionally, in contrast to the 2ER-TD, the drone in the 2E-GU-RP frequently lands on the truck to change or recharge its battery while the truck is moving in the road network, and the 2E-GU-RP assumes a single drone. Moreover, HVDRP shares similarities with the 2ER-TD issue, where the truck is a mobile distribution center transporting drones near customers for deliveries. Nevertheless, in the HVDRP, the writers considered the participation of several trucks, each executing both pickup and delivery tasks. Following the deployment of the drones, the trucks were permitted to move and proceed with their routes. Conversely, the drones could be gathered at different locations, which various trucks might carry out. This setup with multiple trucks and the potential for drone collection by different trucks introduced additional complexities and routing interactions compared to the 2ER-TD issue, where only one truck is considered and the drone collaborates with the same truck during the delivery process.
Two ways of delivering goods involve the coordination of truck and drone delivery: one where drones are launched from trucks and another where drones can operate independently, launched from “micro-depots or the central distribution center”. To tackle this issue, the [135] study researchers created a strategic planning model for a logistics provider to optimize the vehicle fleet and drone station locations and minimize overall costs. Their problem was an extension of the “two-echelon location routing problem (2E-LRP)” described by [136] and was labeled “2E-LRP with drones (2E-LRPD)”. They converted the problem into a MILP, examining different transportation concepts and incorporating various delivery methods. To efficiently handle larger instances, they developed an ALNS algorithm to solve the problem effectively. Ref. [136] comprehensively reviewed UAV routing problems from a two-echelon perspective.
4.4. Charging Infrastructure Planning
UAVs are limited by their battery life, which affects their range and operational time. Managing charging stations (CSs) strategically and integrating them into the delivery network is challenging to ensure continuous operation without excessive downtime.
4.4.1. Charging Station Location
To address the restricted flying distance of drones, the expansion of UAV coverage requires the establishment of refueling or recharging stations. Ref. [137] introduced a fresh location model aimed at creating a network of recharging stations to cater to the needs of UAVs. Unlike surface transportation, UAVs can navigate through unobstructed space directly. The authors put forth a MILP formulation and a proficient heuristic algorithm. Similarly, the research by [138] concentrated on using drones for delivering parcels, taking into account the restricted flight distances caused by limitations in battery capacity. They suggested an algorithmically efficient method that initially positioned CSs in a triangular configuration to cover the entire demand area. Additionally, ref. [139] directed their efforts toward enhancing the operational range of drones from the network design perspective by integrating the CSs. They presented a mathematical model and a heuristic approach for addressing the network design problem, encompassing two main objectives: determining infrastructural investments (i.e., defining the number of CSs to deploy) and minimizing travel distances to optimize service aspects. The proposed model and heuristic approach provided a strategic-level strategy for drone-based delivery.
Moreover, ref. [140] investigated using UAVs in urban operations to reduce greenhouse gas emissions. They developed a model that optimized charging infrastructure coverage using UAV-based operations and solar energy from building envelopes. Additionally, ref. [141] presented a strategy known as a “joint routing and charging strategy (JRCS)” to prolong drone flight time with CSs and enable multiple deliveries in a single mission. This strategy involved customer clustering, drone flight segmentation, and optimized delivery routes considering CSs.
Furthermore, “automated battery swapping machines (ABSMs)” were introduced to recharge drones along their delivery routes. The optimization of ABSM locations, delivery mode choices, drone delivery routes, and the necessary number of drones and batteries is known as DD-ABSM [142], achieved through the introduction of mixed-integer nonlinear programming (NLP). They developed a cutting-plane method to find exact solutions efficiently. Additionally, ref. [143] put forward a drone delivery network design incorporating ABSMs to extend ranges and minimize “long-term delivery costs”, including ABSM investment, drone ownership, and delivery time. The study formulated a mixed-integer NLP algorithm, considering the drones’ waiting time at ABSMs as a nonlinear function. An exact solution approach was developed using a “derivative-supported cutting-plane method” to find the globally optimal solution.
Moreover, the study by [144] tackled the limited drone flight range issue by integrating drone stations for battery replacement or recharging. This approach aimed to minimize the overall travel time from the depot to a customer, a critical factor influencing service quality. The research explored four common scenarios for replenishing drone energy at drone stations: battery replacement, complete recharging, recharging to an optimal level, and station availability. The first two scenarios were addressed using the ILP model, while the latter two involved mixed-integer NLP problems. To address the problem of drone station unavailability, the study introduced a dynamic variation of Dijkstra’s algorithm.
4.4.2. Charging Station Capacity
The issue discussed in [145] dealt with efficiently allocating drones to cater to demands while locating capacitated facilities. The primary goal was to maximize coverage, considering drone energy consumption and range limitations. The problem was defined as the “maximum coverage facility location problem with drones (MCFLPD)”. To balance solution quality and computation time, they introduced innovative greedy and “three-stage heuristics (3SH)”. On average, the solutions obtained using 3SH were nearly 5% off from the best solutions found by Gurobi, a MILP solver, but with significantly faster running times.
In addition, the study by [146] examined the escalating delivery expenses encountered by e-commerce businesses by suggesting a drone-based aerial delivery system as an alternative. Fuzzy variables were utilized to handle the problem’s uncertain nature, resulting in a congested fuzzy capacitated multilevel facility location problem. A probabilistic approach was then employed to solve the problem. Several methods for capacitated CSs for UAVs in LMD systems have been suggested, including heuristic algorithms [55] and NSGA II [147].
4.5. Safety and Security
Ensuring the safety of the UAV’s flight path and avoiding collisions with obstacles or other aircraft is crucial. Adopting UAVs for LMD presents several challenges, encompassing physical and nonphysical aspects. Physical challenges include battery life, drone range, carrying capacity, and the drone’s design. On the other hand, security and privacy concerns are significant factors, as LMD drones operate outside the controlled environment of the warehouse and are exposed to potential threats from external entities. Since drones operate in open airspace, there is a risk of unauthorized access to communication channels between the drone and external entities [148]. Even if communication is authorized, restrictions on the type of information disclosed to specific external entities may be necessary to safeguard privacy. Ref. [148] discussed the critical security and privacy issues in drone-based LMD and general security and privacy concerns that apply to this context. It explored various facets of privacy and security concerns related to using drones for LMD, focusing on risks associated with codes, external entities, and communication signals.
4.6. Trade-off between Efficiency and Sustainability
Balancing the costs associated with UAV acquisition, maintenance, and operation against the environmental benefits is a crucial challenge for sustainable LMD. Ref. [112] proposed a novel multi-objective optimization model to address this issue, explicitly targeting the VRP-D. The proposed model aimed to enhance delivery efficiency and reduce environmental effects. Also, ref. [149] proposed a “mixed-integer green routing model” that considers two common types of traffic restrictions: vehicle-type restrictions and half-side traffic. Moreover, ref. [150] focused on analytically studying the impact of UAVs on CO2 emissions and cost in LMD. They proposed a “binary MILP green routing model” designed explicitly for UAVs to optimize the sustainability aspects of their usage. A GA was developed to solve the complex routing model efficiently. In addition, ref. [151] focused on conducting the “life cycle assessment (LCA)” of drone delivery in Thailand. The study results indicated that an online shopping system utilizing drone delivery emerges as one of the most environmentally friendly transportation options across various scenarios. A realistic parcel delivery system encounters the challenge of stochastic customer presence, where customers may not always be available to receive their deliveries. Ref. [152] introduced a sustainable hybrid truck–drone delivery model that considered the stochastic nature of customer presence. The system was modeled using Markov chain theory, and a linear mathematical model was proposed to optimize the delivery operations. They employed both heuristic and branch-and-bound algorithms to process the problem effectively. Moreover, ref. [153] proposed an innovative dual-objective MILP model to assess drone-assisted truck delivery’s environmental and economic impacts, considering the carbon market price. The results indicated that compared to traditional truck delivery, using drones as an assistive technology led to a reduction of 24.90% in carbon emissions, a decrease of 22.13% in total costs, and a 20.65% reduction in delivery time. Also, the following review papers on UAV-based (drone) operations and delivery are introduced to interested readers: [154,155,156,157,158,159,160,161,162,163,164].
5. Discussion and Future Directions
In previous sections, we examined the gathered papers to explore novel approaches, problems, subproblems, and solution techniques rooted in OR for both eVTOL and UAV applications. Having thoroughly reviewed and analyzed these papers and their contributions, we will now address research gaps and provide recommendations for future studies.
5.1. Integration of UAVs with Delivery Robots
A groundbreaking strategy within the field of LMD involves combining “road autonomous delivery robots (RADRs)” [165] with UAVs, offering a novel perspective on improving delivery efficiency and coverage, which is not paid attention in the literature. In this intriguing scenario, RADRs handle parcel delivery for a specific group of customers, while UAVs are deployed directly from these RADRs. The UAVs are responsible for delivering items to the remaining customers and returning them to a designated drone station or the RADRs. To successfully implement this concept, several crucial factors must be considered. Firstly, the strategic planning and placement of recharging stations for UAVs are of utmost importance. Ensuring that UAVs have access to reliable and strategically located recharging stations is critical to maintaining their operational capabilities during delivery. This infrastructure planning should align with the routes and coverage areas of both RADRs and UAVs. Safety measures are also paramount, particularly for operating RADRs on roads. These road-based robots must adhere to strict safety protocols and regulations to ensure the safety of pedestrians, other vehicles, and cargo. Implementing advanced collision avoidance systems, real-time monitoring, and compliance with traffic regulations are all crucial components of this safety strategy. Furthermore, optimizing the delivery process for UAVs is essential. Ensuring that each UAV can complete its delivery in a single trip conserves energy and reduces operational complexities. Effective route planning, load optimization, and efficient delivery drop-offs should all be integral parts of this approach to maximize the capabilities of UAVs.
5.2. Integration of UAVs with Public Transportation
A burgeoning area of exploration within the field of LMD logistics, which a few studies have addressed, entails merging aerial-based robotic systems, such as UAVs, with the concept of “freight on transit (FOT)” [166]. This innovative amalgamation represents a pioneering approach to LMD, though it comes with operational constraints and challenges that require careful consideration in OR. Utilizing UAVs alongside FOT is particularly well suited for urban settings where the layout of roads and infrastructure renders traditional doorstep parcel delivery impractical [167]. In this visionary concept, public vehicles like buses or trams assume the role of a “mothership fleet”. These vehicles continue to serve the public’s transportation needs, adhering to predetermined schedules while simultaneously accommodating the deployment of UAVs based on specific demands and orders from different parts of the city. One of the primary hurdles in this integrated system is synchronization. This complex decision-making process involves aligning the schedules and movements of UAVs with those of public buses or trams. While buses and trams follow predefined routes and schedules, the use of UAVs depends on real-time demands and orders from various locations within the city. Striking a balance and finding coordination between these dynamic elements is a central challenge. Despite the inherent difficulties and limitations, integrating drones and robots with public transportation can significantly improve the efficiency of parcel delivery and urban logistics concurrently [168]. This approach aligns with sustainability principles and environmentally friendly policies, contributing to more resource-efficient and ecologically conscious solutions for city logistics [169].
5.3. Integration of UAVs with Electric Vehicles and Parcel Lockers
Furthermore, in certain specific scenarios, integrating a UAV-based delivery system with parcel lockers (PLs) [170,171] can significantly improve efficiency, particularly when handling lightweight parcels that are easily transportable by UAVs. Nevertheless, when dealing with heavier products, this system must be supplemented with electric vehicles (EVs) or trucks to ensure successful delivery to customers or PLs. Consequently, a hybrid delivery system encompassing EVs, UAVs, and PLs is emerging as an innovative concept in LMD. Within this hybrid system, denoted as EV-UAV-PL, a key challenge lies in effectively distributing orders to PLs or directly to customers without encountering delivery failures or delays. This necessitates the implementation of sophisticated routing and coordination mechanisms that leverage the strengths of each component. UAVs can be employed for swift deliveries of lightweight items, while EVs or trucks are relied upon for bulkier or heavier goods. Striking this balance ensures that the appropriate delivery method is selected for each parcel, thereby optimizing both speed and reliability.
5.4. An Integrated eVTOL and UAV Transportation System
Combining eVTOL aircraft fleets with UAVs, or drones, for the seamless delivery of products and passengers intracity and intercities presents a promising vision for the future of transportation. However, this integrated system has limitations and complexities, which may explain why it is not studied in the literature yet. One of the primary concerns is the potential for increased air traffic and the risk of collisions in densely populated areas. Stringent safety measures and robust collision avoidance systems will be essential to address this. Additionally, establishing an extensive network of charging stations for eVTOLs and drones will be a critical logistical challenge. Optimal scheduling and sequencing of flights at each vertiport and landing spot will also be necessary to ensure efficient operations and minimize congestion. Nevertheless, the benefits of such an integrated delivery system are immense. It could significantly reduce traffic congestion and greenhouse gas emissions, making urban areas more livable and environmentally friendly. Moreover, it can potentially revolutionize e-commerce, healthcare, and emergency services, offering faster and more efficient delivery options. In the long run, this combined system could contribute to a more sustainable and interconnected world, enhancing the overall quality of life for people in both urban and rural areas and reshaping the future of human transportation.
5.5. Integration of eVTOLs with Sidewalk Robots
Integrating eVTOL aircraft fleets with innovative technologies like “sidewalk autonomous delivery robots (SADRs)” [165] to facilitate the delivery of products, especially in challenging urban areas, represents a pioneering approach to logistics. In this system, which has not been studied in the literature, eVTOLs serve as mothership fleets, transporting SADRs to locations inaccessible by aircraft due to congestion or space constraints. However, this integrated system is not without its complexities. Novelty presents a learning curve for both technology development and public acceptance. Safety and security measures are paramount, given the combination of aerial and ground-based components. Establishing charging stations for eVTOLs and SADRs is essential for sustained operations, while optimal scheduling and sequencing at vertiports and landing spots are critical to minimize congestion. Furthermore, efficiently loading and unloading parcels from eVTOLs to SADRs demands careful planning. Despite these challenges, the benefits are significant. This combined air-and-ground delivery system has the potential to revolutionize urban logistics, reducing traffic congestion, lowering emissions, and improving the overall efficiency of product delivery. It could pave the way for a more sustainable and interconnected future, where goods are transported swiftly and seamlessly to meet the demands of our evolving cities.
5.6. Pricing Decisions for eVTOL
Pricing decisions in eVTOL aircraft, catering to parcel and passenger delivery, are intricate. Novelty factors play a significant role, as these technologies are relatively new and may require consumers to adapt to the concept of UAM. Safety and acceptance from regulatory bodies and the public are paramount, with stringent standards needed to ensure secure operations. Moreover, pricing must consider social and sustainability aspects, ensuring that eVTOLs contribute positively to urban environments and minimize environmental impact. Despite these complexities, the benefits of eVTOLs are immense. They promise to reduce congestion, cut travel times, and mitigate pollution, making them a crucial component of future transportation systems, reshaping our cities, and enhancing the quality of human life.
5.7. UAM Optimization with Modern Methodologies
The development of advanced OR methods is of utmost importance when dealing with the intricacies of UAM (eVTOL and drones) challenges. In this dynamic field, researchers consistently push the boundaries of knowledge by employing innovative and probabilistic mathematical modeling techniques to account for the inherent uncertainties in urban logistics. These models incorporate real-time data on traffic patterns, weather conditions, and consumer behavior, enabling companies to make well-informed decisions for efficient route planning and resource allocation. Furthermore, data mining techniques extract valuable insights from extensive datasets, helping identify recurring patterns and trends that can optimize delivery routes and reduce operational costs. Moreover, the integration of metaheuristic and machine learning-based methodologies has brought about a revolution in UAM optimization. Math-heuristic approaches combine mathematical optimization techniques with heuristic algorithms, allowing for more scalable and adaptable solutions. Conversely, machine learning algorithms empower companies to improve decision making through predictive analytics, enabling proactive problem solving [172]. This multifaceted approach also considers multiple objectives, such as minimizing delivery times, reducing carbon emissions, and maximizing customer satisfaction, aligning with sustainability and efficiency objectives.
5.8. UAM under Uncertainty
Moreover, additional uncertainties within this context relate to factors like demand fluctuations, weather conditions, the availability of public transportation, and the complexities of loading and unloading parcels. These aspects need to be considered when analyzing the challenges associated with emerging parcel delivery methods. This becomes particularly critical because parcel unloading does not always occur seamlessly, and locations may be unsuitable for UAVs to complete their deliveries. Addressing these variables and evaluating how they affect the delivery process presents another intriguing research challenge when developing simulation-based methods like multiagent [173] and discrete-event simulations. Understanding the impact of adverse weather on the delivery operations of these vehicles is essential for developing robust and dependable solutions for UAM systems.
6. Conclusions
Developing urban air mobility (UAM) solutions like electric vertical takeoff and landing aircraft (eVTOLs), air taxis, and unmanned aerial vehicles (UAVs), or drones, for last-mile transportation poses a series of complex challenges when examined through the lens of operations research (OR). This review paper, which focuses on the challenges faced by the applications of eVTOLs and UAVs in last-mile transportation from an OR perspective, holds significant importance in urban mobility and OR literature. Previous reviews in the literature explored UAM implementation challenges and prospects related to its technologies. Despite a shared focus area, our review work stands apart from the existing literature by studying passenger and parcel delivery using eVTOL and UAV technologies from the OR perspective, emphasizing mathematical modeling and solution approaches. By delving into the complexities associated with optimization models and considering environmental sustainability, this review paper plays a crucial role in identifying deficiencies in the current knowledge base and suggesting potential directions for future research efforts. This review categorizes the gathered papers according to eVTOL and UAV technologies. Subsequently, within each technology category, we identify the primary problems, outline the challenges addressed by OR methodologies, and provide an overview of the proposed solution techniques.
Finally, according to the study gaps, several research directions for future studies are suggested as follows: (a) developing a UAM system based on integrated UAVs and delivery robots; (b) integrated UAV delivery systems with public transportation, EVs, and parcel lockers; (c) hybrid eVTOL- and UAV-based transportation system; (d) combined eVTOL and delivery robots; (e) pricing decisions for eVTOLs’ application in UAM; (f) developing new methodologies, such as math heuristics, hybrid metaheuristics, and learn heuristics for UAM optimization problems; and (g) studying the UAM delivery/transportation problem under uncertainty and stochastic parameters. Moreover, future review works on UAM may consider other technologies like VTOL applications in urban, suburban, and intercities areas while focusing on integrated innovative solutions.
Author Contributions
Conceptualization, N.M. and C.W.; methodology, N.M.; software, N.M.; validation, N.M., C.W. and F.M.; formal analysis, N.M.; investigation, N.M. and C.W.; resources, C.W. and F.M.; data curation, N.M.; writing—original draft preparation, N.M.; writing—review and editing, N.M., C.W. and F.M.; visualization, N.M.; supervision, C.W. and F.M.; project administration, C.W.; funding acquisition, C.W. and F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported through funding from the Gina Cody School of Engineering and Computer Science at Concordia University and the Natural Sciences and Engineering Council of Canada (NSERC), grant number # RGPIN-2019-07086.
Data Availability Statement
Data are available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| UAM | Urban air mobility |
| AAM | Advanced air mobility |
| eVTOL | Electric vertical takeoff and landing |
| UAV | Unmanned aerial vehicle |
| OR | Operations research |
| O-D | Origin and destination |
| LMT | Last-mile travel |
| LMD | Last-mile delivery |
| UPS | United Parcel Service |
| RTA | Required time of arrival |
| ASSP-eVTOL | Arrival sequencing and scheduling problem of eVTOL |
| ACS | Adaptive control system |
| TLOF | Touchdown and lift-off |
| ILS | Insertion and local search |
| MILP | Mixed-integer linear programming |
| TA | Time advance |
| ETA | Estimated time of arrival |
| MVS | Multivertiport system |
| CSSP | Charging sequencing and scheduling problem |
| AV | Aerial vehicle |
| ILP | Integer linear program |
| EAV | Electric aerial vehicles |
| RCSP | Routing and charging scheduling problem |
| VRP-TW | Vehicle routing problem with time windows |
| ARP | Aircraft recovery problem |
| NSGA-II | Nondominated sorting genetic algorithm II |
| LODES | LEHD Origin-Destination Employment Statistics |
| AmCS | American Community Survey |
| UAS | Unmanned aerial system |
| UAT | Urban air taxi |
| ATM | Air traffic management |
| FAA | Federal Aviation Administration |
| VDP | Vertiport design problem |
| CLARA | Clustering large applications |
| GA | Genetic algorithms |
| MTVRP | Multitrip VRP |
| VRP | Vehicle routing problem |
| DDP | Drone delivery problem |
| FLP | Facility location problem |
| BCR | Battery consumption rate |
| GV | Ground vehicle |
| TSP | Traveling salesman problem |
| FSTSP | Flying sidekick TSP |
| TSP-D | TSP with drones |
| DP | Dynamic programming |
| GRASP | Greedy randomized adaptive search procedure |
| TSP-DS | TSP with a drone station |
| PDSTSP | Parallel drone scheduling TSP |
| DC | Distribution center |
| m-FSTSP | Multiple-FSTSP |
| mTSP-mD | Multivisit (multiple drops) TSP-mD |
| LARO | Launch and recovery operations |
| VNS | Variable neighborhood search |
| SA | Simulated annealing |
| VRPD | VRP with a single drone |
| ALNS | Adaptive large neighborhood search |
| TS | Tabu search |
| m-TSP-D | Multiple TSP-D |
| m-TSP | Multiple TSP |
| ADI | Adaptive insertion heuristic |
| mTSP-DS | Multiple TSP with drone stations |
| VRP-D | VRP with drones |
| TD-DRP | Truck-based drone delivery routing problem |
| ACO | Ant colony optimization |
| TDRP-TW | Truck–drone routing problem with time windows |
| H-DTRP | Heterogeneous drone–truck routing problem |
| TDHRP-TDRTT | Truck–drone hybrid routing problem with time-dependent road travel time |
| SDDPVD | Same-day delivery problems with vehicles and drones |
| CP | Constraint programming |
| 2E-GU-RP | Two-echelon cooperated routing problem with GV and UAV |
| HVDRP | Hybrid vehicle–drone routing problem |
| 2EVRPD | Two-echelon VRP-D |
| DTRC | Drone truck route construction |
| 2E-RPTD | Two-echelon routing problem for truck and drone |
| 2EVRP | Two-echelon VRP |
| 2E-LRP | Two-echelon location routing problem |
| 2E-LRPD | 2E-LRP with drones |
| JRCS | Joint routing and charging strategy |
| CS | Charging station |
| ABSM | Automated battery swapping machines |
| NLP | Nonlinear programming |
| MCFLPD | Maximum coverage facility location problem with drones |
| 3SH | Three-stage heuristic |
| LCA | Life cycle assessment |
| RADR | Road autonomous delivery robot |
| FOT | Freight on transit |
| PL | Parcel locker |
| EV | Electric vehicle |
| SADR | Sidewalk autonomous delivery robot |
References
- WindRiver.com. What Is Urban Air Mobility? 2023. Available online: https://www.windriver.com/solutions/learning/urban-air-mobility (accessed on 10 October 2023).
- Schrank, D.; Eisele, B.; Lomax, T.; Bak, J. 2015 Urban Mobility Scorecard; Texas Transportation Institute, INRIX, Inc.: College Station, TX, USA, 2015. [Google Scholar]
- Wang, K.; Li, A.; Qu, X. Urban aerial mobility: Network structure, transportation benefits, and Sino-US comparison. Innovation 2023, 4, 100393. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.S.; Fountas, G.; Eker, U.; Still, S.E.; Anastasopoulos, P.C. An exploratory empirical analysis of willingness to hire and pay for flying taxis and shared flying car services. J. Air Transp. Manag. 2021, 90, 101963. [Google Scholar] [CrossRef]
- BuiltIn.com. What Are eVTOLs? Are They the Future of Aviation? 2023. Available online: https://builtin.com/transportation-tech/evtol-aircraft (accessed on 15 October 2023).
- eVTOLNews. Beta Technologies ALIA-250. 2023. Available online: https://evtol.news/beta-technologies-alia/ (accessed on 21 December 2023).
- insiderintelligence.com. Last-Mile Delivery: What It Is and What It Means for Retailers. 2023. Available online: https://www.insiderintelligence.com/insights/last-mile-delivery-shipping-explained/ (accessed on 15 October 2023).
- Boysen, N.; Fedtke, S.; Schwerdfeger, S. Last-mile delivery concepts: A survey from an operational research perspective. OR Spectr. 2021, 43, 1–58. [Google Scholar] [CrossRef]
- Polaczyk, N.; Trombino, E.; Wei, P.; Mitici, M. A review of current technology and research in urban on-demand air mobility applications. In Proceedings of the 8th Biennial Autonomous VTOL Technical Meeting and 6th Annual Electric VTOL Symposium, Mesa, AZ, USA, 28 January–1 February 2019; pp. 333–343. [Google Scholar]
- Sun, X.; Wandelt, S.; Husemann, M.; Stumpf, E. Operational considerations regarding on-demand air mobility: A literature review and research challenges. J. Adv. Transp. 2021, 2021, 3591034. [Google Scholar] [CrossRef]
- Cohen, A.P.; Shaheen, S.A.; Farrar, E.M. Urban air mobility: History, ecosystem, market potential, and challenges. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6074–6087. [Google Scholar] [CrossRef]
- Brunelli, M.; Ditta, C.C.; Postorino, M.N. New infrastructures for Urban Air Mobility systems: A systematic review on vertiport location and capacity. J. Air Transp. Manag. 2023, 112, 102460. [Google Scholar] [CrossRef]
- Garrow, L.A.; German, B.J.; Leonard, C.E. Urban air mobility: A comprehensive review and comparative analysis with autonomous and electric ground transportation for informing future research. Transp. Res. Part C Emerg. Technol. 2021, 132, 103377. [Google Scholar] [CrossRef]
- Wang, L.; Deng, X.; Gui, J.; Jiang, P.; Zeng, F.; Wan, S. A review of Urban Air Mobility-Enabled Intelligent Transportation Systems: Mechanisms, Applications and Challenges. J. Syst. Archit. 2023, 141, 102902. [Google Scholar] [CrossRef]
- Krull, L.F.; Muhammad, B. Urban Air Mobility: Insights into Potentials and Challenges. In Proceedings of the 2022 25th International Symposium on Wireless Personal Multimedia Communications (WPMC), Herning, Denmark, 30 October–2 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 267–272. [Google Scholar]
- Rajendran, S.; Srinivas, S. Air taxi service for urban mobility: A critical review of recent developments, future challenges, and opportunities. Transp. Res. Part E Logist. Transp. Rev. 2020, 143, 102090. [Google Scholar] [CrossRef]
- Kellermann, R.; Biehle, T.; Fischer, L. Drones for parcel and passenger transportation: A literature review. Transp. Res. Interdiscip. Perspect. 2020, 4, 100088. [Google Scholar] [CrossRef]
- Schweiger, K.; Preis, L. Urban air mobility: Systematic review of scientific publications and regulations for vertiport design and operations. Drones 2022, 6, 179. [Google Scholar] [CrossRef]
- Pons-Prats, J.; Živojinović, T.; Kuljanin, J. On the understanding of the current status of urban air mobility development and its future prospects: Commuting in a flying vehicle as a new paradigm. Transp. Res. Part E Logist. Transp. Rev. 2022, 166, 102868. [Google Scholar] [CrossRef]
- Mavraj, G.; Eltgen, J.; Fraske, T.; Swaid, M.; Berling, J.; Röntgen, O.; Fu, Y.; Schulz, D. A systematic review of ground-based infrastructure for the innovative urban air mobility. Trans. Aerosp. Res. 2022, 2022, 1–17. [Google Scholar] [CrossRef]
- Durach, C.F.; Kembro, J.; Wieland, A. A new paradigm for systematic literature reviews in supply chain management. J. Supply Chain. Manag. 2017, 53, 67–85. [Google Scholar] [CrossRef]
- Doo, J.T.; Pavel, M.D.; Didey, A.; Hange, C.; Diller, N.P.; Tsairides, M.A.; Smith, M.; Bennet, E.; Bromfield, M.; Mooberry, J. NASA Electric Vertical Takeoff and Landing (eVTOL) Aircraft Technology for Public Services—A White Paper; Ames Research Center: Washington, DC, USA, 2021. [Google Scholar]
- Pavel, M.D. Understanding the control characteristics of electric vertical take-off and landing (eVTOL) aircraft for urban air mobility. Aerosp. Sci. Technol. 2022, 125, 107143. [Google Scholar] [CrossRef]
- Vieira, D.R.; Silva, D.; Bravo, A. Electric VTOL aircraft: The future of urban air mobility (background, advantages and challenges). Int. J. Sustain. Aviat. 2019, 5, 101–118. [Google Scholar] [CrossRef]
- Daskilewicz, M.; German, B.; Warren, M.; Garrow, L.A.; Boddupalli, S.S.; Douthat, T.H. Progress in vertiport placement and estimating aircraft range requirements for eVTOL daily commuting. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Aerospace Research Central, Atlanta, GA, USA, 25–29 June 2018; p. 2884. [Google Scholar]
- Littell, J.D. Challenges in vehicle safety and occupant protection for autonomous electric vertical take-off and landing (eVTOL) vehicles. In Proceedings of the 2019 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Indianapolis, IN, USA, 22–24 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–16. [Google Scholar]
- Edwards, T.; Price, G. eVTOL Passenger Acceptance; Technical Report; Ames Reaserch Center: Washington, DC, USA, 2020. [Google Scholar]
- Xiang, S.; Xie, A.; Ye, M.; Yan, X.; Han, X.; Niu, H.; Li, Q.; Huang, H. Autonomous eVTOL: A summary of researches and challenges. Green Energy Intell. Transp. 2023, 3, 100140. [Google Scholar] [CrossRef]
- Mohammad, W.A.; Nazih Diab, Y.; Elomri, A.; Triki, C. Innovative solutions in last mile delivery: Concepts, practices, challenges, and future directions. In Proceedings of the Supply Chain Forum: An International Journal; Taylor & Francis: Abingdon, UK, 2023; Volume 24, pp. 151–169. [Google Scholar]
- Aironline.com. Amazon Makes Second Investment in Beta, Following Alia eVTOL Test Flight. 2023. Available online: https://www.ainonline.com/news-article/2022-06-24/amazon-makes-second-investment-beta-following-alia-evtol-test-flight (accessed on 30 March 2023).
- Russo, R.; Tan, E.C. All-electric Vertical Take-off and Landing Aircraft (eVTOL) for Sustainable Urban Travel. In Sustainability Engineering; CRC Press: Boca Raton, FL, USA, 2023; pp. 265–287. [Google Scholar]
- Pradeep, P.; Wei, P. Heuristic approach for arrival sequencing and scheduling for eVTOL aircraft in on-demand urban air mobility. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–7. [Google Scholar]
- Kleinbekman, I.C.; Mitici, M.A.; Wei, P. eVTOL arrival sequencing and scheduling for on-demand urban air mobility. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–7. [Google Scholar]
- Shihab, S.A.M.; Wei, P.; Ramirez, D.S.J.; Mesa-Arango, R.; Bloebaum, C. By schedule or on demand?—A hybrid operation concept for urban air mobility. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3522. [Google Scholar]
- Kleinbekman, I.C.; Mitici, M.; Wei, P. Rolling-horizon electric vertical takeoff and landing arrival scheduling for on-demand urban air mobility. J. Aerosp. Inf. Syst. 2020, 17, 150–159. [Google Scholar] [CrossRef]
- Shao, Q.; Shao, M.; Lu, Y. Terminal area control rules and eVTOL adaptive scheduling model for multi-vertiport system in urban air Mobility. Transp. Res. Part C Emerg. Technol. 2021, 132, 103385. [Google Scholar] [CrossRef]
- Espejo-Díaz, J.A.; Alfonso-Lizarazo, E.; Montoya-Torres, J.R. A heuristic approach for scheduling advanced air mobility aircraft at vertiports. Appl. Math. Model. 2023, 123, 871–890. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y. Optimal eVTOL charging and passenger serving scheduling for on-demand urban air mobility. In Proceedings of the AIAA Aviation 2020 Forum, Virtual Event, 15–19 June 2020; p. 3253. [Google Scholar]
- Rigas, E.S.; Kolios, P.; Ellinas, G. Scheduling aerial vehicles in an urban air mobility scheme. In Proceedings of the 2021 IEEE Vehicular Networking Conference (VNC), New York, NY, USA, 10–12 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 76–82. [Google Scholar]
- Chen, J. Integrated routing and charging scheduling for autonomous electric aerial vehicle system. In Proceedings of the 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 8–12 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–7. [Google Scholar]
- Guo, Z.; Hao, M.; Liu, J.; Yu, B.; Jiang, Y. Joint routing and charging optimization for eVTOL aircraft recovery. Aerosp. Sci. Technol. 2022, 126, 107595. [Google Scholar] [CrossRef]
- Hildemann, M.; Verstegen, J.A. 3D-flight route optimization for air-taxis in urban areas with Evolutionary Algorithms and GIS. J. Air Transp. Manag. 2023, 107, 102356. [Google Scholar] [CrossRef]
- German, B.; Daskilewicz, M.; Hamilton, T.K.; Warren, M.M. Cargo delivery in by passenger evtol aircraft: A case study in the san francisco bay area. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 2006. [Google Scholar]
- Ale-Ahmad, H.; Mahmassani, H.S. Capacitated location-allocation-routing problem with time windows for on-demand urban air taxi operation. Transp. Res. Rec. 2021, 2675, 1092–1114. [Google Scholar] [CrossRef]
- Willey, L.C.; Salmon, J.L. A method for urban air mobility network design using hub location and subgraph isomorphism. Transp. Res. Part Emerg. Technol. 2021, 125, 102997. [Google Scholar] [CrossRef]
- Kai, W.; Jacquillat, A.; Vaze, V. Vertiport planning for urban aerial mobility: An adaptive discretization approach. Manuf. Serv. Oper. Manag. 2022, 24, 3215–3235. [Google Scholar] [CrossRef]
- Park, B.T.; Kim, S.H. Vertiport Design Optimization using Integer Programming. In Proceedings of the 2022 IEEE/AIAA 41st Digital Avionics Systems Conference (DASC), Portsmouth, VA, USA, 18–22 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Rath, S.; Chow, J.Y. Air taxi skyport location problem with single-allocation choice-constrained elastic demand for airport access. J. Air Transp. Manag. 2022, 105, 102294. [Google Scholar] [CrossRef]
- Macias, J.E.; Khalife, C.; Slim, J.; Angeloudis, P. An integrated vertiport placement model considering vehicle sizing and queuing: A case study in London. J. Air Transp. Manag. 2023, 113, 102486. [Google Scholar] [CrossRef]
- Sinha, A.A.; Rajendran, S. Study on facility location of air taxi skyports using a prescriptive analytics approach. Transp. Res. Interdiscip. Perspect. 2023, 18, 100761. [Google Scholar]
- Ferrão, I.G.; Espes, D.; Dezan, C.; Branco, K.R.L.J.C. Security and safety concerns in air taxis: A systematic literature review. Sensors 2022, 22, 6875. [Google Scholar] [CrossRef]
- Bennaceur, M.; Delmas, R.; Hamadi, Y. Passenger-centric Urban Air Mobility: Fairness trade-offs and operational efficiency. Transp. Res. Part C Emerg. Technol. 2022, 136, 103519. [Google Scholar] [CrossRef]
- Velaz-Acera, N.; Álvarez-García, J.; Borge-Diez, D. Economic and emission reduction benefits of the implementation of eVTOL aircraft with bi-directional flow as storage systems in islands and case study for Canary Islands. Appl. Energy 2023, 331, 120409. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle routing problems for drone delivery. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 70–85. [Google Scholar] [CrossRef]
- Shavarani, S.M.; Nejad, M.G.; Rismanchian, F.; Izbirak, G. Application of hierarchical facility location problem for optimization of a drone delivery system: A case study of Amazon prime air in the city of San Francisco. Int. J. Adv. Manuf. Technol. 2018, 95, 3141–3153. [Google Scholar] [CrossRef]
- Torabbeigi, M.; Lim, G.J.; Kim, S.J. Drone delivery scheduling optimization considering payload-induced battery consumption rates. J. Intell. Robot. Syst. 2020, 97, 471–487. [Google Scholar] [CrossRef]
- Yan, S.; Sun, C.S.; Chen, Y.H. Optimal routing and scheduling of unmanned aerial vehicles for delivery services. Transp. Lett. 2023, 1–12. [Google Scholar] [CrossRef]
- Walker, L. Drone Delivery for Amazon and Google Slowed by Headwinds. Newsweek. Available online: https://www.newsweek.com/will-wind-be-end-commercial-drone-delivery-amazon-and-google-275999 (accessed on 7 October 2014).
- Cheng, C.; Adulyasak, Y.; Rousseau, L.M.; Sim, M. Robust drone delivery with weather information. History 2020, 1, 1–37. [Google Scholar] [CrossRef]
- Vural, D.; Dell, R.F.; Kose, E. Locating unmanned aircraft systems for multiple missions under different weather conditions. Oper. Res. 2021, 21, 725–744. [Google Scholar] [CrossRef]
- Gaba, F.T. Solutions to the Generalized UAV Delivery Routing Problem for Last-Mile Delivery with Societal Constraints. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2022. [Google Scholar]
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- de Freitas, J.C.; Penna, P.H.V. A randomized variable neighborhood descent heuristic to solve the flying sidekick traveling salesman problem. Electron. Notes Discret. Math. 2018, 66, 95–102. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Song, B.D.; Lee, S. Truck-drone hybrid delivery routing: Payload-energy dependency and No-Fly zones. Int. J. Prod. Econ. 2019, 214, 220–233. [Google Scholar] [CrossRef]
- de Freitas, J.C.; Penna, P.H.V. A variable neighborhood search for flying sidekick traveling salesman problem. Int. Trans. Oper. Res. 2020, 27, 267–290. [Google Scholar] [CrossRef]
- Gonzalez-R, P.L.; Canca, D.; Andrade-Pineda, J.L.; Calle, M.; Leon-Blanco, J.M. Truck-drone team logistics: A heuristic approach to multi-drop route planning. Transp. Res. Part Emerg. Technol. 2020, 114, 657–680. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Drone-assisted deliveries: New formulations for the flying sidekick traveling salesman problem. Optim. Lett. 2021, 15, 1617–1648. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Algorithms based on branch and bound for the flying sidekick traveling salesman problem. Omega 2021, 104, 102493. [Google Scholar] [CrossRef]
- Boccia, M.; Masone, A.; Sforza, A.; Sterle, C. A column-and-row generation approach for the flying sidekick travelling salesman problem. Transp. Res. Part C Emerg. Technol. 2021, 124, 102913. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Exact models for the flying sidekick traveling salesman problem. Int. Trans. Oper. Res. 2022, 29, 1360–1393. [Google Scholar] [CrossRef]
- Mara, S.T.W.; Rifai, A.P.; Sopha, B.M. An adaptive large neighborhood search heuristic for the flying sidekick traveling salesman problem with multiple drops. Expert Syst. Appl. 2022, 205, 117647. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.; Khojandi, A. The flying sidekick traveling salesman problem with stochastic travel time: A reinforcement learning approach. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102816. [Google Scholar] [CrossRef]
- Boccia, M.; Mancuso, A.; Masone, A.; Sterle, C. A new MILP formulation for the flying sidekick traveling salesman problem. Networks 2023, 82, 254–276. [Google Scholar] [CrossRef]
- Yanpirat, N.; Silva, D.F.; Smith, A.E. Sustainable last mile parcel delivery and return service using drones. Eng. Appl. Artif. Intell. 2023, 124, 106631. [Google Scholar] [CrossRef]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization approaches for the traveling salesman problem with drone. Transp. Sci. 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Bouman, P.; Agatz, N.; Schmidt, M. Dynamic programming approaches for the traveling salesman problem with drone. Networks 2018, 72, 528–542. [Google Scholar] [CrossRef]
- Poikonen, S.; Golden, B.; Wasil, E.A. A branch-and-bound approach to the traveling salesman problem with a drone. INFORMS J. Comput. 2019, 31, 335–346. [Google Scholar] [CrossRef]
- Roberti, R.; Ruthmair, M. Exact methods for the traveling salesman problem with drone. Transp. Sci. 2021, 55, 315–335. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hà, M.H. On the min-cost traveling salesman problem with drone. Transp. Res. Part C Emerg. Technol. 2018, 86, 597–621. [Google Scholar] [CrossRef]
- Yurek, E.E.; Ozmutlu, H.C. Traveling salesman problem with drone under recharging policy. Comput. Commun. 2021, 179, 35–49. [Google Scholar] [CrossRef]
- Kim, S.; Moon, I. Traveling salesman problem with a drone station. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 42–52. [Google Scholar] [CrossRef]
- Murray, C.C.; Raj, R. The multiple flying sidekicks traveling salesman problem: Parcel delivery with multiple drones. Transp. Res. Part C Emerg. Technol. 2020, 110, 368–398. [Google Scholar] [CrossRef]
- Raj, R.; Murray, C. The multiple flying sidekicks traveling salesman problem with variable drone speeds. Transp. Res. Part C Emerg. Technol. 2020, 120, 102813. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Modeling the flying sidekick traveling salesman problem with multiple drones. Networks 2021, 78, 303–327. [Google Scholar] [CrossRef]
- Cavani, S.; Iori, M.; Roberti, R. Exact methods for the traveling salesman problem with multiple drones. Transp. Res. Part C Emerg. Technol. 2021, 130, 103280. [Google Scholar] [CrossRef]
- Chang, Y.S.; Lee, H.J. Optimal delivery routing with wider drone-delivery areas along a shorter truck-route. Expert Syst. Appl. 2018, 104, 307–317. [Google Scholar] [CrossRef]
- Luo, Z.; Poon, M.; Zhang, Z.; Liu, Z.; Lim, A. The multi-visit traveling salesman problem with multi-drones. Transp. Res. Part C Emerg. Technol. 2021, 128, 103172. [Google Scholar] [CrossRef]
- Salama, M.R.; Srinivas, S. Collaborative truck multi-drone routing and scheduling problem: Package delivery with flexible launch and recovery sites. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102788. [Google Scholar] [CrossRef]
- Sacramento, D.; Pisinger, D.; Ropke, S. An adaptive large neighborhood search metaheuristic for the vehicle routing problem with drones. Transp. Res. Part C Emerg. Technol. 2019, 102, 289–315. [Google Scholar] [CrossRef]
- Yin, Y.; Li, D.; Wang, D.; Ignatius, J.; Cheng, T.; Wang, S. A branch-and-price-and-cut algorithm for the truck-based drone delivery routing problem with time windows. Eur. J. Oper. Res. 2023, 309, 1125–1144. [Google Scholar] [CrossRef]
- Boysen, N.; Briskorn, D.; Fedtke, S.; Schwerdfeger, S. Drone delivery from trucks: Drone scheduling for given truck routes. Networks 2018, 72, 506–527. [Google Scholar] [CrossRef]
- Wang, C.; Lan, H.; Saldanha-da Gama, F.; Chen, Y. On optimizing a multi-mode last-mile parcel delivery system with vans, truck and drone. Electronics 2021, 10, 2510. [Google Scholar] [CrossRef]
- Kitjacharoenchai, P.; Ventresca, M.; Moshref-Javadi, M.; Lee, S.; Tanchoco, J.M.; Brunese, P.A. Multiple traveling salesman problem with drones: Mathematical model and heuristic approach. Comput. Ind. Eng. 2019, 129, 14–30. [Google Scholar] [CrossRef]
- Bektas, T. The multiple traveling salesman problem: An overview of formulations and solution procedures. Omega 2006, 34, 209–219. [Google Scholar] [CrossRef]
- Kloster, K.; Moeini, M.; Vigo, D.; Wendt, O. The multiple traveling salesman problem in presence of drone-and robot-supported packet stations. Eur. J. Oper. Res. 2023, 305, 630–643. [Google Scholar] [CrossRef]
- Wang, X.; Poikonen, S.; Golden, B. The vehicle routing problem with drones: Several worst-case results. Optim. Lett. 2017, 11, 679–697. [Google Scholar] [CrossRef]
- Poikonen, S.; Wang, X.; Golden, B. The vehicle routing problem with drones: Extended models and connections. Networks 2017, 70, 34–43. [Google Scholar] [CrossRef]
- Wang, Z.; Sheu, J.B. Vehicle routing problem with drones. Transp. Res. Part B Methodol. 2019, 122, 350–364. [Google Scholar] [CrossRef]
- Schermer, D.; Moeini, M.; Wendt, O. A matheuristic for the vehicle routing problem with drones and its variants. Transp. Res. Part C Emerg. Technol. 2019, 106, 166–204. [Google Scholar] [CrossRef]
- Schermer, D.; Moeini, M.; Wendt, O. A hybrid VNS/Tabu search algorithm for solving the vehicle routing problem with drones and en route operations. Comput. Oper. Res. 2019, 109, 134–158. [Google Scholar] [CrossRef]
- Poikonen, S.; Golden, B. Multi-visit drone routing problem. Comput. Oper. Res. 2020, 113, 104802. [Google Scholar] [CrossRef]
- Han, Y.; Li, J.; Liu, Z.; Liu, C.; Tian, J. Metaheuristic algorithm for solving the multi-objective vehicle routing problem with time window and drones. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420920031. [Google Scholar] [CrossRef]
- Tamke, F.; Buscher, U. A branch-and-cut algorithm for the vehicle routing problem with drones. Transp. Res. Part B Methodol. 2021, 144, 174–203. [Google Scholar] [CrossRef]
- Lei, D.; Cui, Z.; Li, M. A dynamical artificial bee colony for vehicle routing problem with drones. Eng. Appl. Artif. Intell. 2022, 107, 104510. [Google Scholar] [CrossRef]
- Euchi, J.; Sadok, A. Hybrid genetic-sweep algorithm to solve the vehicle routing problem with drones. Phys. Commun. 2021, 44, 101236. [Google Scholar] [CrossRef]
- Ahn, N.; Kim, S. Optimal and heuristic algorithms for the multi-objective vehicle routing problem with drones for military surveillance operations. J. Ind. Manag. Optim. 2022, 18, 1651–1663. [Google Scholar] [CrossRef]
- Kuo, R.; Lu, S.H.; Lai, P.Y.; Mara, S.T.W. Vehicle routing problem with drones considering time windows. Expert Syst. Appl. 2022, 191, 116264. [Google Scholar] [CrossRef]
- Masmoudi, M.A.; Mancini, S.; Baldacci, R.; Kuo, Y.H. Vehicle routing problems with drones equipped with multi-package payload compartments. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102757. [Google Scholar] [CrossRef]
- Gu, R.; Poon, M.; Luo, Z.; Liu, Y.; Liu, Z. A hierarchical solution evaluation method and a hybrid algorithm for the vehicle routing problem with drones and multiple visits. Transp. Res. Part C Emerg. Technol. 2022, 141, 103733. [Google Scholar] [CrossRef]
- Huang, S.H.; Huang, Y.H.; Blazquez, C.A.; Chen, C.Y. Solving the vehicle routing problem with drone for delivery services using an ant colony optimization algorithm. Adv. Eng. Inform. 2022, 51, 101536. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, C.; Yang, J. A multi-objective humanitarian pickup and delivery vehicle routing problem with drones. Ann. Oper. Res. 2022, 319, 291–353. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, S.; Xu, W.; Wang, W. A novel multi-objective optimization model for the vehicle routing problem with drone delivery and dynamic flight endurance. Comput. Ind. Eng. 2022, 173, 108679. [Google Scholar] [CrossRef]
- Kuo, R.; Edbert, E.; Zulvia, F.E.; Lu, S.H. Applying NSGA-II to vehicle routing problem with drones considering makespan and carbon emission. Expert Syst. Appl. 2023, 221, 119777. [Google Scholar] [CrossRef]
- Xia, Y.; Zeng, W.; Zhang, C.; Yang, H. A branch-and-price-and-cut algorithm for the vehicle routing problem with load-dependent drones. Transp. Res. Part B Methodol. 2023, 171, 80–110. [Google Scholar] [CrossRef]
- Tamke, F.; Buscher, U. The vehicle routing problem with drones and drone speed selection. Comput. Oper. Res. 2023, 152, 106112. [Google Scholar] [CrossRef]
- Yin, Y.; Yang, Y.; Yu, Y.; Wang, D.; Cheng, T. Robust vehicle routing with drones under uncertain demands and truck travel times in humanitarian logistics. Transp. Res. Part B Methodol. 2023, 174, 102781. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, C.; Cao, Y.; Roberti, R. Planning robust drone-truck delivery routes under road traffic uncertainty. Eur. J. Oper. Res. 2023, 309, 1145–1160. [Google Scholar] [CrossRef]
- Jiang, J.; Dai, Y.; Yang, F.; Ma, Z. A multi-visit flexible-docking vehicle routing problem with drones for simultaneous pickup and delivery services. Eur. J. Oper. Res. 2024, 312, 125–137. [Google Scholar] [CrossRef]
- Di Puglia Pugliese, L.; Guerriero, F. Last-mile deliveries by using drones and classical vehicles. In Proceedings of the Optimization and Decision Science: Methodologies and Applications: ODS, Sorrento, Italy, 4–7 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; Volume 47, pp. 557–565. [Google Scholar]
- Li, H.; Zhao, J.; Zhan, Z. Truck and Unmanned Vehicle Routing Problem with Time Windows: A Satellite Synchronization Perspective. J. Adv. Transp. 2022, 2022, 6599089. [Google Scholar] [CrossRef]
- Gómez-Lagos, J.; Candia-Véjar, A.; Encina, F. A new truck-drone routing problem for parcel delivery services aided by parking lots. IEEE Access 2021, 9, 11091–11108. [Google Scholar] [CrossRef]
- Das, D.N.; Sewani, R.; Wang, J.; Tiwari, M.K. Synchronized truck and drone routing in package delivery logistics. IEEE Trans. Intell. Transp. Syst. 2020, 22, 5772–5782. [Google Scholar] [CrossRef]
- Dayarian, I.; Savelsbergh, M.; Clarke, J.P. Same-day delivery with drone resupply. Transp. Sci. 2020, 54, 229–249. [Google Scholar] [CrossRef]
- Li, H.; Wang, F. Branch-price-and-cut for the truck–drone routing problem with time windows. Nav. Res. Logist. 2023, 70, 184–204. [Google Scholar] [CrossRef]
- Kang, M.; Lee, C. An exact algorithm for heterogeneous drone-truck routing problem. Transp. Sci. 2021, 55, 1088–1112. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Hu, X.; Xue, G.; Guan, X. Truck–drone hybrid routing problem with time-dependent road travel time. Transp. Res. Part C Emerg. Technol. 2022, 144, 103901. [Google Scholar] [CrossRef]
- Chen, X.; Ulmer, M.W.; Thomas, B.W. Deep Q-learning for same-day delivery with vehicles and drones. Eur. J. Oper. Res. 2022, 298, 939–952. [Google Scholar] [CrossRef]
- Ham, A.M. Integrated scheduling of m-truck, m-drone, and m-depot constrained by time-window, drop-pickup, and m-visit using constraint programming. Transp. Res. Part C Emerg. Technol. 2018, 91, 1–14. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, Z.; Shi, J. A two-echelon cooperated routing problem for a ground vehicle and its carried unmanned aerial vehicle. Sensors 2017, 17, 1144. [Google Scholar] [CrossRef] [PubMed]
- Karak, A.; Abdelghany, K. The hybrid vehicle-drone routing problem for pick-up and delivery services. Transp. Res. Part C Emerg. Technol. 2019, 102, 427–449. [Google Scholar] [CrossRef]
- Kitjacharoenchai, P.; Min, B.C.; Lee, S. Two echelon vehicle routing problem with drones in last mile delivery. Int. J. Prod. Econ. 2020, 225, 107598. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.; Shi, J.; Wu, G.; Pedrycz, W. Two-echelon routing problem for parcel delivery by cooperated truck and drone. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 7450–7465. [Google Scholar] [CrossRef]
- Vu, L.; Vu, D.M.; Hà, M.H.; Nguyen, V.P. The two-echelon routing problem with truck and drones. Int. Trans. Oper. Res. 2022, 29, 2968–2994. [Google Scholar] [CrossRef]
- Perboli, G.; Tadei, R.; Vigo, D. The two-echelon capacitated vehicle routing problem: Models and math-based heuristics. Transp. Sci. 2011, 45, 364–380. [Google Scholar] [CrossRef]
- Rave, A.; Fontaine, P.; Kuhn, H. Drone location and vehicle fleet planning with trucks and aerial drones. Eur. J. Oper. Res. 2023, 308, 113–130. [Google Scholar] [CrossRef]
- Li, H.; Chen, J.; Wang, F.; Bai, M. Ground-vehicle and unmanned-aerial-vehicle routing problems from two-echelon scheme perspective: A review. Eur. J. Oper. Res. 2021, 294, 1078–1095. [Google Scholar] [CrossRef]
- Hong, I.; Kuby, M.; Murray, A.T. A range-restricted recharging station coverage model for drone delivery service planning. Transp. Res. Part C Emerg. Technol. 2018, 90, 198–212. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V.; Huang, C. Reliable path planning for drone delivery using a stochastic time-dependent public transportation network. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4941–4950. [Google Scholar] [CrossRef]
- Pinto, R.; Lagorio, A. Point-to-point drone-based delivery network design with intermediate charging stations. Transp. Res. Part C Emerg. Technol. 2022, 135, 103506. [Google Scholar] [CrossRef]
- ElSayed, M.; Foda, A.; Mohamed, M. Autonomous drone charging station planning through solar energy harnessing for zero-emission operations. Sustain. Cities Soc. 2022, 86, 104122. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Moh, S. JRCS: Joint routing and charging strategy for logistics drones. IEEE Internet Things J. 2022, 9, 21751–21764. [Google Scholar] [CrossRef]
- Cokyasar, T. Delivery drone route planning over a battery swapping network. Procedia Comput. Sci. 2021, 184, 10–16. [Google Scholar] [CrossRef]
- Cokyasar, T.; Dong, W.; Jin, M.; Verbas, İ.Ö. Designing a drone delivery network with automated battery swapping machines. Comput. Oper. Res. 2021, 129, 105177. [Google Scholar] [CrossRef]
- Huang, C.; Ming, Z.; Huang, H. Drone Stations-Aided Beyond-Battery-Lifetime Flight Planning for Parcel Delivery. IEEE Trans. Autom. Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Chauhan, D.; Unnikrishnan, A.; Figliozzi, M. Maximum coverage capacitated facility location problem with range constrained drones. Transp. Res. Part C Emerg. Technol. 2019, 99, 1–18. [Google Scholar] [CrossRef]
- Shavarani, S.M.; Mosallaeipour, S.; Golabi, M.; İzbirak, G. A congested capacitated multi-level fuzzy facility location problem: An efficient drone delivery system. Comput. Oper. Res. 2019, 108, 57–68. [Google Scholar] [CrossRef]
- Shavarani, S.M.; Golabi, M.; Izbirak, G. A capacitated biobjective location problem with uniformly distributed demands in the UAV-supported delivery operation. Int. Trans. Oper. Res. 2021, 28, 3220–3243. [Google Scholar] [CrossRef]
- Tu, Y.J.; Piramuthu, S. Security and privacy risks in drone-based last mile delivery. Eur. J. Inf. Syst. 2023, 1–14. [Google Scholar] [CrossRef]
- Li, Y.; Yang, W.; Huang, B. Impact of UAV delivery on sustainability and costs under traffic restrictions. Math. Probl. Eng. 2020, 2020, 9437605. [Google Scholar] [CrossRef]
- Chiang, W.C.; Li, Y.; Shang, J.; Urban, T.L. Impact of drone delivery on sustainability and cost: Realizing the UAV potential through vehicle routing optimization. Appl. Energy 2019, 242, 1164–1175. [Google Scholar] [CrossRef]
- Koiwanit, J. Analysis of environmental impacts of drone delivery on an online shopping system. Adv. Clim. Change Res. 2018, 9, 201–207. [Google Scholar] [CrossRef]
- Teimoury, E.; Rashid, R. The sustainable hybrid truck-drone delivery model with stochastic customer existence. Res. Transp. Econ. 2023, 100, 101325. [Google Scholar] [CrossRef]
- Meng, Z.; Zhou, Y.; Li, E.Y.; Peng, X.; Qiu, R. Environmental and economic impacts of drone-assisted truck delivery under the carbon market price. J. Clean. Prod. 2023, 401, 136758. [Google Scholar] [CrossRef]
- Coutinho, W.P.; Battarra, M.; Fliege, J. The unmanned aerial vehicle routing and trajectory optimisation problem, a taxonomic review. Comput. Ind. Eng. 2018, 120, 116–128. [Google Scholar] [CrossRef]
- Khoufi, I.; Laouiti, A.; Adjih, C. A survey of recent extended variants of the traveling salesman and vehicle routing problems for unmanned aerial vehicles. Drones 2019, 3, 66. [Google Scholar] [CrossRef]
- Thibbotuwawa, A.; Bocewicz, G.; Nielsen, P.; Banaszak, Z. Unmanned aerial vehicle routing problems: A literature review. Appl. Sci. 2020, 10, 4504. [Google Scholar] [CrossRef]
- Rojas Viloria, D.; Solano-Charris, E.L.; Muñoz-Villamizar, A.; Montoya-Torres, J.R. Unmanned aerial vehicles/drones in vehicle routing problems: A literature review. Int. Trans. Oper. Res. 2021, 28, 1626–1657. [Google Scholar] [CrossRef]
- Poikonen, S.; Campbell, J.F. Future directions in drone routing research. Networks 2021, 77, 116–126. [Google Scholar] [CrossRef]
- Moshref-Javadi, M.; Hemmati, A.; Winkenbach, M. A comparative analysis of synchronized truck-and-drone delivery models. Comput. Ind. Eng. 2021, 162, 107648. [Google Scholar] [CrossRef]
- Li, Y.; Liu, M.; Jiang, D. Application of unmanned aerial vehicles in logistics: A literature review. Sustainability 2022, 14, 14473. [Google Scholar] [CrossRef]
- Liang, Y.J.; Luo, Z.X. A survey of truck–drone routing problem: Literature review and research prospects. J. Oper. Res. Soc. China 2022, 10, 343–377. [Google Scholar] [CrossRef]
- Madani, B.; Ndiaye, M. Hybrid truck-drone delivery systems: A systematic literature review. IEEE Access 2022, 10, 92854–92878. [Google Scholar] [CrossRef]
- Eskandaripour, H.; Boldsaikhan, E. Last-mile drone delivery: Past, present, and future. Drones 2023, 7, 77. [Google Scholar] [CrossRef]
- Zhang, R.; Dou, L.; Xin, B.; Chen, C.; Deng, F.; Chen, J. A review on the truck and drone cooperative delivery problem. Unmanned Syst. 2023, 1–25. [Google Scholar] [CrossRef]
- Figliozzi, M.A. Carbon emissions reductions in last mile and grocery deliveries utilizing air and ground autonomous vehicles. Transp. Res. Part D Transp. Environ. 2020, 85, 102443. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V. Deployment of charging stations for drone delivery assisted by public transportation vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 23, 15043–15054. [Google Scholar] [CrossRef]
- Choudhury, S.; Solovey, K.; Kochenderfer, M.J.; Pavone, M. Efficient large-scale multi-drone delivery using transit networks. J. Artif. Intell. Res. 2021, 70, 757–788. [Google Scholar] [CrossRef]
- Moadab, A.; Farajzadeh, F.; Fatahi Valilai, O. Drone routing problem model for last-mile delivery using the public transportation capacity as moving charging stations. Sci. Rep. 2022, 12, 6361. [Google Scholar] [CrossRef] [PubMed]
- Elsaid, F.; Sanchez, E.T.; Li, Y.; Khamis, A. Optimal Placement of Drone Delivery Stations and Demand Allocation using Bio-inspired Algorithms. In Proceedings of the 2023 IEEE International Conference on Smart Mobility (SM), Thuwal, Saudi Arabia, 19–21 March 2023; pp. 39–44. [Google Scholar]
- Vukićević, M.; Ratli, M.; Rivenq, A.; Zrikem, M. Covering delivery problem with electric vehicle and parcel lockers: Variable neighborhood search approach. Comput. Oper. Res. 2023, 157, 106263. [Google Scholar] [CrossRef]
- Boschetti, M.A.; Novellani, S. Last-mile delivery with drone and lockers. Networks 2024, 83, 213–235. [Google Scholar] [CrossRef]
- Aftabi, N.; Moradi, N.; Mahroo, F. Feed-Forward Neural Networks as a Mixed-Integer Program. arXiv 2024, arXiv:2402.06697. [Google Scholar]
- Aftabi, N.; Moradi, N.; Mahroo, F.; Kianfar, F. A Multi-Method Framework for Information Security Investment. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4730222 (accessed on 14 June 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).