Integrated Thermomechanical Analysis of Tires and Brakes for Vehicle Dynamics and Safety
Abstract
1. Introduction
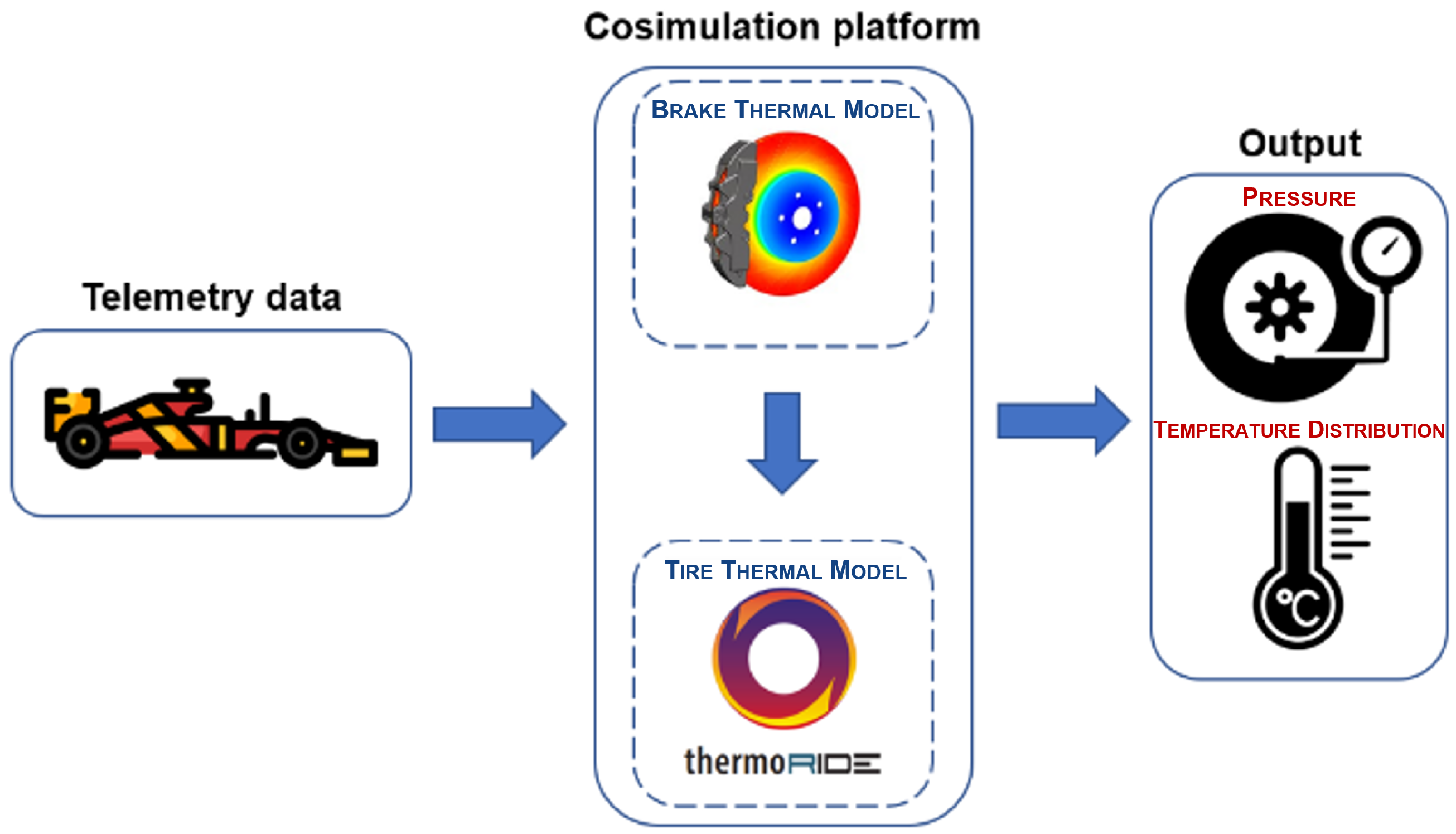
2. Tire and Brake Simulation Platform
2.1. Brake Thermal Model
- is the brake friction power;
- is the brake torque measured by sensor defined in Section 3;
- is the wheel speed.
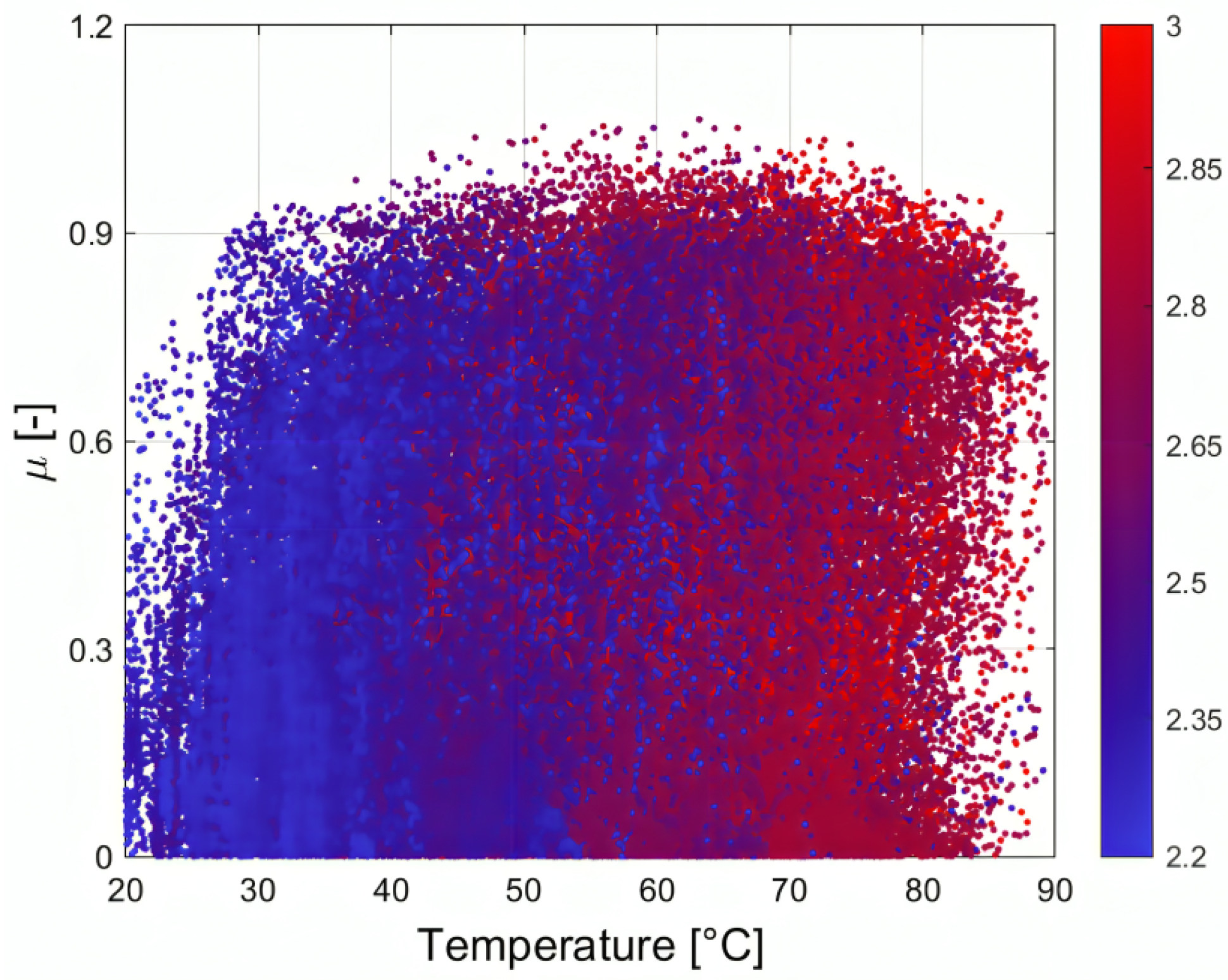
2.2. Tire Thermal Model
3. Experimental Tests
Tire and Vehicle Models Parameterization
- S-Motion: A Correvit S-Motion Type 2055 A sensor is used for the measurement of longitudinal and lateral velocity, sideslip angle, and run distance. It has a range of 400 km/h, a linear velocity measurement accuracy < and an angle resolution <0.01°. The acquisition frequency is 100 Hz.
- IMU: The OXTS 3000 is an inertial platform which measures pitch, roll and yaw rate. It presents the following specifications: accelerometer, bias stability 2 μg, Servo technology, range 10 g, gyroscope, bias stability 2°/h, MEMS technology, and range 100°/s.
- Encoders: The Bosch HA-M is used to measure the wheel angular speed. It has a max frequency of 4.2 kHz and an accuracy repeatability of the falling edge of tooth <4%.
- An infrared sensor is used to measure the tread surface temperature. The acquisition frequency is 10 Hz.
- Internal powered pressure and IR temperature array sensor pressure accuracy <|10 mBar| and temperature accuracy <|3 °C|.
- Wheel force transducers: These are multi-axial measurement systems for use in the development and testing of complete vehicle chassis and components. During measurements, the WFT RoaDyn S6 replaces standard wheel and measures forces (Fx, Fy, and Fz) and torque (Mx, My, and Mz) applied across the tire contact area in the three directions of the wheel coordinate system.
- Brake pressure sensors: AIM M10 0–160 bar comes with 719 black four pin male connectors to fit all AIM loggers and dashboard displays/loggers.
- Piston Area: 18.74 cm2 for brake 1 and 2, 17.62 for brake 3;
- Effective Radius: 134 mm for brake 1, 111 mm for brake 2 and 105 mm for brake 3;
- Pad dimensions: 280 × 22 mm for brake 1 and 2275 × 20 mm for brake 3;
- Friction material: the Ferodo 4209 for all brake systems evaluated;
- Disk material: cast iron for all brake systems evaluated.
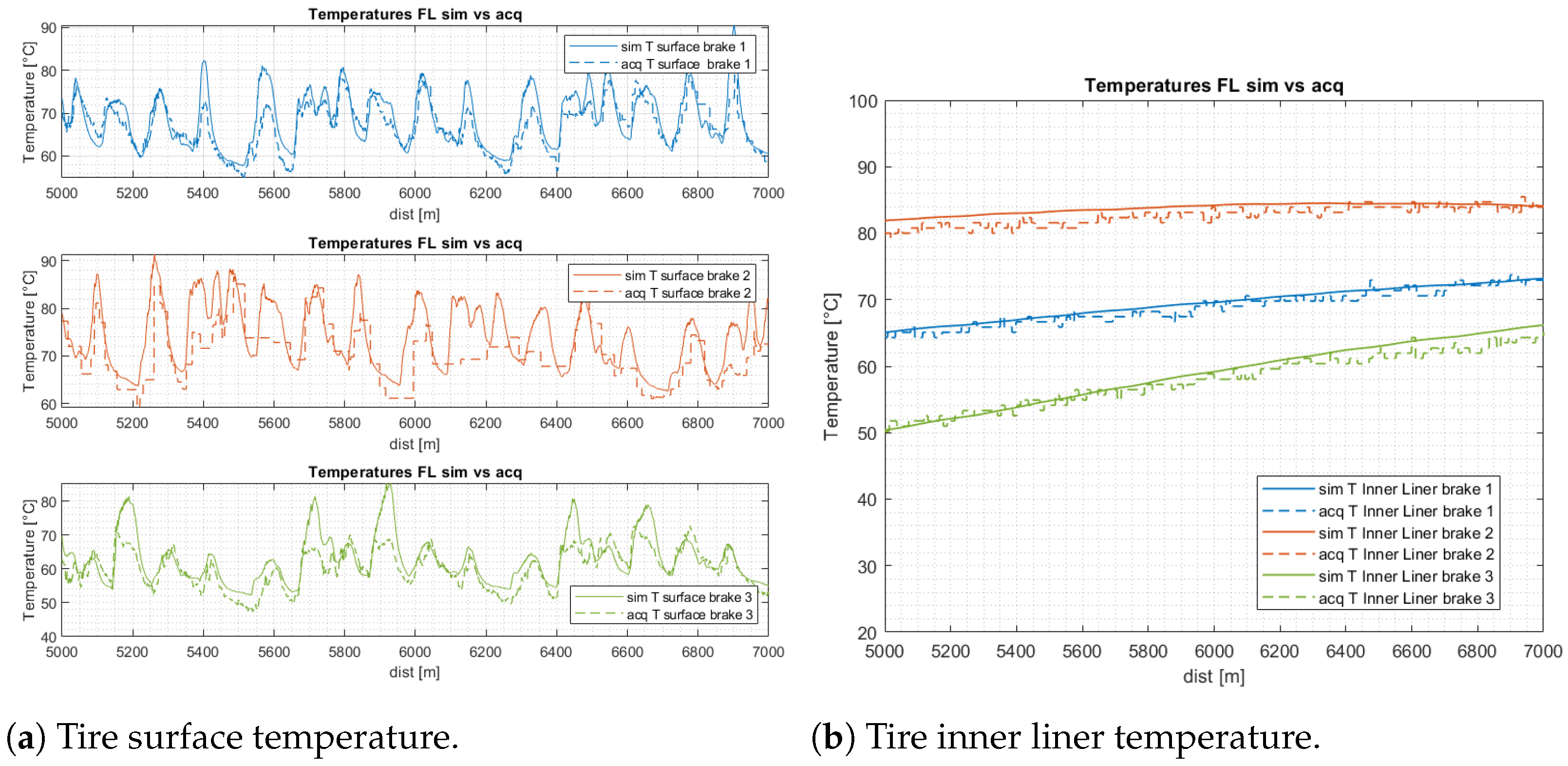
4. Results Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Farroni, F.; Sakhnevych, A. Tire multiphysical modeling for the analysis of thermal and wear sensitivity on vehicle objective dynamics and racing performances. Simul. Model. Pract. Theory 2022, 117, 102517. [Google Scholar] [CrossRef]
- Romano, L.; Sakhnevych, A.; Strano, S.; Timpone, F. A hybrid tyre model for in-plane dynamics. Veh. Syst. Dyn. 2019, 58, 1123–1145. [Google Scholar] [CrossRef]
- Romano, L.; Timpone, F.; Bruzelius, F.; Jacobson, B. Rolling, tilting and spinning spherical wheels: Analytical results using the brush theory. Mech. Mach. Theory 2022, 173, 104836. [Google Scholar] [CrossRef]
- Barbaro, M.; Genovese, A.; Timpone, F.; Sakhnevych, A. Extension of the multiphysical magic formula tire model for ride comfort applications. Nonlinear Dyn. 2024, 112, 4183–4208. [Google Scholar] [CrossRef]
- Niola, V.; Spirto, M.; Savino, S.; Cosenza, C. Vibrational analysis to detect cavitation phenomena in a directional spool valve. Int. J. Mech. Control. 2021, 22, 11–16. [Google Scholar]
- Calabrese, A.; Losanno, D.; Barjani, A.; Spizzuoco, M.; Strano, S. Effects of the long-term aging of glass-fiber reinforced bearings (FRBs) on the seismic response of a base-isolated residential building. Eng. Struct. 2020, 221, 110735. [Google Scholar] [CrossRef]
- Calabrese, A.; Quaglini, V.; Strano, S.; Terzo, M. Online estimation of the friction coefficient in sliding isolators. Struct. Control. Health Monit. 2020, 27, e2459. [Google Scholar] [CrossRef]
- Califano, F.; Cosenza, C.; Niola, V.; Savino, S. Multibody model for the design of a rover for agricultural applications: A preliminary study. Machines 2022, 10, 235. [Google Scholar] [CrossRef]
- Niola, V.; Savino, S.; Quaremba, G.; Cosenza, C.; Nicolella, A.; Spirto, M. Discriminant analysis of the vibrational behavior of a gas micro-turbine as a function of fuel. Machines 2022, 10, 925. [Google Scholar] [CrossRef]
- Teodosio, L.; Timpone, F.; dell’Annunziata, G.N.; Genovese, A. RANS 3D CFD simulations to enhance the thermal prediction of tyre thermodynamic model: A hierarchical approach. Results Eng. 2021, 12, 100288. [Google Scholar] [CrossRef]
- Teodosio, L.; Alferi, G.; Genovese, A.; Farroni, F.; Mele, B.; Timpone, F.; Sakhnevych, A. A numerical methodology for thermo-fluid dynamic modelling of tyre inner chamber: Towards real time applications. Meccanica 2021, 56, 549–567. [Google Scholar] [CrossRef]
- Ballo, F.; Stabile, P.; Gobbi, M.; Mastinu, G. A lightweight ultra-efficient electric vehicle multi-physics modeling and driving strategy optimization. IEEE Trans. Veh. Technol. 2022, 71, 8089–8103. [Google Scholar] [CrossRef]
- Genovese, A.; Strano, S.; Terzo, M. Design and multi-physics optimization of an energy harvesting system integrated in a pneumatic suspension. Mechatronics 2020, 69, 102395. [Google Scholar] [CrossRef]
- Genovese, A.; Pastore, S.R. Development of a portable instrument for non-destructive characterization of the polymers viscoelastic properties. Mech. Syst. Signal Process. 2021, 150, 107259. [Google Scholar] [CrossRef]
- Genovese, A.; Maiorano, A.; Russo, R. A novel methodology for non-destructive characterization of polymers’ viscoelastic properties. Int. J. Appl. Mech. 2022, 14, 2250017. [Google Scholar] [CrossRef]
- Sakhnevych, A.; Genovese, A. Tyre wear model: A fusion of rubber viscoelasticity, road roughness, and thermodynamic state. Wear 2024, 542–543, 205291. [Google Scholar] [CrossRef]
- Sakhnevych, A.; Genovese, A.; Maiorano, A.; Timpone, F.; Farroni, F. An ultrasound method for characterization of viscoelastic properties in frequency domain at small deformations. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2021, 235, 7180–7191. [Google Scholar] [CrossRef]
- Jodhani, J.; Handa, A.; Gautam, A.; Rana, R. Ultrasonic non-destructive evaluation of composites: A review. Mater. Today Proc. 2023, 78, 627–632. [Google Scholar] [CrossRef]
- Mosconi, L.; Farroni, F.; Sakhnevych, A.; Timpone, F.; Gerbino, F.S. Adaptive vehicle dynamics state estimator for onboard automotive applications and performance analysis. Veh. Syst. Dyn. 2023, 61, 3244–3268. [Google Scholar] [CrossRef]
- Strano, S.; Terzo, M.; Tordela, C. Output-only estimation of lateral wheel-rail contact forces and track irregularities. Veh. Syst. Dyn. 2023. [Google Scholar] [CrossRef]
- Kaiser, I.; Salvatore Strano, M.T.; Tordela, C. Estimation of the railway equivalent conicity under different contact adhesion levels and with no wheelset sensorization. Veh. Syst. Dyn. 2022, 61, 19–37. [Google Scholar] [CrossRef]
- Kaiser, I.; Strano, S.; Terzo, M.; Tordela, C. Anti-yaw damping monitoring of railway secondary suspension through a nonlinear constrained approach integrated with a randomly variable wheel-rail interaction. Mech. Syst. Signal Process. 2021, 146, 107040. [Google Scholar] [CrossRef]
- Gandelli, E.; Lomiento, G.; Quaglini, V.; Strano, S.; Terzo, M.; Tordela, C. Estimation of the instantaneous friction coefficients of sliding isolators subjected to bi-directional orbits through a nonlinear state observer. Eng. Struct. 2021, 249, 113374. [Google Scholar] [CrossRef]
- Li, Y.; Zuo, S.; Lei, L.; Yang, X.; Wu, X. Analysis of impact factors of tire wear. J. Vib. Control 2012, 18, 833–840. [Google Scholar] [CrossRef]
- Conant, F. Tire temperatures. Rubber Chem. Technol. 1971, 44, 397–439. [Google Scholar] [CrossRef]
- Mavros, G. A thermo-frictional tyre model including the effect of flash temperature. Veh. Syst. Dyn. 2019, 57, 721–751. [Google Scholar] [CrossRef]
- Calabrese, A.; Gandelli, E.; Quaglini, V.; Strano, S.; Terzo, M.; Tordela, C. Monitoring of hysteretic friction degradation of curved surface sliders through a nonlinear constrained estimator. Eng. Struct. 2021, 226, 111371. [Google Scholar] [CrossRef]
- Romagnuolo, F.; Avolio, S.; Fichera, G.; Ruffini, M.; Stefanelli, R.; Timpone, F. A Co-Simulation Platform with Tire and Brake Thermal Model for the Analysis and Reproduction of Blanking. Vehicles 2023, 5, 1605–1621. [Google Scholar] [CrossRef]
- Schlanger, H. A one-dimensional numerical model of heat transfer in the process of tire vulcanization. Rubber Chem. Technol. 1983, 56, 304–321. [Google Scholar] [CrossRef]
- Whicker, D.; Browne, A.; Segalman, D.; Wickliffe, L. A thermomechanical approach to tire power loss modeling. Tire Sci. Technol. 1981, 9, 3–18. [Google Scholar] [CrossRef]
- Guner, R.; Yavuz, N.; Kopmaz, O.; Ozturk, F.; Korkmaz, I. Validation of analytical model of vehicle brake system. Int. J. Veh. Des. 2004, 35, 331–348. [Google Scholar] [CrossRef]
- Bakar, A.; Abu, R.; Ouyang, H.; Khai, L.C.; Abdullah, M.S. Thermal Analysis of a Disc Brake Model Considering a Real Brake Pad Surface and Wear. Int. J. Veh. Struct. Syst. (IJVSS) 2010, 2, 20–27. [Google Scholar]
- Calabrese, F.; Baecker, M.; Galbally, C.; Gallrein, A. A detailed thermo-mechanical tire model for advanced handling applications. Sae Int. J. Passeng.-Cars-Mech. Syst. 2015, 8, 501–511. [Google Scholar] [CrossRef]
- Li, X.; Han, J.; Dai, X.; Zheng, Z.; Niu, Y. Monitoring overloaded trucks with infrared thermal imaging of tire sidewall. Heliyon 2024, 10, e34358. [Google Scholar] [CrossRef] [PubMed]
- Stoumpos, S.; Bolbot, V.; Theotokatos, G.; Boulougouris, E. Safety performance assessment of a marine dual fuel engine by integrating failure mode, effects and criticality analysis with simulation tools. Proc. Inst. Mech. Eng. Part J. Eng. Marit. Environ. 2022, 236, 376–393. [Google Scholar] [CrossRef]
- Terzo, A.; Gobbato, P.; Masi, M.; Rossi, A. An engine/vehicle model to assess the theoretical increase of car safety by using the spark ignition engine to support the conventional braking system. Int. J. Thermodyn. 2016, 19, 187–196. [Google Scholar]
- Ilie, F.; Cristescu, A.C. Tribological behavior of friction materials of a disk-brake pad braking system affected by structural changes—A review. Materials 2022, 15, 4745. [Google Scholar] [CrossRef]
- Sethupathi, P.B.; Chandradass, J.; Saibalaji, M. Comparative study of disc brake pads sold in Indian market—Impact on safety and environmental aspects. Environ. Technol. Innov. 2021, 21, 101245. [Google Scholar] [CrossRef]
- Kreith, F.; Bohn, M. Principles of Heat Transfer, St; Paul: West Publishing Company: Eagan, MT, USA, 1993. [Google Scholar]
- Stevens, K.; Tirovic, M. Heat dissipation from a stationary brake disc, Part 1: Analytical modelling and experimental investigations. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2018, 232, 1707–1733. [Google Scholar] [CrossRef]
- Rout, S. Design and Analysis of Brake Disc. Ph.D. Thesis, Veer Surendra Sai University of Technology, Odisha, India, 2018. [Google Scholar]
- Thakur, A.S.; Dhakad, P. Thermal analysis of disc brake using ANSYS. Int. J. Tech. Innov. Mod. Eng. Sci. 2018, 4, 8–17. [Google Scholar]
- Day, A.J.; Bryant, D. Braking of Road Vehicles; Butterworth-Heinemann: Oxford, UK, 2022. [Google Scholar]
- Antanaitis, D.; Monsere, P.; Riefe, M. Brake system and subsystem design considerations for race track and high energy usage based on fade limits. SAE Int. J. Passeng.-Cars-Mech. Syst. 2008, 1, 689–708. [Google Scholar] [CrossRef]





| Quantity | Description | Unit |
|---|---|---|
| vWheelFLLong | Tire Longitudinal Velocity | m/s |
| nWheelFL | Tire Rotation Frequency | rad/s |
| FzTireFL | Tire Vertical Load | N |
| FxTireFL | Tire Longitudinal Force | N |
| FyTireFL | Tire Lateral Force | N |
| vSlidingSpeedFLLong | Tire Longitudinal Sliding Speed | m/s |
| vSlidingSpeedFLLat | Tire Lateral Sliding Speed | m/s |
| aCamberFL | Tire Camber Angle | rad |
| TDiscFL | Tire Disc Temperature | °C |
| TAirFL | External Air Temperature | °C |
| TTrackFL | Road Temperature | °C |
| TireFLcompoundThickness | Tire Tread Thickness | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefanelli, A.; Aprea, M.; Carbone, F.; Romagnuolo, F.; Caresia, P.; Suero, R. Integrated Thermomechanical Analysis of Tires and Brakes for Vehicle Dynamics and Safety. Vehicles 2024, 6, 1637-1647. https://doi.org/10.3390/vehicles6030077
Stefanelli A, Aprea M, Carbone F, Romagnuolo F, Caresia P, Suero R. Integrated Thermomechanical Analysis of Tires and Brakes for Vehicle Dynamics and Safety. Vehicles. 2024; 6(3):1637-1647. https://doi.org/10.3390/vehicles6030077
Chicago/Turabian StyleStefanelli, Andrea, Marco Aprea, Fabio Carbone, Fabio Romagnuolo, Pietro Caresia, and Raffaele Suero. 2024. "Integrated Thermomechanical Analysis of Tires and Brakes for Vehicle Dynamics and Safety" Vehicles 6, no. 3: 1637-1647. https://doi.org/10.3390/vehicles6030077
APA StyleStefanelli, A., Aprea, M., Carbone, F., Romagnuolo, F., Caresia, P., & Suero, R. (2024). Integrated Thermomechanical Analysis of Tires and Brakes for Vehicle Dynamics and Safety. Vehicles, 6(3), 1637-1647. https://doi.org/10.3390/vehicles6030077







