Non-Perturbative Approaches to Linear and Nonlinear Responses of Atoms, Molecules, and Molecular Aggregates: A Theoretical Approach to Molecular Quantum Information and Quantum Biology
Abstract
1. Introduction
2. Nonlinear Responses of Molecular Materials
2.1. Linear and Nonlinear Responses of Molecular Materials for Electronic and Magnetic Fields
2.2. Non-Perturbative Methods of Linear and Nonlinear Responses of Materials
2.3. Quasi-Energy Derivative Methods of Linear and Nonlinear Responses
2.4. TD HF and TD DFT Computations of Nonlinear Responses
2.5. Computations of Nonlinear Responses for Open-Shell Atoms and Molecules
2.6. Coupled-Cluster Approaches for Nonlinear Responses
3. Numerical Liouville Approaches to Frequency-Dependent Nonlinear Responses
3.1. Nonperturbative Approach for Higher Nonlinear Responses
3.2. Numerical Liouville Approaches to Frequency-Dependent Nonlinear Responses
3.3. Numerical Liouville Approaches to Frequency-Dependent Nonlinear Responses
4. Discovery of High-Order Harmonic Generation and Developments of Attosecond Chemistry
4.1. Discovery of High-Order Harmonic Generation
4.2. Generation of Attosecond Pulses and Attosecond Spectroscopy
4.3. Molecular Orbital Tomography
4.4. Observations of the Real and Imaginary Parts of Wave Functions
4.5. Dyson Orbitals of Ionized Diradicals and Related Species
5. Quantum Phase Dynamics and Entangled Entropy for Quantum Material Sciences
5.1. Quantum Dynamics Simulations and Level Models for Quantum Optics of Molecules
5.2. Quantum Master Equation and Reduced Density Matrix
5.3. Jaynes–Cummings (JC) Model and Collapse-Revival Phenomena for Atoms and Molecules
5.4. Bose–Einstein Condensation, Quantum Information Sciences and Quantum Computing
5.5. Low-Dimensional Arrays for Organic and Molecular Qubits
6. Exciton Migration and Coherent Energy Transfers in Biological Systems
6.1. Exciton Dynamics in Dendric Structures and Model for Antenna Systems for Photosystem
6.2. Master Equation for Exciton Dynamics in Dendric Structures
6.3. Characteristic Features of Energy Transfers in Dendrimer Systems
6.4. Coherent Energy Transfer and Coherent Control for Quantum Devices
6.5. Quantum Dynamics of Excitons in Dendrimers with and Without Relaxation Term
6.6. Energy Transfers for Phycobilisomes in Cyanobacteria
6.7. Energy Transfers in Light-Harvesting Systems in Photosynthesis
6.8. Quantum Effects for Energy Transfers in Fenna–Mattews–Olson (FMO) Proteins
7. Discussions, Future Prospects, and Concluding Remarks
7.1. Down-Conversion and Four-Wave Mixing for Generation of Entangled Light Pair
7.2. Decoherence, Error Corrections, and Fault-Tolerant Quantum Computer
7.3. Triplet–Triplet Annihilation for Singlet Oxygen Formation and Photochemical Damages
7.4. Triplet–Triplet Annihilation, Upconversion and Frequency Doubling
7.5. Future Prospects of Quantum Effects in Photosynthesis
7.6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Theoretical Computational Methods of Linear and Nonlinear Responses of Materials
Appendix A.2. Functional Behaviors of Nonlinear γ-Value with Diradical Character: Exact Models

Appendix A.3. Quantum Phase Dynamics and Pegg–Barnett Phase Operator
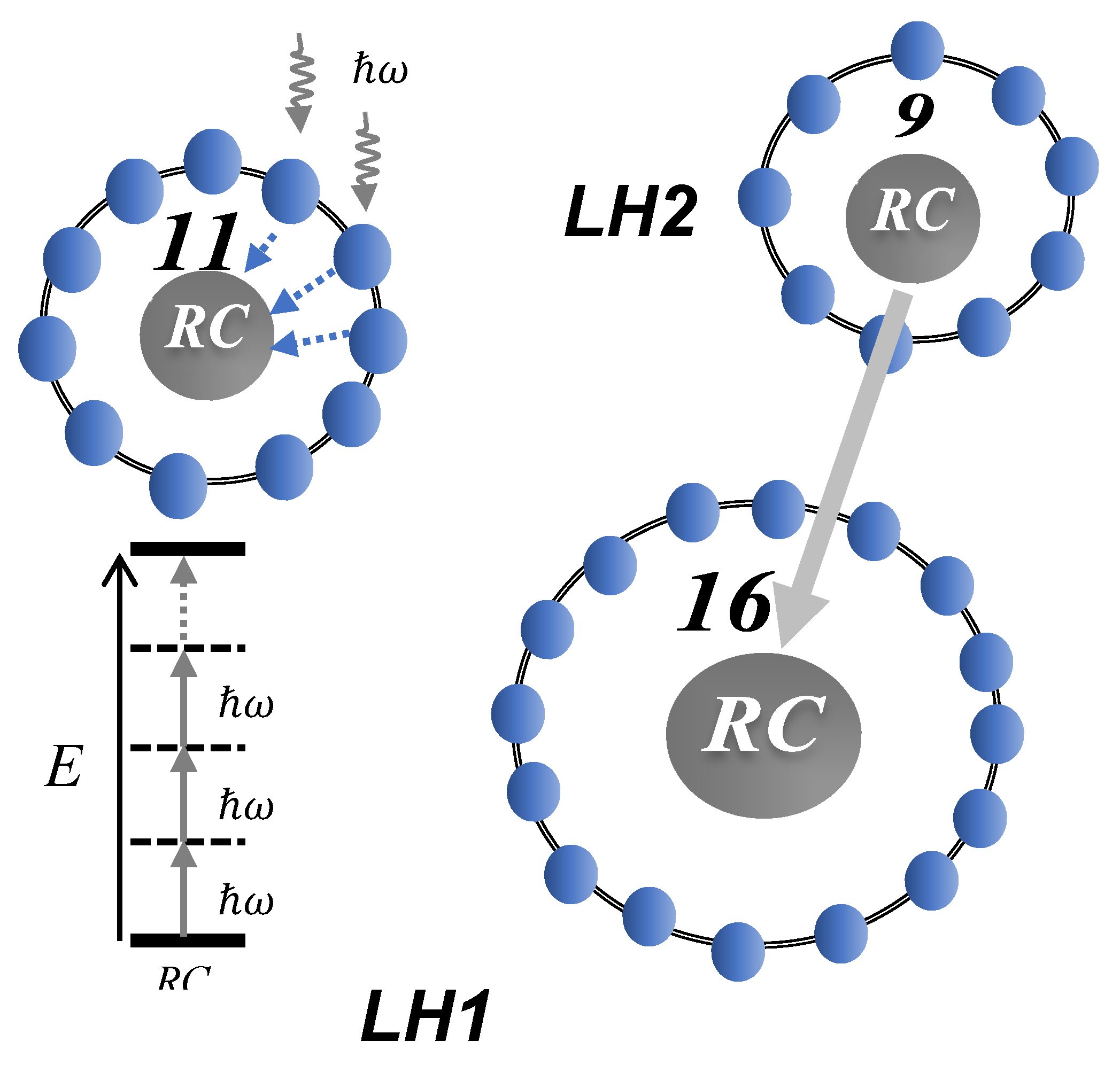
Appendix A.4. Ring Structures of LH1, LH2, and LH2’
References
- Yamada, S.; Shigemoto, I.; Kawakami, T.; Isobe, H.; Shoji, M.; Miyagawa, K.; Yamaguchi, K. Quantum Mechanical Approaches to Strongly Correlated Electron Systems: Structure, Bonding, and Properties of Diradicals, Triradicals, and Polyradicals. Chemistry 2025, 7, 38. [Google Scholar] [CrossRef]
- Heisenberg, W. Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Z. Phys. 1925, 33, 879–893. [Google Scholar] [CrossRef]
- Born, M. Quantenmechanik der Stoßvorgänge. Z. Phys. 1926, 38, 803–827. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The physical interpretation of quantum dynamics. Proc. Roy. Soc. A 1927, 113, 621–641. [Google Scholar]
- Kennard, E.H. Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 1927, 44, 326–352. [Google Scholar] [CrossRef]
- Robertson, H.P. The Uncertainty Principle. Phys. Rev. 1929, 34, 163–164. [Google Scholar] [CrossRef]
- Hirschman, I.J., Jr. A note on entropy. Am. J. Math. 1957, 79, 152–156. [Google Scholar] [CrossRef]
- Ozawa, M. Measurement breaking the standard quantum limit for free-mass position. Phys. Rev. Lett. 1988, 60, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, S. Uncertainty relations in simultaneous measurements for arbitorary observales. Rep. Math. Phys. 1991, 29, 257–273. [Google Scholar] [CrossRef]
- Ozawa, M. Universally valis reformulation of the Heisenberg uncertainity principle on noise and disturbance in measurement. Phys. Rev. A 2003, 67, 042105. [Google Scholar] [CrossRef]
- Erhart, J.; Sponar, S.; Sulypk, G.; Badurek, G.; Ozawa, M.; Hasegawa, Y. Experimental demonstration of a universally valid error-disturbance uncertainty relation in spin measurements. Nat. Phys. 2012, 8, 185–189. [Google Scholar] [CrossRef]
- Rozema, L.A.; Darabi, A.; Mahler, D.H.; Hayat, A.; Soudanger, Y.; Steinberg, A.M. Violation of Heisenberg’s measurement-disturbance relationship by weak measurements. Phys. Rev. Lett. 2012, 109, 100404. [Google Scholar] [CrossRef]
- Kaneda, F.; Baek, S.-Y.; Ozawa, M.; Edamatsu, K. Experimental test of error-disturbance uncertinty relations by weak measurement. Phys. Rev. Lett. 2014, 112, 020402. [Google Scholar] [CrossRef] [PubMed]
- Thome, K.K. Nobel Lecture: LIGO and gravitational waves III. Rev. Mod. Phys. 2018, 90, 040503. [Google Scholar] [CrossRef]
- Einstein, A. Über einen die erzeugung und verwandlung des lichtes betreffenden heuristischen gesichtspunkt (on a heuristic viewpoint concerning the production and transformation of light). Ann. Phys. 1905, 322, 132–148. [Google Scholar] [CrossRef]
- Young, T. A Course of Lectures on Natural Philosophy and the Mechanical Arts; Joseph Johnson: London, UK, 1807. [Google Scholar]
- Tonomura, A.; Endo, J.; Kawasaki, T.; Ezawa, H. Demonstration of single-electron buildup of an interference pattern. Am. J. Phys. 1989, 57, 117–120. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Takeda, S. New era of optical quantum computers: Focused on loop-based approach. JSAP Rev. 2023, 230204. [Google Scholar]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Nakano, M.; Shigemoto, I.; Yamada, S.; Yamaguchi, K. Size-consistent approach and density analysis of hyperpolarizability: Second hyperpolarizabilities of polymeric systems with and without defects. J. Chem. Phys. 1995, 103, 4175–4191. [Google Scholar] [CrossRef]
- Sasagane, K.; Aiga, F.; Itoh, R. Higher-order response theory based on the quasienergy derivatives: The derivation of the frequency-dependent polarizabilities and hyperpolarizabilities. J. Chem. Phys. 1993, 99, 3738–3778. [Google Scholar] [CrossRef]
- Aiga, F.; Sasagane, K.; Itoh, R. Frequency-dependent hyperpolarizabilities in the Møller–Plesset perturbation theory. J. Chem. Phys. 1993, 99, 3779–3789. [Google Scholar] [CrossRef]
- Aiga, F.; Itoh, R. Calculation of frequency-dependent polarizabilities and hyperpolarizabilities by the second-order Møller-Plesset perturbation theory. Chem. Phys. Lett. 1996, 251, 372–380. [Google Scholar] [CrossRef]
- Aiga, F.; Sasagane, K.; Itoh, R. The quadratic response function in the THFD approximation and its application to frequency-dependent hyperpolarizabilities of the FH molecule. Chem. Phys. 1992, 167, 277–290. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Numerical Liouville approach: A calculation method for nonlinear optical susceptibilities of N-state systems. Phys. Rev. A 1994, 50, 2989–3004. [Google Scholar] [CrossRef]
- Keldysh, L.V. Ionization in the field of a strong electromagnetic wave. Sov. Phys. JETP 1965, 20, 1307–1314. [Google Scholar]
- Krainov, V.P. Ionization rates and energy and angular distributions at the barrier-suppression ionization of complex atoms and atomic ions. J. Sov. Phys. JETP 1986, 64, 425–431. [Google Scholar] [CrossRef]
- Li, X.F.; L’Huillier, A.; Ferray, M.; Lompré, L.A.; Mainfray, G. Multiple-harmonic generation in rare gases at high laser intensity. Phys. Rev. A 1989, 39, 5751–5761. [Google Scholar] [CrossRef] [PubMed]
- Moulton, P.F. Spectroscopic and laser characteristics of Ti:Al2O3. J. Opt. Soc. Am. 1986, 2, 125–133. [Google Scholar] [CrossRef]
- Maine, P.; Strickland, D.; Bado, P.; Pessot, M.; Mourou, G. Generation of ultrahigh peak power pulses by chirped pulse amplification. IEEE J. Quantum Electron. 1988, 24, 398–403. [Google Scholar] [CrossRef]
- Tong, X.M.; Zhao, Z.X.; Lin, C.D. Theory of molecular tunneling ionization. Phys. Rev. A 2002, 66, 033402. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- Corkum, P.B.; Burnett, N.H.; Ivanov, M.Y. Subfemtosecond pulses. Opt. Lett. 1994, 15, 1870–1872. [Google Scholar] [CrossRef]
- Constant, E.; Taranukhin, V.D.; Stolow, A.; Corkum, P.B. Methods for the measurement of the duration of high-harmonic pulses. Phys. Rev. A 1997, 56, 3870–3878. [Google Scholar] [CrossRef]
- Kulanderm, K.C.; Shore, B.W. Calculations of Multiple-Harmonic Conversion of 10640 nm Radiation in Xe. Phys. Rev. Lett. 1989, 62, 524–528. [Google Scholar] [CrossRef] [PubMed]
- Brabec, T.; Krausz, F. Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 2000, 72, 545–591. [Google Scholar] [CrossRef]
- Mehendale, M.; Mitchell, S.A.; Likforman, J.; Villeneuve, D.M.; Corkum, P.B. Method for single-shot measurement of the carrier envelope phase of a few-cycle laser pulse. Opt. Lett. 2000, 25, 1672–1674. [Google Scholar] [CrossRef]
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a train of attosecond pulses from high harmonic generation. Science 2001, 292, 1689–1692. [Google Scholar] [CrossRef]
- Hentschel, M.; Kienberger, R.; Spielmann, C.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond metrology. Nature 2001, 414, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Drescher, M.; Hentschel, M.; Kienberger, R.; Uiberacker, M.; Yakovlev, V.; Scrinzi, A.; Westerwalbesloh, T.; Kleineberg, U.; Heinzmann, U.; Krausz, F. Time-resolved atomic inner-shell spectroscopy. Nature 2002, 419, 803–807. [Google Scholar] [CrossRef]
- Kitzler, M.; Milosevic, N.; Scrinzi, A.; Krausz, F.; Brabec, T. Quantum Theory of Attosecond XUV Pulse Measurement by Laser Dressed Photoionization. Phys. Rev. Lett. 2002, 88, 173904. [Google Scholar] [CrossRef]
- Niikura, H.; Légaré, F.; Hasbani, R.; Bandrauk, A.D.; Ivanov, M.Y.; Villeneuve, D.M.; Corkum, P.B. Sub-laser-cycle electron pulses for probing molecular dynamics. Nature 2002, 417, 917–922. [Google Scholar] [CrossRef] [PubMed]
- Mairesse, Y.; Bohan, A.D.; Frasinski, L.J.; Merdji, H.; Dinu, L.C.; Monchicourt, P.; Breger, P.; KovačEv, M.; Taïeb, R.; Carré, B.; et al. Attosecond Synchronization of High-Harmonic Soft X-rays. Science 2003, 302, 1540–1543. [Google Scholar] [CrossRef]
- Baltuška, A.; Udem, T.; Uiberacker, M.; Hentschel, M.; Goulielmakis, E.; Gohle, C.; Holzwarth, R.; Yakovlev, V.S.; Scrinzi, A.; Hänsch, T.W.; et al. Attosecond control of electronic processes by intense light fields. Nature 2003, 421, 611–615. [Google Scholar] [CrossRef]
- Niikura, H.; Légaré, F.; Hasbani, R.; Ivanov, M.Y.; Villeneuve, D.M.; Corkum, P.B. Probing molecular dynamics with attosecond resolution using correlated wave packet pairs. Nature 2003, 421, 826–829. [Google Scholar] [CrossRef] [PubMed]
- Itatani, J.; Levesque, J.; Zeidler, D.; Niikura, H.; Pépin, H.; Kieffer, J.C.; Corkum, P.B.; Villeneuve, D.M. Tomographic imaging of molecular orbitals. Nature 2004, 432, 867–871. [Google Scholar] [CrossRef]
- Sekikawa, T.; Kosuge, A.; Kanai, T.; Watanabe, S. Nonlinear optics in the extreme ultraviolet. Nature 2004, 432, 605–608. [Google Scholar] [CrossRef]
- Litvinyuk, I.V.; Légaré, F.; Dooley, P.W.; Villeneuve, D.M.; Corkum, P.B.; Zanghellini, J.; Pegarkov, A.; Fabian, C.; Brabec, T. Shakeup Excitation during Optical Tunnel Ionization. Phys. Rev. Lett. 2005, 94, 033003. [Google Scholar] [CrossRef]
- Niikura, H.; Légaré, F.; Villeneuve, D.M.; Corkum, P.B. Attosecond dynamics using sub-laser-cycle electron pulses. J. Mod. Opt. 2005, 52, 453–464. [Google Scholar] [CrossRef]
- Niikura, H.; Villeneuve, D.M.; Corkum, P.B. Stopping a Vibrational Wave Packet with Laser-Induced Dipole Forces. Phys. Rev. Lett. 2005, 92, 133002. [Google Scholar] [CrossRef]
- Niikura, H.; Villeneuve, D.M.; Corkum, P.B. Controlling vibrational wave packets with intense, few-cycle laser pulses. Phys. Rev. A 2006, 73, 021402. [Google Scholar] [CrossRef]
- Baker, S.; Robinson, J.S.; Haworth, C.A.; Teng, H.; Smith, R.A.; Chirilă, C.C.; Lein, M.; Tisch, J.W.G.; Marangos, J.P. Probing Proton Dynamics in Molecules on an Attosecond Time Scale. Science 2006, 312, 424–427. [Google Scholar] [CrossRef]
- Patchkovskii, S.; Zhao, Z.; Brabec, T.; Villeneuve, D.M. High Harmonic Generation and Molecular Orbital Tomography in Multielectron Systems: Beyond the Single Active Electron Approximation. Phys. Rev. Lett. 2006, 97, 123003. [Google Scholar] [CrossRef] [PubMed]
- Uiberacker, M.; Uphues, T.; Schultze, M.; Verhoef, A.J.; Yakovlev, V.; Kling, M.F.; Rauschenberger, J.; Kabachnik, N.M.; Schröder, H.; Lezius, M.; et al. Attosecond real-time observation of electron tunnelling in atoms. Nature 2007, 427, 627–632. [Google Scholar] [CrossRef]
- Mairesse, Y.; Dudovich, N.; Levesque, J.; Ivanov, M.Y.; Corkum, P.B.; Villeneuve, D.M. Electron wavepacket control with elliptically polarized laser light in high harmonic generation from aligned molecules. New J. Phys. 2008, 10, 025015. [Google Scholar] [CrossRef]
- Morishita, T.; Le, A.; Chen, Z.; Lin, C.D. Accurate Retrieval of Structural Information from Laser-Induced Photoelectron and High-Order Harmonic Spectra by Few-Cycle Laser Pulses. Phys. Rev. Lett. 2008, 100, 013903. [Google Scholar] [CrossRef]
- Goulielmakis, E.; Schultze, M.; Hofstetter, M.; Yakovlev, V.S.; Gagnon, J.; Uiberacker, M.; Aquila, A.L.; Gullikson, E.M.; Attwood, D.T.; Kienberger, R.; et al. Single-Cycle Nonlinear Optics. Science 2008, 320, 1614–1617. [Google Scholar] [CrossRef]
- Gilbertson, S.; Mashiko, H.; Li, C.; Khan, S.D.; Shakya, M.M.; Moon, E.; Chang, Z. A low-loss, robust setup for double optical gating of high harmonic generation. Appl. Phys. Lett. 2008, 92, 071109. [Google Scholar] [CrossRef]
- Mairesse, Y.; Zeidler, D.; Dudovich, N.; Spanner, M.; Levesque, J.; Villeneuve, D.M.; Corkum, P.B. High-Order Harmonic Transient Grating Spectroscopy in a Molecular Jet. Phys. Rev. Lett. 2008, 100, 143903. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Smirnova, O.; Mairesse, Y.; Patchkovskii, S.; Dudovich, N.; Villeneuve, D.; Corkum, P.; Ivanov, M.Y. High harmonic interferometry of multi-electron dynamics in molecules. Nature 2009, 460, 972–977. [Google Scholar] [CrossRef]
- Akagi, H.; Otobe, T.; Staudte, A.; Shiner, A.; Turner, F.; Dörner, R.; Villeneuve, D.M.; Corkum, P.B. Laser Tunnel Ionization from Multiple Orbitals in HCl. Science 2009, 325, 1364–1367. [Google Scholar] [CrossRef]
- Shafir, D.; Mairesse, Y.; Villeneuve, D.M.; Corkum, P.B.; Dudovich, N. Atomic wavefunctions probed through strong-field light–matter interaction. Nat. Phys. 2009, 5, 412–416. [Google Scholar] [CrossRef]
- Haessler, S.; Caillat, J.; Boutu, W.; Giovanetti-Teixeira, C.; Ruchon, T.; Auguste, T.; Diveki, Z.; Breger, P.; Maquet, A.; Carré, B.; et al. Attosecond imaging of molecular electronic wavepackets. Nat. Phys. 2010, 6, 200–206. [Google Scholar] [CrossRef]
- Niikura, H.; Wörner, H.J.; Villeneuve, D.M.; Corkum, P.B. Probing the Spatial Structure of a Molecular Attosecond Electron Wave Packet Using Shaped Recollision Trajectories. Phys. Rev. Lett. 2011, 107, 093004. [Google Scholar] [CrossRef]
- Tersoff, J.; Hamann, D.R. Theory of the scanning tunneling microscope. Phys. Rev. B 1985, 31, 805–815. [Google Scholar] [CrossRef]
- Repp, J.; Meyer, G.; Stojković, S.M.; Gourdon, A.; Joachim, C. Molecules on Insulating Films: Scanning-Tunneling Microscopy Imaging of Individual Molecular Orbitals. Phys. Rev. Lett. 2005, 94, 026803. [Google Scholar] [CrossRef]
- Pham, B.Q.; Gordon, M.S. Can Orbitals Really Be Observed in Scanning Tunneling Microscopy Experiments? J. Phys. Chem. A 2017, 121, 4851–4852. [Google Scholar] [CrossRef]
- Scerri, E.R. Have Orbitals Really Been Observed ? J. Chem. Educ. 2000, 77, 1492–1494. [Google Scholar] [CrossRef]
- Mulder, P. Are Orbitals Observable? Int. J. Phil. Chem. 2011, 17, 24–35. [Google Scholar]
- Ortiz, J.V. Dyson-orbital concepts for description of electrons in molecules. J. Chem. Phys. 2020, 153, 070902. [Google Scholar] [CrossRef]
- Krylov, A.I. From orbitals to observables and back. J. Chem. Phys. 2020, 153, 080901. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Hiberty, P.C.; Shaik, S.; Gordon, M.S.; Danovich, D. Orbitals and the Interpretation of Photoelectron Spectroscopy and (e,2e) Ionization Experiments. Angew. Chem. Int. Ed. 2019, 58, 12332–12338. [Google Scholar] [CrossRef]
- Fukui, K.; Yonezawa, T.; Shingu, H. A molecular Orbital Theory of Reactivity in Aromatic Hydrocarbons. J. Chem. Phys. 1952, 20, 722–725. [Google Scholar] [CrossRef]
- Fukui, K.; Yonezawa, T.; Shingu, H. Reply to the Comments on the “Frontier Electron Theory”. J. Chem. Phys. 1959, 31, 550–551. [Google Scholar] [CrossRef]
- Pullman, B. Remarks on “Reply to the Comments on ‘Frontier Electron Theory’ by Fukui, Yonezawa, and Nagata”. J. Chem. Phys. 1959, 31, 551–552. [Google Scholar] [CrossRef]
- Shen, Y.R. Optical Second Harmonic Generation at Interfaces. Ann. Rev. Phys. Chem. 1989, 40, 327–350. [Google Scholar] [CrossRef]
- Eisenthal, K.B. Liquid Interfaces Probed by Second-Harmonic and Sum-Frequency Spectroscopy. Chem. Rev. 1996, 96, 1343–1360. [Google Scholar] [CrossRef]
- Cox, G. Biological applications of second harmonic imaging. Biophys. Rev. 2011, 3, 131–141. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sekino, H.; Bartlett, R.J. Frequency dependent nonlinear optical properties of molecules. J. Chem. Phys. 1986, 85, 976–989. [Google Scholar] [CrossRef]
- Sekino, H.; Bartlett, R.J. Molecular hyperpolarizabilities. J. Chem. Phys. 1993, 98, 3022–3037. [Google Scholar] [CrossRef]
- Rice, J.E.; Amos, R.D.; Colwell, S.M.; Handy, N.C.; Sanz, J. Frequency dependent hyperpolarizabilities with application to formaldehyde and methyl fluoride. J. Chem. Phys. 1990, 93, 8828–8839. [Google Scholar] [CrossRef]
- Karna, S.P.; Dupuis, M. Frequency-dependent hyperpolarizabilities of haloforms from ab initio SCF calculations. Chem. Phys. Lett. 1990, 171, 201–208. [Google Scholar] [CrossRef]
- Karna, S.P. Spin-unrestricted time-dependent Hartree–Fock theory of frequency-dependent linear and nonlinear optical properties. J. Chem. Phys. 1996, 104, 6590–6660. [Google Scholar] [CrossRef]
- Bishop, D.M.; Gu, F.L.; Cybulski, S.M. Static and dynamic polarizabilities and first hyperpolarizabilities for CH4, CF4, and CCl4. J. Chem. Phys. 1998, 109, 8407–8415. [Google Scholar] [CrossRef]
- Langhoff, P.W.; Epstein, S.T.; Karplus, M. Aspects of Time-Dependent Perturbation Theory. Rev. Mod. Phys. 1972, 44, 602–644. [Google Scholar] [CrossRef]
- Kobayashi, T.; Sasagane, K.; Yamaguchi, K. Calculations of frequency-dependent polarizabilities for open-shell systems at the second-order Møller-Plesset perturbation theory level based on the quasi-energy derivative method. Int. J. Quantum Chem. 1997, 65, 665–677. [Google Scholar] [CrossRef]
- Kobayashi, T.; Sasagane, K.; Aiga, F.; Yamaguchi, K. Calculation of frequency-dependent first hyperpolarizabilities using the second-order Møller–Plesset perturbation theory. J. Chem. Phys. 1999, 111, 11720–11733. [Google Scholar] [CrossRef]
- Kobayashi, T.; Sasagane, K.; Yamaguchi, K. Frequency-dependent second hyperpolarizabilities in the time-dependent restricted open-shell Hartree-Fock theory: Application to the Li, Na, K and N atoms. J. Chem. Phys. 2000, 112, 7903–7918. [Google Scholar] [CrossRef]
- Yamaki, D.; Shigeta, S.; Yamanaka, S.; Nagao, H.; Yamaguchim, K. Generalized spin orbital calculations of spin-frustrated molecules. Int. J. Quantum Chem. 2001, 84, 546–551. [Google Scholar] [CrossRef]
- Yamaki, D.; Ohsaku, T.; Nagao, H.; Yamaguchim, K. Formulation of unrestricted and restricted Hartree-Fock-Bogoliubov equations. Int. J. Quantum Chem. 2004, 96, 10–16. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Aiga, F.; Tada, T.; Yoshimura, R. Frequency-dependent polarizabilities, hyperpolarizabilities and excitation energies from time-dependent density-functional theory based on the quasi-energy derivative method. J. Chem. Phys. 1999, 111, 2878–2888. [Google Scholar] [CrossRef]
- Bohm, D.; Pines, D. A Collective Description of Electron Interactions III. Coulomb Interactions in a Degenerate Electron Gas. Phys. Rev. 1953, 92, 609–625. [Google Scholar] [CrossRef]
- Thouless, D.J. Vibrational states of nuclei in the random phase approximation. Nucl. Phys. 1961, 22, 78–95. [Google Scholar] [CrossRef]
- McLachlan, A.D.; Ball, M.A. Time-Dependent Hartree—Fock Theory for Molecules. Rev. Mod. Phys. 1964, 38, 844–855. [Google Scholar] [CrossRef]
- Yamaki, D.; Shigeta, Y.; Yamanaka, S.; Nagao, H.; Yamaguchi, K. MP2, Tamm-Dancoff, and RPA methods based on the generalized HF solution. Int. J. Quantum Chem. 2000, 80, 701–707. [Google Scholar] [CrossRef]
- Meyer, H.-D.; Manthe, U.; Cederbaum, L.S. The multi-configurational time-dependent Hartree-Fock approach. Chem. Phys. Lett. 1990, 165, 73–78. [Google Scholar] [CrossRef]
- Albertsen, P.; Jorgensen, P.; Yeager, D.L. Frequency dependent polarizabilities in a multiconfigurational time-dependent Hartree-Fock approximation. Mol. Phys. 1980, 41, 409–420. [Google Scholar] [CrossRef]
- Rice, J.E.; Handy, N.C. The calculation of frequency-dependent hyperpolarizabilities including electron correlation effects. Int. J. Quantum Chem. 1992, 43, 91–118. [Google Scholar] [CrossRef]
- Bishop, D.M.; Cybulski, S.M. Calculation of dynamic magnetic hyperpolarizability anisotropies for He, Ne and Ar. Chem. Phys. Lett. 1992, 200, 153–157. [Google Scholar] [CrossRef]
- Hättig, C.; Heβ, B.A. Correlated frequency-dependent polarizabilities and dispersion coefficients in the time-dependent second-order Møller-Plesset approximation. Chem. Phys. Lett. 1995, 233, 359–370. [Google Scholar] [CrossRef]
- Hättig, C.; Christiansen, O.; Jørgensen, P. Frequency-dependent second hyperpolarizabilities using coupled cluster cubic response theory. Chem. Phys. Lett. 1998, 282, 139–146. [Google Scholar] [CrossRef]
- Hättig, C.; Jørgensen, P. Coupled cluster calculations of the frequency-dependent second hyperpolarizabilities of Ne, Ar, and CH4. J. Chem. Phys. 1998, 109, 2762–2778. [Google Scholar] [CrossRef]
- Gauss, J.; Christiansen, O.; Stanton, J.F. Triple excitation effects in coupled-cluster calculations of frequency-dependent hyperpolarizabilities. Chem. Phys. Lett. 1998, 296, 117–124. [Google Scholar] [CrossRef]
- Rozyczko, P.; Bartlett, R.J. Frequency dependent equation-of-motion coupled cluster hyperpolarizabilities: Resolution of the discrepancy between theory and experiment for HF? J. Chem. Phys. 1997, 107, 10823–10826. [Google Scholar] [CrossRef]
- Hättig, C.; Koch, H.; Jørgensen, P. Comment on “Frequency-dependent equation-of-motion coupled cluster hyperpolarizabilities: Resolution of the discrepancy between theory and experiment for HF?” [J. Chem. Phys. 107, 10823 (1997)]. J. Chem. Phys. 1998, 109, 3293–3295. [Google Scholar] [CrossRef][Green Version]
- Rozyczko, P.; Bartlett, R.J. Response to “Comment on ‘Frequency-dependent equation-of-motion coupled cluster hyperpolarizabilities: Resolution of the discrepancy between theory and experiment for HF?’ ” [J. Chem. Phys. 109, 3293 (1998)]. J. Chem. Phys. 1998, 109, 9201–9203. [Google Scholar] [CrossRef][Green Version]
- Bartlett, R.J.; Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
- Maroulis, G. Electric Polarizability and Hyperpolarizability of Carbon Monoxide. J. Phys. Chem. 1996, 100, 13466–13473. [Google Scholar] [CrossRef]
- Ward, J.F.; Miller, C.K. Measurements of nonlinear optical polarizabilities for twelve small molecules. Phys. Rev. A 1979, 19, 826–833. [Google Scholar] [CrossRef]
- Neogrády, P.; Medveď, M.; Černušák, I.; Urban, M. Benchmark calculations of some molecular properties of O2, CN and other selected small radicals using the ROHF-CCSD(T) method. Mol. Phys. 2001, 100, 541–560. [Google Scholar] [CrossRef]
- Casanova-Páez, M.; Neese, F. Assessment of the similarity-transformed equation of motion (STEOM) for open-shell organic and transition metal molecules. J. Chem. Phys. 2024, 164, 144120. [Google Scholar] [CrossRef]
- Ho, T.-S.; Chu, S.-I. Semiclassical many-mode Floquet theory. The SU(3) dynamical evolution of three-level systems in intense bichromatic fields. Phys. Rev. A 1985, 31, 659–676. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Chu, S.-I. Floquet-Liouville supermatrix approach. II. Intensity-dependent generalized nonlinear optical susceptibilities. J. Chem. Phys. 1987, 86, 3225–3238. [Google Scholar] [CrossRef]
- Ho, T.-S.; Wang, K.; Chu, S.-I. Floquet-Liouville supermatrix approach: Time development of density-matrix operator and multiphoton resonance fluorescence spectra in intense laser fields. Phys. Rev. A 1986, 33, 1798–1816. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Yamaguchi, K. Numerical Liouville approach: Intensity-dependent transient linear and nonlinear optical susceptibilities. Chem. Phys. Lett. 1995, 234, 323–329. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K.; Matsuzaki, Y.; Tanaka, K.; Yamabe, T. Numerical Liouville approach: Formulation of third-order nonlinear optical susceptibilities. J. Chem. Phys. 1995, 102, 2986–2995. [Google Scholar] [CrossRef]
- Nakano, M.; Matsuzaki, Y.; Nagao, H.; Yamada, S.; Shigemoto, I.; Yamaguchi, K. Damping wave packet approach: A calculation method of nonperturbative nonlinear optical susceptibilities including effects of nuclear motion at finite temperature. Chem. Phys. Lett. 1995, 258, 307–315. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Landau, L. Das Dämpfungsproblem in der Wellenmechanik. Z. Phys. 1927, 45, 430–441. [Google Scholar] [CrossRef]
- von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin/Heidelberg, Germany, 1932. [Google Scholar]
- Dirac, P.A.M. Note on Exchange Phenomena in the Thomas Atom. Math. Proc. Camb. Philos. Soc. 1930, 26, 376–385. [Google Scholar] [CrossRef]
- Husimi, K. Some Formal Properties of the Density Matrix. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264–314. [Google Scholar]
- Löwdin, P.-O. Quantum Theory of Many-Particle Systems. I. Physical Interpretations by Means of Density Matrices, Natural Spin-Orbitals, and Convergence Problems in the Method of Configurational Interaction. Phys. Rev. 1955, 97, 1474–1489. [Google Scholar] [CrossRef]
- Fano, U. Description of States in Quantum Mechanics by Density Matrix and Operator Techniques. Rev. Mod. Phys. 1957, 29, 74–93. [Google Scholar] [CrossRef]
- Wigner, E. On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Weyl, H. Quantenmechanik und Gruppentheorie. Z. Phys. 1927, 46, 1–46. [Google Scholar] [CrossRef]
- Moyal, J.E. Quantum mechanics as a statistical theory. Math. Proc. Camb. Phyl. Soc. 1949, 45, 99–124. [Google Scholar] [CrossRef]
- Liouvill, J. Note sur la Théorie de la Variation des constantes arbitraires. J. Mathématiques Pures Appl. 1838, 3, 342–349. [Google Scholar]
- Brittin, W.E.; Chappell, W.R. The Wigner Distribution Function and Second Quantization in Phase Space. Rev. Mod. Phys. 1962, 34, 620–627. [Google Scholar] [CrossRef]
- Kano, Y. A New Phase-Space Distribution Function in the Statistical Theory of the Electromagnetic Field. J. Math. Phys. 1965, 6, 1913–1915. [Google Scholar] [CrossRef]
- Prugovečki, E. Liouville dynamics for optimal stochastic phase-space representations of quantum mechanics. Ann. Phys. 1978, 110, 102–121. [Google Scholar] [CrossRef]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221–260. [Google Scholar] [CrossRef]
- Prugovečki, E. Stochastic phase spaces and master Liouville spaces in statistical mechanics. Found Phys. 1979, 9, 575–587. [Google Scholar] [CrossRef]
- Weissman, Y.; Jortner, J. Quantum manifestations of classical stochasticity. II. Dynamics of wave packets of bound states. J. Chem. Phys. 1982, 77, 1486–1500. [Google Scholar] [CrossRef]
- Carruthers, P.; Zachariasen, F. Quantum collision theory with phase-space distributions. Rev. Mod. Phys. 1983, 55, 245–285. [Google Scholar] [CrossRef]
- Hillery, M.; O’Connell, R.F.; Scully, M.O.; Wigner, E.P. Distribution functions in physics: Fundamentals. Phys. Rep. 1984, 106, 121–167. [Google Scholar] [CrossRef]
- Takahashi, K.; Saitô, N. Chaos and Husimi Distribution Function in Quantum Mechanics. Phys. Rev. Lett. 1985, 55, 645–648. [Google Scholar] [CrossRef]
- Takahashi, K. Wigner and Husimi Functions in Quantum Mechanics. J. Phys. Soc. Jpn. 1986, 55, 762–779. [Google Scholar] [CrossRef]
- Sugita, A. Moments of generalized Husimi distributions and complexity of many-body quantum states. J. Phys. A Math. Gen. 2003, 36, 9081–9103. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Quasiprobability distribution dynamics: An initially one-mode coherent photon field interacting with two- and three-state molecular systems. Chem. Phys. Lett. 1998, 295, 317–327. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Electron-photon field dynamics: A molecular aggregate interacting with an initially one-mode coherent photon field. Chem. Phys. Lett. 1998, 295, 328–336. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Electron–photon field dynamics: Numerically exact calculations of multi-state molecule systems interacting with a single-mode coherent photon field. Chem. Phys. 2000, 252, 115–150. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Quantum-phase and information-entropy dynamics of a two-state molecular system interacting with strongly amplitude- and phase-squeezed fields. J. Chem. Phys. 2000, 112, 2769–2780. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Quantum-Phase and Information-Entropy Dynamics of Dimers Interacting with a Single-Mode Coherent Field: The Difference between One- and Two-Exciton Models. Int. J. Quantum Chem. 2001, 84, 530–545. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Quantum-phase and information-entropy dynamics of a molecular system interacting with a two-mode squeezed coherent field. Phys. Rev. A 2001, 64, 033415. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Quantum-phase dynamics of dimer systems interacting with a two-mode squeezed coherent field. J. Chem. Phys. 2002, 116, 10069–10082. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Nakano, M.; Nagao, H.; Okumura, M.; Yamanaka, S.; Kawakami, T.; Yamaki, D.; Nishino, M.; Shigeta, Y.; Kitagawa, Y.; et al. Spin and Pseudo Spins in Theoretical Chemistry. A Unified View for Superposed and Entangled Quantum Systems. Bull. Korean Chem. Soc. 2003, 24, 864–880. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Nitta, T. Second-order Monte Carlo wave-function approach to the relaxation effects on ringing revivals in a molecular system interacting with a strongly squeezed coherent field. Phys. Rev. A 2004, 70, 033407. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Ohta, S.; Takahashi, H.; Furukawa, S.-I.; Yamaguchi, K. Quantum-phase dynamics of two-component Bose–Einstein condensates: Collapse–revival of macroscopic superposition states. Physica B 2005, 370, 110–120. [Google Scholar] [CrossRef]
- Einstein, A. Quantentheorie des Einatomigen Idealen Gases; Sitzungsberichte der Preussischen Akademie der Wissenschaften: Berlin, Germany, 1925; pp. 261–267. [Google Scholar]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein Condensation in a Dilute Atomic Vaper. Science 1995, 269, 198–201. [Google Scholar] [CrossRef]
- Davis, K.B.; Mewes, M.-O.; Andrews, M.R.; van Druten, N.J.; Dufree, D.S.; Kurn, D.M.; Ketterie, W. Bose-Einstein Condensation in a Gas of Sodium Atoms. Phys. Rev. Lett. 1995, 75, 3969–3973. [Google Scholar] [CrossRef]
- Nakamura, Y.; Pashkin, Y.A.; Tsai, J.S. Coherent control of macroscopic quantum states in a single-Cooper-pair box. Nature 1999, 398, 786–788. [Google Scholar] [CrossRef]
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum Information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313–2363. [Google Scholar] [CrossRef]
- Nogrette, F.; Labuhn, H.; Ravets, S.; Barredo, D.; Béguin, L.; Vernier, A.; Lahaye, T.; Browaeys, A. Single-Atom Trapping in Holographic 2D Arrys of Microtraps with Arbitrary Geometries. Phys. Rev. X 2014, 4, 21034. [Google Scholar]
- Kaufman, A.M.; Lester, B.J.; Foss-Feig, M.; Wall, M.L.; Rey, A.M.; Regel, C.A. Entangling two transportable neutral atoms via local spin exchange. Nature 2015, 527, 208–211. [Google Scholar] [CrossRef]
- Levine, H.; Keesling, A.; Semeghini, G.; Omran, A.; Wang, T.T.; Ebadi, S.; Bernien, H.; Greiner, M.; Vuletić, V.; Pichler, H.; et al. Parallel Implementation of High-Fidelity Multiqubit Gates with Neutral Atoms. Phys. Rev. Lett. 2019, 123, 170503. [Google Scholar] [CrossRef]
- Browaeys, A.; Lahaye, T. Many-body physics with individually controlled Rydberg atoms. Nature Phys. 2020, 16, 132–142. [Google Scholar] [CrossRef]
- Bluvstein, D.; Evered, S.J.; Grein, A.A.; Li, S.H.; Zhou, H.; Manovitz, T.; Ebadi, S.; Cain, M.; Kalinowski, M.; Hangleiter, D.; et al. Logical quantum processor based on reconfigurable atom arrays. Nature 2024, 626, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Graham, T.M.; Song, Y.; Scott, J.; Poole, C.; Phuttitarm, L.; Jooya, K.; Eichler, P.; Jiang, X.; Marra, A.; Grinkemeyer, B.; et al. Multi-qubit entabglement and algorithms on a neutral-atom quantum computer. Nature 2022, 604, 457–462. [Google Scholar] [CrossRef]
- Chew, Y.; Tomita, T.; Mahesh, T.P.; Sugawa, S.; de Leseleuc, S.; Ohmori, K. Unltrafast energy exchange between two single Rydberg atoms on a nanosecond timescale. Nat. Photonics 2022, 16, 724–729. [Google Scholar] [CrossRef]
- Evered, S.J.; Bluvstein, D.; Kalinowski, M.; Ebadi, S.; Manovitz, T.; Zhou, H.; Li, S.H.; Geim, A.A.; Wang, T.T.; Maskara, N.; et al. High-fidelity parallel entangling gates on a neutral-atom quantum computer. Nature 2023, 622, 268–272. [Google Scholar] [CrossRef]
- Bluvstein, D.; Levine, H.; Semeghini, G.; Wang, T.T.; Ebadi, S.; Kalinowski, M.; Keesling, A.; Maskara, N.; Pichler, H.; Greiner, M.; et al. A quantum processor based on coherent transport of entagled atom arrays. Nature 2022, 604, 451–456. [Google Scholar] [CrossRef]
- Xu, M.; Kendrick, L.H.; Kale, A.; Gang, Y.; Feng, C.; Zhang, S.; Young, A.W.; Lebrat, M.; Greiner, M. A neutral-atom Hubbard quantum simulator in the cryogenic regime. arXiv 2025, arXiv:2502.00095. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, A.; Ueyama, N.; Yamaguchi, K. (Eds.) Organometallic Conjugation: Structures, Reactions and Functions of d-d and d-π Conjugated Systems; Springer Series in Chemical Physics: Tokyo, Japan, 2003. [Google Scholar]
- Gatteschi, D.; Yamaguchi, K. Opportunities for New Physics in Molecular Magnetism. In Molecular Magnetism: From Molecular Assemblies to the Devices; Coronado, E., Delhaès, P., Gatteschi, D., Miller, J.S., Eds.; NATO ASI Series; Springer: Dordrecht, The Netherlands, 1996; Volume 321, pp. 561–570. [Google Scholar]
- Nishino, M.; Yamanaka, S.; Yoshioka, Y.; Yamaguchi, K. Theoretical Approaches to Direct Exchange Couplings between Divalent Chromium Ions in Naked Dimers, Tetramers, and Clusters. J. Phys. Chem. A 1997, 101, 705–712. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Nonlinear Field Theory of Large-Spin Heisenberg Antiferromagnets: Semiclassically Quantized Solitons of the One-Dimensional Easy-Axis Néel State. Phys. Rev. Lett. 1983, 50, 1153–1156. [Google Scholar] [CrossRef]
- Mori, W.; Kobayashi, T.C.; Kurobe, J.; Amaya, K.; Narumi, Y.; Kumada, T.; Kindo, K.; Katori, H.A.; Goto, T.; Miura, N.; et al. Magnetic Properties of Oxygen Physisorbed in Cu-Trans-1,4-Cyclohexanedicarboxylic Acid. Mol. Cryst. Liq. Cryst. Sci. Technol. 1997, 306, 1–7. [Google Scholar] [CrossRef]
- Kawakami, T.; Takamizawa, S.; Takenaka, M.; Nishimura, Y.; Kitagawa, Y.; Okumura, M.; Mori, W.; Yamaguchi, K. Theoretical studies of radical spin arrangements in the cavity of nano-porous complexes. Polyhedron 2007, 26, 2367–2374. [Google Scholar] [CrossRef]
- Nagao, H.; Kinugawa, K.; Shigeta, Y.; Ohta, K.; Yamaguchi, K. Quantum spin dynamics in solution applicable to quantum computing. J. Mol. Liq. 2001, 90, 63–68. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yoshioka, Y.; Nakano, M.; Nagao, H.; Okumura, M. Bussei Ryousikagaku Nyuumon; Kodansha Scientific: Tokyo, Japan, 2004. [Google Scholar]
- Hosokoshi, Y.; Katoh, K.; Inoue, K.; Goto, T. Construction of a Quantum-Spin System of S= 1/2 Antiferromagnetic Chain with the Next-Nearest-Neighbor Interactions. J. Phys. Soc. Jpn. 1999, 68, 2910–2913. [Google Scholar] [CrossRef]
- Bader, K.; Dengler, D.; Lenz, S.; Endeward, B.; Jiang, S.-D.; Neugebauer, P.; van Slageren, J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 5304. [Google Scholar] [CrossRef]
- Shiddiq, M.; Komijani, D.; Duan, Y.; Gaita-Ariño, A.; Coronado, E.; Hill, S. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 2016, 531, 348–351. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Toho, A.; Iwase, K.; Ono, T.; Kawakami, T.; Shimokawa, T.; Matsuo, A.; Hosokoshi, Y. Two-Dimensional Honeycomb Lattice Consisting of a New Organic Radical 2-Cl-6-F-V. J. Phys. Soc. Jpn. 2013, 82, 043713. [Google Scholar] [CrossRef]
- Wasielewski, M.R.; Forbes, M.D.E.; Frank, N.L.; Kowalski, K.; Scholes, G.D.; Yuen-Zhou, J.; Baldo, M.A.; Freedman, D.E.; Goldsmith, R.H.; Goodson, T., III; et al. Exploiting chemistry and molecular systems for quantum information science. Nat. Rev. Chem. 2020, 4, 490–504. [Google Scholar] [CrossRef]
- Wojnar, M.K.; Laorenza, D.W.; Schaller, R.D.; Freedman, D.E. Nickel(II) Metal Complexes as Optically Addressable Qubit Candidates. J. Am. Chem. Soc. 2020, 142, 14826–14830. [Google Scholar] [CrossRef]
- Yang, L.-P.; Jacob, Z. Single-photon pulse induced giant response in N > 100 qubit system. npj Quantum Inf. 2020, 6, 76. [Google Scholar] [CrossRef]
- Kimura, S.; Uejima, M.; Ota, W.; Sato, T.; Kusaka, S.; Matsuda, R.; Nishihara, H.; Kusamoto, T. An Open-shell, Luminescent, Two-Dimensional Coordination Polymer with a Honeycomb Lattice and Triangular Organic Radical. J. Am. Chem. Soc. 2021, 143, 4329–4338. [Google Scholar] [CrossRef]
- von Kugelgen, S.; Krzyaniak, M.D.; Gu, M.; Puggioni, D.; Rondinelli, J.M.; Wasielewski, M.R.; Freedman, D.E. Spectral Addressability in a Modular Two Qubit System. J. Am. Chem. Soc. 2021, 143, 8069–8077. [Google Scholar] [CrossRef] [PubMed]
- Kazmierczak, N.P.; Mirzoyan, R.; Hadt, R.G. The Impact of Ligand Field Symmetry on Molecular Qubit Coherence. J. Am. Chem. Soc. 2021, 143, 17305–17315. [Google Scholar] [CrossRef] [PubMed]
- Mani, T. Molecular qubits based on photogenerated spin-correlated radical pairs for quantum sensing. Chem. Phys. Rev. 2022, 3, 021301. [Google Scholar] [CrossRef]
- Bayliss, S.L.; Deb, P.; Laorenza, D.W.; Onizhuk, M.; Galli, G.; Freedman, D.E.; Awschalom, D.D. Enhancing Spin Coherence in Optically Addressable Molecular Qubits through Host-Matrix Control. Phys. Rev. X 2022, 12, 031028. [Google Scholar] [CrossRef]
- Amdur, M.J.; Mullin, K.R.; Waters, M.J.; Puggioni, D.; Wojnar, M.K.; Gu, M.; Sun, L.; Oyala, P.H.; Rondinelli, J.M.; Freedman, D.E. Chemical control of spin–lattice relaxation to discover a room temperature molecular qubit. Chem. Sci. 2022, 13, 7034–7045. [Google Scholar] [CrossRef]
- Garlatti, E.; Albino, A.; Chicco, S.; Nguyen, V.H.A.; Santanni, F.; Paolasini, L.; Mazzoli, C.; Caciuffo, R.; Totti, F.; Santini, P.; et al. The critical role of ultra-low-energy vibrations in the relaxation dynamics of molecular qubits. Nat. Commun. 2023, 14, 1653. [Google Scholar] [CrossRef]
- Fursina, A.A.; Sinitskii, A. Toward Molecular Spin Qubit Devices: Integration of Magnetic Molecules into Solid-State Devices. ACS Appl. Electron. Mater. 2023, 5, 3531–3545. [Google Scholar] [CrossRef]
- Orihashi, K.; Yamauchi, A.; Fujiwara, S.; Asada, M.; Nakamura, T.; Hui, J.K.-H.; Kimizuka, N.; Tateishi, K.; Uesaka, T.; Yanai, N. Spin-Polarized Radicals with Extremely Long Spin–Lattice Relaxation Time at Room Temperature in a Metal–Organic Framework. J. Am. Chem. Soc. 2023, 145, 27650–27656. [Google Scholar] [CrossRef] [PubMed]
- Schäfter, D.; Wischnat, J.; Tesi, L.; De Sousa, J.A.; Little, E.; McGuire, J.; Mas-Torrent, M.; Rovira, C.; Veciana, J.; Tuna, F.; et al. Molecular One- and Two-Qubit Systems with Very Long Coherence Times. Adv. Mater. 2023, 35, 2302114. [Google Scholar] [CrossRef] [PubMed]
- Lee, A.Y.; Colleran, T.A.; Jain, A.; Niklas, J.; Rugg, B.K.; Mani, T.; Poluektov, O.G.; Olshansky, J.H. Quantum Dot–Organic Molecule Conjugates as Hosts for Photogenerated Spin Qubit Pairs. J. Am. Chem. Soc. 2023, 145, 4372–4377. [Google Scholar] [CrossRef]
- Mayländer, M.; Thielert, P.; Quintes, T.; Jentzsch, A.V.; Richert, S. Room Temperature Electron Spin Coherence in Photogenerated Molecular Spin Qubit Candidates. J. Am. Chem. Soc. 2023, 145, 14064–14069. [Google Scholar] [CrossRef]
- Qiu, Y.; Eckvahl, H.J.; Equbal, A.; Krzyaniak, M.D.; Wasielewski, M. Enhancing Coherence Times of Chromophore-Radical Molecular Qubits and Qudits by Rational Design. J. Am. Chem. Soc. 2023, 145, 25903–25909. [Google Scholar] [CrossRef]
- Vujević, L.; Karadeniz, B.; Cindro, N.; Krajnc, A.; Mali, G.; Mazaj, M.; Avdoshenko, S.M.; Popov, A.A.; Žilić, D.; Užarević, K.; et al. Improving the molecular spin qubit performance in zirconium MOF composites by mechanochemical dilution and fullerene encapsulation. Chem. Sci. 2023, 14, 9389–9399. [Google Scholar] [CrossRef]
- Zhou, A.; Li, D.; Tan, M.; Lv, Y.; Pang, S.; Zhao, X.; Shi, Z.; Zhang, J.; Jin, F.; Liu, S.; et al. Phononic modulation of spin-lattice relaxation in molecular qubit frameworks. Nat. Commun. 2024, 15, 10763. [Google Scholar] [CrossRef]
- Morrillo, W.T.; Cumming, H.I.J.; Mattioni, A.; Staab, J.K.; Chilton, N.F. Ab Initio Design of Molecular Qubits with Electric Field Control. J. Am. Chem. Soc. 2024, 146, 25841–25851. [Google Scholar] [CrossRef]
- Orihashi, K.; Yamauchi, A.; Inoue, M.; Parmar, B.; Fujiwara, S.; Kimizuka, N.; Asada, M.; Nakamura, T.; Yanai, N. Radical qubits photo-generated in acene-based metal–organic frameworks. Dalton Trans. 2024, 53, 872–876. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Tominaga, Y.; Kida, T.; Araki, K.; Kawakami, T.; Iwasaki, Y.; Kimura, K.; Hagiwara, M. Realization of a spin-1/2 Kondo necklace model with magnetic field-induced coupling switch. Phys. Rev. Res. 2025, 7, L012023. [Google Scholar] [CrossRef]
- Lin, N.; Tsuji, M.; Bruzzese, I.; Chen, A.; Vrionides, M.; Jian, N.; Kittur, F.; Fay, T.P.; Mani, T. Molecular Engineering of Emissive Molecular Qubits Based on Spin-Correlated Radical Pairs. J. Am. Chem. Soc. 2025, 147, 11062–11071. [Google Scholar] [CrossRef]
- Warner, H.K.; Holzgrafe, J.; Yankelevich, B.; Barton, D.; Poletto, S.; Xin, C.J.; Sinclair, N.; Zhu, D.; Sete, E.; Langley, B.; et al. Coherent control of a superconducting qubit using light. Nat. Phys. 2025, 21, 831–838. [Google Scholar] [CrossRef]
- le Mardelé, F.; Mohelský, I.; Wyzula, J.; Orlita, M.; Turek, P.; Troiani, F.; Boudalis, A.K. Probing spin-electric transitions in a molecular exchange qubit. Nat. Commun. 2025, 16, 1198. [Google Scholar] [CrossRef]
- Cardona, J.; Solé, À.; Mella, P.; Aravena, D.; Ruiz-Hidalgo, J.; Gómez-Coca, S.; Ruiz, E. Exploring hyperfine coupling in molecular qubits. Chem. Sci. 2025, 16, 11291–11303. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Miyagawa, K.; Shoji, M.; Kawakami, T.; Isobe, H.; Yamanaka, S.; Nakajima, T. Theoretical elucidation of the structure, bonding, and reactivity of the CaMn4Ox clusters in the whole Kok cycle for water oxidation embedded in the oxygen evolving center of photosystem II. New molecular and quantum insights into the mechanism of the O–O bond formation. Photosynth. Res. 2024, 162, 291–330. [Google Scholar] [PubMed]
- Yamaguchi, K.; Yamanaka, S.; Nishino, M.; Takano, Y.; Kitagawa, Y.; Nagao, H.; Yoshioka, Y. Symmetry and broken symmetries in molecular orbital descriptions of unstable molecules II. Alignment, flustration and tunneling of spins in mesoscopic molecular magnets. Theor. Chem. Acc. 1999, 102, 328–345. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Schwinger, J. On the Interaction of Mesotrons and Nuclei. Phys. Rev. 1941, 60, 150–152. [Google Scholar] [CrossRef]
- Forster, T. Energiewanderung und Fluoreszenz. Naturwissenschaften 1946, 33, 166–175. [Google Scholar] [CrossRef]
- Frenkel, J. On the Transformation of light into Heat in Solids. I. Phys. Rev. 1931, 46, 17–44. [Google Scholar] [CrossRef]
- Wannier, G.H. The Structure of Electronic Excitation Levels in Insulating Crystals. Phys. Rev. 1937, 52, 191–197. [Google Scholar] [CrossRef]
- Arnold, W.; Oppenheimer, J.R. Internal Conversion in the Photosynthetic Mechanism of Blue-Green Argae. J. Gen. Physiol. 1950, 33, 423–435. [Google Scholar] [CrossRef] [PubMed]
- Förster, T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Ann. Phys. 1948, 437, 55–75. [Google Scholar] [CrossRef]
- Redfield, A.G. On the Theory of Relaxation Processes. IBM J. Res. Dev. 1957, 1, 19–31. [Google Scholar] [CrossRef]
- Simpson, W.T.; Peterson, D.L. Coupling Strength for Resonance Force Transfer of Electronic Energy in van der Waals Solids Available to Purchase. J. Chem. Phys. 1957, 26, 588–593. [Google Scholar] [CrossRef]
- Förster, T. 10th Spiers Memorial Lecture. Transfer mechanisms of electronic excitation. Discuss. Faraday Soc. 1959, 27, 7–17. [Google Scholar] [CrossRef]
- Robinson, G.W.; Frosch, R.P. Theory of Electronic Energy Relaxation in the Solid Phase Available to Purchase. J. Chem. Phys. 1962, 37, 1962–1973. [Google Scholar] [CrossRef]
- Robinson, G.W.; Frosch, R.P. Electronic Excitation Transfer and Relaxation. J. Chem. Phys. 1963, 38, 1187–1203. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Silbey, R. Electronic energy transfer in molecular crystals. Ann. Rev. Phys. Chem. 1976, 27, 203–223. [Google Scholar] [CrossRef]
- Shibata, F.; Takahashi, Y.; Hashitsume, N. A generalized stochastic liouville equation. Non-Markovian versus memoryless master equations. J. Stat. Phys. 1977, 17, 171–187. [Google Scholar] [CrossRef]
- Anderson, P.W. Basic Notions of Condensed Matter Physics; Benjamin Cummings: Menlo Park, CA, USA, 1984. [Google Scholar]
- Leggett, A.J.; Chakravarty, S.; Dorsey, A.T.; Fisher, M.P.A.; Garg, A.; Zwerger, W. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 1995, 59, 725. [Google Scholar] [CrossRef]
- Tomalia, D.A.; Baker, H.; Dewald, J.; Hall, M.; Kallos, G.; Martin, S.; Roeck, J.; Ryder, J.; Smith, P. A New Class of Polymers: Starburst-Dendritic Macromolecules. Polym. J. 1985, 17, 117–132. [Google Scholar] [CrossRef]
- Devadoss, C.; Bharathi, P.; Moore, J.S. Energy Transfer in Dendritic Macromolecules: Molecular Size Effects and the Role of an Energy Gradient. J. Am. Chem. Soc. 1996, 118, 9635–9644. [Google Scholar] [CrossRef]
- Kopelman, R.; Shortreed, M.; Shi, Z.-Y.; Tan, W.; Xu, Z.; Moore, J.S.; Bar-Haim, A.; Klafter, J. Spectroscopic Evidence for Excitonic Localization in Fractal Antenna Supermolecules. Phys. Rev. Lett. 1997, 78, 1239–1242. [Google Scholar] [CrossRef]
- Shortreed, M.R.; Swallen, S.F.; Shi, Z.-Y.; Tan, W.; Xu, Z.; Devadoss, C.; Moore, J.S.; Kopelman, R. Directed Energy Transfer Funnels in Dendrimeric Antenna Supermolecules. J. Phys. Chem. B 1997, 101, 6318–6322. [Google Scholar] [CrossRef]
- Bredas, J.-L.; Beljonne, D.; Coropceanu, V.; Cornil, J. Charge-Transfer and Energy-Transfer Processes in π-Conjugated Oligomers and Polymers: A Molecular Picture. Chem. Rev. 2004, 104, 4971–5004. [Google Scholar] [CrossRef]
- Li, W.-S.; Aoda, T. Dendrimer Porphyrins and Phthalocyanines. Chem. Rev. 2009, 109, 6047–6076. [Google Scholar] [CrossRef]
- Spano, F.C. The Spectral Signatures of Frenkel Polarons in H- and J-Aggregates. Acc. Chem. Res. 2010, 43, 429–439. [Google Scholar] [CrossRef]
- Tretiak, S.; Chernyak, V.; Mukamel, S. Localized Electronic Excitations in Phenylacetylene Dendrimers. J. Phys. Chem. B 1998, 102, 3310–3315. [Google Scholar] [CrossRef]
- Nakano, M.; Takahata, M.; Fujita, H.; Kiribayashi, S.; Yamaguchi, K. Exciton migration dynamics in a dendritic molecular aggregate. Chem. Phys. Lett. 2000, 323, 249–256. [Google Scholar] [CrossRef]
- Kirkwood, J.C.; Scheurer, C.; Chernyak, V.; Mukamel, S. Simulations of energy funneling and time- and frequency-gated fluorescence in dendrimers. J. Chem. Phys. 2001, 114, 2419–2429. [Google Scholar] [CrossRef]
- Takahata, M.; Nakano, M.; Fujita, H.; Yamaguchi, K. Mechanism of exciton migration of dendritic molecular aggregate: A master equation approach including weak exciton–phonon coupling. Chem. Phys. Lett. 2002, 363, 422–428. [Google Scholar] [CrossRef]
- Takahata, M.; Nakano, M.; Yamaguchi, K. Exciton Migration in Dendritic Aggregate Systems Using the Quantum Master Equation Approach Involving Weak Exciton-phonon coupling. J. Theory Comput. Chem. 2003, 2, 459–479. [Google Scholar] [CrossRef]
- Takahata, M.; Nakano, M.; Yamada, S.; Yamaguchi, K. One- and two-exciton migration dynamics of a dendritic molecular aggregate. Int. J. Quantum Chem. 2003, 95, 472–478. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Takahata, M.; Kishi, R.; Nitta, T.; Yamaguchi, K. Ab Initio Study on Nonlinear Optical Properties for Small Dendritic Molecules. J. Nonlinear Optic. Phys. Mat. 2004, 13, 417–422. [Google Scholar] [CrossRef]
- Nakano, M.; Takahata, M.; Yamada, S.; Yamaguchi, K.; Kishi, R.; Nitta, T. Exciton migration dynamics in a dendritic molecule: Quantum master equation approach using ab initio molecular orbital configuration interaction method. J. Chem. Phys. 2004, 120, 2359–2367. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Takahata, M.; Nitta, T.; Yamaguchi, K. Exciton dynamics in nanostar dendritic systems using a quantum master equation approach: Core monomer effects and possibility of energy transport control. J. Lumin. 2005, 111, 359–366. [Google Scholar] [CrossRef]
- Nakano, M.; Ohta, S.; Kishi, R.; Nate, M.; Takahashi, H.; Furukawa, S.-I.; Nitta, H.; Yamaguchi, K. Exciton recurrence motion in aggregate systems in the presence of quantized optical fields. J. Chem. Phys. 2006, 125, 234707. [Google Scholar] [CrossRef]
- Nitta, H.; Shoji, M.; Takahata, M.; Nakano, M.; Yamaki, D.; Yamaguchi, K. Quantum dynamics of exciton recurrence motion in dendritic molecular aggregates. J. Photochem. Photobiol. 2006, 178, 264–270. [Google Scholar] [CrossRef]
- Jelley, E.E. Spectral Absorption and Fluorescence of Dyes in the Molecular State. Nature 1936, 138, 1009–1010. [Google Scholar] [CrossRef]
- Kasha, M.; Rawls, H.R.; El-Bayoumi, M.A. The exciton model in molecular spectroscopy. Pure Appl. Chem. 1965, 11, 371–392. [Google Scholar] [CrossRef]
- Mitani, M.; Mori, H.; Takano, Y.; Yamaki, D.; Yoshioka, Y.; Yamaguchi, K. Density functional study of intramolecular ferromagnetic interaction through m-phenylene coupling unit (I): UBLYP, UB3LYP, and UHF calculations. J. Chem. Phys. 2000, 113, 4035–4051. [Google Scholar] [CrossRef]
- Nagao, H.; Kodama, K.; Shigeta, Y.; Nishikawa, K.; Kawabe, H.; Nakano, M.; Yamaguchi, K. Nonadiabatic treatment of molecular systems by the wavepackets method. Int. J. Quantum Chem. 1996, 60, 1261–1270. [Google Scholar] [CrossRef]
- Nagao, H.; Nakano, M.; Shigeta, Y.; Yamaguchi, K. Quantum Phase Dynamics of Interaction between Photon Field and Magnetic System: Effects of Magnetic Quantum Tunnelling. Opt. Rev. 1999, 6, 227–231. [Google Scholar] [CrossRef]
- Nagao, H.; Nakano, M.; Nishikawa, K.; Yamaguchi, K. Theoretical study on quantum dynamics of bose system interacting with photon field. Int. J. Quantum Chem. 2001, 84, 401–408. [Google Scholar] [CrossRef]
- Takahata, M.; Shoji, M.; Nitta, H.; Takeda, R.; Yamanaka, S.; Okumura, M.; Nakano, M.; Yamaguchi, K. Quantum dynamics in high-spin molecules, spin dendrimers, and spin lattices. Int. J. Quantum Chem. 2005, 105, 615–627. [Google Scholar]
- Yamaguchi, K.; Nakano, M.; Nagao, H.; Okumura, M.; Yamanaka, S.; Kawakami, T.; Yamada, S.; Yamaki, D.; Kitagawa, Y.; Takeda, R.; et al. N-band Hubbard models. III. Boson–fermion and interaction–boson models for high-Tc superconductivity. Int. J. Quantum Chem. 2005, 106, 1052–1075. [Google Scholar]
- Feynman, R.P.; Vernon Jr, F.L. The theory of a general quantum system interacting with a linear dissipative system. Ann. Phys. 1963, 24, 118–173. [Google Scholar] [CrossRef]
- Tanimura, Y.; Kubo, R. Time Evolution of a Quantum System in Contact with a Nearly Gaussian-Markoffian Noise Bath. J. Phys. Soc. Jpn. 1989, 58, 101–114. [Google Scholar] [CrossRef]
- Cao, J. A phase-space study of Bloch–Redfield theory. J. Chem. Phys. 1997, 107, 3204–3209. [Google Scholar][Green Version]
- Mukamel, S. Multidimensional Femtosecond Correlation Spectroscopies of Electronic and Vibrational Excitations. Ann. Rev. Phys. Chem. 2000, 51, 691–729. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, A.; Tanimura, Y. Quantum Dynamics of System Strongly Coupled to Low-Temperature Colored Noise Bath: Reduced Hierarchy Equations Approach. J. Phys. Soc. Jpn. 2005, 74, 3131–3134. [Google Scholar] [CrossRef]
- Tanimura, Y. Reduced hierarchical equations of motion in real and imaginary time: Correlated initial states and thermodynamic quantities. J. Chem. Phys. 2014, 141, 044114. [Google Scholar] [CrossRef]
- Zhu, F.; Galli, C.; Hochstrasser, R.M. The real-time intramolecular electronic excitation transfer dynamics of 9′,9-bifluorene and 2′,2-binaphthyl in solution. J. Chem. Phys. 1993, 98, 1042–1057. [Google Scholar]
- Wynne, K.; Hochstrasser, R.M. Anisotropy as an ultrafast probe of electronic coherence in degenerate systems exhibiting Raman scattering, fluorescence, transient absorption and chemical reactions. J. Raman Spectrosc. 1995, 26, 561–569. [Google Scholar] [CrossRef]
- Yamazaki, I.; Akimoto, S.; Yamazaki, T.; Sato, S.-I.; Sakata, Y. Oscillating Excitation Transfer in Dithiaanthracenophane—Quantum Beat in a Coherent Photochemical Process. J. Phys. Chem. A 2002, 106, 2122–2128. [Google Scholar] [CrossRef]
- Akimoto, S.; Yamazaki, I.; Sakawa, T.; Mimuro, M. Temperature Effects on Excitation Relaxation Dynamics of the Carotenoid β-Carotene and Its Analogue β-Apo-8′-carotenal, Probed by Femtosecond Fluorescence Spectroscopy. J. Phys. Chem. A 2002, 106, 2237–2243. [Google Scholar] [CrossRef]
- Sato, S.-I.; Nishimura, Y.; Sakata, Y.; Yamazaki, I. Coherent Control of Oscillatory Excitation Transfer in Dithia-1,5[3,3]anthracenophane by a Phase-Locked Femtosecond Pulse Pair. J. Phys. Chem. A 2003, 107, 10019–10025. [Google Scholar] [CrossRef]
- Kasajima, T.; Akimoto, S.; Sato, S.-I.; Yamazaki, I. Evidence of vibrational relaxation from non-Boltzmann to Boltzmann distribution over v’=0,1,2 levels in S1 perylene in solution: Franck–Condon analysis of time-resolved fluorescence. Chem. Phys. Lett. 2003, 375, 227–232. [Google Scholar] [CrossRef]
- Kasajima, T.; Akimoto, S.; Sato, S.-I.; Yamazaki, I. Vibrational Energy Relaxation of S1 Perylene in Solution. J. Phys. Chem. A 2004, 108, 3268–3275. [Google Scholar] [CrossRef]
- Yamazaki, I.; Akimoto, S.; Aratani, N.; Osuka, A. Observation of Coherent Recurrence Motion of Excitons in Anthracene Dimers. Bull. Chem. Soc. Jpn. 2004, 77, 1959–1971. [Google Scholar] [CrossRef]
- Grossman, A.R.; Schaefer, M.R.; Chiang, G.G.; Collier, J.L. The phycobilisome, a light-harvesting complex responsive to environmental conditions. Microbiol. Rev. 1993, 57, 725–749. [Google Scholar] [CrossRef] [PubMed]
- MacColl, R. Cyanobacterial Phycobilisomes. J. Struct. Bio. 1998, 124, 311–334. [Google Scholar] [CrossRef]
- Adir, N. Elucidation of the molecular structures of components of the phycobilisome: Reconstructing a giant. Photosynth. Res. 2005, 85, 15–32. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, J.; Liu, D.; Qin, S.; Sun, S.; Zhao, J.; Sui, S.-F. Structure of phycobilisome from the red alga Griffithsia pacifica. Nature 2017, 551, 57–63. [Google Scholar] [CrossRef]
- Watanabe, M.; Ikeuchi, M. Phycobilisome: Architecture of a light-harvesting supercomplex. Photosynth. Res. 2013, 116, 265–276. [Google Scholar] [CrossRef] [PubMed]
- Sui, S.-F. Structure of Phycobilisomes. Ann. Rev. Biophys. 2021, 50, 53–72. [Google Scholar] [CrossRef]
- Ma, J.; You, X.; Sun, S.; Wang, X.; Qin, S.; Sui, S.-F. Structural basis of energy transfer in Porphyridium purpureum phycobilisome. Nature 2020, 579, 146–151. [Google Scholar] [CrossRef]
- Adir, N.; Bar-Zvi, S.; Harris, D. The amazing phycobilisome. Biochim. Biophys. Acta-Bioenerg. 2020, 1861, 148047. [Google Scholar]
- Mishima, K.; Shoji, M.; Umena, Y.; Boero, M.; Shigeta, Y. Estimation of the relative contributions to the electronic energy transfer rates based on Förster theory: The case of C-phycocyanin chromophores. Biophys. Physicobiol. 2021, 18, 196–214. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Zheng, Z.; Li, X.; Wang, G.; Zhang, K.; Wei, P.; Zhao, J.; Gao, N. Structural insight into the mechanism of energy transfer in cyanobacterial phycobilisomes. Nat. Commun. 2021, 12, 5497. [Google Scholar] [CrossRef]
- Kawakami, K.; Nagao, R.; Tahara, Y.O.; Hamaguchi, T.; Suzuki, T.; Dohmae, N.; Kosumi, D.; Shen, J.-R.; Miyata, M.; Yonekura, K.; et al. Structural implications for a phycobilisome complex from the thermophilic cyanobacterium Thermosynechococcus vulcanus. Biochim. Biophys. Acta-Bioenerg. 2021, 1862, 148458. [Google Scholar]
- Kawakami, K.; Hamaguchi, T.; Hirose, Y.; Kosumi, D.; Miyata, M.; Kamiya, N.; Yonekura, K. Core and rod structures of a thermophilic cyanobacterial light-harvesting phycobilisome. Nat. Commun. 2022, 13, 3389. [Google Scholar] [CrossRef]
- Domínguez-Martín, M.A.; Sauer, P.V.; Kirst, H.; Sutter, M.; Bína, D.; Greber, B.J.; Nogales, E.; Polívka, T.; Kerfeld, C.A. Structures of a phycobilisome in light-harvesting and photoprotected states. Nature 2022, 609, 835–845. [Google Scholar] [CrossRef]
- Hill, R.; Bendall, F. Function of the Two Cytochrome Components in Chloroplasts: A Working Hypothesis. Nature 1960, 186, 136–137. [Google Scholar] [CrossRef]
- Duysens, L.N.M.; Amesz, J.; Kamp, B.M. Two photochemical systems in photosynthesis. Nature 1961, 190, 510–511. [Google Scholar] [CrossRef]
- Deisenhofer, J.; Epp, O.; Miki, K.; Huber, R.; Michel, H. Structure of the protein subunits in the photosynthetic reaction centre of Rhodopseudomonas viridis at 3Å resolution. Nature 1985, 318, 618–624. [Google Scholar] [CrossRef] [PubMed]
- McDermott, G.; Prince, S.M.; Freer, A.A.; Hawthornthwaite-Lawless, A.M.; Papiz, M.Z.; Cogdell, R.J.; Isaacs, N.W. Crystal structure of an integral membrane light-harvesting complex from photosynthetic bacteria. Nature 1995, 374, 517–521. [Google Scholar] [CrossRef]
- Leegwater, J.A.; Durrant, J.R.; Klug, D.R. Exciton Equilibration Induced by Phonons: Theory and Application to PS II Reaction Centers. J. Phys. Chem. B 1997, 101, 7205–7210. [Google Scholar] [CrossRef]
- SUMI, H. Bacterial photosynthesis begins with quantum-mechanical coherence. Chem. Rec. 2001, 1, 480–493. [Google Scholar] [CrossRef]
- Mukai, K.; Abe, A.; Sumi, H. Theory of Rapid Excitation-Energy Transfer from B800 to Optically-Forbidden Exciton State of B850 in the Antenna System LH2 of Photosynthetic Purple Bacteria. J. Phys. Chem. B 1999, 103, 6096–6102. [Google Scholar]
- Scholes, G.D.; Fleming, G.R. On the Mechanism of Light Harvesting in Photosynthetic Purple Bacteria: B800 to B850 Energy Transfer. J. Phys. Chem. B 2000, 104, 1854–1868. [Google Scholar] [CrossRef]
- Scholes, G.D.; Jordanides, X.J.; Fleming, G.R. Adapting the Förster Theory of Energy Transfer for Modeling Dynamics in Aggregated Molecular Assemblies. J. Phys. Chem. B 2001, 105, 1640–1651. [Google Scholar] [CrossRef]
- Herek, J.L.; Wohlleben, W.; Cogdell, R.J.; Zeidler, D.; Motzkus, M.; Herek, J.L.; Wohlleben, W.; Cogdell, R.J.; Zeidler, D.; Motzkus, M. Quantum control of energy flow in light harvesting. Nature 2002, 417, 533–535. [Google Scholar] [CrossRef]
- Kimura, A.; Kakitani, T. Theoretical Analysis of the Energy Gap Dependence of the Reconstituted B800→B850 Excitation Energy Transfer Rate in Bacterial LH2 Complexes. J. Phys. Chem. B 2003, 107, 7932–7939. [Google Scholar] [CrossRef]
- Scholes, G.D. Long-Range Resonance Energy Transfer in Molecular Systems. Ann. Rev. Phys. Chem. 2003, 54, 57–87. [Google Scholar]
- Madigan, M.T. Anoxygenic phototrophic bacteria from extreme environments. Photosynth. Res. 2003, 76, 157–171. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Silbey, R.J. Coherence in the B800 Ring of Purple Bacteria LH2. Phys. Rev. Lett. 2006, 96, 28103. [Google Scholar] [CrossRef]
- Beljonne, D.; Curutchet, C.; Scholes, G.D.; Silbey, R.J. Beyond Förster Resonance Energy Transfer in Biological and Nanoscale Systems. J. Phys. Chem. B 2009, 113, 6583–6599. [Google Scholar] [CrossRef]
- Niwa, S.; Yu, L.-J.; Takeda, K.; Hirano, Y.; Kawakami, T.; Wang-Otomo, Z.-Y.; Miki, K. Structure of the LH1–RC complex from Thermochromatium tepidum at 3.0 Å. Nature 2014, 508, 228–232. [Google Scholar] [CrossRef] [PubMed]
- Khrenova, M.G.; Nemukhin, A.V.; Grigorenko, B.L.; Wang, P.; Zhang, J.-P. All-atom structures and calcium binding sites of the bacterial photosynthetic LH1-RC core complex from Thermochromatium tepidum. J. Mol. Model. 2014, 20, 2287. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.-J.; Suga, M.; Wang-Otomo, Z.-Y.; Shen, J.-R. Structure of photosynthetic LH1–RC supercomplex at 1.9 Å resolution. Nature 2018, 556, 209–213. [Google Scholar] [CrossRef]
- Qian, P.; Nguyen-Phan, C.T.; Gardiner, A.T.; Croll, T.I.; Roszak, A.W.; Southall, J.; Jackson, P.J.; Vasilev, C.; Castro-Hartmann, P.; Sader, K.; et al. Cryo-EM structures of light-harvesting 2 complexes from Rhodopseudomonas palustris reveal the molecular origin of absorption tuning. Proc. Natl. Acad. Sci. USA 2022, 119, e2210109119. [Google Scholar] [CrossRef] [PubMed]
- Nagao, R.; Kato, K.; Hamaguchi, T.; Ueno, Y.; Tsuboshita, N.; Shimizu, S.; Furutani, M.; Ehira, S.; Nakajima, Y.; Kawakami, K.; et al. Structure of a monomeric photosystem I core associated with iron-stress-induced-A proteins from Anabaena sp. PCC 7120. Nat. Commun. 2023, 14, 920. [Google Scholar] [CrossRef]
- Bindra, J.K.; Niklas, J.; Jeong, Y.; Jasper, A.W.; Kretzschmar, M.; Kern, J.; Utschig, L.M.; Poluektov, O.G. Coherences of Photoinduced Electron Spin Qubit Pair States in Photosystem I. J. Phys. Chem. B 2023, 127, 10108–10117. [Google Scholar] [CrossRef] [PubMed]
- Tani, K.; Kanno, R.; Harada, A.; Kobayashi, Y.; Minamino, A.; Takenaka, S.; Nakamura, N.; Ji, X.-C.; Purba, E.R.; Hall, M.; et al. High-resolution structure and biochemical properties of the LH1–RC photocomplex from the model purple sulfur bacterium, Allochromatium vinosum. Commun. Biol. 2024, 7, 176. [Google Scholar] [CrossRef]
- Zhu, R.; Li, W.; Zhen, Z.; Zou, J.; Liao, G.; Wang, J.; Wang, Z.; Chen, H.; Qin, S.; Weng, Y. Quantum phase synchronization via exciton-vibrational energy dissipation sustains long-lived coherence in photosynthetic antennas. Nat. Commun. 2024, 15, 3171. [Google Scholar] [CrossRef] [PubMed]
- Yano, J.; Kern, J.; Sauer, K.; Latimer, M.J.; Pushkar, Y.; Biesiadka, J.; Loll, B.; Saenger, W.; Messinger, J.; Zouni, A.; et al. Where Water Is Oxidized to Dioxygen: Structure of the Photosynthetic Mn4Ca Cluster. Science 2006, 314, 821–825. [Google Scholar] [CrossRef]
- Iwai, M.; Yokono, M.; Inada, N.; Minagawa, J. Live-cell imaging of photosystem II antenna dissociation during state transitions. Proc. Natl. Acad. Sci. USA 2009, 107, 2337–2342. [Google Scholar] [CrossRef]
- Umena, Y.; Kawakami, K.; Shen, J.-R.; Kamiya, N. Crystal structure of oxygen-evolving photosystem II at a resolution of 1.9 Å. Nature 2011, 473, 55–60. [Google Scholar] [CrossRef]
- Shen, J.-R. The Structure of Photosystem II and the Mechanism of Water Oxidation in Photosynthesis. Ann. Rev. Plant Bio. 2015, 66, 23–48. [Google Scholar] [CrossRef]
- Pi, X.; Zhao, S.; Wang, W.; Liu, D.; Xu, C.; Han, G.; Kuang, T.; Sui, S.-F.; Shen, J.-R. The pigment-protein network of a diatom photosystem II–light-harvesting antenna supercomplex. Science 2019, 365, 463. [Google Scholar] [CrossRef]
- Croce, R.; van Amerongen, H. Light harvesting in oxygenic photosynthesis: Structural biology meets spectroscopy. Science 2020, 369, 933. [Google Scholar] [CrossRef] [PubMed]
- Sirohiwal, A.; Neese, F.; Pantazis, D.A. Chlorophyll excitation energies and structural stability of the CP47 antenna of photosystem II: A case study in the first-principles simulation of light-harvesting complexes. Chem. Sci. 2021, 12, 4463–4476. [Google Scholar] [CrossRef]
- Hsieh, S.-T.; Zhang, L.; Ye, D.-W.; Huang, X.; Cheng, Y.-C. A theoretical study on the dynamics of light harvesting in the dimeric photosystem II core complex: Regulation and robustness of energy transfer pathways. Faraday Discuss. 2019, 216, 94–115. [Google Scholar] [CrossRef]
- Mattioni, A.; Caycedo-Soler, F.; Huelga, S.F.; Plenio, M.B. Design Principles for Long-Range Energy Transfer at Room Temperature. Phys. Rev. X 2021, 11, 041003. [Google Scholar] [CrossRef]
- Yang, S., Jr.; Arsenault, E.A.; Orcutt, K.; Iwai, M.; Yoneda, Y.; Fleming, G.R. From antenna to reaction center: Pathways of ultrafast energy and charge transfer in photosystem II. Proc. Natl. Acad. Sci. USA 2022, 119, e2208033119. [Google Scholar] [CrossRef]
- Maity, S.; Kleinekathofer, U. Recent progress in atomistic modeling of light-harvesting complexes: A mini review. Photosynth. Res. 2023, 156, 147–162. [Google Scholar] [CrossRef] [PubMed]
- Si, L.; Zhang, S.; Su, X.; Li, M. Structural basis for the distinct core-antenna assembly of cryptophyte photosystem II. Nat. Commun. 2024, 15, 6812. [Google Scholar] [CrossRef] [PubMed]
- Leonardo, C.; Yang, S.-J.; Orcutt, K.; Iwai, M.; Arsenault, E.A.; Fleming, G.R. Bidirectional Energy Flow in the Photosystem II Supercomplex. J. Phys. Chem. B 2024, 128, 7941–7953. [Google Scholar] [CrossRef]
- Yang, S.-J.; Wales, D.J.; Wood, E.J.; Fleming, G.R. Design principles for energy transfer in the photosystem II supercomplex from kinetic transition networks. Nat. Commun. 2024, 15, 8763. [Google Scholar] [CrossRef]
- Rocca, R.L.; Kato, K.; Tsai, P.-C.; Nakajima, Y.; Akita, F.; Shen, J.-R. Structure of a photosystem II-FCPII supercomplex from a haptophyte reveals a distinct antenna organization. Nat. Commun. 2025, 16, 4175. [Google Scholar] [CrossRef]
- Fenna, R.E.; Matthews, B.W. Chlorophyll arrangement in a bacteriochlorophyll protein from Chlorobium limicola. Nature 1975, 258, 573–577. [Google Scholar] [CrossRef]
- Camara-Artigas, A.; Blankenship, R.E.; Allen, J.P. The structure of the FMO protein from Chlorobium tepidum at 2.2 Å resolution. Photosynth. Res. 2003, 75, 49–55. [Google Scholar] [CrossRef]
- Puskar, R.; Truong, C.D.; Swain, K.; Chowdhury, S.; Chan, K.-Y.; Li, S.; Cheng, K.-W.; Wang, T.Y.; Poh, Y.-P.; Mazor, Y.; et al. Molecular asymmetry of a photosynthetic supercomplex from green sulfur bacteria. Nat. Commun. 2022, 13, 5824. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.; Zhang, H.; Gross, M.L.; Blankenship, R.E. Membrane orientation of the FMO antenna protein from Chlorobaculum tepidum as determined by mass spectrometry-based footprinting. Proc. Natl. Acad. Sci. USA 2009, 106, 6134–6139. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Lyratzakis, A.; Khera, R.; Koutantou, M.; Welsch, S.; Michel, H.; Tsiotis, G. Cryo-EM structure of the whole photosynthetic reaction center apparatus from the green sulfur bacterium Chlorobaculum tepidum. Proc. Natl. Acad. Sci. USA 2023, 120, e2216734120. [Google Scholar] [CrossRef]
- Engel, G.S.; Calhoun, T.R.; Read, E.L.; Ahn, T.-K.; Mančal, T.; Cheng, Y.-C.; Blankenship, R.E.; Fleming, G.R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446, 782–786. [Google Scholar] [CrossRef] [PubMed]
- Mohseni, M.; Rebentrost, P.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 2008, 129, 174106. [Google Scholar] [CrossRef]
- Abramavicius, D.; Voronine, D.V.; Mukamel, S. Unravelling Coherent Dynamics and Energy Dissipation in Photosynthetic Complexes by 2D Spectroscopy. Biophys. J. 2008, 94, 3613–3619. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Aspuru-Guzik, A. Role of Quantum Coherence and Environmental Fluctuations in Chromophoric Energy Transport. J. Phys. Chem. B 2009, 113, 9942–9947. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Kassal, I.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum transport. New J. Phys. 2009, 11, 033003. [Google Scholar] [CrossRef]
- Ishizaki, A.; Fleming, G.R. On the adequacy of the Redfield equation and related approaches to the study of quantum dynamics in electronic energy transfer. J. Chem. Phys. 2009, 130, 234110. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, A.; Fleming, G.R. Unified treatment of quantum coherent and incoherent hopping dynamics in electronic energy transfer: Reduced hierarchy equation approach. J. Chem. Phys. 2009, 130, 234111. [Google Scholar] [CrossRef]
- Cheng, Y.-C.; Fleming, G.R. Dynamics of Light Harvesting in Photosynthesis. Ann. Rev. Phys. Chem. 2009, 60, 241–262. [Google Scholar] [CrossRef]
- Panitchayangkoon, G.; Hayes, D.; Fransted, K.A.; Caram, J.R.; Harel, E.; Wen, J.; Blankenship, R.E.; Engel, G.S. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. Proc. Natl. Acad. Sci. USA 2010, 107, 12766–12770. [Google Scholar] [CrossRef] [PubMed]
- Scholes, G.D. Quantum-Coherent Electronic Energy Transfer: Did Nature Think of It First? J. Phys. Chem. Lett. 2010, 1, 2–8. [Google Scholar] [CrossRef]
- Collini, E.; Wong, C.Y.; Wilk, K.E.; Curmi, P.M.G.; Brumer, P.; Scholes, G.D. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 2010, 463, 644–647. [Google Scholar] [CrossRef]
- Scholes, G.D.; Fleming, G.R.; Olaya-Castro, A.; van Grondelle, R. Lessons from nature about solar light harvesting. Nat. Commun. 2011, 3, 763–774. [Google Scholar] [CrossRef]
- Strümpfer, J.; Şener, M.; Schulten, K. How Quantum Coherence Assists Photosynthetis Light-Harvesting. J. Phys. Chem. Lett. 2012, 3, 536–542. [Google Scholar] [CrossRef]
- Ishizaki, A.; Fleming, G.R. Quantum Coherence in Photosynthetic Light Harvesting. Annu. Rev. Condens. Matter Phys. 2012, 3, 333–361. [Google Scholar] [CrossRef]
- Collini, E. Spectroscopic signatures of quantum-coherent energy transfer. Chem. Soc. Rev. 2013, 42, 4932–4947. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Ye, J.; Zhao, Y. Path induced coherent energy transfer in light-harvesting complexes in purple bacteria. J. Chem. Phys. 2014, 141, 124103. [Google Scholar] [CrossRef] [PubMed]
- Romero, E.; Augulis, R.; Novoderezhkin, V.I.; Ferretti, M.; Thieme, J.; Zigmantas, D.; van Grondelle, R. Quantum coherence in photosynthesis for efficient solar-energy conversion. Nat. Phys. 2014, 10, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Chenu, A.; Scholes, G.D. Coherence in Energy Transfer and Photosynthesis. Ann. Rev. Phys. Chem. 2015, 66, 69–96. [Google Scholar] [CrossRef]
- Scholes, G.D.; Fleming, G.R.; Chen, L.X.; Aspuru-Guzik, A.; Buchleitner, A.; Coker, D.F.; Engel, G.S.; van Grondelle, R.; Ishizaki, A.; Jonas, D.M.; et al. Using coherence to enhance function in chemical and biophysical systems. Nature 2017, 543, 647–656. [Google Scholar] [CrossRef]
- Mirkovic, T.; Ostroumov, E.E.; Anna, J.M.; van Grondelle, R.; Govindjee; Scholes, G.D. Light Absorption and Energy Transfer in the Antenna Complexes of Photosynthetic Organisms. Chem. Rev. 2017, 117, 249–293. [Google Scholar] [CrossRef]
- Maeda, N.; Yabuki, T.; Tobita, Y.; Ishikawa, K. Finite-size corrections to the excitation energy transfer in a massless scalar interaction model. Prog. Theor. Exp. Phys. 2017, 2017, 053J01. [Google Scholar] [CrossRef]
- Duan, H.-G.; Prokhorenko, V.I.; Cogdell, R.J.; Ashraf, K.; Stevens, A.L.; Thorwart, M.; Dwayne Miller, R.J. Nature does not rely on long-lived electronic quantum coherence for photosynthetic energy transfer. Proc. Natl. Acad. Sci. USA 2017, 114, 8493–8498. [Google Scholar] [CrossRef]
- Rathbone, H.W.; Davis, J.A.; Michie, K.A.; Goodchild, S.C.; Robertson, N.O.; Curmi, P.M.G. Coherent phenomena in photosynthetic light harvesting: Part two—Observations in biological systems. Biophys. Rev. 2018, 10, 1443–1463. [Google Scholar] [CrossRef]
- Harush, E.Z.; Dubi, Y. Do photosynthetic complexes use quantum coherence to increase their efficiency? Probably not. Sci. Adv. 2021, 7, eabc4631. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, A.; Fleming, G.R. Insights into Photosynthetic Energy Transfer Gained from Free-Energy Structure: Coherent Transport, Incoherent Hopping, and Vibrational Assistance Revisited. J. Phys. Chem. B 2021, 125, 3286–3295. [Google Scholar] [CrossRef] [PubMed]
- Klinger, A.; Lindorfer, D.; Müh, F.; Renger, T. Living on the edge: Light-harvesting efficiency and photoprotection in the core of green sulfur bacteria. Phys. Chem. Chem. Physic 2023, 25, 18698–18710. [Google Scholar] [CrossRef]
- Duan, H.-G.; Jha, A.; Chen, L.; Miller, R.J.D. Quantum coherent energy transport in the Fenna–Matthews–Olson complex at low temperature. Proc. Natl. Acad. Sci. USA 2022, 119, e2212630119. [Google Scholar] [CrossRef]
- Uthailiang, T.; Suntijitrungruang, O.; Issarakul, P.; Pongkitiwanichakul, P.; Boonchui, S. Investigation of quantum trajectories in photosynthetic light harvesting through a quantum stochastic approach. Sci. Rep. 2025, 15, 5220. [Google Scholar] [CrossRef] [PubMed]
- Takeda, S.; Furusawa, A. Toward large-scale fault-tolerant universal photonic quantum computing. APL Photonics 2019, 4, 060902. [Google Scholar] [CrossRef]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513–573. [Google Scholar] [CrossRef]
- Raussendorf, R.; Briegel, H.J. A One-Way Quantum Computer. Phys. Rev. Lett. 2001, 86, 5188–5191. [Google Scholar] [CrossRef]
- Raussendorf, R.; Browne, D.E.; Briegel, H.J. Measurement-based quantum computation on cluster states. Phys. Rev. A 2003, 68, 022312. [Google Scholar] [CrossRef]
- Larsen, M.V.; Guo, X.; Breum, C.R.; Neergaard-Nielsen, J.S.; Andersen, U.L. Deterministic generation of a two-dimensional cluster state. Science 2019, 366, 369–372. [Google Scholar] [CrossRef]
- Larsen, M.V.; Neergaard-Nielsen, J.S.; Andersen, U.L. Architecture and noise analysis of continuous-variable quantum gates using two-dimensional cluster states. Phys. Rev. A 2020, 102, 042608. [Google Scholar] [CrossRef]
- Stephen, D.T.; Ho, W.W.; Wei, T.-C.; Raussendorf, R.; Verresen, R. Universal Measurement-Based Quantum Computation in a One-Dimensional Architecture Enabled by Dual-Unitary Circuits. Phys. Rev. Lett. 2024, 132, 250601. [Google Scholar] [CrossRef]
- Lloyd, S. Ultimate physical limits to computation. Nature 2000, 406, 1047–1054. [Google Scholar] [CrossRef] [PubMed]
- Kitaev, A.Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Bravyi, S.; Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. A 2005, 71, 022316. [Google Scholar] [CrossRef]
- Barends, R.; Kelly, J.; Megrant, A.; Veitia, A.; Sank, D.; Jeffrey, E.; White, T.C.; Mutus, J.; Fowler, A.G.; Campbell, B.; et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 2014, 508, 500–503. [Google Scholar] [CrossRef]
- Google Quantum AI. Suppressing quantum errors by scaling a surface code logical qubit. Nature 2023, 614, 676–681. [Google Scholar] [CrossRef]
- Bravyi, S.; Cross, A.W.; Gambetta, J.M.; Maslov, D.; Rall, P.; Yoder, T.J. High-threshold and low-overhead fault-tolerant quantum memory. Nature 2024, 627, 778–782. [Google Scholar] [CrossRef]
- Bausch, J.; Senior, A.W.; Heras, F.J.H.; Edlich, T.; Davies, A.; Newman, M.; Jones, C.; Satzinger, K.; Niu, M.Y.; Blackwell, S.; et al. Learning high-accuracy error decoding for quantum processors. Nature 2024, 635, 834–840. [Google Scholar] [CrossRef]
- Goto, H. High-performance fault-tolerant quantum computing with many-hypercube codes. Sci. Adv. 2024, 10, eadp6388. [Google Scholar] [CrossRef]
- Google Quantum AI and Collaborators. Quantum error correction below the surface code threshold. Nature 2025, 638, 920–926. [Google Scholar] [CrossRef] [PubMed]
- Itogawa, T.; Takada, Y.; Hirano, Y.; Fujii, K. Efficient Magic State Distillation by Zero-Level Distillation. PRX Quantum 2025, 6, 020356. [Google Scholar] [CrossRef]
- Gidney, C.; Shutty, N.; Jones, C. Magic state cultivation: Growing T states as cheap as CNOT gates. arXiv 2024, arXiv:2409.17595. [Google Scholar] [CrossRef]
- Gottesman, D.; Kitaev, A.; Preskill, J. Encoding a qubit in an oscillator. Phys. Rev. A 2001, 64, 012310. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Optical Computing: Status and Perspectives. Nanomaterials 2022, 12, 2171. [Google Scholar] [CrossRef]
- Takase, K.; Fukui, K.; Kawasaki, A.; Asavanant, W.; Endo, M.; Yoshikawa, J.; van Loock, P.; Furusawa, A. Gottesman-Kitaev-Preskill qubit synthesizer for propagating light. npj Quantum Inf. 2023, 9, 98. [Google Scholar] [CrossRef]
- Foote, C.S. Photosensitized oxygenations and the role of singlet oxygen. Acc. Chem. Res. 1968, 1, 104–110. [Google Scholar] [CrossRef]
- Kasha, M.; Khan, A.U. The Physics, Chemistry, and Biology, of Singlet Molecular Oxygen. Ann. N. Y. Acad. Sci. 1970, 171, 5–23. [Google Scholar] [CrossRef]
- Kearns, D.R. Physical and chemical properties of singlet molecular oxygen. Chem. Rev. 1971, 71, 395–427. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fueno, T.; Fukutome, H. Mechanisms of the reactions of singlet molecular oxygen with olefins. Chem. Phys. Lett. 1973, 22, 466–470. [Google Scholar] [CrossRef]
- Wanga, F.; Liu, X. Recent advances in the chemistry of lanthanide-doped upconversion nanocrystals. Chem. Soc. Rev. 2009, 38, 976–989. [Google Scholar] [CrossRef] [PubMed]
- Singh-Rachford, T.N.; Castellano, F.N. Photon upconversion based on sensitized triplet–triplet annihilation. Coord. Chem. Rev. 2010, 254, 2560–2573. [Google Scholar] [CrossRef]
- Monguzzi, A.; Tubino, R.; Hoseinkhani, S.; Campione, M.; Meinardi, F. Low power, non-coherent sensitized photon up-conversion: Modelling and perspectives. Phys. Chem. Chem. Physic 2012, 14, 4322–4332. [Google Scholar] [CrossRef]
- Chen, G.; Qiu, H.; Prasad, P.N.; Chen, X. Upconversion Nanoparticles: Design, Nanochemistry, and Applications in Theranostics. Chem. Rev. 2014, 114, 5161–5214. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Liu, Q.; Feng, W.; Sun, Y.; Li, F. Upconversion Luminescent Materials: Advances and Applications. Chem. Rev. 2015, 115, 395–465. [Google Scholar] [CrossRef]
- Schulze, T.F.; Schmidt, T.W. Photochemical upconversion: Present status and prospects for its application to solar energy conversion. Energy Environ. Sci. 2015, 8, 103–125. [Google Scholar] [CrossRef]
- Yanai, N.; Kimizuka, N. New Triplet Sensitization Routes for Photon Upconversion: Thermally Activated Delayed Fluorescence Molecules, Inorganic Nanocrystals, and Singlet-to-Triplet Absorption. Acc. Chem. Res. 2017, 50, 2487–2495. [Google Scholar] [CrossRef]
- Bharmoria, P.; Bildirir, H.; Moth-Poulsen, K. Triplet–triplet annihilation based near infrared to visible molecular photon upconversion. Chem. Soc. Rev. 2020, 49, 6529–6554. [Google Scholar] [CrossRef]
- Nonat, A.M.; Charbonnière, L.J. Upconversion of light with molecular and supramolecular lanthanide complexes. Coord. Chem. Rev. 2020, 409, 213192. [Google Scholar] [CrossRef]
- Wang, H.; Liu, W.; Jin, S.; Zhang, X.; Xie, Y. Low-Dimensional Semiconductors in Artificial Photosynthesis: An Outlook for the Interactions Between Particles/Quasiparticles. ACS Cent. Sci. 2020, 6, 1058–1069. [Google Scholar] [CrossRef] [PubMed]
- Richards, B.S.; Hudry, D.; Busko, D.; TurshatovIan, A.; Howard, A. Photon Upconversion for Photovoltaics and Photocatalysis: A Critical Review. Chem. Rev. 2021, 121, 9165–9195. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Bae, K.; Park, W. Enhancement of upconversion luminescence using photonic nanostructures. Nanophotonics 2020, 9, 1359–1371. [Google Scholar] [CrossRef]
- Xu, X.; Shen, R.; Mo, L.; Yang, X.; Chen, X.; Wang, H.; Li, Y.; Hu, C.; Lei, B.; Zhang, X.; et al. Improving Plant Photosynthesis Through Light-Harvesting Upconversion Nanoparticles. ACS Nano 2022, 16, 18027–18037. [Google Scholar] [CrossRef] [PubMed]
- Kurzweil, Y.; Baer, R. Quantum memory effects in the dynamics of electrons in gold clusters. Phys. Rev. B 2006, 73, 075413. [Google Scholar] [CrossRef]
- Ramakrishna, G.; Varnavski, O.; Kim, J.; Lee, D.; Goodson, T. Quantum-Sized Gold Clusters as Efficient Two-Photon Absorbers. J. Am. Chem. Soc. 2008, 130, 5032–5033. [Google Scholar] [CrossRef]
- Bao, K.; Goedecker, S.; Koga, K.; Lançon, F.; Neelov, A. Structure of large gold clusters obtained by global optimization using the minima hopping method. Phys. Rev. B 2009, 79, 041405. [Google Scholar] [CrossRef]
- Russier-Antoine, I.; Bertorelle, F.; Vojkovic, M.; Rayane, D.; Salmon, E.; Jonin, C.; Dugourd, P.; Antoine, R.; Breveta, P.-F. Non-linear optical properties of gold quantum clusters. The smaller the better. Nanoscale 2014, 6, 13572–13578. [Google Scholar] [CrossRef]
- Kurelchuk, U.N.; Vasilyev, O.S.; Borisyuk, P.V. Structure and electronic properties of small gold clusters. J. Phys. Conf. Ser. 2019, 1238, 012021. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Liu, H.; Long, W.; Zhang, X.-D. Enzyme-Like Properties of Gold Clusters for Biomedical Application. Front. Chem. 2020, 8, 219. [Google Scholar] [CrossRef]
- Liu, Z.; Luo, L.; Jin, R. Visible to NIR-II Photoluminescence of Atomically Precise Gold Nanoclusters. Adv. Mater. 2023, 36, 2309073. [Google Scholar] [CrossRef]
- Kong, J.; Zhang, W.; Wu, Y.; Zhou, M. Optical properties of gold nanoclusters constructed from Au13 units. Aggregate 2022, 3, e207. [Google Scholar] [CrossRef]
- Taherpour, M.; van Hoesel, C.; Coehoorn, R.; Bobbert, P.A. Accurate and fast master equation modeling of triplet-triplet annihilation in organic phosphorescent emission layers including correlations. Phys. Rev. B 2022, 105, 085202. [Google Scholar] [CrossRef]
- Edhborg, F.; Olesund, A.; Albinsson, B. Best practice in determining key photophysical parameters in triplet–triplet annihilation photon upconversion. Photochem. Photobiol. Sci. 2022, 21, 1143–1158. [Google Scholar] [CrossRef] [PubMed]
- Carrod, A.J.; Gray, V.; Börjesson, K. Recent advances in triplet–triplet annihilation upconversion and singlet fission, towards solar energy applications. Energy Environ. Sci. 2022, 15, 4982–5016. [Google Scholar] [CrossRef]
- Forecast, R.; Campaioli, F.; Cole, J.H. Magnetic Field Effects in Triplet–Triplet Annihilation Upconversion: Revisiting Atkins and Evans’ Theory. J. Chem. Theory Comput. 2023, 19, 7816–7824. [Google Scholar] [CrossRef] [PubMed]
- Zankel, K.L.; Clayton, R.K. ‘Uphill’ Energy Transfer in a Photosynthetic Bacterium. Photochem. Photobiol. 1969, 9, 7–15. [Google Scholar] [CrossRef]
- Tanaka, A.; Fukushima, Y.; Kamiya, N. Two Different Structures of the Oxygen-Evolving Complex in the Same Polypeptide Frameworks of Photosystem II. J. Am. Chem. Soc. 2017, 139, 1718–1721. [Google Scholar] [CrossRef]
- Kato, K.; Miyazaki, N.; Hamaguchi, T.; Nakajima, Y.; Akita, F.; Yonekura, K.; Shen, J.-R. High-resolution cryo-EM structure of photosystem II reveals damage from high-dose electron beams. Commun. Biol. 2021, 4, 382. [Google Scholar] [CrossRef]
- Wilhelm, C.; Jakob, T. Uphill energy transfer from long-wavelength absorbing chlorophylls to PS II in Ostreobium sp. is functional in carbon assimilation. Photosynth. Res. 2006, 87, 323–329. [Google Scholar] [CrossRef]
- Kotabová, E.; Jarešová, J.; Kaňa, R.; Sobotka, R.; Bína, D.; Prášil, O. Novel type of red-shifted chlorophyll a antenna complex from Chromera velia. I. Physiological relevance and functional connection to photosystems. Biochim. Biophys. Acta 2014, 1837, 734–743. [Google Scholar] [CrossRef]
- Giera, W.; Szewczyk, S.; McConnell, M.D.; Redding, K.E.; van Grondelle, R.; Gibasiewicz, K. Uphill energy transfer in photosystem I from Chlamydomonas reinhardtii. Time-resolved fluorescence measurements at 77 K. Photosynth. Res. 2018, 137, 321–335. [Google Scholar] [CrossRef]
- Wolf, B.M.; Blankenship, R.E. Far-red light acclimation in diverse oxygenic photosynthetic organisms. Photosynth. Res. 2019, 142, 349–359. [Google Scholar] [CrossRef]
- Kosugi, M.; Ozawa, S.-I.; Takahashi, Y.; Kamei, Y.; Itoh, S.; Kudoh, S.; Kashino, Y.; Koike, H. Red-shifted chlorophyll a bands allow uphill energy transfer to photosystem II reaction centers in an aerial green alga, Prasiola crispa, harvested in Antarctica. Biochim. Biophys. Acta-Bioenerg. 2020, 1861, 148139. [Google Scholar] [CrossRef]
- Hamaguchi, T.; Kawakami, K.; Shinzawa-Itoh, K.; Inoue-Kashino, N.; Itoh, S.; Ifuku, K.; Yamashita, E.; Maeda, K.; Yonekura, K.; Kashino, Y. Structure of the far-red light utilizing photosystem I of Acaryochloris marina. Nat. Commun. 2021, 12, 2333. [Google Scholar] [CrossRef]
- Kosugi, M.; Kawasaki, M.; Shibata, Y.; Hara, K.; Takaichi, S.; Moriya, T.; Adachi, N.; Kamei, Y.; Kashino, Y.; Kudoh, S.; et al. Uphill energy transfer mechanism for photosynthesis in an Antarctic alga. Nat. Commun. 2023, 14, 730. [Google Scholar] [CrossRef]
- Waszczak, C.; Carmody, M.; Kangasjärvi, J. Reactive Oxygen Species in Plant Signaling. Ann. Rev. Plant Bio. 2018, 69, 209–236. [Google Scholar] [CrossRef] [PubMed]
- Linker, T.M.; Halavanau, A.; Kroll, T.; Benediktovitch, A.; Zhang, Y.; Michine, Y.; Chuchurka, S.; Abhari, Z.; Ronchetti, D.; Fransson, T.; et al. Attosecond inner-shell lasing at ångström wavelengths. Nature 2025, 642, 934–940. [Google Scholar] [CrossRef] [PubMed]
- Matselyukh, D.; Svoboda, V.; Wörner, H.J. Attosecond X-ray spectroscopy reveals the competing stochastic and ballistic dynamics of a bifurcating Jahn–Teller dissociation. Nat. Commun. 2025, 16, 6540. [Google Scholar] [CrossRef]
- Inoue, I.; Sato, T.; Robles, R.; Seaberg, M.H.; Sun, Y.; Zhu, D.; Cesar, D.; Ding, Y.; Esposito, V.; Franz, P.; et al. Nanofocused attosecond hard x-ray free-electron laser with intensity exceeding 1019 W/cm2. Optica 2025, 12, 309–310. [Google Scholar] [CrossRef]
- Guo, Z.; Driver, T.; Beauvarlet, S.; Cesar, D.; Duris, J.; Franz, P.L.; Alexander, O.; Bohler, D.; Bostedt, C.; Averbukh, V.; et al. Experimental demonstration of attosecond pump–probe spectroscopy with an X-ray free-electron laser. Nat. Photonics 2024, 18, 691–697. [Google Scholar] [CrossRef]
- Yan, J.; Qin, W.; Chen, Y.; Decking, W.; Dijkstal, P.; Guetg, M.; Inoue, I.; Kujala, N.; Liu, S.; Long, T.; et al. Terawatt-attosecond hard X-ray free-electron laser at high repetition rate. Nature Photo. 2024, 18, 1293–1298. [Google Scholar] [CrossRef]
- Bergmann, U. Stimulated X-ray emission spectroscopy. Photosynth. Res. 2024, 162, 371–384. [Google Scholar] [CrossRef]
- Franz, P.; Li, S.; Driver, T.; Robles, R.R.; Cesar, D.; Isele, E.; Guo, Z.; Wang, J.; Duris, J.P.; Larsen, K.; et al. Terawatt-scale attosecond X-ray pulses from a cascaded superradiant free-electron laser. Photosynth. Res. 2024, 18, 698–703. [Google Scholar] [CrossRef]
- Everett, H., III. “Relative State” Formulation of Quantum Mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- Omnès, R. Consistent interpretations of quantum mechanics. Rev. Mod. Phys. 1992, 64, 339–382. [Google Scholar] [CrossRef]
- Arthurs, E.; Kelly, J.L. B.S.T.J. briefs: On the simultaneous measurement of a pair of conjugate observables. Bell Syst. Tech. J. 1965, 44, 725–729. [Google Scholar] [CrossRef]
- Arthurs, E.; Goodman, M.S. Quantum Correlations: A Generalized Heisenberg Uncertainty Relation. Phys. Rev. Lett. 1988, 60, 2447–2449. [Google Scholar] [CrossRef]
- Ozawa, M. Quantum Measurements, Instruments, and Uncertainty Principle. Interdiscip. Inf. Sci. 2004, 10, 69–81. [Google Scholar] [CrossRef]
- Watanabe, Y.; Sagawa, T.; Ueda, M. Uncertainty relation revisited from quantum estimation theory. Phys. Rev. A 2011, 84, 042121. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Petruccione, P. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Wiseman, H.M.; Milburn, G.J. Quantum Measurement and Control; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Bergou, J.A.; Hillery, M.; Saffman, M. Quantum Information Processing; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
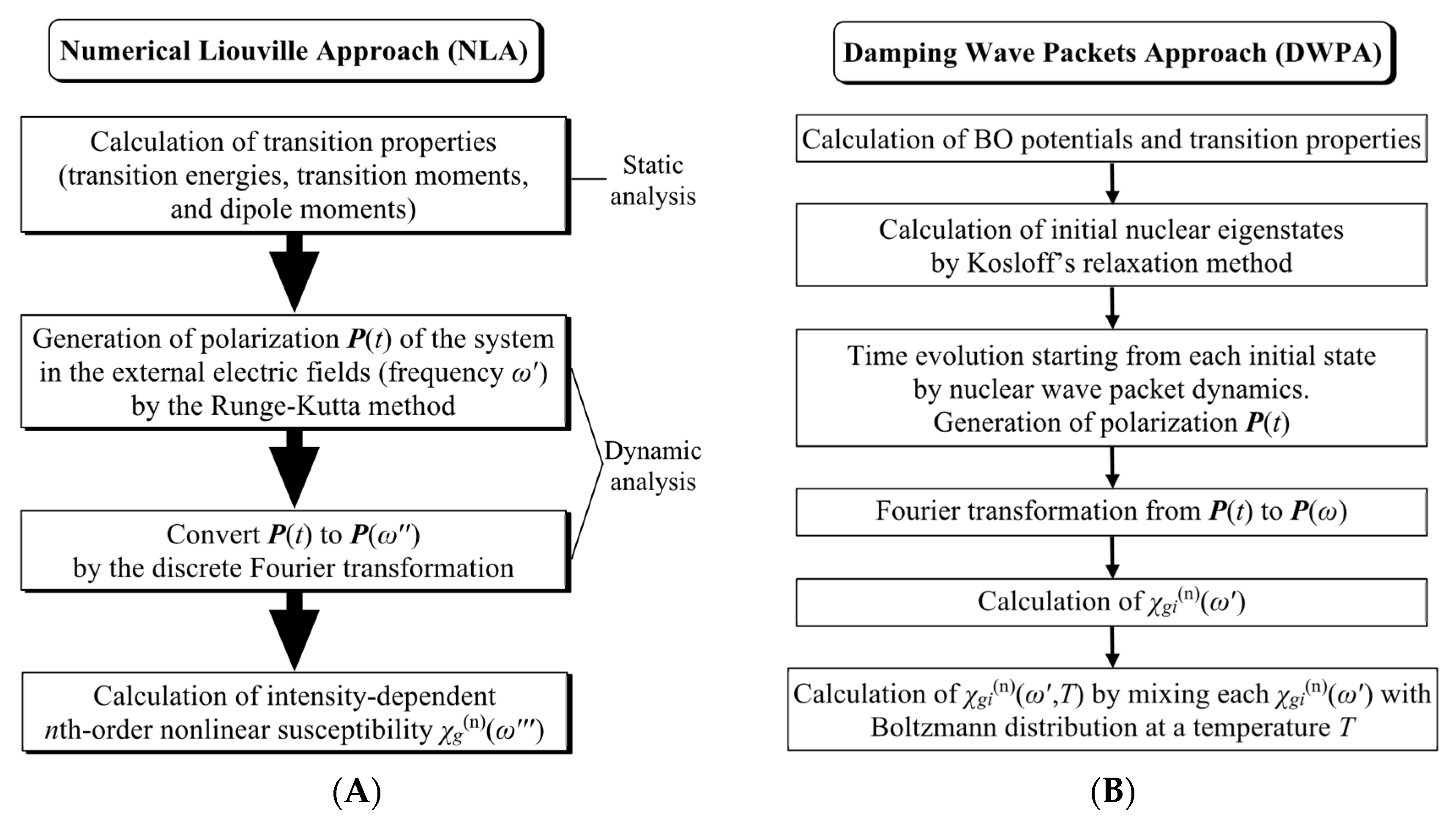
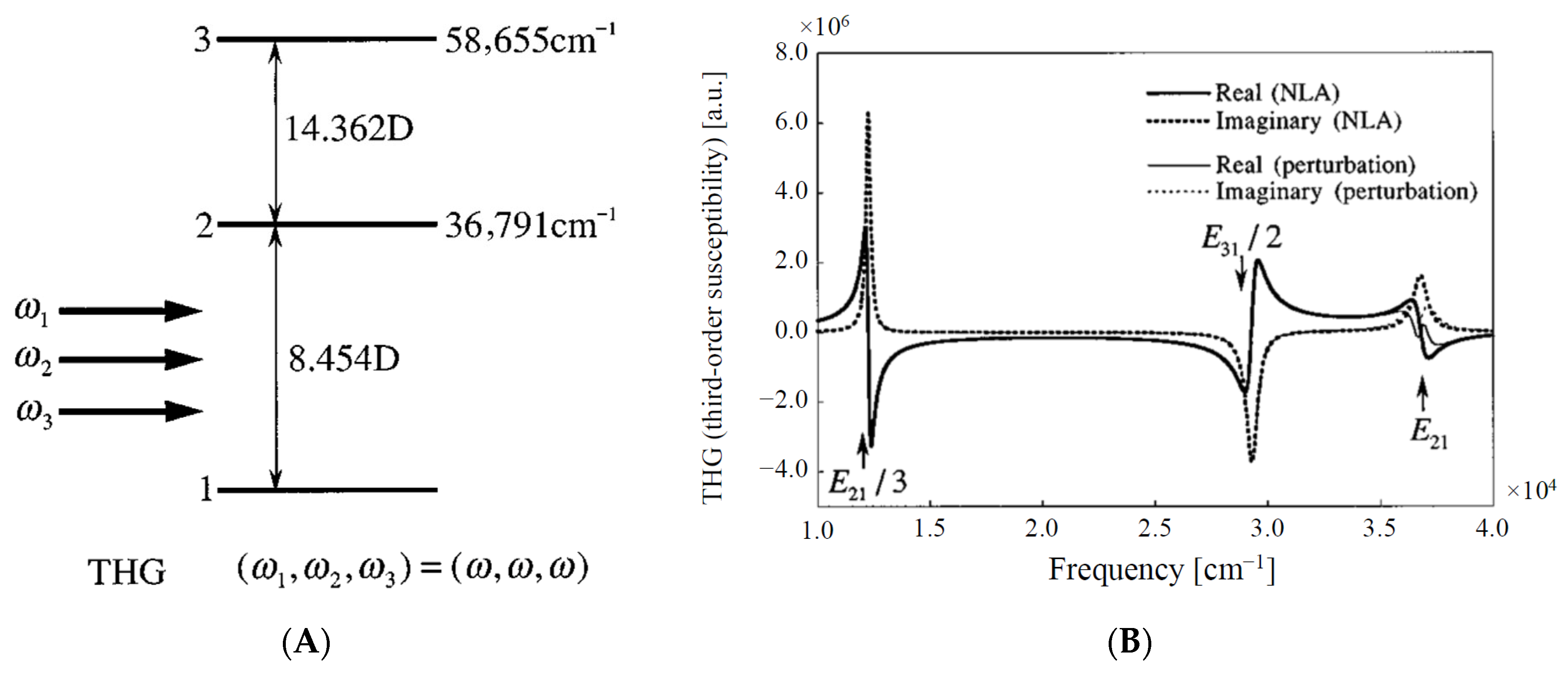

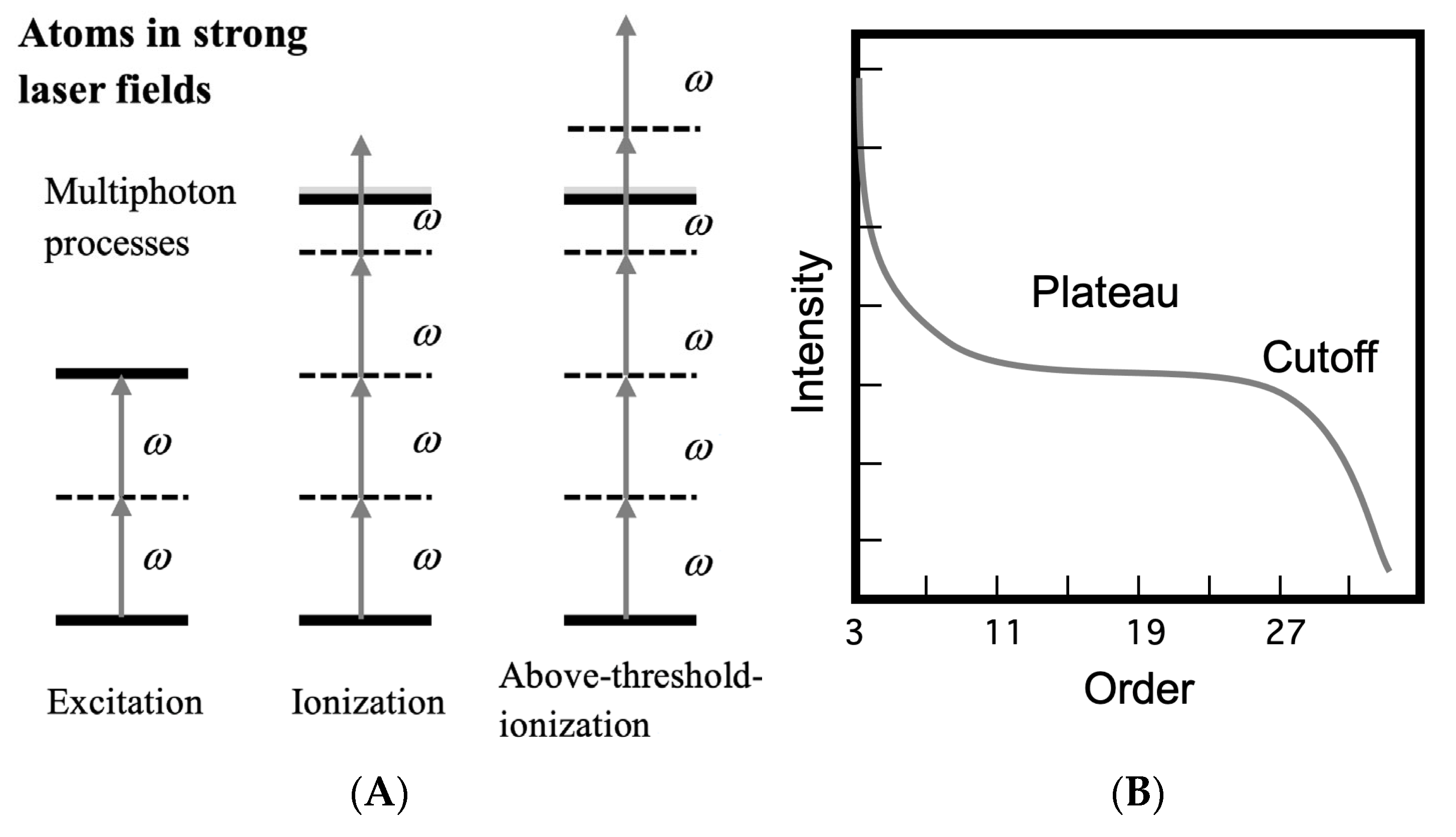
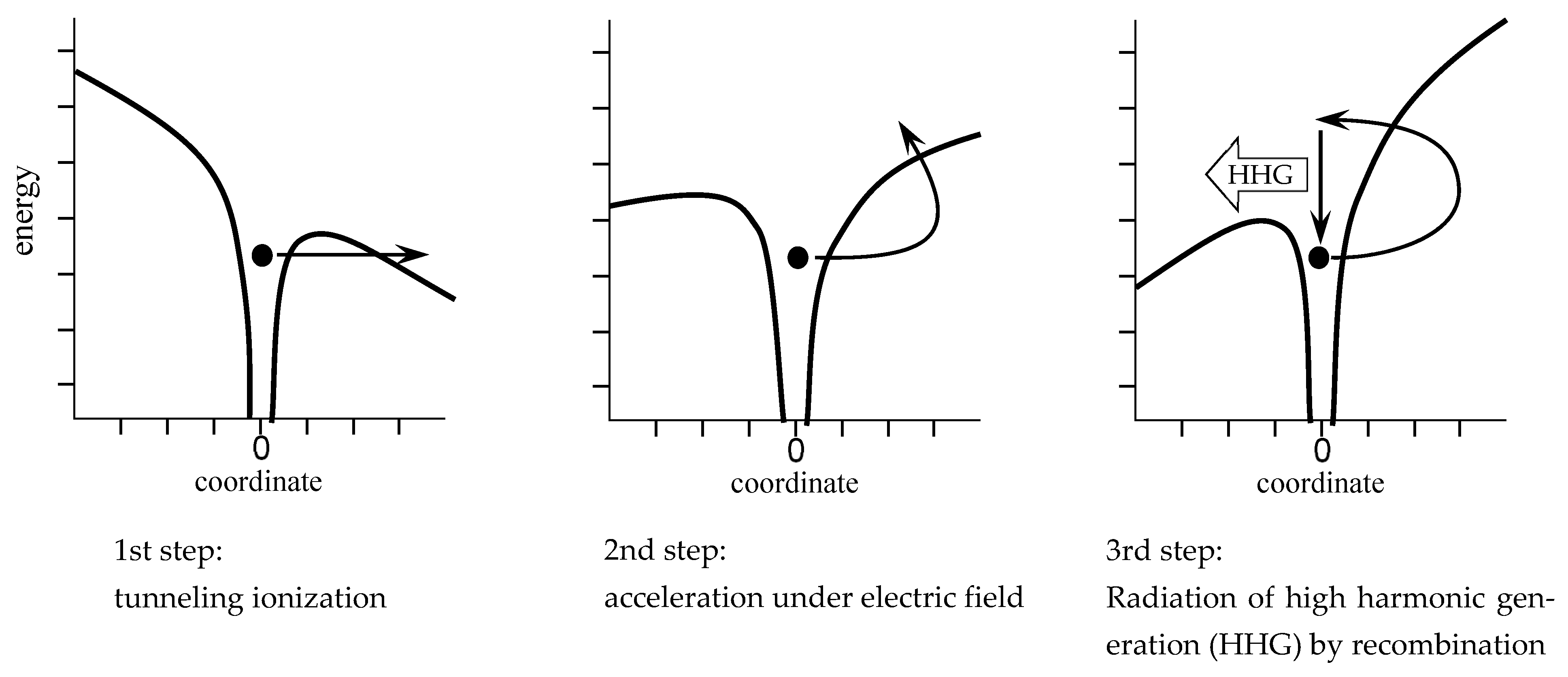


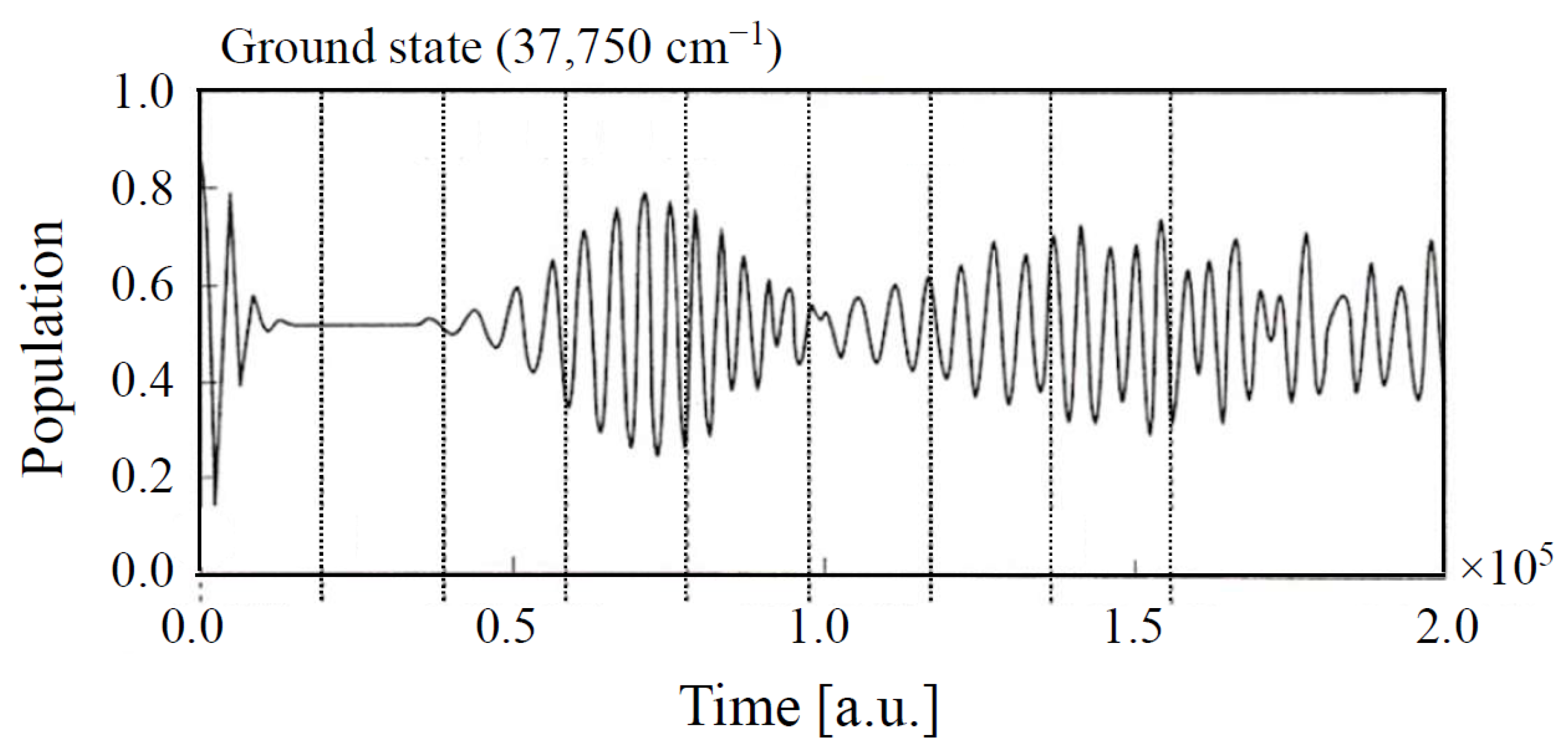
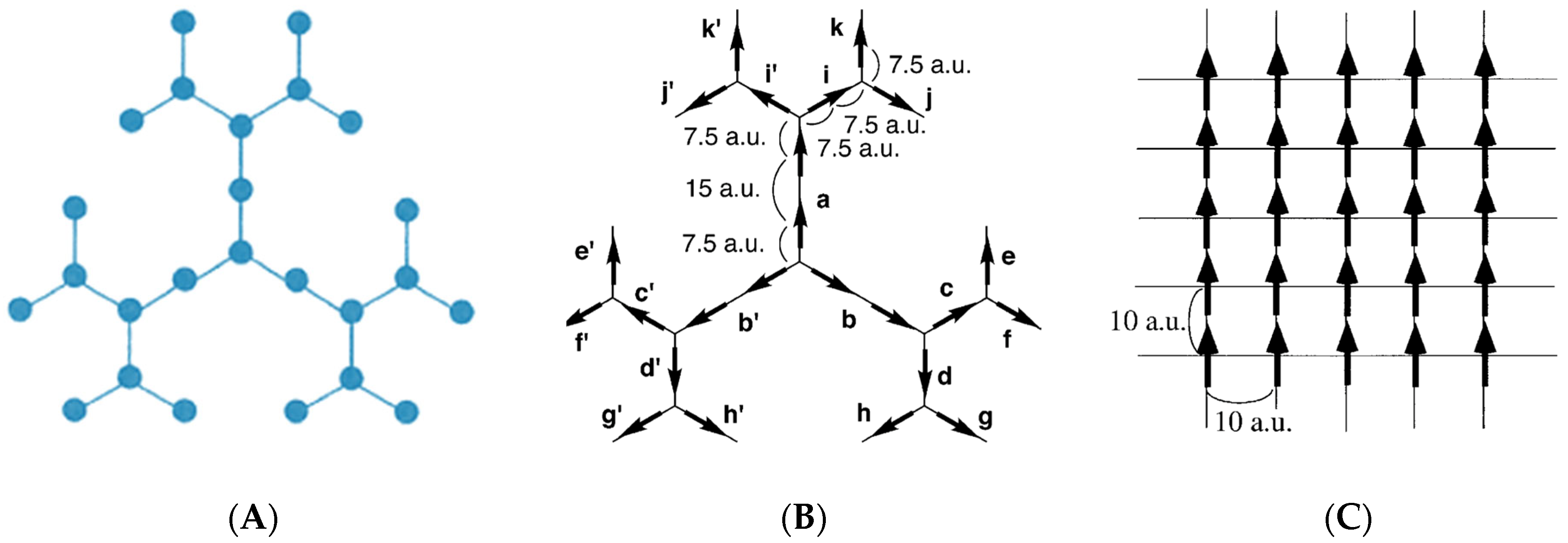


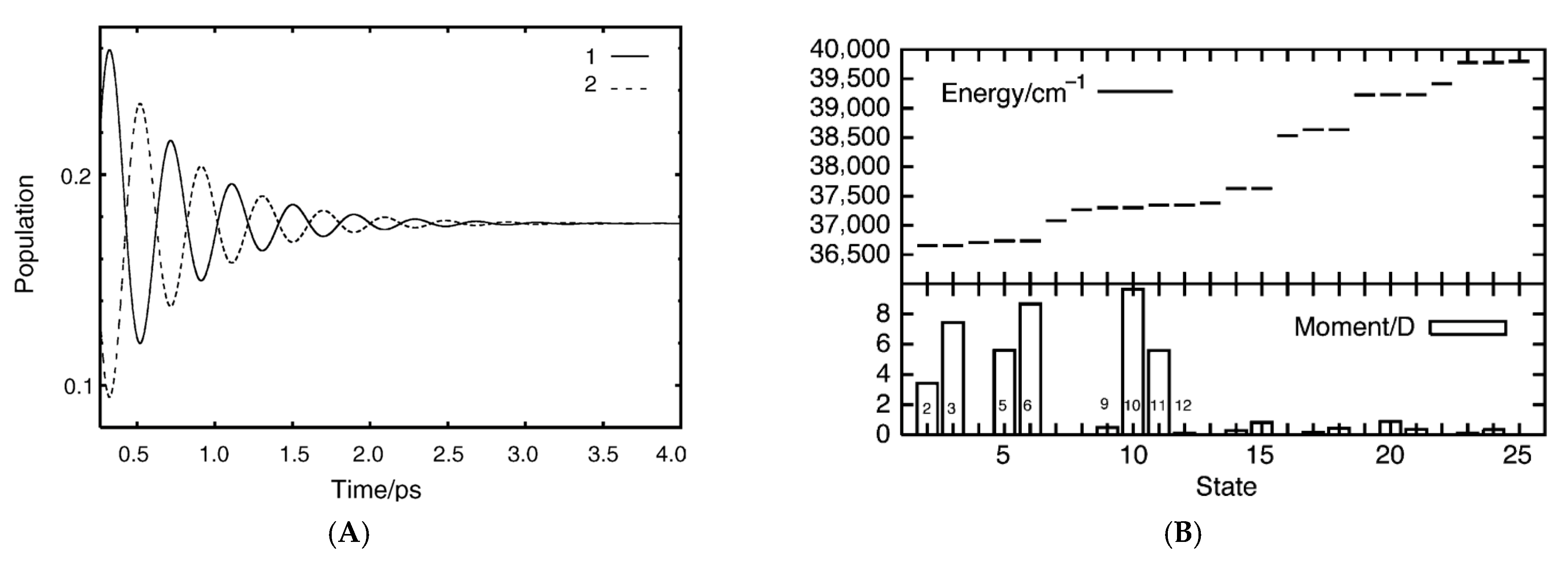

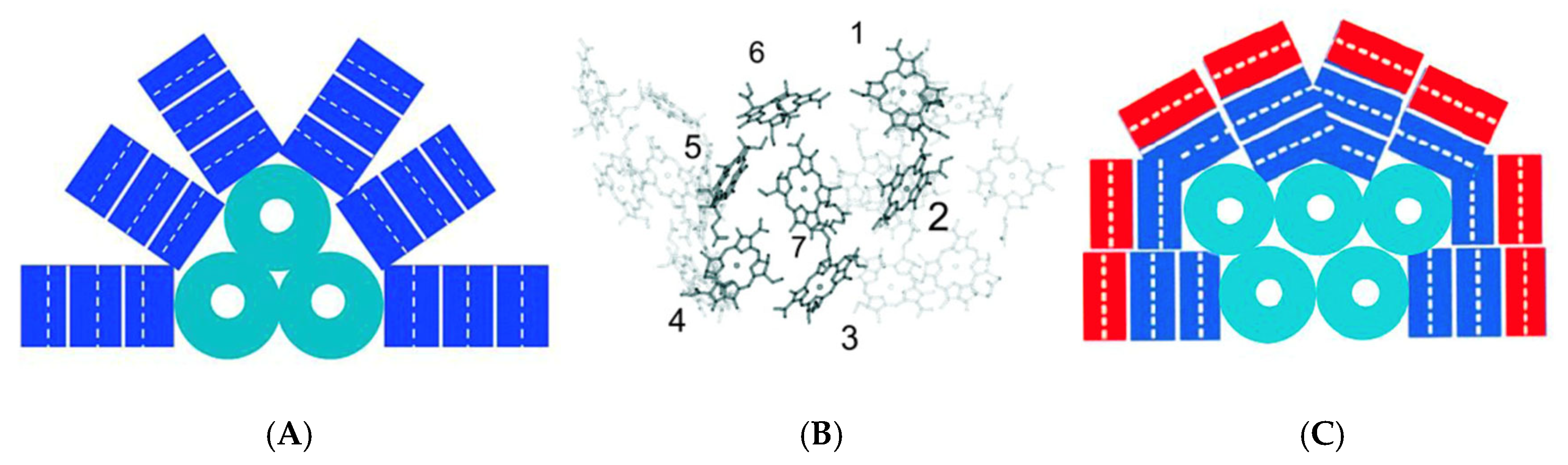
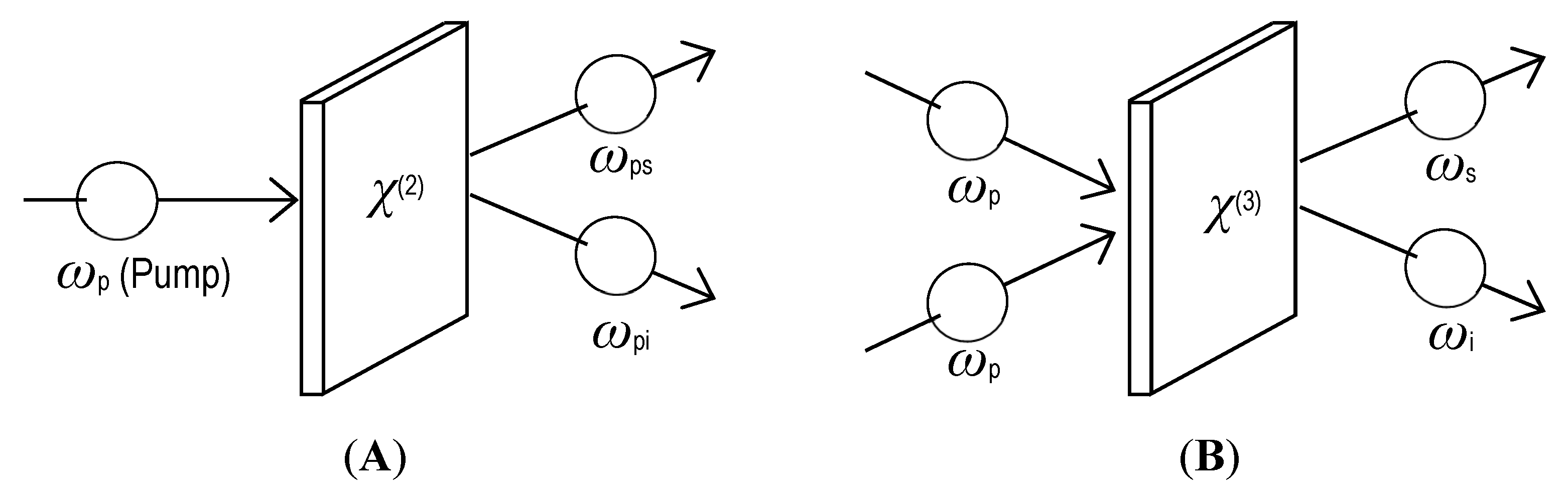
| Response Property | Optical Process | Formula |
|---|---|---|
| Second-order response to the electrostatic field | ||
| Pockels effect | ||
| Second harmonic generation (SHG) | ||
| Third-order response to the electrostatic field | ||
| Third harmonic generation (THG) | ||
| Electric-field-induced second harmonic generation (ESHG) | ||
| Degenerate four-wave mixing (DFWM) | ||
| dc-Kerr effect | ||
| Coherent anti-Stokes Raman scattering (CARS) | ||
| ac-Kerr effect | ||
| Cotton–Mouton effect |
| Method | 0.000 | 0.005 | 0.015 | 0.020 | 0.025 | 0.035 | 0.045 |
|---|---|---|---|---|---|---|---|
| αzz (QED-ROHF) | 11.74 | 11.74 | 11.75 | 11.76 | 11.77 | 11.80 | 11.84 |
| αaver (QED-ROHF) (a) | 11.17 | 11.17 | 11.19 | 11.20 | 11.22 | 11.29 | 11.39 |
| αzz (QED-ROHF + MP2) | 13.18 | 13.18 | 13.20 | 13.21 | 13.22 | 13.26 | 13.32 |
| αaver (QED-ROHF + MP2) | 12.21 | 12.22 | 12.23 | 12.25 | 12.28 | 12.34 | 12.45 |
| αzz (MP2 Contribution) (b) | 10.95 | 10.95 | 10.97 | 10.99 | 11.01 | 11.06 | 11.13 |
| αaver (MP2 Contribution) | 8.57 | 8.57 | 8.57 | 8.57 | 8.67 | 8.56 | 8.55 |
| Method | μz | αzz | αave | βzzz | βzxx | βyxx | β|| |
|---|---|---|---|---|---|---|---|
| RHF SCF (a) | 0.636 | 13.27 | 12.93 | −6.980 | −6.728 | 9.410 | −12.26 |
| RHF SCF (b) | 0.636 | 13.32 | 12.96 | −11.67 | −7.293 | 8.665 | −15.76 |
| RMP2 (a) | 0.600 | 15.71 | 14.41 | −31.15 | −7.553 | 9.086 | −27.75 |
| RMP2 (b) | 0.599 | 15.82 | 14.47 | −37.93 | −8.235 | 6.911 | −32.64 |
| EOM-CCSD (c) | --- | --- | --- | −41.0 | −9.1 | 7.2 | −35.9 |
| RCCSD(T) (d) | 0.590 | 15.71 | 14.38 | −39.6 | −8.8 | --- | −34.3 |
| Exp (e) | 0.578 | --- | 14.56 | --- | --- | --- | --- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, S.; Kobayashi, T.; Takahata, M.; Nitta, H.; Isobe, H.; Kawakami, T.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. Non-Perturbative Approaches to Linear and Nonlinear Responses of Atoms, Molecules, and Molecular Aggregates: A Theoretical Approach to Molecular Quantum Information and Quantum Biology. Chemistry 2025, 7, 164. https://doi.org/10.3390/chemistry7050164
Yamada S, Kobayashi T, Takahata M, Nitta H, Isobe H, Kawakami T, Yamanaka S, Okumura M, Yamaguchi K. Non-Perturbative Approaches to Linear and Nonlinear Responses of Atoms, Molecules, and Molecular Aggregates: A Theoretical Approach to Molecular Quantum Information and Quantum Biology. Chemistry. 2025; 7(5):164. https://doi.org/10.3390/chemistry7050164
Chicago/Turabian StyleYamada, Satoru, Takao Kobayashi, Masahiro Takahata, Hiroya Nitta, Hiroshi Isobe, Takashi Kawakami, Shusuke Yamanaka, Mitsutaka Okumura, and Kizashi Yamaguchi. 2025. "Non-Perturbative Approaches to Linear and Nonlinear Responses of Atoms, Molecules, and Molecular Aggregates: A Theoretical Approach to Molecular Quantum Information and Quantum Biology" Chemistry 7, no. 5: 164. https://doi.org/10.3390/chemistry7050164
APA StyleYamada, S., Kobayashi, T., Takahata, M., Nitta, H., Isobe, H., Kawakami, T., Yamanaka, S., Okumura, M., & Yamaguchi, K. (2025). Non-Perturbative Approaches to Linear and Nonlinear Responses of Atoms, Molecules, and Molecular Aggregates: A Theoretical Approach to Molecular Quantum Information and Quantum Biology. Chemistry, 7(5), 164. https://doi.org/10.3390/chemistry7050164






