Color Transparency in $\overline{p}$A Reactions

Abstract

Exclusive channels of antiproton annihilation on the bound nucleon are sensitive to mesonic interactions with the target residue. If the hard scale is present, then such interactions should be reduced due to color transparency (CT). In this paper, the $d(\overline{p},{\pi }^{-}{\pi }^0)p$ reaction is discussed at a large center-of-mass angle. Predictions for the future PANDA (antiProton ANnihilations at DArmstadt) experiment at FAIR (Facility for Antiproton and Ion Research, Darmstadt, Germany) are given for nuclear transparency ratios calculated within the generalized eikonal approximation and the quantum diffusion model of CT.

The physics program of the future PANDA (antiProton ANnihilations at DArmstadt) experiment [1,2] includes a substantial part related to the studies of antiproton–nucleus reactions at the beam momentum of 1.5–15 GeV/c, with c being the speed of light. At low beam momenta, or by requiring that the particle of interest slows down in the collision with a nucleon, one can study the influence of a nuclear medium on the properties of the antiproton and produced particles such as antibaryon potentials, new decay channels due to the in-medium thresholds (e.g., ${\psi }^{\prime }\to D\overline{D}$), and the partial restoration of chiral symmetry at finite baryon number density. On the other hand, at high beam momenta, it is possible to study the interactions of fast hadrons produced in hard processes induced by the antiproton with the nuclear medium. Thus, one can access color transparency (CT) and short-range nucleon-nucleon ($NN$) correlations in nuclei.

Two-meson annihilation offers a good opportunity to look for the signals of CT, as mesons are generally easier to “squeeze” to point-like configurations (PLC) as compared to baryons. The processes $\overline{p}N\to \pi \pi$ at the center-of-mass (c.m.) polar scattering angle ${\mathsf{\Theta }}_{\mathrm{c}.\mathrm{m}.}\simeq 90$ (i.e., at the standard Mandelstam variables $-t\simeq -u\simeq s/2$) on the bound nucleon seem to be the simplest in this sense and have cross-sections large enough to be studied at the initial stage of the PANDA operation. In contrast to the one-body final state (e.g., $\overline{p}p\to J/\psi$), the beam momentum is not fixed by the mass shell constraint and can be chosen to be sufficiently large (10–20 GeV/c, so that the coherence lengths of the incoming antiproton and the produced pions (see Equation (11) below) would be comparable to the size of the nucleus.

Here, we focus on the process $\overline{p}d\to {\pi }^{-}{\pi }^{0}p$, where the spectator proton is slow in the deuteron rest frame; see details in Ref. [3]. The deuteron wave function (DWF) is relatively well-known, which allows for more robust predictions on exclusive channels as compared with heavier nuclear targets. The CT influences initial-state and final-state interactions due to rescattering on the spectator proton.

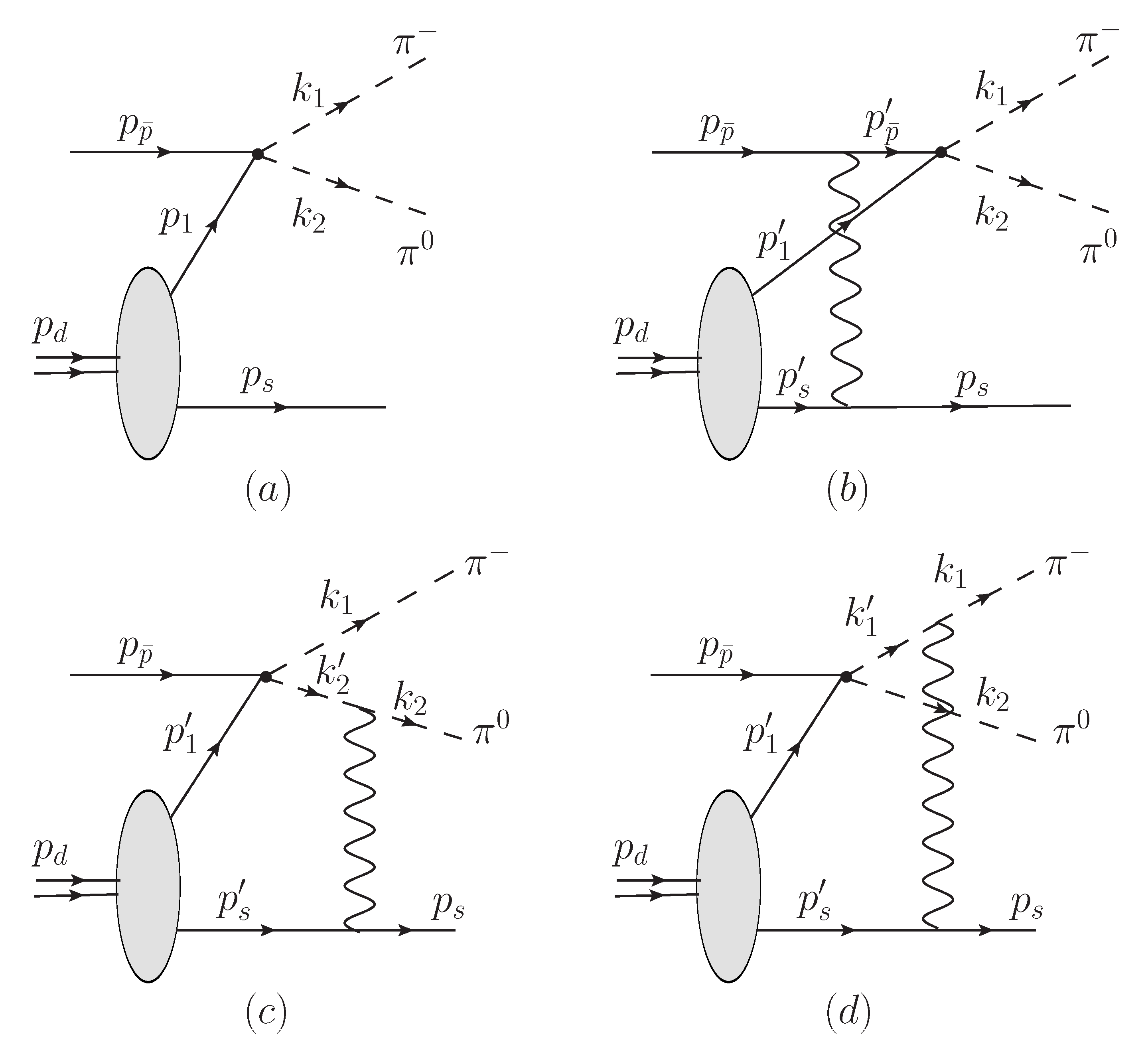
The Feynman diagrams are shown in Figure 1.

The following impulse approximation (IA) invariant amplitude (Figure 1a),

$$M^{\left(a\right)}=M_{\mathrm{ann}}(k_1,k_2,p_{\overline{p}})2m_N^{1/2}{\left(2\pi \right)}^{3/2}\phi \left({\mathbf{p}}_1\right),$$

(1)

is proportional to the annihilation amplitude $\overline{p}n\to {\pi }^{-}{\pi }^0$ denoted as $M_{\mathrm{ann}}(k_1,k_2,p_{\overline{p}})$, and to the DWF $\phi \left({\mathbf{p}}_1\right)$ with ${\mathbf{p}}_1=-{\mathbf{p}}_s$ in the deuteron rest frame. Here, $m_N$ is the nucleon mass, $k_1$, $k_2$, $p_{\overline{p}}$, $p_1$, and $p_s$ are the four-momenta of ${\pi }^{-}$, ${\pi }^0$, antiproton, the intermediate neutron, and the spectator proton, respectively.

Here and below, the spin indices are suppressed for brevity. Summation over intermediate spin states is always implicitly assumed. In numerical calculations, the DWF of the Paris model [4] is applied.

The amplitudes with rescattering are calculated by using the generalized eikonal approximation (GEA) [3,5,6,7,8], which leads to the following expressions (according to Figure 1 diagrams):

$$M^{\left(b\right)}=\frac{i{M}_{\mathrm{ann}}(k_1,k_2,p_{\overline{p}})}{2|{\mathbf{p}}_{\overline{p}}|m_N^{1/2}}\int d^{3}r\phi \left(\mathbf{r}\right)\theta (\mathbf{r}·{\widehat{\mathbf{p}}}_{\overline{p}})e^{i{\mathbf{p}}_s\mathbf{r}-i{\Delta }_{\overline{p}}^0\mathbf{r}·{\widehat{\mathbf{p}}}_{\overline{p}}}\int \frac{d^2{k}_{t,\overline{p}}}{{\left(2\pi \right)}^2}{e}^{-i{\mathbf{k}}_{t,\overline{p}}\mathbf{r}}{M}_{\overline{p}p}\left(t_{\overline{p}}\right),$$

(2)

$$M^{\left(c\right)}=\frac{i{M}_{\mathrm{ann}}(k_1,k_2,p_{\overline{p}})}{2|{\mathbf{k}}_2|m_N^{1/2}}\int d^{3}r\phi \left(\mathbf{r}\right)\theta (-\mathbf{r}·{\widehat{\mathbf{k}}}_2)e^{i{\mathbf{p}}_s\mathbf{r}-i{\Delta }_2^0\mathbf{r}·{\widehat{\mathbf{k}}}_2}\int \frac{d^2{k}_{t,2}}{{\left(2\pi \right)}^2}{e}^{-i{\mathbf{k}}_{t,2}\mathbf{r}}{M}_{{\pi }^{0}p}\left(t_2\right),$$

(3)

where $\mathbf{r}={\mathbf{r}}_n-{\mathbf{r}}_p$ is the relative position vector of a neutron and a proton, ${\widehat{\mathbf{p}}}_{\overline{p}}\equiv {\mathbf{p}}_{\overline{p}}/\left|{\mathbf{p}}_{\overline{p}}\right|$, ${\widehat{\mathbf{k}}}_2\equiv {\mathbf{k}}_2/\left|{\mathbf{k}}_2\right|$, and $\theta \left(x\right)$ is the Heaviside step function ($\theta \left(x\right)=0$ for $x<0$, $\theta \left(x\right)=1/2$ for $x=0$, and $\theta \left(x\right)=1$ for $x>0$). Other variables in Equations (2) and (3) are defined as follows: The momentum transfers to the spectator proton perpendicular to the antiproton and ${\pi }^0$ momenta are denoted as ${\mathbf{k}}_{t,\overline{p}}$ and ${\mathbf{k}}_{t,2}$, respectively, so that ${\mathbf{k}}_{t,\overline{p}}{\widehat{\mathbf{p}}}_{\overline{p}}=0$ and ${\mathbf{k}}_{t,2}{\widehat{\mathbf{k}}}_2=0$. The corresponding four-momentum transfers squared are expressed as $t_{\overline{p}}={(E_s-m_N)}^2-{\left({\Delta }_{\overline{p}}^0\right)}^2-k_{t,\overline{p}}^2$ and $t_2={(E_s-m_N)}^2-{\left({\Delta }_2^0\right)}^2-k_{t,2}^2$ with $E_s=\sqrt{{\mathbf{p}}_s^2+m_N^2}$ being the spectator proton energy,

$$\begin{array}{ccc}& & {\Delta }_{\overline{p}}^0=|{\mathbf{p}}_{\overline{p}}{|}^{-1}[E_{\overline{p}}(E_s-E_s^{\prime })-{(p_s^{\prime }-p_s)}^2/2]\simeq {\left|{\mathbf{p}}_{\overline{p}}\right|}^{-1}(E_{\overline{p}}+m_N)(E_s-m_N),\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& & {\Delta }_2^0=|{\mathbf{k}}_2{|}^{-1}[{\omega }_2(E_s-E_s^{\prime })+{(p_s-p_s^{\prime })}^2/2]\simeq {\left|{\mathbf{k}}_2\right|}^{-1}({\omega }_2-m_N)(E_s-m_N),\hfill \end{array}$$

(5)

being the momentum transfers to the spectator proton along the antiproton and ${\pi }^0$ momenta, respectively. The prime denotes the intermediate particles. Fermi motion is neglected in Equations (4) and (5) in the last step.

The amplitude $M^{\left(d\right)}$ is obtained from Equations (3) and (5) by replacing $2\to 1$ and ${\pi }^0\to {\pi }^{-}$. The DWF in the coordinate space is defined as follows:

$$\phi \left(\mathbf{r}\right)=\int \frac{d^{3}p}{{\left(2\pi \right)}^{3/2}}{e}^{i\mathbf{p}\mathbf{r}}\phi \left(\mathbf{p}\right).$$

(6)

For the annihilation amplitude $\overline{p}n\to {\pi }^{-}{\pi }^0$, the N and $\Delta$ exchange model developed earlier in Ref. [9] is applied. Since we are interested in the kinematics with $-t\simeq -u\simeq s/2$ with $s\simeq$ 10–30 GeV${}^2$, the powers of the form factors in the $\pi NN$ and $\pi N\Delta$ vertices are determined in accordance with the $s\to \infty ,t/s=\mathrm{const}$ asymptotic scaling law [10,11].

The amplitudes of elastic scattering of hadrons by protons are taken in high-energy form:

$$M_{hp}\left(t\right)=2i{p}_h{m}_N{\sigma }_{hp}^{\mathrm{tot}}(1-i{\rho }_{hp})e^{B_{hp}t/2},$$

(7)

where $p_h$ is the hadron momentum in the proton rest frame, ${\sigma }_{hp}^{\mathrm{tot}}$ is the total cross-section of the hadron-proton collision, $B_{hp}$ is the slope parameter of the t-dependence, and ${\rho }_{hp}=\mathrm{Re}{M}_{hp}\left(0\right)/\mathrm{Im}{M}_{hp}\left(0\right)$ is the ratio of the real and imaginary parts of the forward scattering amplitude. It is assumed that elastic scattering conserves the spin projections of the particles. The laboratory momentum $p_{\mathrm{lab}}$-dependent parameterizations of ${\sigma }_{hp}^{\mathrm{tot}}$, $B_{hp}$, and ${\rho }_{hp}$, based on phenomenological fits to experimental data are used for the $\overline{p}p$ and ${\pi }^{-}p$ elastic scattering amplitudes, as described in Appendices A2 and A3 of Ref. [3]. The ${\pi }^{0}p$ amplitude is calculated by using the isospin relation:

$$M_{{\pi }^{0}p}\left(t\right)=\frac{1}{2}(M_{{\pi }^{-}p}\left(t\right)+M_{{\pi }^{+}p}\left(t\right)).$$

(8)

The CT effects are included within the quantum diffusion model [5,12]. In this model, the elastic scattering amplitude (7) is replaced by the coordinate-dependent one:

$$M_{hp}(t,z)=2i{p}_h{m}_N{\sigma }_{hp}^{\mathrm{eff}}(p_h,\left|z\right|)(1-i{\rho }_{hp})e^{B_{hp}t/2}\frac{G_h(t·\frac{{\sigma }_{hp}^{\mathrm{eff}}(p_h,\left|z\right|)}{{\sigma }_{hp}^{\mathrm{tot}}})}{G_h\left(t\right)},$$

(9)

where

$${\sigma }_{hp}^{\mathrm{eff}}(p_h,\left|z\right|)={\sigma }_{hp}^{\mathrm{tot}}\left(\left[\frac{\left|z\right|}{l_h}+\frac{n_h^2\langle k_{ht}^2\rangle }{M_{\mathrm{CT}}^2}\left(1-\frac{\left|z\right|}{l_h}\right)\right]\theta (l_h-\left|z\right|)+\theta \left(\right|z|-l_h)\right),$$

(10)

is the effective hadron-proton cross-section that depends on the distance traveled by the hadron $h=\overline{p},{\pi }^0,{\pi }^{-}$ from/to the hard interaction point, which is expressed as the relative position of the neutron and proton along the hadron momentum, $z=({\mathbf{r}}_n-{\mathbf{r}}_p)·{\widehat{\mathbf{p}}}_h$. The hard interaction scale $M_{\mathrm{CT}}^2$ is set equal to $min(-t_{\mathrm{hard}},-u_{\mathrm{hard}})$, where $t_{\mathrm{hard}}={(p_{\overline{p}}-p_{{\pi }^{-}})}^2,u_{\mathrm{hard}}={(p_{\overline{p}}-p_{{\pi }^0})}^2$. $n_h$ is the number of valence (anti)quarks in the hadron ($n_{\overline{p}}=3$, $n_{\pi }=2$), and $\sqrt{\langle k_{ht}^2\rangle }=0.35$ GeV/c is their average transverse momentum. The coherence length is expressed as follows:

$$l_h=\frac{2p_h}{\Delta M^2},$$

(11)

with the mass denominator of $\Delta M^2\simeq$ 0.7–1.1 GeV${}^2$ [6,13]. Equation (9) describes the expansion of hadronic PLC with increasing distance from the hard interaction point. This expansion also influences the hadronic form factor, $G_h\left(t\right)$, that becomes harder for a smaller transverse size of the hadron. For the antiproton, the Sachs electric form factor of the proton is used, $G_{\overline{p}}\left(t\right)=1/{(1-t/0.71{\mathrm{GeV}}^2)}^2$. The pion form factor is chosen in the monopole form of $G_{\pi }\left(t\right)=1/(1-\langle r_{\pi }^2\rangle t/6)$, where $\langle r_{\pi }^2\rangle =0.439\pm 0.008{\mathrm{fm}}^2$ is the mean square charge radius of the pion [14].

The four-differential cross-section is calculated as follows:

$${\alpha }_s\beta \frac{d^4\sigma }{d{\alpha }_{s}d\beta d\varphi p_{st}d{p}_{st}}=\frac{\overline{|M^{\left(a\right)}+M^{\left(b\right)}+M^{\left(c\right)}+M^{\left(d\right)}{|}^2}{k}_{1t}}{16{\left(2\pi \right)}^4{p}_{\mathrm{lab}}{m}_d{\kappa }_t},$$

(12)

where the bar denotes the summation over spins of final particles and averaging over spins of initial particles, $m_d$ is the deutron mass, $p_{st}$ is the transverse momentum of the spectator proton, ${\kappa }_t=2\left|2k_{1t}/\beta +p_{st}cos\varphi \right|$,

$${\alpha }_s=\frac{2(E_s-p_s^z)}{m_d}$$

(13)

is the light cone (LC) momentum fraction of the spectator proton,

$$\beta =\frac{2({\omega }_1+k_1^z)}{E_{\overline{p}}+m_d-E_s+p_{\mathrm{lab}}-p_s^z}\simeq 1+cos{\mathsf{\Theta }}_{\mathrm{c}.\mathrm{m}.}$$

(14)

is the LC momentum fraction of ${\pi }^{-}$. The last approximate equality, with ${\mathsf{\Theta }}_{\mathrm{c}.\mathrm{m}.}$ being the c.m. polar scattering angle of ${\pi }^{-}$, holds in the limit of zero pion mass. $\varphi$ is the angle between the scattering planes of ${\pi }^{-}$ and the spectator proton,:

$$\varphi ={\varphi }_1-{\varphi }_s.$$

(15)

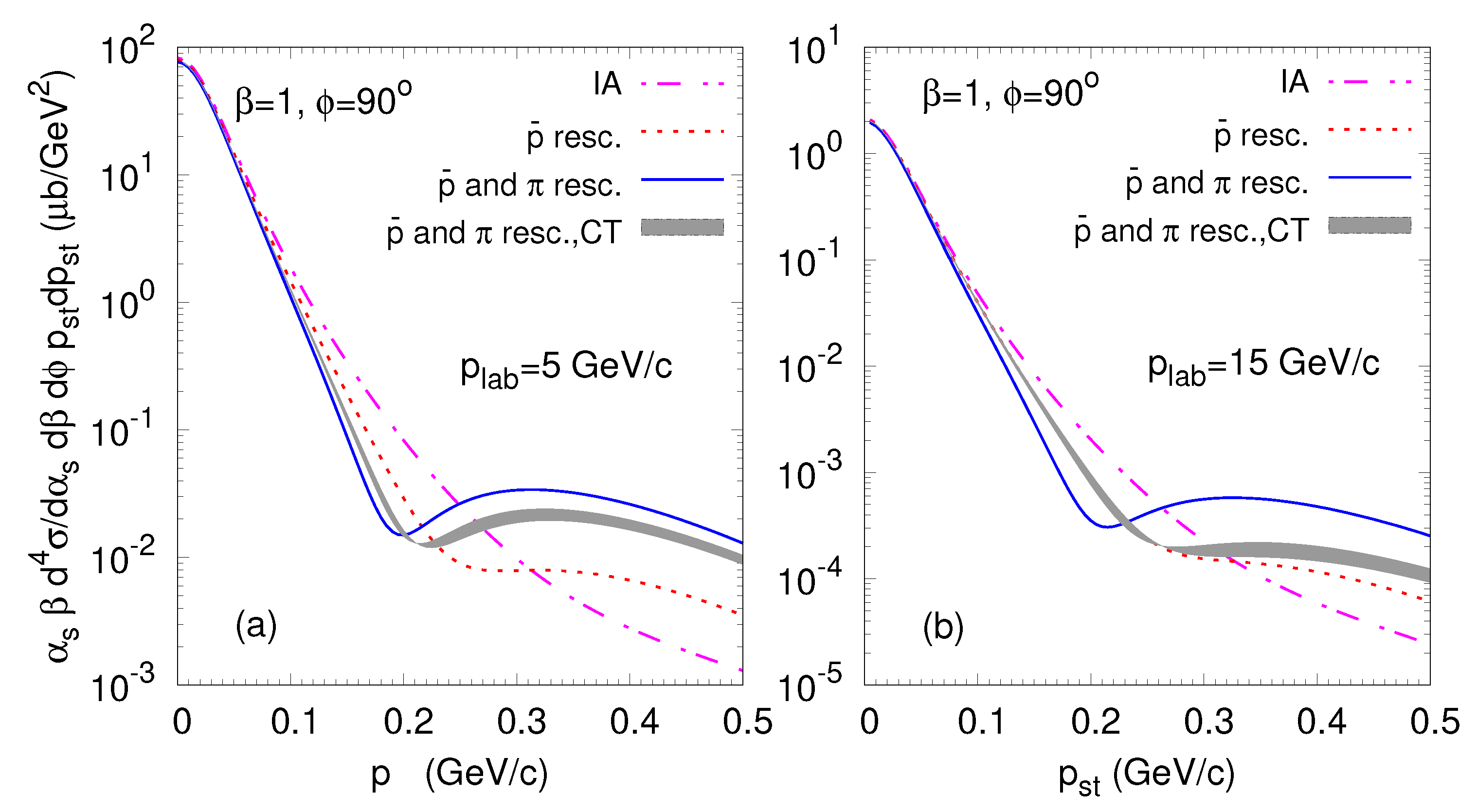
Figure 2 shows the four-differential cross-section, Equation (12), as a function of the transverse momentum of the spectator proton. Rescattering leads to strong deviations from IA: depletion at low and enhancement at high spectator transverse momenta. The inclusion of CT leads to a large difference from GEA, growing with beam momentum.

To see the effects of the rescattering amplitudes better, the transparency ratio can be introduced, i.e. the ratio of the cross section, ${\sigma }^{\mathrm{DWIA}}$, calculated in the distorted wave impulse approximation (DWIA) to the cross section, ${\sigma }^{\mathrm{IA}}$, calculated in the IA (definition adopted from studies of $A(e,e^{\prime }p)$ [5] and $d(p,2p)n$ [6] reactions):

$$T\equiv \frac{{\sigma }^{\mathrm{DWIA}}}{{\sigma }^{\mathrm{IA}}}=\frac{\overline{|M^{\left(a\right)}+M^{\left(b\right)}+M^{\left(c\right)}+M^{\left(d\right)}{|}^2}}{\overline{|M^{\left(a\right)}{|}^2}}.$$

(16)

In the experiment, ${\sigma }^{\mathrm{DWIA}}$ should be replaced by the measured cross-section.

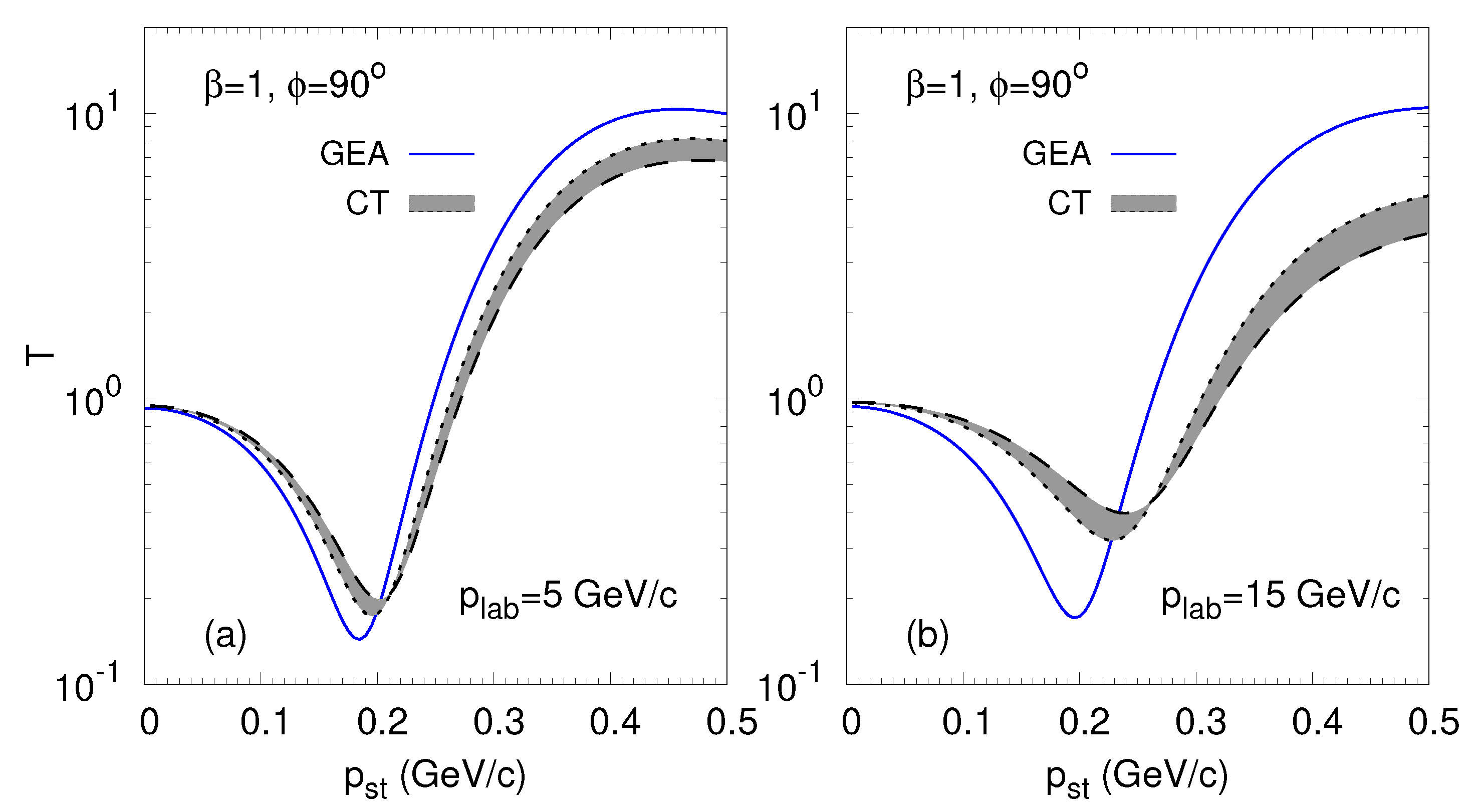
Figure 3 displays the transparency ratio at 5 GeV/c and 15 GeV/c. This observable characterizes the absorption (low $p_{st}$, $T<1$) and rescattering (high $p_{st}$, $T>1$) regions. The CT effects at 5 GeV/c are only modest. However, at 15 GeV/c, CT leads to a factor of two larger transparency ratios at $p_{st}\sim 0.2$ GeV/c and a factor of two smaller ones at $p_{st}\sim 0.3$ GeV/c. Note that a fast variation of the transparency ratio with a transverse momentum is the characteristic prediction of GEA (see also Ref. [6]) and can be used as a clear test of this approach.

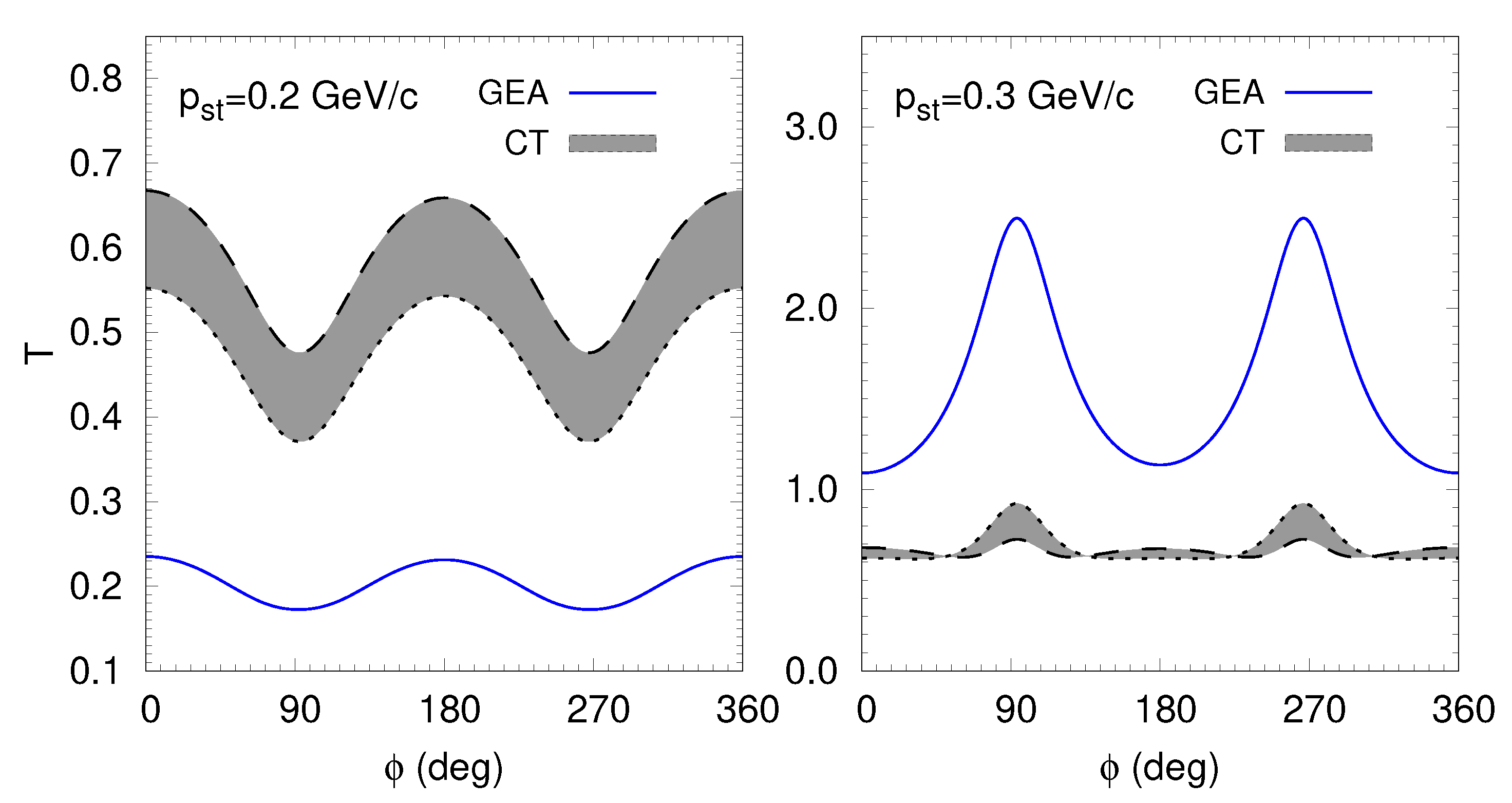
Figure 4 shows the azimuthal angle dependence of the transparency ratio. At $p_{st}=0.2$ GeV/c, the absorption is stronger at $\varphi =90°$ and 270°, while at $p_{st}=0.3$ GeV/c, the rescattering is stronger at the same angles. This behavior can be understood from the structure of the exponents in the amplitude with pion rescattering, as seen in Equation (3). Since ${\alpha }_s=1$, the spectator momentum is almost transverse to the beam momentum. Thus, if $\varphi =90°$ or 270°, then the spectator momentum is also almost transverse to the pion momenta, i.e., ${\mathbf{p}}_s{\mathbf{k}}_1\simeq {\mathbf{p}}_s{\mathbf{k}}_2\simeq 0$. Therefore, the integral over transverse momentum transfer in Equation (3) is dominated by ${\mathbf{k}}_{t,2}\simeq {\mathbf{p}}_s$, which nearly leads to the cancellation of the quickly oscillating exponential factor ${\mathrm{e}}^{i{\mathbf{p}}_s\mathbf{r}}$ at large $|{\mathbf{p}}_s|$. In the case of $\varphi =0°$, such a cancellation is impossible and the amplitudes with pion rescattering get suppressed. Thus, at large $|{\mathbf{p}}_s|$, the pion rescattering amplitude squared is larger for $\varphi =90°$ or 270° than for $\varphi =0°$. This leads to the peaks of the transparency ratio at $\varphi =90°$ and 270° in the GEA calculation at $p_{st}=0.3$ GeV/c. At a smaller value for the spectator transverse momentum, a similar argument pertains to the interference term of the IA and pion rescattering amplitudes, resulting in a larger absorption for $\varphi =90°$ and 270°. CT substantially smoothens the shape of the azimuthal dependence of T at larger transverse momenta of the spectator.

To summarize, the process of $\overline{p}d\to {\pi }^{-}{\pi }^0{p}_s$ at $p_{\mathrm{lab}}$ = 5–15 GeV/c for a large momentum transfer (${\mathsf{\Theta }}_{\mathrm{c}.\mathrm{m}.}\simeq 60°-90°$) in the annihilation $\overline{p}n\to {\pi }^{-}{\pi }^0$ is shown to be well-suited for the studies of CT, which is in qualitative agreement with previous studies of the process $\overline{p}d\to pp{n}_s$ in transverse kinematics (${\alpha }_s=1$) [6]. In both processes, CT significantly influences the nuclear transparency ratio by increasing (reducing) it at small (large) transverse momenta of the spectator, i.e., at $p_{st}<(>)0.2$ GeV/c.

For the targets heavier than the deuteron, the CT effects in the processes $A(\overline{p},\mathrm{meson}+\mathrm{meson})$ are expected to be stronger, although the effects of the nuclear structure such as neutron skin (cf., [15]) should be taken care of since the antiproton is strongly absorbed in the nuclear surface region.

Another interesting process is the quasi-elastic scattering $A(\overline{p},\overline{p}p)$. In the elementary process $\overline{p}p\to \overline{p}p$, only the (multiple) gluon exchange or $\overline{q}q$ annihilation is possible; no quark interchange can occur. Thus, squeezing to PLC might not be present here, in contrast to $pp\to pp$.

In a recent JLab Hall C experiment [16], the nuclear transparency for the ${}^{12}$C$(e,e^{\prime }p)$ process at $Q^2$ = 8–14 GeV${}^2$ appeared to be close to constant value which excludes CT. In hindsight, this result may not be so unexpected since in the BNL data [17] for C$(p,pp)$ at ${\mathsf{\Theta }}_{\mathrm{c}.\mathrm{m}.}=90°$, the nuclear transparency drops with a growing $Q^2$ in the interval 7.6–12.7 GeV${}^2$, which is also in disagreement with CT. Thus, the search for the expected CT effects on the proton propagation in the nucleus should be performed at a larger $Q^2$. Such studies can be performed in large-angle reactions $A(p,pp)$ at NICA-SPD [18], where $Q^2$ up to 50 GeV${}^2$ can be reached.

Finally, in photo-induced reactions $A(\gamma ,\mathrm{meson}+\mathrm{baryon})$, the photon transparency is expected [19]. This is the regime of the unresolved (direct) photon that should take place at large $\left|t\right|$ and $\left|u\right|$ in the elementary $\gamma N\to \mathrm{meson}+\mathrm{baryon}$ process. This expectation is supported by the asymptotic scaling law observed by the CLAS Collaboration for a large number of light-meson photoproduction processes off the nucleon [20]. The complementary studies of photon transparency can be performed for the cross-channel $A(\overline{p},\gamma +\mathrm{meson})$ at PANDA.