Hadronization and Color Transparency ^†

Abstract

In this paper, the earlier studies by us on the production of hadrons in a nuclear environment are reviewed. A string-breaking model for the initial production of hadrons and a quantum-kinetic Giessen-Boltzmann-Uehling-Uhlenbeck (GiBUU) transport model are used to describe the final state interactions of the newly formed (pre)hadrons. The latter are determined both by the formation times and by the time-development of the hadron–hadron cross section. First, it is shown that only a linear time dependence is able to describe the available hadronizatin data. Then, the results are compared with detailed data from HERMES and Jefferson Laboratory (JLAB) experiments; a rather good agreement is reached for all reactions, studied without any tuning of parameters. Predictions of spectra for pions and kaons for JLAB experiments at 12 GeV are also repeated. Finally, the absence of color transparency (CT) effects in the recent experiment on proton transparencies in quasi-elastic (QE) scattering events on nuclei is discussed. We propose to look instead for CT effects on protons in semi-inclusive deep inelastic scattering (SIDIS) events.

1. Introduction

One of the interesting predictions of quantum chromodynamics (QCD) for a nuclear physics phenomenon is that of color transparency (CT). Particles initially produced in a hard, high four-momentum transfer squared, $Q^2$, process on a nuclear target are predicted to be produced as point-like configurations (PLC) with very small transverse dimensions and, correspondingly, also very small cross sections with a surrounding medium. This should have observable consequences for hadrons traversing the nuclear target on their way out to the detector. The search for CT effects has experienced ups and downs. While some experimental results are taken as evidence for CT [1], others are less convincing or even negative such as the recent result on proton transparency in ($e,e^{\prime }p$) quasi-elastic (QE) events [2].

Experimental searches for CT have relied mostly on meson production on nuclear targets. For a given velocity of the produced particle the target radius then provides a time scale for hadronization. An often-cited case is that of the Fermilab experiment E791 that looked at the diffractive dissociation of an incoming 500 GeV pion beam into di-jets [3], which was analyzed in terms of CT by Frankfurt, Miller and Strikman [4], using the Glauber approximation. Later experiments at the Jefferson Laboratory (JLAB) examined both pion and rho productions as a function of $Q^2$. An up-to-date review of these experiments and their theoretical analyses can be found in [1].

One of the problems in identifying CT in such experiments lies in the fact that a reference cross section for a process without CT is needed. For this reference, often, the cross section on an individual nucleon or on deuterium is used. The ratio of particle production cross sections with and without final state interactions, i.e., nuclear transparency, is then also influenced by ‘trivial’ nuclear physics effects, such as nuclear binding and Fermi motions. This complicates the identification of genuine CT effects.

The arguments leading to the prediction of CT are based on perturbative QCD (pQCD), which was generally assumed to be valid for $Q^2>1-2$ GeV². Furthermore, in [5], it was argued that CT is predominantly caused by interactions with longitudinally polarized photons, whereas processes with transversely polarized photons should be suppressed by powers of $1/Q^2$ relative to interactions with longitudinal photons. The exact onset of such suppression is, however, quite uncertain. Experimentally, it was shown in Ref. [6] that at $Q^2$ up to about 4 GeV², the transverse cross section for pion production is larger than the longitudinal one by about a factor of 2, contrary to pQCD expectations. Even for Cornell and HERMES data with much higher $Q^2$ up to 10 GeV², it was shown that the transverse cross section dominates [7]. The arguments from pQCD, thus, need to be taken with caution; indeed, in a recent publication [8], it is assumed that point-like configurations are formed both for longitudinal and transverse photons.

The puzzle of the large transverse cross section at high $Q^2$ was solved in Refs. [7,9,10] by adding a hard scattering amplitude to the t-channel amplitude; the latter alone produced most of the longitudinal strength. This hard-scattering amplitude was connected to the excitation of high-lying resonances, which make up the deep-inelastic scattering (DIS) contribution. The decay of these DIS configurations can be described by a string fragmentation model.

In the studies of CT and cross-section evolution, we take the position that CT is primarily connected with these hard transverse events. The decay times of the high-lying resonances essentially determine the formation times of the final-state hadrons. The purpose of the present paper is to review the results obtained in such an approach; thus, these results are confronted with new data and it is pointed out what one learns about the time development of newly formed hadrons.

2. Model

2.1. Quantum-Kinetic Transport

Any description of CT requires a reliable description of final state interactions of the newly formed hadron with the surrounding nuclear target. To this end, a quantum-kinetic transport model, based on the Kadanoff–Baym equations [11], is used here for the description of the nuclear reaction. The theoretical basis and details of the actual implementation of this model, the Giessen-Boltzmann-Uehling-Uhlenbeck (GiBUU) model, is described in some detail in [12]; the code is freely available from [13]. The treatment of final state interactions within this theory goes well beyond the standard Glauber calculations since it allows coupled channel effects and sidefeeding of the particular channel under investigation.

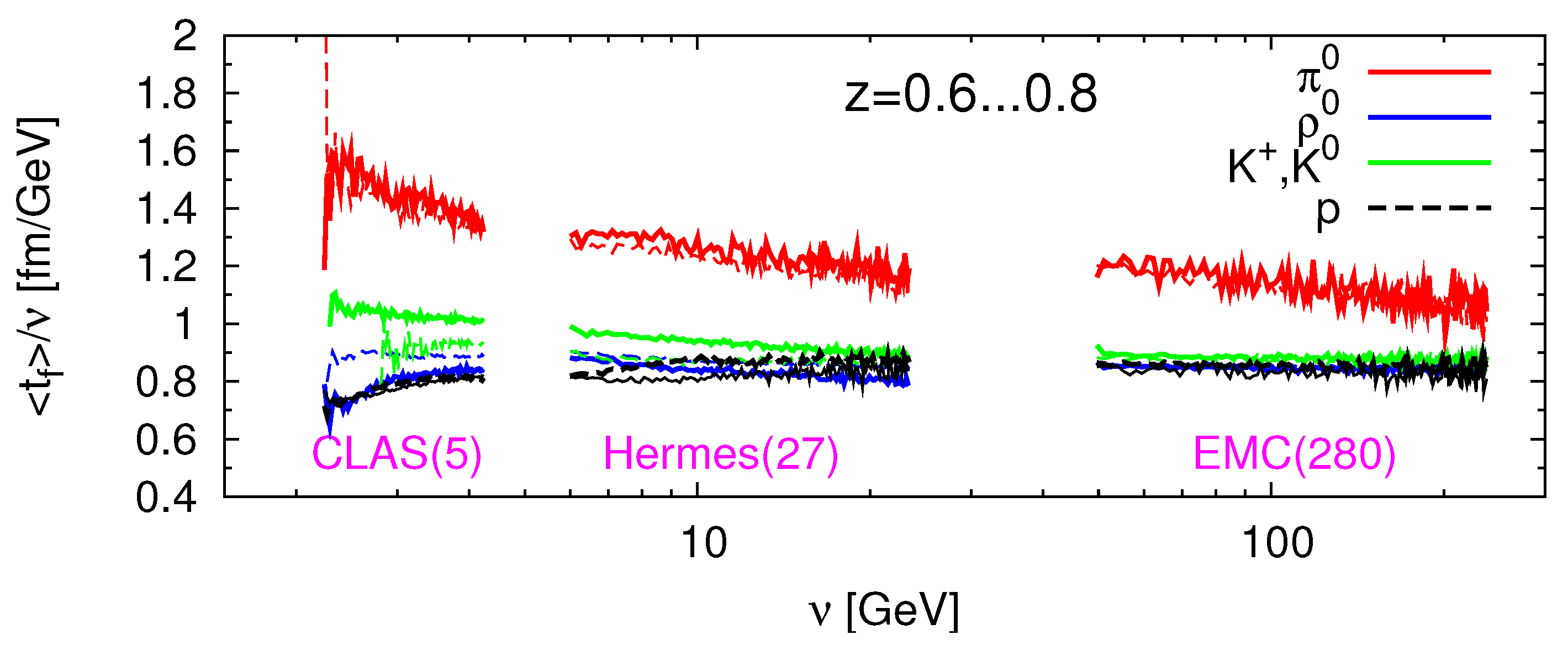
2.2. Formation Times of Hadrons

The fate of hadrons produced in a hard photonuclear reaction on a nuclear target is governed by their formation time and the interaction cross section until the hadron has been fully formed. The formation time is related to the inverse width of the high-lying resonances that make up the DIS doorway state. The actual decay of such a high-lying state (of the energy $W>2-3$ GeV) is described by means of the LUND string fragmentation model as it is implemented in the code PYTHIA [14], which is used by GiBUU. Within PYTHIA, first, a string is formed, which is then fragmented into the final hadrons. The spacetime four-dimensional points where the string breaks determine the production times of the quarks that will make up the final hadrons. In order to form color-neutral hadrons, quarks from different breaking points will have to meet. This happens at a later so-called formation time. In Ref. [15], these two relevant times were extracted from the string-fragmentation process; a detailed discussion of these results can be found in that reference.

Distributions of such times are shown in [15]; they range from a few Fermi up to well above 10 fm, depending on the initial energy transfer. The formation times also depend on mass of the produced hadron, as can be seen from Figure 1, which shows the formation times for the three kinematical regimes JLAB, HERMES and EMC for various hadrons. It is striking to see that all the heavier particles, from kaons up to protons, cluster at values of about $t_f/\nu \approx 0.8$, whereas the lighter pions are connected with larger times $t_f/\nu \approx 1.4$ at the lowest energy transfers; here, $t_f$ is the formation time in the laboratory frame and $\nu$ is the energy transfer. From the results, shown in Figure 1, one obtains estimates for the formation times, ${\tau }_f$ (in fm), in their restframe as a function of the mass, $m_h$ (in GeV), of the produced hadron: ${\tau }_f\approx (1\cdots 2)m_h$. The formation time in the laboratory frame is then given by $t_f=\gamma {\tau }_f=(0.7\cdots 1.4)\nu$; the numerical factors (in fm/GeV) are weakly dependent on $\nu$. It is worth mentioning that, at a given $\nu$, the larger the hadron’s mass, the longer the formation time in the particle’s restframe is, whereas if the time in the laboratory This is a straight consequence of a Lorentz boost when proceeding from the rest frame to the laboratory frame. In particular, at a given $\nu$, the formation time for the proton is less than that of the pion, as shown in Figure 1.

In calculations, these times are extracted from the PYTHIA code for every single particle and for every single event [15]; the times are not free parameters. The formed hadrons are assumed to interact with their full, normal cross section after the formation time.

2.3. Prehadronic Cross Sections

For a description of CT, one must specify the cross sections of the prehadrons during production and formation times. In many high-energy event generators, it is just assumed that the initially formed PLC undergo no (or tuned attenuated) interactions until some formation time occurs, which is usually an adjustable parameter in these generators [16].

Already in 1991, Dokshitzer et al. [17] discussed the problem of how the expansion from an initially compact system to the physical hadron takes place. In their “classical expansion model”, the transverse dimension of a newly formed hadron increases linearly with time, and the cross section then becomes quadratically dependent on time. Such a classical expansion model neglects the quantum-mechanical uncertainty principle, which requires very large momenta for a very compact initial state of the hadron. In their ’quantum expansion model’, which takes the uncertainty principle into account, Dokshitzer et al. [17] arrived at a cross section that increases linearly with time, finally concluding:

“A good, complete experimental program studying almost exclusive reactions in nuclei should be able to tell us which is the better formula at a given momentum transfer.”

In the present calculations, the effects of a small constant cross section before the formation time is exploited, as often used in generators, as well as both a linear and a quadratic time dependence, as discussed in [17]. In all scenarios, the prehadronic cross section is 0 before the production time and assumes the full, asymptotic value after the formation time.

The time-dependences explored thus cover the following [18]:

$$\begin{array}{ccc}\hfill {\sigma }^{*}\left(t\right)& =& 0.5{\sigma }_0,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill {\sigma }^{*}\left(t\right)& =& {\sigma }_0{\left(\frac{t-t_p}{t_f-t_p}\right)}^n,n=1,2,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill {\sigma }^{*}\left(t\right)& =& {\sigma }_0\left[X_0+(1-X_0)·\frac{t-t_p}{t_f-t_p}\right],\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& & \mathrm{with}{X}_0=n_{\mathrm{lead}}\frac{k}{Q^2}.\hfill \end{array}$$

(4)

Here, ${\sigma }^{*}\left(t\right)$ and ${\sigma }_0$ are the time-dependent prehadronic cross section and the final hadronic cross section, respectively. The time-dependence of Equation (3) is quite similar to that proposed by Farrar et al. [19]. Note that only the ’pedestal’ value $X_0$ explicitly depends on $1/Q^2$. The constant k is chosen to be 1 GeV² and quantity $n_{\mathrm{lead}}$ provides the ratio of the number of ’leading’ quarks to total number of quarks (two for a meson and three for a baryon). ’Leading’ quarks are those that are connected directly with the hard interaction point; they are the endpoints of the initial string. ’Leading’ hadrons are those that have at least one leading quark; they have a production time of $t_p=0$. For very large $Q^2$, pedestal value $X_0$ becomes small and the time developments of Equations (2) (for $n=1$) and (3) are essentially identical; this is also the case for all final hadrons that do not contain any leading quarks, i.e., that come from the inner parts of the fragmenting string. These latter particles are not connected to the hard interaction vertex and, thus, do not directly know about the four-momentum transfer.

All these time-dependences of the prehadronic cross sections apply only to hard PYTHIA-generated events. The predominantly longitudinal ‘QE-like’ events are not affected by the time dependences.

Since $t_f\propto \nu$, at high energy transfers a large part of the hadronization occurs outside the nucleus, and, consequently, there is, in general, small sensitivity to the in-medium cross sections and to the details of the time-dependence in CT; see discussion in [18]. In the other extreme, namely, at low energy transfers, hadronization happens very quickly and the full hadronic cross section becomes effective early on. Any observable effects of CT are, thus, intimately connected with the time scales involved in string breaking.

3. Results

In any investigation of color transparency, independent of the specific reaction under study, there are two essential properties that make CT observable:

1.

The nuclear radius must be of the same order as (or smaller than) the distance traveled by the newly formed hadron until it reaches its final, free cross section. If that distance is much larger than the nuclear dimension, most of the formation of the hadron takes place outside the nucleus, and, consequently, the observable effects of CT are maximized.

2.

Even if the geometrical/kinematical constraint just discussed is met, the actual, measurable amount of CT depends on the specific time dependence of the cross section of the newly formed hadron with the target nucleons.

Both of these properties depend on the hadron’s kinematics. Any formation time $\tau$ in the hadron’s restframe is Lorentz-boosted to a larger time in the nuclear restframe. As a consequence, for very fast hadrons, produced in high-energy collisions, the Lorentz-boost is large and most of the formation happens outside the nuclear target, again minimizing PLC expansion and, in particular, the dependence of the attenuation on the specific time-dependence of the prehadronic cross section. It is, thus, essential to investigate first the nuclear modification ratio (called also “nuclear transparency”):

$$R_M^h(\nu ,Q^2,z_h,p_T^2,\cdots )=\frac{{\left[N_h(\nu ,Q^2,z_h,p_T^2,\cdots )/N_e(\nu ,Q^2)\right]}_A}{{\left[N_h(\nu ,Q^2,z_h,p_T^2,\cdots )/N_e(\nu ,Q^2)\right]}_D}$$

(5)

under different kinematical conditions [18]. Here, all hadronic spectra on the nucleus (A) as also on deuterium (D) are normalized to the corresponding number of scattered electrons. Here, $z_h=E_h/\nu$ is the hadron’s relative energy with $E_h$ being the energy of the produced hadron and $p_T$ is the hadron’s transverse momentum.

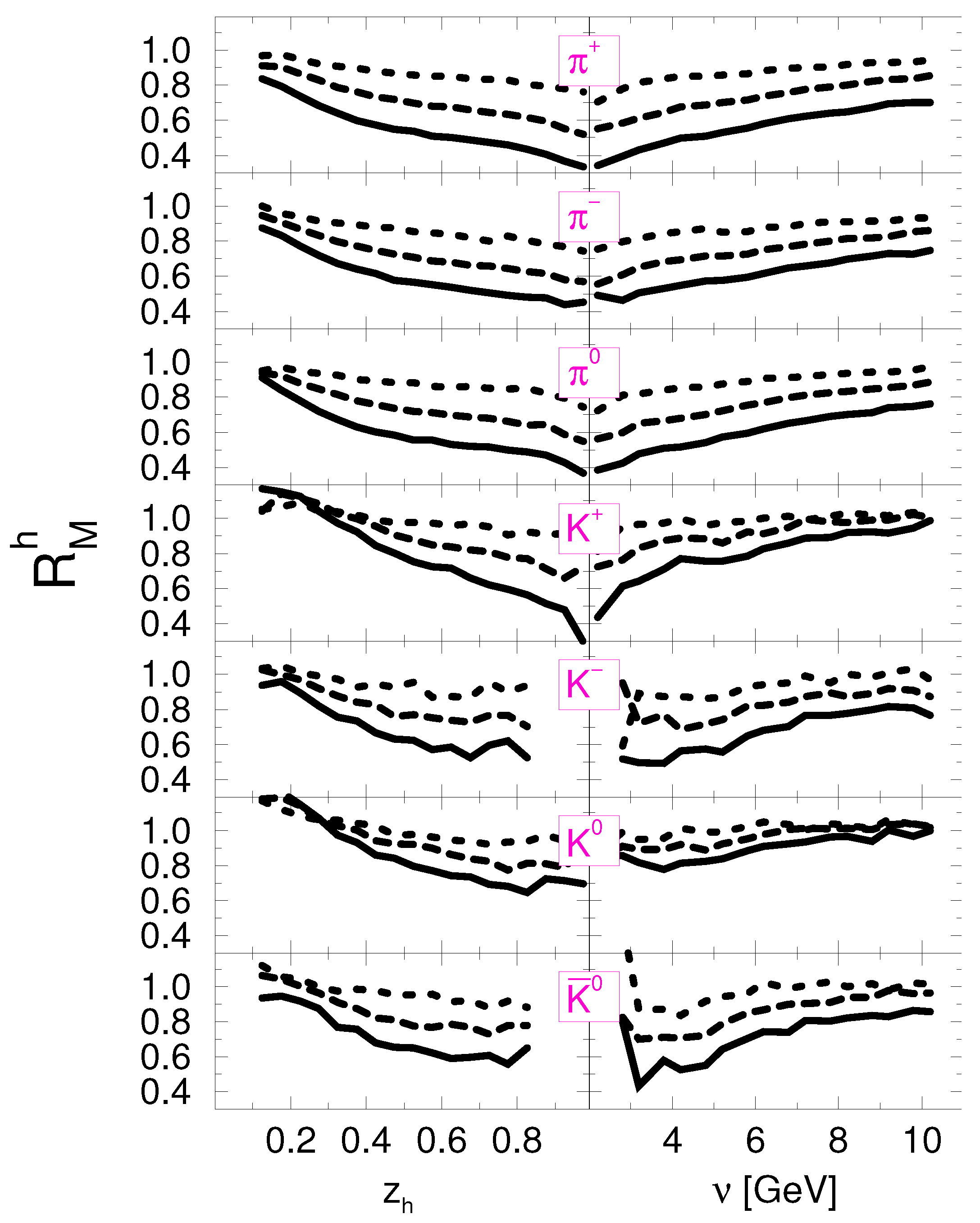
3.1. Time-Dependence of Prehadronic Cross Sections

The results, shown in Figure 2, demonstrate that there is a significant dependence on the special time-dependence of the prehadronic cross section; only a linear dependence can describe the data from these two very different kinematical regimes. For EMC energies, the distance traveled by the produced hadron within its formation time is considerably larger than the nuclear radius. As a consequence, attenuation is quite small and the nuclear modification factor stays close to $R_M^h=1$. Since in this case essentially all the hadronization takes place outside the nucleus, there is relatvely small sensitivity to the special time dependence (linear vs quadratic). On the other hand, at energies lower than that of the HERMES experiment, e.g., at JLAB, the distance traveled within the formation time is small compared to the nuclear radius so that the produced hadron experiences essentially the free, asymptotic cross section.

A closer look at this data/theory comparison shows that the pedestal $Q^2$-dependent term in Equation (3) has a small but visible influence on the modification factor [18]. In the following, only the linear time-dependence with the $1/Q^2$-dependent pedestal in Equation (3) is employed.

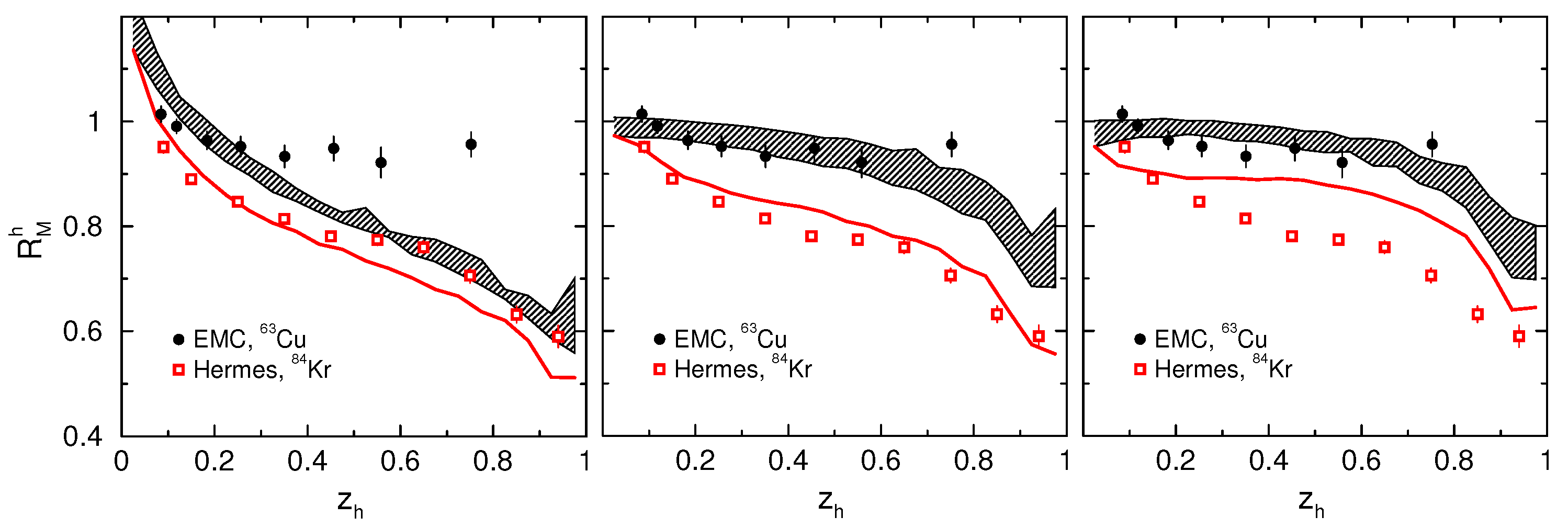
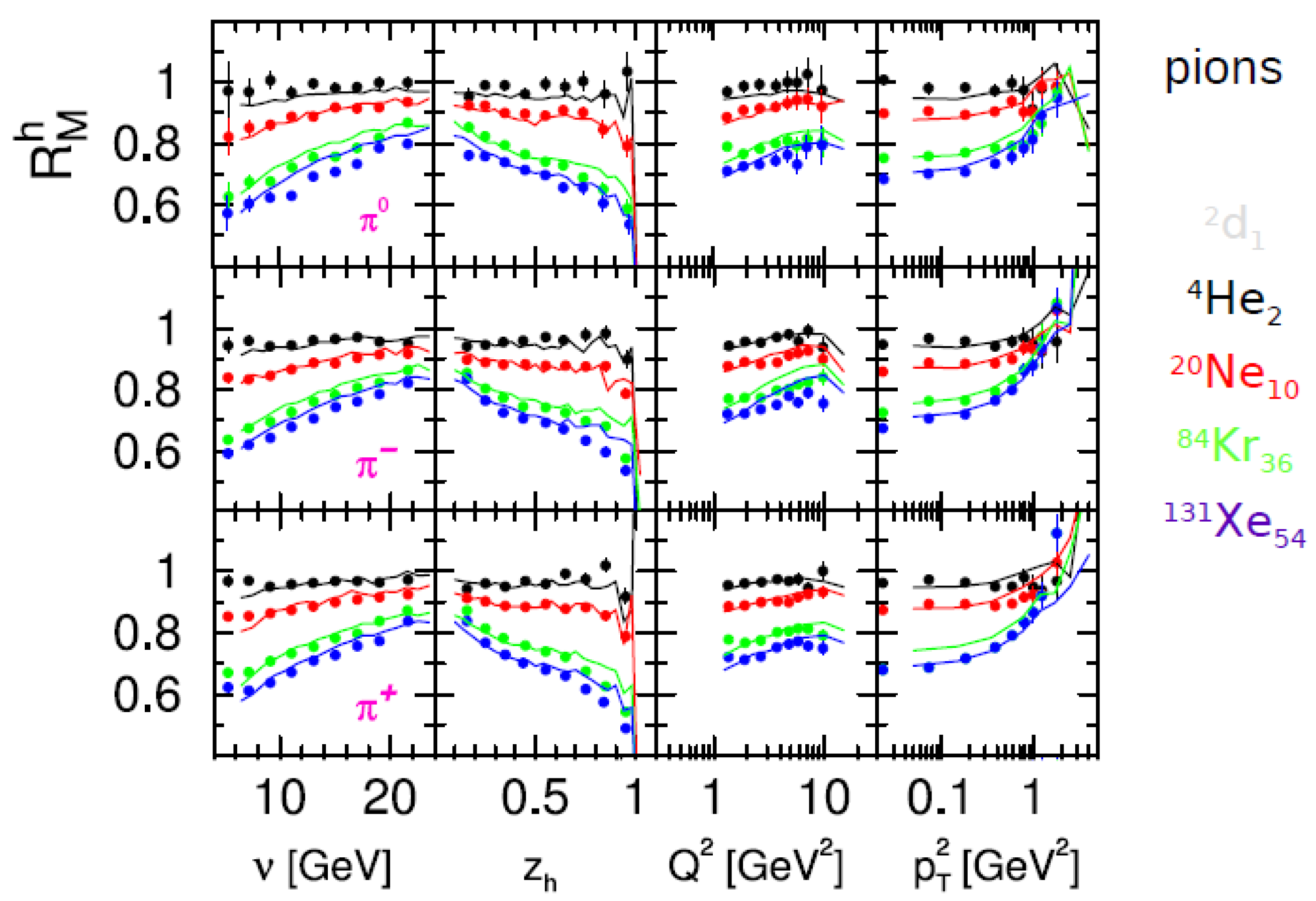
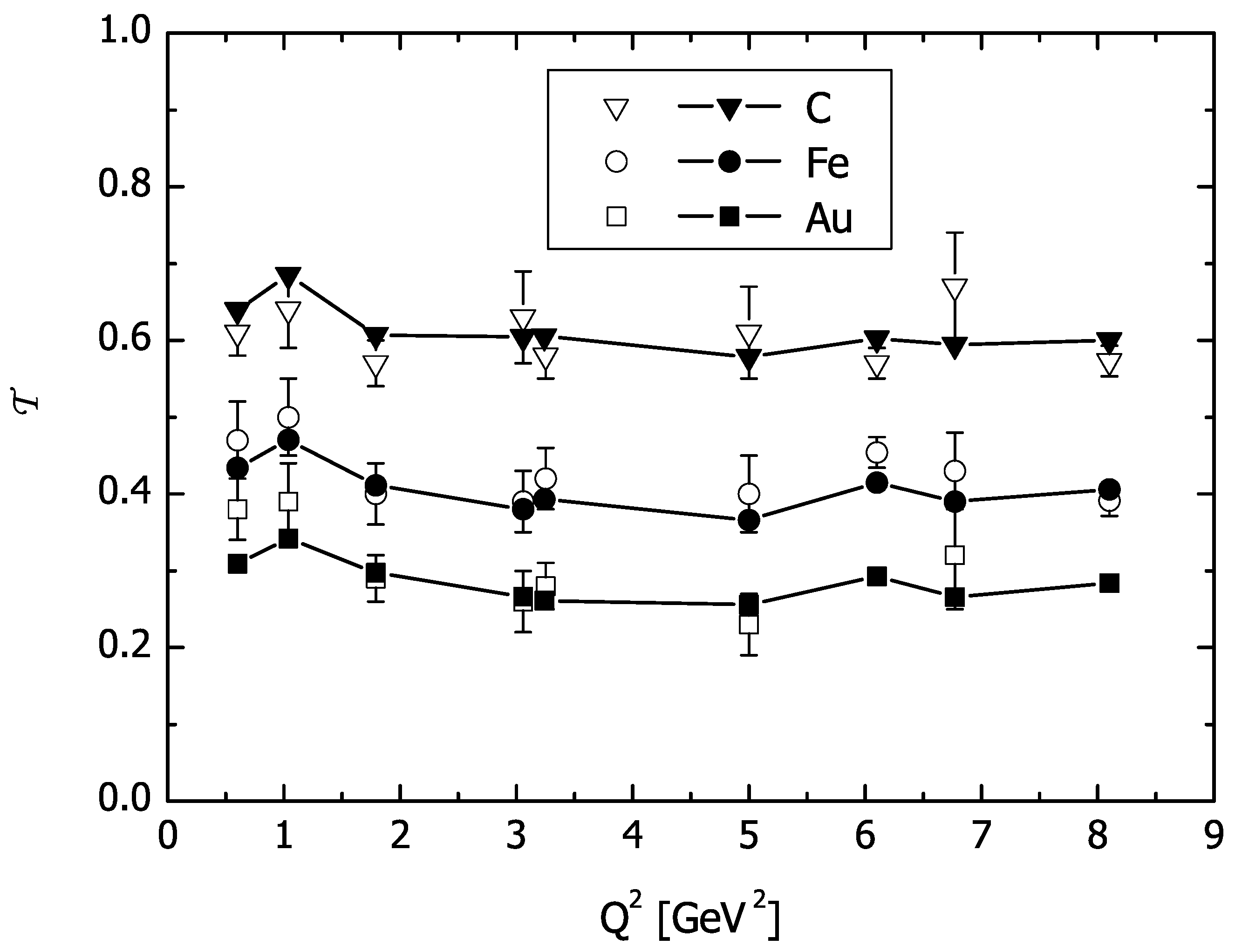
3.2. HERMES Experiment

A more detailed verification of this theory, the modification factors for the identified hadrons were examined in [18]. As an illustration for the results obtained there, is shown in Figure 3, the modification factors for pions produced in the HERMES experiment. A general feature of these distributions is that they are all below 1. This is an effect of detector acceptance that can only be described in calculations that provide complete information about the final state. The actual shape, however, is a consequence of the time-dependence of the prehadronic cross sections. The agreement in all four kinematical variables $\nu ,z_h,Q^2,p_T^2$ and for different target nuclei, from light to heavy, is good enough. Even the two-hadron correlations could be described quite well, while models based on partonic effects fail to describe the correct target-mass dependence (see Figure 3 in [22]).

What is essential for this comparison is that the full final state is modeled so that experimental acceptances can be taken into account. In [23], it was shown that these experimental acceptances have a major influence in particular on $z_h$ and $\nu$ distributions.

3.3. JLAB Experiments

3.3.1. JLAB Experiments with 5 GeV Beam

In Ref. [18], the predictions for the nuclear attenuation of pions and kaons produced at JLAB with a 5 GeV beam were provided. A noticeable feature of the distributions, shown in Figure 6 of [18], was that the modification factor became larger than $R_M^h=1$ for low hadron energies. As mentioned above, this is not due to any time dependence of the prehadronic cross section, and it is, thus, not related to CT. Instead, it is just a conseqence of final state interactions that distribute the initial energy of the primarily produced hadron on other decay products and scattering partners, the so-called “nuclear avalanche effect”.

Pion production data on nuclear targets were obtained with the 5 GeV beam at JLAB [24] for four-momentum transfers squared up to about 4 GeV². The pion transparencies obtained there increase with $Q^2$, and this increase could be rather well reproduced by GiBUU calculations [10]. The essential input for these calculations was a model for the elementary pion production cross section that allowed for a separation of longitudinal and transverse cross sections [25] on the nucleon. Following the philosophy outlined above, CT was included only for the transverse contribution. An essential feature of this calculation is, thus, that both the cross sections on the nucleus and those on the nucleon, which are both needed for the nuclear modification factor, are consistently calculated. Other theoretical descriptions [26,27] did not model the elementary cross section but used experimental values in a Glauber calculation. In effect, this means that CT is applied both to the longitudinal and transverse amplitudes. Moreover, in these studies, the formation times entering into the prehadronic cross section were educated guesses only.

What was similar to these pion production experiments was an experiment at JLAB looking for CT in the electroproduction of $\rho$ mesons [28]. The results of this experiment also show a nuclear modification factor that increases with $Q^2$ (up to only about 2 GeV²); in the Glauber calculations, this behavior was explained by assuming CT in both the transverse and longitudinal constributions [29,30]. The data could also be explained by a calculation in which CT is only active in the transverse channel [31]. The latter calculation again analyzed first the elementary cross section and found a significant hard component on the top of the diffractive production. CT was then applied to the hard component only.

A difficulty in judging the results of this experiment as evidence for color transparency lies in the fact that the experiment applied various kinematical cuts, with the purpose to exclude the resonance region and to select exclusive rho production, among others. It was shown in Ref. [31] that these cuts affect the cross section on the nucleon and on the nucleus differently, mainly because of Fermi motion. Thus, the transparency as a function of $Q^2$ increases steeply for $Q^2>2.5$ GeV² already as a consequence of these cuts alone, even in the absence of any CT. It then becomes a quantitative question in terms of how much of an observed effect below $Q^2=2$ GeV² is due to CT and how much is due to the cuts. This question is discussed in detail in [31]. A clean verification of CT in $\rho$ meson production in an experiment without these kinematical cuts is still outstanding.

In Ref. [18], a number of predictions were made for hadronization experiments at JLAB. In particular, Figure 6 of [18] shows the predictions for the $z_h$-dependence of kaons. This predicted behavior was indeed observed [32], and the data were found to be in quite a good agreement with the prediction. Very recently, a JLAB experiment obtained pion production data from SIDIS events on various nuclear targets [33]. In [33], a detailed comparison with GiBUU calculations is performed and rather overall good agreement is found between the theory and experiment. Discrepancies at the lowest $z_h$, where the theory yields higher $R_M^h$ values than experimentally observed may contain interesting information on in-medium corrections to ’normal’ hadronic cross sections.

3.3.2. JLAB Experiments with 12 GeV Beam

Since experiments with the 12 GeV beam are now running, let us repeat in Figure 4 the prediction we made in Ref. [18] for pions and kaons produced on nuclear targets at that energy. The modification factors for kaons increase above $R_M^h=1$ at small $z_h<0.2$. This is due to the rescattering of the prehadrons. The $K^{-}$ attenuation is seen to be similar to that of $K^{+}$ because prehadronic interactions have a strong influence at this energy level. Since $K^{-}$ are always non-leading particles, they start out with a lower prehadronic cross section; this counteracts the normally stronger absorption of $K^{-}$ mesons. The measurement of these kaon spectra would, thus, provide important information on the actual production and hadronization processes and the prehadronic cross sections inside the medium; see also [34].

3.4. Proton Transparency

Transparency data for protons had been obtained some while ago, both at JLAB and at SLAC; see [35] for the data references. An early GiBUU calculation [35,36] could describe these quasielastic data, which ranged up to $Q^2=8$ GeV², quite well (see Figure 5) without any CT effects.

Quite recently, the Hall C group at JLAB published a result on the absence of CT in quasielastic ¹²C($e,e^{\prime }p$) reactions [2] at even higher $Q^2$. The transparency of the protons was observed to be constant for momentum transfers squared $Q^2$ up to 14 GeV². This actually unexpected result led to some new theoretical studies of this problem. In Ref. [37], it is suggested that the results might be explained by using the so-called Feynman mechanism whereas Brodsky [38] developed arguments for why full color transparency should be set in only at even higher $Q^2$ well beyond the reach of the JLAB experiment.

In the picture developed in the discussions above, the explanation might be rather straight: both the production and the formation times of the proton kicked out in a QE scattering event are $t_p=t_f=0$ since a string was never stretched; this is similar to the Feynman mechanism, advocated as an explanation for the absence of CT in [37]. In such a situation, the proton’s interaction cross section with the surrounding medium does not evolve, but it assumes its ’normal’ value from the time of interaction, which coincides with the production time. The proton’s attenuation is, thus, not sensitive to any time-development of the cross section and, in particular, no attenuation of the ’normal’ final state interactions takes place. This holds also for even higher $Q^2$, as long as the event is QE scattering.

An alternative is to look for the transparency of protons from an SIDIS event. Here, at JLAB energies, the laboratory formation time is about $0.8/\nu$ fm, which translates into about 3–5 fm for $t_f$. This distance is comparable to the nuclear radius; thus, effects from the linear time-dependence could be expected.

4. Summary and Conclusions

In this paper, earlier studies by us on the hadronization process in deep inelastic collisions reviewed and summarized. Semi-inclusive deep-inelastic scattering (SIDIS) events on nuclear targets are sensitive to the duration (and time delays) of the hadronization process and, thus, provide valuable information on hadronization mechanisms.

It is stressed here that any such time-delays are connected only with hard, DIS-like events that require a major reorganization of the struck nucleon and the partons in the reaction product. The initial doorway state in an SIDIS event is connected with a width and, thus, naturally, also with a time span for decay.

The actual decay is handled with a string-fragmentation model as it is implemented in PYTHIA. Contrary to other approaches, the production and formation times are not free parameters or educated guesses, but they are directly obtained from this string-breaking process. Once these times are known, a crucial property then is the time development of the cross section experienced by prehadrons until their formation is over. It is shown that analysis of data in very different kinematical regimes, ranging from Jefferson Laboratory (JLAB) experiments to the EMC experiment, allows one to fix that time-dependence to be linear. The question initially raised in [17] is, thus, answered.

Comparisons of these calculations with data, mainly in the HERMES and JLAB regime, shows excellent agreement for different hadron flavors and as a function of different kinematical variables of the final state particles. In this paper, the predictions made by us in 2007 for pions and kaons at the JLAB 12 GeV beam are also repeated. Such measurements for comparisons are expected to appear soon.

Finally, a solution to the seeming puzzle of why CT was not observed in quasi-elastic (QE) scattering reactions on protons in nuclei are offered. In a QE event, formation times do not appear; thus, no sensitivity to any prehadronic cross section should be expected. Instead, we propose to repeat such studies for protons from SIDIS events where observable effects are expected.