Abstract
The second flavor of hydrogen atoms (SFHA) refers to the kind of hydrogen atoms that have only the states of the zero orbital angular momentum (the S-states), both in the discrete and continuous spectra. They were first discovered theoretically in one of my earlier papers, where a proof of their existence was also provided by analyzing atomic experiments concerning the high-energy tail of the linear momentum distribution in the ground state of hydrogen atoms. From a theoretical point of view, the discovery was based on the standard Dirac equation for hydrogen atoms without changing the existing physical laws. Recently, the existence of the SFHA was seemingly also confirmed by two types of astrophysical observations: the allowance for the SFHA explained the puzzling results concerning both the anomalous absorption of the redshifted 21 cm spectral line from the early Universe, and the observations by the Dark Energy Survey (DES) team where it was found that the distribution of dark matter in the Universe is noticeably smoother than predictions employing Einstein’s relativity. In the present review, we exhibit results from two recent papers where attention was brought to a visible difference in the cross-sections of the resonant charge exchange for collisions of the SFHA with incoming protons, compared to collisions of the usual hydrogen atoms with incoming protons. It was shown that, after taking into account the SFHA, there is a better agreement with the corresponding experimental cross-section. Coupled with the previous evidence of the existence of the SFHA, deduced from the analysis of the other kind of atomic experiments, and evidenced by two different kinds of astrophysical observations, this strengthens the standing of the SFHA as the most probable candidate for all or a part of dark matter.
1. Introduction
The second flavor of hydrogen atoms (SFHA) refers to the kind of hydrogen atoms that have only the states of the zero orbital angular momentum (the S-states), both in the discrete and continuous spectra. They were first discovered theoretically in [1], where proof of their existence was also provided by analyzing atomic experiments concerning the high-energy tail of the linear momentum distribution in the ground state of hydrogen atoms. From a theoretical point of view, the discovery was based on the standard Dirac equation for hydrogen atoms, as follows.
The Dirac equation for hydrogen atoms has two solutions differing by their behavior at relatively small values of the distance r of the electron to the proton. One solution is called “regular” because it has only a weak singularity at small r. The second solution is called “singular” because it has a strong singularity at small r. In all textbooks, the singular solution was rejected. In [1], it was shown that with the allowance for the finite size of the nucleus and for the known (from experiments) distribution of the electric potential inside the nucleus, it is possible to tailor (at the proton boundary) the wave function inside the proton with the singular wave function outside the proton for the ground state of hydrogen atoms, so that there was no reason to reject the singular solution of the standard Dirac equation outside the proton.
Moreover, in [1] a whole class of potentials were derived, for which tailoring and thus the legitimization of the singular solution is possible. Those are potentials inside a sphere of a radius R that rise from r = 0 to r = R faster than for the uniformly charged sphere. They correspond to the charge density that has a maximum at r = 0—just as for the actual charge density inside the proton known from experiments [2,3,4].
In [5], it was shown that singular solutions outside the proton are legitimate not only for the ground state (as in [1]), but also for all S-states in the discrete and continuous energy spectra of hydrogen atoms. Therefore, due to the well-known selection rules, for this kind of hydrogen atom, both diagonal and non-diagonal matrix elements of the radius–vector operator r are zeros (which is why this kind of hydrogen atom does not exhibit any Stark effect in a uniform electric field, or in the non-uniform electric field of the nearest plasma ion, as explained in [6]). Matrix elements of any power of the operator r are zeros because they are the products of the matrix element of the operator r, which are all zeros. Consequently, this kind of hydrogen atom cannot interact with electromagnetic radiation (except for emitting or absorbing the 21 cm spectral line corresponding to the radiative transition between the two hyperfine structure sublevels of the ground state): these hydrogen atoms remain dark (or nearly dark, allowing only for the 21 cm spectral line).
The name “second flavor of hydrogen atoms” was given to this kind of atom in [7] for the following reason. The regular wave function describing the ground state of the usual hydrogen atoms and the singular wave function describing the ground state of the other kind of hydrogen atoms correspond to the same energy and have the same quantum numbers N = 0, k = −1, j = 1/2 (resulting from the solution of the Dirac equation). In other words, they have the same values of the known conserved quantities the energy E, the square of the total angular momentum J2, and K (where the operator K = β(2Ls + 1), β being the Dirac matrix of the rank four and Ls denoting the scalar product of the operators of the orbital angular momentum and spin).
In [7], I notice:
“There is a fundamental theorem of quantum mechanics concerning the cause of any additional degeneracy. Namely, it is caused by the existence of an additional conserved quantity (or quantities), whose operator commutes with the Hamiltonian, but does not commute with other conserved quantities or if it does, but the additional conserved quantity is a multi-component one, then its components do not commute with each other—see, e.g., the textbook [15] (here, [8]). The corresponding degenerate states differ by the eigenvalues (i.e., by additional quantum numbers) of the additional conserved quantity.”
Thus, there is an additional double-degeneracy, in addition to the trivial double-degeneracy with respect to the z- projection of the total angular momentum J. Hydrogen atoms have flavor symmetry: they have two flavors that differ by the eigenvalue of an additional, new conserved quantity. It is appropriate to call it the flavor symmetry by analogy with quarks that are said to have flavors: for instance, there are up and down quarks. As it was written in [7], “for representing this particular flavor symmetry, there was assigned an operator of the isotopic spin (isospin) —the operator having two eigenvalues for its z-projection: = 1/2 assigned to the up quark and = −1/2 assigned to the down quark.” So, the new operator, by eigenvalues of which the singular flavor of hydrogen atoms differ from the regular flavor of hydrogen atoms, was called isohydrogen spin in [7].
Of course, the fact that the SFHA does not interact with the electromagnetic radiation and remains dark, is the objective fact that does not depend on the choice of terminology. In [1], from which the history of the SFHA started, it was shown that the allowance for the SFHA eliminates a really huge discrepancy (of several orders of magnitude) between the experimental high-energy tail of the linear momentum distribution in the ground state of hydrogen atoms and the previous theories that did not allow for the SFHA. This is what constituted the first observational evidence of the existence of the SFHA.
Recently, the existence of the SFHA seemingly was confirmed also by the following two types of astrophysical observations. In [9], the authors presented a puzzling observation of the redshifted 21 cm spectral line from the early Universe. Namely, the observed absorption profile of the 21 cm line turned out to be by a factor of two greater than calculated by the standard cosmology. This meant that the temperature of the primordial hydrogen gas was significantly smaller than expected from the standard cosmological calculations.
In [10], the author hypothesized that the cooling was due to collisions with some unspecified dark matter. According to his estimates, the mass of these unspecified dark matter particles should not be greater than 4.3 GeV—to fit the observational results of [9].
Later, in [11], the author came to the following important conclusion based on the analysis of the results of [9,10]. He stated that these observational results represented an unambiguous proof that dark matter is baryonic, so that non-baryonic models of dark matter should be discarded.
Then, in [5], I addressed the following question: Why not dark matter baryons, responsible for the additional cooling of the primordial hydrogen gas, would be the SFHA —instead of some unspecified dark matter particles suggested in [10]? In [5], it was shown that in the course of the Universe expansion, the SFHA would decouple from the cosmic microwave background radiation much earlier than the usual hydrogen atoms, so that the SFHA temperature was significantly lower than for usual hydrogen atoms. It was demonstrated in [5] that this explained the puzzling astrophysical observation of [9] both qualitatively and quantitatively.
The other recent astrophysical observation seemingly providing an additional confirmation of the existence of the SFHA is the following. From the most detailed map of the distribution of dark matter in the Universe, created from the observations by the DES team, it was determined (and presented in [12]) that this distribution is noticeably smoother than predictions employing the Einstein’s relativity. This motivated suggestions that the explanation would require new physical laws—namely, some type of non-Einsteinian gravitation. In [13], I demonstrated that this perplexing observation can also be explained (qualitatively and quantitatively) by utilizing the SFHA, and no change of physical laws is required.
Namely, in [13] a system of a large number of gravitating neutral particles, equal by their mass to that of hydrogen atoms, was analyzed. The focus was at the subsystem of relatively isolated pairs of these particles that lose energy via gravitational radiation. This causes the decrease in the separation of the particles within the pair. In [13], it was demonstrated that there is a minimum separation, at which the further decrease would stop. It turned out that the calculated minimum separation is of the order of few megaparsecs, which is practically the same as the average observed separation between galaxies. As the pair reaches the minimum separation, the gravitational radiation stops: a partial inhibition of the gravitational radiation occurs within this system. According to the estimate of [13], the percentage of the pairs, for which the inhibition of the unlimited “clumping” takes place, is ≳2.5%. This is in a good agreement with the percentage observed by the DES team—the percentage by which the distribution of dark matter was found to be more smooth, less clumpy, than predicted by general relativity.
What are the dark matter particles that interact only gravitationally (no electromagnetic interaction) and whose mass is equal to the mass of hydrogen atoms? In [13], it was pointed out that such dark matter particles could only be the SFHA.
Thus, the SFHA seems to be the most probable candidate for dark matter (or at least for a part of it) because it has the following four advantages over other hypotheses. First, the SFHA has the experimental confirmation from the analysis of atomic experiments [1]. Second, it is favored by the Occam razor principle because it does not go beyond the Standard Model. Third, its theoretical discovery was based on the standard the Dirac equation without resorting to change the physical laws (and thus once again it is favored by the Occam razor principle). Fourth, using the SFHA it was possible to explain qualitatively and quantitatively the two puzzling astrophysical observations: one of [9], another of [12].
For reinforcing the status of the SFHA as the most probable candidate for dark matter, it would be good to find further evidence of the existence of the SFHA from atomic experiments—in addition to the experimental evidence presented in [1]. It turned out that such additional evidence can be indeed obtained—from analysis of experiments on the resonant charge exchange between hydrogen atoms and incoming protons, as shown in [6,14]. In the present review, I exhibit the results of [6,14].
2. Resonant Charge Exchange Involving the Second Flavor of Hydrogen Atoms: A Classical Description for Excited States
For an electron transiting from being bound to one proton to being bound to another proton, the classical cross-section σ of the resonant charge exchange is (see, e.g., [15]):
where v is the relative velocity of the two protons and I is the ionization potential from the particular state of the atom. Here and below we use atomic units, unless specified to the contrary. Equation (1) is valid under the condition:
The ionization potential I in the zeroth approximation is related to the principal quantum number n, as follows:
Therefore, in the zeroth approximation, Equation (1) yields:
In the next approximation for the usual hydrogen atoms, in [6] the linear Stark shift in the field of the proton located at the distance R from the atom was allowed for:
In Equation (5), and are the parabolic quantum numbers.
According to [15], the potential barrier for the transition of the electron from one proton to another vanishes when the interaction potential between the electron and the protons in the middle of the internuclear axis becomes greater than the ionization potential. This condition results in the following charge-exchange-effective separation between the two protons [15]:
On substituting in the 2nd term in the parenthesis in Equation (5) and utilizing , Equation (5) can be represented in the form:
After combining Equations (1) and (7) and taking into account that the 2nd term in the right side of Equation (7) is relatively small, the author of paper [6] finally obtained:
In distinction to the usual hydrogen atoms, for the SFHA there is no Stark effect in any order, as explained in [6] and noted above. Therefore, for the SFHA the corresponding cross-section is:
In Equation (9), the number 2 in the subscript means the “second flavor”.
Figure 1 shows the relative difference versus the principal quantum number n for the quantum number q = n − 1 and the relative velocity of the colliding particles v = 0.1. One can see that the relative difference can become of the order of unity.
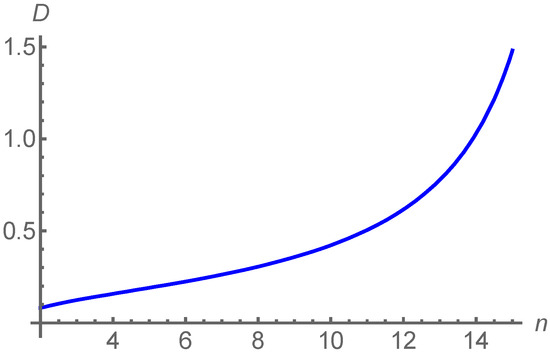
Figure 1.
The relative difference in the cross-sections of the resonant charge exchange for the usual hydrogen atoms and the second flavor of hydrogen atoms (SFHA) versus the principal quantum number n for the quantum number q = n − 1 and the relative velocity of the colliding particles v = 0.1.
3. Resonant Charge Exchange Involving the Second Flavor of Hydrogen Atoms: A Classical Description for the Ground State and the Analysis of Experiments
In this section, I follow [14]. For relatively large internuclear distances R. the ground state energy of usual hydrogen atoms can be written as follows (in accordance with Equation (4.59) in [16]):
In Equation (10), the higher order terms of the expansion have been omitted; the subscript “large” means that Equation (10) is valid for relatively large R. Therefore, the ionization potential for the ground state of the usual hydrogen atoms can be represented as follows:
By combining Equations (6) and (11) (and omitting the subscript “0”) one obtains:
Out of the roots of Equation (12), the one that is relevant to the problem under consideration is:
As for the SFHA, the energy of the ground state for relatively large R is:
We remind that the SFHA does not exhibit any Stark shift. Therefore,
so that (in accordance to Equation (5)):
Next, in [14], I analyzed the situation for a relatively small R. In this case, the ground state energy of the usual hydrogen atoms can be expressed as follows (according to Equation (5.13) in [16]):
In Equation (17), the higher order terms have been omitted; the subscript “small” signifies that this expansion is valid for a relatively small R. So, the ionization potential for the ground state has the form:
where the subscript “small” means that Equation (18) is valid for a relatively small R.
After combining Equations (6) and (18), in [14] the following was obtained:
Out of the roots of Equation (19), the one that is relevant to the problem under consideration is:
As for the SFHA, the energy of the ground state for relatively small R is:
Once again, since there is no shift in the energy levels of the SFHA in the electric field, consequently:
so that (in accordance to Equation (6)):
Further, in [14] I wrote:
“For calculating the cross-sections of the charge exchange by using Equation (6), it is necessary to add the corresponding contributions from both channels, i.e., from both the “large R” case and the “small R” case. For obtaining the ratio of the resonant charge exchange cross-section from the ground state of the SFHA to the corresponding result for the usual hydrogen atoms in the simplest form—just to get the message across—we will consider the limit of v approaching zero.”
In this limit, the ratio becomes:
After substituting the data from Equations (13), (16), (20) and (23) in Equation (24), in [14] the following was finally obtained:
Thus, the is by 5% larger than .
Then, in [14], I compared the results with the most precise experiment on the resonant charge exchange between hydrogen atoms in the ground state and protons of a relatively low energy—the experiment performed by Fite et al. [17]. Figure 2 (reproduced from Figure 1 of [14]) shows the following: (i) the experimental cross-sections—circles, some with error margins—reproduced from Figure 2 of [17]; (ii) the experimental cross-sections—crosses (with error margins) connected by the solid line—from the earlier measurements by Fite et al. [18], reproduced from Figure 2 of [17]; (iii) the theoretical cross-sections—filled circles connected by the solid line—calculated by Dalgarno and Yadav [19], reproduced from Figure 2 of [17]; (iv) the theoretical cross-sections for the case of the SFHA—the dashed line—from the present calculations.
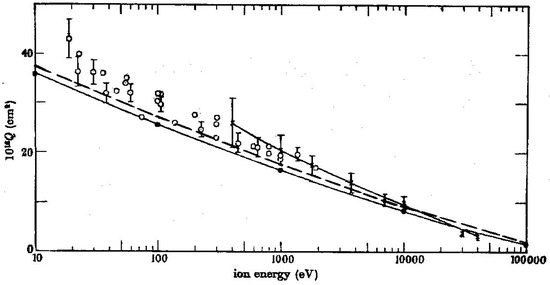
Figure 2.
Experimental cross-sections of the resonant charge exchange between hydrogen atoms and low-energy protons in comparison to the corresponding theoretical cross-sections (the cross-sections are in units of 10−16 cm2). Circles (some with error margins)—experiment reported in [17]; crosses (with error margins) connected by the solid line—experiment reported in [18]; filled circles connected by the solid line—theory of [19], allowing only for the usual hydrogen atoms; the dashed line—theory from the present paper, allowing for the SFHA [14].
One can see that the theoretical cross-sections calculated with the allowance for the SFHA exhibit a noticeably better agreement with the corresponding experimental cross-sections.
4. Conclusions
In [6,14], reviewed in the present paper, it was shown that there is a noticeable difference in the cross-sections of the resonant charge exchange for collisions of usual hydrogen atoms with incoming protons compared to collisions of second flavour hydrogen atoms (SFHA) with incoming protons. It was demonstrated that the allowance for the SFHA exhibits a noticeably better agreement with the corresponding experimental cross-sections.
In addition to the earlier evidence of the existence of the SFHA obtained from the analysis of the other kind of atomic experiments [1], as well as the evidence related to the two different kinds of astrophysical observations [5,9,10,11,12,13], the results of [14] reinforce the status of the SFHA as the most probable candidate for dark matter (or at least for a part of it).
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Oks, E. High-Energy tail of the linear momentum distribution in the ground state of hydrogen atoms or hydrogen-like ions. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 2235–2243. [Google Scholar] [CrossRef]
- Simon, G.G.; Schmitt, C.; Borkowski, F.; Walther, V.H. Absolute electron-proton cross sections at low momentum transfer measured with a high pressure gas target system. Nucl. Phys. A 1980, 333, 381–391. [Google Scholar] [CrossRef]
- Perkins, D.H. Introduction to High Energy Physics; Addison-Wesley Publishing Company Inc.: Menlo Park, CA, USA, 1987; Section 6.5. [Google Scholar]
- Feynman, R.P. Photon-Hadron Interactions; Addison-Wesley Publishing Company: Redwood City, CA, USA, 1989; Lecture 24. [Google Scholar]
- Oks, E. Alternative kind of hydrogen atoms as a possible explanation for the latest puzzling observation of the 21 cm radio line from the early Universe. Res. Astron. Astrophys. 2020, 20, 109. [Google Scholar] [CrossRef]
- Oks, E. Classical description of resonant charge exchange involving the second flavor of hydrogen atoms. Atoms 2021, 9, 41. [Google Scholar] [CrossRef]
- Oks, E. Two flavors of hydrogen atoms: A possible explanation of dark matter. Atoms 2020, 8, 33. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics; Pergamon: Oxford, UK, 1965. [Google Scholar]
- Bowman, J.D.; Rogers, A.E.E.; Monsalve, R.; Mozdzen, T.; Mahesh, N. An absorption profile centred at 78 megahertz in the sky-averaged spectrum. Nature 2018, 555, 67–70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barkana, R. Possible interaction between baryons and dark-matter particles revealed by the first stars. Nature 2018, 555, 71–74. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGaugh, S.S. Strong hydrogen absorption at cosmic dawn: The signature of a baryonic universe. Res. Notes AAS 2018, 2, 37. [Google Scholar] [CrossRef] [Green Version]
- Jeffrey, N.; Gatti, M.; Chang, C.; Whiteway, L.; Demirbozan, U.; Kovacs, A.; Pollina, G.; Bacon, D.; Hamaus, N.; Kacprzak, T.; et al. Dark Energy Survey Year 3 results: Curved-sky weak lensing mass map reconstruction. Mon. Not. R. Astron. Soc. 2021, 505, 4626–4645. [Google Scholar] [CrossRef]
- Oks, E. DES Map shows a smoother distribution of matter than expected: A possible explanation. Res. Astron. Astrophys. 2021, 10, 241. [Google Scholar] [CrossRef]
- Oks, E. Analysis of experimental cross-sections of charge exchange between hydrogen atoms and protons yields another evidence of the existence of the second flavor of hydrogen atom. Foundations 2021, 1, 265–270. [Google Scholar] [CrossRef]
- Smirnov, B.M. The classical theory of resonant charge exchange. Sov. Phys. JETP 1971, 32, 670–672. Available online: http://jetp.ras.ru/cgi-bin/e/index/e/32/4/p670?a=list (accessed on 10 January 2022).
- Komarov, I.V.; Ponomarev, L.I.; Slavyanov, S.Y. Spheroidal and Coulomb Spheroidal Functions; Nauka: Moscow, USSR, 1976. (In Russian) [Google Scholar]
- Fite, W.L.; Smith, A.C.H.; Stebbings, R.F. Charge transfer in collisions involving symmetric and asymmetric resonance. Proc. R. Soc. A Math. Phys. Eng. Sci. 1962, A268, 527–536. [Google Scholar] [CrossRef]
- Fite, W.L.; Brackmann, R.T.; Snow, W.R. Charge exchange in proton-hydrogen-atom collisions. Phys. Rev. 1958, 112, 1161–1169. [Google Scholar] [CrossRef]
- Dalgarno, A.; Yadav, H.N. Electron capture II: Resonance capture from hydrogen atoms by slow protons. Proc. Phys. Soc. (Lond.) Sect. A 1953, 66, 173–177. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).