Enhancing Temperature Data Quality for Agricultural Decision-Making with Emphasis to Evapotranspiration Calculation: A Robust Framework Integrating Dynamic Time Warping, Fuzzy Logic, and Machine Learning
Abstract
1. Introduction
- Implementing a Spatial Consistency Test using Dynamic Time Warping (DTW) and Fuzzy Logic to detect anomalies in temperature measurements.
- Applying ML-based reconstruction (using XGBoost) to fill missing values while preserving seasonal and spatial temperature patterns.
- Developing a Data Quality Index (DQI) to quantify the overall reliability of temperature measurements, ensuring transparency and usability for water management and agricultural applications.
2. Temperature Dataset Characteristics and Data Quality Challenges
2.1. Temperature Time Series and Types of Observed Errors
2.2. Challenges of Network Operation and Data Analysis
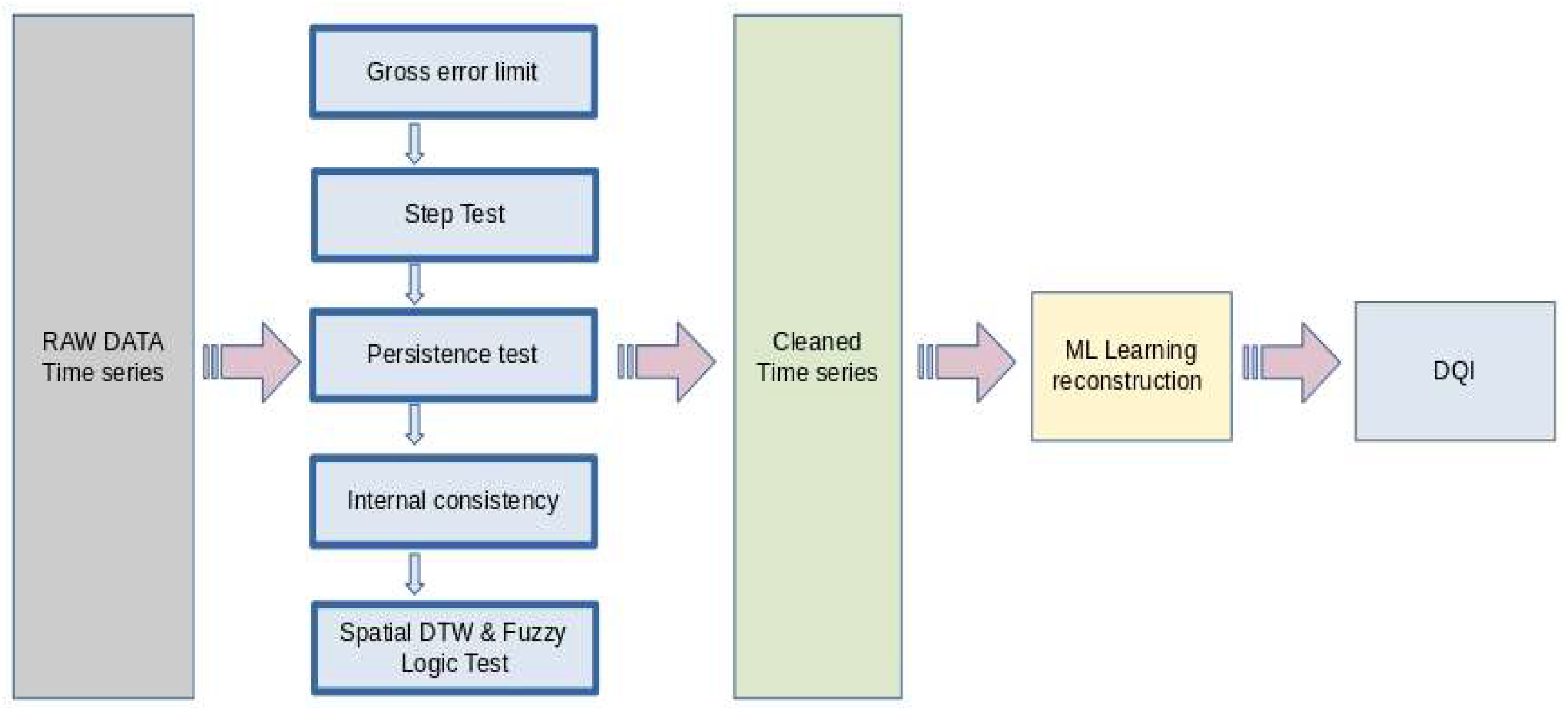
3. Materials and Methods
3.1. Area Description and Weather Station Network
3.2. QC Tests
3.2.1. Basic QC: Gross Error Limit
3.2.2. Basic QC: Step Test
3.2.3. Basic QC: Persistence Test
3.2.4. Basic QC: Internal Consistency
3.2.5. Basic QC: Spatial Consistency Test
3.3. Extended QC: Spatial DTW and Fuzzy Logic Test
- Dynamic Time Warping (DTW) to compare temperature time series across multiple stations, allowing for temporal shifts and capturing underlying similarities.
- Fuzzy Logic to handle uncertainty in anomaly classification, reducing the risk of false positives and false negatives.
- Dynamic adaptations to seasonal and diurnal temperature variations, ensuring the accurate detection of anomalies within different meteorological conditions.
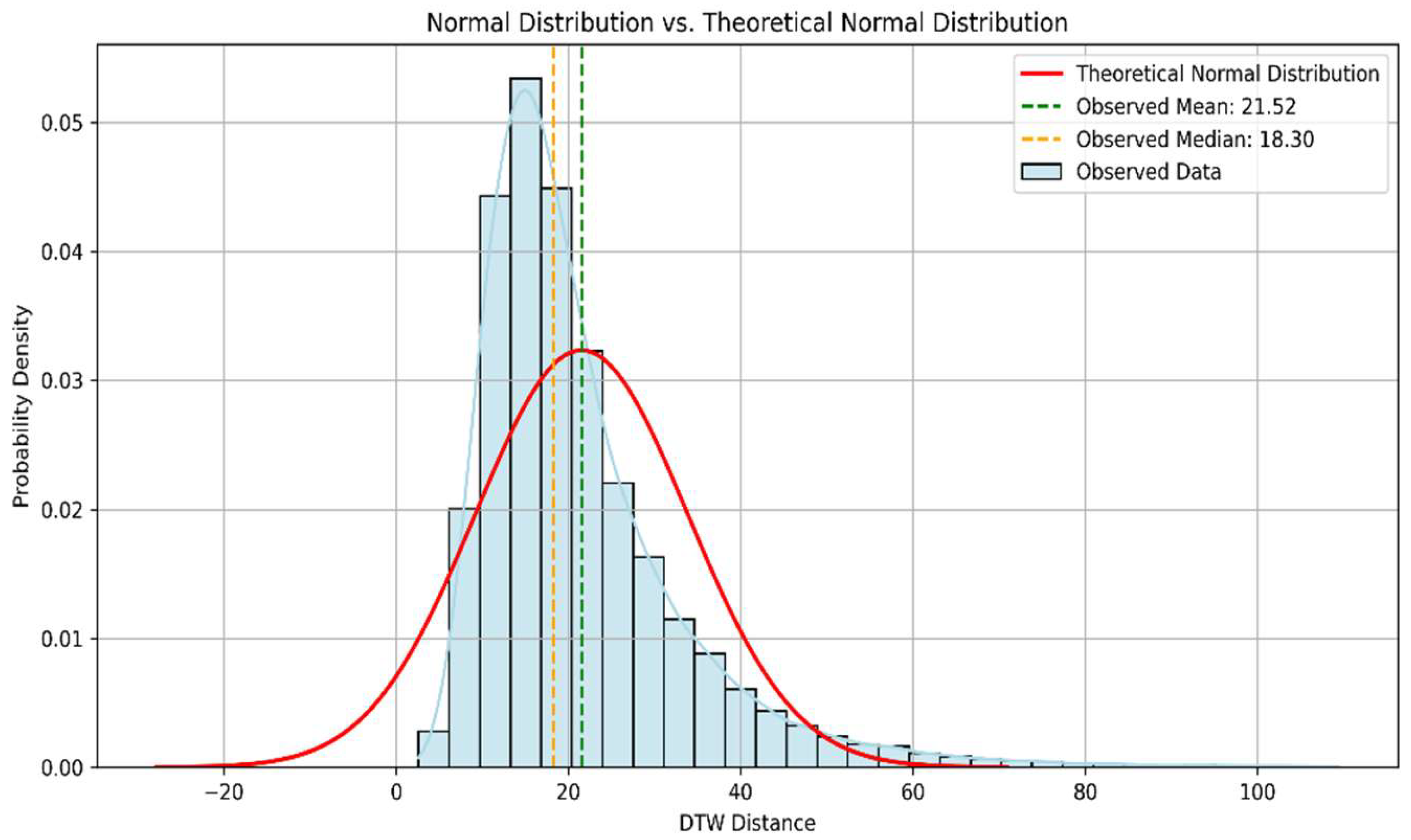
3.3.1. DTW Methodology Description
- Stabilizing variance: Log transformation compresses large values and expands smaller values, reducing the influence of extreme anomalies while maintaining the relative relationships between distances.
- Enhancing normality: The original DTW distance distribution exhibited a mean of 21.52 and a median of 18.30, with significant right skewness. After transformation, the distribution became more symmetric, with a mean of 2.94 and a standard deviation of 0.50, facilitating the use of standard-deviation-based thresholding techniques.
- Daily isolation: Each day’s temperature data were treated as a separate time series, consisting of 24-hourly measurements per station.
- DTW pairwise comparisons: DTW distances were computed for daily temperature time series across all station pairs.
- Log transformation and thresholding: The log transformation was applied to the DTW distances, and the anomaly threshold was established using the three-standard-deviation criterion.
3.3.2. Fuzzy Logic Model
- Time of day: Classified as either “Night” or “Day”.
- Absolute temperature difference: Between a reference station (e.g., Ag) and all other stations in the network.
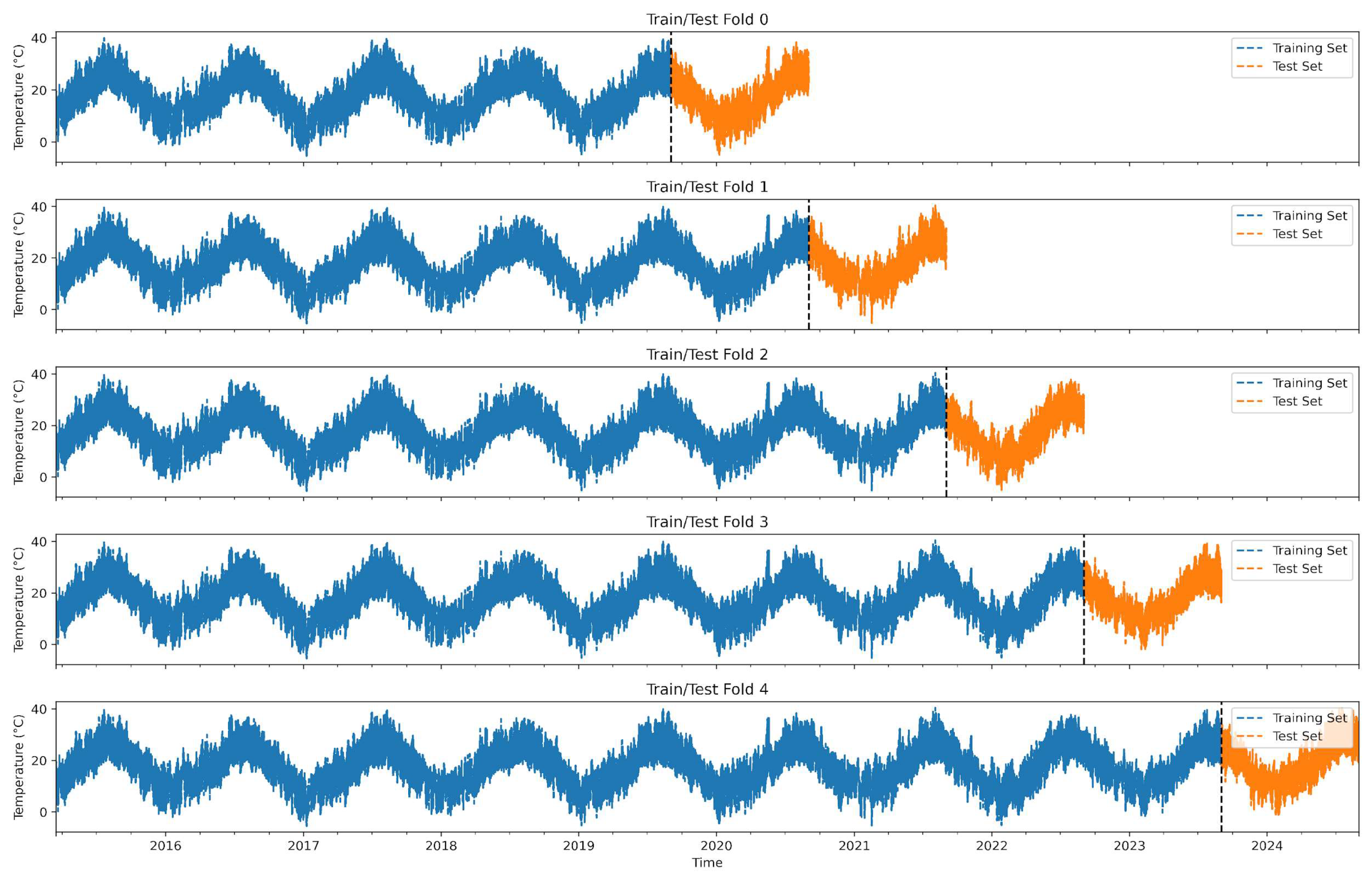
3.4. ML for the Reconstruction of Time Series
- First, to ensure that the training dataset remains viable even if data from one station are missing.
- Second, because the final ML model—intended for real-time processing—must be able to produce results even if one or more stations are offline.
3.5. DQI
3.5.1. Completeness Assessment
3.5.2. Accuracy Assessment
3.5.3. Data Quality Index (DQI) Computation
4. Results
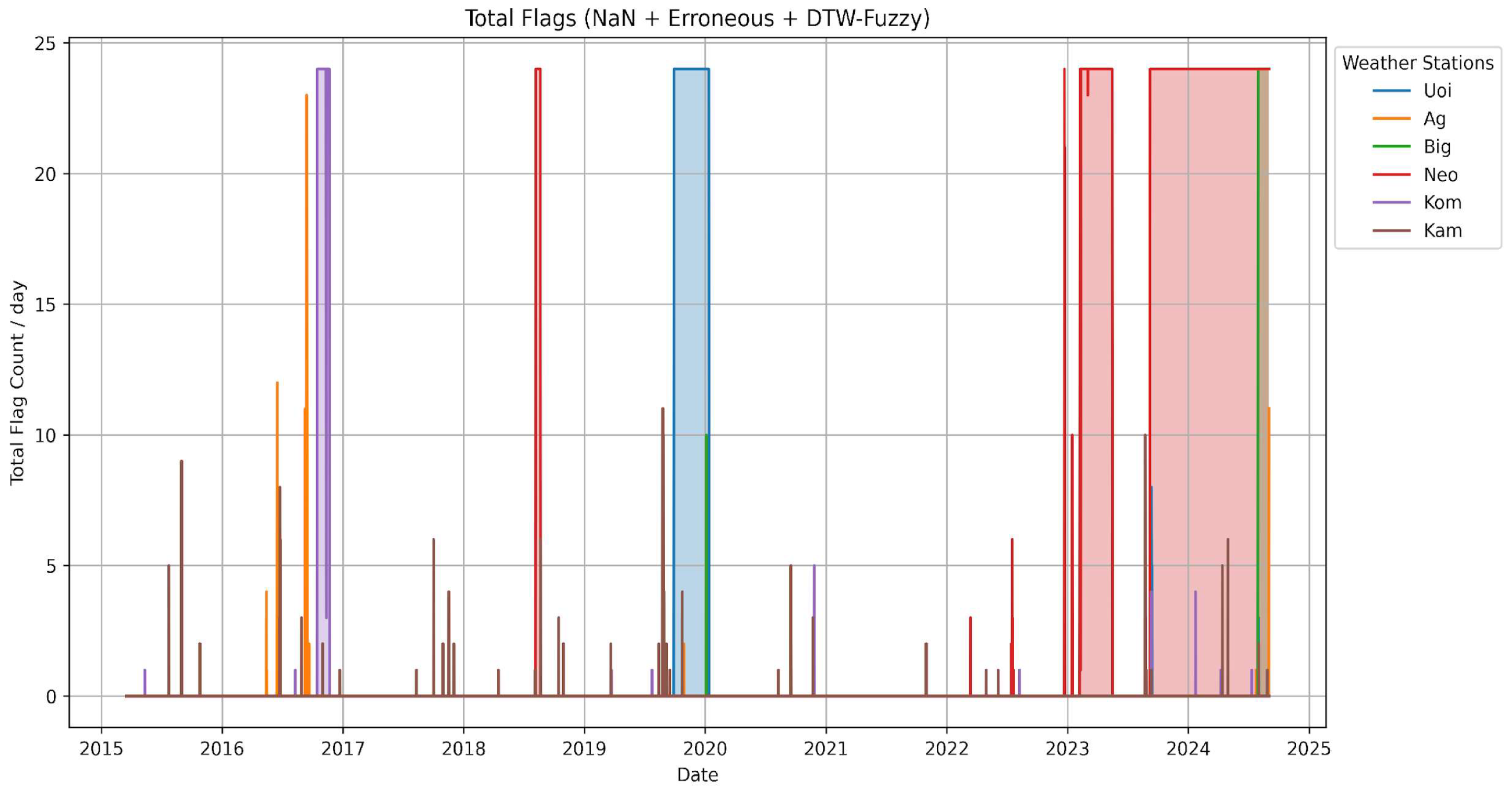
4.1. Basic QC Tests’ Results
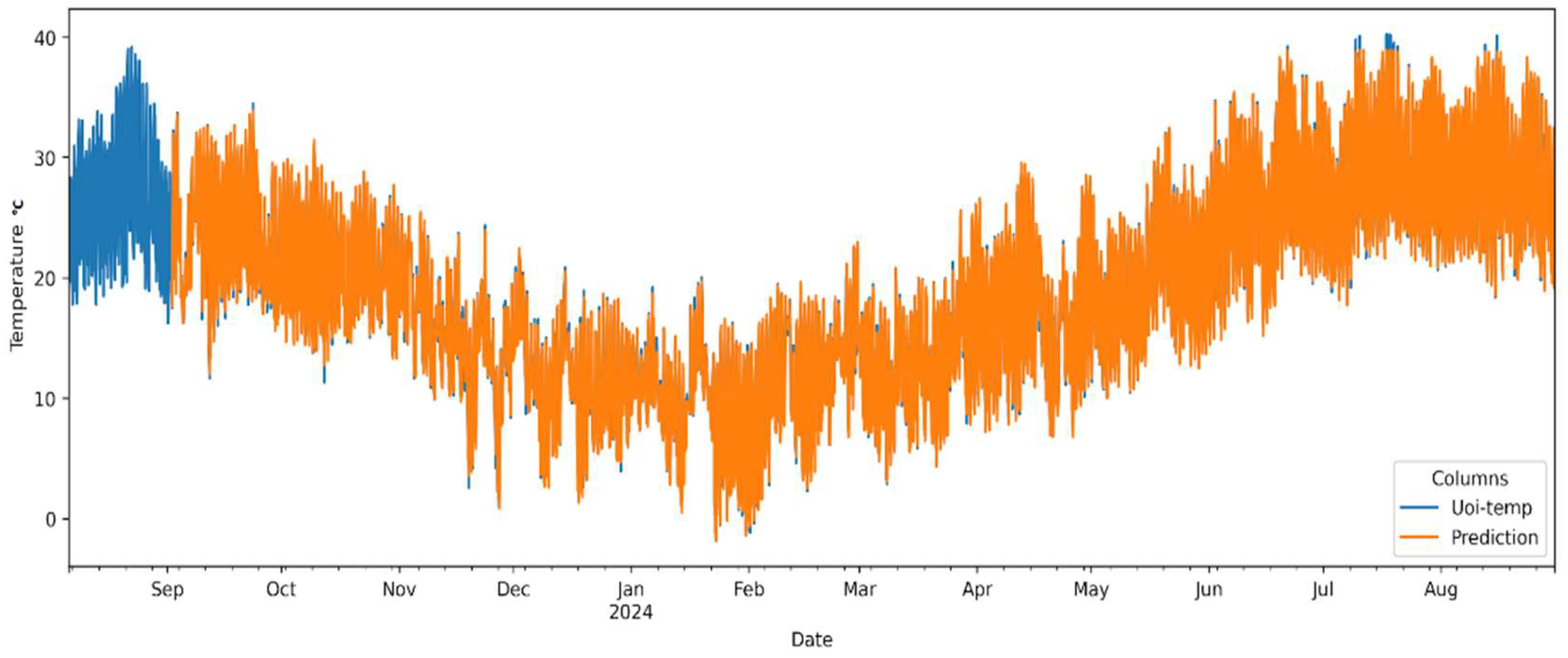
4.2. ML Reconstruction Results
- The XGBoost model achieved high reconstruction accuracy, with RMSE values ranging between 0.40 °C and 0.66 °C across the weather station network.
- The Big station exhibited the lowest RMSE (0.40 °C), indicating stable temperature patterns and a strong spatial correlation with neighboring stations.
- The Kom station recorded the highest RMSE (0.66 °C), suggesting that prolonged missing data periods and localized temperature anomalies may have introduced higher reconstruction uncertainty.
- Spatial correlation was the dominant factor influencing reconstruction accuracy, with temperature observations from nearby stations serving as the most significant predictors.
- The proposed method provides a computationally efficient and interpretable solution for reconstructing missing meteorological data, offering a practical framework for ensuring data completeness in automated weather station networks.
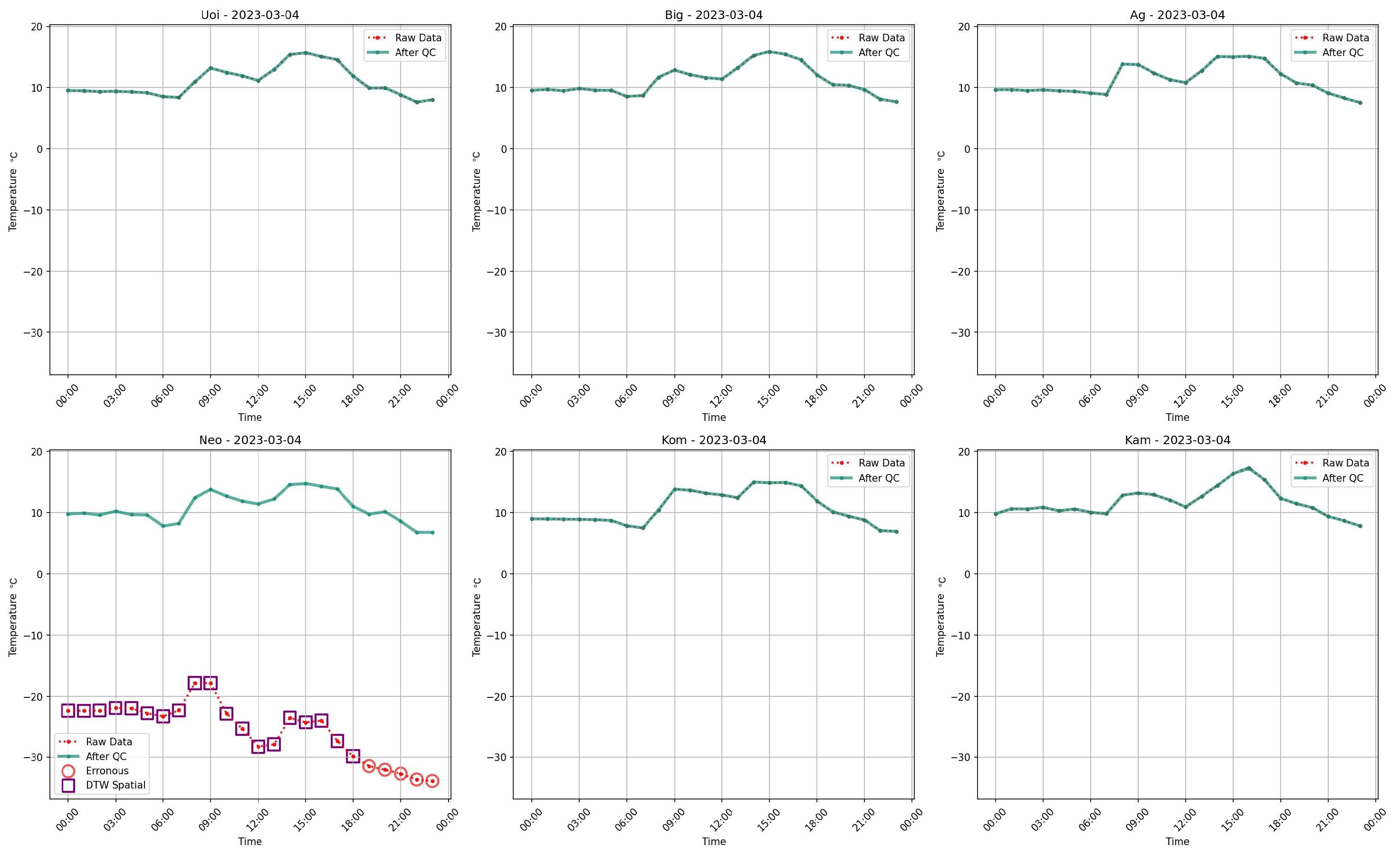
4.3. Results of the Proposed DTW–Fuzzy Spatial Test
- Better resilience to missing values.
- Higher detection sensitivity to local anomalies.
- Lower false alarm rates, improving the trustworthiness of spatial quality control assessments.
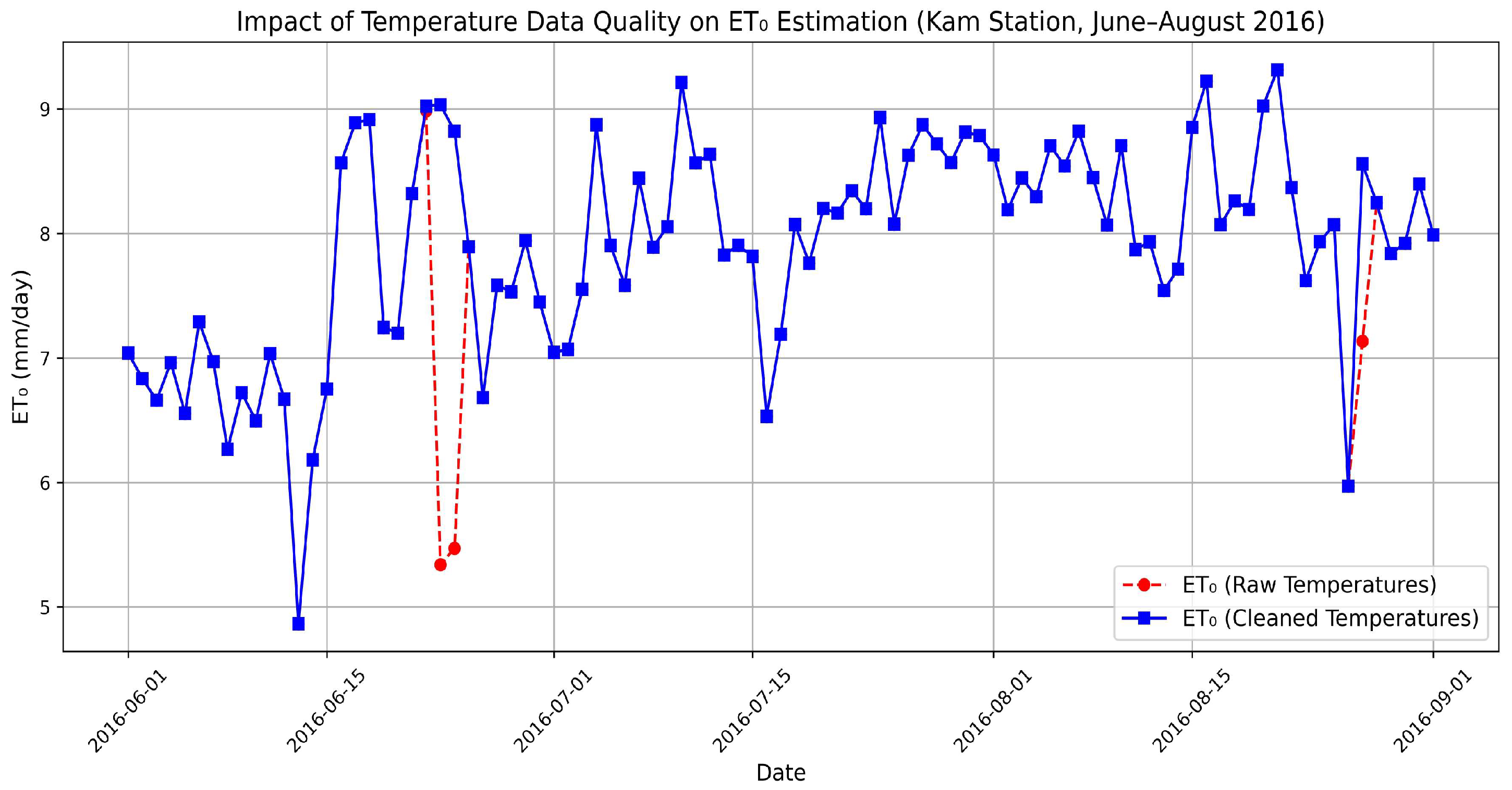
4.4. Preliminary Assessment of Temperature Data Quality Impact on Evapotranspiration Estimation
4.5. DQI Results
5. Discussion
6. Conclusions
- Extending the DQI framework to incorporate additional meteorological variables such as humidity, solar radiation, and wind speed.
- Exploring alternative machine learning models (e.g., LSTMs, transformers) for even more robust time series reconstructions.
- Evaluating the impact of improved data quality on real-world irrigation practices using field experiments and case studies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Faybishenko, B.; Versteeg, R.; Pastorello, G.; Dwivedi, D.; Varadharajan, C.; Agarwal, D. Challenging problems of quality assurance and quality control (QA/QC) of meteorological time series data. Stoch. Environ. Res. Risk Assess. 2022, 36, 1049–1062. [Google Scholar] [CrossRef]
- Lopez-Guerrero, A.; Cabello-Leblic, A.; Fereres, E.; Vallee, D.; Steduto, P.; Jomaa, I.; Owaneh, O.; Alaya, I.; Bsharat, M.; Ibrahim, A.; et al. Developing a Regional Network for the Assessment of Evapotranspiration. Agronomy 2023, 13, 11. [Google Scholar] [CrossRef]
- Estévez, J.; Gavilán, P.; Berengena, J. Sensitivity analysis of a Penman–Monteith type equation to estimate reference evapotranspiration in southern Spain. Hydrol. Process. 2009, 23, 3342–3353. [Google Scholar] [CrossRef]
- Cerlini, P.; Silvestri, L.; Saraceni, M. Quality control and gap-filling methods applied to hourly temperature observations over Central Italy. Meteorol. Appl. 2020, 27, e1913. [Google Scholar] [CrossRef]
- Boujoudar, M.; El Ydrissi, M.; Abraim, M.; Bouarfa, I.; El Alani, O.; Ghennioui, H.; Bennouna, E.G. Comparing machine learning algorithms for imputation of missing time series in meteorological data. Neural Comput. Appl. 2024. [Google Scholar] [CrossRef]
- WMO. Guide to Meteorological Instruments and Methods of Observation; No. 8; WMO: Geneva, Switzerland, 2023. [Google Scholar]
- WMO. Guide to Agricultural Meteorological Practices (GAMP); No. 134; WMO: Geneva, Switzerland, 2010. [Google Scholar]
- Orlanski, I. A rational subdivision of scales for atmospheric processes. Bull. Am. Meteorol. Soc. 1975, 56, 527–530. [Google Scholar]
- High Precision Miniature Humidity and Temperature Probe. Available online: https://www.epluse.com/products/humidity-instruments/humidity-modules-and-probes/ee08 (accessed on 29 March 2025).
- A753 UHF Radio Telemetry Unit. ADCON. Available online: https://www.rshydro.fr/wireless-telemetry-systems/wireless-radio-data-loggers/radio-rtus/a753-uhf-radio-telemetry-unit/ (accessed on 29 March 2025).
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Aguilar, E.; Auer, I.; Brunet, M.; Peterson, T.; Wieringa, J. Guidelines on Climate Metadata and Homogenization; No. 1186; WMO: Geneva, Switzerland, 2003. [Google Scholar]
- Eaton, B.; Gregory, J.; Drach, B.; Taylor, K.; Hankin, S.; Caron, J.; Signell, R.; Bentley, P.; Rappa, G.; Höck, H.; et al. NetCDF Climate and Forecast (CF) Metadata Conventions. NetCDF. Available online: https://cfconventions.org/cf-conventions/cf-conventions.html (accessed on 29 March 2025).
- Fiebrich, C.; Crawford, K. The Impact of Unique Meteorological Phenomena Detected by the Oklahoma Mesonet and ARS Micronet on Automated Quality Control. Bull. Am. Meteorol. Soc. 2001, 82, 2173–2188. [Google Scholar] [CrossRef]
- Snyder, R.L.; Pruitt, W.O. Evapotranspiration data management in California. In Proceedings of the Irrigation and Drainage Sessions at Water Forum ‘92, Baltimore, ML, USA, 2–6 August 1992; pp. 128–133. [Google Scholar]
- Shafer, M.A.; Fiebrich, C.A.; Arndt, D.S.; Fredrickson, S.E.; Hughes, T.W. Quality assurance procedures in the Oklahoma Mesonet. J. Atmos. Ocean. Technol. 2000, 17, 474–494. [Google Scholar] [CrossRef]
- Estévez, J.; Gavilán, P.; Giráldez, J.V. Guidelines on validation procedures for meteorological data from automatic weather stations. J. Hydrol. 2011, 402, 144–154. [Google Scholar] [CrossRef]
- Meek, D.; Hatfield, J. Data Quality Checking for Single Station Meteorological Databases. Agric. For. Meteorol. 1994, 69, 85. [Google Scholar] [CrossRef]
- Reek, T.; Doty, S.R.; Owen, T.W. A deterministic approach to the validation of historical daily temperature and precipitation data from the Cooperative Network. Bull. Am. Meteorol. Soc. 1992, 73, 753–762. [Google Scholar] [CrossRef]
- Feng, S.; Hu, Q.; Qian, Q. Quality control of daily meteorological data in China, 1951–2000: A new dataset. Int. J. Climatol. 2004, 24, 853–870. [Google Scholar] [CrossRef]
- Lawrence, M. The Relationship between Relative Humidity and the Dewpoint Temperature in Moist Air: A Simple Conversion and Applications. Bull. Am. Meteorol. Soc. 2005, 86, 225–233. [Google Scholar] [CrossRef]
- Hubbard, K.G.; You, J. Spatial regression test for climate data. J. Appl. Meteorol. 2005, 44, 634–643. [Google Scholar]
- Fiebrich, C.A.; Morgan, C.R.; McCombs, A.G.; Hall, P.K.; McPherson, R.A. Quality assurance procedures for mesoscale meteorological data. J. Atmos. Ocean. Technol. 2010, 27, 1565–1582. [Google Scholar] [CrossRef]
- Durre, I.; Menne, M.J.; Vose, R.S. Strategies for evaluating quality assurance procedures. J. Appl. Meteorol. Climatol. 2008, 47, 1785–1791. [Google Scholar] [CrossRef]
- WMO. Guide on the Global Data-Processing System; No. 305; WMO: Geneva, Switzerland, 1993. [Google Scholar]
- Yaro, A.S.; Maly, F.; Prazak, P. Outlier Detection in Time-Series Receive Signal Strength Observation Using Z-Score Method with Sn Scale Estimator for Indoor Localization. Appl. Sci. 2023, 13, 6. [Google Scholar] [CrossRef]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J. A Review on Outlier/Anomaly Detection in Time Series Data. ACM Comput. Surv. 2021, 54, 56. [Google Scholar] [CrossRef]
- Li, K.; Sward, K.; Deng, H.; Morrison, J.; Habre, R.; Franklin, M.; Chiang, Y.-Y.; Ambite, J.L.; Wilson, J.P.; Eckel, S.P. Using dynamic time warping self-organizing maps to characterize diurnal patterns in environmental exposures. Sci. Rep. 2021, 11, 24052. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Ren, X.; Zhao, G. Machine-Learning-Based Imputation Method for Filling Missing Values in Ground Meteorological Observation Data. Algorithms 2023, 16, 9. [Google Scholar] [CrossRef]
- Hayawi, K.; Shahriar, S.; Hacid, H. Climate Data Imputation and Quality Improvement Using Satellite Data. J. Data Sci. Intell. Syst. 2025, 3, 2. [Google Scholar] [CrossRef]
- RandomForestClassifier. Scikit-Learn. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html (accessed on 29 March 2025).
- XGBoost Documentation—Xgboost 3.0.0 Documentation. Available online: https://xgboost.readthedocs.io/en/release_3.0.0/ (accessed on 29 March 2025).
- LightGBM Documentation. Available online: https://lightgbm.readthedocs.io/en/stable/ (accessed on 29 March 2025).
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Kong, L.; Xi, Y.; Lang, Y.; Wang, Y.; Zhang, Q. A Data Quality Evaluation Index for Data Journals. In Big Scientific Data Management; BigSDM 2018. Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11473. [Google Scholar] [CrossRef]
- Ehrlinger, L.; Wöß, W. A Survey of Data Quality Measurement and Monitoring Tools. Front. Big Data 2022, 5, 850611. [Google Scholar] [CrossRef]
- Batini, C.; Barone, D.; Mastrella, M.; Maurino, A.; Ruffini, C. A Framework and a Methodology for Data Quality Assessment and Monitoring. In Proceedings of the 12th International Conference on Information Quality, MIT, Cambridge, MA, USA, 9–11 November 2007; p. 346. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, R.; Li, Y. Sensitivity analysis of reference evapotranspiration (ETo) to climate change in Beijing, China. Desalin. Water Treat. 2014, 52, 2799–2804. [Google Scholar] [CrossRef]
- Emeka, N.; Ikenna, O.; Okechukwu, M.; Chinenye, A.; Emmanuel, E. Sensitivity of FAO Penman–Monteith Reference Evapotranspiration (ETo) to Climatic Variables Under Different Climate Types in Nigeria. J. Water Clim. Change 2021, 12, 858–878. [Google Scholar] [CrossRef]
- Stahl, K.; Moore, R.D.; Floyer, J.A.; Asplin, M.G.; McKendry, I.G. Comparison of approaches for spatial interpolation of daily air temperature in a large region with complex topography and highly variable station density. Agric. For. Meteorol. 2006, 139, 224–236. [Google Scholar] [CrossRef]
- Paredes, P.; Pereira, L.S.; Almorox, J.; Darouich, H. Reference grass evapotranspiration with reduced data sets: Parameterization of the FAO Penman-Monteith temperature approach and the Hargeaves-Samani equation using local climatic variables. Agric. Water Manag. 2020, 240, 106210. [Google Scholar] [CrossRef]
- Tegos, A.; Malamos, N.; Efstratiadis, A.; Tsoukalas, I.; Karanasios, A.; Koutsoyiannis, D. Parametric Modelling of Potential Evapotranspiration: A Global Survey. Water 2017, 9, 795. [Google Scholar] [CrossRef]
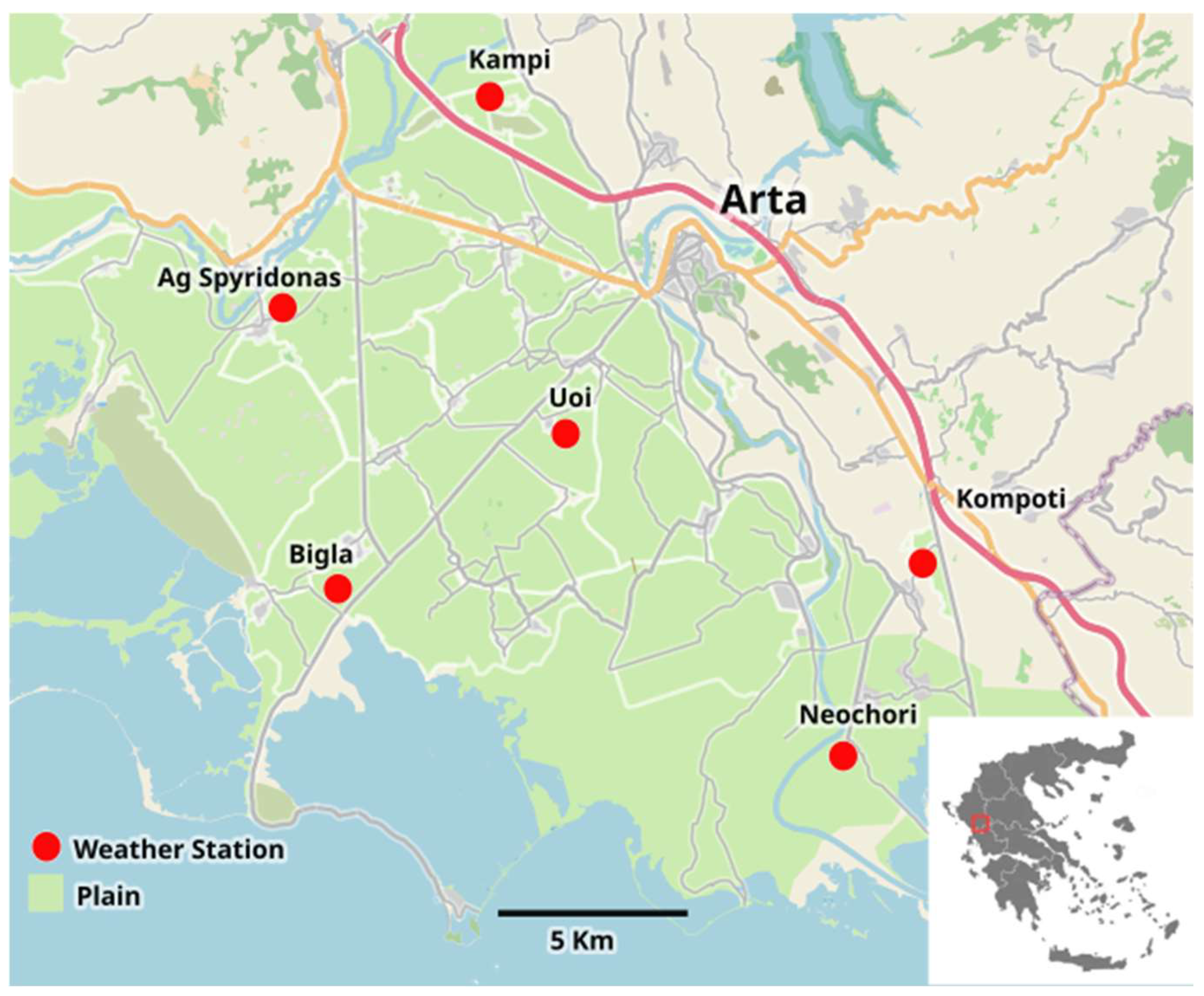
| Uoi | Big | Ag | Neo | Kom | Kam | |
|---|---|---|---|---|---|---|
| Latitude (°) | 39.12208 | 39.07888 | 39.14904 | 39.05061 | 39.09518 | 39.21634 |
| Longitude (°) | 20.94737 | 20.88525 | 20.87591 | 21.01207 | 21.06071 | 20.91295 |
| Altitude (m) | 10 | 0 | 10 | 10 | 15 | 20 |
| Test | Formulation | Reference |
|---|---|---|
| Gross error limit | −30 °C < Th < 50 °C | Shafer et al., 2000 [16] |
| Step Test | |Th − Th−1| < 10 °C | WMO No.8 [6] |
| Persistence Test | Th≠Th−1≠Th−2≠Th−3 | Estévez et al. (2011) [17], Meek and Hatfield (1994) [18] |
| Internal Consistency | Thmin < Th < Thmax Th > Tdew (Th, RH) | WMO (2010) [7] Reek et al., 1992 [19] Feng et al. (2004) [20] Magnus-Tetens formula [21] |
| Spatial Consistency | T* − fσ* < Th < T* + fσ* f = 3 σ* = weighting root mean square error; | Hubbard et al. (2005) [22] |
| Spatial DTW and Fuzzy Logic Test | Proposed in this work | |
| ML Reconstructed data | Proposed in this work |
| Station | Initial Nan | Gross Errors | Step Test (10 °C) | Step Test (4 °C) | Persistence | Internal Consistency | Spatial Consistency | DTW Fuzzy | Final NaN |
|---|---|---|---|---|---|---|---|---|---|
| Uoi | 2547 (3.07%) | 0 | 19 | 2290 (2.76%) | 1 | 0 | 0 | 4 | 2571 (3.1%) |
| Big | 823 | 0 | 5 | 1642 (1.98%) | 0 | 0 | 413 (0.5%) | 0 | 828 (0.01%) |
| Ag | 30 | 19 | 51 | 2961 (3.57%) | 0 | 0 | 0 | 16 (0.02%) | 116 |
| Neo | 8664 (10.4%) | 2543 (3.07%) | 51 | 2788 (3.35%) | 0 | 0 | 0 | 185 (0.21%) | 11,443 (13.7%) |
| Kom | 846 | 20 | 13 | 4649 (5.59%) | 0 | 0 | 8084 (9.73%) | 21 (0.03%) | 900 (0.01%) |
| Kam | 9 | 0 | 15 | 2950 (3.56%) | 0 | 0 | 11,370 (13.7%) | 145 (0.16%) | 169 |
| Uoi | Big | Ag | Neo | Kom | Kam | |
|---|---|---|---|---|---|---|
| RMSE | 0.43 | 0.40 | 0.42 | 0.47 | 0.66 | 0.52 |
| Station | Most Important | Less Important <10% | Min Importance <1% |
|---|---|---|---|
| Uoi | Big 49% Ag 23% Neo 13.7% | Kam 6% Kom 5% Uoi-lag1h 1.3% | Uoi-lag2h, Uoi-lag1h, Uoi-lag24h * month, quarter |
| Big | Uoi 48% Ag 24% Neo 17% | Kam 6% Big-lag1h 2% | Kom, Big-lag2h, Big-lag1h, Big-lag24h month quarter |
| Ag | Big 37% Kam 35% Uoi 19.5% | Neo 3% Ag-lag1h 2.6% | Kom, Ag-lag2h, Ag-lag1h, Ag-lag24h month, quarter |
| Neo | Kom 38% Uoi 32% Big 23% | Ag 2.6% Neo-lag1h 2.5% | Kam Neo-lag1h, Neo-lag2h, Neo-lag24h month, quarter |
| Kom | Neo 59% Uoi 25% | Ag 6.5% Kom-lag1h 4% Big 3.6% | Kam Kom-lag1h, Kom-lag2h, Kom-lag24h month, quarter |
| Kam | Ag 46% Uoi 25% Big 14% Kam-lag1h 10% | Kom 1.5% Neo 1% | Kam lag2h, Kam-lag1h, Kam-lag24h month, quarter |
| Station | Anomalies Detected (n) | Anomalies Detected (%) |
|---|---|---|
| Uoi | 4 | 0.005% |
| Big | 0 | 0.000% |
| Ag | 16 | 0.02% |
| Neo | 185 | 0.21% |
| Kom | 21 | 0.03% |
| Kam | 145 | 0.16% |
| Start | End | Nan | Erroneous | DTW-Fuzzy | |
|---|---|---|---|---|---|
| Uoi | 27 July 2019 | 11 January 2020 | 2 | 2542 | 1 |
| Ag | 14 June 2016 | 12 September 2016 | 55 | 13 | 7 |
| Big | 29 July 2024 | 31 August 2024 | 0 | 809 | 0 |
| Neo | 2 March 2023 | 31 August 2024 | 1663 | 8659 | 120 |
| Kom | 13 October 2016 | 20 November 2016 | 22 | 842 | 4 |
| Kam | 23 August 2019 | 24 August 2019 | 0 | 0 | 13 |
| Initial Completeness | Final Completeness | Initial Accuracy | Final Accuracy | Initial DQI | Final DQI | Improvement | |
|---|---|---|---|---|---|---|---|
| Uoi | 37.25% | 100.00% | 68.66% | 98.79% | 52.96% | 99.40% | 46.44% |
| Ag | 96.57% | 100.00% | 99.70% | 98.46% | 98.13% | 99.23% | 1.10% |
| Big | 0.61% | 100.00% | 50.31% | 83.59% | 25.46% | 91.79% | 66.33% |
| Neo | 20.72% | 100.00% | 67.14% | 98.86% | 43.93% | 99.43% | 55.50% |
| Kom | 7.26% | 100.00% | 55.02% | 97.74% | 31.14% | 98.87% | 67.73% |
| Kam | 72.92% | 100.00% | 100.00% | 100.00% | 86.46% | 99.98% | 13.52% |
| Initial Completeness | Final Completeness | Initial Accuracy | Final Accuracy | Initial DQI | Final DQI | Improvement | |
|---|---|---|---|---|---|---|---|
| Uoi | 99.90% | 100.00% | 98.47% | 99.06% | 97.68% | 99.53% | 1.85% |
| Ag | 99.86% | 100.00% | 99.98% | 99.09% | 99.93% | 99.54% | −0.39% |
| Big | 99.00% | 100.00% | 99.50% | 99.07% | 99.25% | 99.53% | 0.28% |
| Neo | 86.21% | 100.00% | 94.78% | 99.10% | 90.49% | 99.55% | 9.06% |
| Kom | 98.92% | 100.00% | 99.49% | 99.15% | 99.20% | 99.57% | 0.37% |
| Kam | 99.80% | 100.00% | 99.99% | 99.15% | 99.90% | 99.58% | −0.32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koliopanos, C.; Gemitzi, A.; Kofakis, P.; Malamos, N.; Tsirogiannis, I. Enhancing Temperature Data Quality for Agricultural Decision-Making with Emphasis to Evapotranspiration Calculation: A Robust Framework Integrating Dynamic Time Warping, Fuzzy Logic, and Machine Learning. AgriEngineering 2025, 7, 174. https://doi.org/10.3390/agriengineering7060174
Koliopanos C, Gemitzi A, Kofakis P, Malamos N, Tsirogiannis I. Enhancing Temperature Data Quality for Agricultural Decision-Making with Emphasis to Evapotranspiration Calculation: A Robust Framework Integrating Dynamic Time Warping, Fuzzy Logic, and Machine Learning. AgriEngineering. 2025; 7(6):174. https://doi.org/10.3390/agriengineering7060174
Chicago/Turabian StyleKoliopanos, Christos, Alexandra Gemitzi, Petros Kofakis, Nikolaos Malamos, and Ioannis Tsirogiannis. 2025. "Enhancing Temperature Data Quality for Agricultural Decision-Making with Emphasis to Evapotranspiration Calculation: A Robust Framework Integrating Dynamic Time Warping, Fuzzy Logic, and Machine Learning" AgriEngineering 7, no. 6: 174. https://doi.org/10.3390/agriengineering7060174
APA StyleKoliopanos, C., Gemitzi, A., Kofakis, P., Malamos, N., & Tsirogiannis, I. (2025). Enhancing Temperature Data Quality for Agricultural Decision-Making with Emphasis to Evapotranspiration Calculation: A Robust Framework Integrating Dynamic Time Warping, Fuzzy Logic, and Machine Learning. AgriEngineering, 7(6), 174. https://doi.org/10.3390/agriengineering7060174










