Design and Experimental Evaluation of a Two-Stage Domain-Segmented Harvesting Device for Densely Planted Dwarf Apple Orchards
Abstract
1. Introduction
2. Materials and Methods
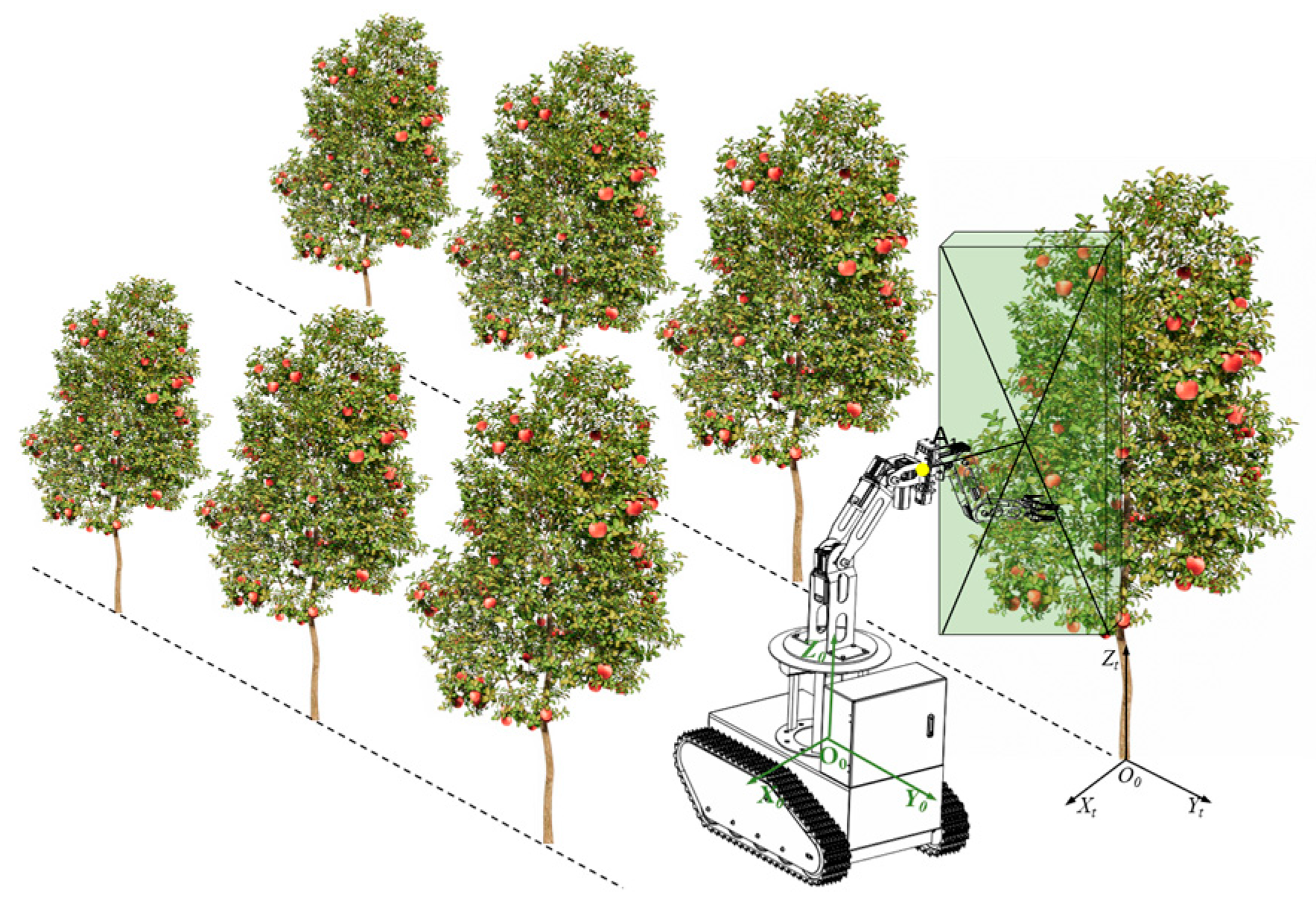
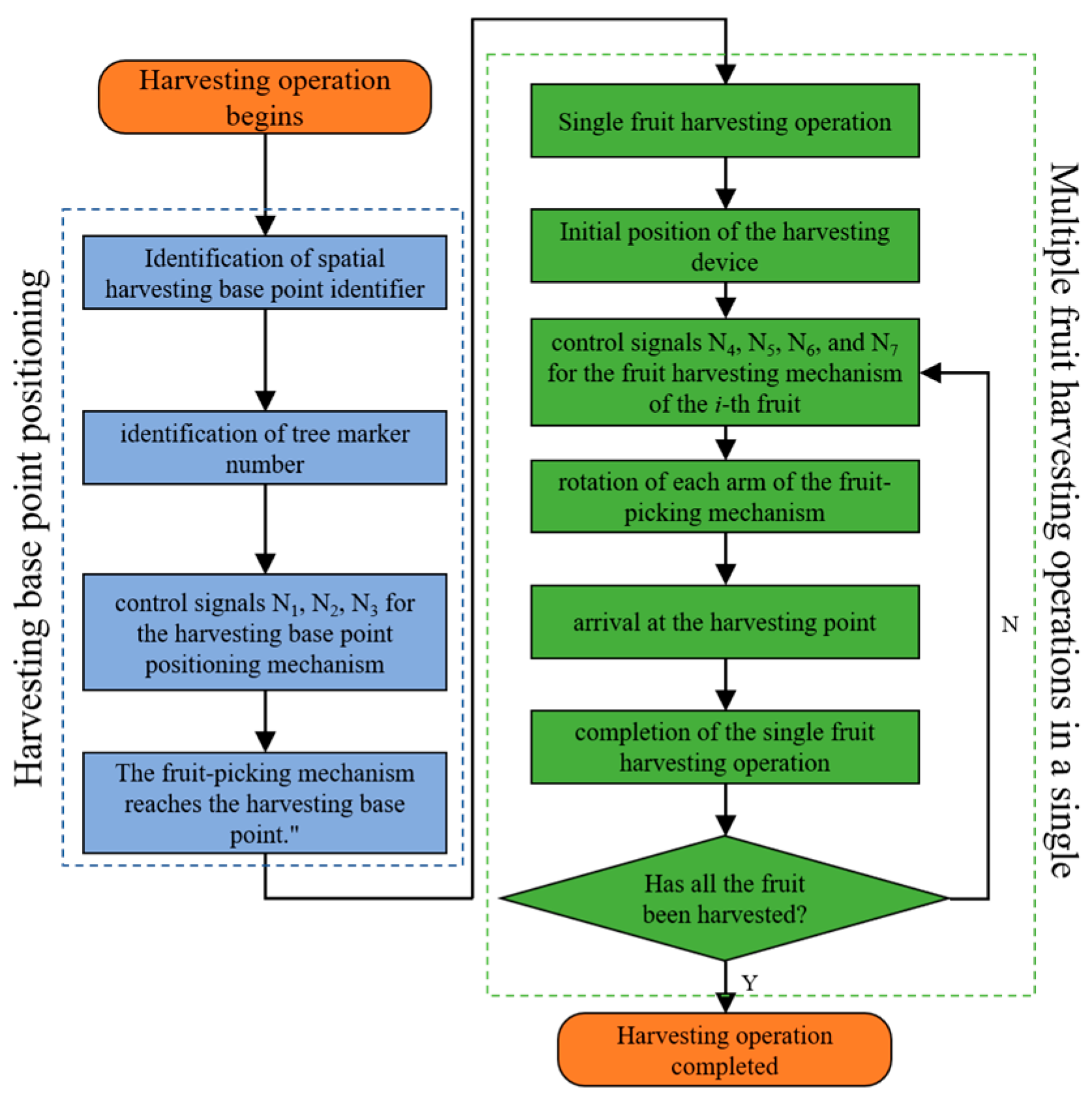
2.1. Machine Structure and Working Principle
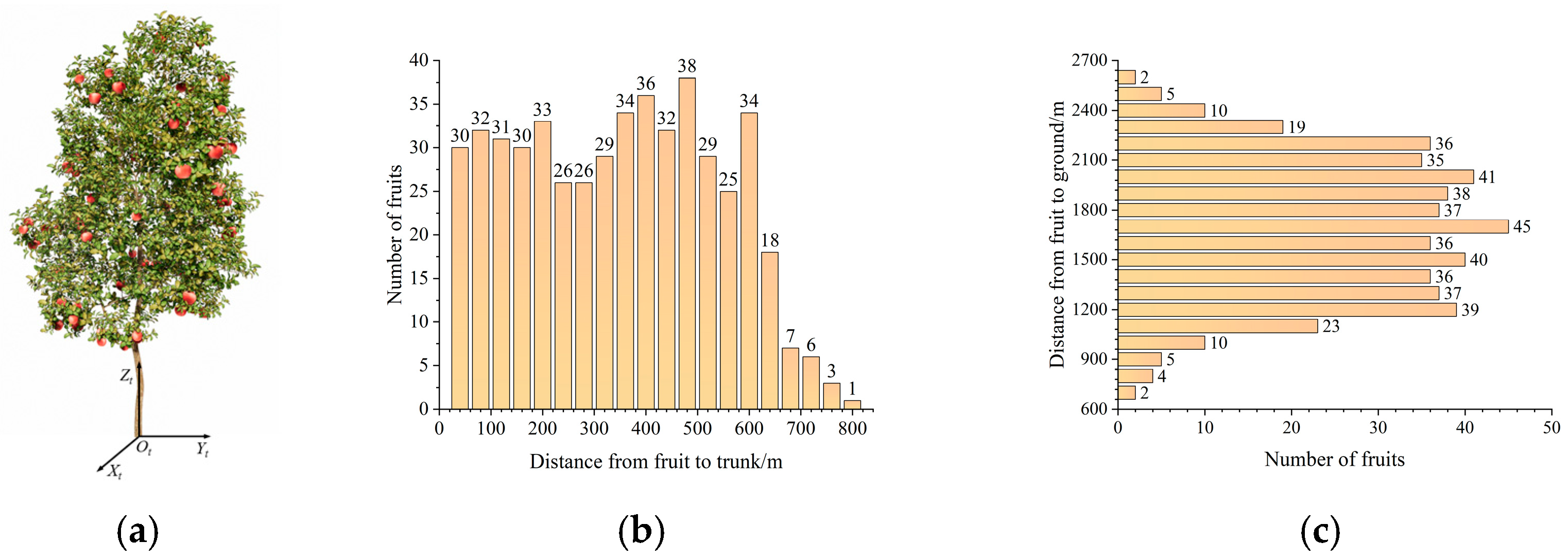
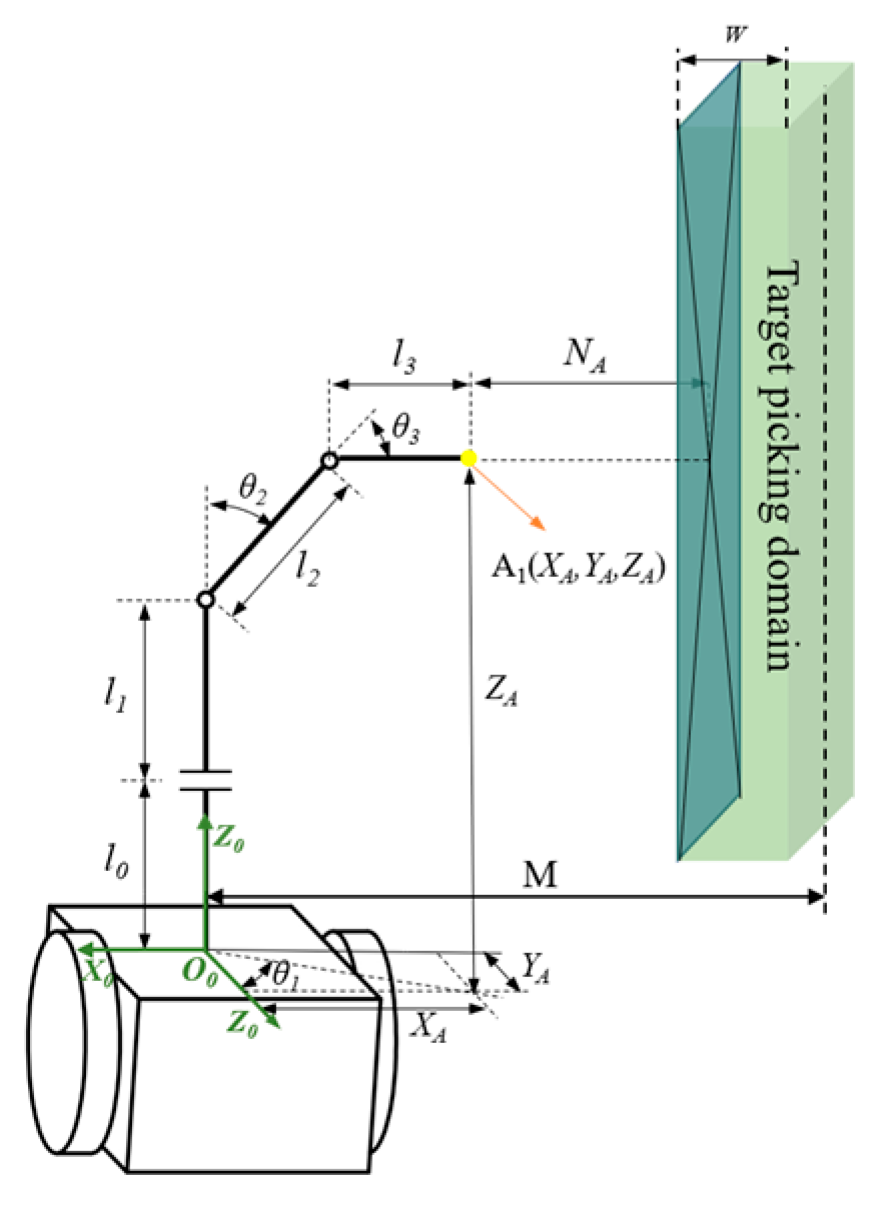
2.1.1. Fruit Distribution Characteristics and Single-Domain Picking Base Point Positioning
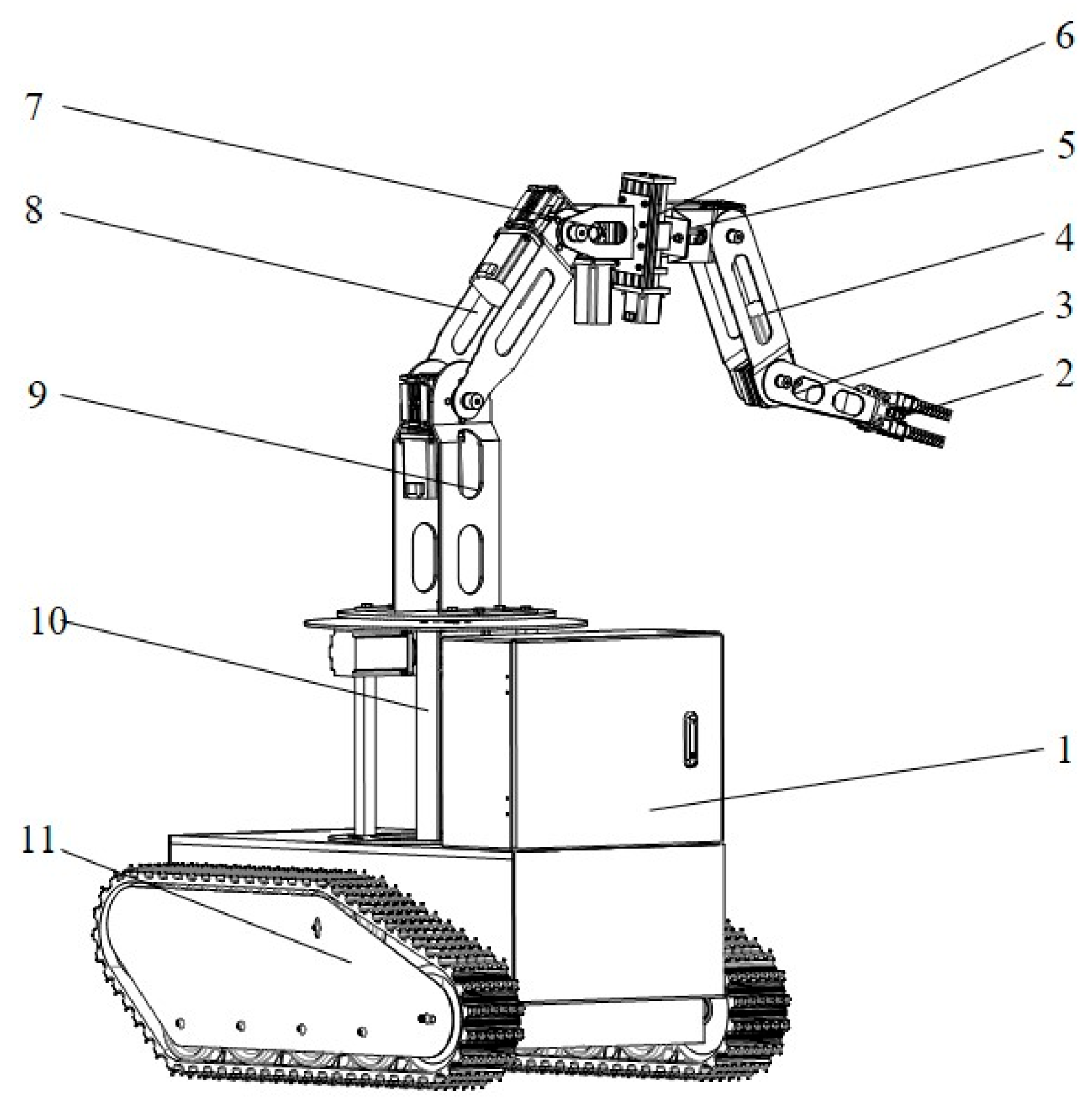
2.1.2. Machine Structure
2.1.3. Working Principle
2.2. Key Component Design
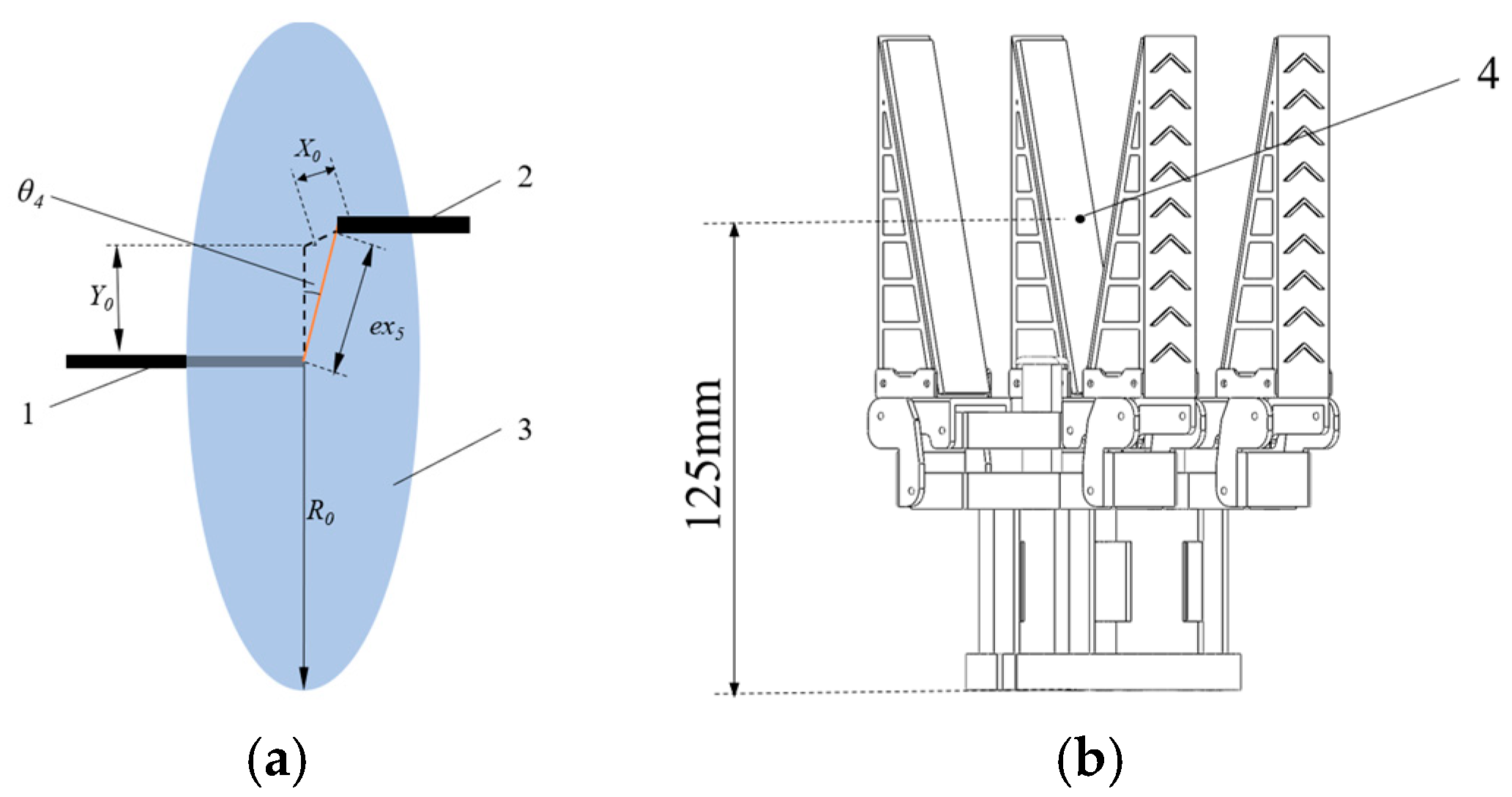
2.2.1. Harvesting Reference Point Positioning Mechanism
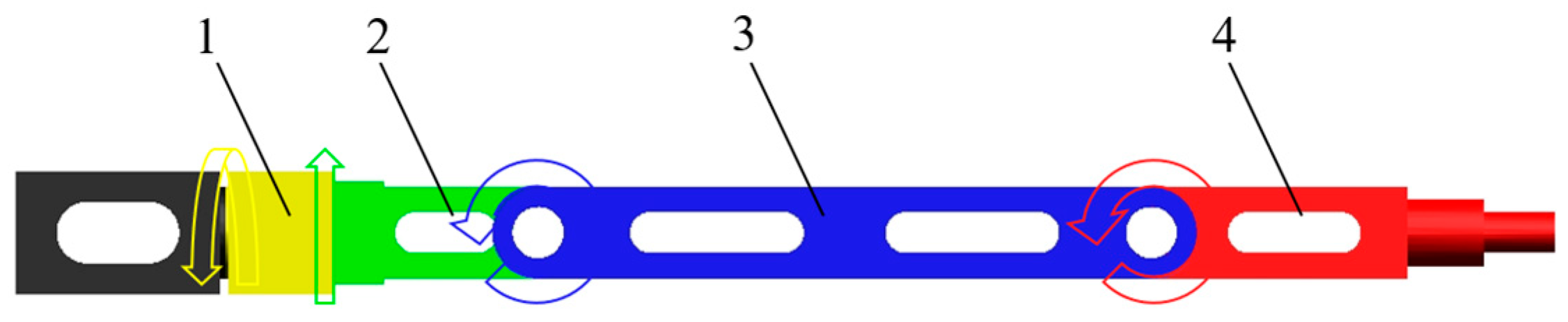
2.2.2. Fruit-Picking Mechanism
2.3. Forward Kinematics Model of Picking Device
2.4. Control System Design
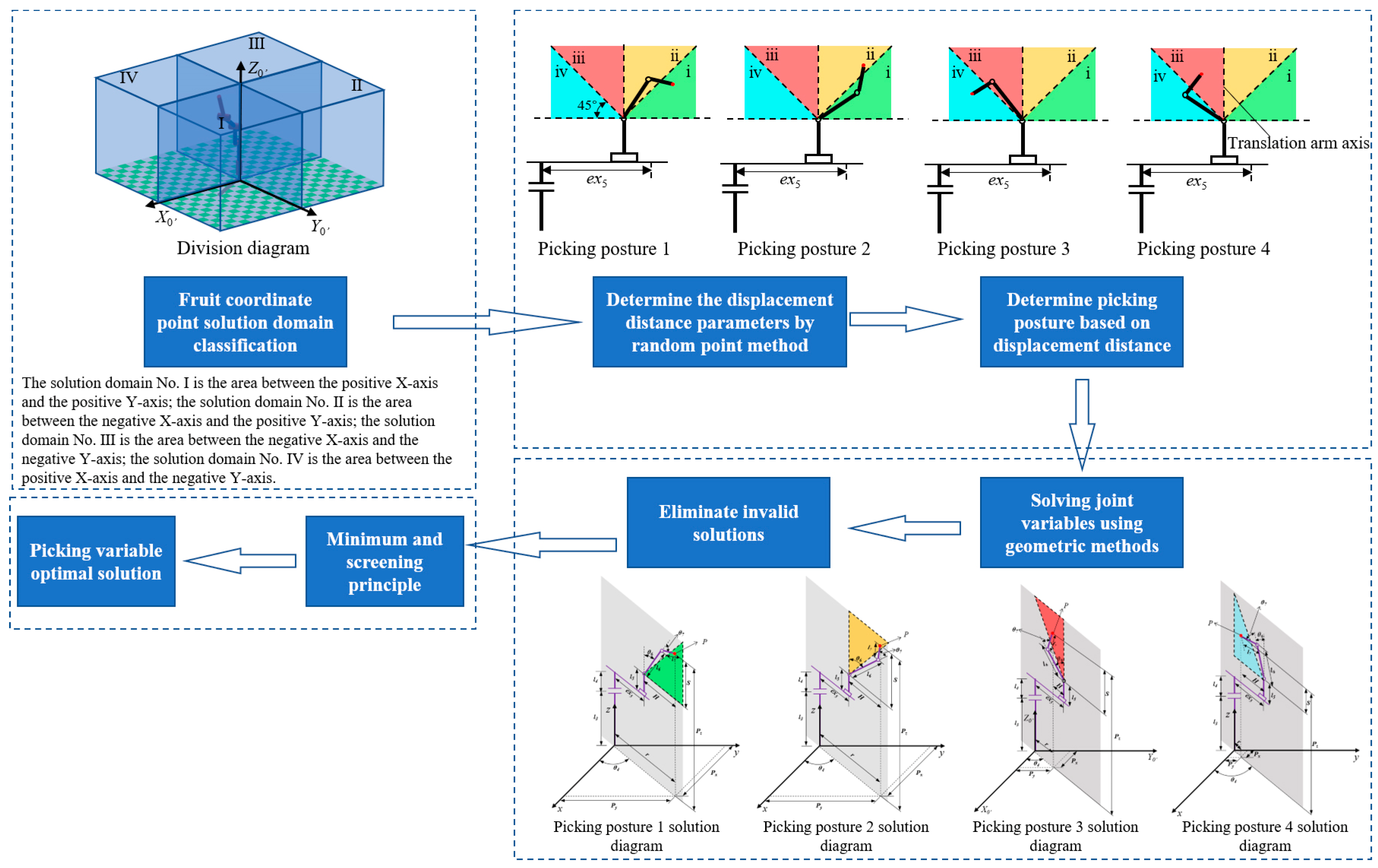
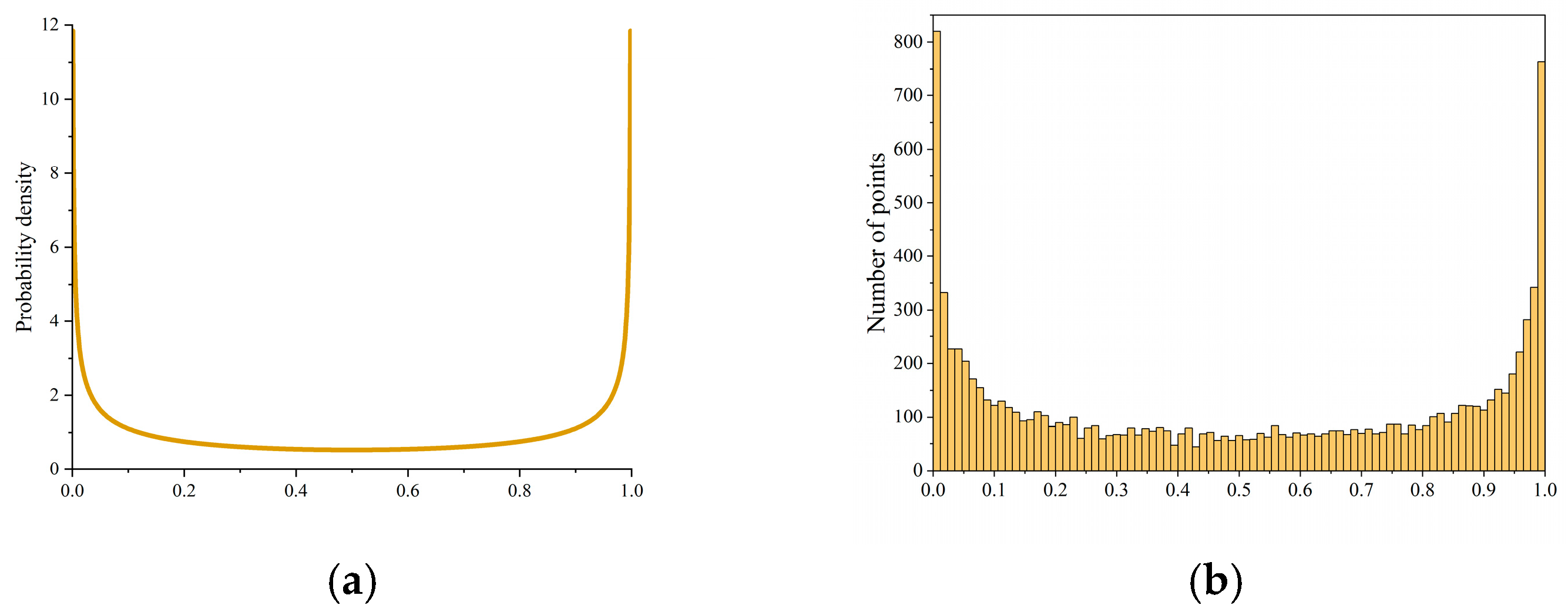
2.4.1. Inverse Kinematics Model Based on Random Point-Geometry Fusion Method
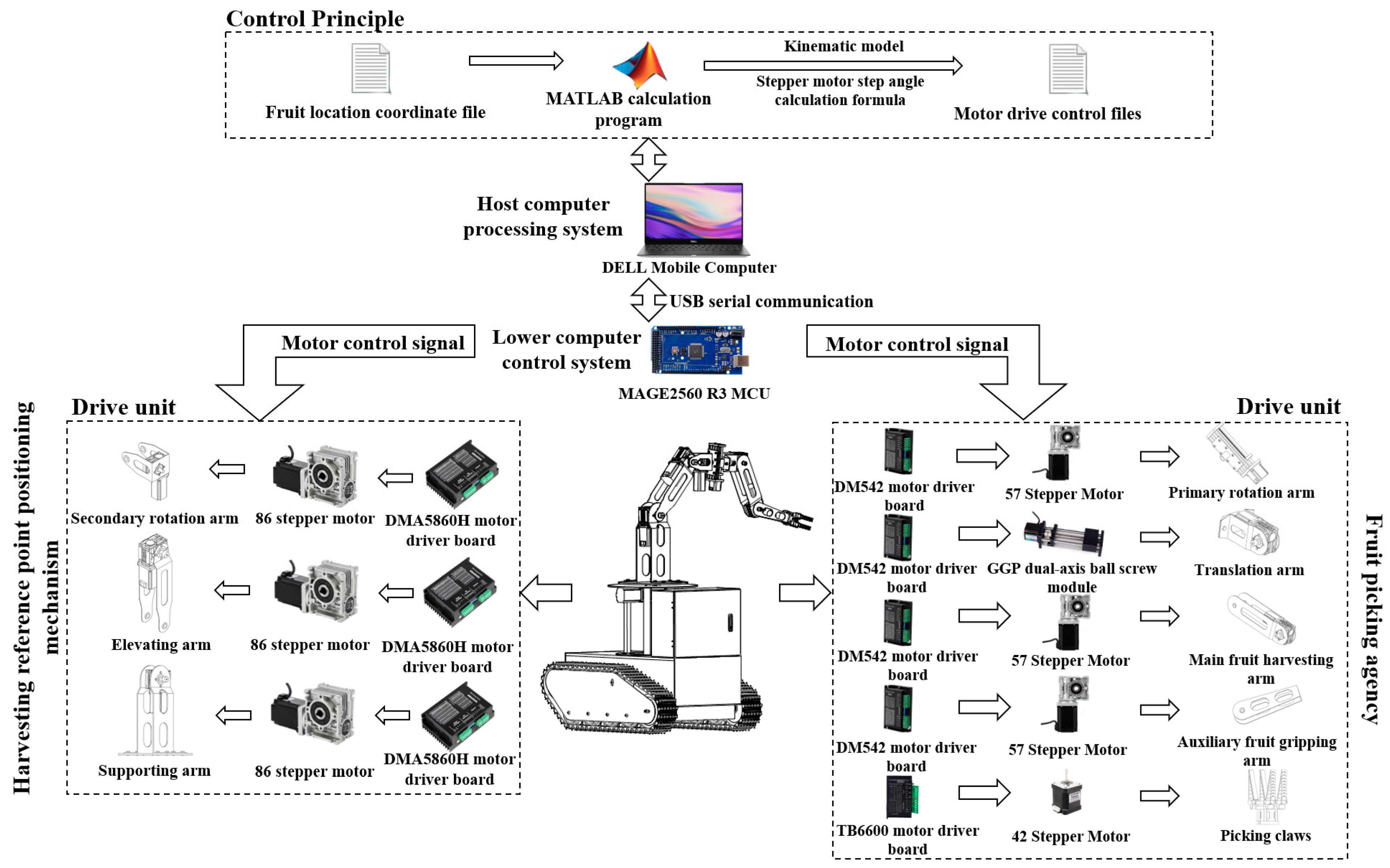
2.4.2. Control System
2.5. Picking Device Performance and Simulation Test
2.5.1. Tilt-Shift Structure Enhances Range Performance
2.5.2. Driving Force Distance Simulation Test
2.6. Prototype Experiment
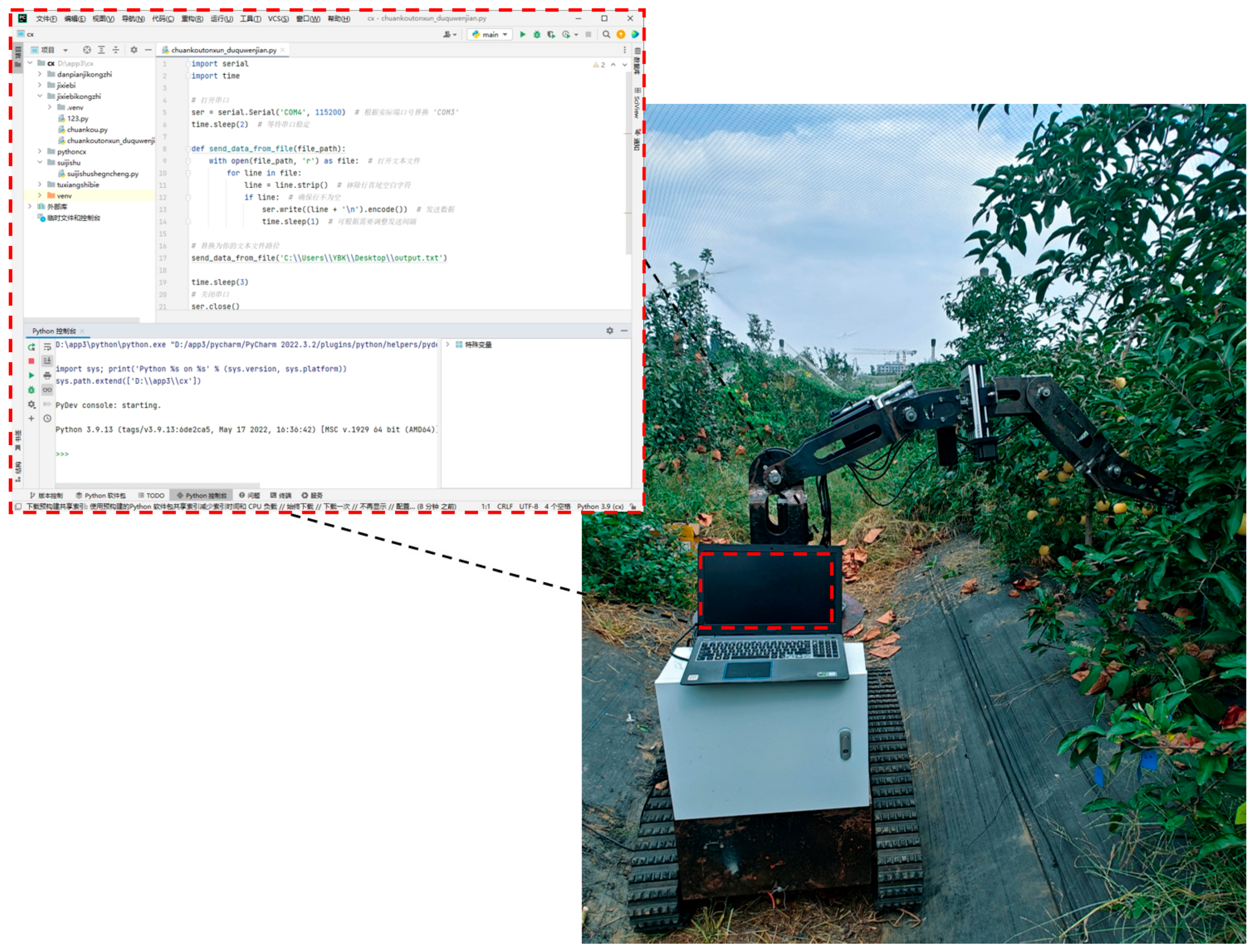
2.6.1. Experimental Instruments
2.6.2. Positioning and Fruit-Picking Reference Point Tracking Experiment
2.6.3. Harvesting Experiment
3. Results and Discussion
3.1. Simulation of Harvesting Domain Analysis
3.1.1. Analysis of Harvesting Domain Expansion Effect
3.1.2. Simulation Analysis of the Harvesting Domain
3.2. Simulation Experiment Analysis
Joint Driving Force Simulation Analysis
3.3. Prototype Experiment Results and Analysis
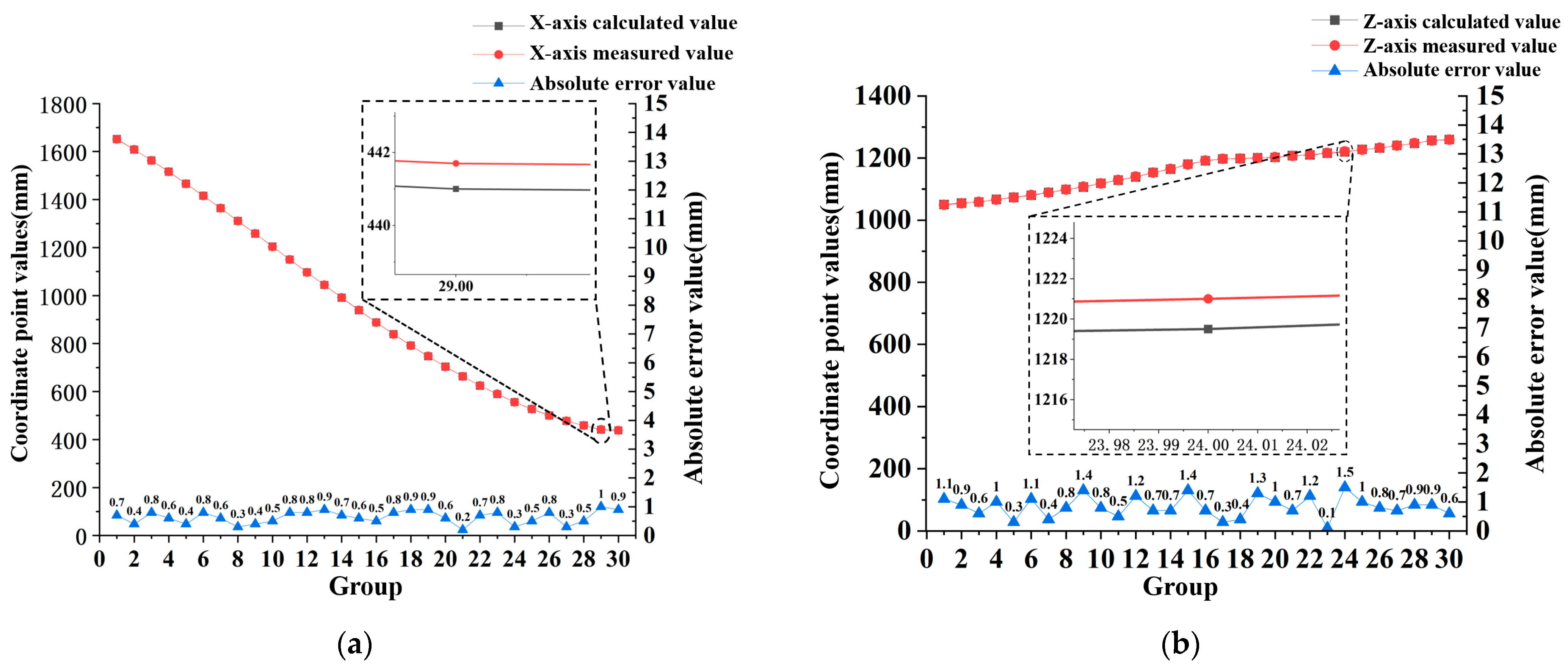
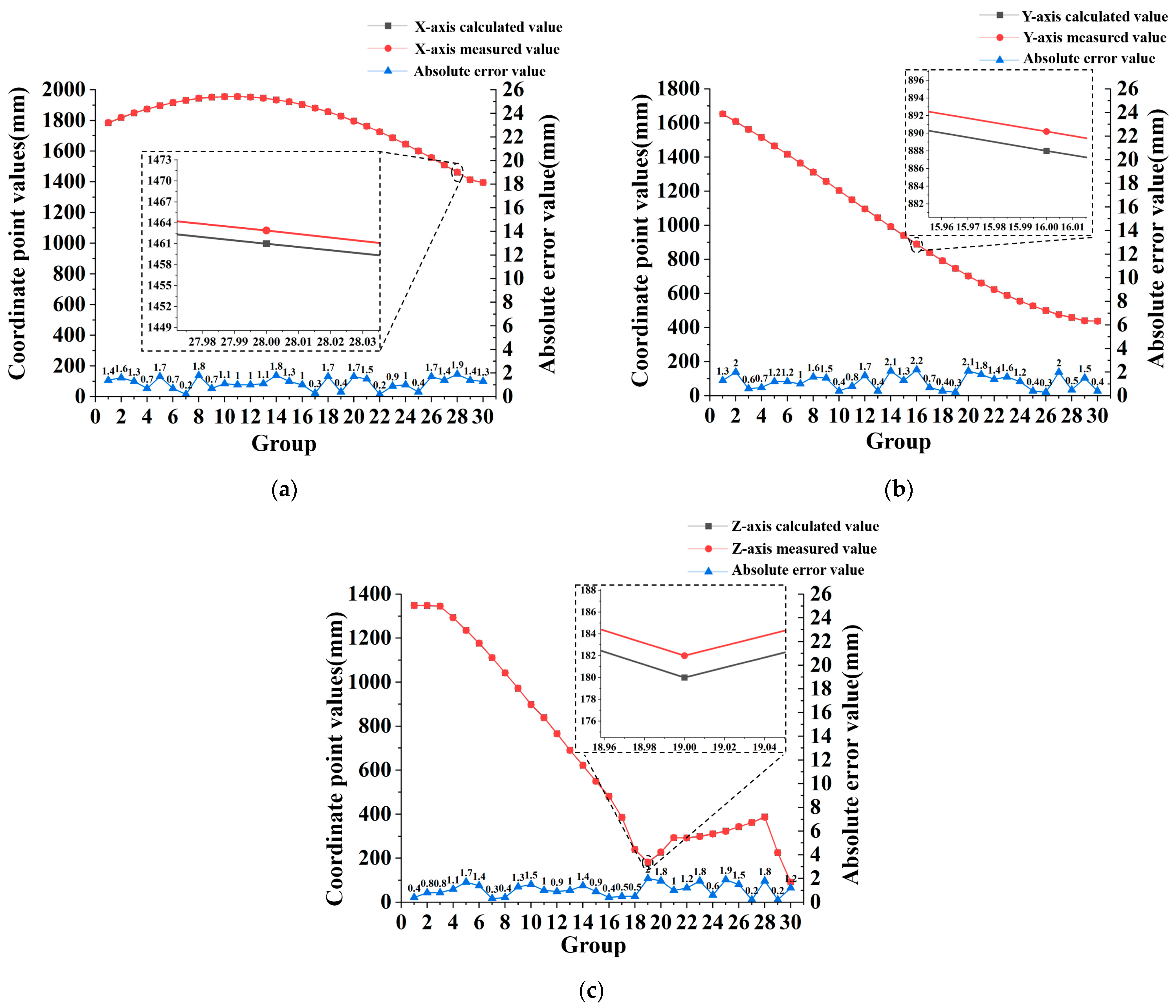
3.3.1. Position Analysis of the Localization and Fruit-Picking Reference Points
3.3.2. Fruit Picking Experiment Results Analysis
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Annual News: China’s Fruit Production Trend and Structure Data Analysis Briefing in 2024. Available online: https://baijiahao.baidu.com/s?id=1819584679956396190&wfr=spider&for=pc&searchword=%E4%B8%96%E7%95%8C%E6%B0%B4%E6%9E%9C%E6%80%BB%E4%BA%A7%E9%87%8F&sShare=2 (accessed on 5 April 2025).
- Rural Social and Economic Survey Department of National Bureau of Statistics. China Rural Statistical Yearbook; China Statistics Press: Beijing, China, 2024. [Google Scholar]
- Li, T.; Sun, J.; Huang, J.; Lu, S. Fruit quality analysis and evaluation of ‘Fuji’ apples from different producing areas. J. China Agric. Univ. 2024, 29, 23–29. [Google Scholar]
- Li, S.; Tang, X. Research, Status; Development and Analysis of Apple Picking Robot. Equip. Manuf. Technol. 2016, 1, 185–186+192. [Google Scholar]
- Cao, P.; Wang, T.; Zhai, L.; Niu, S.; Liu, L.; Shi, Y. Design of 6-DOF Tomato Picking Lifting Platform. Agriculture 2022, 12, 1945. [Google Scholar] [CrossRef]
- Li, W.; Yin, H.; Li, Y.; Liu, X.; Liu, J.; Wang, H. Research on the Jet Distance Enhancement Device for Blueberry Harvesting Robots Based on the Dual-Ring Model. Agriculture 2024, 14, 1563. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, Y. Structural Design and Testing of a Vibrating Apple Picker. J. Inn. Mong. Agric. Univ. (Nat. Sci. Ed.) 2023, 44, 39–49. [Google Scholar] [CrossRef]
- Chen, Q.; Yin, C.; Guo, Z.; Wang, J.; Zhou, H.; Jiang, X. Current status and future development of the key technologies for apple picking robots. Trans. Chin. Soc. Agric. Eng. 2023, 39, 1–15. [Google Scholar]
- Wang, Y.; Yang, C.; Gao, Y.; Lei, Y.; Ma, L.; Qu, A. Design and Testing of an Integrated Lycium barbarum L. Harvester. Agriculture 2024, 14, 1370. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.; Yang, X.; Li, J.; Wang, P. Design and Experiment of Hand-held Shaking Branch Type Jujube Vibration Picker. Trans. Chin. Soc. Agric. Mach. 2024, 55, 194–204+215. [Google Scholar]
- Shang, S.; Li, C.; He, X.; Wang, D.; Wang, H.; Yang, S. Design and Experiment of High-acid Apple Vibrating Picker. Trans. Chin. Soc. Agric. Mach. 2023, 54, 115–125+168. [Google Scholar]
- Zhang, Z.; Igathinathane, C.; Li, J.; Cen, H.; Lu, Y.; Flores, P. Technology progress in mechanical harvest of fresh market apples. Comput. Electron. Agric. 2020, 175, 105606. [Google Scholar] [CrossRef]
- Huang, S.; Pan, K.; Wang, S.; Zhu, Y.; Zhang, Q.; Su, X.; Yu, H. Design and Test of an Automatic Navigation Fruit-Picking Platform. Agriculture 2023, 13, 882. [Google Scholar] [CrossRef]
- Luo, H.; Wei, G. System design and implementation of a novel robot for apple harvest. INMATEH-Agric. Eng. 2015, 46, 85. [Google Scholar]
- Zhang, K.; Lammers, K.; Chu, P.; Li, Z.; Lu, R. System design and control of an apple harvesting robot. Mechatronics 2021, 79, 102644. [Google Scholar] [CrossRef]
- Silwal, A.; Davidson, J.R.; Karkee, M.; Mo, C.; Zhang, Q.; Lewis, K. Design, integration, and field evaluation of a robotic apple harvester. J. Field Robot. 2017, 34, 1140–1159. [Google Scholar] [CrossRef]
- Davidson, J.R.; Hohimer, C.J.; Mo, C.; Karkee, M. Dual robot coordination for apple harvesting. In Proceedings of the 2017 ASABE Annual International Meeting, Spokane, WA, USA, 16–19 July 2017; Volume 1. [Google Scholar]
- Feng, Q.; Zhao, C.; Li, T.; Chen, L.; Guo, X.; Xie, F.; Xiong, Z.; Chen, K.; Liu, C.; Yan, T. Design and test of a four-arm apple harvesting robot. Trans. Chin. Soc. Agric. Eng. 2023, 39, 25–33. [Google Scholar]
- Xue, X.; Chen, R.; Li, F.; Yu, S.; Meng, C.; Yu, X. High-quality and high-yield technology of super-dense cultivation of dwarf apple rootstock. China Fruits 2024, 2, 101–104. [Google Scholar] [CrossRef]
- Chang, L. SE(3)based extended Kalman filter for attitude estimation. J. Chin. Inert. Technol. 2020, 28, 499–504+550. [Google Scholar] [CrossRef]
- Chang, C.-L.; Huang, C.-C. Design and lmplementation of an Al-Based Robotic Arm for Strawberry Harvesting. Agriculture 2024, 14, 2057. [Google Scholar] [CrossRef]
- Li, Z.; Fan, G.; Liang, Z.; Niu, C. Workspace analysis and experiments of orchard platform based on D-H method. Trans. Chin. Soc. Agric. Eng. 2020, 36, 25–34. [Google Scholar]
- Singh, A.; Singla, A.; Soni, S. Extension of DH parameter method to hybrid manipulators used in robot-assisted surgery. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2015, 229, 703–712. [Google Scholar] [CrossRef]
- Liang, X.; Yao, Z.; Deng, W.; Yao, J. Research on Kinematic Calibration and Inverse Solution of 6-DOF Hydraulic Manipulator. J. Mech. Eng. 2025, 61, 346–357. [Google Scholar]
- Gong, Y.; Jin, Z.; Bai, X.; Wang, S.; Wu, L.; Huang, W. Design and Experiment of Servo Control System for Sugarcane Header. Trans. Chin. Soc. Agric. Mach. 2023, 54, 119–128+138. [Google Scholar]
- Wang, C.; Li, C.; Han, Q.; Wu, F.; Zou, X. A Performance Analysis of a Litchi Picking Robot System for Actively Removing Obstructions, Using an Artificial Intelligence Algorithm. Agronomy 2023, 13, 2795. [Google Scholar] [CrossRef]
- Lou, K.; Wang, Z.; Zhang, B.; Xu, Q.; Fu, W.; Gu, Y.; Liu, J. Analysis and Experimentation on the Motion Characteristics of a Dragon Fruit Picking Robot Manipulator. Agriculture 2024, 14, 2095. [Google Scholar] [CrossRef]
- Wan, M.; Zhou, Z.; Wang, Y.; Xu, J.; Cui, Y. Design and experiment of facility elevated planting strawberry continuous picking manipulator. Comput. Electron. Agric. 2025, 228, 109703. [Google Scholar] [CrossRef]
- Kong, F.; Wang, D.; Shi, L.; Huang, H.; Xie, Q.; Wu, T.; Sun, Y.; Chen, C. Dynamic Analysis and Parameter Optimization of the Cutting System for Castor Harvester Picking Devices. Appl. Sci. 2023, 13, 2116. [Google Scholar] [CrossRef]
- Ramzy, M.R.; Hammad, S.; Maged, S.A. Kinematic and Dynamic Modeling of 3DOF Variable Stiffness Links Manipulator with Experimental Validation. Appl. Sci. 2024, 14, 5285. [Google Scholar] [CrossRef]
- GB/T5667-2008; National Agricultural Machinery Standardization Technical Committee. Agricultural Machinery Production Test Methods. China Standards Press: Beijing, China, 2009.



 ” represents a revolute joint with a rotational direction parallel to the plane of the
paper. The symbol “
” represents a revolute joint with a rotational direction parallel to the plane of the
paper. The symbol “ ” denotes a
prismatic joint with a translational direction parallel to the plane of the
paper. The symbol “
” denotes a
prismatic joint with a translational direction parallel to the plane of the
paper. The symbol “ ” also
indicates a revolute joint with a rotational direction parallel to the plane of
the paper. The symbol “
” also
indicates a revolute joint with a rotational direction parallel to the plane of
the paper. The symbol “ ” signifies
a coordinate axis perpendicular to the plane of the paper and pointing outward.
The symbol “
” signifies
a coordinate axis perpendicular to the plane of the paper and pointing outward.
The symbol “ ” represents
a coordinate axis perpendicular to the plane of the paper and pointing inward.
To simplify the forward kinematic model of the fruit-picking mechanism, a base
coordinate system O0′X0′Y0′Z0′
has been established. Additionally, to accurately determine the picking point
location, an auxiliary coordinate system O8X8Y8Z8
has been introduced.
” represents
a coordinate axis perpendicular to the plane of the paper and pointing inward.
To simplify the forward kinematic model of the fruit-picking mechanism, a base
coordinate system O0′X0′Y0′Z0′
has been established. Additionally, to accurately determine the picking point
location, an auxiliary coordinate system O8X8Y8Z8
has been introduced.
 ” represents a revolute joint with a rotational direction parallel to the plane of the
paper. The symbol “
” represents a revolute joint with a rotational direction parallel to the plane of the
paper. The symbol “ ” denotes a
prismatic joint with a translational direction parallel to the plane of the
paper. The symbol “
” denotes a
prismatic joint with a translational direction parallel to the plane of the
paper. The symbol “ ” also
indicates a revolute joint with a rotational direction parallel to the plane of
the paper. The symbol “
” also
indicates a revolute joint with a rotational direction parallel to the plane of
the paper. The symbol “ ” signifies
a coordinate axis perpendicular to the plane of the paper and pointing outward.
The symbol “
” signifies
a coordinate axis perpendicular to the plane of the paper and pointing outward.
The symbol “ ” represents
a coordinate axis perpendicular to the plane of the paper and pointing inward.
To simplify the forward kinematic model of the fruit-picking mechanism, a base
coordinate system O0′X0′Y0′Z0′
has been established. Additionally, to accurately determine the picking point
location, an auxiliary coordinate system O8X8Y8Z8
has been introduced.
” represents
a coordinate axis perpendicular to the plane of the paper and pointing inward.
To simplify the forward kinematic model of the fruit-picking mechanism, a base
coordinate system O0′X0′Y0′Z0′
has been established. Additionally, to accurately determine the picking point
location, an auxiliary coordinate system O8X8Y8Z8
has been introduced.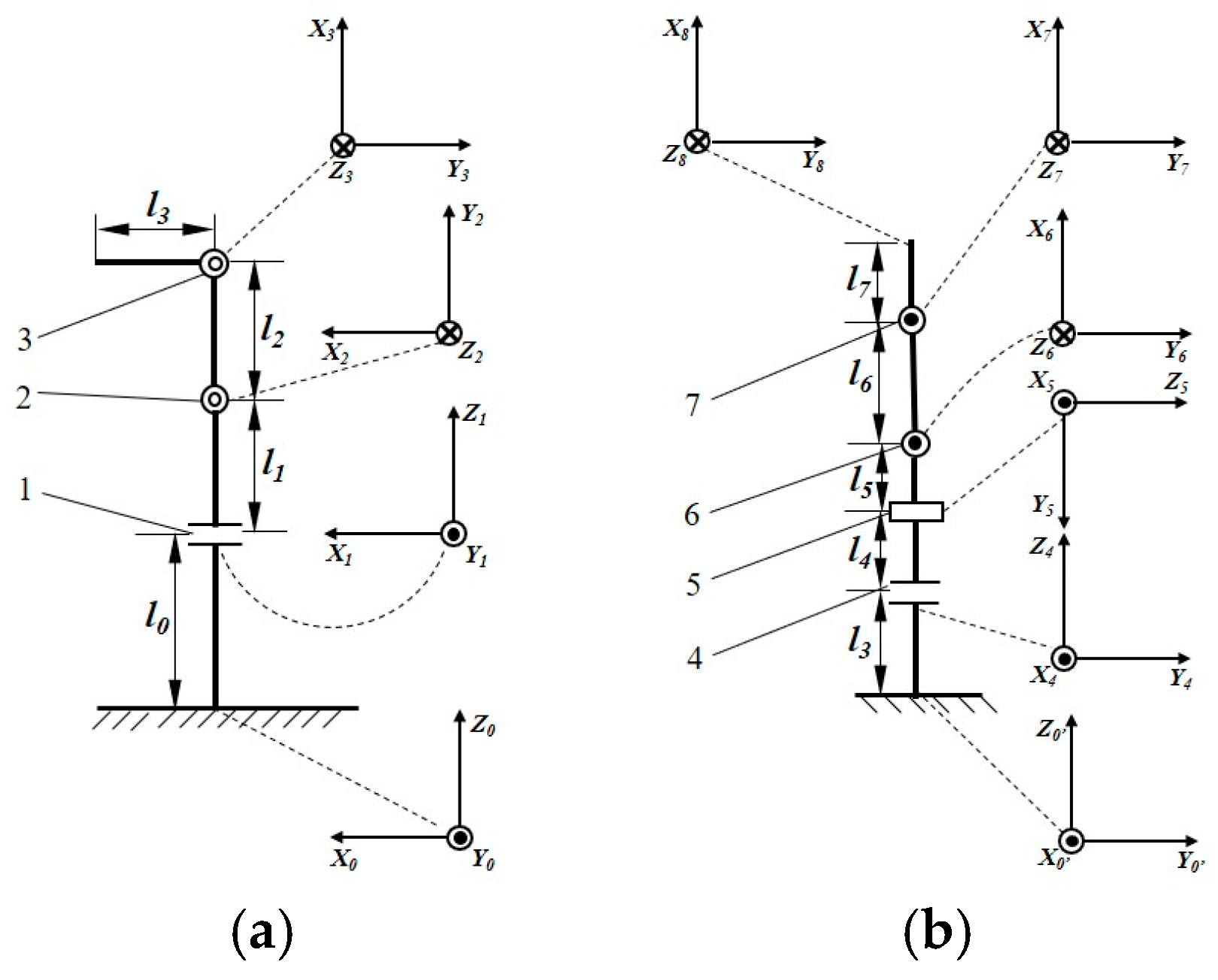




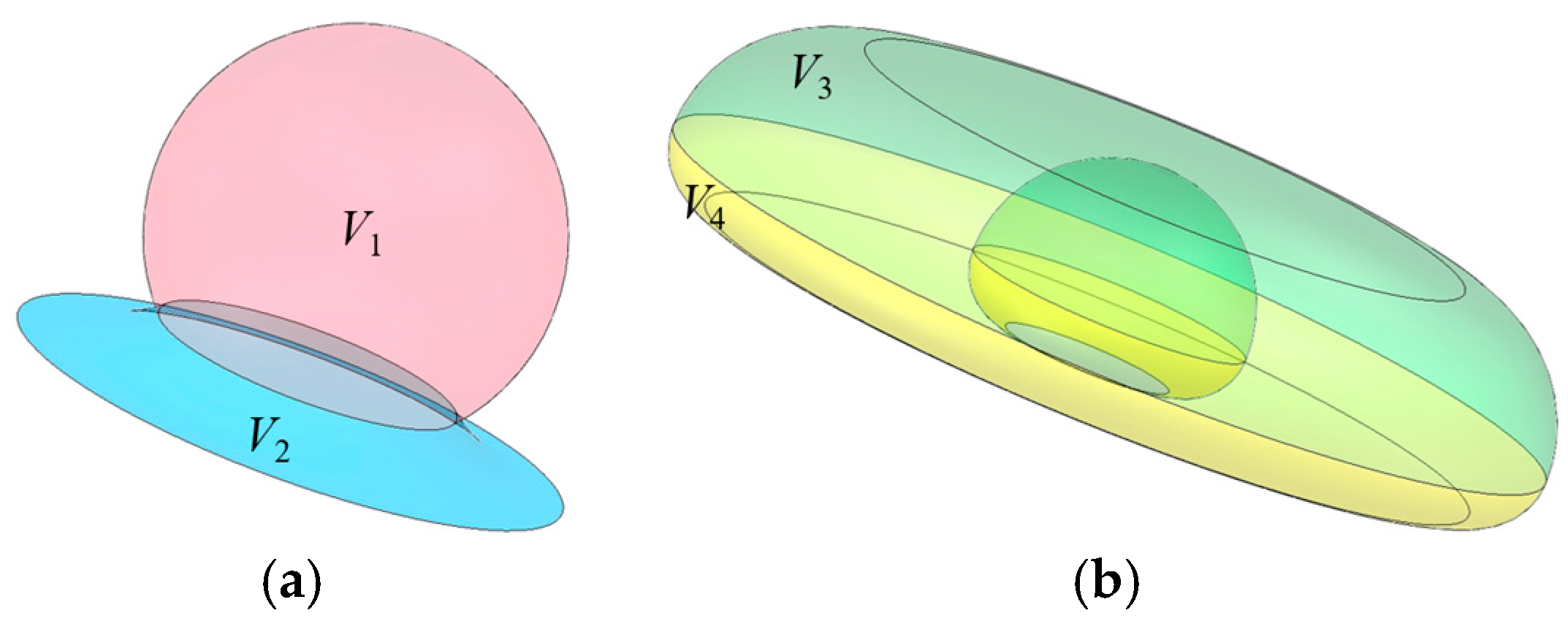
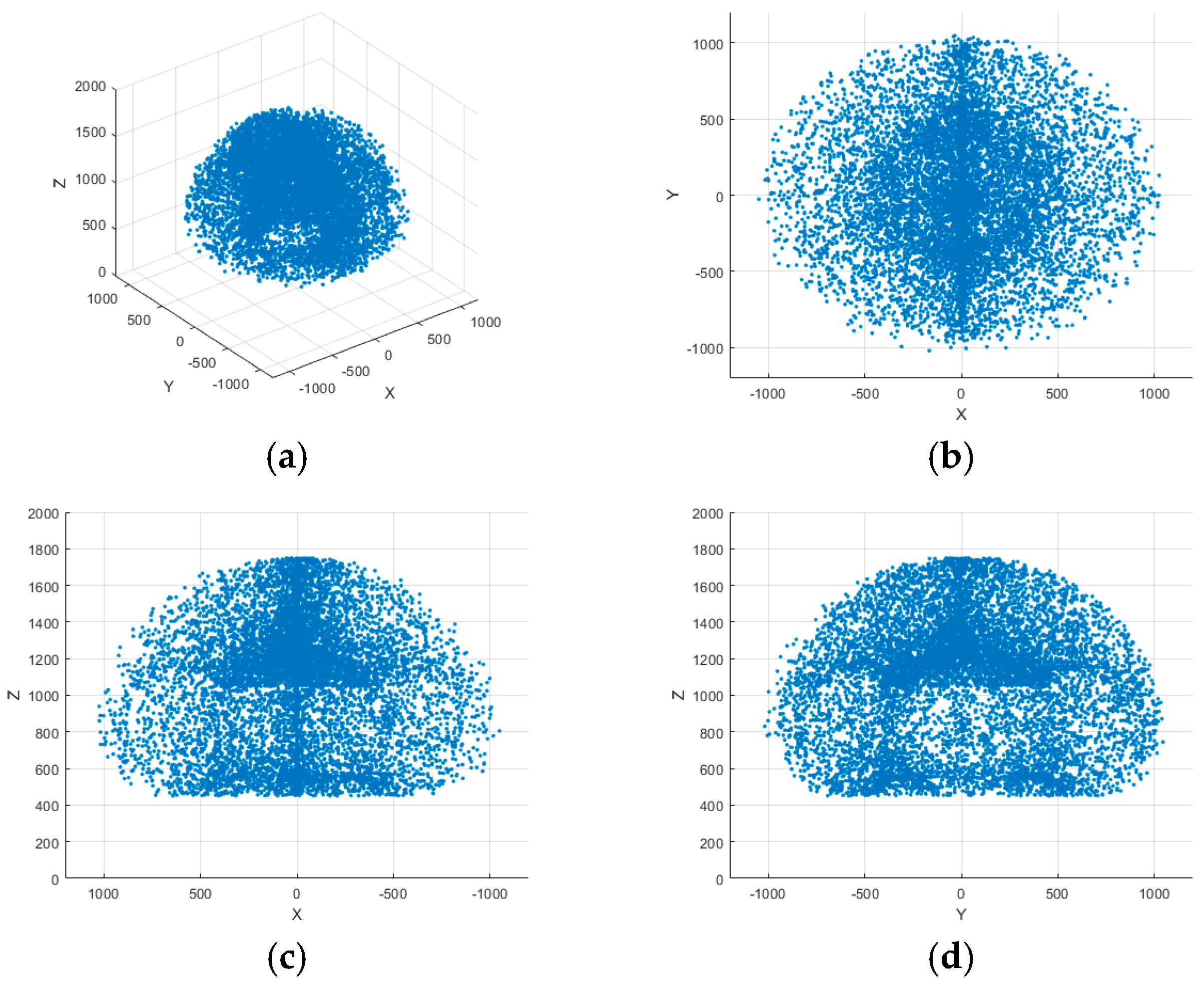



| Name | Fruit Tree Row Spacing | Plant Spacing | Fruit Tree Height | Crown Width | Crown Thickness | |
|---|---|---|---|---|---|---|
| Fruit Tree Shape | ||||||
| Spindle tree shape | 3.5~4.2 m | 1.0~1.2 m | 2.8~3.1 m | 1.0~1.5 m | 1.0~1.2 m | |
| Hedge tree shape | 3.6~4.2 m | 1.5~1.7 m | 2.7~3.2 m | 1.4~1.6 m | 0.4~0.6 m | |
| Parameter | Value |
|---|---|
| Suitable planting row spacing/m | 2.5~3.5 |
| Working height/m | 2.4 |
| Working width/m | 2.0~2.1 |
| Degrees of Freedom/piece | 7 |
| Walking speed/m·s−1 | 0.9~1.1 |
| Name | Range |
|---|---|
| primary rotation arm angle (θ4) | [−180°, 180°] |
| translation arm displacement distance (ex5) | [−100 mm, 100 mm] |
| main fruit harvesting arm angle (θ6) | [−90°, 90°] |
| auxiliary fruit gripping arm angle (θ7) | [−120°, 120°] |
| Joint Number | θi/(°) | di/mm | ai/mm | αi/(°) | Joint Range |
|---|---|---|---|---|---|
| 0 | 0 | l0 | 0 | 0 | 0 |
| 1 | θ1 | l1 | 0 | 90 | [−45°, 45°] |
| 2 | 90 + θ2 | 0 | l2 | 0 | [30°, 105°] |
| 3 | −90 + θ3 | 0 | l3 | 90 | [−60°, 60°] |
| Joint Number | θi/(°) | di/mm | ai/mm | αi/(°) | Joint Range |
|---|---|---|---|---|---|
| 3 | 0 | l3 | 0 | 0 | 0 |
| 4 | θ4 | l4 | 0 | 90 | [−180°,180°] |
| 5 | 90 | ex5 | l5 | 90 | [−100 mm,100 mm] |
| 6 | θ5 | 0 | l6 | 0 | [−30°,30°] |
| 7 | θ6 | 0 | l7 | 0 | [−120°,120°] |
| Group | Number of Successful Fruits | Picking Success Rate/% | Time for Single-Domain Picking/s | Average Time for Single Fruit Picking/s |
|---|---|---|---|---|
| 1 | 43 | 78.7 | 316.5 | 7.36 |
| 2 | 35 | 77.1 | 246 | 7.05 |
| 3 | 41 | 75.9 | 300 | 7.32 |
| 4 | 36 | 75.6 | 264 | 7.34 |
| 5 | 39 | 78.7 | 278 | 7.13 |
| 6 | 41 | 76.6 | 298.5 | 7.28 |
| 7 | 35 | 75.4 | 257 | 7.34 |
| 8 | 36 | 77.4 | 268 | 7.44 |
| 9 | 43 | 73.5 | 303.5 | 7.06 |
| 10 | 38 | 76.4 | 271 | 7.14 |
| Average value | 76.53 | 7.24 | ||
| Standard Deviation | 1.5720 | 0.1385 | ||
| Coefficient of variation | 2.06% | 1.91% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, B.; Zhang, H.; Li, Y.; Cao, X.; Sun, L.; Jing, L.; Xue, L.; Liu, C.; Fan, G.; Wang, J. Design and Experimental Evaluation of a Two-Stage Domain-Segmented Harvesting Device for Densely Planted Dwarf Apple Orchards. AgriEngineering 2025, 7, 135. https://doi.org/10.3390/agriengineering7050135
Yuan B, Zhang H, Li Y, Cao X, Sun L, Jing L, Xue L, Liu C, Fan G, Wang J. Design and Experimental Evaluation of a Two-Stage Domain-Segmented Harvesting Device for Densely Planted Dwarf Apple Orchards. AgriEngineering. 2025; 7(5):135. https://doi.org/10.3390/agriengineering7050135
Chicago/Turabian StyleYuan, Bingkun, Hongjian Zhang, Yanfang Li, Xinpeng Cao, Linlin Sun, Linlong Jing, Longzhen Xue, Chunyang Liu, Guiju Fan, and Jinxing Wang. 2025. "Design and Experimental Evaluation of a Two-Stage Domain-Segmented Harvesting Device for Densely Planted Dwarf Apple Orchards" AgriEngineering 7, no. 5: 135. https://doi.org/10.3390/agriengineering7050135
APA StyleYuan, B., Zhang, H., Li, Y., Cao, X., Sun, L., Jing, L., Xue, L., Liu, C., Fan, G., & Wang, J. (2025). Design and Experimental Evaluation of a Two-Stage Domain-Segmented Harvesting Device for Densely Planted Dwarf Apple Orchards. AgriEngineering, 7(5), 135. https://doi.org/10.3390/agriengineering7050135





