Abstract
The ear is able to detect low-level acoustic signals by a highly specialized system including a parametric amplifier in the cochlea. This is verified by a numerical mechanical model of the cochlea, which reduces the three-dimensional (3D) system to a one-dimensional (1D) approach. A formerly developed mechanical model permits the consideration of the fluid and the orthotropic basilar membrane in a 1D fluid-structure coupled system. This model shows the characteristic frequency to place transformation of the traveling wave in the cochlea. The additional inclusion of time and space dependent stiffness of outer hair cells and the signal level dependent stiffness of the string enables parametric amplification of the input signal. Due to the nonlinear outer hair cell stiffness change, nonlinear distortions follow as a byproduct of the parametric amplification at low levels constituting the compressive nonlinearity. More distortions are generated by the saturating displacements of the string at high input levels, which can be distinguished from the low-level distortions by the order of additional harmonics. Amplification factors of and are calculated, and a change of the traveling-wave mapping is postulated with parametric amplification representing the healthy state of the cochlea.
1. Introduction
The hearing system, including the cochlea of the inner ear, has the ability to detect low level acoustic signals in the subnanometer range to enable efficient and sensitive communication. This extraordinary feature is induced by a highly specialized mechano-electrical system transforming air-guided sound to vibrations along the basilar membrane (BM) surrounded by waterlike fluid. It is accepted that traveling waves in the mammalian cochlea show a frequency to place mapping, in the sense that the place of maximum displacement along the BM depends on the frequency of the stapes movement. This work confirms that statement and extends it by including small axial nonlinear stiffness changes of outer hair cells (OHC), with the effect of parametric amplification and a place shift of maximum BM displacement during propagation of the traveling wave. The concept of parametric traveling-wave amplification was predicted considering strings [1] and electric network circuits [2]. Furthermore, it was shown in the theory of nonlinear oscillations that two harmonic forces with circular frequencies and will produce additional components which contain not only these circular frequencies but combination tones with multiple and also subharmonic frequencies [3,4].
The cochlear model presented is a 1D approach of the fluid-structure coupled mechanics formulated by a partial differential equation (PDE) in time and one-space dimension. The solution of the PDE is executed by a finite difference scheme including a loss term in a damped wave equation. Another nonlinear term, standing for the restoring force, which increases with the cube of displacements, becomes relevant for large displacements. Recently similar approaches for strings with viscoelastic foundations [5] and formerly with hydrodynamic bearings have been presented [6,7].
2. Methods
2.1. Partial Differential Equation (Parametric Traveling-Wave Amplifier)
To prove the effect of parametric amplification (PA) of acoustic signals for increasing the hearing sensitivity of the cochlea, we study a 1D cochlear mechanical model in the form of a partial differential equation based on a former passive approach [8]. The reduction of dimensionality from 3D to 1D or 2D involves various limitations. One of these is the impossibility to calculate sound wave reflections at rigid walls or walls having limited mechanical impedance values. Even more important is the inability to simulate the 3D field generated by the superposition of propagating sound waves in a complex fluid-filled geometry, like the cochlea, including the coupling to the elastic BM. An alternative hypothesis of a 2D approach relies on the same assumption of a 1D model concerning the structure (BM), namely, representing the orthotropic elastic shell (BM) as a 1D embedded elastic beam. Therefore, boundary layers and interactions of 3D sound fields cannot be calculated properly as well. The derivation of the PDE for the traveling-wave amplifier in the cochlea is based on a structural cochlear model which reduces the 3D geometry to a 1D approach, representing the BM as an elastic embedded beam [8] (Figure 1 and Figure 2). The fluid structure coupling relies on the assumption that the BM displacement is equal to the fluid (volume) velocity gradient in the longitudinal direction of the cochlea. The 3D box-model of the uncoiled cochlea includes the fluid (perilymph) filled Scala vestibuli (S.v.) and Scala tympani (S.t.). The Scala media is disregarded in a first approach. For simplification, the bending stiffness of the resulting elastic embedded beam (Figure 2) is neglected and Equation (1)—similar to an equation describing the transverse displacements of a string—is developed. If the effects of the longitudinal BM coupling and the inertial forces caused by the low BM mass compared to the fluid mass are neglected, Equation (1) obtains the pressure results. The displacement is a function of space and time.
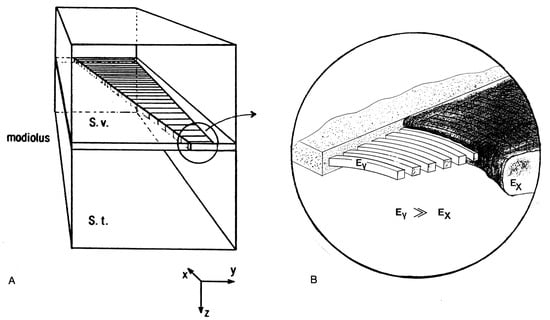
Figure 1.
Box model of the human cochlea (A). The upper front area (representing the oval window attaching the Scala vestibuli (S.v.)) is excited by a sinusoidal velocity with the frequency 2 kHz and amplitude 1 nm/s. The magnified view of the basilar membrane (BM) (B) illustrates the orthotropic consistency of the BM with collagen containing stiff transverse fibers with Young’s modulus embedded into softer elastic tissue .
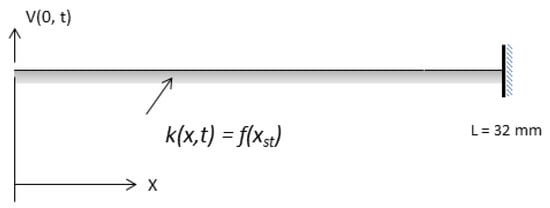
Figure 2.
Elastic string representing the BM with nonlinear stiffness , produced by outer hair cells (OHC) in the cochlea.
Though known physical damping mechanisms such as boundary layer damping [9,10] are relevant in the cochlea, an overall standard viscous damping term is included in PDE (2). Furthermore, a time and space dependent Young’s modulus change , representing the stiffness change by OHC along the BM, is included in (2). With the so far mentioned physical portions, an unlimited increase of displacements would result with increasing input signal amplitude. A displacement limiting cubic nonlinear term , considering the stiffening of a string with increasing displacement amplitude, is added. The cubic term assures the increasing restoring force for positive and negative displacements of the string representing the BM. Therefore, the transversal displacements cannot grow beyond all limits as in the unphysiological linear case.
The equations so far are noted in the time domain without the restriction of the stationarity of input signals. Multifrequency and transient stimulations, as used in otological diagnostics, can be utilized and associated BM displacements are calculated. Table 1 summarizes the geometric and physical parameters of the 1D cochlear model.

Table 1.
Physical parameters constituting the 1D cochlear model with parametric amplification.
Equation (2) is solved for the BM from 0 mm to mm. The width of the BM increases linearly from mm at the base of the cochlea to mm at the helicotrema. If a constant value mm is assumed, Equation (1) reduces to the standard wave equation with constant coefficients describing the propagation of displacements with the velocity
2.2. Finite Difference Scheme (Damped Wave Equation)
Equation (2) is solved by applying an explicit finite difference scheme (3) according to those presented in [11].
The terms are time independent but space variable-normed BM width factors. The normed damping constant of dimension is . Further abbreviations are
with i, denoting space and time indices, respectively. The resolution in space is mm/200 = 0.16 mm; and in time μs. All results are evaluated 100 ms after onset, according to time steps. The average calculation time is 30 minutes using a Z800 Workstation (Hewlett Packard, Palo Alto, CA, USA) equipped with 160 GByte RAM.
2.3. Nonlinear Stiffness Function of Outer Hair Cells
We assume that nonlinear stiffness changes of OHC cause time dependent variations of the Young’s modulus and the generation of nonlinear distortions and parametric amplification in the cochlea. For a derivation, we follow the assumption that the nonlinear BM motion is due to the nonlinear growth function of the OHC membrane potential [12]. The outer hair cell membrane potential is fitted by the second-order Boltzmann function
is the peak-to-peak value and is the membrane potential for maximum hyperpolarization. The constants and , and displacements and , are determined by the Levenberg–Marquardt algorithm, respectively, and is the product of the Boltzmann-constant k and the temperature T (Table 2). In the next step, the somatic axial stiffness of an OHC as a function of the membrane potential is derived. This is impossible for the in vivo case, and therefore experimental results of isolated OHCs are used [13,14]. Applying again the Levenberg–Marquardt algorithm to fit experimental data of OHC stiffness measurements, a stiffness function is obtained
with constants , and —the constant OHC stiffness is developed (Table 2). The nonlinear Equations (4) and (5) describe the axial somatic stiffness change in dependence of the OHC stereocilia bundle displacements . The stiffness multiplied by a factor is inserted into Equation (3) and corresponds to a velocity change and Young’s modulus change in Equation (2). The factor was optimised by numerical experiments before an instability (unlimited growth) of displacements occured. The equivalent acoustic velocity change according to the nonlinear stiffness of OHC is 1.7 m s, and therefore, a small amount of the undisturbed velocity which is ms.

Table 2.
Electrical and mechanical parameters constituting the parametric amplification by outer hair cells.
3. Results
The input signal is the time-dependent displacement at mm, with nm representing the displacement amplitude of the oval window at the base of the cochlea. The solution of Equation (2) is evaluated by the finite-difference scheme (3). We study six cases and present four of them, which are collected in Table 3 using a switched sinusoidal signal of frequency 2 kHz and two input amplitudes 1 nm and 100 nm, respectively.

Table 3.
Passive and active cases with 40 dB input level difference.
Initially the linear passive case with the constant Young’s modulus is presented in space (Figure 3) after 100 ms and frequency (Figure 5) at a basal location (6.4 mm) or n = 40 with = 1 nm stimulating displacement amplitude. The maximum displacement is located basally, and the output frequency remains the input frequency because of the linearity of the system. In case of parametric amplification by the time and space dependent Young’s modulus, the amplitude of BM displacement increases to 18.8 nm and the place of maximum displacement shifts to the center of the BM length at 16 mm or (Figure 4). This increase corresponds to a BM displacement amplification of 15.53 dB, evaluated by the fraction of the maximum displacement at half of the BM length with parametric amplification to the maximum at the more basal place 6.4 mm (n = 40) in the passive case. Figure 6 shows the corresponding frequency spectrum for the active case. The examples considered so far would lead to an unlimited increase of displacements.
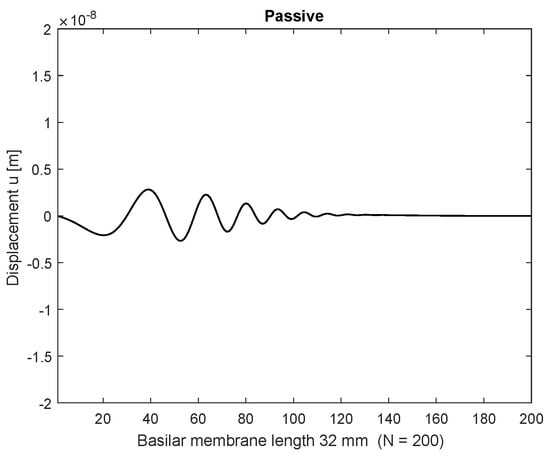
Figure 3.
Displacements along the BM with stimulation frequency 2000 Hz at the base (passive), stimulation amplitude nm.
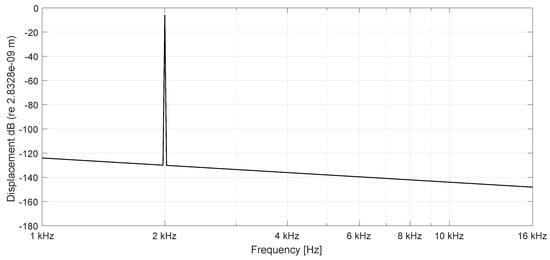
Figure 5.
Spectrum of BM displacement at 6.4 mm (n = 40) stimulation frequency 2000 Hz (passive), stimulation amplitude nm.
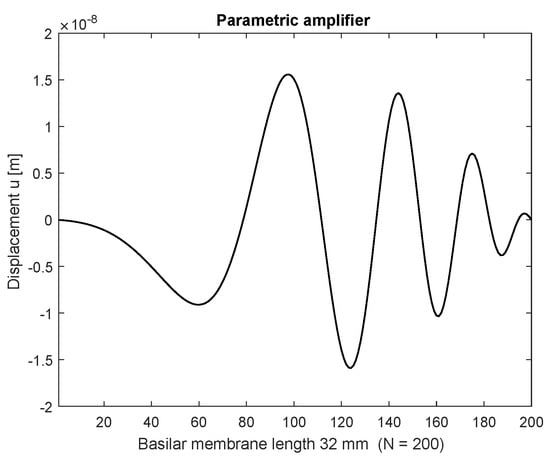
Figure 4.
Displacements with stimulation frequency 2000 Hz (parametric amplified), stimulation amplitude nm. Nonlinear distortions are generated by the OHC nonlinear stiffness function.
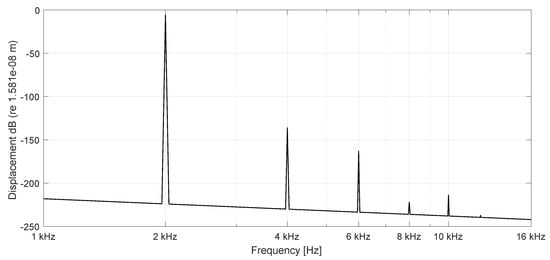
Figure 6.
Spectrum of BM displacements at 16 mm (n = 100) stimulation frequency 2000 Hz (active), stimulation amplitude nm.
Therefore, the cubic term in Equations (2) and (3) representing the nonlinear increase of the restoring force with increasing displacement is included. The passive case in Figure 7 shows the spectrum of displacements at the base (6.4 mm) of the BM with a higher stimulating amplitude of nm. The odd harmonics are the distortion components of a string, limited in its vibration amplitude by a geometrical nonlinearity caused by an increased stiffness with increasing displacement amplitudes. Figure 8 presents displacements of the healthy cochlea with parametric amplification and an increase of displacements by 23.97 dB compared to the passive case. It even shows odd harmonics, caused by the nonlinear OHC stiffness and the saturating displacements induced by the stiffening of the nonlinear string (BM).
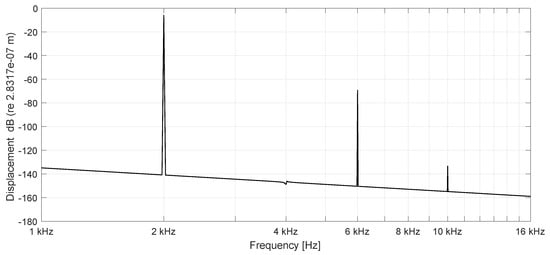
Figure 7.
Spectrum of BM displacements at 6.4 mm (n = 40) stimulation frequency 2000 Hz (passive), stimulation amplitude nm. Nonlinear distortions are generated by the cubic nonlinearity of the string.
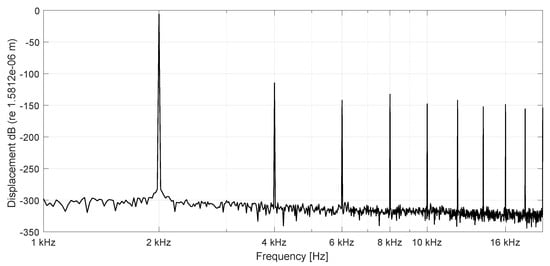
Figure 8.
Spectrum of BM displacements at 16 mm (n = 100) stimulation frequency 2000 Hz (active), stimulation amplitude nm. Nonlinear distortions are generated by the OHC stiffness functions and the saturating cubic nonlinearity of the string.
4. Discussion and Conclusions
The BM represented as a string vibrates with the characteristics of a traveling wave, namely, the frequency to characteristic place transformation. A main result of this work is the dependence of this transformation by the time-varying Young’s modulus, causing parametric amplification (PA). The numerical examples prove the effect of PA in a 1D mechanical–mathematical model of the cochlea. Therefore, the frequency to place-map is largely dependent on the PA demonstrated by the difference in Figure 3 and Figure 4, which are supplied by input signals of identical amplitude and frequency. The amplification of 15.53 dB for the low level case; 24.0 dB for the high level case; and the place shift of maximum displacement along the BM with the same input frequency, corresponds to experimental data from the squirrel monkey [15]. The PA is achieved by changing the axial stiffness of OHC represented by the Young’s modulus change . In contrast to former approaches of PA applied to the cochlea [16], where the OHC contraction is in common mode with the input signal frequency and also constant in space, the stiffness is time and space dependent according to arbitrary and variable BM displacements. Another work includes the PA by outer hair cells, but reduces it to one location along the BM without considering traveling waves [17]. Therefore, the inclusion of a signal-dependent stiffness change along the space coordinate is a main advantage to former approaches. For higher input levels, geometric nonlinearities of the cells of the organ of Corti become relevant [18] and saturate the displacements leading to the limitation of BM displacements by geometrical nonlinearities. For simplicity, these saturation mechanisms are represented by a cubic nonlinearity of the transversal vibrations of a string neglecting bending stiffness and longitudinal deformations in the present work.
A comparison of the results with experimental data is merely possible fractionally. The fact of the frequency-dependent maximum BM displacements is fulfilled by displacements shown in Figure 3 (passive) and Figure 4 (active). They show the maximum displacements in the medial part of the string, or BM as it was measured by von Békésy in human temporal bones [19]. The shift of BM displacement amplitudes from the active (in vivo) case to the passive (dead) case is observable in Figure 3 and Figure 4. The experimental validation of this progression is given by the data of Rhode et al. (1974). In Figure 3 of this work [15], the ratio of basilar membrane displacement/malleus displacement is presented log-scaled (amplitude and frequency). At the frequency kHz, which should correspond to the frequency kHz in this work, an amplitude decrease of 20 dB is found from the active in vivo case to the passive (1 h after death) case. This measurement was conducted at one place and it is impossible to measure BM displacements at many places simultaneously, as it is possible in numerical models of the organ. Nonetheless, the experiments confirm the place shift of the maximum BM displacement along the cochlea to the base (direction of the stapes) without the parametric amplification of OHC (passive case). Therefore, the in vivo activity shifts the maximum BM displacement to the apex (direction of the helicotrema), as can be seen in Figure 3 and Figure 4 of this work.
Another comparison with experimental data could be conducted with measured otoacoustic emissions (OAE) e.g., distortion product otoacoustic emissions (DPOAE), applying two tones with a frequency ratio of e.g., and different levels of primary tones at the base of the string. However, a comparison with measured DPOAE requires a three-dimensional (3D) mechanical mathematical model of the cochlea because the generator of the DPOAE, which is the nonlinear stiffness of OHC, leads to high frequency mechanical waves in the surrounding fluid. These waves interfere and are measurable with a sensor in the cochlea [20] or in the ear canal [21]. As the fluid is not modeled as a dimensional continuum yet, it is not possible to evaluate the interfering components and produce realistic signals to be comparable with measured OAE.
Nevertheless, it is shown that the inclusion of small stiffness changes of the BM enables a parametric amplification of acoustic signals caused by nonlinear distortions at low levels in a 1D model of cochlear mechanics. Though nonlinear cochlear preprocessing has been proposed before [22,23], these physical concepts did not include the PA and therefore the level dependent BM displacements did not show frequency-dependent shifts along the BM to be inferred from PA.
The PA causes nonlinear distortions, measurable as OAE propagating inside the cochlea which are emitted into the ear canal. An evaluation of OAE requires a 3D model of the cochlea to be presented in a future work. These simulations will include the 3D wave propagation in the fluid and the active BM with nonlinear OHC functions introduced by time and space variable Young’s moduli of the solid or BM. This approach will prove the concept of PA and will enable the calculation of OAE, which are by-products of the cochlear amplifier, which has been evolved to increase the hearing sensitivity.
Funding
This research received no external funding.
Acknowledgments
All calculations were executed using MATLAB R2016b.
Conflicts of Interest
The author declares no conflict of interest.
References
- Melde, F. Über die Erregung stehender Wellen eines fadenförmigen Körpers [On the excitation of standing waves on a string]. Annalen der Physik und Chemie (Ser. 2) 1859, 109, 193–215. [Google Scholar]
- Cullen, A.L. Theory of the travelling-wave parametric amplifier. Proc. IEE-Part B 1959, 107, 101–107. [Google Scholar] [CrossRef][Green Version]
- Morse, P.M.; Ingard, K.U. Theoretical Acoustics; Princeton University Press: Princeton, NJ, USA, 1986. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Pure & Applied Mathematics; John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- Cheng, X.; Blanchard, A.; Tan, C.A.; Lu, H.; Bergman, L.A.; McFarland, D.M.; Vakakis, A.F. Separation of traveling and standing waves in a finite dispersive string with partial or continuous viscoelastic foundation. J. Sound Vibr. 2017, 411, 193–209. [Google Scholar] [CrossRef]
- Tan, C.A.; Yang, B.; Mote, C.D., Jr. More On the vibration of a translating string coupled to hydrodynamic bearings. J. Vib. Acoust. 1990, 112, 337–345. [Google Scholar] [CrossRef]
- Huang, F.Y.; Mote, C.D., Jr. On the translating damping caused by a thin viscous fluid layer between a translating string and a translating rigid surface. J. Vib. Acoust. 1995, 181, 251–260. [Google Scholar] [CrossRef]
- Böhnke, F.; Janssen, T.; Steinhoff, H.-J.; Zimmermann, P. Structural Cochlear Model including the Coupling of Basilar Membrane Fibers in the Longitudinal Direction. Il Valsalva 1989, 54 (Suppl. 1), 10–16. [Google Scholar]
- Elliott, S.J. Wave propagation in a constrained fluid layer bounded by an elastic half-space and its relevance in cochlear micromechanics. J. Sound Vib. 2007, 305, 918–924. [Google Scholar] [CrossRef]
- Böhnke, F.; Semmelbauer, S. Acoustic boundary layer attenuation in ducts with rigid and elastic walls applied to cochlear mechanics. J. Fluids Eng. 2017, 139, 101202. [Google Scholar] [CrossRef]
- Najafi, H.S.; Izadi, F. Comparison of two finite-difference methods for solving the damped wave equation. Int. J. Math. Eng. Sci. 2014, 3, 35–49. [Google Scholar]
- Preyer, S.; Gummer, A.W. Nonlinearity of mechanoelectrical transduction of outer hair cells as the source of nonlinear basilar-membrane motion and loudness recruitment. Audiol. Neuro-Otol. 1996, 1, 3–11. [Google Scholar] [CrossRef]
- He, D.Z.; Dallos, P. Somatic stiffness of cochlear outer hair cells is voltage-dependent. Proc. Natl. Acad. Sci. USA 1999, 96, 8223–8228. [Google Scholar] [CrossRef]
- Deo, N.; Grosh, K. Two-State Model for Outer Hair Cell Stiffness. Biophys. J. 2004, 86, 3519–3528. [Google Scholar] [CrossRef] [PubMed]
- Rhode, W.S.; Robles, L. Evidence from Mössbauer experiments for nonlinear vibration in the cochlea. J. Acoust. Soc. Am. 1974, 55, 588–596. [Google Scholar] [CrossRef] [PubMed]
- Ko, W.; Stockie, J.M. An immersed boundary model of the cochlea with parametric forcing. SIAM J. Appl. Math. 2015, 75, 1065–1089. [Google Scholar] [CrossRef][Green Version]
- Kielczynski, P. Power amplification and selectivity in the cochlear amplifier. Arch. Acoust. 2013, 38, 83–92. [Google Scholar] [CrossRef]
- Böhnke, F.; Arnold, W. Mechanics of the Organ of Corti Caused by Deiters Cells. IEEE Trans. Biomed. Eng. 1998, 45, 1227–1233. [Google Scholar] [CrossRef] [PubMed]
- von Békésy, G. Zur Theorie des Hörens, Die Schwingungsform der Basilarmembran. Physikalische Zeitschrift 1928, 29, 793–810. [Google Scholar]
- Dong, W. Simultaneous intracochlear pressure measurements from two cochlear locations: Propagation of distortion products in gerbil. J. Assoc. Res. Otolaryngol. 2017, 18, 209–225. [Google Scholar] [CrossRef][Green Version]
- Kemp, D.T. Evidence of mechanical nonlinearity and frequency selective wave amplification in the cochlea. Arch. Otorhinolaryngol. 1979, 224, 37–45. [Google Scholar] [CrossRef]
- Zwicker, E. A hardware cochlear nonlinear preprocessing model with active feedback. J. Acoust. Soc. Am. 1986, 80, 146–153. [Google Scholar] [CrossRef]
- Verhulst, S.; Dau, T.; Shera, C.A. Nonlinear time-domain cochlear model for transient stimulation and human otoacoustic emission. J. Acoust. Soc. Am. 2012, 132, 3842–3848. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).