The Present and Future Role of Acoustic Metamaterials for Architectural and Urban Noise Mitigations
Abstract
1. Introduction
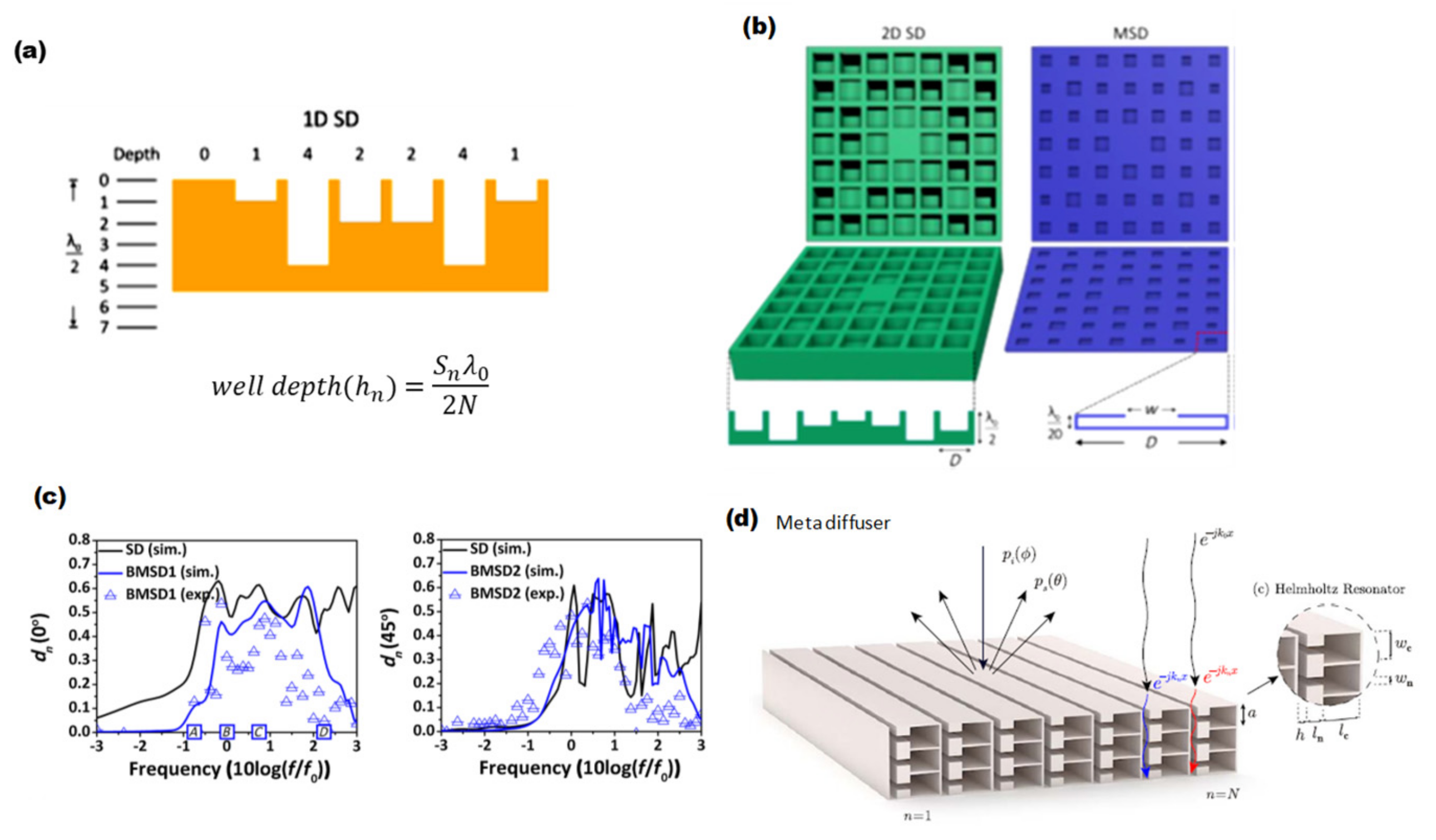
2. Applications of Acoustic Metamaterials
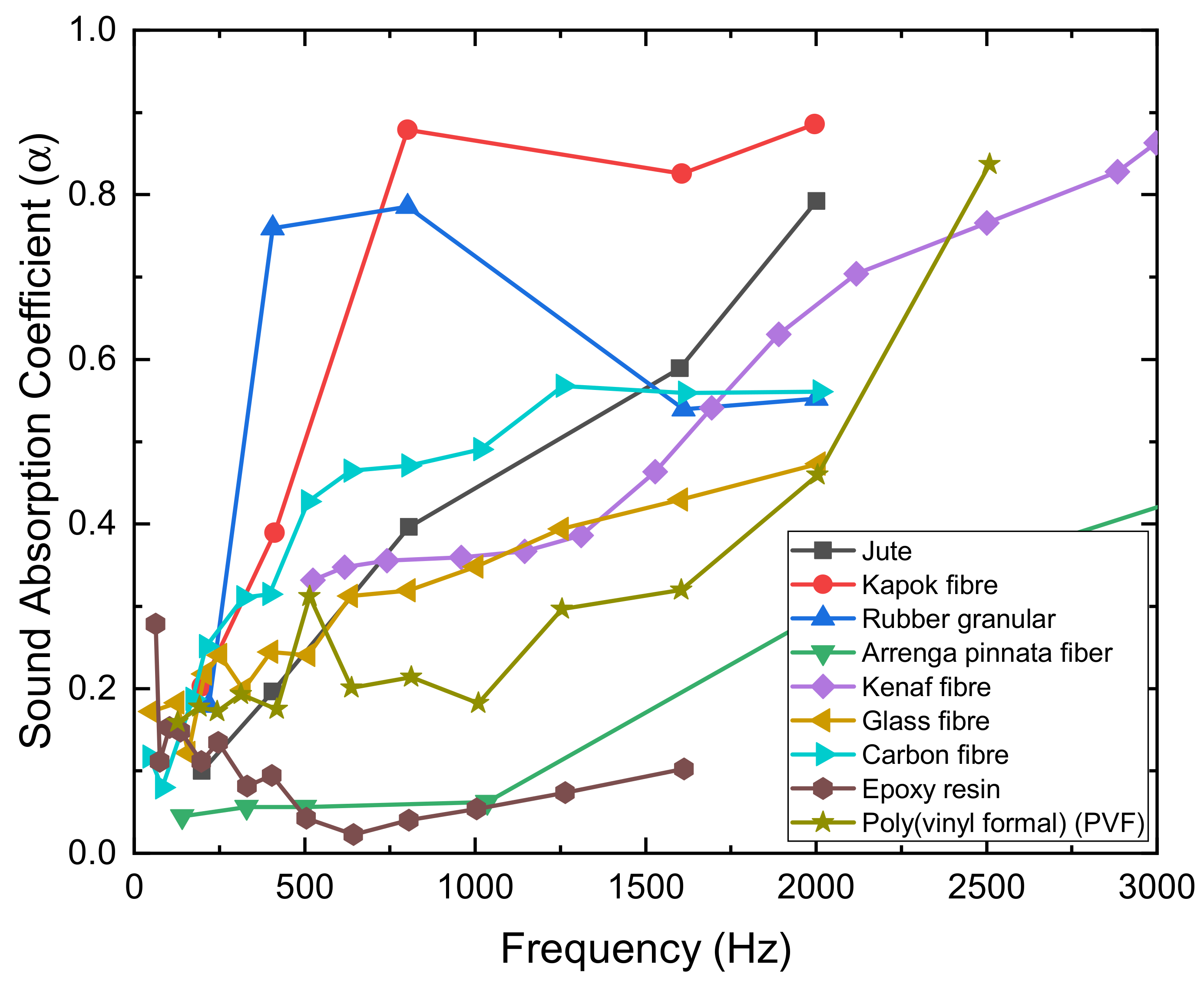
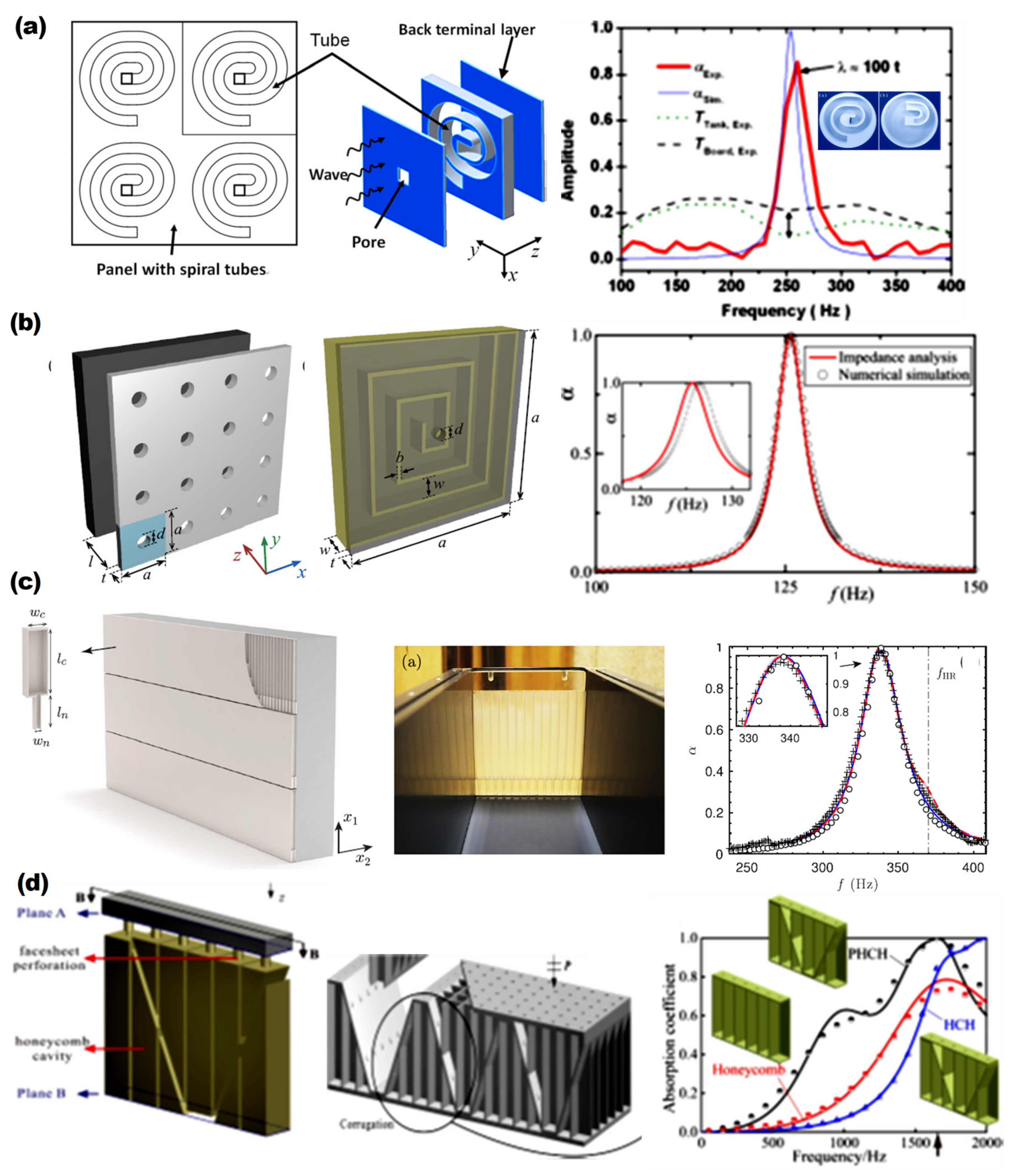
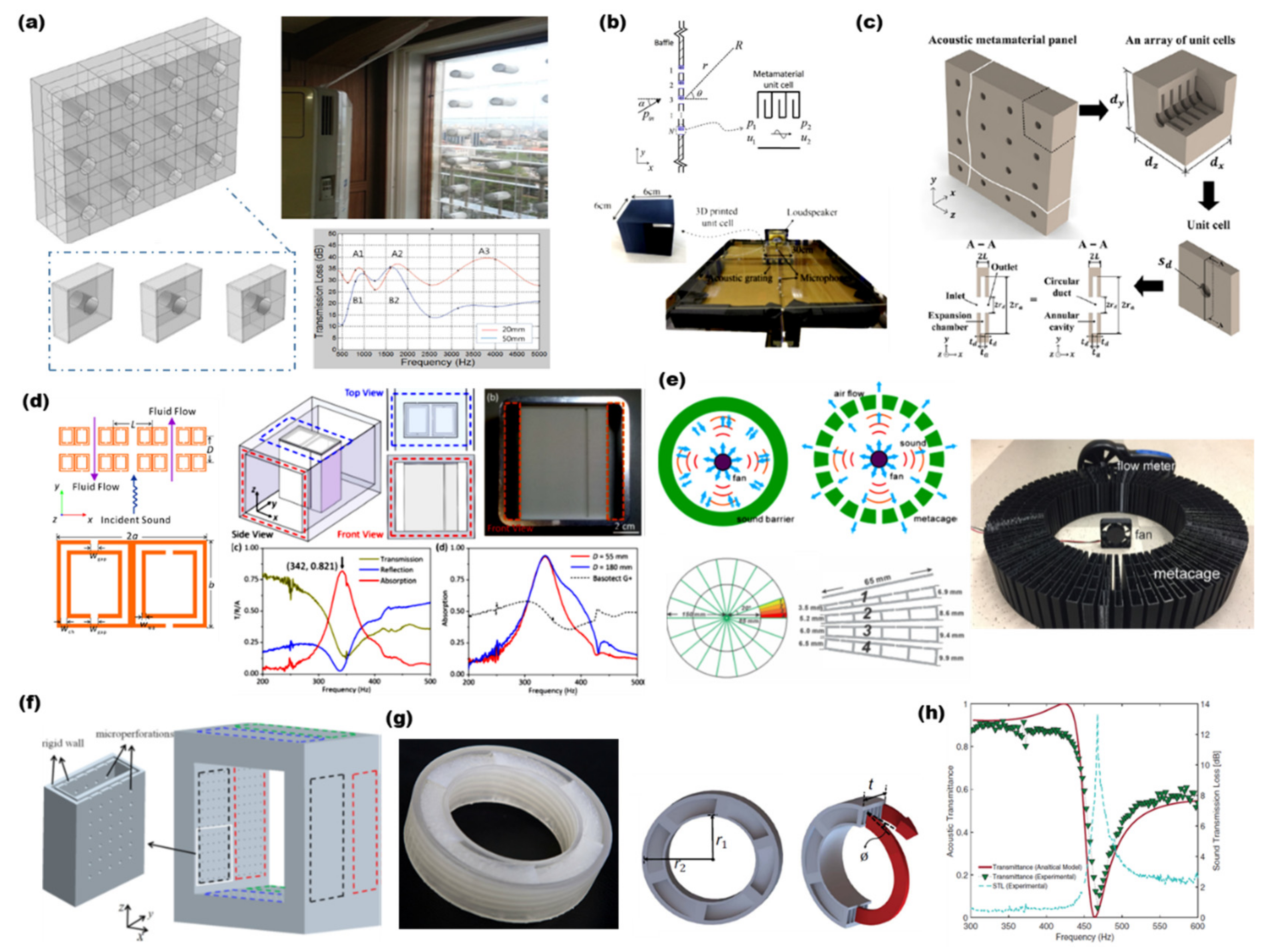
2.1. Acoustic Metamaterials as Sound Absorbers
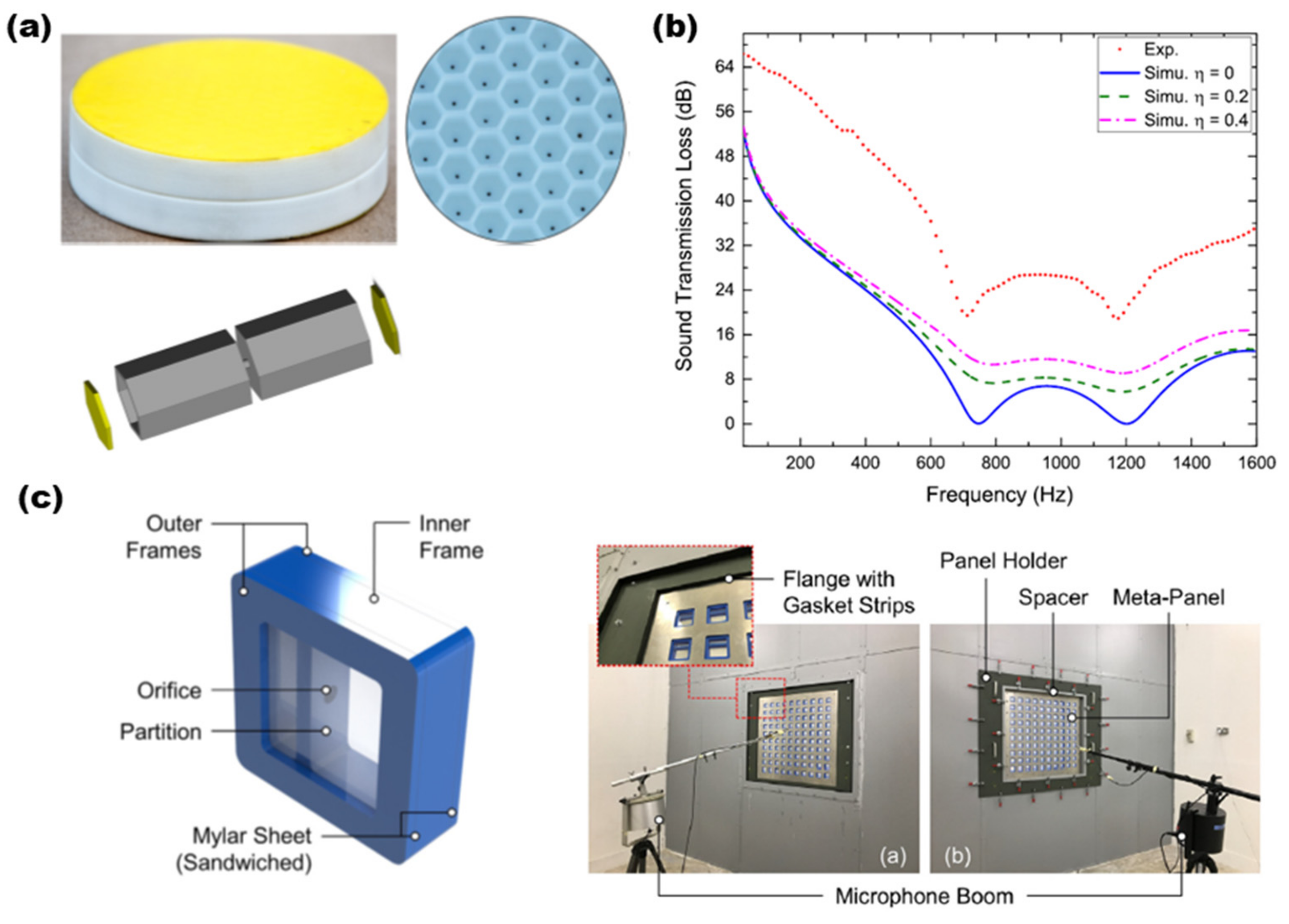
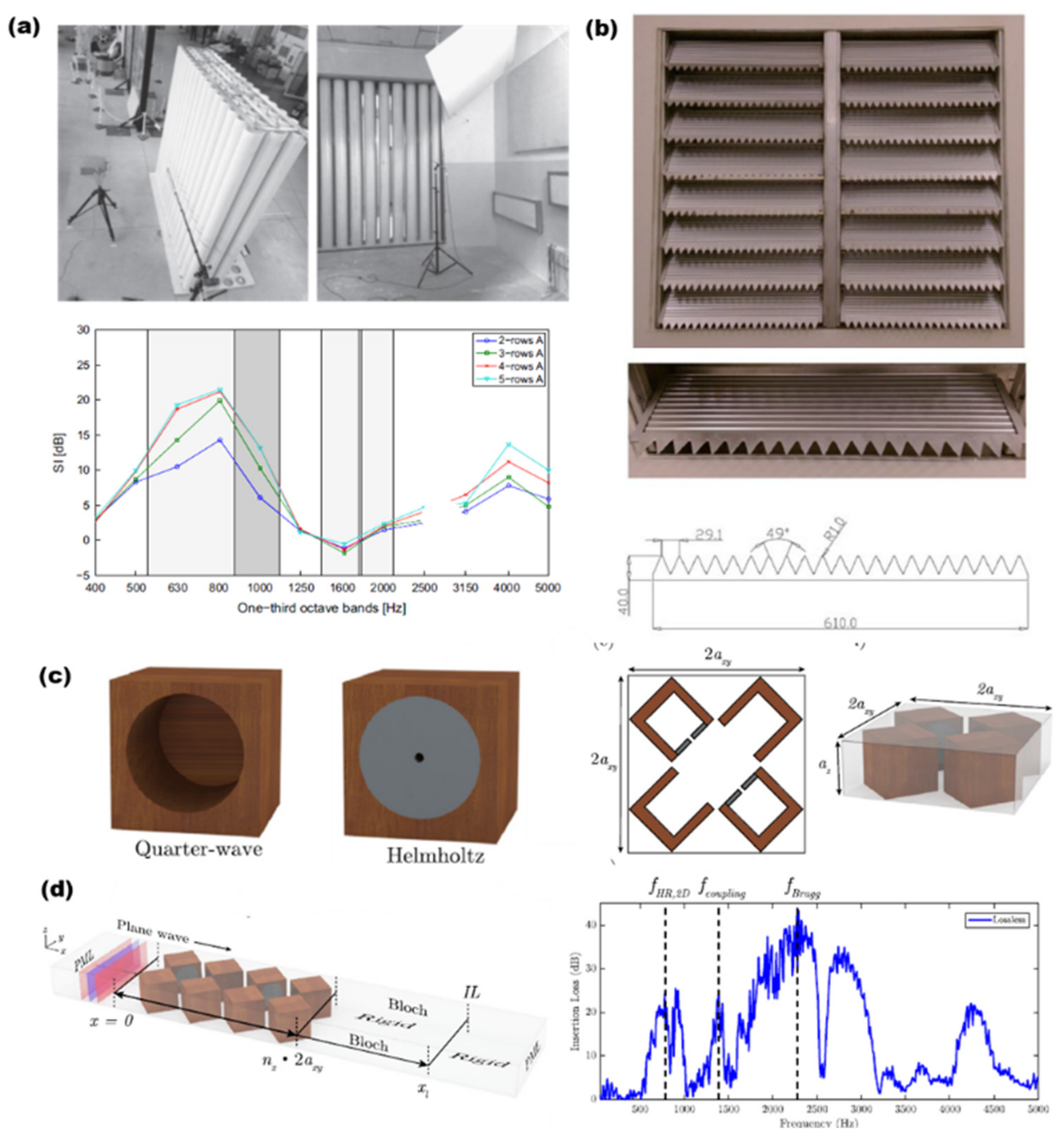
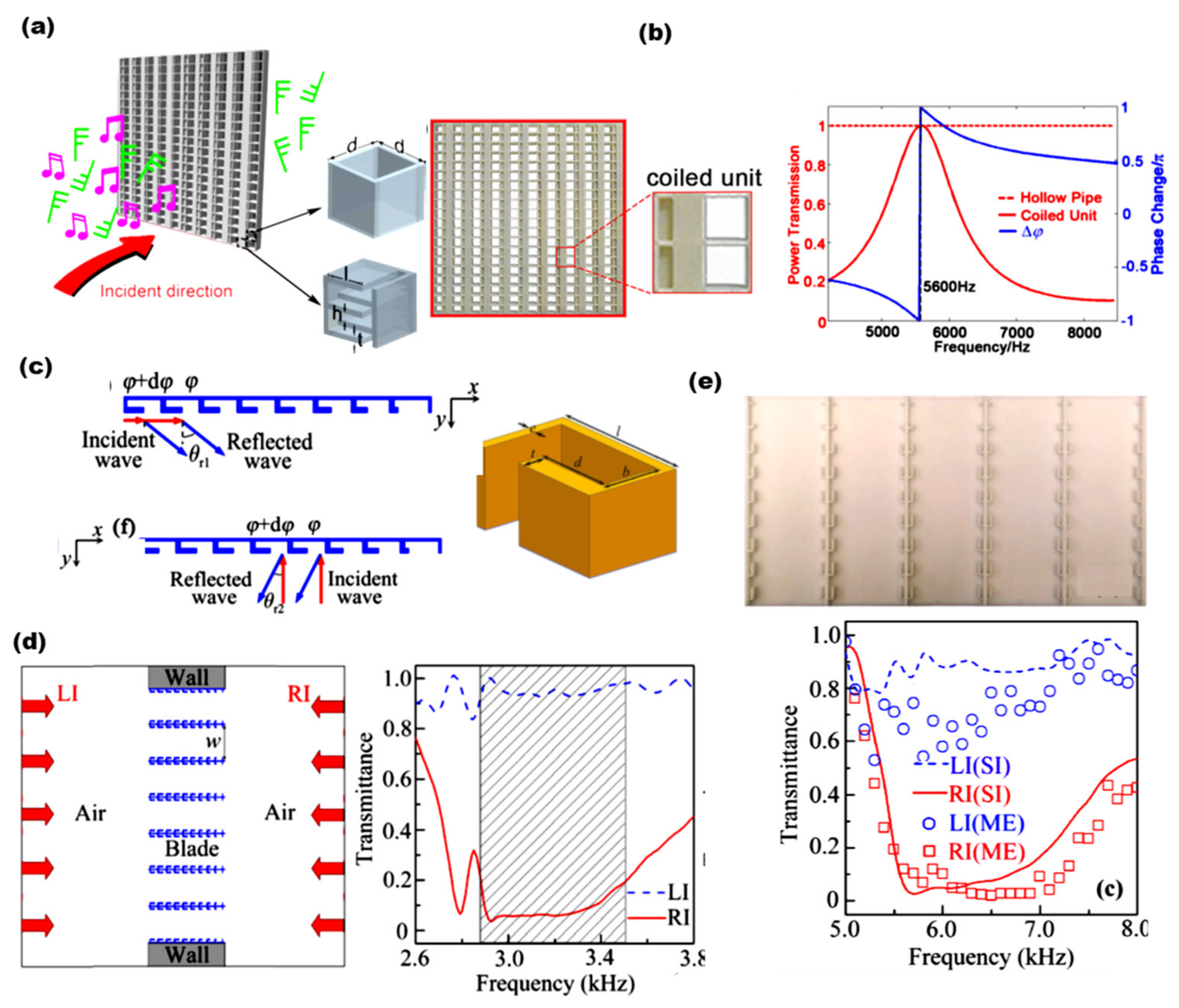
2.2. Acoustic Metamaterials as Sound Barriers
2.3. Acoustic Metamaterials as Soundproof Ventilated Windows
3. Challenges and Future Outlook
4. Conclusions
Funding
Conflicts of Interest
References
- Buss, R. United Nations Conference on the Human Environment (UNCHE). In Proceedings of the Stockholm Conference, Stockholm, Sweden, 5–16 June 1972. [Google Scholar]
- Morillas, J.M.B.; Gozalo, G.R.; González, D.M.; Moraga, P.A.; Vílchez-Gómez, R. Noise Pollution and Urban Planning. Curr. Pollut. Rep. 2018, 4, 1–12. [Google Scholar] [CrossRef]
- Walter Jensen, J.R.; Duke, N.S.; Edward, M.M. Noise Pollution and Abatement Act of 1972. In New Efforts Toward A Quieter Environment; Wiley: Hoboken, NJ, USA, 1975; Volume 13, pp. 45–46. [Google Scholar]
- Bateni, H.; Vaizasatya, A.; Blaschak, M. The Effect of 80 dB Environmental Noise on Control of Posture in Healthy Young Adults. Hum. Factors Ergon. Manuf. 2013, 23, 213–221. [Google Scholar] [CrossRef]
- World Health Organization. Environmental Noise Guidelines for the European Region; World Health Organization, Regional Office for Europe: Copenhagen, Denmark, 2018. [Google Scholar]
- Stansfeld, S.A.; Matheson, M.P. Noise pollution: Non-auditory effects on health. Br. Med. Bull. 2003, 68, 243–257. [Google Scholar] [CrossRef] [PubMed]
- Goines, L.; Hagler, L. Noise pollution: A modern plague. South. Med. J. 2007, 100, 287–294. [Google Scholar] [CrossRef] [PubMed]
- Haralabidis, A.S.; Dimakopoulou, K.; Vigna-Taglianti, F.; Giampaolo, M.; Borgini, A.; Dudley, M.-L.; Pershagen, G.; Bluhm, G.; Houthuijs, D.; Babisch, W. Acute effects of night-time noise exposure on blood pressure in populations living near airports. Eur. Heart J. 2008, 29, 658–664. [Google Scholar] [CrossRef] [PubMed]
- Dzhambov, A.M. Long-term noise exposure and the risk for type 2 diabetes: A meta-analysis. Noise Health 2015, 17, 23. [Google Scholar] [CrossRef] [PubMed]
- Arenas, J.P.; Crocker, M.J. Recent trends in porous sound-absorbing materials. Sound Vibration 2010, 44, 12–18. [Google Scholar]
- Magrini, U.; Ricciardi, P. Surface sound acoustical absorption and application of panels composed of granular porous materials. Proc. Inter Noise 2000 2000, 27–30. [Google Scholar]
- Frank, W.; Irregeher, J.F. Foam material sound absorption. United States Patent 4584232, 1986. [Google Scholar]
- Haines, J.C.; Fay, R.M. Sound Absorption Laminate. WO 97/04445, 1995. [Google Scholar]
- Pilaar, J.G. Inflatable Sound Attenuation System. 7992678, 9 August 2011. [Google Scholar]
- Crocker, M.J. Handbook of Noise and Vibration Control; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Rossing, T.D. Springer Handbook of Acoustics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Cox, T.; d’Antonio, P. Acoustic Absorbers and Diffusers: Theory, Design and Application, 3rd ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group, LLC: New York, NY, USA, 2017. [Google Scholar]
- Yang, Z.; Dai, H.; Chan, N.; Ma, G.; Sheng, P. Acoustic metamaterial panels for sound attenuation in the 50–1000 Hz regime. Appl. Phys. Lett. 2010, 96, 041906. [Google Scholar] [CrossRef]
- London, A. Transmission of reverberant sound through single walls. J. Res. Nat. Bur. Stand 1949, 42, 2. [Google Scholar] [CrossRef]
- Mei, J.; Ma, G.; Yang, M.; Yang, Z.; Wen, W.; Sheng, P. Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat. Commun. 2012, 3, 756. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Sheng, P. Sound Absorption Structures: From Porous Media to Acoustic Metamaterials. Annu. Rev. Mater. Res. 2017, 47, 83–114. [Google Scholar] [CrossRef]
- Broner, N. The effects of low frequency noise on people? A review. J. Sound Vib. 1978, 58, 483–500. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Maa, D.-Y. Potential of microperforated panel absorber. J. Acoust. Soc. Am. 1998, 104, 2861–2866. [Google Scholar] [CrossRef]
- Song, G.Y.; Cheng, Q.; Huang, B.; Dong, H.Y.; Cui, T.J. Broadband fractal acoustic metamaterials for low-frequency sound attenuation. Appl. Phys. Lett. 2016, 109, 131901. [Google Scholar] [CrossRef]
- Ma, G.; Sheng, P. Acoustic metamaterials: From local resonances to broad horizons. Sci. Adv. 2016, 2, e1501595. [Google Scholar] [CrossRef]
- Fok, L.; Ambati, M.; Zhang, X. Acoustic metamaterials. MRS Bull. 2008, 33, 931–934. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nature Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Haberman, M.R.; Norris, A.N. Acoustic metamaterials. Phys. Today 2016, 12, 31–39. [Google Scholar] [CrossRef]
- Huang, T.-Y.; Shen, C.; Jing, Y. Membrane-and plate-type acoustic metamaterials. J. Acoust. Soc. Am. 2016, 139, 3240–3250. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Wright, O.B. Origin of negative density and modulus in acoustic metamaterials. Phys. Rev. B 2016, 93, 024302. [Google Scholar] [CrossRef]
- Ge, H.; Yang, M.; Ma, C.; Lu, M.-H.; Chen, Y.-F.; Fang, N.; Sheng, P. Breaking the barriers: Advances in acoustic functional materials. Natl. Sci. Rev. 2017, 5, 159–182. [Google Scholar] [CrossRef]
- Lee, D.; Nguyen, D.M.; Rho, J. Acoustic wave science realized by metamaterials. Nano Converg. 2017, 4, 3. [Google Scholar] [CrossRef] [PubMed]
- Assouar, B.; Liang, B.; Wu, Y.; Li, Y.; Cheng, J.-C.; Jing, Y. Acoustic metasurfaces. Nat. Rev. Mater. 2018, 1. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, M.; Sheng, P. Perspective: Acoustic metamaterials in transition. J. Appl. Phys. 2018, 123, 090901. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Fleury, R. Active times for acoustic metamaterials. Rev. Phys. 2019, 100031. [Google Scholar] [CrossRef]
- Lee, J.; Kim, G.H.; Ha, C.S. Sound absorption properties of polyurethane/nano-silica nanocomposite foams. J. Appl. Polym. Sci. 2012, 123, 2384–2390. [Google Scholar] [CrossRef]
- Yang, W.; Li, Y. Sound absorption performance of natural fibers and their composites. Sci. China Technol. Sci. 2012, 55, 2278–2283. [Google Scholar] [CrossRef]
- Xue, B.; Li, R.; Deng, J.; Zhang, J. Sound absorption properties of microporous poly (vinyl formal) foams prepared by a two-step acetalization method. Ind. Eng. Chem. Res. 2016, 55, 3982–3989. [Google Scholar] [CrossRef]
- Rajappan, S.; Bhaskaran, P.; Ravindran, P. An Insight into the Composite Materials for Passive Sound Absorption. J. Appl. Sci. 2017, 17, 339–356. [Google Scholar] [CrossRef]
- Lim, Z.; Putra, A.; Nor, M.J.M.; Yaakob, M. Sound absorption performance of natural kenaf fibres. Appl. Acoust. 2018, 130, 107–114. [Google Scholar] [CrossRef]
- Chen, C.; Du, Z.; Hu, G.; Yang, J. A low-frequency sound absorbing material with subwavelength thickness. Appl. Phys. Lett. 2017, 110, 221903. [Google Scholar] [CrossRef]
- Huang, S.; Fang, X.; Wang, X.; Assouar, B.; Cheng, Q.; Li, Y. Acoustic perfect absorbers via spiral metasurfaces with embedded apertures. Appl. Phys. Lett. 2018, 113, 233501. [Google Scholar] [CrossRef]
- Cai, X.; Guo, Q.; Hu, G.; Yang, J. Ultrathin low-frequency sound absorbing panels based on coplanar spiral tubes or coplanar Helmholtz resonators. Appl. Phys. Lett. 2014, 105, 121901. [Google Scholar] [CrossRef]
- Ingard, U. On the theory and design of acoustic resonators. J. Acoust. Soc. Am. 1953, 25, 1037–1061. [Google Scholar] [CrossRef]
- Li, Y.; Assouar, B.M. Acoustic metasurface-based perfect absorber with deep subwavelength thickness. Appl. Phys. Lett. 2016, 108, 063502. [Google Scholar] [CrossRef]
- Jiménez, N.; Huang, W.; Romero-García, V.; Pagneux, V.; Groby, J.-P. Ultra-thin metamaterial for perfect and quasi-omnidirectional sound absorption. Appl. Phys. Lett. 2016, 109, 121902. [Google Scholar] [CrossRef]
- Tang, Y.; Ren, S.; Meng, H.; Xin, F.; Huang, L.; Chen, T.; Zhang, C.; Lu, T.J. Hybrid acoustic metamaterial as super absorber for broadband low-frequency sound. Sci. Rep. 2017, 7, 43340. [Google Scholar] [CrossRef]
- Yang, Z.; Mei, J.; Yang, M.; Chan, N.; Sheng, P. Membrane-type acoustic metamaterial with negative dynamic mass. Phys. Rev. Lett. 2008, 101, 204301. [Google Scholar] [CrossRef]
- Naify, C.J.; Chang, C.-M.; McKnight, G.; Nutt, S. Transmission loss and dynamic response of membrane-type locally resonant acoustic metamaterials. J. Appl. Phys. 2010, 108, 114905. [Google Scholar] [CrossRef]
- Yang, M.; Ma, G.; Yang, Z.; Sheng, P. Coupled membranes with doubly negative mass density and bulk modulus. Phys. Rev. Lett. 2013, 110, 134301. [Google Scholar] [CrossRef] [PubMed]
- Ang, L.Y.L.; Koh, Y.K.; Lee, H.P. Broadband sound transmission loss of a large-scale membrane-type acoustic metamaterial for low-frequency noise control. Appl. Phys. Lett. 2017, 111, 041903. [Google Scholar] [CrossRef]
- Kumar, S.; Bhushan, P.; Prakash, O.; Bhattacharya, S. Double negative acoustic metastructure for attenuation of acoustic emissions. Appl. Phys. Lett. 2018, 112, 101905. [Google Scholar] [CrossRef]
- Prakash, O.; Bhattacharya, S.; Kumar, S.; Bhushan, P. Composite Sound Absorption Panel Assembly. US 2019/0103089 A1, 2019. [Google Scholar]
- Ma, F.; Huang, M.; Wu, J.H. Ultrathin lightweight plate-type acoustic metamaterials with positive lumped coupling resonant. J. Appl. Phys. 2017, 121, 015102. [Google Scholar] [CrossRef]
- Ma, F.; Huang, M.; Xu, Y.; Wu, J.H. Bi-layer plate-type acoustic metamaterials with Willis coupling. J. Appl. Phys. 2018, 123, 035104. [Google Scholar] [CrossRef]
- Ang, L.Y.L.; Koh, Y.K.; Lee, H.P. Plate-type acoustic metamaterial with cavities coupled via an orifice for enhanced sound transmission loss. Appl. Phys. Lett. 2018, 112, 051903. [Google Scholar] [CrossRef]
- Ang, L.Y.L.; Koh, Y.K.; Lee, H.P. Plate-Type Acoustic Metamaterials: Experimental Evaluation of a Modular Large-Scale Design for Low-Frequency Noise Control. Acoustics 2019, 1, 354–368. [Google Scholar] [CrossRef]
- Ang, L.Y.L.; Koh, Y.K.; Lee, H.P. Plate-type acoustic metamaterials: Evaluation of a large-scale design adopting modularity for customizable acoustical performance. Appl. Acoust. 2019, 149, 156–170. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022. [Google Scholar] [CrossRef]
- Romero-García, V.; Picó, R.; Cebrecos, A.; Sánchez-Morcillo, V.J.; Staliunas, K. Enhancement of sound in chirped sonic crystals. Appl. Phys. Lett. 2013, 102, 091906. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.; Yang, Z.; Chan, C.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Sala, R.; Sancho, J.; Sánchez, J.V.; Gómez, V.; Llinares, J.; Meseguer, F. Sound attenuation by sculpture. Nature 1995, 378, 241. [Google Scholar] [CrossRef]
- Romero-García, V.; Sánchez-Pérez, J.V.; Garcia-Raffi, L. Tunable wideband bandstop acoustic filter based on two-dimensional multiphysical phenomena periodic systems. J. Appl. Phys. 2011, 110, 014904. [Google Scholar] [CrossRef]
- Romero-García, V.; Lagarrigue, C.; Groby, J.; Richoux, O.; Tournat, V. Tunable acoustic waveguides in periodic arrays made of rigid square-rod scatterers: Theory and experimental realization. J. Phys. D Appl. Phys. 2013, 46, 305108. [Google Scholar] [CrossRef]
- Alagoz, S. A sonic crystal diode implementation with a triangular scatterer matrix. Appl. Acoust. 2014, 76, 402–406. [Google Scholar] [CrossRef]
- Rubio, C.; Castiñeira-Ibáñez, S.; Uris, A.; Belmar, F.; Candelas, P. Numerical simulation and laboratory measurements on an open tunable acoustic barrier. Appl. Acoust. 2018, 141, 144–150. [Google Scholar] [CrossRef]
- Jia, D.; Sun, H.-x.; Xia, J.-p.; Yuan, S.-q.; Liu, X.-j.; Zhang, C. Acoustic topological insulator by honeycomb sonic crystals with direct and indirect band gaps. New J. Phys. 2018, 20, 093027. [Google Scholar] [CrossRef]
- Morandi, F.; Miniaci, M.; Marzani, A.; Barbaresi, L.; Garai, M. Standardised acoustic characterisation of sonic crystals noise barriers: Sound insulation and reflection properties. Appl. Acoust. 2016, 114, 294–306. [Google Scholar] [CrossRef]
- Lee, H.M.; Tan, L.B.; Lim, K.M.; Lee, H.P. Experimental study of the acoustical performance of a sonic crystal window in a reverberant sound field. Build. Acoust. 2017, 24, 5–20. [Google Scholar] [CrossRef]
- Lee, H.M.; Lim, K.M.; Lee, H.P. Reduction of Ceiling Fan Noise by Serrated Trailing Edge. Fluct. Noise Lett. 2018, 17, 1850026. [Google Scholar] [CrossRef]
- Lee, H.M.; Tan, L.B.; Lim, K.M.; Xie, J.; Lee, H.P. Field experiment of a sonic crystal window. Fluct. Noise Lett. 2018, 17, 1850032. [Google Scholar] [CrossRef]
- Lee, H.M.; Haris, A.; Lim, K.M.; Xie, J.; Lee, H.P. Environmental Noise Mitigation by Plenum Window with Sonic Crystals and Jagged Flap. Fluct. Noise Lett. 2019, 18, 1950001. [Google Scholar] [CrossRef]
- Cavalieri, T.; Cebrecos, A.; Groby, J.-P.; Chaufour, C.; Romero-García, V. Three-dimensional multiresonant lossy sonic crystal for broadband acoustic attenuation: Application to train noise reduction. Appl. Acoust. 2019, 146, 1–8. [Google Scholar] [CrossRef]
- Schröder, M.R. Diffuse sound reflection by maximum–length sequences. J. Acoust. Soc. Am. 1975, 57, 149–150. [Google Scholar] [CrossRef]
- Schroeder, M.R. Binaural dissimilarity and optimum ceilings for concert halls: More lateral sound diffusion. J. Acoust. Soc. Am. 1979, 65, 958–963. [Google Scholar] [CrossRef]
- Zhu, Y.; Fan, X.; Liang, B.; Cheng, J.; Jing, Y. Ultrathin Acoustic Metasurface-Based Schroeder Diffuser. Phys. Rev. X 2017, 7, 021034. [Google Scholar] [CrossRef]
- Jiménez, N.; Cox, T.J.; Romero-García, V.; Groby, J.-P. Metadiffusers: Deep-subwavelength sound diffusers. Sci. Rep. 2017, 7, 5389. [Google Scholar] [CrossRef]
- Song, G.Y.; Cheng, Q.; Cui, T.J.; Jing, Y. Acoustic planar surface retroreflector. Phys. Rev. Mater. 2018, 2, 065201. [Google Scholar] [CrossRef]
- Kim, S.-H.; Lee, S.-H. Air transparent soundproof window. AIP Adv. 2014, 4, 117123. [Google Scholar] [CrossRef]
- Yu, X.; Lu, Z.; Liu, T.; Cheng, L.; Zhu, J.; Cui, F. Sound transmission through a periodic acoustic metamaterial grating. J. Sound Vib. 2019, 449, 140–156. [Google Scholar] [CrossRef]
- Jung, J.W.; Kim, J.E.; Lee, J.W. Acoustic metamaterial panel for both fluid passage and broadband soundproofing in the audible frequency range. Appl. Phys. Lett. 2018, 112, 041903. [Google Scholar] [CrossRef]
- Wu, X.; Au-Yeung, K.Y.; Li, X.; Roberts, R.C.; Tian, J.; Hu, C.; Huang, Y.; Wang, S.; Yang, Z.; Wen, W. High-efficiency ventilated metamaterial absorber at low frequency. Appl. Phys. Lett. 2018, 112, 103505. [Google Scholar] [CrossRef]
- Shen, C.; Xie, Y.; Li, J.; Cummer, S.A.; Jing, Y. Acoustic metacages for sound shielding with steady air flow. J. Appl. Phys. 2018, 123, 124501. [Google Scholar] [CrossRef]
- Li, L.J.; Zheng, B.; Zhong, L.M.; Yang, J.; Liang, B.; Cheng, J.C. Broadband compact acoustic absorber with high-efficiency ventilation performance. Appl. Phys. Lett. 2018, 113, 103501. [Google Scholar] [CrossRef]
- Ghaffarivardavagh, R.; Nikolajczyk, J.; Anderson, S.; Zhang, X. Ultra-open acoustic metamaterial silencer based on Fano-like interference. Phys. Rev. B 2019, 99, 024302. [Google Scholar] [CrossRef]
- Zhang, H.-l.; Zhu, Y.-f.; Liang, B.; Yang, J.; Yang, J.; Cheng, J.-c. Omnidirectional ventilated acoustic barrier. Appl. Phys. Lett. 2017, 111, 203502. [Google Scholar] [CrossRef]
- Ge, Y.; Sun, H.-X.; Yuan, S.-Q.; Lai, Y. Broadband unidirectional and omnidirectional bidirectional acoustic insulation through an open window structure with a metasurface of ultrathin hooklike meta-atoms. Appl. Phys. Lett. 2018, 112, 243502. [Google Scholar] [CrossRef]
- Ge, Y.; Sun, H.-X.; Yuan, S.-Q.; Lai, Y. Switchable omnidirectional acoustic insulation through open window structures with ultrathin metasurfaces. Phys. Rev. Mater. 2019, 3, 065203. [Google Scholar] [CrossRef]
- Elford, D.; Chalmers, L.; Wilson, R. Acoustic attenuator. US Patent 20170263235 A1, 14 September 2017. [Google Scholar]
- Acoustic screen with the NoiseTrap technology. Transformer Substation Noise Reduction Acoustic Attenuator. Available online: https://www.sonobex.com/portfolio-item/substation-transformer-noise/ (accessed on 16 June 2019).
- Bishop-Moser, J.; Spadaccini, C.; Andres, C. Metamaterials Manufacturing: Pathway to Industrial Competitiveness; Metamaterials Manufacturing: Ann Arbor, MI, USA, 2018; pp. 1–42. [Google Scholar]
- Babaee, S.; Viard, N.; Wang, P.; Fang, N.X.; Bertoldi, K. Harnessing deformation to switch on and off the propagation of sound. Adv. Mater. 2016, 28, 1631–1635. [Google Scholar] [CrossRef]
- Yu, K.; Fang, N.X.; Huang, G.; Wang, Q. Magnetoactive Acoustic Metamaterials. Adv. Mater. 2018, 30, 1706348. [Google Scholar] [CrossRef] [PubMed]
- Fan, S.-W.; Zhao, S.-D.; Chen, A.-L.; Wang, Y.-F.; Assouar, B.; Wang, Y.-S. Tunable Broadband Reflective Acoustic Metasurface. Phys. Rev. Appl. 2019, 11, 044038. [Google Scholar] [CrossRef]
- Tian, Z.; Shen, C.; Li, J.; Reit, E.; Gu, Y.; Fu, H.; Cummer, S.A.; Huang, T.J. Programmable Acoustic Metasurfaces. Adv. Funct. Mater. 2019, 1808489. [Google Scholar] [CrossRef] [PubMed]
- Harris, C.M. Absorption of sound in air versus humidity and temperature. J. Acoust. Soc. Am. 1966, 40, 148–159. [Google Scholar] [CrossRef]
- Bohn, D.A. Environmental effects on the speed of sound. In Proceedings of the Audio Engineering Society Convention 83, New York, NY, USA, 16–19 October 1987. [Google Scholar]
- Qi, S.; Oudich, M.; Li, Y.; Assouar, B. Acoustic energy harvesting based on a planar acoustic metamaterial. Appl. Phys. Lett. 2016, 108, 263501. [Google Scholar] [CrossRef]
- Oudich, M.; Li, Y. Tunable sub-wavelength acoustic energy harvesting with a metamaterial plate. J. Phys. D Appl. Phys. 2017, 50, 315104. [Google Scholar] [CrossRef]
- Qi, S.; Assouar, B. Acoustic energy harvesting based on multilateral metasurfaces. Appl. Phys. Lett. 2017, 111, 243506. [Google Scholar] [CrossRef]
- Mir, F.; Saadatzi, M.S.; Ahmed, R.U.; Banerjee, S. The possibility of harvesting electrical energy from industrial noise barriers using meta-wall bricks. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, Denver, CO, USA, 5–8 March 2018; p. 105982S. [Google Scholar]

| Source | Average Noise Exposure | Night Noise Exposure |
|---|---|---|
| Road traffic noise | <53 dB | <45 dB |
| Railway noise | <54 dB | <44 dB |
| Aircraft noise | <45 dB | <40 dB |
| Wind turbine noise | <45 dB | No recommendation |
| Leisure noise | <70 dB |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, S.; Lee, H.P. The Present and Future Role of Acoustic Metamaterials for Architectural and Urban Noise Mitigations. Acoustics 2019, 1, 590-607. https://doi.org/10.3390/acoustics1030035
Kumar S, Lee HP. The Present and Future Role of Acoustic Metamaterials for Architectural and Urban Noise Mitigations. Acoustics. 2019; 1(3):590-607. https://doi.org/10.3390/acoustics1030035
Chicago/Turabian StyleKumar, Sanjay, and Heow Pueh Lee. 2019. "The Present and Future Role of Acoustic Metamaterials for Architectural and Urban Noise Mitigations" Acoustics 1, no. 3: 590-607. https://doi.org/10.3390/acoustics1030035
APA StyleKumar, S., & Lee, H. P. (2019). The Present and Future Role of Acoustic Metamaterials for Architectural and Urban Noise Mitigations. Acoustics, 1(3), 590-607. https://doi.org/10.3390/acoustics1030035






