1. Introduction
Nonlinear dielectric ceramics have attracted considerable attention due to their promising applications in electronic integrated circuits, transistors, ferroelectric random-access memories, and energy storage systems [
1,
2,
3]. Among these materials, strontium titanate, SrTiO
3 (STO) is a widely studied model electroceramic crystal due to its optical transparency, high dielectric constant, and thermal stability [
4]. Previous studies have established that the distinctive properties of STO are intimately linked to interface characteristics, including oxygen vacancies and local strain [
5,
6,
7]. Research suggests that aging and electrical failures in STO are primarily driven by the migration of oxygen vacancies at interfaces, grain boundaries, and the formation of extensive dendritic structures [
5,
6,
7]. Notably, oxygen vacancies tend to remain confined at the interfaces, even following oxidation treatments, rather than diffusing away [
8]. A more profound understanding of the dynamics of oxygen vacancy migration and local strain evolution is critical for elucidating the underlying mechanisms of ionic degradation and thermal breakdown dynamics [
9,
10,
11,
12].
STO bicrystals with well-defined tilt boundaries offer an ideal platform to investigate how crystallographic discontinuities affect their local transport properties, oxygen vacancy migrations, and dielectric responses. The low-angle grain boundaries (typically < 15°) in bicrystals offer desired structural dislocations by controlling the GB plane and orientation. Also, a periodic array of dislocations can be achieved at a certain interval. This dislocation array and interfacial strain impact the local symmetry and domain behavior, especially ferroelectrics like STO. Studies have revealed that compressive and tensile strain fields are concentrated along tilt boundaries, where oxygen vacancies preferentially form between dislocation cores [
13,
14]. These bicrystals exhibit distinct domain configurations, governed by crystallographic orientation and boundary geometry, which in turn influence their ferroelectric and piezoelectric properties. Tilted phase boundaries can act either as channels or barriers for charge transport and defect migration, thereby modulating the macroscopic behavior of the material. However, capturing detailed information on local strain distributions and polarization dynamics at these interfaces remains challenging with conventional bulk or film-based characterization methods, such as electrical transport measurements, microstructural analysis, and high-resolution transmission electron microscopy.
Second-harmonic generation (SHG), a second-order nonlinear optical process, is highly sensitive to nanoscale variations in material symmetry and polarization, making it a powerful tool for investigating complex local domain structures. Most recently, the polarization-dependent SHG technique has been developed to accurately distinguish domain orientations in dielectric and ferroelectric thin films [
14,
15,
16,
17,
18,
19]. This method involves the systematic variation of the polarization angle of the incident beam, combined with controlled rotation of the sample relative to the beam axis. By analyzing the resulting azimuth- and polarization-dependent SHG signals, both the orientations of individual domains and their corresponding volume fractions can be precisely determined [
20,
21,
22,
23,
24,
25]. Building upon these advancements, scanning SHG imaging and employing spatially resolved detection of nonlinear optical signals facilitate the direct visualization of domain distributions and structural inhomogeneities [
26,
27,
28]. Mapping the spatial modulation of
χ(2) components reconstructs strain fields near phase boundaries, uncovering complex, interwoven domain architectures and their associated elastic textures [
29,
30,
31].
In this invited paper, we present the polarization-dependent SHG imaging approaches to explore local symmetry breaking and complex domain structures in STO bicrystals. We show that anisotropic strain from a tilted grain boundary induces significant structural distortions, leading to the formation of tetragonal and rhombohedral domains. By analyzing SHG intensity variations and nonlinear susceptibility, we achieve spatial mapping of elastic strain fields and local domain configurations near the grain boundary. Our results reveal that the grain boundary creates a strain gradience, stabilizing symmetry-breaking distortions, and phase evolution. The SHG imaging microscopy provides new insights into the interplay between localized strain, symmetry breaking, and phase transitions, offering valuable perspectives for designing strain-engineered functional oxide devices. Our SHG imaging technique provides unique access to both microscopic symmetry and nanoscale structural behavior to map domain distributions which cannot be obtained by TEM or XRD characterization techniques.
2. Experiments
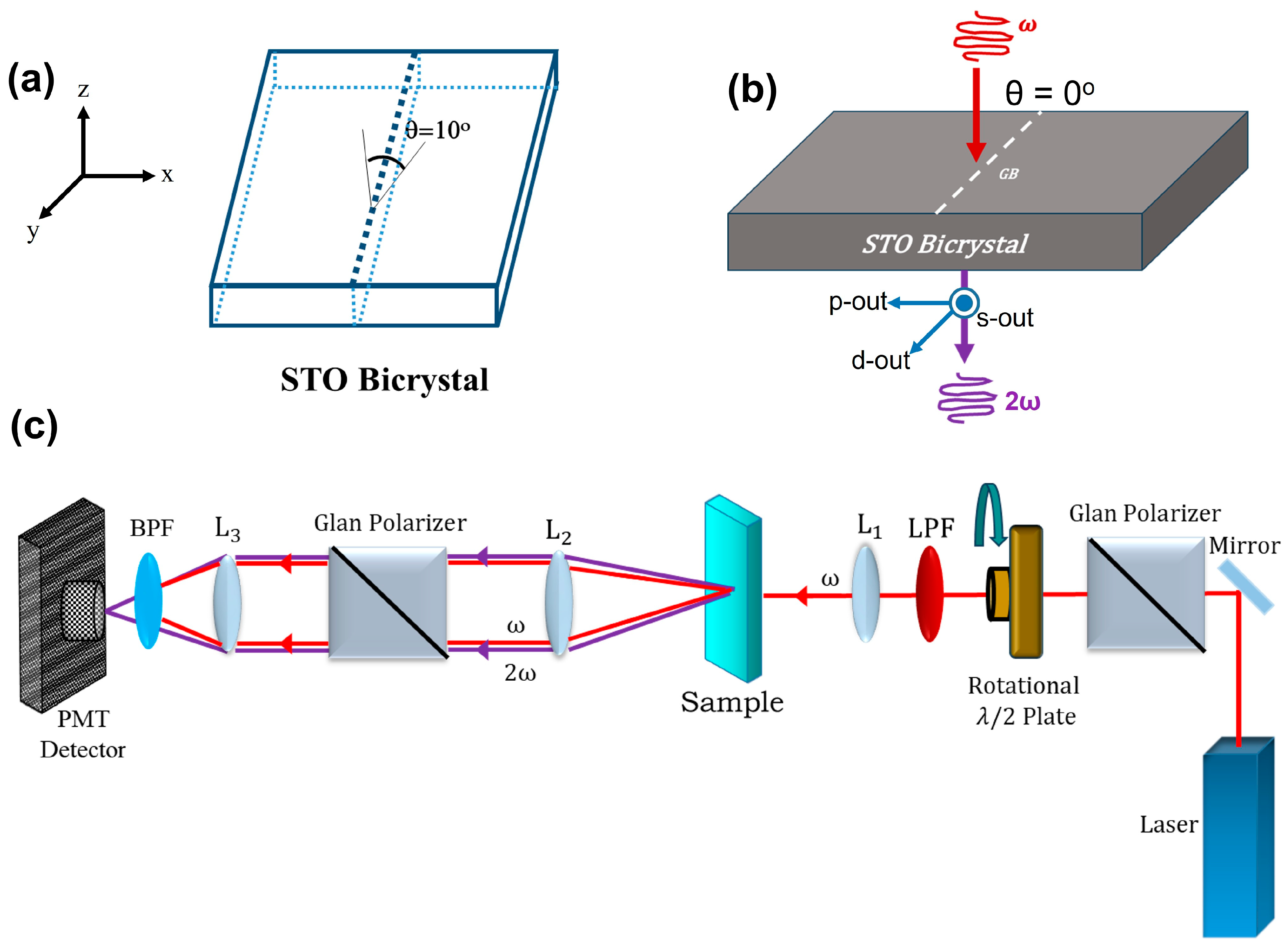
The STO bicrystals were prepared by thermal diffusion bonding (Shinkosha, Tokyo, Japan), with a 10° grain boundary (GB) tilt along the (100) plane in the [001] direction. As shown in
Figure 1a, the bicrystal was cut and polished into 3 × 3 × 0.5 mm
3 pieces from the same undoped STO single crystal, ensuring consistent defect chemistry across both halves. The bicrystals were then annealed in a tube furnace at 900 °C under a reducing atmosphere (pO
2 × 10
−5 bar) to achieve n-type doping. To degrade the STO bicrystals, 100 nm lateral amorphous platinum electrodes were deposited in ab ambient atmosphere along the sample edges for transverse
dc field application. The samples were subsequently placed in a temperature bath at 250 °C with an applied
dc voltage of 40 V to induce oxygen ion and vacancy migrations.
Figure 1b,c show the schematic setup for optical SHG measurements at normal incidence (θ = 0°) and schematics of optical setup in the transmission geometry. The coordinate system is defined such that the x-axis lies along the bicrystal and crosses the phase boundary, the y-axis runs parallel to the boundary within the sample plane, and the z-axis is oriented along the laser propagation direction, normal to the sample surface as shown in
Figure 1a.
Ultrashort optical pulses from an 800 nm femtosecond amplifier laser (Coherent Libra, 1 kHz repetition rate) were used as the fundamental light source. Two polarizers, combined with a half-waveplate, were employed to control the polarization of the incident and transmitted laser light. We focused the laser beam through a 10× objective lens with a numerical aperture (NA ~0.25) with a 2 mm input beam and 0.05 mW average power, yielding an estimated lateral spatial resolution of approximately 2 μm, and the estimated peak power density at focus is ~8 × 10
11 W/cm
2. The generated SHG signal was collected by a photomultiplier tube (PMT) detector (Hamamatsu, H9305-04). In
Figure 1c, L1, L2, and L3 depict focusing lenses while LPF and BPF represent longpass filter and bandpass filter, respectively. We measured the SHG intensity both near and far from the grain boundary to validate our domain evolution results. To control laser-induced artifacts, we monitored the sample under both short- and long-term exposures and confirmed that the observed signal changes were not caused by laser damage.
We performed the polarization-resolved SHG measurements by varying the input polarization angle (γ) while fixing the output polarization (γ′) to p-out (parallel to the xz-plane, γ′ = 0°), s-out (parallel to the y-axis, γ′ = 90°), or d-out (γ′ = ±45°, corresponding to 45° between s- and p-polarizations). Here p-out, s-out, and d-out indicate the p-, s-, and d- output polarization, respectively. There are only three nonzero independent second-order susceptibility components, and , available for 4 mm and 3 m point group symmetries, respectively.
For scanning SHG imaging, we utilized the lateral distribution of SHG signals arising from nonzero χ(2) components to directly visualize local structural distortions across the film near the bicrystal GB. To ensure high spatial accuracy and resolution, SHG measurements were carried out in transmission geometry with the incident beam aligned normal to the sample surface (θ = 0°), thereby eliminating angular distortions. In addition, measurements at an oblique incidence angle of 45° were performed to reveal out-of-plane susceptibility tensor components such as χzzz, which are inaccessible under strictly normal incidence. To minimize experimental uncertainties, reduce noise levels, and maintain alignment stability, the sample was carefully monitored under both short and extended exposure durations. Specifically, we carefully monitored the sample during both short and extended exposures and performed repeated measurements at the same bicrystal position to ensure the signal evolution was consistent and reproducible. These checks confirmed that the observed domain behavior reflects intrinsic material properties rather than photoinduced changes. The typical error bar for our SHG intensity measurements is estimated to be approximately ±5%, reflecting the combined effects of instrumental noise and alignment tolerance.
3. Results and Discussion
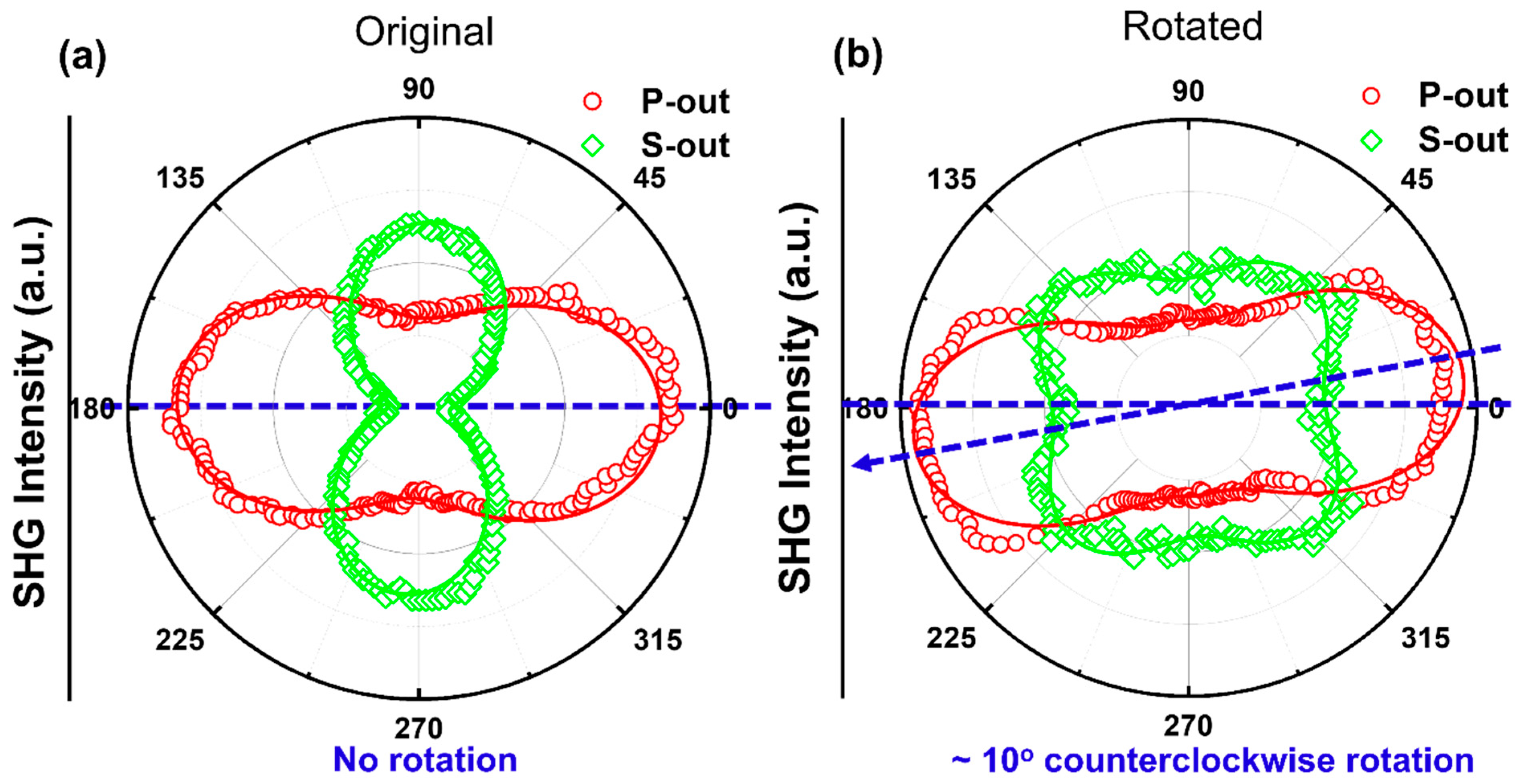
Figure 2a,b show the
s- and
p-polarized SHG intensities as functions of the incident polarization angle
γ for the pristine STO bicrystal near the grain boundary. These measurements were taken in the transmission geometry. We note that both
p-out and
s-out SHG responses show a strong dependence on the measured location. We identified a
clockwise rotation for both
p-out and
s-out SHG spectra on the rotated (R) side of the GB in the pristine crystal, while no obvious rotation is observed on the original (O) side of the GB. The
p-out SHG response on both sides of the GB features a twofold rotational symmetry with a pair of major peaks. The
s-out SHG response on the R side of the GB shows a four-fold structure with equal pairs of major and minor peaks. The s-out SHG spectra on the O side of the GB deviated from a two-peak structure. We notice that both the
p-out and
s-out SHG intensities decreased as the detection spot moved across the GB from the R side to O side.
Although the SHG responses are dominated by the strain-induced tetragonal phases, we also detect a contribution from the rhombohedral phases near the grain boundary. We were able to fit the SHG spectra by using the nonzero second-order susceptibility
χ(2) components,
,
,
(4 mm) and
,
,
(3 m-like). Three 3 m-like tensor components distinguish the rhombohedral 3 m phase from the tetragonal 4 mm phase, and these components are mutually independent. To assess both the tetragonal and rhombohedral structures, the SHG intensity is expressed as a function of the second-order susceptibility components [
32]:
where
is the effective nonlinear second-order susceptibility and
Fu is the volume fraction of the uth variant of the domains.
For the rhombohedral phase with a 3 m symmetry, the SHG intensities,
,
can be expressed as functions of the polarization angle γ of the incident pump pulses for an effective surface region:
where
with
and
being the diagonal elements of the Fresnel transformation tensors relevant to the fundamental and SHG lights at frequencies of
⍵ and 2
⍵, respectively.
At transmission (θ = 0°),
For
p-polarized SHG output, the total
p-polarized SHG output intensity is as follows [
33]:
For S-polarized SHG output, the total
s-polarized SHG output intensity is as follows:
Moreover, SHG measurements at an oblique incidence angle of 45° were conducted to reveal an out-of-plane susceptibility tensor component,
χzzz. The SHG response is highly sensitive to the polarization angle of the incident light,
γ. To map the distribution of structural distortions associated with dislocation cores across the bulk of the STO bicrystal, we performed transmitted SHG measurements at normal incidence along the GB. As shown in
Figure 2a,b, the SHG patterns exhibit clear spatial variations in both shape and signal intensity. The SHG signal intensity polar plots were fitted with Equations (10) and (11). In the original STO bicrystal, the bulk retains a broken 4 mm symmetry. However, as the detection spot moves across the GB, the
s-polarized SHG response gradually shifts toward a 3 m-like symmetry. This evolution is attributed to the emergence of a new interface structural symmetry and a corresponding modification of the second-order nonlinear susceptibility tensor, induced by the structural distortion near the GB. The strain-induced local structural distortions alter the nonzero elements of the nonlinear susceptibility tensor, resulting in the observed transition from a two-fold SHG pattern to a four-fold s-SHG pattern. The presence of strong lattice distortions—driven by lattice mismatch and symmetry breaking between the adjoining grains—leads to clear signatures of a local structural phase transition from tetragonal (T) to rhombohedral (R) within the GB region.
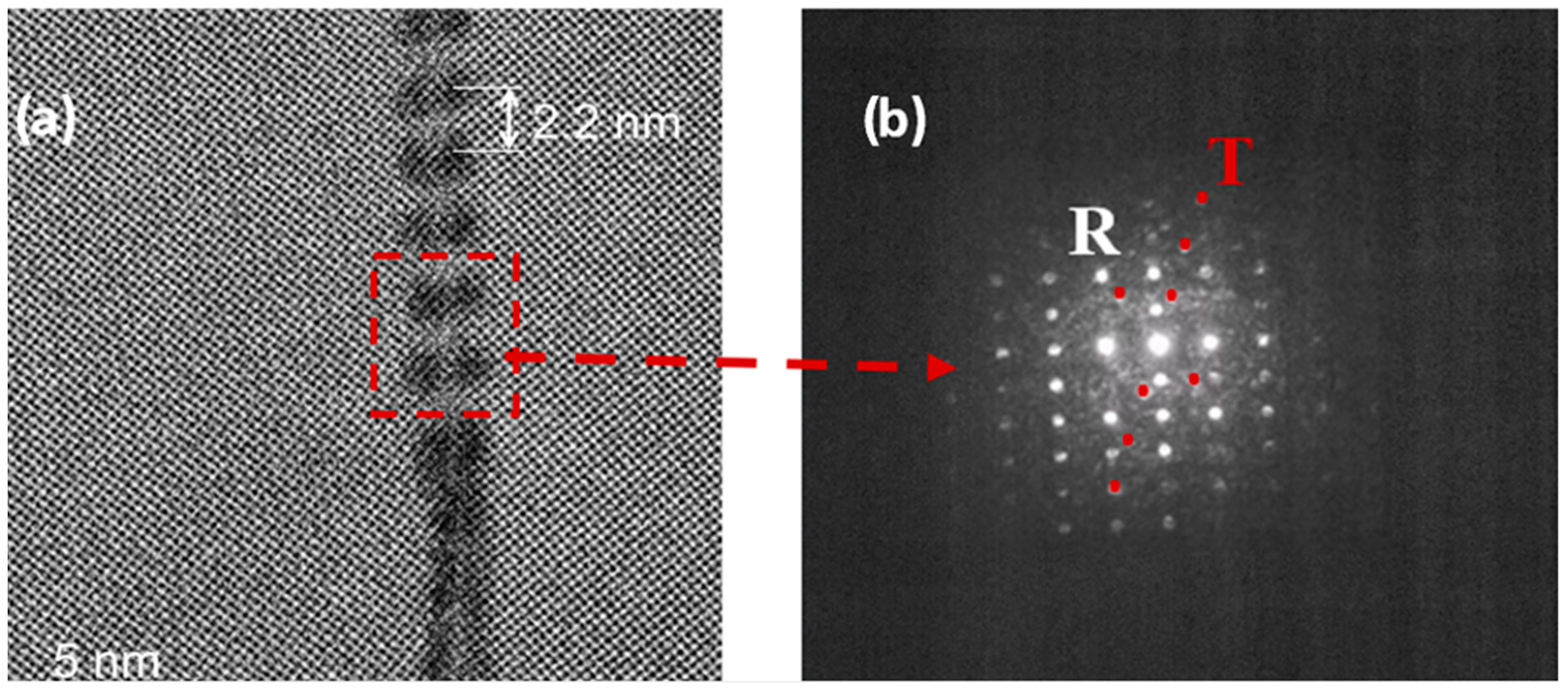
The SHG-based phase identification is supported by high-resolution transmission electron microscopy (HRTEM) and FFT-selected area electron diffraction (FFT-SAED) analyses. The SHG data are consistent with the HRTEM results shown in
Figure 3a. In the STO pristine bicrystal with a 10° misorientation angle across the grain boundary, the HRTEM image reveals a well-defined tilt boundary formed by a periodic array of dislocations that accommodate the angular mismatch between the adjoining crystalline domains. The dislocation spacing is approximately 2.2 nm, in good agreement with Frank’s formula for small-angle grain boundaries in perovskite oxides. Each dislocation acts as a localized distortion center, generating strain fields that extend into the adjacent grains and induce a periodic modulation of the lattice. FFT-SAED analysis (
Figure 3b) confirms the coexistence of tetragonal and rhombohedral symmetries across the boundary, indicating a phase boundary between structurally distinct domains. The dislocation cores exhibit pronounced strain-induced lattice distortions, which can significantly influence defect migration, polarization rotation, and local symmetry breaking.
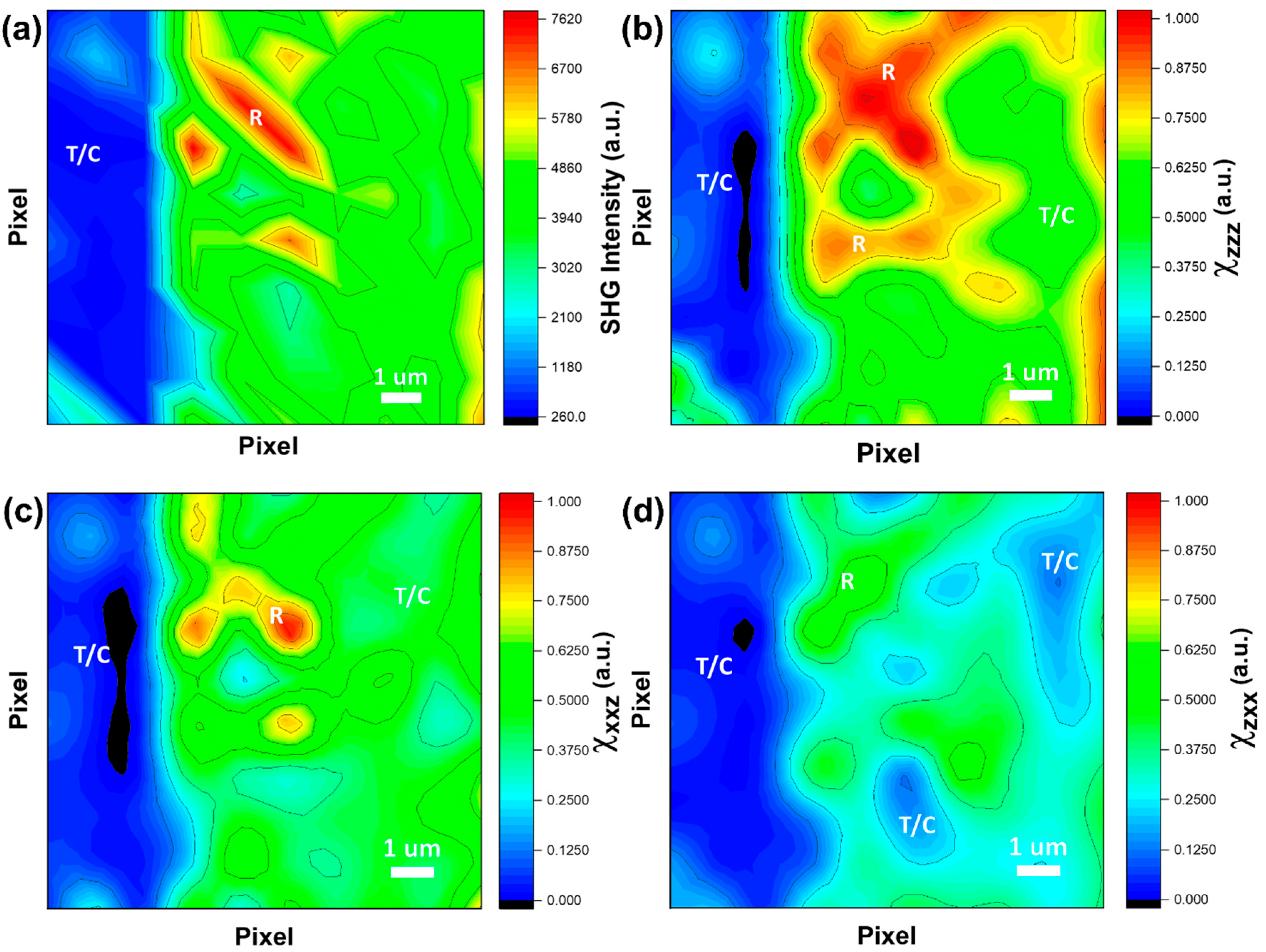
The mixed rhombohedral and tetragonal phases near the GB can be further revealed using spatially resolved SHG polarimetry.
Figure 4a demonstrates the SHG intensity image for the pristine STO bicrystal bulk.
Figure 4b–d display SHG images (
and
) of the second-order susceptibility tensor components:
χzzz,
χxxz, and
χzxx, via scanning SHG spectroscopy. Out-of-plane stretching and compressing of
Ti-O bonds along the crystallographic
c-axis influences the magnitude of
χzzz while in-plane stretching and compressing of
Ti-O bonds in the crystallographic
ab-plane influences the magnitude of
χxxz. Out-of-plane bending of crystallographic
a- and
b-axis
Ti-O bonds contributes to the magnitude of
χzxx. We identify the T-like and R-like polar structures based on the characteristic bright–dark SHG contrast, facilitating polarimetric analysis of local structural symmetries.
SHG intensities for the polarization combinations at
pp (
pin-pout),
ps (
pin-sout), and
ds (
din-sout) were directly measured from the sample surface. These measured values were then used in Equations (4), (5), and (9) to extract the second-order nonlinear susceptibility
χ(2) components,
,
,
. The corresponding Fresnel transformation factors, which account for field transmission at interfaces, are given as follows:
These expressions describe the diagonal components of the Fresnel transformation tensor
, where
Lω and
L2ω denote the Fresnel tensors at the fundamental and second harmonic frequencies, respectively. Here,
is the effective refractive index of the SHG-active region at frequency ω,
n(ω) is the refractive index of the incident medium (air), and
n(2ω) is the refractive index of the STO) at the second harmonic frequency. In most cases, we approximate
. The angles
θ and
θ′ represent the incidence angle in air and the refracted angle inside the nonlinear medium, respectively, and are related through Snell’s law:
, where
ω corresponds to the fundamental input light and 2
ω to the second harmonic output. The refractive index of STO as a function of wavelength
λ (in μm) at room temperature is described by the Sellmeier equation:
From this, the refractive indices at the fundamental and second harmonic wavelengths are determined to be
n(
ω) = 2.34 and
n(2
ω) = 2.65, respectively.
The R-phase domains are expected to exhibit similar
χzzz and
χxxz amplitudes due to their inclined polarization orientations, which possess equivalent out-of-plane and in-plane components. However, the
χzxx amplitude significantly decreases for R-phase domains with out-of-plane polarization orientations. In contrast, the T-phase domains display maximum
χzzz amplitudes, as their polarizations are strongly influenced by out-of-plane stretching, while their
χxxz amplitudes remain negligible due to the absence of an in-plane polarization component. Furthermore, because T-phase domains lack shear deformation, they contribute negligibly to the
χzxx amplitudes averaged over the film thickness. As a result, the high-amplitude “islands” (red and yellow regions) in
Figure 4a correspond to R-phase (red and yellow) domain-rich areas in the rotated GB, whereas the surrounding matrix regions (blue and green) are T-phase rich.
Figure 4b–d present the contour images of different susceptibility components
χzzz, χxxz, and
χzxx associated with tetragonal (4 mm) symmetry, respectively. The SHG image reflects the structural evolution from tetragonal to rhombohedral phases across the grain boundary. These susceptibilities were evaluated based on theoretical models for both 4 mm and 3 m point group symmetries. The domain patterns are distinctly resolved in each SHG component, revealing strong spatial contrasts between regions of differing phase symmetries. The SHG responses clearly delineate the domain boundaries, which align with the crystallographic orientations at the GB, highlighting the structural distortions associated with dislocation cores in the STO bicrystals [
14].
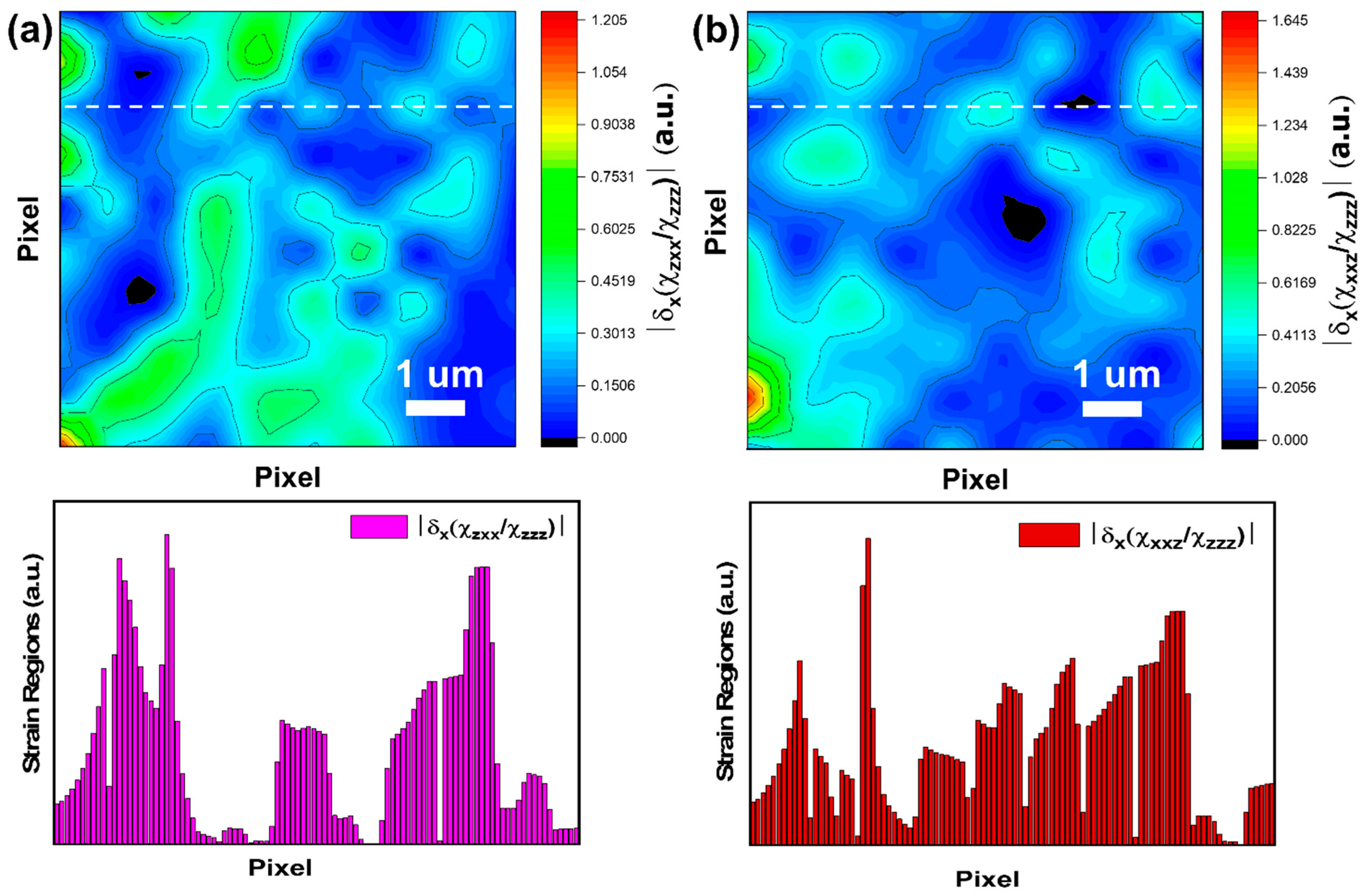
The locally strained regions arising from GB structural distortions in the STO bicrystals can be further visualized by numerically differentiating the ratios of nonlinear susceptibilities obtained from spatially resolved SHG polarimetry [
19].
Figure 5a,b demonstrate the contour images of the first order derivative changes of
χzxx/χzzz (out-of-plane
Ti-O bending/out-of-plane
Ti-O stretching) and the first order derivative changes of
χxxz/χzzz (in-plane
Ti-O stretching/out-of-plane
Ti-O stretching) across the film. The ratios of these components reveal the relative strengths of bond stretching and bending in each region, which directly correlate with the distribution of the internal elastic strain near GB. From the first-order derivative changes of
, we observe that the R-phase domain structures exhibit significant
Ti-O bond out-of-plane bending, while the derivative changes
ratio highlights pronounced stress field due to in-plane and out-of-plane
Ti-O bond stretching. In the STO bicrystals, stress relaxation occurs through the formation of elastic polydomains near the dislocation cores. The bottom panel in
Figure 5a,b, displays the corresponding the spatial variation in the derivative change of the ratio of off-diagonal χ
(2) components
and
, strain distribution (absolute values of susceptibility ratio derivatives) throughout the bicrystal surface indicated by white dashed line. While SHG imaging offers high spatial and symmetry resolution, it does not provide absolute values of strain; rather, it reflects relative variations associated with symmetry-breaking effects. Both ratios of off-diagonal χ
(2) components provide direct evidence of local strain fields, directly related to the lattice mismatch and broken symmetry at GB. The spatial mapping of these components reveals regions of enhanced shear or uniaxial distortion at specific domain interfaces, which act collectively as a relaxation mechanism of misfit strains with the dislocation cores.
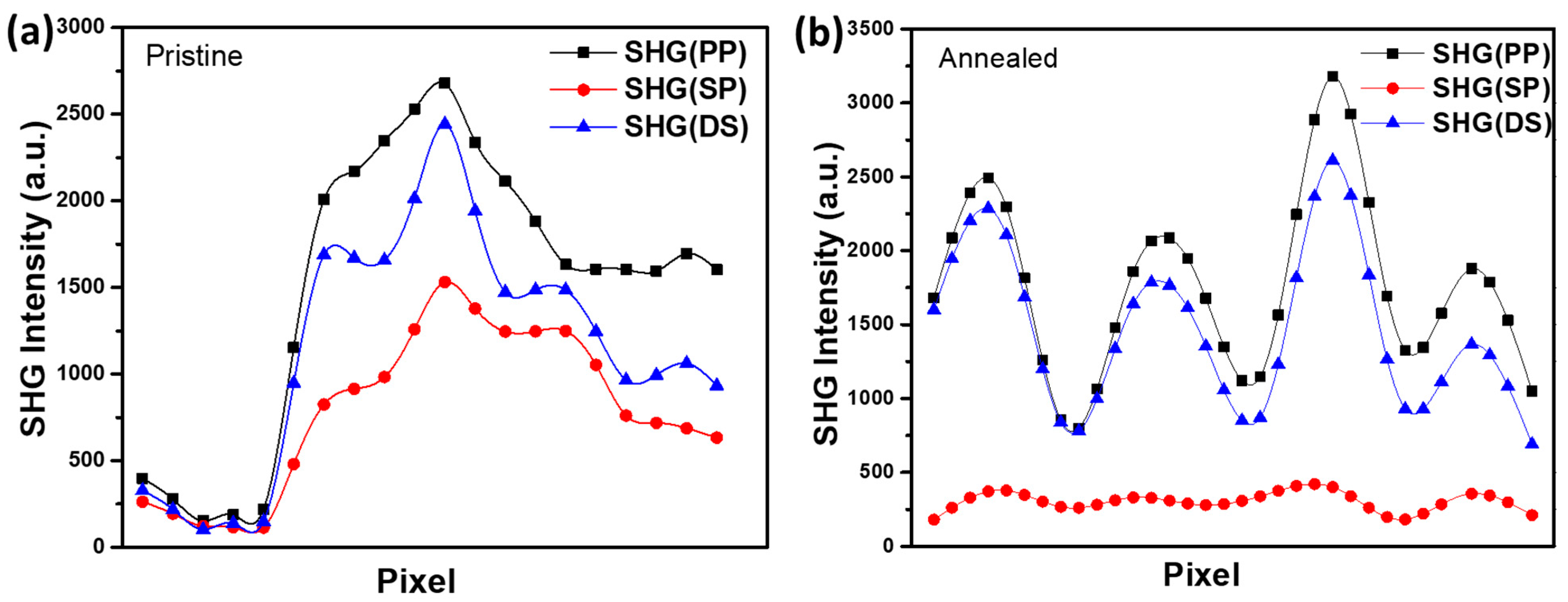
To compare the structural responses before and after degradation, we performed transmission SHG measurements on both pristine and annealed STO bicrystals.
Figure 6a,b show the SHG intensity distributions across the two samples. The SHG profiles exhibit a clear correlation with strain and defect distributions near the GB. In the pristine sample, the SHG intensity is low in the original crystal bulk, peaks sharply at the GB, and gradually diminishes across the rotated domain. This behavior reflects strain accumulation and local broken symmetry near the GB, primarily due to dislocation cores and lattice mismatch. In contrast, the annealed sample exhibits a broadened and more uniform SHG response, indicative of strain relaxation throughout the crystal. This relaxation is attributed to oxygen vacancy migration under a
dc electric field applied during the degradation process: O
2− anions migrate toward the anode, while oxygen vacancies move in the opposite direction. The GB impedes vacancy diffusion, resulting in vacancy accumulation and the generation of internal electric fields that redistribute and mitigate the localized strain. These observations demonstrate the high sensitivity of SHG to lattice distortions and defect dynamics, providing direct optical evidence of field-induced degradation and internal field formation in perovskite oxide bicrystals [
34,
35,
36].
Our SHG measurements reveal the localized nonlinear responses at GB in wide-band-gap perovskite bicrystal STO. Understanding and controlling local strain and domain structures at grain boundaries can directly impact the performance and reliability of perovskite oxide–based devices. For example, in photovoltaics and other optoelectronic applications, strain and defect distributions influence charge carrier dynamics, recombination rates, and ionic migration pathways—factors critical for device efficiency and stability. Our results thus provide a foundation for strain engineering strategies aimed at optimizing functional oxide materials in such technologies.