Accurate Absorption Energy Calculations in Solution Using the Reference Interaction Site Model Self-Consistent Field Including the Constrained Spatial Electron Density Distribution
Abstract
:1. Introduction
2. Methods
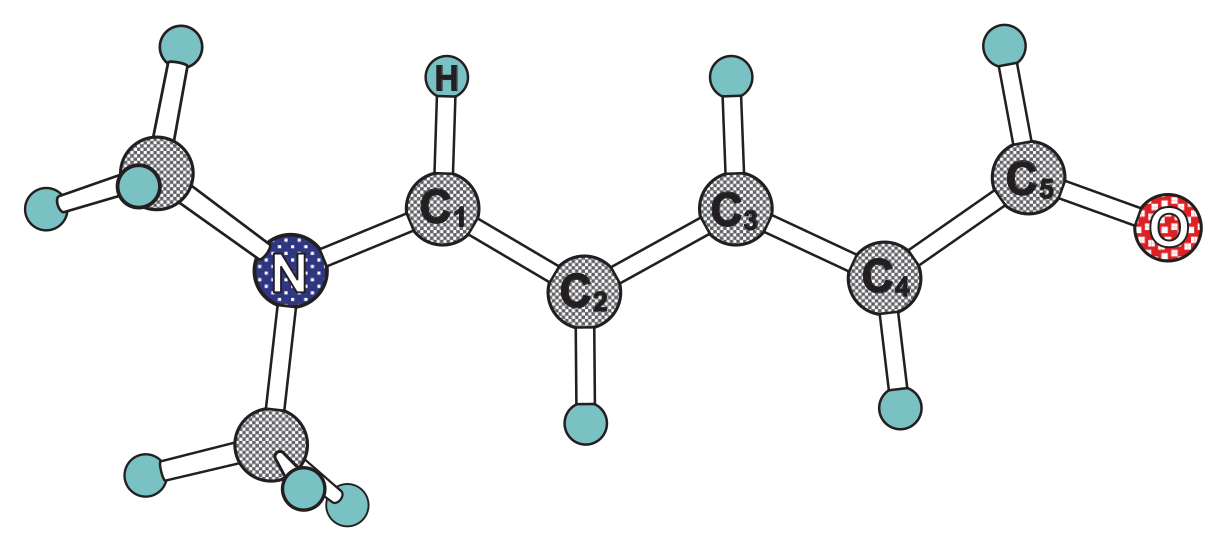
3. Computational Details
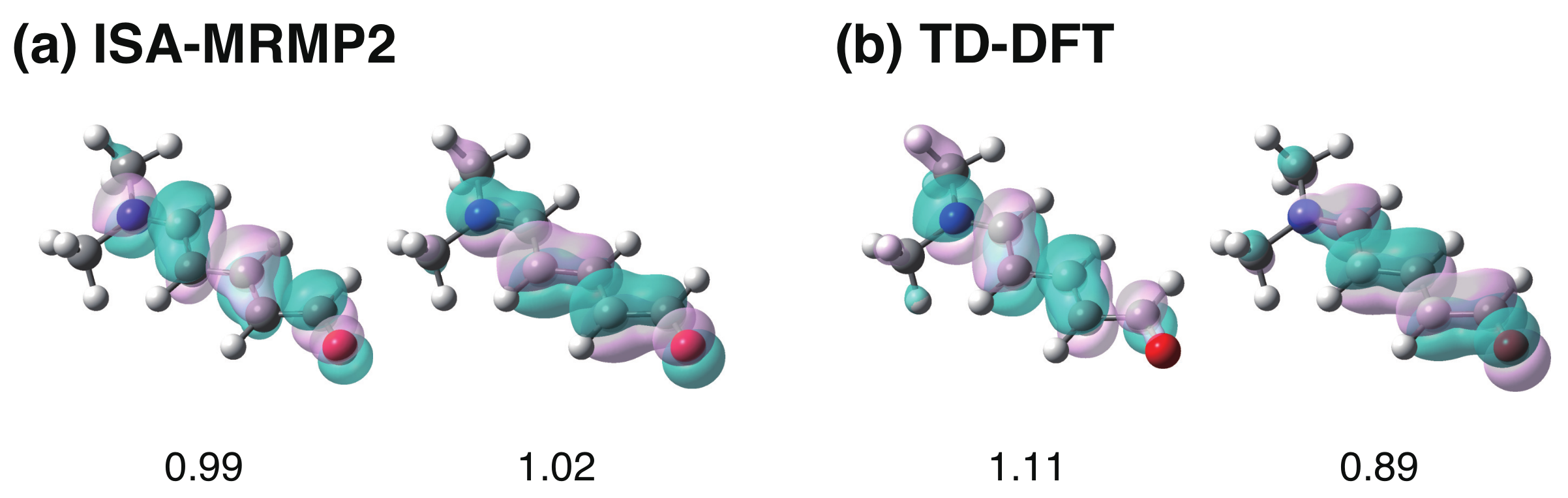
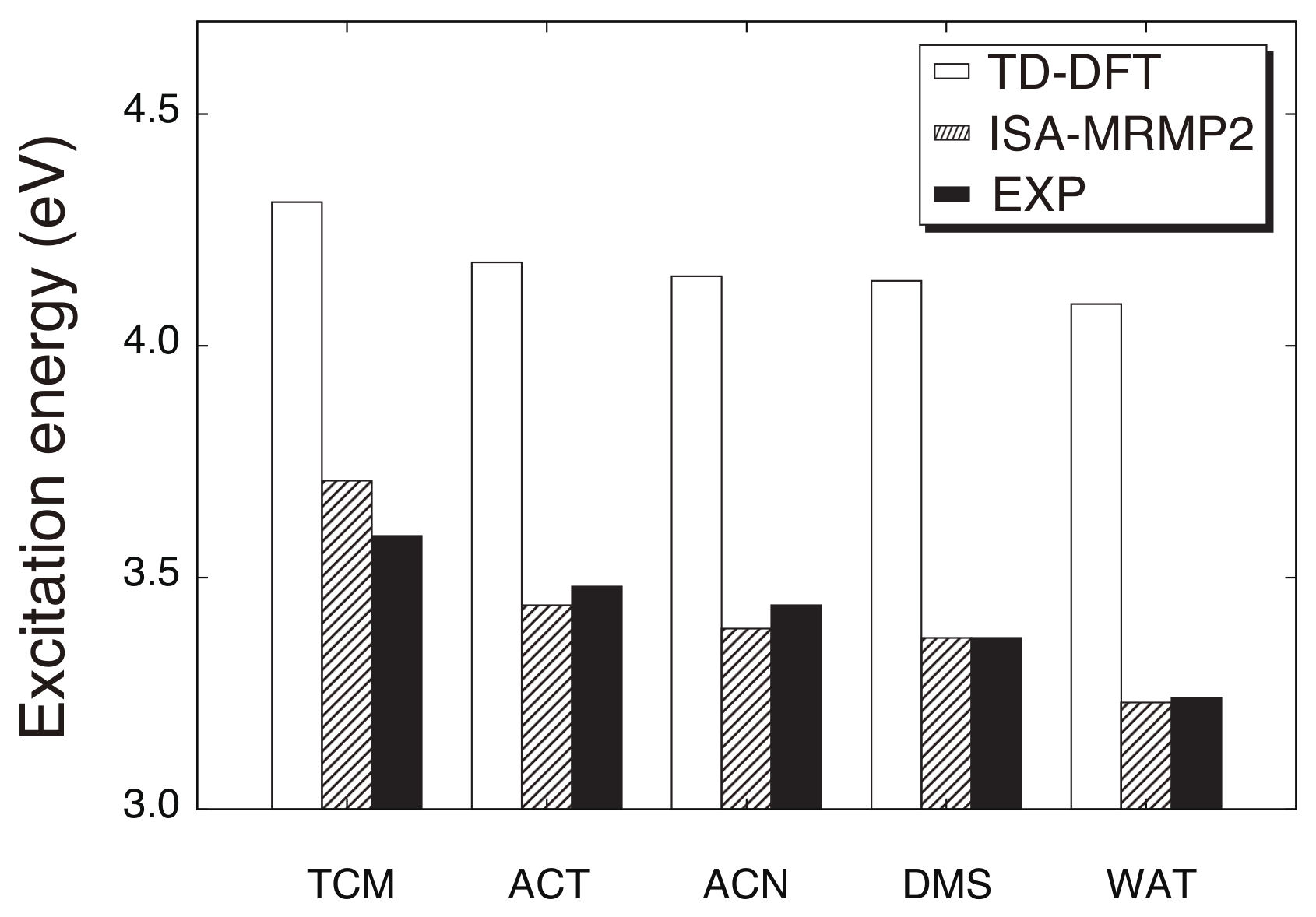
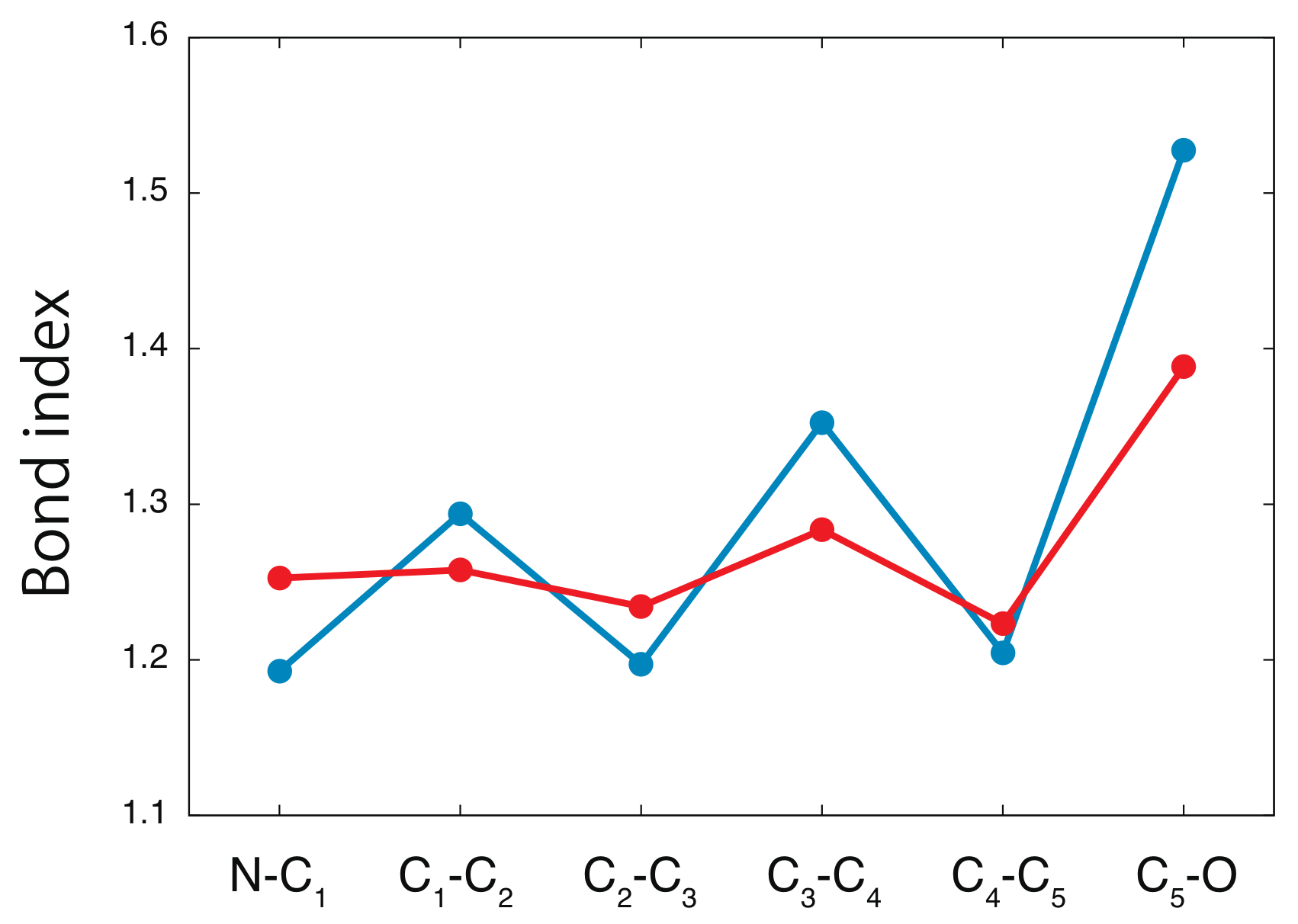
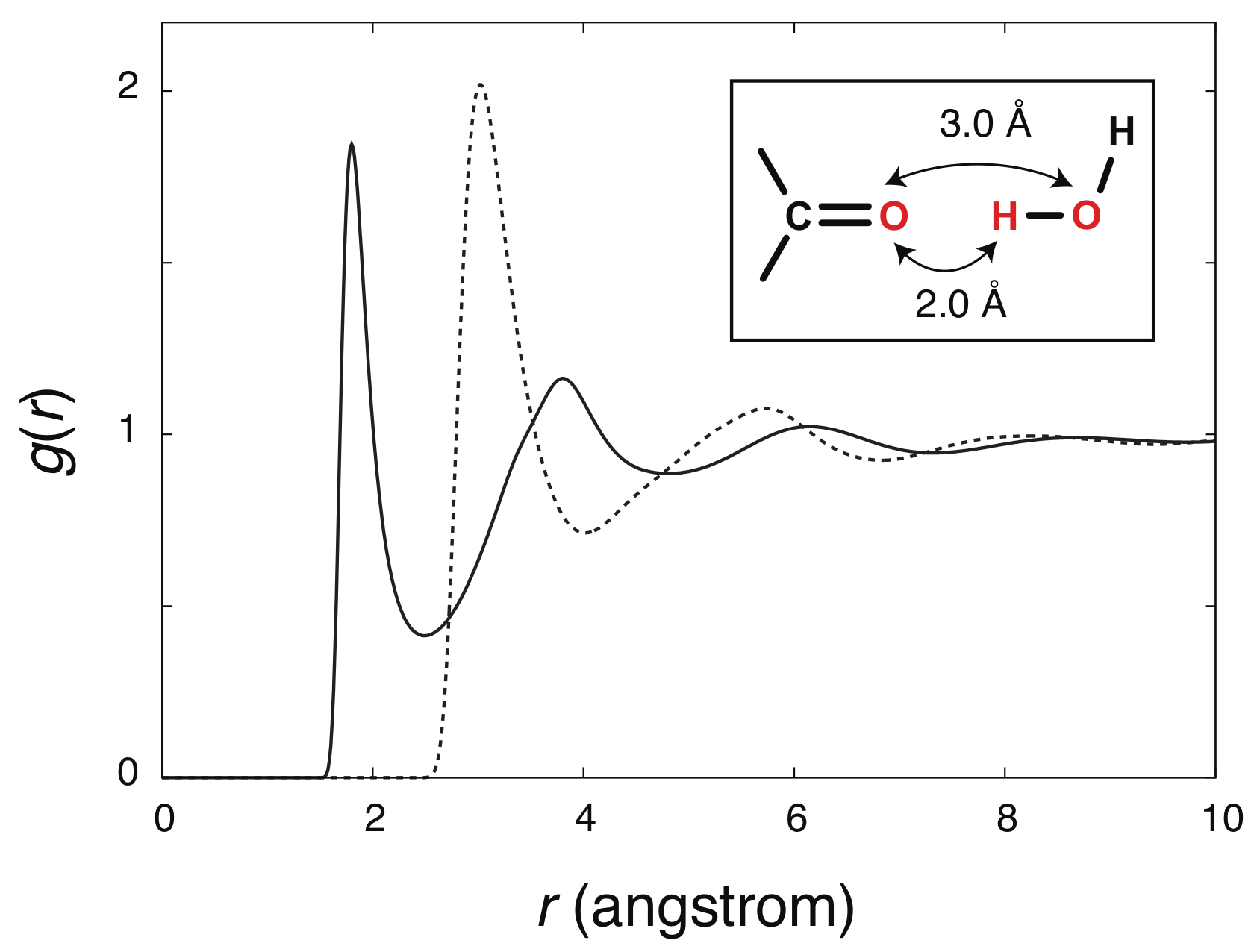
4. Results and Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Naka, K.; Sato, H.; Morita, A.; Hirata, F.; Kato, S. RISM-SCF study of the free-energy profile of the Menshutkin-type reaction NH3 + CH3Cl− → NH3CH3 + Cl− in aqueous solution. Theor. Chem. Acc. 1999, 102, 165. [Google Scholar] [CrossRef]
- Sato, H.; Sakaki, S. Comparison of Electronic Structure Theories for Solvated Molecules: RISM-SCF versus PCM. J. Phys. Chem. A 2004, 108, 1629–1634. [Google Scholar] [CrossRef]
- Nakano, H.; Yamamoto, T. Variational calculation of quantum mechanical/molecular mechanical free energy with electronic polarization of solvent. J. Chem. Phys. 2012, 136, 134107. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, E.; Fukazawa, A.; Kosaka, Y.; Yokogawa, D.; Irle, S.; Yamaguchi, S. A Benzophosphole P-Oxide with an Electron-Donating Group at 3-Position: Enhanced Fluorescence in Polar Solvents. Bull. Chem. Soc. Jpn. 2015, 88, 1545–1552. [Google Scholar] [CrossRef]
- Shimizu, R.Y.; Yanai, T.; Kurashige, Y.; Yokogawa, D. Electronically Excited Solute Described by RISM Approach Coupledwith Multireference Perturbation Theory: Vertical Excitation Energies of Bioimaging Probes. J. Chem. Theory Comput. 2018, 14, 5673–5679. [Google Scholar] [CrossRef] [PubMed]
- Arifin; Yokogawa, D.; Schnupf, U.; Irle, S. Statistical Mechanics-Based Theoretical Investigation of Solvation Effects on Glucose Anomer Preferences. J. Phys. Chem. B 2018, 122, 290–296. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids, 2nd ed.; Academic: London, UK, 1986. [Google Scholar]
- Chandler, D.; Andersen, H.C. Optimized Cluster Expansions for Classical Fluids. II. Theory of Molecular Liquids. J. Chem. Phys. 1972, 57, 1930–1937. [Google Scholar] [CrossRef]
- Hirata, F.; Rossky, P.J. An extended RISM equation for molecular polar fluids. Chem. Phys. Lett. 1981, 83, 329–334. [Google Scholar] [CrossRef]
- Hirata, F. (Ed.) Molecular Theory of Solvation; Kluwer: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Ten-no, S.; Hirata, F.; Kato, S. A hybrid approach for the solvent effect on the electronic-structure of a solute based on the RISM and Hartree-Fock equations. Chem. Phys. Lett. 1993, 214, 391–396. [Google Scholar] [CrossRef]
- Sato, H.; Hirata, F.; Kato, S. Analytical energy gradient for the reference interaction site model multiconfiguration self-consistent-field method: Application to 1,2-difluoroethylene in aqueous solution. J. Chem. Phys. 1996, 105, 1546–1551. [Google Scholar] [CrossRef]
- Yokogawa, D.; Sato, H.; Sakaki, S. New generation of the reference interaction site model self-consistent field method: Introduction of spatial electron density distribution to the solvation theory. J. Chem. Phys. 2007, 126, 244504. [Google Scholar] [CrossRef] [Green Version]
- Yokogawa, D. New Generation of the Reference Interaction Site Model Self-Consistent Field Method: Introduction of Constrained Spatial Electron Density Distribution (cSED). Bull. Chem. Soc. Jpn. 2018, 91, 1540–1545. [Google Scholar] [CrossRef]
- Yokogawa, D.; Sato, H.; Sakaki, S. Analytical energy gradient for reference interaction site model self-consistent field explicitly including spatial electron density distribution. J. Chem. Phys. 2009, 131, 214504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yokogawa, D. New fitting approach of electrostatic potential for stable quantum mechanical calculations using the reference interaction site model. Chem. Phys. Lett. 2013, 587, 113–117. [Google Scholar] [CrossRef]
- Bayly, C.I.; Cieplak, P.; Cornell, W.D.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Hayaki, S.; Kido, K.; Yokogawa, D.; Sato, H.; Sakaki, S. A theoretical analysis of a Diels-Alder reaction in ionic liquids. J. Phys. Chem. B 2009, 113, 8227–8230. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, Y.; Yokogawa, D.; Irle, S. Theoretical study of cellobiose hydrolysis to glucose in ionic liquids. Chem. Phys. Lett. 2014, 603, 7–12. [Google Scholar] [CrossRef]
- Arifin; Puripat, M.; Yokogawa, D.; Parasuk, V.; Irle, S. Glucose Transformation to 5-Hydroxymethylfurfural in Acidic Ionic Liquid: A Quantum Mechanical Study. J. Comput. Chem. 2016, 37, 327–335. [Google Scholar] [CrossRef] [PubMed]
- Iida, K.; Yokogawa, D.; Sato, H.; Sakaki, S. The barrier origin on the reaction of CO2+OH− in aqueous solution. Chem. Phys. Lett. 2007, 443, 264–268. [Google Scholar] [CrossRef]
- Iida, K.; Yokogawa, D.; Ikeda, A.; Sato, H.; Sakaki, S. Carbon dioxide capture at the molecular level. Phys. Chem. Chem. Phys. 2009, 11, 8556–8559. [Google Scholar] [CrossRef] [Green Version]
- Yokogawa, D.; Sato, H.; Sakaki, S.; Kimura, Y. Aqueous Solvation of p-Aminobenzonitrile in the Excited States: A Molecular Level Theory on Density Dependence. J. Phys. Chem. B 2010, 114, 910–914. [Google Scholar] [CrossRef] [PubMed]
- Yokogawa, D.; Ono, K.; Sato, H.; Sakaki, S. Theoretical study on aquation reaction of cis-platin complex: RISM-SCF-SEDD, a hybrid approach of accurate quantum chemical method and statistical mechanics. Dalton Trans. 2011, 40, 11125–11130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yokogawa, D. Coupled Cluster Theory Combined with Reference Interaction Site Model Self-Consistent Field Explicitly Including Spatial Electron Density Distribution. J. Chem. Theory Comput. 2018, 14, 2661–2666. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, R.Y.; Yanai, T.; Yokogawa, D. Improved RISM-CASSCF Optimization via State-Average Treatment and Damping for Characterizing Excited Molecules in Solution with Multireference Perturbation Theory. J. Chem. Theory Comput. 2020, 16, 4865–4873. [Google Scholar] [CrossRef] [PubMed]
- Yokogawa, D. Time-dependent density functional theory (TD-DFT) coupled with reference interaction site model self-consistent field explicitly including spatial electron density distribution (RISM-SCF-SEDD). J. Chem. Phys. 2016, 145, 094101. [Google Scholar] [CrossRef] [PubMed]
- Negishi, N.; Yokogawa, D. Analytical energy gradient for the second order Møller-Plesset perturbation theory coupled with the reference interaction site model self-consistent field explicitly including spatial electron density distribution. J. Chem. Phys. 2021, 154, 154101. [Google Scholar] [CrossRef] [PubMed]
- Suda, K.; Sarinastiti, A.; Arifin; Kimura, Y.; Yokogawa, D. Understanding Structural Changes through Excited-State Intramolecular Proton Transfer in 4′-N,N-Diethylamino-3-hydroxyflavone (DEAHF) in Solution Based on Quantum Chemical Calculations. J. Phys. Chem. B 2019, 123, 9872–9881. [Google Scholar] [CrossRef] [PubMed]
- Yokogawa, D. Linear response approximation to reference interaction site model self-consistent field explicitly including spatial electron density distribution. Free energy. J. Chem. Phys. 2013, 138, 164109. [Google Scholar] [CrossRef] [PubMed]
- Hirao, K. Multireference Møller-Plesset method. Chem. Phys. Lett. 1992, 190, 374–380. [Google Scholar] [CrossRef]
- Witek, H.A.; Choe, Y.K.; Finley, J.P.; Hirao, K. Intruder State Avoidance Multireference Møller-Plesset Perturbation Theory. J. Comput. Chem. 2002, 23, 957–965. [Google Scholar] [CrossRef] [PubMed]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Papajak, E.; Zheng, J.; Xu, X.; Leverentz, H.R.; Truhlar, D.G. Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions. J. Chem. Theory Comput. 2011, 7, 3027–3034. [Google Scholar] [CrossRef]
- Jorgensen, W.L. OPLS and OPLS-AA Parameters for Organic Molecules, Ions, and Nucleic Acids; Yale University: New Haven, CT, USA, 1997. [Google Scholar]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Dähne, S.; Schob, F.; Nolte, K.D. Die Lösungsmittelabhängigkeit der Oszillatorenstärke des 5-Dimethylaminopentadienals, eines einfachen McRocyanin-Farbstoffes. Z. Chem. 1973, 13, 471–473. [Google Scholar] [CrossRef]
- Wiberg, K.B. Application of the Pople-Santry-Segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yokogawa, D. Accurate Absorption Energy Calculations in Solution Using the Reference Interaction Site Model Self-Consistent Field Including the Constrained Spatial Electron Density Distribution. J 2021, 4, 638-644. https://doi.org/10.3390/j4040046
Yokogawa D. Accurate Absorption Energy Calculations in Solution Using the Reference Interaction Site Model Self-Consistent Field Including the Constrained Spatial Electron Density Distribution. J. 2021; 4(4):638-644. https://doi.org/10.3390/j4040046
Chicago/Turabian StyleYokogawa, Daisuke. 2021. "Accurate Absorption Energy Calculations in Solution Using the Reference Interaction Site Model Self-Consistent Field Including the Constrained Spatial Electron Density Distribution" J 4, no. 4: 638-644. https://doi.org/10.3390/j4040046
APA StyleYokogawa, D. (2021). Accurate Absorption Energy Calculations in Solution Using the Reference Interaction Site Model Self-Consistent Field Including the Constrained Spatial Electron Density Distribution. J, 4(4), 638-644. https://doi.org/10.3390/j4040046





