Computational Prediction of New Series of Topological Ternary Compounds LaXS (X = Si, Ge, Sn) from First-Principles
Abstract
:1. Introduction
2. Computational Method
3. Results and Discussion
3.1. Crystal Structure
3.2. Volume Optimization
3.3. Formation Energy
3.4. Elastic Properties
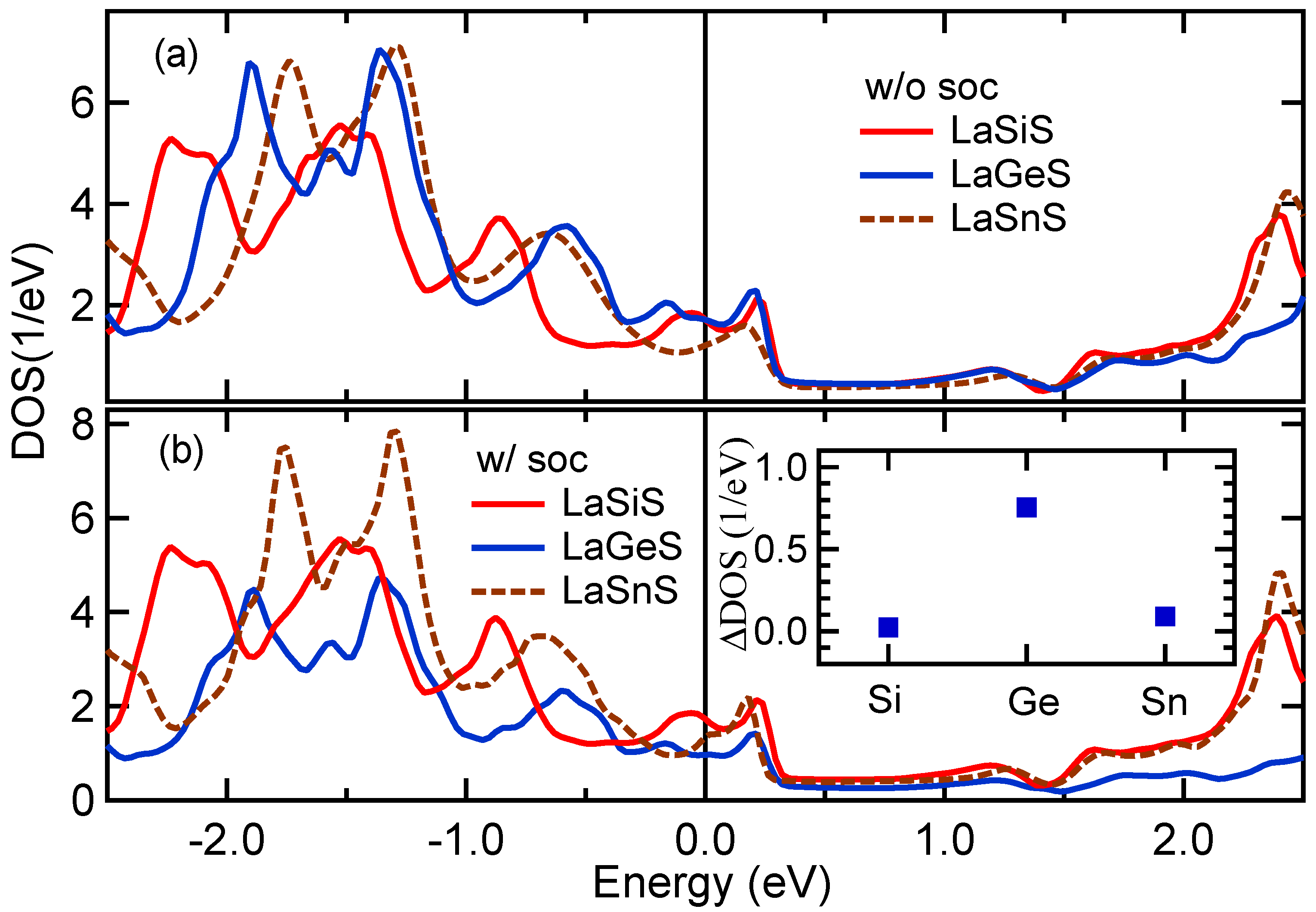
3.5. Band Structure and DOS Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liang, T.; Gibson, Q.; Ali, M.N.; Liu, M.; Cava, R.J.; Ong, N.P. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 2015, 14, 280–284. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.Z.; Kane, C.L. Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.-J.; Nagaosa, N. Classification of stable three-dimensional Dirac semimetals with nontrivial topology. Nat. Commun. 2014, 5, 4898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, G.; Weng, H.; Wang, Z.; Dai, X.; Fang, Z. Chern Semimetal and the Quantized Anomalous Hall Effect in HgCr2Se4. Phys. Rev. Lett. 2011, 107, 186806. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zyuzin, A.A.; Wu, S.; Burkov, A.A. Weyl semimetal with broken time reversal and inversion symmetries. Phys. Rev. B 2012, 85, 165110. [Google Scholar] [CrossRef] [Green Version]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; NPeres, N.M.R.; Geim, A.K. Fine structure constant defines visual transparency of graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Tan, Y.-W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Z.K.; Jiang, J.; Zhou, B.; Wang, Z.J.; Zhang, Y.; Weng, H.M.; Prabhakaran, D.; Mo, S.-K.; Peng, H.; Dudin, P.; et al. A stable three-dimensional topological Dirac semimetal Cd3As2. Nat. Mater. 2014, 13, 677–681. [Google Scholar] [CrossRef] [PubMed]
- Rui, Y.; Weng, H.; Fang, Z.; Dai, X.; Hu, X. Topological Node-Line Semimetal and Dirac Semimetal State in Antiperovskite Cu3PdN. Phys. Rev. Lett. 2015, 115, 036807. [Google Scholar]
- Young, S.M.; Zaheer, S.; Teo, J.C.Y.; Kane, C.L.; Mele, E.J.; Rappe, A.M. Dirac Semimetal in Three Dimensions. Phys. Rev. Lett. 2012, 108, 140405. [Google Scholar] [CrossRef]
- Liu, Z.K.; Zhou, B.; Zhang, Y.; Wang, Z.J.; Weng, H.M.; Prabhakaran, D.; Mo, S.-K.; Shen, Z.X.; Fang, Z.; Dai, X.; et al. Discovery of a Three-Dimensional Topological Dirac Semimetal, Na3Bi. Science 2014, 343, 864–867. [Google Scholar] [CrossRef] [Green Version]
- Neupane, M.; Xu, S.-Y.; Sankar, R.; Alidoust, N.; Bian, G.; Liu, C.; Belopolski, I.; Chang, T.-R.; Jeng, H.-T.; Lin, H.; et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2. Nat. Commun. 2014, 5, 3786. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Xu, S.-Y.; Liu, C.; Kushwaha, S.K.; Sankar, R.; Krizan, J.W.; Belopolski, I.; Neupane, M.; Bian, G.; Alidoust, N.; et al. Observation of Fermi arc surface states in a topological metal. Science 2015, 347, 294–298. [Google Scholar] [CrossRef] [Green Version]
- Borisenko, S.; Gibson, Q.; Evtushinsky, D.; Zabolotnyy, V.; Büchner, B.; Cava, R.J. Experimental Realization of a Three-Dimensional Dirac Semimetal. Phys. Rev. Lett. 2014, 113, 027603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, M.; Huang, H.; Zhang, K.; Wang, E.; Yao, W.; Deng, K.; Wan, G.; Zhang, H.; Arita, M.; Yang, H.; et al. Lorentz-violating type-II Dirac fermions in transition metal dichalcogenide PtTe2. Nat. Commun. 2017, 8, 257. [Google Scholar] [CrossRef]
- Noh, H.-J.; Jeong, J.; Cho, E.-J.; Kim, K.; Min, B.I.; Park, B.-G. Experimental Realization of Type-II Dirac Fermions in a PdTe2 Superconductor. Phys. Rev. Lett. 2017, 119, 016401. [Google Scholar] [CrossRef] [Green Version]
- Gibson, Q.D.; Schoop, L.M.; Muechler, L.; Xie, L.S.; Hirschberger, M.; Ong, N.P.; Car, R.; Cava, R.J. Three-dimensional Dirac semimetals: Design principles and predictions of new materials. Phys. Rev. B 2015, 91, 205128. [Google Scholar] [CrossRef] [Green Version]
- Schoop, L.M.; Pielnhofer, F.; Lotsch, B.V. Chemical Principles of Topological Semimetals. Chem. Mater. 2018, 30, 3155–3176. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.-R.; Chang, T.-R.; Xu, S.-Y.; Sanchez, D.S.; Tsai, W.-F.; Huang, S.-M.; Chang, G.; Hsu, C.-H.; Bian, G.; Belopolski, I.; et al. Type-II Symmetry-Protected Topological Dirac Semimetals. Phys. Rev. Lett. 2017, 119, 026404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, S.-Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.-C.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science. 2015, 349, 613–617. [Google Scholar] [CrossRef] [Green Version]
- Lv, B.Q.; Weng, H.M.; Ma, J.Z.; Richard, P.; Huang, X.C.; Zhao, L.X.; Chen, G.F.; Matt, C.E.; Bisti, F.; Strocov, V.N.; et al. Observation of Weyl nodes in TaAs. Nat. Phys. 2015, 11, 724–727. [Google Scholar] [CrossRef]
- Lv, B.Q.; Gresch, D.; Wang, Z.; Wu, Q.; Troyer, M.; Dai, X.; Bernevig, B.A. Type-II Weyl semimetals. Nature 2015, 527, 495–498. [Google Scholar]
- Deng, K.; Wan, G.; Deng, P.; Zhang, K.; Ding, S.; Wang, E.; Yan, M.; Huang, H.; Zhang, H.; Xu, Z.; et al. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2. Nat. Phys. 2016, 12, 1105–1110. [Google Scholar] [CrossRef]
- Xu, N.; Weng, H.M.; Lv, B.Q.; Matt, C.E.; Park, J.; Bisti, F.; Strocov, V.N.; Gawryluk, D.; Pomjakushina, E.; Conder, K.; et al. Observation of Weyl nodes and Fermi arcs in tantalum phosphide. Nat Commun. 2016, 7, 11006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, L.X.; Liu, Z.K.; Sun, Y.; Peng, H.; Yang, H.F.; Zhang, T.; Zhou, B.; Zhang, Y.; Guo, Y.F.; Rahn, M.; et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat. Phys. 2015, 11, 728–732. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.-M.; Xu, S.-Y.; Belopolski, I.; Lee, C.-C.; Chang, G.; Wang, B.; Alidoust, N.; Bian, G.; Neupane, M.; Zhang, C.; et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 2015, 6, 7373. [Google Scholar] [CrossRef]
- Xie, L.S.; Schoop, L.M.; Seibel, E.M.; Gibson, Q.D.; Xie, W.; Cava, R.J. A new form of Ca3P2 with a ring of Dirac nodes. APL Mater. 2015, 3, 083602. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Yu, R.; Fang, Z.; Dai, X.; Weng, H. Topological nodal line semimetals in the CaP3 family of materials. Phys. Rev. B. 2017, 95, 045136. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Wang, G. A new strongly topological node-line semimetal β-PbO2. Phys. Lett. A. 2017, 381, 2856–2859. [Google Scholar] [CrossRef]
- Yamakage, A.; Yamakawa, Y.; Tanaka1, Y.; Okamoto1, Y. Line-Node Dirac Semimetal and Topological Insulating Phase in Noncentrosymmetric Pnictides CaAgX (X = P, As). J. Phys. Soc. Jpn. 2016, 85, 013708. [Google Scholar] [CrossRef] [Green Version]
- Feng, X.; Yue, C.; Song, Z.; Wu, Q.; Wen, B. Topological Dirac nodal-net fermions in AlB2 -type TiB2 and ZrB2. Phys. Rev. Mater. 2018, 2, 014202. [Google Scholar] [CrossRef] [Green Version]
- Hirayama, M.; Okugawa, R.; Miyake, T.; Murakami, S. Topological Dirac nodal lines and surface charges in fcc alkaline earth metals. Nat. Commun. 2017, 8, 14022. [Google Scholar] [CrossRef] [PubMed]
- Mikitik, G.P.; Sharlai, Y.V. Band-contact lines in the electron energy spectrum of graphite. Phys. Rev. B. 2006, 73, 235112. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Liu, J.; Vanderbilt, D.; Duan, W. Topological nodal-line semimetals in alkaline-earth stannides, germanides, and silicides. Phys. Rev. B 2016, 93, 201114. [Google Scholar] [CrossRef] [Green Version]
- Lou, R.; Ma, J.-Z.; Xu, Q.-N.; Fu, B.-B.; Kong, L.-Y.; Shi, Y.-G.; Richard, P.; Weng, H.-M.; Fang, Z.; Sun, S.-S.; et al. Emergence of topological bands on the surface of ZrSnTe crystal. Phys. Rev. B. 2016, 93, 241104. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Wang, L.-L.; Mun, E.; Johnson, D.D.; Mou, D.; Huang, L.; Lee, Y.; Bud’ko, S.L.; Canfield, P.C.; Kaminski, A. Dirac node arcs in PtSn4. Nat. Phys. 2016, 12, 667–671. [Google Scholar] [CrossRef]
- Bian, G.; Chang, T.-R.; Sankar, R.; Xu, S.-Y.; Zheng, H.; Neupert, T.; Chiu, C.-K.; Huang, S.-M.; Chang, G.; Belopolski, I.; et al. Topological nodal-line fermions in spin–orbit metal PbTaSe2. Nat. Commun. 2016, 7, 10556. [Google Scholar] [CrossRef]
- Takane, D.; Wang, Z.; Souma, S.; Nakayama, K.; Trang, C.X.; Sato, T.; Takahashi, T.; Ando, Y. Dirac-node arc in the topological line-node semimetal HfSiS. Phys. Rev. B. 2016, 94, 121108. [Google Scholar] [CrossRef] [Green Version]
- Topp, A.; Lippmann, J.M.; Varykhalov, A.; Duppel, V.; Lotsch, B.V.; Ast, C.R.; Schoop, L.M. Non-symmorphic band degeneracy at the Fermi level in ZrSiTe. New J. Phys. 2016, 18, 125014. [Google Scholar] [CrossRef] [Green Version]
- Haubold, E.; Koepernik, K.; Efremov, D.; Khim, S.; Fedorov, A.; Kushnirenko, Y.; van den Brink, J.; Wurmehl, S.; Büchner, B.; Kim, T.K.; et al. Experimental realization of type-II Weyl state in noncentrosymmetric TaIrTe4. Phys. Rev. B 2017, 95, 241108(R). [Google Scholar] [CrossRef] [Green Version]
- Schoop, L.; Ali, M.N.; Straβer, C.; Topp, A.; Varykhalov, A.; Marchenko, D.; Duppel, V.; Parkin, S.S.P.; Lotsch, B.V.; Ast, C.R. Dirac cone protected by non-symmorphic symmetry and three-dimensional Dirac line node in ZrSiS. Nat. Commun. 2016, 7, 11696. [Google Scholar] [CrossRef]
- Hu, J.; Tang, Z.; Liu, J.; Liu, X.; Zhu, Y.; Graf, D.; Myhro, K.; Tran, S.; Lau, C.N.; Wei, J.; et al. Evidence of Topological Nodal-Line Fermions in ZrSiSe and ZrSiTe. Phys. Rev. Lett. 2016, 117, 016602. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Zhou, S.; Duan, W. Type-II Dirac fermions in the PtSe2 class of transition metal dichalcogenides. Phys. Rev. B 2016, 94, 121117. [Google Scholar] [CrossRef] [Green Version]
- Muechler, L.; Alexandradinata, A.; Neupert, T.; Car, R. Topological Nonsymmorphic Metals from Band Inversion. Phys. Rev. X 2016, 6, 041069. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Xie, Y.; Yang, S.A.; Pan, H.; Zhang, F.; Cohen, M.L.; Zhang, S. Nanostructured Carbon Allotropes with Weyl-like Loops and Points. Nano Lett. 2015, 15, 6974–6978. [Google Scholar] [CrossRef] [Green Version]
- Young, S.; Kane, C.L. Dirac Semimetals in Two Dimensions. Phys. Rev. Lett. 2015, 115, 126803. [Google Scholar] [CrossRef] [Green Version]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter. 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter. 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Singh, D.J.; Nordstrom, L. Planewaves, Pseudopotentials, and the LAPW Method, 2nd ed.; Springer: New York, NY, USA, 2006; pp. 1–134. [Google Scholar]
- Sjöstedt, E.; Nordström, L.; Singh, D.J. An alternative way of linearizing the augmented plane-wave method. Solid State Commun. 2000, 114, 15–20. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Blaha, P.; Schwarz, K.; Sjöstedt, E.; Nordström, L. Efficient linearization of the augmented plane-wave method. Phys. Rev. B 2001, 64, 195134. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef] [Green Version]
- Blaha, P.; Schwarz, K.; Sorantin, P.; Trickey, S.B. Full-potential, linearized augmented plane wave programs for crystalline systems. Commput. Phys. Commun. 1990, 59, 399–415. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.H.; Marks, L.D. WIEN2k: An APW+lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef] [PubMed]
- Golesorkhtabar, R.; Pavone, P.; Spitaler, J.; Puschniga, P.; Draxl, C. ElaStic: A tool for calculating second-order elastic constants from first principles. Comp. Phys. Commun. 2013, 184, 1861–1873. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef] [Green Version]
- Lee, I.; Hyun, S.I.; Shim, J.H. Topological classification of nodal-line semimetals in square-net materials. Phys. Rev. B 2021, 103, 165106. [Google Scholar] [CrossRef]
- Born, M. On the stability of crystal lattices. I. Math. Proc. Camb. Philos. Soc. 1940, 36, 160–172. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef] [Green Version]
- Kittle, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons: New York, NY, USA, 2004; pp. 1–704. [Google Scholar]
- Koster, G.F.; Dimmock, J.D.; Wheeler, R.G.; Statz, H. Properties of the Thirty-Two Point Groups, 1st ed.; MIT Press: Cambridge, MA, USA, 1963; pp. 1–104. [Google Scholar]
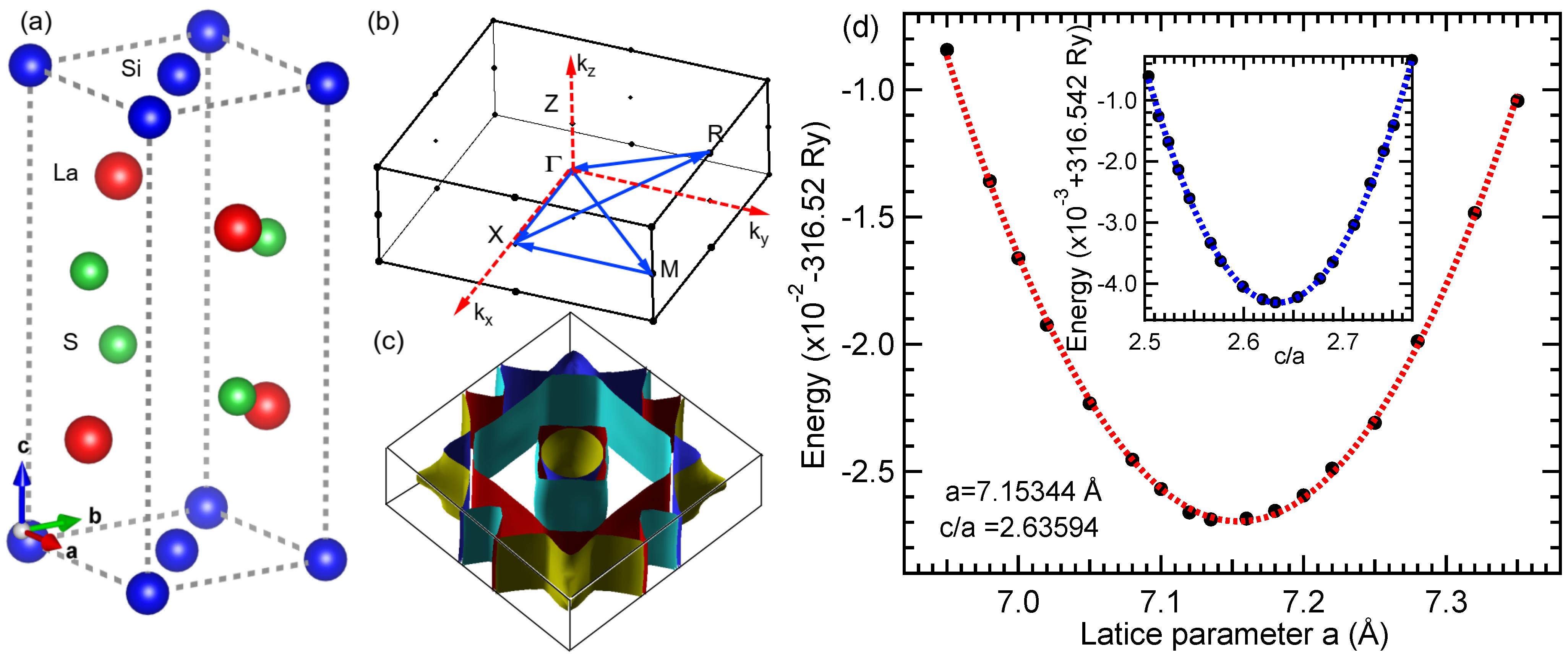
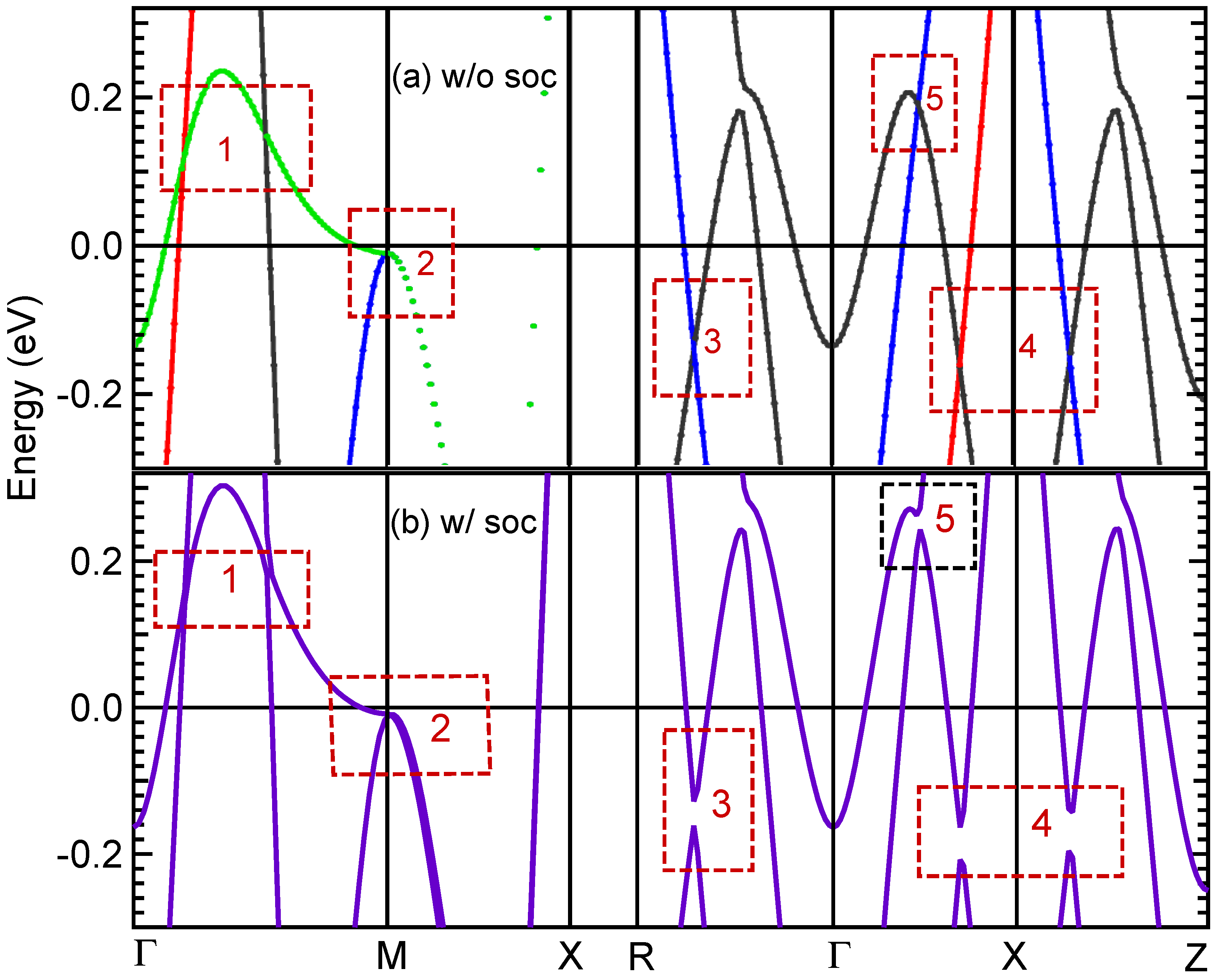
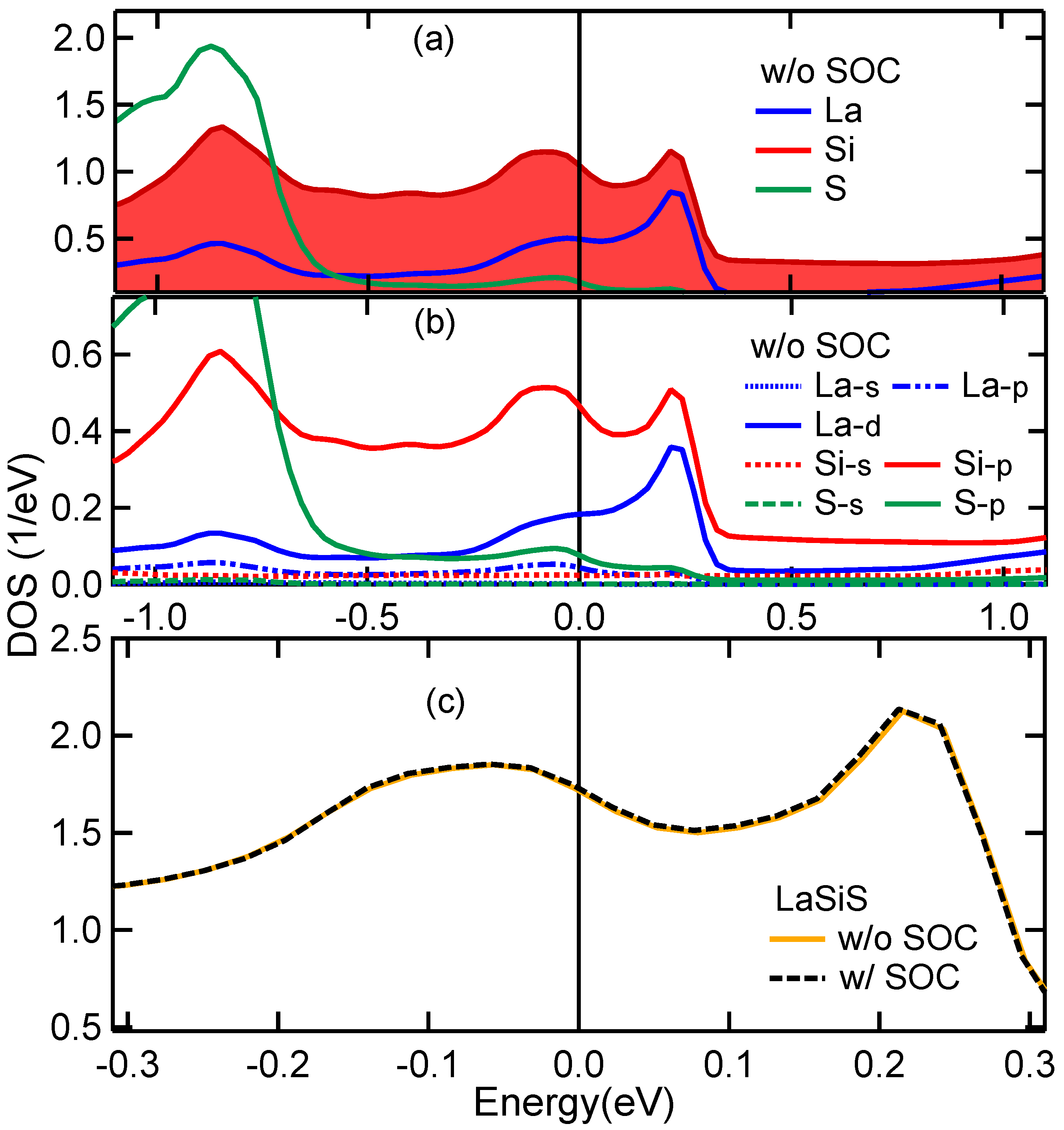
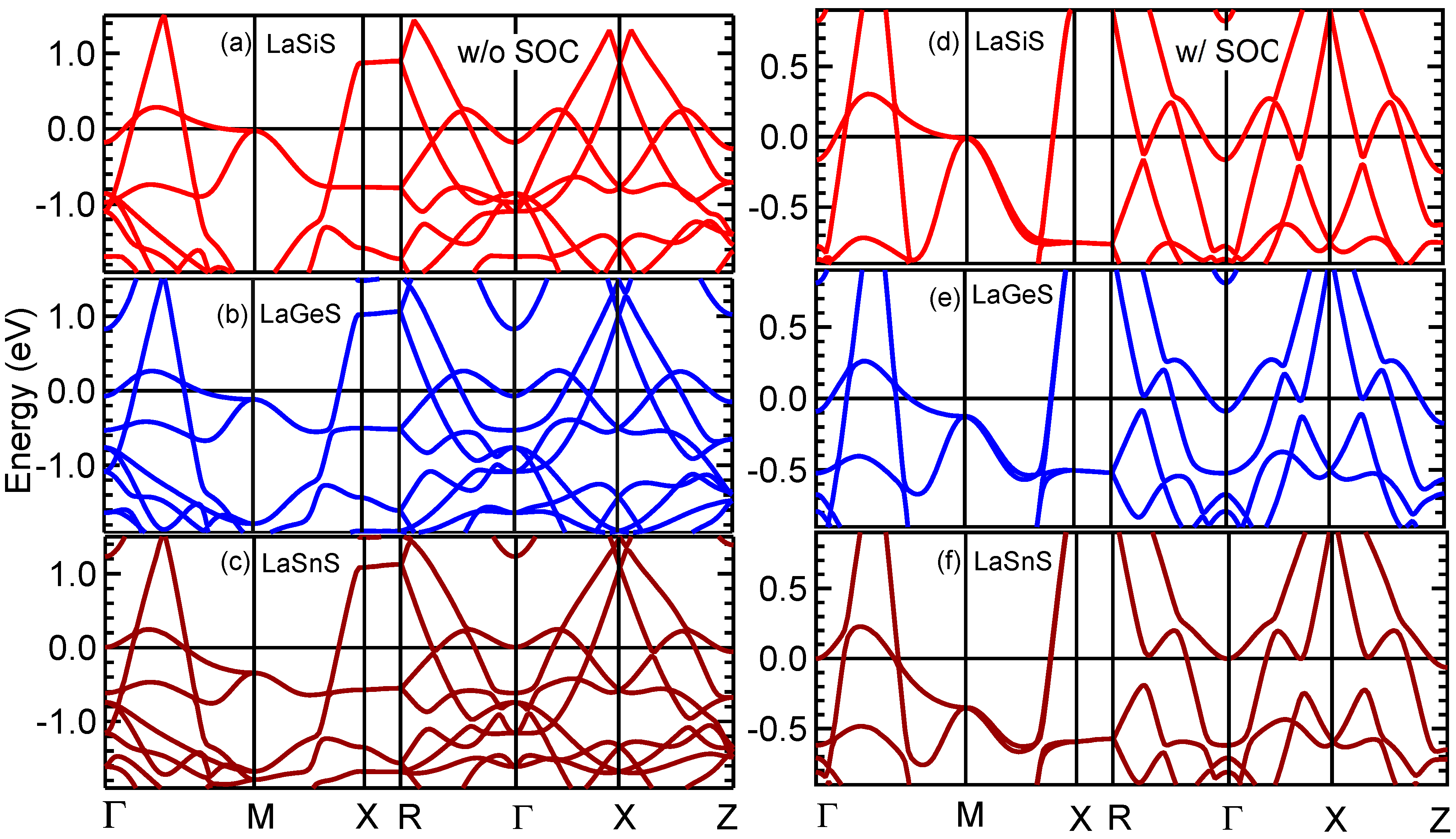
| a (Å) | c (Å) | E (eV/atom) | |
|---|---|---|---|
| LaSiS | 3.7854 | 9.9782 | −1.1898 |
| LaGeS | 3.8581 | 9.9772 | −1.2830 |
| LaSnS | 4.0546 | 10.1559 | −1.2089 |
| B | G | E | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LaSiS | 139.9 | 31.4 | 39.8 | 32.8 | 21.8 | 23.9 | 45.44 | 21.85 | 56.50 | 0.29 |
| LaGeS | 134.1 | 57.0 | 39.7 | 47.1 | 14.7 | 52.3 | 55.82 | 24.20 | 63.42 | 0.31 |
| LaSnS | 112.3 | 78.2 | 21.4 | 63.8 | 1.0 | 90.7 | 53.65 | 16.00 | 43.65 | 0.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Howard, J.; Steier, J.; Haldolaarachchige, N.; Hettiarachchilage, K. Computational Prediction of New Series of Topological Ternary Compounds LaXS (X = Si, Ge, Sn) from First-Principles. J 2021, 4, 577-588. https://doi.org/10.3390/j4040042
Howard J, Steier J, Haldolaarachchige N, Hettiarachchilage K. Computational Prediction of New Series of Topological Ternary Compounds LaXS (X = Si, Ge, Sn) from First-Principles. J. 2021; 4(4):577-588. https://doi.org/10.3390/j4040042
Chicago/Turabian StyleHoward, Jack, Joshua Steier, Neel Haldolaarachchige, and Kalani Hettiarachchilage. 2021. "Computational Prediction of New Series of Topological Ternary Compounds LaXS (X = Si, Ge, Sn) from First-Principles" J 4, no. 4: 577-588. https://doi.org/10.3390/j4040042
APA StyleHoward, J., Steier, J., Haldolaarachchige, N., & Hettiarachchilage, K. (2021). Computational Prediction of New Series of Topological Ternary Compounds LaXS (X = Si, Ge, Sn) from First-Principles. J, 4(4), 577-588. https://doi.org/10.3390/j4040042






