Quantum Matter Overview
Abstract
:1. Introduction
1.1. Quantum Matter
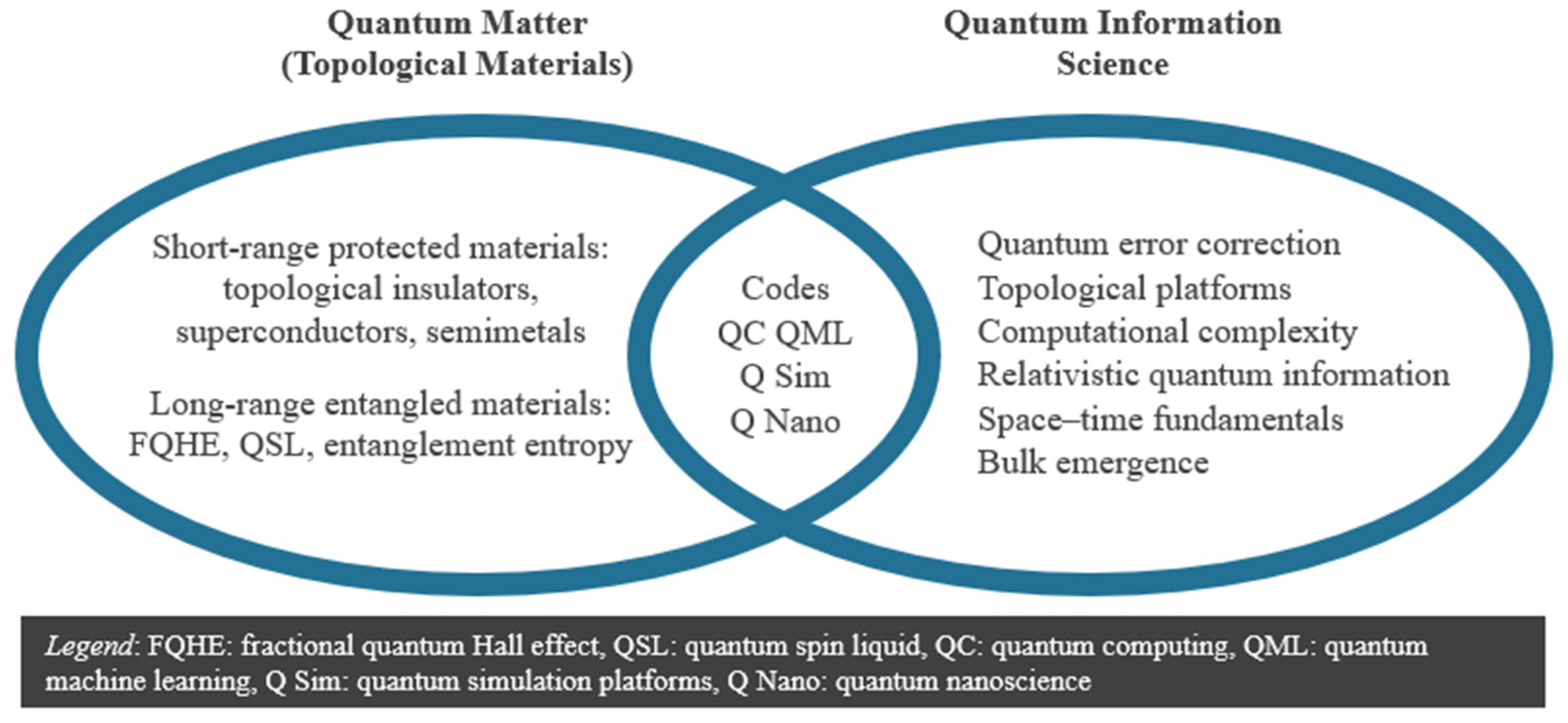
The Relation of Quantum Matter and Quantum Information Science
1.2. Symmetry and Topology
1.2.1. Quasiparticles (Fermions) and Collective Excitations (Bosons)
1.2.2. Anyons: Third Kind of Particle
1.3. Hyperbolic Space (Negative Curvature)
1.3.1. Hyperbolic Bloch Theorem and Hyperbolic Band Theory
1.3.2. Magnetics
1.3.3. Condensates
2. Short-Range Protected Topological Materials
2.1. Introduction to Short-Range Protected Topological Order
2.2. Topological Semimetals
2.2.1. Weyl and Dirac Topological Semimetals
2.2.2. Nodal-Line Topological Semimetals
2.2.3. Magnetic Topological Semimetals
2.2.4. Chiral Topological Semimetals
3. Long-Range Entangled Topological Materials
3.1. Quantum Hall States
3.2. Quantum Spin Liquids
3.2.1. Initial Discovery of Quantum Spin Liquids
3.2.2. Creating Quantum Spin Liquids from Scratch
3.2.3. Topological Qubits, Non-Locality, and Quantum Error Correction
3.3. Entanglement Entropy and Quantum Phase Transition
3.3.1. Topological Entanglement Entropy
3.3.2. Topological Quantum Field Theory
4. Codes (Toric, etc.)
4.1. Stabilizer Codes
4.1.1. The Toric Code
4.1.2. Quantum Error Correction
4.1.3. Stabilizer Codes in Quantum Error Correction
4.2. Bosonic Codes
5. Application Example: Quantum Neuroscience
5.1. Quantum Neuroscience
5.1.1. Neural Signaling Phase Transitions
5.1.2. AdS/Brain Theory (Anti-de Sitter Space)
5.2. Quantum Biology of Deformable Soft Solids
6. Discussion
6.1. Quantum Matter and Quantum Information Science Integration
6.1.1. Universal Quantum Computing
6.1.2. Quantum Machine Learning
6.1.3. Quantum Simulation Platforms
6.1.4. Quantum Nanoscience
6.2. Future Outlook for Quantum Matter Science
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Abelian | Commuting (order of terms does not matter) |
| AdS/Brain | Multi-tier holographic theory of neural signaling based on the AdS/CFT correspondence |
| AdS/CFT correspondence | (Anti-de Sitter space/Conformal Field Theory) Theory positing that a physical system with a bulk volume can be described by a boundary theory in one fewer dimensions |
| Angular momentum | Measure of a body’s tendency to roll, spin, or orbit; measured by amount (magnitude), direction (projection), and intrinsic angular momentum (spin) |
| Anyon | Third type of particle between a fermion and a boson, not fundamental but emerges in many-body systems |
| Anyonic exchange statistics | Computable measure of particles changing places, exchanging wavefunctions by ‘braiding’ |
| Artificial lattice | Atomic-scale structure designed to confine electrons or spins on a chosen lattice (made with scanning tunneling microscopy or electron beam) |
| Band gap | Prohibited range of energy in a system |
| Berry curvature | Gauge-invariant geometrical property of a band; invariant under changes in the phase of the wavefunction |
| Bloch theorem | Solution to the Schrödinger equation for periodic systems |
| Boson | Force particle (photon, gluon, graviton) with integer spin |
| Bosonic code | Photon-based system in which physical and protective logical qubits can be encoded in a self-contained continuous value system in a single bosonic mode (state) |
| Bosonic mode | Photon state controllable with standard Gaussian operations such as squeezing, displacement, phase rotation, and beam splitting |
| Brillouin zone | Geometric zone inside a reciprocal lattice or crystal |
| Cat code | (Schrödinger’s cat) error correction based on superpositioned coherent states |
| Charge | Electrical valence of a particle (particle properties: spin, charge, angular momentum) |
| Chern number | Topological invariant of the Berry curvature flux over a closed momentum surface (global system property) |
| Chern–Simons theory | Mathematical model of topological invariance |
| Chiral topological semimetals | Topological semimetals in crystals with a chiral structure (handedness due to lack of mirror and inversion symmetries) |
| cQED Circuit quantum electrodynamics | Experimental platform for modeling and synthesizing quantum matter phases in hyperbolic space |
| Code (error correction) | Allowed values (or structure of values) for data in a system, may include parameters re: how many ancilla (extra) bits protect one logical bit over what distance |
| Codespace | Error-correction domain; possibly denoted by lattice grid states or graph states |
| Coherent state | Oscillatory quantum state (the quantum state of the harmonic oscillator) |
| Correlation function | The average (expectation value) of field operators at different positions; the amplitude for propagation of a particle or excitation between two points |
| Crystal | Atoms organized in a regular array (lattice); has discrete translation symmetry |
| Crystal lattice | Symmetrical three-dimensional arrangement of atoms inside a crystal |
| Dimer | Molecule of two identical molecules linked together |
| Discrete time crystal | Non-equilibrium state of matter that breaks time translation symmetry (repeating time structure) |
| Eigenvalues | Values at allowable scale tiers in a system, levels; characteristic system values |
| Electron holes | Positively charged quasiparticles denoting the lack of an electron in a state in the valence band of a semiconductor |
| Energy band theory | Allowed/prohibited energy bands/band gaps in systems |
| Entanglement | Quantum property of correlated physical attributes among particles (position, momentum, spin, polarization) |
| Fermion | Matter particle (electron, quark) with half-odd integer (1/2, 3/2, etc.) spin |
| Fractional quantum Hall effect | Quantized plateaus at fractional values of charge, giving rise to quasiparticles (collective states) in which electrons bind magnetic flux lines to make new quasiparticles that have a fractional charge and obey anyonic statistics |
| Floquet engineering | Control of periodically driven time cycles in quantum matter systems |
| Floquet theorem | Periodic system (Bloch) transform to solvable linear differential equations |
| Frontier orbitals | Highest occupied/lowest unoccupied orbitals of a molecule |
| Fuchsian model | Hyperbolic Riemannian surface model |
| Gapless | No band gap in spacing between energy levels in a system |
| Gapped | Gaps in energy bands in a system |
| GKP codes (Gottesman, Kitaev, Preskill) | Error-corrected qubit encoding in an oscillator with superpositions of squeezed states, protected against shifts in position and amplitude damping |
| Hall effect (Hall conductance) | Production of a voltage difference (the Hall voltage) across an electrical conductor that is transverse (perpendicular) to an electric current in the conductor and to an applied magnetic field perpendicular to the current (Hall 1879) |
| Hamiltonian | Operator (function) used to calculate the energy levels of a quantum system |
| Herbertsmithite | Mineral with quantum spin liquid magnetic properties (neither ferromagnet nor antiferromagnet); magnetic particles with constantly fluctuating, scattered orientations on a kagome lattice; (Zinc, Copper, Oxygen, Hydrogen, Chlorine); (Iran, Chile, Arizona, Greece) |
| Hilbert space | Infinite-dimensional space of quantum mechanics (vs 3D Euclidean space) |
| Honeycomb lattice | Standard hexagonal/triangular lattice (e.g., graphene) (generally looks the same from any direction) |
| Hyperbolic band theory | Energy band theory in hyperbolic space |
| Hyperbolic lattice | Synthetic quantum matter in which particles hop on a discrete tessellation of two-dimensional hyperbolic space |
| Hyperbolic space | Geometric space with negative curvature (vs Euclidean space (zero curvature) and elliptic space (positive curvature) |
| Josephson junction | Quantum tunneling superconducting device used in quantum computing |
| Josephson junction-based superconducting circuits | Superconducting qubits controlled with microwave photons (quantized electromagnetic fields stored in the superconducting circuits) |
| K-space | Wave vector space of possible values of momentum for a particle (also the spatial frequency domain of a Fourier transform or a compactly generated topological space) |
| Kagome lattice | Uniform tiling of equilateral triangles and hexagons |
| Kitaev honeycomb lattice | Exactly solvable spin model in two dimensions; spins are on the vertices of a honeycomb lattice with nearest-neighbor interactions |
| Lattice | Regular array geometric arrangement of matter in a space (e.g., crystal); scaffolding |
| Lattice surgery | Switching between error-correcting codes on the fly |
| Magnon | Collective excitation of electron spins in a crystal lattice |
| Many-body problem | Physical systems with many interacting particles (three/more) |
| Majorana fermions | Exotic fermions that are their own antiparticles |
| Many-body localization (MBL) | Many-body interactions causing quantum particles to be localized and maintained in an out-of-equilibrium state |
| Multi-scale entanglement renormalization ansatz (MERA) | Tensor network representation for ground states of critical quantum spin chains (with a network that extends in an additional dimension corresponding to scale) |
| Mode | Characteristic state, normal frequency, allowable value |
| Molecular code | GKP codes for asymmetric bodies (molecules) in free space |
| Nodal-line semimetals | Topological semimetals with energy band-touching manifolds in the shape of closed loops |
| Non-abelian | Non-commuting (order of terms matters) (v. abelian) |
| Nonsymmorphic | Not comparable on a symmetry basis (symmetry operations do not have a common point on the lattice) |
| Paramagnet | Material weakly attracted by an external magnetic field |
| Particle properties | Spin, charge, angular momentum, polarization |
| Phonon | Collective excitation of atoms in a rigid crystal structure |
| Plasmon | Collective excitation of electrons simultaneously oscillating with respect to ions |
| Quantum droplet | Quantum matter phase defined by properties emerging from the interactions of bosonic or fermionic constituents |
| Quantum error-correcting code | Logical codespace corresponding to the physical subspace of a lattice |
| Quantum Hall effect | Quantum version of the Hall effect; obtained by applying a strong magnetic field perpendicular to a two-dimensional electron system |
| Quantum matter | Novel phases of matter at zero temperature with emergent order and exotic properties, possibly including the emergence of quasiparticles (collective excitations) with anyonic exchange statistics, gauge theory, quantum phase transitions, and low-energy effective theories of topologically ordered states |
| Quantum nanoscience | Nanostructure fabrication that exploits quantum effects |
| Quantum phase transition | Phase transition between different quantum phases via parameter change such as magnetic field or pressure |
| Quantum spin Hall states | Quantum Hall effect based on the flow of spin currents (as opposed to charge currents) |
| Quantum spin liquid | Quantum matter phase with magnetic spins (qubits) degrees of freedom; a magnetic system that does not settle into a long-range ordered configuration, even at zero temperature, residing in a nontrivial quasi-disordered ground state |
| Quantum topology | Novel properties of topological shapes in quantum systems |
| Quasiparticle | Long-lived, low-energy excitation of a many-body state in fermions (collective excitations in bosons); examples: electron holes, phonons, plasmons, magnons |
| Rényi entropy | Composite of Shannon, Hartley, collision, and minimum entropy |
| “Schrödinger cat” states | Superpositioned quantum states |
| Soliton | Stable solitary wavepacket in nonlinear systems |
| Spin | Intrinsic form of angular momentum carried by elementary particles (depicted as an axis of rotation, but actual particles do not rotate); particles with spin may possess a magnetic dipole moment (exploited in electronic devices) |
| Spin chain | Linear collection of magnetic moments with spin–spin coupling interactions |
| Spin engineering | Control of spin systems in devices and materials, including the precise arrangement of magnetic atoms as a probe |
| Spinors | More complicated version of vectors and tensors needed to describe the rotations of particle spin |
| Spintronics (spin electronics) | Using electron spins as the internal degree of freedom to store 0 s/1 s for information processing |
| Squeezed (coherent) state | Pinched oscillatory quantum state (to reduce the quantum noise (environmental interference)) |
| Stabilizer code | Quantum error-correction code (quantum version of linear codes), based on X-, Y-, Z-axis Pauli operators to measure entangled states and correct (bit flip, spin flip) a corrupt quantum state to its original state; commuting operators |
| Subsystem code | Quantum error code with non-commuting operators |
| Surface code | Stabilizer code, topology-based, defined on a two-dimensional spin lattice, taking various shapes |
| Symmetry | Features of particles and spacetime which are unchanged under some transformation; property of looking the same from different points of view (face, cube, laws of physics) |
| Symmetry breaking | Phase transition, rupturing a system’s symmetry (e.g., time-reversal, particle-hole, chiral) |
| Symmetry-protected topological (SPT) order | Quantum matter phases with trivial topological order (short-range entanglement), symmetry, and a finite energy gap (e.g., topological insulator) |
| Tessellation | Tiling of a plane using geometric shapes (tiles) |
| Time-reversal symmetry breaking | System property: the dynamics of a process remain well-defined when the sequence of time-states is reversed |
| Topological entanglement entropy | Topology-based measure of entanglement entropy specific to quantum matter and quantum phase transition calculated from the quasiparticle excitations of the many-body state or in a comparison between the system and the von Neumann entropy (tripartite information; two time, one space dimension) |
| Topological insulator | Material with a conducting surface and an insulating interior; surface states are symmetry-protected (e.g., time-reversal, particle-hole, chiral symmetry) |
| Topological quantum field theory | Quantum field theory emphasizing topological invariants and impervious to spacetime contraction; explains quantum matter phases |
| Topological qubits | Computational qubits made with quantum matter phases (e.g., by putting quantum spin liquids into a geometrical array) |
| Topological semimetals | Material with energy band-touching manifolds (at zero-dimensional points or one-dimensional nodal lines/rings) |
| Topological strings | Strings linking atoms entangled in a quantum spin liquid |
| Topology | The property of geometric form being preserved under deformation (such as bending, stretching, twisting, and crumpling, but not cutting or gluing) |
| Toric code | Stabilizer code defined on a two-dimensional lattice with periodic boundary conditions (torus-shaped); stabilizer operators on the spins around vertex and plaquette (face) |
| Trotterization | Operation to simulate the evolution of a Hamiltonian |
| Valleytronics (valley electronics) | Using valleys in the electronic band structure of the first Brillouin zone of a crystal as the internal degree of freedom to store 0 s/1 s for information processing |
| von Neumann entropy | (Quantum mechanical entropy) minimum over all measurement bases of Shannon entropy |
| Wavefunction | Quantum system state description (positions or speeds (momenta) of entire system configurations); generally intractable Schrödinger equation applied (complex-valued probability amplitudes with real and imaginary wave-shaped components) |
| Weyl and Dirac topological semimetals | Topological semimetals created by two energy bands crossing at a single node (Weyl node), with two-fold (Weyl) and four-fold (Dirac) degenerate Fermi points |
References
- Cirac, J.I.; Pérez-García, D.; Schuch, N.; Verstraete, F. Matrix product states and projected entangled pair states: Concepts, symmetries, and theorems. Rev. Mod. Phys. 2021, 93, 045003. [Google Scholar] [CrossRef]
- Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef] [Green Version]
- Pines, D.; Nozieres, P. Theory of Quantum Liquids: Normal Fermi Liquids. Advanced Book Classics; Addison-Wesley: New York, NY, USA, 1994. [Google Scholar]
- Wilczek, F. Quantum Mechanics of Fractional-Spin Particles. Phys. Rev. Lett. 1982, 49, 957–959. [Google Scholar] [CrossRef]
- Bartolomei, H.; Kumar, M.; Bisognin, R.; Marguerite, A.; Berroir, J.-M.; Bocquillon, E.; Plaçais, B.; Cavanna, A.; Dong, Q.; Gennser, U.; et al. Fractional statistics in anyon collisions. Science 2020, 368, 173–177. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, J.; Liang, S.; Gardner, G.C.; Manfra, M.J. Direct observation of anyonic braiding statistics. Nat. Phys. 2020, 16, 931–936. [Google Scholar] [CrossRef]
- Yu, S.; Piao, X.; Park, N. Topological Hyperbolic Lattices. Phys. Rev. Lett. 2020, 125, 053901. [Google Scholar] [CrossRef] [PubMed]
- Pastawski, F.; Yoshida, B.; Harlow, D.; Preskill, J. Holographic quantum error-correcting codes: Toy models for the bulk/boundary correspondence. J. High Energy Phys. 2015, 2015, 149. [Google Scholar] [CrossRef]
- Kollár, A.J.; Fitzpatrick, M.; Houck, A.A. Hyperbolic lattices in circuit quantum electrodynamics. Nature 2019, 571, 45–50. [Google Scholar] [CrossRef] [Green Version]
- Maciejko, J.; Rayanc, S. Automorphic Bloch theorems for hyperbolic lattices. Proc. Natl. Acad. Sci. USA 2022, 119, e2116869119. [Google Scholar] [CrossRef]
- Maciejko, J.; Rayan, S. Hyperbolic band theory. Sci. Adv. 2021, 7, eabe9170. [Google Scholar] [CrossRef]
- Ikeda, K.; Aoki, S.; Matsuki, Y. Hyperbolic band theory under magnetic field and Dirac cones on a higher genus surface. J. Phys. Condens. Matter 2021, 33, 485602. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, K.; Matsuki, Y.; Aoki, B. Algebra of Hyperbolic Band Theory under Magnetic Field. arXiv 2021, arXiv:2107.10586v2. [Google Scholar]
- Lemm, M.; Siebert, O. Bose-Einstein condensation on hyperbolic spaces. arXiv 2022, arXiv:2202.01538v2. [Google Scholar]
- Cohen-Tannoudji, G.; Gazeau, J.-P. Cold Dark Matter: A Gluonic Bose–Einstein Condensate in Anti-de Sitter Space Time. Universe 2021, 7, 402. [Google Scholar] [CrossRef]
- Yang, W.-C.; Xia, C.-Y.; Nitta, M.; Zeng, H.-B. Fractional and integer vortex dynamics in strongly coupled two-component Bose-Einstein condensates from AdS/CFT correspondence. Phys. Rev. D 2020, 102, 046012. [Google Scholar] [CrossRef]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor. Science 1995, 269, 198–201. [Google Scholar] [CrossRef] [Green Version]
- Norcia, M.A.; Ferlaino, F. Developments in atomic control using ultracold magnetic lanthanides. Nat. Phys. 2021, 17, 1349–1357. [Google Scholar] [CrossRef]
- Wei, Y.; Macheda, F.; Zhao, Z.; Tse, T.; Plekhanov, E.; Bonini, N.; Weber, C. High-Temperature Superconductivity in the Lanthanide Hydrides at Extreme Pressures. Appl. Sci. 2022, 12, 874. [Google Scholar] [CrossRef]
- Böttcher, F.; Schmidt, J.-N.; Hertkorn, J.; Ng, K.S.H.; Graham, S.D.; Guo, M.; Langen, T.; Pfau, T. New states of matter with fine-tuned interactions: Quantum droplets and dipolar supersolids. Rep. Prog. Phys. 2020, 84, 012403. [Google Scholar] [CrossRef]
- Pyrkov, A.N.; Byrnes, T. Nontrivial solitonic attractors of nonlinear quantum equations: Application to associative memory. In Proceedings of the AIP Conference Proceedings, Kovilpatti, India, 23 June 2020; Volume 2241, p. 020032. [Google Scholar] [CrossRef]
- Pan, J.; Yi, S.; Shi, T. Quantum phases of self-bound droplets of bose-bose mixtures. arXiv 2021, arXiv:2102.02361. [Google Scholar]
- Ezawa, M. Chiral edge soliton in nonlinear Chern systems. arXiv 2022, arXiv:2201.01891v1. [Google Scholar]
- Yan, Z.; Bi, R.; Shen, H.; Lu, L.; Zhang, S.-C.; Wang, Z. Nodal-link semimetals. Phys. Rev. B 2017, 96, 041103. [Google Scholar] [CrossRef] [Green Version]
- Chiu, C.-K.; Teo, J.C.Y.; Schnyder, A.P.; Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 2016, 88, 035005. [Google Scholar] [CrossRef]
- Sato, M.; Ando, Y. Topological superconductors: A review. Rep. Prog. Phys. 2017, 80, 076501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Lu, H.-Z.; Hou, J.-M. Topological semimetals with a double-helix nodal link. Phys. Rev. B 2017, 96, 041102. [Google Scholar] [CrossRef] [Green Version]
- Burkov, A.A. Topological semimetals. Nat. Mat. 2016, 15, 1145–1148. [Google Scholar] [CrossRef]
- Chan, Y.-H.; Chiu, C.-K.; Chou, M.-Y.; Schnyder, A.P. Ca3P2 and other topological semimetals with line nodes and drumhead surface states. Phys. Rev. B 2016, 93, 205132. [Google Scholar] [CrossRef] [Green Version]
- Wieder, B.J.; Wang, Z.; Cano, J.; Dai, X.; Schoop, L.M.; Bradlyn, B.; Bernevig, B.A. Strong and fragile topological Dirac semimetals with higher-order Fermi arcs. Nat. Commun. 2020, 11, 627. [Google Scholar] [CrossRef] [Green Version]
- Rui, W.B.; Zhao, Y.X.; Schnyder, A.P. Topological transport in Dirac nodal-line semimetals. Phys. Rev. B 2018, 97, 161113. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Chan, Y.-H.; Chiu, C.-K.; Vergniory, M.G.; Schoop, L.M.; Schnyder, A.P. Topological band crossings in hexagonal materials. Phys. Rev. Mater. 2018, 2, 074201. [Google Scholar] [CrossRef]
- Joshi, D.G.; Schnyder, A.P. Topological quantum paramagnet in a quantum spin ladder. Phys. Rev. B 2017, 96, 220405. [Google Scholar] [CrossRef] [Green Version]
- Joshi, D.G.; Schnyder, A.P. Z2 topological quantum paramagnet on a honeycomb bilayer. Phys. Rev. B 2019, 100, 020407. [Google Scholar] [CrossRef] [Green Version]
- Bernevig, B.A.; Felser, C.; Beidenkopf, H. Progress and prospects in magnetic topological materials. Nature 2022, 603, 41–51. [Google Scholar] [CrossRef]
- Nguyen, T.; Tsurimaki, Y.; Pablo-Pedro, R.; Bednik, G.; Liu, T.; Apte, A.; Andrejevic, N.; Li, M. Topological Signatures in Nodal Semimetals through Neutron Scattering. New J. Phys. 2022, 24, 013016. [Google Scholar] [CrossRef]
- Xu, B.; Fang, Z.; Sánchez-Martínez, M.; Venderbos, J.W.F.; Ni, Z.; Qiu, T.; Manna, K.; Wang, K.; Paglione, J.; Bernhard, C.; et al. Optical signatures of multifold fermions in the chiral topological semimetal CoSi. Proc. Natl. Acad. Sci. USA 2020, 117, 27104–27110. [Google Scholar] [CrossRef]
- Schröter, N.B.M.; Pei, D.; Vergniory, M.G.; Sun, Y.; Manna, K.; De Juan, F.; Krieger, J.A.; Süss, V.; Schmidt, M.; Dudin, P.; et al. Chiral topological semimetal with multifold band crossings and long Fermi arcs. Nat. Phys. 2019, 15, 759–765. [Google Scholar] [CrossRef]
- Liu, C.-X.; Zhang, S.-C.; Qi, X.-L. The Quantum Anomalous Hall Effect: Theory and Experiment. Annu. Rev. Condens. Matter Phys. 2015, 7, 301–321. [Google Scholar] [CrossRef]
- Frenkel, A.; Hartnoll, S.A. Entanglement in the Quantum Hall Matrix Model. arXiv 2021, arXiv:2111.05967v2. [Google Scholar]
- Broholm, C.; Cava, R.J.; Kivelson, S.A.; Nocera, D.G.; Norman, M.R.; Senthil, T. Quantum spin liquids. Science 2020, 367, 6475. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, A.; Bridges, C.A.; Yan, J.-Q.; Aczel, A.A.; Li, L.; Stone, M.B.; Granroth, G.E.; Lumsden, M.D.; Yiu, Y.; Knolle, J.; et al. Proximate Kitaev quantum spin liquid behavior in a honeycomb magnet. Nat. Mat. 2016, 15, 733–740. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bartlett, S.D. Programming a quantum phase of matter. Science 2021, 374, 1200–1201. [Google Scholar] [CrossRef] [PubMed]
- Satzinger, K.J.; Liu, Y.-J.; Smith, A.; Knapp, C.; Newman, M.; Jones, C.; Chen, Z.; Quintana, C.; Mi, X.; Dunsworth, A.; et al. Realizing topologically ordered states on a quantum processor. Science 2021, 374, 1237–1241. [Google Scholar] [CrossRef] [PubMed]
- Semeghini, G.; Levine, H.; Keesling, A.; Ebadi, S.; Wang, T.T.; Bluvstein, D.; Verresen, R.; Pichler, H.; Kalinowski, M.; Samajdar, R.; et al. Probing topological spin liquids on a programmable quantum simulator. Science 2021, 374, 1242–1247. [Google Scholar] [CrossRef]
- Kalinowski, M.; Samajdar, R.; Melko, R.G. Bulk and Boundary Quantum Phase Transitions in a Square Rydberg Atom Array. arXiv 2021, arXiv:2112.10790v1. [Google Scholar]
- Khajetoorians, A.A.; Wegner, D.; Otte, A.F.; Swart, I. Creating designer quantum states of matter atom-by-atom. Nat. Rev. Phys. Rev. 2019, 1, 703–715. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum Phase Transitions; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Kitaev, A.; Preskill, J. Topological Entanglement Entropy. Phys. Rev. Lett. 2006, 96, 110404. [Google Scholar] [CrossRef] [Green Version]
- Hosur, P.; Qi, X.-L.; Roberts, D.A.; Yoshida, B. Chaos in quantum channels. J. High Energy Phys. 2016, 2016, 4. [Google Scholar] [CrossRef] [Green Version]
- Savary, L.; Balents, L. Quantum spin liquids: A review. Rep. Prog. Phys. 2017, 80, 016502. [Google Scholar] [CrossRef]
- Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 2006, 321, 2–111. [Google Scholar] [CrossRef] [Green Version]
- Chapman, A.; Flammia, S.T.; Kollar, A.J. Free-Fermion Subsystem Codes. arXiv 2022, arXiv:2201.07254v1. [Google Scholar]
- Swan, M.; dos Santos, R.P.; Witte, F. Quantum Information Science. IEEE Internet Comput. Spec. J. Issue Quantum Post-Moore’s Law Comput. 2022, 26, 5–6. [Google Scholar] [CrossRef]
- Royer, B.; Singh, S.; Girvin, S.M. Stabilization of Finite-Energy Gottesman-Kitaev-Preskill States. Phys. Rev. Lett. 2020, 125, 260509. [Google Scholar] [CrossRef] [PubMed]
- Gottesman, D.; Kitaev, A.; Preskill, J. Encoding a qubit in an oscillator. Phys. Rev. A 2001, 64, 012310. [Google Scholar] [CrossRef] [Green Version]
- Chamberland, C.; Noh, K.; Arrangoiz-Arriola, P.; Campbell, E.T.; Hann, C.T.; Iverson, J.; Putterman, H.; Bohdanowicz, T.C.; Flammia, S.T.; Keller, A.; et al. Building a Fault-Tolerant Quantum Computer Using Concatenated Cat Codes. PRX Quantum 2021, 3, 010329. [Google Scholar] [CrossRef]
- Albert, V.V.; Covey, J.P.; Preskill, J. Robust Encoding of a Qubit in a Molecule. Phys. Rev. X 2020, 10, 031050. [Google Scholar] [CrossRef]
- Sejnowski, T.J. The unreasonable effectiveness of deep learning in artificial intelligence. Proc. Natl. Acad. Sci. USA 2020, 117, 30033–30038. [Google Scholar] [CrossRef] [Green Version]
- Poirazi, P.; Papoutsi, A. Illuminating dendritic function with computational models. Nat. Rev. Neurosci. 2020, 21, 303–321. [Google Scholar] [CrossRef]
- Swan, M.; dos Santos, R.P.; Witte, F. Quantum Neurobiology. Quantum Rep. 2022, 4, 107–126. [Google Scholar] [CrossRef]
- Swan, M.; dos Santos, R.P.; Lebedev, M.A.; Witte, F. Quantum Computing for the Brain; World Scientific: London, UK, 2022. [Google Scholar]
- Maldacena, J. The Large-N Limit of Superconformal Field Theories and Supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef] [Green Version]
- Morningstar, A.; Hauru, M.; Beall, J.; Ganahl, M.; Lewis, A.G.M.; Khemani, V.; Vidal, G. Simulation of quantum many-body dynamics with Tensor Processing Units: Floquet prethermalization. arXiv 2021, arXiv:2111.08044v1. [Google Scholar]
- Mi, X.; Ippoliti, M.; Quintana, C.; Greene, A.; Chen, Z.; Gross, J.; Arute, F.; Arya, K.; Atalaya, J.; Babbush, R.; et al. Observation of Time-Crystalline Eigenstate Order on a Quantum Processor. arXiv 2021, arXiv:2107.13571. [Google Scholar]
- Bajardi, F.; Altucci, L.; Benedetti, R.; Capozziello, S.; Del Sorbo, M.R.; Franci, G.; Altucci, C. DNA Mutations via Chern–Simons Currents. Eur. Phys. J. Plus 2021, 136, 1080. [Google Scholar] [CrossRef] [PubMed]
- Treado, J.D.; Wang, D.; Boromand, A.; Murrell, M.P.; Shattuck, M.D.; O’Hern, C.S. Bridging particle deformability and collective response in soft solids. Phys. Rev. Mater. 2021, 5, 055605. [Google Scholar] [CrossRef]
- Ma, Q.; Grushin, A.G.; Burch, K.S. Topology and geometry under the nonlinear electromagnetic spotlight. Nat. Mater. 2021, 20, 1601–1614. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.-G. Choreographed entanglement dances: Topological states of quantum matter. Science 2019, 363, eaal3099. [Google Scholar] [CrossRef] [Green Version]
- Giustino, F.; Bibes, M.; Lee, J.H.; Trier, F.; Winter, S.M.; Valentí, R.; Son, Y.-W.; Taillefer, L.; Heil, C.; Figueroa, A.I.; et al. The 2021 quantum materials roadmap. J. Phys. Mater. 2021, 3, 042006. [Google Scholar] [CrossRef]
- Polash, M.H.; Yalameha, S.; Zhou, H.; Ahadi, K.; Nourbakhsh, Z.; Vashaee, D. Topological quantum matter to topological phase conversion: Fundamentals, materials, physical systems for phase conversions, and device applications. Mater. Sci. Eng. R Rep. 2021, 145, 100620. [Google Scholar] [CrossRef]
- Yang, H. Quantum Materials: A New Open Section in Materials. Materials 2021, 14, 3142. [Google Scholar] [CrossRef]
- Knolle, J.; Moessner, R. A Field Guide to Spin Liquids. Annu. Rev. Condens. Matter Phys. 2019, 10, 451–472. [Google Scholar] [CrossRef] [Green Version]
- Ball, P. Major Quantum Computing Strategy Suffers Serious Setbacks. Available online: https://www.quantamagazine.org/major-quantum-computing-strategy-suffers-serious-setbacks-20210929/ (accessed on 13 February 2022).
- Preskill, J. Quantum computing 40 years later. arXiv 2021, arXiv:2106.10522. [Google Scholar]
- Carrasquilla, J. Machine learning for quantum matter. Adv. Phys. X 2020, 5, 1797528. [Google Scholar] [CrossRef]
- Carrasquilla, J.; Luo, D.; Perez, F.; Milsted, A.; Clark, B.K.; Volkovs, M.; Aolita, L. Probabilistic Simulation of Quantum Circuits with the Transformer. Phys. Rev. A 2021, 104, 032610. [Google Scholar] [CrossRef]
- Verdel, R.; Schmitt, M.; Huang, Y.-P.; Karpov, P.; Heyl, M. Variational classical networks for dynamics in interacting quantum matter. Phys. Rev. B 2021, 103, 165103. [Google Scholar] [CrossRef]
- Stephen, D.T.; Nautrup, H.P.; Bermejo-Vega, J.; Eisert, J.; Raussendorf, R. Subsystem symmetries, quantum cellular automata, and computational phases of quantum matter. Quantum 2019, 20, 142. [Google Scholar] [CrossRef]
- Sapra, N.V.; Yang, K.Y.; Vercruysse, D.; Leedle, K.J.; Black, D.S.; England, R.J.; Su, L.; Trivedi, R.; Miao, Y.; Solgaard, O.; et al. On-chip integrated laser-driven particle accelerator. Science 2020, 367, 79–83. [Google Scholar] [CrossRef] [Green Version]
- Pikulin, D.I.; Franz, M. Black Hole on a Chip: Proposal for a Physical Realization of the Sachdev-Ye-Kitaev model in a Solid-State System. Phys. Rev. X 2017, 7, 031006. [Google Scholar] [CrossRef] [Green Version]
- Brown, A.R.; Gharibyan, H.; Leichenauer, S.; Lin, H.W.; Nezami, S.; Salton, G.; Susskind, L.; Swingle, B.; Walter, M. Quantum gravity in the lab: Teleportation by size and traversable wormholes. arXiv 2021, arXiv:1911.06314v2. [Google Scholar]
- Heinrich, A.J.; Oliver, W.D.; Vandersypen, L.M.K.; Ardavan, A.; Sessoli, R.; Loss, D.; Jayich, A.B.; Fernandez-Rossier, J.; Laucht, A.; Morello, A. Quantum-coherent nanoscience. Nat. Nanotechnol. 2021, 16, 1318–1329. [Google Scholar] [CrossRef]
- Laucht, A.; Hohls, F.; Ubbelohde, N.; Gonzalez-Zalba, M.F.; Reilly, D.J.; Stobbe, S.; Schroder, T.; Scarlino, P.; Koski, J.V.; Dzurak, A.; et al. Roadmap on quantum nanotechnologies. Nanotechnology 2021, 32, 162003. [Google Scholar] [CrossRef]
- Belenchia, A.; Carlesso, M.; Bayraktar, O.; Dequal, D.; Derkach, I.; Gasbarri, G.; Herr, W.; Li, Y.L.; Rademacher, M.; Sidhu, J.; et al. Quantum physics in space. Phys. Rep. 2022, 951, 1–70. [Google Scholar] [CrossRef]
- Barzen, J.; Leymann, F. Quantum Humanities: A First Use Case for Quantum-ML in Media Science. Digit. Welt 2020, 4, 102–103. [Google Scholar] [CrossRef]
- Miranda, E.R. Quantum Computing in the Arts and Humanities: An Introduction to Core Concepts, Theory and Applications; Springer International Publishing: London, UK, 2022. [Google Scholar]
- Oka, T.; Kitamura, S. Floquet Engineering of Quantum Materials. Annu. Rev. Condens. Matter Phys. 2019, 10, 387–408. [Google Scholar] [CrossRef] [Green Version]
| Building Blocks | Short-Range Protection | Long-Range Entanglement |
|---|---|---|
| Symmetry and topology | Topological insulators | Quantum spin liquids |
| Anyons/quasiparticles | Topological superconductors | Quantum Hall states |
| Hyperbolic space | Topological semimetals | Entanglement entropy |
| Code | Description | |
|---|---|---|
| 1 | Code (general) | Allowed values (or value structure) for data or other parameters |
| 2 | QEC code | Logical codespace corresponding to a physical lattice model space |
| 3 | Stabilizer code | Topology-based Pauli operators (X, Y, Z) to restore bit/spin flip |
| 4 | Toric code | Stabilizer codes defined on a 2D torus-shaped spin lattice |
| 5 | Surface code | Stabilizer codes defined on a 2D spin lattice in any shape |
| 6 | Bosonic code | Self-contained photon-based oscillator system with bosonic modes |
| 7 | GKP code | Bosonic code: squeezed states protect position-amplitude shifts |
| 8 | Molecular code | GKP codes extended to asymmetric bodies (molecules) in free space |
| 9 | Cat code | Superpositioned states (Schrödinger) used as error-correction codes |
| Model Parameter | Quantum Information | Quantum Matter | |
|---|---|---|---|
| 1 | Multiscalar model | AdS/CFT correspondence | Condensed matter bulk–boundary |
| 2 | Phase transition | Neural signal integration | Topological entanglement entropy |
| 3 | Symmetry | Symmetry rebalancing | Short-range: topological semimetal |
| 4 | Entanglement | Non-local measurement | Long-range: quantum spin liquid |
| 5 | Renormalization | bMERA tensor network | MERA (wavefunction) TPUs |
| 6 | Floquet dynamics | Neural signal periodicity | Floquet circuits with NISQ QC |
| 7 | Matrix mechanics | Diagonalize matrices | Quantum Hall matrix mechanics |
| 8 | Quantum walks | Faster lattice search | Molecular code rotation |
| 9 | Optimization | Chern–Simons curvature | High Chern numbers (invariance) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swan, M.; Dos Santos, R.P.; Witte, F. Quantum Matter Overview. J 2022, 5, 232-254. https://doi.org/10.3390/j5020017
Swan M, Dos Santos RP, Witte F. Quantum Matter Overview. J. 2022; 5(2):232-254. https://doi.org/10.3390/j5020017
Chicago/Turabian StyleSwan, Melanie, Renato P. Dos Santos, and Frank Witte. 2022. "Quantum Matter Overview" J 5, no. 2: 232-254. https://doi.org/10.3390/j5020017
APA StyleSwan, M., Dos Santos, R. P., & Witte, F. (2022). Quantum Matter Overview. J, 5(2), 232-254. https://doi.org/10.3390/j5020017






