Global Stability and Exponential Decay of Processes in Nonlinear Feedback Systems with Different Fractional Orders

Abstract

The global stability of continuous-time multi-input multi-output nonlinear feedback systems with different fractional orders and interval matrices of positive linear parts is investigated. New sufficient conditions for the global stability of this class of positive nonlinear systems are established. Sufficient conditions for the exponential decay of processes in fractional nonlinear systems are given. Procedures for computation of a gain matrix characterizing the class of nonlinear elements are proposed and illustrated by examples.

1. Introduction

In positive systems inputs, state variables and outputs take only nonnegative values for any nonnegative inputs and nonnegative initial conditions [1,2,3]. Examples of positive systems are industrial processes involving chemical reactors, heat exchangers and distillation columns, storage systems, compartmental systems, water and atmospheric pollutions models. A variety of models having positive behavior can be found in engineering, management science, economics, social sciences, biology and medicine, etc. An overview of state of the art positive systems theory is given in the monographs [1,2,3,4,5].

Mathematical fundamentals of the fractional calculus are given in the monographs [4,5,6,7]. The positive fractional linear systems have been investigated in [4,5,8,9,10,11,12,13,14,15,16,17,18,19]. Positive linear systems with different fractional orders have been addressed in [11,12,19]. Descriptor positive systems have been analyzed in [13,20] and their stabilization in [18,19]. Linear positive electrical circuits with state feedbacks have been addressed in [20,21]. The superstabilization of positive linear electrical circuits by state feedbacks have been analyzed in [22] and the stability of nonlinear systems in [21,23]. The global stability of nonlinear systems with negative feedbacks and positive not necessary asymptotically stable linear parts has been investigated in [9,24,25]. The global stability of nonlinear standard and fractional positive feedback systems has been considered in [23].

In this paper the global stability of continuous-time multi-input multi-output nonlinear feedback systems with different fractional orders and interval matrices of positive linear parts will be addressed, and sufficient conditions for exponential decay of processes in fractional nonlinear systems with different orders will be proposed.

The paper is organized as follows. In Section 2 the basic definitions and theorems concerning the positive linear systems with different fractional orders are recalled. The stability of fractional interval positive linear systems is analyzed in Section 3. New sufficient conditions for the global stability of these feedback nonlinear systems with interval matrices of positive linear parts are established in Section 4. In Section 5, a procedure for calculation of a gain matrix characterizing the class of nonlinear elements is presented and illustrated by numerical examples. Sufficient conditions for the exponential decay of processes in fractional nonlinear systems with different orders are proposed in Section 6. Concluding remarks are given in Section 7.

The following notation will be used: $\Re$—the set of real numbers, ${\Re }^{n\times m}$—the set of $n\times m$ real matrices, ${\Re }_{+}^{n\times m}$—the set of $n\times m$ real matrices with nonnegative entries and ${\Re }_{+}^n={\Re }_{+}^{n\times 1}$, $M_n$—the set of $n\times n$ Metzler matrices (real matrices with nonnegative off-diagonal entries), $I_n$— the $n\times n$ identity matrix, ${\displaystyle \sum A(:,n)}$—the sum of all elements of nth column.

2. Positive Different Fractional Orders Linear Systems

Consider the fractional continuous-time linear system

$$\frac{d^{\alpha }x(t)}{d{t}^{\alpha }}=Ax(t)+Bu(t), 0<\alpha <1$$

(1)

$$y(t)=Cx(t)+Du(t),$$

(2)

where $x(t)\in {\Re }^n$, $u(t)\in {\Re }^m$, $y(t)\in {\Re }^p$ are the state, input and output vectors and $A\in {\Re }^{n\times n}$, $B\in {\Re }^{n\times m}$, $C\in {\Re }^{p\times n}$, $D\in {\Re }^{p\times m}$,

$$\frac{d^{\alpha }x(t)}{d{t}^{\alpha }}=\frac{1}{\Gamma (1-\alpha )}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{\dot{x}(\tau )}{{(t-\tau )}^{\alpha }}d\tau }, \dot{x}(\tau )=\frac{dx(\tau )}{d\tau }$$

(3)

is the Caputo fractional derivative and

$$\Gamma (z)={\displaystyle \underset{0}{\overset{\infty }{\int }}{t}^{z-1}{e}^{-t}dt}, \mathrm{Re}(z)>0$$

(4)

is the gamma function [4,5].

Definition 1.

[4,5] The fractional system (1), (2) is called (internally) positive if $x(t)\in {\Re }_{+}^n$ and $y(t)\in {\Re }_{+}^p$ ,$t\ge 0$ for any initial conditions $x(0)\in {\Re }_{+}^n$ and all inputs$u(t)\in {\Re }_{+}^m$ ,$t\ge 0$.

Theorem 1.

[4,5] The fractional system (1), (2) is positive if and only if

$$A\in M_n, B\in {\Re }_{+}^{n\times m}, C\in {\Re }_{+}^{p\times n}, D\in {\Re }_{+}^{p\times m}.$$

(5)

Definition 2.

[4,5] The positive fractional system (1), (2) (for $u(t)=0$) is called asymptotically stable (the matrix A is Hurwitz) if

$$\underset{t\to \infty }{\lim }x(t)=0 \mathit{for} \mathit{any} x(0)\in {\Re }_{+}^n.$$

(6)

Theorem 2.

[4,5] The positive linear system (1), (2) is asymptotically stable if and only if one of the following equivalent conditions is satisfied:

 (1) 

All coefficient of the characteristic polynomial

$$p_n(s)=\det [I_{n}s-A]=s^n+a_{n-1}{s}^{n-1}+\dots +a_{1}s+a_0$$

(7)

are positive, i.e., $a_i>0$for $i=0,1,\dots ,n-1$.

 (2) 

There exists strictly positive vector ${\lambda }^T=[\begin{array}{ccc}{\lambda }_1& \cdots & {\lambda }_n{]}^T\end{array}$, ${\lambda }_k>0$, $k=1,\dots ,n$such that

$$A\lambda <0 \mathit{or} {\lambda }^{T}A<0.$$

(8)

Theorem 3.

The positive system (1), (2) is asymptotically stable if the sum of entries of each column (row) of the matrix A is negative.

Proof. 

Using (8) we obtain

$$A\lambda =\left[\begin{array}{ccc}{a}_{11}& \dots & a_{1n}\\ ⋮& \dots & ⋮\\ a_{n1}& \dots & a_{nn}\end{array}\right]\left[\begin{array}{c}{\lambda }_1\\ ⋮\\ {\lambda }_n\end{array}\right]=\left[\begin{array}{c}{a}_{11}\\ ⋮\\ a_{1n}\end{array}\right]{\lambda }_1+\dots +\left[\begin{array}{c}{a}_{n1}\\ ⋮\\ a_{nn}\end{array}\right]{\lambda }_n<\left[\begin{array}{c}0\\ ⋮\\ 0\end{array}\right]$$

(9)

and the sum of entries of each column of the matrix A is negative since ${\lambda }_k>0$, $k=1,\dots ,n$. The proof for rows is similar. □

Now consider the fractional linear system with two different fractional orders

$$\left[\begin{array}{c}\frac{d^{\alpha }{x}_1(t)}{d{t}^{\alpha }}\\ \frac{d^{\beta }{x}_2(t)}{d{t}^{\beta }}\end{array}\right]=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\left[\begin{array}{c}{x}_1(t)\\ x_2(t)\end{array}\right]+\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]u(t),$$

(10)

$$y(t)=[\begin{array}{cc}{C}_1& C_2\end{array}]\left[\begin{array}{c}{x}_1(t)\\ x_2(t)\end{array}\right],$$

(11)

where $0<\alpha ,\beta <1$, $x_1(t)\in {\Re }^{n_1}$ and $x_2(t)\in {\Re }^{n_2}$ are the state vectors, $A_{ij}\in {\Re }^{n_i\times n_j}$, $B_i\in {\Re }^{n_i\times m}$, $C_i\in {\Re }^{p\times n_i}$; i, j = 1,2; $u(t)\in {\Re }^m$ is the input vector and $y(t)\in {\Re }^p$ is the output vector. Initial conditions for (10) have the form

$$x_1(0)=x_{10}, x_2(0)=x_{20} \mathrm{and} x_0=\left[\begin{array}{c}{x}_{10}\\ x_{20}\end{array}\right].$$

(12)

Remark 1.

The state Equation (10) of fractional continuous-time linear systems with two different fractional orders has a similar structure to the 2D Roeesser type models.

Definition 3.

The fractional system (10), (11) is called positive if$x_1(t)\in {\Re }_{+}^{n_1}$,$x_2(t)\in {\Re }_{+}^{n_2}$and$y(t)\in {\Re }_{+}^p$,$t\ge 0$for any initial conditions$x_{10}\in {\Re }_{+}^{n_1}$,$x_{20}\in {\Re }_{+}^{n_2}$and all input vectors$u\in {\Re }_{+}^m$,$t\ge 0$.

Theorem 4.

[11,12] The fractional system (10), (11) for $0<\alpha <1;\begin{array}{c}\end{array}0<\beta <1$ is positive if and only if

$$\tilde{A}=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\in M_N, \tilde{B}=\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right]\in {\Re }_{+}^{N\times m}, \tilde{C}=[\begin{array}{cc}{C}_1& C_2\end{array}]\in {\Re }_{+}^{p\times n}(N=n_1+n_2).$$

(13)

Theorem 5.

[4] The positive fractional system (10), (11) is asymptotically stable if and only if one of the following equivalent conditions is satisfied:

 (1) 

All coefficients of the characteristic polynomial

$$\det [I_{n}s-\tilde{A}]=s^n+{\tilde{a}}_{n-1}{s}^{n-1}+\dots +{\tilde{a}}_{1}s+{\tilde{a}}_0$$

(14)

are positive, i.e.,${\tilde{a}}_i>0$for$i=0,1,\dots ,n-1$

 (2) 

There exists a strictly positive vector$\lambda =[\begin{array}{ccc}{\lambda }_1& \cdots & {\lambda }_n]\end{array}$, ${\lambda }_k>0$, $k=1,\dots ,n$such that

$$\tilde{A}\lambda <0\mathit{or}{\lambda }^T\tilde{A}<0.$$

(15)

Theorem 6.

The positive system (10), (11) is asymptotically stable if the sum of entries of each column (row) of the matrix $\tilde{A}$is negative.

Proof. 

Proof is similar to the proof of Theorem 3. □

Theorem 7.

The solution of the Equation (10) for$0<\alpha <1;\begin{array}{c}\end{array}0<\beta <1$with initial conditions (12) has the form

$$x(t)=\left[\begin{array}{c}{x}_1(t)\\ x_2(t)\end{array}\right]={\Phi }_0(t)x_0+{\displaystyle \underset{0}{\overset{t}{\int }}M(t-\tau )u(\tau )d\tau },$$

(16)

where

$$\begin{gathered} M\left(t\right)={\mathsf{\Phi }}_1\left(t\right)B_{10}+{\mathsf{\Phi }}_2\left(t\right)B_{01}=\left[\begin{array}{cc}{\mathsf{\Phi }}_{11}^1\left(t\right)& {\mathsf{\Phi }}_{12}^1\left(t\right)\\ {\mathsf{\Phi }}_{21}^1\left(t\right)& {\mathsf{\Phi }}_{22}^1\left(t\right)\end{array}\right]\left[\begin{array}{c}{B}_1\\ 0\end{array}\right]+\left[\begin{array}{cc}{\mathsf{\Phi }}_{11}^2\left(t\right)& {\mathsf{\Phi }}_{12}^2\left(t\right)\\ {\mathsf{\Phi }}_{21}^2\left(t\right)& {\mathsf{\Phi }}_{22}^2\left(t\right)\end{array}\right]\left[\begin{array}{c}0\\ B_2\end{array}\right] \\ =\left[\begin{array}{c}{\mathsf{\Phi }}_{11}^1\left(t\right)B_1+{\mathsf{\Phi }}_{12}^2\left(t\right)B_2\\ {\mathsf{\Phi }}_{21}^1\left(t\right)B_1+{\mathsf{\Phi }}_{22}^2\left(t\right)B_2\end{array}\right]=\left[\begin{array}{cc}{\mathsf{\Phi }}_{11}^1\left(t\right)& {\mathsf{\Phi }}_{12}^2\left(t\right)\\ {\mathsf{\Phi }}_{21}^1\left(t\right)& {\mathsf{\Phi }}_{22}^2\left(t\right)\end{array}\right]\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right] \end{gathered}$$

(17)

and

$${\Phi }_0(t)={\displaystyle \sum _{k=0}^{\infty }{\displaystyle \sum _{l=0}^{\infty }{T}_{kl}\frac{t^{k\alpha +l\beta }}{\Gamma (k\alpha +l\beta +1)}}},$$

(18)

$${\Phi }_1(t)={\displaystyle \sum _{k=0}^{\infty }{\displaystyle \sum _{l=0}^{\infty }{T}_{kl}\frac{t^{(k+1)\alpha +l\beta -1}}{\Gamma \left[(k+1)\alpha +l\beta \right]}}},$$

(19)

$${\Phi }_2(t)={\displaystyle \sum _{k=0}^{\infty }{\displaystyle \sum _{l=0}^{\infty }{T}_{kl}\frac{t^{k\alpha +(l+1)\beta -1}}{\Gamma \left[k\alpha +(l+1)\beta \right]}}},$$

(20)

$$T_{kl}=\left\{\begin{array}{c}{I}_n\begin{array}{c}\end{array}\mathrm{for}\begin{array}{c}\end{array}k=l=0\\ \left[\begin{array}{cc}{A}_{11}& A_{12}\\ 0& 0\end{array}\right]\begin{array}{c}\end{array}\mathrm{for}\begin{array}{c}\end{array}k=1,l=0\\ \left[\begin{array}{cc}0& 0\\ A_{21}& A_{22}\end{array}\right]\begin{array}{c}\end{array}\mathrm{for}\begin{array}{c}\end{array}k=0,l=1\\ T_{10}{T}_{k-1,l}+T_{01}{T}_{k,l-1}\begin{array}{c}\end{array}\mathrm{for}\begin{array}{c}\end{array}k+l>1\end{array}\right.$$

(21)

Proof. 

Proof is given in [12]. □

Note that if $\alpha =\beta$ then from (18) we have

$${\left.{\Phi }_0\right|}_{\alpha =\beta }(t)={\displaystyle \sum _{k=0}^{\infty }\frac{A^k{t}^{k\alpha }}{\Gamma (k\alpha +1)}}.$$

(22)

3. Stability of Fractional Interval Positive Linear Systems

Consider the fractional interval positive linear continuous-time system

$$\frac{d^{\alpha }x}{d{t}^{\alpha }}=Ax,\hspace{1em}\hspace{1em}0<\alpha <1,$$

(23)

where $x=x(t)\in {\Re }^n$ is the state vector and the interval matrix $A\in M_n$ is defined by

$$\underset{¯}{A}\le A\le \overline{A} \mathrm{or} \mathrm{equivalently} A\in [\overline{A},\underset{¯}{A}].$$

(24)

Definition 4.

The fractional interval positive system (23) is called asymptotically stable if the system is asymptotically stable for all matrices $A\in M_n$satisfying the condition (24).

By condition (8) of Theorem 2, the positive system (23) is asymptotically stable if there exists a strictly positive vector $\lambda >0$ such that the condition (8) is satisfied.

For two fractional positive linear systems

$$\frac{d^{\alpha }x}{d{t}^{\alpha }}=\overline{A}x, \overline{A}\in M_n$$

(25)

and

$$\frac{d^{\alpha }x}{d{t}^{\alpha }}=\underset{¯}{A}x, \underset{¯}{A}\in M_n$$

(26)

there exists a strictly positive vector $\lambda \in {\Re }_{+}^n$ such that

$$\overline{A}\lambda <0 \mathrm{and} \underset{¯}{A}\lambda <0$$

(27)

if and only if the systems (25), (26) are asymptotically stable.

Theorem 8.

If the matrices$\overline{A}$and$\underset{¯}{A}$of fractional positive systems (25), (26) are asymptotically stable then their convex linear combination

$$A=(1-k)\underset{¯}{A}+k\overline{A} \mathrm{for} 0\le k\le 1$$

(28)

is also asymptotically stable.

Proof. 

By condition (8) of Theorem 2, if the fractional positive linear systems (25), (26) are asymptotically stable then there exists a strictly positive vector $\lambda \in {\Re }_{+}^n$ such that (27) holds. Using (8) and (27) we obtain

$$A\lambda =[(1-k)\underset{¯}{A}+k\overline{A}]\lambda =(1-k)\underset{¯}{A}\lambda +k\overline{A}\lambda <0$$

(29)

for $0\le k\le 1$. Therefore, if the positive linear systems (25), (26) are asymptotically stable then their convex linear combination (28) is also asymptotically stable. □

Theorem 8.

The interval positive systems (23) are asymptotically stable if and only if the positive linear systems (25), (26) are asymptotically stable.

Proof. 

By condition (8) of Theorem 2 if the matrices $\overline{A}\in M_n$, $\underset{¯}{A}\in M_n$ are asymptotically stable, then there exists a strictly positive vector $\lambda \in {\Re }_{+}^n$ such that (8) holds. The convex linear combination (28) satisfies the condition $A\lambda <0$ if and only if (29) holds. Therefore, the interval system (23) is asymptotically stable if and only if the positive linear system is asymptotically stable. □

Example 1.

Consider the fractional interval positive linear continuous-time system (23) with the matrices

$$\overline{A}=\left[\begin{array}{cc}-3& 2\\ 2& -4\end{array}\right],\hspace{0.33em}\hspace{0.33em}\underset{¯}{A}=\left[\begin{array}{cc}-2& 1\\ 1& -3\end{array}\right].$$

(30)

Using the condition (8) of Theorem 2, we choose $\lambda ={[1\hspace{0.33em}\hspace{0.33em}1]}^T$ and we obtain

$$\overline{A}\lambda =\left[\begin{array}{cc}-3& 2\\ 2& -4\end{array}\right]\left[\begin{array}{c}1\\ 1\end{array}\right]=\left[\begin{array}{c}-1\\ -2\end{array}\right]<0$$

(31)

and

$$\underset{¯}{A}\lambda =\left[\begin{array}{cc}-2& 1\\ 1& -3\end{array}\right]\left[\begin{array}{c}1\\ 1\end{array}\right]=\left[\begin{array}{c}-1\\ -2\end{array}\right]<0.$$

(32)

Therefore, the matrices (30) are Hurwitz.

These considerations can be easily extended to positive different fractional orders linear systems (10), (11).

4. Global Stability of Fractional Nonlinear Positive Feedback Systems

Consider the m-input p-output (MIMO) nonlinear feedback system shown in Figure 1 which consists of the positive fractional linear part, the nonlinear element with the matrix characteristic $u=f(e)$ and the feedback with positive gain matrix H. The positive fractional linear part is described by the equations (25), (26) with the interval matrices

$$\tilde{A}\in [\overline{A},\hspace{0.33em}\underset{¯}{A}]\in M_n,\tilde{B}\in [\overline{B},\hspace{0.33em}\underset{¯}{B}]\in {\Re }_{+}^{n\times m},\tilde{C}\in [\overline{C},\hspace{0.33em}\underset{¯}{C}]\in {\Re }_{+}^{p\times n}.$$

(33)

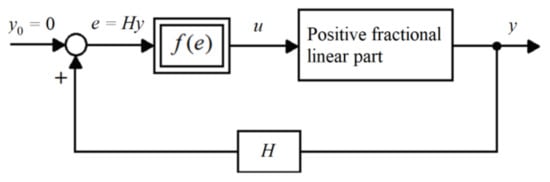
Figure 1. The nonlinear feedback system.

It is assumed that the interval matrix $\tilde{A}\in M_n$ is Hurwitz.

The characteristic $f(e)$ of the nonlinear element satisfies the condition

$$0\le f(e)\le Ke \mathrm{or} 0\le u\le Ke,$$

(34)

where

$$u=\left[\begin{array}{c}{u}_1\\ ⋮\\ u_m\end{array}\right],K=\left[\begin{array}{ccc}{k}_{11}& \cdots & k_{1p}\\ ⋮& \ddots & ⋮\\ k_{m1}& \cdots & k_{mp}\end{array}\right],e=\left[\begin{array}{c}{e}_1\\ ⋮\\ e_p\end{array}\right]$$

(35)

and

$$f(0)=0, u_i=f(e_1,\dots ,e_p)\le k_{i1}{e}_1+\dots +k_{ip}{e}_p,i=1,\dots ,m.$$

(36)

Remark 2.

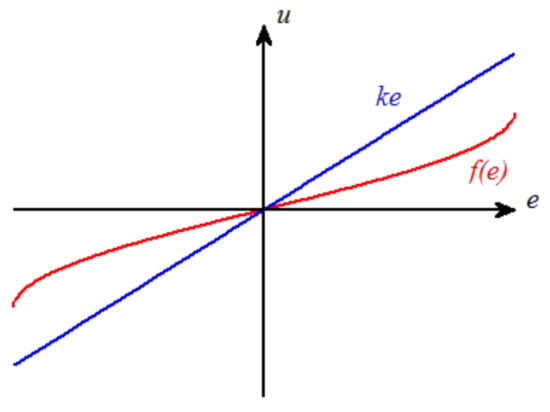
The matrix K forms m, p-dimensional convex surfaces which constricts possible dynamics of nonlinear elements, i.e., for m = p = 1 the nonlinear characteristicf(e) is presented in Figure 2.

Figure 2. Characteristic of single-input single-output nonlinear element.

Definition 5.

The fractional nonlinear positive system is called globally stable if it is asymptotically stable for all nonnegative initial conditions $x(0)\in {\Re }_{+}^n.$

The following theorem gives sufficient conditions for the global stability of the positive nonlinear system.

Theorem 9.

The fractional nonlinear system consisting of the positive asymptotically stable linear part described by (25), (26) with interval matrices (33), the nonlinear element satisfying the condition (34) and the feedback with positive gain matrix $H\in {\Re }_{+}^{m\times p}$is globally stable if the sum of entries of each column (row) of the matrix

$$(1-q)\underset{¯}{A}+q\overline{A}+\tilde{B}KH\tilde{C}=\left\{\begin{array}{c}\overline{A}+\overline{B}\overline{K}H\overline{C}\in M_n\hspace{1em}\mathrm{for}\hspace{1em}q=0\\ \underset{¯}{A}+\underset{¯}{B}\underset{¯}{K}H\underset{¯}{C}\in M_n\hspace{1em}\mathrm{for}\hspace{1em}q=1\end{array}\right.$$

(37)

is negative.

Proof. 

The proof will be accomplished by the use of the Lyapunov method [26,27]. As the Lyapunov function $V(x)$ we choose

$$V_1(x_1)+V_2(x_2)={\lambda }_1^T{x}_1+{\lambda }_2^T{x}_2\ge 0 \mathrm{for} x=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\in {\Re }_{+}^n,\lambda =\left[\begin{array}{c}{\lambda }_1\\ {\lambda }_2\end{array}\right]\in {\Re }_{+}^n,$$

(38)

where $\lambda$ is a strictly positive vector, i.e., ${\lambda }_{ij}>0$, $i=1,2;$ $j=1,\dots ,n.$

Using (37) and (25) we obtain

$$\begin{array}{l}\frac{d^{\alpha }{V}_1(x_1)}{d{t}^{\alpha }}+\frac{d^{\beta }{V}_2(x_2)}{d{t}^{\beta }}=[\begin{array}{cc}{\lambda }_1^T& {\lambda }_2^T\end{array}]\left[\begin{array}{c}\frac{d^{\alpha }{x}_1}{d{t}^{\alpha }}\\ \frac{d^{\beta }{x}_2}{d{t}^{\beta }}\end{array}\right]\\ ={\lambda }^T(\tilde{A}x+\tilde{B}u)={\lambda }^T(\tilde{A}x+\tilde{B}f(e))\le {\lambda }^T(\tilde{A}+\tilde{B}KH\tilde{C})x\end{array}$$

(39)

since $u=f(e)\le Ke=KH\tilde{C}x.$

From (39) it follows that $\frac{d^{\alpha }{V}_1(x_1)}{d{t}^{\alpha }}+\frac{d^{\beta }{V}_2(x_2)}{d{t}^{\beta }}<0$ if the sum of entries of each column (row) of the matrix (37) is negative (Theorem 3) and the nonlinear positive system is globally stable. □

5. Procedure and Example

To find the $K\in {\Re }_{+}^{m\times p}$ satisfying the condition (37) for the nonlinear positive system, the following procedure can be used.

Procedure 1.

Step 1.

Using the matrices $\overline{A},$ $\overline{B},$ $\overline{C}$ of the positive linear system and the matrix $H$ compute the maximum value of the matrix $\overline{K}$ such that the sum of all entries of each column (row) of the matrix

$$\overline{\overline{A}}=\overline{A}+\overline{B}\overline{K}H\overline{C}$$

(40)

is negative. Entries of the matrix $K$ can be computed as the solution of the linear matrix equation

$$Gk=h,$$

(41)

where the matrix $G$ and the column vector $h$ are defined by the sum of entries of each column (row) of the matrix (40) and vector k contains components of matrix K. If $m p>n$ or/and $\mathrm{rank} G\ne n,$ then we choose arbitrarily $m p-\mathrm{rank} G$ nonnegative entries of the matrix K.

Step 2.

Using the matrices $\underset{¯}{A},$ $\underset{¯}{B},$ $\underset{¯}{C}$ of the positive linear system and the matrix $H$ compute the maximum value of the matrix $\underset{¯}{K}$ such that the sum of all entries of each column (row) of the matrix

$$\underset{¯}{\underset{¯}{A}}=\underset{¯}{A}+\underset{¯}{B}\underset{¯}{K}H\underset{¯}{C}$$

(42)

is negative.

Step 3.

Taking into consideration $\overline{K}$ computed in Step 1 and $\underset{¯}{K}$ from Step 2, find the desired $K\in {\Re }_{+}^{m\times p}$ for which the matrices $\overline{\overline{A}}$ and $\underset{¯}{\underset{¯}{A}}$ are Hurwitz, i.e., the characteristic f(e) satisfy the condition (34).

Remark 3.

The conditions of Theorem 2 can be also used to compute the entries of the matrix$K$. Usually in this case the computations are more complicated.

Example 2.

Consider the nonlinear feedback system shown in Figure 1 with the interval matrices of the positive linear part

$$\begin{array}{l}\overline{A}=\left[\begin{array}{ccc}-15.8& 0.2& 0.9\\ 0.4& -14.1& 0.5\\ 0.5& 0.4& -20.1\end{array}\right],\begin{array}{c}\end{array}\underset{¯}{A}=\left[\begin{array}{ccc}-7.9& 0.1& 0.7\\ 0.2& -7.9& 0.3\\ 0.1& 0.2& -12.1\end{array}\right],\begin{array}{c}\end{array}\\ \overline{B}=\left[\begin{array}{cc}0.5& 0.4\\ 0.3& 0.5\\ 0.8& 0.6\end{array}\right],\begin{array}{c}\end{array}\underset{¯}{B}=\left[\begin{array}{cc}0.4& 0.3\\ 0.2& 0.4\\ 0.6& 0.5\end{array}\right],\\ \overline{C}=\left[\begin{array}{ccc}0.4& 0.6& 0.8\\ 0.6& 0.4& 0.6\end{array}\right],\begin{array}{c}\end{array}\underset{¯}{C}=\left[\begin{array}{ccc}0.3& 0.5& 0.6\\ 0.4& 0.3& 0.5\end{array}\right]\end{array}$$

(43)

and the gain matrix

$$H=\left[\begin{array}{cc}2& 1\\ 1& 5\end{array}\right].$$

(44)

From (43) it follows that m = p = 2 and $u_1=f(e_1,e_2)\le k_{11}{e}_1+k_{12}{e}_2,$ $u_2=f(e_1,e_2)\le k_{21}{e}_1+k_{22}{e}_2$, then we are looking for

$$K=\left[\begin{array}{cc}{k}_{11}& k_{12}\\ k_{21}& k_{22}\end{array}\right]\in {\Re }_{+}^{2\times 2},$$

(45)

for which the nonlinear feedback system is globally stable.

Using Procedure 1 we obtain:

Step 1.

Using (40), (43) and (44) we determined that the sum of columns are the following:

$$\begin{array}{l}{\displaystyle \sum \overline{\overline{A}}(:,1)}=2.24k_{11}+5.44k_{12}+2.1k_{21}+5.1k_{22}-14.9,\\ {\displaystyle \sum \overline{\overline{A}}(:,2)}=2.56k_{11}+4.16k_{12}+2.4k_{21}+3.9k_{22}-13.5,\\ {\displaystyle \sum \overline{\overline{A}}(:,3)}=3.52k_{11}+6.08k_{12}+3.3k_{21}+5.7k_{22}-18.7\end{array}$$

(46)

and taking into consideration (5.2), we have

$$G=\left[\begin{array}{cccc}2.24& 5.44& 2.1& 5.1\\ 2.56& 4.15& 2.4& 3.9\\ 3.52& 6.08& 3.3& 5.7\end{array}\right],\begin{array}{c}\end{array}k=\left[\begin{array}{c}{k}_{11}\\ k_{12}\\ k_{21}\\ k_{22}\end{array}\right],\begin{array}{c}\end{array}h=\left[\begin{array}{c}14.9\\ 13.5\\ 18.7\end{array}\right].$$

(47)

Since $\mathrm{rank} G=2$, then we choose $mp-\mathrm{rank} G=2$ elements of the vector k (entries of the matrix K) as $k_{21}=1,\begin{array}{c}\end{array}{k}_{22}=1$. The solution for (41) with (47) is the following

$$\left[\begin{array}{c}{k}_{11}\\ k_{12}\\ k_{21}\\ k_{22}\end{array}\right]=\left[\begin{array}{c}1.309\\ 0.869\\ 1\\ 1\end{array}\right]$$

(48)

and for

$$\overline{K}<=\left[\begin{array}{cc}1.309& 0.869\\ 1& 1\end{array}\right]$$

(49)

the system with $\overline{A},$ $\overline{B},$ $\overline{C}$ is stable.

Step 2.

Similar to Step 1, using (42), (43) and (44) we can write the linear matrix Equation (41) in the form

$$\left[\begin{array}{cccc}1.1& 2.53& 1.2& 2.76\\ 1.43& 2.2& 1.56& 2.4\\ 1.87& 3.41& 2.04& 3.72\end{array}\right]\left[\begin{array}{c}{k}_{11}\\ k_{12}\\ k_{21}\\ k_{22}\end{array}\right]=\left[\begin{array}{c}7.6\\ 7.6\\ 11.1\end{array}\right].$$

(50)

Since $\mathrm{rank} \left[\begin{array}{cccc}1.1& 2.53& 1.2& 2.76\\ 1.43& 2.2& 1.56& 2.4\\ 1.87& 3.41& 2.04& 3.72\end{array}\right]=2$, then we choose two elements of the vector k as $k_{11}=1,\begin{array}{c}\end{array}{k}_{12}=1$. The solution for (50) is

$$\left[\begin{array}{c}{k}_{11}\\ k_{12}\\ k_{21}\\ k_{22}\end{array}\right]=\left[\begin{array}{c}1\\ 1\\ 1.013\\ 1.002\end{array}\right],$$

(51)

and

$$\underset{¯}{K}<=\left[\begin{array}{cc}1& 1\\ 1.013& 1.002\end{array}\right]$$

(52)

Therefore, the system with $\underset{¯}{A},$ $\underset{¯}{B},$ $\underset{¯}{C}$ is stable.

Step 3.

Taking into consideration (49) and (52), we have that for

$$K=\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]$$

(53)

the matrices $\overline{\overline{A}}$ and $\underset{¯}{\underset{¯}{A}}$ are Hurwitz since

$$\begin{array}{l}{\displaystyle \sum \overline{\overline{A}}(:,1)}=-0.01,\\ {\displaystyle \sum \overline{\overline{A}}(:,2)}=-0.01,\\ {\displaystyle \sum \overline{\overline{A}}(:,3)}=-0.06,\end{array}\begin{array}{l}{\displaystyle \sum \underset{¯}{\underset{¯}{A}}(:,1)}=-0.02,\\ {\displaystyle \sum \underset{¯}{\underset{¯}{A}}(:,2)}=-0.48,\\ {\displaystyle \sum \underset{¯}{\underset{¯}{A}}(:,3)}=-0.1.\end{array}$$

(54)

Therefore, for nonlinear elements satisfying the condition

$$\left[\begin{array}{c}0\\ 0\end{array}\right]\le f(e_1,e_2)\le \left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]\left[\begin{array}{c}{e}_1\\ e_2\end{array}\right],$$

(55)

the nonlinear feedback system with interval matrices (43) of positive linear parts and for the gain matrix (53), the nonlinear system is globally stable.

6. Exponential Decay of Processes in Nonlinear Feedbacks Systems

Consider the nonlinear feedback system shown in Figure 3 which consists of the positive linear part, the nonlinear element with characteristic $u=f(e)$ and positive dynamical feedback. The linear part is described by the equations

$$\begin{array}{l}\dot{x}=Ax+Bu,\\ y=Cx,\end{array}$$

(56)

with interval matrices

$$\underset{¯}{A}\le A\le \overline{A},\begin{array}{c}\end{array}\underset{¯}{B}\le B\le \overline{B},\begin{array}{c}\end{array}\underset{¯}{C}\le C\le \overline{C},$$

(57)

where $x=x(t)\in {\Re }_{+}^{n_1},$ $u=u(t)\in {\Re }_{+},$ $y=y(t)\in {\Re }_{+}$ is the state, input and output vectors of the system (56) and $A\in M_{n_1},$ $B\in {\Re }_{+}^{n_1\times 1},$ $C\in {\Re }_{+}^{1\times n_1}.$ It is assumed that the matrix $A$ of (56) has all eigenvalues $s_k$ with real parts smaller than

$$\mathrm{Re}{s}_k<-\gamma , \mathrm{i}.\mathrm{e}., \gamma >0,k=1,\dots ,n.$$

(58)

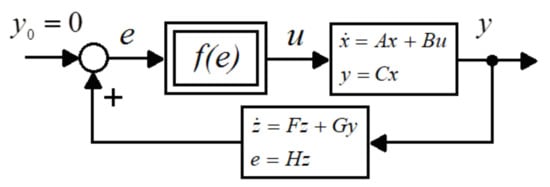
Figure 3. The nonlinear feedback system.

The characteristic of the nonlinear element is shown in Figure 2 and it satisfies the condition

$$0\le \frac{f(e)}{e}\le k<\infty .$$

(59)

The positive feedback system is described by the equations

$$\begin{array}{l}\dot{z}=Fz+Gy,\\ e=Hz,\end{array}$$

(60)

with interval matrices

$$\underset{¯}{F}\le F\le \overline{F},\begin{array}{c}\end{array}\underset{¯}{G}\le G\le \overline{G},\begin{array}{c}\end{array}\underset{¯}{H}\le H\le \overline{H},$$

(61)

where $z=z(t)\in {\Re }_{+}^{n_2},$ $e=e(t)\in {\Re }_{+}$ are the state vector and output vectors. It is assumed that the matrix $F+I_n\gamma \in M_{n_2}$ is also asymptotically stable. From (56) and (60) we have

$$\left[\begin{array}{c}\dot{x}\\ \dot{z}\end{array}\right]=\widehat{A}\left[\begin{array}{c}x\\ z\end{array}\right]+\widehat{B}u,$$

(62)

where

$$\widehat{A}=\left[\begin{array}{cc}A& 0\\ GC& F\end{array}\right]\in M_n,\begin{array}{c}\end{array}\widehat{B}=\left[\begin{array}{c}B\\ 0\end{array}\right]\in {\Re }_{+}^{n\times 1},\begin{array}{c}\end{array}n=n_1+n_2.$$

(63)

The following theorem gives sufficient conditions for the exponential decay of transient values in the positive feedback nonlinear system faster than $e^{-\gamma t}$.

Theorem 10.

The state variables of the nonlinear system consisting of the positive linear part (56), the nonlinear element satisfying the condition (34), (35), (36) and positive asymptotically stable dynamical feedback system (60) are decaying exponentially faster than $e^{-\gamma t}$if the matrix

$$\left[\begin{array}{cc}\underset{¯}{A}+I_{n_1}\gamma & k\overline{B}\overline{H}\\ \overline{G}\overline{C}& \underset{¯}{F}+I_{n_2}\gamma \end{array}\right]\in M_n$$

(64)

is asymptotically stable.

Proof. 

The proof will be accomplished by the use of the Lyapunov method [26,27]. As the Lyapunov function $V(x,z)$ we choose

$$V(x,z)={\lambda }^T\left[\begin{array}{c}x\\ z\end{array}\right]\ge 0 \mathrm{for} x\in {\Re }_{+}^{n_1},\begin{array}{c}\end{array}z\in {\Re }_{+}^{n_2},$$

(65)

where $\lambda \in {\Re }_{+}^n$ is a strictly positive vector, i.e., ${\lambda }_k>0$, $k=1,\dots ,n.$

It is well-known that if the matrix $A\in M_n$ is asymptotically stable, then the state variables of the system $\dot{x}=(A+I_n\gamma )x$ are decaying exponentially faster than $e^{-\gamma t}$.

Using (56), (60) and (65) we obtain

$$\begin{array}{l}\dot{V}(x,z)={\lambda }^T\left[\begin{array}{c}\dot{x}\\ \dot{z}\end{array}\right]={\lambda }^T\left\{\left[\begin{array}{cc}A& 0\\ GC& F\end{array}\right]\left[\begin{array}{c}x\\ z\end{array}\right]+\left[\begin{array}{c}B\\ 0\end{array}\right]u\right\}\\ ={\lambda }^T\left\{\left[\begin{array}{cc}A& 0\\ GC& F\end{array}\right]\left[\begin{array}{c}x\\ z\end{array}\right]+\left[\begin{array}{c}B\\ 0\end{array}\right]kHz\right\}={\lambda }^T\left[\begin{array}{cc}A& kBH\\ GC& F\end{array}\right]\left[\begin{array}{c}x\\ z\end{array}\right]\le 0\end{array}$$

(66)

since $Bu=Bf(e)\le kBHz$ by the condition (6.2).

From (66) it follows that $\dot{V}(x,z)\le 0$ if the matrix (64) is asymptotically stable, and therefore the state variables decay exponentially faster than $e^{-\gamma t}$. □

Theorem 6.1 can be applied to solve the following two problems.

Problem 1.

Given matrices A, B, C and F, G, H of the positive systems (56), (60) and the nonlinear characteristic $u=f(e)$ of the nonlinear element. Knowing the value of $k$ satisfying the condition (59), check if the transient processes in the nonlinear system decay faster than $e^{-\gamma t}$.

Problem 2.

Given matrices A, B, C and F, G, H of the positive systems (56), (60) and the nonlinear characteristic $u=f(e)$ of the nonlinear element. Find the maximal value of $k$ for which the characteristic $u=f(e)$ of the nonlinear element satisfies the condition (59) and the transient values of the nonlinear system decay faster than $e^{-\gamma t}$.

The Problem 1 can be solved by the use of the following:

Procedure 2.

Step 1.

Knowing the characteristic $u=f(e)$, find the minimal value of $k$ satisfying the condition (59).

Step 2.

Using Theorem 10, find the sum of entries of each column (row) of the matrix (64). If all these sums are negative, then the transient processes in the nonlinear system decay faster than $e^{-\gamma t}$.

The Problem 2 can be solved by the use of the following:

Procedure 2.

Step 1.

Using Theorem 10, find the sum of entries of each column (row) of the matrix (64).

Step 2.

Find the maximal value of $k_c(k_r)$ for which the sums of entries of all columns (rows) of (64) are negative.

Step 3.

Find $k_{\max }=\min (k_c,k_r)$.

In this case, the transient process in the nonlinear system decrease faster than $e^{-\gamma t}$ for all nonlinear characteristics $u=f(e)$ satisfying the condition

$$0<f(e)<k_{\max }e.$$

(67)

Remark 4.

The value of$k_{\max }$depends only on the first$n_1$rows and of the last$n_2$columns of the matrix (64).

Example 3.

Consider the nonlinear system shown in Figure 3 with linear positive parts described by (56) and (60) with

$$\begin{array}{l}\underset{¯}{A}=\left[\begin{array}{cc}-6.5& 1\\ 2& -6.2\end{array}\right],\begin{array}{c}\end{array}\overline{A}=\left[\begin{array}{cc}-7& 1.5\\ 2.3& -6.5\end{array}\right],\begin{array}{c}\end{array}\underset{¯}{B}=\left[\begin{array}{c}0.5\\ 0.7\end{array}\right],\begin{array}{c}\end{array}\overline{B}=\left[\begin{array}{c}0.5\\ 0.7\end{array}\right],\\ \underset{¯}{C}=[\begin{array}{cc}0.4& 0.5\end{array}],\begin{array}{c}\end{array}\overline{C}=[\begin{array}{cc}0.5& 0.6\end{array}]\end{array}$$

(68)

and

$$\begin{array}{l}\underset{¯}{F}=\left[\begin{array}{cc}-6& 2\\ 1.6& -7\end{array}\right],\begin{array}{c}\end{array}\overline{F}=\left[\begin{array}{cc}-6.2& 2.2\\ 1.8& -7.3\end{array}\right],\begin{array}{c}\end{array}\underset{¯}{G}=\left[\begin{array}{c}0.8\\ 0.6\end{array}\right],\begin{array}{c}\end{array}\overline{G}=\left[\begin{array}{c}1\\ 0.8\end{array}\right],\hspace{1em}\hspace{1em}(6.10)\\ \underset{¯}{H}=[\begin{array}{cc}0.4& 0.2\end{array}],\begin{array}{c}\end{array}\overline{H}=[\begin{array}{cc}0.5& 0.4\end{array}]\end{array}$$

(69)

respectively, and the nonlinear element with characteristics satisfying the condition (59).

Case 1.

Using$k=1$, check the global stability of the nonlinear system for$\gamma =-2.$In this case, using (6.5), (6.9) and (6.10) we obtain

$$\left[\begin{array}{cc}\underset{¯}{A}+I_{n_1}\gamma & k\overline{B}\overline{H}\\ \overline{G}\overline{C}& \underset{¯}{F}+I_{n_2}\gamma \end{array}\right]=\left[\begin{array}{cccc}-4.5& 1& 0.3& 0.24\\ 2& -4.2& 0.4& 0.32\\ 0.5& 0.6& -4& 2\\ 0.4& 0.48& 1.6& -5\end{array}\right]$$

(70)

The sums of the entries of columns of the matrix (6.11) are: column 1:$=-1.6,$column 2:$=-2.12,$column 3:$=-1.7,$column 4:$=-2.44$. Therefore, by Theorem 6.1, the nonlinear system is globally stable.

Case 2.

Find the maximal value of$k_{\max }$satisfying the condition (4.2) for which the transient process in the nonlinear system decreases faster than$e^{-\gamma t}$. Using Procedure 2 we obtain the following:

Step 1.

The sums of entries of each column (row) of the matrix

$$\left[\begin{array}{cc}\underset{¯}{A}+I_{n_1}\gamma & k\overline{B}\overline{H}\\ \overline{G}\overline{C}& \underset{¯}{F}+I_{n_2}\gamma \end{array}\right]=\left[\begin{array}{cccc}-4.5& 1& 0.3k& 0.24k\\ 2& -4.2& 0.4k& 0.32k\\ 0.5& 0.6& -4& 2\\ 0.4& 0.48& 1.6& -5\end{array}\right]$$

(71)

are: column 1:$=-1.6,$column 2:$=-2.12,$column 3:$=0.7k-2.4,$column 4:$=0.56k-3,$row 1:$=-2.96,$row 2:$=-1.48,$row 3:$=0.54k-3.5,$row 4:$=0.72k-2.2.$

Step 2.

From Theorem 10 we have: for column 3: k < 3.428 and for column 4: k < 5.357 and for row 1: k < 6.482, row 2: k < 3.0555.

Step 3.

The desired value of k is$k_{\max }=\min (k_c,k_r)=3.0555$.

Therefore, the transient process in the nonlinear system with characteristics satisfying the condition (34), (35), (36) for$k<3.0555$decreases faster than$e^{-\gamma t}$.

Remark 3.

From matrix (6.5) and the computation procedure, it follows that the k depends only on the matrices F, G, H and is independent of the matrices A, C, G.

7. Concluding Remarks

The global stability of continuous-time nonlinear feedback systems with different fractional orders and interval matrices of positive linear parts has been investigated. New sufficient conditions for the global stability of this class of positive nonlinear systems are established (Theorem 9). The procedure for the calculation of a gain matrix characterizing the class of nonlinear elements is presented and illustrated by numerical example. Sufficient conditions for the exponential decay of processes in nonlinear systems have been proposed (Theorem 10) and illustrated by numerical example. The considerations can be extended to the discrete-time nonlinear systems with different fractional orders and interval matrices of positive linear parts. Further investigation could address the extension of the considerations to nonlinear different fractional order systems with e time-varying linear parts.