Porting MADGRAPH to FPGA Using High-Level Synthesis (HLS)

Abstract

The escalating demand for data processing in particle physics research has spurred the exploration of novel technologies to enhance the efficiency and speed of calculations. This study presents the development of an implementation of MADGRAPH, a widely used tool in particle collision simulations, to Field Programmable Gate Array (FPGA) using High-Level Synthesis (HLS). This research presents a proof of concept limited to a single, relatively simple process $e^{+}{e}^{-}\to {\mu }^{+}{\mu }^{-}$. The experimental evaluation methodology is described, focusing on performance comparison between traditional CPU implementations, GPU acceleration, and the new FPGA approach. This study describes the complex process of adapting MADGRAPH to FPGA using HLS, focusing on optimizing algorithms for parallel processing. These advancements could enable faster execution of complex simulations, highlighting FPGA’s crucial role in advancing particle physics research. The encouraging results obtained in this proof of concept prove potential interest in testing the performance of the FPGA implementation of more complex processes.

1. Introduction

Physics event generators are a necessary part of the software infrastructure in High-Energy Physics (HEP) experiments. For example, in the ATLAS [1] and CMS [2] experiments at the Large Hadron Collider (LHC) [3], they are the entry point for simulation workflows and take 5–20% of the annual CPU resource allocation. These generators use Monte Carlo (MC) methods to randomly sample events, where each event requires an independent computation of the Matrix Element (ME). Each event generation involves multiple steps, ranging from parton distribution function sampling and hard scattering to parton showering, hadronization, and detector simulation. This workflow easily allows data parallelism, especially on Graphics Processing Unit (GPU) and vector CPUs, which are optimized for lockstep processing.

As the complexity of high-energy physics experiments grows, so does the computational cost of event generation. For example, for multi-jet processes, the computation of the number of Feynman diagrams is high, which leads to a corresponding increase in the number of associated MEs, resulting in high computation times. In fact, more than 95% of the runtime in such workflows is due to the calculation of the ME alone and hence the major computational bottleneck. Beyond this, processes with high jet multiplicities or beyond the Standard Model can require several seconds of CPU time per event such that large-scale simulations may become very resource-intensive.

These challenges are overcome by exploring new hardware architectures, such as GPU, FPGA, and application-specific accelerators, which have great potential to accelerate ME computations by using parallelism, reducing latency, or optimising specific domains. The growing computational requirements of modern event generators impose the necessity to work out efficient solutions at both the software and hardware levels. In future facilities, the luminosity and energy of collisions will increase (High-Luminosity LHC). This will further increase the complexity of simulated processes. This points to the urgent need for scalable, high-performance solutions for the computational challenges of next-generation HEP experiments.

Recent years have seen a variety of GPU-based approaches that tackle the matrix-element calculation and other time-critical parts of event generation [4,5], leading to significant speed-ups in platforms like MadGraph5_aMC. However, large-scale simulations still demand further optimization to manage power efficiency and handle increasingly complex processes. Reconfigurable hardware such as FPGAs has drawn attention in HEP data processing pipelines, for instance, in trigger systems and real-time inference [6,7], due to their capacity for fine-grained parallelism and deterministic latency control.

Beyond high-energy physics, a distinct trend in high-performance computing (HPC) reveals that FPGAs can be effectively utilized in areas such as deep learning and customized numerical kernels, suggesting significant opportunities for improvements in performance and energy efficiency. However, transferring large and complex physics codes to hardware presents considerable challenges. High-Level Synthesis (HLS) [8] tools such as Vitis HLS have simplified this task by allowing developers to code kernel logic in C/C++, though complex refactoring is frequently necessary to restructure loops, memory accesses, and data dependencies. Specifically, in the case of MadGraph5_aMC, the computation of the matrix element is the primary contributor to the total runtime for multi-jet events; therefore, it represents a sensible target for an FPGA-based acceleration strategy that could help reduce performance bottlenecks while preserving or enhancing energy efficiency.

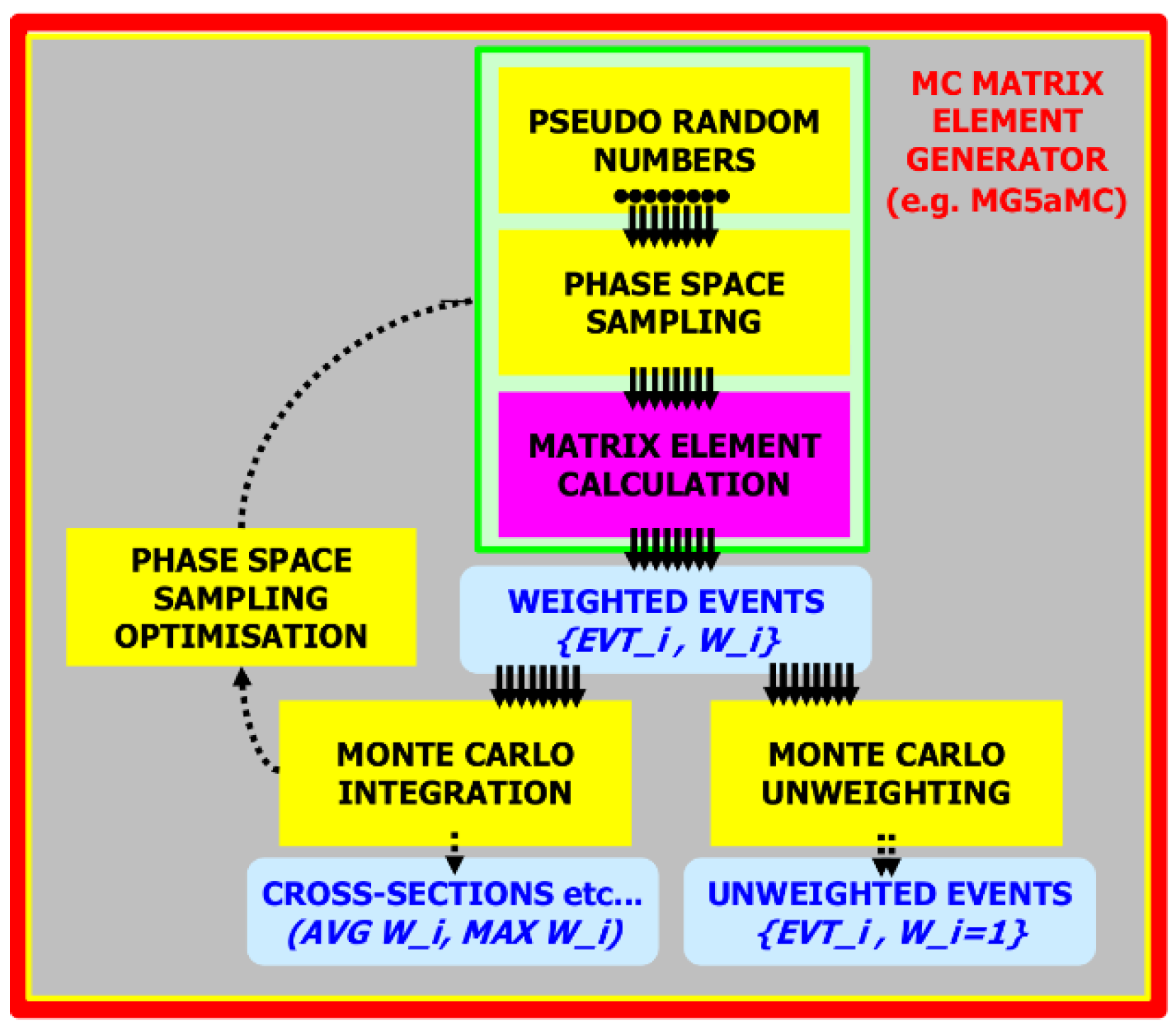
MadGraph5_aMC@NLO [9] is an event generator that provides a platform developed to study both Standard Model (SM) and Beyond Standard Model (BSM) physics with a suite of tools: cross-section calculations, event generation at the hard scattering level, merging with event generators, and interfacing with various packages for manipulating and analyzing events. The framework allows a user to simulate Leading Order (LO)-accurate processes starting from an arbitrary user-provided Lagrangian while providing fully automated Next to Leading Order (NLO)-accurate Quantum Chromodynamics (QCD) corrections to any SM process. Simultaneously, it calculates Matrix Element at the tree level and one-loop calculation (Figure 1).

This study describes porting a core part of MadGraph5_aMC, specifically the matrix element (ME) calculation, to an Alveo FPGA Accelerator. The ME evaluation is often the primary workload that needs to be processed in simulations with many Feynman diagrams. Such workloads are process-intensive, especially when large particle multiplicities are involved. Modifying the existing code to meet HLS requirements means that data structures and loop constructs have to be changed with the core physics algorithms remaining unchanged. The goal of this is to demonstrate how specialized hardware accelerators can help achieve greater speed and energy savings in real HEP simulations.

2. Materials and Methods

2.1. Hardware and Software Setup

2.1.1. Host System and FPGA Board

Experiments were carried out on a workstation featuring an Intel Core i7-13700 CPU (24 cores, 3.4 GHz base frequency) with 32 GB of RAM, running Ubuntu 22.04. The FPGA accelerator used was an AMD Xilinx Alveo U250 board; we configured the FPGA to operate at a synthesis target frequency of 120 MHz.

2.1.2. Tools and Libraries

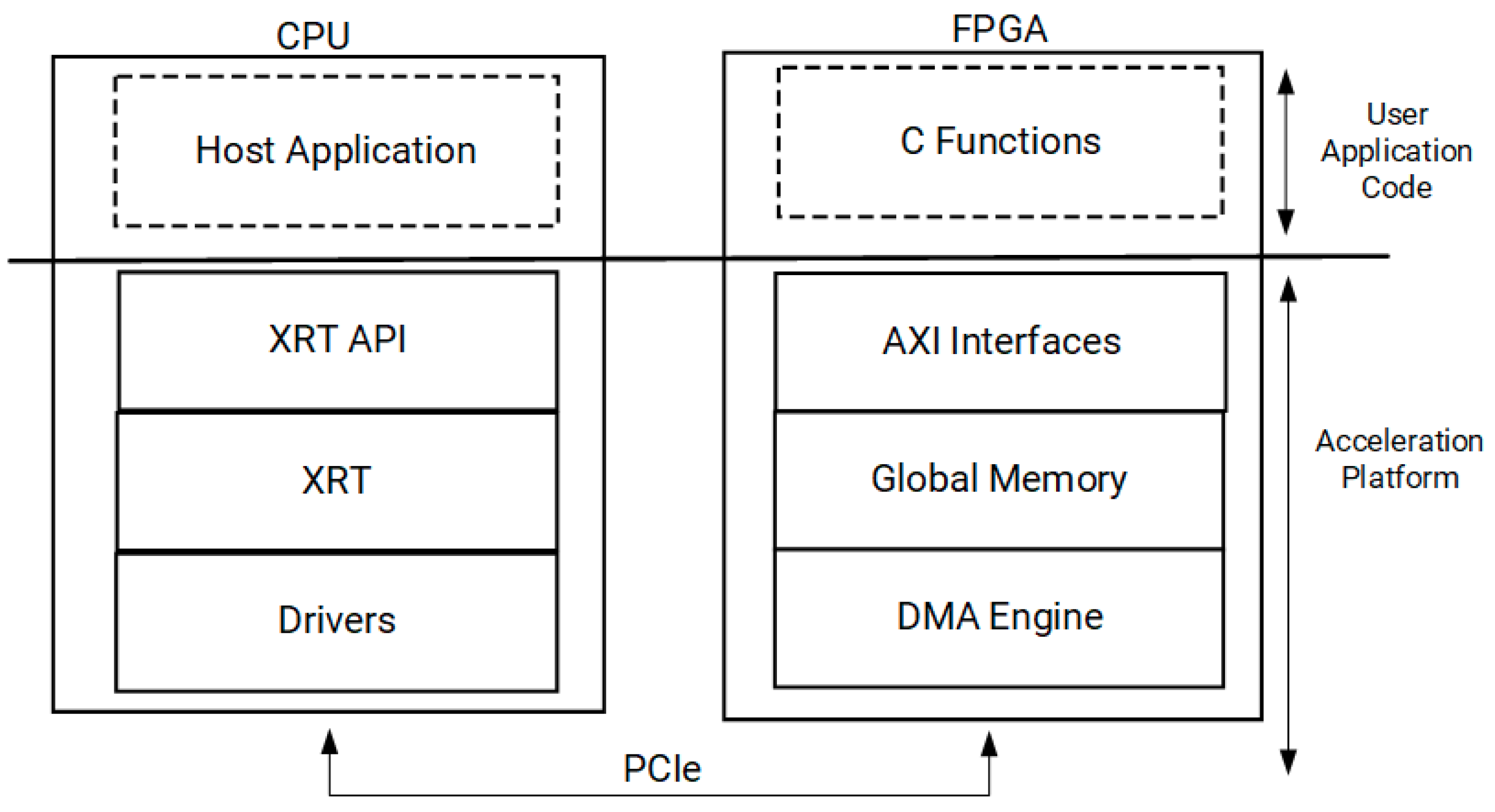
The FPGA kernels were developed using Vitis HLS (version 2023.2) and integrated with the platform through the Xilinx Vitis toolchain (Figure 2). All host applications were compiled with g++ (version 11.3) and linked against the Xilinx Runtime (XRT, version 2.16.204). Random number generation on the host used the C++11 Mersenne Twister engine (std::mt19937_64) to create pseudo-random seeds for Monte Carlo simulations.

We also make performance comparisons on two additional platforms:

• CPU Only: Using the same Intel Core i7-13700 and single-threaded and multi-threaded versions of the MadGraph code.
• GPU: An NVIDIA GeForce RTX 3050 8 GB running CUDA 12.3, using the madgraph4gpu branch of MadGraph5_aMC [11].

2.2. Code Porting and HLS Adaptation

We implemented a GPU-adapted version of the MadGraph5_aMC ME calculation, which uses CUDA kernels and standard C++ library calls for parallel event generation. Although this approach takes advantage of GPU thread blocks for concurrency, the code includes functions that are not supported or are not optimal in the context of FPGA synthesis.

• Dynamic memory allocations (e.g., calls to new/delete or high-level C++ containers like std::vector), which complicate the static resource mapping required for an FPGA design.
• Complex function call hierarchies and partial inlining constraints that required flattening or restructuring for pipeline efficiency.
• CUDA-specific kernels and parallel constructs that had no direct analog in HLS.

Figure 2. Interaction between the CPU and FPGA in an acceleration platform. The Host Application runs on the CPU, interfacing with the FPGA via the XRT stack and PCIe for data transfer. Computation is offloaded to FPGA kernels, which communicate with AXI interfaces, global memory, and the DMA engine to optimize performance [12].

Figure 2. Interaction between the CPU and FPGA in an acceleration platform. The Host Application runs on the CPU, interfacing with the FPGA via the XRT stack and PCIe for data transfer. Computation is offloaded to FPGA kernels, which communicate with AXI interfaces, global memory, and the DMA engine to optimize performance [12].

These guidelines required eliminating dynamic allocations, replacing certain library calls with HLS-ready intrinsics, and limiting function recursion or the use of function pointers. The original code organized physical data, such as 4-moments, coupling constants and partial amplitude matrices. For FPGA synthesis, the memory organization had to be explicitly defined at compile time.

• Static Buffers and Fixed-Size Arrays: Wherever possible, we replaced dynamic containers with fixed-size arrays. For instance, four vectors representing particle momenta were stored in double momenta [MAX_EVENTS] [4], thus avoiding any runtime allocation. A compile-time MAX_EVENTS could be tuned based on resource constraints (e.g., BRAM availability on the FPGA).
• HLS Streams: In parts of the code that required sequential data processing (especially random seed distribution), we employed HLS hls::stream<> objects to pass data in a pipelined way. This approach allowed us to separate data production (e.g., random momentum generation) from ME consumption, potentially improving concurrency within the FPGA kernel.

In the GPU implementation, each event can be processed independently for matrix element computation, enabling large-scale parallelization. In FPGAs, parallelism is realized in another way: through custom pipelines and concurrency of data streams instead of thousands of threads.

• Function Inlining and Loop Unrolling: We applied #pragma HLS UNROLL factor=N on small loops with known iteration bounds. Larger loops were pipelined (#pragma HLS PIPELINE) to allow new data to enter the arithmetic pipeline at each clock cycle, thus increasing performance.
• Consolidating Kernel Logic: The hierarchical function structure used in GPU code, where small CUDA kernels are separately compiled, was merged into a single monolithic HLS kernel or a small set of interconnected kernels. This allowed the Vitis HLS tool to optimize dataflow between subroutines without incurring significant overhead from function calls.
• Dataflow Optimization: We enabled #pragma HLS DATAFLOW on sections that continuously produce and consume data (e.g., generating four random vectors and then passing them to the ME calculator). This allowed partial results to be produced and consumed in a chain, rather than waiting for one complete step to finish before starting the next.

By default, MadGraph5_aMC uses double-precision (64-bit) floating-point arithmetic to ensure the accuracy required for most physical processes. In typical high-energy physics (HEP) simulations, especially those involving delicate interference patterns or higher-order corrections, double precision can be crucial to maintaining numerical stability. Although single- or mixed-precision approaches can significantly reduce the use of FPGA resources, our preliminary tests indicated that it was preferable to keep double-precision arithmetic in all major routines because simple-precision can introduce rounding errors, affecting the physical analysis.

2.3. FPGA Deployment Workflow

The final step in our design process was to synthesize the high-level synthesis (HLS) cores into hardware, generate the corresponding bit stream, and connect the host program with the FPGA design. This subsection describes how the Vitis toolchain, runtime libraries, and custom host code are joined to enable accelerated execution of the array element (ME) calculation on the Alveo board (Figure 3).

2.4. Experimental Procedure

As a proof of concept for the FPGA-accelerated matrix element (ME) calculation, we focused on the $e^{+}{e}^{-}\to {\mu }^{+}{\mu }^{-}$ process, generating event samples ranging from $N=2^{11}$ to $N=2^{24}$ to examine scaling behaviour. Random seeds were initially provided on the host side, then transferred to the FPGA, where a phase-space sampling procedure internally computed the final-state particle momenta. Once each event’s kinematics were established, the FPGA kernel performed the ME calculation, thus completing the core high-throughput step of the simulation.

All run-time measurements recorded the total time just before loading the input data (random seed + num_events) in the accelerator to retrieve the resulting ME values from the FPGA memory. This approach captured the overhead from data transfers over PCIe as well as the hardware computation time. After collecting the output from each run, we cross-checked the FPGA-computed MEs against a reference CPU implementation of MadGraph5_aMC, allowing a floating-point difference tolerance of ${10}^{-7}$. No discrepancies exceeding this threshold were observed, confirming that our hardware kernel preserved numerical accuracy relative to the established software baseline.

3. Results

This section presents the evaluation of FPGA-based matrix element (ME) calculation, compared to CPU- and GPU-accelerated implementations. We mainly focus on runtime scaling through different event counts, discuss the use of FPGA resources, and detail numerical validation. Finally, we interpret the implications of these results for larger or more complex physical processes.

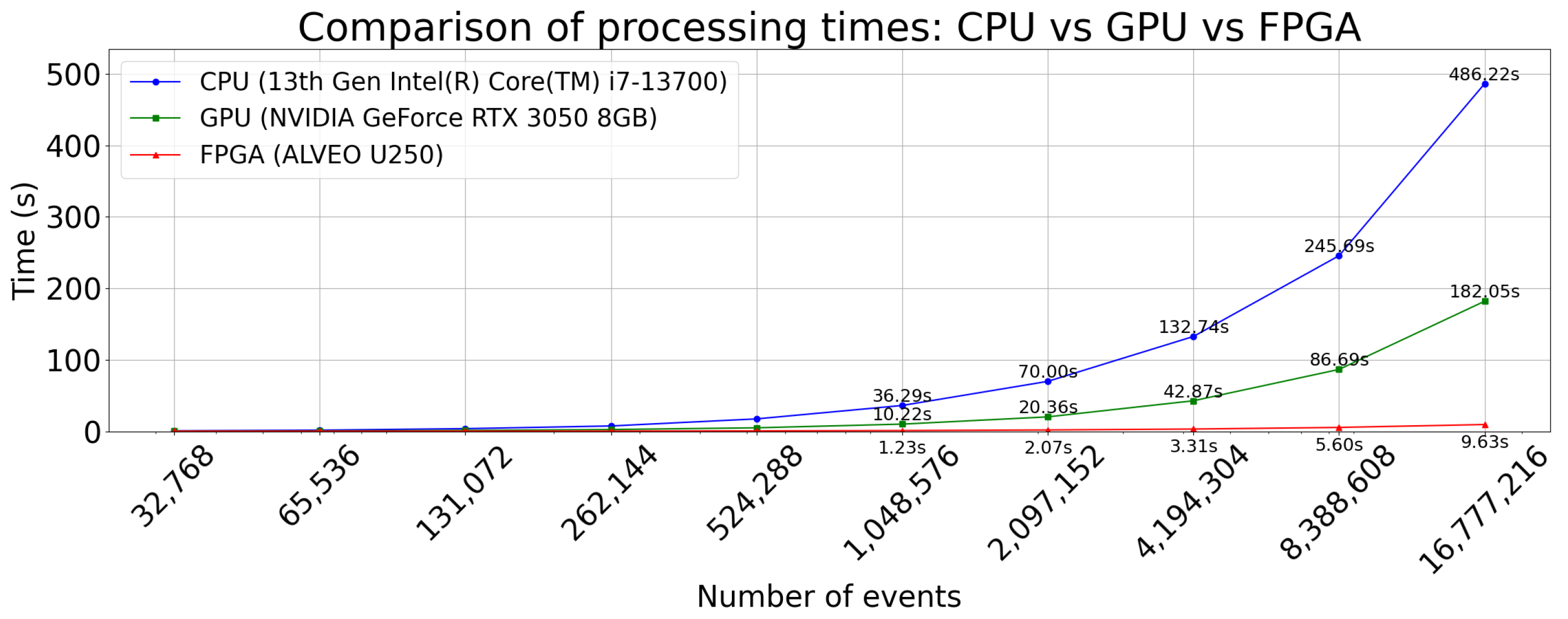
The runtime includes data transfers between host and device, the kernel execution itself, and any necessary synchronization steps. Figure 4 compares the performance of the following:

• CPU-Only: 13th Gen Intel(R) Core(TM) i7-13700).
• GPU-Accelerated: NVIDIA RTX 3050 8 GB.
• FPGA-Accelerated: Alveo U250 board operating at 120 MHz.

For the range of events ($2^{15}$ up to $2^{18}$ events), the time related to core configuration and PCIe transfer decreases gains from hardware acceleration, resulting in almost equal performance between CPU, GPU, and FPGA. However, once the batch size increases beyond $2^{20}$ events, the FPGA implementation begins to outperform both the CPU and the GPU. At $2^{24}$ events, these factors reach approximately 51× and 19×, respectively, with the FPGA. This improvement arises largely from the FPGA’s pipeline-level concurrency, which keeps arithmetic units utilized at a high rate once data streaming is underway. Meanwhile, the overhead associated with scheduling numerous GPU threads or relying on CPU thread management becomes less efficient at these larger event counts.

We obtained the final design for the Alveo U250 platform;

Table 1. Resource utilization of the FPGA design, including LUTs, FF, BRAMs, DSP slices, and the operating frequency (120 MHz). The design demonstrates efficient computation within the resource constraints.

Resource	Utilization	Available	Utilization (%)
LUT	404,715	1,759,631	23
FF	549,021	3,660,140	15
DSP	5218	12,424	42
BRAM	22	3280	0.6

summarizes the resource usage, highlighting Look-Up Tables (LUTs), Flip Flops (FFs), Digital Signal Processing (DSP) blocks, and on-chip Block RAM (BRAM):

The kernel meets timing closure at 120 MHz, with around a quarter of the LUTs and fewer than half of the available DSP slices utilized. This leaves some scope for kernel replication—in principle, multiple copies of the same kernel could run concurrently on the same device to push throughput higher, though the overall speed-up would then be limited by memory bandwidth and PCIe transfer rates. Double-precision arithmetic moderately increased DSP usage, but was still well within device limits. While it might be possible to reduce resource usage further by employing single-precision or hybrid-precision strategies, we prioritized numerical integrity.

Figure 4. Execution time comparison for matrix element calculation across different platforms: CPU (13th Gen Intel(R) Core(TM) i7-13700), GPU (NVIDIA GeForce RTX 3050 8GB), and FPGA (ALVEO U250).

Figure 4. Execution time comparison for matrix element calculation across different platforms: CPU (13th Gen Intel(R) Core(TM) i7-13700), GPU (NVIDIA GeForce RTX 3050 8GB), and FPGA (ALVEO U250).

4. Conclusions

This work demonstrates the significant performance improvement achieved by porting the Matrix Element calculation of MadGraph5_aMC to FPGA. By using the parallelism and hardware optimization capabilities of FPGA, the implementation drastically reduces the computational time compared to traditional CPU-based solutions. In particular, the FPGA performs a 51× speed-up concerning CPU and a 19× speed-up concerning the GPU. The FPGA design, operating at a frequency of 120 MHz, shows substantial efficiency gains in high-energy physics simulations, proving the viability of hardware acceleration for such complex calculations.

It is important to note that the comparison of the GPU and FPGA performance has been carried out between concrete models available in our test-bench. In the case of the GPU, the model used, an NVIDIA GeForce RTX 3050 8 GB, is a low-end consumer GPU. The reader might wonder about the outcome of a direct comparison with state-of-the-art GPU implementations such as MadGraph4GPU running on high-end GPUs (A100 or H100) commonly used in HPC systems for large-scale Monte Carlo production. This significant difference suggests that our current results may considerably underestimate the true potential of high-performance GPU-based solutions. In future comparisons, it would be valuable to include these more advanced GPU platforms to establish a more balanced assessment of the relative performance between FPGA and state-of-the-art GPU solutions available in HPC environments.

Despite the promising results, the implementation is currently limited to a single process, $e^{+}{e}^{-}\to {\mu }^{+}{\mu }^{-}$, due to the complexity of porting more intricate processes to hardware. While this first step validates the FPGA approach for simpler processes, future work will involve expanding the scope of the implementation to handle more complex matrix element calculations.

The design effectively utilizes FPGA resources, including LUT, FF, BRAM, and DSP slices, without exceeding the available hardware resources. This demonstrates the potential for scaling the FPGA design to handle more processes and larger datasets in the future.

Although reduced energy consumption was mentioned as a potential advantage of FPGA implementations, this study does not provide comparative energy measurements. The Alveo U250 FPGA used in our experiments has a maximum power rating of 225 W, higher than the RTX 3050 8 GB GPU’s power rating of approximately 130 W. However, the FPGA executes the matrix element calculation approximately 19 times faster than the GPU, which could potentially result in lower total energy consumption despite its higher power draw. Future work will include comprehensive energy efficiency evaluations to quantify the actual energy benefits of FPGA implementations for matrix element computation, especially considering the trade-offs between performance gains and energy consumption across hardware platforms.

The next steps in this work will focus on improving the implementation for more complex physics processes, optimizing the hardware design further, and integrating additional features such as energy efficiency evaluation. Moreover, incorporating broader FPGA models with increased processing power will allow for more demanding simulations to be executed efficiently.

The ability to accelerate MadGraph5_aMC on FPGA opens up new opportunities for high-energy physics research, where large-scale simulations are integral to understanding particle interactions. By moving from traditional CPU or GPU-based approaches to FPGA-based acceleration, this work provides a foundation for more efficient, faster, and energy-efficient simulation workflows, which can be crucial for future discoveries in particle physics.