Delayed Discharge Bridging Two Sputtering Modes from Modulated Pulsed Power Magnetron Sputtering (MPPMS) to Deep Oscillation Magnetron Sputtering (DOMS)
Abstract
1. Introduction
2. Materials and Methods
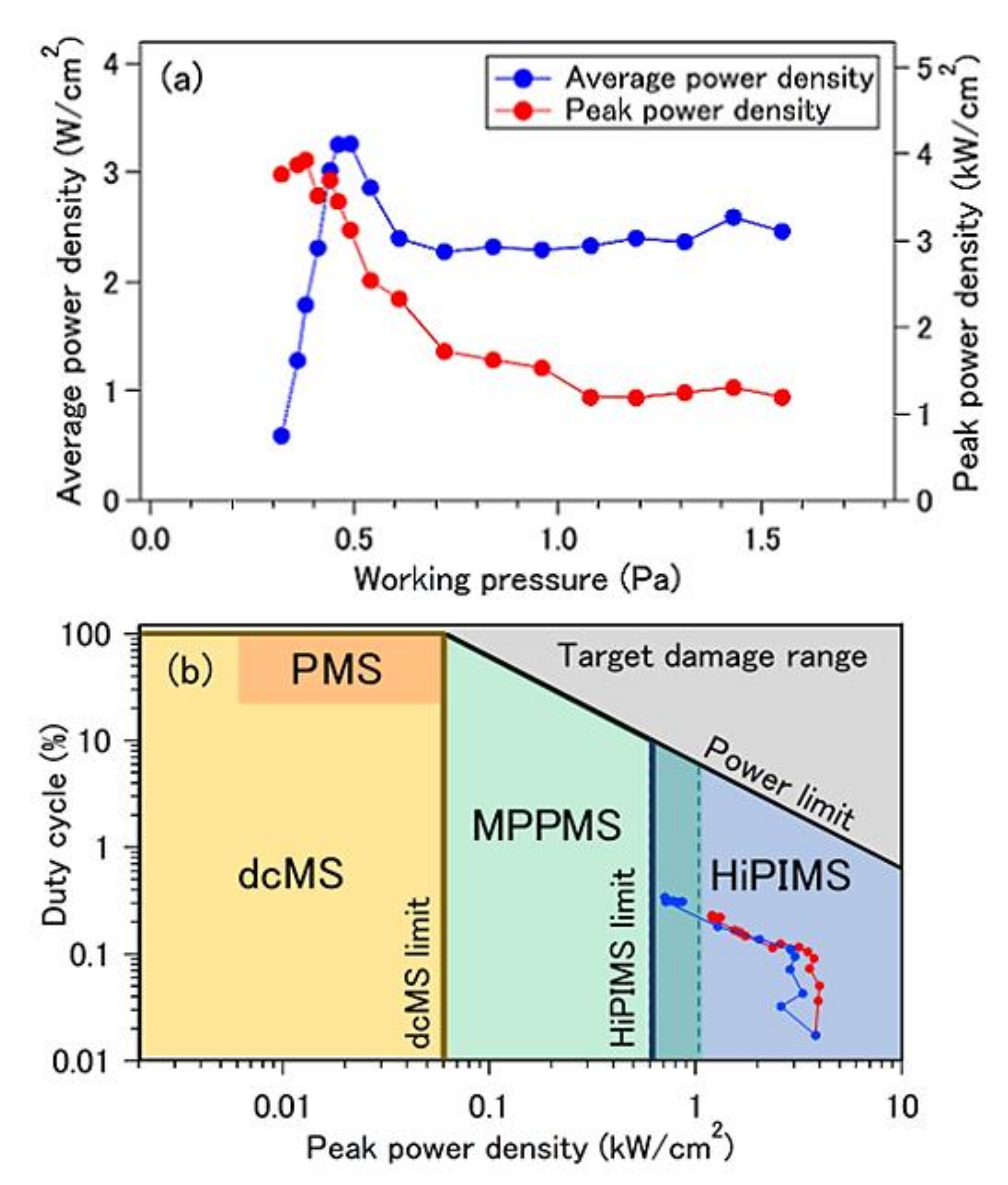
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gudmundsson, J.T.; Brenning, N.; Lundin, D.; Helmersson, U. High power impulse magnetron sputtering discharge. J. Vac. Sci. Technol. A 2012, 30, 030801. [Google Scholar] [CrossRef]
- Lin, J.; Moore, J.J.; Sproul, W.D.; Mishra, B.; Wu, Z. Modulated pulse power sputtered chromium coatings. Thin Solid Films 2009, 518, 1566–1570. [Google Scholar] [CrossRef]
- Lin, J.; Moore, J.; Sproul, W.; Mishra, B.; Rees, J.; Wu, Z.; Chistyakov, R.; Abraham, B. Ion energy and mass distributions of the plasma during modulated pulse power magnetron sputtering. Surf. Coat. Technol. 2009, 203, 3676–3685. [Google Scholar] [CrossRef]
- Lin, J.; Moore, J.J.; Sproul, W.D.; Mishra, B.; Wu, Z.; Wang, J. The structure and properties of chromium nitride coatings deposited using dc, pulsed dc and modulated pulse power magnetron sputtering. Surf. Coat. Technol. 2010, 204, 2230–2239. [Google Scholar] [CrossRef]
- Lin, J.; Moore, J.J.; Sproul, W.D.; Lee, S.L.; Wang, J. Effect of Negative Substrate Bias on the Structure and Properties of Ta Coatings Deposited Using Modulated Pulse Power Magnetron Sputtering. IEEE Trans. Plasma Sci. 2010, 38, 3071–3078. [Google Scholar] [CrossRef]
- Liebig, B.; Braithwaite, N.S.J.; Kelly, P.; Chistyakov, R.; Abraham, B.; Bradley, J. Time-resolved plasma characterisation of modulated pulsed power magnetron sputtering of chromium. Surf. Coat. Technol. 2011, 205, S312–S316. [Google Scholar] [CrossRef]
- Papa, F.; Gerdes, H.; Bandorf, R.; Ehiasarian, A.; Kolev, I.; Braeuer, G.; Tietema, R.; Krug, T. Deposition rate characteristics for steady state high power impulse magnetron sputtering (HIPIMS) discharges generated with a modulated pulsed power (MPP) generator. Thin Solid Films 2011, 520, 1559–1563. [Google Scholar] [CrossRef]
- Hála, M.; Čapek, J.; Zabeida, O.; Klemberg-Sapieha, J.; Martinu, L. Pulse management in high power pulsed magnetron sputtering of niobium. Surf. Coat. Technol. 2012, 206, 4186–4193. [Google Scholar] [CrossRef]
- Hála, M.; Capek, J.; Zabeida, O.; Klemberg-Sapieha, J.E.; Martinu, L. Hysteresis-free deposition of niobium oxide films by HiPIMS using different pulse management strategies. J. Phys. D Appl. Phys. 2012, 45, 055204. [Google Scholar] [CrossRef]
- Zheng, B.C.; Wu, Z.L.; Wu, B.; Li, Y.G.; Lei, M.K. A global plasma model for reactive deposition of compound films by modulated pulsed power magnetron sputtering discharges. J. Appl. Phys. 2017, 121, 171901. [Google Scholar] [CrossRef]
- Helmersson, U.; Lattemann, M.; Bohlmark, J.; Ehiasarian, A.P.; Gudmundsson, J.T. Ionized physical vapor deposition (IPVD): A review of technology and applications. Thin Solid Films 2006, 513, 1–24. [Google Scholar] [CrossRef]
- Sarakinos, K.; Alami, J.; Konstantinidis, S. High power pulsed magnetron sputtering: A review on scientific and engineering state of the art. Surf. Coat. Technol. 2010, 204, 1661–1684. [Google Scholar] [CrossRef]
- Britun, N.; Minea, T.; Konstantinidis, S.; Snyders, R. Plasma diagnostics for understanding the plasma–surface interaction in HiPIMS discharges: A review. J. Phys. D Appl. Phys. 2014, 47, 224001. [Google Scholar] [CrossRef]
- Anders, A. Tutorial: Reactive high-power impulse magnetron sputtering (R-HiPIMS). J. Appl. Phys. 2017, 121, 171101. [Google Scholar] [CrossRef]
- Hopwood, J.A. Thin Films Vol. 27: Ionized Physical Vapor Deposition; Hopwood, J.A., Ed.; Academic Press: San Diego, CA, USA, 2000; pp. 181–207. [Google Scholar]
- Lin, J.; Wang, B.; Sproul, W.D.; Ou, Y.; Dahan, I. Anatase and rutile TiO2 films deposited by arc-free deep oscillation magnetron sputtering. J. Phys. D Appl. Phys. 2013, 46, 84008. [Google Scholar] [CrossRef]
- Lin, J.; Sproul, W.D.; Wei, R.; Chistyakov, R. Diamond like carbon films deposited by HiPIMS using oscillatory voltage pulses. Surf. Coat. Technol. 2014, 258, 1212–1222. [Google Scholar] [CrossRef]
- Ferreira, F.; Serra, R.; Oliveira, J.; Cavaleiro, A. Effect of peak target power on the properties of Cr thin films sputtered by HiPIMS in deep oscillation magnetron sputtering (DOMS) mode. Surf. Coat. Technol. 2014, 258, 249–256. [Google Scholar] [CrossRef]
- Lin, J.; Sproul, W.D. Structure and properties of Cr2O3 coatings deposited using DCMS, PDCMS, and DOMS. Surf. Coat. Technol. 2015, 276, 70–76. [Google Scholar] [CrossRef]
- Ou, Y.; Lin, J.; Tong, S.; Che, H.; Sproul, W.D.; Lei, M. Wear and corrosion resistance of CrN/TiN superlattice coatings deposited by a combined deep oscillation magnetron sputtering and pulsed dc magnetron sputtering. Appl. Surf. Sci. 2015, 351, 332–343. [Google Scholar] [CrossRef]
- Ferreira, F.; Oliveira, J.; Cavaleiro, A. CrN thin films deposited by HiPIMS in DOMS mode. Surf. Coat. Technol. 2016, 291, 365–375. [Google Scholar] [CrossRef]
- Oliveira, J.; Fernandes, F.; Serra, R.; Cavaleiro, A. On the role of the energetic species in TiN thin film growth by reactive deep oscillation magnetron sputtering in Ar/N2. Thin Solid Films 2018, 645, 253–264. [Google Scholar] [CrossRef]
- Ferreira, F.; Aijaz, A.; Kubart, T.; Cavaleiro, A.; Oliveira, J. Hard and dense diamond like carbon coatings deposited by deep oscillations magnetron sputtering. Surf. Coat. Technol. 2018, 336, 92–98. [Google Scholar] [CrossRef]
- Oliveira, J.C.; Ferreira, F.; Anders, A.; Cavaleiro, A. Reduced atomic shadowing in HiPIMS: Role of the thermalized metal ions. Appl. Surf. Sci. 2018, 433, 934–944. [Google Scholar] [CrossRef]
- Antonin, O.; Tiron, V.; Costin, C.; Popa, G.; Minea, T.M. On the HiPIMS benefits of multi-pulse operating mode. J. Phys. D Appl. Phys. 2015, 48, 015202. [Google Scholar] [CrossRef]
- Fekete, M.; Hnilica, J.; Vitelaru, C.; Minea, T.; Vašina, P. Ti atom and Ti ion number density evolution in standard and multi-pulse HiPIMS. J. Phys. D Appl. Phys. 2017, 50, 365202. [Google Scholar] [CrossRef]
- Tiron, V.; Velicu, I.-L.; Dobromir, M.; Demeter, A.; Samoila, F.; Ursu, C.; Sirghi, L. Reactive multi-pulse HiPIMS deposition of oxygen-deficient TiOx thin films. Thin Solid Films 2016, 603, 255–261. [Google Scholar] [CrossRef]
- Tiron, V.; Velicu, I.-L.; Mihǎilǎ, I.; Popa, G. Deposition rate enhancement in HiPIMS through the control of magnetic field and pulse configuration. Surf. Coat. Technol. 2018, 337, 484–491. [Google Scholar] [CrossRef]
- Tiron, V.; Ursu, E.-L.; Cristea, D.; Munteanu, D.; Bulai, G.; Ceban, A.; Velicu, I.-L. Overcoming the insulating materials limitation in HiPIMS: Ion-assisted deposition of DLC coatings using bipolar HiPIMS. Appl. Surf. Sci. 2019, 494, 871–879. [Google Scholar] [CrossRef]
- Hnilica, J.; Klein, P.; Vašina, P.; Snyders, R.; Britun, N. Revisiting particle dynamics in HiPIMS discharges. I. General effects. J. Appl. Phys. 2020, 128, 043303. [Google Scholar] [CrossRef]
- Hnilica, J.; Klein, P.; Vašina, P.; Snyders, R.; Britun, N. Revisiting particle dynamics in HiPIMS discharges. II. Plasma pulse effects. J. Appl. Phys. 2020, 128, 043304. [Google Scholar] [CrossRef]
- Sanekata, M.; Nishida, H.; Nakagomi, Y.; Hirai, Y.; Nishimiya, N.; Tona, M.; Hirata, N.; Yamamoto, H.; Tsukamoto, K.; Ohshimo, K.; et al. to be submitted to Plasma.
- Musil, J.; Leština, J.; Vlček, J.; Tölg, T. Pulsed dc magnetron discharge for high-rate sputtering of thin films. J. Vac. Sci. Technol. A 2001, 19, 420–424. [Google Scholar] [CrossRef]
- Gudmundsson, J.; Alami, J.; Helmersson, U. Spatial and temporal behavior of the plasma parameters in a pulsed magnetron discharge. Surf. Coat. Technol. 2002, 161, 249–256. [Google Scholar] [CrossRef]
- Von Engel, A. Ionized Gases; American Vacuum Society Classics; American Institute of Physics: New York, NY, USA, 1994; pp. 204–212. [Google Scholar]
- Kuffel, E.; Zaengl, W.; Kuffel, J. High Voltage Engineering Fundamentals; Elsevier BV: Amsterdam, The Netherlands, 2000; pp. 383–391. [Google Scholar]
- Raizer, Y.P. Gas Discharge Physics; Allen, J.E., Ed.; Springer: New York, NY, USA, 1991; pp. 52–56, 128–137. [Google Scholar]
- Yushkov, G.Y.; Anders, A. Origin of the Delayed Current Onset in High-Power Impulse Magnetron Sputtering. IEEE Trans. Plasma Sci. 2010, 38, 3028–3034. [Google Scholar] [CrossRef]
- Nakano, T.; Murata, C.; Baba, S. Effect of the target bias voltage during off-pulse period on the impulse magnetron sputtering. Vacuum 2010, 84, 1368–1371. [Google Scholar] [CrossRef]
- Zuo, X.; Chen, R.; Ke, P.; Wang, A. Gas Breakdown and Discharge Formation in High-Power Impulse Magnetron Sputtering. IEEE Trans. Plasma Sci. 2019, 47, 1215–1222. [Google Scholar] [CrossRef]
- Han, M.; Luo, Y.; Li, H.; Li, L.; Xu, Y.; Luo, S.; Zhang, P.; Xu, H.; Xu, C. Auxiliary capacitor to enhance oscillation in circuit and reduce current onset delay in HiPIMS discharge: Theory, experiment and simulation. Surf. Coat. Technol. 2021, 405, 126518. [Google Scholar] [CrossRef]
- Vašina, P.; Meško, M.; Imbert, J.C.; Ganciu, M.; Boisse-Laporte, C.; De Poucques, L.; Touzeau, M.; Pagnon, D.; Bretagne, J. Experimental study of a pre-ionized high power pulsed magnetron discharge. Plasma Sour. Sci. Technol. 2007, 16, 501–510. [Google Scholar] [CrossRef]
- Mozgrin, D.V.; Fetisov, I.K.; Khodachenko, G.V. High-current low-pressure quasi-stationary discharge in a magnetic field: Experimental research. Plasma Phys. Rep. 1995, 21, 422. [Google Scholar]
- Tsukamoto, K.; Tamura, T.; Matsusaki, H.; Tona, M.; Yamamoto, H.; Nakagomi, Y.; Nishida, H.; Hirai, Y.; Nishimiya, N.; Sanekata, M.; et al. Time-of-flight mass spectrometric diagnostics for ionized and neutral species in high-power pulsed magnetron sputtering of titanium. Jpn. J. Appl. Phys. 2020, 59, SHHB05. [Google Scholar] [CrossRef]
- Kudrle, V.; LeDuc, E.; Fitaire, M. Breakdown delay times and memory effects in helium at low pressure. J. Phys. D Appl. Phys. 1999, 32, 2049–2055. [Google Scholar] [CrossRef]
- Phelps, A.V.; Petrović, Z.L. Cold-cathode discharges and breakdown in argon: Surface and gas phase production of secondary electrons. Plasma Sour. Sci. Technol. 1999, 8, R21–R44. [Google Scholar] [CrossRef]
- Walker, C.G.H.; El-Gomati, M.M.; Assa’d, A.M.D.; Assa’d, A.M.D. The secondary electron emission yield for 24 solid elements excited by primary electrons in the range 250-5000 ev: A theory/experiment comparison. Scanning 1999, 32, 2049–2055. [Google Scholar] [CrossRef] [PubMed]
- Schade, R. Über die Aufbauzeit einer Glimmentladung. Z. Phys. 1937, 104, 487–510. [Google Scholar] [CrossRef]
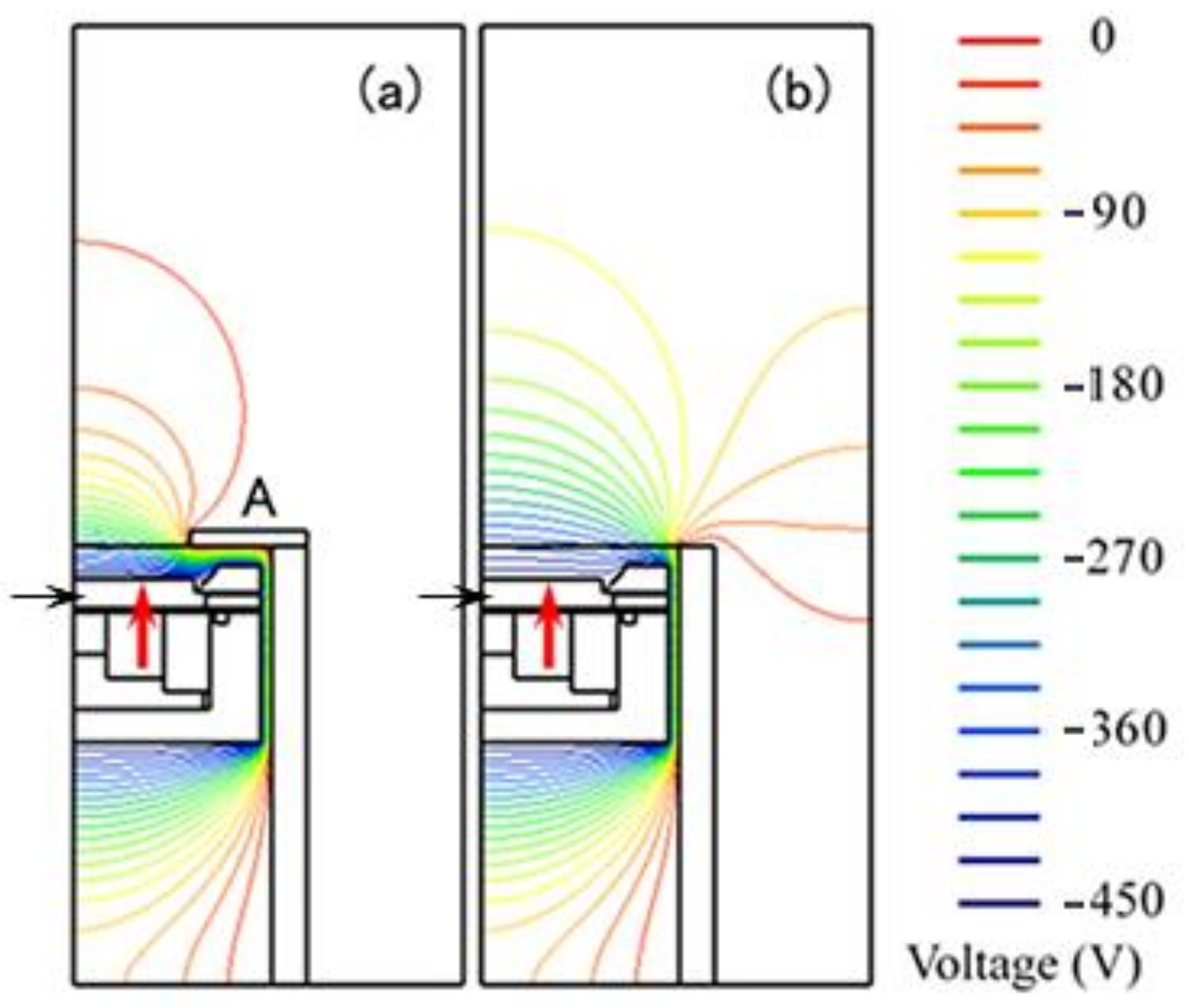
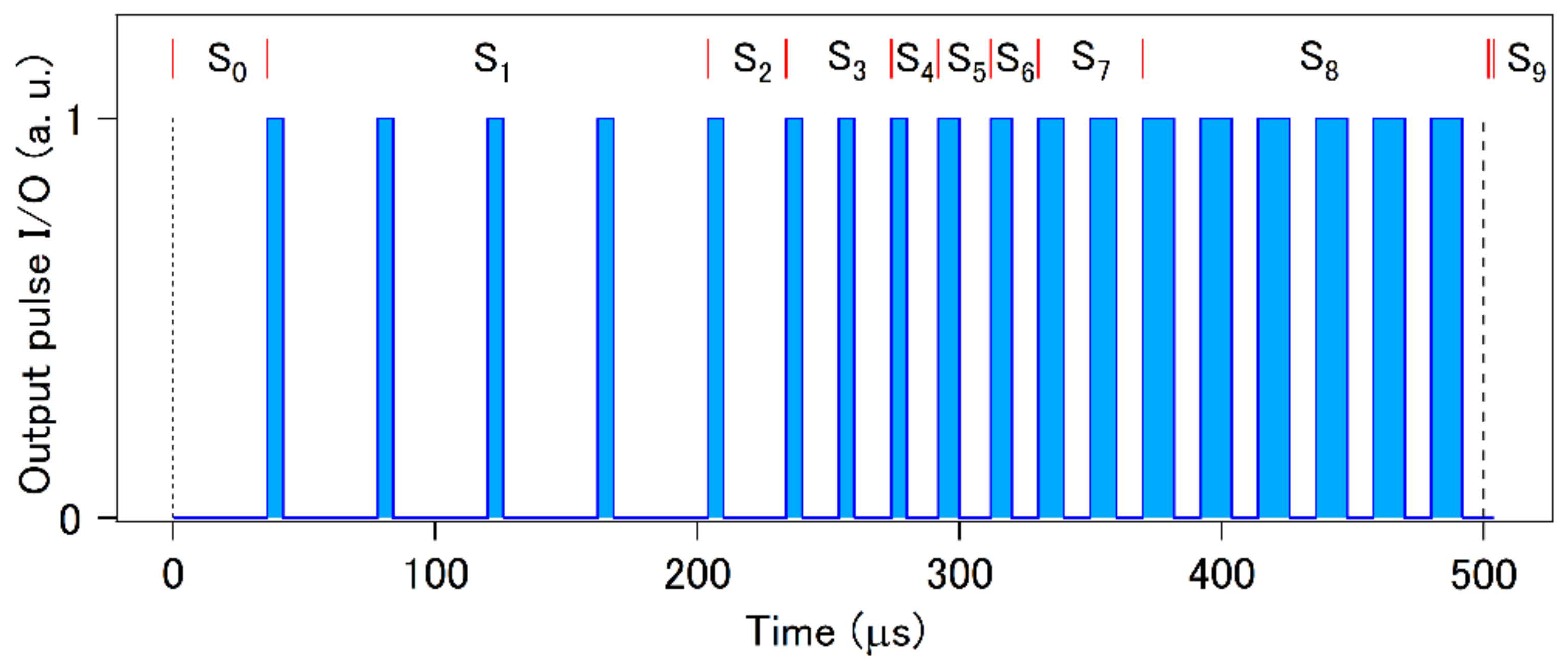
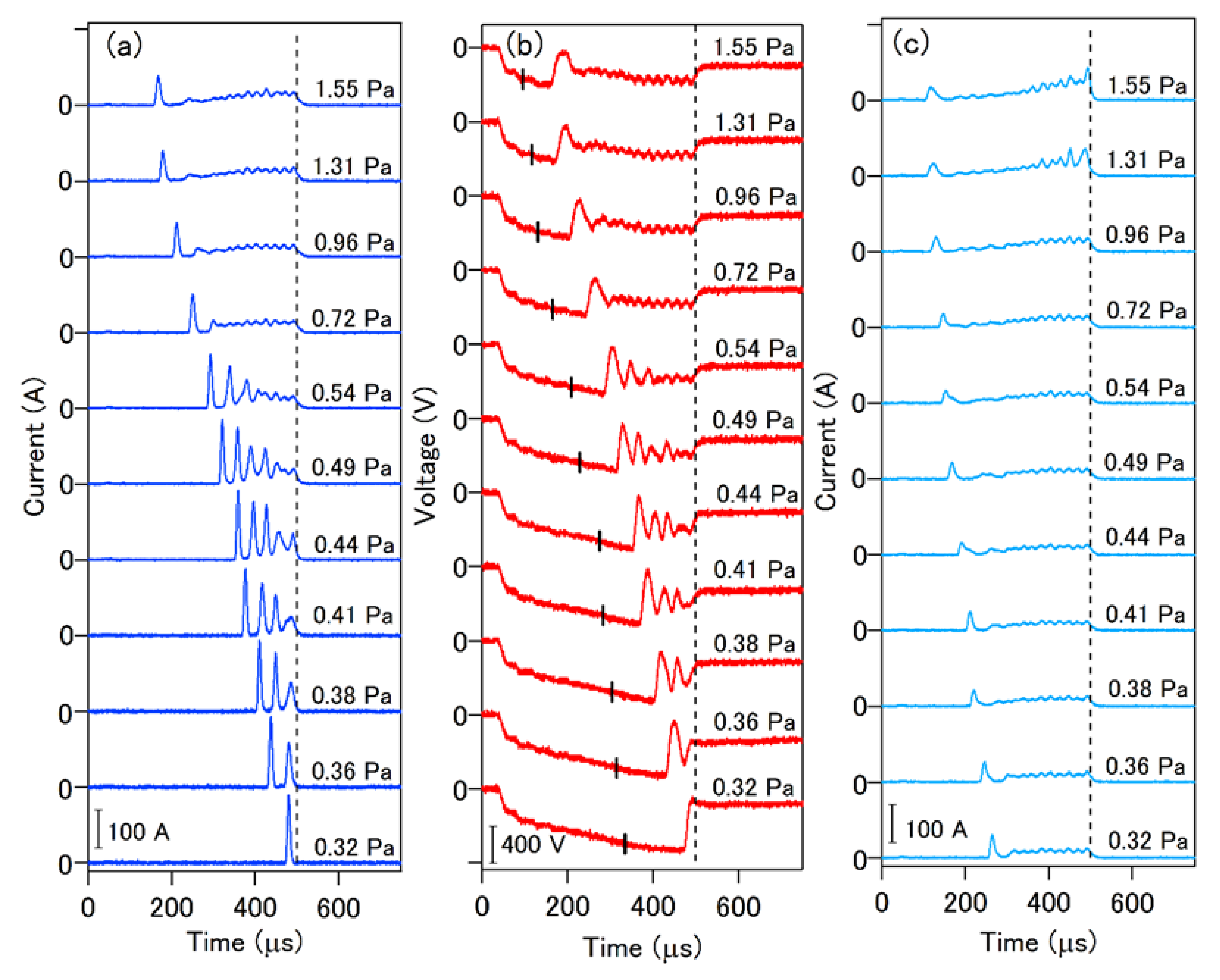
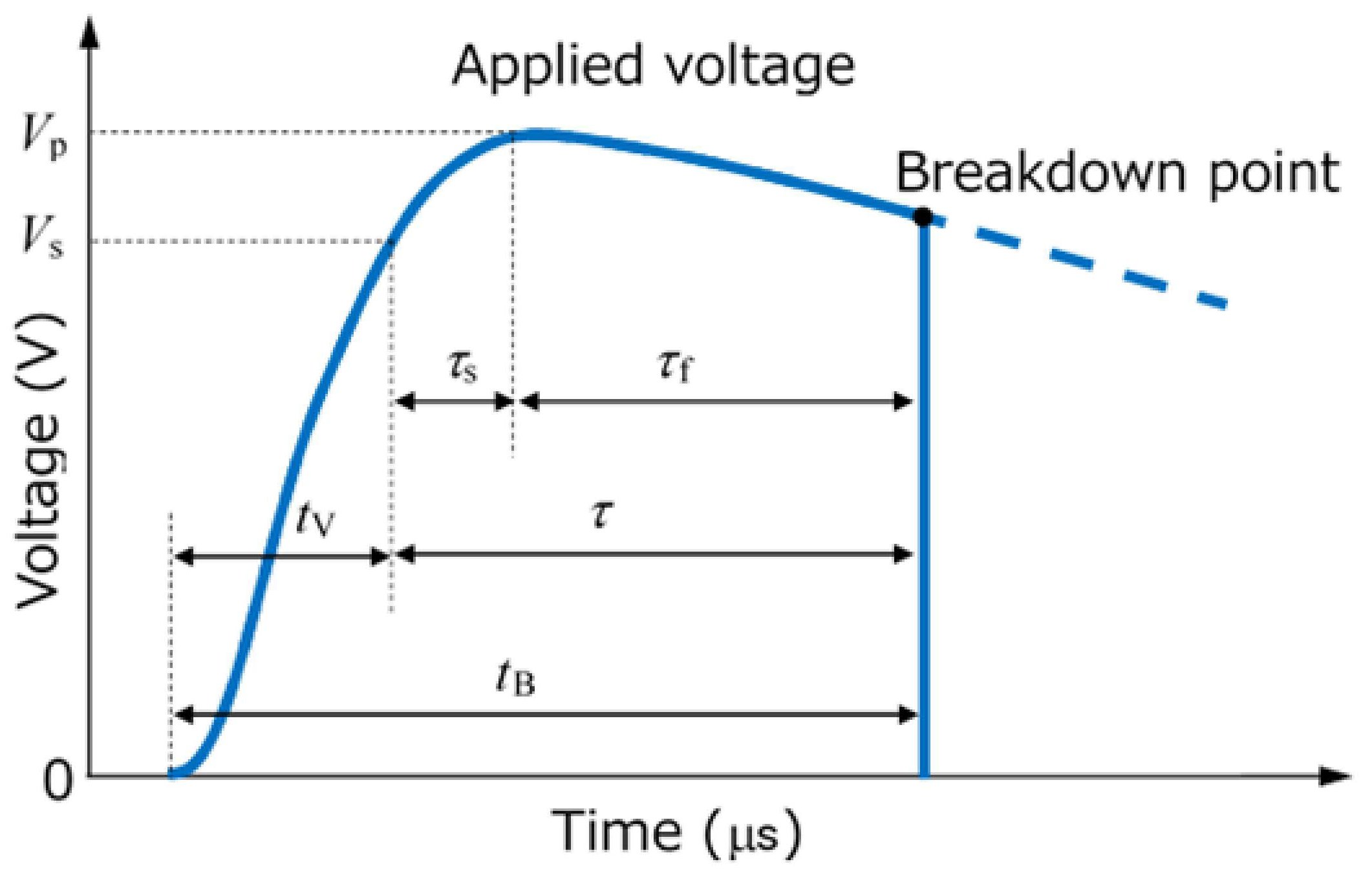
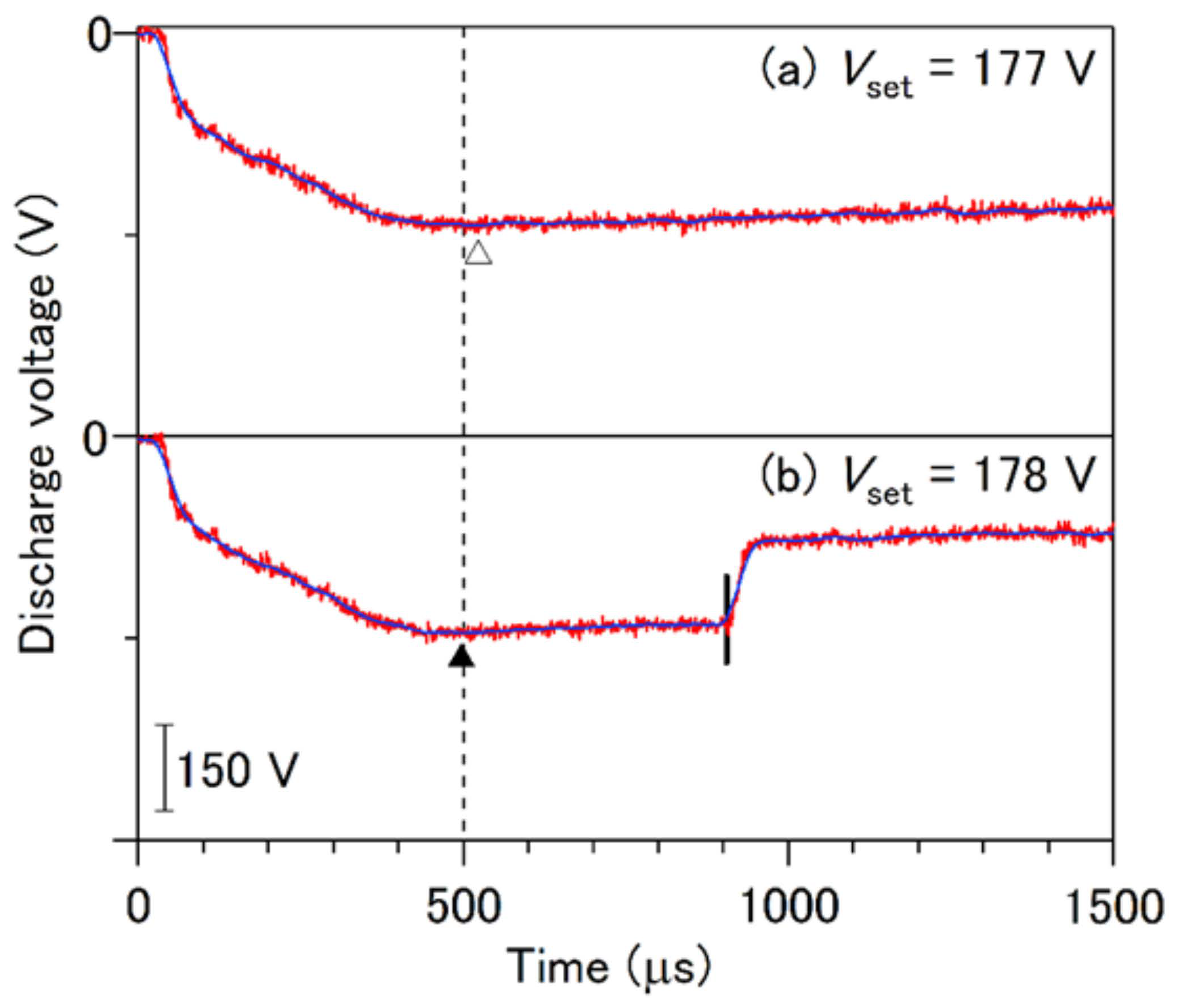
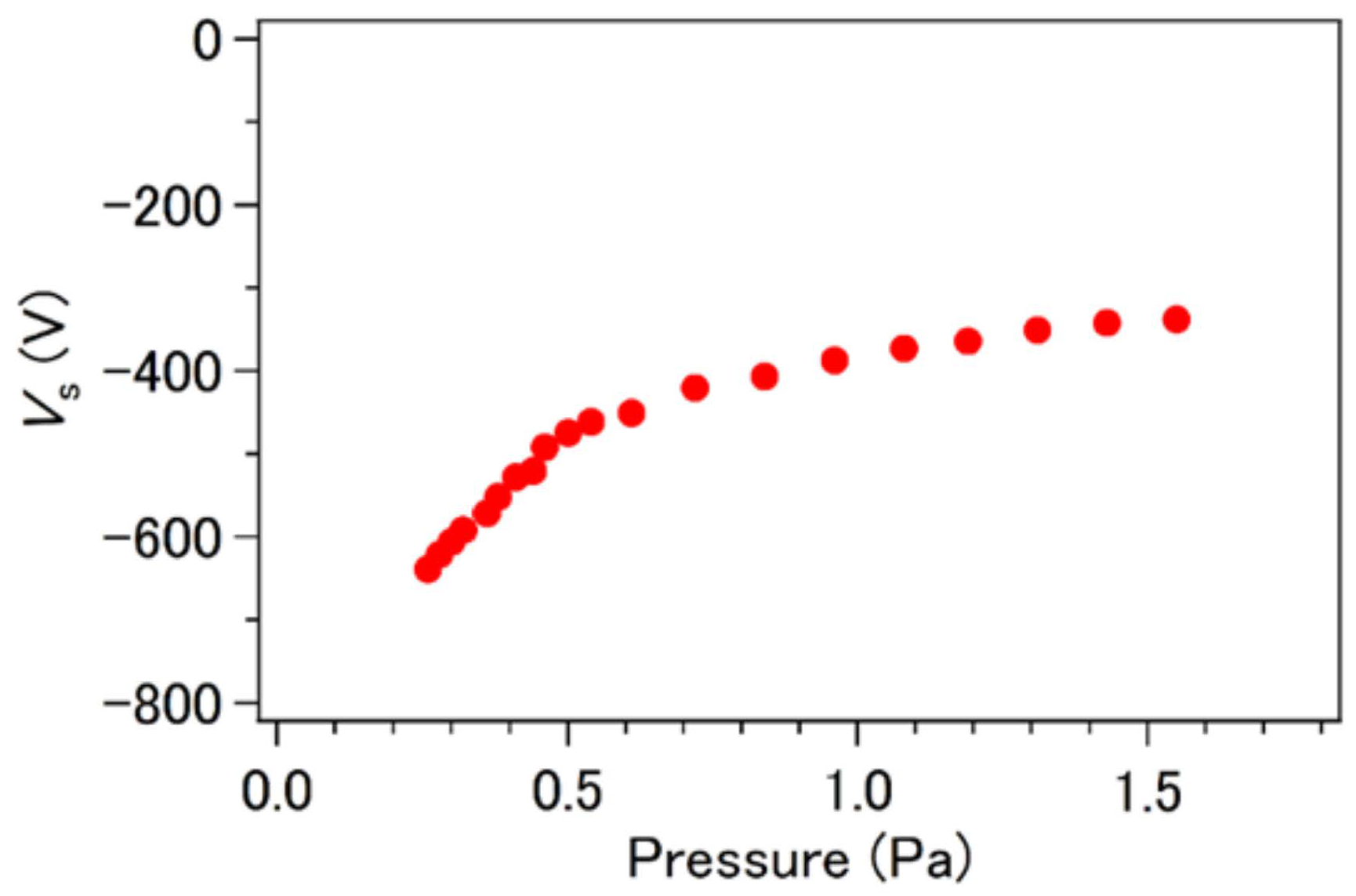
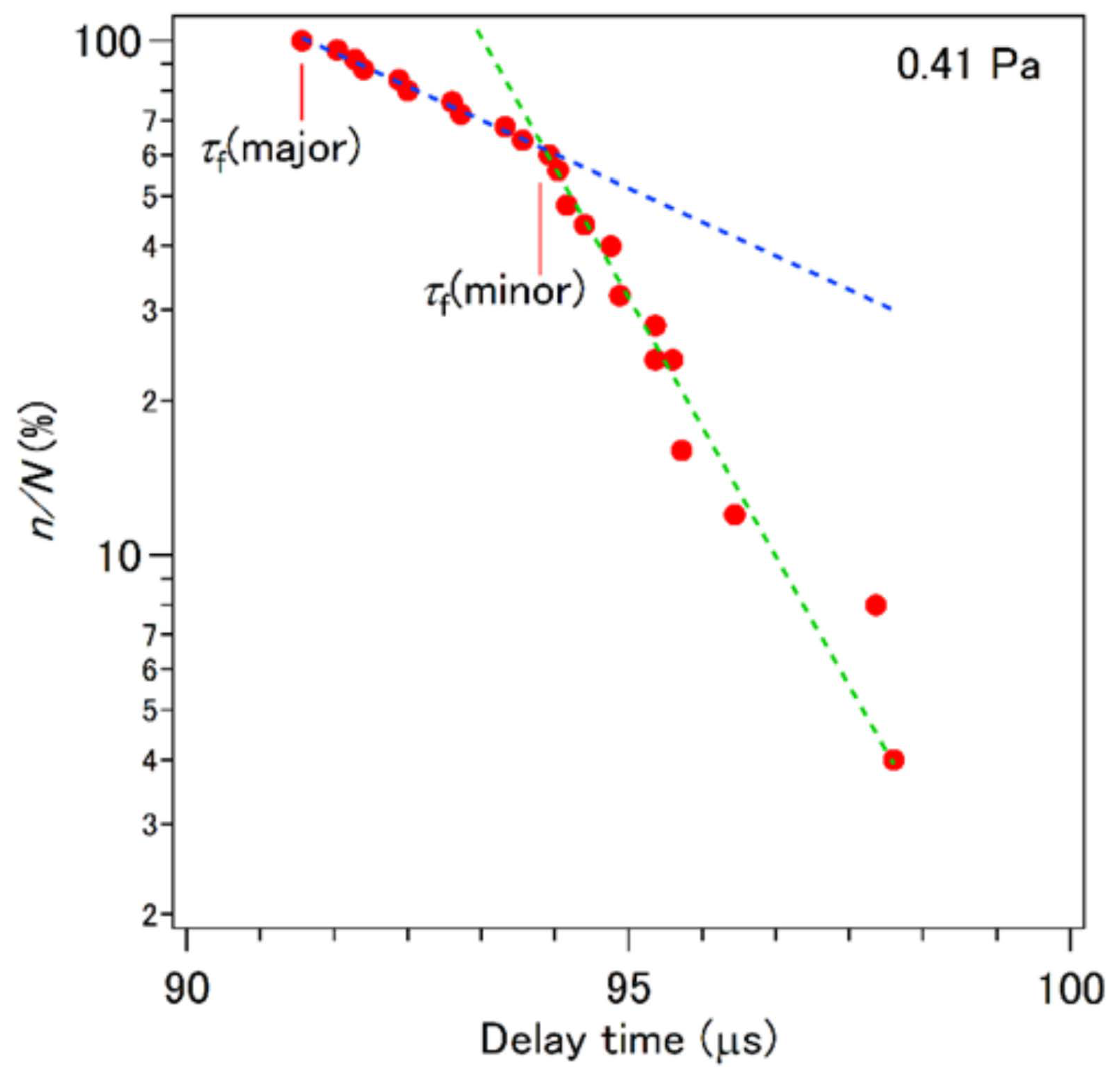
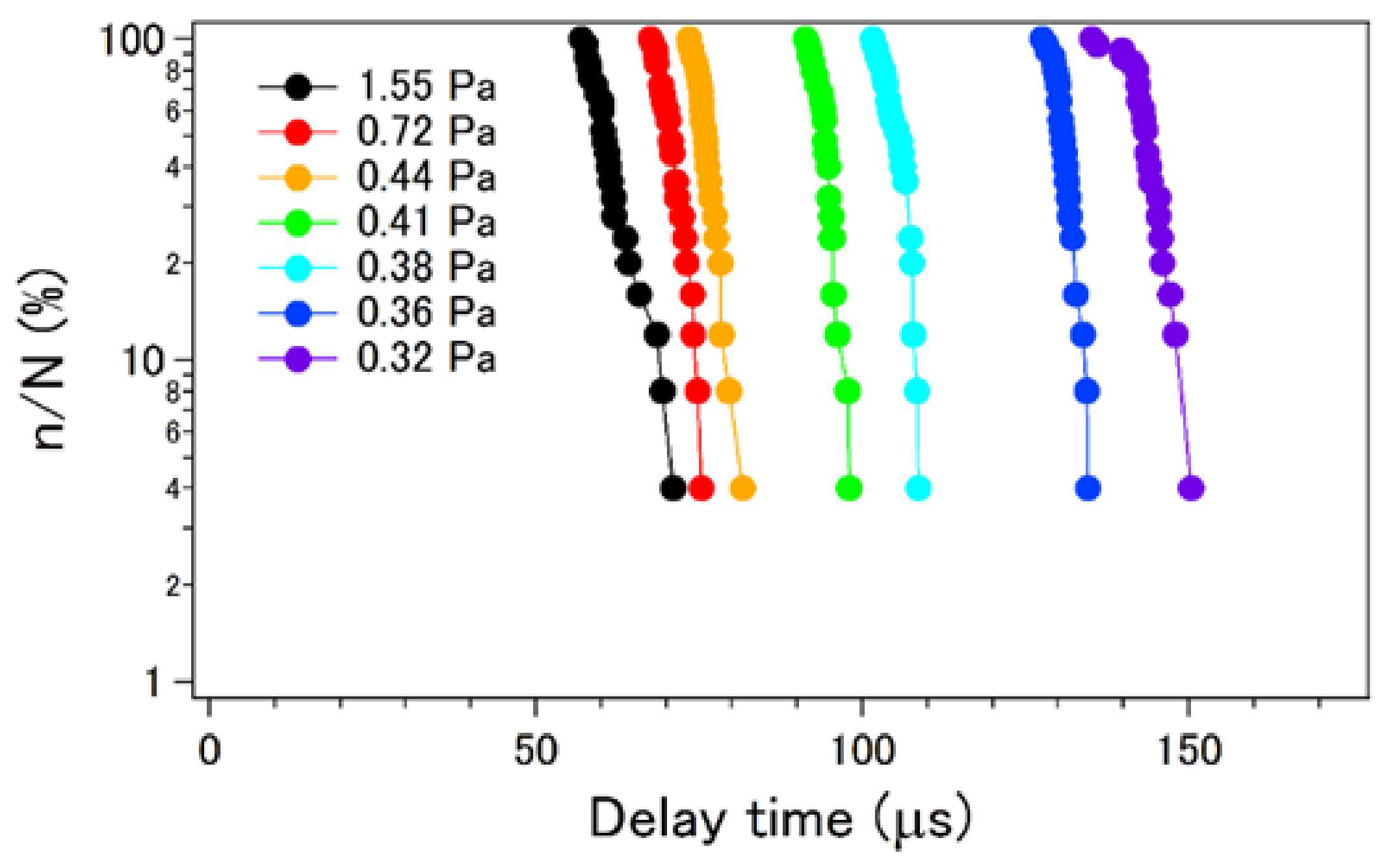

| Segment | On Time (μs) | Off Time (μs) | Number of Micro-Pulses |
|---|---|---|---|
| S0 | 0 | 36 | 1 |
| S1 | 6 | 36 | 4 |
| S2 | 6 | 24 | 1 |
| S3 | 6 | 14 | 2 |
| S4 | 6 | 12 | 1 |
| S5 | 8 | 12 | 1 |
| S6 | 8 | 10 | 1 |
| S7 | 10 | 10 | 2 |
| S8 | 12 | 10 | 6 |
| S9 | 0 | 2 | 1 |
| p (Pa) | τf (μs) | τs (μs) | ||
|---|---|---|---|---|
| Major | Minor | Major | Minor | |
| 0.32 | 135 | 142 | 36.4 | 3.21 |
| 0.36 | 128 | 130 | 8.07 | 1.98 |
| 0.38 | 102 | 107 | 5.10 | 0.743 |
| 0.41 | 91.4 | 94.0 | 5.51 | 1.44 |
| 0.44 | 73.4 | 74.9 | 5.31 | 2.29 |
| 0.72 | 67.8 | 73.6 | 3.72 | 1.12 |
| 1.55 | 57.3 | 69.9 | 4.63 | 2.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanekata, M.; Nishida, H.; Watabe, T.; Nakagomi, Y.; Hirai, Y.; Nishimiya, N.; Tona, M.; Yamamoto, H.; Hirata, N.; Tsukamoto, K.; et al. Delayed Discharge Bridging Two Sputtering Modes from Modulated Pulsed Power Magnetron Sputtering (MPPMS) to Deep Oscillation Magnetron Sputtering (DOMS). Plasma 2021, 4, 239-251. https://doi.org/10.3390/plasma4020016
Sanekata M, Nishida H, Watabe T, Nakagomi Y, Hirai Y, Nishimiya N, Tona M, Yamamoto H, Hirata N, Tsukamoto K, et al. Delayed Discharge Bridging Two Sputtering Modes from Modulated Pulsed Power Magnetron Sputtering (MPPMS) to Deep Oscillation Magnetron Sputtering (DOMS). Plasma. 2021; 4(2):239-251. https://doi.org/10.3390/plasma4020016
Chicago/Turabian StyleSanekata, Masaomi, Hiroshi Nishida, Tatsuya Watabe, Yuki Nakagomi, Yoshihiro Hirai, Nobuo Nishimiya, Masahide Tona, Hiroaki Yamamoto, Naoyuki Hirata, Keizo Tsukamoto, and et al. 2021. "Delayed Discharge Bridging Two Sputtering Modes from Modulated Pulsed Power Magnetron Sputtering (MPPMS) to Deep Oscillation Magnetron Sputtering (DOMS)" Plasma 4, no. 2: 239-251. https://doi.org/10.3390/plasma4020016
APA StyleSanekata, M., Nishida, H., Watabe, T., Nakagomi, Y., Hirai, Y., Nishimiya, N., Tona, M., Yamamoto, H., Hirata, N., Tsukamoto, K., Ohshimo, K., Misaizu, F., & Fuke, K. (2021). Delayed Discharge Bridging Two Sputtering Modes from Modulated Pulsed Power Magnetron Sputtering (MPPMS) to Deep Oscillation Magnetron Sputtering (DOMS). Plasma, 4(2), 239-251. https://doi.org/10.3390/plasma4020016






