A Computationally Assisted Ar I Emission Line Ratio Technique to Infer Electron Energy Distribution and Determine Other Plasma Parameters in Pulsed Low-Temperature Plasma
Abstract
1. Introduction
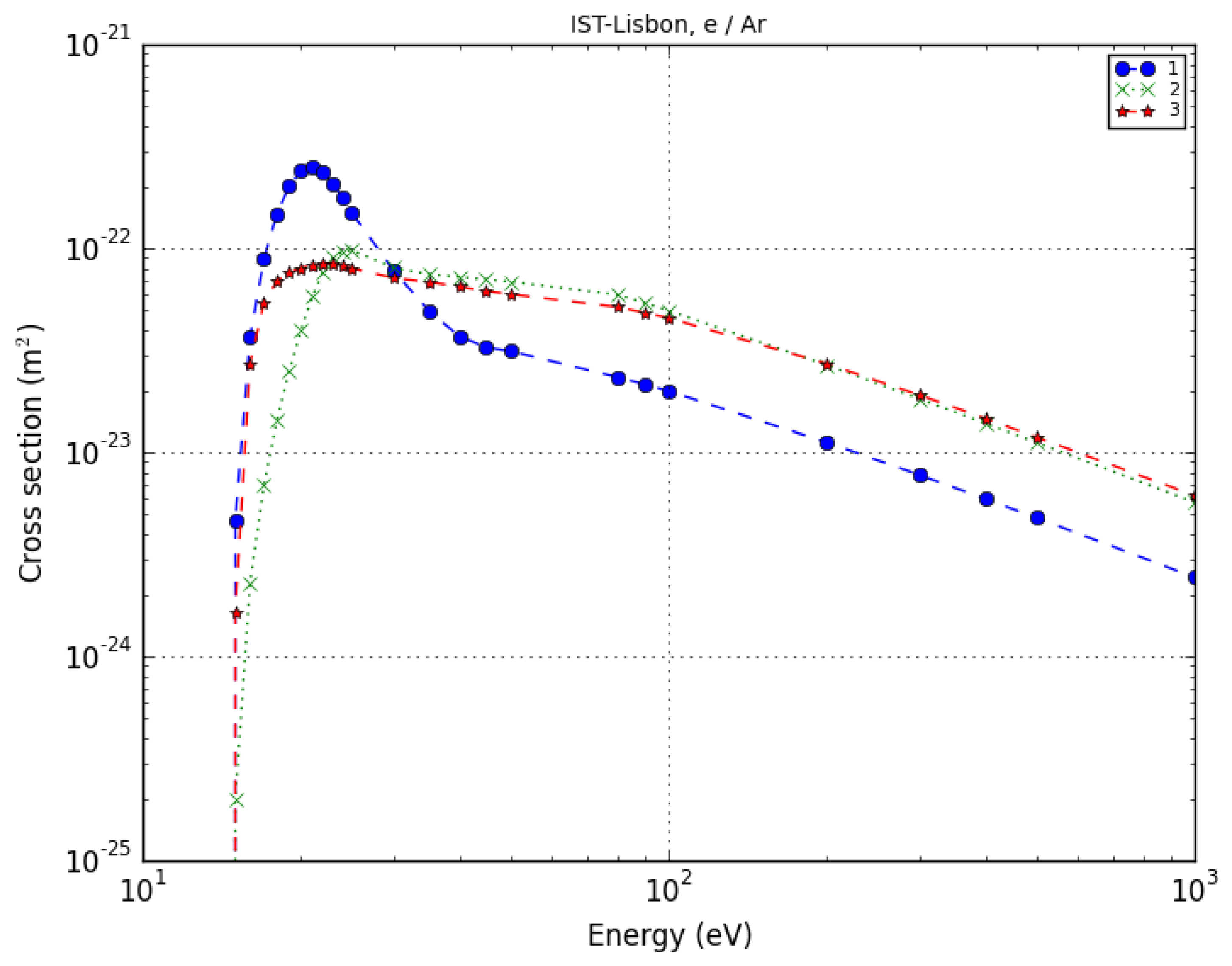
2. Excitation of 3p States
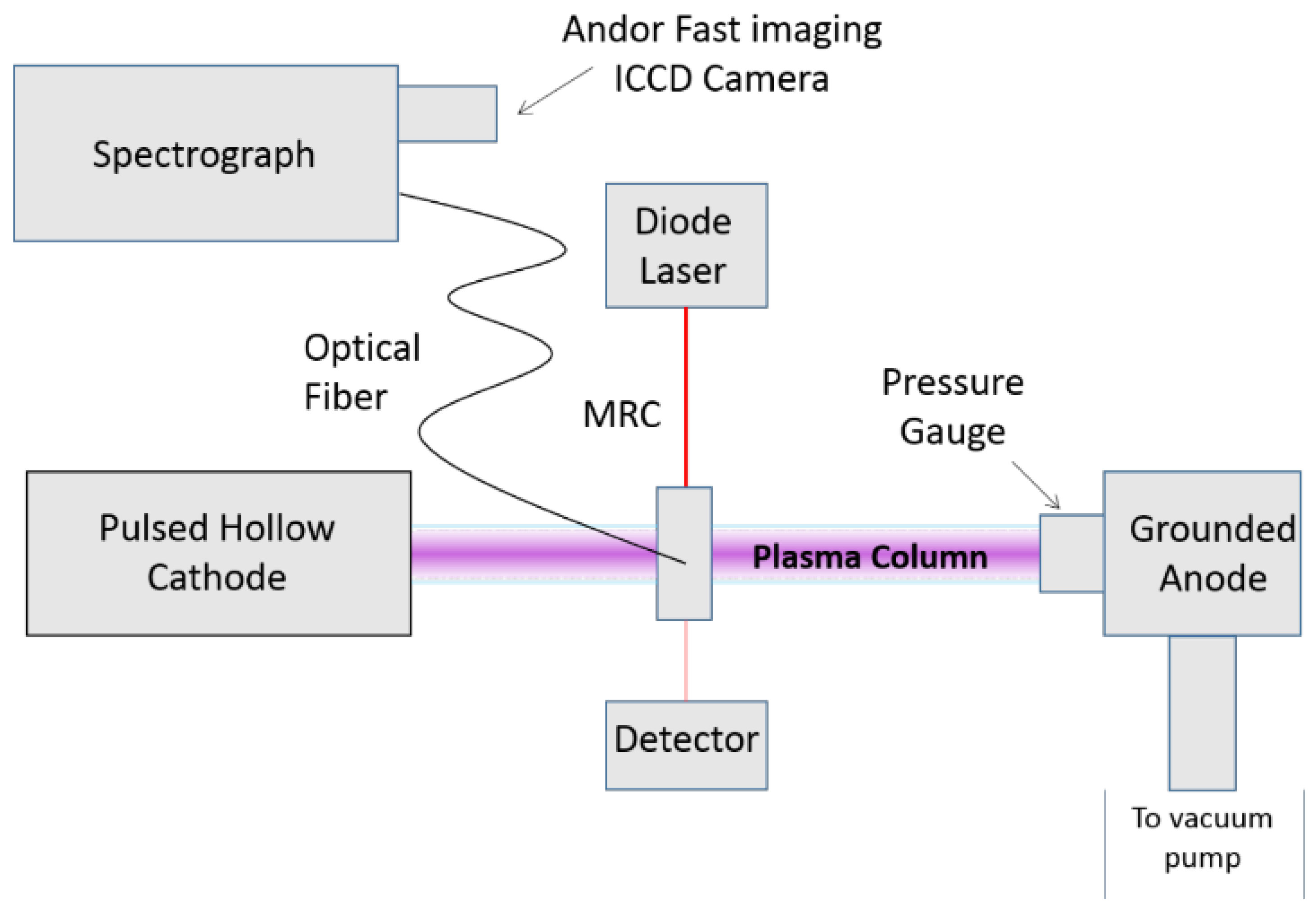
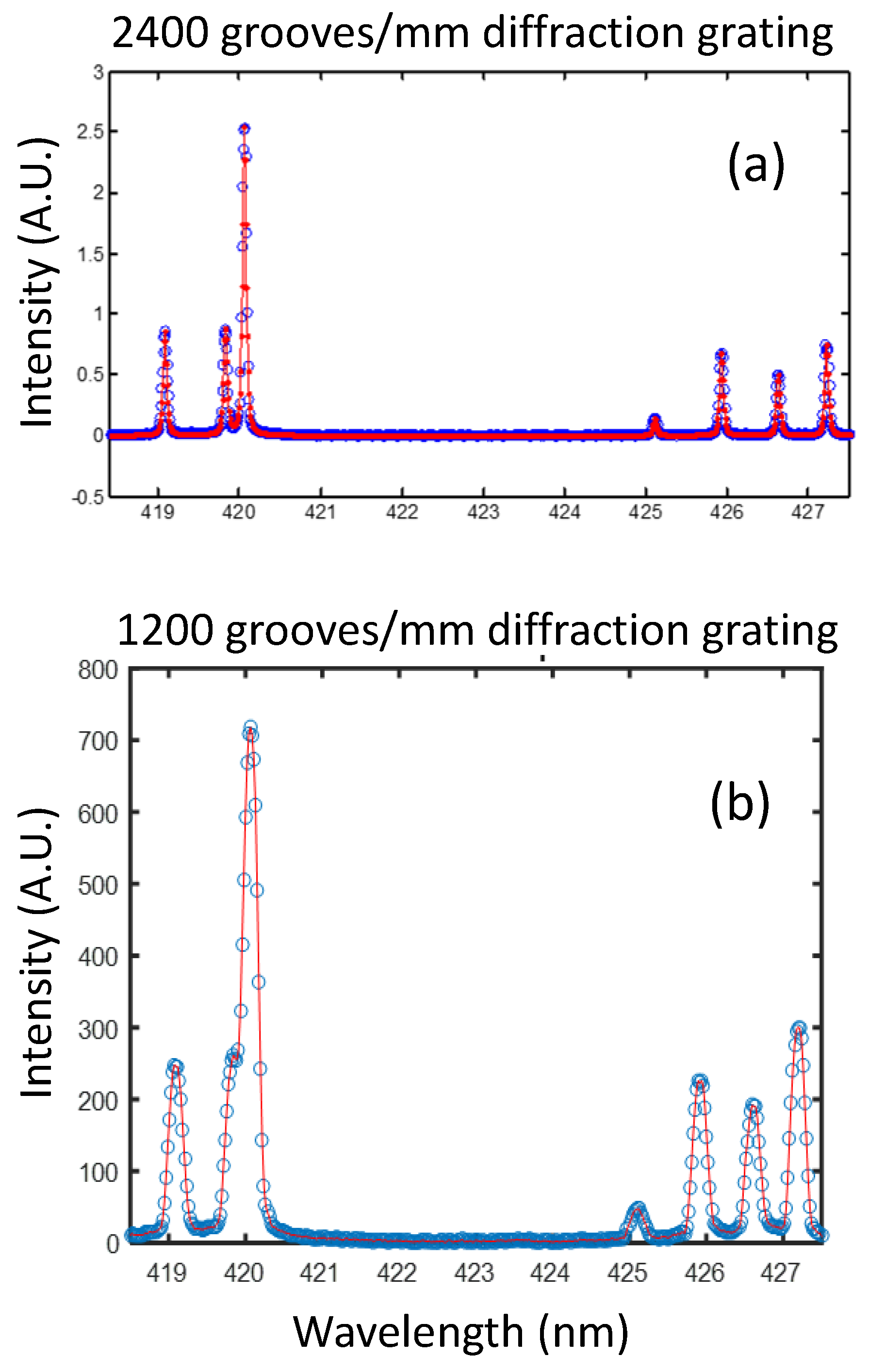
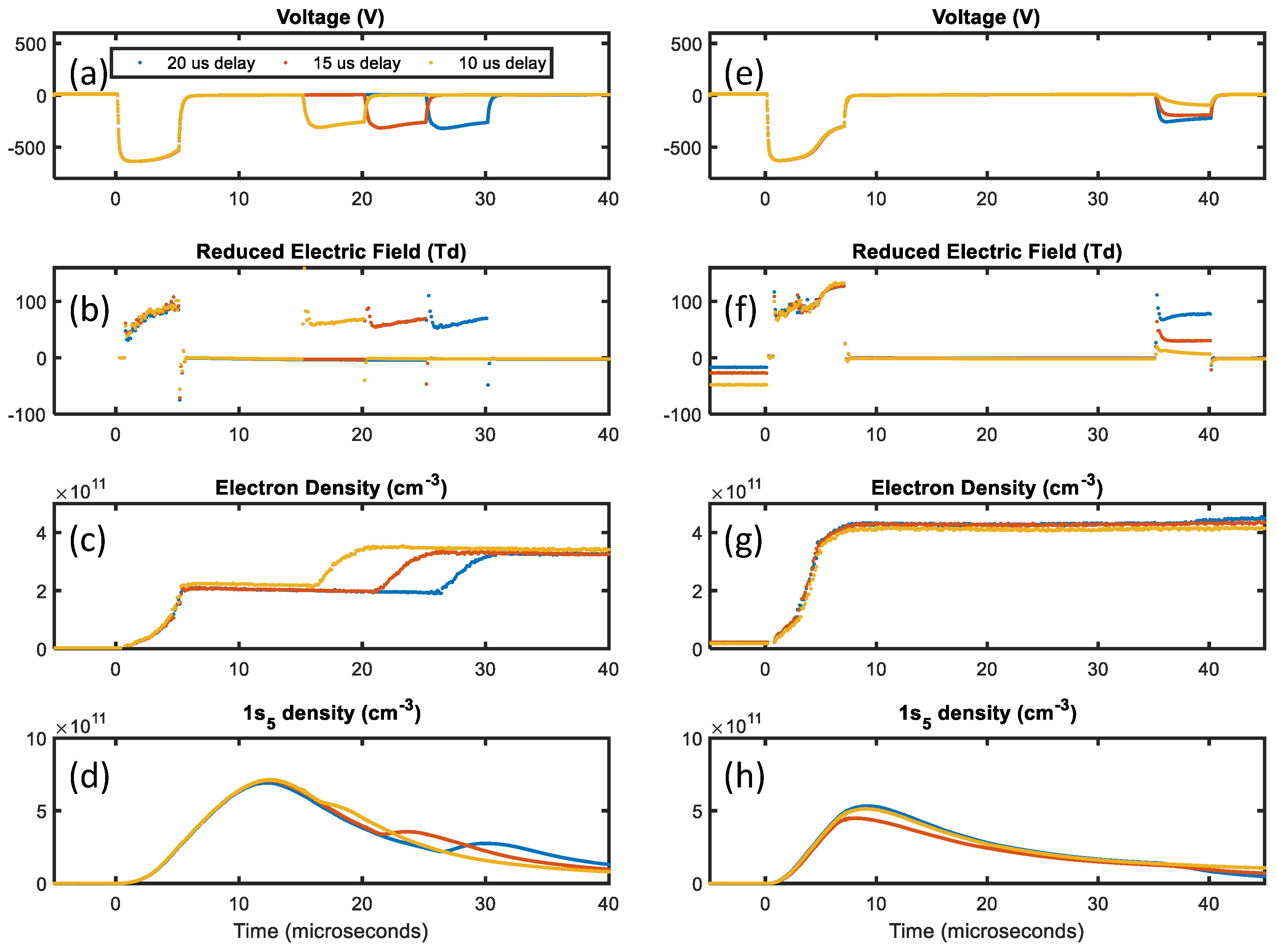
3. Experiment
Microwave Resonant Cavity
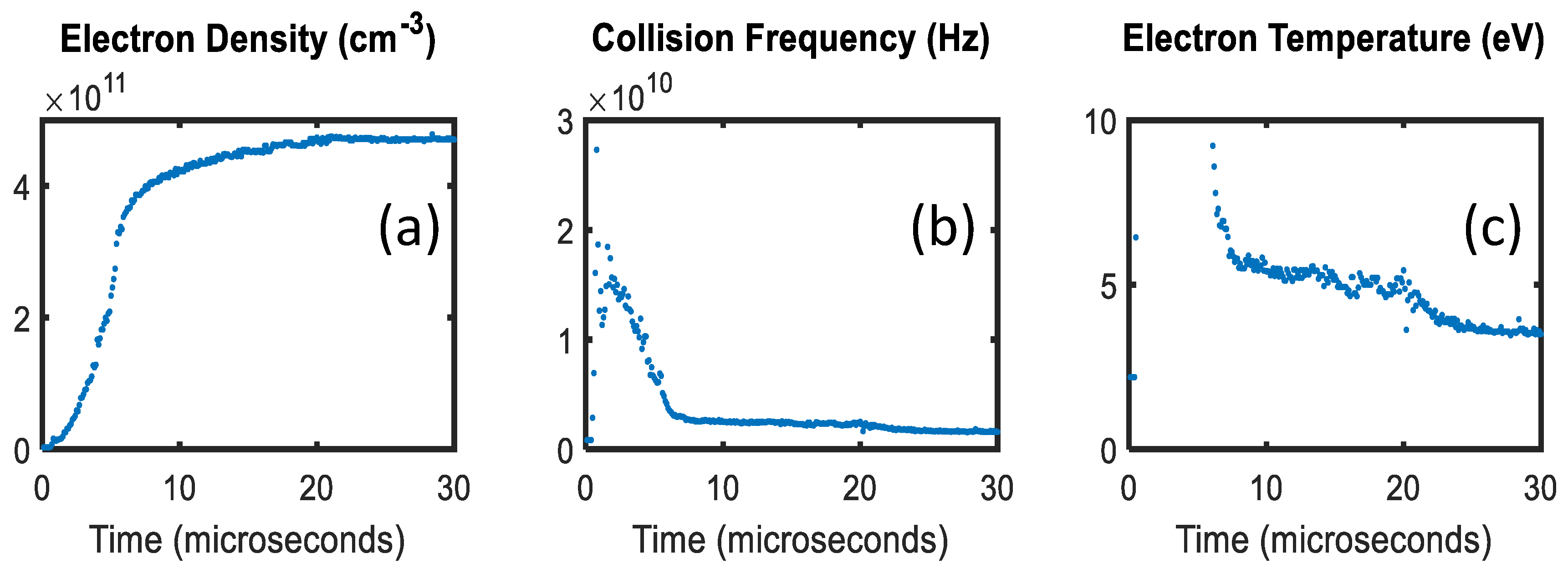
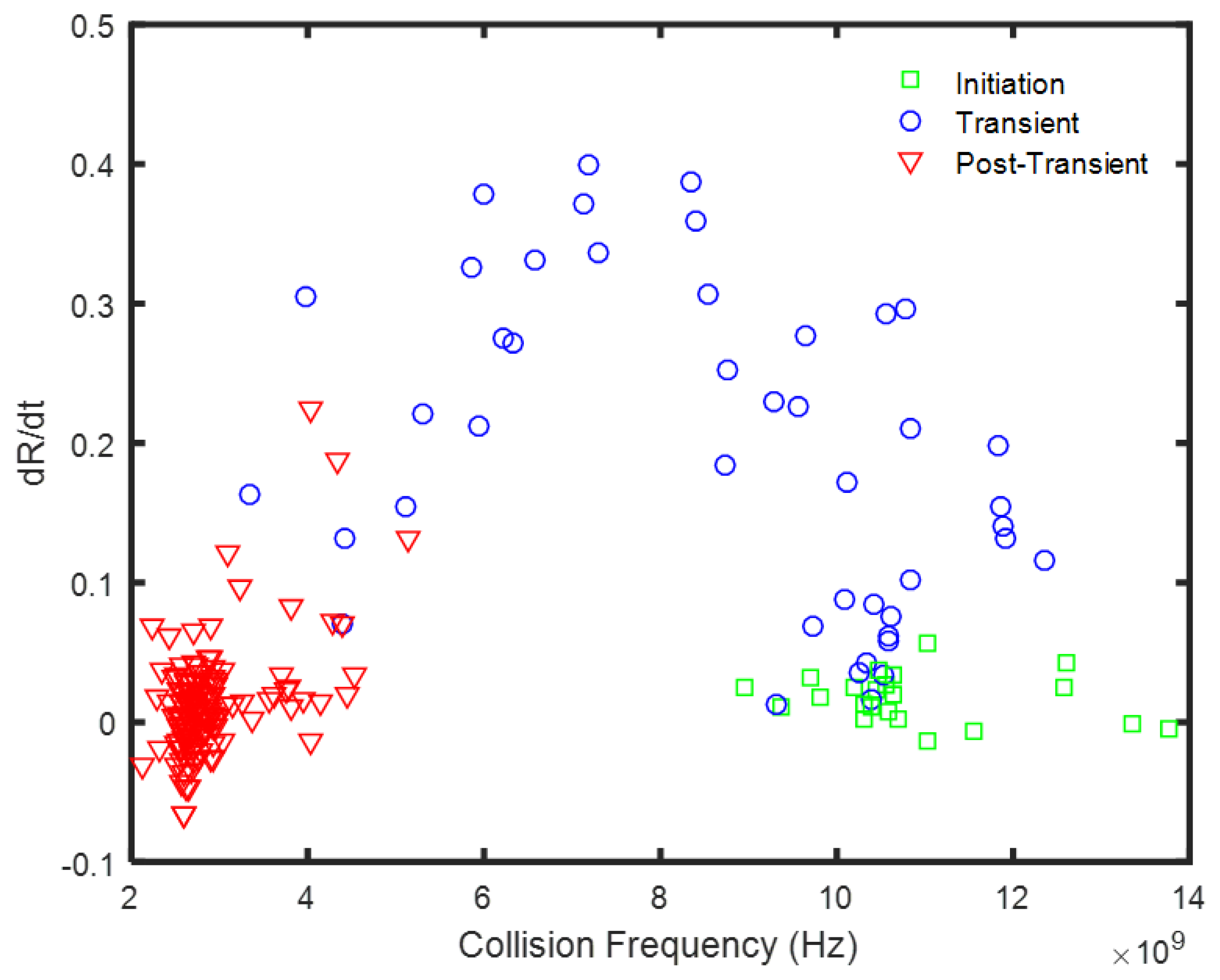
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Koepke, M.E.; Marchand, R. A modelling challenge facility for advancing model and simulation through design of experiments methodology. 2019. in preparation. [Google Scholar]
- Franek, J.B.; Nogami, S.H.; Demidov, V.I.; Koepke, M.E.; Barnat, E.V. Correlating metastable-atom density, reduced electric field, and electron energy distribution in the post-transient stage of a 1-Torr argon discharge. Plasma Sources Sci. Technol. 2015, 24, 034009. [Google Scholar] [CrossRef]
- Adams, S.F.; Bogdanov, E.A.; Demidov, V.I.; Koepke, M.E.; Kudryavtsev, A.A. Metastable atom and electron density diagnostic in the initial stage of a pulsed discharge in Ar and other rare gases by emission spectroscopy. Phys. Plasmas 2012, 19, 023510. [Google Scholar] [CrossRef]
- Boffard, J.B.; Jung, R.O.; Lin, C.C.; Aneskavich, L.E.; Wendt, A.E. Argon 420.1–419.8 nm emission line ratio for measuring plasma effective electron temperatures. J. Phys. D Appl. Phys. 2012, 45, 045201. [Google Scholar] [CrossRef]
- Fox-Lyon, N.; Knoll, A.J.; Franek, J.B.; Demidov, V.I.; Godyak, V.A.; Koepke, M.E.; Oehrlein, G.S. Determination of Ar metastable atom densities in Ar and Ar/H2 inductively coupled low-temperature plasmas. J. Phys. D Appl. Phys. 2013, 46, 485202. [Google Scholar] [CrossRef]
- Franek, J.B.; Nogami, S.H.; Koepke, M.E.; Demidov, V.I.; Barnat, E.V. Dynamics of atomic kinetics in pulsed positive-column discharge at 100 Pa. Plasma Phys. Control. Fusion 2016, 59, 014005. [Google Scholar] [CrossRef]
- Boffard, J.B.; Wang, S.; Lin, C.C.; Wendt, A.E. Detection of fast electrons in pulsed argon inductively-coupled plasmas using the 420.1–419.8 nm emission line pair. Plasma Sources Sci. Technol. 2015, 24, 065005. [Google Scholar] [CrossRef]
- Franek, J.B. Correlating metastable atom density, reduced electric field, and electron energy distribution in the initiation, transient, and post-transient stages of a pulsed argon discharge. In Argon Dissertation; West Virginia University: Morgantown, WV, USA, 2017; ProQuest Dissertations and Theses, Publication number: 10276362. [Google Scholar]
- DeJoseph, C.A.; Demidov, V.I.; Kudryavtsev, A.A. Modification of a nonlocal electron energy distribution in a bounded plasma. Phys. Rev. E 2005, 72, 036410. [Google Scholar] [CrossRef] [PubMed]
- Boffard, J.B.; Chiaro, B.; Weber, T.; Lin, C.C. Electron-impact excitation of argon: Optical emission cross sections in the range of 300–2500 nm. At. Data Nucl. Tables 2007, 93, 831. [Google Scholar] [CrossRef]
- Reader, J.; Corliss, C.H.; Wiese, W.L.; Martin, G.A. Wavelengths and Transition Probabilities for Atoms and Atomic Ions, Part I. Wavelengths, Part II. Transition Probabilities. In National Standard Reference Data System, NSRDS-NBS 68; U.S. Government Printing Office: Washington, DC, USA, 1980. [Google Scholar] [CrossRef]
- Jung, R.O.; Boffard, J.B.; Anderson, L.W.; Lin, C.C. Excitation into the 3p55p levels from the metastable levels of Ar. Phys. Rev. A 2007, 75, 052707. [Google Scholar] [CrossRef]
- Franek, J.B.; Nogami, S.H.; Demidov, V.I.; Koepke, M.E.; Barnat, E.V. Reply to Comment on ‘Correlating metastable-atom density, reduced electric field, and electron energy distribution in the post-transient stage of a 1 Torr argon discharge’. Plasma Sources Sci. Technol. 2016, 25, 038002. [Google Scholar] [CrossRef]
- Pack, J.L.; Phelps, A.V. Drift velocities of slow electrons in helium, neon, argon, hydrogen, and nitrogen. Phys. Rev. 1961, 121, 789. [Google Scholar]
- Barnat, E.V.; Weatherford, B.R. 2D laser-collision induced fluorescence in low-pressure argon discharges. Plasma Sources Sci. Technol. 2015, 24, 055024. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franek, J.B.; Nogami, S.H.; Koepke, M.E.; Demidov, V.I.; Barnat, E.V. A Computationally Assisted Ar I Emission Line Ratio Technique to Infer Electron Energy Distribution and Determine Other Plasma Parameters in Pulsed Low-Temperature Plasma. Plasma 2019, 2, 65-76. https://doi.org/10.3390/plasma2010007
Franek JB, Nogami SH, Koepke ME, Demidov VI, Barnat EV. A Computationally Assisted Ar I Emission Line Ratio Technique to Infer Electron Energy Distribution and Determine Other Plasma Parameters in Pulsed Low-Temperature Plasma. Plasma. 2019; 2(1):65-76. https://doi.org/10.3390/plasma2010007
Chicago/Turabian StyleFranek, James B., Samuel H. Nogami, Mark E. Koepke, Vladimir I. Demidov, and Edward V. Barnat. 2019. "A Computationally Assisted Ar I Emission Line Ratio Technique to Infer Electron Energy Distribution and Determine Other Plasma Parameters in Pulsed Low-Temperature Plasma" Plasma 2, no. 1: 65-76. https://doi.org/10.3390/plasma2010007
APA StyleFranek, J. B., Nogami, S. H., Koepke, M. E., Demidov, V. I., & Barnat, E. V. (2019). A Computationally Assisted Ar I Emission Line Ratio Technique to Infer Electron Energy Distribution and Determine Other Plasma Parameters in Pulsed Low-Temperature Plasma. Plasma, 2(1), 65-76. https://doi.org/10.3390/plasma2010007




