Abstract
Understanding the production mechanisms of ozone and other reactive species in atmospheric pressure dielectric barrier discharges (DBDs) has become increasingly important for the optimization and commercial success of these plasma devices in emerging applications, such as plasma medicine, plasma agriculture, and plasma catalysis. In many of these applications, input power modulation is exploited as a means to maintain a low gas temperature. Although the chemical pathways leading to ozone production/destruction and their strong temperature dependence are relatively well understood, the effect of the on-time duration on the performance of these modulated DBDs remains largely unexplored. In this study, we use electrical and optical diagnostics, as well as computational methods, to assess the performance of a modulated DBD device. The well-established Lissajous method for measuring the power delivered to the discharge is not suitable for modulated DBDs because the transients generated at the beginning of each pulse become increasingly important in short on-time modulated plasmas. It is shown that for the same input power and modulation duty-cycle, shorter on-time pulses result in significantly enhanced ozone production, despite their operation at slightly higher temperatures. The key underpinning mechanism that causes this counter-intuitive observation is the more efficient net generation rate of ozone during the plasma on-time due to the lower accumulation of NO2 in the discharge volume.
1. Introduction
Atmospheric pressure dielectric barrier discharges have gained renewed interest in recent years due to their use in emerging applications such as plasma medicine [1], plasma agriculture [2,3], treatment of liquids [4], plasma catalysis [5,6,7], and preparation and processing of materials [8,9,10]. Arguably, the most established use of dielectric barrier discharges is the generation of ozone [11]. Due to ozone’s high oxidation potential (2.07 V) compared to that of chlorine (1.36 V), and the possibility of generating it in-situ and on-demand, ozone is a water treatment method widespread across Europe and North America [12]. This has led to extensive research and development into efficiency improvements of ozone generators [13]. Feed gas composition, gas temperature, cooling systems, and electrode geometry, have all been investigated to maximize ozone production efficacy [14,15,16].
Ozone production efficacy also depends on the voltage waveform applied. Sinusoidal voltages are the most commonly used, and the typical operating frequency is 1–50 kHz [17]. Higher frequencies (e.g., 13.56 MHz) can generate higher density plasmas. However, due to their increased power density, these tend to operate at a higher gas temperature, which leads to poor ozone generation efficacy [18]. This can be mitigated by using helium or argon with an admixture of oxygen as feed gases [19,20]. Although noble gases offer a potential solution for low-volume large-value applications (e.g., biomedical treatments), the increase in cost associated with the use of noble gases means large-scale use is not economically viable.
Avoiding heating up the gas is essential to prevent ozone thermal degradation and to minimize the generation of reactive nitrogen species (RNS), such as NO2 and NO3, when air is used in the feed gas [21,22]. This can be achieved through intelligent reactor design and with cooling systems integrated within the reactor. One needs to bear in mind that the cost of cooling can be high and affect the final cost of ozone generation [16]. A second method often used to reduce the gas temperature is to modulate or pulse the discharge, so that the gas can cool down when the plasma is off [18]. Changing both the on-time and the duty cycle (i.e., the ratio of on-time to the modulation period) can influence the ozone production. For a fixed voltage amplitude, low duty cycles have low average power and, therefore, cause a limited gas temperature increase. However, they also produce weak discharges, which can lead to limited ozone generation [23,24]. The optimal duty cycle varies between reactors, with the cooling efficiency of the electrodes being an influential parameter.
In this study, we investigate the influence of the on-time duration on the ozone production for a fixed duty-cycle. This has received little attention, and existing literature has reported contradicting trends. Olszewski et al. observed that in their system, on-time periods of 20 ms were marginally more effective than periods of 2 ms and significantly more effective than a 2 min period [25]. On the other hand, Barni et al. found that ozone production with a 0.5 ms on-time was more efficient than 2.8 ms [26]. The effect of on-time on ozone production has also been studied recently by Seri et al., who by means of adjustable square waveforms showed that shorter on-times can increase the ozone concentration. In their study, they also found that when pulses are too short, there is a decrease in efficacy. [27]. They explained their experimental observations in terms of residence time and argued that during the pulse off-time, ozone generated in the previous on-time escapes the discharge region, which in turn gets replenished with fresh background gas. If the off-time is not sufficiently long to allow for ozone to diffuse (or be convected) away from the discharge region, the subsequent discharge breaks down some of the previously generated ozone, affecting the overall production efficacy. Here, we expand these studies and explore the influence of the on-time (at a fixed duty-cycle) in the performance of a pulsed sinusoidal dielectric barrier discharge.
2. Materials and Methods
2.1. Microbubble Dielectric Barrier Discharges (DBD) Plasma Reactor
Figure 1 shows a schematic of the plasma source used throughout this study. The reactor can be separated into two parts. The lower part of the reactor is the plasma module, which consists of 19 electrode assemblies housed in a plenum chamber. Each electrode assembly is made up of an 80 mm stainless steel rod with a 3.5 mm hemispherical cap at the tip. These are then placed within a quartz crucible with a wall thickness of 1.5 mm, which acts as the dielectric barrier. A polytetrafluoroethylene (PTFE) plug holds each rod within the crucible. Each rod is connected to a stainless-steel ring, which is also connected to the output of the power supply. At a gap of 2 mm above the tip of each crucible is a grounded nickel membrane. The nickel membrane (Micropore Ltd) has a pore size of 20 µm and a pitch of 180 µm. Compressed air is supplied to the bottom of the plasma module at 1 standard litre per minute (SLPM) from a mass flow controller (PR 4000B, MKS, Andover, MA, USA) and flows upwards through the plasma module housing. The plasma forms between the crucibles and the membrane, and the plasma effluent passes through the pores of the nickel membrane into the upper part of the reactor, the reaction tank. The tank has a height of 100 mm and a diameter of 140 mm, with a typical liquid treatment volume of ~1 litre. At the centre of the reaction tank is a draft tube with a height of 50 mm and diameter of 80 mm, allowing for good mixing within the reactor when treating a liquid [28]. For the work reported in this paper, the reactor was operated without liquid; however, the reactor can be used for pre-treatment of biomass [29,30] and wastewater [31]. The gas exits the reactor through a port in the centre of the top lid. Further details of the reactor used can be found elsewhere [32].
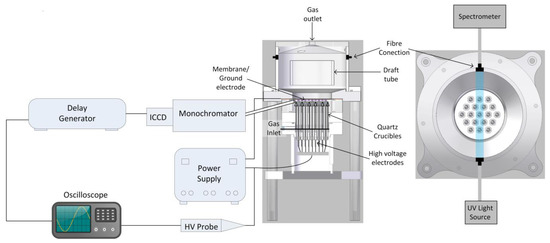
Figure 1.
Schematic of the DBD plasma source used in this work and the experimental setup.
2.2. Power Supply
The power supply used for this study is a full-bridge resonant power supply built in-house. For the experiments reported in this work, the plasmas were sustained with a voltage of 31 kVpp at a frequency of 21.6 kHz. The voltage was modulated at a 30% duty cycle and three different on-times were investigated in the study: 1 ms, 10 ms and 100 ms.
2.3. Ozone Measurements
The concentration of ozone was measured using UV absorption. This was carried out by directing a 255 nm LED light source (LLS-255, Ocean Optics, Largo, FL, USA) through the upper region of the reaction tank using a fibre optic cable (QP600-1-XSR, Ocean Optics, Largo, FL, USA) and a collimating lens (see Figure 1). The transmitted light was detected using a second collimating lens, an optic fibre cable, and a UV spectrometer (HR2000+, Ocean Optics, Largo, FL, USA).
2.4. Temperature Measurements
The gas temperature between the electrodes was measured using a fibre optic thermometer (FOB102, Omega Inc., Norwalk, CT, USA). The fibre was placed through a sealable hole on the side of the plasma module and data was logged using a personal computer.
2.5. Electrical Measurements
A current probe (2877 Pearson, Pearson Electronics, Palo Alto, CA, USA), a high voltage (HV) probe (P6015, Tektronix, Beaverton, OR, USA) and an oscilloscope (DP4104B Tektronix, Beaverton, OR, USA) were used to measure the current and voltage waveforms. Waveforms were sampled at least at 100 MHz as lower sampling rates affect the temporal resolution of the current waveform, causing an underestimation of the power delivered to the plasma (see Figure 2). The voltage and current waveforms were recorded and post-processed to calculate the power, taking into account the different delays introduced by the probes. The power was calculated multiplying the instantaneous voltage and current traces and then averaging over a period. For plasmas sustained with a continuous wave, the power calculation was in agreement (±2%) with the power measured using a sensing capacitor and the Lissajous method [33]. Given the pulsed nature of the waveforms under study and the transients observed in the experimental data (see discussion below), the Lissajous method was found to be unsuitable for the present study.
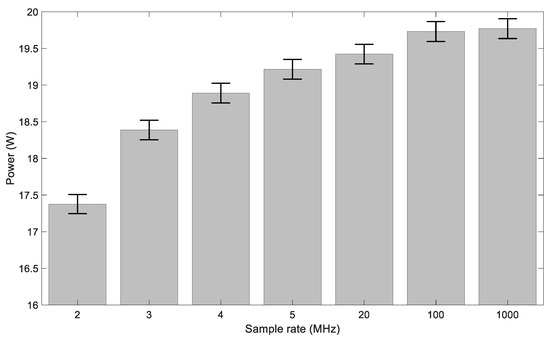
Figure 2.
The change in power when changing the sample rate.
The optical emission intensity of the nitrogen second positive system (0–2) was tracked over time as a proxy for the overall discharge intensity. This was done using a fibre optic cable (QP600-1-XSR, Ocean Optics, Largo, FL, USA) inserted through a port in the plasma module side wall, as shown in Figure 1, and a spectrometer (Andor SR-303i-A, 100 µm slit, grating 2400 l/mm, Andor, Oxford, UK). The angle of the hole and fibre’s orientation ensured direct line of sight of the discharge region. An iCCD camera (Andor iStar) was synchronized with the power supply and the oscilloscope, and a delay generator (7075, Berkeley Nucleonics, San Rafael, CA, UK) was used to trigger the iCCD camera (exposure time 5 µs) at different times within the plasma on-time.
Figure 3 shows the comparison of the measured instantaneous power and the emission intensity, with both measurements revealing a transient response at the beginning of the on-time pulse. Regardless of the on-time duration, at the beginning of the on-time pulse the power and light intensity recorded in the experiments show a transient with an “overshoot” that oscillates and attenuates exponentially as time progresses. The cause of this damped oscillating overshoot is a combination of the topology of the resonant power supply and the plasma impedance, which combined create an RLC equivalent load for the H-bridge. After approximately 300 μs, the oscillation was damped and the average power delivered during the rest of the on-time was fairly constant.
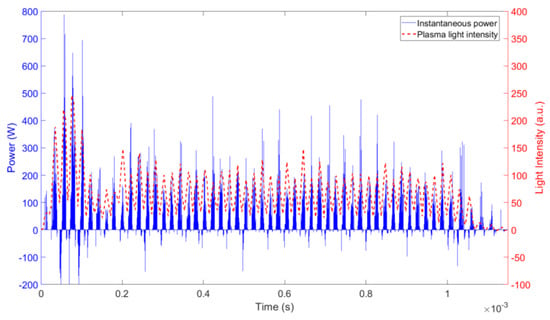
Figure 3.
Instantaneous power and the nitrogen second positive system (SPS) emission intensity during a 1 ms on-time pulse.
This initial transient (~300 μs) takes a significant portion of the on-time period when this is set to 1ms (Figure 3), but a much smaller fraction when the on-time period is 10 or 100 ms (data not shown explicitly). The presence of this transient means that a different average power is delivered at different on-times, even when the power supply is set to deliver the same voltage. As a result of the increased power delivered at the beginning of the on-time period and the tailing off at the end of the on-time pulse (Figure 3), shorter on-times have a higher average power. For the particular conditions of this study, as the on-time was reduced from 100 ms to 10ms and 1 ms, the average power delivered to the plasma increased by 8% and 25%, respectively. This draws attention to the care required when measuring power in pulsed sinusoidal DBDs. In some respects, this behaviour is similar to the enhanced power delivery observed in pulsed microwave plasmas at the beginning of each pulse [34]. Transient responses in modulated RF systems have also been observed, and in this case, they were attributed to thermal effects and ambient air mixing [19].
2.6. Computational Model
A 0-D numerical model was used to gain insights into the key chemical pathways in the discharge. The reactor is modelled as a cylindrical DBD reactor with circular electrodes of 12 cm in diameter. This gives an electrode surface area comparable to that of the plasma forming region in the actual reactor. The gap between the electrodes is set to 2 mm and the gas flow rate to 1 SLPM. The reactor overall heat capacity was measured experimentally and determined to be 0.015 W/K. The ambient air temperature and the initial gas temperature were set to 300 K.
The model solves the particle balance equation for each species, the electron energy balance equation, and the neutral gas energy balance equation, according to [35,36,37]. The flux to the electrodes of neutral species is assumed to be the thermal flux, with that of positive ions being given by the modified Bohm velocity [35,38]. For negatively charged ions, the flux to the electrode depends on the ion temperature and the electrode potential. This flux is estimated as:
During the plasma on time, the electron density and their thermal velocity are much larger than that of anions, and, therefore, the flux of negative ions is negligible. Nonetheless, this flux can be significant during the off-time once the electron density decreases and the remaining electrons cool down.
The chemical reaction set used in the model includes 37 species and 376 reactions taken from [39]. Reactions involving humidity were excluded from the reaction set as no humidity was introduced in the experiments. Where possible, the reaction rates of electron impact reactions were obtained from cross section data using the Boltzmann solver Bolsig+ [40] and cross-section data from LxCat [41], accounting for electron collisions with nitrogen molecules [42], oxygen molecules [43], nitrogen atoms [44], oxygen atoms [45,46], and nitric oxide [47]. The Boltzmann solver was used to pre-populate a look-up table with reaction rates for different effective electron temperatures, without constraining the electron energy distribution function (EEDF) to any particular distribution. The global model then used reaction rates from the look-up table based on the time evolution of the effective electron temperature (solution of the energy balance equation). When the density of any of the neutral species changes more than an order of magnitude, the look-up table is updated to make sure that reaction rates remain consistent with the actual plasma composition.
As shown in Figure 3, the average power delivered to the plasma is not constant throughout the on-time pulse, and, therefore, in the model we incorporate a damping sinusoidal waveform on the input power. The input power during the on time is given by Equation (2):
where is the desired peak power after the initial transient, , and parameters to characterize the overshoot and damped oscillations, t the time with respect to the beginning of the on-time pulse, and fAC the AC frequency of the sinusoidal signal (21.6 kHz). The resulting power function is shown in Figure 4a for the case of an on-time of 1ms. For comparison purposes, Figure 4b shows a sinusoidal waveform with the same frequency and duty cycle, in which no overshoot or transient is present.
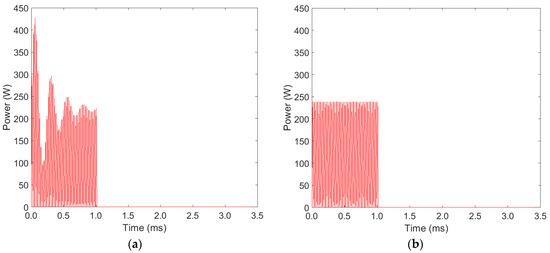
Figure 4.
(a) Power waveform incorporating the overshoot and damping observed in experiments (b) Theoretical pulsed sinusoidal power waveform. Both signals deliver the same average power.
3. Results and Discussion
3.1. Ozone Concentration
Figure 5 shows the time evolution of the ozone concentration generated in the reactor when the on-times are 1, 10, and 100 ms, respectively. Experimental and computational results agree qualitatively, and both show that 1 ms on-time is more efficient in generating ozone than longer on-time periods and that the ozone concentration initially increases, reaches a maximum after ~20 s, and then decreases, becoming negligible after ~80 s. This non-monotonous trend has been observed in other DBD systems and in has been attributed to increasing poisoning of the background gas by NOx species [48]. Indeed, as NOx species accumulate in the reactor, the model shows that the catalytic action of NO and NO2 quenches ozone and atomic oxygen:
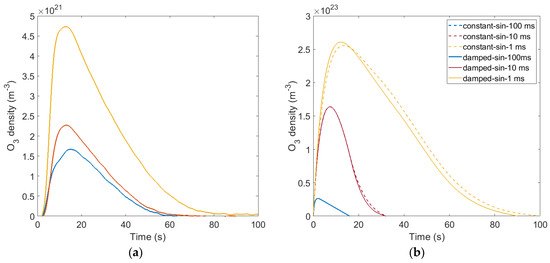
Figure 5.
Time evolution of the ozone concentration (a) experimental measurements and (b) computational results.
The computational model overestimates the amount of ozone generated in the system by a factor of ~50. This is attributed to the limitations of the zero dimensional model in capturing the actual geometry of the real device. In the actual reactor, not all the gas flowing through the system becomes ionized because the plasma forms only in between the 19-electrode ensemble and the ground mesh. As a result, the plasma forms only in about an eighth of the volume and, therefore, reactive species generated in the plasma are diluted in background gas before they are even transferred into the tank volume. Given the larger volume of the tank, plasma species are further diluted in the tank volume before being measured. At a flow rate of 1 SLPM, the concentration in the tank after 10 s is only ~15% of that of the gas entering the tank. These two dilutions that take place in the experimental setup, but are not captured in the global model, are responsible for the quantitative discrepancy between experimental and computational results. Despite this limitation, the zero dimensional model captures the general trends observed in experiments and provides valuable insights into the chemical pathways at play during the on- and off-time periods.
The better efficacy of the shorter on-time (Figure 5a) could be erroneously attributed to the higher input power delivered to the plasma, due to the transient oscillation induced at the beginning of each pulse (see discussion in Section 2.5). This is not the case, and Figure 5b allows us to assess the effect of the power overshoot at the beginning of the pulse on the ozone production. For the two largest on-times (10 ms and 100 ms), there is virtually no difference between the “damped” (Figure 4a) and “constant” (Figure 4b) sinusoidal waveforms. This result is expected, as the overshoot at the beginning of each pulse lasts for a very short time when compared to the total duration of the on-time pulse. For the 1 ms on-time, a difference between the two waveforms is observed because the transient at the beginning of the pulse takes a significant fraction of the on-time of the pulse. However, this difference is negligible when compared with the difference cause by the change in on-time.
Since the simulation results capture the same trend, even when no oscillation is incorporated in the input power waveform (Figure 5b), it follows that the increased power delivered with the shorter on-times is not the main factor contributing to the enhanced ozone production. The underpinning mechanism is discussed in the Plasma Chemistry section below.
3.2. Temperature Evolution
Figure 6 shows the temporal evolution of the discharge gas temperature for the three on-times. Shorter on-times result in higher gas temperature, with 1 ms reaching 359 K after 100 s, 10 ms 355 K and 100 ms 343 K. The temperature rise is faster over the first 20 s for all cases.
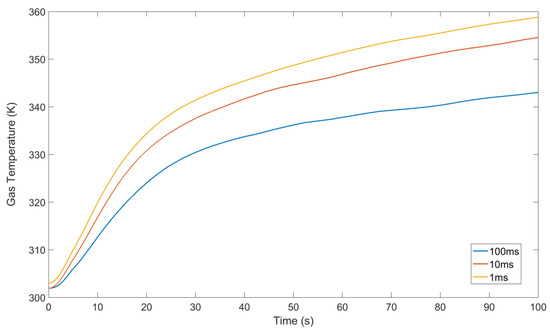
Figure 6.
Time evolution of the gas temperature as measured by the optical fibre thermometer.
The increase in temperature contributes to turning the system from one where ozone is predominantly generated to one in which it is effectively destroyed [48,49]. This explains the trends seen in Figure 5, where the ozone density rises and then falls back to zero again. Simulation results in which the gas temperature is kept constant do not show a decrease in ozone concentration (data not shown explicitly). It is interesting to note that 1 ms on-time results in the hottest discharge, yet 1 ms on-time is also the one that produces most ozone. Therefore, the transition from an ozone-producing to an ozone-destroying regime although triggered by temperature, must also rely on the actual discharge composition. In particular, the dissociation of N2O5 into NO2 and NO3 is favoured at higher temperature, and, as will be discussed in the next section, NO2 plays a critical role in determining the ozone production/destruction efficacy.
3.3. Plasma Chemistry
The enhanced ozone production with the 1 ms on-time is somewhat surprising, as this on-time is obtained at the highest gas temperature. The fact that the three on-time cases result in different ozone concentrations indicates that the net ozone generation rate during the on-times, the net ozone destruction rate during the off-times, or both are different. Although it is not possible to fully resolve the temporal evolution of the ozone concentration in our experimental setup, simulation results indicate that the main difference can be attributed to the faster net production rate of ozone during the on-time of shorter on-time periods.
Ozone generation during the on-time is driven by the three body reaction O + O2 + M→O3 + M, but during the on-time, other competing reactions destroy ozone. In the first seconds of the discharge, ozone is quenched by collisions with electrons (e + O3→ O2− + O) and singlet oxygen (1O2 + O3→2O2 + O), primarily. Since singlet oxygen builds-up relatively slowly during the on-time pulse and decreases relatively quickly during the off-time, longer on-time pulses favour the accumulation of higher concentrations of singlet oxygen in the discharge during the on-time, which leads to enhanced ozone destruction. The ozone destruction rates associated with these reactions, however, are typically two orders of magnitude smaller than the generation rates and hence have little bearing on the net generation rate of ozone.
Instead the main mechanism affecting the net generation rate of ozone in the first seconds of the discharge is the availability of atomic oxygen. Longer on-times result in lower concentrations of atomic oxygen, which leads to the slower ozone production (O + O2 + M→O3 + M). This is the case because longer on-times favour the accumulation of NO2, which, besides reacting with ozone directly (O3 + NO2 → O2 + NO3), quenches atomic oxygen (O + NO2 → NO + O2). Although during the first 10–20 s there is a net positive production of ozone, eventually, the accumulation of both NO and NO2 leads to the catalytic destruction of O and O3 (see Figure 5).
Therefore, the ozone production efficacy is dependent on the generation/destruction of NO2, as this affects the balance of atomic oxygen. NO2 is involved in the catalytic reaction with O and in the formation of N2O5. These reactions change the composition of the NOx cocktail in the discharge but retain the total amount of nitrogen, and subsequently other NOx species lead to the formation of NO2. Significantly, however, NO2 also reacts with atomic nitrogen (N + NO2 → N2O + O). This is an important reaction because, on one hand, it releases O, which can subsequently lead to ozone production, and on the other, it produces N2O. Unlike other NOx species, N2O is fairly stable and escapes the plasma removing nitrogen from the system, thereby preventing it from becoming NO2 again. Short on-times are found to produce a higher average density of atomic nitrogen and, therefore, are more efficient in converting NO2 into N2O, thereby favouring ozone production. This occurs, because atomic nitrogen is generated during the on-time and consumed during the off-time. For long on/off-times, atomic nitrogen is completely depleted for most part of the off time, whereas in short on/off-time atomic nitrogen is present during the whole period.
Therefore, shorter on-times produce more ozone from a combination of effects. Previous studies have found that more frequent off-time periods allow for ozone to escape the discharge region and the discharge to form in the replenished gas between the electrodes [27]. In addition, the current study has found that shorter on-time periods favour a higher concentration of atomic oxygen and lower concentration of singlet oxygen, which contribute to a more efficient net production of ozone. The higher atomic oxygen concentration is a direct consequence of the lower NO2 accumulation in discharges with short on-times, as these discharges present larger concentrations of atomic nitrogen (N) that converts NO2 into long-lived N2O.
4. Conclusions
Atmospheric pressure dielectric barrier discharges (DBD) have been used for decades in the production of ozone and have recently gained renewed interest for their potential application in a number of emerging fields, such as plasma medicine, plasma catalysis, and plasma agriculture. Although extensive work has been done on the dependence of the ozone production efficacy on the feed gas composition, gas temperature, cooling systems, and electrode geometry, the influence of the on-time duration on modulated DBDs remains largely unexplored.
In this work, we show that for fixed average power and duty-cycle, the on-time duration can have a marked influence on the performance of the DBD. Care must be exercised when measuring power in modulated DBD systems, as the varying plasma impedance and the output stage of the power supply can cause transients that become increasingly important in short on-time pulses.
The experimental and computational results presented here show that shorter on-time pulses lead to enhanced ozone production, even despite their operation at slightly higher temperature. The key underpinning mechanism that causes this important observation is the more efficient net generation rate of ozone during the plasma on-time due to the lower accumulation of NO2 in the discharge, as this leads to a lower competing quenching rate of ozone and atomic oxygen. The lower accumulation of NO2 is favoured by the larger average density of atomic nitrogen that converts NO2 into the less reactive, longer lived N2O.
Therefore, applications that rely on ozone production using DBDs should consider short on-times as a means of enhancing their efficacy.
Author Contributions
F.M., A.W., J.R., A.S.: methodology and investigation; G.N., H.B., F.I.: supervision, formal analysis; F.M., A.W., J.R.: writing-original draft; H.B., F.I.: Review and preparation of the final manuscript.
Funding
A.W. would like to thank EPSRC (EP/M507908/1) for the studentship. A.W. & H.B. would like to thank Plants to Products BBSRC NIBB for funding (POC-HD_RD0300 C and BB/L013819/1).
Acknowledgments
The authors would like to acknowledge Micropore technology Ltd. for providing nickel membranes and Perlemax Ltd. for advice and support on plasma reactors. The authors are also grateful to Mark Barron and Steve Bowler for the fabrication of the reactor. FI & HB would also like to acknowledge the support provided by the Loughborough University’s Centre for Doctoral Training in Gas Plasma Interactions with Organic Liquids.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lu, X.; Naidis, G.V.; Laroussi, M.; Reuter, S.; Graves, D.B.; Ostrikov, K. Reactive Species in Non-Equilibrium Atmospheric-Pressure Plasmas: Generation, Transport, and Biological Effects. Phys. Rep. 2016, 630, 1–84. [Google Scholar] [CrossRef]
- Park, D.P.; Davis, K.; Gilani, S.; Alonzo, C.A.; Dobrynin, D.; Friedman, G.; Fridman, A.; Rabinovich, A.; Fridman, G. Reactive Nitrogen Species Produced in Water by Non-Equilibrium Plasma Increase Plant Growth Rate and Nutritional Yield. Curr. Appl. Phys. 2013, 13 (Suppl. 1), S19–S29. [Google Scholar] [CrossRef]
- Shaw, A.; Shama, G.; Iza, F. Emerging Applications of Low Temperature Gas Plasmas in the Food Industry. Biointerphases 2015, 10, 029402. [Google Scholar] [CrossRef] [PubMed]
- Bruggeman, P.J.; Kushner, M.J.; Locke, B.R.; Gardeniers, J.G.E.; Graham, W.G.; Graves, D.B.; Hofman-Caris, R.C.H.M.; Maric, D.; Reid, J.P.; Ceriani, E.; et al. Plasma–liquid Interactions: A Review and Roadmap. Plasma Sources Sci. Technol. 2016, 25, 053002. [Google Scholar] [CrossRef]
- Xu, S.; Chansai, S.; Stere, C.; Inceesungvorn, B.; Goguet, A.; Wangkawong, K.; Taylor, S.F.R.; Al-Janabi, N.; Hardacre, C.; Martin, P.A.; et al. Sustaining Metal–organic Frameworks for Water–gas Shift Catalysis by Non-Thermal Plasma. Nat. Catal. 2019, 2, 142–148. [Google Scholar] [CrossRef]
- Tou, A.; Kim, H.H.; Einaga, H.; Teramoto, Y.; Ogata, A. Ozone-Assisted Catalysis of CO: In Situ Fourier Transform IR Evidence of the Cooperative Effect of a Bimetallic Ag-Pd Catalyst. Chem. Eng. J. 2019, 355, 380–389. [Google Scholar] [CrossRef]
- Jia, Z.; Ben Amar, M.; Yang, D.; Brinza, O.; Kanaev, A.; Duten, X.; Vega-González, A. Plasma Catalysis Application of Gold Nanoparticles for Acetaldehyde Decomposition. Chem. Eng. J. 2018, 347, 913–922. [Google Scholar] [CrossRef]
- Mariotti, D.; Sankaran, R.M. Microplasmas for Nanomaterials Synthesis. J. Phys. D Appl. Phys. 2010, 43, 323001. [Google Scholar] [CrossRef]
- Lisco, F.; Shaw, A.; Wright, A.; Walls, J.M.; Iza, F. Atmospheric-Pressure Plasma Surface Activation for Solution Processed Photovoltaic Devices. Sol. Energy 2017, 146, 287–297. [Google Scholar] [CrossRef]
- Vandenbossche, M.; Hegemann, D. Recent Approaches to Reduce Aging Phenomena in Oxygen- and Nitrogen-Containing Plasma Polymer Films: An Overview. Curr. Opin. Solid State Mater. Sci. 2018, 22, 26–38. [Google Scholar] [CrossRef]
- Kogelschatz, U. Dielectric-Barrier Discharges: Their History, Discharge Physics, and Industrial Applications. Plasma Chem. Plasma Process. 2003, 23, 1–46. [Google Scholar] [CrossRef]
- Langlain, B.; Reckhow, D.; Brink, D. Ozone in Water Treatment: Application and Engineering; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Vezzu, G.; Lopez, J.L.; Freilich, A.; Becker, K.H. Optimization of Large-Scale Ozone Generators. IEEE Trans. Plasma Sci. 2009, 37, 890–896. [Google Scholar] [CrossRef]
- Brueggemann, N.; Puehmeier, T.; Fiekens, R.; Richardt, F.J.; Salvermoser, M. Cooling Conditions of Ozone Generators. Ozone Sci. Eng. 2017, 39, 196–201. [Google Scholar] [CrossRef]
- Murata, T.; Okita, Y.; Noguchi, M.; Takase, I. Basic Parameters of Coplanar Discharge Ozone Generator. Ozone Sci. Eng. 2004, 26, 429–442. [Google Scholar] [CrossRef]
- Panjeshahi, M.H.; Ataei, A. Application of an Environmentally Optimum Cooling Water System Design in Water and Energy Conservation. Int. J. Environ. Sci. Technol. 2008, 5, 251–262. [Google Scholar] [CrossRef]
- Suksri, A.; Karnchanalekha, K.; Tonmitra, K.; Apiratikul, P. A Comparative Study on Suitable High Voltage Sources for Ozone Generation. In Proceedings of the 2009 6th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Pattaya, Thailand, 6–9 May 2009; pp. 296–299. [Google Scholar] [CrossRef]
- Šimek, M.; Pekárek, S.; Prukner, V. Influence of Power Modulation on Ozone Production Using an AC Surface Dielectric Barrier Discharge in Oxygen. Plasma Chem. Plasma Process. 2010, 30, 607–617. [Google Scholar] [CrossRef]
- Zhang, S.; Sobota, A.; van Veldhuizen, E.M.; Bruggeman, P.J. Temporally Resolved Ozone Distribution of a Time Modulated RF Atmospheric Pressure Argon Plasma Jet: Flow, Chemical Reaction, and Transient Vortex. Plasma Sources Sci. Technol. 2015, 24, 045015. [Google Scholar] [CrossRef]
- Park, J.; Henins, I.; Herrmann, H.W.; Selwyn, G.S.; Jeong, J.Y.; Hicks, R.F.; Shim, D.; Chang, C.S. An Atmospheric Pressure Plasma Source. Appl. Phys. Lett. 2000, 76, 288–290. [Google Scholar] [CrossRef]
- Sung, Y.-M.; Sakoda, T. Optimum Conditions for Ozone Formation in a Micro Dielectric Barrier Discharge. Surf. Coat. Technol. 2005, 197, 148–153. [Google Scholar] [CrossRef]
- Chirokov, A.; Gutsol, A.; Fridman, A. Atmospheric Pressure Plasma of Dielectric Barrier Discharges. Pure Appl. Chem. 2005, 77, 487–495. [Google Scholar] [CrossRef]
- Ma, T.; Jiang, H.; Liu, J.; Zhong, F. Decomposition of Benzene Using a Pulse-Modulated DBD Plasma. Plasma Chem. Plasma Process. 2016, 36, 1533–1543. [Google Scholar] [CrossRef]
- Díaz, R.; Márquez, A.; Menéndez, D.; Pérez, R. Medium Frequency Pulse Train Ozone Generation. Ozone Sci. Eng. 1999, 21, 635–642. [Google Scholar] [CrossRef]
- Olszewski, P.; Li, J.F.; Liu, D.X.; Walsh, J.L. Optimizing the Electrical Excitation of an Atmospheric Pressure Plasma Advanced Oxidation Process. J. Hazard. Mater. 2014, 279, 60–66. [Google Scholar] [CrossRef] [PubMed]
- Barni, R.; Biganzoli, I.; Dell’Orto, E.C.; Riccardi, C. Effect of Duty-Cycles on the Air Plasma Gas-Phase of Dielectric Barrier Discharges. J. Appl. Phys. 2015, 118. [Google Scholar] [CrossRef]
- Seri, P.; Wright, A.; Shaw, A.; Iza, F.; Bandulasena, H.; Borghi, C.A.; Neretti1, G. Influence of the Shape and On-Time Duration of the Voltage Waveform on the Performance of a DBD Micro-Bubble Reactor. Plasma Sources Sci. Technol. 2018. under review. [Google Scholar]
- Ying, K.; Al-mashhadani, M.K.H.; Hanotu, J.O.; Gilmour, D.J.; Zimmerman, W.B. Enhanced Mass Transfer in Microbubble Driven Airlift Bioreactor for Microalgal Culture. Engineering 2013, 5, 735–743. [Google Scholar] [CrossRef]
- Wright, A.; Ibenegbu, C.; Holmes, T.; Shaw, A.; Zimmerman, W.; Iza, F.; Leak, D.; Bandulasena, H. Dielectric Barrier Discharge Plasma Microbubble Reactor for Pretreatment of Lignocellulosic Biomass. AIChE J. 2018, 64, 3803–3816. [Google Scholar] [CrossRef]
- Wright, A.; Marsh, A.; Ricciotti, F.; Shaw, A.; Iza, F.; Holdich, R.; Bandulasena, H.C.H. Microbubble-Enhanced Dielectric Barrier Discharge Pretreatment of Micro Crystalline Cellulose. Biomass Bioenergy 2018, 118, 46–54. [Google Scholar] [CrossRef]
- Wright, A.; Uprety, B.; Shaw, A.; Shama, G.; Iza, F.; Bandulasena, H.C.H. Effect of Humic Acid on E. coli Disinfection Using a Microbubble-Gas Plasma Reactor. J. Water Process Eng. 2019. under review. [Google Scholar]
- Wright, A.; Taglioli, M.; Montazersadgh, F.; Shaw, A.; Iza, F.; Bandulasena, H.C.H. Microbubble-Enhanced DBD Plasma Reactor: Design, Characterisation and Modelling. Chem. Eng. Res. Des. 2019, 144, 159–173. [Google Scholar] [CrossRef]
- Manley, T.C. The Electric Characteristics of the Ozonator Discharge. Trans. Electrochem. Soc. 1943, 84, 83–96. [Google Scholar] [CrossRef]
- Jeong, S.Y.; Nam, W.J.; Lee, J.K.; Yun, G.S. Dependence of Reactive Species Generation on Microwave Pulse Parameters in Atmospheric Argon/Oxygen Plasma. J. Phys. D Appl. Phys. 2018, 51. [Google Scholar] [CrossRef]
- Lieberman, M.; Lichtenberg, A. Discharges and Materials Processing Principles of Plasma Discharges and Materials; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Liu, D.-X.; Iza, F.; Wang, X.-H.; Ma, Z.-Z.; Rong, M.-Z.; Kong, M.G. A Theoretical Insight into Low-Temperature Atmospheric-Pressure He+H2 Plasmas. Plasma Sources Sci. Technol. 2013, 22, 055016. [Google Scholar] [CrossRef]
- Lietz, A.M.; Kushner, M.J. Air Plasma Treatment of Liquid Covered Tissue: Long Timescale Chemistry. J. Phys. D Appl. Phys. 2016, 49. [Google Scholar] [CrossRef]
- Khoramabadi, M.; Ghomi, H.; Shukla, P.K. The Bohm-sheath Criterion in Plasmas Containing Electrons and Multiply Charged Ions. J. Plasma Phys. 2013, 79, 267–271. [Google Scholar] [CrossRef]
- Sakiyama, Y.; Graves, D.B.; Chang, H.-W.; Shimizu, T.; Morfill, G.E. Plasma Chemistry Model of Surface Microdischarge in Humid Air and Dynamics of Reactive Neutral Species. J. Phys. D Appl. Phys. 2012, 45, 425201. [Google Scholar] [CrossRef]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann Equation to Obtain Electron Transport Coefficients and Rate Coefficients for Fluid Models. Plasma Sources Sci. Technol. 2005, 14, 722–733. [Google Scholar] [CrossRef]
- Plasma Data Exchange Project. Available online: www.lxcat.net (accessed on 17 June 2018).
- Phelps, A.V.; Pitchford, L.C. Anisotropic Scattering of Electrons by N2 and Its Effect on Electron Transport. Phys. Rev. A 1985, 31, 2932–2949. [Google Scholar] [CrossRef]
- Ionin, A.A.; Kochetov, I.V.; Napartovich, A.P.; Yuryshev, N.N. Physics and Engineering of Singlet Delta Oxygen Production in Low-Temperature Plasma. J. Phys. D Appl. Phys. 2007, 40, R25–R61. [Google Scholar] [CrossRef]
- Wang, Y.; Zatsarinny, O.; Bartschat, K. B-Spline R-Matrix-with-Pseudostates Calculations for Electron-Impact Excitation and Ionization of Nitrogen. Phys. Rev. A 2014, 89, 062714. [Google Scholar] [CrossRef]
- Alves, L.L.; Coche, P.; Ridenti, M.A.; Guerra, V. Electron Scattering Cross Sections for the Modelling of Oxygen-Containing Plasmas. Eur. Phys. J. D 2016, 70. [Google Scholar] [CrossRef]
- Laher, R.R.; Gilmore, F.R. Updated Excitation and Ionization Cross Sections for Electron Impact on Atomic Oxygen. J. Phys. Chem. Ref. Data 1990, 19, 277–305. [Google Scholar] [CrossRef]
- Itikawa, Y. Cross Sections for Electron Collisions with Nitric Oxide. J. Phys. Chem. Ref. Data 2016, 45, 033106. [Google Scholar] [CrossRef]
- Shimizu, T.; Sakiyama, Y.; Graves, D.B.; Zimmermann, J.L.; Morfill, G.E. The Dynamics of Ozone Generation and Mode Transition in Air Surface Micro-Discharge Plasma at Atmospheric Pressure. New J. Phys. 2012, 14, 103028. [Google Scholar] [CrossRef]
- Gardoni, D.; Vailati, A.; Canziani, R. Decay of Ozone in Water: A Review. Ozone Sci. Eng. 2012, 34, 233–242. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).