Experiments Designed to Study the Non-Linear Transition of High-Power Microwaves through Plasmas and Gases
Abstract
1. Introduction
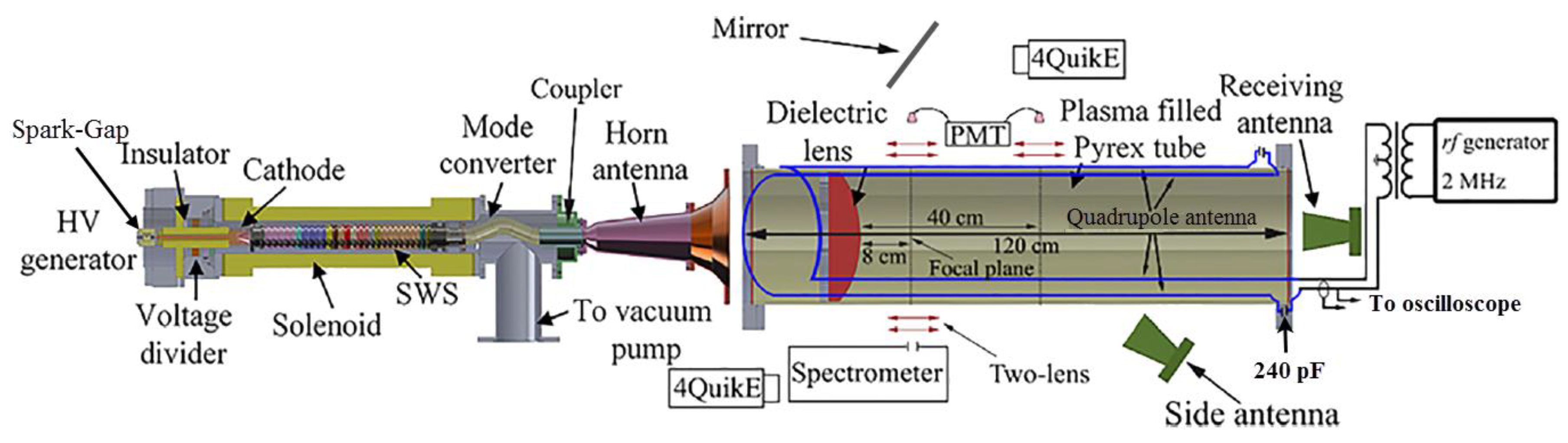
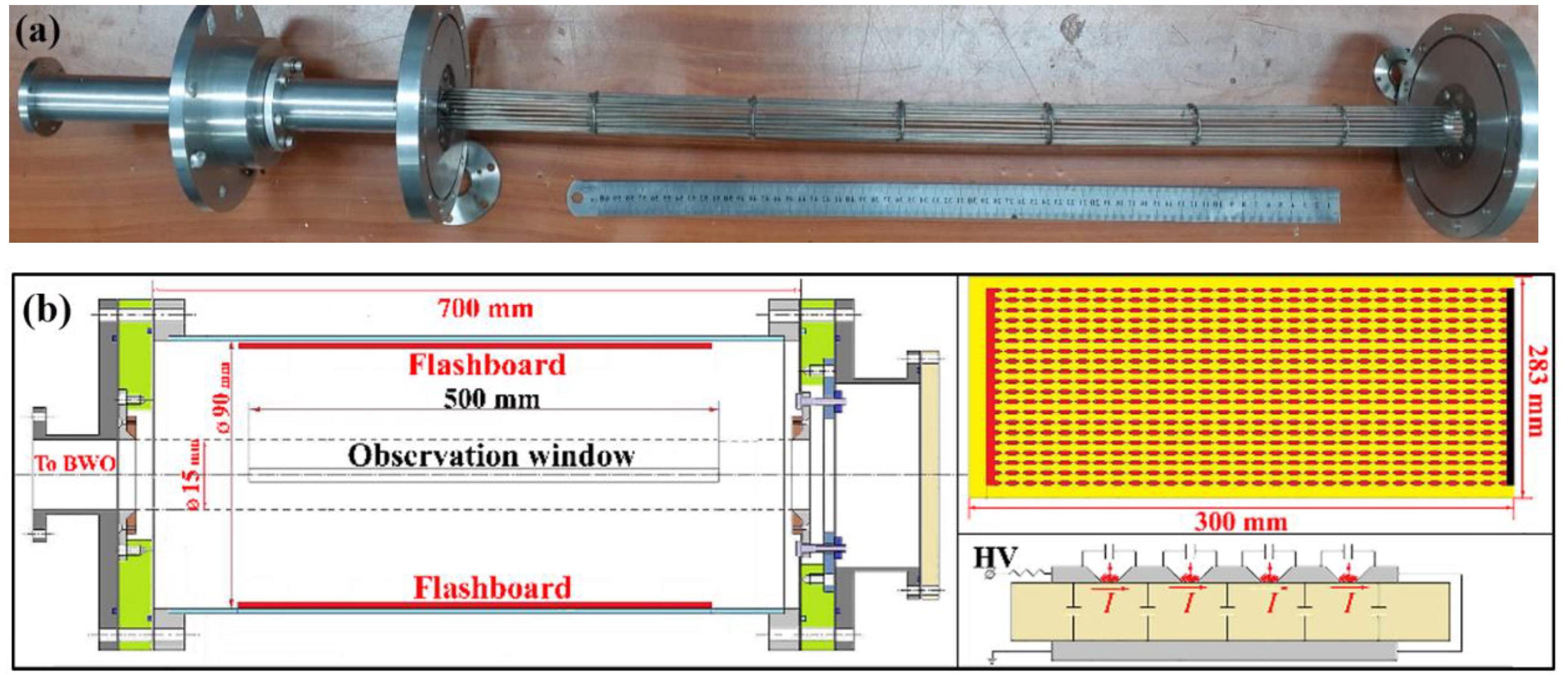
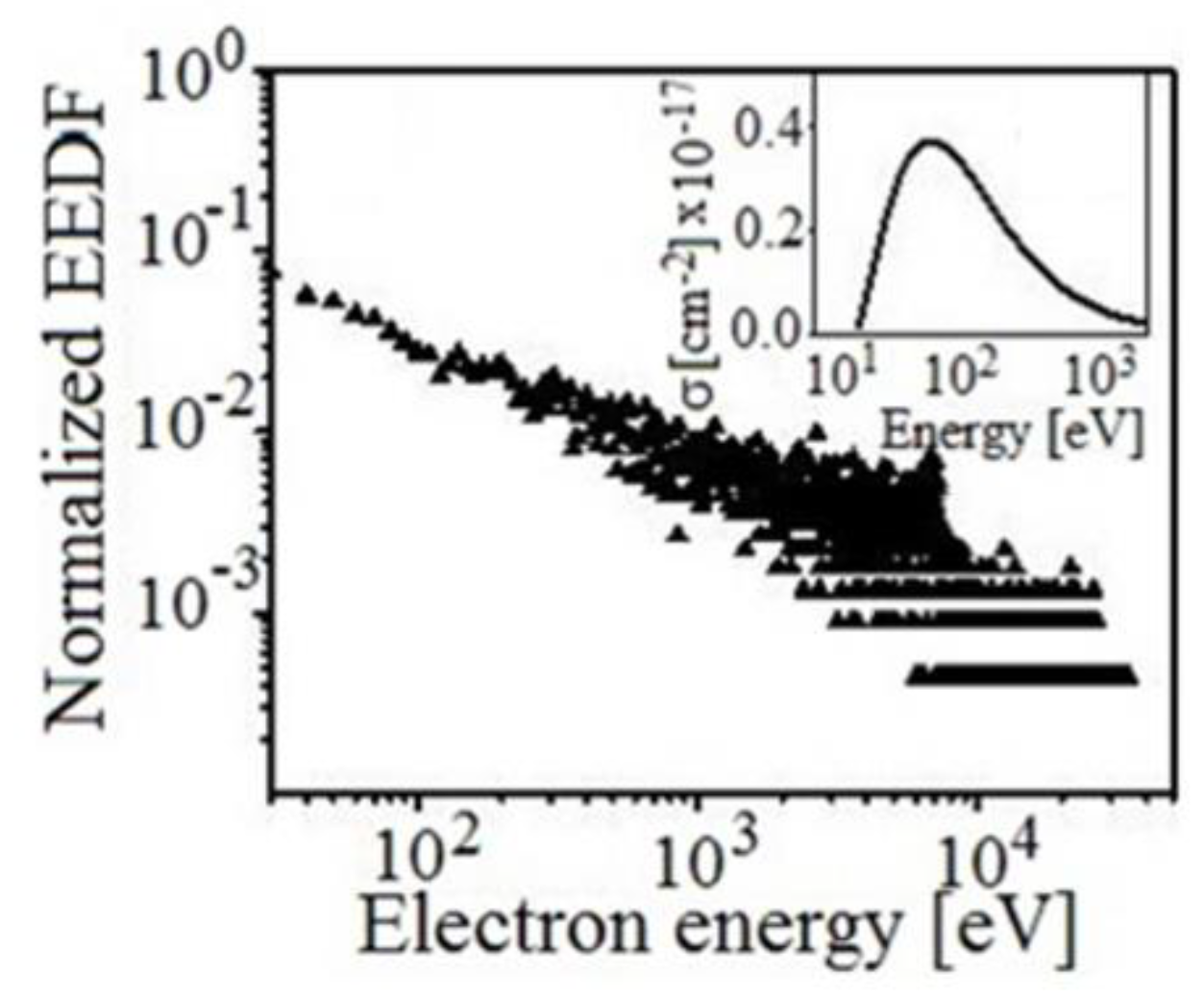
2. The Experiment
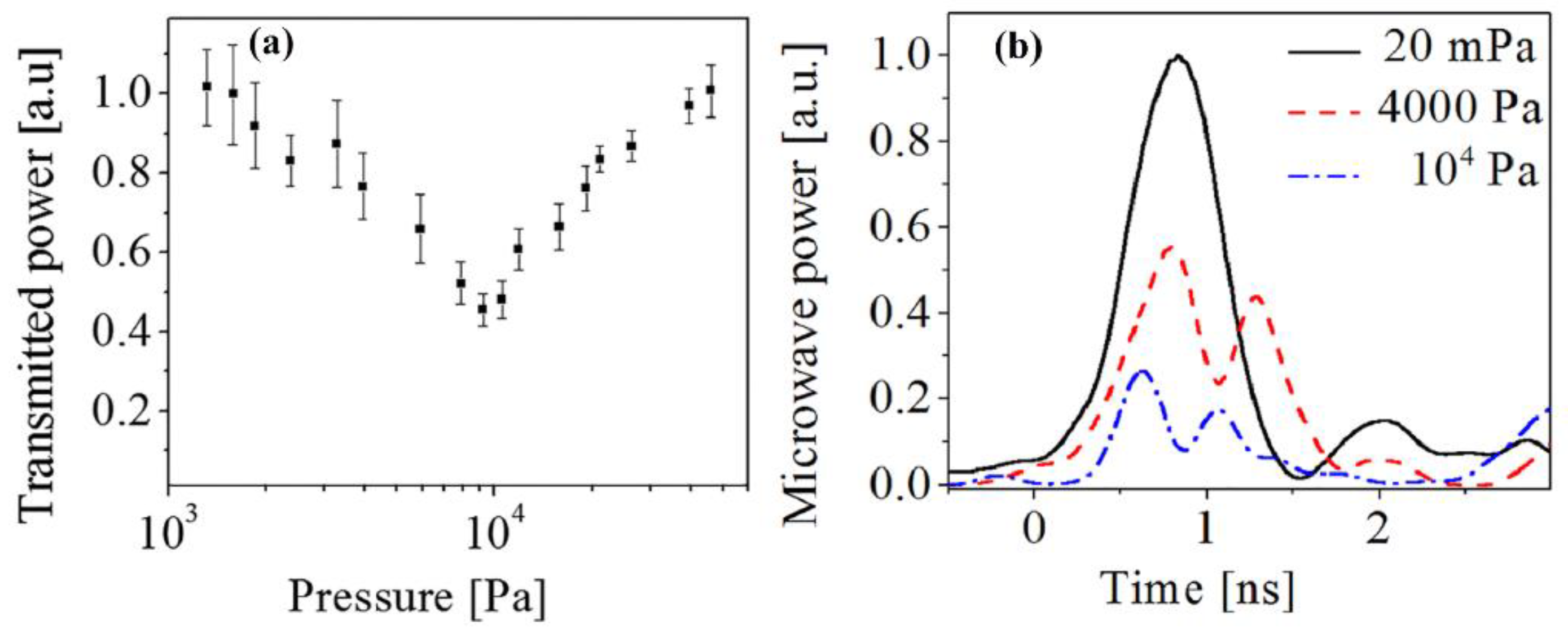
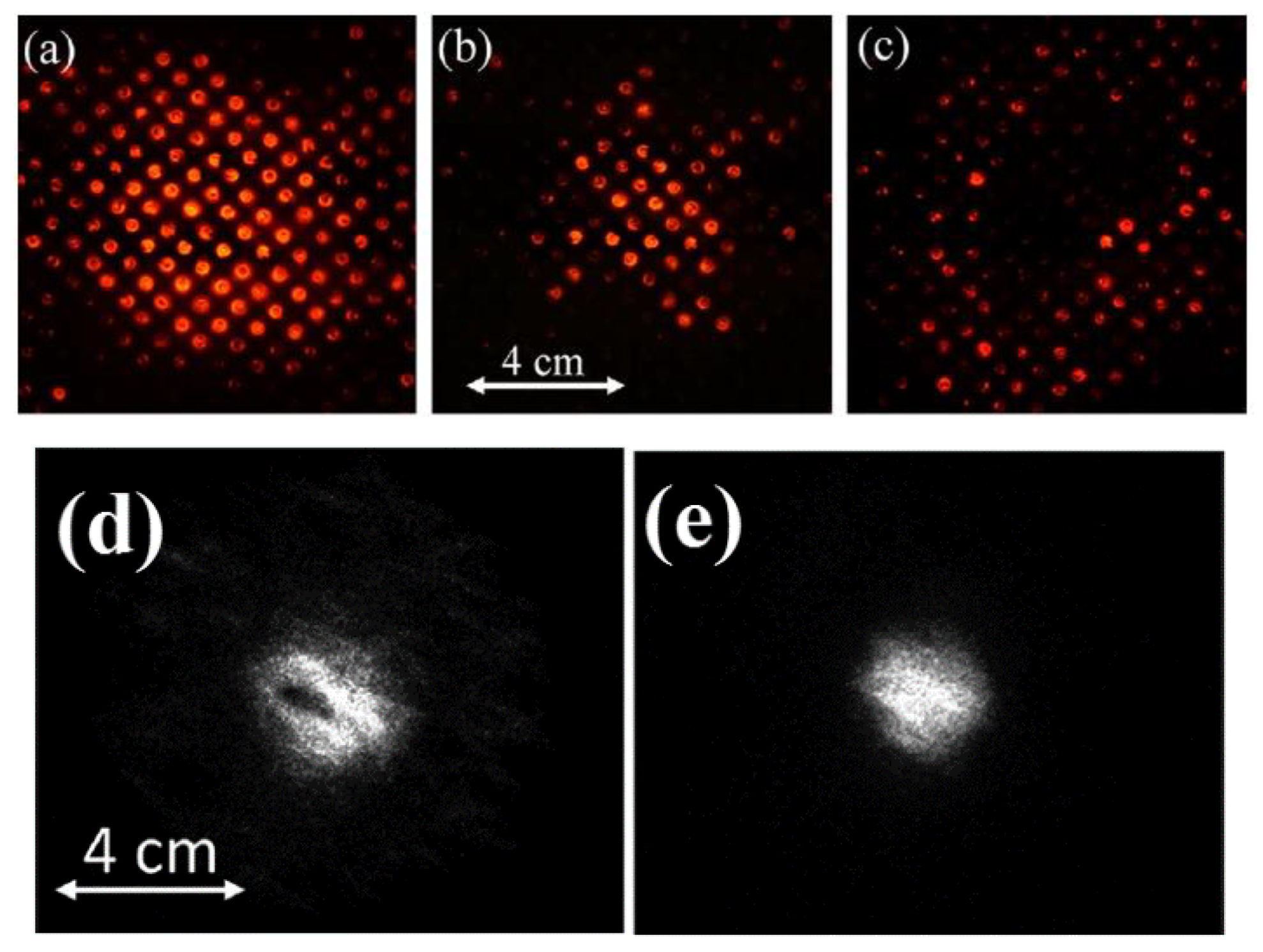
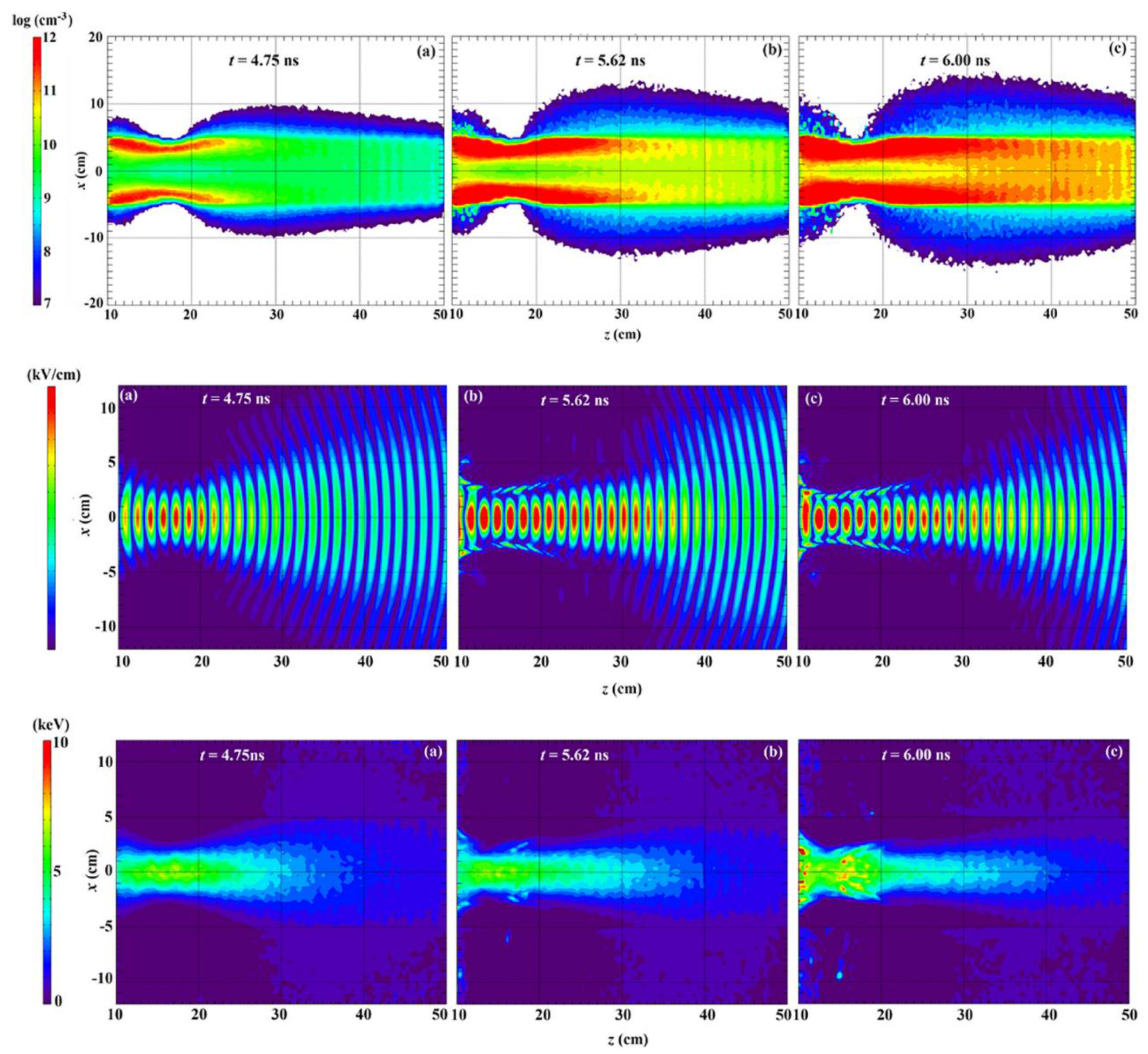
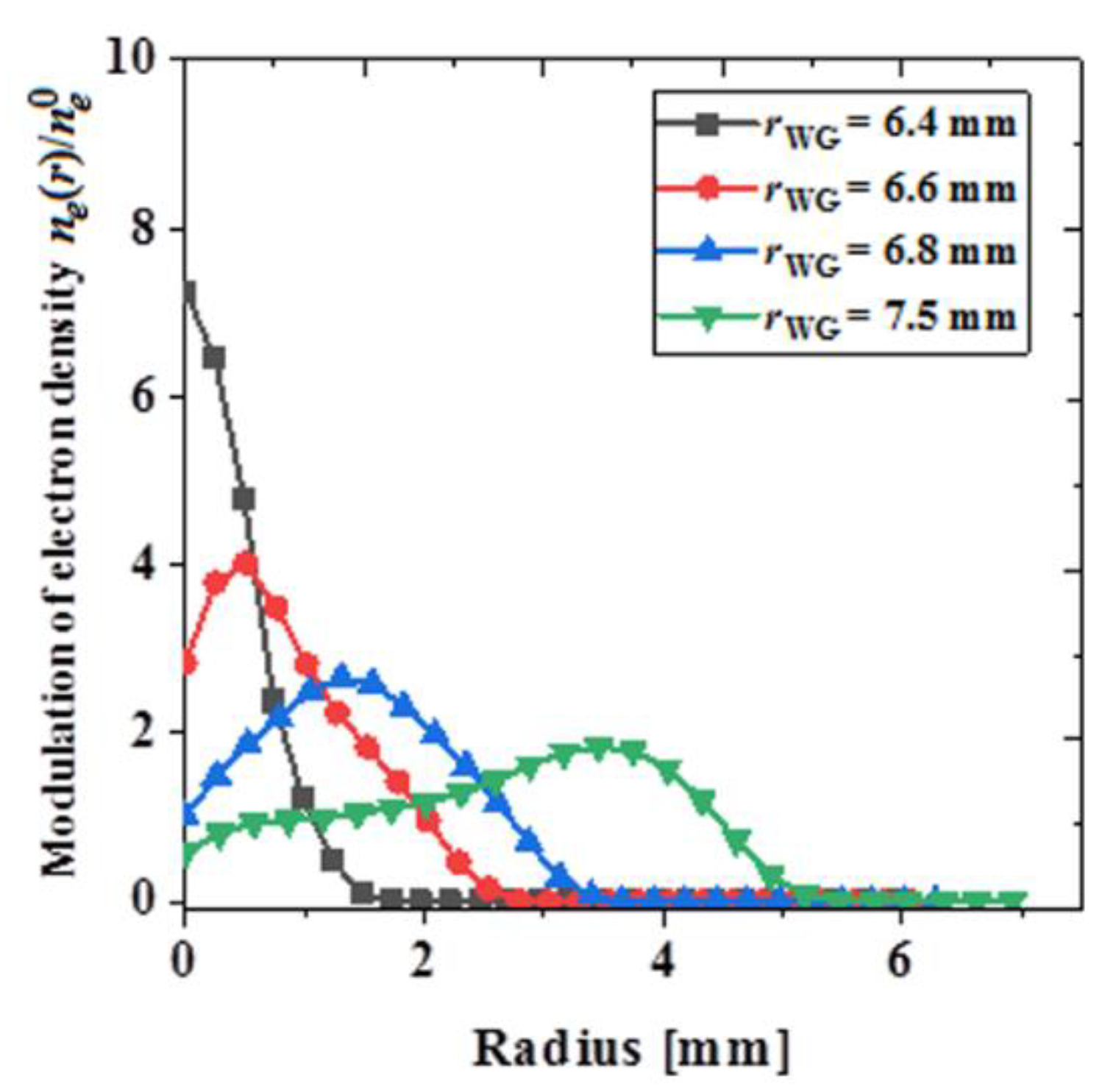
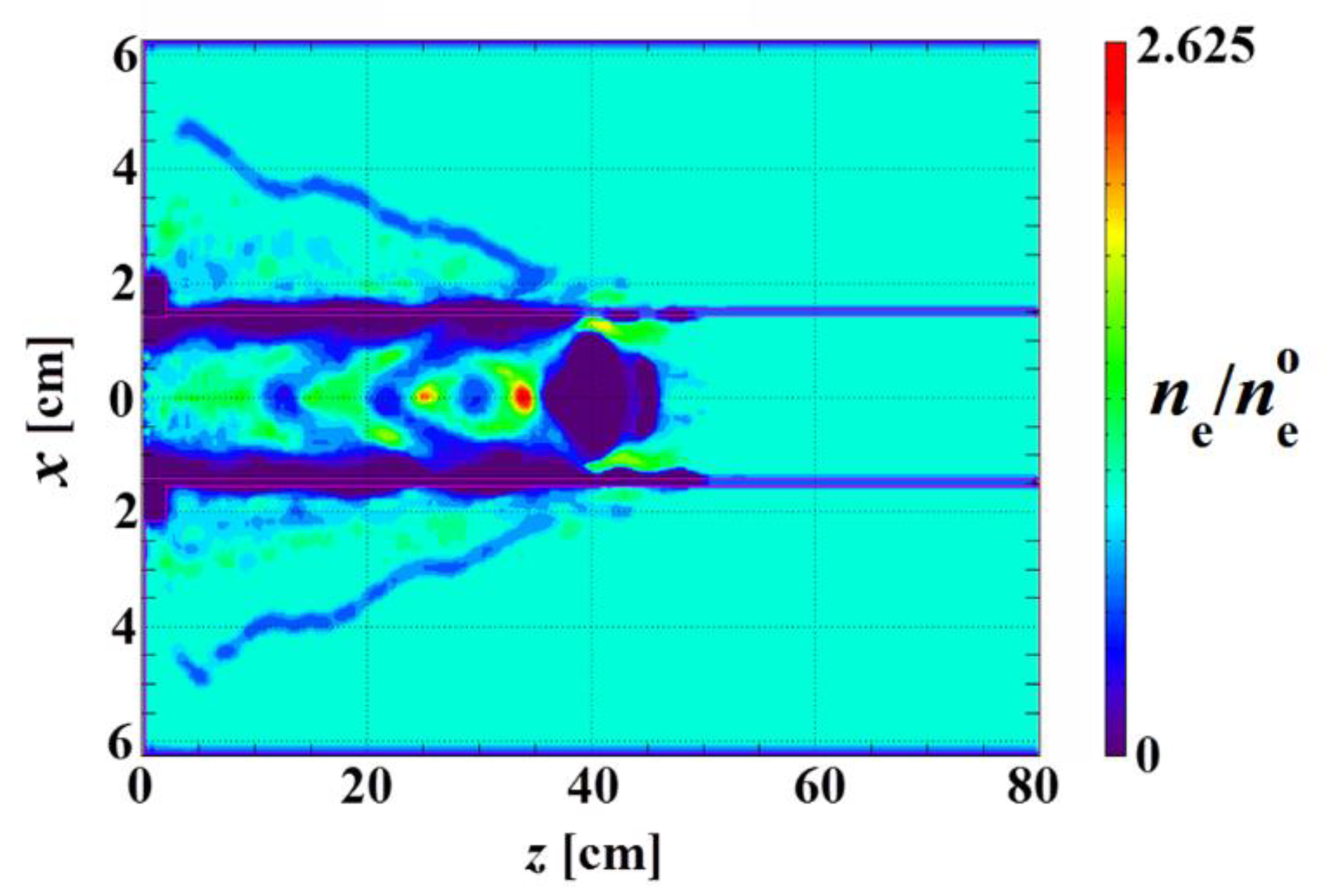
3. Self-Channeling Experiments
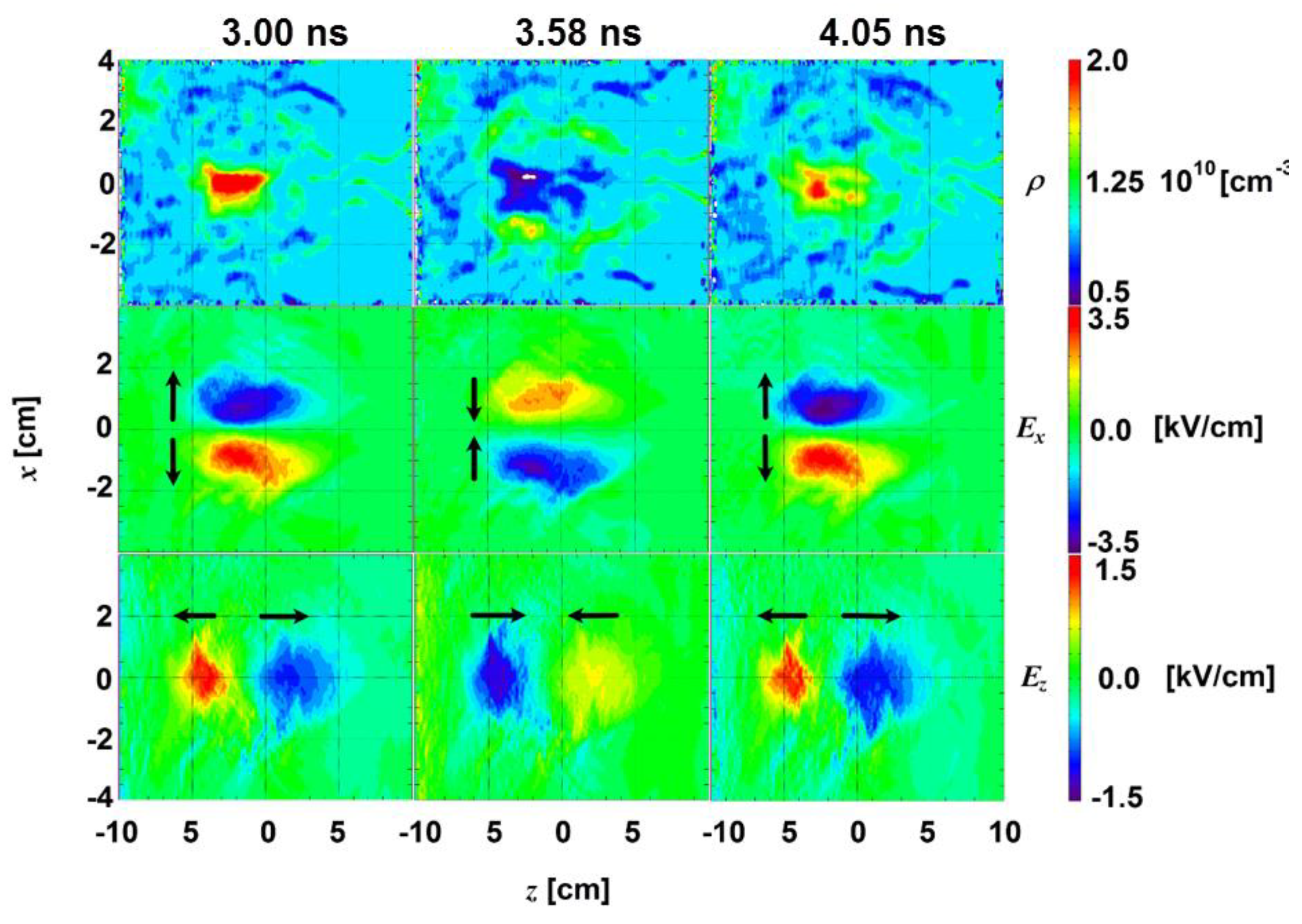
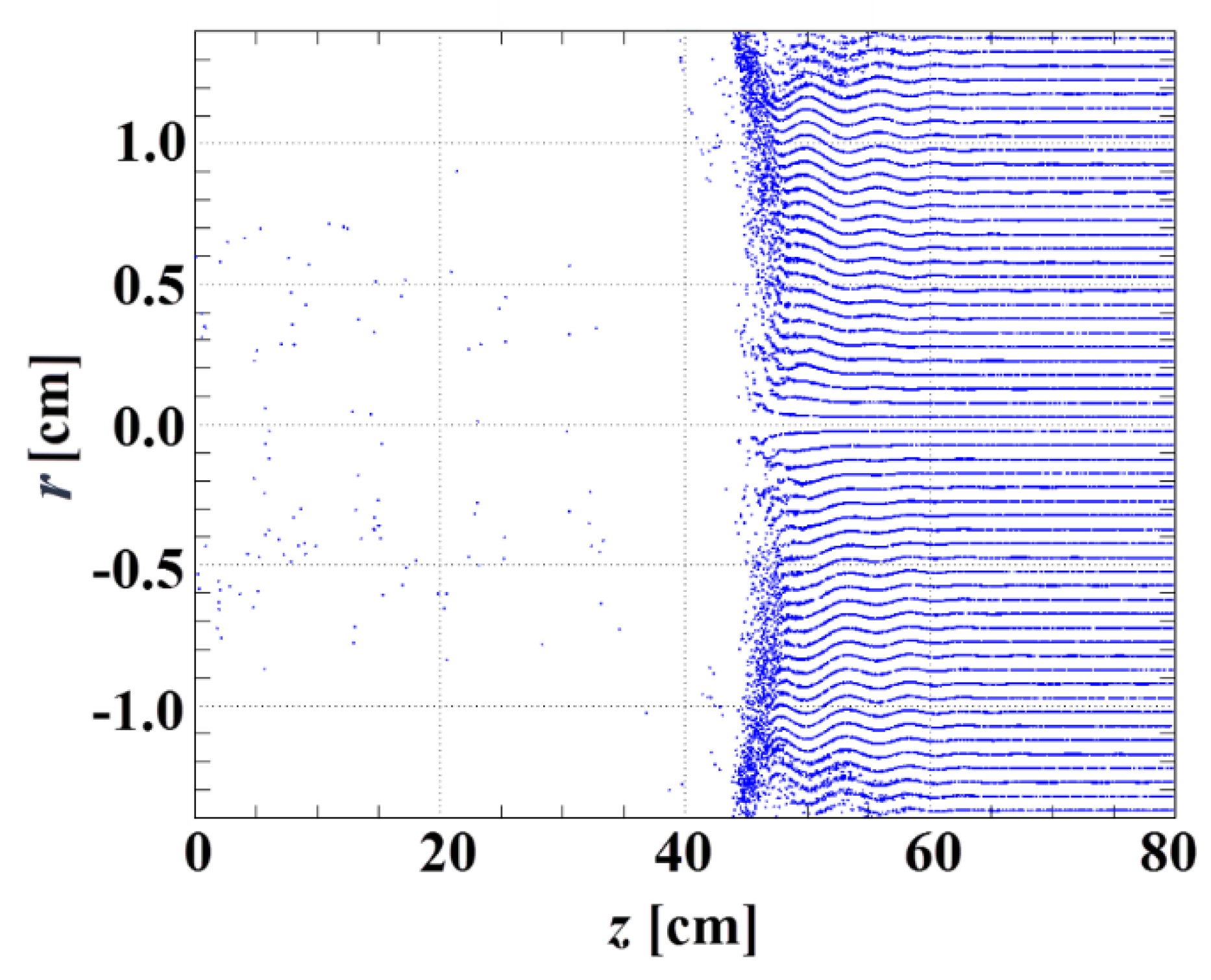
4. Wakefield Experiments
5. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Tajima, T.; Dawson, J.M. Laser Electron Accelerator. Phys. Rev. Lett. 1979, 43, 267–270. [Google Scholar] [CrossRef]
- Esaray, E.; Schroeder, C.; Lemans, W. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 2009, 81, 1229–1285. [Google Scholar]
- Malka, V. Laser plasma accelerators. Phys. Plasmas 2012, 19, 055501. [Google Scholar] [CrossRef]
- Leemans, W.P.; Nagler, B.; Gonsalves, A.J.; Toth, C.; Nakamura, K.; Geddes, C.G.R.; Esarey, E.; Schroeder, C.B.; Hooker, S.M. GeV electron beams from a centimetre-scale accelerator. Nat. Phys. 2006, 2, 696–699. [Google Scholar]
- Siders, C.W.; le Blanc, S.P.; Fisher, D.; Tajima, T.; Downer, M.W.; Babine, A.; Stepanov, A.; Sergeev, A. Laser wakefield excitation and measurement by femtosecond longitudinal interferometry. Phys. Rev. Lett. 1996, 76, 3570–3573. [Google Scholar] [CrossRef] [PubMed]
- Buck, A.; Nicolai, M.; Schmid, K.; Sears, C.M.S.; Sävert, A.; Mikhailova, J.M.; Krausz, F.; Kaluza, M.C.; Veisz, L. Real-time observation of laser-driven electron acceleration. Nat. Phys. 2011, 7, 543–548. [Google Scholar]
- Mangles, S.P.D.; Murphy, C.D.; Najmudin, Z.; Thomas, A.G.R.; Collier, J.L.; Dangor, A.E.; Divall, E.J.; Foster, P.S.; Gallacher, J.G.; Hooker, C.J.; et al. Monoenergetic beams of relativistic electrons from intense laser–plasma interactions. Nature 2004, 431, 535–538. [Google Scholar] [CrossRef]
- Litos, M.; Adli, E.; An, W.; Clarke, C.I.; Clayton, C.E.; Corde, S.; Delahaye, J.P.; England, R.J.; Fisher, S.; Frederico, J.; et al. High-efficiency acceleration of an electron beam in a plasma wakefield accelerator. Nature 2014, 515, 92–95. [Google Scholar]
- Matlis, N.H.; Reed, S.; Bulanov, S.S.; Chvykov, V.; Kalintchenko, G.; Matsuoka, T.; Rousseau, P.; Yanovsky, V.; Maksimchuk, A.; Kalmykov, S.; et al. High-efficiency acceleration of an electron beam in a plasma wakefield accelerator. Nat. Phys. 2006, 2, 749–753. [Google Scholar] [CrossRef]
- Schwab, M.B.; Savert, A.; Jackel, O.; Polz, J.; Schnell, M.; Rinck, T.; Veisz, L.; Moller, M.; Hansinger, P.; Paulus, G.G.; et al. Few-cycle optical probe-pulse for investigation of relativistic laser-plasma interactions. Appl. Phys. Lett. 2013, 103, 191118. [Google Scholar]
- Ito, H.; Rajyaguru, C.; Yugami, N.; Nishida, Y.; Hosoya, T. Propagation characteristics and guiding of a high-power microwave in plasma waveguide. Phys. Rev. E 2004, 69, 066406. [Google Scholar] [CrossRef] [PubMed]
- Kichigin, G.N. Relativistic waves raised by explosions in space as sources of ultra-high-energy cosmic rays. Adv. Space Res. 2013, 2, 309–314. [Google Scholar] [CrossRef]
- Aria, A.K.; Malik, H.K. Wakefield Generation in a Plasma Filled Rectangular Waveguide. Open Plasma Phys. J. 2008, 1, 1–8. [Google Scholar] [CrossRef]
- Niknam, A.R.; Akhlaghipour, N. Microwave ponderomotive action on the inhomogeneous collisionless and collisional plasmas. Waves Rand. Compl. Med. 2013, 23, 183–199. [Google Scholar] [CrossRef]
- Nishida, Y.; Kusaka, S.; Yugami, N. Excitation of wakefield and electron acceleration by short microwave pulse. Phys. Scr. 1994, T52, 65–68. [Google Scholar] [CrossRef]
- Yugami, N.; Kusaka, S.; Nishida, Y. Observation of plasma-wave echoes in an ion-wave regime. Phys. Rev. E 1994, 49, 2276–2281. [Google Scholar] [CrossRef]
- Ito, H.; Nishida, Y.; Yugami, N. Formation of Duct and Self-Focusing in Plasma by High Power Microwave. Phys. Rev. Lett. 1996, 76, 4540–4543. [Google Scholar] [CrossRef]
- Kamal-Al-Hassan, M.; Ito, J.; Yugami, N.; Nishida, Y. Dynamic of ion density perturbations observed in a microwave-plasma interaction. Phys. Plasmas 2005, 12, 112307. [Google Scholar] [CrossRef]
- Nishida, Y.; Ito, H.; Rajyaguru, C.; Yugami, N. On the experiments of Surfatron concept with use of capillary plasma. Aip Conf. Proc. 2004, 737, 957. [Google Scholar]
- Martins, S.F.; Fonseca, R.A.; Lu, W.; Mori, W.B.; Silva, L.O. Exploring laser-wakefield-accelerator regimes for near-term lasers using particle-in-cell simulation in Lorentz-boosted frames. Nat. Phys. 2010, 6, 311–316. [Google Scholar] [CrossRef]
- Holkundkar, A.; Brodin, G.; Marklund, M. Wakefield generation in magnetized plasmas. Phys. Rev. E 2011, 84, 036409. [Google Scholar] [CrossRef] [PubMed]
- Jha, P.; Saroch, A.; Mishra, R.K.; Upadhyay, A.K. Laser wakefield acceleration in magnetized plasma. Phys. Rev. St Accel. Beams 2012, 15, 081301. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Esirkepov, T.Z.; Kando, M.; Koga, J.K.; Hosokai, T.; Zhidkov, A.G.; Kodama, R. Nonlinear plasma wave in magnetized plasmas. Phys. Plasmas 2013, 20, 083113. [Google Scholar] [CrossRef]
- Shvets, G.; Wurtele, J.S.; Hur, M. Applications of Magnetized Plasma to Particle Acceleration. Aip Conf. Proc. 2002, 647, 681. [Google Scholar]
- Gad, R.; Leopold, J.G.; Fisher, A.; Fredkin, D.R.; Ron, A. Observation of Magnetically Induced Transparency in a Classical Magnetized Plasma. Phys. Rev. Lett. 2012, 108, 15503. [Google Scholar] [CrossRef] [PubMed]
- Beilin, L.; Shlapakovski, A.; Donskoy, M.; Queller, T.; Krasik, Y.E. Plasma density temporal evolution in a high-power microwave pulse compressor switch. Epl (Europhys. Lett.) 2015, 109, 25001. [Google Scholar] [CrossRef]
- Shlapakovski, A.S.; Beilin, L.; Hadas, Y.; Schamiloglu, E.; Krasik, Y.E. Self-consistent evolution of plasma discharge and electromagnetic fields in a microwave pulse compressor. Phys. Plasmas 2015, 22, 073111. [Google Scholar] [CrossRef]
- Ginzburg, N.S.; Novozhilova, N.Y.; Zotova, I.V.; Sergeev, A.S.; Peskov, N.Y.; Phelps, A.D.; Wiggins, S.M.; Cross, A.W.; Ronald, K.; He, W.; et al. Generation of powerful subnanosecond microwave pulses by intense electron bunches moving in a periodic backward wave structure in the superradiative regime. Phys. Rev. E Stat. Phys. Plasmasfluidsrelat. Interdiscip. Top. 1999, 60, 3297–3304. [Google Scholar] [CrossRef]
- Eltchaninov, A.A.; Korovin, S.D.; Rostov, V.V.; Pegel, I.V.; Mesyats, G.A.; Rukin, S.N.; Shpak, V.G.; Yaladin, M.I.; Ginzburg, N.S. Production of short microwave pulses with a peak power exceeding the driving electron beam power. Laser Part. Beams 2003, 21, 187–196. [Google Scholar] [CrossRef]
- Ginzburg, N.S.; Zotova, I.V.; Cross, A.W.; Phelps, A.D.R.; Yalandin, M.I.; Rostov, V.V. Generation, Amplification, and Nonlinear Self-Compression of Powerful Superradiance Pulses. IEEE Trans. Plasma Sci. 2013, 41, 646–660. [Google Scholar] [CrossRef]
- El’chaninov, A.A.; Korovin, S.D.; Rostov, V.V.; Pegel, I.V.; Mesyats, G.A.; Yalandin, M.I.; Ginzburg, N.S. Cherenkov superradiance with a peak power higher than electron flow power. JETP Lett. 2003, 77, 266–269. [Google Scholar] [CrossRef]
- Ginzburg, N.S.; Zotova, I.V.; Pegel, I.V.; Rostov, V.V.; Shpak, V.G.; Yalandin, M.I. Generation of high-power ultrashort electromagnetic pulses on the basis of effects of superradiance of electron bunches. Radiophys. Quantum Electron. 2007, 50, 762–779. [Google Scholar] [CrossRef]
- Rostov, V.V.; Totmeninov, E.M.; Yalandin, M.I. High-Power Relativistic Microwave Sources Based on the Backward Wave Oscillator with a Modulating Resonant Reflector. Radiophysics 2008, 78, 85–92. [Google Scholar] [CrossRef]
- Bogomolov, Y.L.; Lirin, S.F.; Semenov, V.E.; Sergeev, A.M. ionization self-channeling of extreme intense electromagnetic waves in a plasma. JETP Lett. 1987, 45, 680–683. [Google Scholar]
- Shafir, G.; Shlapakovski, A.; Siman-Tov, M.; Bliokh, Y.; Leopold, J.G.; Gleizer, S.; Gad, R.; Rostov, V.V.; Krasik, Y.E. High power microwave source for a plasma wakefield experiment. J. Appl. Phys. 2017, 121, 033301. [Google Scholar] [CrossRef]
- Rostov, V.V.; Romanchenko, I.V.; Pedos, M.S.; Rukin, S.N.; Sharypov, K.S.; Shpak, V.G.; Shunailov, S.A.; Yalandin, M.I. Superradiant Ka-band Cherenkov oscillator with 2-GW peak power. Phys. Plasmas 2016, 23, 093103. [Google Scholar] [CrossRef]
- Cao, Y.; Bliokh, Y.; Leopold, J.G.; Rostov, V.; Slutsker, Y.; Krasik, Y.E. Wakefield excitation by a powerful sub-nanosecond 28.6 GHz microwave pulse propagating in a plasma filled waveguide. Phys. Plasmas 2019, 25, 023102. [Google Scholar] [CrossRef]
- Rukin, S.N. High-power nanosecond pulse generators based on semiconductor opening switches. Instrum. Exp. Tech. 1999, 42, 439–467. [Google Scholar]
- Shafir, G.; Kreif, M.; Gleizer, J.Z.; Gleizer, S.; Krasik, Y.E.; Gunin, A.V.; Kutenkov, O.P.; Pegel, I.V.; Rostov, V.V. Experimental research of different plasma cathodes for generation of high-current electron beams. J. Appl. Phys. 2015, 118, 193302. [Google Scholar] [CrossRef]
- Goplen, B.; Ludeking, L.; Smith, D.; Warren, G. User-configurable MAGIC for electromagnetic PIC calculations. Comp. Phys. Commun. 1995, 87, 54–86. [Google Scholar] [CrossRef]
- Shafir, G.; Zolotukhin, D.; Godyak, V.; Shlapakovski, A.; Gleizer, S.; Slutsker, Y.; Gad, R.; Bernshtam, V.; Ralchenko, Y.; Krasik, Y.E. Characterization of inductively coupled plasma generated by quadruple antenna. Plasma Sources Sci. Technol. 2017, 26, 025005. [Google Scholar] [CrossRef]
- Shafir, G.; Cao, Y.; Bliokh, Y.; Leopold, J.G.; Levko, D.; Rostov, V.; Gad, R.; Fisher, A.; Bernshtam, V.; Krasik, Y.E. The interaction of intense, ultra-short microwave beams with the plasma generated by gas ionization. Phys. Plasmas 2018, 25, 032308. [Google Scholar] [CrossRef]
- Shafir, G.; Krasik, Y.E.; Bliokh, Y.P.; Levko, D.; Cao, Y.; Leopold, J.G.; Rostov, V.; Gad, R.; Bernshtam, V.; Fisher, A. Ionization-Induced Self-Channeling of an Ultrahigh-Power Subnanosecond Microwave Beam in a Neutral Gas. Phys. Rev. Lett. 2018, 120, 135003. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Leopold, J.G.; Bliokh, Y.P.; Krasik, Y.E. Self-channeling of powerful microwave beams in preliminarily formed plasma. Phys. Plasmas 2018, 25, 103101. [Google Scholar] [CrossRef]
- Krasik, Y.E.; Weingarten, A. Energetic Electron and Ion Beam Generation in Plasma Opening Switches. IEEE Trans. Plasma Sci. 1998, 26, 208–219. [Google Scholar] [CrossRef]
- Burrell, C.F.; Kunze, H.-J. Two-photon absorption and stimulated Raman scattering on excited Helium atoms in a plasma. Phys. Rev. Lett. 1972, 29, 1445–1448. [Google Scholar] [CrossRef]
- Brizhinev, M.P.; Gavrilenko, V.P.; Egorov, S.V.; Eremin, B.G.; Kostrov, A.V.; Oks, E.A.; Shagiev, Y.M. Procedure for quasilocal measurements of electric fields in a plasma by using satellites of helium forbidden lines. Zh. Eksp. Teor. Fiz. 1983, 85, 893–908. [Google Scholar]
- Rebhan, U.; Wiegart, N.J.; Kunze, H.-J. Measurements of fluctuating electric fields by means of high frequency Stark effect in a laser excited lithium beam. Phys. Lett. 1981, 85, 228–230. [Google Scholar] [CrossRef]
- Shefer, R.E.; Bekefi, G. Stark broadening induced by the intense electric field of a pulsed relativistic magnetron. Phys. Fluids 1979, 22, 1584–1586. [Google Scholar] [CrossRef]
- Oks, E.A. Plasma spectroscopy with quasimonochromatic electric fields. Sov. Phys. Dokl. 1984, 29, 224–226. [Google Scholar]
- Kamp, A.; Himmel, G. Determination of rf electric in deuterium from satellite of Balmer lines field strengths structure. Appl. Phys. B 1988, 47, 177–185. [Google Scholar] [CrossRef]
- Polushkin, I.N.; Ryabikin, M.Y.; Shagiev, Y.M.; Yazenkov, V.V. Local microwave field measurements in plasmas by resonant laser-induced fluorescence of hydrogen atoms. Zh. Eksp. Teor. Fiz. 1985, 89, 1648–1655. [Google Scholar]
- Akhmedzhanov, R.A.; Polushkin, I.N.; Rostovstev, Y.V.; Ryabikin, M.Y.; Shagiev, Y.M.; Yazenkov, V.V. Observation of the fine structure of a hydrogen plasma in a microwave field by intracavity laser spectroscopy. Zh. Eksp. Teor. Fiz. 1986, 63, 52–58. [Google Scholar]
- Ralchenko, Y.; Janev, R.K.; Kato, T.; Fursa, D.V.; Bray, I.; de Heer, F.J. Electron-impact excitation and ionization cross sections for ground state and excited helium atoms. At. Data Nucl. Data Tables 2008, 94, 603–622. [Google Scholar] [CrossRef]
- Welch, D.R.; Rose, D.V.; Oliver, B.V.; Clark, R.E. Simulation techniques for heavy ion fusion chamber transport. Nucl. Instrum. Methods Phys. Res. Sect. A 2001, 464, 134–139. [Google Scholar] [CrossRef]
- Welch, D.R.; Rose, D.V.; Cuneo, M.E.; Campbell, R.B.; Mehlhorn, T.A. Integrated simulation of the generation and transport of proton beams from laser-target interaction. Phys. Plasmas 2006, 13, 063105. [Google Scholar] [CrossRef]
- Bliokh, Y.P.; Leopold, J.G.; Shafir, G.; Shlapakovski, A.; Krasik, Y.E. Wakefield in a waveguide. Phys. Plasmas 2018, 24, 063112. [Google Scholar] [CrossRef]
- Dogariu, A.; Goldberg, B.M.; O’Byrne, S.; Miles, R.B. Species-Independent Femtosecond Localized Electric Field Measurement. Phys. Rev. Appl. 2017, 7, 024024. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krasik, Y.E.; Leopold, J.G.; Shafir, G.; Cao, Y.; Bliokh, Y.P.; Rostov, V.V.; Godyak, V.; Siman-Tov, M.; Gad, R.; Fisher, A.; et al. Experiments Designed to Study the Non-Linear Transition of High-Power Microwaves through Plasmas and Gases. Plasma 2019, 2, 51-64. https://doi.org/10.3390/plasma2010006
Krasik YE, Leopold JG, Shafir G, Cao Y, Bliokh YP, Rostov VV, Godyak V, Siman-Tov M, Gad R, Fisher A, et al. Experiments Designed to Study the Non-Linear Transition of High-Power Microwaves through Plasmas and Gases. Plasma. 2019; 2(1):51-64. https://doi.org/10.3390/plasma2010006
Chicago/Turabian StyleKrasik, Yakov E., John G. Leopold, Guy Shafir, Yang Cao, Yuri P. Bliokh, Vladislav V. Rostov, Valery Godyak, Meytal Siman-Tov, Raanan Gad, Amnon Fisher, and et al. 2019. "Experiments Designed to Study the Non-Linear Transition of High-Power Microwaves through Plasmas and Gases" Plasma 2, no. 1: 51-64. https://doi.org/10.3390/plasma2010006
APA StyleKrasik, Y. E., Leopold, J. G., Shafir, G., Cao, Y., Bliokh, Y. P., Rostov, V. V., Godyak, V., Siman-Tov, M., Gad, R., Fisher, A., Bernshtam, V., Gleizer, S., Zolotukhin, D., & Slutsker, Y. (2019). Experiments Designed to Study the Non-Linear Transition of High-Power Microwaves through Plasmas and Gases. Plasma, 2(1), 51-64. https://doi.org/10.3390/plasma2010006






