Abstract
This work shows a three-dimensional (3D) layerwise model for static and free vibration analyses of functionally graded piezomagnetic materials (FGPM) spherical shell structures where magnetic and elastic fields are completely coupled. The 3D magneto-elastic governing equations for spherical shells are made of the three equations of equilibrium in three-dimensional form and the three-dimensional divergence equation for the magnetic induction. Governing equations are written in the orthogonal mixed curvilinear reference system (, , z) allowing the analysis of several curved and flat geometries (plates, cylindrical shells and spherical shells) thanks to proper considerations of the radii of curvature. The static cases, actuator and sensor configurations and free vibration investigations are proposed. The resolution method uses the imposition of the Navier’s harmonic forms in the two in-plane directions and the exponential matrix methodology in the transverse normal direction. Single-layered and multilayered simply-supported FGPM structures have been investigated. In order to understand the behavior of FGPM structures, numerical values and trends along the thickness direction for displacements, stresses, magnetic potential, magnetic induction and free vibration modes are proposed. In the results section, a first assessment phase is proposed to demonstrate the validity of the formulation and to fix proper values for the convergence of results. Therefore, a new benchmark section is presented. Different cases are proposed for several material configurations, load boundary conditions and geometries. The possible effects involved in this problem (magneto-elastic coupling and effects related to embedded materials and thickness values of the layers) are discussed in depth for each thickness ratio. The innovative feature proposed in the present paper is the exact 3D study of magneto-elastic coupling effects in FGPM plates and shells for static and free vibration analyses by means of a unique and general formulation.
1. Introduction
In aerospace structures, innovative materials can be employed in the design of the next generation of aircraft and spacecraft or in health monitoring. In this framework, smart structures (in particular, piezomagnetic smart structures) are always of great interest. The main peculiarity of smart structures is their own dual behavior: a sensor, when a mechanical load produces a magnetic field in output, and actuator, when a magnetic field produces specific values of deformations [1,2,3,4,5,6]. For this reason, a complete study the behavior of piezomagnetic smart structures is crucial in several applications such as those in the aerospace, biomedical, civil and automotive fields.
The present work is devoted to a closed-form solution for the 3D magneto-elastic static and free vibration investigations of spherical shells. The present three-dimensional magneto-elastic model allows to analyze different geometries such as plates, cylindrical shells and spherical shells made of at least one functionally graded piezomagnetic material (FGPM) layer. These analyses are possible thanks to the use of an orthogonal mixed curvilinear reference system and specific considerations regarding the radii of curvature of the proposed structures.
Researchers from all over the world have always demonstrated a strong interest in smart structures. For this reason, different analytical and numerical formulations for beams, plates and shells have been proposed in the past years. However, all these works have gaps in terms of generality, since they presented formulations developed only for particular geometries of structures and, therefore, a general model capable of analyzing plates, cylinders, cylindrical shells and spherical shells by means of a unique formulation is missing. In works [7,8], 3D free vibration and static analyses for functionally graded materials (FGMs), anisotropic and linear magneto-electro-elastic (MEE) plates were presented considering a semi-analytical finite element method (FEM). A series solution was assumed in the plane directions and the FEM procedure was adopted in the thickness direction. Esen and Özmen [9] investigated the thermal vibration and buckling behaviors of a porous nanoplate made of an FGM layer of barium-titanate and cobalt-ferrite. Haitao et al. [10] presented 3D coupled equations of MEE structures derived from the Hamilton principle where the problem of single sorts of variables was converted into double sorts of variables: The dynamic characteristics of simply supported FG MEE plates and pipes were studied. Hung et al. [11] investigated the natural vibration of MEE FG porous plates. The methodology involved a moving Kriging mesh-free method to analyze the MEE-FG porous plates composed of piezoelectric and piezomagnetic materials with distributions of porosity. Li et al. [12] considered a transversely isotropic FG MEE circular plate uniformly loaded. The displacements and electric potential were modeled by polynomials in radial coordinates. In [13], Pan and Han presented an exact solution for a simply supported multilayered rectangular plate made of FG, anisotropic and linear MEE materials. The homogeneous solution in each layer was obtained using the pseudo-Stroh formalism. Phoenix et al. [14] showed the analysis of multilayered plates embedding piezoelectric/magnetostrictive layers using layerwise mixed FEM derived from the Reissner mixed variational theorem. Ramirez et al. [15] calculated free frequencies for orthotropic MEE graded composite plates via two different approaches based on the concept of discrete layers. In [16], the frequency analysis of edge-cracked MEE FG plates was investigated using the extended FEM; first-order shear deformation theory, von Karman’s nonlinear strain-displacement equations and a modified power-law were considered. In [17], a higher-order finite element model for the static and free vibration analyses of thick and thin MEE plates was presented. Sladek et al. [18] presented a meshless local Petrov–Galerkin method based on the Reissner-Mindlin shear deformation theory for the analysis of FGM plates with a sensor or actuator MEE layer localized on the top surface of the structures. In [19], Thai et al. showed a nonlocal strain gradient isogeometric model for free vibration analyses of FG nanoplates made of MEE materials. Vinyas [20] showed a finite element model derived from Hamilton’s principle and applied to the vibrational behavior of porous FG MEE circular and annular plates. In [21], a finite element model was proposed to analyze FG MEE structures when hygrometric, thermal, magnetic, electric and elastic fields were coupled. In [22], a modified Pagano method was developed by Wu and Lu for the 3D dynamic response of simply supported, multilayered and FG MEE plates with three different lateral surface conditions. Xiao et al. [23] investigated the characteristics of elastic guided waves in an infinite FG MEE plate. The formulation was based on Hamilton’s principle with the Chebyshev spectral element method applied along the thickness direction to obtain the dispersion equation. In [24], a Reissner–Mindlin model was developed for heterogeneous multilayer laminates made of FG MEE material using the variational asymptotical method. A semi-analytical flexural analysis of FG MEE plates was proposed in [25], with material coefficients mathematically expressed as arbitrary functions in terms of in-plane coordinates utilizing the scaled boundary FEM in association with the precise integration method. Zheng and Wang [26] presented a theoretical model to describe a magnetic force arising from an interaction between the nonlinear magnetization of structures made of soft ferromagnetic materials and an external applied magnetic field. Thanks to the introduction of displacements, electric potential, magnetic potential and their dual counterparts as state variables, Zhao and Chen [27] proposed a symplectic analysis to solve the plane problem of FG MEE materials. A coupled multi-physical cell-based smoothed FEM which took into account the coupling effects among elastic, electric, magnetic and thermal fields was proposed by Zhou et al. [28] to investigate the static behavior of FG MEE structures under thermal conditions. In [29], Heyliger and Pan showed a mathematical formulation where the weak form of the equations of motion/equilibrium and Gauss law for magnetism were adopted for the static analysis of rectangular laminates with arbitrary edge boundary conditions. The same two authors [30] also proposed an analytical solution for free vibrations of 3D, linear anisotropic, MEE and multilayered rectangular plates under simply supported edge conditions; the general solution was obtained via the pseudo-Stroh formalism. Shishesaz et al. [31] proposed a general differential quadrature method based on classical plate theory where the radial and circumferential stresses in an annular FGM plate with a uniform thickness under a transverse axisymmetric load were investigated.
In the framework of curved structures, Bhangale and Ganesan [32,33] proposed the free vibration analysis for FG MEE non-homogeneous cylindrical shells by using a semi-analytical finite element formulation involving series solution in the circumferential and axial directions and finite elements in the radial direction. Annigeri et al. [34] presented a semi-analytical FE model for the influence of the piezomagnetic effect on the frequencies of clamped-clamped MEE cylindrical shells. Buckling and vibration analyses of FG magneto-electro-thermo-elastic circular cylindrical shells were investigated [35]. Ni et al. [36] presented an analytical buckling solution for a cylindrical shell made of two-phase magneto-electro-thermo-elastic composites under multi-physical fields. A solid-shell FE model for free vibrations of FG MEE plates and cylindrical shells was developed by Shijie et al. [37] on the basis of the assumed natural strain and enhanced assumed strain method. In [38], Tsai and et al. showed a 3D solution for the static analysis of doubly curved FG MEE shells considering an asymptotic approach. The same authors also proposed a 3D asymptotic free-vibration analysis with open-circuit surface conditions [39] and a static analysis under the action of mechanical loads, electric displacements and magnetic fluxes [40] for simply supported, doubly curved FG MEE shells. Zenkour et al. [41] proposed an electro-magneto-thermo-elastic analysis for an infinite FG hollow cylinder in the framework of the thermoelasticity theory. Zhao et al. [42] studied FGM shells with porosity using a FE formulation based on the first-order shear deformation theory for the evaluation of static and dynamic behavior under thermal loads. In [43], a fully geometrically nonlinear FEM formulation was proposed for the analysis of large deflections of FG carbon nanotubes reinforced with MEE materials. The first-order shear deformation theory and strain–displacement relations of large rotations were employed. Zhen and Wang [44] developed a theoretical model for soft ferromagnetic shells to describe their magneto-elastic behavior when a magnetic field was applied. Pezzulla et al. [45] developed a 2D reduced model for hard-magnetic, thin, linear-elastic shells that could be actuated through an external magnetic field, with geometrically exact strain measures and assuming a reduced kinematics model based on Kirchhoff–Love assumptions.
The present article is devoted to the analysis of the behavior of FGPM smart structures using three-dimensional coupled magneto-elastic equations for spherical shell panels. The proposed model is a general three-dimensional layer-wise model able to investigate the magneto-elastic coupling in several geometries (plates, cylinders and cylindrical/spherical shells) including different lamination schemes embedding classical and functionally graded piezomagnetic materials. These investigations are possible by means of a unified and general formulation. The 3D set of equations for the magneto-elastic problem is composed of the three 3D equilibrium equations and the 3D divergence equation for the magnetic induction for spherical shells. The present set of four 3D second-order differential equations is solved considering harmonic forms in the in-plane directions for displacements and magnetic potential and the exponential matrix method in the thickness direction. This formulation is an extension of the electro-elastic model for piezoelectric multilayered structures proposed in [46,47] and the magneto-elastic model for classical piezomagnetic multilayered smart structures proposed in [48].
2. 3D Coupled Magneto-Elastic Equations for Spherical Shells
In the present section, a coupled model for the 3D magneto-elastic problem regarding spherical shells is proposed. In the first two subsections, the three 3D equilibrium equations and the 3D divergence equation for magnetic induction are presented for spherical shell panels as a set of four second-order differential equations governing the 3D coupled magneto-elastic problem. These equations are written specifically for FGPM structures in an orthogonal reference system having two curved in-plane coordinates and a rectilinear transverse normal coordinate. This reference system degenerates from that for spherical shells to that for plates with easy consideration of the radii of curvature and . In Figure 1, all possible geometries are clearly indicated with the related reference middle surface and curvilinear-rectilinear orthogonal reference system and . This set of equations has four basic variables: the three displacements u, v and w and the magnetic potential . In the last subsection, the resolution method involving harmonic forms and the exponential matrix method is described. Thanks to the proposed mathematical formulation, FGPM smart structures can be investigated for static and free frequency problems.
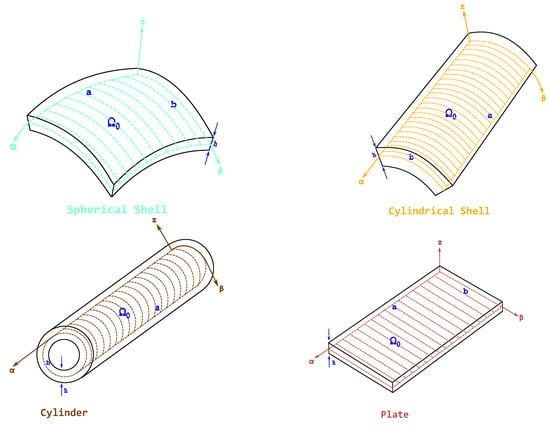
Figure 1.
Reference geometries for the proposed three-dimensional coupled elasto-magnetic formulation (3D-u-) and for proposed assessments and benchmarks.
2.1. Geometrical and Constitutive Relations
Geometrical and constitutive equations allow the connection between the magnetic and the elastic field. These equations are written as follows:
where is the strain vector, is the geometric matrix for displacements, is the displacement vector, is the magnetic field vector, is the geometrical matrix for magnetic fields for spherical shells, is the scalar magnetic potential, is the stress vector, is the elastic coefficient matrix in the structural reference system for functionally graded materials, is the piezomagnetic coefficient matrix for functionally graded materials, is the magnetic induction vector and is the magnetic permittivity coefficient matrix for functionally graded materials. Superscripts k and T in Equations (1) and (2) identify a general physical layer of the structure and the transpose of a matrix, respectively.
As can be seen in Equation (1), matrices and involve the curvature terms and that can be written as follows:
In matrices and , the z dependence is obvious, as and terms are included. In the thickness direction, the z axis is rectilinear and no curvature is involved: This feature means . The variable z written in Equation (3) varies from to but it is also possible to include a shifted coordinate called that goes from 0 to h. h is the global thickness of the structure. Terms and are radii of curvature evaluated on the reference surface in the and directions, respectively.
In order to perform a closed-form solution for the proposed three-dimensional magneto-elastic formulation, only 0° and 90° orthotropic angles are possible. Therefore, the following coefficients in matrices , and must be set to zero:
2.2. Governing Equations for Static and Free Vibration Analysis
The present subsection is devoted to the presentation of the 3D governing equations for the magneto-elastic problem for spherical panels. The set of equations comprises the three 3D equations of equilibrium and the 3D equation of divergence for magnetic induction. The 3D divergence magnetic induction equation has been proposed in analogy with [46] for the case of electric displacement.
The governing relations for the three-dimensional coupled magneto-elastic analysis of spherical panels are as follows:
is the mass density of each k layer. , and indicate the second derivatives in time of the three displacement components. Partial derivatives in the , and z directions are indicated as , and , respectively. The same set of 3D equations is also valid in the static case considering the inertial loads equal zero (they are all the second parts of Equations (4a)–(4c)).
2.3. Solution Procedure
The solution methodology for the three-dimensional magneto-elastic problem for FGPM structures can be performed when geometrical relations (Equation (1)) and constitutive equations (Equation (2)) are introduced in the 3D governing equations (Equation (4)). In this way, the three-dimensional magneto-elastic problem is proposed in terms of the basic variables and .
The resolution method consists in the imposition of harmonic forms for the four basic variables in the in-plane directions and :
The exponential term is equal to one when the static analysis is performed as the mechanical loads and magnetic potential are in steady-state conditions. Terms and are the maximum amplitudes for each primary variable. and are two numerical terms expressed as follows:
The inclusion of harmonic forms (Equation (5)) leads to a magneto-elastic problem where amplitudes , , and are the primary unknowns of the problem. Derivatives in the in-plane directions and can be exactly computed as trigonometric function derivatives are well known.
Governing equations regarding the 3D coupled magneto-elastic problem for FGPM structures become
Static and free frequency problems differ only for the and terms that include inertial loads in the case of free frequency analyses. These inertial loads are zero for static problems. Equation (7) comprises four differential equations of second order in z: They contain amplitudes, their first derivatives in z (subscript, ) and their second-order derivatives in z (subscript, ).
In order to conclude the resolution procedure, the exponential matrix methodology is adopted in the tranverse normal direction. In Equation (7), coefficients depend on the z because of the curvature terms and elastic, piezomagnetic and permittivity coefficients for FGPMs. The exponential matrix method can be applied if a system of first-order differential equations with constant coefficients is obtained. For this reason, in the thickness direction, a proper number of thin f fictitious layers for each k physical layer is introduced. Therefore, a generic fictitious layer will be named as j and the total number of fictitious layers will be . In each j layer, elastic, piezomagnetic and magnetic permittivity properties and curvature terms are defined as constant. If the mathematical formulation is proposed for a common j fictitious layer, no differences are involved in the equations. In order to have a set of first-order differential equations, the three-dimensional governing Equation (7) is redoubled by also adding and as primary variables. This feature makes this resolution method very powerful as stresses, strains, magnetic field components and magnetic induction components along transverse normal direction can be exactly calculated.
The redoubling of primary variables in Equation (7) results in a set of eight differential equations of first order in z having constant coefficients written; its matrix form is
The explicit matrix form of Equation (8) can be seen in [46]. The solution of Equation (8), adopting the exponential matrix methodology, is
Interlaminar continuity conditions have to be imposed to perform a layer-wise approach. This approach is mandatory in order to correctly depict the trends of basic variables through the thickness direction, stresses, strains and magnetic induction. Interlaminar continuity conditions are valid for both static and free frequency problems. The explicit form is here written as follows:
The interlaminar continuity conditions state the continuity at each interface for displacements and magnetic potential (congruence conditions) and for transverse shear/normal stresses and transverse normal magnetic induction (equilibrium conditions). t indicates the top of the layer and b indicates the bottom of the layer j. The interlaminar continuity conditions can be written in matrix form as follows:
Considering a recursive introduction of Equation (11) in Equation (9), the complete solution along the thickness direction of the structure can be computed as follows:
considers all the peculiarities of the structural configuration in terms of geometry and material properties. In addition, it even includes the layer-wise approach thanks to the transfer matrices computed for each interface. Despite the chosen total number M of fictitious layers, computation always gives a matrix.
Simply supported boundary conditions must be imposed at the edges of the structure as follows:
Considering harmonic forms of Equation (5), these boundary conditions are automatically satisfied at the edges.
Load boundary conditions have also to be imposed. Regarding the 3D static analysis, two different load boundary conditions can be imposed: the first ones for the sensor configuration (Equation (15)) and the second ones for the actuator configuration (Equation (16)):
As the presented model adopts a closed-form solution, the explicit form of the transverse normal mechanical load is also harmonic:
A compact form for the load boundary conditions in the case of static and free vibration analysis can be written as
considering and as the load boundary matrices at the external surfaces of the structure.
Introducing Equation (12) in Equation (18), Equations (18) and (19) can be compacted as follows:
For static configurations, the solution of the linear system in Equation (20) evaluates basic variables at the bottom of the first mathematical layer. Introducing recursively Equation (11) in Equation (9), the computation of the unknown trends in the thickness direction occurs.
For the free vibration analysis cases, vector is zero. Therefore, the minimum eigenvalue of matrix that makes the space null must be found out. Having found this value, eigenvalues and the respective eigenvectors that depict circular frequencies and connected vibration modes, respectively, for the structure can be computed. In the same way, as described for the static case, the computation of unknown thickness modes along the thickness direction, starting from the bottom of the first layer, can be performed by introducing recursively Equation (11) in Equation (9).
Free vibration analysis in closed circuit configuration considers zero imposed magnetic potential at external surfaces (). Free vibration analysis in open circuit configuration considers zero imposed transverse normal magnetic induction at external surfaces ().
The proposed formulation has been implemented in the Matlab R2022a environment within an in-house academic software called 3DES (3D Elasticity Solutions) which was initially developed only for pure elastic problems and then subsequently extended to multi-field problems.
3. Results
In this section, an “Assessments” part and a “New Benchmarks” part are proposed. In the “Assessments” part, the proposed formulation is validated by means of comparisons with other three-dimensional magneto-elastic results obtainable from the open literature. The assessment part is mandatory in order to deeply know the potentiality of the proposed 3D-u- model (this acronym comes from the main peculiarities of the model: a 3D formulation with displacements u and magnetic potential as primary variables). The 3D-u- model has been assessed in terms of elasto-magnetic coupling, material and thickness layer effects (for both static and free frequency analyses). This first step is also mandatory to set the correct values of fictitious layers and the order of the exponential matrix to have convergent results. Then, considering these values, a new benchmark step is proposed. In this second subsection, new cases are shown involving all possible geometries (plates, cylindrical shells and spherical shells) embedding at least one functionally graded piezomagnetic material (FGPM). The aim of this section is to provide reference results for those scientists interested in the smart piezomagnetic structures behavior. These results can also be used to validate further 2D/3D numerical and analytical models regarding magneto-elastic problems.
3.1. Assessments
Five different assessment cases involving different geometries and material configurations are proposed in the present subsection. Material layer configurations can be single-layered FGPM, single-layered magnetostrictive material and single-layered FGM. Single-layered configuration was obtained as a degeneration of the FGPM configuration. In addition, 3D models available in the literature regarding piezomagnetic structures are not so numerous; some assessment cases can take into account only FG non-piezomagnetic materials. The assessment cases proposed are always related to simply supported boundary conditions for both static and free frequency analyses.
For both flat and curved panels, a total number of fictitious layers has been adopted and the exponential matrix has been truncated at the third order () according to the Taylor approximation of Equation (9). These two values, as stated in previous work by Brischetto and Torre [49], are always sufficient to obtain convergent results.
The first assessment (A1) is an open-circuit () static analysis of a FGPM thick square plate. A transverse normal mechanical load is applied at the top. The bottom of the plate is made of magnetostrictive material and the top is made of piezoelectric material. The FGP law along the thickness direction for mechanical, piezomagnetic and magnetic permittivity coefficients is [8]
where is the volume fraction of the top phase, are Young moduli, are shear moduli, are Poisson ratios, are piezomagnetic coefficients and are magnetic permittivities. Mechanical, piezomagnetic and magnetic permittivity values regarding and are collected in Table 1. Column A1 in Table 2 shows data for geometry, half-wave number couples and load conditions for boundaries. In Table 3, three different exponential terms ( and ) are considered for comparisons with the reference solution. In Table 3, reference solution results have been obtained taking into account both tabular results and trends along the thickness direction given in [8]. The results shown in Table 3 are computed in and in-plane coordinates. For all investigated variables, it is possible to notice a very good accordance between the results provided by the reference solution and the proposed 3D-u- model. Thanks to this assessment case, magneto-elastic coupling and the correct depiction of the thickness layer effect can be considered confirmed in the case of static analyses for flat structures.

Table 1.
Elastic, piezomagnetic and permittivity properties for materials used in assessment and new benchmark cases.

Table 2.
Data for geometry, half-wave number couples and load conditions for boundaries for the five assessment cases.

Table 3.
Assessment 1, static analysis of a simply supported open-circuit single-layered FGP square plate. Maximum values through the thickness direction z in and .
The second assessment is devoted to an open-circuit ( T) free frequency analysis of a single-layered thick square plate. This configuration has been obtained as a degeneration of the A1 material case. The material properties are shown in the column in Table 1. The mass density of the material is constant through the thickness direction (). In the A2 column of Table 2, data for geometry and half-wave number couples for this assessment are shown. The reference solution used for comparisons is the 3D model for electro-magneto-elastic plates by Chen et al. [50]. In Table 4, the first four circular frequencies in non-dimensional form for are compared with the ones computed using the proposed 3D-u- formulation. The results shown in Table 4 state an accordance between the two different formulations. The results shown for this assessment permit to attest the validity of the 3D-u- model for the magneto-elastic free vibration analyses of piezomagnetic flat structures.

Table 4.
Assessment 2, free frequency analysis of a simply supported open-circuit single-layered square plate in . is the maximum elastic coefficient of matrix for the material.
The third assessment regards an open-circuit static analysis of a FG cylindrical panel. The bottom of the cylindrical panel is made of a metallic material (mechanical, piezomagnetic and magnetic permittivity properties are reported in the metallic column of Table 1) and the top is made of ceramic material (mechanical, piezomagnetic and magnetic permittivity properties are reported in the ceramic column of Table 1). The FG laws are the same shown in the first assessment. Column A3 of Table 2 gives data for the geometry, half-wave number couples and load conditions for boundaries. The reference solution for this assessment is the quasi-3D layer-wise mechanical model proposed in [51]. Comparisons between the quasi-3D model in [51] and the proposed 3D-u- formulation are performed considering different thickness ratios and different p exponential values. As can be seen in Table 5, a very good match between the present 3D-u- model and the reference solution is highlighted. This assessment permits to validate the correct depiction of curvature terms and effects connected with the thickness of the layers for the case of static analysis involving FGMs.

Table 5.
Assessment 3, static analysis of a simply supported open-circuit single-layered FG cylindrical panel. The transverse normal displacement is evaluated in the middle of the thickness ().
The fourth assessment is devoted to the free vibration analysis of a closed-circuit () single-layered FG cylindrical panel. The same FGM configuration used for the third case is here adopted (metallic material at the bottom and ceramic material at the top). The mechanical, piezomagnetic and magnetic permittivity properties are reported in the proper columns of Table 1. Data for the geometry and half-wave number couples used for this assessment can be seen in column A4 of Table 2. The FGM laws used for this assessment are the same as those seen in Equation (21) for the first case, except for a different definition of the volume fraction and a different FGM law for the mass density :
where and . The reference solution is the 3D model by Zahedinejad et al. [52]. In Table 6, the first circular frequency in non-dimensional form is compared for different thickness ratios and different p values. The results proposed by the 3D-u- formulation are very similar to those proposed by the 3D reference solution [52]. For this reason, curvature terms and thickness layer effects can be considered as validated also in the case of magneto-elastic free vibration analysis for curved structures.

Table 6.
Assessment 4, free frequency analysis of a simply supported open-circuit single-layered FG cylindrical panel.
The last assessment takes into account an open-circuit () free vibration analysis of a single-layered FGPM spherical shell. The bottom layer is made of material and the top layer is made of material. The mechanical, piezomagnetic and magnetic permittivity properties of both constituent phases are collected in Table 1; the geometrical data and load conditions are collected under the A5 column in Table 2. The FGPM laws adopted are the following:
where the two mass densities are and . The reference solution is the 3D asymptotic approach for the free-vibration analysis of spherical shells by Tsai and Wu [39]. In Table 7, the first circular frequencies in non-dimensional form for four different exponential laws and for three different thickness ratios are compared. Very good conforming between the results given by the present formulation and the 3D asymptotic results in [39] is shown. In terms of percentage, the relative error is always around 1% for each presented case. This last assessment allows to validate the free-vibration analysis of curved structures involving FGPMs.

Table 7.
Assessment 5, free frequency analysis of a simply supported open-circuit single-layered FGP spherical shell. and are the elastic coefficient and the mass density of the material, respectively.
According to the presentation of these results and each comment at the end of each assessment case, the 3D-u- model can be considered validated for the static and free vibration analysis for flat and curved FGPM structures. Correct results are obtained when fictitious layers and truncation at the third order () of the exponential matrix are employed. Considering these two values, elasto-magnetic coupling, thickness and material layer effects are always properly evaluated for all thickness values and for both static and free frequency investigations.
3.2. New Benchmarks
In the present part, three new cases involving static and free frequency analysis of flat and curved panels have been proposed. As concerns static analyses, displacements, stresses, magnetic potential and transverse normal magnetic induction at several thickness locations are given in tabular form for several thickness ratios (from thick to thin panels). In addition, the trend along the thickness direction of the same six tabular variables is proposed in graphical form for moderately thin structures. In the case of free vibration analysis, the first three circular frequencies are presented for different half-wave numbers and different thickness ratios. Even for this case, thickness modes are proposed in graphical form for moderately thin structures. The aim of these new benchmark cases is to investigate elasto-magnetic coupling and effects connected with the embedded materials and the thickness of each layer for FGPM structures. As clearly stated in the assessments subsection, the tabular and graphical results are computed using fictitious layers and truncation at the third order () of the exponential matrix.
In the first benchmark (B1), the static analysis of a square FGPM plate is proposed. The actuator configuration has and values imposed at the external surfaces of the plate. The bottom of the plate is made of magnetostrictive material and the top is made of piezoelectric material. The mechanical and magnetic properties of both materials are collected in Table 1 under the related columns. The FGPM laws adopted in the thickness direction are the same as those already proposed in Equation (21). Geometrical data can be seen in Table 8 under the B1 column. In Table 9, the results for variables u, w, , , , , and are proposed for different thickness ratios (from thick to thin panels) and for three different p exponential terms ( and 2). In Figure 2, trends along the thickness direction for the same variables of Table 9 are proposed for and . Thanks to the opportune inclusion in the model of the interlaminar continuity conditions, no discontinuities are present for any of the presented variables: The mechanical and magnetic properties of the FGPM plate vary with continuity along the thickness direction. The correct imposition of the load boundary conditions for the actuator case can be seen in values of variable at the external surfaces ( and ). is zero at the top and bottom of the structure configuration because mechanical loads are not applied at the outer surfaces of the plate. For this benchmark, elasto-magnetic coupling and effects connected with the thickness of the layers are clearly shown in Table 9 and Figure 2.

Table 8.
Data for geometry, half-wave number couples and load conditions for boundaries for the three benchmark cases.

Table 9.
Benchmark 1, simply supported FGPM square plate. Actuator configuration.
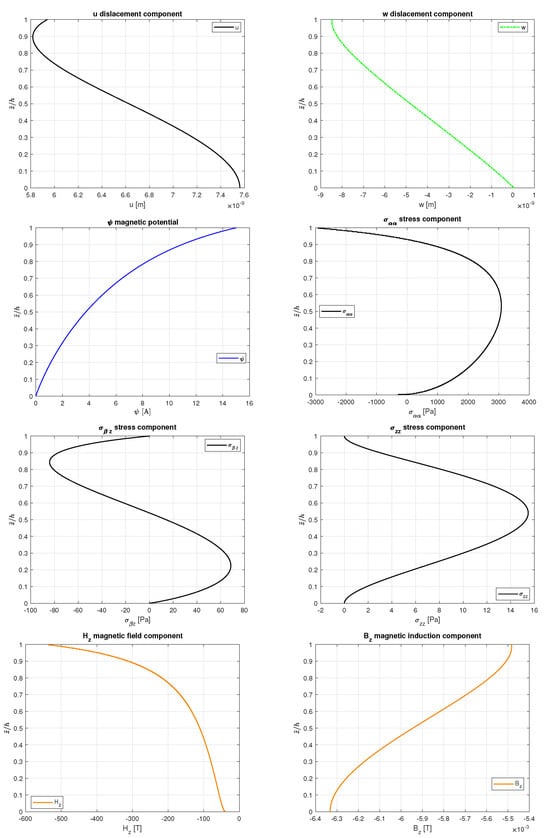
Figure 2.
Benchmark 1, simply supported FGPM square plate in actuator configuration. Thickness ratio and .
In the second benchmark (B2), a static analysis of a cylindrical shell made of FGPM is presented. The sensor configuration considers a transverse normal mechanical load imposed on the external surfaces ( Pa and Pa). The magnetic potential is not imposed as zero at external surfaces but it is free. The material configuration is the same as that proposed in the B1 case (bottom constituent is and top constituent is ). Both the mechanical and magnetic material properties are given in Table 1 and data for the geometry, half-wave number coupled and load conditions for boundaries are summarized in Table 8. Mechanical and magnetic FGPM laws are the same as those presented for the B1 case (see also Equation (21)). Table 10 shows the tabular results for different p values and different thickness ratios at specific locations for the following variables: v, w, , , , , and . The same variables as those in Table 10 are shown for and for in Figure 3. The trends in Figure 3 are typical of FGM structures as mechanical and magnetic properties continuously vary in the thickness direction according to the laws in Equation (21). Differently from multilayered structures, no changes in slope and/or discontinuities are present. So, it can be stated that interlaminar continuity conditions are correctly imposed. In addition, elasto-magnetic coupling and effects connected with the thickness of the layer are perfectly depicted. Load boundary conditions are satisfied considering the values at the top and at the bottom of the structure. No impositions at the outer surfaces on the magnetic potential profile are used, as can be seen from the trend along the thickness direction in Figure 3.

Table 10.
Benchmark 2, simply supported FGPM cylindrical shell. Sensor configuration.
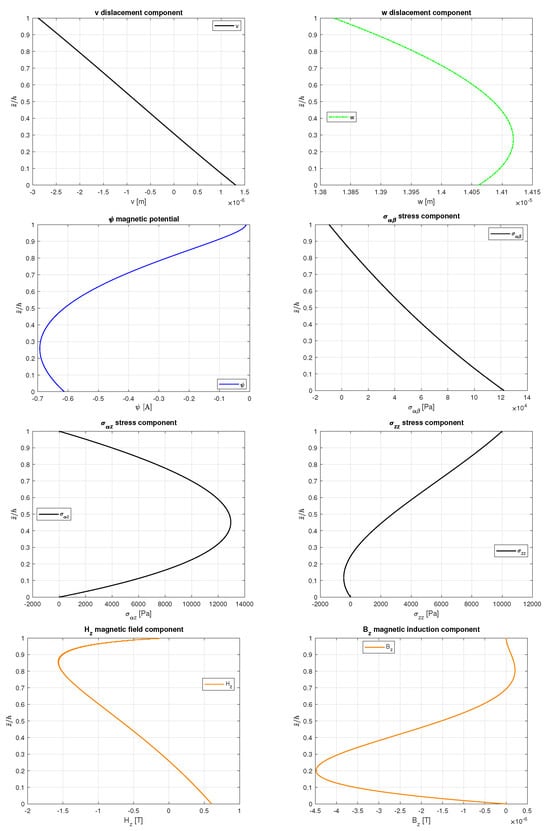
Figure 3.
Benchmark 2, simply supported FGPM cylindrical shell in sensor configuration. Thickness ratio and .
In the third benchmark (B3), an open-circuit ( T) free vibration analysis of a multilayered FGPM spherical shell is investigated. The bottom external lamina is totally made of magnetostrictive material, the top external lamina is totally made of piezoelectric material and the central lamina is made of FGPM. The thickness of each external lamina is h and the thickness of the central lamina is h (h is the total thickness). The FGPM laws in the thickness direction are the same as those presented for the B1 case (see also Equation (21)). Mass density has the following exponential law:
where and . The mechanical and magnetic properties of the two constituents are written explicitly in Table 1 under the and columns. The data for geometry are reported in Table 8 under the B3 column. In Table 11, the first three circular frequency values for different half-wave number couples and different thickness ratios are given by considering as an exponential term. It is possible to notice that the curvature effect of the configuration is clearly marked because the circular frequency related to the I mode decreases from thick to thin thickness ratios. In Figure 4, the thickness modes related to the first three vibration modes for half-wave numbers, and , are shown in terms of normalized values , , , and . The normalization is performed by dividing u, v, w, and by their own maximum values. From Figure 4, the correct imposition of the open-circuit conditions is clear in the trend, together with the thickness layer effect and the correct impositions of conditions for the interlaminar continuity.

Table 11.
Benchmark 3, simply supported multilayered FGPM spherical shell. First three circular frequencies for different half-wave number couples. Open-circuit configuration.
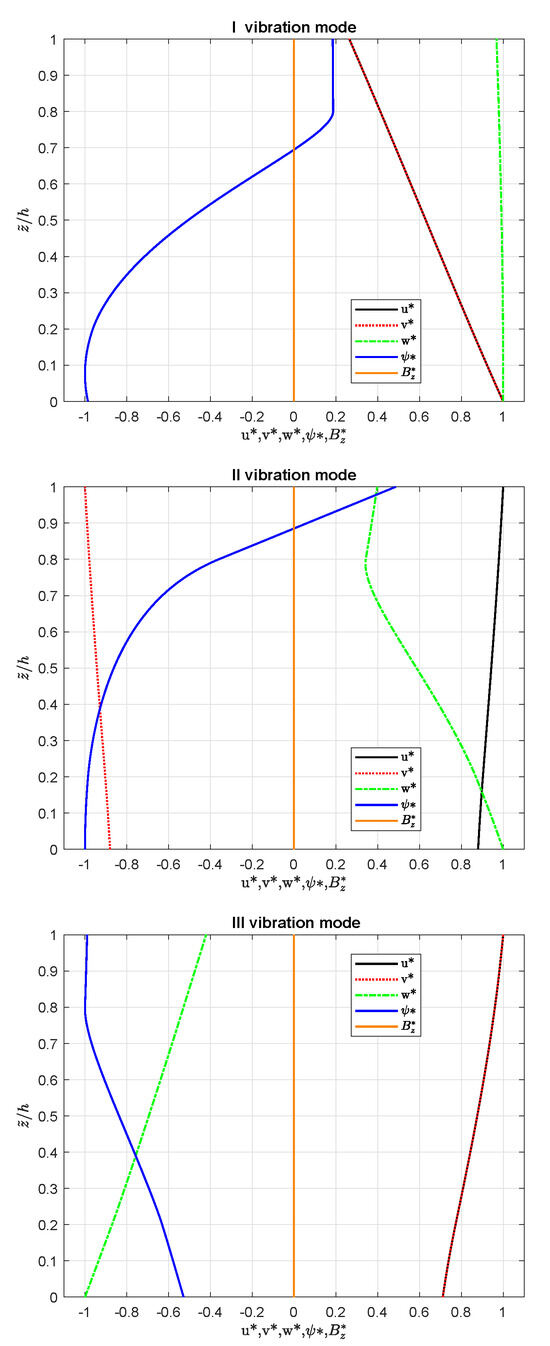
Figure 4.
Benchmark 3, simply-supported FGPM spherical shell in open-circuit configuration. First three thickness vibration modes for half-wave numbers. Thickness ratio and .
4. Conclusions
The present work shows an exact 3D coupled magneto-elastic analysis for shells and plates taking into account functionally graded piezomagnetic materials (FGPMs). The present model solves the 3D governing equations for the elasto-magnetic problem for spherical panels; the three three-dimensional equations of equilibrium are coupled with the three-dimensional equation of divergence for the magnetic induction. Static and free vibration problems are analyzed. The resolution method to solve the governing equations of the three-dimensional elasto-magnetic problem considers harmonic forms in the in-plane directions and the exponential matrix methodology in the thickness direction. The three-dimensional elasto-magnetic problem is solved in a closed-form solution: Only simply-supported structures can be solved. In the assessment part, the present three-dimensional mathematical formulation was validated considering other 3D magneto-elastic models from the literature for both static and free frequency investigations. Therefore, new benchmarks were discussed and presented in terms of elasto-magnetic variables (tabular and graphical forms) and in terms of circular frequencies. Different thickness ratios and several exponential laws for FGPMs are considered for each benchmark case. The present three-dimensional coupled elasto-magnetic model correctly describes all three-dimensional features in the static case and it correctly calculates circular frequencies and thickness vibration modes in the free vibration case. Functionally graded typical effects are perfectly evaluated thanks to a correct imposition of interlaminar continuity in terms of congruence and equilibrium conditions. The use of FGPM layers always allows the continuity of each variable through the thickness direction. The typical zigzag effect of multilayered structures is shown for both static and free frequency analyses. For both static and free frequency investigations, load boundary conditions are always satisfied. The present model can be adopted to understand the 3D behavior of FGPM spherical shell panels with the possibility to also analyze simpler geometries, such as plates and cylindrical shells, by simply considering proper radii of curvature. A future development of the proposed 3D model will be a 3D elasto-electro-magnetic model able to investigate the generation of a magnetic potential due to electric or mechanical loadings. Future developments will also consider the coupling of further physical fields such as thermal and hygroscopic ones and the finite element extension in order to consider further boundary conditions different from the simply supported ones, more complicated geometries and new materials different from the isotropic or orthotropic ones. The proposed 3D model is very suitable for a finite element extension because it is simple and light in terms of computational costs. The proposed 3D analytical results will be used as validation assessments for the future finite element extension where the Navier harmonic forms will be replaced by the shape functions and weak forms typical of the finite element formulation.
Author Contributions
Conceptualization, S.B.; methodology, S.B.; software, D.C.; validation, D.C.; formal analysis, S.B.; investigation, D.C.; resources, S.B.; data curation, S.B. and D.C.; writing—original draft preparation, D.C.; writing—review and editing, S.B.; visualization, S.B. and D.C.; supervision, S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arefi, M.; Zenkour, A.M. Effect of thermo-magneto-electro-mechanical fields on the bending behaviors of a three-layered nanoplate based on sinusoidal shear deformation plate theory. J. Sandw. Struct. Mater. 2019, 21, 639–669. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Zhao, Y.F.; Wang, X.; Chen, M.; Schmidt, R. Static and dynamic analysis of functionally graded magneto-electro-elastic plates and shells. Compos. Struct. 2022, 281, 114950. [Google Scholar] [CrossRef]
- Jiang, W.-W.; Gao, X.-W.; Liu, H.-Y. Multi-physics zonal Galerkin free element method for static and dynamic responses of functionally graded magneto-electro-elastic structures. Compos. Struct. 2023, 321, 117217. [Google Scholar] [CrossRef]
- Pang, Y.; Wang, Y.S.; Liu, J.X.; Fang, D.N. A study of the band structures of elastic wave propagating in piezoelectric/piezomagnetic layered periodic structures. Smart Mater. Struct. 2010, 19, 055012. [Google Scholar] [CrossRef]
- Esayas, L.S.; Kattimani, S. Effect of porosity on active damping of geometrically nonlinear vibrations of a functionally graded magneto-electro-elastic plate. Def. Technol. 2022, 18, 891–906. [Google Scholar] [CrossRef]
- Kattimani, S.; Joladarashi, S.; Mahesh, V. Geometrically nonlinear vibration attenuation of functionally graded magneto-electro-elastic shells. In Proceedings of the ASME 2019 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Louisville, KY, USA, 9–11 September 2019. [Google Scholar]
- Bhangale, R.K.; Ganesan, N. Free vibration of simply supported functionally graded and layered magneto-electro-elastic plates by finite element method. J. Sound Vib. 2006, 294, 1016–1038. [Google Scholar] [CrossRef]
- Bhangale, R.K.; Ganesan, N. Static analysis of simply supported functionally graded and layered magneto-electro-elastic plates. Int. J. Solids Struct. 2006, 43, 3230–3253. [Google Scholar] [CrossRef]
- Esen, I.; Özmen, R. Thermal vibration and buckling of magneto-electro-elastic functionally graded porous nanoplates using nonlocal strain gradient elasticity. Compos. Struct. 2022, 296, 115878. [Google Scholar] [CrossRef]
- Haitao, D.; Wei, C.; Mingzhi, L. Static/dynamic analysis of functionally graded and layered magneto-electro-elastic plate/pipe under Hamiltonian system. Chin. J. Aeronaut. 2008, 21, 35–42. [Google Scholar] [CrossRef]
- Hung, P.T.; Thai, C.H.; Phung-Van, P. A C0-HSDT free vibration of magneto-electro-elastic functionally graded porous plates using a moving Kriging meshfree method. Aerosp. Sci. Technol. 2023, 137, 108266. [Google Scholar] [CrossRef]
- Li, X.Y.; Ding, H.J.; Chen, W.Q. Three-dimensional analytical solution for functionally graded magneto–electro-elastic circular plates subjected to uniform load. Compos. Struct. 2008, 83, 381–390. [Google Scholar] [CrossRef]
- Pan, E.; Han, F. Exact solution for functionally graded and layered magneto-electro-elastic plates. Int. J. Eng. Sci. 2005, 43, 321–339. [Google Scholar] [CrossRef]
- Phoenix, S.S.; Satsangi, S.K.; Singh, B.N. Layer-wise modelling of magneto-electro-elastic plates. J. Sound Vib. 2009, 324, 798–815. [Google Scholar] [CrossRef]
- Ramirez, F.; Heyliger, P.R.; Pan, E. Discrete layer solution to free vibrations of functionally graded magneto-electro-elastic plates. Mech. Adv. Mater. Struct. 2006, 13, 249–266. [Google Scholar] [CrossRef]
- Sh, E.L.; Kattimani, S.; Trung, N.T. Frequency response analysis of edge-cracked magneto-electro-elastic functionally graded plates using extended finite element method. Theor. Appl. Fract. Mech. 2022, 120, 103417. [Google Scholar] [CrossRef]
- Moita, J.M.S.; Soares, C.M.M.; Soares, C.A.M. Analyses of magneto-electro-elastic plates using a higher order finite element model. Compos. Struct. 2009, 91, 421–426. [Google Scholar] [CrossRef]
- Sladek, J.; Sladek, V.; Krahulec, S.; Pan, E. Analyses of functionally graded plates with a magnetoelectroelastic layer. Smart Mater. Struct. 2013, 22, 035003. [Google Scholar] [CrossRef]
- Thai, C.H.; Fereira, A.M.J.; Nguyen-Xuan, H.; Hung, P.T.; Phung-Van, P. A nonlocal strain gradient isogeometric model for free vibration analysis of magneto-electro-elastic functionally graded nanoplates. Compos. Struct. 2023, 316, 117005. [Google Scholar] [CrossRef]
- Vinyas, M. On frequency response of porous functionally graded magneto-electroelastic circular and annular plates with different electro-magnetic conditions using HSDT. Compos. Struct. 2020, 240, 112044. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, L.; Chai, Y. The adaptive hygrothermo–magneto–electro–elastic coupling improved enriched finite element method for functionally graded magneto–electro–elastic structures. Thin-Walled Struct. 2024, 200, 111970. [Google Scholar] [CrossRef]
- Wu, C.-P.; Lu, Y.-C. A modified Pagano method for the 3D dynamic responses of functionally graded magneto-electro-elastic plates. Compos. Struct. 2009, 90, 363–372. [Google Scholar] [CrossRef]
- Xiao, D.; Han, Q.; Liu, Y.; Li, C. Guided wave propagation in an infinite functionally graded magnetoelectro-elastic plate by the Chebyshev spectral element method. Compos. Struct. 2016, 153, 704–711. [Google Scholar] [CrossRef]
- Yifeng, Z.; Lei, C.; Yu, W.; Xiaopin, Z.; Liangliang, Z. Asymptotical construction of a Reissner-like model for multilayer functionally graded magneto-electro-elastic plates. Compos. Struct. 2013, 96, 786–798. [Google Scholar] [CrossRef]
- Zhang, P.; Qi, C.; Fang, H.; Sun, X. A semi-analytical approach for the flexural analysis of in-plane functionally graded magneto-electro-elastic plates. Compos. Struct. 2020, 250, 112590. [Google Scholar] [CrossRef]
- Zheng, X.-J.; Wang, X. Analysis of magnetoelastic interaction of rectangular ferromagnetic plates with nonlinear magnetization. Int. J. Solids Struct. 2001, 38, 8641–8652. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, W.-Q. Plane analysis for functionally graded magneto-electro-elastic materials via the symplectic framework. Compos. Struct. 2010, 92, 1753–1761. [Google Scholar] [CrossRef]
- Zhou, L.; Li, M.; Tian, W.; Liu, P. Coupled multi-physical cell-based smoothed finite element method for static analysis of functionally graded magneto-electro-elastic structures at uniform temperature. Compos. Struct. 2019, 226, 111238. [Google Scholar] [CrossRef]
- Heyliger, P.R.; Pan, E. Static fields in magnetoelectroelastic laminates. AIAA J. 2004, 42, 1435–1443. [Google Scholar] [CrossRef]
- Heyliger, P.R.; Pan, E. Free vibrations of simply supported and multilayered magneto-electro-elastic plates. J. Sound Vib. 2002, 252, 429–442. [Google Scholar]
- Shishesaz, M.; Zakipour, A.; Jafarzadeh, A. Magneto-elastic analysis of an annular FGM plate based on classical plate theory using GDQ method. Lat. Am. J. Solids Struct. 2016, 13, 2736–2762. [Google Scholar] [CrossRef]
- Bhangale, R.K.; Ganesan, N. Free vibration of functionally graded non-homogeneous magneto-electro-elastic cylindrical shell. Int. J. Comput. Methods Eng. Sci. Mech. 2006, 7, 191–200. [Google Scholar] [CrossRef]
- Bhangale, R.K.; Ganesan, N. Free vibration studies of simply supported non-homogeneous functionally graded magneto-electro-elastic finite cylindrical shells. J. Sound Vib. 2005, 288, 412–422. [Google Scholar] [CrossRef]
- Annigeri, A.R.; Ganesan, N.; Swarnamani, S. Free vibrations of clamped–clamped magneto-electro-elastic cylindrical shells. J. Sound Vib. 2006, 292, 300–314. [Google Scholar] [CrossRef]
- Lang, Z.; Xuewu, L. Buckling and vibration analysis of functionally graded magneto-electro-thermo-elastic circular cylindrical shells. Appl. Math. Model. 2013, 37, 2279–2292. [Google Scholar] [CrossRef]
- Ni, Y.; Zhu, S.; Sun, J.; Tong, Z.; Zhou, Z.; Xu, X. Analytical buckling solution of magneto-electro-thermo-elastic cylindrical shells under multi-physics fields. Compos. Struct. 2020, 239, 112021. [Google Scholar] [CrossRef]
- Shijie, Z.; Yan, F.; Hongtao, W. Free vibration studies of functionally graded magneto-electro-elastic plates/shells by using solid-shell elements. J. Vibroeng. 2012, 14, 1787–1796. [Google Scholar]
- Tsai, Y.-H.; Wu, C.-P. Three-dimensional analysis of doubly curved functionally graded magneto-electro-elastic shells. Eur. J. Mech. Solids 2008, 27, 79–105. [Google Scholar] [CrossRef]
- Tsai, Y.-H.; Wu, C.-P. Dynamic responses of functionally graded magneto-electro-elastic shells with open-circuit surface conditions. Int. J. Eng. Sci. 2008, 46, 843–857. [Google Scholar] [CrossRef]
- Wu, C.-P.; Tsai, Y.-H. Static behavior of functionally graded magneto-electro-elastic shells under electric displacement and magnetic flux. Int. J. Eng. Sci. 2007, 45, 744–769. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I.A. Electro-magneto-thermo elastic response of infinite functionally graded cylinders without energy dissipation. J. Magn. Magn. Mater. 2015, 395, 123–129. [Google Scholar] [CrossRef]
- Zhao, Y.F.; Gao, Y.S.; Wang, X.; Markert, B.; Zhang, S.Q. Finite element analysis of functionally graded magneto-electro-elastic porous cylindrical shells subjected to thermal loads. Mech. Adv. Mater. Struct. 2023, 31, 4003–4018. [Google Scholar] [CrossRef]
- Zhao, Y.F.; Wang, X.; Zhao, G.Z.; Markert, B.; Zhang, S.Q. Large deflections of magneto-electro-elastic cylindrical shells reinforced with functionally graded carbon nanotubes. Mech. Adv. Mater. Struct. 2024, 31, 2494–2508. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, X. A magnetoelastic theoretical model for soft ferromagnetic shell in magnetic field. Int. J. Solids Struct. 2003, 40, 6897–6912. [Google Scholar] [CrossRef]
- Pezzulla, M.; Yan, D.; Reis, P.M. A geometrically exact model for thin magneto-elastic shells. J. Mech. Phys. Solids 2022, 166, 104916. [Google Scholar] [CrossRef]
- Brischetto, S.; Cesare, D. Three-dimensional vibration analysis of multilayered composite and functionally graded piezoelectric plates and shells. Compos. Struct. 2024, 346, 118413. [Google Scholar] [CrossRef]
- Brischetto, S.; Cesare, D. 3D electro-elastic static analysis of advanced plates and shells. Int. J. Mech. Sci. 2024, 280, 109620. [Google Scholar] [CrossRef]
- Brischetto, S.; Cesare, D. A 3D shell model for static and free vibration analysis of multilayered magneto-elastic structures. Thin-Walled Struct. 2025, 206, 112620. [Google Scholar] [CrossRef]
- Brischetto, S.; Torre, R. Effects of order of expansion for the exponential matrix and number of mathematical layers in the exact 3D static analysis of functionally graded plates and shells. Appl. Sci. 2018, 8, 110. [Google Scholar] [CrossRef]
- Chen, W.Q.; Lee, K.Y.; Ding, H.J. On free vibration of non-homogeneous transversely isotropic magneto-electro-elastic plates. J. Sound Vib. 2005, 279, 237–251. [Google Scholar] [CrossRef]
- Carrera, E.; Brischetto, S.; Cinefra, M.; Soave, M. Refined and advanced models for multilayered plates and shells embedding functionally graded material layers. Mech. Adv. Mater. Struct. 2010, 17, 603–621. [Google Scholar] [CrossRef]
- Zahedinejada, P.; Malekzadehb, P.; Farida, M.; Karami, G. A semi-analytical three-dimensional free vibration analysis of functionally graded curved panels. Int. J. Press. Vessel. Pip. 2010, 87, 470–480. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).