Free Vibration Characteristics of Functionally Graded Material (FGM) Beams on Three-Parameter Viscoelastic Foundation
Abstract
1. Introduction
2. Governing Differential Equations
2.1. Governing Equations of Dynamic System
2.2. Governing Equations of Damped Free Vibration System
3. MGDQ Method for Solving for Complex Characteristic Frequencies
3.1. Introduction of Beam Boundary Condition Control Parameters
3.2. Weighting Coefficients in the MGDQ Method
3.3. Unified Discretized Equations via the MGDQ Method
3.4. Complex Characteristic Frequency Equation
4. Analysis and Discussion
4.1. Validation of Numerical Results
4.2. Influence of GBT Order n on Output Response Parameters
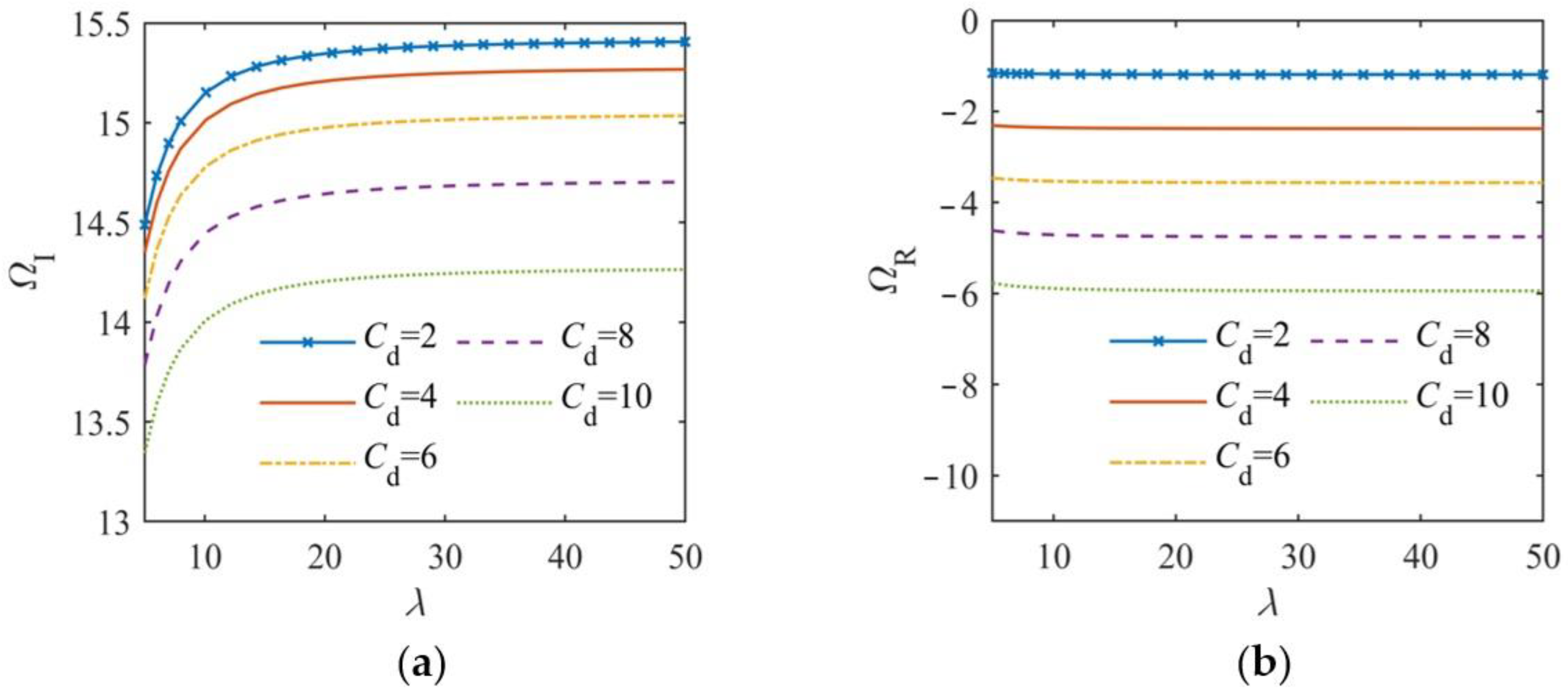
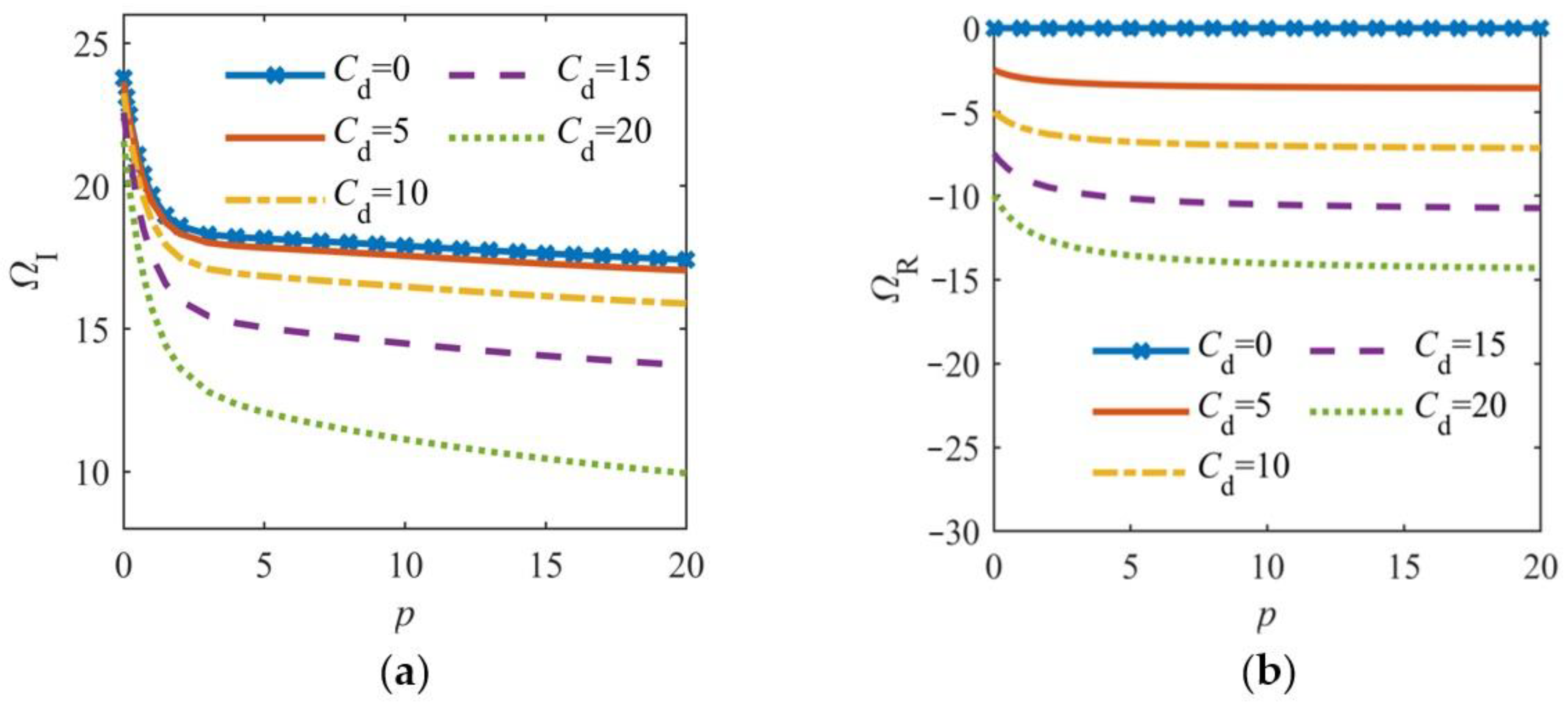
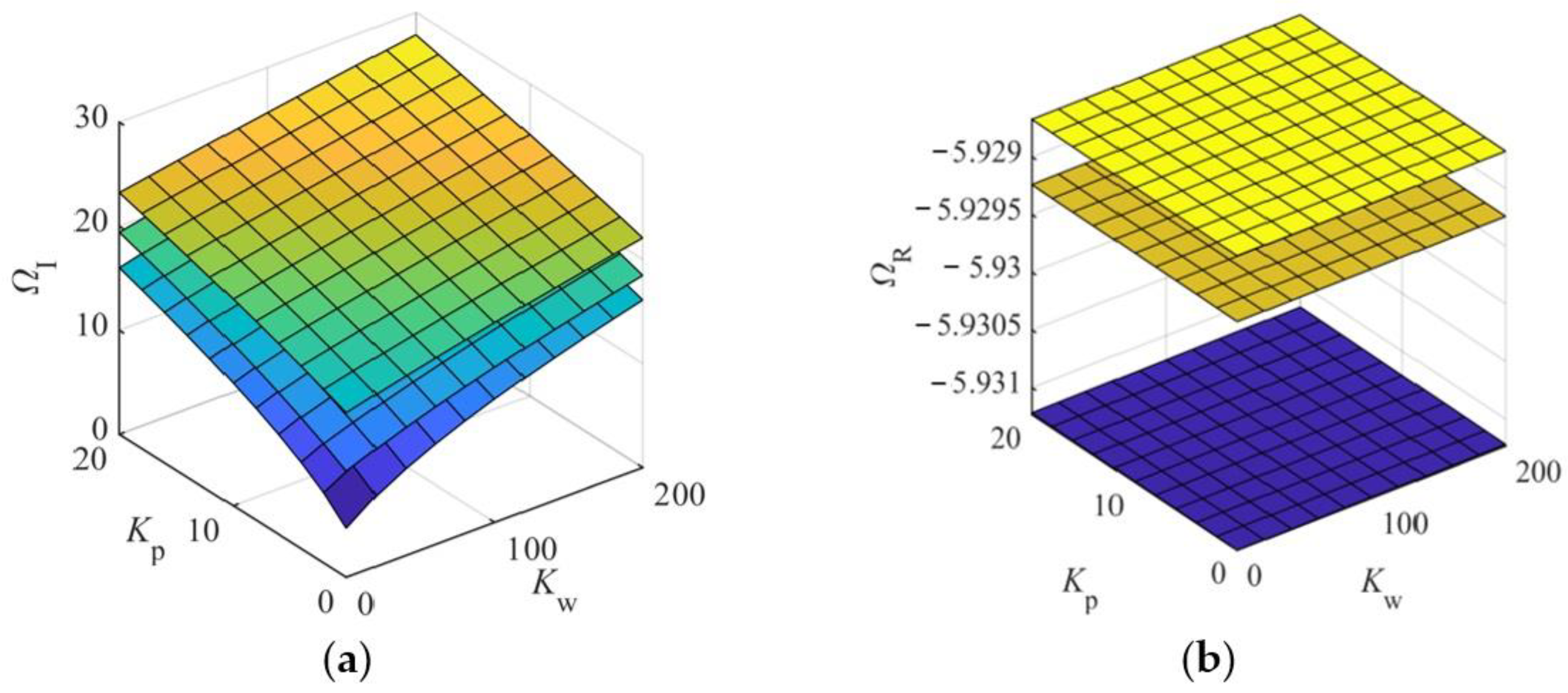
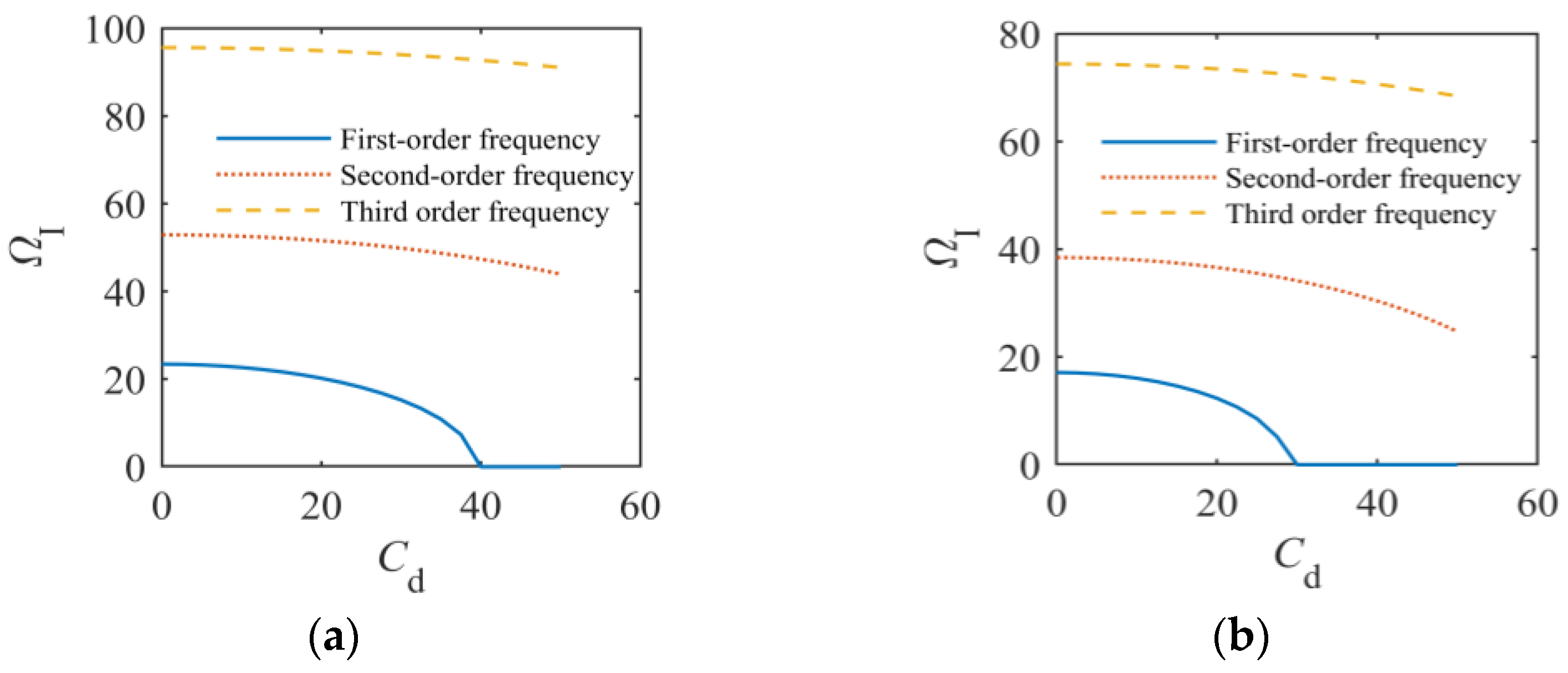
4.3. Influence of Other Factors on Output Response Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- De Rosa, M.A.; Maurizi, M.J. The Influence of Concentrated Masses and Pasternak Soil on the Free Vibrations of Euler Beams—Exact Solution. J. Sound Vib. 1998, 212, 573–581. [Google Scholar] [CrossRef]
- Zhou, H.; Jiang, J.; Zhang, T. Steady-state response of infinite beam on Kelvin foundation under moving loads. J. Zhejiang Univ. 2004, 38, 91–96. [Google Scholar]
- Ayvaz, Y.; Özgan, K. Application of Modified Vlasov Model to Free Vibration Analysis of Beams Resting on Elastic Foundations. J. Sound Vib. 2002, 255, 111–127. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, H.; Zhang, D.; Huang, X. Steady-state response of an infinite Euler-Bernoulli beam on Kerr foundation subjected to a moving oscillating load. J. Vib. Shock 2018, 37, 14–20. [Google Scholar] [CrossRef]
- Wang, C.M.; Lam, K.Y.; He, X.Q. Exact Solutions for Timoshenko Beams on Elastic Foundations Using Green’s Functions∗. Mech. Struct. Mach. 1998, 26, 101–113. [Google Scholar] [CrossRef]
- Chen, W.Q.; Lü, C.F.; Bian, Z.G. A Mixed Method for Bending and Free Vibration of Beams Resting on a Pasternak Elastic Foundation. Appl. Math. Model. 2004, 28, 877–890. [Google Scholar] [CrossRef]
- Thambiratnam, D.; Zhuge, Y. Dynamic Analysis of Beams on an Elastic Foundation Subjected to Moving Loads. J. Sound Vib. 1996, 198, 149–169. [Google Scholar] [CrossRef]
- Kim, S.-M.; Roesset, J.M. Dynamic Response of a Beam on a Frequency-Independent DAMPED elastic Foundation to Moving Load. Can. J. Civ. Eng. 2003, 30, 460–467. [Google Scholar] [CrossRef]
- Sun, L. A Closed-Form Solution of Beam on Viscoelastic Subgrade Subjected to Moving Loads. Comput. Struct. 2002, 80, 1–8. [Google Scholar] [CrossRef]
- Peng, L.; Ding, H.; Chen, L. Transverse free vibration of a beam resting on a three-parameter viscoelastic foundation. J. Vib. Shock 2014, 33, 101–105. [Google Scholar] [CrossRef]
- Zhang, D.; Lie, Y. Free vibration characteristics of an euler-bernoulli beam on a viscoelastic foundation based on nonlocal continuum theory. J. Vib. Shock 2017, 36, 88–95. [Google Scholar] [CrossRef]
- Sorrentino, S.; Fasana, A. Finite Element Analysis of Vibrating Linear Systems with Fractional Derivative Viscoelastic Models. J. Sound Vib. 2007, 299, 839–853. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Benyoucef, S.; Tounsi, A.; Benachour, A.; Bedia, E.A.A. On the Effect of the Micromechanical Models on the Free Vibration of Rectangular FGM Plate Resting on Elastic Foundation. Earthq. Struct. 2018, 14, 117–128. [Google Scholar] [CrossRef]
- Şimşek, M. Fundamental Frequency Analysis of Functionally Graded Beams by Using Different Higher-Order Beam Theories. Nucl. Eng. Des. 2010, 240, 697–705. [Google Scholar] [CrossRef]
- Kahya, V.; Turan, M. Finite Element Model for Vibration and Buckling of Functionally Graded Beams Based on the First-Order Shear Deformation Theory. Compos. Part B Eng. 2017, 109, 108–115. [Google Scholar] [CrossRef]
- Lesieutre, G.A.; Lee, U. A Finite Element for Beams Having Segmented Active Constrained Layers with Frequency-Dependent Viscoelastic Material Properties; Davis, L.P., Ed.; IOP Publishing Ltd.: San Diego, CA, USA, 1997; pp. 315–328. [Google Scholar]
- Trinh, L.C.; Vo, T.P.; Thai, H.-T.; Nguyen, T.-K. An Analytical Method for the Vibration and Buckling of Functionally Graded Beams under Mechanical and Thermal Loads. Compos. Part B Eng. 2016, 100, 152–163. [Google Scholar] [CrossRef]
- Pu, Y.; Zhou, F. Vibration and stability characteristics of FGM beams under thermal-mechanical loads based on a n-th generalized shear beam theory. J. Vib. Eng. 2020, 33, 64–73. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Jafari, A. A Four-Variable Refined Shear-Deformation Beam Theory for Thermo-Mechanical Vibration Analysis of Temperature-Dependent FGM Beams with Porosities. Mech. Adv. Mater. Struct. 2018, 25, 212–224. [Google Scholar] [CrossRef]
- Zhou, F.; Pu, Y. Dynamic behaviors of porous FGVM beams ubjected to thermal mechanical viscoelastic effects. Eng. Mech. 2021, 38, 16–26. [Google Scholar]
- Ying, J.; Lü, C.F.; Chen, W.Q. Two-Dimensional Elasticity Solutions for Functionally Graded Beams Resting on Elastic Foundations. Compos. Struct. 2008, 84, 209–219. [Google Scholar] [CrossRef]
- Pu, Y.; Teng, Z. Two-dimensional elasticity solutions for free vibration of FGM beams resting on Winkler-Pasternak elastic foundation. J. Vib. Shock 2015, 34, 74–79. [Google Scholar] [CrossRef]
- Zahedinejad, P. Free Vibration Analysis of Functionally Graded Beams Resting on Elastic Foundation in Thermal Environment. Int. J. Struct. Stab. Dyn. 2016, 16, 1550029. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, W.; Wei, H.; Chen, Y.Q. A Comparative Study of Constant-Order and Variable-Order Fractional Models in Characterizing Memory Property of Systems. Eur. Phys. J. Spec. Top. 2011, 193, 185–192. [Google Scholar] [CrossRef]
- Deng, H.; Chen, K.; Cheng, W.; Zhao, S. Vibration and Buckling Analysis of Double-Functionally Graded Timoshenko Beam System on Winkler-Pasternak Elastic Foundation. Compos. Struct. 2017, 160, 152–168. [Google Scholar] [CrossRef]
- Pu, Y.; Zhou, F. Vibration characteristics of FGM beams under the action of initial axial load based on a n-th generalized shear beam theory. J. Vib. Shock 2020, 39, 100–106. [Google Scholar] [CrossRef]
- Duc, N.D.; Quan, T.Q.; Luat, V.D. Nonlinear Dynamic Analysis and Vibration of Shear Deformable Piezoelectric FGM Double Curved Shallow Shells under Damping-Thermo-Electro-Mechanical Loads. Compos. Struct. 2015, 125, 29–40. [Google Scholar] [CrossRef]
- Loghman, E.; Kamali, A.; Bakhtiari-Nejad, F.; Abbaszadeh, M. Nonlinear Free and Forced Vibrations of Fractional Modeled Viscoelastic FGM Micro-Beam. Appl. Math. Model. 2021, 92, 297–314. [Google Scholar] [CrossRef]
- Pu, Y. Static and Dynamic Responses of Functionally Graded Micro-Beams Subjected to Multi-Field Coupling Effects. Ph.D. Thesis, Lanzhou University of Technology, Lanzhou, China, 2020. [Google Scholar]




| Boundary | Method | p = 0 | p = 0.2 | p = 1 | p = 10 |
|---|---|---|---|---|---|
| C-C | Ref. [14] * | 10.0705 | 9.46641 | 7.95034 | 6.16515 |
| This study | 10.0756 | 9.46932 | 7.95395 | 6.16797 | |
| S-S | Ref. [14] * | 5.15274 | 4.80924 | 3.99042 | 3.28160 |
| This study | 5.15274 | 4.80807 | 3.99041 | 3.28160 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, S.; Yang, G.; Pu, Y.; Ma, P.; Li, K. Free Vibration Characteristics of Functionally Graded Material (FGM) Beams on Three-Parameter Viscoelastic Foundation. J. Compos. Sci. 2025, 9, 215. https://doi.org/10.3390/jcs9050215
Jia S, Yang G, Pu Y, Ma P, Li K. Free Vibration Characteristics of Functionally Graded Material (FGM) Beams on Three-Parameter Viscoelastic Foundation. Journal of Composites Science. 2025; 9(5):215. https://doi.org/10.3390/jcs9050215
Chicago/Turabian StyleJia, Shuming, Guojiang Yang, Yu Pu, Pengfei Ma, and Kan Li. 2025. "Free Vibration Characteristics of Functionally Graded Material (FGM) Beams on Three-Parameter Viscoelastic Foundation" Journal of Composites Science 9, no. 5: 215. https://doi.org/10.3390/jcs9050215
APA StyleJia, S., Yang, G., Pu, Y., Ma, P., & Li, K. (2025). Free Vibration Characteristics of Functionally Graded Material (FGM) Beams on Three-Parameter Viscoelastic Foundation. Journal of Composites Science, 9(5), 215. https://doi.org/10.3390/jcs9050215








