Author Contributions
Conceptualization, K.C., J.N., H.M., M.W., and O.F.; methodology, O.F., M.S. and M.F.B.; formal analysis, O.F., and M.F.B.; investigation, O.F., K.C., and J.N.; resources, H.M. and M.W.; writing—original draft preparation, O.F., K.C., J.N. and M.F.B.; writing—review and editing, O.F., K.C., J.N., M.F.B., H.M., and M.W.; visualization, O.F., M.S. and M.F.B.; supervision, K.C. and J.N.; project administration, K.C.
Figure 1.
SEM observations of the 304L powder used in this work, showing its morphology at different magnifications: (a) 500 μm, (b) 190 μm, and (c) 100 μm.
Figure 1.
SEM observations of the 304L powder used in this work, showing its morphology at different magnifications: (a) 500 μm, (b) 190 μm, and (c) 100 μm.
Figure 2.
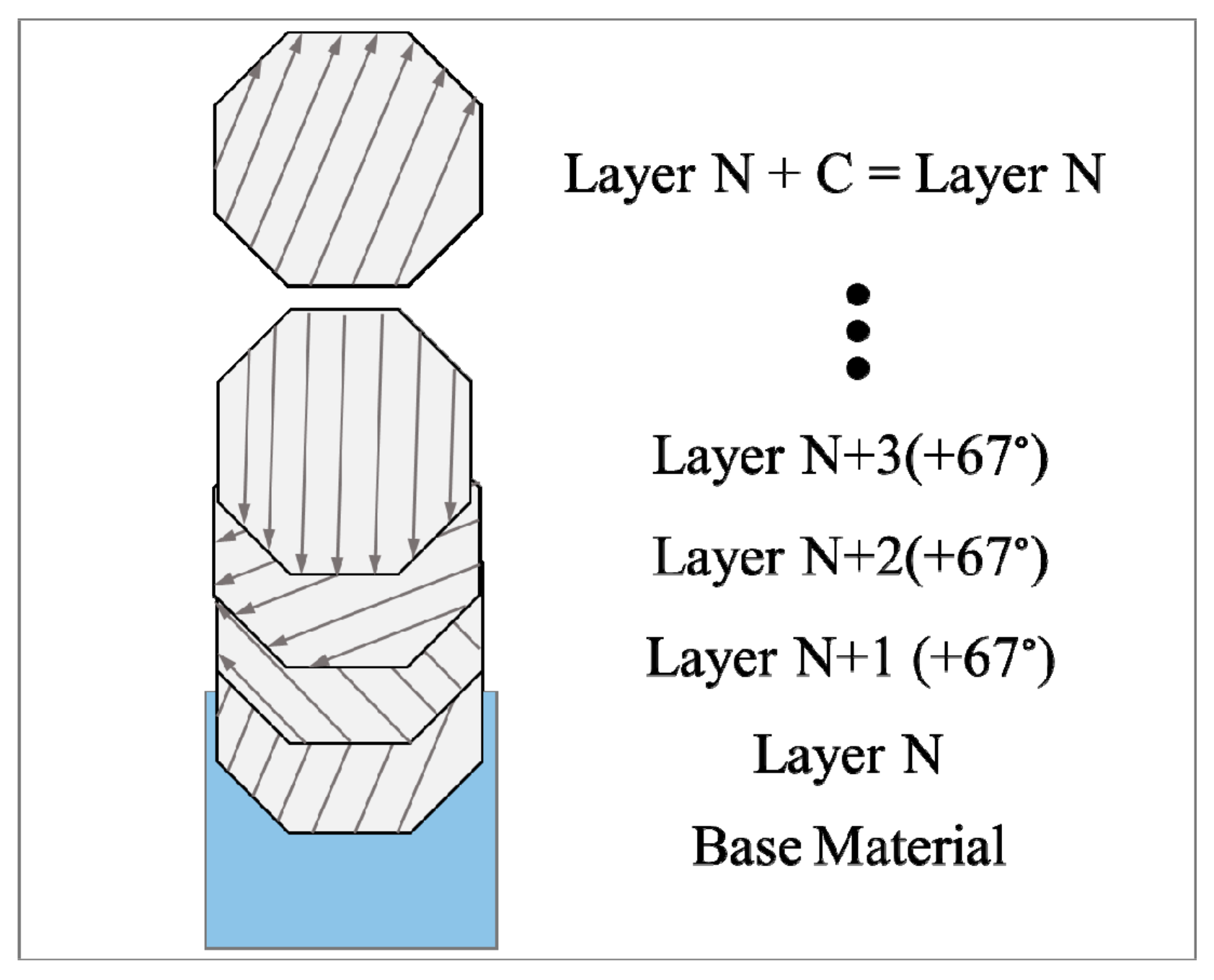
Schematic view of the scan direction in-between layers (configuration (f) in
Table 3).
Figure 2.
Schematic view of the scan direction in-between layers (configuration (f) in
Table 3).
Figure 3.
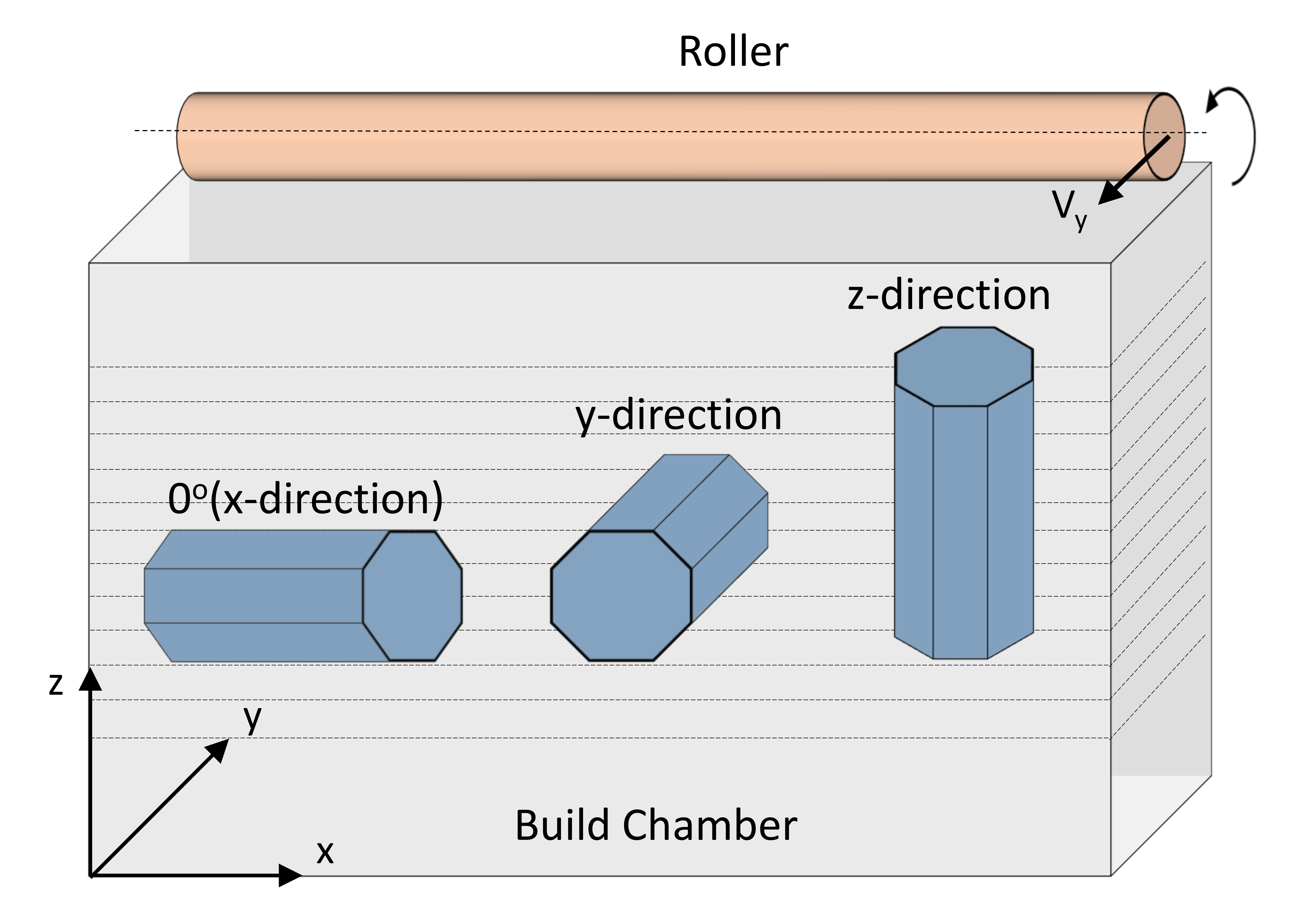
Schematic view of build orientations for manufacturing SLM parts.
Figure 3.
Schematic view of build orientations for manufacturing SLM parts.
Figure 4.
Major and minor Feret measurement illustration.
Figure 4.
Major and minor Feret measurement illustration.
Figure 5.
Microstructure side-by-side comparison of (a) 0°, (b) 67°, and (c) 105° hatch angle specimens built in the y-direction before compression test. Electrolytic etchant in 60:40 nitric acid:water solution.
Figure 5.
Microstructure side-by-side comparison of (a) 0°, (b) 67°, and (c) 105° hatch angle specimens built in the y-direction before compression test. Electrolytic etchant in 60:40 nitric acid:water solution.
Figure 6.
Close inspection of the 0° hatch angle, y-direction specimen showing the cellular structure and melt pool boundary, at two different magnifications: (a) 50 µm and (b) 10 µm.
Figure 6.
Close inspection of the 0° hatch angle, y-direction specimen showing the cellular structure and melt pool boundary, at two different magnifications: (a) 50 µm and (b) 10 µm.
Figure 7.
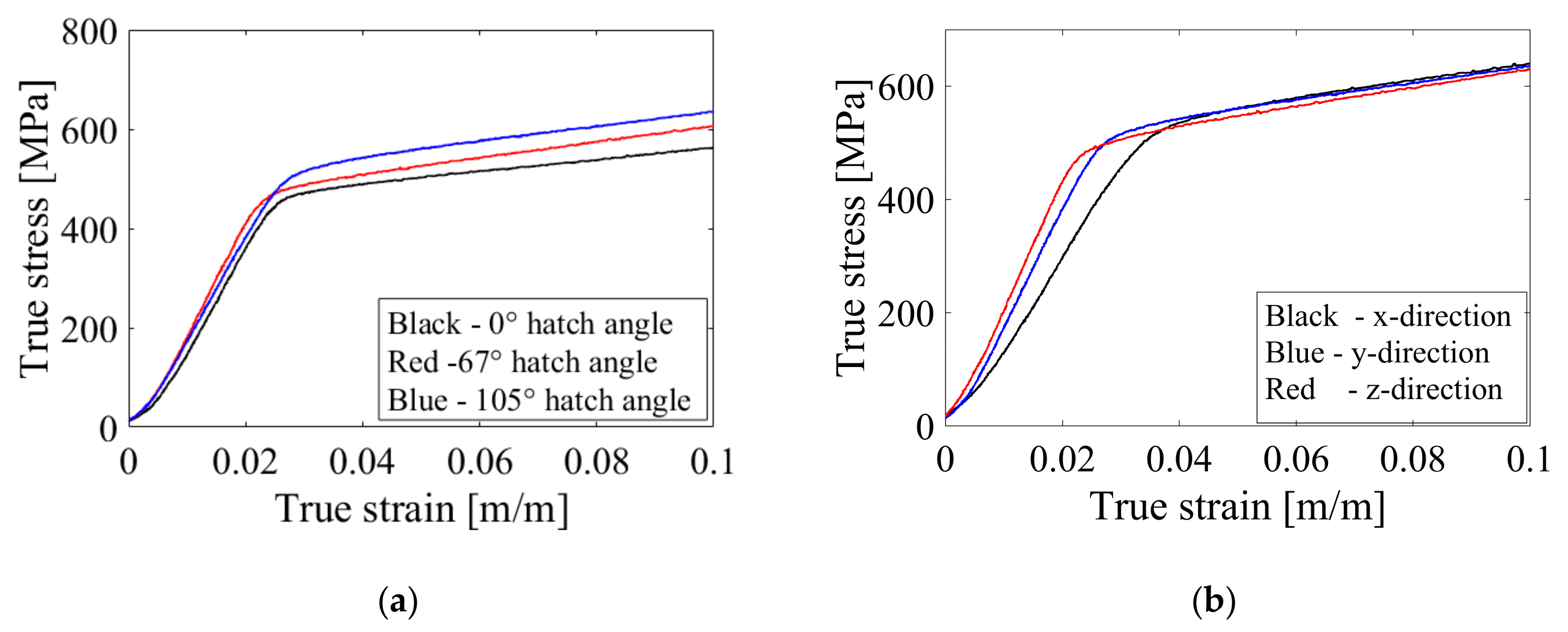
True stress–strain curve of SLM 304L stainless steel showing the elastic region: (a) samples built with three hatch angles in the y-direction, (b) samples built in three orientations using hatch angle of 105°.
Figure 7.
True stress–strain curve of SLM 304L stainless steel showing the elastic region: (a) samples built with three hatch angles in the y-direction, (b) samples built in three orientations using hatch angle of 105°.
Figure 8.
Geometry of untested and tested samples (where a–c equals samples built with a 0° hatch angle in the x-, y-, and z-direction, respectively, d–f equals samples built with a 67° hatch angle in the x-, y-, and z-direction, respectively, and g–i equals samples built with a 105° hatch angle in the x-, y-, and z-direction, respectively).
Figure 8.
Geometry of untested and tested samples (where a–c equals samples built with a 0° hatch angle in the x-, y-, and z-direction, respectively, d–f equals samples built with a 67° hatch angle in the x-, y-, and z-direction, respectively, and g–i equals samples built with a 105° hatch angle in the x-, y-, and z-direction, respectively).
Figure 9.
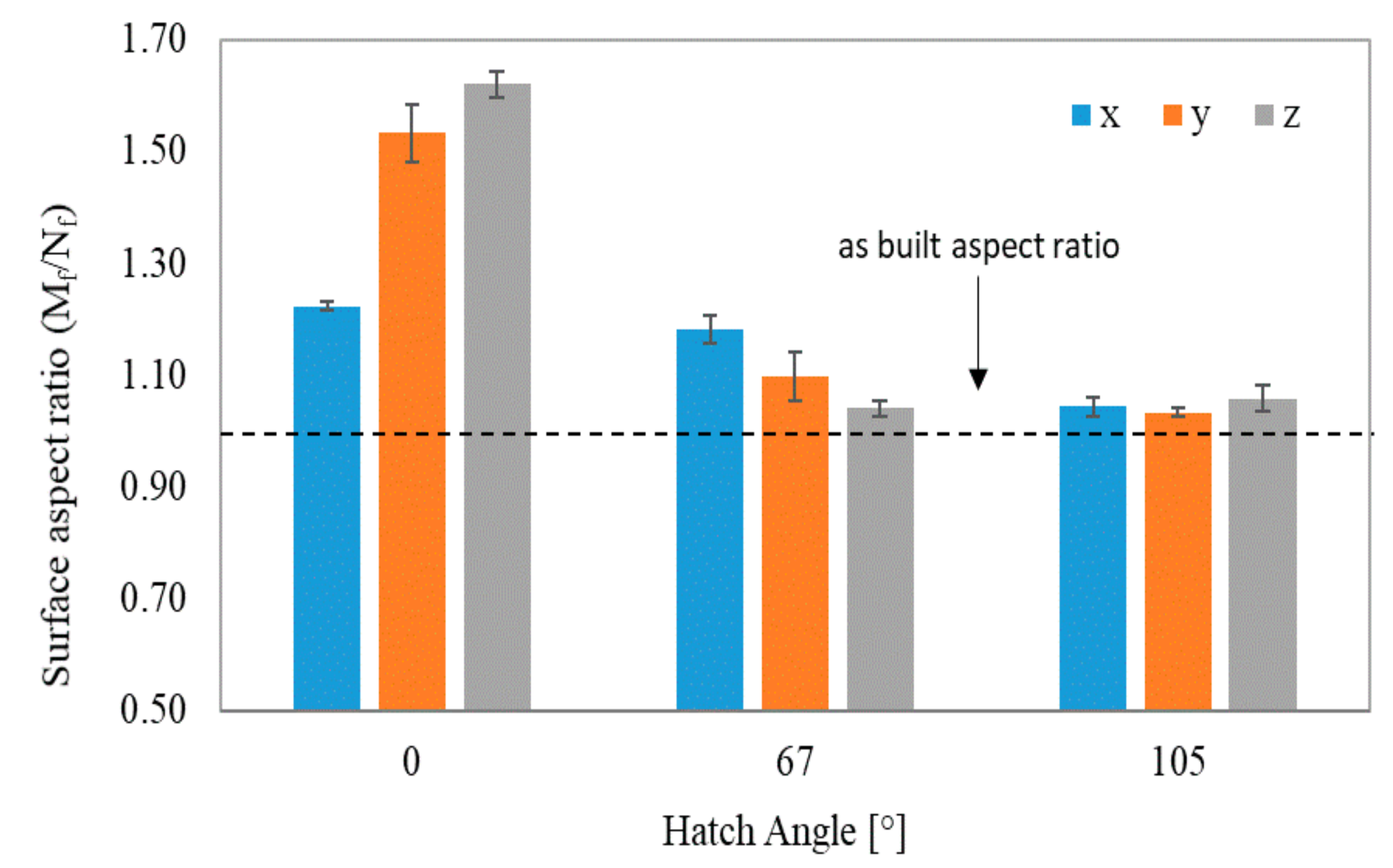
Surface aspect ratio comparison of compressed samples built using different hatch angles and build orientations.
Figure 9.
Surface aspect ratio comparison of compressed samples built using different hatch angles and build orientations.
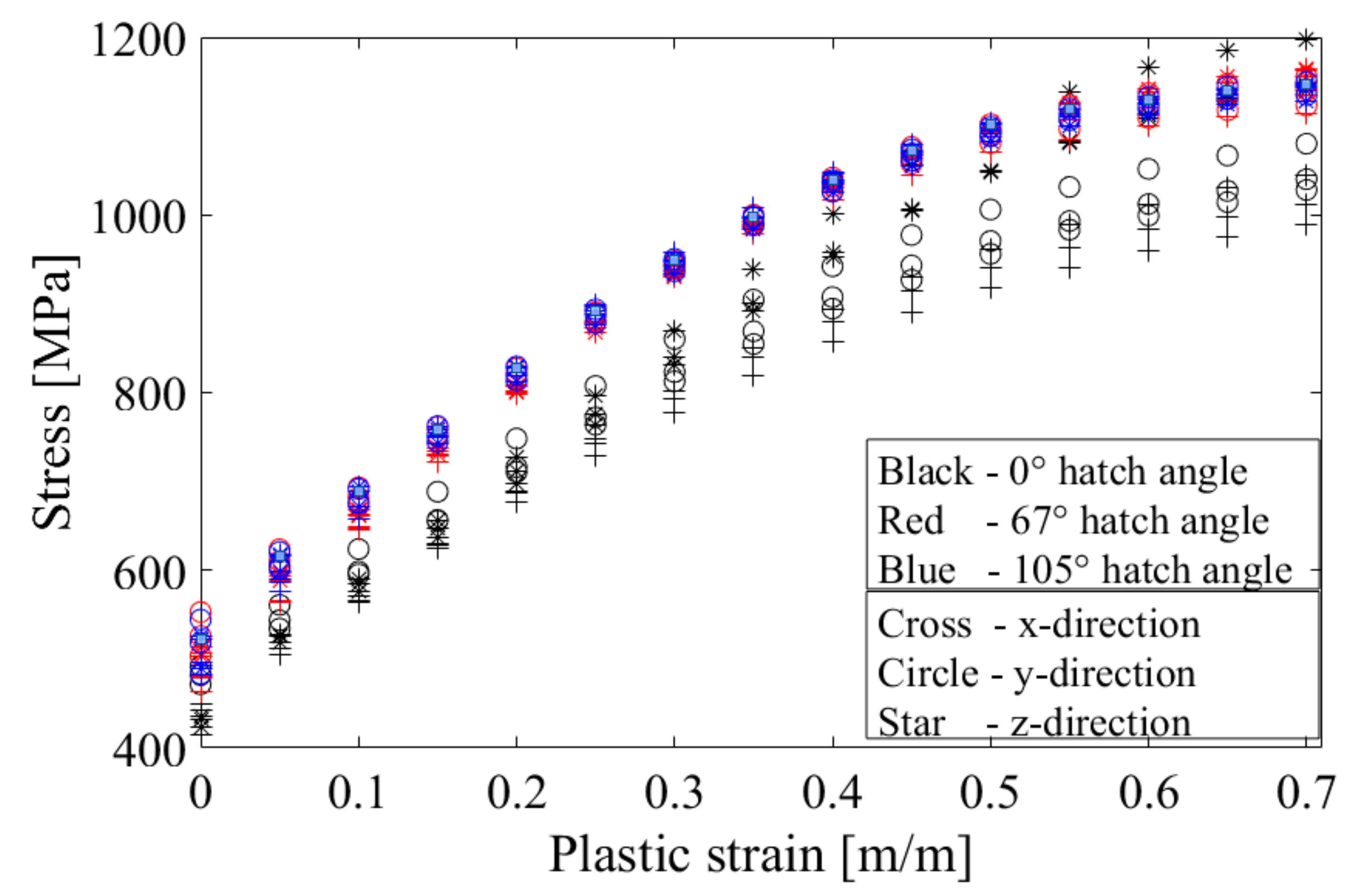
Figure 10.
Plastic true stress–strain curve showing the compressive results for all tested conditions.
Figure 10.
Plastic true stress–strain curve showing the compressive results for all tested conditions.
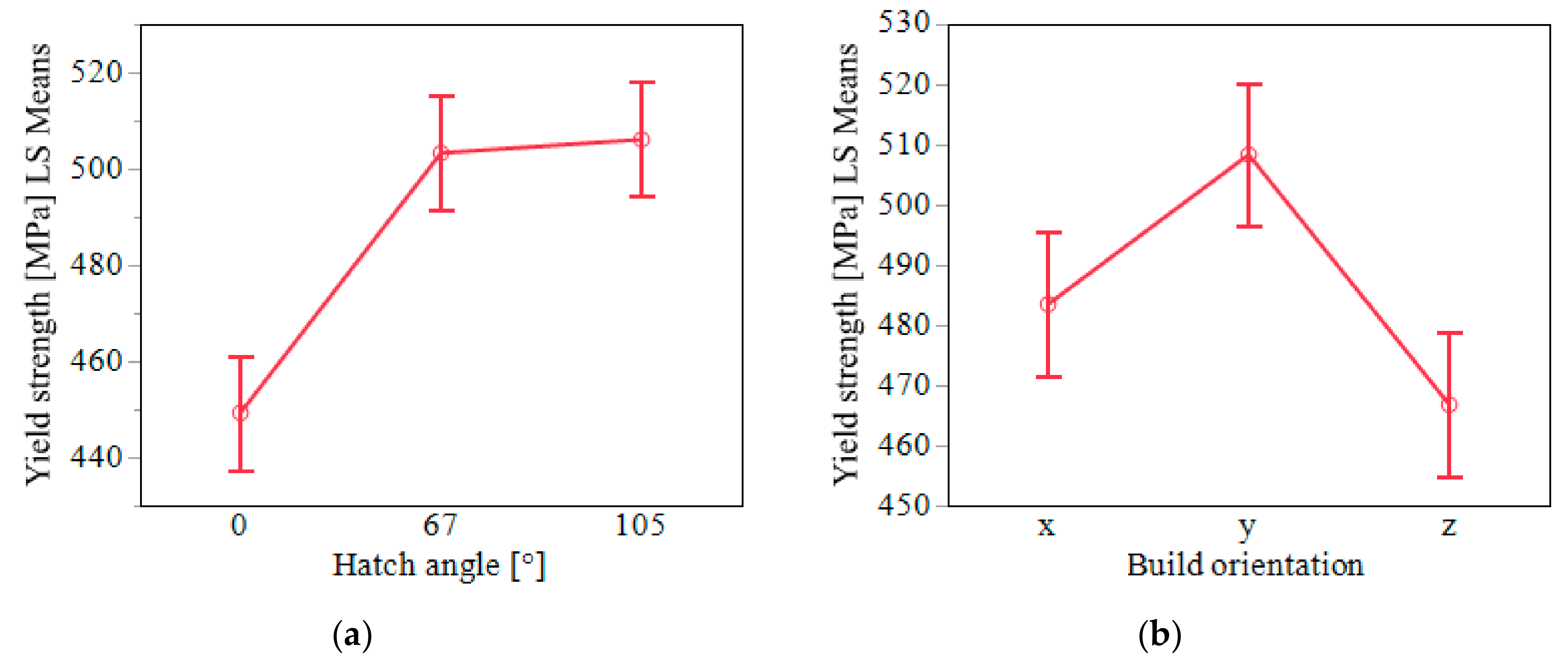
Figure 11.
Least square mean plot (yield strength) for the two factors: (a) hatch angle, and (b) build orientation.
Figure 11.
Least square mean plot (yield strength) for the two factors: (a) hatch angle, and (b) build orientation.
Figure 12.
Least squares mean plot (flow stress at 35% plastic strain).
Figure 12.
Least squares mean plot (flow stress at 35% plastic strain).
Table 1.
Chemical composition (in wt.%) of 304L stainless steel powder.
Table 1.
Chemical composition (in wt.%) of 304L stainless steel powder.
| Element | Cr | Ni | Mn | Si | Cu | N | O | C | P | S | Fe |
|---|
| wt.% | 18.5 | 9.9 | 1.4 | 0.63 | 0.1 | 0.09 | 0.02 | 0.015 | 0.012 | 0.004 | Balance |
Table 2.
Selective laser melting (SLM) machine parameters.
Table 2.
Selective laser melting (SLM) machine parameters.
| Parameter | Value |
|---|
| Laser type | 1070 nm NdYAG |
| Laser power (W) | 200 |
| Effective build volume (mm × mm× mm) | 248 × 248 × 280 |
| Laser spot | 70 |
| Hatch distance (mm) | 0.085 |
| Fill pattern | Stripes |
| Exposure time (μs) | 75 |
| Point distance (μm) | 60 |
| Layer thickness (μm) | 50 |
| Inert gas during production | Argon |
Table 3.
Summary of different build configurations studied during this study.
Table 3.
Summary of different build configurations studied during this study.
| Configuration | Hatch Angle (°) | Build Orientation |
|---|
| (a) | 0 | x |
| (b) | 0 | y |
| (c) | 0 | z |
| (d) | 67 | x |
| (e) | 67 | y |
| (f) | 67 | z |
| (g) | 105 | x |
| (h) | 105 | y |
| (i) | 105 | z |
Table 4.
Full-factorial design.
Table 4.
Full-factorial design.
| Factors | Levels |
|---|
| Hatch angle (I) | 0° | 67° | 105° |
| Build orientation (II) | x-direction | y-direction | z-direction |
Table 5.
ANOVA table for the factorial experiment.
Table 5.
ANOVA table for the factorial experiment.
| Source | Degrees of Freedom (DF) | Sum of Squares (SS) | Mean Square (MS) | F Ratio |
|---|
| Treatment combinations | a*b − 1 | SSTreat.comb | MSTreat. comb | MSTreat. Comb/MSError |
| Hatch angle (I) | a − 1 | SSI | MSI | MSI/MSError |
| Build orientation (II) | b − 1 | SSII | MSII | MSII/MSError |
| Factor I*II | (a − 1)*(b − 1) | SSI*II | MSI*II | MSI*II/MSError |
| Error | a*b*(n − 1) | SSError | MSError | |
| Total | (a*b*n) − 1 | SSTotal | | |
Table 6.
Full factorial design of the two control factors with three replicates.
Table 6.
Full factorial design of the two control factors with three replicates.
| | | Response: Yield Strength
(MPa) | Response: Flow Stress at 35% Plastic Strain Strength (MPa) |
|---|
| Factor | Replication | Replication |
|---|
| Sample | A | B | 1 | 2 | 3 | Mean | St.Dev | 1 | 2 | 3 | Mean | St.Dev |
|---|
| 1 | 0 | x | 431 | 436 | 424 | 430 | 6 | 892 | 900 | 939 | 911 | 25 |
| 2 | 0 | y | 481 | 492 | 471 | 482 | 10 | 869 | 904 | 854 | 876 | 26 |
| 3 | 0 | z | 442 | 415 | 449 | 436 | 18 | 819 | 851 | 841 | 837 | 16 |
| 4 | 67 | x | 504 | 507 | 513 | 508 | 5 | 990 | 988 | 985 | 987 | 2 |
| 5 | 67 | y | 553 | 528 | 504 | 528 | 25 | 991 | 1000 | 998 | 993 | 6 |
| 6 | 67 | z | 481 | 479 | 463 | 474 | 10 | 996 | 979 | 992 | 989 | 9 |
| 7 | 105 | x | 522 | 526 | 489 | 512 | 20 | 998 | 998 | 983 | 993 | 9 |
| 8 | 105 | y | 483 | 544 | 518 | 515 | 31 | 997 | 987 | 998 | 995 | 5 |
| 9 | 105 | z | 483 | 497 | 492 | 491 | 7 | 1007 | 1008 | 996 | 1004 | 7 |
Table 7.
ANOVA results for yield strength (α = 0.05).
Table 7.
ANOVA results for yield strength (α = 0.05).
| Source | DF | Sum of Squares | Mean Square | F Ratio |
|---|
| Model | 8 | 28,743.027 | 3592.88 | 12.4699 |
| Error | 18 | 5186.220 | 288.12 | Prob > F |
| C. Total | 26 | 33,929.246 | | <0.0001* |
Table 8.
Effects test for yield strength (α = 0.05).
Table 8.
Effects test for yield strength (α = 0.05).
| Source | Nparm | DF | Sum of Squares | F Ratio | Prob > F |
|---|
| Hatch angle | 2 | 2 | 18,438.828 | 31.9982 | <0.0001* |
| Build orientation | 2 | 2 | 7864.314 | 13.6475 | 0.0002* |
| Hatch angle*Build orientation | 4 | 4 | 2439.885 | 2.1170 | 0.1207 |
Table 9.
ANOVA results for flow stress at 35% plastic strain (α = 0.05).
Table 9.
ANOVA results for flow stress at 35% plastic strain (α = 0.05).
| Source | DF | Sum of Squares | Mean Square | F Ratio |
|---|
| Model | 8 | 93,496.572 | 11687.1 | 58.00850 |
| Error | 18 | 3626.491 | 201.5 | Prob > F |
| C. Total | 26 | 97,123.062 | | <0.0001* |
Table 10.
Effects table for flow stress at 35% plastic strain (α = 0.05).
Table 10.
Effects table for flow stress at 35% plastic strain (α = 0.05).
| Source | Nparm | DF | Sum of Squares | F Ratio | Prob > F |
|---|
| Hatch angle | 2 | 2 | 85,115.62 | 211.2348 | <0.0001* |
| Build orientation | 2 | 2 | 1897.766 | 4.7098 | 0.0226* |
| Hatch angle*Build orientation | 4 | 4 | 6483.144 | 8.0447 | 0.0007* |
Table 11.
Least square means (LS Means) Differences Tukey honestly significant difference (HSD) (yield strength); α = 0.050.
Table 11.
Least square means (LS Means) Differences Tukey honestly significant difference (HSD) (yield strength); α = 0.050.
| Level | | | Least Sq. Mean |
|---|
| 105 | A | | 506.07706 |
| 67 | A | | 503.27145 |
| 0 | | B | 449.29164 |
| y | A | | 508.34234 |
| x | | B | 483.49386 |
| z | | B | 466.80394 |
Table 12.
LSMeans Differences Tukey HSD (flow stress at 35% plastic strain); α = 0.050.
Table 12.
LSMeans Differences Tukey HSD (flow stress at 35% plastic strain); α = 0.050.
| Level | | | | Least Sq. Mean |
|---|
| 105,z | A | | | 1003.8160 |
| 105,y | A | | | 994.5960 |
| 67,y | A | | | 993.2092 |
| 105,x | A | | | 992.9778 |
| 67,z | A | | | 988.9414 |
| 67,x | A | | | 987.4619 |
| 0,x | | B | | 910.5729 |
| 0,y | | B | C | 876.1423 |
| 0,z | | | C | 836.9911 |