A Two-Layer Framework for Cooperative Standoff Tracking of a Ground Moving Target Using Dual UAVs
Abstract
1. Introduction
2. Problem Formulation
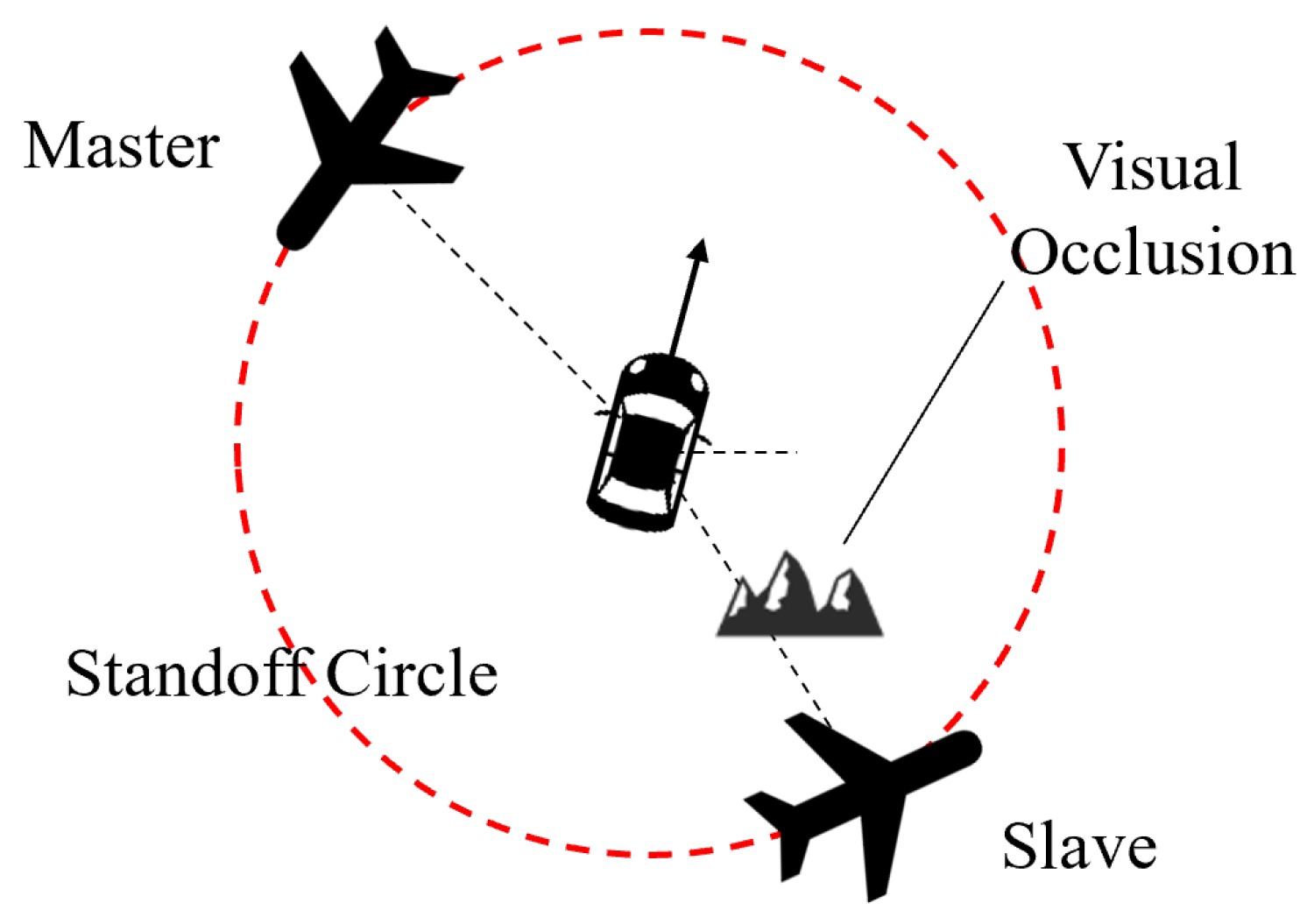
2.1. Role Transition Model
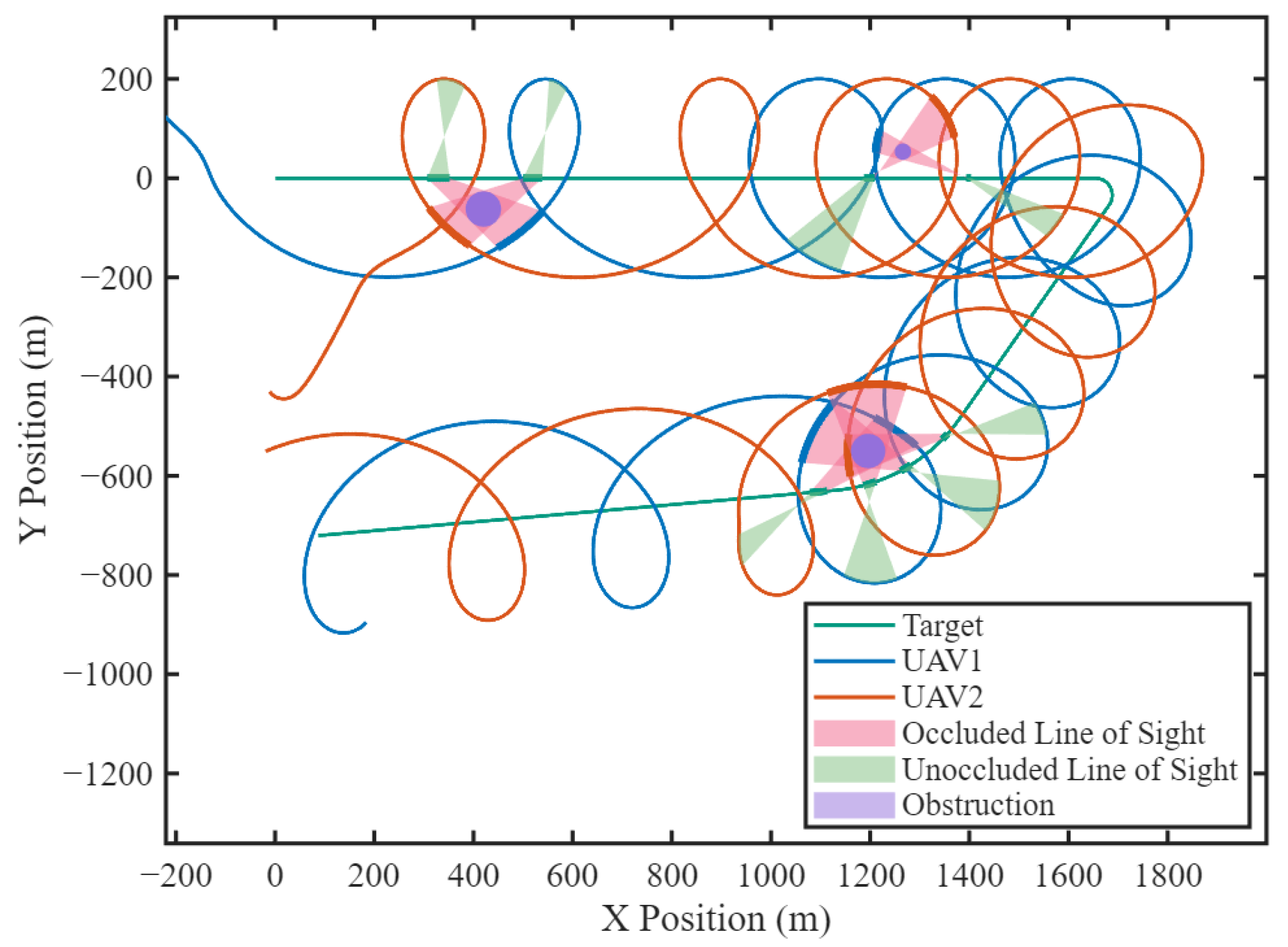
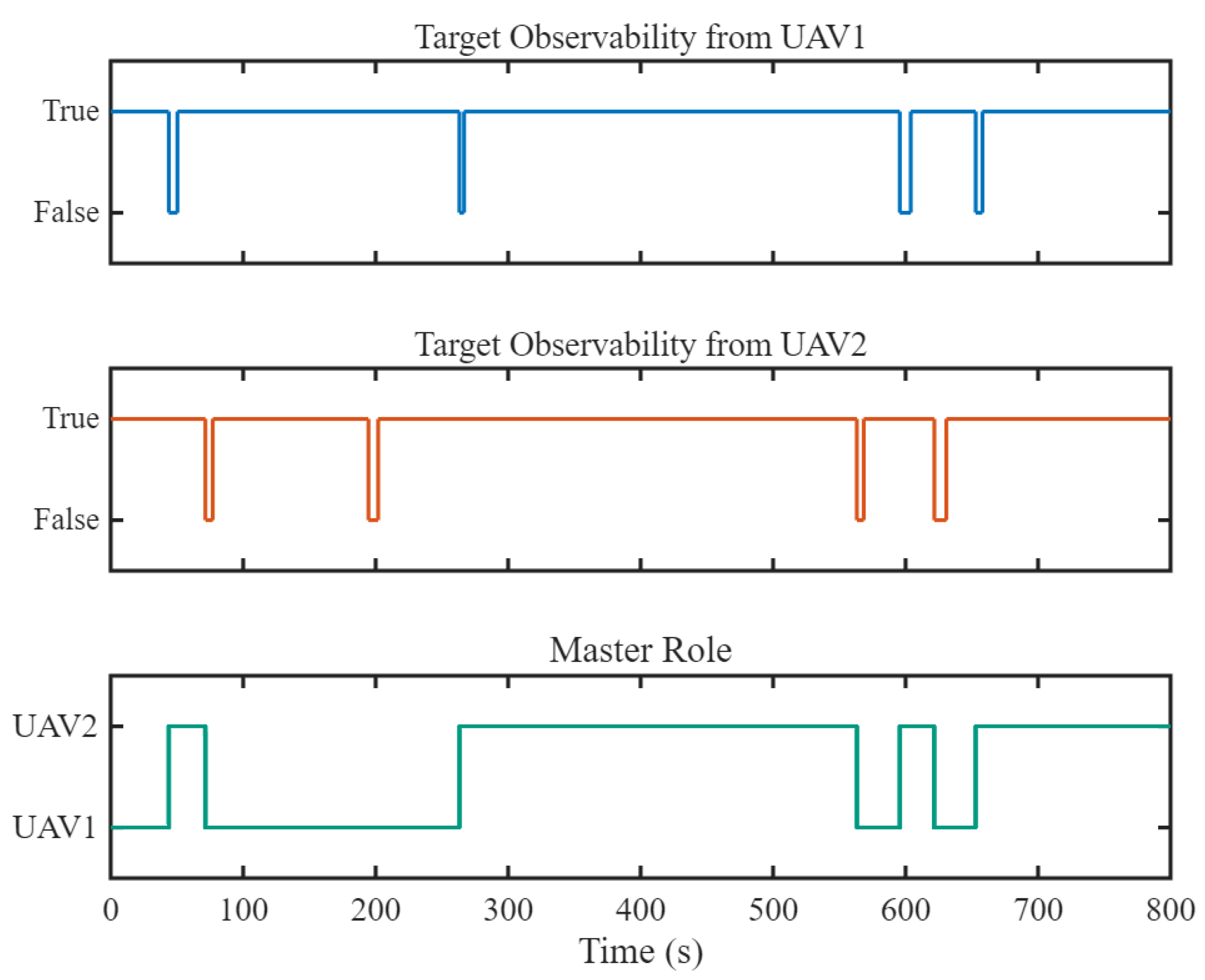
- Single-Observer Mode: When a UAV ensures continuous and stable observation of the target, it assumes the role of Master, providing the target states to the Slave, which is unable to ensure stable observation caused by occlusion.
- Dual-Observer Mode: When the Slave UAV’s visual occlusion is cleared, the system activates Dual-Observer Mode, retaining the Master–Slave roles established in Single-Observer Mode. Both UAVs share the target states they acquire, allowing for an exchange of acquired target states.
- If either the Master or Slave UAV is unable to maintain target observation during Dual-Observer Mode, resulting in a loss of target sight, the system automatically reverts to Single-Observer Mode.
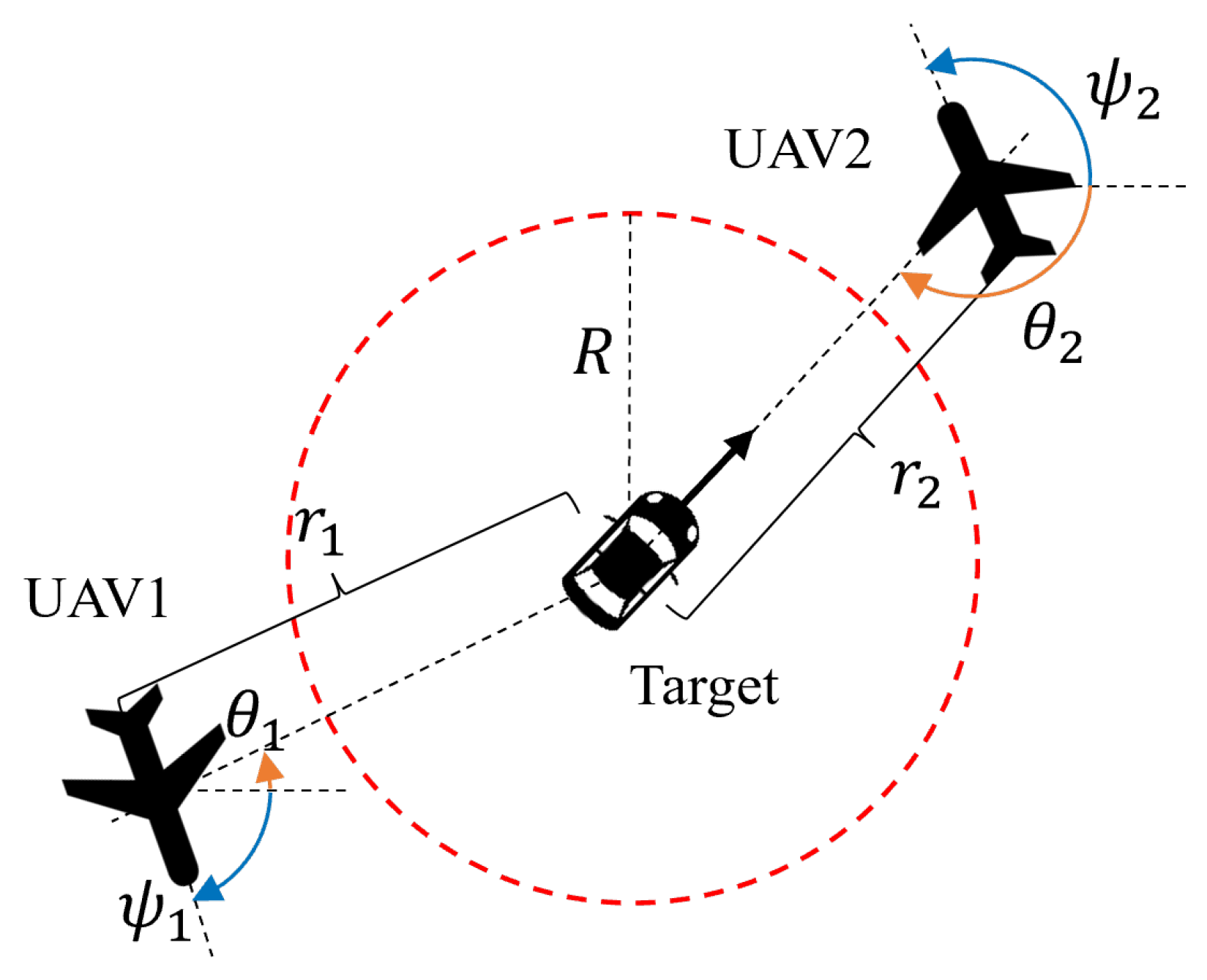
2.2. UAV Kinematic Model
3. Two-Layer Tracking Framework Design
3.1. Decision-Making Layer
- Identity Independence: Both nodes execute identical code, and UAV roles dynamically transition in real-time based on target observability.
- Bounded Delay: The decision synchronization delay is bounded by .
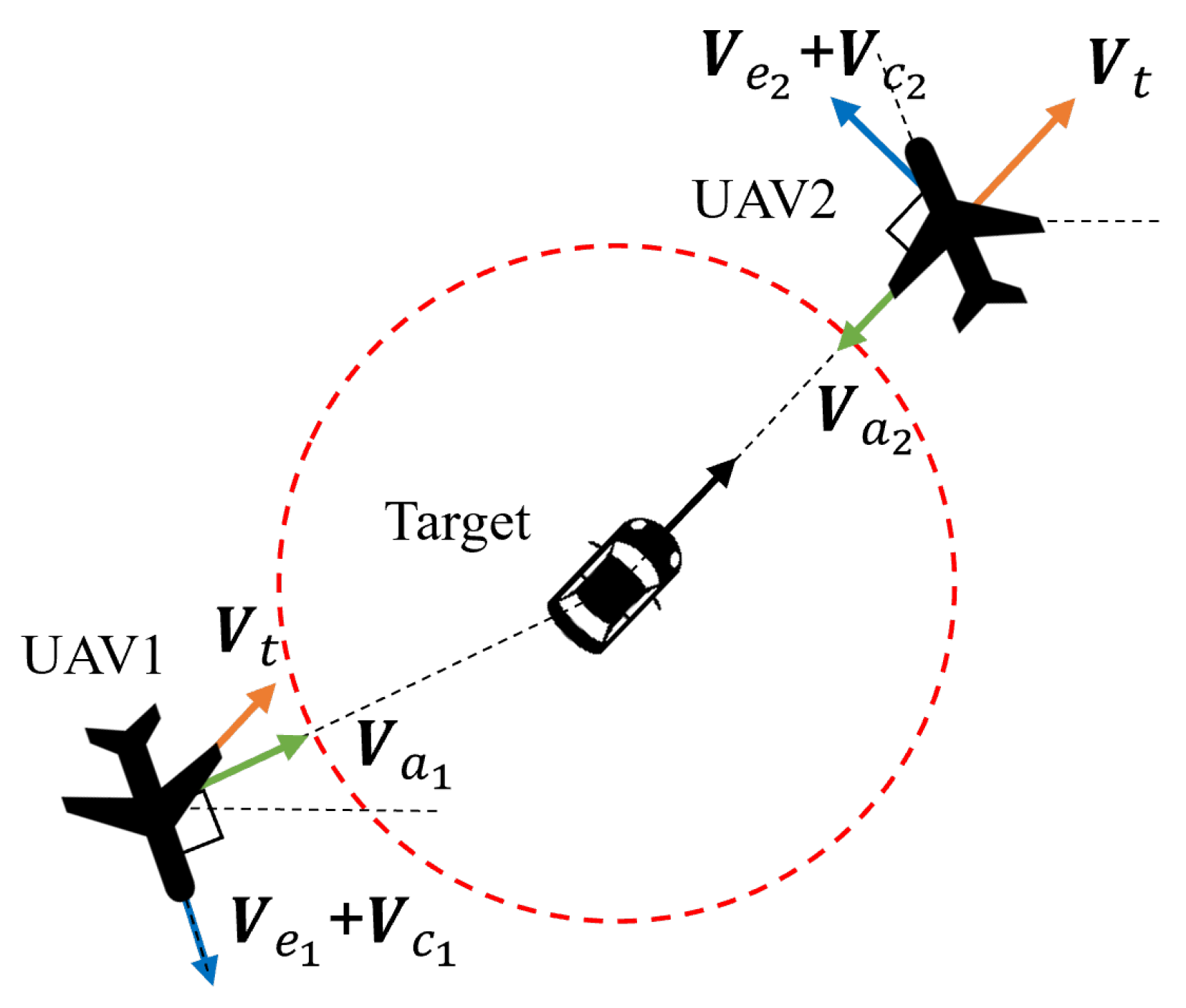
3.2. Guidance Layer
4. Stability Analysis
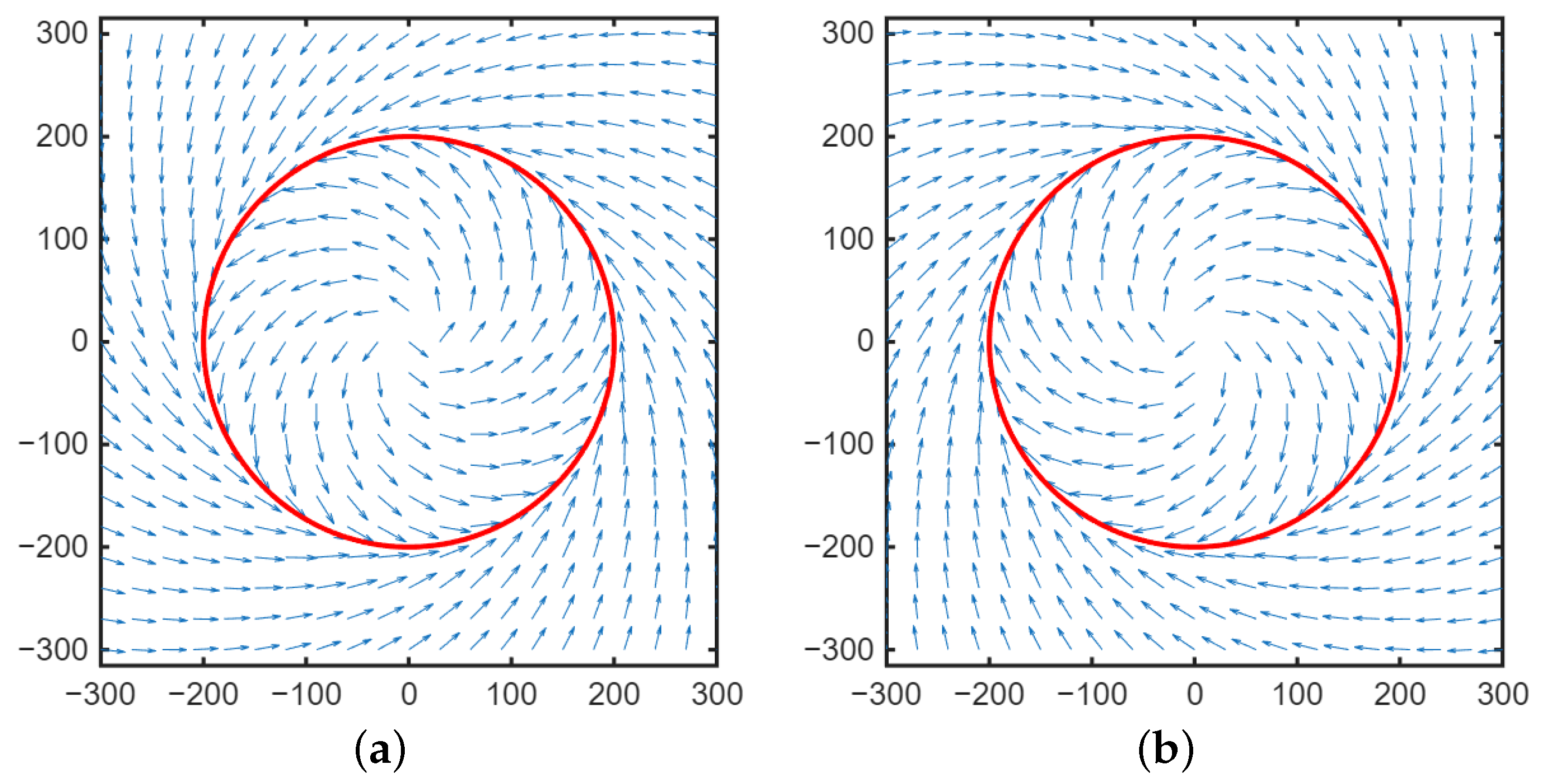
4.1. Radial Distance Stability
- When , the vector field diverges outward toward the circle of radius ;
- When , the vector field converges inward toward the circle of radius .
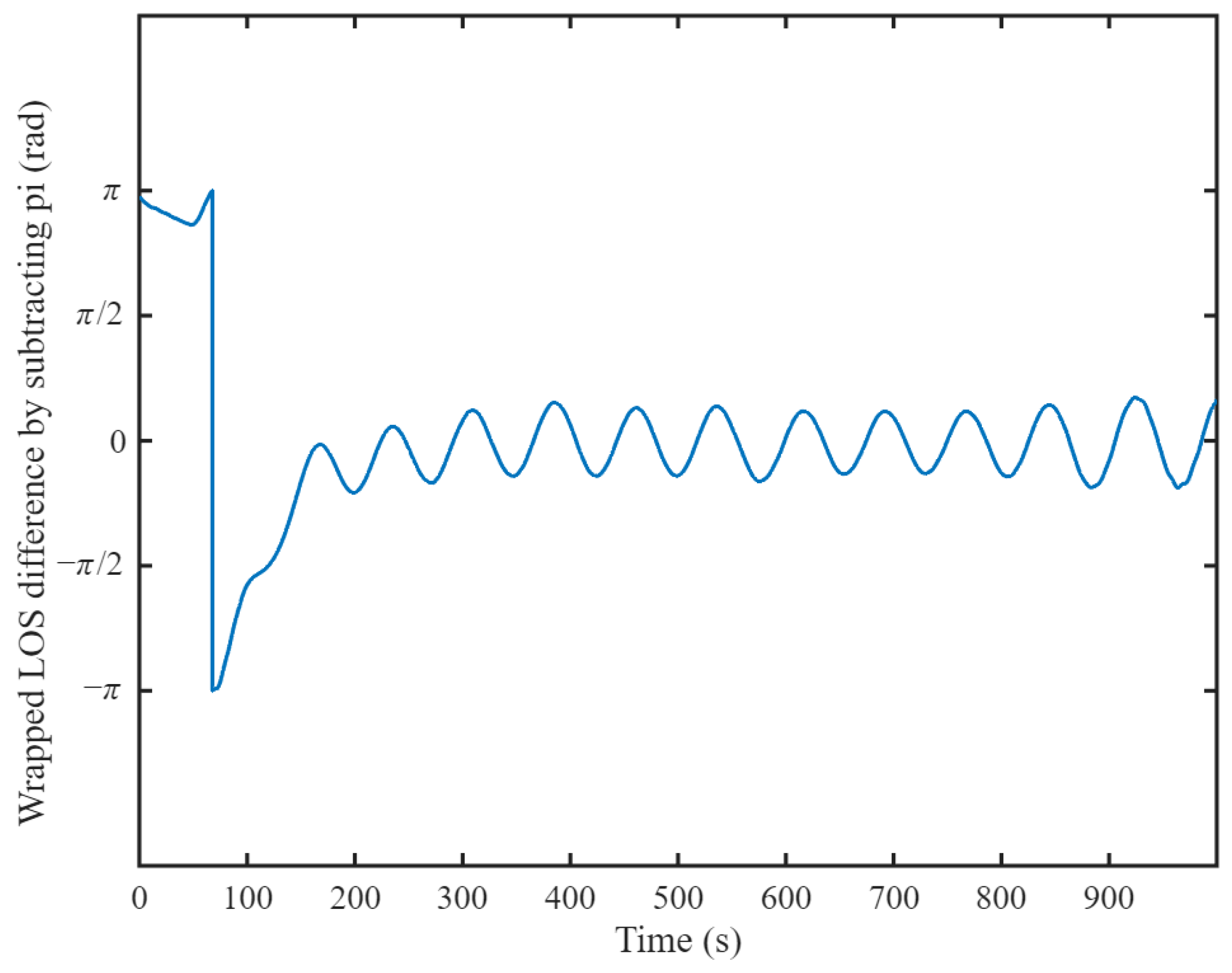
4.2. Phase Synchronization Stability
4.3. Comprehensive Analysis
5. Simulation and Analysis
5.1. Numerical Simulation Setup
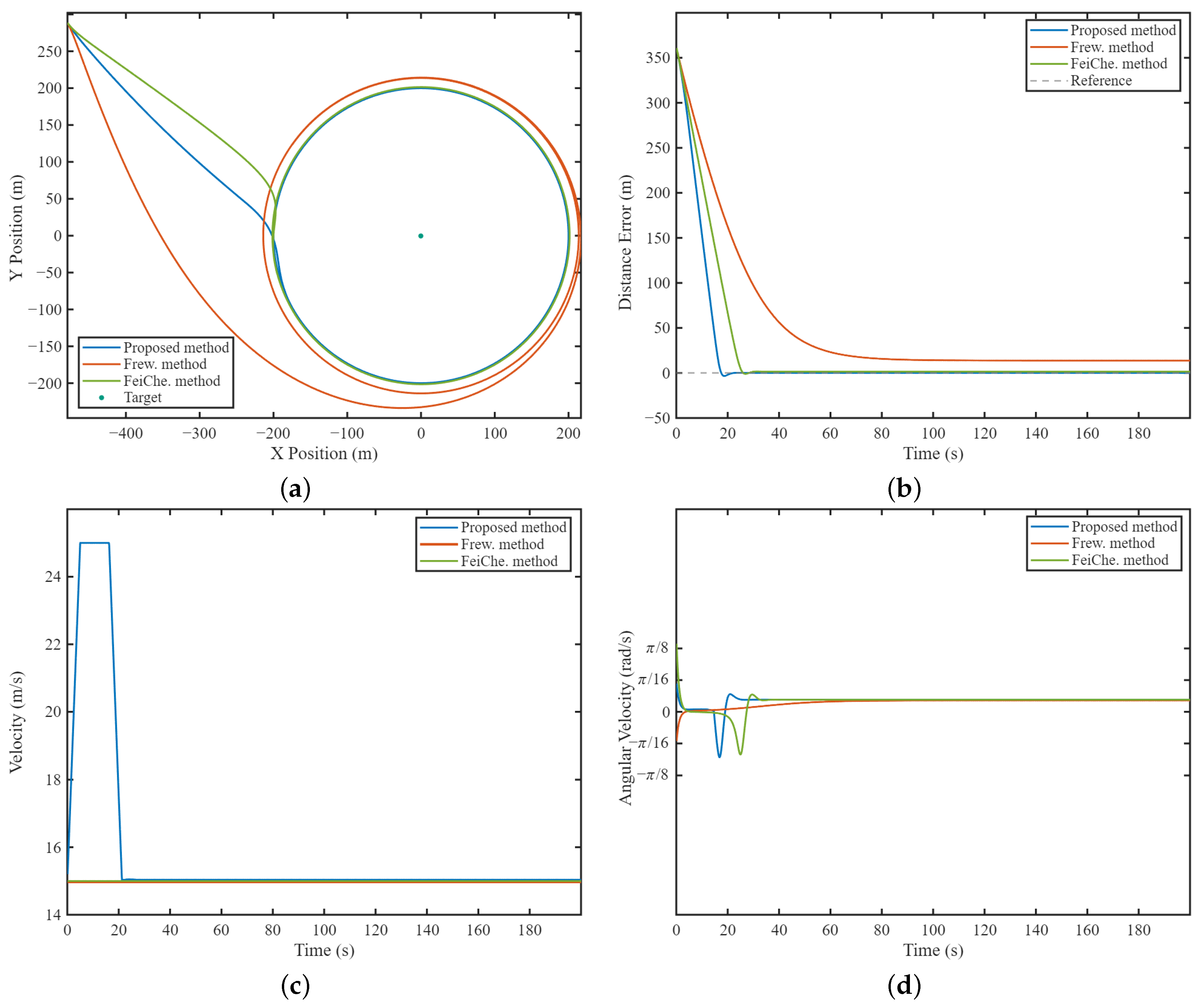
5.1.1. Stationary Target Tracking
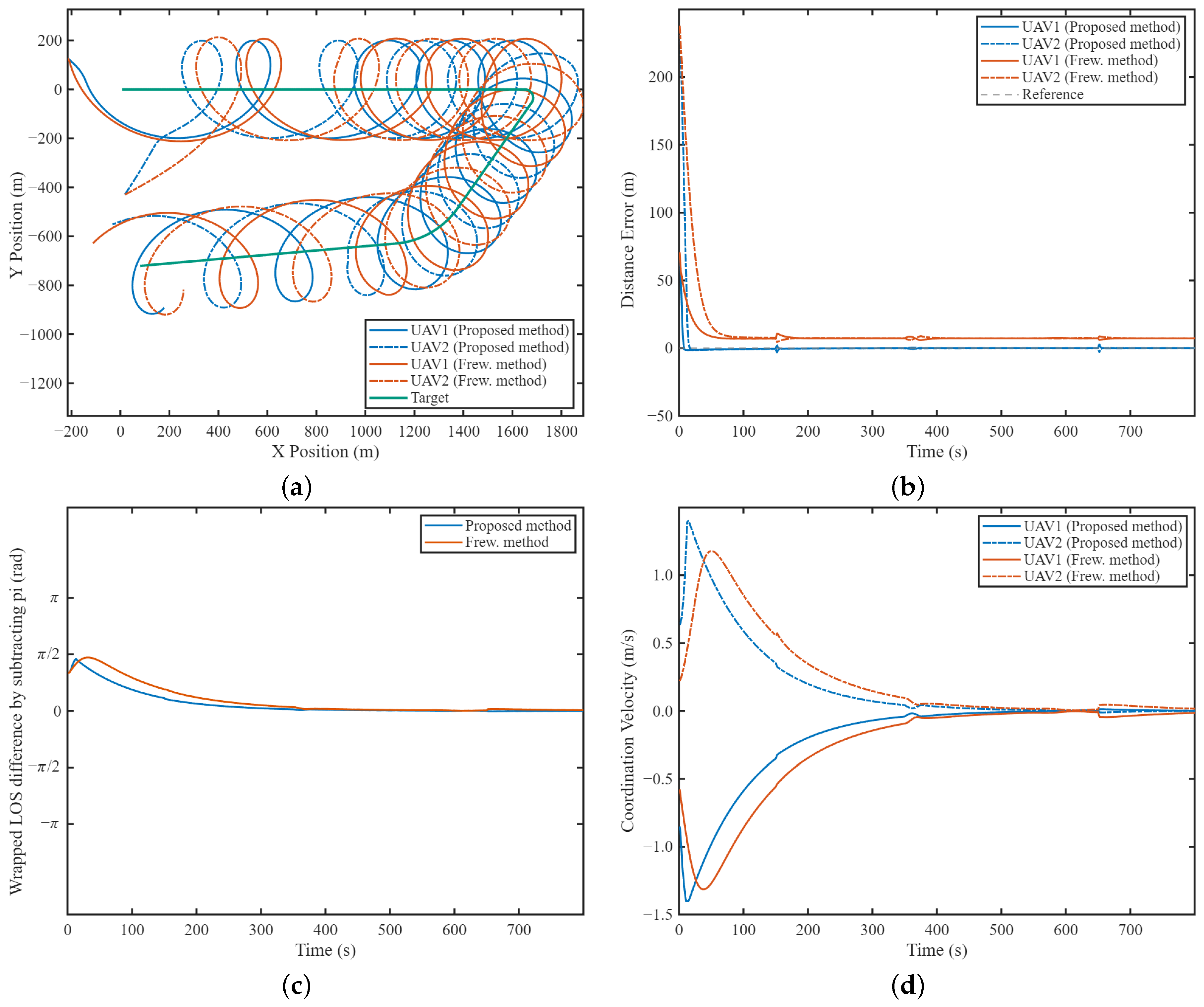
5.1.2. Phase-Synchronized Cooperative Tracking of Maneuvering Target
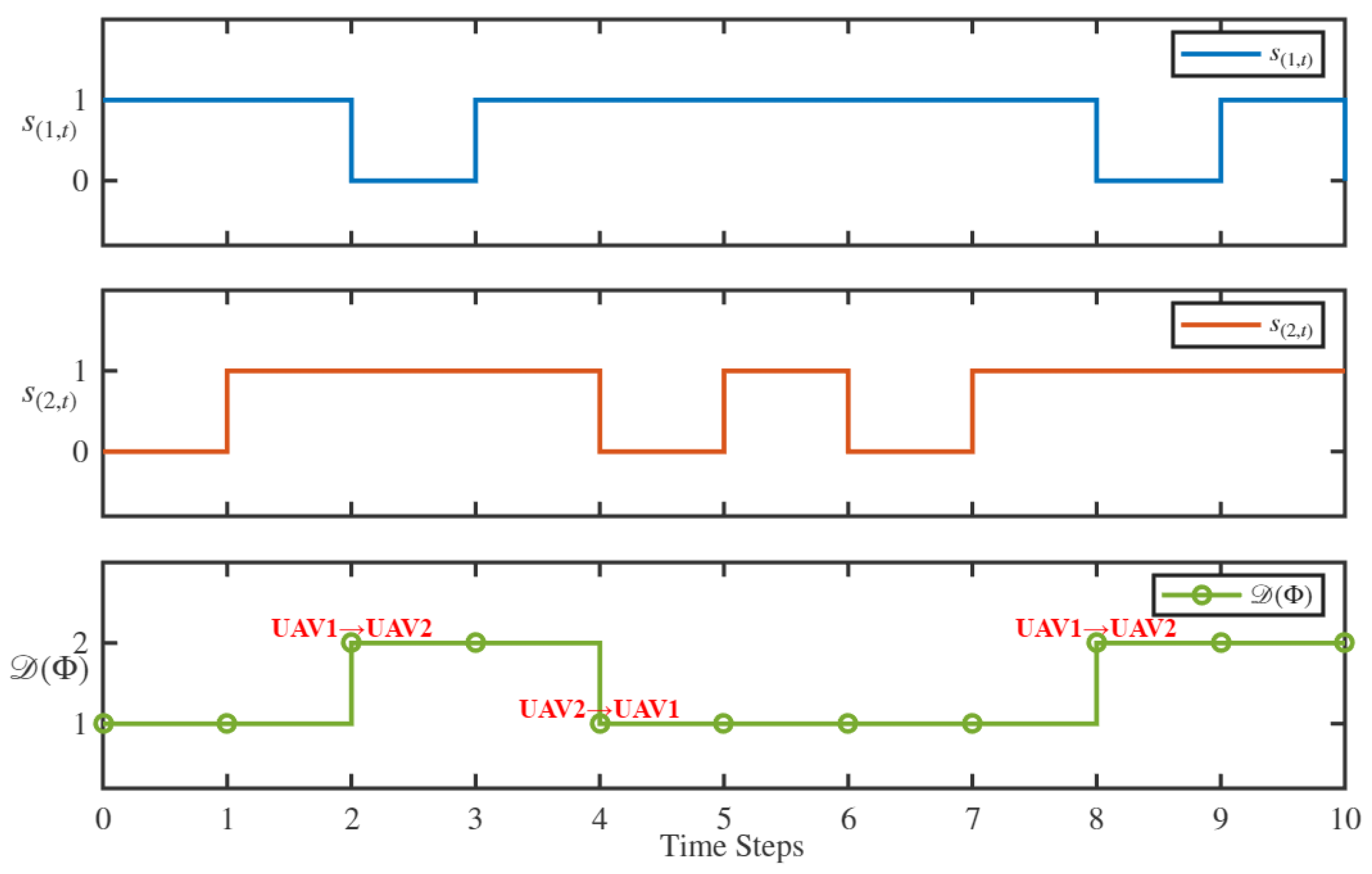
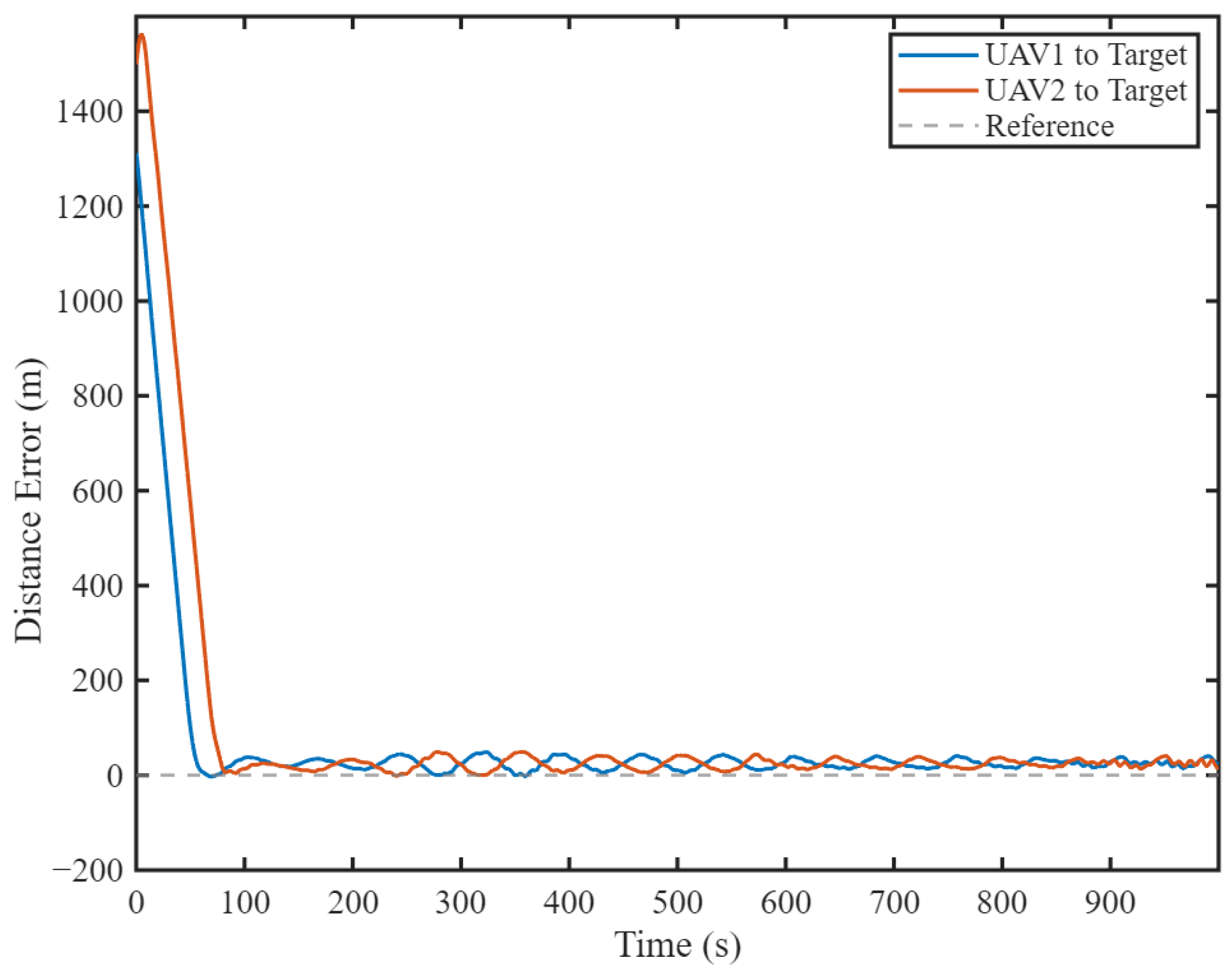
5.1.3. Occlusion-Robust Tracking with Dynamic Role Transition
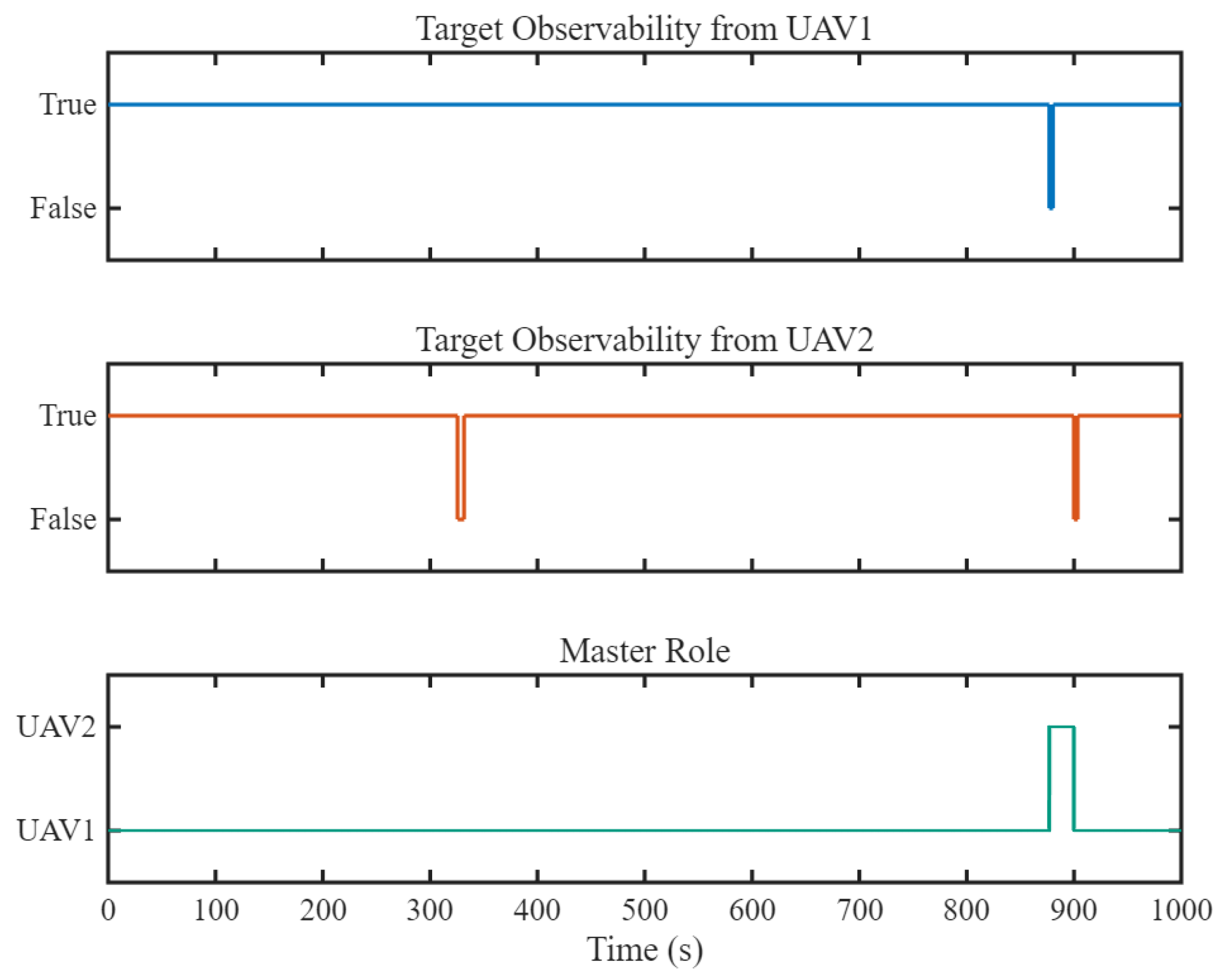
5.2. Hardware-in-the-Loop Simulation
5.2.1. HIL Simulation Setup
5.2.2. HIL Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, L.; Leng, S.; Liu, Q.; Wang, Q. Intelligent UAV Swarm Cooperation for Multiple Targets Tracking. IEEE Internet Things J. 2022, 9, 743–754. [Google Scholar] [CrossRef]
- Hayat, S.; Yanmaz, E.; Muzaffar, R. Survey on Unmanned Aerial Vehicle Networks for Civil Applications: A Communications Viewpoint. IEEE Commun. Surv. Tutor. 2016, 18, 2624–2661. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Luo, Y.; Zhang, H.; Zhang, X.; Ding, W. Iterative Trajectory Planning and Resource Allocation for UAV-Assisted Emergency Communication with User Dynamics. Drones 2024, 8, 149. [Google Scholar] [CrossRef]
- Huang, Z.; Wu, W.; Wu, K.; Yuan, H.; Fu, C.; Shan, F.; Wang, J.; Luo, J. LI2: A New Learning-Based Approach to Timely Monitoring of Points-of-Interest With UAV. IEEE Trans. Mob. Comput. 2025, 24, 45–61. [Google Scholar] [CrossRef]
- Zhou, X.; Jia, W.; He, R.; Sun, W. High-Precision Localization Tracking and Motion State Estimation of Ground-Based Moving Target Utilizing Unmanned Aerial Vehicle High-Altitude Reconnaissance. Remote Sens. 2025, 17, 735. [Google Scholar] [CrossRef]
- Frew, E.W.; Lawrence, D.A.; Morris, S. Coordinated Standoff Tracking of Moving Targets Using Lyapunov Guidance Vector Fields. J. Guid. Control. Dyn. 2008, 31, 290–306. [Google Scholar] [CrossRef]
- Oh, H.; Kim, S. Persistent Standoff Tracking Guidance Using Constrained Particle Filter for Multiple UAVs. Aerosp. Sci. Technol. 2019, 84, 257–264. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Zhou, Q. Real-Time Multi-Target Localization from Unmanned Aerial Vehicles. Sensors 2017, 17, 33. [Google Scholar] [CrossRef]
- Yılmaz, C.; Ozgun, A.; Erol, B.A.; Gumus, A. Open-Source Visual Target-Tracking System Both on Simulation Environment and Real Unmanned Aerial Vehicles. In Proceedings of the 2nd International Congress of Electrical and Computer Engineering, Bandirma, Turkey, 22–25 November 2023; Seyman, M.N., Ed.; Springer: Cham, Switzerland, 2024; pp. 147–159. [Google Scholar]
- Liu, Z.; Xiang, L.; Zhu, Z. Cooperative Standoff Target Tracking Using Multiple Fixed-Wing UAVs with Input Constraints in Unknown Wind. Drones 2023, 7, 593. [Google Scholar] [CrossRef]
- Yao, P.; Wang, H.; Su, Z. Cooperative Path Planning with Applications to Target Tracking and Obstacle Avoidance for Multi-UAVs. Aerosp. Sci. Technol. 2016, 54, 10–22. [Google Scholar] [CrossRef]
- Fu, Y.; Xiong, H.; Dai, X.; Nian, X.; Wang, H. Multi-UAV Target Localization Based on 3D Object Detection and Visual Fusion. In Proceedings of the 3rd 2023 International Conference on Autonomous Unmanned Systems (3rd ICAUS 2023), Nanjing, China, 8–11 September 2023; Qu, Y., Gu, M., Niu, Y., Fu, W., Eds.; Springer: Singapore, 2024; pp. 226–235. [Google Scholar]
- Sun, T.; Cui, J. Multi-Agents Cooperative Localization with Equivalent Relative Observation Model Based on Unscented Transformation. Unmanned Syst. 2024, 12, 1063–1071. [Google Scholar] [CrossRef]
- Rao, K.; Yan, H.; Yang, P.; Wang, M.; Lv, Y. Multi-UAV Trajectory Planning with Field-of-view Sharing Mechanism in Cluttered Environments:Application to Target Tracking. Sci. China Inf. Sci. 2025, 68, 89–102. [Google Scholar] [CrossRef]
- Lawrence, D. Lyapunov Vector Fields for UAV Flock Coordination. In Proceedings of the 2nd AIAA “Unmanned Unlimited” Conference and Workshop & Exhibit, San Diego, CA, USA, 15–18 September 2003. [Google Scholar] [CrossRef]
- Chen, H.; Chang, K.; Agate, C.S. UAV Path Planning with Tangent-plus-Lyapunov Vector Field Guidance and Obstacle Avoidance. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 840–856. [Google Scholar] [CrossRef]
- Oh, H.; Kim, S.; Tsourdos, A.; White, B.A. Decentralised Standoff Tracking of Moving Targets Using Adaptive Sliding Mode Control for UAVs. J. Intell. Robot. Syst. 2013, 76, 169–183. [Google Scholar] [CrossRef]
- Lim, S.; Kim, Y.; Lee, D.; Bang, H. Standoff Target Tracking Using a Vector Field for Multiple Unmanned Aircrafts. J. Intell. Robot. Syst. 2013, 69, 347–360. [Google Scholar] [CrossRef]
- Pothen, A.A.; Ratnoo, A. Curvature-Constrained Lyapunov Vector Field for Standoff Target Tracking. J. Guid. Control. Dyn. 2017, 40, 2729–2736. [Google Scholar] [CrossRef]
- Sun, S.; Wang, H.; Liu, J.; He, Y. Fast Lyapunov Vector Field Guidance for Standoff Target Tracking Based on Offline Search. IEEE Access 2019, 7, 124797–124808. [Google Scholar] [CrossRef]
- Hu, C.; Zhang, Z.; Tao, Y.; Wang, N. Decentralized Real-Time Estimation and Tracking for Unknown Ground Moving Target Using UAVs. IEEE Access 2019, 7, 1808–1817. [Google Scholar] [CrossRef]
- Sun, S.; Liu, Y.; Guo, S.; Li, G.; Yuan, X. Observation-Driven Multiple UAV Coordinated Standoff Target Tracking Based on Model Predictive Control. Tsinghua Sci. Technol. 2022, 27, 948–963. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhou, R.; Dong, Z.N.; Li, H. Coordinated Standoff Target Tracking Using Two UAVs with Only Bearing Measurement. J. Beijing Univ. Aeronaut. Astronaut. 2015, 41, 2116–2123. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Fang, Z.; Li, P. Cooperative Standoff Tracking For Multi-UAVs Based on tau Vector Field Guidance. J. Zhejiang Univ. Eng. Sci. 2016, 50, 984. [Google Scholar] [CrossRef]
- Park, S.; Deyst, J.; How, J. A New Nonlinear Guidance Logic for Trajectory Tracking. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, TX, USA, 16 August 2004; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. [Google Scholar] [CrossRef]
- Park, S.; Deyst, J.; How, J.P. Performance and Lyapunov Stability of a Nonlinear Path Following Guidance Method. J. Guid. Control. Dyn. 2007, 30, 1718–1728. [Google Scholar] [CrossRef]
- Huang, S.; Lyu, Y.; Zhu, Q.; Su, L.; Li, K.; Shi, J. UAV Fast Standoff Tracking of a Moving Target Based on a Composite Guidance Law. In Proceedings of the 2024 36th Chinese Control and Decision Conference (CCDC), Xi’an, China, 25–27 May 2024; pp. 1358–1363. [Google Scholar] [CrossRef]
- Wang, Y.; Shan, M.; Wang, D. Motion Capability Analysis for Multiple Fixed-Wing UAV Formations with Speed and Heading Rate Constraints. IEEE Trans. Control Netw. Syst. 2020, 7, 977–989. [Google Scholar] [CrossRef]
- Che, F.; Niu, Y.; Li, J.; Wu, L. Cooperative Standoff Tracking of Moving Targets Using Modified Lyapunov Vector Field Guidance. Appl. Sci. 2020, 10, 3709. [Google Scholar] [CrossRef]

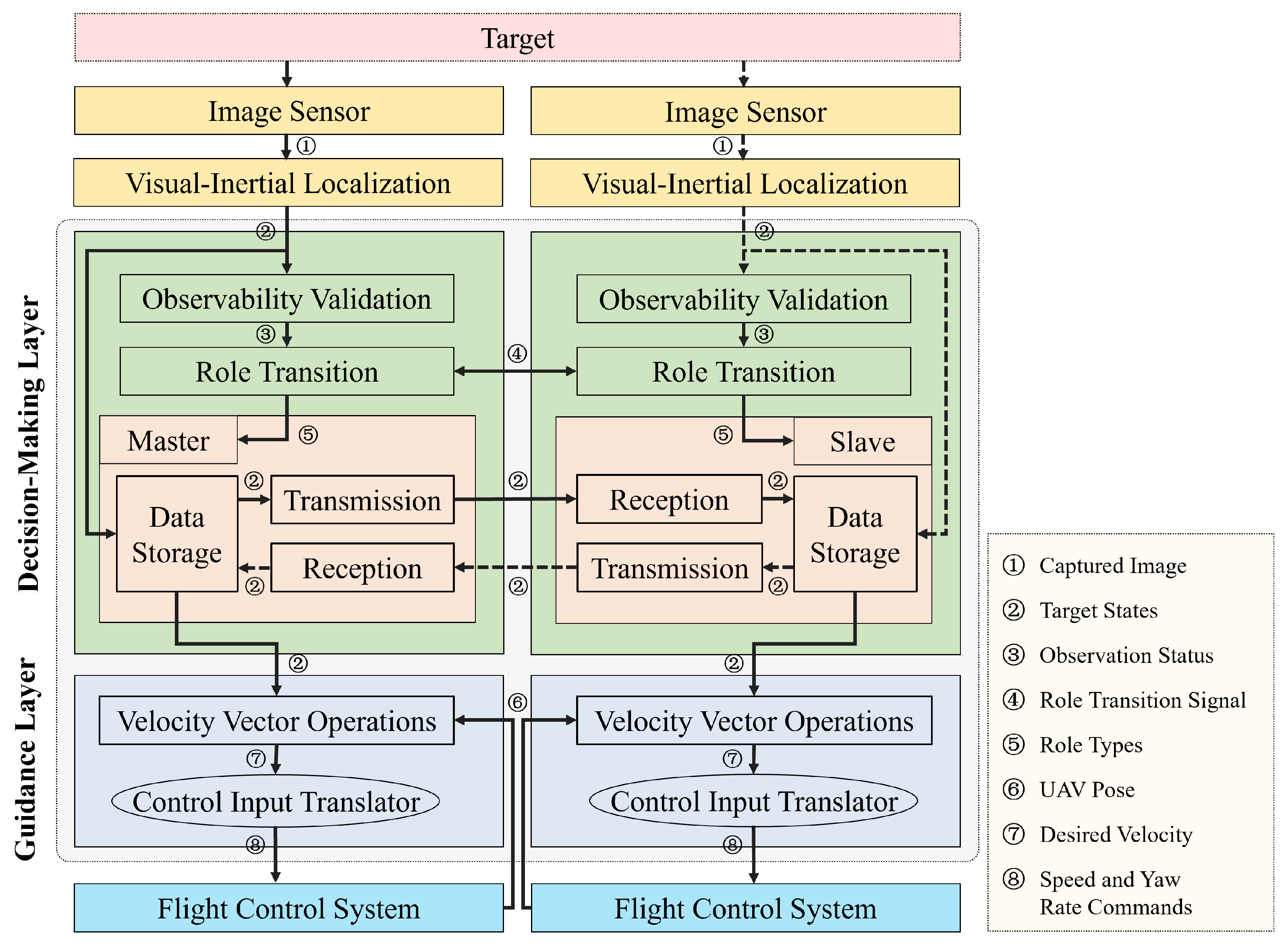

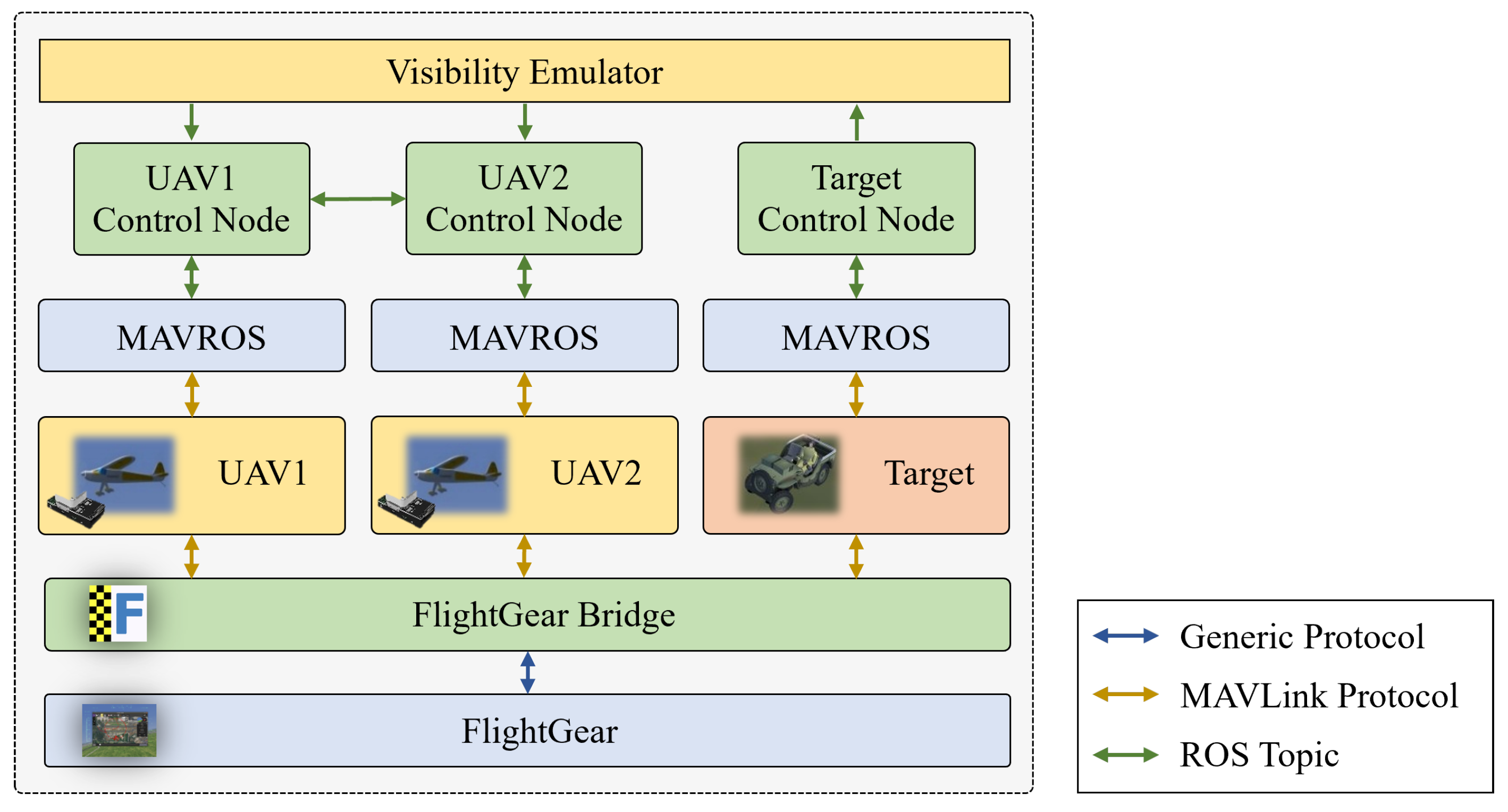


| Layer | Module | Function |
|---|---|---|
| Decision-Making Layer | Observability Validation | Evaluates target state validity; flags observation failure if no data received for >0.5 s |
| Role Transition | Maintains current/previous states to execute role transition algorithm | |
| Data Storage | Acquires target states via visual-inertial localization or inter-UAV comms | |
| Transmission/Reception | Manages target states exchange between UAVs per Section 2.1 | |
| Guidance Layer | Velocity Vector Operations | Performs velocity vector synthesis |
| Control Input Translator | Converts vector speeds to executable flight commands |
| 0 | 0 | 1 | 1 | 2 |
| 0 | 1 | 1 | 0 | 2 |
| 0 | 1 | 1 | 1 | 2 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 2 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| Parameter | Target | UAVs |
|---|---|---|
| Speed (m/s) | 0–8 | 7–23 |
| Acceleration (m/s2) | ≤10 | ≤2 |
| Yaw rate (°/s) | ≤10 | ≤5 |
| Time (s) | Target Maneuver | Method | UAV1 Error (m) | UAV2 Error (m) |
|---|---|---|---|---|
| 150 | Deceleration | Proposed | 2.36 | 2.82 |
| Frew et al. [6] | 3.86 | 3.11 | ||
| 350 | Sharp turn | Proposed | 0.75 | 0.72 |
| Frew et al. [6] | 2.72 | 2.74 | ||
| 550 | Gentle turn | Proposed | <0.2 | <0.2 |
| Frew et al. [6] | <0.2 | <0.2 | ||
| 650 | Acceleration | Proposed | 2.88 | 2.88 |
| Frew et al. [6] | 1.38 | 1.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Yin, D.; Fu, J.; Cong, Y.; Chen, H.; Yang, X.; Zhao, H.; Liu, L. A Two-Layer Framework for Cooperative Standoff Tracking of a Ground Moving Target Using Dual UAVs. Drones 2025, 9, 560. https://doi.org/10.3390/drones9080560
Chen J, Yin D, Fu J, Cong Y, Chen H, Yang X, Zhao H, Liu L. A Two-Layer Framework for Cooperative Standoff Tracking of a Ground Moving Target Using Dual UAVs. Drones. 2025; 9(8):560. https://doi.org/10.3390/drones9080560
Chicago/Turabian StyleChen, Jing, Dong Yin, Jing Fu, Yirui Cong, Hao Chen, Xuan Yang, Haojun Zhao, and Lihuan Liu. 2025. "A Two-Layer Framework for Cooperative Standoff Tracking of a Ground Moving Target Using Dual UAVs" Drones 9, no. 8: 560. https://doi.org/10.3390/drones9080560
APA StyleChen, J., Yin, D., Fu, J., Cong, Y., Chen, H., Yang, X., Zhao, H., & Liu, L. (2025). A Two-Layer Framework for Cooperative Standoff Tracking of a Ground Moving Target Using Dual UAVs. Drones, 9(8), 560. https://doi.org/10.3390/drones9080560








