A Survey on UAV Control with Multi-Agent Reinforcement Learning

Abstract

Unmanned Aerial Vehicles (UAVs) have become increasingly prevalent in both governmental and civilian applications, offering significant reductions in operational costs by minimizing human involvement. There is a growing demand for autonomous, scalable, and intelligent coordination strategies in complex aerial missions involving multiple Unmanned Aerial Vehicles (UAVs). Traditional control techniques often fall short in dynamic, uncertain, or large-scale environments where decentralized decision-making and inter-agent cooperation are crucial. A potentially effective technique used for UAV fleet operation is Multi-Agent Reinforcement Learning (MARL). MARL offers a powerful framework for addressing these challenges by enabling UAVs to learn optimal behaviors through interaction with the environment and each other. Despite significant progress, the field remains fragmented, with a wide variety of algorithms, architectures, and evaluation metrics spread across domains. This survey aims to systematically review and categorize state-of-the-art MARL approaches applied to UAV control, identify prevailing trends and research gaps, and provide a structured foundation for future advancements in cooperative aerial robotics. The advantages and limitations of these techniques are discussed along with suggestions for further research to improve the effectiveness of MARL application to UAV fleet management.

1. Introduction

Unmanned Aerial Vehicles (UAVs), commonly referred to as drones, have experienced a significant surge in popularity due to their versatility, cost-effectiveness, and ability to access hard-to-reach areas. In search-and-rescue (SAR) operations, UAVs provide real-time aerial surveillance, enabling fast response in challenging terrains such as forests, mountains, or disaster-stricken zones. Being equipped with thermal imaging and high-resolution cameras allows them to operate in low-visibility and obstructed environments. In the commercial sector, UAVs are revolutionizing delivery services by offering faster, contactless transportation of goods, especially in remote or urban areas where traditional delivery methods face logistical challenges. Additionally, in geographical mapping [1], UAVs enable the creation of highly accurate topographical maps and 3D models by capturing detailed aerial imagery [2] and LiDAR data, aiding in urban planning, agriculture [3], and environmental monitoring [4]. UAVs also offer a viable alternative to conventional platforms for acquiring high-resolution remote sensing data [5]. In military operations, UAVs play a critical role in reconnaissance [6,7], surveillance [8,9], target acquisition [10], detecting mines [11], and even precision strikes [12], offering strategic advantages while minimizing the risk to human personnel.

Traditionally, UAVs are controlled through methods such as remote piloting via radio frequency (RF) links, ground control stations (GCS) with dedicated software interfaces, and pre-programmed GPS waypoint navigation. In manual control modes, human operators rely on handheld transmitters or laptops connected to the drone to manage flight paths, altitude, and onboard sensors. The manual control mode often requires constant line of sight, stable communication channels, and skilled human operators, especially for complex maneuvers or in unpredictable environments. Traditional control methods present several challenges that can limit the effectiveness and scalability of UAV operations. RF communication is susceptible to signal interference, latency, and range limitations, particularly in urban or mountainous regions where signal obstruction is common. This can compromise the drone’s responsiveness or even result in its loss. Ground control stations, while powerful, are often bulky and rely on stable network connections, making rapid deployment in disaster zones or battlefield conditions more difficult. Pre-programmed GPS navigation, though useful for repetitive tasks like mapping, lacks adaptability to real-time changes such as dynamic obstacles or weather conditions. In all cases, manual piloting requires trained personnel, which can be a bottleneck in emergency situations whenever fast deployment is critical. These challenges highlight the need for more intelligent, autonomous UAV systems that can operate reliably with minimal human intervention, adapt to changing environments, and maintain operational continuity even under adverse conditions.

The limitations of traditional UAV control methods have led researchers to integrate Machine Learning (ML) techniques to enhance drone autonomy, adaptability, and performance [13,14]. ML algorithms enable UAVs to interpret complex environmental data, make decisions in real time, and learn from previous experiences without requiring constant human input [15]. For instance, in search-and-rescue operations, ML-based image recognition can analyze live video feeds to detect human shapes or anomalies in terrain more accurately and faster than human operators [16]. In navigation, Machine Learning allows drones to dynamically adjust their flight paths in response to obstacles, changing weather, or GPS signal loss, outperforming rigid, pre-programmed routes [17]. Additionally, ML techniques used for optimal sensor fusion and predictive modeling can improve situational awareness by combining data from multiple onboard sensors (e.g., cameras, LiDAR, IMUs) to infer surroundings and anticipate future decisions, thereby reducing collision risks and enhancing stability [18,19,20].

The use of ML also reduces the reliance on high-bandwidth, low-latency communication channels by allowing the UAV to operate semi- or fully autonomously [21,22,23,24]. This is especially beneficial in remote areas or signal-compromised environments like dense forests, urban canyons, or disaster zones. Furthermore, Machine Learning can support fleet-level coordination or swarms [25], enabling multiple UAVs to collaborate, optimize coverage areas, and share learned experiences across missions. By embedding intelligence directly into the UAV’s onboard systems, these approaches not only address the shortcomings of traditional control methods but also unlock new levels of operational efficiency, scalability, and resilience. As hardware capabilities continue to improve and ML algorithms become more sophisticated, their integration into UAV systems is becoming not just a technological advancement but a necessity for meeting the demands of increasingly complex aerial missions.

The methodology used to analyze the surveyed papers in this study was structured around a systematic and comparative framework to evaluate the effectiveness of Multi-Agent Reinforcement Learning (MARL) techniques in UAV control applications. First, a comprehensive collection of recent and relevant peer-reviewed papers was assembled from high-impact journals and conferences, focusing on those that implemented MARL for UAV coordination, navigation, exploration, target tracking, and area coverage. Each paper was then examined based on a set of predefined systematic performance metrics, including environment type (e.g., discrete, continuous, simulated, or real-world), training technique (centralized, decentralized, or hybrid), swarm size, success rate, scalability, fault tolerance, and convergence speed.

For consistency, quantitative values such as swarm size and success rate were extracted directly from experimental results or approximated when reported in graphical form. Qualitative attributes like scalability were categorized as high, moderate, or low based on the authors’ claims, observed performance under varying conditions, and robustness to agent failure or environmental changes. When possible, convergence behavior was assessed through reported training curves or episode counts. This structured comparison enabled a cross-paper analysis, revealing trends, strengths, and limitations of existing approaches. The findings were tabulated and used to identify promising methods, gaps in current research, and areas requiring further investigation.

This paper is organized as follows: first, in Section 2, we present the different methods of drone control, followed by Section 3 on Reinforcement Learning (RL) and how it could be used in drone control. Section 4 presents Value-Based Multi-Agent Reinforcement Learning Techniques, followed by Policy-Based Multi-Agent Reinforcement Learning Techniques in Section 5. Multi-agent Federated Reinforcement Learning Techniques are presented in Section 6. A comparison between all three of the techniques is presented in Section 7. Open research problems and discussions are presented in Section 8 followed by the Conclusion in Section 9.

2. Methods of Drone Control

The primary purpose of Unmanned Aerial Vehicles (UAVs) is to enable commercial, cargo, and military aircraft to undertake missions without a human pilot onboard. UAVs can be operated individually or in groups and are categorized based on their level of autonomy, as shown in Figure 1: manually controlled, semi-automatic, and fully autonomous drones. Each category has distinct applications in today’s world. In this discussion, we will explore various methods and examples of how drones can be controlled, highlighting the technological diversity and the range of functionalities that UAVs provide.

2.1. Manually Controlled Drones

These UAVs are typically controlled entirely by human operators or require significant human intervention during operation. A common example of manual drone control involves using a programmed remote controller. Control signals are transmitted to UAVs via radio frequency antennas, Bluetooth technology, or Wi-Fi, depending on factors like distance, cost implications, and the quality and quantity of information to be exchanged between the drone and controller. While this approach grants operators full control over the UAVs, it is generally constrained by distance, and the controllers themselves become increasingly complex and challenging to design and implement depending on the required functionalities.

Manually controlled drones are well-suited for close-range tasks such as taking aerial photographs and conducting surveys. However, they are not effective when controlling long-range swarms; coordinating multiple drones simultaneously and accurately by several operators to avoid collisions is difficult. One potential solution is to control multiple UAVs from a single point using a single controller, but this approach complicates control as the number of UAVs increases and is not scalable.

These limitations prompted researchers, as discussed in [26], to develop a drone control system utilizing tactile feedback and impedance control, which responds to the operator’s hand signals. This system is based on the principle of impedance matching. Impedance matching is a critical concept in radio frequency (RF) communication systems, which plays a significant role in ensuring effective long-range control of Unmanned Aerial Vehicles (UAVs). In the context of UAVs, impedance matching typically refers to aligning the impedance of the transmitter and the antenna to a common standard value—usually 50 ohms. This alignment is essential because any mismatch leads to signal reflection and loss of power, which degrades the signal quality and reduces the communication range. For UAVs operating over long distances, maintaining a high-quality RF link is crucial to ensure reliable command and control [27]. Impedance matching enables efficient and reliable RF communication [28], which is essential for UAV operators to maintain stable long-range control, especially in critical applications such as search and rescue, surveillance, or remote inspection missions. While impedance matching is essential for maximizing power transfer and communication efficiency in UAV systems, it introduces design challenges, sensitivity to environmental factors, and potential limitations in adaptability and system efficiency. It also poses practical and technical challenges in swarm configurations that require dynamic, adaptable, and interference-resilient communication systems. These significant drawbacks highlight the need for enhancements in UAV control technologies, leading to the development of semi-automatic drones. These UAVs offer several advantages over fully manual drones, particularly in terms of usability, efficiency, and reliability. These UAVs can perform certain tasks—such as takeoff, landing, hovering, and waypoint navigation—autonomously while still allowing the operator to intervene or guide key decisions. This reduces the cognitive load and training requirements for users, making drone operation more accessible and less error-prone [29]. Additionally, semi-automatic systems enhance mission consistency and accuracy, especially in repetitive or complex tasks like surveying, inspection, and search and rescue. They also improve safety by providing built-in fail-safe behaviors such as return-to-home and obstacle avoidance. Overall, semi-automatic drones strike a practical balance between full autonomy and manual control, offering more reliability and efficiency without completely removing human oversight, resulting in improved efficiency, safety, and data reliability across various applications.

2.2. Semi-Automatic Drones

These drones operate with a blend of human input and autonomous decision-making. The UAVs are equipped with built-in controllers but require occasional updates on operational parameters from the operator. An example of this approach is the L1 adaptive control model proposed in [30]. This control strategy adjusts the motion control parameters of a UAV based on relevant performance and robustness metrics predefined by the system designer. While this approach enables the UAV to adapt according to established metrics, it necessitates frequent updates of these metrics by the operator to accommodate changing environmental conditions and other external factors, introducing the potential for human error and delays in adjustments.

Semi-automatic UAVs are suitable for tasks that do not require constant modifications during operation. They are particularly effective in applications like image projection, where maintaining a stable position is crucial for generating holographic images. Additionally, they are well-suited for short-duration, repetitive tasks such as delivery services, where the complexity and frequency of operational adjustments are minimal. In [31], the use of a proportional differential (PD) controller for UAV control is detailed. A proportional-derivative (PD) compensator is used to help the drone approach the desired location. The PD gains are adjusted by the operator as needed. This method aims to ensure that the drones reach their intended positions as accurately as possible. While this system significantly narrows the steady state error, it still requires human intervention to adjust the proportional and differential gains based on the drone’s position and accounting for the environmental conditions and drone dynamics. The overarching goal is to minimize human input, enhancing the autonomy of the UAVs while maintaining precise control over their operation. Reference [32] proposes a safe deployment of semi-autonomous drones in populated areas within visual line-of-sight of operators. It focuses on reducing the workload of human operators, enhancing mission efficiency, and ensuring safety through system-centric approaches. The proposed system integrates standard procedures to optimize predictability and simplicity. It includes a safety analysis to validate its reliability, and its effectiveness is demonstrated through a bridge inspection case study using simulations and scenario analysis. Its success lies in its strict predictability requirement, which enhances situational awareness and the use of the CAE block methodology to formally verify safety claims through deductive and inductive reasoning. This approach balances operational simplicity, safety, and reliability, making it both practical and effective. The research in [33] introduces a semi-autonomous drone swarm system for persistent airborne surveillance, addressing limitations of traditional methods like static cameras and helicopters. The proposed system uses a swarm mobility model optimized for maximum utility and energy efficiency, enabling drones to follow predefined trajectories without manual control. The drones stream video to a ground control station (GCS), where an object detection framework based on the YOLOv3 Real-Time Object Detection Algorithm [34] identifies objects of interest. The work of [35] describes a system and method for verifying aviation navigation signals using a semi-automated drone platform. This invention addresses the limitations of traditional flight inspection methods—which typically require manned aircraft—and proposes a cost-effective, safer, and more flexible alternative using Unmanned Aerial Vehicles (UAVs) by measuring the accuracy of signals transmitted by a localizer. It also determines the accuracy of signals transmitted by a glide slope station to perform a flight check of one or more navigational aid systems. Hutton [36] explores the use of augmented reality (AR) as a natural user interface for controlling task-oriented semi-automatic drones. The core idea is that while drone hardware has advanced rapidly, user interfaces—especially for non-expert users—remain intuitive and cognitively demanding. The research proposes leveraging AR to simplify drone control using intuitive gestures and visual overlays that reduce the training burden and enhance usability. As the capabilities of semi-autonomous drones continue to evolve—enabling users to guide drone behavior through intuitive interfaces—the natural progression is toward full autonomy. While semi-autonomous systems reduce operator workload and increase usability, they still rely on human oversight for complex decision-making and task execution. Fully autonomous drones, on the other hand, are designed to operate independently, leveraging onboard sensors, artificial intelligence, and advanced path-planning algorithms to perform missions without real-time human input. Transitioning to full autonomy not only enables greater operational efficiency and scalability but also allows drones to function reliably in environments that are too dynamic, hazardous, or remote for continuous human supervision. This shift represents a critical step in unlocking the full potential of UAVs across applications such as logistics, surveillance, infrastructure inspection, and environmental monitoring.

2.3. Fully Autonomous Drones

Efforts to further reduce human intervention in UAV operations have led to the development of various methods aimed at enhancing machine intelligence and autonomy. Autonomous machines are designed to operate with no human input, typically requiring only the initial setup and final instructions. These systems are equipped to autonomously make decisions based on assigned tasks, guided by information provided by onboard sensors and mapping of the environment. The integration of Machine Learning (ML) techniques has significantly enhanced the intelligence of Unmanned Aerial Vehicles (UAVs), enabling them to make precise decisions during operations. Recent studies highlight the pivotal role of ML in advancing UAV capabilities across various domains. For instance, Rezwan and Choi [37] provides a comprehensive survey of artificial intelligence approaches for UAV navigation, emphasizing how ML algorithms facilitate autonomous decision-making in dynamic environments. Their work categorizes different AI methodologies, including optimization-based and learning-based approaches, that contribute to efficient UAV navigation. As a result, drones have become versatile tools, applicable to a broad range of activities including military [38], search-and-rescue missions [39], disaster recovery [40], security surveillance [41], and even unsupervised package delivery [42]. The work of [43] utilized a PID controller, a semi-automated control method for UAVs, and integrated a technique called fuzzy logic to minimize human intervention during operations. Fuzzy logic, a form of logical computation, uses degrees of truth rather than the binary true or false states typical of Boolean logic. In fuzzy logic, truths are expressed on a continuum from 0 to 1, allowing for more nuanced representations, such as depicting the likelihood of an event occurring as 0.9. This approach was employed to automate the tuning of the PID controller, dynamically adjusting the gains based on the fuzzy logic algorithm. While the method demonstrates improved disturbance reduction and robust trajectory tracking compared to conventional PID controllers, the fuzzy-logic-based control algorithm can be complex for sophisticated and complex applications, which require significant computational resources.

A more straightforward approach involves employing meta-heuristic Machine Learning algorithms, such as Swarm Intelligence and Genetic Algorithms. The authors in [44] investigated the use of the Particle Swarm Optimization Algorithm (PSO), a Swarm Intelligence technique, to manage the formation of a drone swarm. Simultaneously, they utilized a PID controller to maintain the stability of individual drones. While this method simplifies some aspects of control, it still relies on the traditional PID control technique, which works well only for linear systems. Additional human intervention is needed to accomplish system stability and accurate tracking. The researchers in [45] explored a combination of Particle Swarm Optimization (PSO) and the Genetic Algorithm (GA) for controlling both individual drones and their collective behavior in a swarm. The Genetic Algorithm tailors individual control traits within the drones, whereas PSO governs the overall swarm behavior. Despite the sophistication of this combined approach, a significant drawback is the convergence issues of the meta-heuristic algorithms, which can affect the efficiency, stability, and reliability of the system. This challenge has prompted researchers to investigate alternative strategies for achieving full autonomy in UAV machines.

3. Reinforcement Learning

To possibly overcome the previously discussed limitations, researchers have turned to the use of Reinforcement Learning (RL), one of the three main paradigms of Machine Learning. Unlike data-training-based Machine Learning, RL uses learning through experience in which an agent learns to accomplish a goal by performing actions and receiving feedback in the form of rewards or penalties. The rewards inform the agent of the effectiveness of the action, influencing subsequent decisions [46]. The goal is to maximize the total reward over time. This approach is inspired by behavioral psychology and is commonly used in areas such as robotics, game playing, and autonomous systems, where learning from direct experience is essential. RL, particularly Deep Reinforcement Learning (DRL), has been instrumental in enabling Unmanned Aerial Vehicles (UAVs) to autonomously execute specific tasks with minimal human oversight. This advancement is evident across various applications, including navigation, obstacle avoidance, and mission planning [47,48]. However, a major ongoing challenge is managing a group of these UAVs, each tasked with individual and collective tasks, particularly under demanding conditions like high turbulence and severe storms. In [49], a DRL algorithm known as Proximal Policy Optimization (PPO) was implemented to control two drones equipped with distinct memory capabilities. Additionally, Curriculum Learning was employed to progressively train the drones to navigate environments ranging from those with few obstacles to others featuring multiple and complex obstacles. For example, in [50], the authors present a path planning method that combines goal-conditioned Reinforcement Learning (RL) with Curriculum Learning to enable Unmanned Aerial Vehicles (UAVs) to handle increasingly complex missions. The training begins with simple tasks, such as reaching a single target, and progressively advances to more challenging scenarios, including round-trip navigation involving multiple sub-goals. This structured approach allows the UAVs to build upon foundational skills, leading to improved performance in environments with varying levels of complexity. This method demonstrated remarkable improvements with a 92% success rate in relatively complex tasks and a 77% success rate in round-trip missions. However, the agent did not take the most efficient route to the goal in some cases. This efficiency limitation becomes more evident in complex missions involving multiple waypoints or round-trip scenarios.

The concept of RL is straightforward when applied to a single agent. In this setting, the agent interacts with an environment by making actions based on a policy, observes the impact of the actions, and receives rewards or penalties. The agent’s goal is to learn an optimal policy that maximizes the cumulative reward over time. The environment is typically considered stationary, meaning its dynamics do not change based on the agent’s actions. This allows the agent to gradually improve its decision-making through trial and error, leveraging algorithms like Q-learning [51,52], SARSA [53], or policy gradient methods [54]. The simplicity of this setup—one agent, one policy, one learning objective—makes it easier to model, analyze, and implement. It provides a controlled framework where concepts such as exploration vs. exploitation, reward shaping, and value estimation can be clearly defined and systematically improved. However, complexities arise when multiple agents are involved. Optimizing the learning process to train multiple agents efficiently, with minimal computational resources and script usage, becomes a challenge. Additionally, for parameters that provide a continuous action space—such as drone velocity, acceleration, or angular control—selecting the most suitable algorithm to handle such dynamics is crucial. In other words, adapting Reinforcement Learning (RL) algorithms for such scenarios requires the use of specialized methods beyond traditional discrete-action algorithms like Q-learning. In such environments, policy-based and actor–critic algorithms are preferred, as they are better suited for learning continuous control policies. More advanced actor–critic approaches like Deep Deterministic Policy Gradient (DDPG) [55], Twin Delayed DDPG (TD3) [56] and Soft Actor–Critic (SAC) [57] offer improved stability and performance. These methods combine a value function (critic) with a policy function (actor), allowing for efficient learning in high-dimensional, continuous domains.

Reinforcement Learning (RL) relies on the assumption that an agent operates within a Markovian environment, leading to decision problems commonly modeled by the Markov Decision Process (MDP) [58]. The foundational concept in this model is the Markov Property, which asserts that the probability of transitioning to the next state depends solely on the current state and not on any previous states [59].

A Markov Decision Process (MDP) is a mathematical framework for modeling decision-making in environments where outcomes are partly random and partly under the control of an agent. A Markov Decision Process (MDP) is defined as a 5-tuple:

$$\mathcal{M}=(\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma )$$

where

• $\mathcal{S}$ is a finite set of states.
• $\mathcal{A}$ is a finite set of actions.
• $\mathcal{P}(s^{\prime }\mid s,a)$ is the transition probability function, giving the probability of transitioning to state $s^{\prime }$ from state s after taking action a.
• $\mathcal{R}(s,a)$ is the reward function, specifying the expected reward received after taking action a in state s.
• $\gamma \in [0,1]$ is the discount factor, representing the importance of future rewards.

The agent’s objective is to learn a policy $\pi :\mathcal{S}\to \mathcal{A}$ that maximizes the expected cumulative discounted reward:

$${\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^t\mathcal{R}(s_t,a_t)\right]$$

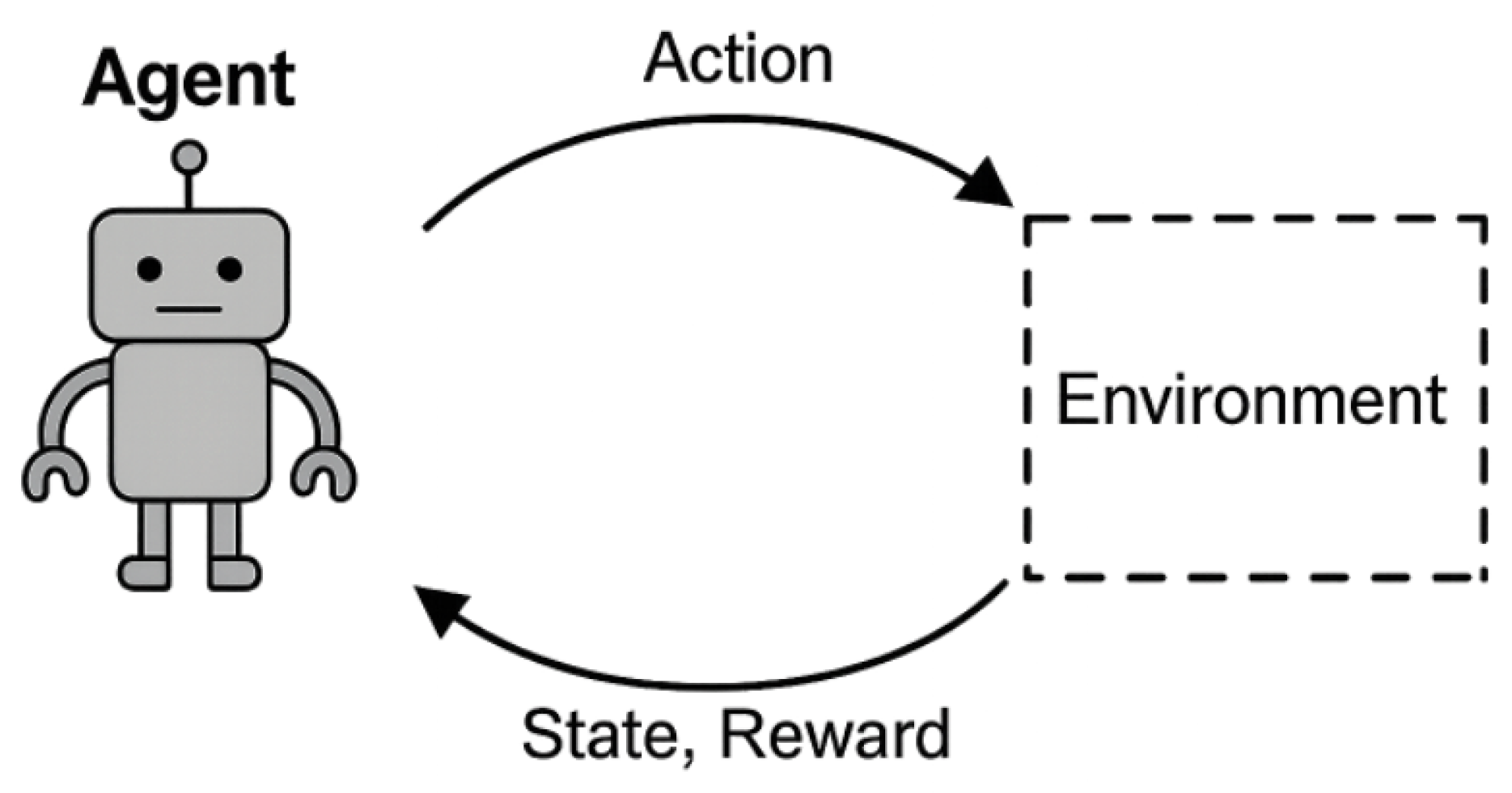
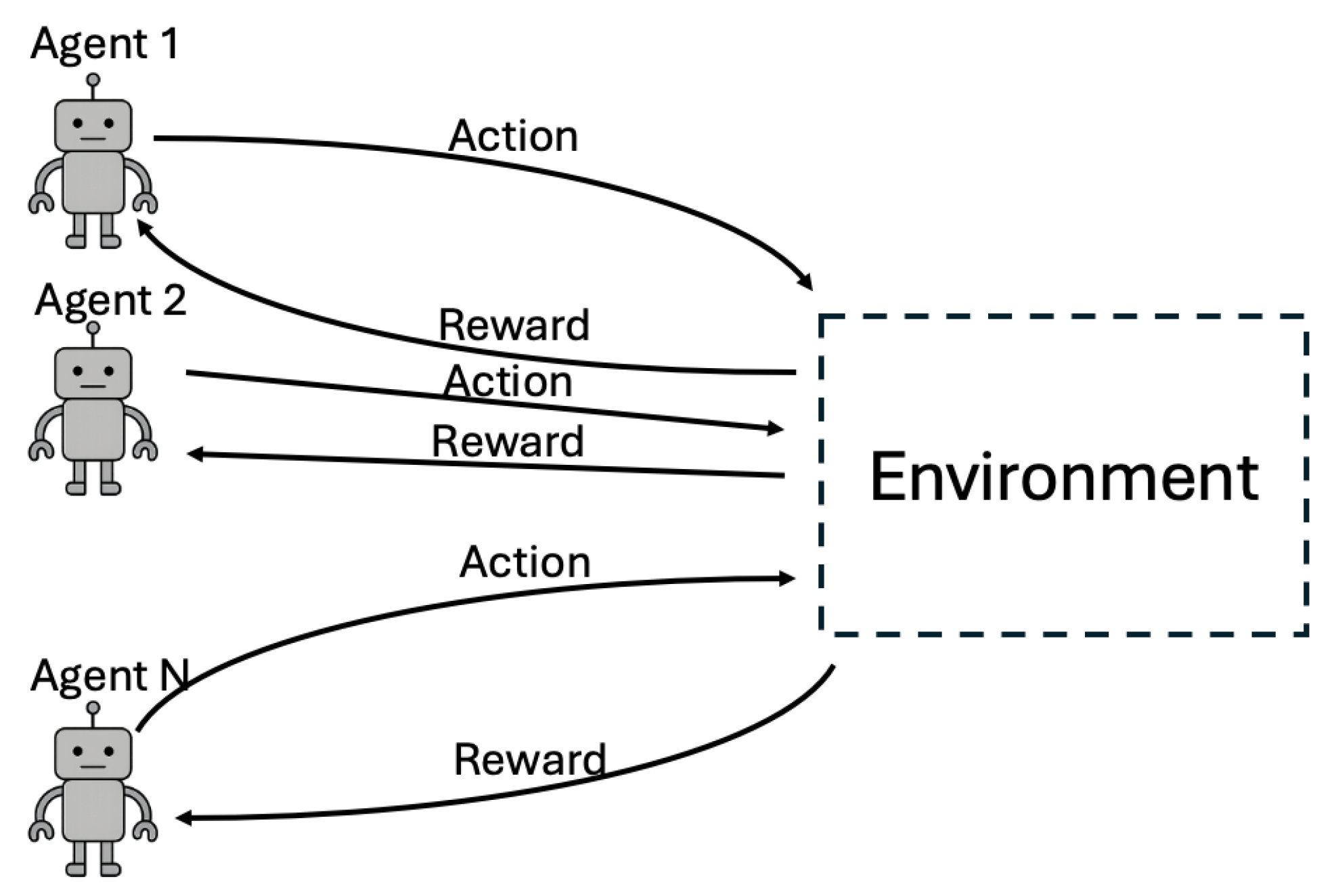
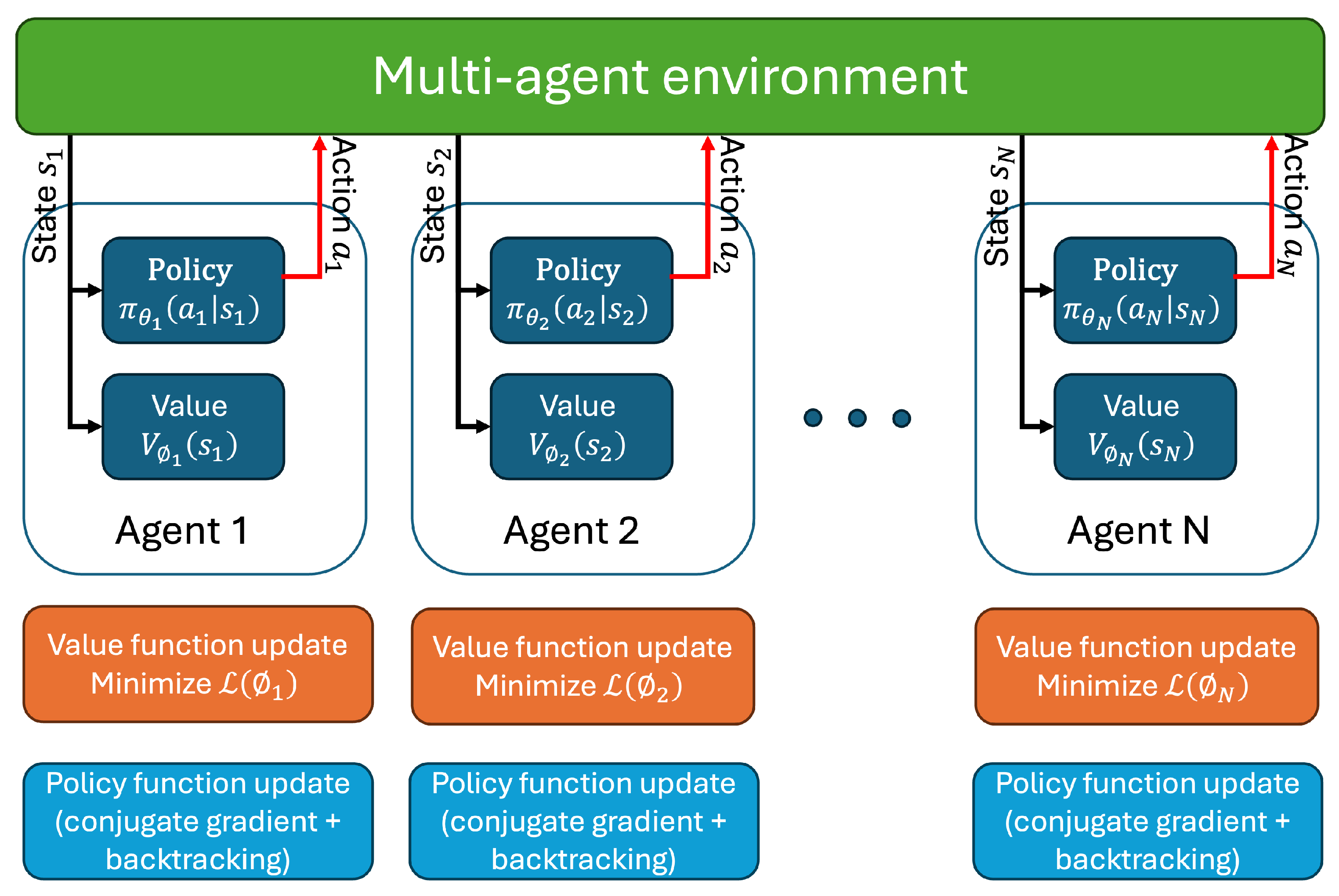
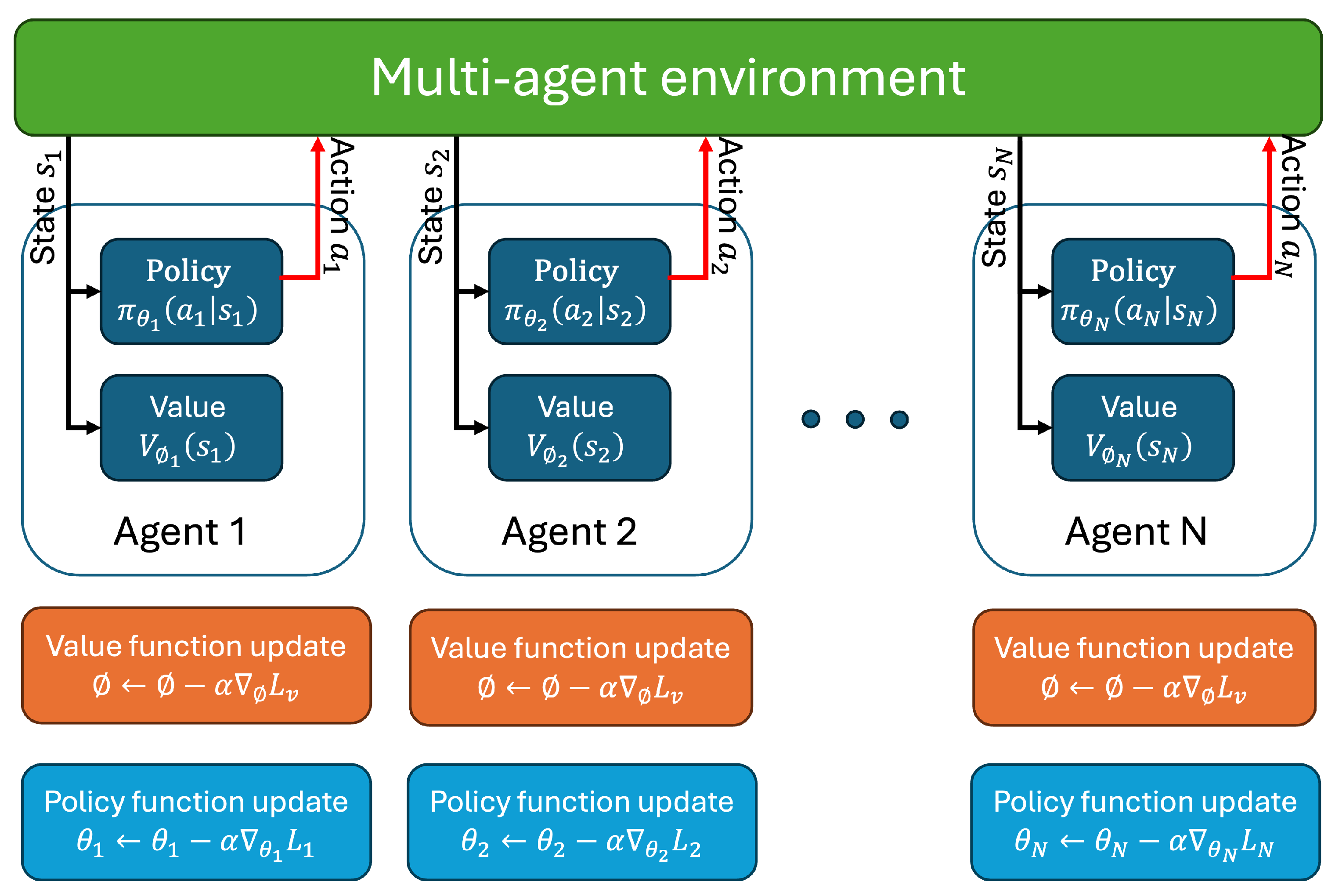
The Multi-Agent Reinforcement Learning (MARL) algorithm and its variations address the complexities of controlling multiple agents, such as a swarm of UAVs. This paper explores a broad spectrum of drone control methods, focusing on how MARL facilitates the coordination of UAV swarms during specific operations. Unlike Single-Agent Reinforcement Learning (SARL), which involves one agent interacting solely with its environment Figure 2, MARL introduces multiple agents into the same environment Figure 3. A Multi-Agent Reinforcement Learning (MARL) environment can be modeled as a Markov Game (Stochastic Game), defined by the tuple

$$\mathcal{G}=(\mathcal{S},{\left\{{\mathcal{A}}^i\right\}}_{i=1}^N,\mathcal{P},{\left\{{\mathcal{R}}^i\right\}}_{i=1}^N,\gamma )$$

where

• $\mathcal{S}$ is the set of global states.
• ${\mathcal{A}}^i$ is the action space for agent i, and the joint action space is $\mathcal{A}={\mathcal{A}}^1\times \cdots \times {\mathcal{A}}^N$.
• $\mathcal{P}(s^{\prime }\mid s,a^1,\dots ,a^N)$ is the transition function, determining the probability of transitioning to state $s^{\prime }$ given current state s and joint action $(a^1,\dots ,a^N)$.
• ${\mathcal{R}}^i(s,a^1,\dots ,a^N)$ is the reward function for agent i.
• $\gamma \in [0,1]$ is the discount factor.

Figure 2. Pictorial representation of Single-Agent Reinforcement Learning. The figure shows the flow of interaction in a typical Single-Agent Reinforcement Learning algorithm.

Figure 2. Pictorial representation of Single-Agent Reinforcement Learning. The figure shows the flow of interaction in a typical Single-Agent Reinforcement Learning algorithm.

Figure 3. Pictorial representation of Multi-Agent Reinforcement Learning. The figure shows the flow of interaction in a typical Multi-Agent Reinforcement Learning Algorithm.

Figure 3. Pictorial representation of Multi-Agent Reinforcement Learning. The figure shows the flow of interaction in a typical Multi-Agent Reinforcement Learning Algorithm.

Each agent i seeks to learn a policy ${\pi }^i:\mathcal{S}\to {\mathcal{A}}^i$ that maximizes its own expected return:

$${\mathbb{E}}_{{\pi }^1,\dots ,{\pi }^N}\left[\sum _{t=0}^{\infty }{\gamma }^t{\mathcal{R}}^i(s_t,a_t^1,\dots ,a_t^N)\right]$$

In MARL, these agents interact not only with the environment but also with each other  [60]. While each agent individually observes the shared environment’s state and decides on an action, it must also consider the actions and potential reactions of other agents. This scenario presents a unique challenge: although there is only one environment and one collective state, the presence of multiple agents necessitates individual policies and results in diverse rewards. Other major challenges arise from the non-stationarity of the environment and the scaling or dimensionality [61,62]. MARL algorithms can be broadly categorized into three types [63]: value-based MARL, which focuses on updating the value functions of state–action pairs; policy-based MARL, which directly optimizes the policy functions guiding the agents’ actions; and actor–critic methods, which combine the strengths of both value-based and policy-based approaches. The “actor” updates the policy directly, while the “critic” evaluates the action by estimating value functions [64]. This combination allows for more stable and efficient learning in complex environments [65]. Actor–critic methods are generally considered a subclass of policy-based methods in the field of Reinforcement Learning [66].

As mentioned before, Reinforcement Learning (RL) algorithms can be categorized based on several criteria. Firstly, they are divided into value-based and policy-based algorithms, depending on whether the updates are applied to value functions or policies. Secondly, they can be classified according to the nature of their state and action spaces into discrete- or continuous-time states and action RL algorithms. Lastly, RL algorithms are differentiated based on the number of agents they manage, categorized as Single-Agent and Multi-Agent Reinforcement Learning algorithms. In subsequent sections, these classifications are explored in greater detail.

4. Value-Based Multi-Agent Reinforcement Learning Techniques

The primary goal of value-based Reinforcement Learning (RL) methods is to accurately estimate the optimal state–action or state–value function, commonly referred to as the optimal Q-function ($Q_{\ast }^{\pi }$). The optimal policy can be attained by utilizing a greedy action of the estimated Q-value [67]. Value-based RL algorithms aim to achieve convergence by consistently updating the Q-function values to reflect the expected rewards. In the context of UAVs, which are often modeled in grid world environments where the operational space is represented as a discrete grid of cells, the actions can be discretized, with the primary actions being movements from one grid cell to another. Value-based Multi-Agent Reinforcement Learning (MARL), which operates in discrete action spaces, is well-suited for managing such tasks.

4.1. QMIX

QMIX is a deep Multi-Agent Reinforcement Learning (MARL) technique designed to learn decentralized policies within a centralized training framework, effectively utilizing additional state information [68]. This approach enables the learning of an optimal joint action–value function that can be decomposed into individual action–value functions for each agent, simplifying control and coordination. In [43], MARL was applied to the strategy game StarCraft, where multiple agents are controlled to defeat opponents, simulating the coordination of unmanned vehicle movements. Two MARL techniques, QMIX and Value Decomposition Network (VDN), were used, both employing a centralized reward system for the agents. It was observed that QMIX outperformed VDN in terms of efficacy. However, the discrete nature of the actions in this scenario made them particularly well-suited for value-based methods.

The QMIX learning technique high level structure is presented in Figure 4, and the algorithm is presented in Algorithm 1. The key idea of the algorithm is to allow centralized training with access to the global state s and decentralized execution, where each agent selects actions based only on its local observation $o_i$. Each agent learns an individual action–value function $Q_i(o_i,a_i)$, conditioned only on its local observation $o_i$. During training, these individual Q-values are combined through a mixing network into a global action–value pair:

$$Q_{\mathrm{tot}}(s,a)=f_{\varphi }(Q_1,Q_2,\dots ,Q_N;s)$$

Here, $f_{\varphi }$ is a mixing network parameterized by $\varphi$ that incorporates the global state s to guide the learning process. To ensure that decentralized execution is feasible, the mixing network is constrained to be monotonic in each agent’s Q-value:

$${\displaystyle \frac{\partial Q_{\mathrm{tot}}}{\partial Q_i}}\ge 0,\forall i$$

Algorithm 1 QMIX Algorithm

1: Parameters $\theta$ of agent networks $\left\{Q_i\right\}$ for $i=1$ to N   2: Parameters $\varphi$ of the mixing network $Q_{\mathrm{tot}}$   3: Target networks $\left\{Q_i^{\prime }\right\}$ and $Q_{\mathrm{tot}}^{\prime }$ initialized with $\theta$ and $\varphi$   4: Replay buffer $\mathcal{D}$   5: for episode $=1$ to $MaxEpisodes$ do   6:       Initialize environment, get global state s and local observations $\{o_1,\dots ,o_N\}$   7:       for $t=1$ to T (episode length) do   8:             for each agent $i=1$ to N do   9:                   Select action $a_i$ using $ϵ$-greedy policy from $Q_i\left(o_i\right)$ 10:             end for 11:             Execute joint action $a=(a_1,\dots ,a_N)$ 12:             Observe reward r, next state $s^{\prime }$, next observations $\{o_1^{\prime },\dots ,o_N^{\prime }\}$ 13:             Store $(s,\left\{o_i\right\},a,r,s^{\prime },\left\{o_i^{\prime }\right\})$ in replay buffer $\mathcal{D}$ 14:       end for 15:       for training_step = 1 to NumUpdates do 16:             Sample mini-batch from $\mathcal{D}$ each transition $(s,\left\{o_i\right\},a,r,s^{\prime },\left\{o_i^{\prime }\right\})$ 17:             for each agent $i=1$ to N do 18:                   Compute $a_i^{\prime }=arg{max}_{a^{\prime }}{Q}_i^{\prime }(o_i^{\prime },a^{\prime };{\theta }_i^{\prime })$ 19:                   Compute $Q_i^{\mathrm{next}}=Q_i^{\prime }(o_i^{\prime },a_i^{\prime };{\theta }_i^{\prime })$ 20:             end for 21:             Compute $Q_{\mathrm{tot}}^{\mathrm{next}}=\mathrm{MixingNetwork}(Q_1^{\mathrm{next}},\dots ,Q_N^{\mathrm{next}}\mid s^{\prime };{\varphi }^{\prime })$ 22:             $y=r+\gamma Q_{\mathrm{tot}}^{\mathrm{next}}$ 23:             for each agent $i=1$ to N do 24:                   Compute $Q_i^{\mathrm{current}}=Q_i(o_i,a_i;{\theta }_i)$ 25:             end for 26:             Compute $Q_{\mathrm{tot}}^{\mathrm{current}}=\mathrm{MixingNetwork}(Q_1^{\mathrm{current}},\dots ,Q_N^{\mathrm{current}}\mid s;\varphi )$ 27:             Compute loss $\mathcal{L}={(y-Q_{\mathrm{tot}}^{\mathrm{current}})}^2$ 28:       end for 29:       Update $\theta$ and $\varphi$ using gradient descent on L 30:       Every C steps: update target networks: ${\theta }^{\prime }\leftarrow \theta$, ${\varphi }^{\prime }\leftarrow \varphi$ 31: end for

This constraint guarantees that maximizing $Q_i(o_i,a_i)$ for each agent leads to an increase in the joint $Q_{\mathrm{tot}}$, making decentralized greedy action selection effective. During training, transitions are stored in a replay buffer in the form

$$(s,\left\{o_i\right\},\mathbf{a},r,s^{\prime },\left\{o_i^{\prime }\right\})$$

The update rule uses the target

$$y=r+\gamma Q_{\mathrm{tot}}^{\prime }(s^{\prime },{\mathbf{a}}^{\prime })$$

where each agent i selects $a_i^{\prime }=arg{max}_a{Q}_i^{\prime }(o_i^{\prime },a)$ using the target networks. The loss is computed as:

$$\mathcal{L}={\left(y-Q_{\mathrm{tot}}(s,\mathbf{a})\right)}^2$$

Gradient descent is then applied to minimize this loss and update both agent networks and the mixing network.

There are many systems where the the QMIX algorithm was employed to control multiple agents such as in the StarCraft Multi-Agent Competition and in a multi-player soccer game, as described in [69]. In the soccer simulation, the environment featured 22 players, each with a specific objective: either attacking or defending by moving towards the ball. QMIX was effectively implemented in this context, enabling the simulation of straightforward decision-making and actions. In contrast, the StarCraft game presents a more complex scenario. As a strategy game requiring numerous decisions, the actions in StarCraft are more intricate than those in the soccer game, though they remain discrete. The game’s rapidly changing states and environmental complexity add further challenges. Despite these complexities, QMIX was successfully applied to StarCraft, demonstrating its adaptability to environments with discrete actions and varying levels of decision-making complexity.

4.2. Deep Q Network (DQN)

The core concept of Q-learning involves updating the values of $Q(.)$ iteratively for all state–action pairs in a structure known as the Q-table [70]. This approach can become computationally intensive in scenarios involving large action spaces [71,72]. In such cases, function approximation is employed to estimate Q values [71]. For instance, a function with parameter $\theta$ to compute Q values can be denoted as $Q(s,a;\theta )$. Function approximation is typically nonlinear, which can lead to instability in Q-learning [73,74]. To address the computational challenges and improve stability, the Deep Q-Network (DQN) was developed. It enhances the training process of Q-learning by incorporating experience replay and periodically updating the Q-values toward specified target values. It combines Q-learning with deep neural networks to handle environments with high-dimensional state spaces. It was introduced by DeepMind in 2013 and gained attention after successfully playing Atari 2600 games directly from pixel inputs, as detailed in [75].

The Multi-Agent Deep Q-Network (MADQN) algorithm extends the classical Deep Q-Network (DQN) to environments involving multiple agents. Each agent independently learns its own Q-function, as shown in Figure 5, using local observations and rewards. The algorithm shown in Algorithm 2 is fully decentralized during both training and execution. During the initialization phase, each agent initializes its Q-networks $Q_i$ and target networks $Q_i^{\mathrm{target}}$ with weights ${\theta }_i$ and ${\theta }_i^{\prime }$, respectively, and creates a replay buffer ${\mathcal{D}}_i$ for each agent $i\in \{1,\dots ,N\}$. During each episode, the environment resets and obtains initial states $\{s_1,s_2,\dots ,s_N\}$. Each agent i selects an action $a_i$ and then executes a joint action $\{a_1,\dots ,a_N\}$ in the environment while observing next states $\{s_1^{\prime },\dots ,s_N^{\prime }\}$ and rewards $\{r_1,\dots ,r_N\}$. Each agent stores its experience $(s_i,a_i,r_i,s_i^{\prime })$ in its replay buffer ${\mathcal{D}}_i$. After sampling, a minibatch of transitions from ${\mathcal{D}}_i$ the target is computed:

$$y_i=r_i+\gamma \underset{a^{\prime }}{max}{Q}_i^{\mathrm{target}}(s_i^{\prime },a^{\prime };{\theta }_i^{\prime })$$

Algorithm 2 Multi-Agent Deep Q-Network (MADQN) Algorithm

1: Initialize replay buffer ${\mathcal{D}}_i$ for each agent $i\in \{1,\dots ,N\}$   2: Initialize Q-network $Q_i(s_i,a_i;{\theta }_i)$ with random weights ${\theta }_i$ for each agent   3: Initialize target Q-network $Q_i^{\mathrm{target}}(s_i,a_i;{\theta }_i^{\prime })$ with ${\theta }_i^{\prime \leftarrow {\theta }_i}$   4: for episode $=1$ to $MaxEpisodes$ do   5:       Initialize environment and get initial states $\{s_1,s_2,\dots ,s_N\}$   6:       for $t=1$ to T do   7:             for each agent $i=1$ to N do   8:                   Select action $a_i$: with probability $ϵ$, select random $a_i$ otherwise, select $a_i=arg{max}_a{Q}_i(s_i,a;{\theta }_i)$   9:             end for 10:             Execute joint action $\{a_1,\dots ,a_N\}$ in environment 11:             Observe next states $\{s_1^{\prime },\dots ,s_N^{\prime }\}$ and rewards $\{r_1,\dots ,r_N\}$ 12:             for each agent $i=1$ to N do 13:                   Store transition $(s_i,a_i,r_i,s_i^{\prime })$ in buffer ${\mathcal{D}}_i$ 14:             end for 15:             for each agent $i=1$ to N do 16:                   Sample minibatch of transitions $(s_i,a_i,r_i,s_i^{\prime })$ from ${\mathcal{D}}_i$ 17:                   Compute target: $$y_i=r_i+\gamma \underset{a^{\prime }}{max}{Q}_i^{\mathrm{target}}(s_i^{\prime },a^{\prime };{\theta }_i^{\prime })$$ 18:                   Update ${\theta }_i$ by minimizing: $$\mathcal{L}\left({\theta }_i\right)={(y_i-Q_i(s_i,a_i;{\theta }_i))}^2$$ 19:             end for 20:             if every C steps then 21:                   Update target networks: ${\theta }_i^{\prime }\leftarrow {\theta }_i$ for all agents i 22:             end if 23:       end for 24: end for

Parameters ${\theta }_i$ are then updated by minimizing the loss:

$$\mathcal{L}\left({\theta }_i\right)={\left(y_i-Q_i(s_i,a_i;{\theta }_i)\right)}^2$$

In [76], DQN was implemented in swarms of two and three drones tasked with surveilling four targets on a simulated 2D grid plane. Transfer Learning was integrated into the DQN algorithm to facilitate adapting the learning model to new drones added to the network. The drones operated within discrete grid boxes, allowing the DQN algorithm to effectively manage the swarm. Initially, a swarm of two drones was created by transferring the model from the primary UAV to the additional drone, which was effective in the absence of an established UAV network. However, when a third drone was added to the established network, the Transfer Learning process became less efficient, slowing the learning rate, but eventual convergence was achieved. The main issues with the presented results are scalability, the lack of a realistic scenario, and limited evaluation against benchmarks such as QMIX, MADDPG, and MAPPO. In [77], combat drones were simultaneously trained using both the Multi-Agent Deep Q-Network (MADQN) and Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithms for strike force and mobility tasks. The authors explored three training strategies for MADQN. The first strategy, scenario transfer, involved transferring learned models from simple combat tasks to other drones. The second strategy, self-play training, allowed agents to continually learn by iterating the training algorithm. The third strategy, rule-coupled training, incorporated rules from aerial combat operations into the training algorithm. Combining these three strategies significantly enhanced both the training effectiveness and post-training functionality of the UAVs. In [78], SERT-DQN, a novel Reinforcement Learning algorithm was presented. It was designed to optimize multi-agent coverage path planning (CPP) for UAV-UGV systems, particularly in uncertain and fault-prone environments like Mars. The framework combines decentralized DQN-based primary networks for individual UAVs with a centralized intermediate Q-network located on the UGV, allowing coordination through a hybrid local-global policy structure. The SERT-DQN algorithm significantly improves upon both regular DQN and QMIX in the context of multi-agent coverage path planning (CPP) but also introduces new trade-offs. For example, SERT-DQN introduces greater computational complexity and dependency on centralized updates, making it more demanding to implement in real-world scenarios

The effectiveness of decomposition in Value-Based Multi-Agent Reinforcement Learning (MARL) lies in the ability to approximate a global action–value function $Q_{\mathrm{tot}}(\mathbf{s},\mathbf{a})$ using individual agent value functions $Q_i(s_i,a_i)$, thereby enabling decentralized execution while retaining the advantages of centralized training. In simple settings such as Value Decomposition Networks (VDNs), the total value function is linearly decomposed as $Q_{\mathrm{tot}}\approx {\sum }_i{Q}_i$, which is theoretically sound under the assumptions of additive rewards and independent agent transitions. However, this linear formulation cannot capture complex inter-agent dependencies. To address this limitation, QMIX introduces a monotonic mixing network that guarantees $\partial Q_{\mathrm{tot}}/\partial Q_i\ge 0$, ensuring that individual greedy actions with respect to $Q_i$ still correspond to the maximization of the global action–value function. This allows QMIX to be more expressive than VDN while supporting decentralized policies. Nonetheless, QMIX cannot model non-monotonic interactions or highly coordinated joint behaviors. Advanced methods such as QTRAN [79,80] relax the monotonicity constraint via constrained optimization, achieving theoretically complete representational power, albeit with increased computational cost. Further extensions like MAVEN [81] and ROMA incorporate latent variables or role-based decompositions to capture diverse coordination patterns among agents. Overall, while decomposition facilitates scalable learning and decision-making, it imposes structural biases that may limit the algorithm’s ability to learn optimal joint policies in environments with complex agent interactions.

Table 1. Comparison between QMIX and MADQN in Multi-Agent Reinforcement Learning.

Feature	QMIX	MADQN
Mode of Operation	Utilizes a mixing network to derive decentralized policies from centralized action–state value functions.	Integrates Q-learning with deep neural networks to enhance the approximation capability of Q-functions.
Performance in Partially Observable Environments	Highly effective due to its decentralized policy design. Ideal for defense or combat scenarios where agents must act on limited information, such as hidden enemy locations.	Less suitable for partially observable settings. Limited ability to disambiguate ally vs. enemy behavior makes it inadequate for military rescue missions.
Scalability	Scalability is limited; the addition of agents after training may degrade performance due to reliance on a fixed network structure.	Highly scalable; supports dynamic swarm expansion without significant loss in performance, learning stability, or accuracy.
Computational Complexity	Requires frequent value function updates, increasing computational demands. This can affect drone payload constraints and swarm design.	Performs periodic updates, reducing overall computational load. Enables compact hardware deployment and energy-efficient swarm operations.

presents a brief comparison between the two most common Value-Based Multi-Agent Reinforcement Learning Techniques, QMIX and MADQN, in Multi-Agent Reinforcement Learning. On the other hand,

Table 2. Comparison between articles on Value-Based Multi-Agent Reinforcement Techniques.

Paper ID	Environment Type	Training Technique	Swarm Size	S.R. 4	Scal. 5	F.T. 7	T.L. 3	Conv. 6
[76]	Grid-based UAV surveillance	Distributed DQN,	3 UAVs	60–80%	High	N/A 1	Yes	40,000
[77]	Multi-UAV combat (RTS-style)	MADQN, MADDPG	Two teams, ∼5 UAVs	70–90%	Mod. 2	Partial	Yes	15 × 106
[78]	Hybrid UAV–UGV coverage mission	SERT-DQN	5 UAVs	90%	Mod. (UGV-limited)	Yes	N/A	N/A
[69]	Multi-task StarCraft micromanagement	REFIL (QMIX)	Variable (6–20 agents)	60–80%	High	N/A	Yes	107

¹ N/A stands for Not available. ² Mod. stands for Moderate. ³ T.L. stands for Transfer Learning. ⁴ S.R. stands for Success Rate. ⁵ Scal.. stands for Scalability. ⁶ Conv. stands for Convergence (#of Steps). ⁷ F.T. stands for Fault Tolerance.

compares four recent value-based Multi-Agent Reinforcement Learning (MARL) frameworks applied to UAV and multi-agent coordination tasks. The algorithms span a range of domains, including UAV swarm surveillance [76], combat scenarios [77], hybrid UAV–UGV coverage missions [78], and multi-task micromanagement in UAVs [69]. Key metrics such as scalability, training technique, fault tolerance, and convergence speed are considered. Notably, [78] stands out for its explicit fault-tolerant design using SERT-DQN, while [76] demonstrates strong scalability and effective Transfer Learning, whereas [77] achieves improved training efficiency through scenario-transfer and self-play.

5. Policy-Based Multi-Agent Reinforcement Learning Techniques

Policy-based methods, also known as policy gradient methods, aim to directly model and optimize the policy. The parameterized policy, represented as ${\pi }_{\theta }\left(a\right|s)$, is defined as a function of $\theta$ [82]. The objective function’s value depends on this policy, and various algorithms are employed to optimize the parameter $\theta$ to maximize the reward, as outlined in [82]. Policy-Based Multi-Agent Reinforcement Learning (MARL) techniques are a pivotal framework in the field of Reinforcement Learning, especially when dealing with environments involving multiple interacting agents [67,83]. These methods synergize policy-based (actor) and value-based (critic) approaches, enabling agents to learn optimal behaviors in complex, dynamic, and often partially observable settings [84,85]. At the core of policy-based methods lies the direct optimization of policies, which can be particularly advantageous in high-dimensional or continuous action spaces [86,87]. Unlike value-based methods that derive policies indirectly through value functions, policy-based approaches adjust the policy parameters directly to maximize expected returns. This direct optimization can lead to more stable and efficient learning, especially in scenarios where value estimation is challenging [88]. In multi-agent scenarios, policy-based methods must account for the non-stationarity introduced by concurrently learning agents, making the design of effective algorithms particularly challenging [83,89]. Techniques such as Centralized Training with Decentralized Execution (CTDE) have been proposed to address these challenges, allowing agents to learn coordinated behaviors while operating independently during execution [84,90]. Policy-based MARL techniques have been applied across various domains, including autonomous driving, robotic coordination, and resource management [91,92]. For instance, in network load balancing, these methods have been utilized to dynamically distribute traffic, optimizing performance and reducing congestion [92]. In robotic swarms, policy-based algorithms facilitate coordinated behaviors without centralized control, enhancing adaptability and robustness [93,94]. One can conclude that these methods are particularly well-suited for applications requiring continuous action control, such as robotic manipulations and drone speed adjustments. Despite their successes, policy-based MARL methods face challenges such as scalability to large agent populations, efficient communication protocols, and robustness to partial observability [62,67]. Future research is directed toward developing more scalable architectures, incorporating meta-learning for adaptability, and designing algorithms that can operate effectively with limited communication [67,68]. In the following subsections, we will explore three Policy-Gradient Multi-Agent Reinforcement Learning (MARL) algorithms and their applications in UAV control.

5.1. Deep Deterministic Policy Gradient (DDPG)

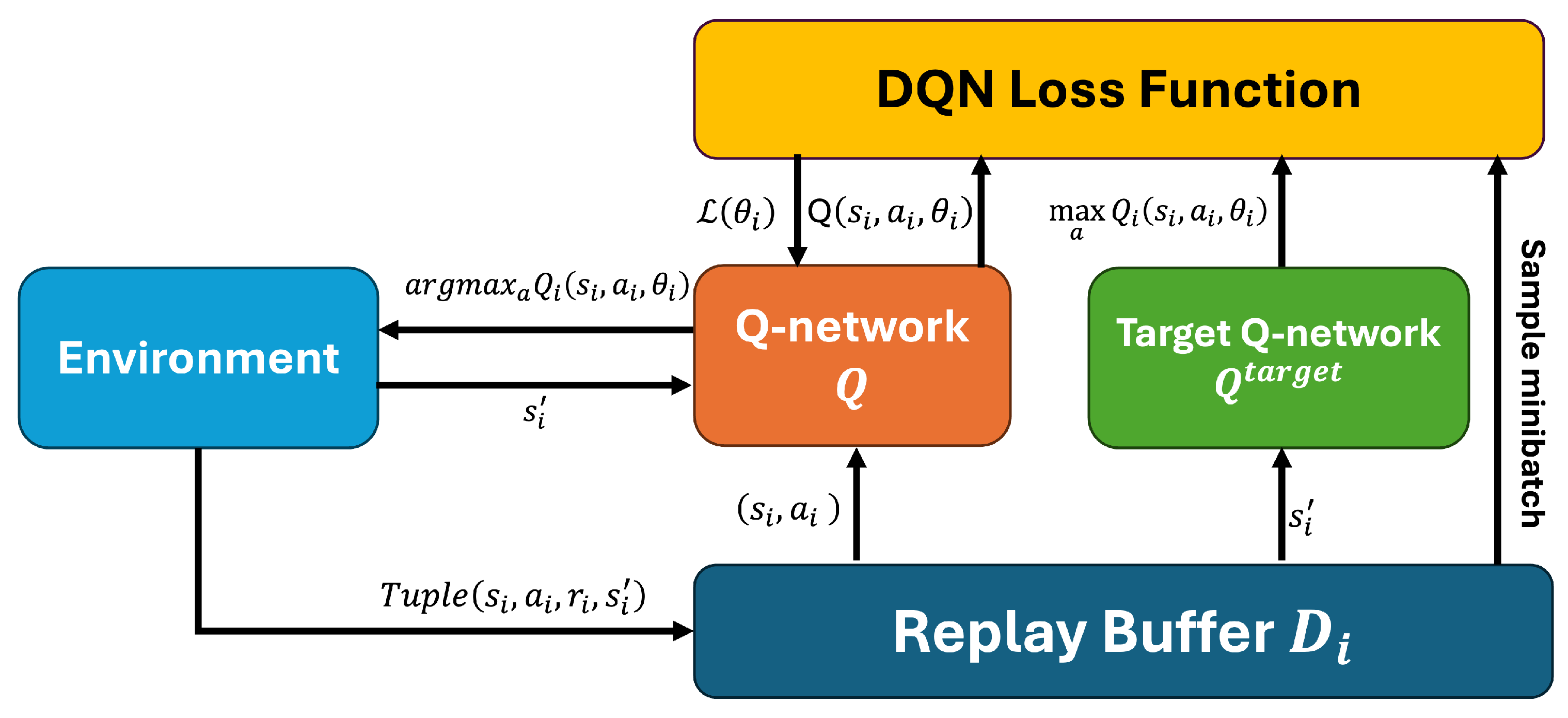
Deep Deterministic Policy Gradient (DDPG) is a model-free, off-policy actor–critic algorithm that employs a deterministic policy to address the challenge of discrete action spaces inherent in Deep Q-Networks (DQNs) [95]. In contrast, DQNs stabilize the Q-function learning process through experience replay and a frozen target network. Multi-agent DDPG (MADDPG) extends the DDPG framework to environments with multiple agents operating synchronously, each using locally observed information [84]. In MADDPG, each agent perceives the environment as dynamic due to the continuous policy updates from other agents, whose policies are unknown. It was designed to address the challenges posed by decentralized decision-making and non-stationarity in multi-agent systems. It was introduced by [84] as an extension of the Deep Deterministic Policy Gradient (DDPG) algorithm [55] to cooperative and competitive environments involving multiple agents. In Single-Agent Reinforcement Learning, DDPG has been shown to perform well in continuous action spaces using a deterministic actor–critic architecture. However, applying DDPG independently in multi-agent environments leads to non-stationary learning dynamics, as the environment’s state distribution changes with the evolving policies of other agents [83,89]. This non-stationarity can degrade learning performance or even lead to divergence. To address this, MADDPG introduces a centralized training and decentralized execution (CTDE) paradigm. During training, each agent has access to a centralized critic that takes into account the global state and actions of all agents. This allows the critic to estimate more accurate gradients despite the non-stationarity caused by other learning agents. However, the actor (policy network) for each agent uses only local observations during execution, enabling scalability and applicability in real-world distributed systems [84].

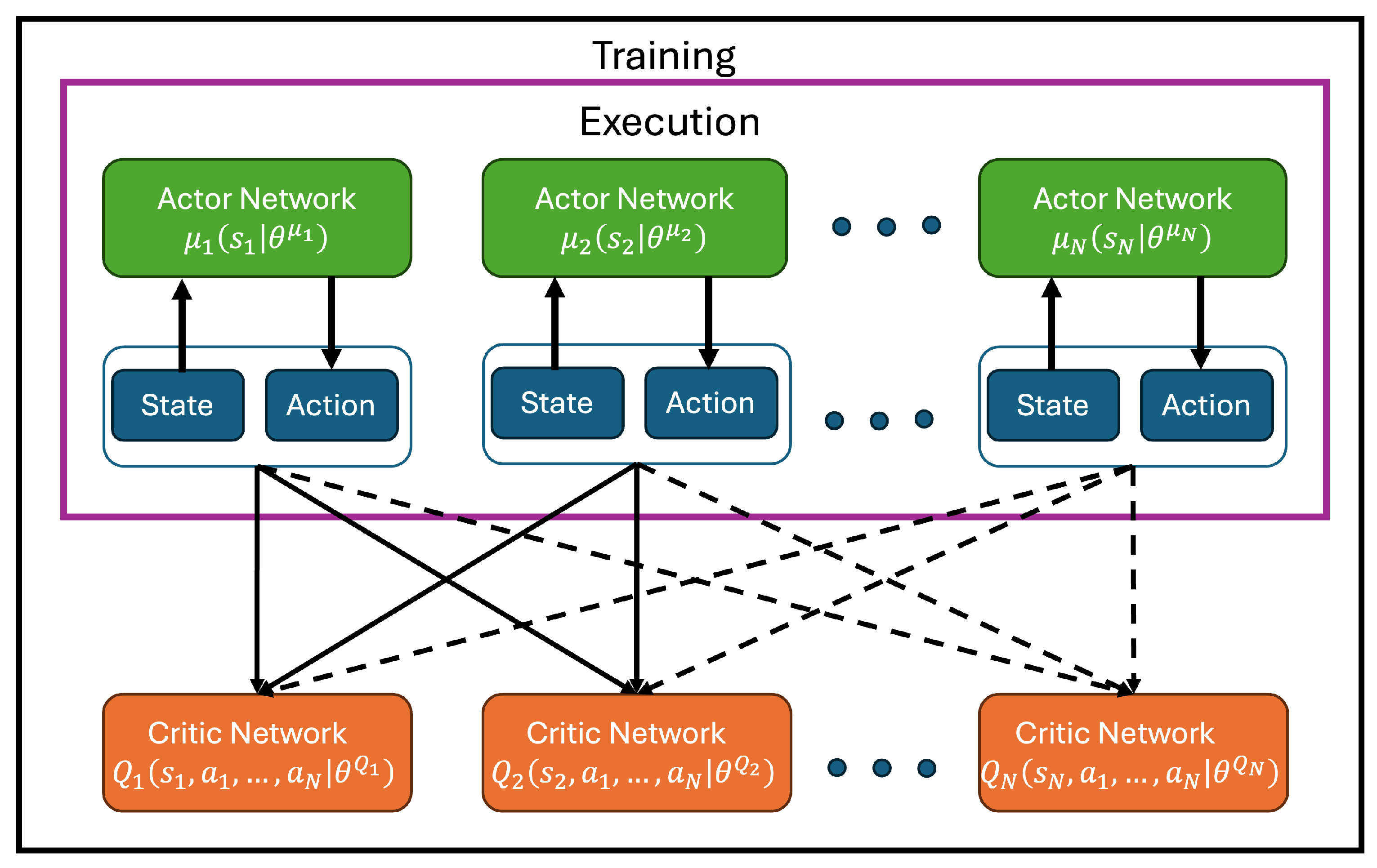
The Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithm structure is shown in Figure 6, while the algorithm is shown in Algorithm 3. It extends the Deep Deterministic Policy Gradient (DDPG) method to multi-agent environments by adopting the Centralized Training with Decentralized Execution (CTDE) paradigm. In MADDPG, each agent $i\in \{1,\dots ,N\}$ learns a deterministic policy (actor) ${\mu }_i(s_i;{\theta }^{{\mu }_i})$, where $s_i$ is the local observation of agent i and ${\theta }^{{\mu }_i}$ represents the parameters of the actor network. The corresponding action is given by $a_i={\mu }_i\left(s_i\right)$.

During training, each agent also maintains a centralized critic network $Q_i(s_i,a_1,\dots ,a_N;$${\theta }^{Q_i})$, where x is the global state (which may include all agents’ observations), $a_1,\dots ,a_N$ are the actions of all agents, and ${\theta }^{Q_i}$ are the critic’s parameters. The target value for critic training is computed as

$$y_i=r_i+\gamma Q_i^{\prime }(s_i^{\prime },a_1^{\prime },\dots ,a_N^{\prime };{\theta }^{Q_i^{\prime }}),$$

(1)

where $r_i$ is the reward received by agent i, $\gamma \in [0,1]$ is the discount factor, $Q_i^{\prime }$ is the target critic network, and $a_j^{\prime }={\mu }_j^{\prime }(s_j^{\prime };{\theta }^{{\mu }_j^{\prime }})$ are the actions predicted by the target actor networks at the next state $s_j^{\prime }$ for all agents j.

The critic network is updated by minimizing the following loss function:

$$\mathcal{L}\left({\theta }^{Q_i}\right)={\displaystyle \frac{1}{K}}\sum _{k=1}^K{\left(y_i^{\left(k\right)}-Q_i(x^{\left(k\right)},a_1^{\left(k\right)},\dots ,a_N^{\left(k\right)};{\theta }^{Q_i})\right)}^2,$$

(2)

where K is the minibatch size and $(x^{\left(k\right)},a_1^{\left(k\right)},\dots ,a_N^{\left(k\right)},y_i^{\left(k\right)})$ are sampled from the replay buffer.

Algorithm 3 Multi-Agent Deep Deterministic Policy Gradient (MADDPG)

1: Initialize environment with N agents   2: for each agent $i\in \{1,...,N\}$ do   3:       Initialize actor network ${\mu }_i\left(s_i\right|{\theta }^{{\mu }_i})$ and critic network $Q_i(s_i,a_1,...,a_N|{\theta }^{Q_i})$   4:       Initialize target networks: ${\theta }^{{\mu }_i^{\prime }}\leftarrow {\theta }^{{\mu }_i}$, ${\theta }^{Q_i^{\prime }}\leftarrow {\theta }^{Q_i}$   5:       Initialize replay buffer ${\mathcal{D}}_i$   6: end for   7: for episode = 1 to M do   8:       Initialize random process ${\mathcal{N}}_i$ for exploration   9:       Receive initial State $s=(s_1,...,s_N)$ 10:       for time step $t=1$ to T do 11:             for each agent i do 12:                   Select action $a_i={\mu }_i\left(s_i\right|{\theta }^{{\mu }_i})+{\mathcal{N}}_i$ 13:             end for 14:             Execute joint action $(a_1,...,a_N)$ and observe reward $r_i$ and next State $s_i^{\prime }$ for each agent 15:             for each agent i do 16:                   Store $(s_i,a_t,r_t,s_i^{\prime })$ in ${\mathcal{D}}_i$ 17:                   Sample a minibatch of K transitions from ${\mathcal{D}}_i$ 18:                   Set target: $$y_i=r_i+\gamma Q_i^{\prime }(s_i^{\prime },a_1^{\prime },...,a_N^{\prime }|{\theta }^{Q_i^{\prime }})$$ 19:                   where $a_j^{\prime }={\mu }_j^{\prime }\left(s_j^{\prime }\right|{\theta }^{{\mu }_j^{\prime }})$ for all agents j 20:                   Update critic by minimizing: $$\mathcal{L}\left({\theta }^{Q_i}\right)={\displaystyle \frac{1}{K}}\sum {(y_i-Q_i(s,a_1,...,a_N|{\theta }^{Q_i}))}^2$$ 21:                   Update actor using the policy gradient: $${\nabla }_{{\theta }^{{\mu }_i}}J\approx {\displaystyle \frac{1}{K}}\sum {\nabla }_{a_i}{Q}_i(s,a_1,...,a_i,...,a_N){\nabla }_{{\theta }^{{\mu }_i}}{\mu }_i\left(s_i\right)$$ 22:                   Update target networks: $${\theta }^{Q_i^{\prime }}\leftarrow \tau {\theta }^{Q_i}+(1-\tau ){\theta }^{Q_i^{\prime }}$$ $${\theta }^{{\mu }_i^{\prime }}\leftarrow \tau {\theta }^{{\mu }_i}+(1-\tau ){\theta }^{{\mu }_i^{\prime }}$$ 23:             end for 24:       end for 25: end for

The actor is updated using the deterministic policy gradient, given by

$${\nabla }_{{\theta }^{{\mu }_i}}J\approx {\displaystyle \frac{1}{K}}\sum _{k=1}^K{\nabla }_{a_i}{Q}_i(x,a_1,\dots ,a_N){|}_{a_i={\mu }_i\left(s_i\right)}·{\nabla }_{{\theta }^{{\mu }_i}}{\mu }_i\left(s_i\right).$$

(3)

Target networks for both the actor and critic are updated using soft updates as follows:

$${\theta }^{\prime }\leftarrow \tau \theta +(1-\tau ){\theta }^{\prime },$$

(4)

where $\tau \ll 1$ is the soft update rate.

MADDPG has demonstrated significant success in cooperative navigation tasks, autonomous vehicle coordination, and multi-robot systems. In the Multi-Agent Particle Environment (MPE) benchmark, MADDPG outperformed independent DDPG and Q-learning baselines by enabling agents to learn coordinated strategies [84]. It has also been adopted in domains such as autonomous drone swarms [67] and smart grid energy management [92], showcasing its flexibility. Despite its success, MADDPG is not without limitations. The use of separate critics for each agent limits scalability to large agent populations. Furthermore, it assumes that agents can access the actions and observations of others during training, which may not always be feasible in partially observable settings. These limitations have inspired variants and improvements, such as MAAC and MAPPO, that aim to improve coordination, scalability, and robustness [90,93]. In [77], MADDPG was compared with the Multi-agent Deep Q-Network (MADQN) algorithm, incorporating three learning strategies to enhance the speed and accuracy of UAV training for combat tasks. MADDPG demonstrated superior performance, achieving better convergence and providing more decision-making options for UAVs due to its operation in the continuous domain and the use of a continuous action space. Article [96] compares the implementation of the DDPG, TRPO, and PPO algorithms in drone control against each other and a well-tuned PID controller. Specifically, DDPG was used to train drones for flight and stability maintenance. Although DDPG required a lengthy training period, it achieved convergence more quickly than TRPO. MADDPG works well for drones as it supports continuous action spaces, suitable for the control of thrust, pitch, and yaw, and it allows decentralized execution, which is necessary for independent UAV operation. It also enables the scalable training of multiple drones via centralized critics and finally, it is adaptable to partial observability and communication-constrained environments. In [67], MADDPG was used to train quadrotors to maintain formations while avoiding collisions, using only partial observations in simulated environments like AirSim or Gazebo. In [92] MADDPG allows drones to navigate between buildings and through air lanes by learning optimal control under flight constraints in urban air mobility simulations. In [97], an artificial intelligence approach called Simultaneous Target Assignment and Path Planning (STAPP) is used to solve the multi-UAV target assignment and path planning (MUTAPP problem), which leverages the Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithm to model and train agents to handle both target assignment and path planning concurrently, guided by a specially designed reward structure.

5.2. Multi-Agent Trust Region Policy Optimization (MATRPO)

Trust Region Policy Optimization (TRPO) aims to limit excessive changes in policy updates by incorporating a KL divergence constraint, thereby reducing the number of parameter updates per step [98]. However, TRPO has not fully resolved the issue of minimizing parameter updates, making it less reliable for controlling hardware agents. This limitation led to the development of the PPO algorithm.

Multi-Agent Trust Region Policy Optimization (MA-TRPO) extends the principles of Trust Region Policy Optimization (TRPO) to Multi-Agent Reinforcement Learning (MARL) scenarios. While TRPO has demonstrated stability and performance in single-agent settings by ensuring monotonic policy improvements through constrained updates, its direct application to multi-agent environments introduces challenges due to the dynamic interactions among multiple learning agents [83]. In MARL, each agent’s learning process can affect and be affected by the learning processes of other agents, leading to a non-stationary environment from any individual agent’s perspective. This interdependence complicates the application of TRPO, which assumes a stationary environment for its theoretical guarantees to hold. To address this, researchers have developed adaptations of TRPO tailored for multi-agent settings. One such adaptation is the Multi-Agent Trust Region Policy Optimization (MATRPO) algorithm proposed by [99], which reformulates the TRPO update as a distributed consensus optimization problem. This approach allows agents to optimize their policies based on local observations and private rewards without requiring access to other agents’ information, promoting a decentralized and privacy-preserving learning process. Empirical evaluations have demonstrated MATRPO’s robust performance in cooperative multi-agent tasks.

The Multi-Agent Trust Region Policy Optimization (MATRPO) structure is shown in Figure 7, while the algorithm is shown in Algorithm 4 [100,101]. In this framework, a set of agents $\{1,2,\dots ,N\}$ interact with a shared environment modeled as a Markov Game. Each agent i has its own policy ${\pi }_{{\theta }_i}(a_i\mid s_i)$ and value function $V_{{\varphi }_i}\left(s_i\right)$, where ${\theta }_i$ and ${\varphi }_i$ denote the respective parameter vectors. Agents observe local states $s_i$, take actions $a_i$, and receive rewards $r_i$, aiming to maximize the expected return $\mathbb{E}\left[R_i\right]$. Training is conducted under the Centralized Training with Decentralized Execution (CTDE) paradigm.

During each iteration, each agent collects trajectories ${\tau }_i$ by executing its current policy in the environment. The advantage function $A_i(s,a_i)$, often estimated using Generalized Advantage Estimation (GAE), is computed to evaluate the benefit of taking action $a_i$ in state s. The policy gradient for agent i is computed as

$$g_i={\nabla }_{{\theta }_i}{\mathbb{E}}_{{\tau }_i}\left[log{\pi }_{{\theta }_i}(a_i\mid s_i)·A_i(s,a_i)\right].$$

To ensure stable updates, MATRPO imposes a trust region constraint using the Kullback–Leibler (KL) divergence between the old and new policies. This leads to the following constrained optimization problem:

$$\underset{\Delta {\theta }_i}{max}{g}_i^{\top }\Delta {\theta }_i\mathrm{subject}\mathrm{to}\Delta {\theta }_i^{\top }{H}_i\Delta {\theta }_i\le \delta ,$$

where $H_i$ is the Hessian of the sample average KL-divergence, approximated as

$$H_i\approx {\mathbb{E}}_{{\tau }_i}\left[{\nabla }_{{\theta }_i}log{\pi }_{{\theta }_i}(a_i\mid s_i)·{\nabla }_{{\theta }_i}log{\pi }_{{\theta }_i}{(a_i\mid s_i)}^{\top }\right],$$

and $\delta$ is a predefined KL-divergence bound. The optimal update direction $\Delta {\theta }_i$ is computed using the conjugate gradient method, followed by a backtracking line search to enforce the KL constraint. Finally, each agent updates its value function by minimizing the mean squared error between predicted and actual returns:

$$\mathcal{L}\left({\varphi }_i\right)={\mathbb{E}}_{{\tau }_i}\left[{\left(V_{{\varphi }_i}\left(s_i\right)-R_i\right)}^2\right].$$

MATRPO allows each agent to learn a stable and effective decentralized policy while leveraging centralized training to improve coordination and performance in multi-agent environments.

Algorithm 4 Multi-Agent Trust Region Policy Optimization (MATRPO)

1: Initialize policy parameters ${\left\{{\theta }_i\right\}}_{i=1}^N$ and value function parameters ${\left\{{\varphi }_i\right\}}_{i=1}^N$   2: Set KL-divergence constraint $\delta >0$   3: for each iteration do   4:       for each agent $i\in \{1,\dots ,N\}$ do   5:             Collect trajectories ${\tau }_i$ using policy ${\pi }_{{\theta }_i}$ in the environment   6:             Estimate advantage function $A_i(s,a_i)$ using value function $V_{{\varphi }_i}\left(s\right)$   7:             Compute policy gradient: $$g_i\leftarrow {\nabla }_{{\theta }_i}{\mathbb{E}}_{{\tau }_i}\left[log{\pi }_{{\theta }_i}\left(a_i\right|s_i)·A_i(s,a_i)\right]$$   8:             Compute the Hessian of the sample average KL-divergence: $$H_i\approx {\mathbb{E}}_{{\tau }_i}\left[{\nabla }_{{\theta }_i}log{\pi }_{{\theta }_i}\left(a_i\right|s_i)·{\nabla }_{{\theta }_i}log{\pi }_{{\theta }_i}{\left(a_i\right|s_i)}^T\right]$$   9:             Solve constrained optimization: $$\begin{array}{ccc}& \underset{\Delta {\theta }_i}{\mathrm{maximize}}\hfill & g_i^T\Delta {\theta }_i\hfill \\ & \hfill \mathrm{subject}\mathrm{to}& \hfill \Delta {\theta }_i^T{H}_i\Delta {\theta }_i\le \delta \end{array}$$ 10:             Use conjugate gradient to compute step direction $\Delta {\theta }_i$ 11:             Perform backtracking line search to ensure KL-divergence $\le \delta$ 12:             Update policy: ${\theta }_i\leftarrow {\theta }_i+\Delta {\theta }_i$ 13:             Update value function parameters ${\varphi }_i$ by minimizing: $$\mathcal{L}\left({\varphi }_i\right)={\mathbb{E}}_{{\tau }_i}\left[{\left(V_{{\varphi }_i}\left(s\right)-R_i\right)}^2\right]$$ 14:       end for 15: end for

Another significant development is the Heterogeneous-Agent Trust Region Policy Optimization (HATRPO) algorithm [102], which introduces a sequential policy update scheme and a multi-agent advantage decomposition lemma. HATRPO enables agents with different policy and value function structures to learn effectively without sharing parameters or relying on restrictive assumptions about the decomposability of the joint value function. This method has shown superior performance in various benchmarks, including Multi-Agent MuJoCo and StarCraft II tasks. In parallel, Wen et al. [103] proposed a game-theoretic formulation of trust-region optimization in multi-agent systems, resulting in the Multi-Agent Trust-Region Learning (MATRL) method. MATRL uses Nash equilibrium concepts to guide policy updates and ensure convergence in competitive and cooperative environments, further strengthening the theoretical underpinnings of trust-region approaches in multi-agent learning.

Multi-Agent Trust-Region Policy Optimization (MATRPO) has shown significant promise in the field of autonomous drones (UAVs), particularly in scenarios that require decentralized coordination, robustness, and policy stability in dynamic environments. MATRPO extends the Trust Region Policy Optimization (TRPO) framework into multi-agent systems by reformulating the policy optimization as a distributed consensus optimization problem [99]. This formulation is particularly suitable for UAV applications where each drone must act autonomously using local observations while collectively achieving a global task. In many UAV missions, such as aerial surveying, disaster relief, and military surveillance, individual drones have access to only partial state information due to limited sensing and communication constraints. MATRPO enables each agent to update its policy independently without needing access to the policies or observations of other agents, a critical advantage over fully centralized algorithms [83,99]. This makes MATRPO ideal for distributed drone swarms operating in GPS-denied or bandwidth-constrained environments, where decentralized execution is not just efficient but also necessary [104]. UAVs are often deployed in non-stationary environments, such as regions with changing wind patterns, moving obstacles, or adversarial interference. MATRPO’s trust region mechanism, which restricts the KL divergence between consecutive policies, ensures that policy updates are stable and conservative, avoiding performance collapses due to overly aggressive updates [86,99]. This is particularly important for aerial applications, where erratic behavior can lead to mission failure or hardware loss. Applications of MATRPO spans areas for coverage and exploration [105], search and rescue (SAR) [106], and emergency communication and network access [107]. Compared to methods like MADDPG or MAPPO, which often require centralized critics or synchronized updates, MATRPO offers a fully decentralized and privacy-preserving framework with the stability benefits of trust region optimization. This makes it highly suitable for UAVs operating in real-world scenarios where central coordination is infeasible or unsafe [99]. The major drawback is that TRPO exhibits the longest training times compared to MADDPG and MAPPO, explaining its infrequent use in UAV control. Despite this drawback, TRPO achieves precise convergence during training, making it beneficial for controlling ground vehicles and robotics.

5.3. Proximal Policy Optimization (PPO)

PPO performs optimization using a batch of navigation examples and minibatch stochastic gradient descent to maximize the objective [87], simplifying the algorithm by eliminating the KL penalty and the need for versatile updates. It balances updates between the current policy $\pi$ and the previous policy ${\pi }_{old}$ that created the batch, preventing excessive updates beyond the region where the sample provides a reliable estimate. PPO also integrates with the actor–critic framework, where each agent uses one actor and multiple critic networks for faster and distributed learning. Multi-Agent Proximal Policy Optimization (MAPPO) is an extension of the Proximal Policy Optimization (PPO) algorithm tailored for Multi-Agent Reinforcement Learning (MARL) environments. It employs a Centralized Training with Decentralized Execution (CTDE) framework, where each agent learns its policy while a centralized critic evaluates the joint actions, facilitating stable learning in cooperative settings.

The Multi-Agent Proximal Policy Optimization (MAPPO)structure is shown in Figure 8, while the algorithm is shown in Algorithm 5 [108]. In MAPPO, each agent i learns a decentralized policy ${\pi }_{{\theta }_i}\left(a_i\right|s_i)$ based on its own local observation $s_i$, while benefiting from a centralized critic $V_{\varphi }\left(s\right)$ that has access to the global state s during training.

Algorithm 5 Multi-Agent Proximal Policy Optimization (MAPPO)

1: Initialize policy parameters $\theta =\{{\theta }_1,{\theta }_2,\dots ,{\theta }_N\}$ for n agents   2: Initialize centralized value function parameters $\varphi$   3: for each iteration do   4:       for each environment rollout do   5:             for $t=1$ to T do   6:                   for each agent $i=1$ to N do   7:                         Observe local state $s_i$   8:                         Sample action $a_i\sim {\pi }_{{\theta }_i}\left(a_i\right|s_i)$   9:                   end for 10:                   Execute joint action $a=(a_1,\dots ,a_n)$ 11:                   Observe next state s and joint reward $r=(r_1,\dots ,r_N)$ 12:                   Store $(s,a,r,s^{\prime })$ in buffer 13:             end for 14:       end for 15:       for each agent $i=1$ to N do 16:             Compute advantages ${\widehat{A}}_i$ using Generalized Advantage Estimation (GAE): $${\delta }_i=r_i+\gamma V_{\varphi }\left(s^{\prime }\right)-V_{\varphi }\left(s\right)$$ $${\widehat{A}}_i=\sum _{l=0}^{T-t}{\left(\gamma \lambda \right)}^l{\delta }_i^{t+l}$$ 17:             Compute the PPO objective: $$L_i=min\left({\displaystyle \frac{{\pi }_{{\theta }_i}\left(a_i\right|s_i)}{{\pi }_{{\theta }_i}^{\mathrm{old}}\left(a_i\right|s_i)}}{\widehat{A}}_t^i,\mathrm{clip}\left({\displaystyle \frac{{\pi }_{{\theta }_i}\left(a_i\right|s_i)}{{\pi }_{{\theta }_i}^{\mathrm{old}}\left(a_i\right|s_i)}},1-ϵ,1+ϵ\right){\widehat{A}}_i\right)$$ 18:             Update policy parameters: $${\theta }_i\leftarrow {\theta }_i+\alpha {\nabla }_{{\theta }_i}{L}_i$$ 19:       end for 20:       Update value function parameters by minimizing: $$L_v=\sum _t{\left(V_{\varphi }\left(s\right)-R\right)}^2$$ $$\varphi \leftarrow \varphi -\alpha {\nabla }_{\varphi }{L}_v$$ 21: end for

The learning objective of each agent is adapted from PPO’s clipped surrogate loss, which stabilizes policy updates by preventing large deviations between the new and old policy. The surrogate loss function for agent i is defined as

$$L_i\left({\theta }_i\right)=\mathbb{E}\left[min\left(r_i\left({\theta }_i\right){\widehat{A}}_i,\mathrm{clip}(r_i\left({\theta }_i\right),1-ϵ,1+ϵ){\widehat{A}}_i\right)\right],$$

where the probability ratio $r_i\left({\theta }_i\right)$ is given by

$$r_i\left({\theta }_i\right)={\displaystyle \frac{{\pi }_{{\theta }_i}\left(a_i\right|s_i)}{{\pi }_{{\theta }_i}^{\mathrm{old}}\left(a_i\right|s_i)}},$$

and ${\widehat{A}}_i$ denotes the advantage function for agent i, which is estimated using Generalized Advantage Estimation (GAE):

$${\delta }_i=r_i+\gamma V_{\varphi }\left(s^{\prime }\right)-V_{\varphi }\left(s\right),$$

$${\widehat{A}}_i=\sum _{l=0}^{T-t}{\left(\gamma \lambda \right)}^l{\delta }_i^{t+l}.$$

Here, $\gamma$ is the discount factor and $\lambda$ controls the bias-variance tradeoff in advantage estimation.

The centralized value function $V_{\varphi }\left(s\right)$ is updated by minimizing the mean squared error between the predicted value and the actual return R:

$$L_v=\sum _t{\left(V_{\varphi }\left(s\right)-R\right)}^2$$

MAPPO has demonstrated strong empirical performance in several benchmark environments, such as the StarCraft Multi-Agent Challenge (SMAC) and Multi-Agent MuJoCo, by leveraging stable and efficient policy optimization for cooperative multi-agent systems. In [49], PPO was used to train two UAVs individually and as a pair for navigation recommendations, while the drone control was manually handled by a remote pilot. This semi-autonomous control approach is suitable for military operations in war zones, where distinguishing between allies and foes is challenging, providing precise navigation paths for manual operation by a remote pilot. In [109], PPO was employed to train 50 UAVs for cooperative persistent surveillance in an unknown environment. A neural network using PPO enabled the swarm to navigate and avoid collisions effectively in a complex environment with numerous obstacles. PPO was also used to train UAVs for stability in multi-agent environments in [110], simulated using the PyBullet gym in OpenAI. The dynamic environment created various scenarios and obstacles, and PPO was found to be well-balanced in training time and convergence accuracy compared to other algorithms. In [77], a complex UAV-to-UAV combat situation was simulated, requiring UAVs to gather information from teammates and enemies. A decentralized PPO approach with decentralized actors and a centralized critic was implemented in a four-UAV swarm combating a two-UAV swarm. This approach outperformed a centralized PPO, which struggled with convergence as the number of UAVs increased. PPO remains the most versatile training algorithm in robotics [7]. In [111], the authors introduce a multi-UAV escape target search algorithm based on MAPPO to address the escape target search difficulty problem. The authors of [90] demonstrated the effectiveness of MAPPO across various MARL benchmarks, including the StarCraft Multi-Agent Challenge (SMAC) and Google Research Football, highlighting its superior performance over other algorithms like MADDPG and COMA. Further advancements, such as the MAPPO-PIS algorithm introduced in [112], incorporates intent-sharing mechanisms to enhance cooperative decision-making among connected and autonomous vehicles (CAVs), showcasing improved safety and efficiency in complex traffic scenarios. Liu et al. [113] presents a path planning approach utilizing an action-mask-based Multi-Agent Proximal Policy Optimization (AM-MAPPO) algorithm to coordinate multiple UAVs in the search for moving targets within three-dimensional (3D) environments. Specifically, it introduces a multi-UAV high–low altitude collaborative search architecture that combines the wide detection range offered by high-altitude UAVs with the enhanced detection accuracy provided by low-altitude UAVs. Multi-Agent Proximal Policy Optimization (MAPPO) has demonstrated significant potential in enhancing the coordination and control of multi-UAV systems, particularly in complex, dynamic, and partially observable environments. By leveraging the Centralized Training with Decentralized Execution (CTDE) paradigm, MAPPO allows for scalable and robust policy learning across fleets of autonomous drones [90]. Despite this decentralized execution, the training process embeds cooperative behavior learned centrally, ensuring coordinated action across the fleet. This separation of training and execution allows MAPPO to scale to large numbers of agents, as the centralized training phase can efficiently exploit inter-agent dependencies while keeping the execution decentralized and lightweight, which enhances convergence speed. Applications of MAPPO in drone systems span a wide array of domains, including target tracking, surveillance, collaborative exploration, and search-and-rescue missions. These techniques not only improve search efficiency but also enhance mission safety and redundancy, which are critical in real-world deployments. Moreover, MAPPO’s ability to maintain stable policy updates through clipped objectives while effectively handling the non-stationarity inherent in multi-agent systems, makes it an ideal candidate for UAV Swarm Intelligence and autonomous aerial systems. As research continues, integrating MAPPO with communication-aware strategies, intent prediction, and sensor fusion is expected to further extend its capabilities in urban air mobility, precision agriculture, and disaster response operations.

The comparative analysis across Policy-Based Multi-Agent Reinforcement Learning (MARL) techniques reveals distinct performance trade-offs tied to each algorithm’s environment and coordination strategy.

Table 3. Comparison of Policy Gradient-Based Algorithms for UAV Swarm Control.

Criteria	MADDPG	TRPO	PPO
Mode of Operation	Uses a deterministic policy gradient with actor–critic networks to enable continuous action spaces.	Minimizes policy updates by enforcing a KL-divergence constraint during optimization.	Uses a clipped objective to limit policy deviation, enabling more stable updates via stochastic gradient descent.
Action Space	Continuous	Continuous (extensions exist for discrete)	Discrete and Continuous
Stochastic / Deterministic	Deterministic policy	Stochastic policy	Stochastic policy
Stability	Stable in moderate-scale applications	High theoretical stability but sensitive in practice	Very stable; robust across diverse tasks
Scalability	Moderate; more suitable for small-to-medium swarms	Poor; not ideal for large-scale applications	High; excellent for large multi-agent systems
Use in Multi-Agent RL	Widely used (e.g., MADDPG) with decentralized actors	Less common due to complexity; experimental in MARL	Very common; MAPPO is widely used in cooperative MARL
Computational Requirements	Requires moderate computational resources—higher than PPO but lower than TRPO. Suitable if drone memory capacity is sufficient and updates are infrequent.	Most computationally demanding due to second-order derivatives. Best suited for high-resource platforms or offline learning.	Most efficient computationally. Suitable for large drone swarms with limited onboard processing capabilities.
Convergence Rate	Exhibits the slowest convergence among the three, requiring more training time for UAV swarms.	Faster than MADDPG but slower than PPO. Adequate for swarm applications with infrequent decision-making.	Fastest convergence. Ideal for real-time UAV applications requiring rapid responses to dynamic environments.
Convergence Accuracy	Offers stable and reliable convergence but slightly less accurate than PPO. Effective in tasks where precision is secondary, such as search and rescue.	Comparable to MADDPG in accuracy but suffers from instability, making it less suitable for real-world deployment.	Delivers the most accurate and stable convergence. Suitable for precision-critical tasks like UAV-based targeting or surveillance.
Implementation Complexity	Moderately complex. Easier than TRPO but more involved than PPO due to its reliance on multi-agent architecture.	Complex implementation due to second-order KL-divergence constraints. Best used in controlled research environments.	Simplest among the three. Its clipped objective makes it straightforward and practical for fast deployment in drone swarms.

presents a brief comparison between the most common Policy Gradient-Based Algorithms for UAV Swarm Control in Multi-Agent Reinforcement Learning.

Table 4. Comparison between articles on Policy-Based Multi-Agent Reinforcement techniques.

Paper ID	Environment Type	Training Technique	Swarm Size	S.R. 2	Scal. 3	F.T. 5	Conv. 4
[49]	UAV Target Search	DRL with reward shaping	1	∼85%		Limited Basic avoidance	Mod. > 2000
[67]	Dynamic 3D obstacle environment	Q-learning	4	∼85%	Limited	Poor Basic collision avoidance	Mod. > 2000
[90]	2D Static Environment	MAPPO	5 agents	∼80%	Low (static setup)	Limited	Mod 1. > 800
[97]	Dynamic threat environment	MADDPG in STAPP framework	5 UAVs	90–95%	Mod.	Yes (not tested)	slow > 150,000.
[105]	Variable-size UAV network	Transformer-based MARL	8 UAVs	∼97% coverage	High	Robust	Fast
[106]	UAV path planning	Centralized MADDPG	20 UAVs	∼95% target coverage	Mod.	Limited	Fast <100
[107]	Urban simulated environment for resource sharing	DDPG	10 UAVs	∼90%	Mod.	Mod. (Backup UAV)	Mod. < 1000
[109]	Urban Intersection (CAVs)	MAPPO	3–5 (50)	∼88%	Limited to CAV scope	Safety constraints	Mod. >2000
[111]	Moving targets and obstacle	ETS–MAPPO + STEE	29	>30% vs. baselines	Mod.	STEEN facilitates reallocation	Mod <1600
[112]	Traffic Merging (CAVs)	MAPPO-PIS	6–10	Better than MAPPO	High	Safety Enhanced Module	Slow >10,000
[113]	multi-UAV target tracking	AM-MAPPO	3–8	Better in target search only	High	redundant coverage	Mod. < 2000

¹ Mod. stands for Moderate. ² S.R. stands for Success Rate. ³ Scal. stands for Scalability. ⁴ Conv. stands for Convergence (#of Steps). ⁵ F.T. stands for Fault Tolerance.

presents a comparison between many of the research articles cited in this section. For example, [113], using AM-MAPPO, demonstrates strong scalability and moderate convergence for multi-UAV target tracking by leveraging redundant coverage, while [112] applies PIS-MAPPO in traffic merging scenarios, achieving enhanced safety but at the cost of slower convergence (>10,000 steps). In contrast, Liao et al. [111] introduces ETS-MAPPO with STEE for obstacle-rich, moving-target environments, offering a 30% success rate improvement and moderate convergence (<1600 steps) due to dynamic agent reallocation. Classical methods such as Q-learning [67] and DRL with reward shaping [49] show moderate success (85%) but suffer from poor scalability and slower convergence due to their discrete and environment-specific designs. Transformer-based MARL in [105] offers the highest coverage (97%) with fast convergence and high scalability, while centralized MADDPG in [106] delivers 95% target coverage with rapid convergence (<100 steps) but limited fault tolerance. Chen et al. [107] and Qie et al. [97] explore urban and threat-aware UAV scenarios, respectively, where both demonstrate moderate convergence and fault resilience, with [97] notably requiring over 150,000 steps due to its complex STAPP framework. Overall, advanced MARL frameworks such as AM-MAPPO, Transformer-based MARL, and ETS-MAPPO stand out in handling larger swarms and dynamic environments and achieving higher success rates with relatively stable training dynamics.

6. Multi-Agent Federated Reinforcement Learning Techniques

Federated Learning (FL) has emerged as a powerful framework for enabling decentralized intelligence, particularly in scenarios where data privacy and communication constraints are critical. When combined with Multi-Agent Reinforcement Learning (MARL), FL facilitates the training of distributed agents across multiple edge devices or environments without requiring direct access to local data. This synergy allows agents to collaboratively learn shared policies or value functions while preserving data locality and reducing bandwidth usage. In federated MARL, each agent or a group of agents independently interacts with its environment to collect experience and update local models, which are then periodically aggregated using techniques such as Federated Averaging (FedAvg) on a central server or coordinator. These methods help address key challenges in MARL, including scalability, heterogeneity of agent experiences, and security concerns. As such, federated MARL is increasingly being explored in domains such as autonomous vehicle coordination, distributed robotics, and smart IoT systems, where collaborative learning must occur without centralized data collection.

Multi-Agent Federated Reinforcement Learning (MAFRL) techniques have become a powerful paradigm for establishing stable [114] and intelligent communication networks, particularly in scenarios involving distributed and mobile agents such as UAVs. By combining the decentralized decision-making capabilities of Multi-Agent Reinforcement Learning with the privacy-preserving and communication-efficient nature of federated learning, MAFRL enables each agent to learn locally from its environment while benefiting from global knowledge through periodic model aggregation. This architecture is particularly advantageous in dynamic wireless networks, where maintaining stability in terms of connectivity, data throughput, and fairness is critical. For instance, UAVs acting as aerial relays can collaboratively learn optimal flight paths, power allocations, and scheduling policies without sharing raw data, thereby reducing latency and enhancing scalability. Moreover, the federated approach ensures robustness against network failures or mobility-induced disruptions by enabling asynchronous updates and distributed training. As demonstrated in recent studies, MAFRL achieves improved convergence [115], reduced interference, and enhanced fairness in access to limited communication resources [116], making it a highly effective solution for the future of resilient and adaptive communication networks. It was also used to improve spectrum utilization [117]. MAFRL was applied to optimize the quality of service in various LoRa network slices.

Recent research in Multi-Agent Federated Reinforcement Learning (MAFRL) for UAV applications has yielded a diverse range of frameworks aimed at optimizing communication efficiency, trajectory planning, and resource allocation in dynamic environments. Gao et al. [118] introduced a federated Deep Reinforcement Learning framework for UAV trajectory design, enabling privacy-preserving collaboration across multiple UAVs serving mobile users. Their focus on trajectory learning demonstrated strong performance under mobile user scenarios. However, the study focused on a limited number of UAVs (only five), which raises questions about the scalability. It lacks real-life applications, as it was only validated by simulation. Nie et al. [119] addressed semi-distributed resource management in UAV-aided mobile edge computing (MEC) systems by proposing an MAFRL algorithm that balances computation offloading and power minimization while preserving user privacy using Gaussian noise. But this framework has scalability concerns as it was validated by simulations on a limited number of UAVs, as well as its dependence on a central server. In contrast, Wang et al. [120] applied a distributed federated Deep Reinforcement Learning (DFDRL) approach to optimize UAV trajectories in emergency communication networks, with an emphasis on adaptability and reduced latency in air–ground cooperation. Tarekegn et al. [121] proposed a federated multi-agent DRL system for trajectory control and fair communication (TCFC), which uniquely emphasized fairness in user data rates and applied real channel measurements for link estimation—setting it apart in terms of practical realism. Finally, Han et al. [122] proposed a collaborative learning model for UAV deployment and resource allocation using environment-centric learning, focusing on system-wide throughput and fair access. This framework poses potential privacy concerns as raw observations may still be shared among agents. While all papers demonstrate the scalability and privacy-preserving benefits of federated learning, they differ in primary focus: [118,119,120] target performance and latency, [121] centers on fairness and real-world deployment, and [122] integrates collaborative policy learning for UAV deployment.

Table 5. Comparison between the MAFRL techniques referenced.

Article	Swarm Size	(Avg. Time of Episode)/#Episodes	Accum. Reward	Application	Pros	Cons
[118]	5	8.093 s/420	2000	Trajectory Design for UAV-assisted networks	Incorporates dueling DDQN and multi-step bootstrapping	It did not converge in some cases, and in others it took >2000 s, scalability and static Server UAV
[119]	10	0.5664 s/20,000	0.4	Resource Management in UAV	use of PPO provides stable convergence	Dependence on Central Server, Scalability
[121]	3	0.738 s/1000	80	Trajectory Control for Multi-UAV Networks	Joint Optimization of Trajectory and Fairness	Assumes stable and reliable communication between UAVs and the server; the use of MADDPG increases training complexity
[122]	6	1.492 s/1200	200	UAV Deployment and Resource Allocation	Decentralized scalability, optimizes UAV positioning and communication resource allocation	No Federated Privacy Mechanism, Energy Efficiency Ignored
[120]	6	-/4000	1.5	Optimizing UAV trajectories	Distributed Privacy-Preserving Design, Trajectory Optimization for Emergency Response	Central Aggregator Dependency, Simplified Channel Models

presents a comparison between these different research articles.

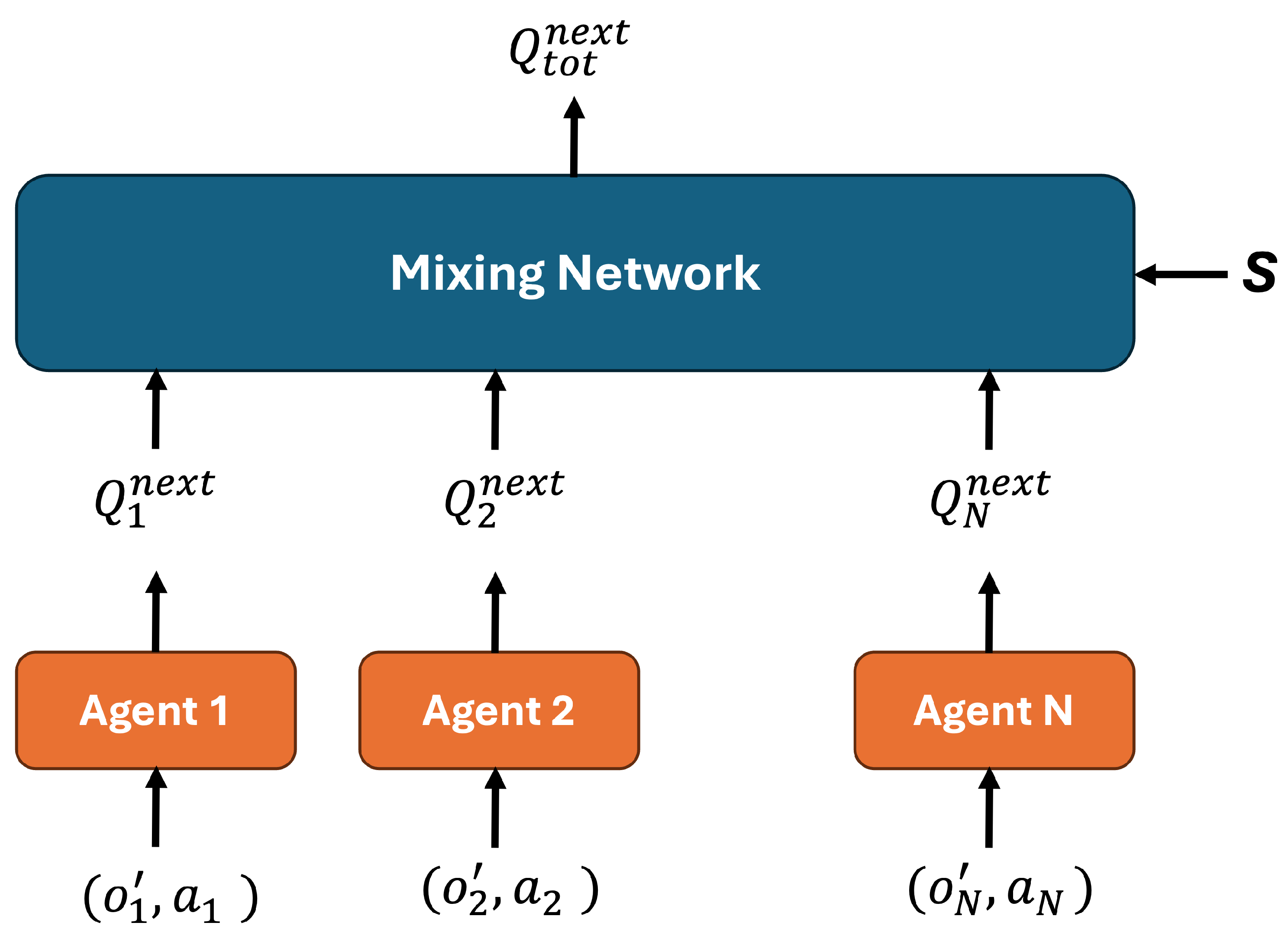
7. Comparison Between MARL Learning Techniques

Table 6. Expanded comparison of MARL learning techniques.

Criterion	Value-Based MARL	Policy-Based MARL	Federated MARL
Core Idea	Learns joint or factorized value functions (e.g., Q-values)	Learns decentralized or centralized policies directly	Distributes learning across agents while preserving data locality
Representative Algorithms	QMIX, VDN, QTRAN, WQMIX	MAPPO, MADDPG, TRPO, HAPPO	FedRL, FedMARL, FedAvg+MARL
Action Space	Discrete	Continuous and discrete	Both (depends on local model)
Performance	High in structured/cooperative tasks	High in continuous, dynamic tasks	Moderate to high; depends on aggregation frequency and bandwidth
Environment	Best in fully observable or low-noise discrete settings	Works well in dynamic, partially observable, or continuous environments	Well-suited for distributed, privacy-sensitive, and bandwidth-limited environments
Scalability	Moderate (limited by value function complexity)	High (decentralized execution is effective)	High (supports large-scale distributed systems)
Communication Overhead	Low to moderate	Moderate (depends on policy sharing)	Low (only model parameters shared)
Training Stability	Sensitive to agent number and observability	More stable with proper exploration (e.g., GAE)	Depends on sync method and local training accuracy
Convergence Speed	Fast in simple settings	Moderate; requires more samples but is stable	Slower due to delayed aggregation and heterogeneity
Adaptability to Dynamic Environments	Low to moderate	High	High (supports model personalization)
Privacy Preservation	Not supported inherently	Not supported inherently	Strong (data remains local)
Suitability for UAV Applications	Suitable for cooperative discrete tasks (e.g., coverage)	Ideal for continuous control (e.g., formation, tracking)	Ideal for distributed UAV systems with privacy and bandwidth constraints

presents a brief comparison between Multi-Agent Reinforcement Learning (MARL) techniques. This comparison summarizes the key points relevant to UAV control, depending on factors such as the environment, application, and performance requirements. The comparison of Value-Based, Policy-Based, and Federated Multi-Agent Reinforcement Learning (MARL) techniques reveals distinct strengths and limitations across key performance dimensions. Value-based methods, such as QMIX and QTRAN, focus on learning joint or decomposed value functions and are generally efficient in simpler or discrete environments, but they can suffer from scalability issues and instability in partially observable or dynamic settings. In contrast, policy-based approaches like MAPPO and MADDPG directly optimize decentralized or centralized policies, offering better adaptability to continuous control tasks such as UAV formation flying and cooperative maneuvering. These methods typically require more training episodes but yield greater robustness and flexibility in complex multi-agent scenarios. Federated MARL introduces an additional layer of scalability and privacy by enabling agents to train locally while sharing model parameters rather than raw data. Although convergence may be slower due to asynchronous updates and communication delays, federated approaches excel in settings where data locality, communication efficiency, or privacy is a concern—making them highly suitable for distributed UAV swarms or edge AI systems. Ultimately, the choice among these techniques depends on the application’s control complexity, environmental dynamics, system scale, and communication constraints.

When comparing some of the most common MARL techniques used for applications related to UAVs, as presented in

Table 7. Comparative analysis of MARL techniques for UAV applications.

Technique	Scalability	Fault Tolerance	Success Rate	Exploration Strategy	Training Time/ Convergence	Special Features/ Use Case
SERT-QDN [78]	High	Strong	High	Similarity-based	Moderate	Fault-tolerant swarms in harsh environments
QMIX [68]	Moderate	Limited	High	$\epsilon$-greedy	Fast	Cooperative exploration, low training complexity
QTRAN [79]	Low	None	Moderate	Constraint-based	Slow	Computationally heavy, resource-intensive coordination
MAVEN [81]	Moderate	None	High	Latent variable	Moderate	Supports diverse behavior patterns
VDAC [123]	Moderate	None	Moderate	Decentralized advantage	Fast	Entropy-regularized learning
ROMA [124]	High	None	High	Role assignment	Fast	Structured swarm roles for robust coordination
MAPPO [90]	High	Limited	High	GAE	Fast	Stable formation control, scalable and robust
HAPPO [102]	High	Limited	High	GAE	Moderate	Precision missions, hierarchical advantage policy
FACMAC [125,126]	Moderate	None	High	Entropy maximization	Moderate	Bandwidth-aware policies, decentralized training
WQMIX [127]	Moderate	None	High	Weighted mixing	Moderate	Energy-efficient swarm learning

, one should note that the training time of Multi-Agent Reinforcement Learning (MARL) techniques is influenced by several critical factors. These include the number of agents involved, as more agents increase the dimensionality of the joint action space and coordination complexity. The algorithm type also plays a role; for example, value-based methods like QMIX may train faster but struggle with scalability, whereas policy-based methods like MAPPO can offer stability at the cost of longer convergence. Communication overhead, especially in centralized or hybrid systems, can slow training when agents frequently exchange state or policy information. Additionally, environmental complexity, such as dynamic obstacles or partial observability, and the reward structure (sparse vs. dense) significantly affect the sample efficiency and number of episodes required to reach optimal performance. This comparison also highlights a diverse landscape of algorithmic strengths tailored to different operational demands. SERT-QDN [78] stands out with high scalability, robust fault tolerance, and high success rates, making it ideal for fault-tolerant swarm operations in harsh environments, although it demands moderate computational resources. QMIX [68] and QTRAN [79] present trade-offs; QMIX offers high success with moderate scalability but limited fault tolerance and lower training complexity, whereas QTRAN, while constrained in scalability and convergence, demands high computational and energy resources due to its constraint-based exploration. MAVEN [81] and VDAC [123] both feature moderate capabilities but diverge in exploration strategy, with MAVEN leveraging latent variables and VDAC using decentralized advantages suitable for entropy-regularized applications. ROMA [124] and MAPPO [90] deliver high performance in scalability and convergence, with ROMA employing role assignment for structured swarm behavior and MAPPO suited for formation control with general advantage estimation. HAPPO [102], a hierarchical variant, matches MAPPO’s strengths and adds precision for coordinated missions. Lastly, FACMAC [125,126] and WQMIX [127] focus on bandwidth-awareness and energy efficiency, respectively, with both showing strong success rates and scalability. Overall, the selection of a method depends on mission-specific requirements such as fault tolerance, deployment readiness, and computational constraints.

8. Open Research Problems

Despite the significant advancements and promising results achieved in UAV control [128] using Multi-Agent Reinforcement Learning (MARL), several open research problems remain. Addressing these issues is crucial for the further development and deployment of MARL in UAV systems [129]. This section outlines key areas that require further investigation.

• Scalability to Large-Scale Systems: The growing demand for scalable, efficient, and real-time aerial operations has underscored the need for deploying large numbers of UAVs across various domains. In search-and-rescue missions, fleets of UAVs can rapidly survey expansive or hazardous areas; in agriculture, they enable large-scale crop monitoring and precision farming. Military and defense sectors rely on multiple UAVs for surveillance, reconnaissance, and coordinated strikes. Similarly, environmental monitoring, logistics, and infrastructure inspection benefit from UAV swarms that provide wide coverage, improve redundancy, and enhance operational efficiency. These applications collectively justify the push toward large-scale UAV coordination and automation. However, while MARL has shown success in controlling small to medium-sized UAV swarms, scaling these techniques to larger networks remains a challenge. Research is needed to develop algorithms that can efficiently manage a large number of UAVs without compromising performance or increasing computational complexity. In [130], a novel multi-layer topology network and consensus control approach for a large-scale UAV swarm moving under a stable configuration was presented. The proposed topology can make the swarm remain robust in spite of the large number of UAVs. Although this control approach is a solid contribution to UAV swarm coordination, it lacks provisions for handling agent failures, communication breakdowns, or adversarial conditions, which are critical for resilient swarm coordination. The simulation environment also lacks dynamic complexity such as moving obstacles and wind turbulence. In [131], the authors introduced an agent masking technique that allows a standard Deep Q-Network (DQN) algorithm to scale effectively to large swarms, even when training is performed on comparatively smaller swarm sizes. The paper does not analyze convergence behavior, learning curves, or policy variance across training runs. It is unclear how stable or sample-efficient the proposed approach is. Also, no analysis is provided on how performance degrades or scales with increasing swarm size or communication complexity.
• Real-Time Learning and Adaptation: In dynamic and unpredictable environments, UAVs must be able to learn and adapt in real-time. Developing MARL algorithms that can quickly respond to changes and learn from new experiences without extensive retraining is a critical area for future research. For example, [131] presents a simulation of a large swarm size, but the simulation environment is relatively simplistic, lacking dynamic elements such as mobile obstacles, environmental noise, or sensor failures. Real-world UAV operations often involve uncertainties (e.g., GPS noise and wind) and constrained communication bandwidth, which are not modeled or discussed. While [132] presents some promising results, it lacks scaling to large-scale swarms.
• Control of a Swarm of UAVs in areas of high turbulence: Controlling a swarm of UAVs in areas of high turbulence involves significant challenges that necessitate advanced strategies and robust algorithms due to the unpredictable nature of turbulent airflows. Key issues include maintaining stability amid rapidly changing conditions, managing increased computational complexity, ensuring robustness and stability, and dealing with communication disruptions. While [133] presents a framework for optimizing UAV performance in turbulent environments using a cascaded model predictive control algorithm and Pixhawk hardware, it lacks scalability as it focuses only on the control of one UAV. It also lacks the generalization of the convergence and resource management, which is expected to be significant in such environments. Research on the control of a swarm of UAVs in areas of high turbulence is scarce.
• Energy Efficiency and Resource Management: UAVs typically have limited energy resources. Efficient energy management is crucial for prolonged operation. Future research should focus on integrating energy-aware strategies into MARL frameworks to optimize the use of power and computational resources. Jung et al. [134] presents a framework for enabling cooperative UAV teams to track multiple dynamic ground targets. While the proposed method reduces communication delay by 64% and energy consumption by 78% compared with traditional MESH networks for 10 UAVs, several limitations and weaknesses reduce the generalizability and robustness of the work as it lacks scalability and convergence studies. Ma et al. [135] presents an improved DRL-based energy-efficient UAV control for maximum lifecycle which is based on DDPG. It lacks the study of Transfer Learning as well as convergence in case of large scale swarms.
• Transfer Learning and Generalization: Developing MARL algorithms that can generalize across different tasks and environments is a significant challenge. Transfer Learning techniques, which allow knowledge gained in one context to be applied in another, could significantly enhance the flexibility and applicability of MARL for UAV control. The learned policies in [129,131,132,134] are not tested on new environments, larger team sizes, or with altered dynamics (e.g., target speed or number). This absence of generalization testing makes it hard to trust the method’s robustness. Reference [136] presents Real-Time Policy Optimization for UAV Swarms based on evolution strategies but lacks scalability and does not guarantee convergence.
• Convergence: UAVs must make decisions in real time under stringent safety constraints and uncertain environmental dynamics (e.g., wind disturbances, obstacle movement), which means the RL agent must generalize well from limited, high-risk data. This often results in sparse and delayed reward signals, further slowing convergence. Additionally, simulation-to-real-world transfer is another major hurdle: policies trained in a simulation may not converge effectively in the real world due to discrepancies between simulated and physical dynamics (the “reality gap”). In multi-agent UAV systems, convergence is even more complex. The environment becomes non-stationary from each agent’s perspective because other agents are simultaneously learning and changing their policies. This non-stationarity breaks the standard assumptions of RL algorithms, degrading learning performance and making stable convergence much harder to achieve. Techniques like Centralized Training with Decentralized Execution (CTDE) and frameworks like MAPPO and QMIX have been proposed to address this, but convergence still depends heavily on careful hyperparameter tuning, reward shaping, and training stability mechanisms. Wang et al. [130], Blais and Akhloufi [131] provide control approaches for large-scale systems but did not present any studies on the convergence. Jung et al. [134] present an energy efficient approach but lacks the study of convergence.

9. Conclusions

This paper provided a comprehensive survey of the control of drone swarms using Multi-Agent Reinforcement Learning (MARL). The integration of UAVs with MARL has emerged as a promising solution for tackling complex control and coordination challenges in dynamic and uncertain environments. The limitations of MARL in providing a robust and flexible framework for managing multiple UAVs in intricate scenarios have been pointed out. Further research is needed to enhance the efficiency, autonomy, and reliability of UAV systems to unlock the full potential of UAVs across diverse sectors.