Abstract
In recent years, UAV (unmanned aerial vehicle)-UGV (unmanned ground vehicle) collaborative systems have played a crucial role in emergency disaster rescue. To improve rescue efficiency, heterogeneous network and task chain methods are introduced to cooperatively develop rescue sequences within a short time for collaborative systems. However, current methods also overlook resource overload for heterogeneous units and limit planning to a single task chain in cross-platform rescue scenarios, resulting in low robustness and limited flexibility. To this end, this paper proposes Gemini, a cascaded dual-agent deep reinforcement learning (DRL) framework based on the Heterogeneous Service Network (HSN) for multiple task chains planning in UAV-UGV collaboration. Specifically, this framework comprises a chain selection agent and a resource allocation agent: The chain selection agent plans paths for task chains, and the resource allocation agent distributes platform loads along generated paths. For each mission, a well-trained Gemini can not only allocate resources in load balancing but also plan multiple task chains simultaneously, which enhances the robustness in cross-platform rescue. Simulation results show that Gemini can increase rescue effectiveness by approximately 60% and improve load balancing by approximately 80%, compared to the baseline algorithm. Additionally, Gemini’s performance is stable and better than the baseline in various disaster scenarios, which verifies its generalization.
1. Introduction
1.1. Background
In recent years, Unmanned Aerial Vehicles (UAVs) have evolved from auxiliary tools to task execution entities possessing capabilities for situational awareness, intelligent decision-making, and action implementation, finding extensive applications in disaster response [1,2,3,4,5]. Benefiting from its high flexibility, scalability, and rapid response ability, the UAV-UGV collaboration can quickly detect and locate disaster sites, continuously monitor the environmental conditions, and perform rapid rescue [6]. Moreover, even in the global navigation satellite system (GNSS)-denied subterranean rescue missions, the collaborative system can also efficiently achieve positioning by fusing the sensor information on UAVs and UGVs with each other [7]. Therefore, the UAV-UGV collaboration has been proven to be effective in disaster rescue tasks [8,9,10,11,12].
In UAV-UGV collaborative disaster rescue, the heterogeneous network was introduced to integrate diverse communication methods and provide ubiquitous and highly reliable connections [13]. To efficiently associate the collaboration between UAVs and UGVs, heterogeneous network-based task chain methods were introduced for collaborative scheduling tasks in the task planning module [14,15]. By utilizing information on intelligent algorithms, data links, and distributed architectures, task chain methods can efficiently dispatch rescue forces across platforms through predefined cooperation protocols, which significantly improve the rescue effectiveness in disaster environments [16].
The current task chain methods can be divided into two main categories. The first category aims to enhance cross-platform service capability, typically defining service capability as the maximum number of task chains that can be supported. Subsequently, optimization is performed on the network topology using specific connectivity metrics to generate the optimal task chain [14,17]. The second category focuses on load balancing of service network resources, dynamically planning task chains based on real-time network load conditions with the objectives of minimizing latency and enhancing the network’s rapid response capability [18,19,20].
However, current task chain planning methods remain limited for cross-platform disaster rescue scenarios: Traditional methods focus primarily on addressing communication resources to overcome connectivity challenges [18], but inadequately consider characteristics specific to disasters such as dynamic situations, mission urgency, and extreme resource constraints. Additionally, traditional methods can only generate a single task chain for each rescue mission [21]. When any node in the planned chain becomes disabled, the rescue mission may be forced to terminate, severely harming the continuity of the entire rescue process. Moreover, the resource allocation in traditional methods relies on pre-programming by external systems [22,23], which cannot deal with the extreme resource constraints arising from the dynamic evolution of disaster situations, such as sudden bandwidth drops and depleted computing resources.
Therefore, achieving effective collaboration among cross-platform rescue teams with efficient resource allocation to enhance emergency rescue efficiency still faces several significant challenges.
1.2. Challenges
This paper concludes the main challenges of task chain planning in the UAV-enabled HSN for disaster rescue scenarios as the “3H” (How) framework:
- How to plan task chains to simultaneously consider communication and platform resources constrained by disaster conditions to serve more rescue missions? For service capability enhancement methods: It performs resource pooling by allocating resource loads to UAVs and UGVs according to multi-dimensional mission requirements in disaster zones; For network resource load balancing methods: It performs pooling by connecting UAVs and UGVs tasked with serving the same disaster response mission to improve capability.
- How to plan task chains to effectively cooperate UAVs with UGVs in disaster-altered environments to serve complex rescue missions? Complex missions often demand that UAV and UGV platforms cooperate effectively to dispatch resources; Current methods rarely consider collaborative service policies within the UAV-UGV collaboration under dynamic disaster disturbances.
- How to plan task chains to timely return feedback for dealing with large-scale disaster scenarios? The current methods, based on mathematical programming and rule-based heuristic algorithms, are inefficient and incapable of addressing large-scale disaster scenarios in real time.
1.3. Contributions
To address these critical challenges in cross-platform disaster rescue missions, this paper models disaster-response task chain planning as an integer programming problem and proposes Gemini, a cascaded dual-agent DRL framework for Heterogeneous Service Network (HSN) based task chain generation method in UAV-UGV collaborative disaster rescue missions. The principal innovations are shown as follows:
- Task chain Planning Model: This paper comprehensively considers the limitations of communication and platform resources in UAV-UGV collaboration, then formalizes the task chain planning problem as an integer programming model, which decouples the problem into a joint optimization of chain selection and resource allocation. It ensures that the limited resources and services for missions can be considered simultaneously in the planned task chains (Addresses Challenge 1).
- Cooperation Policy: This paper proposes a cooperation policy for task chain planning to compensate for the low robustness of a single task chain. By planning multiple task chains for each rescue mission, the cooperation policy enhances platforms’ coordination capabilities, enabling the UAVs to cooperate with UGVs to serve for more complex rescue missions (Addresses Challenge 2).
- Cascaded DRL Framework: By applying the proposed integer programming model, this paper proposes Gemini, a cascaded dual-agent DRL framework that handles chain selection and resource allocation simultaneously. Gemini independently trains two agents: DRL-P and DRL-R. They collaboratively optimize the overall performance to dynamically plan task chains according to the HSN state and resource requirements. The trained Gemini can generate task chains quickly in large-scale disaster scenarios (Addresses Challenge 3).
1.4. Organization
The rest of the paper is organized as follows: Section 2 introduces the research related to our study. Section 3 introduces the concepts of HSN and task chain, and presents the problem formulation. Section 4 establishes the integer programming model for task chain planning. Section 5 proposes the Gemini, a cascaded dual-agent DRL framework. Section 6 presents the numerical simulation results. Section 7 is the conclusion.
2. Related Work
In single-platform task chain planning with UAV-network, current methods focus on improving planning efficiency and adaptability [24,25,26]. To enhance the efficiency of the multi-UAV system in complex task scenarios, Zhang et al. [24] integrated the task chain planning problem as a sub-problem into a joint optimization problem and proposed a task chain selection algorithm, which handle the task chain, power and UAV trajectory planning in same optimization framework. To improve the adaptability of task planning methods, Yue et al. [25] proposed a vulnerability-based topology reconstruction mechanism, which automatically ranks the importance of nodes in the task chain. When nodes are vulnerable, the UAV network will be reconstructed using the node ranking obtained. Duan et al. [26] formulated a distributed source-task-capability allocation problem and developed a dynamic task chain planning method, which enhanced the online adaptability of task chain links in multi-UAV missions.
When traditional task chain planning methods are extended to cross-platform scenarios, the singular UAV network cannot satisfy the increasing information exchange requirements due to the diversity of entities and platforms [27]. For this reason, the heterogeneous network has been introduced to facilitate the scheduling among different kinds of entities or platforms [28,29]. Nevertheless, the high flexibility of UAVs causes highly dynamic changes in the network topology, presenting more conflicts and challenges to heterogeneous networks [30,31]. To alleviate conflicts among time, space, and resource, Li et al. [28] proposed the Task Heterogeneous Information Network (THIN) to model scheduling tasks and constraints, such that the conflicts in the heterogeneous network can be detected and resolved dynamically. To enhance the collaboration between heterogeneous platforms, Xu et al. [29] proposed an integrated architecture for the heterogeneous network with UAVs and UGVs, which improved the service quality for their delivery mission.
In the past decade, high-efficiency communication models and safety routing protocols have been proposed successively, alleviating the communication problem in UAV-enabled heterogeneous networks and mitigating their heterogeneity [28,32]. This makes cross-platform heterogeneous network-based task chain planning feasible [11]. Xiao et al. [33] combined reinforcement learning and game theory for resource management in chain planning tasks. By treating resource consumption as a negative reward during the training process, the proposed method plans the chain to consume as few resources as possible. However, the negative reward cannot precisely control resource consumption; compared to our proposed method, this method cannot be applied to scenarios with fixed and limited resources. Compared to single-platform scenarios, task chain planning in cross-platform scenarios faces more collaborative challenges, such as inefficient load balancing, limited resources, and low robustness [11,34,35]. To alleviate the computational load imbalance, Wang et al. [11,34] proposed a high-efficiency information sharing scheme named RescueChain and a two-tier reinforcement learning-based incentive algorithm for cross-platform disaster rescue with UAV-aided, which improves collaboration effectiveness. To alleviate the limited resources, Zhou et al. [35] established an air-ground integration network architecture with UAV-UGV collaboration in the task chain, which improved the resource utilization.
Notably, existing research predominantly designs task chains from a unilateral perspective, rarely considering the systematic impact of adversarial interactions on the network. It innovatively adopts an adversarial perspective. While planning task chains, it evaluates the service effectiveness and quantifies the potential threat these tasks pose to the network. By establishing comprehensive evaluation indicators, the study maximizes overall effectiveness.
3. Preliminaries
This section introduces the concept of HSN and the task chain, defines the mathematical model of the HSN with UAV-UGV collaboration, and formalizes the task chain planning process as a two-stage optimization problem comprising resource allocation and path planning.
3.1. HSN and Task Chain
Heterogeneous service network refers to a networked architecture comprising operating entities and platforms interconnected by predefined communication protocols. From the task chain perspective, the core of the operational process can be concluded as the following sequential phases: acquiring intelligence, making decisions, and executing missions. Furthermore, by combining the operational workflows, the entity of the service network can be categorized into three classes:
- Sensing entity : Responsible for environmental monitoring and data collection. Equipped with sensors and reconnaissance modules, sensing platforms generate dynamic situational awareness by aggregating mission intelligence.
- Deciding entity : Making decision through embedded reasoning algorithms. Deciding entities analyze inputs from sensing entities, evaluate the benefit of executable actions, and generate the best decision.
- Influencing entity : Implements actions based on received directives. Influencing entities are configured with restricted loads to perform missions.
According to the entity types in service network, denote the entity type set as and the entities relationship set as . Then, the HSN can be defined as follows:
Definition 1
(Heterogeneous Service Network). For a given undirected network , where is the set of nodes, is the set of edges, is the node type mapping, and is the edge type mapping. For any node , there is a node type , and for any edge , there is also an edge type . If the graph has node-type or edge-type , the network is considered a heterogeneous service network.
In addition, considering the UAV and UGV platforms simultaneously, each entity type can be further divided. As shown in Figure 1, in the UAV platform, the UAVs can also be divided into sensing, deciding, and influencing UAVs, which correspond to the entity types sensing entity (S), deciding entity (D), and influencing entity (I). Specifically, see Figure 1, HSN organizes each entity from UAV and UGV platforms to complete four missions. Sensing UAVs and UGVs are employed to gather intelligence, serving as S. Deciding UAVs and UGVs are employed to formulate task completion strategies based on the acquired intelligence, serving as D. Influencing UAVs and UGVs are employed to execute actions, serving as I.
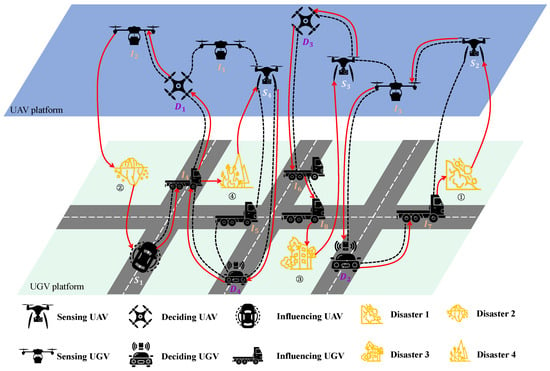
Figure 1.
The schematic diagram of the task chain in UAV-UGV collaboration.
After the entities’ respective functions are completed, sensing, deciding, and influencing entities must be connected to complete the mission execution process. If the missions are within the scope of sensing entities, the workflow can be operated through the following phased protocol: Firstly, a sensing entity is selected to maintain persistent surveillance while propagating processed data packets to a deciding entity. Then, a deciding entity synthesizes received information and generates optimized tasking directives for an influencing entity. At last, an influencing entity executes missions within specified resource budgets. This workflow constitutes the multi-stage operational process, which connects the sensing entity, deciding entity, and influencing entity in a specific sequence: . Based on the multi-stage operational process, the task chain can be defined as follows:
Definition 2
(Task Chain). A task chain is a path that sequentially traverses sensing, deciding, and influencing entities, where designated entities are assigned to perform situational awareness, intelligent decision-making, and action implementation. Planning task chains constitutes a critical method for executing missions through HSN in complex mission scenarios.
Furthermore, the task chain can be abstracted as a functional path: a sequence of connected nodes following predefined topological rules. Such a path is formally termed a meta-path.
Definition 3
(Meta-Path). A heterogeneous network contains multiple meta-paths, which can be denoted by a set . For an arbitrary meta-path l, it can be represented by , in which , and can be respectively mapped with a corresponding type by .
To meet the mission capability requirements, the meta-path of the task chain needs to satisfy the following constraints:
- the head node is a sensing entity, .
- the tail node is an influencing entity, .
- there is an intermediate node which is a deciding entity, .
It is worth noting that in the meta-path, only the first sensing entity, the last influencing entity, and one of the deciding entities in the middle engage in the mission execution. The other nodes in the meta-path only serve to relay information.
As illustrated in Figure 1, four rescue missions need to be executed. HSN plans task chains to complete missions, denoted as , , and . For the task chain , the sensing, deciding, and influence entities can simply plan. However, information flow cannot always be transferred directly. For and , which cannot be completed by the specific sequence “” because of the communication constraint. Thus, forwarding entities, which any entity can execute, are required to rely on the workflow and complete the task chain. For example, and are treated as forwarding entities for and . It is worth noting that they only perform relaying and do not execute any other missions.
3.2. Problem Description
Planning task chains will occupy the entity’s resources. However, the resource quantity is limited. To maximize the utilization of resources on the entities, we need to plan task chains strategically. As shown in Figure 2, four meta-paths can be used to plan task chains to execute the three detected missions, which are respectively . Since the entities and are deciding entities, and each task chain involves only one deciding entity, making the decision. By using to denote the x-th candidate task chain for executing the k-th mission, six task chains can be chosen according to the different choices of deciding entity:
where is used to identify the deciding entity responsible for making a decision, when multiple decision entities are included in the task chain. To completing all missions, we combined all feasible task chains and obtained eight candidate solutions as follows:
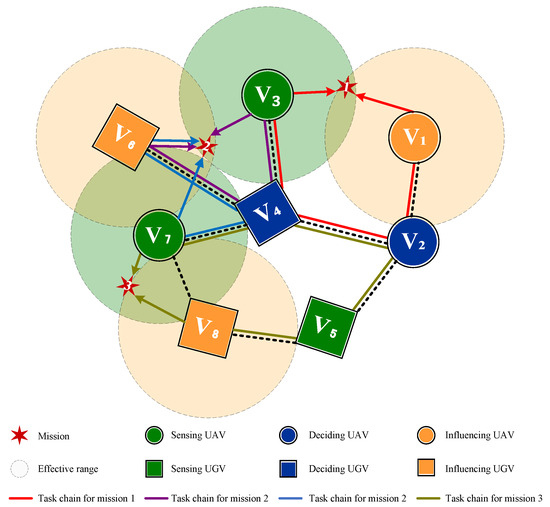
Figure 2.
The task chain planning process for a given HSN.
Assuming that the minimum required resource for completing missions are , which respectively donate the resource that the sensing entity, the deciding entity and the influencing entity need. The maximum capability of each entity can be known in advance, which can be respectively denoted by . As depicted in Figure 3, the line chart illustrates the maximum resource capacity for each entity, while the bar chart presents the resource consumption associated with each entity. The expected resource consumption for all solutions, except for , exceeds the maximum load capacity of entities and . Thus, the solution can only be used to plan task chains for the missions.
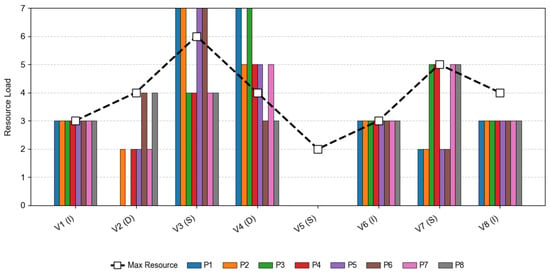
Figure 3.
The load and capability of entities.
Generally, task chains are always issued in an order-based method, and each order represents a mission that needs to deploy a task chain. However, the complex missions are always hard to complete with a single task chain. Assuming that the required resource of mission 2 is changed, the sensing resource is changed from to . For the changed requirement, it can be observed that none of the solutions can be chosen to complete the mission. In fact, the quantity of resources within the effective range is sufficient; the reason why we can not complete all missions is that the existing order-based method can not effectively schedule the available resources. Thus, this paper proposes a cooperation-based policy to plan task chains, instead of strictly planning one task chain for each mission. This policy adjusts the number of task chains according to the requirements of the missions. In this way, the resources can be allocated flexibly and more missions can be destroyed.
Based on the cooperation-based method, we try to plan an additional task chain based on . In this way, can work with to complete the mission commonly. Then we need to decide the resource allocation strategy for these two task chains. Since and are only different with the sensing entity, thus, we only need to consider how to allocate sensing resources to satisfy the demand. Three different policies can be got as and , which respectively represents allocation policies for entity in and entity in . These new solutions is respectively named as and . We determine the feasibility of the solution based on whether the entity’s load rate exceeds 1, with the load rate being defined as the ratio of the entity’s resource consumption to its capacity. The maximum load rate of these new solutions is respectively. Thus, and are reasonable to complete all missions. To this end, we can find that different path planning and resource allocation policies can lead to different service effectiveness. Therefore, we define the task chain planning problem as follows:
Definition 4
(Task chain planning problem). The task chain planning problem involves selecting feasible meta-paths and allocating heterogeneous resources across sensing, deciding, and influencing entities. Its objective is to maximize benefit by completing more missions.
4. Task Chain Planning Model
This section simultaneously considers the communication and platform resources to model the task chain planning problem and establishes an integer programming model.
4.1. Assumption
For establishing the task chain planning model, this paper takes the following assumptions:
- All missions are simultaneously detected and maintain positional stasis while HSN plans task chains.
- Entities can share intelligence with all entities quickly through communication protocols. Task chains have the same communication requirement for each connection.
- Task chains can be executed successfully while they are planned. The mission takes a relatively long time to execute, so the consumed resources during the execution process cannot be released.
4.2. Entity Model
We consider a continuous scenario, using to define the time step. At each time step t, the sensing entity detects disasters and generates rescue missions . The attribution of can be denoted by a three-tuple . The vector represents the generating location, the vector represents the required resources quantity for each type, and represents the threat if is not completed.
HSN organizes entities to complete missions, according to Definition 1, which is described as . For each entity , attributions can be described as a four-tuple . The vector denotes the location of the i-th entity, vector denotes the type of , where is a binary, which is 1 if the type of is . Since each entity has only one type, satisfies the normalized condition: . The denotes the capability of , which limits the resource usage. denotes the effective range of the i-th entity. Sensing and influencing entities only work when the missions are within the effective range. denotes the resource consumption at t time step.
Considering the communication in the previous assumptions, we assume that the HSN can share the information with the communication protocol among entities. However, entities can not be connected entirely due to the limitations of communication distance and communication protocols. Meanwhile, the communication frequency of each edge is limited due to the restriction on bandwidth. For each edge , the attribution can be described as a two-tuple . where denotes the capability of , which limits the communication frequency. When and can exchange information through the connection , otherwise, when , the connection does not exist; denotes the communication frequency of at t time step.
4.3. Resource Allocation
Denote X as the maximum number of task chains for mission ; For mission , its x-th task chain () can be denoted as . Especially, the represents that the x-th task chain of does not exist. To indicate the x-th task chain planning situation on mission , we denote a binary variable as follows:
In this way, the overall task chain planning situation on mission can also be indicated by a binary variable that satisfies the following equation:
By judging if the value of is 1, a rescue mission subset can be filtered. We denote the mission with as , traverse the mission set , we have a new set: . Only the rescue mission in is considered complete. When , HSN will choose entities and allocate resources to execute the task chain .
We use three-dimensional vector to denote the consumption of type resources on . For all task chains and entities involved in mission , the allocated resource must satisfy the requirement, so we have:
To ensure the mission can be completed successfully, entities can not overload. The generated load at each time step can be computed as follows:
Simultaneously, for entity , its load is non-recyclable and cannot exceed its capability during the entire mission process. Therefore, we have the following resource restriction:
According to Definition 2, the task chain has a construction restriction: it requires a sensing entity, a deciding entity, and an influencing entity to cooperate. To ensure the task chain concludes these entities, a binary variable is defined to denote if allocates type resource to plan as follows:
Next, when the following equation is held, the task chain would conclude all the entities:
4.4. Task Chain Planning
The chosen entity needs to be connected to plan a whole task chain. is defined as a binary variable to denote if is chosen at t step, when is chosen for planning , otherwise . To ensure effective communication, edges can not be overloaded. The generated load at each time step can be computed as follows:
The load of each edge cannot exceed the capability during the whole mission process; the restriction should be made as follows:
According to the location in the task chain, the entity can be divided into three types: the head entity, the middle entity, and the irrelevant entity. The head entities are the first entity and the last entity on the task chain; the middle entities are the other entities on the task chain; the irrelevant entities are the entities outside the task chain. According to Definition 3, head entities are sensing entities and influencing entities, and middle entities are used to deliver the message without any consumption, except that a deciding entity makes the decision. When is decided to be planned, the entities can be distinguished. and are defined as binary variables as follow, denotes that is a head entity within and denotes that is a middle entity within .
Since a chain has only one start entity and one end entity, it is necessary to ensure that the quantity of head entities is two to guarantee the rationality of as follows:
Then we need to ensure the entities that are allocated resources are correctly deployed on the task chain:
Besides, sensing entities and influencing entities have a limited effective range. When it is chosen as a head entity, we need to ensure the distance between the mission and the head entity is within the effective range:
4.5. Optimization Objective
According to the restrictions, we can deploy appropriate task chains to complete missions. The destination is to reduce the threat from missions as much as possible, which can be denoted as:
4.6. Complexity Analysis
P can be transferred into the combination of a resource-constrained project scheduling problem (RCPSP) [36] and a Steiner tree problem (STP) [37] at each time step; both of these problems have been proven to be NP-hard.
Assuming that the variable is known at the t step, P can be transferred as an RCPSP. The RCPSP considers a mission set and a resource set . For each mission , the requirement to complete is . For each kind of resource , the maximum capability is . When solving the RCPSP, the objective is to produce an appropriate cooperation policy to employ limited resources to complete missions for the maximum benefit. for P, the rescue mission can be regarded as , where the entities can be regarded as . The demanded resource to complete the rescue mission can be regarded as d, and the entities’ maximum capability can be considered as c. Due to the limited capabilities of entities in HSN, the objective of P is to determine the optimal corporate policy for organizing entities to complete rescue missions, thereby reducing the threat posed by disasters as much as possible.
Assuming that the variable is known at t step. P can be transferred as an STP. The STP considers an undirected graph where N denotes the node set and B denotes the edge set, and a final point set F is also given. The objective is to find a sub-tree that connects the given final points at the lowest possible cost. For P, the entities can be regarded as N and the edges between can be considered as B; thus, the HSN can be regarded as K. Since the given head node and the tail node can be regarded as F. Sub-trees are needed for completing missions, which not only connect the given finals but also contain a D-type entity. Due to the limited communication capability of each edge, the objective is to establish an appropriate routing policy that maximizes mission completion. Based on the above analysis, we prove that P is NP-hard.
5. Gemini Design
In this section, we propose the Gemini, a cascaded dual-agent DRL framework for cooperation-based task chain planning. Gemini decouples the task chain planning problem into two sub-problems: resource allocation and path planning. Subsequently, it trains two specialized agents, DRL-R and DRL-P, to address these sub-problems respectively.
5.1. General Overview
The proposed algorithm adopts an Actor-Critic framework to construct a cascaded optimization model, which consists of a chain selector and resource allocator, as shown in Figure 4. The chain selector (DRL-P) sequentially plans paths according to the mission priorities. It first filters out invalid UAVs through a masking mechanism and then employs an embedded shortest-path algorithm to determine optimal paths based on the mission locations. Subsequently, DRL-R verifies whether the number of planned task chains satisfies the predefined requirements. If the requirements are met, the paths are confirmed as outputs, and the process moves on to the next mission. Otherwise, the planning is terminated, and communication resources in the selected paths are immediately released. The resource allocator (DRL-R) allocates loads to UAVs along the generated paths. It extracts specific service subgraphs that are solely relevant to the current mission from the HSN. Then, it incrementally allocates loads to UAVs (one unit per decision) based on UAV load status and mission demands. After each allocation, the agent assesses the mission. If the mission can be struck successfully, the agent outputs the allocation and proceeds to the next mission; otherwise, the allocation is terminated, and the loads on the UAVs are immediately released.
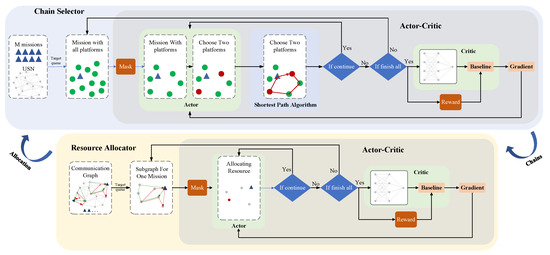
Figure 4.
The workflow of Gemini.
5.2. Elements of Gemini
State, action, transition and reward are the four most important elements for achieving reinforcement learning and are also the key to the interaction between the reinforcement learning agent and the environment [38]. The reinforcement learning agent acquires the current state representation of the environment through observation and takes corresponding actions based on its policy. Actions change the environment through transitions, and rewards are obtained from the changes in the environment [39,40]. In this way, the reinforcement learning agent can gradually learn a policy to maximize its rewards by continuously interacting with the environment and obtaining rewards. These elements are represented as follows.
5.2.1. Element of DRL-R
Based on the input paths, DRL-R distributes resources for entities to plan task chains.
State: State is comprised of HSN state and mission states. HSN state is determined by entities’ load and capability, which can be represented by and , where represents the load of the entity and denotes the capability of the entity. Mission states are determined by the demand for missions and executable UAVs. Demand of missions is denoted as , where respectively represent the required resource quantities for successful completing. Executable entities, derived from input paths, are denoted as , where is structured as , representing the sensing entity (S), the deciding entity (D) and the influencing entity (I) in the i-th task chain planned for mission . Thus, the state can be denoted as:
Action: We traverse the mission sequence based on preset priorities and execute actions for each mission. Action is a decision sequence, for each decision, we select an entity and use one unit of resource. The action process iterates multiple rounds until either the resource requirements of the mission are fully satisfied or all available resources become exhausted. If the mission is successfully destroyed, we record the deployed task chain, otherwise, we release the allocated resources.
Transition: After allocating resource for a mission, the entity load need to be updated. This allows the agent to more comprehensively consider the current load of the entities during subsequent decision-making, thereby increasing its propensity to select entities with more abundant remaining resources.
Reward: The core objective of DRL-R is to complete as many missions as possible under the strictly constrained resources of entities. To enhance the capability of exploring global optimal solutions, we employ a delayed reward mechanism that computes rewards after the allocation for all missions is completed. This enables agents to optimize decisions from a long-term perspective.
Since we consider an interaction process, the mission value is decided by both its importance and adversarial impact on HSN. Fan et al. quantified the importance of missions based on resource consumption within the network [41]. We adopt this approach to quantify a mission’s importance through the sum of demanded resources, defining the importance of a mission as the sum of resources demanded for completing it, which can be formalized as follows:
Yang et al. established a multiple objective decision-making model to assess the threat of the mission [42]. We adopt this measure to compute the threat level of a mission by aggregating the weighted entity’s value within its effective threat range. The value of each entity is determined by its capability. To measure its importance for HSN, the weight is quantified based on the degree. Thus, the threat of a mission can be expressed as:
When constructing a comprehensive reward function, there is a key challenge: the two core components ( and ) typically possess different physical dimensions and numerical ranges. This difference may cause the part with the large numerical range to completely dominate the final result, while the part with the small numerical range loses almost all influence, regardless of its actual importance. To eliminate this unfair influence caused by differences in dimension and scale as much as possible, we employ logarithmic normalization to process and separately. The core advantage of this method lies in significantly compressing the range of large numerical values, especially exerting a stronger inhibitory effect on extreme values. This process ensures the fairness of reward calculation effectively.
When integrating the processed and to form the final reward, we abandon the simple additive form and instead choose the multiplicative form. This choice is based on profound consideration: addition essentially allows for linear compensation between different parts. However, and are interdependent and inseparable relative factors. Multiplication perfectly fits this characteristic, it naturally strengthens the “bottleneck effect” or “constraint enforcement”. This characteristic enables the multiplicative form to more authentically reflect the essential requirement of non-substitutability and synergy of key factors in reality.
Based on the above, adopting multiplication on the logarithmically normalized indicators can construct a comprehensive reward mechanism that is more aligned with actual decision-making logic and possesses stronger robustness, which can be denoted as follows:
5.2.2. The Element of DRL-P
DRL-P plans paths based on the HSN state and mission states, which serve as inputs for DRL-R to allocate resources.
State: State consists of HSN state and mission state. HSN state is determined by the adjacency matrix, the communication protocol and the type of entities, which can be represented as , and . if there the entity and are connected by topology, otherwise . indicates the load rate of each edge. represents the type of entity . Mission state can be expressed as the positional relationship between the entity and the mission, which is represented as , where if the mission lies within the effective operational range of entity , otherwise . In summary, the state can be expresses as:
Action: We traverse the mission sequence based on preset priorities and execute actions for each mission. Action is a decision sequence, for each decision, we plan a path. Specifically, we employ the depth-first search algorithm to identify reasonable chains as a candidate set. Subsequently, we select the optimal path from the candidate set based on an evaluation metric that combines chain length with load. To implement the cooperation strategy, we plan 3 task chains for each mission. Consequently, we plan 3 paths for a mission and permit repeated selection of the same chain to avoid unnecessary coordination.
Transition: After the planning for a mission, the communication load need to be updated. This allows the agent to more comprehensively consider the current communication load, thereby increasing its propensity to select the path with more remaining communication resources. Notably, each update restricts the communication load increment to a maximum of one unit, thereby preventing excessive load resulting from repeated selection of the same path under the cooperation strategy.
Reward: We implement a delayed reward mechanism wherein the reward for action sequences is calculated after planning task chains for all missions. The generated paths are fed into the trained DRL-R to make allocations. Then, DRL-R outputs the reward computed by the planned task chains with Equation (18) as the reward of DRL-P, which is used to evaluate the effectiveness of the path planning strategies.
5.3. Training Process
DRL-R is trained to make decisions in Algorithm 1, which aims to generate a satisfied resource allocation policy to complete more missions based on given paths.
| Algorithm 1: Training Process of DRL-R. |
 |
At the start of training DRL-R, we define the number of missions N, initialize the parameters of the Actor network and Critic network , set the initial state of the HSN , and use a depth-first search algorithm (DFS) to plan the chain. For each instance, the HSN state is obtained to form the instance states . Each instance contains some batches, for each batch, a random sequence containing N missions is generated. The sequential execution of missions follows the predefined sequence is used to simulate the dynamic task generation process. For each mission , the demand resource amounts can be known. To satisfy , DFS is used to find the shortest path candidate P which obeys the task chain definition. According to our model, no more than three task chains p are chosen randomly from the candidate path set P. Within the chosen task chain p, the S entities, D entities, and I entities that execute for are determined. Before the agent takes action, the state is updated by concatenating and with . Based on the updated state, the actor network performs sequentially to choose entity v, each choice means that one unit of resource is allocated to execute . The decision process terminates when the available resources are depleted or the current mission is completed. To evaluate the quality of generated policies, we compute the reward and utilize the critic network to assess the state value based on the initial instance state, thereby establishing a performance baseline for comparison:
and represent the parameter matrices of the first and second layers, respectively, while and denote the corresponding bias terms.
Finally, we jointly optimize the actor and critic networks to enhance the policy value. On one hand, the actor network generates higher-value action sequences, and we compute the policy gradient weighted by the advantage function. The parameters of the actor network are updated by the gradient descent method to maximize the expected return (Line 18):
On the other hand, the critic network evaluates the expected return of the current state to quantify the relative advantage of the action sequence, which is used to provide a baseline value for the actor network. We calculate the value estimation error and obtain the parameter gradients by differentiating the error, then update the parameters of the critic network using the gradient descent method. Additionally, we update the parameters in Equation (20) through backpropagation to generate a better baseline to minimize the value estimation error (Line 19):
The trained DRL-R is used to train DRL-P in Algorithm 2, which aims to plan satisfied chains as an effective input to adopt the allocation policy generated by DRL-R. At the start of training DRL-P, we define the same variable as in Algorithm 1 with the trained DRL-R and a permitted maximum number of chains to plan for each mission X.
For each instance, the HSN state is obtained to form the instance states . Each instance contains some batches, for each batch, a random sequence containing N missions is generated. The sequential execution of missions follows the predefined sequence is used to simulate the dynamic task generation process. For each mission , the demand resource amounts and the coordinate can be known. Then, the state is update by concatenating and with . A masking mechanism is used to restrict the agent can only choose the entity, whose effective range is . After the data preparation, the actor network performs sequentially to choose entity and according to the probability distribution, and paths are planned by DFS. Before planning paths for the next mission, the trained DRL-R is used to generate the allocation policy, compute the action reward r, and return the HSN state Then, DRL-P executes the same process as DRL-R to evaluate and optimize.
| Algorithm 2: Training Process of DRL-P. |
 |
6. Performance Evaluation
In this section, we make multiple simulations to evaluate the performance of Gemini and demonstrate its superiority by comparing it with the baseline. Furthermore, we validate the generalization capability by testing it on HSN with larger scales, more missions, and stricter conditions.
6.1. Settings for Numerical Simulation
6.1.1. Data Preparation
We constructed a fictional HSN as follows: Firstly, a square scenario of size is defined, and 50 entities are randomly generated within it, including UAVs and UGVs. The capability of each entity is sampled from uniform distributions within the ranges of . The coordinates of the entities are sampled from a uniform distribution of , and probabilistically assigned as sensing entity, deciding entity, and influence entity with probabilities of 0.35, 0.3, and 0.35, respectively. If the distance between entities is less than 25, an edge will be established with a probability of 0.4. Additionally, 30 missions are randomly generated on the scenario, with their coordinates sampled from a uniform distribution of . The required resources to complete the mission are sampled from uniform distributions within the ranges of . Besides, other hyperparameter settings are shown in Table 1.

Table 1.
Hyperparameters of DRL-R and DRL-P.
6.1.2. Device Configuration
We conduct simulation experiments on a server with the following specifications: CPU: 18 vCPU AMD EPYC 9754 128-Core Processor; GPU: NVIDIA RTX4090; Memory: 24GB; OS: Ubuntu 22.04. All algorithms are developed using Python 3.12.
6.1.3. Metrics
To comprehensively evaluate our method, we propose two metrics: action benefit and load balance rate. Given that the action benefit can be represented as the reward, we focus primarily on introducing the load balance rate. Kurose et al. [43] thought that taking the load balancing rate into account in network resource scheduling can lead to the construction of a highly available and high-performance network architecture, which enhances resource utilization and ensures system reliability. Thus, we design the load balance rate as an important metric to evaluate our approach, which can be expressed as:
where and are used to respectively denote the load balance rate of entities and communications, where represents the average load rate and denotes the standard deviation of the load rate. According to the formulation, a smaller value of b signifies a more balanced network load.
6.1.4. Comparison Method
Order-Based strategy: To verify the effectiveness of Gemini, we propose the order-based strategy as the baseline. Based on the planning process, we propose the following specific algorithm: First, the missions are sorted according to their priority, and then the task chain is planned based on this order. Subsequently, the entities capable of sensing and influencing the mission are respectively assigned to a sensing entity candidate set and an influencing entity candidate set. Then, the entities with the lowest load rate from these sets are selected as the head node and tail node. Subsequently, the depth-first search algorithm (DFS) is used to find a candidate path set. Finally, a path characterized by the lowest decision entity load rate and the shortest path length is selected from the candidate path set for planning the task chain. Simultaneously, the load of the relevant entities and communications is updated for planning task chains to complete the next mission.
Random strategy: To prove the order-based strategy is reasonable, we design a random strategy. In the beginning, the random strategy sorts missions the same way as the order-based strategy. Then, the sensing and influencing entities are randomly selected from the executable entities. Finally, DFS is used to find a path candidate set, then choose a path to plan the task chain randomly and update the load of the relevant entities and communications simultaneously.
6.2. Training Performance of Gemini
Figure 5a,b illustrate the loss changes during the training of DRL-R and DRL-P, respectively. To better highlight the overall data trends, we smooth the raw data, setting the factors to 0.8 and 0.6 for DRL-R and DRL-P, respectively. The data shows that the loss function decreases progressively as the number of training iterations increases, which is indicative of model convergence. As training proceeds, the learning algorithm updates the parameters based on reward signals and state values. The figures demonstrate that DRL-R converges after approximately 20,000 tasks, whereas DRL-P, with a larger action space, requires around 30,000 tasks to converge. This confirms that the Gemini achieves stable solutions post-training and possesses practical applicability.
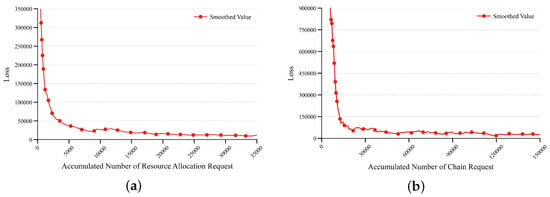
Figure 5.
Metrics comparison with different quantities of missions. (a) Train process for DRL-R. (b) Train process for DRL-P.
6.3. Numerical Simulation Result
In the simulation experiments conducted in this section, to ensure data reliability while quantifying the impact of randomness on the experimental results, we conducted 40 repeated experiments for each data point and calculated the confidence intervals at .
6.3.1. Simulation in Task Chain Planning
As shown in Figure 6, Gemini, order-based strategy, and random strategy are respectively used to plan task chains, with the setting assumed in Section 6.1.1. Notably, varying intensities of red denote the differing importance of missions, with a deeper hue of red indicating greater significance. Gemini and order-based strategies perform better, as shown by the number of task chains, which proves the rationality of the scenario and the task chain planning strategy. Furthermore, Gemini outperforms the order-based strategy. On one hand, Gemini plans multiple task chains to complete the same mission collaboratively, on the other hand, Gemini provides a DRL framework that enables the distribution of limited resources to complete more significant missions.
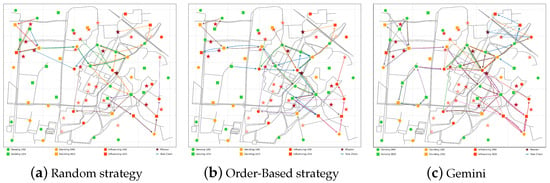
Figure 6.
Task chain planning effectiveness with different strategy.
6.3.2. Simulation in the Service Benefit
The service benefit on missions of different intensities: We evaluate the performance when handling missions of differing intensities. Mission intensity refers to the quantity of resources demanded for completion. Resource requirements are determined as follows: Given an average resource requirement x (where ), the demands for sensing, decision-making, and influencing resources are randomly generated within the interval , with their arithmetic mean fixed at x. Based on these settings, we compare the task chain planning method across seven distinct mission scenarios corresponding to x values ranging from 2 to 8. In addition, since the significant variation in the magnitudes of the experimental data, we applied logarithmic standardization. This process compresses the data values while preserving their underlying trends, facilitating clearer visualization.
Taking the service benefit of the order-based strategy when as the reference point and normalizing the remaining simulation results, which are shown in Figure 7a. Data analysis indicates that Gemini achieves the best effectiveness under all scenarios. In low-demand scenarios (), Gemini outperforms the order-based strategy slightly since the overall resources of the network are abundant and a single task chain can complete most missions. In high-demand scenarios (), the advantages of Gemini are even more prominent, which is attributed to the mission decoupling mechanism. The decoupling mechanism dynamically distributes resources to plan multiple task chains for each mission, enabling HSN to complete more complex missions.
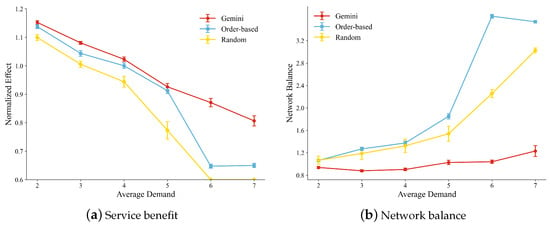
Figure 7.
Compare the service benefit of different methods with different average demands.
Regarding network load balancing, Figure 7b demonstrates that Gemini’s advantages become progressively more pronounced with increasing mission resource demands. Under low resource demand conditions, entities and links experience full utilization as most missions can be accomplished through task chain planning, resulting in balanced network loads. Consequently, all methods exhibit low values in such scenarios. As resource demands escalate: the number of successfully completed missions gradually decreases, while high-value central entities tend to sustain elevated loads. This leads to significantly unbalanced network loads and consequently higher NB metric values. However, leveraging its unique decoupling mechanism, Gemini maintains relatively balanced network loads through collaborative planning of additional task chains, thereby sustaining lower b values compared to alternative approaches.
The service benefit on missions in different generation areas: We evaluated performance under varying mission distribution patterns, categorized as centralized or distributed [44]. Centralized distribution concentrates missions in specific areas for focused services, while distributed distribution disperses missions across the service network. By dynamically adjusting the mission distribution range defined as (where ), we constructed scenarios transitioning continuously from distributed () to centralized () services. The simulation results, which are normalized against the order-based strategy’s service benefit at , which is shown in Figure 8a, demonstrate Gemini’s consistent superiority.
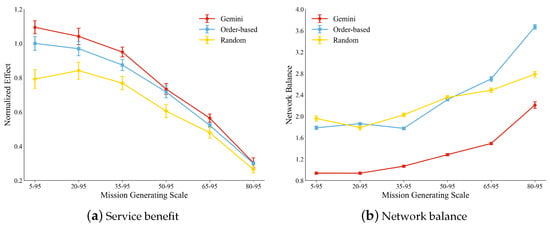
Figure 8.
Compare the service benefit of different methods with different mission generating scales.
In terms of network load balancing, Gemini exhibits significant advantages, as shown in Figure 8b. When missions are distributed (), the load balancing metric remains the lowest. This performance arises because the distributed nature of the missions allows entities to be utilized more reasonably during task chain planning. However, as missions become more centralized (), distance constraints increasingly limit the number of entities available for planning task chains. Consequently, the performance of load balancing progressively deteriorates for typical methods. In contrast, Gemini achieves a relatively balanced load within the region by leveraging its collaborative planning capabilities to utilize more entities effectively, sharing the load. This mitigates the aggravation of network load imbalance. This approach enables Gemini to maintain better overall load balancing performance compared to other methods, especially centralized mission distributions.
The service benefit on missions of different quantities: We evaluated the performance under different quantities of missions. The number of missions is determined as (). Comparative methods are conducted for the task chain planning method across 7 different mission scenarios, where the mission quantity ranges from 6 to 30.
We normalize the simulation results by using the service benefit of the order-based strategy for 18 missions as a benchmark. As shown in Figure 9a, the result indicates that Gemini consistently outperforms the order-based strategy across all scenarios. When the quantity of missions is small (), Gemini has a slight advantage since the resources are enough. However, when the quantity of missions is big (), Gemini maintains superior service benefits by prioritizing to complete high-threat missions. By contrast, the lack of global coordination capability in the order-based strategy compels it to rely on local optimizations, thereby resulting in a significant decline under constrained resource conditions.
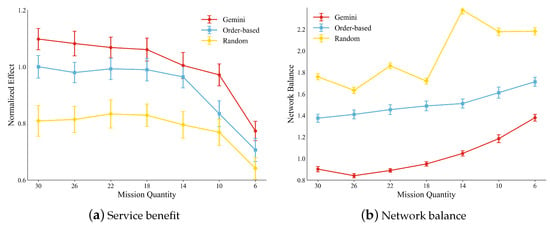
Figure 9.
Compare the service benefit of different methods with different mission quantity.
The proposed algorithm demonstrates significant advantages in network load balancing. As shown in Figure 9b, it maintains optimal load-balancing performance when mission quantities scale from 6 to 30. For larger mission volumes, Gemini’s task chain planning achieves superior load balancing compared to alternative methods. As mission quantities decrease, Gemini consistently sustains lower b values. However, its relative advantage in load balancing diminishes with reduced mission volumes due to constrained optimization space. Crucially, these results confirm that Gemini maintains effective performance even in small-scale scenarios, demonstrating robust generalization capability.
6.3.3. Simulation in Different Proportions of Entities
We evaluated the service benefit under varying network conditions. In real-world operational scenarios, the composition of entities may experience substantial alterations as a result of factors such as faults, operational demands, or network reconfiguration. To validate the generalization capability of the proposed model, we simulate these dynamic changes by adjusting the proportions of entity types. Specifically, the proportion of deciding entity is set to , while the proportions of sensing and influencing entities are adjusted to (). By adjusting the parameter x, we progressively alter the proportion of deciding entities from 0.1 to 0.7. This process not only provides a comprehensive evaluation of the algorithm’s generalization performance but also conducts a rigorous examination of its adaptability and stability under extreme conditions.
We take the service benefit of the order-based strategy when the proportion of decision nodes is 0.3 as the benchmark and normalize the simulation results. As shown in Figure 10a, when the proportion of deciding entities is not greater than 0.2 (), Gemini is slightly better than the order-based strategy since the number of available task chains is already limited, and Gemini is hard to make better decisions. As the proportion of the deciding entities increases, the performance of Gemini improves faster because it can more efficiently distribute resources to complete high-threat missions with limited resources. When the proportion of decision entities reaches 0.4, the service benefit of both the Gemini and the order-based strategy reaches its peak. This means that in the current network configuration, the proportion of deciding entities that can bring the greatest service benefit to HSN is 0.4. As the proportion of the decision entities continues to increase, the service benefit declines, and Gemini still maintains an advantage.
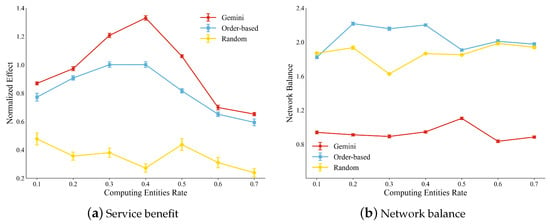
Figure 10.
Compare the service benefit with different entities’ proportions.
In terms of network load balancing, Gemini demonstrates a significant advantage as shown in Figure 10b. Specifically, Gemini consistently sustains the lowest load balance value and demonstrates significantly superior performance compared to the order-based strategy. For the order-based strategy, the best service benefit is achieved when the proportion of deciding entities is 0.4. This is because, during the mission generation phase, we ensure that the aggregate demand for each type of resource remains consistent. When the proportion of entities is uniform, the rate of each resource type is equal, thereby enhancing the overall service benefit. In conclusion, Gemini can perform a greater service benefit, maintain better load balancing, and possess superior generalization capabilities.
6.3.4. Sensitivity Analysis
To demonstrate the rationality of the network balance metric proposed in Equation (24), we conduct a sensitivity analysis of its parameters . Different values of shift the focus of network attention: when approaching 0, the network prioritizes link load balancing, while near 1, it emphasizes node load balancing. However, our defined network balance metric is relative. To further highlight the relationship between network load balancing and mission effectiveness while avoiding a good performance caused by mission failure, we proposed the metric as follows before the sensitivity analysis:
where E represents the overall mission effectiveness after logarithmic normalization. Using this metric, we perform a sensitivity analysis with parameter values ranging from 0.3 to 0.8 in increments of 0.1.
Taking the scenario in Figure 7a as an example, the sensitivity analysis of parameters after processing the network balance metric b is shown in Figure 11. We observe that within the given range, regardless of how we adjust the focus on the load balancing of edge or node, Gemini consistently achieves the lowest values. This indicates that Gemini can learn strategies that optimize global load balancing while maximizing overall effectiveness.
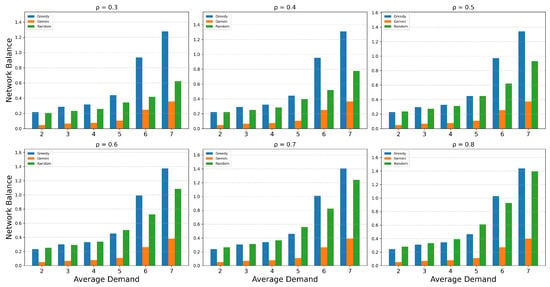
Figure 11.
Evaluation the sensitivity of .
7. Conclusions
Existing task chain planning methods can not generate multiple task chains or handle resource allocation and capability optimization simultaneously for the same rescue mission. It limits the efficiency and robustness of the UAV-UGV collaboration in emergency disaster rescue. To address these limitations, we propose Gemini, a cascaded dual-agent DRL framework that is capable of planning cooperation-based task chains in UAV-UGV collaboration. Specifically, by integrating communication protocols and resource constraints, Gemini enables multi-platform task chain planning for individual missions. This process is executed through two modules: a task chain selection agent, which plans task chain paths based on real-time rescue scenarios, and a resource allocation agent, which distributes resources along the generated task chains. Numerical simulation results demonstrate that Gemini outperforms baseline algorithms in service benefit, network load balancing, and generalization capability.
Author Contributions
Conceptualization, M.W. and C.Q.; methodology, M.W., C.Q. and B.R.; software, M.W. and Y.G.; validation, C.Q., Y.G. and B.R.; formal analysis, M.W., Y.G., C.Q. and M.Z.; investigation, M.W., Y.G., C.Q., M.Z., B.R. and X.L.; resources, C.Q. and B.R.; writing—original draft preparation, M.W., Y.G. and M.Z.; writing—review and editing, M.W., Y.G., C.Q., B.R., M.Z. and X.L.; supervision, C.Q., B.R., M.Z. and X.L.; funding acquisition, B.R., M.Z. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be made available on request.
Acknowledgments
The authors sincerely thank Runhao Zhao from the Laboratory for Big Data and Decision, National University of Defense Technology, for his expert technical assistance in software debugging and paper editing.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sun, L.; Kong, S.; Yang, Z.; Gao, D.; Fan, B. Modified Siamese Network Based on Feature Enhancement and Dynamic Template for Low-Light Object Tracking in UAV Videos. Drones 2023, 7, 483. [Google Scholar] [CrossRef]
- Adam, M.S.; Abdullah, N.F.; Abu-Samah, A.; Amodu, O.A.; Nordin, R. Advanced Path Planning for UAV Swarms in Smart City Disaster Scenarios Using Hybrid Metaheuristic Algorithms. Drones 2025, 9, 64. [Google Scholar] [CrossRef]
- Wang, C.; Wu, L.; Yan, C.; Wang, Z.; Long, H.; Yu, C. Coactive design of explainable agent-based task planning and deep reinforcement learning for human-UAVs teamwork. Chin. J. Aeronaut. 2020, 33, 2930–2945. [Google Scholar] [CrossRef]
- Xu, D.; Guo, Y.; Long, H.; Wang, C. A Novel Variable Step-size Path Planning Framework with Step-Consistent Markov Decision Process For Large-Scale UAV Swarm. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 10447–10452. [Google Scholar] [CrossRef]
- Shi, Z.; Feng, Z.; Wang, Q.; Dong, X.; Lü, J.; Ren, Z.; Wang, D. Prescribed-Time Time-Varying Output Formation Tracking for Heterogeneous Multi-Agent Systems. IEEE Internet Things J. 2024, 12, 11622–11632. [Google Scholar] [CrossRef]
- Nowakowski, M.; Berger, G.S.; Braun, J.; Mendes, J.a.; Bonzatto Junior, L.; Lima, J. Advance Reconnaissance of UGV Path Planning Using Unmanned Aerial Vehicle to Carry Our Mission in Unknown Environment. In Robot 2023: Sixth Iberian Robotics Conference; Marques, L., Santos, C., Lima, J.L., Tardioli, D., Ferre, M., Eds.; Springer Nature Switzerland: Cham, Switzerland, 2024; pp. 50–61. [Google Scholar]
- Akhihiero, D.; Olawoye, U.; Das, S.; Gross, J. Cooperative Localization for GNSS-Denied Subterranean Navigation: A UAV–UGV Team Approach. NAVIGATION J. Inst. Navig. 2024, 71. [Google Scholar] [CrossRef]
- Ribeiro, R.G.; Cota, L.P.; Euzébio, T.A.M.; Ramírez, J.A.; Guimarães, F.G. Unmanned-Aerial-Vehicle Routing Problem With Mobile Charging Stations for Assisting Search and Rescue Missions in Postdisaster Scenarios. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6682–6696. [Google Scholar] [CrossRef]
- Zhang, J.; Yue, X.; Zhang, H.; Xiao, T. Optimal Unmanned Ground Vehicle—Unmanned Aerial Vehicle Formation-Maintenance Control for Air-Ground Cooperation. Appl. Sci. 2022, 12, 3598. [Google Scholar] [CrossRef]
- Han, S.; Wang, M.; Duan, J.; Zhang, J.; Li, D. Research on Unmanned Aerial Vehicle Emergency Support System and Optimization Method Based on Gaussian Global Seagull Algorithm. Drones 2024, 8, 763. [Google Scholar] [CrossRef]
- Wang, Y.; Su, Z.; Xu, Q.; Li, R.; Luan, T.H. Lifesaving with RescueChain: Energy-Efficient and Partition-Tolerant Blockchain Based Secure Information Sharing for UAV-Aided Disaster Rescue. In Proceedings of the 40th IEEE Conference on Computer Communications, INFOCOM 2021, Vancouver, BC, Canada, 10–13 May 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Munasinghe, I.; Perera, A.; Deo, R.C. A Comprehensive Review of UAV-UGV Collaboration: Advancements and Challenges. J. Sens. Actuator Netw. 2024, 13, 81. [Google Scholar] [CrossRef]
- Bravo-Arrabal, J.; Toscano-Moreno, M.; Fernandez-Lozano, J.J.; Mandow, A.; Gomez-Ruiz, J.A.; García-Cerezo, A. The Internet of Cooperative Agents Architecture (X-IoCA) for Robots, Hybrid Sensor Networks, and MEC Centers in Complex Environments: A Search and Rescue Case Study. Sensors 2021, 21, 7843. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, K.; Li, X.; Shin, H.; Liu, P. Joint Task Chain, Power and UAV Trajectory Optimization Based on an Integrated Multi-UAV System. IEEE Trans. Veh. Technol. 2025, 1–15. [Google Scholar] [CrossRef]
- Wang, Y.; Su, Z.; Xu, Q.; Li, R.; Luan, T.H.; Wang, P. A Secure and Intelligent Data Sharing Scheme for UAV-Assisted Disaster Rescue. IEEE/ACM Trans. Netw. 2023, 31, 2422–2438. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, J.; Tang, Y.; Deng, Y.; Tian, X.; Yue, Y.; Yang, Y. GACF: Ground-Aerial Collaborative Framework for Large-Scale Emergency Rescue Scenarios. In Proceedings of the 2023 IEEE International Conference on Unmanned Systems (ICUS), Hefei, China, 13–15 October 2023; pp. 1701–1707. [Google Scholar] [CrossRef]
- Orhan, D.; Idouar, Y.; Pilla, L.L.; Cassagne, A.; Barthou, D.; Jégo, C. Scheduling Strategies for Partially-Replicable Task Chains on Two Types of Resources. arXiv 2025. [Google Scholar] [CrossRef]
- Qun, T.; Li, P.; Zhimeng, L.; Wei, Q. A Load Balancing Method for Matching Reconnaissance Tasks and Satellite Resources. J. Natl. Univ. Def. Technol. 2011, 33, 95–99. [Google Scholar]
- Jairam Naik, K. A Dynamic ACO-Based Elastic Load Balancer for Cloud Computing (D-ACOELB). In Data Engineering and Communication Technology; Raju, K.S., Senkerik, R., Lanka, S.P., Rajagopal, V., Eds.; Springer: Singapore, 2020; pp. 11–20. [Google Scholar]
- Liang, Y.; Lan, Y. TCLBM: A Task Chain-Based Load Balancing Algorithm for Microservices. Tsinghua Sci. Technol. 2021, 26, 251–258. [Google Scholar] [CrossRef]
- Mondal, M.S.; Ramasamy, S.; Humann, J.D.; Dotterweich, J.M.; Reddinger, J.P.F.; Childers, M.A.; Bhounsule, P. A robust uav-ugv collaborative framework for persistent surveillance in disaster management applications. In Proceedings of the 2024 International Conference on Unmanned Aircraft Systems (ICUAS), Chania, Crete, Greece, 4–7 June 2024; pp. 1239–1246. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, K.; Ma, J.; Li, X.; LI, D.; Sun, M.; Gao, F.; Xing, H.; Feng, L. Dynamic integration model of time-sensitive strike chain in naval battlefield. Chin. J. Ship Res. 2024, 19, 290–298. [Google Scholar] [CrossRef]
- Gowda, V.D.; Sharma, A.; Prasad, K.; Saxena, R.; Barua, T.; Mohiuddin, K. Dynamic Disaster Management with Real-Time IoT Data Analysis and Response. In Proceedings of the 2024 International Conference on Automation and Computation (AUTOCOM), Dehradun, India, 14–16 March 2024; pp. 142–147. [Google Scholar] [CrossRef]
- Xu, H. Joint All-domain Command and Control Technology Based on Networked Information System and its Future Perspectives. Aerosp. Shanghai (Chin. Engl.) 2024, 41, 1–8. [Google Scholar] [CrossRef]
- Yue, Q.; Li, J.; Huang, Z.; Xie, X.; Yang, Q. Vulnerability Assessment and Topology Reconstruction of Task Chains in UAV Networks. Electronics 2024, 13, 2126. [Google Scholar] [CrossRef]
- Duan, T.; Li, Q.; Zhou, X.; Li, X. An Adaptive Task Planning Method for UAVC Task Layer: DSTCA. Drones 2024, 8, 553. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, H.; Zhu, D.; Wang, J.; Zhang, C.; Ding, W.; Luo, X.; Hua, C.; Meng, M.Q. Air-Ground Collaborative Robots for Fire and Rescue Missions: Towards Mapping and Navigation Perspective. arXiv 2024. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, R.; Li, X.; Yu, Z.; Li, X.; Zhao, W.; Zhang, X.; Li, L. Conflict detection in Task Heterogeneous Information Networks. Web Intell. 2022, 20, 21–35. [Google Scholar] [CrossRef]
- Xu, J.; Liu, X.; Jin, J.; Pan, W.; Li, X.; Yang, Y. Holistic Service Provisioning in a UAV-UGV Integrated Network for Last-Mile Delivery. IEEE Trans. Netw. Serv. Manag. 2025, 22, 380–393. [Google Scholar] [CrossRef]
- Qin, C.; Niu, M.; Zhang, P.; He, J. Exploiting Cascaded Channel Signature for PHY-Layer Authentication in RIS-Enabled UAV Communication Systems. Drones 2024, 8, 358. [Google Scholar] [CrossRef]
- Xu, S. Research on the Key Techniques of Unmanned Operation Network Based on Connectivity. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2017. [Google Scholar]
- Li, R.; Jiang, B.; Zong, Y.; Lu, N.; Guo, L. Event-Triggered Collaborative Fault Diagnosis for UAV–UGV Systems. Drones 2024, 8, 324. [Google Scholar] [CrossRef]
- Xiao, H.; Sun, S.; Li, D. Research on Kill Chain Resource Allocation Optimization Based on Reinforcement Learning and Game Theory. In Proceedings of the 2024 2nd International Conference on Computer, Vision and Intelligent Technology (ICCVIT), Huaibei, China, 24–27 November 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, F.; Chen, B.; Xi, L.; Deng, F.; Chen, J. Weighted Decentralized Information Filter for Collaborative Air-Ground Target Geolocation in Large Outdoor Environments. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 7292–7302. [Google Scholar] [CrossRef]
- Zhou, Y.; Jin, Z.; Shi, H.; Shi, L.; Lu, N.; Dong, M. Enhanced Emergency Communication Services for Post–Disaster Rescue: Multi-IRS Assisted Air-Ground Integrated Data Collection. IEEE Trans. Netw. Sci. Eng. 2024, 11, 4651–4664. [Google Scholar] [CrossRef]
- Asadujjaman, M.; Rahman, H.F.; Chakrabortty, R.K.; Ryan, M.J. Supply chain integrated resource-constrained multi-project scheduling problem. Comput. Ind. Eng. 2024, 194, 110380. [Google Scholar] [CrossRef]
- Hsie, M.; Wu, M.Y.; Huang, C.Y. Optimal urban sewer layout design using Steiner tree problems. Eng. Optim. 2019, 51, 1980–1996. [Google Scholar] [CrossRef]
- Dai, Y.; Ouyang, H.; Zheng, H.; Long, H.; Duan, X. Interpreting a deep reinforcement learning model with conceptual embedding and performance analysis. Appl. Intell. 2023, 53, 6936–6952. [Google Scholar] [CrossRef]
- Zhao, R.; Tang, J.; Zeng, W.; Guo, Y.; Zhao, X. Towards human-like questioning: Knowledge base question generation with bias-corrected reinforcement learning from human feedbac. Inf. Process. Manag. 2025, 62, 1–23. [Google Scholar] [CrossRef]
- Zhao, R.; Xu, D.; Jian, S.; Tan, L.; Sun, X.; Zhang, W. Quadratic Exponential Decrease Roll-Back: An Efficient Gradient Update Mechanism in Proximal Policy Optimization. In Proceedings of the 2023 2nd International Conference on Machine Learning, Cloud Computing and Intelligent Mining (MLCCIM), Sichuan, China, 25–29 July 2024; pp. 65–70. [Google Scholar] [CrossRef]
- Fan, Q.; Pan, P.; Li, X.; Wang, S.; Li, J.; Wen, J. DRL-D: Revenue-Aware Online Service Function Chain Deployment via Deep Reinforcement Learning. IEEE Trans. Netw. Serv. Manag. 2022, 19, 4531–4545. [Google Scholar] [CrossRef]
- Gao, Y.; Lyu, N. A New Multi-Target Three-Way Threat Assessment Method with Heterogeneous Information and Attribute Relevance. Mathematics 2024, 12, 691. [Google Scholar] [CrossRef]
- Kurose, J.F.; Ross, K.W. Computer Networking: A Top-Down Approach Featuring the Internet, 1st ed.; Addison-Wesley: Boston, MA, USA, 2002. [Google Scholar]
- Xu, K.; Li, Z.; Liang, N.; Kong, F.; Lei, S.; Wang, S.; Paul, A.; Wu, Z. Research on Multi-Layer Defense against DDoS Attacks in Intelligent Distribution Networks. Electronics 2024, 13, 3583. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).