Rotor Failure Compensation in a Biplane Quadrotor Based on Virtual Deflection
Abstract
1. Introduction
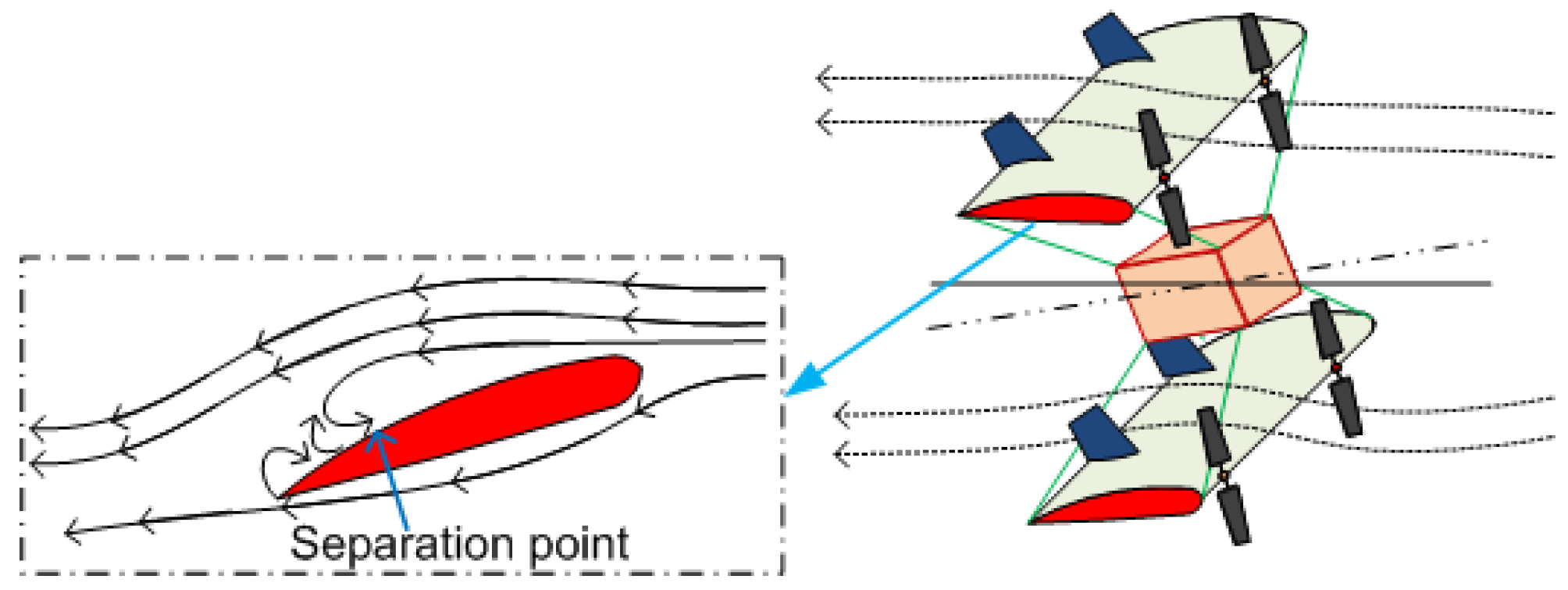
2. Biplane Dynamics and Rotor Failure
3. Mathematical Mode of the SJA
- The actuator non-linearity’s output is not measurable.
- Parameters of the actuator non-linearity are unknown.
- Jet momentum does not vary during the entire period of the diaphragm motion.
- The air-stream density and control of flow along the width are constant.
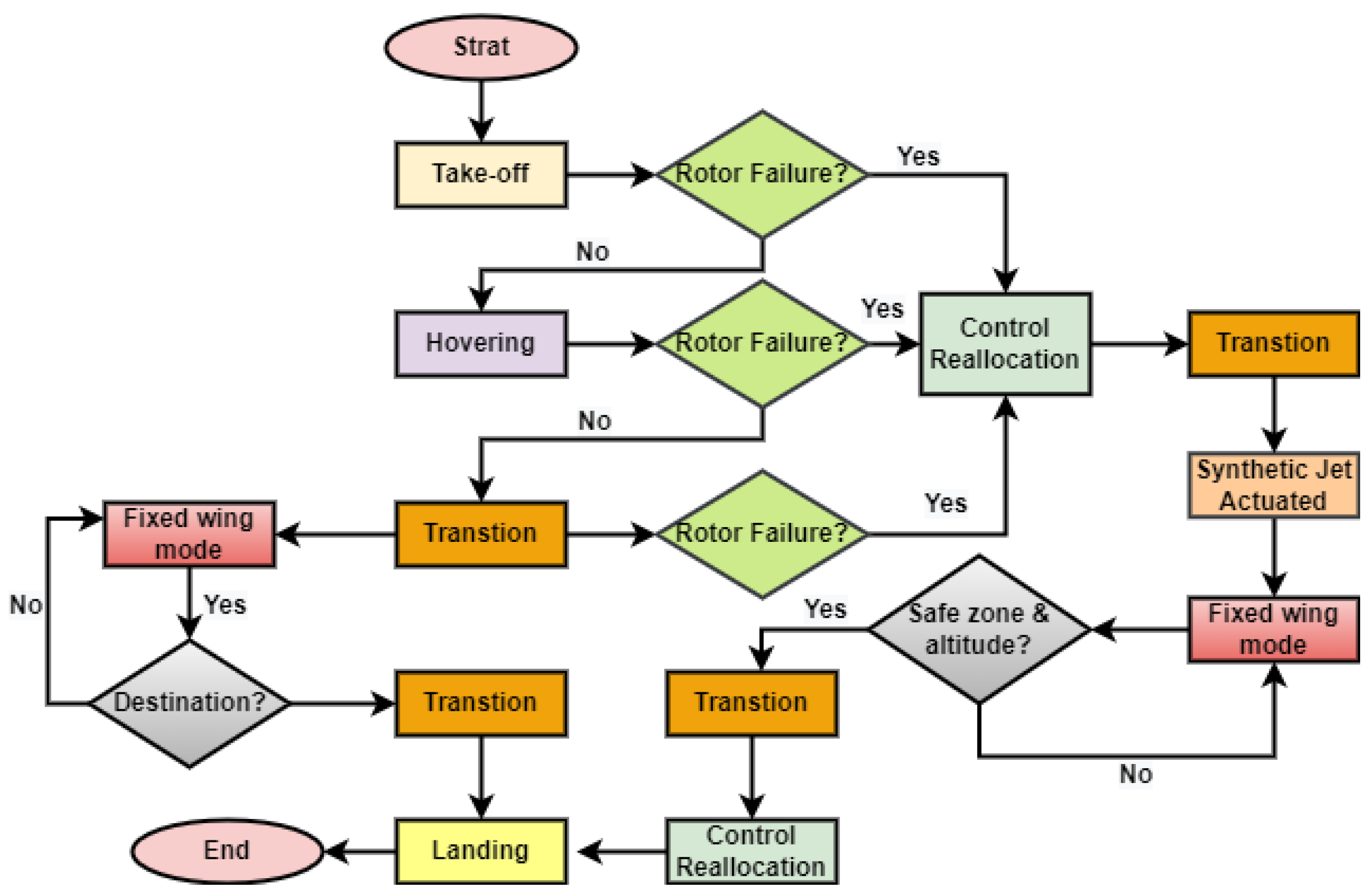
4. Control Architecture
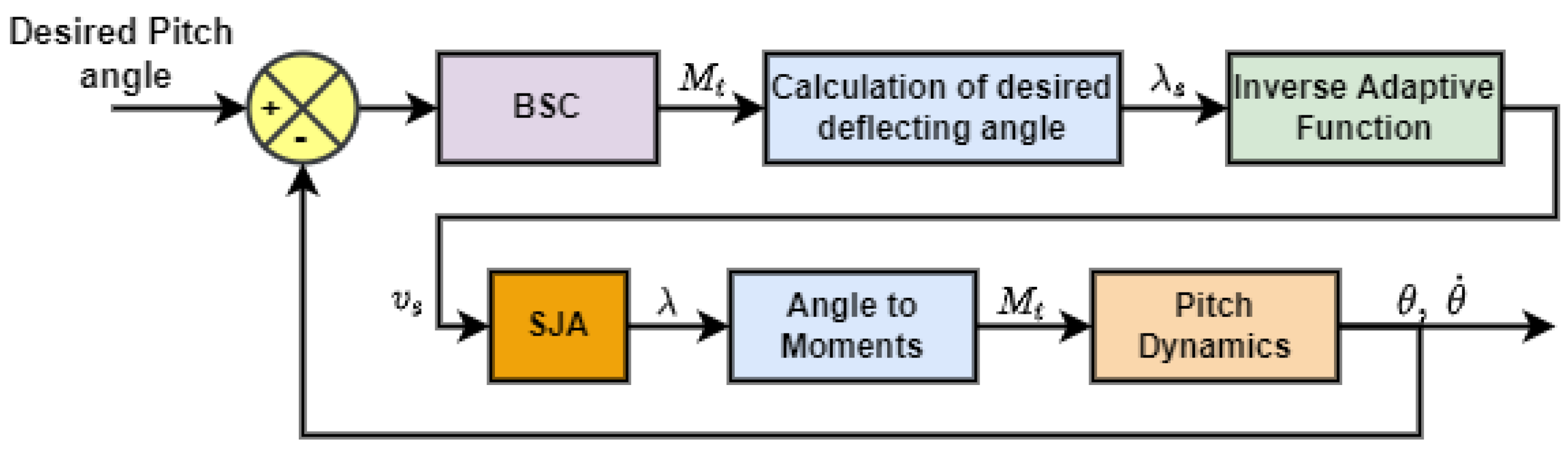
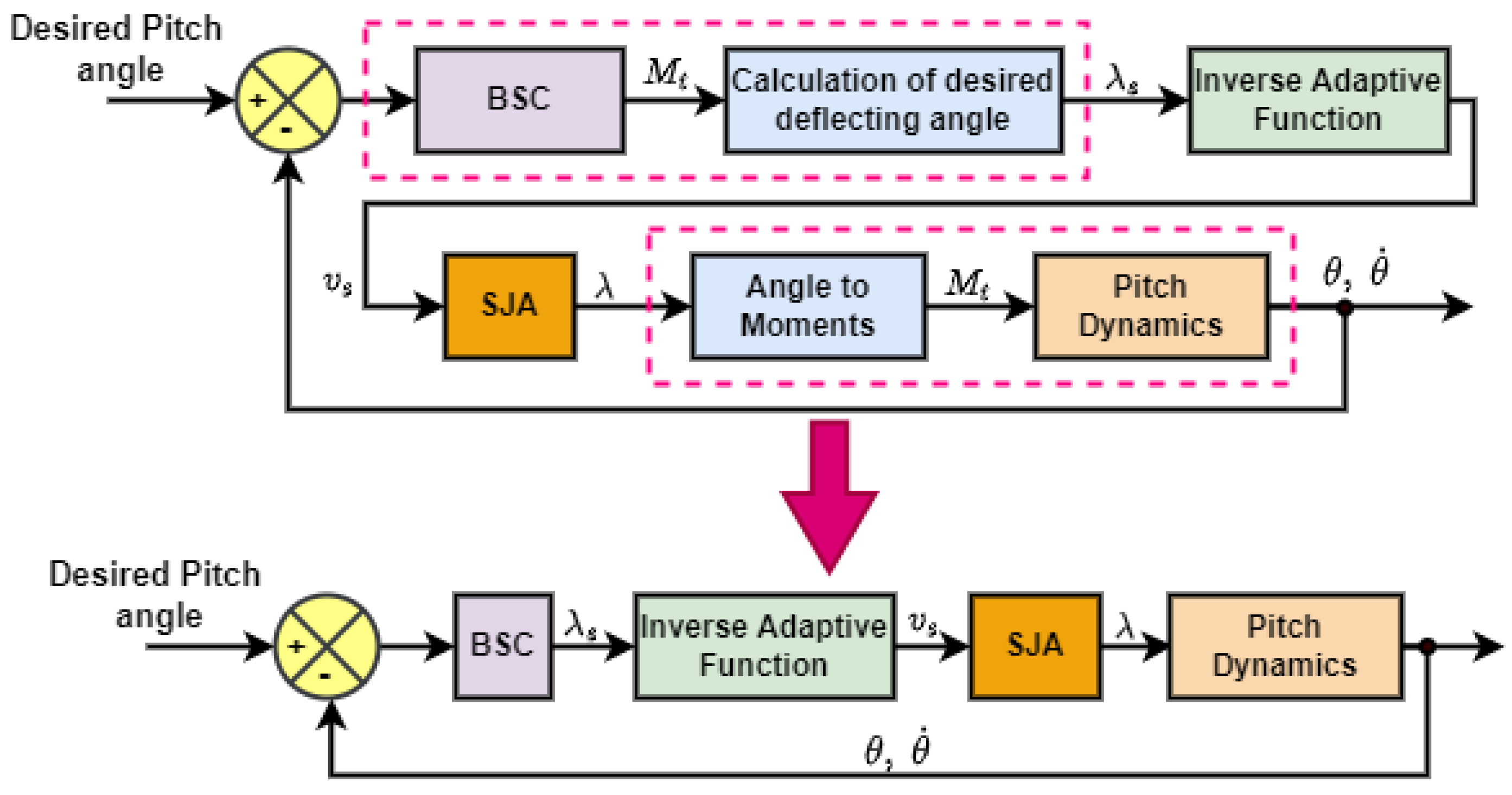
5. Controller Design
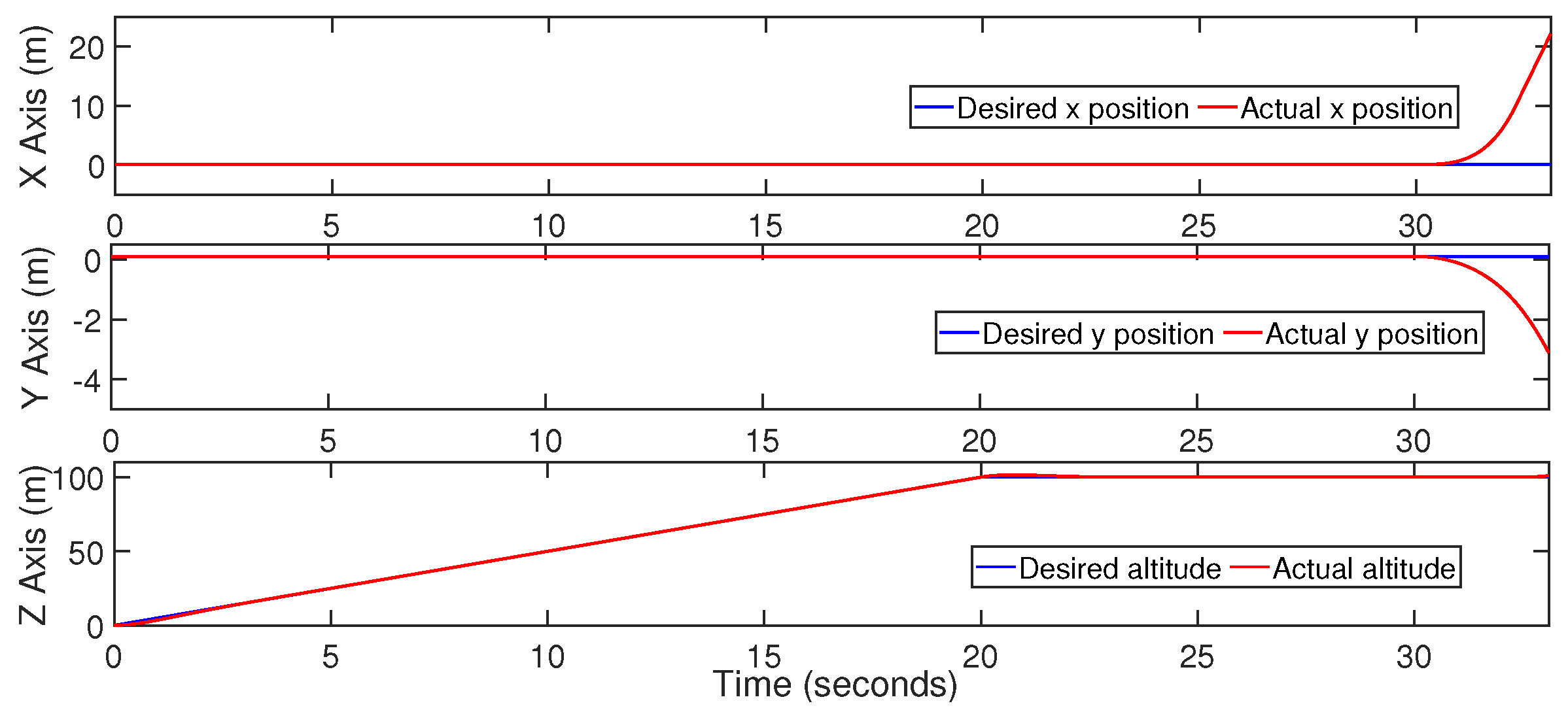
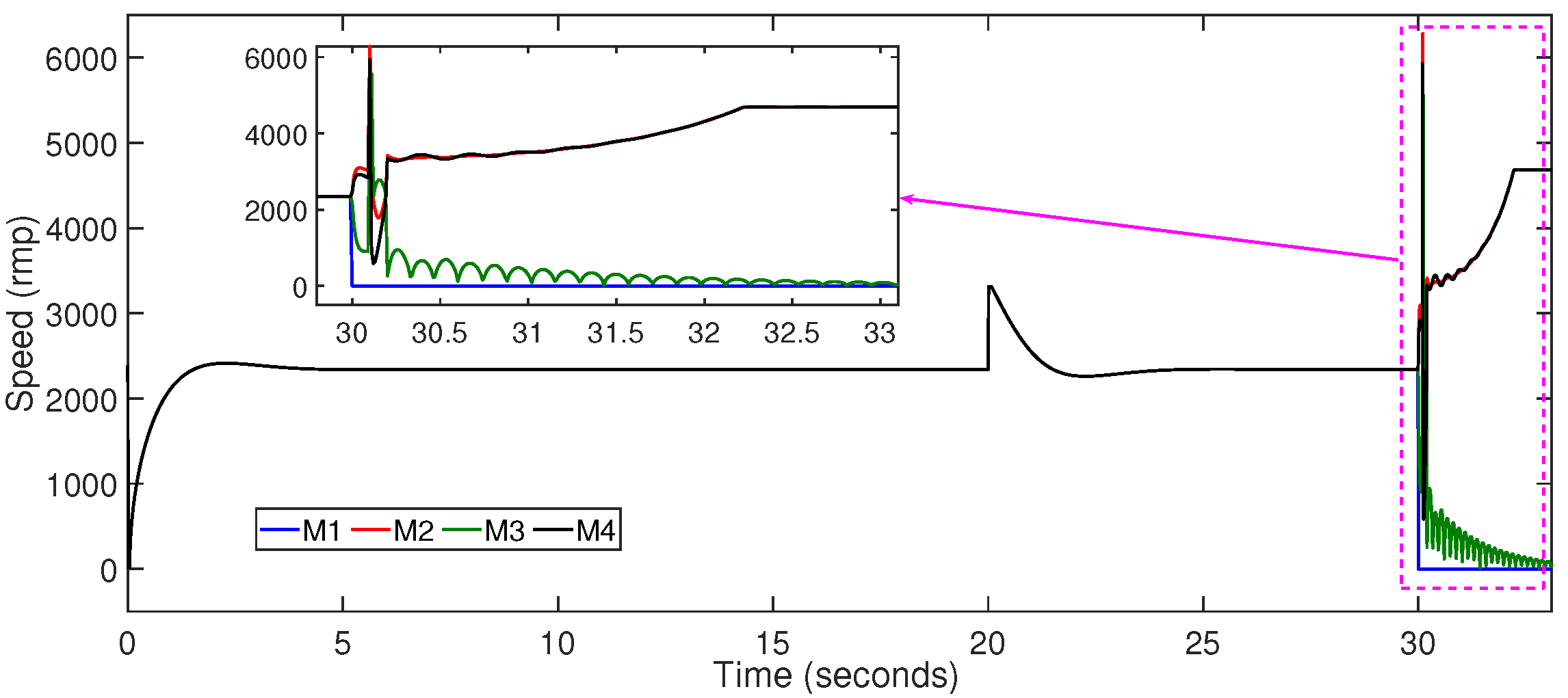
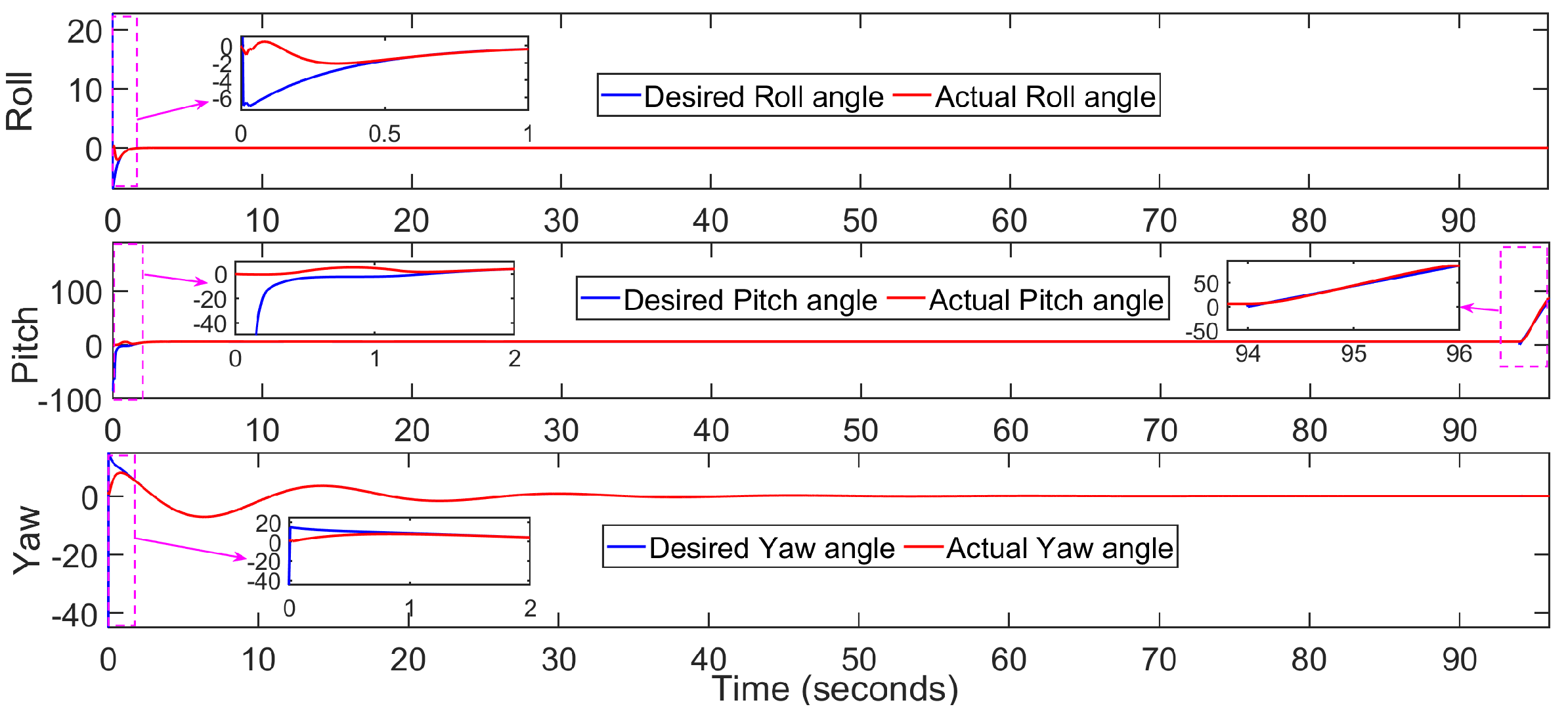
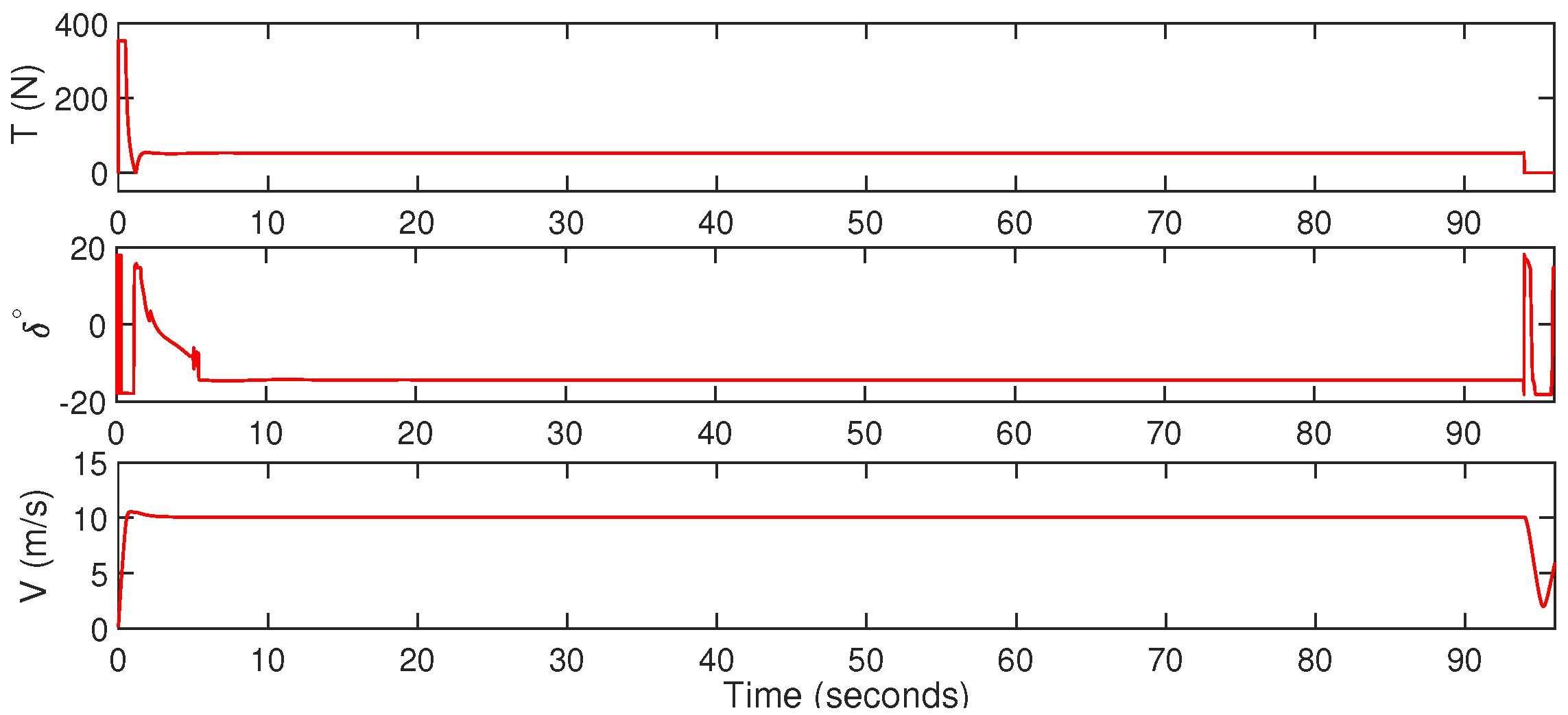
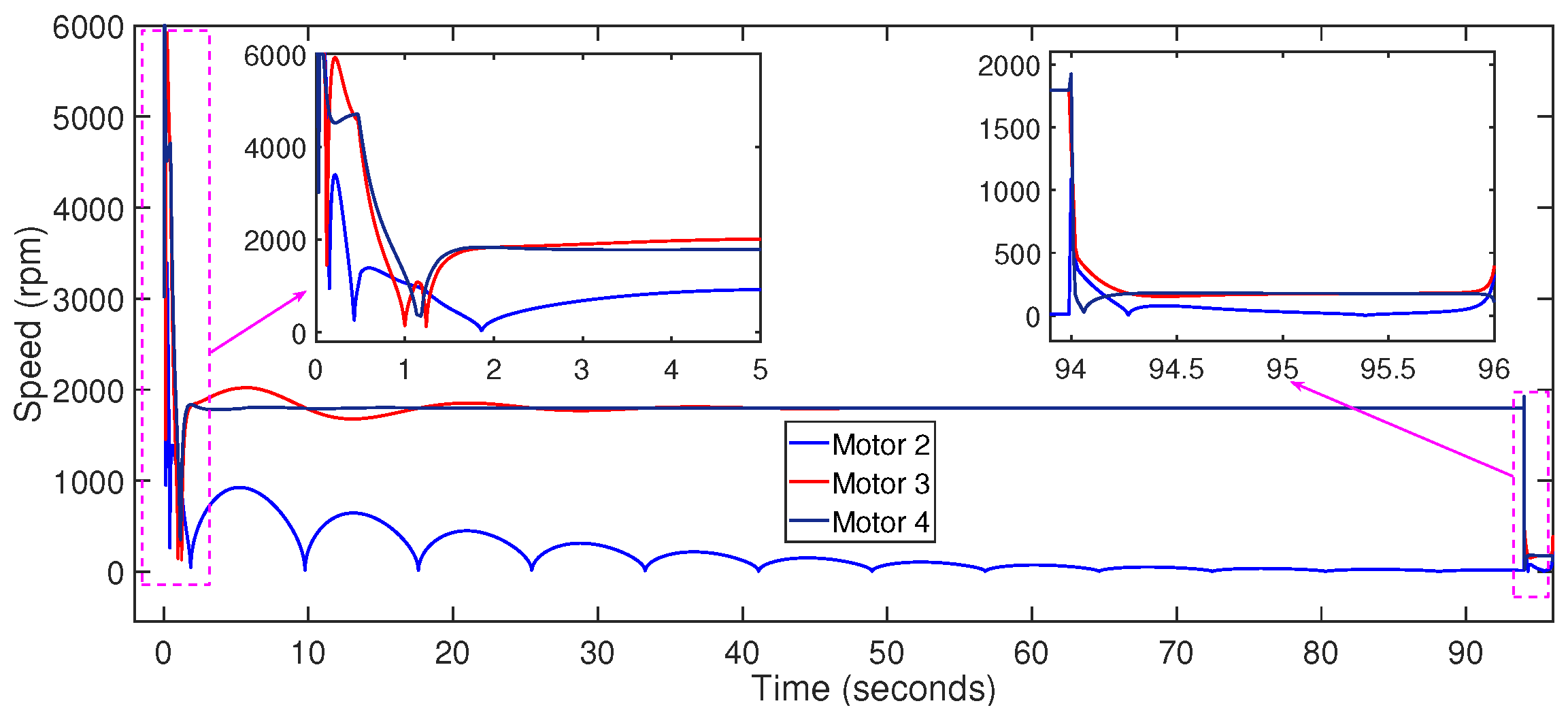
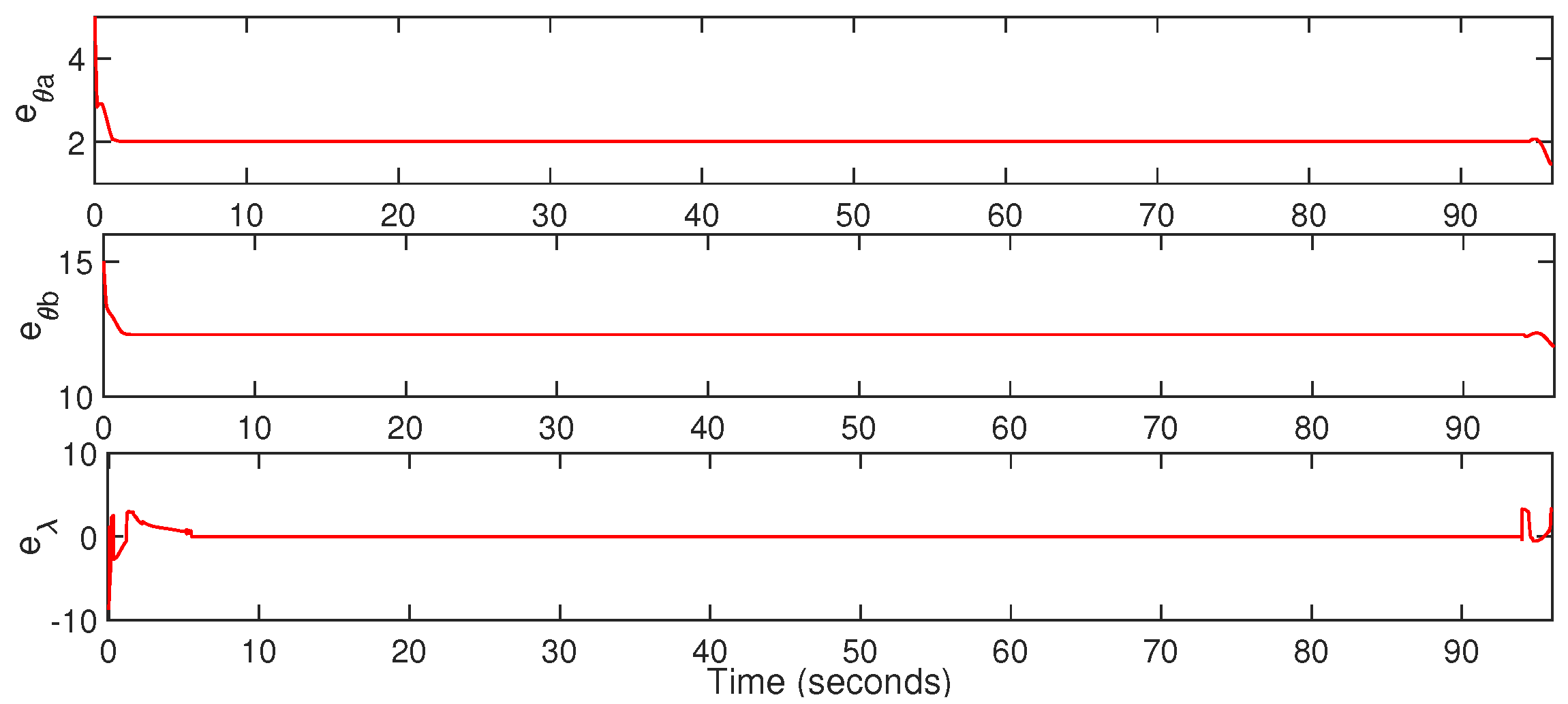
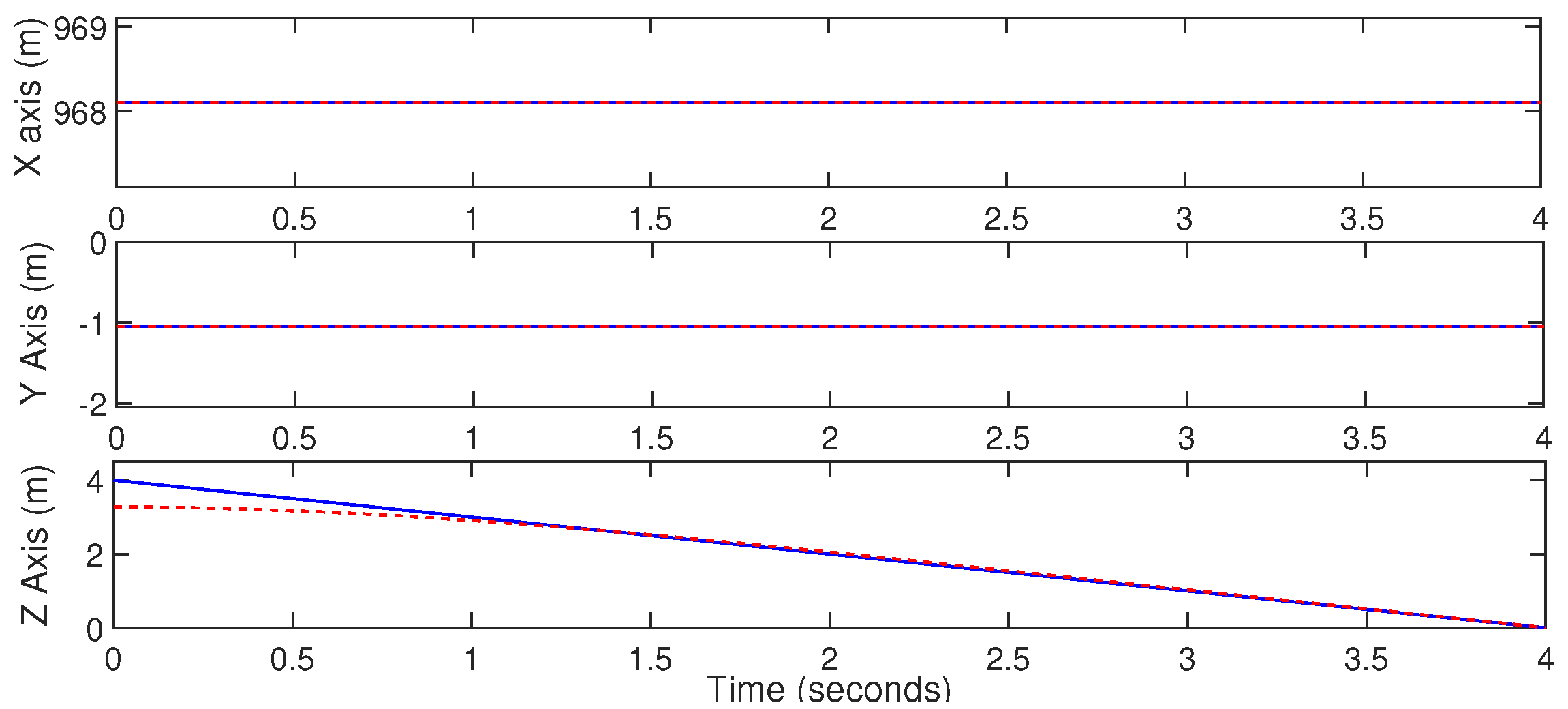
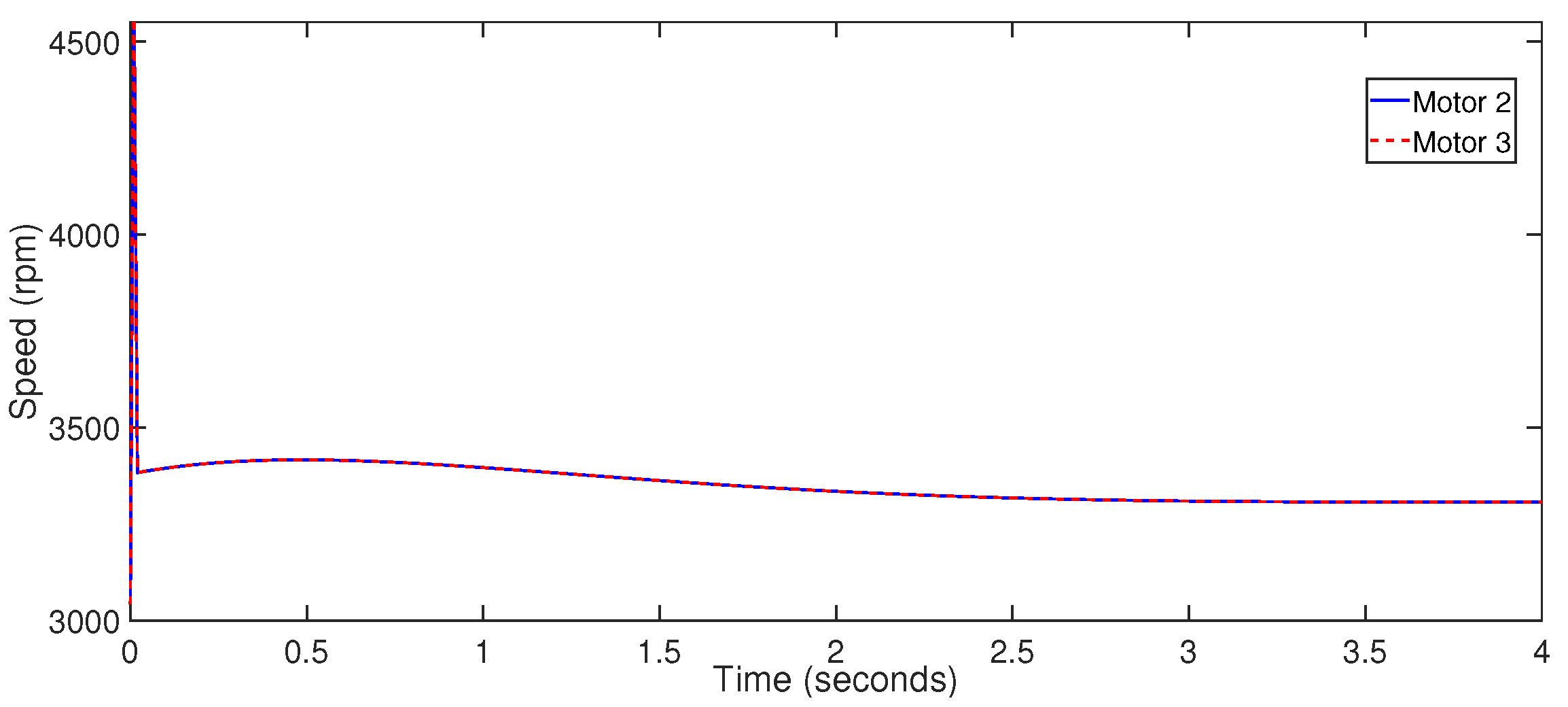
6. Results and Discussion
7. Conclusions
- The biplane quadrotor is able to perform the transition maneuver even after the total rotor failure.
- In fixed-wing mode, after the reallocation of the control signals, the desired altitude, roll, and pitch angles are tracked.
- SJA is able to deliver the desired virtual deflection for controlling the pitching movement.
- By using the adaptive inverse compensation scheme, non-linearity in the SJA is effectively compensated.
- Based on the Lyapunov method, closed-loop stability of the overall control architecture is proven.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alioua, A.; Djeghri, H.; Cherif, M.E.T.; Senouci, S.M.; Sedjelmaci, H. UAVs for traffic monitoring: A sequential game-based computation offloading/sharing approach. Comput. Netw. 2020, 177, 107273. [Google Scholar] [CrossRef]
- Messina, G.; Modica, G. Applications of UAV thermal imagery in precision agriculture: State of the art and future research outlook. Remote Sens. 2020, 12, 1491. [Google Scholar] [CrossRef]
- Bravo, R.; Leiras, A. Literature review of the application of UAVs in humanitarian relief. In Proceedings of the XXXV Encontro Nacional de Engenharia de Producao, Fortaleza, Brazil, 10–13 October 2015; pp. 13–16. [Google Scholar]
- Specht, M.; Stateczny, A.; Specht, C.; Widźgowski, S.; Lewicka, O.; Wiśniewska, M. Concept of an Innovative Autonomous Unmanned System for Bathymetric Monitoring of Shallow Waterbodies (INNOBAT System). Energies 2021, 14, 5370. [Google Scholar] [CrossRef]
- Wang, D.; Xing, S.; He, Y.; Yu, J.; Xu, Q.; Li, P. Evaluation of a New Lightweight UAV-Borne Topo-Bathymetric LiDAR for Shallow Water Bathymetry and Object Detection. Sensors 2022, 22, 1379. [Google Scholar] [CrossRef]
- Dalwadi, N.; Deb, D.; Muyeen, S.M. Adaptive backstepping controller design of quadrotor biplane for payload delivery. IET Intell. Transp. Syst. 2022. [Google Scholar] [CrossRef]
- Chipade, V.S.; Abhishek; Kothari, M.; Chaudhari, R.R. Systematic design methodology for development and flight testing of a variable pitch quadrotor biplane VTOL UAV for payload delivery. Mechatronics 2018, 55, 94–114. [Google Scholar] [CrossRef]
- Ryseck, P.; Yeo, D.; Hrishikeshavan, V.; Chopra, I. Aerodynamic and Mechanical Design of a Morphing Winglet for a Quadrotor Biplane Tail-sitter. In Proceedings of the Vertical Flight Society 8th Autonomous VTOL Symposium, Mesa, AZ, USA, 26–28 January 2019. [Google Scholar]
- Sandiwan, A.P.; Cahyadi, A.; Herdjunanto, S. Robust proportional-derivative control on SO(3) with disturbance compensation for quadrotor UAV. Int. J. Control Autom. Syst. 2017, 15, 2329–2342. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Noth, A.; Siegwart, R. PID vs LQ control techniques applied to an indoor micro quadrotor. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2451–2456. [Google Scholar] [CrossRef]
- Xi, L.; Zhu, Q.; Zhang, D. Sliding mode control design based on fuzzy reaching law for yaw angle of a Tail-sitter UAV. In Proceedings of the 2016 22nd International Conference on Automation and Computing (ICAC), Colchester, UK, 7–8 September 2016; pp. 238–243. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, H.H. Tracking a Moving Target by a Fixed-wing UAV Based on Sliding Mode Control. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, American Institute of Aeronautics and Astronautics, Chicago, IL, USA, 10–13 August 2013. [Google Scholar] [CrossRef]
- Gambhire, S.J.; Kishore, D.R.; Londhe, P.S.; Pawar, S.N. Review of sliding mode based control techniques for control system applications. Int. J. Dyn. Control 2020, 9, 363–378. [Google Scholar] [CrossRef]
- Dalwadi, N.; Deb, D.; Kothari, M.; Ozana, S. Disturbance Observer-Based Backstepping Control of Tail-Sitter UAVs. Actuators 2021, 10, 119. [Google Scholar] [CrossRef]
- Dalwadi, N.; Deb, D.; Rath, J.J. Biplane Trajectory Tracking Using Hybrid Controller Based on Backstepping and Integral Terminal Sliding Mode Control. Drones 2022, 6, 58. [Google Scholar] [CrossRef]
- Wen, F.H.; Hsiao, F.Y.; Shiau, J.K. Analysis and Management of Motor Failures of Hexacopter in Hover. Actuators 2021, 10, 48. [Google Scholar] [CrossRef]
- Hou, Z.; Lu, P.; Tu, Z. Nonsingular terminal sliding mode control for a quadrotor UAV with a total rotor failure. Aerosp. Sci. Technol. 2020, 98, 105716. [Google Scholar] [CrossRef]
- Saied, M.; Lussier, B.; Fantoni, I.; Shraim, H.; Francis, C. Fault Diagnosis and Fault-Tolerant Control of an Octorotor UAV using motors speeds measurements. IFAC Pap. 2017, 50, 5263–5268. [Google Scholar] [CrossRef]
- Park, J.; Jung, Y.; Kim, J.H. Multiclass Classification Fault Diagnosis of Multirotor UAVs Utilizing a Deep Neural Network. Int. J. Control Autom. Syst. 2022, 20, 1316–1326. [Google Scholar] [CrossRef]
- Lin, C.E.; Shao, P.C. Failure Analysis for an Unmanned Aerial Vehicle Using Safe Path Planning. J. Aerosp. Inf. Syst. 2020, 17, 358–369. [Google Scholar] [CrossRef]
- Wang, X.; Sun, S. Incremental fault-tolerant control for a hybrid quad-plane UAV subjected to a complete rotor loss. Aerosp. Sci. Technol. 2022, 125, 107105. [Google Scholar] [CrossRef]
- Guzmán-Rabasa, J.A.; López-Estrada, F.R.; González-Contreras, B.M.; Valencia-Palomo, G.; Chadli, M.; Pérez-Patricio, M. Actuator fault detection and isolation on a quadrotor unmanned aerial vehicle modeled as a linear parameter-varying system. Meas. Control 2019, 52, 1228–1239. [Google Scholar] [CrossRef]
- Tahavori, M.; Hasan, A. Fault recoverability for nonlinear systems with application to fault tolerant control of UAVs. Aerosp. Sci. Technol. 2020, 107, 106282. [Google Scholar] [CrossRef]
- Chung, W.; Son, H. Fault-Tolerant Control of Multirotor UAVs by Control Variable Elimination. IEEE/ASME Trans. Mechatron. 2020, 25, 2513–2522. [Google Scholar] [CrossRef]
- Lu, P.; van Kampen, E.J. Active fault-tolerant control for quadrotors subjected to a complete rotor failure. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 4698–4703. [Google Scholar] [CrossRef]
- Allahverdy, D.; Fakharian, A.; Menhaj, M.B. Fault-Tolerant Control of Quadrotor UAVs Based on Back-Stepping Integral Sliding Mode Approach and Iterative Learning Algorithm. Math. Probl. Eng. 2021, 2021, 1–15. [Google Scholar] [CrossRef]
- Yel, E.; Bezzo, N. A Meta-Learning-based Trajectory Tracking Framework for UAVs under Degraded Conditions. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 6884–6890. [Google Scholar] [CrossRef]
- Sharma, P.; Poddar, P.; Sujit, P. A Model-free Deep Reinforcement Learning Approach To Maneuver A Quadrotor Despite Single Rotor Failure. arXiv 2021, arXiv:2109.10488. [Google Scholar]
- Kim, M.; Lee, H.; Kim, J.; hun Kim, S.; Kim, Y. Hierarchical Fault Tolerant Control of a Hexacopter UAV Against Actuator Failure. In Robot Intelligence Technology and Applications 6; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 79–90. [Google Scholar] [CrossRef]
- Dalwadi, N.; Deb, D.; Muyeen, S. Observer based rotor failure compensation for biplane quadrotor with slung load. Ain Shams Eng. J. 2022, 13, 101748. [Google Scholar] [CrossRef]
- Smith, B.L.; Swift, G.W. A comparison between synthetic jets and continuous jets. Exp. Fluids 2003, 34, 467–472. [Google Scholar] [CrossRef]
- Deb, D.; Burkholder, J.; Tao, G. Synthetic jet actuators and arrays: Modeling and control. In Adaptive Compensation of Nonlinear Actuators for Flight Control Applications; Springer: Singapore, 2021; pp. 11–41. [Google Scholar] [CrossRef]
- Tang, H.; Zhong, S. A static compressible flow model of synthetic jet actuators. Aeronaut. J. 2007, 111, 421–431. [Google Scholar] [CrossRef]
- Zong, H.h.; Wu, Y.; Li, Y.h.; Song, H.m.; Zhang, Z.B.; Jia, M. Analytic model and frequency characteristics of plasma synthetic jet actuator. Phys. Fluids 2015, 27, 027105. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X. Active flow control for supersonic aircraft: A novel hybrid synthetic jet actuator. Sens. Actuators Phys. 2020, 302, 111770. [Google Scholar] [CrossRef]
- MacKunis, W.; Subramanian, S.; Mehta, S.; Ton, C.; Curtis, J.W.; Reyhanoglu, M. Robust nonlinear aircraft tracking control using synthetic jet actuators. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 220–225. [Google Scholar]
- Duvigneau, R.; Visonneau, M. Optimization of a synthetic jet actuator for aerodynamic stall control. Comput. Fluids 2006, 35, 624–638. [Google Scholar] [CrossRef]
- Deb, D.; Tao, G.; Burkholder, J.; Smith, D. An adaptive inverse control scheme for a synthetic jet actuator model. In Proceedings of the 2005, American Control Conference, Portland, OR, USA, 8–10 June 2005; Volume 4, pp. 2646–2651. [Google Scholar] [CrossRef]
- Deb, D.; Tao, G.; Burkholder, J.O.; Smith, D.R. Adaptive Compensation Control of Synthetic Jet Actuator Arrays for Airfoil Virtual Shaping. J. Aircr. 2007, 44, 616–626. [Google Scholar] [CrossRef]
- Deb, D.; Sonowal, S. Synthetic jet actuator based adaptive neural network control of nonlinear fixed pitch wind turbine blades. In Proceedings of the 2013 IEEE International Conference On Control Applications (CCA), Hyderabad, India, 28–30 August 2013; pp. 152–157. [Google Scholar]
- Trancossi, M.; Dumas, A. Coanda Synthetic Jet Deflection Apparatus and Control. SAE Tech. Pap. 2011, 2011. [Google Scholar] [CrossRef]
- Hong, M.H.; Cheng, S.Y.; Zhong, S. Effect of geometric parameters on synthetic jet: A review. Phys. Fluids 2020, 32, 031301. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, Z. Study on longitudinal stability improvement of flying wing aircraft based on synthetic jet flow control. Aerosp. Sci. Technol. 2015, 46, 287–298. [Google Scholar] [CrossRef]
- Jabbal, M.; Liddle, S.; Potts, J.; Crowther, W. Development of design methodology for a synthetic jet actuator array for flow separation control applications. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2013, 227, 110–124. [Google Scholar] [CrossRef]
- Li, C.; Zhang, T.; Yang, J. Attitude Control of Aircraft Using Only Synthetic Jet Actuators When Stall Occurs. IEEE Access 2018, 6, 37910–37917. [Google Scholar] [CrossRef]
- Post, M.; Corke, T. Separation Control on High Angle of Attack Airfoil Using Plasma Actuators. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit. American Institute of Aeronautics and Astronautics, Reno, NV, USA, 6–9 January 2003. [Google Scholar] [CrossRef]
- Shan, H.; Jiang, L.; Liu, C.; Love, M.; Maines, B. Numerical study of passive and active flow separation control over a NACA0012 airfoil. Comput. Fluids 2008, 37, 975–992. [Google Scholar] [CrossRef]
- Lee, D.; Nonomura, T.; Oyama, A.; Fujii, K. Comparison of numerical methods evaluating airfoil aerodynamic characteristics at low Reynolds number. J. Aircr. 2015, 52, 296–306. [Google Scholar] [CrossRef]
- Yousefi, K.; Saleh, R. Three-dimensional suction flow control and suction jet length optimization of NACA 0012 wing. Meccanica 2015, 50, 1481–1494. [Google Scholar] [CrossRef]
- Balakumar, P. Direct numerical simulation of flows over an NACA-0012 airfoil at low and moderate Reynolds numbers. In Proceedings of the 47th AIAA Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3978. [Google Scholar]
- Pranesh, C.; Sivapragasam, M.; Deshpande, M.; Narahari, H. Negative lift characteristics of NACA 0012 aerofoil at low Reynolds numbers. Sādhanā 2019, 44, 21. [Google Scholar] [CrossRef]
- Castelli, M.R.; Garbo, F.; Benini, E. Numerical investigation of laminar to turbulent boundary layer transition on a NACA 0012 airfoil for vertical-axis wind turbine applications. Wind Eng. 2011, 35, 661–685. [Google Scholar] [CrossRef]
- Mejia, O.D.L.; Moser, R.D.; Brzozowski, D.P.; Glezer, A. Effects of trailing-edge synthetic jet actuation on an airfoil. AIAA J. 2011, 49, 1763–1777. [Google Scholar] [CrossRef]
- Wei, Q.; Niu, Z.; Chen, B.; Huang, X. Bang-bang control applied in airfoil roll control with plasma actuators. J. Aircr. 2013, 50, 670–677. [Google Scholar] [CrossRef][Green Version]
- Li, C.; Yang, J. Roll control using only synthetic jet actuators at high angle of attack. J. Aircr. 2016, 54, 371–376. [Google Scholar] [CrossRef]
- Hasegawa, H.; Obayashi, S. Active stall control system on NACA0012 by using synthetic jet actuator. J. Flow Control Meas. Vis. 2018, 7, 61–72. [Google Scholar] [CrossRef][Green Version]
- Li, W.; Wang, W.; Huang, X.; Zhang, S.; Li, C. Roll Control of Morphing Aircraft with Synthetic Jet Actuators at a High Angle of Attack. Appl. Sci. 2021, 11, 505. [Google Scholar] [CrossRef]
- Tang, H.; Salunkhe, P.; Zheng, Y.; Du, J.; Wu, Y. On the use of synthetic jet actuator arrays for active flow separation control. Exp. Therm. Fluid Sci. 2014, 57, 1–10. [Google Scholar] [CrossRef]
- Montazer, E.; Mirzaei, M.; Salami, E.; Ward, T.; Romli, F.; Kazi, S. Optimization of a synthetic jet actuator for flow control around an airfoil. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; Volume 152, p. 012023. [Google Scholar]
- Jee, S.K.; Lopez, O.; Moser, R.; Kutay, A.; Muse, J.; Calise, A. Flow Simulation of a Controlled Airfoil With Synthetic Jet Actuators. In Proceedings of the 19th AIAA Computational Fluid Dynamics, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar] [CrossRef]
- de Luca, L.; Girfoglio, M.; Coppola, G. Modeling and Experimental Validation of the Frequency Response of Synthetic Jet Actuators. AIAA J. 2014, 52, 1733–1748. [Google Scholar] [CrossRef]
- Geng, L.; Hu, Z.; Lin, Y. Thrust and flow characteristic of double synthetic jet actuator underwater. Ocean Eng. 2019, 176, 84–96. [Google Scholar] [CrossRef]
- Caruana, D.; Rogier, F.; Dufour, G.; Gleyzes, C. The Plasma Synthetic Jet Actuator, Physics, Modeling and Flow Control Application on Separation; Aerospace Lab. 2013, pp. 1–13. Available online: https://hal.archives-ouvertes.fr/hal-01184643/ (accessed on 13 June 2022).
- Singhal, C.; Tao, G.; Burkholder, J. Neural Network-Based Compensation of Synthetic Jet Actuator Nonlinearities for Aircraft Flight Control. In Proceedings of the AIAA Guidance, Navigation, and Control Conference. American Institute of Aeronautics and Astronautics, Chicago, IL, USA, 10–13 August 2009. [Google Scholar] [CrossRef]
- Ramos-Pedroza, N.; MacKunis, W.; Reyhanoglu, M. Sliding mode control-based limit cycle oscillation suppression for UAVs using synthetic jet actuators. In Proceedings of the 2015 International Workshop on Recent Advances in Sliding Modes (RASM), Istanbul, Turkey, 9–11 April 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Swarnkar, S.; Parwana, H.; Kothari, M.; Abhishek, A. Biplane-Quadrotor Tail-Sitter UAV: Flight Dynamics and Control. J. Guid. Control Dyn. 2018, 41, 1049–1067. [Google Scholar] [CrossRef]
- Deb, D.; Tao, G.; Burkholder, J.O.; Smith, D.R. Adaptive Synthetic Jet Actuator Compensation for A Nonlinear Aircraft Model at Low Angles of Attack. IEEE Trans. Control Syst. Technol. 2008, 16, 983–995. [Google Scholar] [CrossRef]









| AoA | Re = | Re = | Re = |
|---|---|---|---|
| 0 | 0.869 | 0.979 | 0.869 |
| 1.5 | 0.713 | 0.832 | 0.781 |
| 3 | 0.582 | 0.713 | 0.770 |
| 4.5 | 0.461 | 0.575 | 0.674 |
| 6 | 0.340 | 0.429 | 0.556 |
| 7.5 | 0.198 | 0.209 | 0.409 |
| 9.0 | 0.082 | 0.056 | 0.115 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 1.86 kg | 2.03 kg | ||
| 3.617 kg | Aspect ratio | 6.9 | |
| g | 9.8 | Wing Span | 2.29 m |
| Wing area (single) | 0.754 | Mass (m) | 12 kg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dalwadi, N.; Deb, D.; Ozana, S. Rotor Failure Compensation in a Biplane Quadrotor Based on Virtual Deflection. Drones 2022, 6, 176. https://doi.org/10.3390/drones6070176
Dalwadi N, Deb D, Ozana S. Rotor Failure Compensation in a Biplane Quadrotor Based on Virtual Deflection. Drones. 2022; 6(7):176. https://doi.org/10.3390/drones6070176
Chicago/Turabian StyleDalwadi, Nihal, Dipankar Deb, and Stepan Ozana. 2022. "Rotor Failure Compensation in a Biplane Quadrotor Based on Virtual Deflection" Drones 6, no. 7: 176. https://doi.org/10.3390/drones6070176
APA StyleDalwadi, N., Deb, D., & Ozana, S. (2022). Rotor Failure Compensation in a Biplane Quadrotor Based on Virtual Deflection. Drones, 6(7), 176. https://doi.org/10.3390/drones6070176







