Abstract
This article presents a formation tracking control method for the operation of multi-agent systems under disturbances. This study aims to ensure that the followers of a quadcopter converge into the desired formation while the center formation of the follower quadcopters tracks the leader’s trajectory within a finite time. The distributed finite-time formation control problem is first investigated using the fast terminal sliding mode control (FTSMC) theory. A disturbance observer is then integrated into the FTSMC to overcome the model uncertainties and bounded disturbances. Subsequently, the Lyapunov function is proposed to ensure the stability of the system. It is shown that formation tracking control can be achieved even in the presence of disturbances. Simulation and experimental results verify the effectiveness of the proposed formation tracking control method compared to existing ones.
1. Introduction
In recent years, the research into the cooperative control of multi-agent systems has gained widespread interest. It has been increasingly implemented in various applications, such as flocking [1,2], target tracking [3], consensus [4], and machine learning [5,6]. As a classification of formation, formation tracking control can retain the formation configuration, and also track the reference trajectory of the leader’s (or virtual leader’s) position. It has been widely employed in various applications, such as unmanned aerial vehicles [7], maritime search and rescue [8], mobile robots [9], and so on. The formation tracking problem has drawn considerable attention in the academic domain with regard to overcoming the external disturbances and model uncertainties.
Various control methods have been analyzed to overcome the formation tracking control problem. The formation control based on output consensus feedback control for multiple nonlinear systems was proposed in [10]. The adaptive consensus method combined with a neural-network-based observer was proposed in [11] for nonlinear multi-agent systems. Cooperative controllers were presented in [12] for mobile robots using a constructive algorithm. A synchronized control method was proposed in [13] to maintain the time-varying formation of a multi-agent system. Several formation control methods have been applied effectively to optimize the energy consumption and interaction frequency, such as impulse control and even-triggered control [14,15]. In [16], a distributed formation tracking control approach was proposed for mobile robots considering collision avoidance and the effects of unknown slippage. The cooperative tracking control approach based on neural networks was proposed for high-order systems in [17]. However, most studies mentioned above focused on asymptotic stability, where the settling time is unlimited. The high-speed convergence from the finite-time control strategy provides some merits, such as disturbance rejection [18] and faster convergence [19]. Therefore, the finite-time control problem considering disturbances is crucial for practical applications, but has not been addressed thus far.
Numerous studies have been conducted recently focusing on the design of cooperative control in the presence of disturbances. The finite-time tracking problem for multiple quadrotors was presented in [20]. Liu et al. [21] presented a fast terminal sliding mode (TSM) algorithm for multi-agent systems with finite-time convergence. In [22], the cooperative tracking control problem was analyzed for multi-agent systems in the presence of multiple delays and impulse issues. The authors of [23] proposed a consensus strategy for a group of network robots. Furthermore, several robust control techniques based on an observer were proposed in [24,25,26,27]. Recent methods proposed novel formation tracking control with good results, such as finite-time criteria design [28,29,30], optimal design with Q-learning [31], consensus design [32], command filtered backstepping [33], the adaptive backstepping technique [34], robust sliding mode with fixed-time stability [35], data driven-based formation control [36], output feedback formation [37], adaptive nonsingular terminal sliding mode [38], and neural networks [39]. However, most studies mentioned above lack experimental results or asymptotical convergence in quadcopter systems. The finite-time distributed even-triggered formation is proposed in [40] in the presence of disturbances, but this method may not consider the faster response from the exponential convergent property. Therefore, analyzing the cooperative tracking control of multi-agent systems with finite-time convergence and an unknown upper bound of disturbances is essential. This study aims to extend the article [41] by analyzing the finite-time consensus formation tracking control for multi-agent systems in the presence of external disturbances. This means that the follower agents maintain the geometric configuration under external disturbances in a finite time and also track the desired trajectory of the leader agent within the finite time. Consequently, a fast terminal sliding mode control method is proposed for the multi-agent system, which can handle finite-time consensus control in the presence of unknown bounded disturbances. When compared to [41], this study considers the external disturbances in the model of multi-agent systems and can be verified with the help of experimental results. The main contributions of this manuscript can be summarized as follows:
- We develop formation tracking control with a disturbance observer—the proposed method can provide faster finite-time convergence, less steady-state errors, and robustness;
- The stability of the whole system is validated using Lyapunov theory;
- We compare the proposed method with the existing algorithm in [41];
- We implement it on a real quadcopter platform for verification, which is lacking in [41].
The remainder of the article is organized as follows. The notations, graph theory, and the multi-agent system used in this study are presented in Section 2, while the observers in the external disturbances are shown in Section 3. The fast terminal sliding mode control methodology is presented in Section 4. Section 5 presents the numerical simulations and experimental results. Finally, Section 6 draws the conclusions of this paper.
2. Preliminaries and Multi-Agent System
2.1. Notation
In this study, certain notations are defined for the formation control as follows. The real number is denoted as R. The real matrices in dimensions are represented as . For and the vector , is denoted. Consider as a diagonal matrix with the entries, . Let , , . Note that denotes the Kronecker product and represents the Euclidean norm. For a given matrix represents its transpose.
2.2. Graph Theory
A weighted digraph, , is denoted as the information interaction of formation with N agents, where , and represent a vertex set with N nodes, a link edge set, and a weighted adjacency matrix, respectively. If , it indicates that the agent can receive the information of the agent . The element of A satisfies if ; otherwise, . For all , it is assumed that there are no self-loops (). Furthermore, the Laplacian matrix of a digraph, , is defined as , where , and . A digraph is defined as a directed spanning tree if a directed path exists from one node to all the other nodes.
It is assumed that there is one leader agent and followers. The root node is called the leader, which is labelled as 0, and the other nodes are called the followers, and are defined as . The information interaction between follower agents is described by . Consider a digraph with agents. Subsequently, the Laplacian matrix of the digraph, , can be defined as , where is the communication weight matrix between the leader and the followers [28].
2.3. Multi-Agent System
This study considers a multi-agent system with agents. We assume that the position model of each quadrotor is linearized [42] in a second-order system. The dynamics of the leader quadrotor can be assumed as:
where , , are the position, velocity, and control input of the leader, respectively. The dynamics of the follower can be assumed as:
where , , are the position, velocity, and control inputs of the followers, and represents the disturbance. It is assumed that:
Lemma 1.
([28]). If a positive-definite Lyapunov function candidate, , satisfies with and , can be defined as the fast-finite-time stability, and is the settling time required to reach , for all .
2.4. Control Objective
The control objective of the proposed method is to design a formation tracking control approach based on fast terminal sliding mode control and a disturbance observer to achieve the following objectives:
where , represents the designed formation and is the finite time.
Remark 1.
It can be easily concluded that the finite-time fast terminal sliding mode formation tracking control is converted into a finite-time consensus problem when.
Remark 2.
Equations (4) and (5) are the basic criteria of formation tracking control—that is, the forming of the formation, position, and velocity tracking. Equations (6) and (7) can guarantee that the geometric center from the follower agents can track the leader agent in finite time.
3. Disturbance Observer Design
This section is divided into subsections. It provides a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn. In this section, the disturbance observer is introduced to estimate the in (2).
Theorem 1.
Consider the multi-agent system (2) under assumption (1). A disturbance observer is designed via an auxiliary variable,,as follows:
Proof.
The Lyapunov function is selected as:
The first derivative of the Lyapunov function is achieved as:
Since , (10) is written as:
Let . From Lemma 1, it is clear that can be reached in finite time with . Therefore, for .
From (8), the disturbance error can be calculated as:
From the conclusion of Equation (11), we can obtain . □
4. Formation Tracking Control Design
The design of the formation tracking control approach includes two steps. A fast terminal sliding mode (FTSM) is first designed for a closed-loop system. A finite formation tracking control approach based on the disturbance observer and FTSM is then proposed for each follower agent.
We define the formation tracking errors as:
Let . The entire group of formation tracking control errors can be achieved as
where .
A sliding surface vector can be defined as:
where and .
Theorem 2.
Consider the multi-agent system, formation tracking errors, and the sliding surface given by (1), (2), (14), and (15). Consider that the following formation tracking control approach is implemented as:
Proof.
The first derivative of sliding surface (15) can be achieved as:
The Lyapunov function is selected as:
Let . The first derivative of the Lyapunov function (18) can be written as:
where is the maximum eigenvalue of the corresponding matrix.
From the conclusion of Equation (12), we can obtain:
Based on Lemma 1, the multi-agent system can converge within fast finite time, , with . Therefore, all the follower agents form the formation and track the leader’s trajectory within the finite time. □
Remark 3.
Equation (2) has two parts: formation tracking control and disturbance rejection. In the case of no disturbance in the whole system, the disturbance observershould be zero. This means that the algorithm only conducts the formation tracking control task. In the presence of disturbance, the value ofshould be different to zero, which is used for disturbance compensation.
Remark 4.
In Equation (16), to achieve good formation tracking performance, the parametersneed to be tuned. To obtain disturbance rejection, the parametersin (4) need to be adjusted. These parameters should be chosen carefully by trial and error to achieve the desired performance.
5. Simulation Results
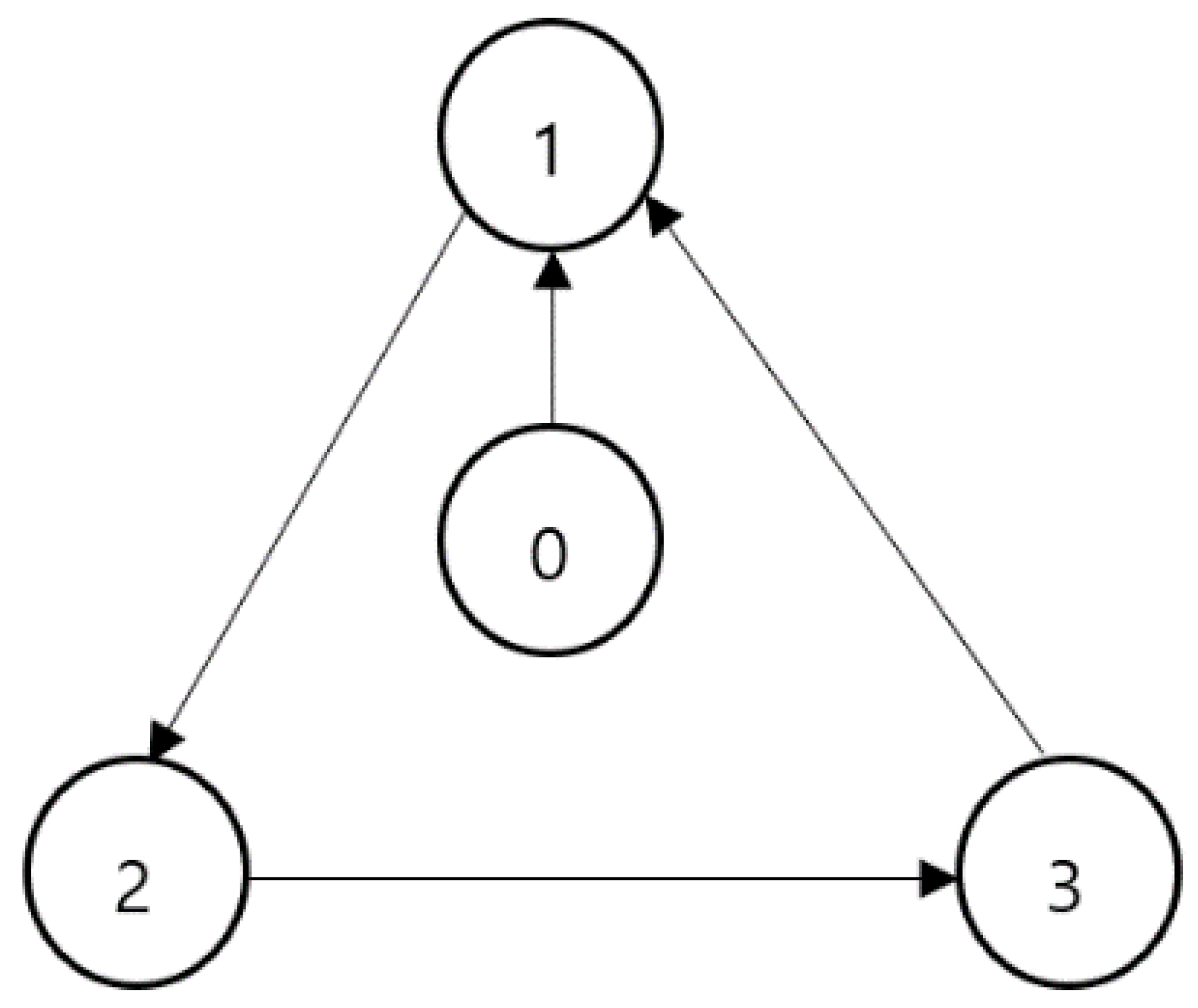
In this section, the performance of the proposed method is compared with the original FTSM formation tracking control presented in [41]. Consider a team of three follower agents and one virtual leader agent in a network with a directed graph, as shown in Figure 1. The leader is labelled as 0, whereas the followers are labelled as 1, 2, 3. The initial positions of each agent are configured as: , , , . The leader’s trajectory is configurated as:
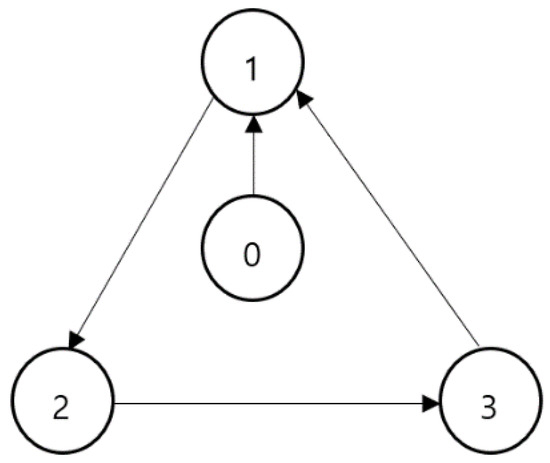
Figure 1.
Desired formation of multi-agent system.
We assume that the disturbance is injected into quadrotor 1 in the -direction as . The desired formation is set as , , . Two numerical examples will be considered. The parameters for formation tracking control are chosen as: , , , , , , , , .
5.1. Case 1: Absence of Disturbance Observer Mechanism
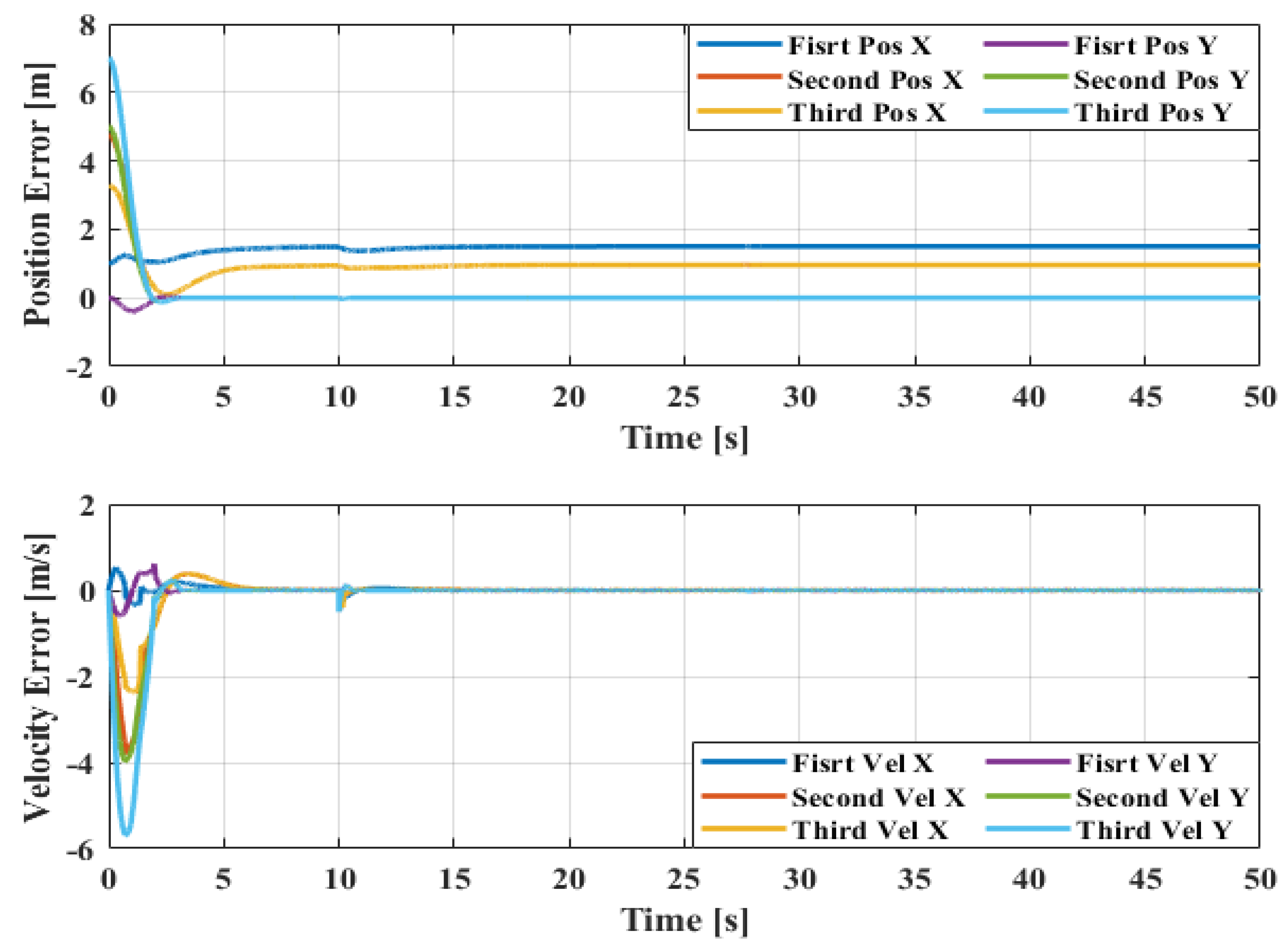
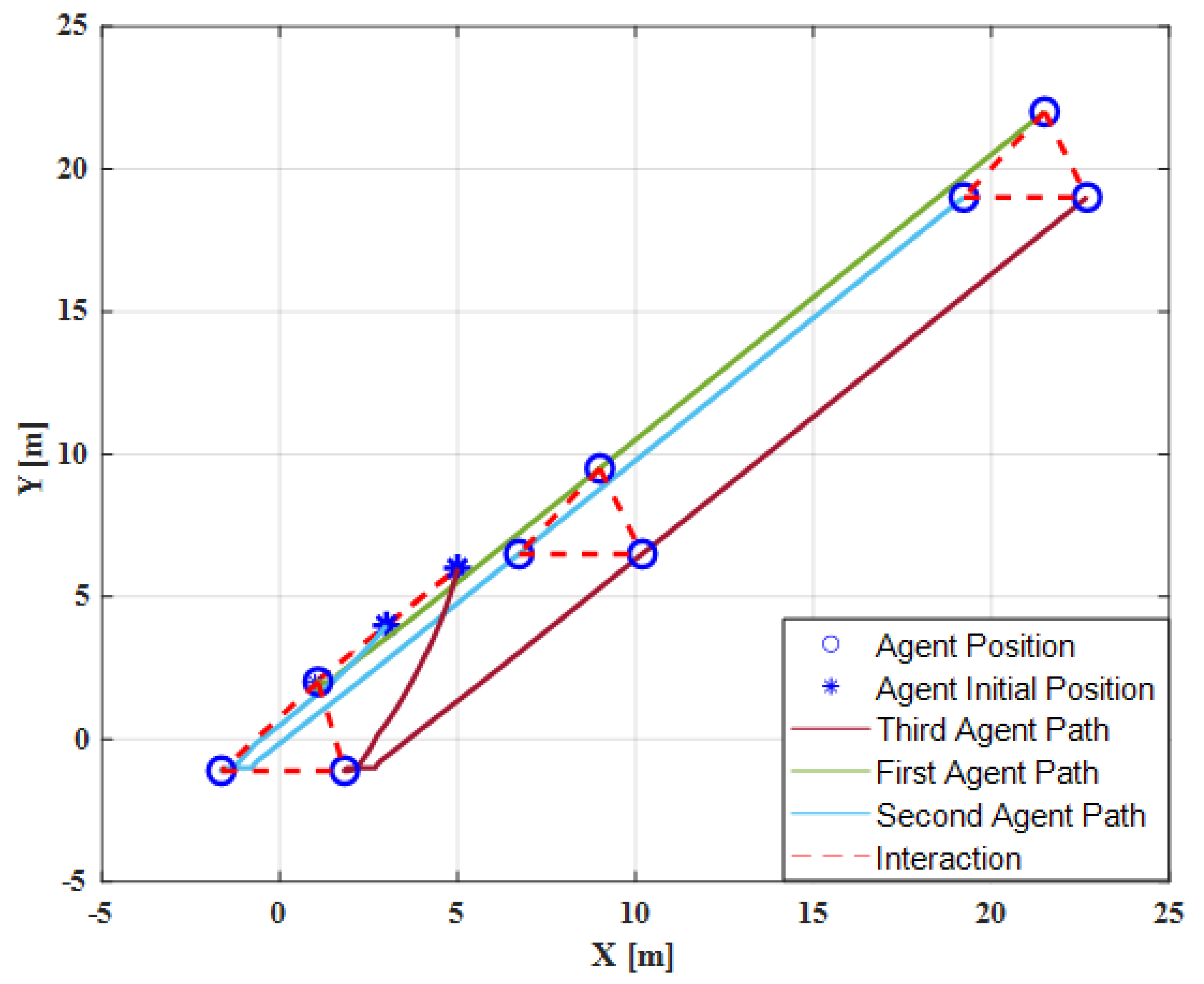
In this case, with the original method in [41] (without the disturbance observer algorithm), the formation cannot be maintained well when tracking the leader’s trajectory. To be more specific, the responses of the position errors in the second and third quadrotor cannot converge to zero values as in Figure 2. It should be mentioned that all velocity errors converge to zero values because the position errors converge to constant values, although there is an abrupt change at 10 s due to the injection of a disturbance in the first quadrotor. The corresponding 2D formation tracking control is shown in Figure 3.
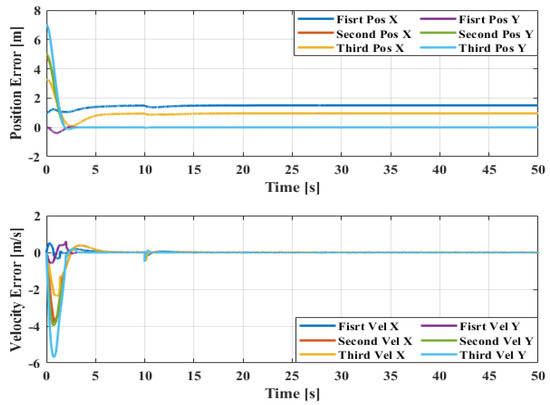
Figure 2.
Position and velocity error without disturbance observer.
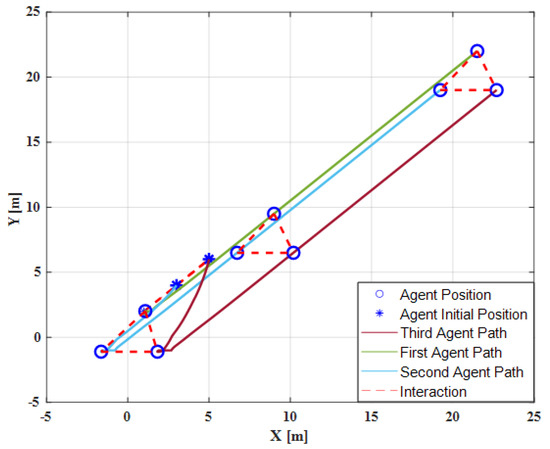
Figure 3.
Two-dimensional formation tracking control without disturbance observer.
5.2. Case 2: Presence of Disturbance of Observer Mechanism
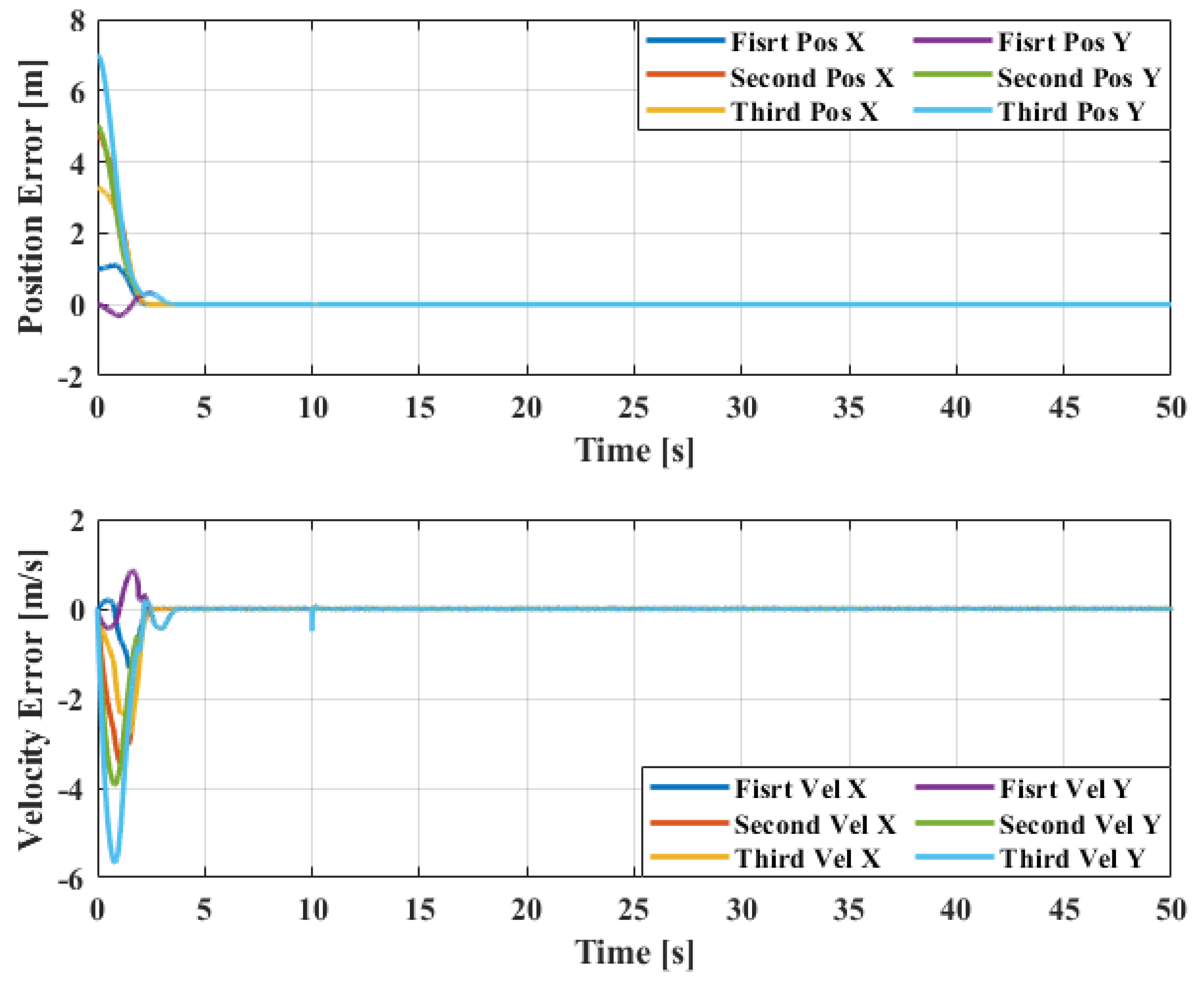
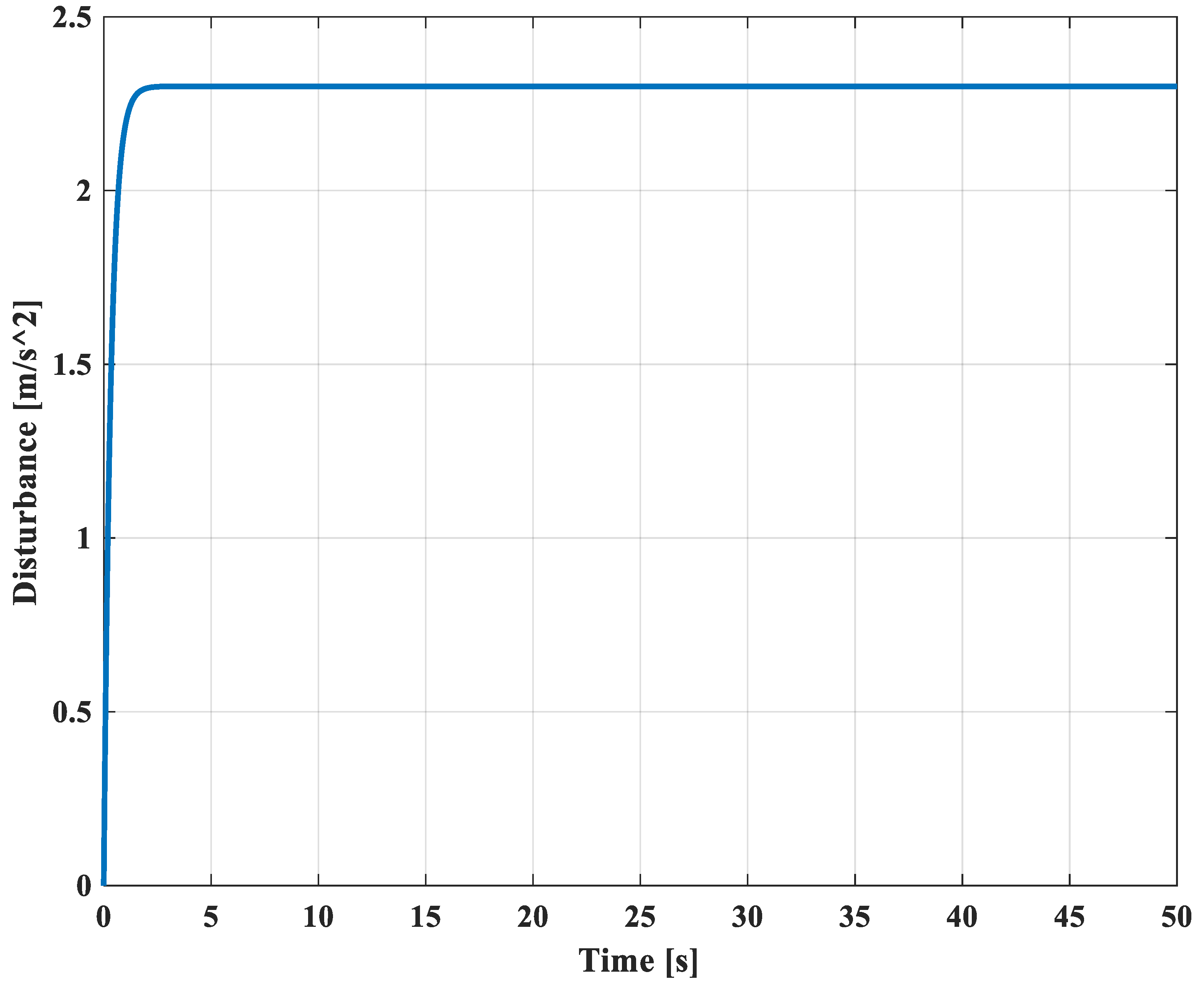
In this case, the disturbance observer algorithm is considered in the formation control algorithm. In Figure 4, the position errors converge to 0 from the initial positions within 3 s. This means that all followers can track the desired position within 3 s. From 3 s to 50 s, the position errors can be maintained at 0 m, although there is a disturbance injected into the first agents in the x-direction, as mentioned above. This means that all agents can maintain the formation and track the desired leader’s trajectory well under a disturbance. The corresponding 2D formation tracking control is shown in Figure 5. The disturbance estimation is shown in Figure 6. It is presented that the disturbance observer can provide a good estimation of the disturbance. Its value converges to 2.3.
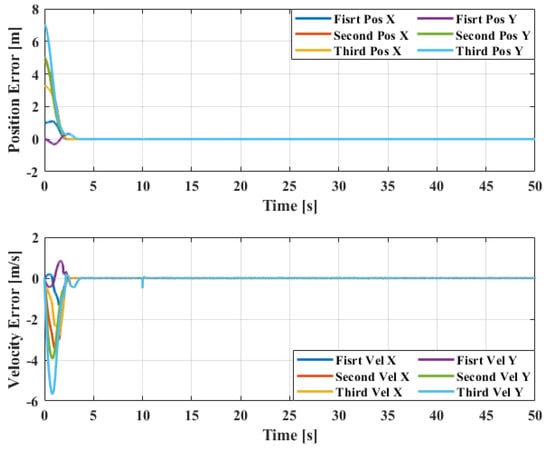
Figure 4.
Position and velocity error with disturbance observer.
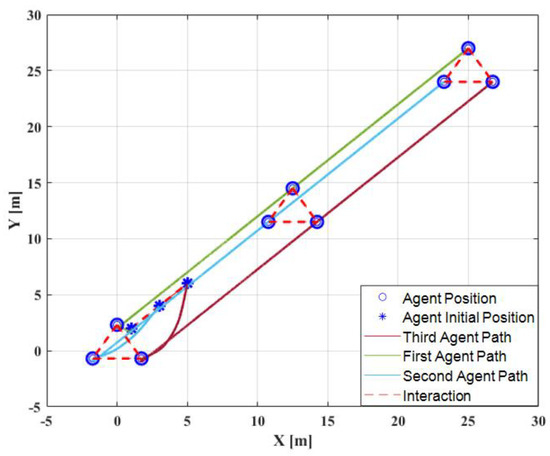
Figure 5.
Two-dimensional formation tracking control with disturbance observer.
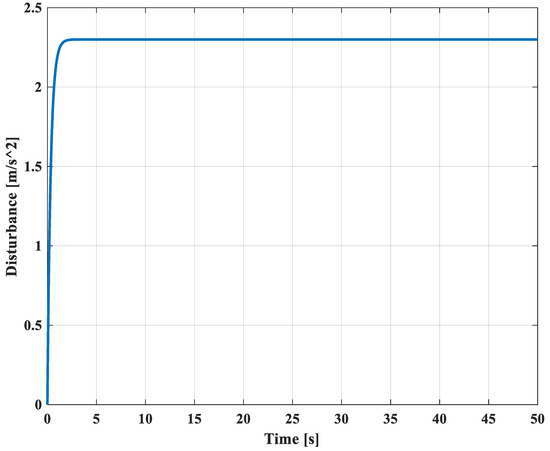
Figure 6.
The estimation of disturbance.
6. Experiment
6.1. Experimental Setup
Consider a directed graph with three follower agents and one virtual leader agent. The formation topology is shown in Figure 1. The Laplacian matrix and communication weight matrix are given as:
The desired formation is set as , ,.
The setup for the flight test is presented in Figure 7, which includes the three quadrotors and the Vicon capture system. The Vicon cameras can capture the position through markers attached to the quadrotor and send the images to the processing computer. Before the Vicon system starts to capture the object, the calibration of the reflective markers is conducted to determine the current position and orientation of the objects in real time. The processing computer is used to send the Vicon data to a laptop through the local area network (LAN).

Figure 7.
Experimental setup for micro quadrotor.
The attitude, position control, and the sensor fusion algorithm are conducted onboard a Crazy quadcopter [43]. The attitude and position control loop are running at 500 Hz and 100 Hz, respectively. The GCS, which is run on the laptop, is used to receive the position data from the Vicon system, computing the formation tracking control algorithm, sending the commands to the follower quadcopter, and providing a user interface to switch between various missions and operational modes.
6.2. Experimental Results
6.2.1. Case 1: Straight Line
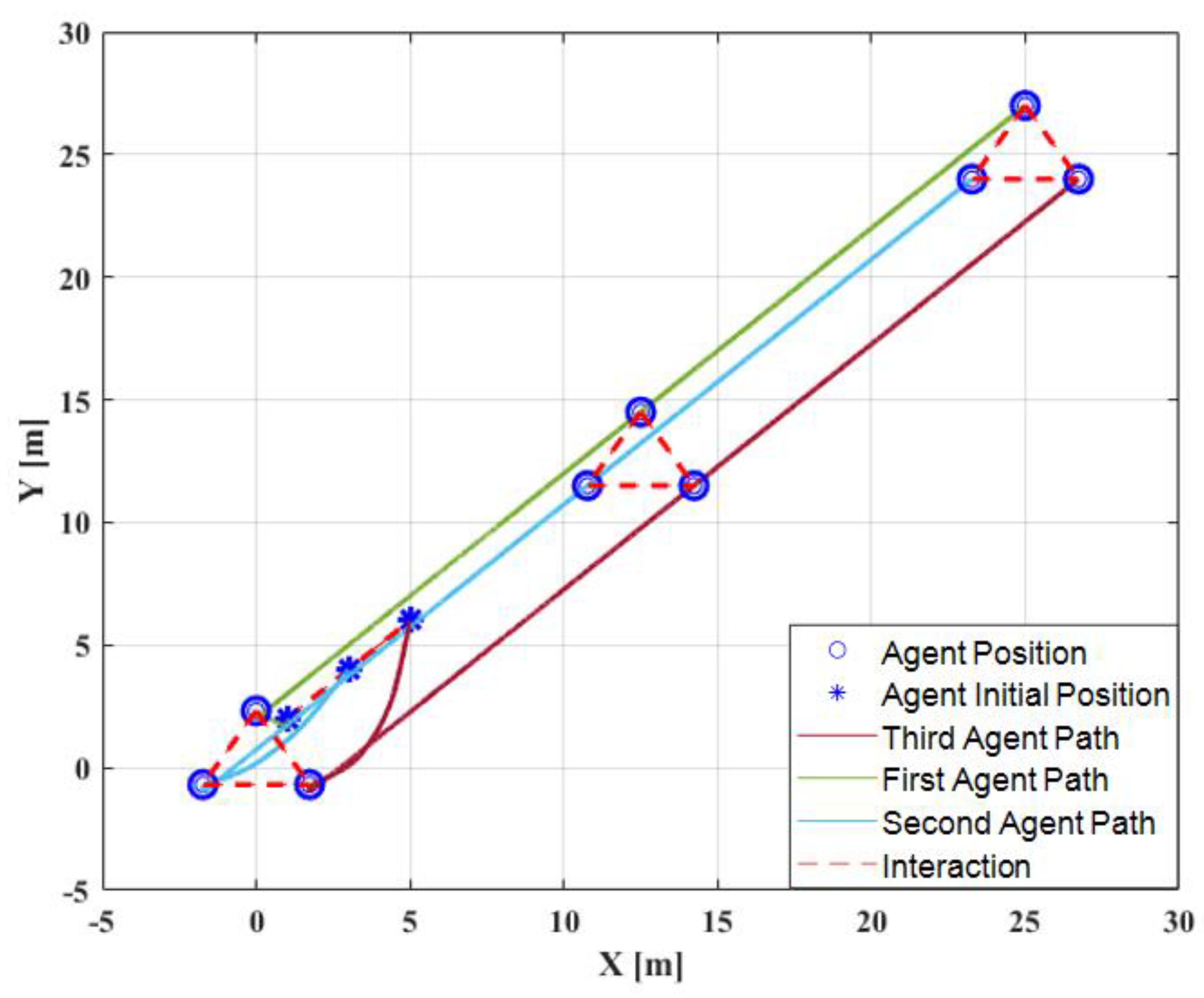
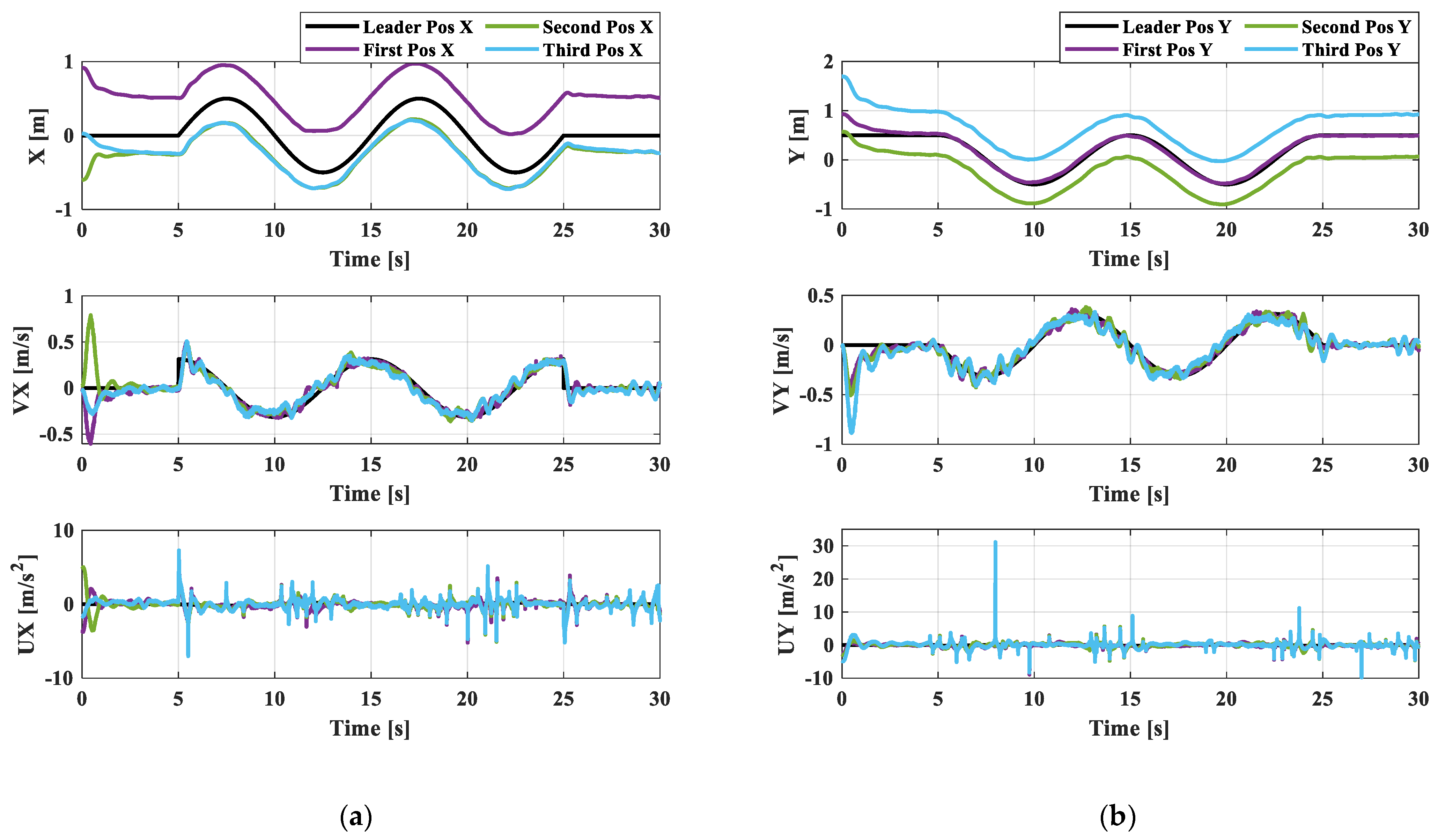
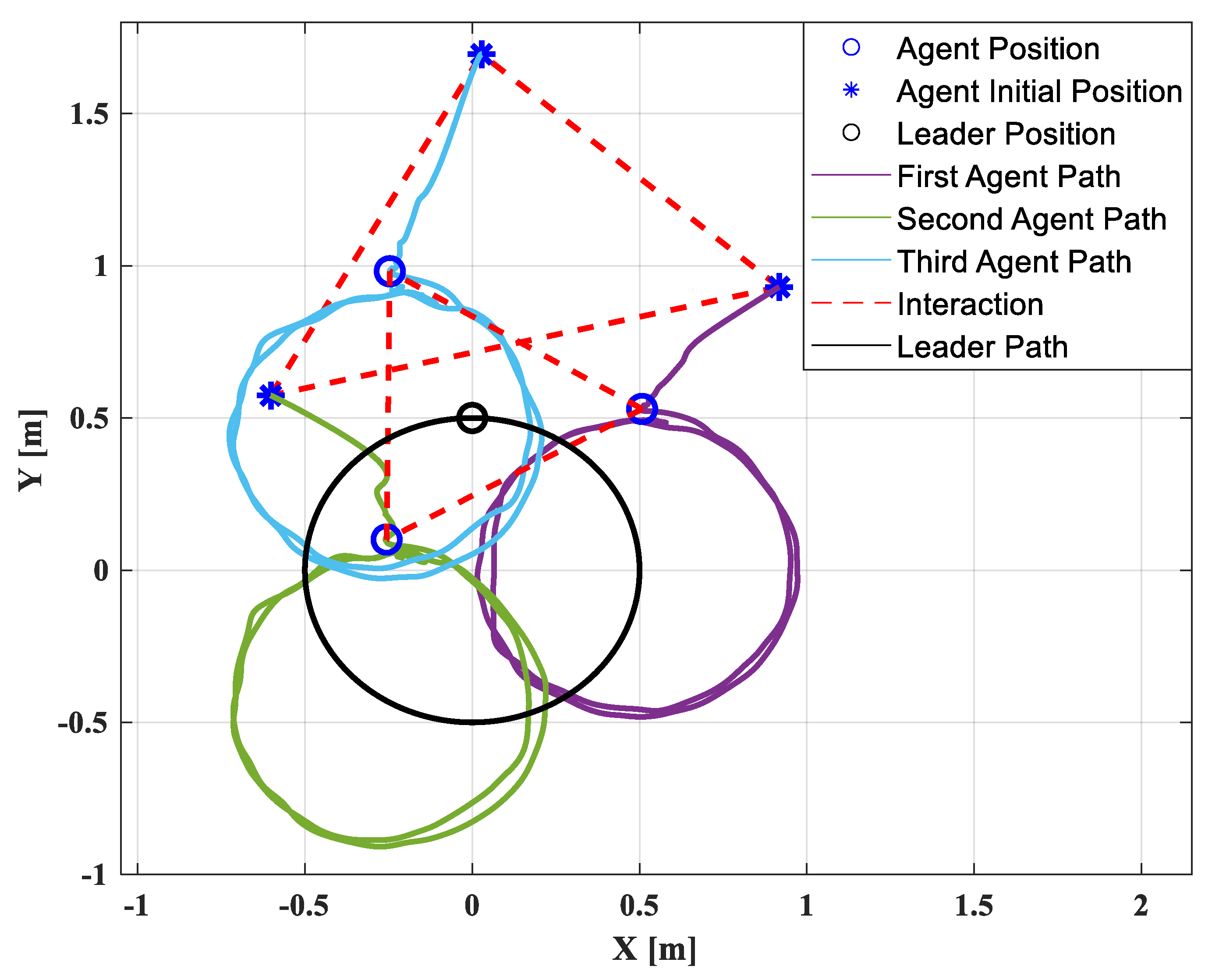
The desired trajectory of the virtual leader is configured by if and , if , if , if . The follower agents are assumed to track the desired trajectory of the leader agent. The movement of the quadrotor in the x- and y-directions is controlled by the formation tracking control law presented in (12). The experiment is conducted in three steps. All the quadrotors are hovered at the altitude of 0.3 m in the first step, but these data are not presented for simplification. In the second step, the formation tracking control law is activated at 0 s after hovering at 0.3 m. Figure 8 illustrates the corresponding position, velocity, and acceleration of each agent in the x- and y-directions. After 5 s, the follower agents can precisely track the desired trajectory from the leader agent. It must be noted that the velocity and acceleration of the quadrotors are kept within the desired ranges. The 2D performance of the formation is presented in Figure 9. It is shown that the follower agents can maintain the triangular shape while tracking the desired trajectory.
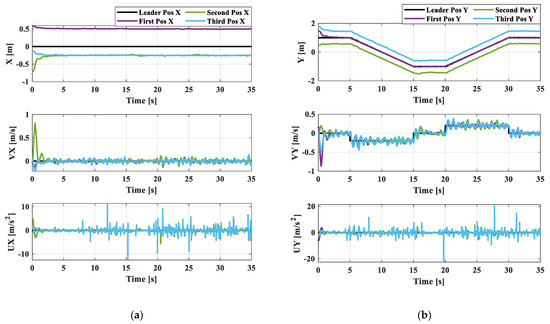
Figure 8.
(a) Position, velocity, and acceleration in x-direction of straight line; (b) position, velocity, and acceleration in y-direction of straight line.
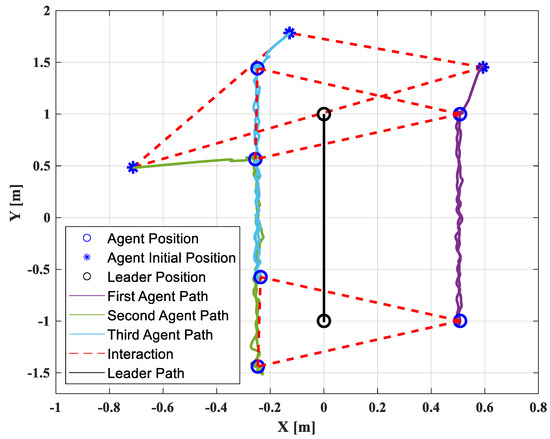
Figure 9.
Trajectory performance in two dimensions of straight line.
6.2.2. Case 2: Circular Trajectory
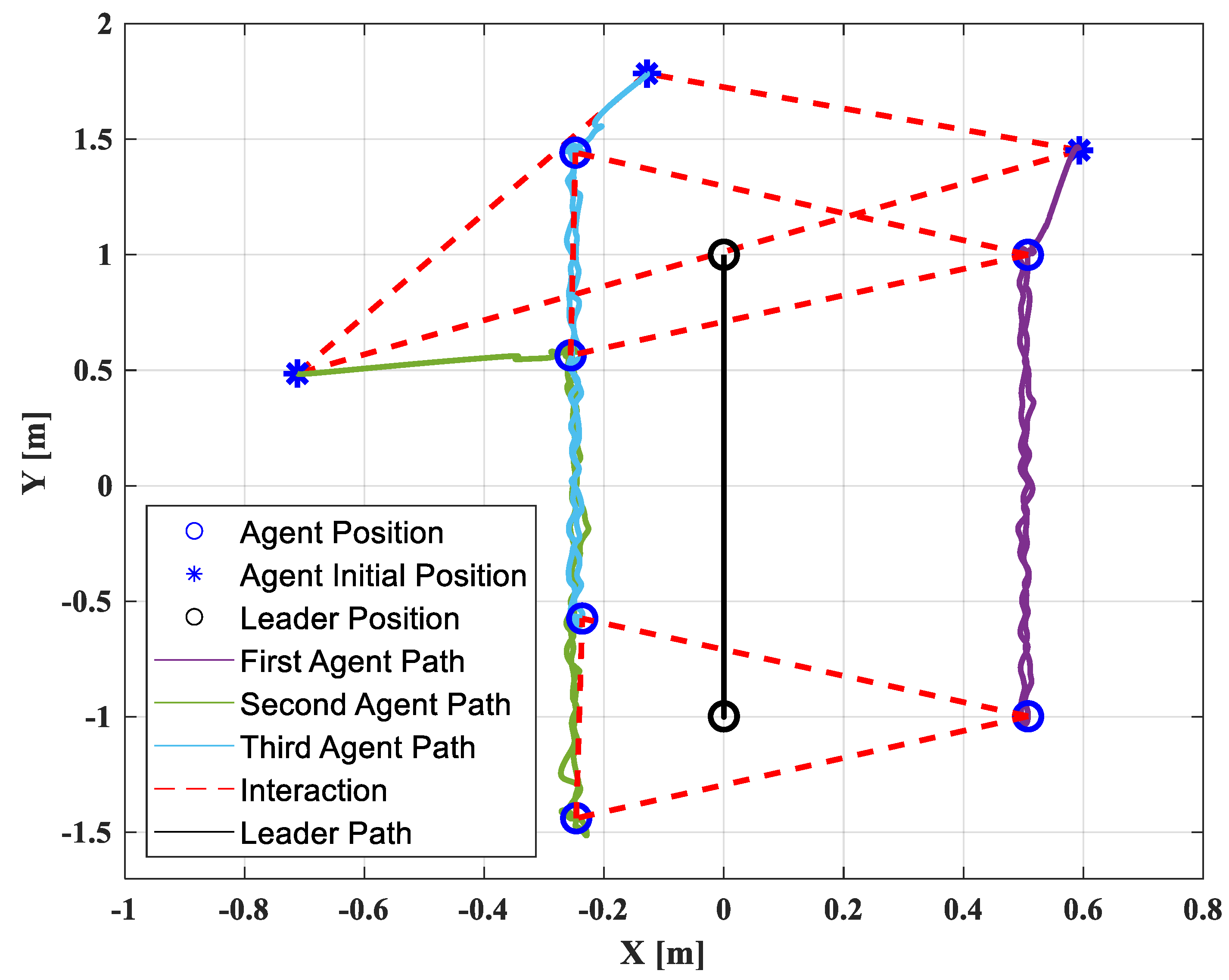
The follower agents are designed to track the circular trajectory of the virtual leader, given by if , if . The experiment is conducted in two steps. All the quadrotors are hovered at the initial position, but these data are not presented for simplification. In the second step, the formation tracking control law is activated at 0 s. Figure 10 presents the corresponding position, velocity, and acceleration of each agent in the x- and y-directions. After activating the formation control law (after 0 s), the three follower agents move towards the desired position, from where they can accurately track the circular trajectory after 5 s. The 2D performance of the formation is presented in Figure 11. It is demonstrated that the follower agents can maintain the circular shape while tracking the desired trajectory.
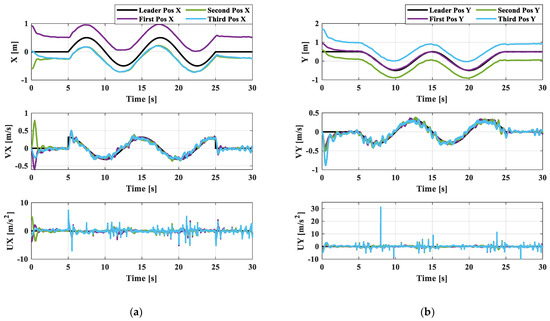
Figure 10.
(a) Position, velocity, and acceleration in x-direction of circular trajectory; (b) position, velocity, and acceleration in y-direction of circular trajectory.
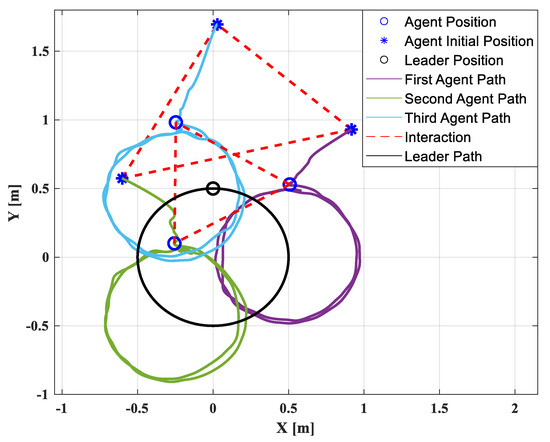
Figure 11.
Trajectory performance in two dimensions of circular trajectory.
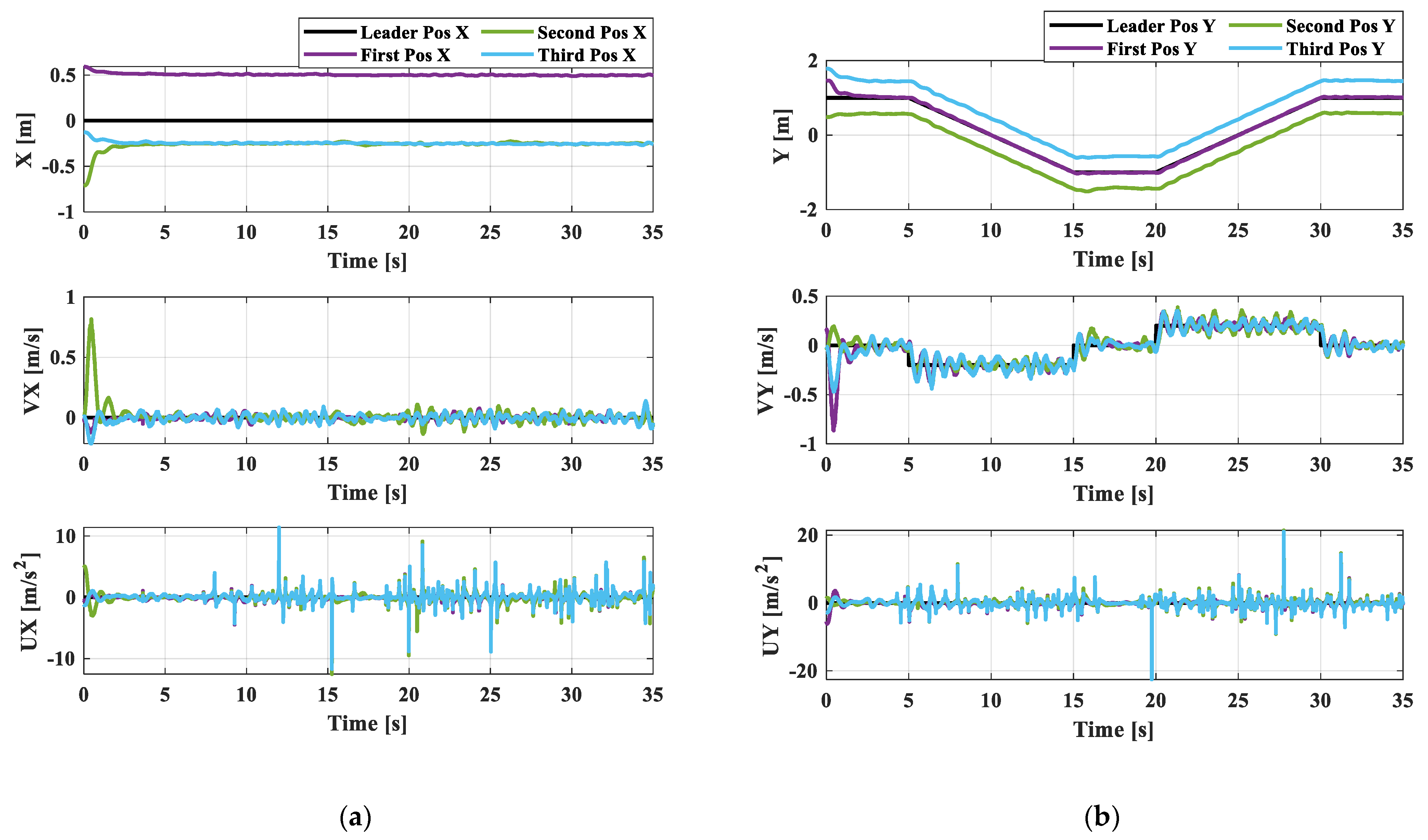
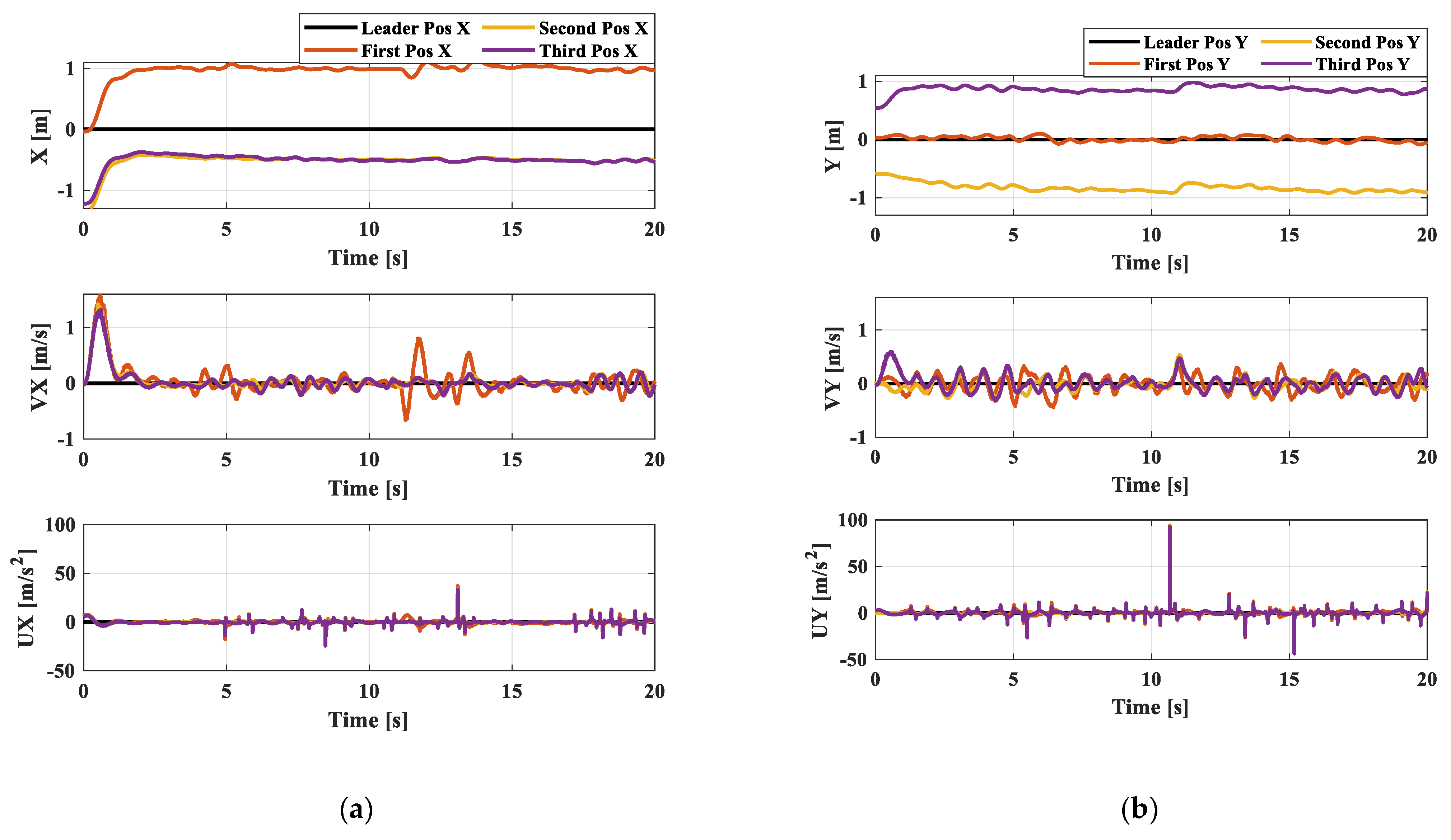
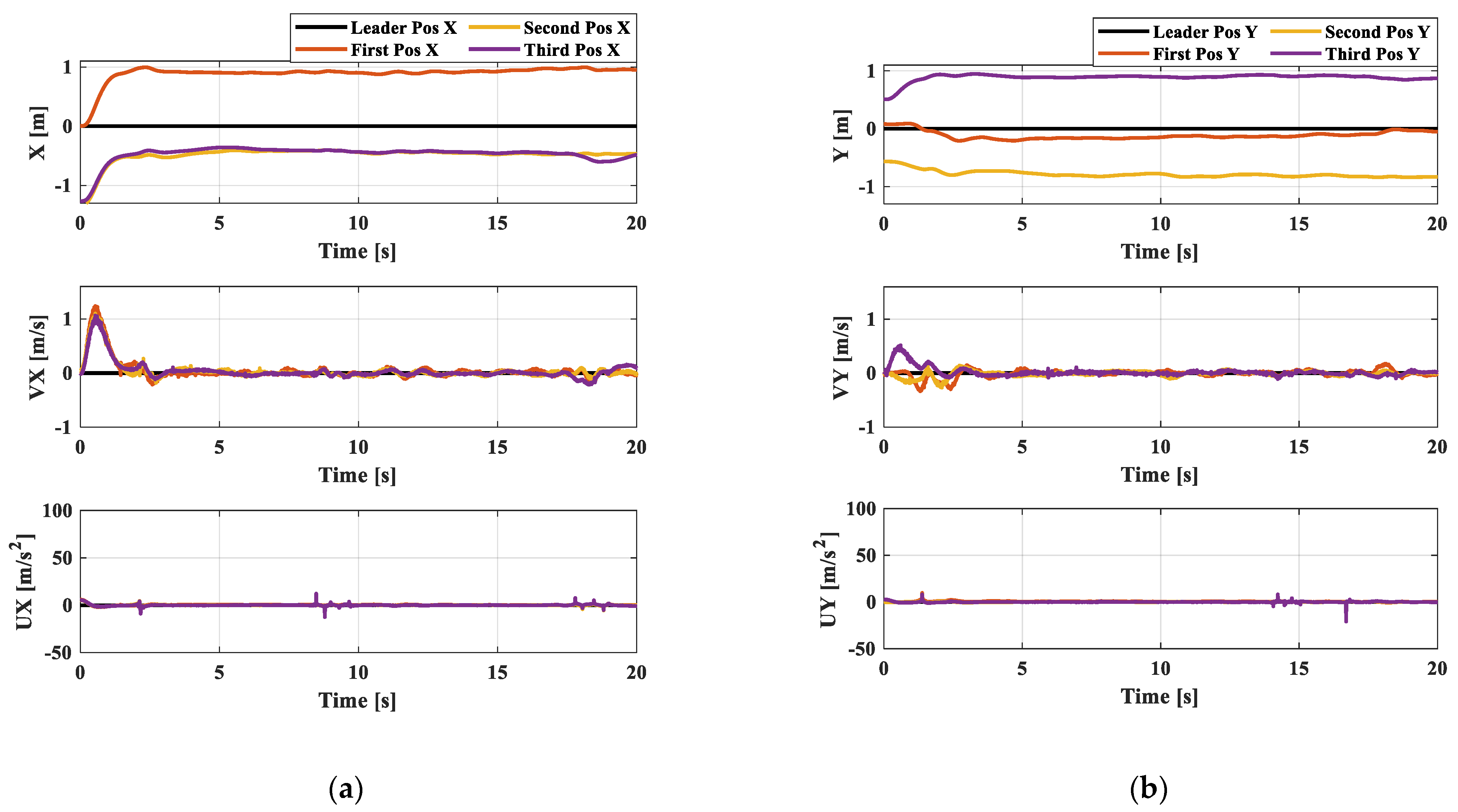
6.2.3. Case 3: Formation with External Disturbances
To demonstrate the effectiveness of the disturbance observer, an electric fan is used to generate a disturbance in the y-direction for the first follower agent. Figure 12 and Figure 13 show the position, velocity, and acceleration performance of the quadrotors with and without the use of the disturbance observer, respectively. It is evident that the position of the first quadrotor and the formation shape obtained from the proposed method can be effectively maintained when a disturbance is introduced into the first quadrotor. However, when the disturbance observer method is not used, the first quadrotor deviates from the desired position and the formation shape is also affected. The full experiment work of Section 6.2 is conducted as video’s link in Supplementary Materials.
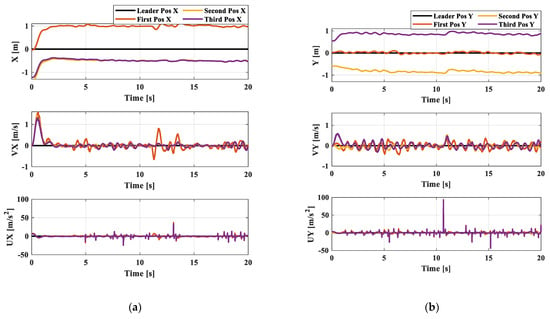
Figure 12.
(a) Position, velocity, and acceleration in x-direction; (b) Position, velocity, and acceleration in y-direction with disturbance observer.
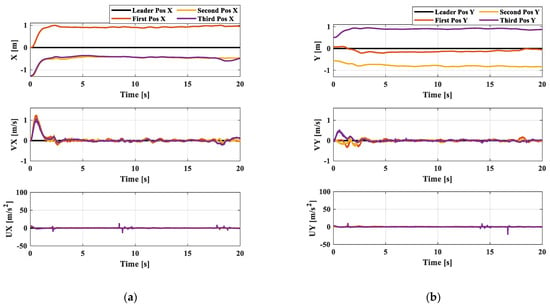
Figure 13.
(a) Position, velocity, and acceleration in x-direction; Position, velocity, and acceleration in y-direction without disturbance observer.
7. Conclusions
In this study, the formation tracking control problem for multi-agent systems under external disturbances has been analyzed. Based on graph theory, the disturbance observer, finite-time stability theory, the properties of the Laplacian matrix, and the formation tracking control have been analyzed. The formation of the follower agents can achieve the desired configuration within a finite time and the center of the formation can simultaneously track the leader’s trajectory. Three scenarios have been analyzed to verify the proposed theory. The results indicate that the follower can maintain the shape in a straight line or in a circular trajectory. It is observed that the advantage of the proposed method is that it is superior to the original method in the presence of disturbance. The results showed that with the integration of a disturbance observer (Equation (8)) into the control law (Equation (16)), the formation shape with the proposed method can be maintained well. This means that the convergence time for obtaining the desired formation shape is reduced. Therefore, the errors between the formation shape and desired formation in the proposed method converge to zero quicker than in the conventional one. However, the disadvantage of the proposed method is that the bound of the disturbance is known, and the velocity and acceleration cause some oscillations due to the high gain of the disturbance observer. Therefore, a future study will design a disturbance observer with unknown bounded disturbance and will consider the problem caused by the high gain of the disturbance observer. Moreover, future research will integrate collision avoidance into the control law to maintain the formation shape in the presence of obstacles.
Supplementary Materials
The full demonstration is shown at the following link: https://www.youtube.com/watch?v=RqXU-YW_sfQ&t=54s (accessed on 30 June 2021).
Author Contributions
Conceptualization, N.P.N. and S.K.H.; Methodology, N.P.N. and D.P.; Software, N.P.N. and D.N.N.; Validation, N.P.N. and T.T.H.; Formal Analysis, N.P.N., D.P., T.N.N. and S.K.H.; Investigation, N.P.N., T.N.N. and S.K.H.; Resources, N.P.N., N.X.-M. and T.N.N.; Data Curation, N.P.N., D.P., D.N.N., N.X.-M., T.T.H., T.N.N. and S.K.H.; Writing—Original Draft Preparation, N.P.N.; Writing—Review and Editing, N.X.-M., D.N.N., T.T.H. and T.N.N.; Visualization, N.P.N.; Supervision, S.K.H.; Project Administration, S.K.H.; Funding Acquisition, S.K.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP-2022-2018-0-01423) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation). This research also was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (2020R1A6A1A03038540).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, H.; Cheng, Z.; Chen, G.; Li, C. Model predictive flocking control for second-order multi-agent systems with input constraints. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 1599–1606. [Google Scholar] [CrossRef]
- Fang, H.; Wei, Y.; Chen, J.; Xin, B. Flocking of Second-Order Multiagent Systems with Connectivity Preservation Based on Algebraic Connectivity Estimation. IEEE Trans. Cybern. 2016, 47, 1067–1077. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Li, S.; Guan, X. Flocking algorithm with multi-target tracking for multi-agent systems. Pattern Recognit. Lett. 2010, 31, 800–805. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Wen, G.; Liu, Y.; Wang, F. Adaptive Consensus Control for a Class of Nonlinear Multiagent Time-Delay Systems Using Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1217–1226. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Hien, T.D.; Nguyen-Thoi, T.; Lee, J. A unified adaptive approach for membrane structure: Form finding and large deflection iso-geometric analysis. Comput. Methods Appl. Mech. Eng. 2020, 369, 113239. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Lee, J.; Dinh-Tien, L.; Dang, L.M. Deep learned one-iteration nonlinear solver for solid mechanics. Int. J. Numer. Methods Eng. 2022, 123, 1841–1860. [Google Scholar] [CrossRef]
- Duan, H.; Liu, S. Non-linear dual-mode receding horizon control for multiple unmanned air vehicles formation flight based on chaotic particle swarm optimization. IET Control Theory Appl. 2010, 4, 2565–2578. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.; Yang, T.; Zhou, L.; Yuan, Y.; Feng, H. Maritime Search and Rescue Networking Based on Multi-Agent Cooperative Communication. J. Commun. Inf. Netw. 2019, 4, 42–53. [Google Scholar] [CrossRef]
- Jennings, J.S.; Whelan, G.; Evans, W.F. Cooperative search and rescue with a team of mobile robots. In Proceedings of the 1997 8th International Conference on Advanced Robotics. Proceedings, ICAR’97, Monterey, CA, USA, 7–9 July 1997; pp. 193–200. [Google Scholar]
- Wang, W.; Huang, J.; Wen, C.; Fan, H. Distributed adaptive control for consensus tracking with application to formation control of nonholonomic mobile robots. Automatica 2014, 50, 1254–1263. [Google Scholar] [CrossRef]
- Mao, J.; Karimi, H.R.; Xiang, Z. Observer-based adaptive consensus for a class of nonlinear multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1893–1900. [Google Scholar] [CrossRef]
- Do, K.D. Formation tracking control of unicycle-type mobile robots with limited sensing ranges. IEEE Trans. Control Syst. Technol. 2008, 16, 527–538. [Google Scholar] [CrossRef] [Green Version]
- Sanhoury, I.M.; Amin, S.H.; Husain, A.R. Formation control of multiple mobile robots utilizing synchronization approach. Int. J. Mechatron. Manuf. Syst. 2013, 6, 94–114. [Google Scholar]
- Chen, L.; Li, C.; Sun, Y.; Ma, G. Cooperative impulsive formation control for networked uncertain euler-lagrange systems with communication delays. Chin. Phys. B 2017, 26, 068703. [Google Scholar] [CrossRef]
- Chen, L.; Li, C.; Xiao, B.; Guo, Y. Formation-containment control of networked euler-lagrange systems: An event-triggered framework. ISA Trans. 2019, 86, 87–97. [Google Scholar] [CrossRef]
- Yoo, S.J.; Kim, T.H. Distributed formation tracking of networked mobile robots under unknown slippage effects. Automatica 2015, 54, 100–106. [Google Scholar] [CrossRef]
- Cui, R.; Ren, B.; Ge, S. Synchronized tracking control of multi-agent system with high order dynamics. IET Control. Theory Appl. 2012, 6, 603–614. [Google Scholar] [CrossRef] [Green Version]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Franceschelli, M.; Pisano, A.; Giua, A.; Usai, E. Finite-time consensus with disturbance rejection by discontinuous local interactions in directed graphs. IEEE Trans. Autom. Control 2015, 60, 1133–1138. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, J.; Li, B.; Yang, Y. Finitetime formation tracking control for quadrotor UAVs based on fast non-singular terminal sliding mode. In Proceedings of the 2018 International Symposium in Sensing and Instrumentation in IoT Era (ISSI), Shanghai, China, 6–7 September 2018. [Google Scholar]
- Liu, H.; Cheng, L.; Tan, M.; Wang, Y. Consensus tracking of general linear multi-agent systems: Fast sliding-mode algorithms. In Proceedings of the IEEE 2013 32nd Chinese Control Conference (CCC), Xi’an, China, 26–28 July 2013; pp. 7302–7307. [Google Scholar]
- Nazarova, A.V.; Zhai, M. Distributed solution of problems in multi agent robotic systems. In Smart Electromechanical Systems; Springer: Cham, Switzerland, 2019; pp. 107–124. [Google Scholar]
- Tang, Y.; Xing, X.; Karimi, H.R.; Kocarev, L.; Kurths, J. Tracking control of networked multi-agent systems under new characterizations of impulses and its applications in robotic systems. IEEE Trans. Ind. Electron. 2015, 63, 1299–1307. [Google Scholar] [CrossRef]
- Li, B.; Qin, K.; Xiao, B.; Yang, Y. Finite-time extended state observer based fault tolerant output feedback control for attitude stabilization. ISA Trans. 2019, 91, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Hu, Q.; Yang, Y. Continuous finite-time extended state observer based fault tolerant control for attitude stabilization. Aerosp. Sci. Technol. 2019, 89, 204–213. [Google Scholar] [CrossRef]
- Xiao, B.; Yang, X.; Huo, X. A novel disturbance estimation scheme for formation control of ocean surface vessels. IEEE Trans. Ind. Electron. 2016, 64, 4994–5003. [Google Scholar] [CrossRef]
- Lazim, I.M.; Husain, A.R.; Mohamed, Z.; Basri, M.A.M.; Adilla, N. Disturbance observer-based formation tracking control of multiple quadrotors in the presence of disturbances. Trans. Inst. Meas. Control. 2019, 41, 4129–4141. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.; Zhao, Y.; Ghosh, B.K. Finite-time velocity-free observer-based consensus tracking for heterogeneous uncertain AUVs via adaptive sliding mode control. Ocean. Eng. 2021, 237, 109565. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.; Zhao, Y.; Ghosh, B.K. Finite-time velocity-free rendezvous control of multiple AUV systems with intermittent communication. IEEE Trans. Syst. Man Cybern. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.; Zhao, Y.; Ghosh, B.K. Finite-time observer-based tracking control of uncertain heterogeneous underwater vehicles using adaptive sliding mode approach. Neurocomputing 2022, 481, 322–332. [Google Scholar] [CrossRef]
- Peng, Z.; Luo, R.; Hu, J.; Shi, K.; Nguang, S.K.; Ghosh, B.K. Optimal tracking control of nonlinear multiagent systems using internal reinforce Q-learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Wu, Y. Interventional bipartite consensus on coopetition networks with unknown dynamics. J. Frankl. Inst. 2017, 354, 4438–4456. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, J.; Shi, P. Command filtered backstepping-based attitude containment control for spacecraft formation. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1278–1287. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, J.; Wang, Q.G. Adaptive finite-time containment control of uncertain multiple manipulator systems. IEEE Trans. Cybern. 2022, 52, 556–567. [Google Scholar] [CrossRef]
- Mechalo, O.; Xu, L.; Xie, X.; Iqbal, J. Theory and practice for autonomous formation flight of quadrotors via distributed robust sliding mode control protocol with fixed-time stability guarantee. Control. Eng. Pract. 2022, 123, 105150. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, H.; Wan, Y. Data-driven fault-tolerant formation control for nonlinear quadrotors under multiple simultaneous actuator faults. Syst. Control. Lett. 2021, 158, 105063. [Google Scholar] [CrossRef]
- Shojaeim, K. Output-feedback formation control of wheeled mobile robots with actuators saturation compensation. Nonlinear Dyn. 2017, 89, 2867–2878. [Google Scholar] [CrossRef]
- Meng, C.-C.; Zhang, X.-Y. Distributed leaderless formation control for multiple autonomous underwater vehicles based on adaptive nonsingular terminal sliding mode. Appl. Ocean. Res. 2021, 115, 102781. [Google Scholar] [CrossRef]
- Shojaei, K. Neural network formation control of a team of tractor-trailer systems. Robotica 2018, 36, 39–56. [Google Scholar] [CrossRef]
- Wang, J.; Bi, C.; Wang, D.; Kuang, C.W.Q. Finite-time distributed event-triggered formation control for quadrotor UAVs with experimentation. ISA Trans. 2021, 126, 585–596. [Google Scholar] [CrossRef]
- Han, T.; Guan, Z.H.; Liao, R.Q.; Chen, J.; Chi, M.; He, D.X. Distributed finite-time formation control of multi-agent systems via FTSMC approach. IET Control. Theory Appl. 2017, 11, 2585–2590. [Google Scholar] [CrossRef]
- Okyere, E.; Bousbaine, A.; Poyi, G.T.; Joseph, A.K.; Andrade, J.M. LQR controller design for quad-rotor helicopters. J. Eng. 2019, 17, 4003–4007. [Google Scholar] [CrossRef]
- Available online: https://store.bitcraze.io/products/crazyflie-2–1 (accessed on 20 May 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).