Abstract
The study examined the intricate relationships between embankment slope configurations, toe drain designs, and drawdown scenarios. It utilized a unique combination of numerical, physical, and mathematical models. The investigation involved 16 numerical models and 8 physical models with distinct characteristics. The research explored the correlations of key parameters: matric suction, horizontal water conductivity, time, and factor of safety. The factor of safety values varied from 0.62 to 1.03 as a result of the different investigated combinations. For instance, a 1:2 embankment slope without a toe drain under instantaneous drawdown led to the factor of safety values ranging from 1.22 to 1.57. Additionally, incorporating elements like a 30 m toe drain and a 1 m per day drawdown rate influenced these values, with extremes recorded from 1.337 to 2.21, shedding light on embankment stability under diverse conditions and configurations. When subjected to a 1 m per day drawdown, water flow rates decreased significantly at the upstream face and increased downstream, accompanied by an increase in water mass flux at the upstream face and a decrease at the downstream toe, suggesting dynamic changes in water behavior in response to drawdown. Moreover, the findings unveiled significant correlations between matric suction and time (correlation coefficient of 0.950) and factor of safety and water conductivity (correlation coefficient of 0.750). Conversely, a distinct negative correlation emerged between matric suction and factor of safety (correlation coefficient of −0.864). The study’s distinctive insights contribute to our understanding of seepage behavior and dam stability across varied scenarios, offering valuable input for resilient dam construction approaches that will ensure the longevity and effectiveness of these essential structures.
1. Introduction
Embankment dams, also referred to as earth dams, hold a vital role in global water resource management, flood control in flood-prone regions, and irrigation systems. Nevertheless, the intricate process of designing and constructing these dams entails grappling with the challenge of effectively managing seepage [1]. Profound behaviors related to the stability mechanisms of embankment dams encompass complex interactions and responses within the dam structure, such as gradual changes in pore water pressure and soil consolidation, which may influence factors like factor of safety and deformation patterns under various loading conditions [2]. These behaviors also involve the nuanced effects of factors like hydraulic conductivity variations [3], embankment slope configurations [4], toe drain effectiveness [5], and drawdown rates [6], which can impact the dam’s overall stability and performance, often requiring analysis and consideration in dam design and management to ensure long-term safety and resilience. The consequences of unchecked seepage can be dire, encompassing potential failures and safety risks. In response to this concern, engineers and researchers persistently seek innovative approaches to mitigate seepage-related hazards. As the demands for water resources and flood control escalate, the indispensability of earth dams as critical infrastructure becomes increasingly evident [7]. Carefully handling seepage is crucial to make sure these important structures last a long time.
Regrettably, improper design can render these dams perilous and catastrophic in the event of structural failure [8]. As previously emphasized, seepage represents a paramount issue that can precipitate potential embankment dam failures. Seepage arises when water navigates pathways through the dam’s materials or foundation, fostering internal erosion and the looming threat of dam collapse [9]. Inadequate consideration of permeability and seepage control measures can erode the dam’s stability and compromise its capacity to retain water securely [10]. The question of slope stability further compounds the challenges stemming from flawed embankment design. Excessive slope steepness or inaccurately assessed material properties can render the dam susceptible to slope failure, with dire implications such as extensive erosion, slumping, or even a catastrophic rupture that jeopardizes lives and property downstream [11]. Moreover, neglecting the thorough analysis of the dam’s foundation conditions can engender settlement, differential settlement, or embankment heaving. The repercussions of uneven settlement extend to structural damage and the creation of seepage pathways, further weakening the dam’s stability and performance over time. It is important to recognize that the geometric configuration of an earth dam exerts a significant influence on its seepage behavior.
The slope of an embankment dam plays a critical role in its stability and overall performance, as it directly influences factors such as seepage control, erosion resistance, and structural integrity [12]. Steeper slopes can reduce the amount of land required for dam construction but may increase the risk of slope failure and seepage, necessitating more robust engineering measures and materials [13]. Conversely, gentler slopes can enhance dam stability but often require larger land areas for construction. Striking the right balance in slope design is essential to ensure the dam’s safety, longevity, and effective management of water resources while considering local geological conditions and engineering constraints. In their embankment stability investigation, Li and Wang [14] considered the influence of slope and found that when embankment dams of equal height experience identical seismic intensities, the stability and safety factor of the dam slope decrease as the slope ratio increases. Additionally, when dams share both the same height and slope configuration, the stability and safety factor of the dam slope decrease with increasing seismic intensity. On the other hand, by providing a controlled path for the dissipation of seepage and pore water pressure that may accumulate at the base of the dam, a properly designed toe drain helps to reduce the risk of internal erosion and piping, which are major threats to dam integrity. The toe drain effectively prevents the build-up of excessive hydrostatic pressure within the dam’s foundation, enhancing its overall stability. Moreover, it can contribute to improved long-term performance by maintaining a stable foundation and preventing saturation-related issues. Malekpour et al. [15] conducted a study focusing on how the size of horizontal drains affects the stability of an embankment dam under both steady-state and transient seepage conditions. Their findings revealed that under steady-state seepage, increasing the drain thickness effectively prevented piping issues, while under transient seepage conditions, it ensured the stability of the upstream slope. However, it is worth noting that the thickest drain employed in their research displayed varying levels of efficiency depending on the length to which it was applied. Moreover, a rapid drawdown in an embankment dam, characterized by a sudden and substantial lowering of the reservoir water level, can have significant and potentially adverse impacts on dam stability [16,17]. During such events, the quick reduction in water pressure against the dam’s upstream face can induce a series of challenges. Firstly, it may trigger internal erosion and piping within the dam, as the rapid drawdown can create strong seepage forces that may displace soil particles and initiate erosion pathways. Secondly, the decreased water load on the dam can lead to increased pore water pressure within the embankment, potentially compromising its stability. Moreover, the sudden change in stress distribution across the dam can result in slope instability, which may lead to slumping or even catastrophic failure [3]. In their study, Alfatlawi et al. [18] conducted an assessment of the upstream slope stability of earth dams using the Khassa Chai Dam as a case study, with a particular focus on drawdown conditions. Their findings indicated that the stability of the slope during the drawdown process is significantly influenced by the rate at which pore water pressure dissipates. The research outcomes also demonstrated that, in the scenario of a one-day water drawdown, a minimum factor of safety (F.S.) value was reached within 10 h, resulting in a reduction in the F.S. by approximately 60.66%.
Over time, scholars have explored the consequences arising from different design components, particularly focusing on the central impervious core and toe drain and their impacts on the seepage attributes of earthen dams. A noteworthy illustration comes from the work of Kumar et al. [19], who investigated the effects of a central impervious core and drainage arrangement on seepage behaviors within earth dams. From their findings, a consequential observation emerged, wherein these alterations led to a discernible reduction in the phreatic line, illustrating the intricate relationship between the geometrical attributes of dam components and the intricate behavior of seepage within earth dams. The central impervious core functions as a barrier to mitigate seepage [20], while the downstream filter is tasked with controlled regulation and conveyance of seepage [21]. Darcy’s pioneering experiments on fluid flow through porous media laid the groundwork for comprehending fluid mechanics and hydrogeology [22]. Darcy’s investigations unveiled a fundamental relationship linking flow velocity, head loss, and the length of the flow path [23]. The observed direct proportionality between flow velocity and head loss elucidates the energy loss sustained by the fluid as it traverses the porous medium. These insights underpin Darcy’s law, an indispensable cornerstone across multiple disciplines that guides the study and practical application of fluid flow in porous media [24].
In the context of embankment dams, the role of the toe drain—a supplementary structure to manage seepage—merits attention. However, comprehensive information regarding the influence of toe drains in tandem with varied drawdown rates remains scarce. While embankment dams endure long-term steady-state conditions, instances requiring rapid drawdown can nullify the stabilizing effects of such states, potentially leading to failure. Yet a dearth of comprehensive insights persists concerning the impact of diverse drawdown rates on the seepage dynamics and stability of embankment dams, particularly when coupled with variations in embankment slope and the presence of a toe drain. The intricate interaction between these multifaceted aspects has not been comprehensively explored, leaving a critical gap in our understanding of how these factors synergistically influence the performance and stability of embankment structures under dynamic drawdown scenarios. As a result, there is an urgent need for innovative research projects that explore the complexity of this phenomenon and reveal the numerous interdependencies that influence how embankments react to situations of rapid drawdown [25]. A comprehensive investigation into the combined effects of geometric features, embankment filters, and rapid drawdown is not only pivotal for advancing state-of-the-art geotechnical engineering but also holds profound implications for ensuring the safety, resilience, and sustainability of embankment structures worldwide. By embarking on such groundbreaking research, the engineering community can gain unprecedented insights into mitigating potential hazards and devising more informed design strategies, thus forging a path toward more reliable and optimized embankment solutions for future endeavors. To be more specific, the domain of embankment dams, encompassing seepage and slope stability analyses, has seen extensive exploration due to the intricate nature of the underlying mechanisms. Nevertheless, there remain uncharted territories within this realm. One particularly challenging area is the optimization of dam designs, which poses a formidable task due to the myriad of factors that demand consideration. These factors include hydraulic conductivity, slope configurations, toe drain characteristics, and flow conditions. It is worth noting that existing research often examines these factors in isolation, limiting the scope of comprehensive dam design optimization. This study represents a groundbreaking approach by concurrently examining the combined impacts of these factors, specifically focusing on embankment slopes, toe drain configurations, and diverse drawdown conditions. This holistic methodology signifies a significant leap forward in the field, mirroring the intricate realities faced by dam designers and engineers.
This research extensively explored the complex interaction between seepage occurrence and slope stability, investigating the cumulative impacts of diverse embankment slope arrangements, toe drain configurations, and varying drawdown scenarios. The study employed a combination of physical and analytical models to examine seepage discharge. Statistical tools such as analysis of variance (ANOVA) and correlation analysis were utilized. The study encompassed a range of models representing embankment slopes operating within steady-state conditions. These models were contrasted with analytical solutions derived from established methodologies, including the Dupuit formulation, Casagrande equation, Pavlovsky’s expression, and the Schaffernak formula.
2. Materials and Methods
2.1. Soil Material Characterization
Before starting to build physical models for seepage discharge analysis and the subsequent development of numerical models, it was decided to conduct a laboratory examination of soil properties to learn more about the characteristics of the soil. The results of the soil investigation were particularly significant because they were essential inputs for the numerical models, highlighting their significance in the larger research project. The procedure began with several crucial tests that included not only determining the natural moisture content but also carefully analyzing the contents of sieves to reveal the precise pattern of particle size distribution. Important components of plasticity characterization and liquid and plastic limit tests provided complex insights into the behavior of the soil. Permeability tests, which shed light on the soil’s innate ability to convey water, uncovered deeper insights. The common compaction test, which was equally important, contributed to a comprehensive understanding of the soil’s compaction ability. Consolidation tests, a challenging field, revealed the soil’s settlement behavior under various loads. Direct shear testing was used to examine the shear strength domain, providing still another level of information. The crystalline forms encasing the very center and periphery of the earth dam models were examined using rigorous X-ray diffraction (XRD) as we delved deeper into the maze of the soil’s composition. The powerful Bruker D8 machine opened the door for an excellent XRD study by utilizing the complex Bragg–Brentano technique. This groundbreaking strategy, at the forefront of scientific inquiry, provided the tools to identify and decipher the subtleties of the crystalline phases dwelling within the soil, illuminating its complex mineralogical makeup. The result of this extensive battery of geotechnical tests, which was harmoniously intertwined with the complex XRD analysis, served as the cornerstone for the painstaking and accurate construction of the earth dam prototypes inside the sacred walls of the hydraulics laboratory.
2.2. Study Design
The research simultaneously investigated various slope configurations for embankments, different designs for toe drains, and multiple scenarios for drawdown. It employed a diverse approach, combining numerical simulations, mathematical models, and laboratory-scale physical replicas. In the case of numerical models, models 1 to 12 were thoroughly examined without a central core presence. Moreover, the investigation included an analysis of supplementary models (models 13, 14, 15, and 16) that featured an impermeable clay core. The coordination of this experimental setup, supported by innovative seepage control methods, provided a unique and comprehensive way to explore numerous dam configurations. This effort yielded invaluable insights to enhance the safety and efficiency of earthen dam design and construction. The study was dedicated to improving research accuracy and reliability. To provide greater specificity, the study involved eight unique physical models, each replicated three times, resulting in a total of 24 physical experiments. Simultaneously, 16 numerical models were developed, each featuring four different scenarios: steady-state conditions, instantaneous drawdown, a 10-day drawdown, and a gradual drawdown rate of 1 m per day. This approach resulted in the creation of 64 numerical models.
2.2.1. Lab-Scale Models
To investigate the intricate seepage characteristics of an earthen dam featuring an impermeable foundation, a crafted scaled-down experimental model took center stage. Employing a scale factor of 1/100, the dam’s dimensions were adjusted to ensure an accurate representation. Within a spacious hydraulic flume, eight earth dam models were expertly fashioned, a strategic choice aimed at minimizing any potential measurement fluctuations during the rigorous discharge analysis. To ensure precise compaction, the Proctor penetrometer was adroitly utilized, acknowledging the pronounced impact of scaling effects on the ultimate outcomes. A meticulous approach was adopted to track the elusive phreatic line within the experimental models. Fluorescent dye endowed with radiation-emitting properties was deftly harnessed for this purpose. The resulting phreatic line, a vibrant and vivid green light, was masterfully captured onto transparent polymer sheets and transferred to A3-sized graph paper. This set of coordinates was then subjected to a rigorous comparison with data emanating from SEEP/W software, subsequently providing robust validation of the experimental insights. A comprehensive exploration of the seepage characteristics was undertaken, encompassing a spectrum of dam configurations that encompassed both homogeneous earth dams and those that featured central clay cores. Quantification of seepage discharge was achieved through precise volumetric discharge measurements, adapted to accommodate the intricacies of the two-dimensional earth dam models. Furthermore, the investigative scope of the study was extended to ascertain the effects of changes in the longitudinal slope and fluid viscosity, gauging their individual impacts on the phenomenon of seepage discharge. Rigorous measurements were obtained through the application of a rotational rheometer, securing adept control over the fluid parameters. Innovative strategies to control seepage were introduced, among them the ingenious development of a horizontal drainage filter that was seamlessly integrated within the dam structure. The toe drain installation process downstream of the embankment began with proper planning, considering the specific location and drain specifications tailored to the embankment material and drainage requirements. A trench was excavated at the base of the embankment model, thoughtfully designed to align with the established criteria and facilitate optimal water flow. To promote effective filtration, a layer of coarse aggregate was strategically placed at the trench’s base. A perforated drainage pipe was then positioned atop the aggregate layer, ensuring a consistent slope to facilitate efficient water collection. The drainage pipe was securely covered with additional aggregate, and the trench was carefully backfilled using compacted soil or backfill material. A well-constructed outlet was established for the toe drain system, ensuring the safe discharge of seepage water.
2.2.2. Numerical Models
To attain precise outcomes while optimizing computational efficiency, a methodical strategy was employed to select a finite element mesh size of 0.1 m. This determination was arrived at after conducting a series of iterative computations, exploring a range of mesh sizes. This mesh selection approach was aimed at achieving a delicate equilibrium between the quality of analysis and computational speed. Employing an advanced finite element methodology, the investigation aimed to scrutinize the potential implications of swift reservoir drawdown on embankment slope stability, accounting for diverse soil parameters. Varied drawdown scenarios were examined, encompassing long-term steady-state conditions, instantaneous drawdown, a 10-day drawdown, and a drawdown rate of 1 m per day. The analytical exploration was initiated with a thorough evaluation of the embankment’s performance under the conditions of long-term equilibrium. This was sequentially followed by an assessment of the response during rapid drawdown events (instantaneous, 10-day, and 1 m per day rates). Notably, the scenario of instantaneous drawdown entailed the assumption of immediate drainage of the dam or reservoir water, representing an extreme or worst-case circumstance. Simultaneously, comprehensive seepage analysis was concurrently carried out alongside the investigations into slope stability. The study harnessed the use of GeoStudio’s 2023 (23.1.0.520) sub-software components, namely SEEP/W and SLOPE/W. SEEP/W, grounded in the finite element method (FEM), was effectively utilized for two-dimensional seepage analysis across specific sections. To replicate the embankment’s behavior during drawdown, the analytical procedure commenced with the establishment of a long-term equilibrium state using GeoStudio’s steady-state analysis methodology. Subsequent to this foundational state, transient flow analysis was undertaken to capture the dynamics of the drawdown process. This transient flow analysis was intricately factored into the pore pressure generated by seepage during the long-term equilibrium analysis. Throughout this transient seepage analysis, the temporal fluctuations in water levels during the drawdown phase was artfully represented through a linear function employed as a boundary condition at the upstream embankment face.
2.3. General Cases Investigated in the Numerical Modeling
To elaborate further, the slope stability analysis was conducted utilizing the esteemed Morgenstern–Price method, which adheres to the overarching principles of the general limit equilibrium (GLE). This rigorous methodology entailed distinct analyses for each of the slope stability scenarios, yielding a comprehensive investigation. In essence, the study encompassed four principal groups of cases. Firstly, an examination of seepage and slope stability was undertaken for embankments devoid of drains, alongside counterparts equipped with 5 m, 15 m, and 30 m drains, all accentuated by a 1:1 (vertical-to-horizontal) slope configuration. The second group of cases encompassed a similar investigation, albeit with a 1:2 slope. The third group examined the seepage and slope stability for embankments with a 1:4 slope configuration. Lastly, the fourth group probed into the intricate interplay of seepage and slope stability for embankments with a central core while adhering to a 1:2 slope (Table 1). The implementation of the toe drain within GeoStudio software was successfully achieved through the utilization of boundary conditions. This involved a systematic approach to define and integrate the necessary boundary conditions into the model. In all the models, a consistent top width of 20 m and initial water level of 20 m were consistently maintained.

Table 1.
The cases investigated in the study.
To provide greater detail, slope stability analysis was conducted using the SLOPE/W module within GeoStudio software. Each analysis was defined individually, and the Morgenstern–Price method [26] was applied within the framework of the general limit equilibrium (GLE) approach [27]. In this general limit equilibrium formulation, two distinct equations for the factor of safety are employed:
- The first equation computes the factor of safety with respect to the moment equilibrium (Fm).
- The second equation calculates the factor of safety considering the horizontal force equilibrium (Ff).
It is worth noting that the utilization of these two equations in factor of safety computations was initially introduced by Spencer [28], as documented in Equations (1) and (2). Spencer’s method can be viewed as an extended and modified version of Bishop’s simplified method. In Bishop’s simplified method, the factor of safety (F) is determined as the ratio of the total available strength (S) along the slip surface to the total mobilized shear strength (Sm) [29], as summarized in Equation (1).
Furthermore, within Spencer’s analytical framework, the resultant of the pair of interslice forces (Q) is determined through the application of Equation (2). This equation plays a critical role in the calculation of forces and stability considerations within the slope stability analysis. It is a fundamental component of the method developed by Spencer, which extends and refines Bishop’s simplified approach. The calculation of Q involves the evaluation of various parameters and force interactions along the slip surface, contributing to a comprehensive assessment of slope stability. Spencer’s method represents a valuable refinement of classical slope stability analysis techniques, allowing for a more detailed and accurate examination of the factors influencing the stability of slopes and embankments.
In this context, a set of crucial parameters plays distinct roles: “b” and “h” signify the width and mean height of the slice, respectively, while “α” represents the slope angle of the base of the slice. The pivotal factor of safety denoted as “F,” the angle “θ” characterizing the resultant slope of a pair of interslice forces, and the pore-pressure coefficient “ru” all contribute to the comprehensive analysis. Additionally, the bulk density “ɣ,” the height of the embankment “H”, the angle of shearing resistance with respect to effective stress “ø,′” and the cohesion with respect to effective stress “c′” play essential roles in this geotechnical assessment.
The Morgenstern–Price method, as applied in this study, is a versatile technique grounded in the principles of limit equilibrium, ensuring the equilibrium of forces and moments acting on individual blocks. This method involves the systematic partitioning of the soil above the slip surface into discrete blocks using dividing planes [30]. Moreover, within the framework of general limit equilibrium, the calculation of interslice shear forces is addressed through an equation initially introduced by Morgenstern and Price [31], exemplified in Equation (3). This equation serves as a fundamental component of the analytical approach, enabling a comprehensive examination of slope stability by considering the equilibrium of forces and moments acting on these divided blocks.
In this context, there is a mathematical representation wherein “f(x)” denotes a function, and “λ” represents the percentage of this function in decimal form. Additionally, we consider “E” as the interslice normal force, and “X” represents the interslice shear force. This formulation enables personnel to express and evaluate the role of the function within the context of interslice forces, allowing for quantitative analysis of their interplay.
Figure 1 encapsulates a comprehensive portrayal of the overall outlook or configuration of the embankments scrutinized in the study. This visual representation offers a concise and informative overview of the key attributes and features characterizing the investigated embankments.
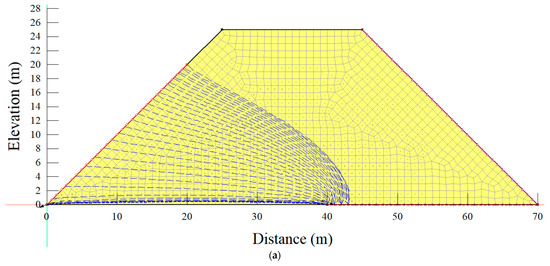
Figure 1.
The general outlook of the investigated embankments (a) 1:1 (V:H) slope, (b) 1:2 (V:H) slope, (c) 1:4 (V:H) slope, and (d) 1:2 (V:H) slope with a core.
The fundamental characteristics of the soil underwent thorough testing, and the outcomes are summarized in Table 2. These critical findings were subsequently utilized as essential input parameters in the SLOPE/W and SEEP/W modules within the GeoStudio 2018 software suite. By integrating these data into the analysis platforms, the research team sought to unravel the intricate behaviors and interactions governing the slope stability and seepage phenomena, thereby advancing the frontiers of geotechnical understanding and paving the way for more robust engineering solutions.

Table 2.
Soil properties.
Figure 2 provides a comprehensive overview of the volumetric water content and hydraulic conductivity functions associated with the homogeneous embankments examined in this study. These functions have been precisely generated, taking into account the specific material characteristics attributed to the embankment.
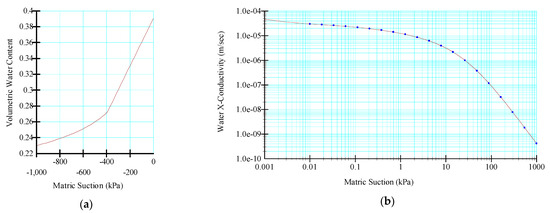
Figure 2.
Functions of (a) volumetric water content, and (b) hydraulic conductivity.
2.4. Validation of Seepage Discharge Calculations
In the pursuit of validating the seepage discharge calculations, the study’s authors adroitly utilized an assortment of analytical methodologies, including the Dupuit formulation, Casagrande equation, Pavlovsky’s expression, and Schaffernak formula. These results were carefully cross-referenced against both experimental and computational models, ensuring a robust verification process. With attention to adhering to stringent input prerequisites and a finely orchestrated numerical modeling procedure, an exhaustive investigation into the intricate interactions of seepage and slope stability within the realm of earth dam models was unequivocally ensured.
2.5. Statistical Methods
2.5.1. Investigation of the Relationship between Seepage and Stability Parameters
Pearson correlation analysis, a statistical tool, stands as a paramount method for quantifying the magnitude and direction of the linear association between continuous variables. This powerful analysis method illuminates the extent to which changes in one variable proportionally parallel changes in another, yielding profound insights into their interconnection. The correlation coefficient, symbolized as “r,” assumes values within the range of −1 to +1, where a positive value unveils a positive correlation, signifying that an increase in one variable coincides with a concomitant rise in the other. Conversely, a negative value reveals a negative correlation, indicating that an increase in one variable corresponds to a decline in the other. A correlation coefficient of 0 signifies an absence of any linear relationship between the variables.
2.5.2. Variance Analysis
This statistical approach entails a rigorous examination of the variance levels present within the distinct groups by carefully extracting representative samples from each of them. By subjecting the data to ANOVA, the study sought to elucidate the extent to which the observed variations between groups could be attributed to actual differences in the population means, rather than mere chance occurrence. This analysis aids in drawing well-founded conclusions about the significance of group disparities and plays a crucial role in discerning meaningful patterns and trends amidst the data’s complexity. By adopting such a robust statistical methodology, the research endeavored to foster greater rigor and credibility in its findings, facilitating a deeper understanding of the underlying phenomena at play.
3. Results
3.1. Seepage Analysis from 1:1 (V:H) Slope
As previously elucidated, the initial phase of the modeling endeavor encompassed a comprehensive seepage analysis conducted under the auspices of a 1:1 (vertical to horizontal) slope configuration. This analysis was performed for both steady-state and transient scenarios, specifically addressing instantaneous conditions as well as time frames of 10 days and 1 m per day. In the context of the 1:1 (vertical to horizontal) embankment slope, diverse embankment models were examined, thereby comprising the following variants: the absence of any drainage system, a 5 m drainage implementation, a 15 m drainage implementation, and finally, a 30 m drainage implementation.
3.1.1. Without a Drain
Figure 3 presents a summary of the water conductivity in the horizontal direction vs. matric suction. It should be noted that the concept of matric suction emerges as a pivotal soil parameter, wielding a profound influence over the intricate behaviors of unsaturated soils, encompassing shear strength and permeability characteristics. This fundamental property, arising from the dynamic interplay between pore water and the solid matrix, imparts a remarkable ability to unsaturated soils, enabling them to retain moisture against the forces of gravity, thereby defying conventionally anticipated patterns of flow and drainage. By virtue of matric suction, unsaturated soils attain an exquisite balance between attractive and repulsive forces acting within their pore spaces, thereby culminating in a fine equilibrium that governs their response to external stresses and loads. Moreover, the intricate interplay between matric suction and soil particle interaction underlies the intriguing phenomenon of capillary rise and its corollary, capillary fall, wherein the ascendancy and subsidence of liquid in narrow capillaries counterintuitively transgress the conventional gravitational flow regime.
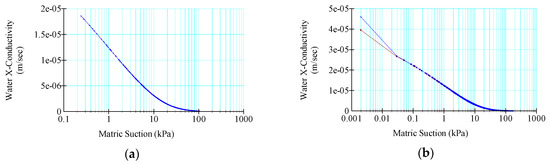
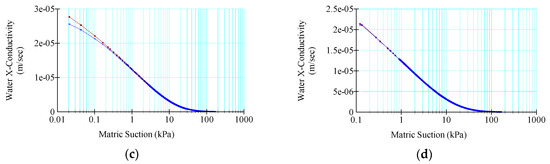
Figure 3.
Water conductivity and matric suction without a drain under (a) steady-state, (b) instantaneous, (c) 10-day, and (d) 1 m per day drawdown.
Table 3 presents a condensed overview of the findings obtained from the seepage analysis conducted with a 1:1 (horizontal to vertical) ratio, excluding the implementation of any drainage system. From Table 3, it can be observed that under long-term steady-state conditions, the 1:1 (horizontal to vertical) sloped embankment yielded a water flow rate of 1.35 × 10−5 m3/s at the upstream side and −1.60 × 10−5 m3/s at the downstream side. However, when the embankment experienced a drawdown rate of 1 m per day, a water flow rate of −1.1 × 10−8 m3/s was obtained at the upstream face and 9.73 × 10−7 m3/s was retrieved at the downstream base of the embankment. From the water mass flux data, it becomes evident that under steady-state conditions, a water mass flux of 0.022 kg/s/m2 was discerned at the upstream face of the embankment. Notably, a larger water mass flux of 0.045 kg/s/m2 was observed at the downstream toe of the embankment. Interestingly, when the embankment was exposed to a drawdown rate of 1 m per day, the water mass flux escalated. Specifically, a heightened value of 2.05 × 10−5 kg/s/m2 was extracted from the upstream face, while the downstream toe exhibited a water mass flux of 0.012 kg/s/m2.

Table 3.
Summary of the results from the seepage analysis with 1:1 (H:V) without a drain.
3.1.2. With a 30 m Drain
Water conductivity and matric suction are of paramount importance in the analysis of seepage within embankment dams. These factors play a pivotal role in understanding the flow of water through the dam structure and its surrounding foundation. Water conductivity provides insights into the ease with which water can move through the soil and rock, affecting potential pathways for seepage. Higher conductivity implies greater permeability, which could lead to more significant seepage concerns. Matric suction, on the other hand, reflects the tension in the soil due to moisture content. As matric suction increases, the soil becomes drier, reducing its ability to transmit water and altering seepage patterns. Monitoring changes in water conductivity and matric suction allows engineers to anticipate variations in seepage rates, identify potential seepage zones, and implement necessary measures to prevent excessive water flow. This comprehensive understanding aids in ensuring the stability and integrity of embankment dams, ultimately contributing to their long-term safety and performance. The graphical representation in Figure 4 offers a vivid portrayal of the matric suction dynamics, emanating from a steady-state context with an approximate measure of 0.0012 kPa, in stark contrast to the matric suction invoked by an instantaneous drawdown, enunciated at a notable level of approximately 0.048 kPa. In a parallel vein, the matric suction resulting from the 10-day drawdown rate was unveiled with a magnitude of approximately 0.07 kPa, whereas its counterpart stemming from a drawdown rate of one meter per day was unveiled at a discernible magnitude of approximately 0.031 kPa, as discerned from the insights gleaned from Figure 4. Furthermore, within the very contours of Figure 4, the graphical depiction that entwined water conductivity and matric suction adorned itself with the compelling form of a descending exponential curve. This distinctive curve, characterized by its downward trajectory, stands as a symbol of the intricate reciprocity governing water conductivity and matric suction—an elucidation that heralds an augmentation in one parameter accompanied by a propensity for diminution in the other. This finding articulated a profound inverse relationship between the two variables, wherein the augmentation of one corresponds to the attenuation of the other.
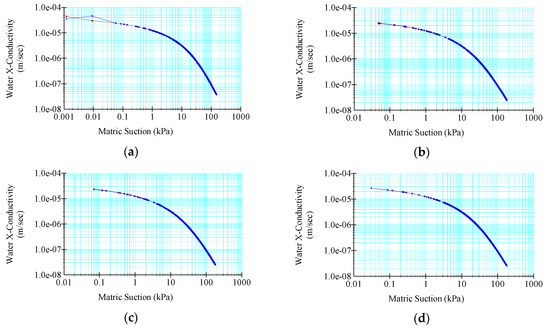
Figure 4.
Water conductivity and matric suction with a 30 m drain under (a) steady-state, (b) instantaneous, (c) 10-day, and (d) 1 m per day drawdown.
The modeling procedure also considered the potential impact of the toe drain on the overall seepage behavior of the embankment, especially when encountering both steady-state and transient flow circumstances within a 1:1 (horizontal to vertical) slope. As indicated in Table 4, it became evident that over extended durations of steady state, the embankment demonstrated a water flow rate of 1.73 × 10−7 m3/s at the upstream side, along with a minor discharge of −5.10 × 10−11 m3/s at the downstream side. In contrast, under the condition of a drawdown rate of 1 m per day, the embankment exhibited a notably diminished water flow rate of 7.78 × 10−23 m3/s at the upstream face, while similarly minimal outflow of −1.70 × 10−11 m3/s was observed at the downstream base. Under steady-state conditions, an observable water mass flux of 0.03384 kg/s/m2 was noted at the embankment’s upstream face. Meanwhile, a water mass flux of 1.13 × 10−6 kg/s/m2 was identified at the downstream toe, indicating intensified water movement in this specific area. During the embankment’s exposure to a drawdown rate of 1 m per day, a water mass flux of 1.79 × 10−5 kg/s/m2 was extracted from the upstream face, whereas the downstream toe showcased a water mass flux of 3.65 × 10−7 kg/s/m2.

Table 4.
Summary of the results from the seepage analysis with 1:1 (H:V) and 30 m drain.
3.2. Seepage Analysis from 1:2 (H:V) Slope
3.2.1. Without a Drain
The examination also considered the potential impact of the toe drain on the overall seepage behavior of the embankment, particularly when dealing with both steady-state and transient flow circumstances within a 1:2 (horizontal to vertical) embankment slope. As showcased in Table 5, it became apparent that during prolonged periods of equilibrium, the embankment exhibited a water flow rate of 1.24 × 10−5 m3/s at the upper part of the upstream side and 6.56 × 10−7 m3/s at the midpoint of the upstream face, along with a minor outflow of −5.10 × 10−6 m3/s at the downstream side. Conversely, in the context of a 1 m per day drawdown rate, the embankment displayed a notably reduced water flow rate of 0 m3/s at the upper part of the upstream face, −5.40 × 10−9 m3/s at the midpoint of the upstream face, and a similarly modest outflow of −1.70 × 10−11 m3/s at the downstream base. Also, under conditions of equilibrium, a noticeable water mass flux of 0.02 kg/s/m2 was observed at the upper part of the embankment’s upstream face and 0.0012 kg/s/m2 at the midpoint of the upstream face. Impressively, a relatively greater water mass flux of 0.023 kg/s/m2 was identified at the downstream toe, indicating heightened water movement in that specific region. Significantly, the scenario shifted when the embankment experienced a drawdown rate of 1 m per day. The water mass flux encountered a substantial surge, with an increased value of 1.28 × 10−5 kg/s/m2 observed at the upper part of the upstream face and 1.06 × 10−5 kg/s/m2 at the midpoint of the upstream face. Concurrently, the downstream toe showcased a water mass flux of 0.02 kg/s/m2. These findings underscored the embankment’s sensitivity to variations in flow conditions, illustrating how such alterations can lead to noteworthy adjustments in the flux of water masses across distinct sections of the embankment. In a nutshell, Table 5 succinctly summarizes the outcomes derived from the seepage investigation carried out employing a 1:2 (horizontal to vertical) ratio and without the presence of a drain.

Table 5.
Summary of the results from the seepage analysis with 1:2 (H:V) without a drain.
3.2.2. With a 30 m Drain
Table 6 provides the outcomes stemming from the examination of a 1:2 (horizontal to vertical) embankment slope integrated with a 30 m drain size. As elucidated in Table 6, it became evident that over extended periods of equilibrium, the embankment demonstrated a water flow rate of 1.63 × 10−5 m3/s at the upper segment of the upstream side and 9.64 × 10−7 m3/s at the midpoint of the upstream face, coupled with a negligible outflow of 2.07 × 10−14 m3/s at the downstream side. In a contrasting scenario, under the circumstances of a drawdown rate of 1 m per day, the embankment showcased a considerably diminished water flow rate of 1.57 × 10−23 m3/s at the upper section of the upstream face, −4.70 × 10−9 m3/s at the midpoint of the upstream face, and a comparably modest outflow of 2.19 × 10−15 m3/s at the downstream base.

Table 6.
Summary of the results from the seepage analysis with 1:2 (H:V) and 30 m drain.
3.3. Seepage Analysis from 1:4 (H:V) Slope
3.3.1. Without a Drain
Table 7 presents a concise overview of the findings obtained from the 1:4 (horizontal to vertical) embankment slope in the absence of a toe drain. A discernible water mass flux of 0.012 kg per second per square meter (kg/s/m2) was noted at the upper region of the embankment’s upstream face and 8.66 × 10−5 kg/s/m2 at the midpoint of the upstream face. Remarkably, a comparatively higher water mass flux of 0.0115 kg/s/m2 was detected at the downstream toe, indicating elevated water movement within that specific area. Importantly, the scenario altered when the embankment encountered a drawdown rate of 1 m per day. The water mass flux underwent a substantial increase, with an elevated measurement of 6.90 × 10−6 kg/s/m2 observed at the upper portion of the upstream face and 9.74 × 10−6 kg/s/m2 at the midpoint of the upstream face. Concurrently, the downstream toe showcased a water mass flux of 0.012 kg/s/m2.

Table 7.
Summary of the results from the seepage analysis with 1:4 (H:V) without a drain.
3.3.2. With a 30 m Drain
Table 8 provides an extensive summary of the results arising from the 1:4 (horizontal to vertical) embankment slope configuration, incorporating a toe drain dimension of 30 m. It became apparent that a discernible water mass flux of 0.014 kg per second per square meter (kg/s/m2) was derived from the upper portion of the embankment’s upstream face, under conditions of equilibrium. Additionally, a measure of 0.0001 kg/s/m2 was observed at the midpoint of the upstream face. Furthermore, a markedly lower water mass flux of 2.63 × 10−16 kg/s/m2 was identified at the downstream toe. When the embankment encountered a drawdown rate of 1 m per day, the water mass flux experienced a significant upsurge. Specifically, a reading of 6.89 × 10−6 kg/s/m2 was noted at the upper region of the upstream face, while a value of 8.20 × 10−6 kg/s/m2 was registered at the midpoint of the upstream face. Simultaneously, the downstream toe exhibited a notably constrained water mass flux of 1.83 × 10−16 kg/s/m2.

Table 8.
Summary of the results from the seepage analysis with 1:4 (H:V) and 30 m drain.
3.4. Seepage Analysis from 1:2 (H:V) Slope and Central Core
3.4.1. Without a Drain
The examination also explored the influence of integrating a central core and toe drain on the overall seepage behavior of the embankment, a critical consideration for both steady-state and transient flow scenarios within a 1:2 (horizontal to vertical) embankment slope. Table 9 succinctly presents the seepage analysis results, excluding the toe drain factor. The data showed that under steady-state conditions, the embankment exhibited a water flow rate of 9.41 × 10−7 m3/s at the upper segment of the upstream side, 61.59 × 10−8 m3/s at the midpoint of the upstream face, and an outflow of 2.14 × 10−6 m3/s at the downstream side. Conversely, with a drawdown rate of 1 m per day, the water flow rate reduced significantly to −1.20 × 10−22 m3/s at the upper portion of the upstream face, accompanied by 2.20 × 10−8 m3/s at the midpoint of the upstream face and an outflow of 2.06 × 10−6 m3/s at the downstream base. Furthermore, under equilibrium conditions, the water mass flux was 0.001 kg per second per square meter (kg/s/m2) at the upper region of the embankment’s upstream face and 2.98 × 10−5 kg/s/m2 at the midpoint of the upstream face, while the downstream toe exhibited a heightened water mass flux of 0.0079 kg/s/m2, indicating increased water movement in that specific zone. Notably, these dynamics shifted when the embankment encountered a drawdown rate of 1 m per day, with water mass flux values of 5.29 × 10−5 kg/s/m2 at the upper part of the upstream face, 3.95 × 10−5 kg/s/m2 at the midpoint of the upstream face, and 0.0065 kg/s/m2 at the downstream toe.

Table 9.
Summary of the results from the seepage analysis with 1:2 (H:V), without a drain, but with a central core.
3.4.2. With a 30 m Drain
Table 10 presents an extensive overview of the results stemming from the amalgamation of a central core and 30 m toe drain. The analysis revealed a conspicuous water mass flux of 0.001 kg per second per square meter (kg/s/m2) at the upper region of the embankment’s upstream face. This measure stood in contrast to the reading of 2.98 × 10−5 kg/s/m2 observed at the midpoint of the upstream face, denoting a lower yet still noticeable value. Interestingly, the downstream toe displayed a significantly reduced water mass flux, quantified at 1.70 × 10−11 kg/s/m2. A critical transformation occurred as the embankment underwent a drawdown rate of 1 m per day. The water mass flux experienced a marked escalation, with a heightened reading of 5.29 × 10−5 kg/s/m2 observed at the upper portion of the upstream face. This reading was in contrast to the measurement of 3.95 × 10−5 kg/s/m2 taken at the midpoint of the upstream face, subtly altered due to the imposed drawdown condition. Concurrently, the downstream toe maintained a water mass flux of 1.66 × 10−11 kg/s/m2, indicative of its consistent albeit minor influence in the revised seepage dynamics. In essence, the nuanced variations in water mass flux underscored the intricate interplay between structural integration, positional influence, and hydraulic behavior. The data highlighted how manipulating these factors can orchestrate significant shifts in the complex tapestry of seepage patterns along the embankment.

Table 10.
Summary of the results from the seepage analysis with 1:2 (H:V), 30 m drain, and central core.
3.5. Slope stability Analysis
In a comprehensive exploration of the depicted embankments (Figure 5), it became apparent that modifications in the incline of the embankment wielded a more profound sway over the factor of safety, surpassing the impact attributed to the presence of the toe drain. This observation underscored the pivotal role that slope adjustments play in influencing the overall stability of the embankment. Moreover, an evident pattern arose, unveiling that heightened rates of drawdown accentuated the complexities associated with reinstating the embankment’s equilibrium. This phenomenon can be attributed to the intricate interplay between the rapid decrease in water levels and the embankment’s ability to adapt to these abrupt changes. Adding to the intricate narrative, the thorough analysis brought into focus the behavior of the 1:1 (vertical to horizontal) embankment slope model. When subjected to scenarios of swift drawdown, the factor of safety values consistently dipped below the critical threshold of 1 across all configurations within the 1:1 (V:H) embankment slope model. This intriguing discovery further underscored the challenges that such conditions pose to the embankment’s overall stability and the importance of considering both slope adjustments and drawdown rates when assessing and designing embankment systems.
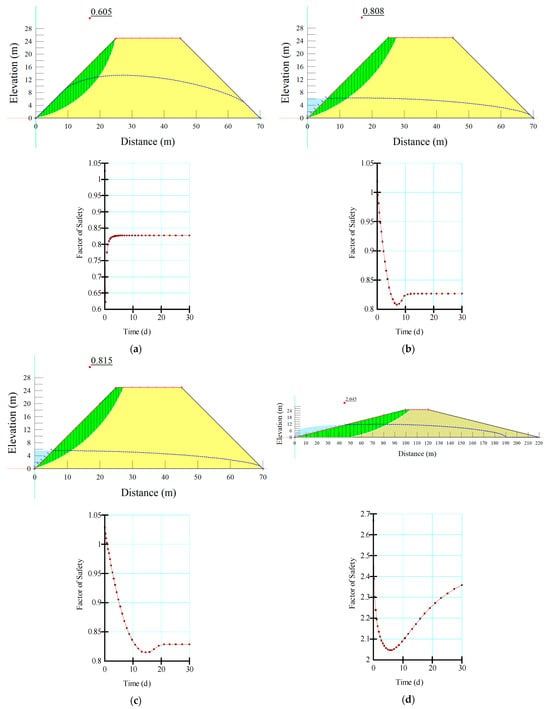
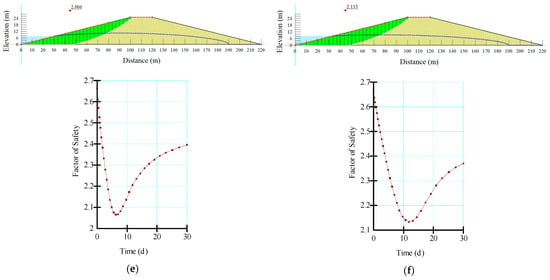
Figure 5.
Trends in the factor of safety values for (a) 1:1 (V:H) without toe drain and instantaneous drawdown (b) 1:1 (V:H) without toe drain and 10-day drawdown (c) 1:1 (V:H) without toe drain and 1 m per day drawdown (d) 1:4 (V:H) with 30 m toe drain and instantaneous drawdown (e) 1:4 (V:H) with 30 m toe drain and 10-day drawdown (f) 1:4 (V:H) with 30 m toe drain and 1 m per day drawdown.
Table 11 provides a concise summary of the factor of safety values derived from a meticulous investigation of various scenarios within this study. The combinations of different parameters resulted in a wide range of outcomes. For example, in scenarios like a 1:1 embankment slope without a toe drain and instantaneous drawdown, the factor of safety values varied from 0.62 to 1.03. Similarly, different configurations, such as a 1:2 embankment slope without a toe drain under instantaneous drawdown, led to the factor of safety values ranging from 1.22 to 1.57. Additionally, incorporating elements like a 30 m toe drain and a 1 m per day drawdown rate influenced these values, with extremes recorded from 1.337 to 2.21, shedding light on embankment stability under diverse conditions and configurations.

Table 11.
Summary of the factor of safety values.
3.6. Analysis of Variance
3.6.1. Matric Suction
Table 12 offers a comprehensive summation of the outcomes derived from the ANOVA analysis of matric suction data, gathered across distinct scenarios encompassing steady-state conditions and transient flows, each coupled with varying embankment slopes and drain conditions. With heightened specificity, each model investigated within the study underwent exposure to the aforementioned conditions, allowing for the examination of the resultant datasets. Subsequently, these datasets were subjected to analysis of variance, scrutinizing the potential presence of notable distinctions amongst the various scenarios. It is pertinent to note that an alpha value of 0.05 served as the benchmark against which the derived p-values were juxtaposed, enabling the assessment of the significance of observed distinctions. Notably, the p-values across all scenarios were consistently below 0.05, decisively signifying the presence of substantial disparities within the datasets.

Table 12.
Summary of the ANOVA results from matric suction.
3.6.2. Water Conductivity
Table 13 provides an inclusive summary of the results stemming from the ANOVA analysis conducted on water conductivity data. These data were collected across diverse scenarios encompassing steady-state conditions, instantaneous drawdown, 10-day drawdown, and a drawdown rate of 1 m per day. These scenarios were executed alongside varying embankment slopes and drain conditions. With refined precision, each model scrutinized in this study was exposed to these distinctive conditions, facilitating an exploration of the resultant datasets. Subsequently, these datasets underwent analysis of variance, aiming to discern significant differentiations among the various scenarios. It is noteworthy that an alpha value of 0.05 was employed as a baseline against which the computed p-values were assessed, thereby enabling the evaluation of the statistical significance of the observed variations. Importantly, across all scenarios, the computed p-values consistently registered below the 0.05 threshold, unequivocally indicating the presence of considerable dissimilarities within the datasets.

Table 13.
Summary of the ANOVA results from water conductivity.
3.6.3. Factor of Safety
Table 14 provides a comprehensive synthesis of the results emanating from the ANOVA analysis applied to the factor of safety data. This analysis encompassed a spectrum of scenarios, ranging from steady-state conditions to instantaneous drawdown, 10-day drawdown, and a drawdown rate of 1 m per day. These scenarios were further nuanced by diverse embankment slopes and drainage conditions. With intricate precision, each model subjected to investigation underwent exposure to this array of conditions, enabling an exhaustive examination of the ensuing datasets. Subsequent to this, the datasets were subjected to a rigorous analysis of variance, probing for discernible differentiations among the diverse scenarios. It is worth noting that a prespecified alpha value of 0.05 was deployed as a statistical threshold against which the derived p-values were assessed. This process facilitated the determination of the significance of the observed disparities. Importantly, it was evident that across all scenarios, the p-values consistently fell below the 0.05 threshold, thus affirming the compelling presence of substantive distinctions within the datasets.

Table 14.
Summary of the ANOVA results from the factor of safety values.
3.6.4. Factor of Safety for Models with a Central Core
In this phase of the research, the factor of safety datasets obtained from the model’s instantaneous drawdown scenarios were subjected to ANOVA analysis. This encompassed variations such as the presence of a central core without a toe drain, as well as configurations involving central cores paired with 5 m, 15 m, and 30 m drain sizes. Comparable investigations were also performed for the 10-day drawdown and 1 m per day drawdown rate. As demonstrated in Table 15, it became evident that all computed p-values were below the threshold of 0.05, unequivocally indicating a notable and statistically significant difference across the analyzed datasets.

Table 15.
Summary of the ANOVA results from models with a central core.
3.7. Seepage Discharge Analysis
An examination of seepage discharge was additionally carried out, involving a comparison between the physical models and numerical simulations. Within this phase of the study, a total of eight physical models were utilized. Figure 6 presents a concise overview of the outcomes stemming from the seepage discharge analysis. Notably, the analysis revealed that the greatest seepage discharge was observed in model 1, characterized by a 1:1 (vertical to horizontal) embankment slope without a toe drain.
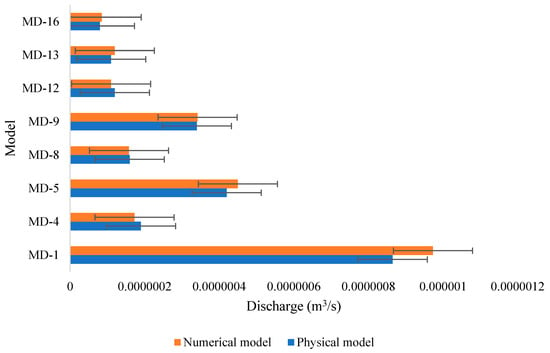
Figure 6.
Seepage discharge analysis.
Figure 7 showcases the outcomes derived from a comprehensive comparison between the computational models and analytical solutions. These models pertained to various embankment slopes operating under steady-state conditions, and their performances were contrasted against analytical solutions derived from established methodologies such as the Dupuit formulation, Casagrande equation, Pavlovsky’s expression, and Schaffernak formula. Notably, congruence between the analytical and computational outcomes was evident across the majority of the models, barring models 1, 2, 5, and 9. Analysis of the results underscored a pertinent observation: instances where steeper embankment slopes were employed in tandem with the absence of a toe drain exhibited greater disparities between the computational models and analytical solutions. This nuanced understanding sheds light on the influence of slope inclination and drainage provisions on the alignment between analytical predictions and computational simulations.
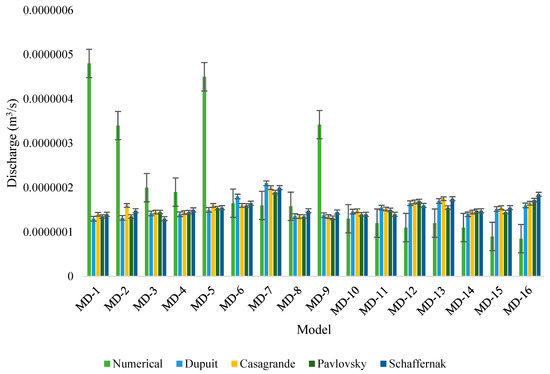
Figure 7.
Seepage discharge comparison between numerical model and equations.
3.8. Relationships among Different Parameters
Various parameters, such as matric suction, water conductivity in the horizontal direction, time, and factor of safety, were subjected to thorough investigation to unveil potential interrelationships. Analysis of the data presented in Table 16 revealed that matric suction and time exhibited the most substantial correlation among the parameters explored, boasting a noteworthy correlation coefficient of 0.950. Similarly, factor of safety and water conductivity of the embankment showcased a relatively robust correlation, substantiated by a correlation coefficient of 0.750. Conversely, a markedly pronounced negative correlation emerged between matric suction and factor of safety, as evidenced by a correlation coefficient of −0.864. This indicated that an escalation in matric suction precipitated a decline in the factor of safety, while conversely, a reduction in matric suction corresponded to an augmentation in the factor of safety.

Table 16.
Relationships among seepage stability parameters.
4. Discussion
From the results, it was apparent that when subjected to long-term steady-state conditions, the embankment characterized by the 1:1 slope ratio exhibited a water flow rate of 1.35 × 10−5 m3/s at the upstream side. Conversely, an intriguing observation was made at the downstream side, where a negative water flow rate of −1.60 × 10−5 m3/s was recorded. The presence of this negative value could indicate a reversal of water flow direction, suggesting that seepage might have occurred into the embankment at that particular location. However, the scenario transformed when the embankment was subjected to a drawdown rate of 1 m per day. During this dynamic condition, the water flow behavior shifted significantly. The upstream face of the embankment displayed a notably reduced water flow rate of −1.1 × 10−8 m3/s, indicating an inward flow, which might be attributed to rapidly decreasing water levels. On the other hand, the downstream base of the embankment exhibited contrasting behavior, with a relatively higher water flow rate of 9.73 × 10−7 m3/s, suggesting potentially increased seepage outflow as the water levels decreased. The existing literature also highlights that as the water level in front of the slope steadily decreases, there is a corresponding gradual augmentation in the seepage gradient within the slope’s seepage field. This alteration becomes more pronounced as the rate of descent increases [32].
Examining the water mass flux data provided further insights into the behaviors of embankment under varying conditions [33]. During steady-state conditions, a discernible water mass flux of 0.022 kg/s/m2 was observed at the embankment’s upstream face, indicating the movement of water through the embankment. Strikingly, a more substantial water mass flux of 0.044967 kg/s/m2 was recorded at the downstream toe, emphasizing the heightened water movement in that specific area. This could be attributed to the differences in hydraulic gradients and local flow patterns within the embankment. Remarkably, when the embankment was subjected to a drawdown rate of 1 m per day, the water mass flux experienced a notable escalation. Specifically, an elevated value of 2.05 × 10−5 kg/s/m2 was extracted from the upstream face, signifying a heightened rate of water movement through the embankment. Simultaneously, the downstream toe exhibited a water mass flux of 0.01 kg/s/m2, reinforcing the significance of this location in terms of water seepage. The results reveal the intricate interplay between various factors, such as slope configuration and drawdown rate, showcasing the dynamic behavior of seepage within embankments. The observed patterns of water flow and water mass flux underscore the complexity of seepage processes and necessity of considering these factors when designing and managing embankment systems.
From the factor of safety results, it became readily apparent that adjustments in the embankment’s inclination exerted a notably more profound influence on the factor of safety than the presence of the toe drain. This observation underscores the paramount importance of slope alterations in dictating the overall stability of the embankment. Furthermore, a discernible pattern emerged, shedding light on the fact that heightened drawdown rates intricately exacerbate the complexities entailed in reestablishing the embankment’s state of equilibrium. This phenomenon can be attributed to the intricate interplay between the rapid reduction in water levels and the embankment’s capacity to adeptly respond to these abrupt and dynamic changes. Embedded within this intricate narrative, the analysis brought to the forefront the intriguing behavior exhibited by the 1:1 (vertical to horizontal) embankment slope model. When subjected to scenarios characterized by rapid drawdown, the factor of safety values consistently fell below the critical threshold of 1 across all configurations within the 1:1 (V:H) embankment slope model. This significant revelation underscores the formidable challenges that such conditions impose upon the overall stability of the embankment. The research carried out by Indraratna and colleagues revealed that a reduction in the embankment slope resulted in an augmentation of the embankment height at the point of failure, escalating it from 1.8 to 2.1 [34].
The study systematically compared computational models to established analytical methods, including the Dupuit formulation, the Casagrande equation, Pavlovsky’s expression, and Schaffernak formula. Notably, a significant degree of agreement was observed between computational simulations and analytical predictions for most of the models studied. However, exceptions were noted for models 1, 2, 5, and 9. The analysis of the results revealed a crucial observation: when steeper embankment slopes were combined with the absence of a toe drain, more significant discrepancies occurred between the computational models and analytical solutions. These findings shed light on the intricate relationship between factors such as slope steepness and the presence of drainage systems. Several other scholars, like Varkey et al. [35], Maula and Zhang [36], Roshan et al. [37], and Liu et al. [38], also underscored the possible influences of the geometric attributes of embankments on slope stability.
The study also embarked on a comprehensive investigation of a spectrum of parameters, encompassing matric suction, water conductivity in the horizontal direction, time, and factor of safety, with the intent of unraveling potential interrelationships that might shed light on the complex behaviors of embankments. Moreover, from the results, it became evident that certain parameters exhibited significant correlations, offering insights into their mutual influences. A focal point was the correlation between matric suction and time, which emerged as a standout interrelationship with a substantial correlation coefficient of 0.950. This observation implies a close association between changes in matric suction and the temporal aspect of the embankment’s behavior. Similarly, factor of safety and water conductivity of the embankment showcased a relatively robust correlation, underpinned by a correlation coefficient of 0.750. This connection between factor of safety and water conductivity underscores the interplay between hydraulic properties and overall stability, indicating that variations in water conductivity can impact the embankment’s safety factor. Conversely, an intriguing insight emerged from the notably pronounced negative correlation between matric suction and factor of safety, evident through a correlation coefficient of −0.864. This correlation suggests an intricate relationship wherein an escalation in matric suction, which signifies the ability of the soil to retain water, corresponds to a reduction in the factor of safety. This implies that as matric suction increases, the embankment’s stability diminishes, emphasizing the significance of moisture content in influencing structural integrity. Conversely, a decrease in matric suction aligned with an augmentation in the factor of safety, indicating that the embankment becomes more stable as the soil’s water retention capacity diminishes. In essence, these findings showcase the interconnected nature of the investigated parameters and offer a deeper understanding of the complex dynamics governing embankment behavior. They underscore the importance of considering a multifaceted approach when analyzing embankment performance, as various factors converge to shape their responses to different conditions. This nuanced comprehension has implications for embankment designs, management, and decision-making processes, facilitating more informed and effective strategies for ensuring stability and optimal performance in various scenarios.
5. Conclusions
This study provided a comprehensive analysis of the relationships between embankment slope configurations, toe drain designs, and drawdown scenarios, utilizing a diverse set of models. The investigation revealed significant variations in factor of safety values, ranging from 0.62 to 1.03, across different combinations. For instance, a 1:2 embankment slope without a toe drain during an instantaneous drawdown resulted in factor of safety values between 1.22 and 1.57, while the incorporation of a 30 m toe drain and a 1 m per day drawdown rate led to values ranging from 1.337 to 2.21. These findings highlight the critical role of slope design and drainage elements in embankment stability. Furthermore, the study observed dynamic changes in water behavior in response to drawdown, with a notable decrease in water flow rates at the upstream face and an increase downstream. Additionally, water mass flux displayed variations, further emphasizing the impact of drawdown on seepage behavior. Significant correlations were identified, including a strong positive correlation between matric suction and time (correlation coefficient of 0.950), a positive correlation between factor of safety and water conductivity (correlation coefficient of 0.750), and a distinct negative correlation between matric suction and factor of safety (correlation coefficient of −0.864). In the ANOVA analysis of matric suction data collected from different situations, which included steady-state conditions and transient flows, as well as different combinations of embankment slopes and drain conditions, it is noteworthy that the p-values consistently remained below 0.05 in all scenarios, unequivocally indicating significant differences within the datasets. Likewise, through the application of ANOVA analysis to the factor of safety data, it became apparent that in all scenarios, the p-values consistently remained below the 0.05 threshold, confirming the clear existence of significant differences within the datasets. The study compared computational models to analytical solutions for various embankment slopes under steady-state conditions, finding a generally congruent alignment between the two, except for specific cases involving steeper slopes without a toe drain, highlighting the impact of slope inclination and drainage on their alignment. Overall, these unique insights contribute significantly to our understanding of seepage behavior and dam stability in various scenarios. They offer valuable guidance for the development of resilient dam construction approaches, ensuring the long-term durability and effectiveness of these vital structures.
Author Contributions
Conceptualization, T.M. and Y.B.U.; methodology, T.M.; software, S.B.A.; validation, N.A.S.; formal analysis, U.B.A. and A.M.B.; investigation, T.M., Y.B.U. and A.K.A.; resources, A.K.A.; data curation, Z.A.S.; writing—original draft preparation, T.M.; writing—review and editing, Z.A.S.; visualization, T.M.; supervision, Y.B.U.; project administration, A.K.A.; funding acquisition, A.K.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP09258790).
Data Availability Statement
Available upon request.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Kheiri, G.; Javdanian, H.; Shams, G. A Numerical Modeling Study on the Seepage under Embankment Dams. Model. Earth Syst. Environ. 2020, 6, 1075–1087. [Google Scholar] [CrossRef]
- Markovic, M.; Radivojevic, N.; Andrejevic Stosovic, M.; Markovic Brankovic, J.; Zivkovic, S. High Embankment Dam Stability Analysis Using Artificial Neural Networks. Teh. Vjesn. Tech. Gaz. 2022, 29, 1733–1740. [Google Scholar] [CrossRef]
- Noori, K.; Salim, S. The Influence of Shell Permeability on Stability of Upstream Slope during Rapid Drawdown–Khassa Chai Earth Dam as a Case Study. Iraqi Natl. J. Earth Sci. 2021, 21, 15–28. [Google Scholar] [CrossRef]
- Shole, D.G.; Belayneh, M.Z. The Effect of Side Slope and Clay Core Shape on the Stability of Embankment Dam: Southern Ethiopia. Int. J. Environ. Sci. Technol. 2019, 16, 5871–5880. [Google Scholar] [CrossRef]
- Mkilima, T. Toe Drain Size and Slope Stability of Homogeneous Embankment Dam under Rapid Drawdown. Technobius 2021, 1, 0001. [Google Scholar] [CrossRef]
- Utepov, Y.B.; Aldungarova, A.K.; Mkilima, T.; Pidal, I.M.; Tulebekova, A.S.; Zharassov, S.Z.; Abisheva, A.K. Dynamics of Embankment Slope Stability under Combination of Operating Water Levels and Drawdown Conditions. Infrastructures 2022, 7, 65. [Google Scholar] [CrossRef]
- Shrestha, B.B.; Kawasaki, A. Quantitative Assessment of Flood Risk with Evaluation of the Effectiveness of Dam Operation for Flood Control: A Case of the Bago River Basin of Myanmar. Int. J. Disaster Risk Reduct. 2020, 50, 101707. [Google Scholar] [CrossRef]
- Adinehvand, R.; Raeisi, E.; Hartmann, A. An Integrated Hydrogeological Approach to Evaluate the Leakage Potential from a Complex and Fractured Karst Aquifer, Example of Abolabbas Dam (Iran). Environ. Earth Sci. 2020, 79, 1–19. [Google Scholar] [CrossRef]
- Torabi Haghighi, A.; Tuomela, A.; Hekmatzadeh, A.A. Assessing the Efficiency of Seepage Control Measures in Earthfill Dams. Geotech. Geol. Eng. 2020, 38, 5667–5680. [Google Scholar] [CrossRef]
- Al-Janabi, A.M.S.; Ghazali, A.H.; Ghazaw, Y.M.; Afan, H.A.; Al-Ansari, N.; Yaseen, Z.M. Experimental and Numerical Analysis for Earth-Fill Dam Seepage. Sustainability 2020, 12, 2490. [Google Scholar] [CrossRef]
- Jiang, X.; Zhanyuan, Z.; Chen, H.; Deng, M.; Niu, Z.; Deng, H.; Zuyin, Z. Natural Dam Failure in Slope Failure Mode Triggered by Seepage. Geomatics, Nat. Hazards Risk 2020, 11, 698–723. [Google Scholar] [CrossRef]
- Zewdu, A. Modeling the Slope of Embankment Dam during Static and Dynamic Stability Analysis: A Case Study of Koga Dam, Ethiopia. Model. Earth Syst. Environ. 2020, 6, 1963–1979. [Google Scholar] [CrossRef]
- Akhmetov, D.A.; Pukharenko, Y.V.; Vatin, N.I.; Akhazhanov, S.B.; Akhmetov, A.R.; Jetpisbayeva, A.Z.; Utepov, Y.B. The Effect of Low-Modulus Plastic Fiber on the Physical and Technical Characteristics of Modified Heavy Concretes Based on Polycarboxylates and Microsilica. Materials 2022, 15, 2648. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Wang, Y.; Sun, P. Research on Safety Factor of Dam Slope of High Embankment Dam under Seismic Condition. MATEC Web Conf. 2015, 22, 04001. [Google Scholar] [CrossRef]
- Malekpour, A.; Farsadizadeh, D.; Hosseinzadeh Dalir, A.; Sadrekarimi, J. Effect of Horizontal Drain Size on the Stability of an Embankment Dam in Steady and Transient Seepage Conditions. Turkish J. Eng. Environ. Sci. 2012, 36, 139–152. [Google Scholar] [CrossRef]
- Bhutto, A.H.; Bhurgri, G.S.; Zardari, S.; Zardari, M.A.; Bhanbhro, R.; Memon, B.A. Numerical Analysis of Rapid Drawdown of an Embankment Dam. Eng. Technol. Appl. Sci. Res. 2020, 10, 5496–5500. [Google Scholar] [CrossRef]
- Aldungarova, A.K.; Mkilima, T.M.; Utepov, Y.B.; Tulebekova, A.S.; Zharassov, S.Z. Heterogeneous Embankment Dam under Rapid Drawdown. Mag. Civ. Eng. 2023, 117, 11708. [Google Scholar] [CrossRef]
- Alfatlawi, T.J.M.; Al-Temimi, Y.K.; Alomari, Z.M. Evaluation of the Upstream Slope Stability of Earth Dams Based on Drawdown Conditions–Khassa Chai Dam: A Case Study. IOP Conf. Ser. Mater. Sci. Eng. 2020, 671, 012072. [Google Scholar] [CrossRef]
- Kumar, S.; Sahu, A.K.; Kumar, M. Modeling the Effect of Central Impervious Core and Downstream Filter Geometry on Seepage through Earth Dams. Ain Shams Eng. J. 2022, 13, 101510. [Google Scholar] [CrossRef]
- Vasoya, K.; Soni, N. Seepage Analysis of Core Section of Jhuj Dam. Int. J. Res. Appl. Sci. Eng. Technol. 2022, 10, 713–717. [Google Scholar] [CrossRef]
- Salmasi, F.; Nouri, M.; Abraham, J. Upstream Cutoff and Downstream Filters to Control of Seepage in Dams. Water Resour. Manag. 2020, 34, 4271–4288. [Google Scholar] [CrossRef]
- Verschoor, H. Experimental Data on the Viscous Force Exerted by a Flowing Fluid on a Dense Swarm of Particles. Appl. Sci. Res. 1951, 2, 155–161. [Google Scholar] [CrossRef]
- O’Sullivan, C.; Arson, C.; Coasne, B. A Perspective on Darcy’s Law across the Scales: From Physical Foundations to Particulate Mechanics. J. Eng. Mech. 2022, 148, 04022064. [Google Scholar] [CrossRef]
- Le Reun, T.; Hewitt, D.R. High-Rayleigh-Number Convection in Porous–Fluid Layers. J. Fluid Mech. 2021, 920, A35. [Google Scholar] [CrossRef]
- Zhussupbekov, A.; Mkilima, T. Stability Analysis of an Old Earth Samarkand Dam in Kazakhstan under Rapid Drawdown Conditions. Environ. Eng. 2022, 9, 11–20. [Google Scholar] [CrossRef]
- El-Ramly, H.; Morgenstern, N.R.; Cruden, D.M. Probabilistic Slope Stability Analysis for Practice. Can. Geotech. J. 2002, 39, 665–683. [Google Scholar] [CrossRef]
- Lam, L.; Fredlund, D.G. A General Limit Equilibrium Model for Three-Dimensional Slope Stability Analysis. Can. Geotech. J. 1993, 30, 905–919. [Google Scholar] [CrossRef]
- Spencer, E. A Method of Analysis of the Stability of Embankments Assuming Parallel Inter-Slice Forces. Geotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Agam, M.W.; Hashim, M.H.M.; Murad, M.I.; Zabidi, H. Slope Sensitivity Analysis Using Spencer’s Method in Comparison with General Limit Equilibrium Method. Procedia Chem. 2016, 19, 651–658. [Google Scholar] [CrossRef]
- Atashband, S. Evaluate Reliability of Morgenstern–Price Method in Vertical Excavations. In Numerical Methods for Reliability and Safety Assessment; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Morgenstern, N.R.; Price, V.E. The Analysis of the Stability of General Slip Surfaces. Géotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.; Yang, K.; Wang, G.; Hu, R. Analysis of the Influence of Water Level Change on the Seepage Field and Stability of a Slope Based on a Numerical Simulation Method. Water 2023, 15, 216. [Google Scholar] [CrossRef]
- Li, Y.; Pan, D.Z. A Simulation of Salt Transport in Nacl-Laden Soil Barrier to Control Subterranean Termites in an Earth Embankment. Water 2021, 13, 1204. [Google Scholar] [CrossRef]
- Indraratna, B.; Sathananthan, I.; Bamunawita, C.; Balasubramaniam, A.S. Theoretical and Numerical Perspectives and Field Observations for the Design and Performance Evaluation of Embankments Constructed on Soft Marine Clay. In Ground Improvement Case Histories; Elsevier: Amsterdam, The Netherlands, 2015; pp. 83–122. [Google Scholar]
- Varkey, D.; Hicks, M.A.; Vardon, P.J. Effect of Uncertainties in Geometry, Inter-Layer Boundary and Shear Strength Properties on the Probabilistic Stability of a 3D Embankment Slope. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2023, 17, 262–276. [Google Scholar] [CrossRef]
- Maula, B.H.; Zhang, L. Assessment of Embankment Factor Safety Using Two Commercially Available Programs in Slope Stability Analysis. Procedia Eng. 2011, 14, 559–566. [Google Scholar] [CrossRef][Green Version]
- Roshan, M.J.; Rashid, A.S.A.; Wahab, N.A.; Hezmi, M.A.; Jusoh, S.N.; Azmi, M. Stability of Railway Embankment in Saturated and Unsaturated Conditions. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1, 1153. [Google Scholar] [CrossRef]
- Liu, C.; Hounsa, U.S.F. Analysis of Road Embankment Slope Stability. Open J. Civ. Eng. 2018, 08, 121–128. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).