Abstract
Modern society’s very existence is tied to the proper and reliable functioning of its Critical Infrastructure (CI) systems. In the seismic risk assessment of an infrastructure, taking into account all the relevant uncertainties affecting the problem is crucial. While both aleatory and epistemic uncertainties affect the estimate of seismic risk to an infrastructure and should be considered, the focus herein is on the latter. After providing an up-to-date literature review about the treatment of and sensitivity to epistemic uncertainty, this paper presents a comprehensive framework for seismic risk assessment of interdependent spatially distributed infrastructure systems that accounts for both aleatory and epistemic uncertainties and provides confidence in the estimate, as well as sensitivity of uncertainty in the output to the components of epistemic uncertainty in the input. The logic tree approach is used for the treatment of epistemic uncertainty and for the sensitivity analysis, whose results are presented through tornado diagrams. Sensitivity is also evaluated by elaborating the logic tree results through weighted ANOVA. The formulation is general and can be applied to risk assessment problems involving not only infrastructural but also structural systems. The presented methodology was implemented into an open-source software, OOFIMS, and applied to a synthetic city composed of buildings and a gas network and subjected to seismic hazard. The gas system’s performance is assessed through a flow-based analysis. The seismic hazard, the vulnerability assessment and the evaluation of the gas system’s operational state are addressed with a simulation-based approach. The presence of two systems (buildings and gas network) proves the capability to handle system interdependencies and highlights that uncertainty in models/parameters related to one system can affect uncertainty in the output related to dependent systems.
1. Introduction
Modern societies are increasingly dependent on their Critical Infrastructure (CI) to produce and distribute the essential goods and services they need. From a system-theoretic point of view, the infrastructure is a system of systems including several systems, which can be area-like (i.e., buildings), line-like (i.e., lifelines, utilities) and point-like (i.e., critical facilities). The first two categories are spatially distributed.
The best practice for the seismic risk assessment of an infrastructure encompasses taking into account all the relevant uncertainties affecting the problem, as well as providing the confidence in the estimate and the sensitivity of the total output uncertainty to each input model.
This issue applies to all problems, but is particularly pertinent for CI systems, in light of their growing interdependence. In fact, input uncertainty related to one system can affect output uncertainty in all other systems included in the infrastructure.
Uncertainty affects the estimate of seismic risk to an infrastructure in the following aspects:
- Cause or hazard: regional seismicity.
- Physical damage: fragility of vulnerable components as a function of local seismic intensities.
- Functional consequences: network flow analysis for the considered systems.
- Impact: injured, fatalities, displaced population, economic loss.
Uncertainties can be classified as aleatory, if the modeller does not foresee the possibility of reducing them, or epistemic. Epistemic uncertainty can be reduced by increasing the “knowledge”, i.e., by improving the models and the estimates of their parameters (Der Kiureghian and Ditlevsen, 2009) [1]. In general, and with reference to the above list, aleatory uncertainty is related to the seismic hazard, while epistemic uncertainty affects, in relative terms, more the physical systems (in terms of damage, functional consequences and impact). However, both uncertainties may characterise the seismic hazard as well as the physical systems. Examples of quantities affected by epistemic uncertainty and related to the seismic hazard evaluation are the geometry of seismic sources, their activity rate and the maximum magnitude of earthquakes they can generate, whilst an example of aleatory uncertainty affecting the system is the damage state of a component given an intensity measure.
This paper, while also accounting for aleatory uncertainty in the regional seismicity (in terms of event magnitude and location, and local seismic intensities at vulnerable components’ sites), focuses on epistemic uncertainty, which can affect the selection of a model among different candidate models or the parameters of a chosen model, or both.
In the current literature, many works address the treatment and sensitivity of output epistemic uncertainty in seismic risk assessment (e.g., Gokkaya et al., 2016 [2]). However, most of these works give only a partial view of the problem, as they deal with either the treatment of uncertainties (e.g., Rokneddin et al., 2015 [3]) or the computation of confidence bounds (e.g., Rubinstein and Kroese, 2016 [4], and Petty, 2012 [5]), or the sensitivity (e.g., Visser et al., 2000 [6], and Saltelli et al., 2010 [7]). Moreover, most of the available works focus on seismic hazard only (e.g., Bommer and Scherbaum, 2008 [8]) or structural reliability (e.g., Zhang et al., 2010 [9], and Alam and Barbosa, 2018 [10]). Tate et al. (2015) [11] addressed both uncertainty and sensitivity analysis with reference to economic loss estimates due to riverine flooding. To the best of the authors’ knowledge, the work by Cavalieri and Franchin (2019) [12] is currently the only one tackling both treatment of and sensitivity to epistemic uncertainty with reference to interdependent critical infrastructural systems subjected to seismic hazard.
This paper aims to provide an additional contribution to this field. In particular, the goals of the manuscript are to (i) summarise relevant approaches in the current literature about the treatment of and sensitivity to epistemic uncertainty, (ii) propose feasible solutions to some critical issues, (iii) present a comprehensive framework for seismic risk assessment of interdependent infrastructure systems that accounts for both aleatory and epistemic uncertainties and provides confidence in the estimate as well as sensitivity of output epistemic uncertainty, and (iv) exemplify the implemented methodology with reference to an infrastructure composed of buildings and a gas network. The novelties of the paper include an efficient approach for considering parameter correlation in a logic tree (see Section 2.2) and several effective recommendations for the analyst to better investigate the sensitivity of uncertainty in the output to the components of epistemic uncertainty in the input (see Section 3.4).
Risk assessment in this work is carried out according to the performance-based Earthquake Engineering framework adapted to spatially distributed systems, addressing (i) the seismic hazard characterisation in terms of both transient and permanent ground deformation, (ii) the vulnerability assessment for systems’ components using fragility models, and (iii) the simulation-based evaluation of the infrastructure’s performance, adopting a flow-based performance metric for the gas system.
The employed steady-state gas flow formulation is the one presented by Cavalieri (2017, 2020) [13,14], encompassing multiple pressure levels, the pressure-driven mode and the correction for pipe elevation change. Flow equations for high, medium and low pressure are available, allowing one to handle both distribution and transmission networks. Models for reduction groups and compressor stations, which allow the pressure to be locally reduced or increased, are included. The flow-based gas system model was implemented by the first author into an open-source simulation tool for civil infrastructures, namely Object-Oriented Framework for Infrastructure Modelling and Simulation (OOFIMS) [15], coded in MATLAB® [16] language and initially developed within the EU-funded project SYNER-G (2012) [17]. OOFIMS is an integrated framework for reliability analysis that allows one to consider multiple interdependent infrastructure systems, accounting for the relevant uncertainties.
The remaining sections of this article are organised as follows. Section 2 presents a state-of-the-art review about the treatment of and sensitivity to epistemic uncertainty, offering suggestions on the best practice and presenting a novel approach to handle parameter correlation in a logic tree. A seismic risk assessment, encompassing the proposed methodology, was carried out for demonstration purposes on a “synthetic” city, composed of buildings and a gas network, as described in Section 3. Before presenting and discussing the results, Section 3 briefly describes the models and the performance metrics adopted in the framework. Conclusions and future work are reported in Section 4.
2. Treatment of and Sensitivity to Epistemic Uncertainty
2.1. Modelling of Input Epistemic Uncertainty
The possible approaches to the treatment of epistemic uncertainty vary depending on its type, denoted as I and II in the following:
- Epistemic uncertainty on model form (Type I): a logic tree is commonly used, composed of a chain of sequential modules, the latter intended as groups of parallel branches or choices. In this framework, alternative models Θ, corresponding to logic tree branches within each module, are considered in each step of the analysis. Individual simulations are carried out for each different combination of sequential branches (i.e., of models), thus yielding multiple results, for instance in terms of mean annual frequency (MAF) of exceedance curves of a performance metric. Weights, summing up to one, are attached to branches to indicate subjective degrees of belief of the analyst in each model. This is common practice in probabilistic seismic hazard analysis (PSHA), where a typical uncertainty in model form is represented by the ground motion prediction equation (GMPE). The outcome is usually expressed in terms of mean hazard curve over the logic tree, obtained as a weighted average of the curves from all branches (Bommer and Scherbaum, 2008) [8]. Upper and lower fractile curves and/or a confidence interval around the mean curve are often computed based on the set of curves from the tree, so as to quantify the effect of epistemic uncertainty on the results.
- Epistemic uncertainty on model parameters (Type II): each model parameter θ is modelled with a random variable, whose distribution describes its epistemic uncertainty. (a) The parameters (e.g., the maximum magnitude Mmax) are arranged in a hierarchical model together with aleatory uncertainty (e.g., the magnitude M). In this case, only one simulation is carried out and the risk analysis provides a single result (i.e., a single MAF curve of a performance metric, for instance), embedding the effects of both aleatory and epistemic uncertainty (e.g., Franchin and Cavalieri, 2015 [18], Su et al., 2020 [19], Morales-Torres et al., 2016 [20]). This approach prevents the analyst from properly treating Type II epistemic uncertainty, in terms of computing confidence intervals or fractiles, and identifying distinct contributions of input aleatory and epistemic uncertainty within the output uncertainty (refer to Figure 8 for an example). (b) Alternatively, the risk analysis is repeated for discrete values of each parameter θ (e.g., 16%, 50% and 84% fractiles). This approach, involving a higher associated computational effort, allows one, however, to arrange parameters in a logic tree, as done for Type I uncertainty. Since the discrete values of the model parameters are values from a probability distribution, their choice, as well as that of the corresponding weights attached to tree branches, could be assigned, for instance, according to Miller and Rice (1983) [21].
- Epistemic uncertainty of both Type I and II: (a) The analyst can decide to adopt approach (2a) for Type II uncertainty. This cheaper approach leads to carrying out the expectation over all sources of uncertainty, presenting the results as the mean over the logic tree. However, in this case, confidence intervals or fractiles would refer only to part of the total epistemic uncertainty (i.e., the one related to models). (b) The second option, involving approach (2b) for Type II uncertainty, consists of building an expanded logic tree for the treatment of both Type I and II uncertainties.
It should be clear from the above that the best practice for the treatment of epistemic uncertainty on model parameters is the adoption of approaches (2b) or (3b). However, one issue with the logic tree including model parameters is that, strictly speaking, sequential modules can only be used when all parameters are statistically independent. In the presence of parameter correlation, a variation in one parameter, belonging to one module, changes the (conditional) distribution of the others, thus making the results dependent on the ordering of modules. Such correlation is often disregarded, as it occurs for instance in PSHA with reference to the parameters of the Gutenberg–Richter recurrence relationship, namely a, b and Mmax, for which independent sequential modules are commonly adopted, thus neglecting, at least, the correlation between a and b. This leads the possible combinations to probably cover an unrealistically wide range of values, thus presenting a range of uncertainty much wider than the analyst actually intends to model (Bommer and Scherbaum, 2008) [8]. A possible solution to this issue, proposed by Cavalieri and Franchin (2019) [12], is reported in Section 2.2, together with a novel and more efficient solution developed in the current work.
2.2. Case of Correlated Parameter Values
As pointed out above, in the presence of correlation between parameters in logic trees (approaches (2b) and (3b)), sequential modules can still be used, but the results will be dependent, regardless, on the ordering of modules. Care should be taken in conditioning the values of the subsequent parameter to those of the preceding one. One possible option would be to change the weights, so that they are obtained from the distribution of each parameter conditional on the value of the correlated parameter that precedes it (e.g., Yilmaz et al., 2020 [22]). This approach would lead to having different weights for the same choices within a module depending on the choice of the preceding module, or to the same weights attached to different choices (parameter values). However, it can work only as far as there are no other constraints involved. One case that arises in the context of seismic risk analysis, where simple adjustment of the weights does not solve the problem, is related to the uncertainty in damage to a component given the input seismic intensity, uncertainty that is represented by fragility functions. The latter describe the probability of reaching or exceeding a given limit state conditional on intensity at the component’s site. These functions are commonly postulated as lognormal and are thus defined by two parameters, the log-mean and the log-standard deviation. Epistemic uncertainty on these parameters, which are obviously correlated, is sometimes available. As long as the component’s state is defined as binary and thus a single fragility function is employed to determine the damage state, modifying the weights is a viable option. The problem arises when the component is not modelled as binary and multiple limit states are therefore considered, and hence two or more fragility curves are used, which must never intersect.
To overcome these issues, Cavalieri and Franchin (2019) [12] proposed to avoid the use of sequential modules corresponding to correlated parameters, and instead to lump them all together into the same module, accounting for their dependence within the module itself. Needed input data are the marginal distributions (e.g., normal with mean μ and standard deviation σ) of the parameters and their correlation matrix. One parameter is fixed to a certain fractile and the same fractile of the remaining parameters is obtained using the conditional mean and standard deviation. For the formulation to be exhaustive, all combinations of conditioning and conditioned parameters are included. Indicating with ρ the correlation coefficient, with x1 the conditioning parameter (fixed to a fractile) and with x2 the vector of the conditioned parameters, it is possible to write the diagonal matrix of standard deviations, Dxx, the correlation matrix, Rxx, and the covariance matrix, Cxx, as follows:
where , and are partitions of the covariance matrix Cxx. The conditional mean vector, , and covariance matrix, , are obtained as (Benjamin and Cornell, 1970) [23]:
The conditional standard deviations are simply the square root of the diagonal elements of . Starting from the conditional means and standard deviations, one can retrieve any fractile of the conditioned parameters, using the inverse of the cumulative distribution function (CDF).
The method proposed by Cavalieri and Franchin (2019) [12] is flawed. In fact, the fractile chosen for the parameters on their respective marginal distributions does not correspond to the same fractile of the joint distribution, which is the actual target. For illustrative purposes, this is illustrated with reference to an example including only the first two correlated fragility parameters used in the application (see Section 3.2), related to the yield limit state fragility curve, namely, μln,Y and σln,Y. Taking only two parameters over a set of four correlated parameters allows the joint CDF to be visualised in a 3D plot. In particular, only the first two columns in Table 1 and the first 2 × 2 submatrix in Table 2 are considered for this example (the description of such tables is given in Section 3.2). First, the extreme values of μln,Y and σln,Y, extracted from a large sample of parameter values obtained from their marginal normal distributions, were used for a discretisation of the parameter supports, thus building a grid of points. Then, the joint CDF was evaluated at such grid points, as displayed in Figure 1. The latter shows the process of deriving the fractile of the joint distribution corresponding to a given fractile of the two parameters, according to the method proposed in [12]. For simplicity, and without loss of generality, the 50% fractile is considered, leading to the retrieval of only one set of parameter values, extracted from their marginal unconditional distributions (the set and marginal CDFs are shown in the figure). Figure 1 clearly shows that the 50% fractile of both parameters corresponds to the 27% fractile (black dot) of the joint distribution, which is thus quite different from the desired (target) 50% fractile. This shortcoming may occur, of course, also in the case of parameter fractiles different from 50%, when one parameter is fixed and the other one is extracted from the conditional distribution (see procedure outlined above).

Table 1.
Mean and coefficient of variation (CoV) of parameters of reinforced concrete (RC) fragility curves.

Table 2.
Correlation matrix for parameters of RC fragility curves.
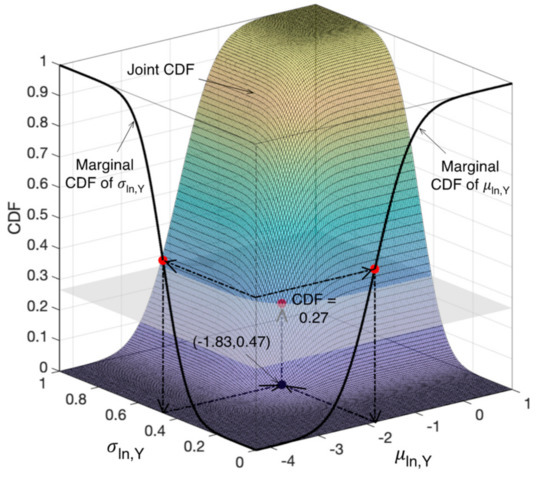
Figure 1.
Example showing the derivation of the fractile (black dot) of the joint distribution corresponding to the 50% fractile of the two fragility parameters, according to the approach proposed in [12].
In order to overcome this issue and properly handle the case of correlated parameters in a logic tree, a novel approach, which is also more efficient, is proposed in this work. The procedure is straightforward and encompasses the following steps:
- The extreme values of all parameters are obtained from their marginal distributions. Based on this, a sufficiently accurate discretisation of the parameter supports is carried out, thus building a grid of points.
- The joint CDF and probability density function (pdf) are evaluated at all grid points, using the parameters of the multivariate distribution (e.g., normal with mean vector μX and covariance matrix Cxx).
- For each desired fractile of the joint distribution, corresponding to a CDF value F*, the points characterised by CDF = F* are extracted, as displayed with cyan dots in Figure 2a with reference to the example described above and the 50% fractile. The same cyan dots are also shown in Figure 2b, each with its joint pdf value. The accuracy in this step is of course a function of the discretisation employed in step #1 and the tolerance fixed for CDF around F*.
 Figure 2. Example showing the selection of the 50% fractile of the joint distribution, according to the approach proposed herein. (a) 50% fractile (black dot) as one of the points with joint CDF = 0.5 (cyan dots); (b) 50% fractile (black dot) selected as the one that maximises the joint pdf.
Figure 2. Example showing the selection of the 50% fractile of the joint distribution, according to the approach proposed herein. (a) 50% fractile (black dot) as one of the points with joint CDF = 0.5 (cyan dots); (b) 50% fractile (black dot) selected as the one that maximises the joint pdf. - Among the extracted points, the desired fractile of the joint distribution is selected as the one with the highest value of the joint pdf, as shown with a black dot in Figure 2b. The same selected point is also shown in Figure 2a. The selected set of values is the most likely parameter set; as such, it is not supposed to lead to extreme combinations of values and, in the case of fragility parameters, to intersection of fragility curves related to different limit states.
The point selected in Figure 2 is the same reported in Figure 3 with a black dot. It can be clearly noted how the (target) 50% fractile of the joint distribution corresponds to the 70% and 69% fractiles of μln,Y and σln,Y, respectively. This is a further reassurance on the fact that, in general, the fractiles of the parameters and the joint distribution do not coincide, and that the proposed approach is the correct one to properly handle the desired fractiles of joint distributions within a logic tree. In fact, the approach (i) is fully consistent with the parameter correlation structure, (ii) keeps the independence of results on the ordering of modules, and (iii) is also much more efficient than the one presented in [12]; indeed, it allows one to considerably reduce the number of branches in the logic tree and thus the required computational effort, as will be better highlighted in Section 3.3.
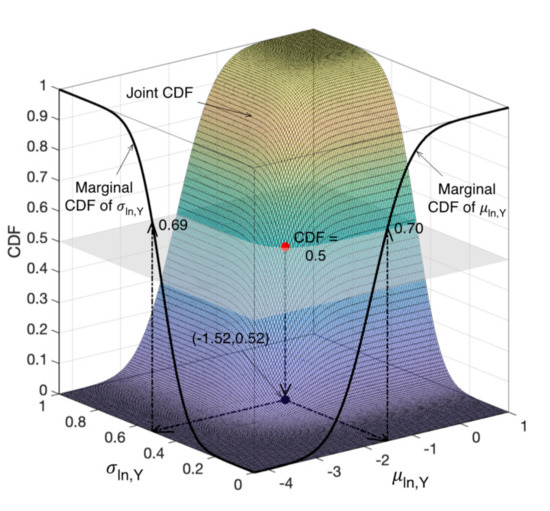
Figure 3.
Example showing the derivation of the fractiles of the two fragility parameters corresponding to the 50% fractile (black dot) of the joint distribution, according to the approach proposed herein.
2.3. Quantification of Output Uncertainty Due to the Epistemic Component
As already said, in a probabilistic framework where a logic tree is used to account for epistemic uncertainty (approaches 1, (2b) and (3b)), risk is estimated through a chain of modules, each composed of parallel choices (i.e., alternative models or model parameter values). The logic tree provides multiple results, for instance in terms of a number N of MAF of exceedance (λ) curves, denoted λ-curves in the following, for a performance metric of interest. Each λ-curve is related to one out of N simulations (e.g., Monte Carlo), each encompassing multiple runs.
Propagation of epistemic uncertainty through the logic tree results in a distribution of the output X. The latter may express either λ values for a fixed performance metric value or performance metric values for a fixed value of λ. This choice is dictated by the goal of the analyst, who can be interested in the mean value of for fixed performance metric values or for fixed λ values. The two approaches can yield very different results for the mean value. Bommer and Scherbaum (2008) [8], referring to hazard curves, pointed out that in current engineering design practice the procedure is to retrieve the expected value of intensity measure at a preselected frequency of exceedance (or return period). This is the choice adopted also in this work, with reference to a performance metric (refer to Figure 8).
As a minimum, can be summarised through its mean μX and variance σ2X. Computing the mean is commonly termed harvesting the logic tree in PSHA practice, while using the variance it is possible to estimate a confidence interval around the mean curve. Finally, variability in X is also often expressed through weighted fractiles, as an alternative to σ2X.
For a tree with NΘ models and Nθ parameters (see example in Figure 4), μX can be estimated as the weighted average of X [12]:
with:
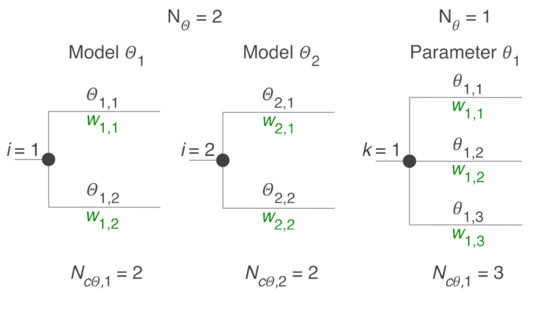
Figure 4.
An example logic tree for a problem with two models and one uncertain model parameter.
In Equation (4), NcΘ,i and Ncθ,k are the numbers of choices for the i-th model and the k-th parameter, respectively, xn is the MAF or performance metric value corresponding to the n-th branch of the tree, formed from the sequence j(1), …, j(NΘ) of models and m(1), …, m(Nθ) of parameter values, while wn is the associated weight. It is noted that the final weights wn, as well as all other weights within each module, are “reliability weights”, as opposed to “frequency weights”, therefore they sum up to unity:
The variance σ2X can be estimated through the weighted sample variance:
which is the unbiased estimator when weights sum up to unity as in Equation (5).
The weighted p% fractile is defined as the element xp of X satisfying the following condition:
where I is an indicator function equal to 1 if xn is lower than or equal to xp, and 0 otherwise.
Finally, the confidence interval around the estimate of μX, following, e.g., Rubinstein and Kroese (2016) [4] or Petty (2012) [5], can be obtained, recalling that the estimator has approximately a normal distribution, (μX,σ2X/N), where N is the samples size. When σ2X is estimated as in Equation (6), the confidence interval at the confidence level (1 − α)100% (e.g., α = 0.05 yields a confidence level of 95%), is:
where tN−1,1−α/2 is the critical value for the Student t distribution with (N−1) degrees of freedom.
2.4. Sensitivity to Input Epistemic Uncertainty
In order to assess which component of (input) epistemic uncertainty contributes more to the uncertainty in the output, sensitivity analysis should be carried out. Most of the works found in the current literature about sensitivity analysis can be grouped in three main threads, based on the one-at-a-time (OAT) approach, the logic tree and analysis of variance, respectively.
According to the OAT approach, sensitivity is evaluated by varying one uncertain input variable or model at a time, while holding all the others constant (at their median value or best estimate). Visser et al. (2000) [6] and Merz and Thieken (2009) [24] proposed indices based on the difference between the maximum “uncertainty” range, MUR(λ), i.e., the difference between maximum and minimum value of the metric for a fixed λ (they use T = 1/λ), and the corresponding range URi(λ) obtained by switching off the i-th module (i.e., setting it to its best estimate choice):
Other authors, for instance, Celik and Ellingwood (2010) [25] and Celarec et al. (2012) [26], with reference to seismic risk assessment of structures, performed sensitivity of selected seismic response parameters (drifts, forces, etc.) to the input random variables—the latter also including Type II epistemic uncertainty. In these works, output is commonly computed first with all input variables set to their medians, and then setting one input variable at a time to a lower or upper fractile (typically 16% and 84%): the resulting variations are represented with tornado diagrams. Along the same lines, Porter et al. (2002) [27] used the OAT approach to carry out a deterministic sensitivity analysis of building loss estimates to major uncertain variables, which include spectral acceleration, mass, damping and structural force–deformation behaviour. Tornado diagrams were also used by Pourreza et al. (2020) [28] to eliminate the least influential modelling variables on the collapse capacity of a five-storey steel special moment resisting frame (SMRF). Similar approaches were followed, for instance, by Easa et al. (2020) [29] and Sevieri et al. (2020) [30].
The findings of all these studies are limited by their use of the OAT method. As pointed out by Saltelli and Annoni (2010) [31], sensitivity analyses employing the OAT approach are incomplete, as they are fundamentally unable to quantify the portion of uncertainty arising from interactions between input variables. In other words, correlations cannot be considered in OAT analyses because this would require the simultaneous movement of more than one input variable, as also highlighted by Cremen and Baker (2020) [32].
Frameworks including a logic tree are instead capable of taking into account interactions, since each combination of sequential branches involves variations within all modules (the latter including parallel choices of models or model parameters). For each choice within a module, it is possible to compute the weighted average considering only the logic tree branches involving that choice. The sensitivity of output epistemic uncertainty to logic tree choices can still be presented through tornado diagrams (see, e.g., Figure 10b). Crowley et al. (2005) [33] evaluated the impact of epistemic uncertainty on earthquake loss models. In particular, they used systematic combined variations of the parameters defining the demand (i.e., ground motion) and the capacity (i.e., vulnerability) to identify the relative impacts on the resulting losses, finding that the influence of the epistemic uncertainty in the capacity is larger than that of the demand for a single earthquake scenario. Sensitivity results were presented through tornado diagrams. The logic tree approach was also used by Tyagunov et al. (2014) [34], who estimated the sensitivity of seismic risk curves to several input parameters belonging to three different modules of risk analysis, namely, hazard, vulnerability and loss. As a further, recent example, Bensi and Weaver (2020) [35] used a logic tree to treat both Type I and Type II epistemic uncertainties associated with the estimation of tropical cyclone storm recurrence rates. A sensitivity analysis, presented through tornado diagrams, was also carried out to show how storm rate (input) epistemic uncertainty impacts estimates of storm surge hazards.
An alternative way to account for interaction effects between input variables requires the use of Global Sensitivity Analysis (GSA), which allows for the identification of the parameters that have the largest influence on a set of model performance metrics and the identification of non-influential parameters (Saltelli et al., 2008) [36]. GSA is typically undertaken using variance-based techniques. The latter aim to quantify the contribution of each input parameter to the total variance of the output, by means of the analysis of variance (ANOVA) decomposition.
Tate et al. (2015) [11], after providing an understanding of the total variation and central tendency of the loss (i.e., output) estimates through an uncertainty analysis, carried out a sensitivity analysis based on the method of Sobol’ (1993) [37]. The latter decomposes the variance to determine the proportional contribution of each model component to the total uncertainty. Based on the original version of the Sobol’ sensitivity indices, among which the first order sensitivity index (or main effect) of the i-th uncertain variable, Si, Homma and Saltelli (1996) [38] introduced the total sensitivity index, STi. While Si gives the effect of the i-th uncertain variable by itself, STi indicates its “total” effect, which includes the fraction of variance accounted for by the variable alone, as well as the fraction accounted for by any combination of it with the remaining variables [7,31]. These indices, whose computation is carried out via sampling schemes, were indeed also mentioned by Helton et al. (2006) [39], who reviewed sampling-based methods for uncertainty and sensitivity analysis, and used by Cremen and Baker (2020) [32] within a variance-based sensitivity analysis for the FEMA P-58 methodology.
For complete variance decomposition, in addition to the method of Sobol’, techniques based on the Fourier Amplitude Sensitivity Test (FAST) are also available [40,41]. Bovo and Buratti (2019) [42] used an ANOVA procedure based on a two-way crossed classification model [43], in order to evaluate the effect of epistemic uncertainty in plastic-hinge constitutive models on the definition of fragility curves for reinforced concrete (RC) frames. It was found that the uncertainty associated with the hysteretic model definition has a magnitude similar to the one related to record-to-record variability.
Among all the algorithms proposed in the literature for GSA, several methods consider the entire pdf of the model output, rather than its variance only. Such methods, which are moment-independent, are preferable in cases where variance is not a suitable proxy of uncertainty, for instance, when the output distribution is highly skewed or multi-modal. However, the adoption of density-based methods has been limited so far, owing to its difficulty to be implemented. In order to overcome this issue, Pianosi and Wagener (2015) [44] introduced the PAWN method, which efficiently enables the computation of density-based sensitivity indices. It is based on the concept of characterising output distributions by their CDF, which is easier to derive than pdf. Zadeh et al. (2017) [45] provided an interesting comparison between the commonly used variance-based method of Sobol’ and the recently proposed moment-independent PAWN method, with reference to the Soil and Water Assessment Tool (SWAT), which is an environmental simulator applied all over the world for watershed management purposes. Sobol’ and PAWN identified the same non-influential parameters, but the ranking of the influential ones was better quantified by the PAWN method. This was probably due to the asymmetric character of the output distributions, thus undermining the Sobol’ implicit assumption that variance is a good proxy for output uncertainty.
Following an alternative approach, Cavalieri and Franchin (2019) [12] employed (modified) ANOVA combined with logic tree to perform sensitivity analysis of output uncertainty to input epistemic uncertainty. ANOVA allows one to test the assumption that a sample is divided into groups, by expressing the total variance in the sample, s2X, as the sum of a variance “within” each group, s2X,W, and a variance “between” groups, s2X,B. A large ratio s2X,B/s2X indicates that the difference between groups is large. If each module in the logic tree is taken in turn as a criterion for grouping and the set of results xn is divided into NG sub-groups, each corresponding to a different choice in the module, the ratio s2X,B/s2X can be used to rank modules. The classical ANOVA expression is derived for a sample where all realisations have the same weight and reflect the underlying distribution, which is assumed to be normal. If the sample is weighted, as in the case of results derived from a logic tree, the following relation for weighted ANOVA holds:
where xgj and wgj are the output value and the associated weight corresponding to the j-th branch within the ng branches in the g-th group (g-th option in the considered module), and is the weighted average within the g-th group. Note that weights within a group do not sum up to unity. To summarise, the importance of the i-th module according to weighted ANOVA, based on which a module ranking can be derived, is obtained as:
This is one of the approaches adopted for sensitivity analysis in the current work (see Section 3.4).
3. Application
The methodology presented above for the treatment of and sensitivity to epistemic uncertainty was implemented in OOFIMS. For demonstration purposes, a seismic risk assessment was carried out on a “synthetic” city composed of buildings and a gas network (see Section 3.2) and subjected to distributed seismic hazard.
3.1. Hazard, Vulnerability and Performance Metric for Gas System
The hazard probabilistic model adopted herein takes into account both transient ground deformation (TGD) and permanent ground deformation (PGD). TGD is related to ground shaking due to travelling seismic waves, while PGD is induced by geotechnical hazards (e.g., landslides) and causes large permanent soil deformations. In the application, the intensity measures (IMs) used to express TGD are the peak ground acceleration (PGA) and the peak ground velocity (PGV). For further details on the implemented hazard model, interested readers are referred to [46].
After computing the relevant IMs at the surface, namely, PGA, PGV and PGD (the latter acronym also indicates the resulting displacement) for each site, the physical damage state of the components is obtained through fragility models. Concerning gas pipelines, the model proposed by the American Lifelines Alliance (ALA) (2001) [47] for water pipelines was adopted. Two Poisson repair rates of faults (leaks/breaks) per unit length are assumed to be lognormally distributed, with an expression for the median, (returned in in km−1, with PGV in cm/s and PGD in m), and a logarithmic standard deviation:
The residual terms and are both lognormal with unit median and log-standard deviation equal to 1.15 and 0.74, respectively, whilst K1 and K2 are modification factors, functions of the pipe material, soil, joint type and diameter. For the generic pipe, the highest repair rate, , is used to estimate the number of repairs (i.e., leaks or breaks). The outflow associated to such repairs is then lumped to the end nodes of the pipe as additional loads. Any leak or break thus plays a role in the flow analysis in damaged conditions.
The metering/reduction (M/R) stations, which function as source nodes, were assumed to behave as binary components (i.e., intact/broken) and were assigned the same fragility model used for compressor stations, and provided by HAZUS (2007) [48]. Their lognormal fragility curve is characterised by a median PGA of 0.77 g and a logarithmic standard deviation of 0.65. The seismic vulnerability of the remaining components in the taxonomy of gas systems was neglected because no fragility models are available in the literature, to the authors’ knowledge. The adopted fragility model for buildings will be introduced in Section 3.2.
Being that the focus of this work is on epistemic uncertainty, rather than on the comparison of metrics, it was decided to consider only one metric for the gas system, namely, the System Serviceability Index, SSI (Wang and O’Rourke, 2008) [49]. It is defined at system level and is flow-based, meaning that it requires a flow analysis and thus gives insight into the system’s actual serviceability. SSI, ranging between 0 and 1, is defined as the ratio between the sum, over the n load nodes, of the delivered gas flows Qi(P1,i)s after an earthquake (subscript s), and the sum of node demands Qi.
The term P1,i is the pressure at the i-th load node, needed to possibly reduce the demands according to the pressure-driven formulation (see [13]). This is a deterministic metric. Starting from the values computed within the single simulation runs, new probabilistic metrics can be retrieved at the end of the simulation, thus accounting for aleatory uncertainty. Examples of probabilistic metrics are given by moments or distributions of a deterministic metric (see Section 3.4).
3.2. The Synthetic City
The topology of the gas distribution network, already used by Cavalieri (2017) [13], is sketched in Figure 5a, together with the indication of node types. The graph is characterised by a grid or mesh-like topological structure, typical in urban areas where the main pipes connect suburbs or districts, and can be considered as a transmission/distribution (TD) system. The topology was generated using the network model developed by Dueñas-Osorio (2005) [50], which aims to represent real TD systems based on the ideal class of the d-lattice-graph.
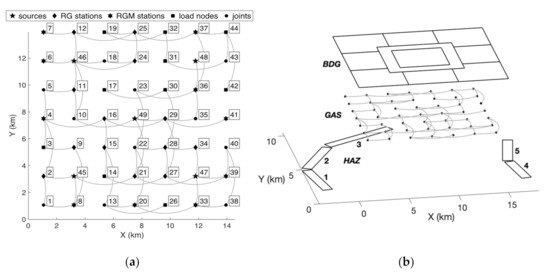
Figure 5.
The synthetic city used as case-study. (a) Sketch of the realistic gas network with multiple pressure levels; (b) the gas network together with the building and hazard layers.
Out of the total 49 nodes, five are sources (i.e., M/R stations) and the remaining ones are RG/RGM stations, load nodes and joints. Note that RG (reduction group) stations operate pressure reduction between two pressure ranges (i.e., low, medium, high) or two pressure levels within the same range, while RGM (reduction group and metering) stations also serve as sink (or load) nodes for industrial users (at high or medium pressure). In load nodes, gas is delivered to end-users.
Three pressure levels are present, namely, two medium pressure (three bar and two bar) and one low pressure (0.05 bar). A total of 65 high-density polyethylene (HDPE) pipes connect the nodes. Pressure reduction is operated by reduction groups, which are automatically split into two nodes (see [13]). Elevation is 0 m for all nodes, while all pipes were assigned a D = 300 mm diameter.
Figure 5b displays the gas network (GAS) together with two other layers, namely, the seismic hazard (HAZ) and buildings (BDG). The 15 by 15 km square footprint of the city is subdivided into nine geometrically coincident subcity districts (SCDs) and building census areas (BCAs), each of size 5 by 5 km. A park surrounds the central area. The total population is 1,800,000, corresponding to an average density equal to 8000 inhabitants/km2. For simplicity, only reinforced concrete buildings are present. The corresponding seismic fragility model was assigned on the basis of a comprehensive literature survey conducted within the SYNER-G (2012) project [17]. A set of two lognormal fragility curves is provided (in terms of PGA, in units of g), for the yield and collapse limit states. The curve parameters (μln,Y and σln,Y for the yield limit state, μln,C and σln,C for the collapse limit state) are themselves characterised as joint normal variables (epistemic uncertainty of Type II). Table 1 above reports the mean and coefficient of variation (CoV) of fragility parameters for RC buildings (mid-rise, seismically designed, non-ductile bare frames, according to Crowley et al., 2014 [51]), while Table 2 reports the corresponding correlation matrix, which is needed to ensure that the yield and collapse fragility curves do not intersect.
The seismic environment (i.e., the HAZ layer) consists of two sources, which are discretised into three and two rectangular seismogenic areas, displayed and numbered in Figure 5b. Their activity is characterised in terms of the parameters for the truncated Gutenberg–Richter recurrence law. In particular, λ0 (i.e., the mean annual rate of the events in the source with M greater than the lower limit Mmin) values are 0.014, 0.016, 0.020, 0.018, and 0.022 for the five areas, while the magnitude slope β and lower and upper magnitude limits Mmin and Mmax are set to 2.72, 4.5 and 6.5 for the first three areas, and 1.70, 5.0 and 6.5 for the remaining two areas.
3.3. Adopted Logic Tree
Following approach (3b) in Section 2.1, a logic tree was used to provide confidence in the estimate of the risk assessment results, as well as the sensitivity of the total output uncertainty to the components of epistemic uncertainty in the input. The four employed modules, related to models or parameter values, concern (weights are indicated in curly braces):
- Mmax for all the seismic sources
- (a)
- 6.5 {0.4};
- (b)
- 7.0 {0.6}
- GMPE
- (a)
- Akkar and Bommer (2010) [52] {0.7};
- (b)
- Boore and Atkinson (2008) [53] {0.3}.
- Fractiles of both residual terms in the HAS fragility model
- (a)
- 91.5% {0.25};
- (b)
- 50% {0.5};
- (c)
- 8.5% {0.25}.
- Fractiles of joint normal distribution of fragility curve parameters for RC buildings
- (a)
- 91.5% {0.25};
- (b)
- 50% {0.5};
- (c)
- 8.5% {0.25}.
The fractiles and corresponding weights in modules #3 and #4 were set according to the work by Miller and Rice (1983) [21]. A Gaussian quadrature procedure and a selected weighting function are employed to approximate a continuous cumulative distribution with a user-defined number of pairs of random variable values and cumulative probability. Each value is paired with a probability, so as to obtain the probability mass function of the discretised random variable. Such probabilities are used as branch weights in a logic tree module containing several parameter values. For the case at hand, the parameter distributions in modules #3 and #4 were discretised with three points, namely, the 91.5%, 50% and 8.5% fractiles with weights 0.25, 0.5 and 0.25, respectively.
Concerning module #3, the two variables belong to the same fragility model and could be correlated. However, only their (lognormal) marginal distributions are available [47], while their correlation structure is unknown. In order to handle this case, both parameters are lumped together in the same module, rather than in two subsequent modules, as done for the case of known correlation. Then, in the absence of the needed information, for each of the three branches the same fractile is derived for the two parameters by using their inverse marginal lognormal CDF, with zero log-mean and the log-standard deviations reported in Section 3.1.
As already mentioned, the four parameters of the two lognormal fragility curves for RC buildings are correlated (see Table 2). According to the approach by Cavalieri and Franchin (2019) [12], to handle parameter correlation, the RC fragility module (#4 above) in the logic tree would include four branches for each fractile. However, for the 50% fractile, all branches provide the same set of fragility curves (i.e., the mean curves), so that the four branches are lumped in just one. To summarise, such an approach would require four combinations for both 8.5% and 91.5% fractiles and one combination for the 50% fractile, for a total of nine branches to include in module #4, and consequently a total of 2 × 2 × 3 × 9 = 108 branches in the logic tree. On the other hand, the approach proposed herein for handling parameter correlation leads the RC fragility module to include only one branch per fractile (i.e., just three branches), for a total of 2 × 2 × 3 × 3 = 36 branches in the whole logic tree, thus entailing a significant reduction in computational effort.
The fragility curves related to the three branches in module #4 were thus retrieved according to the proposed approach (see Figure 2 above), employing a 25 point discretisation for each of the four parameters (for a total of 254 = 390,625 grid points) and fixing a 10−3 tolerance for CDF around each of the three considered F* values, namely, 0.915, 0.50 and 0.085. The curves are displayed (with thicker lines) in Figure 6, where the mean fragility curves are also reported (with thinner lines) for reference. Three aspects deserve to be highlighted. First, the fragility curves for the 50% fractile branch (see Figure 6b) are quite different from the mean ones, thus confirming once more that the parameter values corresponding to the 50% fractile of the joint normal distribution are not the 50% fractiles of their marginal distributions. Second, the 50% fractile fragility curves (in Figure 6b) are not very distant from the 91.5% fractile ones (in Figure 6a), owing to the steep slope of the joint CDF in the [0.5,1] range: this leads the 50% and 91.5% fractiles of the joint distribution to be reflected by similar (high) fractiles of the parameters. Third, selecting the point with the highest joint pdf value (see Section 2.2) leads the fractiles of the parameters to be different from the target fractile of the joint distribution, but similar between each other, as can also be gathered from the example with two parameters in Figure 3. As a consequence, it can be noted in Figure 6 that the fragility curves gradually decrease both their median and slope (controlled by the log-mean and the log-standard deviation, respectively), when moving from 91.5% to 8.5% fractiles.
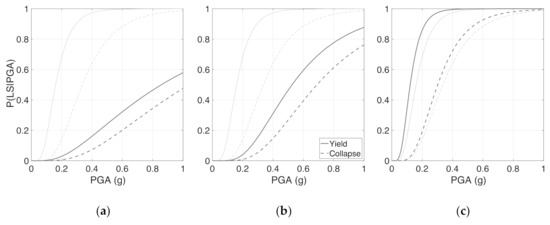
Figure 6.
Fragility curves (thicker lines) for RC buildings with correlated parameters: (a) 91.5% fractile; (b) 50% fractile; (c) 8.5% fractile. The mean fragility curves are also displayed, with thinner lines.
3.4. Results and Discussion
In order to carry out the seismic risk assessment in OOFIMS, a Monte Carlo simulation scheme was adopted. Distinct simulations were executed for each different combination of branches in the logic tree (see Section 3.3), thus yielding multiple results. Within the generic simulation, before starting the sampling, the implemented steady-state flow formulation is used to assess the operational state of the undamaged gas network. Then, in each simulation run, the following activities are undertaken:
- The IMs of interest (i.e., PGA, PGV and PGD) at vulnerable components’ sites are estimated using the OOFIMS hazard module;
- The damage state of the components at risk, belonging to both gas and building systems, is estimated through the adopted fragility models;
- The connectivity and operational state are assessed for the damaged gas network;
- The gas system’s performance is estimated through the adopted flow-based metric;
- A second performance metric of interest for this application is computed, namely, the displaced population, Pd. In the implemented model, people can be displaced from their homes either because of direct physical damage (building usability) or because of lack of basic services/utilities (building habitability), resulting from damage to interdependent utility systems (only gas system in this case). See Franchin and Cavalieri (2015) [18] for further details.
As mentioned above, the logic tree resulting from the adoption of the proposed approach for correlated parameters is composed of 36 branches, thus entailing the execution of 36 Monte Carlo simulations. Each single simulation consists of 1000 runs (i.e., iterations or samples), a number deemed to be sufficient in consideration of the illustrative character of the paper, and appropriate to show the main features of the implemented methodology for the treatment of and sensitivity to epistemic uncertainty. Overall, the analyses required a computational time of about 14 h, using a computer with a 3.50 GHz eight-core CPU and 64 GB RAM.
The subplots in Figure 7 show twelve λ-curves of SSI, obtained from different combinations of choices in the first three modules, concerning Mmax, the GMPE and both variables in the GAS fragility model. An important feature characterising this application is that the highest attainable value of SSI, corresponding to the reference undamaged conditions and called here SSI0, results in being lower than 1, and in particular, 0.976. This effect owes to the pressure-driven mode adopted in the flow formulation, combined with the assigned pressure levels and thresholds in the network (see [13,14]). As a result, several node loads are reduced even in non-seismic conditions, yielding a SSI0 value lower than 1. Looking at the curves, it is possible to see the amount of epistemic uncertainty in the output and also qualitatively assess its sensitivity to the considered modules. It is noted that the maximum magnitude practically does not affect the curves, while the influence of the residuals and especially the GMPE is more evident. In particular, the upper fractiles for cause the λ-curves to be slightly shifted towards lower exceedance rates for SSI values, as expected, whilst in all cases the Akkar and Bommer (2010) [52] GMPE leads to more severe λ-curves of SSI, laying below the ones related to the Boore and Atkinson (2008) [53] model.
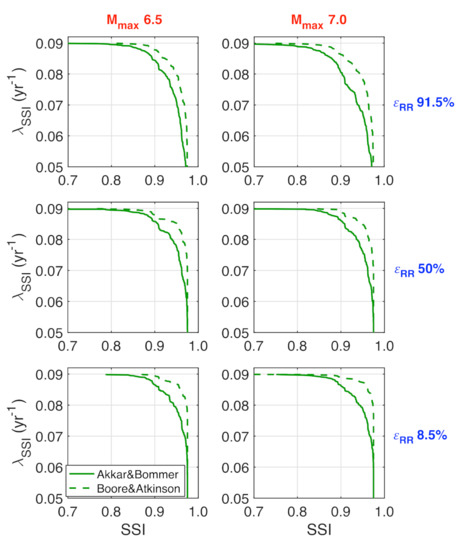
Figure 7.
Mean annual frequency (MAF) curves of System Serviceability Index (SSI), due to different choices of ground motion prediction equation (GMPE), Mmax and residuals in the gas network (GAS) fragility model.
Figure 8 shows the MAF curves of the displaced population normalised to the total population, Pd/P. The λ-curves shown are 36, as the number of simulations carried out. Each curve corresponds to a single branch of the logic tree and quantifies the aleatory uncertainty contained in the employed models and parameters, whilst the spread of the curves around the average gives a clear indication of the epistemic uncertainty. As a consequence, the distribution of Pd/P corresponding to the full suite of curves captures both aleatory and epistemic uncertainties (Bommer and Scherbaum, 2008) [8]. Figure 8 displays the weighted average curve of Pd/P (for fixed MAF values), as well as the 95% confidence bounds and 16% and 84% weighted fractile curves. In fact, while the confidence in the estimate increases with the number of simulations, N, thus leading the confidence interval to reduce, the weighted fractiles are only a function of the sampled values.
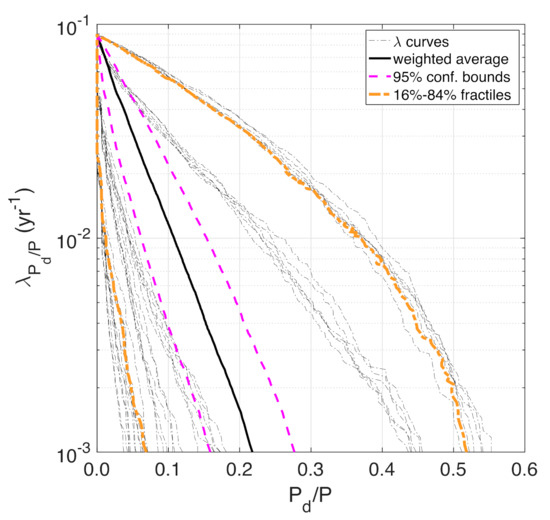
Figure 8.
MAF curves of Pd/P, with weighted average curve, 95% confidence bounds and 16% and 84% weighted fractile curves.
To gain qualitative insight into the sensitivity of uncertainty in the final output (i.e., the MAF of Pd/P) to the input modules, the subplots in Figure 9 show a disaggregation of the total epistemic uncertainty according to the fractiles of the RC fragility distribution, and following the same order of subplots in Figure 6. Thus, subplots (a), (b) and (c) show the λ-curves obtained by fixing the RC fragility distribution at 91.5%, 50% and 8.5% fractiles, respectively. The curves appear to be clearly grouped into clusters, related to the considered fractiles: naturally, the higher the fractile, the lower the estimated number of displaced people. The similarity of the 50% and 91.5% fractile fragility curves (see Figure 6a,b) leads to two almost overlapped clusters (in Figure 9a,b). In each subplot, two further clusters of curves, related to the two adopted GMPEs, can be identified. In particular, as already seen for SSI, the Akkar and Bommer (2010) [52] GMPE leads to more severe λ-curves of Pd/P, laying on the right of the ones related to the Boore and Atkinson (2008) [53] model. The other two modules, namely, Mmax and , do not cause clustering of curves, and therefore are deemed to contribute less to output epistemic uncertainty.
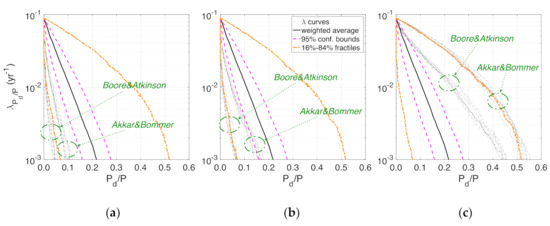
Figure 9.
Disaggregation of total epistemic uncertainty in MAF curves of Pd/P, according to the two adopted GMPEs and the fractiles of the RC fragility distribution: (a) 91.5%; (b) 50%; (c) 8.5%.
Quantitative information about sensitivity can be gained from Figure 10a, showing the module importance ranking obtained from weighted ANOVA (see Section 2.4), for return periods of 100 and 500 years. Each module is displayed with two bars indicating the total variance for the two return periods; the hatched portion of the bars indicates the variance between groups and thus the importance of the module in terms of contribution to the total epistemic uncertainty. It can be readily observed that the building fragility model has the highest importance, whilst the contributions of Mmax and are negligible. Figure 10a provides a clear indication of the modules having the largest impact and thus deserving increased “knowledge” (in terms of enhanced modelling, additional data for calibration, etc.), in the effort to reduce the total epistemic uncertainty in the problem.
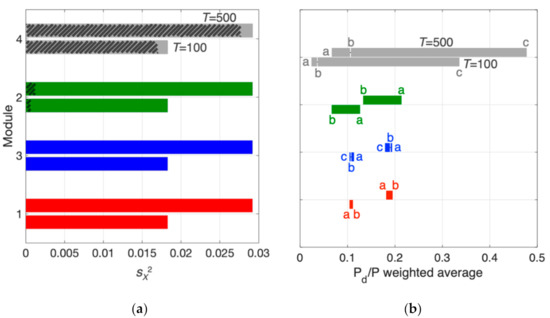
Figure 10.
Importance ranking of modules (from top to bottom), (a) according to the weighted ANOVA method and (b) based on tornado diagram Colours red, green, blue and grey are used for modules #1, #2, #3 and #4, respectively. Which is consistent where pertinent, namely in Figure 6 (RC fragility curves in grey), 7, 9 (text about GMPE in green) and 10.
The tornado diagram shown in Figure 10b presents the sensitivity of the weighted average of Pd/P to the different choices in the considered modules, for the same two return periods used for weighted ANOVA. The plot partly reflects the importance ranking of modules gained from Figure 10a, since the modules characterised by larger distance between the extreme choices, for the generic return period, clearly give higher contribution to uncertainty. Once again, the close values (especially for the 100 years’ return period) of the Pd/P weighted average for choices (a) and (b) in module #4 reflect the similarity of the 50% and 91.5% fractile fragility curves (see Figure 6a,b). Concerning the only module containing models, namely, #2 above, the Akkar and Bommer (2010) [52] GMPE yields higher values of Pd/P weighted average, and thus it is confirmed to provide more severe shaking intensities than the Boore and Atkinson (2008) [53] model, as already seen in Figure 7 and Figure 9. Finally, for all three modules containing parameter values, the sensitivity results are consistent with the input settings, since higher magnitude, upper fractile for and lower fractile for RC fragility distribution yield higher values of displaced population, and vice versa, as expected.
4. Conclusions and Future Work
The best practice for the seismic risk assessment of interdependent Critical Infrastructure systems encompasses taking into account all the relevant uncertainties affecting the problem, as well as providing confidence in the estimate and sensitivity of the total output uncertainty to uncertainty in the input.
Focusing on epistemic uncertainty, this paper presents a comprehensive framework for seismic risk assessment of infrastructure systems that (i) accounts for both aleatory and epistemic uncertainties and (ii) provides the confidence in the estimate, as well as (iii) the sensitivity of output epistemic uncertainty to the components of epistemic uncertainty in the input. Both models and model parameters, affected by epistemic uncertainty, are arranged in a chain of sequential modules within a logic tree. The latter is used for the treatment of epistemic uncertainty and, in combination with weighted ANOVA and tornado diagrams, to evaluate the sensitivity of uncertainty in the output to input epistemic uncertainty. The formulation is general and can be applied to risk assessment problems involving not only infrastructural but also structural systems (an example of treatment of Type II epistemic uncertainty using a logic tree is given in Gabbianelli et al., 2020 [54], related to steel storage pallet racks). The main novel contribution of the paper concerns a method for properly handling parameter correlation in a logic tree. This is a crucial aspect that is often disregarded by analysts in different sectors (e.g., in PSHA) and leads the possible combinations of parameter values to probably cover an unrealistically wide range, thus impairing the entire analysis.
The presented methodology was implemented within an open-source simulation tool for civil infrastructures, OOFIMS, and exemplified with reference to a synthetic city composed of buildings and a gas network. A simulation-based (Monte Carlo) approach was adopted, in which the seismic hazard is characterised in terms of both TGD and PGD, and a flow-based performance metric was used to evaluate the serviceability of the gas system. The employed steady-state gas flow formulation encompasses multiple pressure levels. The presence of the building layer allows showing the possibility to handle system interdependencies, in terms of displaced population evaluated as a function of utility loss in the gas network, as well as highlighting that uncertainty in models/parameters related to one system can affect uncertainty in the output related to dependent systems. Sensitivity results showed that the building fragility model has the highest importance, the GMPE model has a quite low impact, while the contributions (in the uncertainty of the output) of maximum magnitude and residuals in the gas fragility model are negligible. These results suggest that increased “knowledge” is needed to reduce epistemic uncertainty, especially in the derivation of building fragility curves. Such knowledge may be related to an enhanced modelling approach, or additional data for model calibration, or both. For example, instead of employing generic or typological fragility functions, one could use structure-specific fragility curves, obtained with a Bayesian Network (BN) model (e.g., the one proposed by Franchin et al., 2016 [55] for bridges). In the case of complete information available for model calibration, it would be possible to retrieve a single set of fragility curves: epistemic uncertainty in the input will be still somehow present, albeit to a lesser extent, but not treated in the framework (for the case-study considered herein, this would mean removing module #4 in the logic tree). On the other hand, in cases of incomplete information, the BN model can still be used and may lead to obtaining a probabilistic fragility model (such as the one used in this work) characterised by reduced uncertainty (with respect to a generic model). In both cases, the MAF curves of the performance metric of interest will produce a tighter “fan” around the weighted average (see Figure 8 above).
The proposed methodology for treatment of and sensitivity to epistemic uncertainty, as well as its software implementation, can be used by emergency managers, infrastructure owners and all the stakeholders engaged in mitigating the seismic risk of communities in earthquake-prone regions.
Future work aims to consider additional sources of epistemic uncertainty in this field, to compare or develop further methods for sensitivity analysis, as well as to explore the sensitivity of the ANOVA-based importance ranking to the number of runs in the logic tree parallel simulations and to the performance metrics considered.
Author Contributions
Conceptualisation, F.C. and P.F.; methodology, F.C. and P.F.; software, F.C.; validation, F.C. and P.F.; formal analysis, F.C.; investigation, F.C. and P.F.; resources, F.C. and P.F.; data curation, F.C.; writing—original draft preparation, F.C.; writing—review and editing, F.C. and P.F.; visualisation, F.C. and P.F.; supervision, F.C. and P.F.; project administration, F.C. and P.F.; funding acquisition, P.F. Both authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the European Commission, for the SYNER-G collaborative research project, grant number 244061.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Der Kiureghian, A.; Ditlevsen, O. Aleatory or epistemic? Does it matter? Struct. Saf. 2009, 31, 105–112. [Google Scholar] [CrossRef]
- Gokkaya, B.U.; Baker, J.W.; Deierlein, G.G. Quantifying the impacts of modeling uncertainties on the seismic drift demands and collapse risk of buildings with implications on seismic design checks. Earthq. Eng. Struct. Dyn. 2016, 45, 1661–1683. [Google Scholar] [CrossRef]
- Rokneddin, K.; Ghosh, J.; Dueñas-Osorio, L.; Padgett, J.E. Uncertainty Propagation in Seismic Reliability Evaluation of Aging Transportation Networks. In Proceedings of the 12th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP12), Vancouver, BC, Canada, 12–15 July 2015. [Google Scholar]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Petty, M.D. Calculating and Using Confidence Intervals for Model Validation. In Proceedings of the 2012 Fall Simulation Interoperability Workshop, Orlando, FL, USA, 10–14 September 2012. [Google Scholar]
- Visser, H.; Folkert, R.J.M.; Hoekstra, J.; De Wolff, J.J. Identifying key sources of uncertainty in climate change projections. Clim. Chang. 2000, 45, 421–457. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Bommer, J.J.; Scherbaum, F. The use and misuse of logic trees in probabilistic seismic hazard analysis. Earthq. Spectra 2008, 24, 997–1009. [Google Scholar] [CrossRef]
- Zhang, H.; Mullen, R.L.; Muhanna, R.L. Interval Monte Carlo methods for structural reliability. Struct. Saf. 2010, 32, 183–190. [Google Scholar] [CrossRef]
- Alam, M.S.; Barbosa, A.R. Probabilistic seismic demand assessment accounting for finite element model class uncertainty: Application to a code-designed URM infilled reinforced concrete frame building. Earthq. Eng. Struct. Dyn. 2018, 47, 2901–2920. [Google Scholar] [CrossRef]
- Tate, E.; Muñoz, C.; Suchan, J. Uncertainty and sensitivity analysis of the HAZUS-MH flood model. Nat. Hazards Rev. 2015, 16, 04014030. [Google Scholar] [CrossRef]
- Cavalieri, F.; Franchin, P. Treatment of and Sensitivity to Epistemic Uncertainty in Seismic Risk Assessment of Infrastructures. In Proceedings of the 13th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP13), Seoul, Korea, 26–30 May 2019. [Google Scholar]
- Cavalieri, F. Steady-state flow computation in gas distribution networks with multiple pressure levels. Energy 2017, 121, 781–791. [Google Scholar] [CrossRef]
- Cavalieri, F. Seismic risk assessment of natural gas networks with steady-state flow computation. Int. J. Crit. Infrastruct. Prot. 2020, 28, 100339. [Google Scholar] [CrossRef]
- Franchin, P.; Cavalieri, F. OOFIMS (Object-Oriented Framework for Infrastructure Modelling and Simulation). Available online: https://sites.google.com/a/uniroma1.it/oofims/home/ (accessed on 13 October 2020).
- MATLAB® R2019b; The MathWorks Inc.: Natick, MA, USA, 2019.
- SYNER-G Collaborative Research Project, Funded by the European Union within Framework Programme 7 (2007–2013), under Grant Agreement No. 244061, 2012. Available online: http://www.syner-g.eu/ (accessed on 13 October 2020).
- Franchin, P.; Cavalieri, F. Probabilistic assessment of civil infrastructure resilience to earthquakes. Comput. Civ. Infrastruct. Eng. 2015, 30, 583–600. [Google Scholar] [CrossRef]
- Su, L.; Li, X.L.; Jiang, Y.P. Comparison of methodologies for seismic fragility analysis of unreinforced masonry buildings considering epistemic uncertainty. Eng. Struct. 2020, 205, 110059. [Google Scholar] [CrossRef]
- Morales-Torres, A.; Escuder-Bueno, I.; Altarejos-García, L.; Serrano-Lombillo, A. Building fragility curves of sliding failure of concrete gravity dams integrating natural and epistemic uncertainties. Eng. Struct. 2016, 125, 227–235. [Google Scholar] [CrossRef]
- Miller III, A.C.; Rice, T.R. Discrete approximations of probability distributions. Manag. Sci. 1983, 29, 352–362. [Google Scholar] [CrossRef]
- Yilmaz, C.; Silva, V.; Weatherill, G. Probabilistic framework for regional loss assessment due to earthquake-induced liquefaction including epistemic uncertainty. Soil Dyn. Earthq. Eng. 2020, 106493. [Google Scholar] [CrossRef]
- Benjamin, J.R.; Cornell, C.A. Probability, Statistics, and Decision for Civil Engineers; McGraw Hill, Inc.: New York, NY, USA, 1970. [Google Scholar]
- Merz, B.; Thieken, A.H. Flood risk curves and uncertainty bounds. Nat. Hazards 2009, 51, 437–458. [Google Scholar] [CrossRef]
- Celik, O.C.; Ellingwood, B.R. Seismic fragilities for non-ductile reinforced concrete frames–Role of aleatoric and epistemic uncertainties. Struct. Saf. 2010, 32, 1–12. [Google Scholar] [CrossRef]
- Celarec, D.; Ricci, P.; Dolšek, M. The sensitivity of seismic response parameters to the uncertain modelling variables of masonry-infilled reinforced concrete frames. Eng. Struct. 2012, 35, 165–177. [Google Scholar] [CrossRef]
- Porter, K.A.; Beck, J.L.; Shaikhutdinov, R.V. Sensitivity of building loss estimates to major uncertain variables. Earthq. Spectra 2002, 18, 719–743. [Google Scholar] [CrossRef]
- Pourreza, F.; Mousazadeh, M.; Basim, M.C. An efficient method for incorporating modeling uncertainties into collapse fragility of steel structures. Struct. Saf. 2021, 88, 102009. [Google Scholar] [CrossRef]
- Easa, S.M.; Ma, Y.; Liu, S.; Yang, Y.; Arkatkar, S. Reliability Analysis of Intersection Sight Distance at Roundabouts. Infrastructures 2020, 5, 67. [Google Scholar] [CrossRef]
- Sevieri, G.; De Falco, A.; Marmo, G. Shedding Light on the Effect of Uncertainties in the Seismic Fragility Analysis of Existing Concrete Dams. Infrastructures 2020, 5, 22. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Cremen, G.; Baker, J.W. Variance-based sensitivity analyses and uncertainty quantification for FEMA P-58 consequence predictions. Earthq. Eng. Struct. Dyn. 2020. [Google Scholar] [CrossRef]
- Crowley, H.; Bommer, J.J.; Pinho, R.; Bird, J. The impact of epistemic uncertainty on an earthquake loss model. Earthq. Eng. Struct. Dyn. 2005, 34, 1653–1685. [Google Scholar] [CrossRef]
- Tyagunov, S.; Pittore, M.; Wieland, M.; Parolai, S.; Bindi, D.; Fleming, K.; Zschau, J. Uncertainty and sensitivity analyses in seismic risk assessments on the example of Cologne, Germany. Nat. Hazards Earth Syst. Sci. 2014, 14, 1625–1640. [Google Scholar] [CrossRef]
- Bensi, M.; Weaver, T. Evaluation of tropical cyclone recurrence rate: Factors contributing to epistemic uncertainty. Nat. Hazards 2020, 103, 3011–3041. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: West Sussex, UK, 2008. [Google Scholar]
- Sobol’, I.M. Sensitivity analysis for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef]
- Sallaberry, C.J.; Helton, J.C. An introduction to complete variance decomposition. Shock Vib. Dig. 2006, 38, 542–543. [Google Scholar]
- Cannavó, F. Sensitivity analysis for volcanic source modeling quality assessment and model selection. Comput. Geosci. 2012, 44, 52–59. [Google Scholar] [CrossRef]
- Bovo, M.; Buratti, N. Evaluation of the variability contribution due to epistemic uncertainty on constitutive models in the definition of fragility curves of RC frames. Eng. Struct. 2019, 188, 700–716. [Google Scholar] [CrossRef]
- Searle, S.R.; Casella, G.; McCulloch, C.E. Variance Components; John Wiley & Sons: Hoboken, NJ, USA, 2006; ISBN 978-0-470-00959-8. [Google Scholar]
- Pianosi, F.; Wagener, T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environ. Model. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef]
- Zadeh, F.K.; Nossent, J.; Sarrazin, F.; Pianosi, F.; van Griensven, A.; Wagener, T.; Bauwens, W. Comparison of variance-based and moment-independent global sensitivity analysis approaches by application to the SWAT model. Environ. Model. Softw. 2017, 91, 210–222. [Google Scholar] [CrossRef]
- Weatherill, G.; Esposito, S.; Iervolino, I.; Franchin, P.; Cavalieri, F. Framework for Seismic Hazard Analysis of Spatially Distributed Systems. In SYNER-G: Systemic Seismic Vulnerability and Risk Assessment of Complex Urban, Utility, Lifeline Systems and Critical Facilities: Methodology and Applications; Pitilakis, K., Franchin, P., Khazai, B., Wenzel, H., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 31, pp. 57–88. [Google Scholar] [CrossRef]
- ALA (American Lifelines Alliance). Seismic Fragility Formulations for Water Systems. Part 1—Guideline; ASCE-FEMA: Reston, VA, USA, 2001. [Google Scholar]
- NIBS; FEMA. HAZUSMH MR4 Multi-Hazard Loss Estimation Methodology—Earthquake Model—Technical Manual; FEMA: Washington, DC, USA, 2007. [Google Scholar]
- Wang, Y.; O’Rourke, T.D. Seismic Performance Evaluation of Water Supply Systems; Technical Report MCEER-08-0015; MCEER: Buffalo, NY, USA, 2008. [Google Scholar]
- Dueñas-Osorio, L. Interdependent Response of Networked Systems to Natural Hazards and Intentional Disruptions. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2005. [Google Scholar]
- Crowley, H.; Colombi, M.; Silva, V. Epistemic Uncertainty in Fragility Functions for European RC Buildings. In SYNER-G: Typology Definition and Fragility Functions for Physical Elements at Seismic Risk; Pitilakis, K., Crowley, H., Kaynia, A.M., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 27, pp. 95–109. [Google Scholar]
- Akkar, S.; Bommer, J.J. Empirical equations for the prediction of PGA, PGV and spectral accelerations in Europe, the Mediterranean region and the Middle East. Seismol. Res. Lett. 2010, 81, 195–206. [Google Scholar] [CrossRef]
- Boore, D.M.; Atkinson, G.M. Ground-motion prediction equations for the average horizontal component of PGA, PGV, and 5%-damped PSA at spectral periods between 0.01 s and 10.0 s. Earthq. Spectra 2008, 24, 99–138. [Google Scholar] [CrossRef]
- Gabbianelli, G.; Cavalieri, F.; Nascimbene, R. Seismic vulnerability assessment of steel storage pallet racks. Ing. Sismica 2020, 37, 18–40. [Google Scholar]
- Franchin, P.; Lupoi, A.; Noto, F.; Tesfamariam, S. Seismic fragility of reinforced concrete girder bridges using Bayesian belief network. Earthq. Eng. Struct. Dyn. 2016, 45, 29–44. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).