Durability-Based Design of Structures Made with Ultra-High-Performance/Ultra-High-Durability Concrete in Extremely Aggressive Scenarios: Application to a Geothermal Water Basin Case Study
Abstract
1. Introduction
- −
- A superior performance in the fresh state, highly conducive to self-compacting and self-levelling consistency. This, besides the inborn technological advantage of an easier fabrication of even complex shapes, also results in the possibility of aligning the fibers coherently with the direction of the casting flow. The latter can be designed in such a way that the preferential direction of fiber alignment matches, as close as possible, with the direction of the principal tensile stresses within the structural element when in service. The structural use of the material can thus greatly benefit from such a tailored alignment of the fibers. The suitably balanced fresh-state performance would allow to mould the shape of an element and, thanks to a tailored casting process, to align the fibers along the direction of the principal tensile stresses resulting from its structural function. A closer correspondence between the shape of an element and its structural function [14,15,16,17,18,19,20,21] can be thus effectively pursued;
- −
- A superior durability in the un-cracked state, because of the high compactness of the matrix, as due to the high content of binders as well as to the use of small maximum aggregate sizes [22];
- −
- −
- Probabilistic safety format;
- −
- Partial safety factor format;
- −
- Deemed-to-satisfy approach;
- −
- Avoidance-of-deterioration approach.
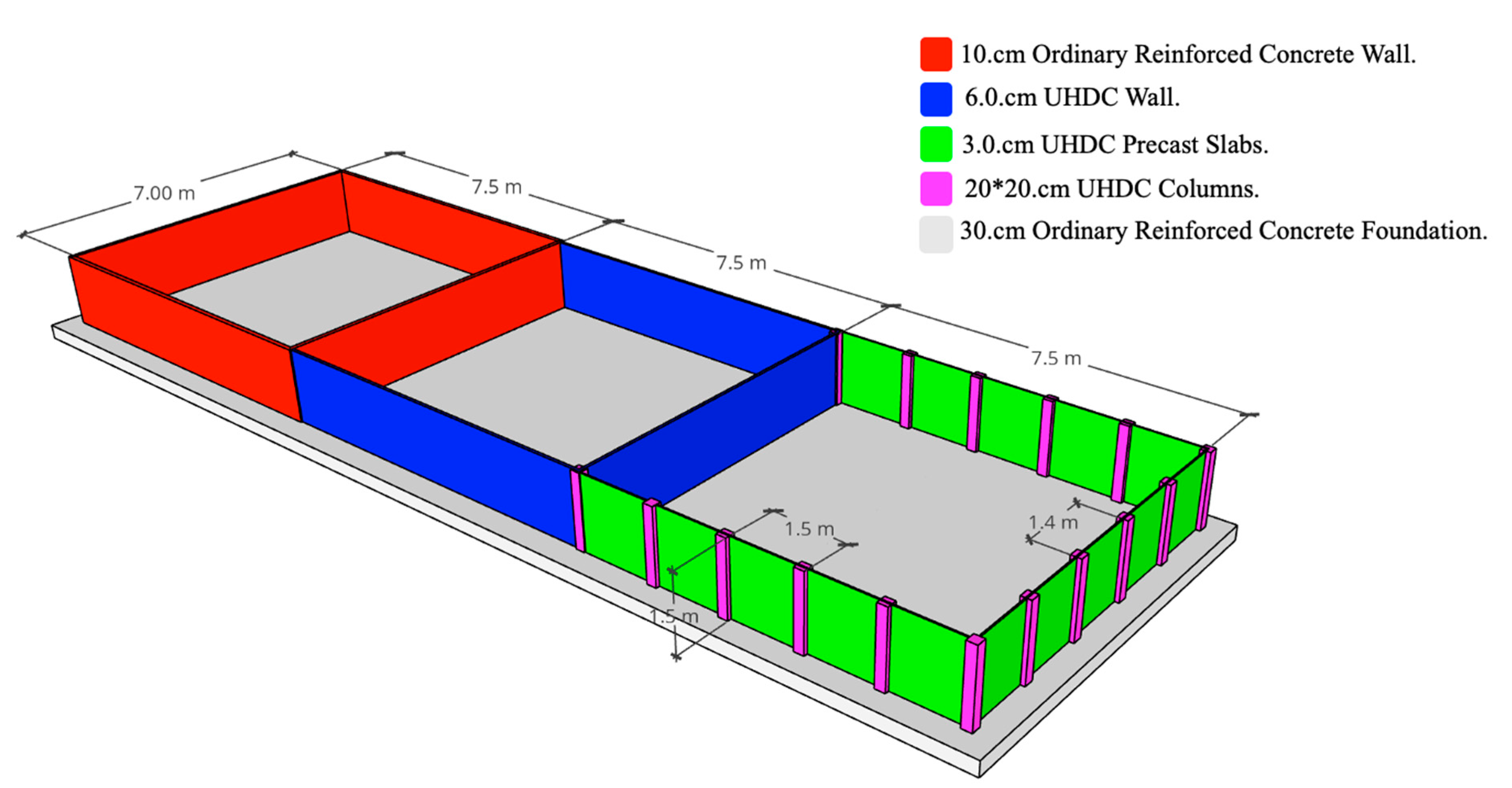
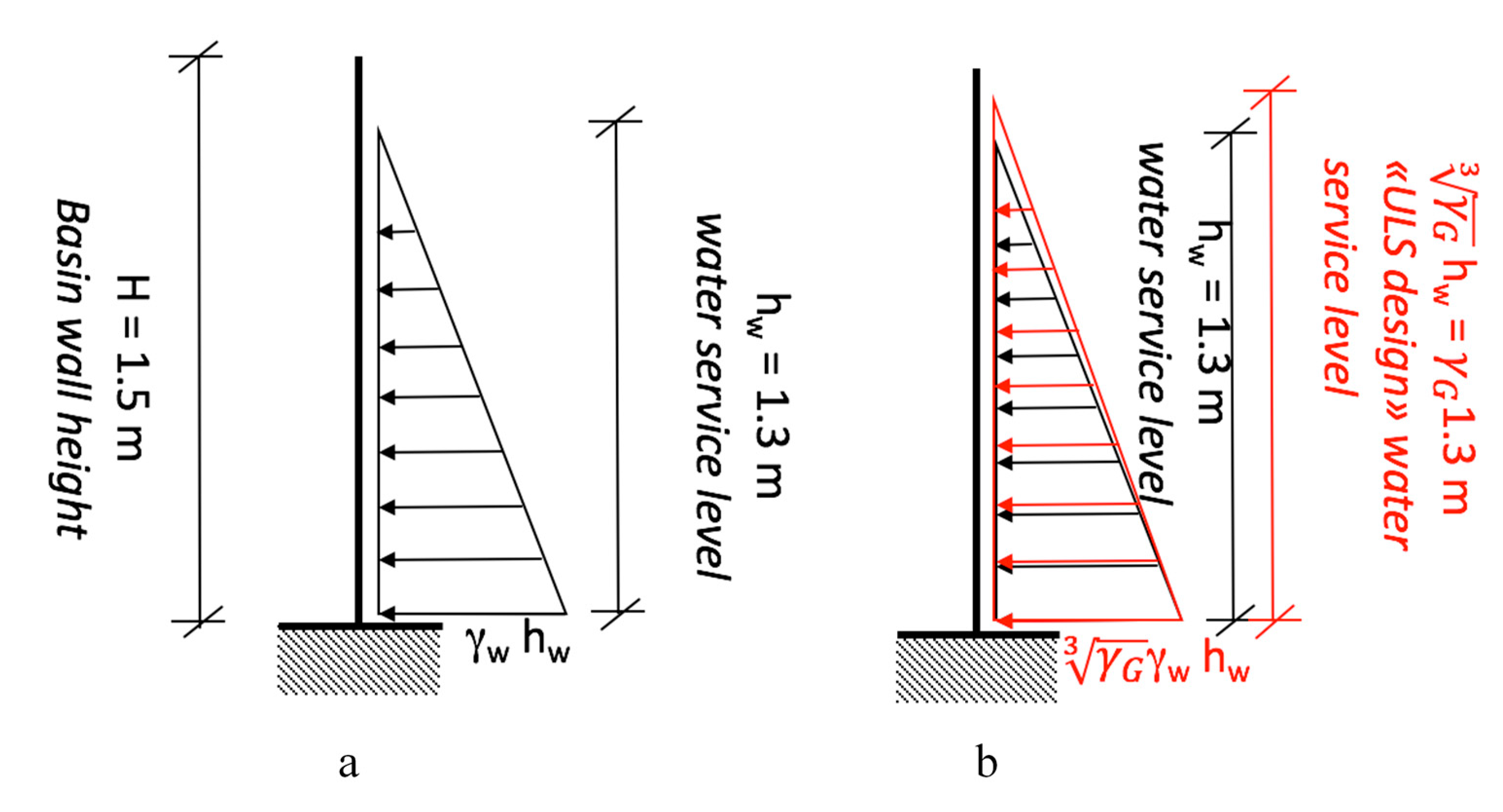
2. Description of the Pilot Case Study: A Water Basin in a Geothermal Power Plant
3. Current Design and Construction Practice for Structures in Geothermal Power Plants (XA Exposure Condition)
- −
- Maximum water/cement ratio according to the Code or the National Application Document (NAD).
- −
- Documents (NAD—in the case of Eurocodes) as well as depending on the type on structure (mass concrete, reinforced concrete, pre-stressed concrete) ranges from 0.4 for XS3 conditions (Danish code for offshore concrete structures DNV-OS-C502 2012 [73]) to 0.65 for XS1 conditions (German code ZTV-W-LB215 issued by Federal Waterways Engineering and Research Institute BAW [74]). Similar prescriptions hold for XA exposure conditions.
- −
- A minimum content of cement, accompanied in some case by cement type prescription (see the Irish NAD to EN 1992-1-1), which, once again according to the Code and depending on the type of structure, ranges from about 300 kg/m3 (Spanish NDA to EN 1992-1-1 for XS1 condition) to 350 kg/m3 (Spanish NAD to EN 1992-1-1) or even more than 400 kg/m3 (Danish code for offshore concrete structures) for XS3 conditions. As for XA conditions, while the Spanish NAD to EN 1992-1-1 reports similar values as for XS, the Irish NAD recommends dosages from 320 kg/m3 for XA1 to 400 kg/m3 for XA3, also depending on the type of cement and on the always recommended total content of ground granulated blast furnace slag (GGBS).
- −
- Minimum cover to reinforcement, to increase the distance to the aggression front, which depends on the structural class and on the level of aggressiveness. EN 1992-1-1 and related NADs recommend a minimum cover ranging from 20 to 45 mm for XS1 condition and from 30 to 55 mm for XS3 condition (structural classes from S1 to S6). No cover prescriptions hold for XA conditions. This is meant to delay, complying with the intended service life of the structure, the penetration of chloride ions and their accumulation up to the critical threshold at the reinforcement depth. In this respect, an acceptable chloride content in the hardened state, also known as chloride threshold, is recommended, e.g., by the Spanish standard EHE-08, equal to 0.3% and 0.6% (by weight of the dried sample) for prestressed and reinforced concrete and for both XS and XA exposures, respectively.
- −
- Cracking limit state, with low maximum allowable crack widths, or the use of prestressing to avoid the formation of cracks, keeping the maximum tensile stress below the cracking strength or even guaranteeing a decompression stress state. EN 1992-1-1 recommends a maximum crack width below 0.3 mm for reinforced concrete members, and prestressed members with unbonded tendons, calculated under quasi-permanent combination of actions, and a decompression state, calculated under frequent combination of actions, for prestressed members with bonded tendons. These prescriptions refer to XS conditions, no explicit requirement holding for XA, even if similar ones may be adopted. More strict requirements may be found in some EN 1992-1-1 NADs, such as 0.2 mm maximum crack width for reinforced concrete members and even 0.1 for XS3 condition for prestressed members with bonded tendons (Danish, Finnish, German and Spanish NAD). In some cases, the prescription also considering the expected service life of the structure (Swedish NAD). Specific rules for the cracking limit state are also contained in EN 1992-3, depending on the Tightness Class (from 0, when some degree of leakage is acceptable, to 3, when no leakage is permitted). Prescriptions for tightness classes above class 1 include maximum crack widths that are defined on the basis of the ratio between height of the stored liquid and thickness of the retaining structure (i.e., on the maximum pressure value), and the need to guarantee a minimum compression zone along the thickness (Table 3).
- −
- Specific criteria, including, e.g., the use of galvanized or stainless steel.
4. Materials and Design Actions
4.1. Reinforced Concrete (Basin 1)
- Characteristic cylindrical compressive strength: fck = 25 MPa
- Average direct tensile strength: fctm = 2.6 MPa
- Average indirect tensile strength (in bending): fcfm = 3.1 MPa
- Instantaneous modulus of elasticity: Ecm = 31 GPa
4.2. UHDC (Basins 2 and 3)
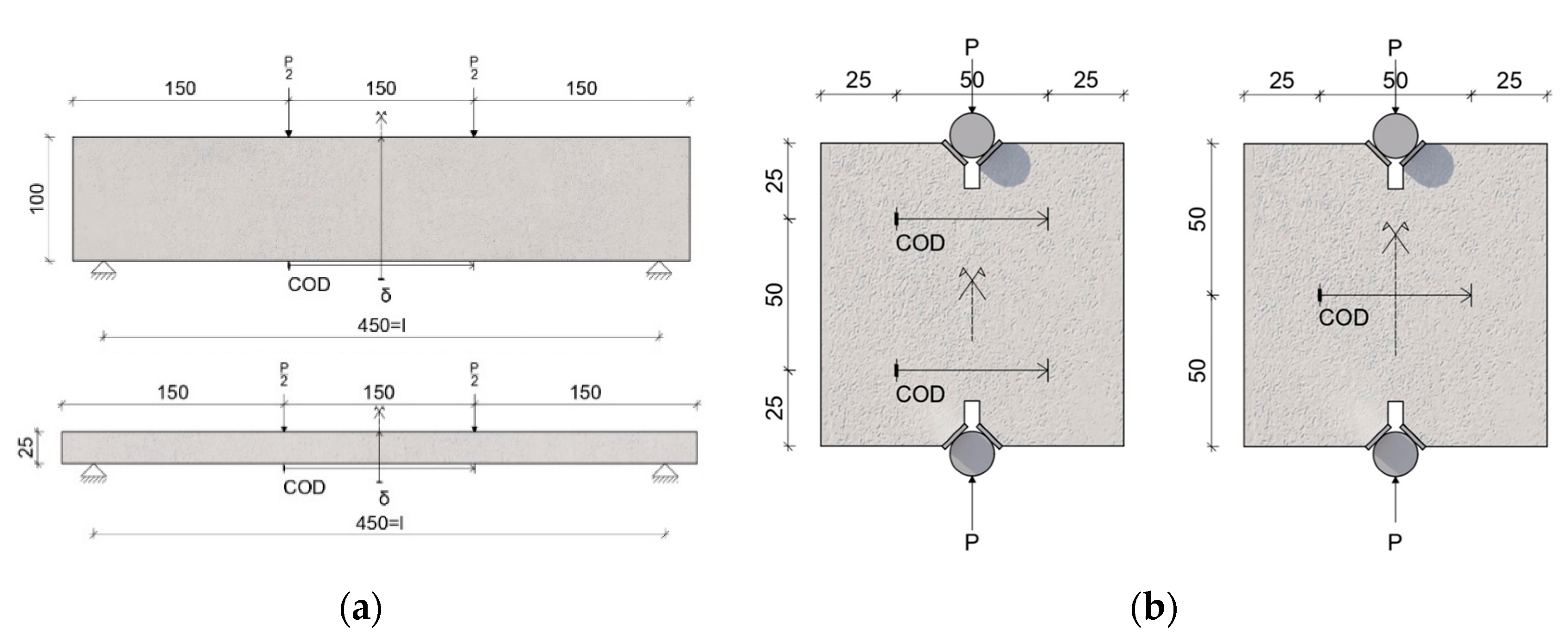
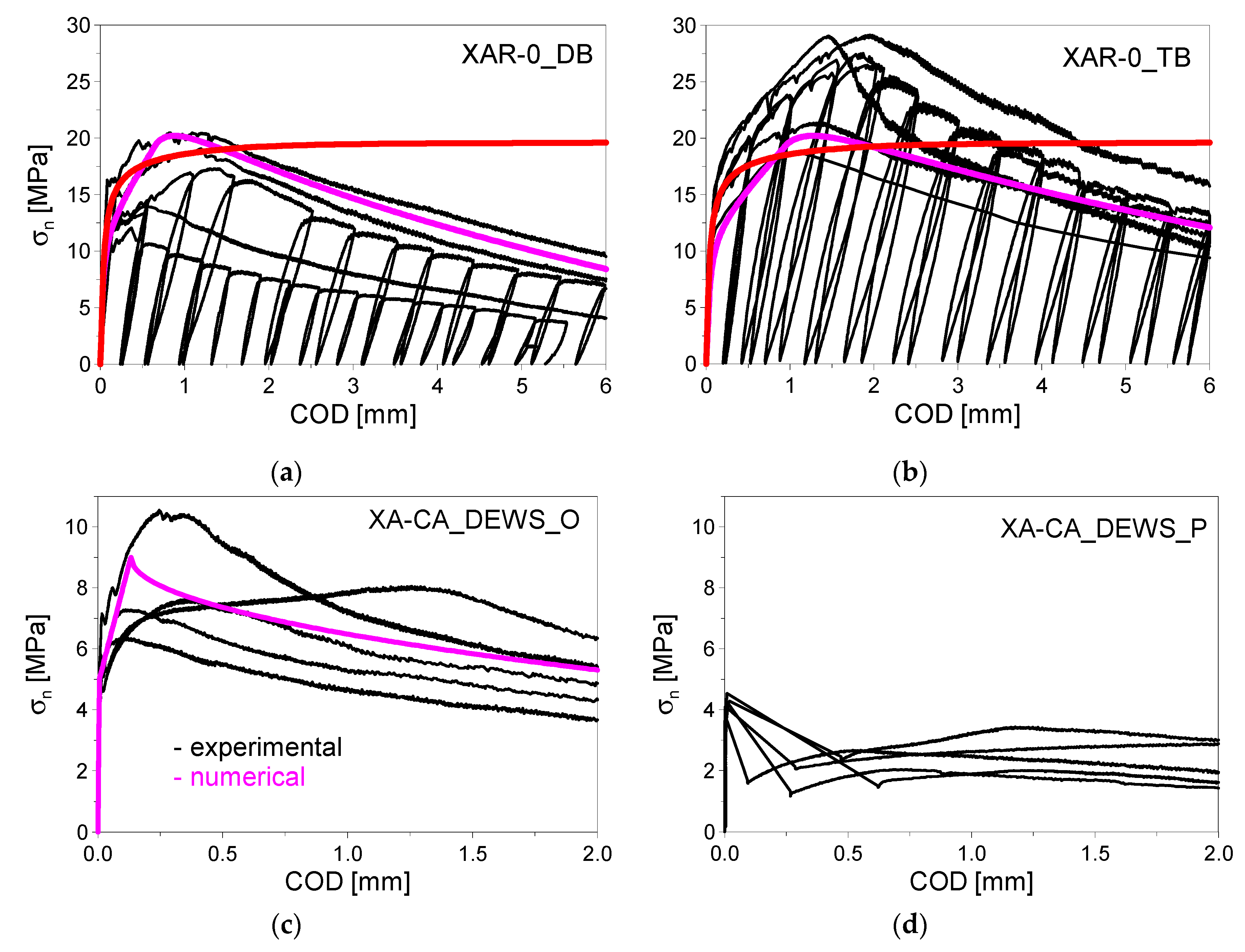
- Deep Beams—DB (L × b × h = 500 × 100 × 100 mm3) (five tests per mix);
- Thin Beams—TB (L × b × h = 500 × 100 × 25 mm3) (five tests per mix).
- Average direct tensile strength: fctm = 7.0/1.25 = 5.6 MPa
- Average indirect tensile strength (in bending): fcfm = 12.0/1.25 = 9.6 MPa
- Instantaneous modulus of elasticity: Ecm = 45 GPa
4.3. Design Actions
5. Durability Assessment: Degradation Mechanisms and Models and Durability Indicator Calibration
5.1. Chloride Diffusion and Chloride Induced Corrosion
- C(x,t): chloride concentration at depth x and time t (%wt binder).
- xcrit: critical chloride depth.
- Ci: initial chloride content of concrete (%wt binder).
- Cs: chloride concentration at surface (x = 0).
- Ccrit: critical chloride concentration.
- T: degradation time (year);
- Ti: time of corrosion initiation (year);
- icorr; corrosion current density (mm/(mA/m2).
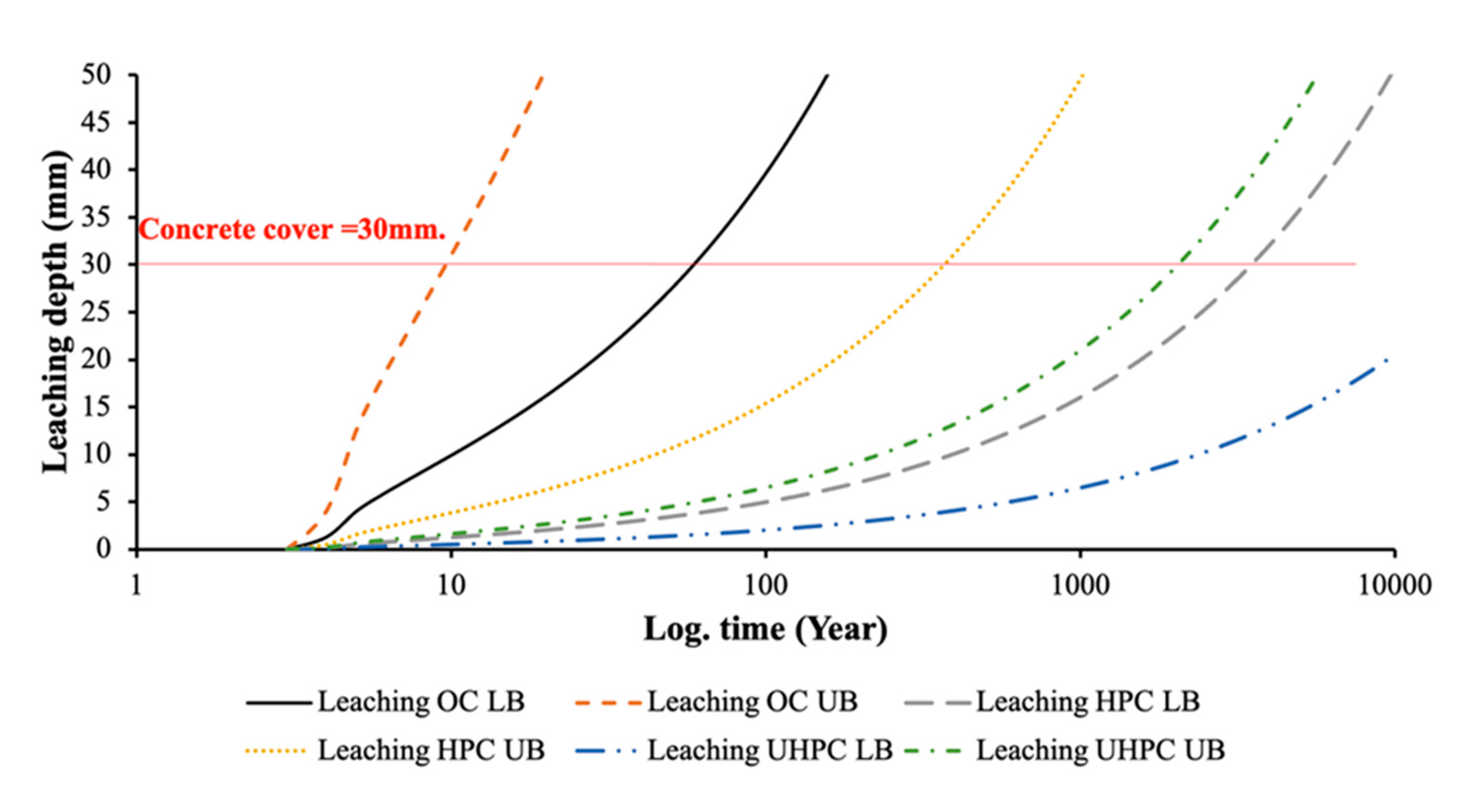
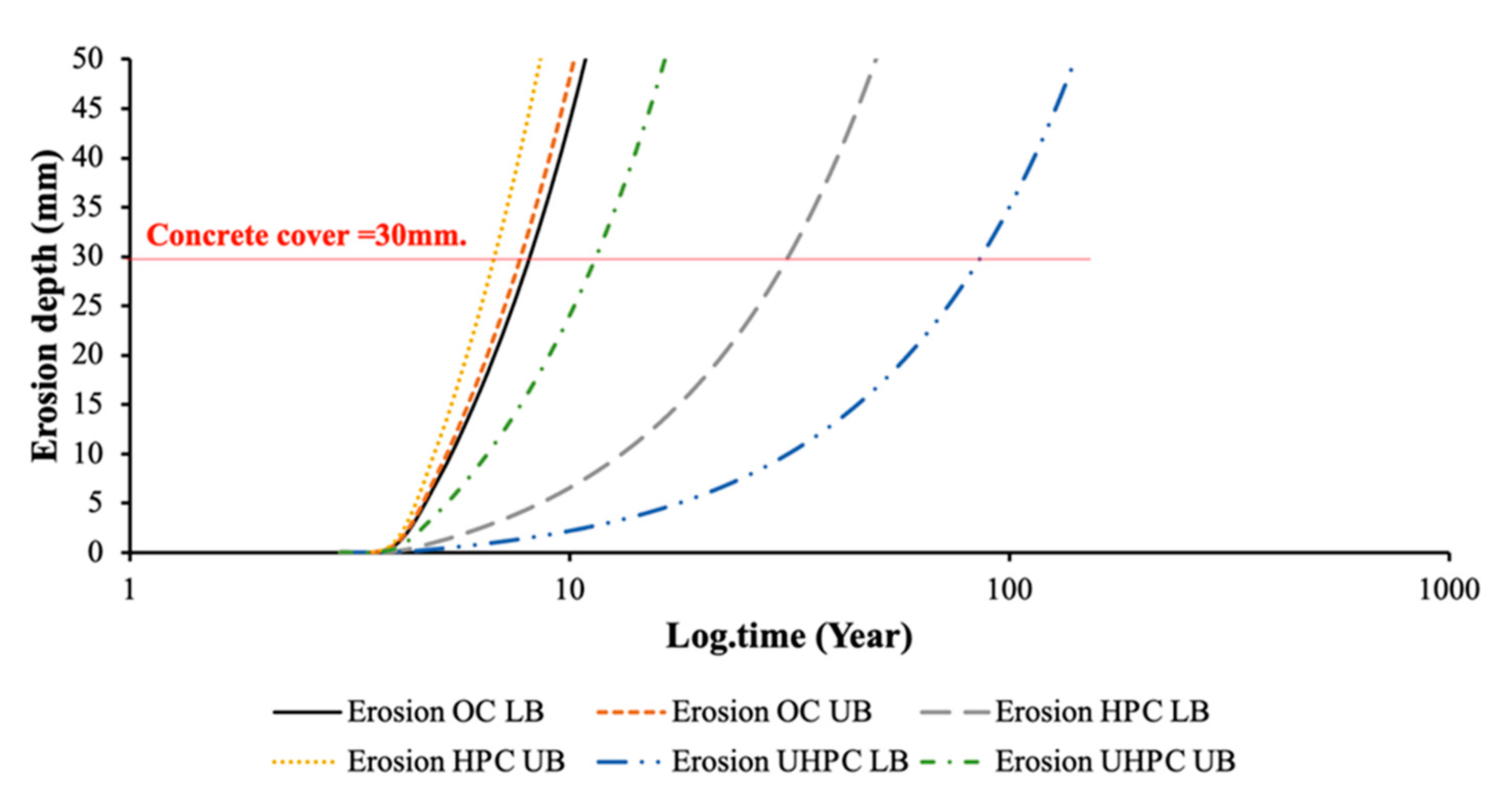
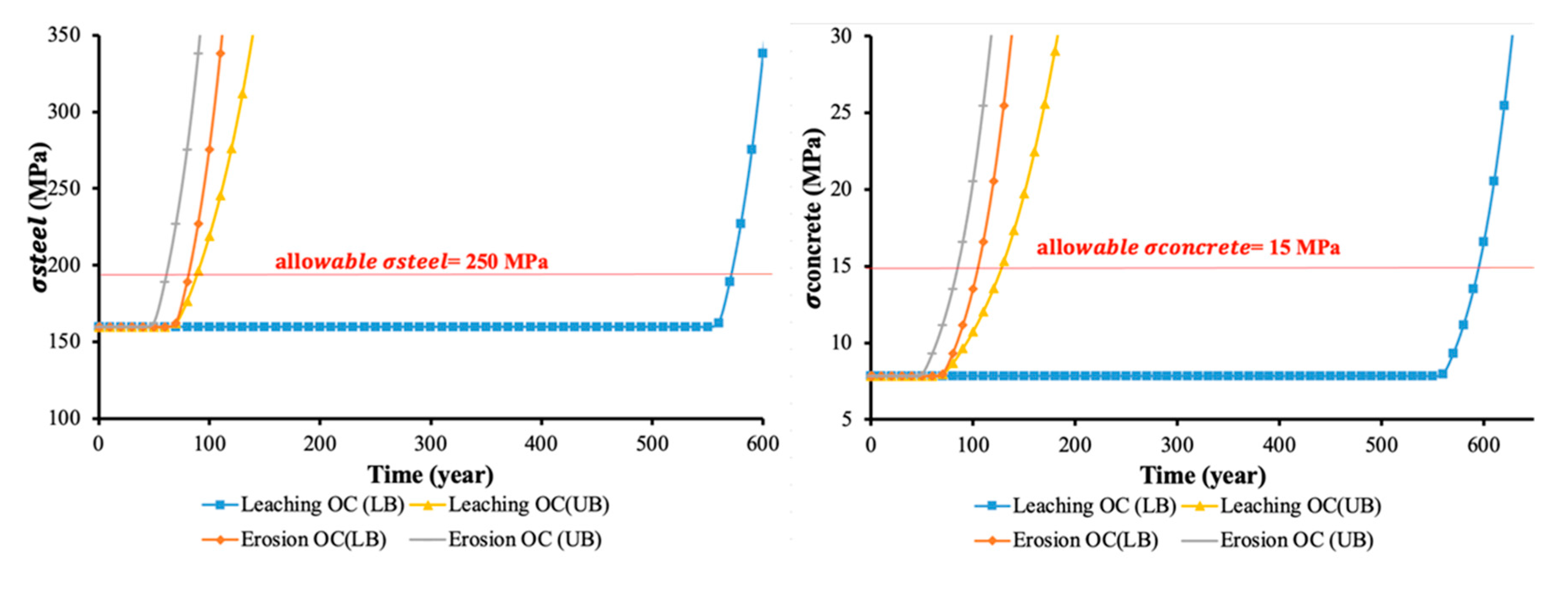
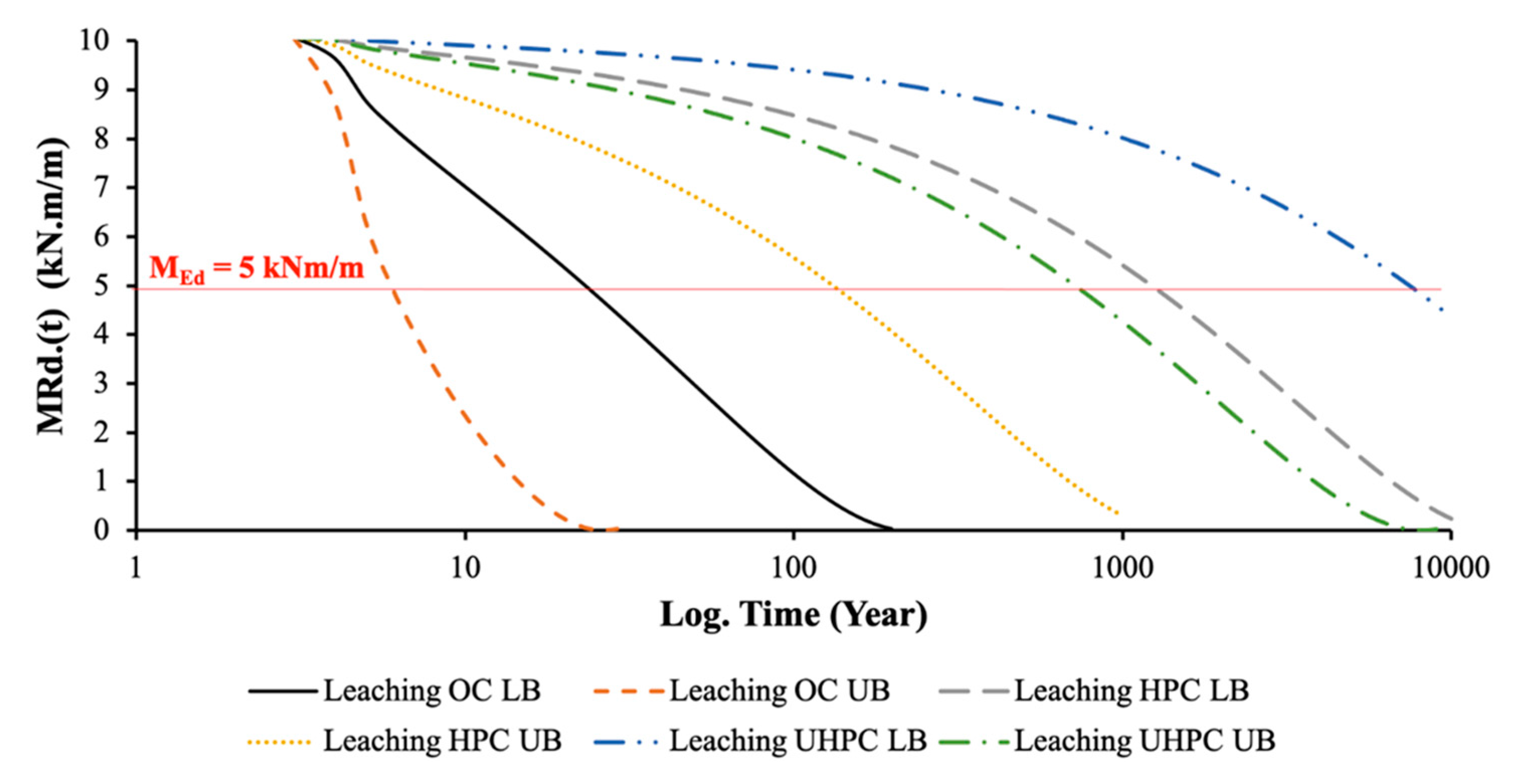
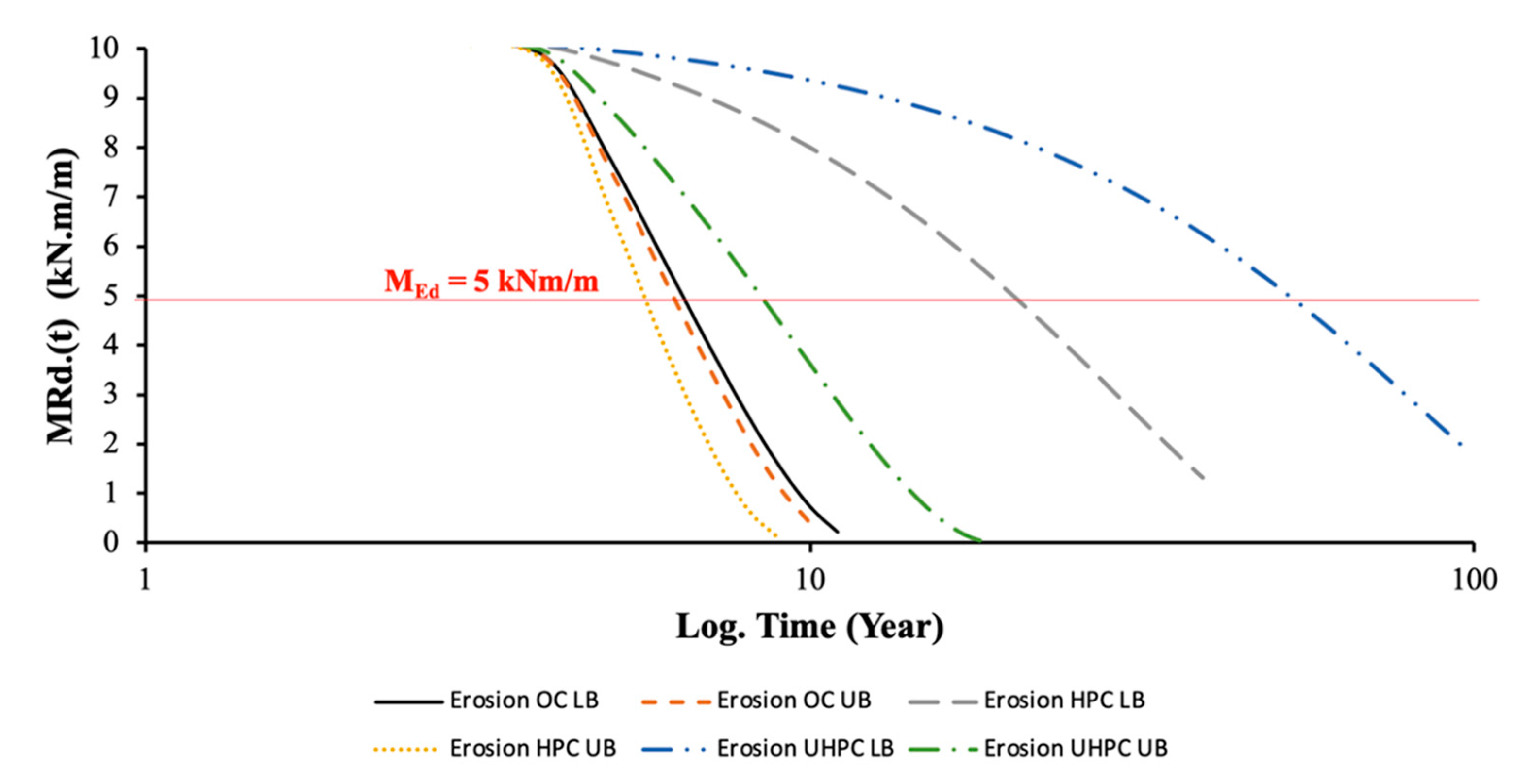
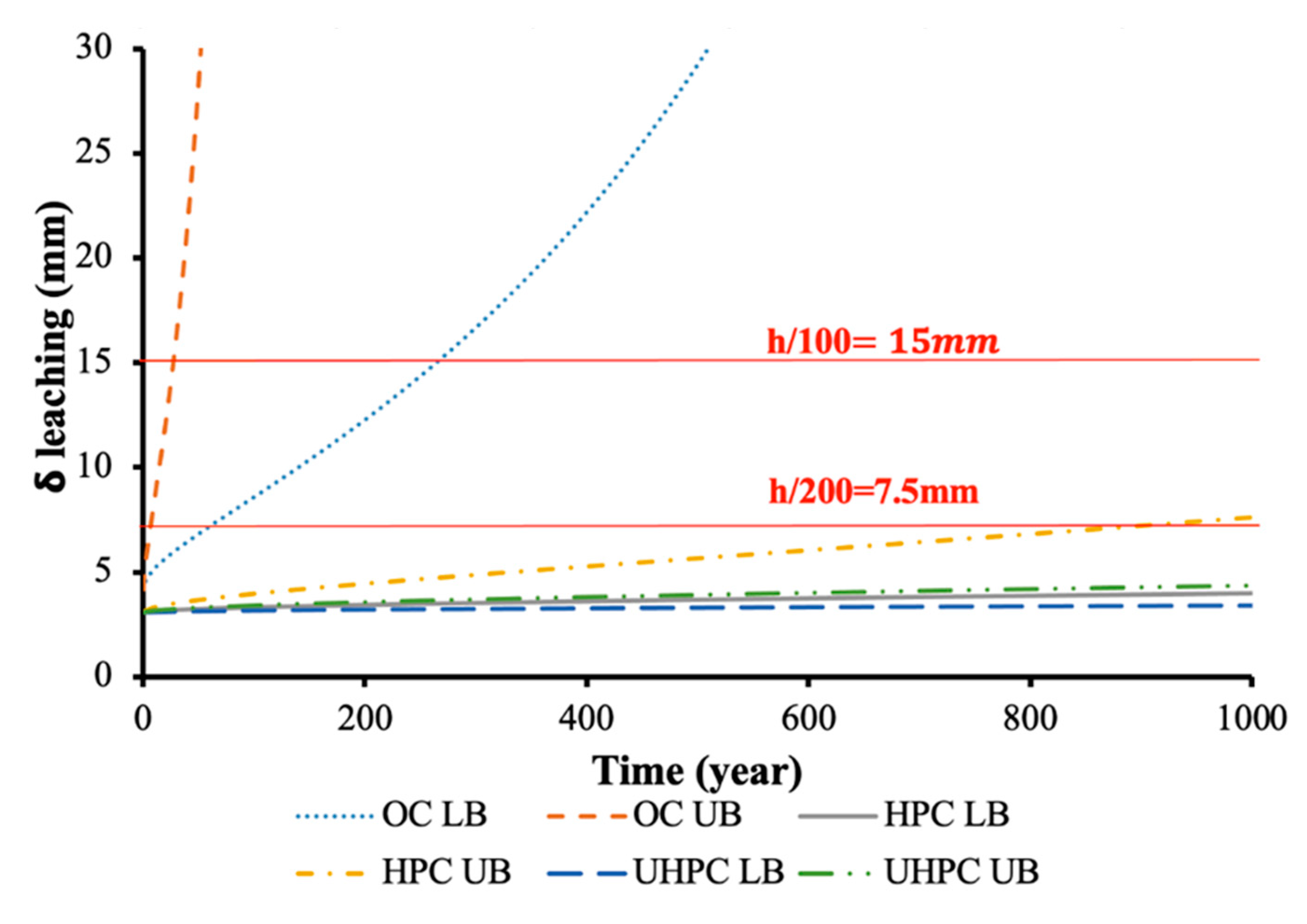
5.2. Acid Attack: Leaching and Erosion
- (1)
- Surface leaching with no erosion and no water pressure gradient: In dense concrete, the reaction only occurs on the surface, so that a dissolution process occurs as a moving boundary and is diffusion controlled [122]. In this case, the thickness of the dissolved zone grows with the square-root of time.
- (2)
- Surface leaching with erosion: If the water is flowing along the surface at high speed and if it brings with it sand and other erosive particles, the dissolved and weakened surface layer can be eroded. When this occurs the leaching process does no longer feature a linear dependence with time in log-scale [122].
- D—diffusion coefficient of the gel layer.
- —ratio of volume of soluble constituents to the total volume.
- ms—mass of soluble matter [g] of CaO per cm3 of concrete.
- cs—Ca(HCO3)2 concentration, or highest concentration of Ca2+ ions, in the solution at the face of intact concrete (g/cm3).
- cm—Ca(HCO3)2 concentration, or highest concentration of Ca2+ ions, in the solution unaffected by the concrete (g/cm3).
- ke—the erosion coefficient (mm d−1).
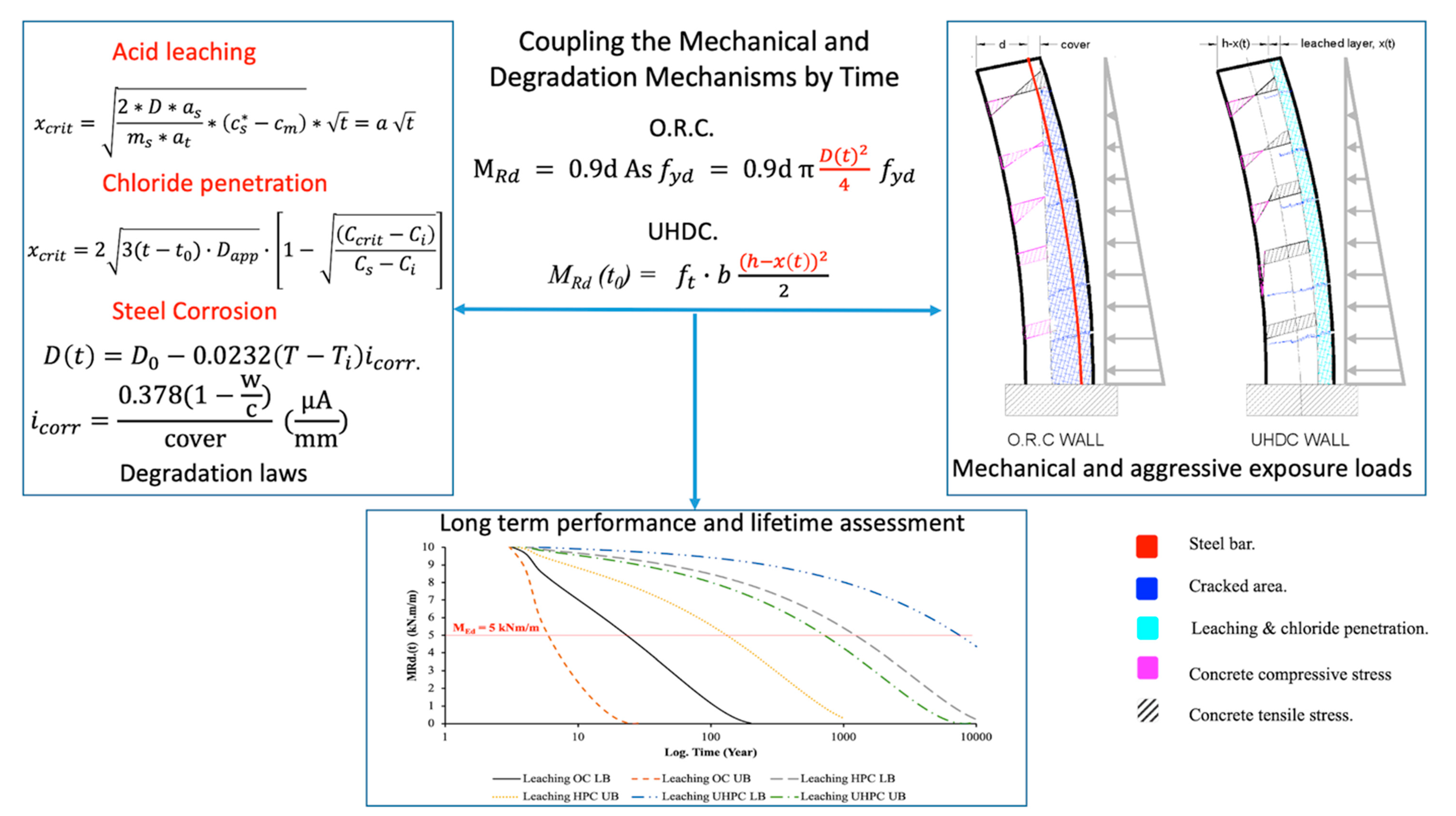
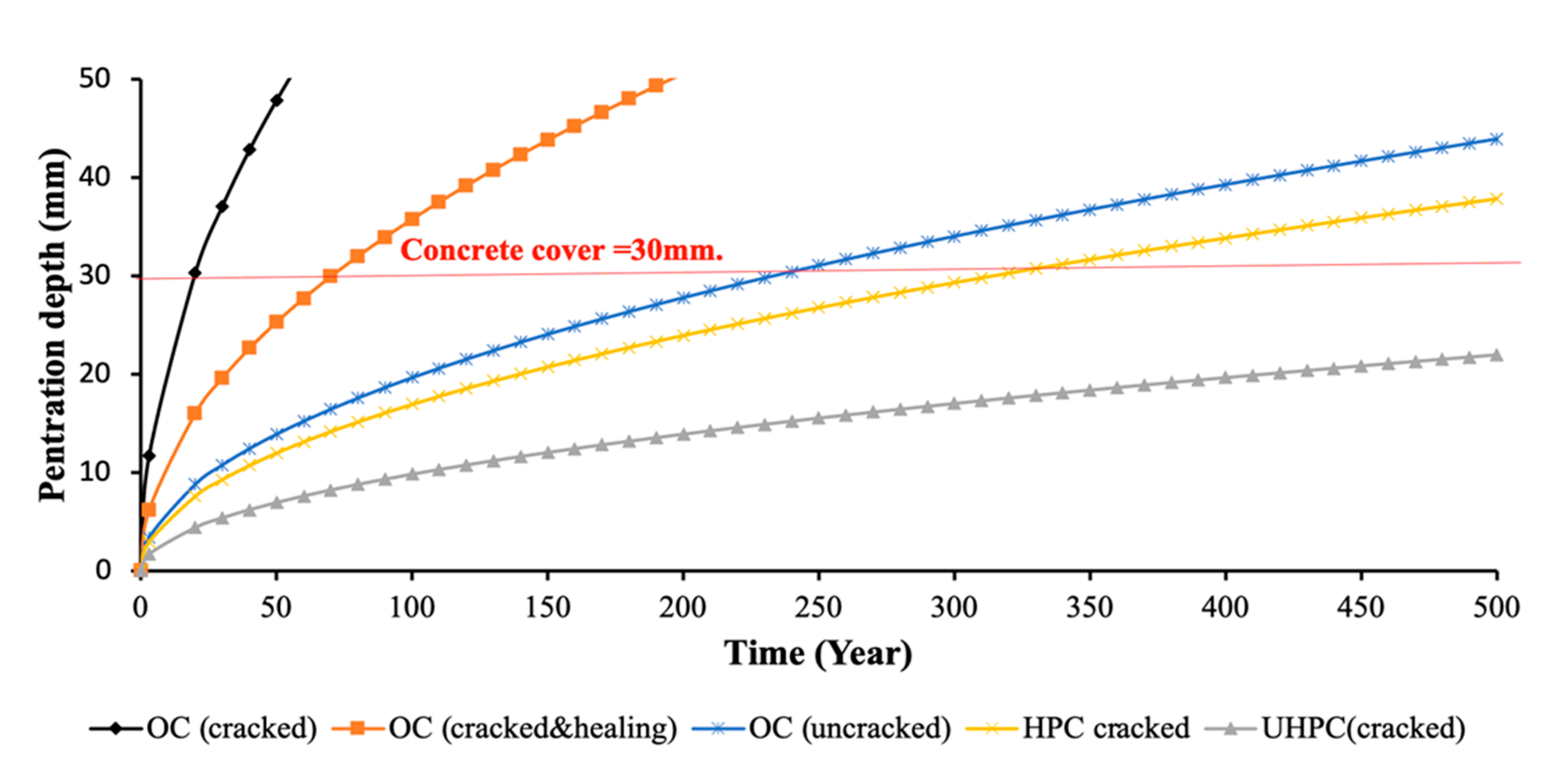
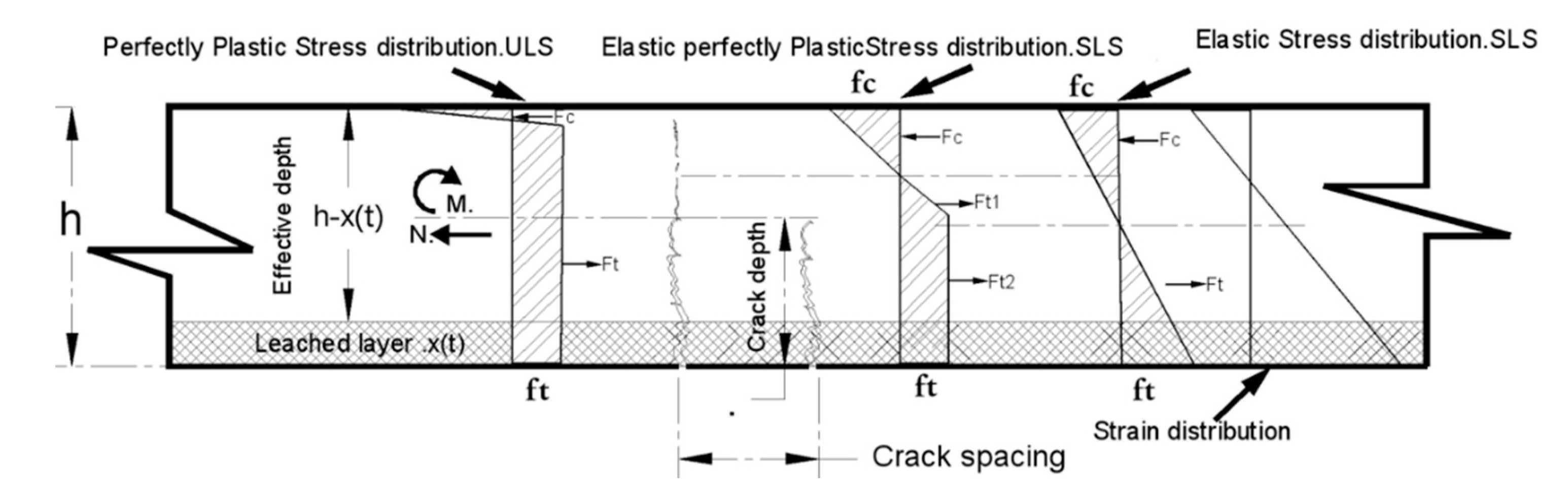
6. Structural Durability Assessment: Embedding Degradation Models into Structural Design Algorithms
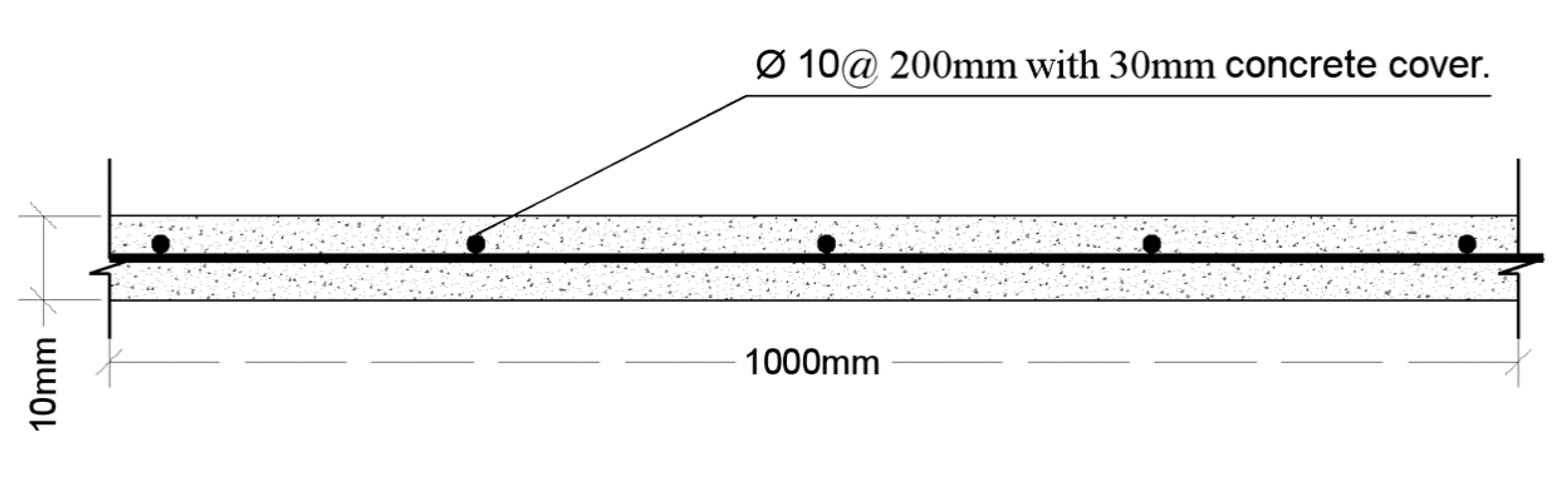
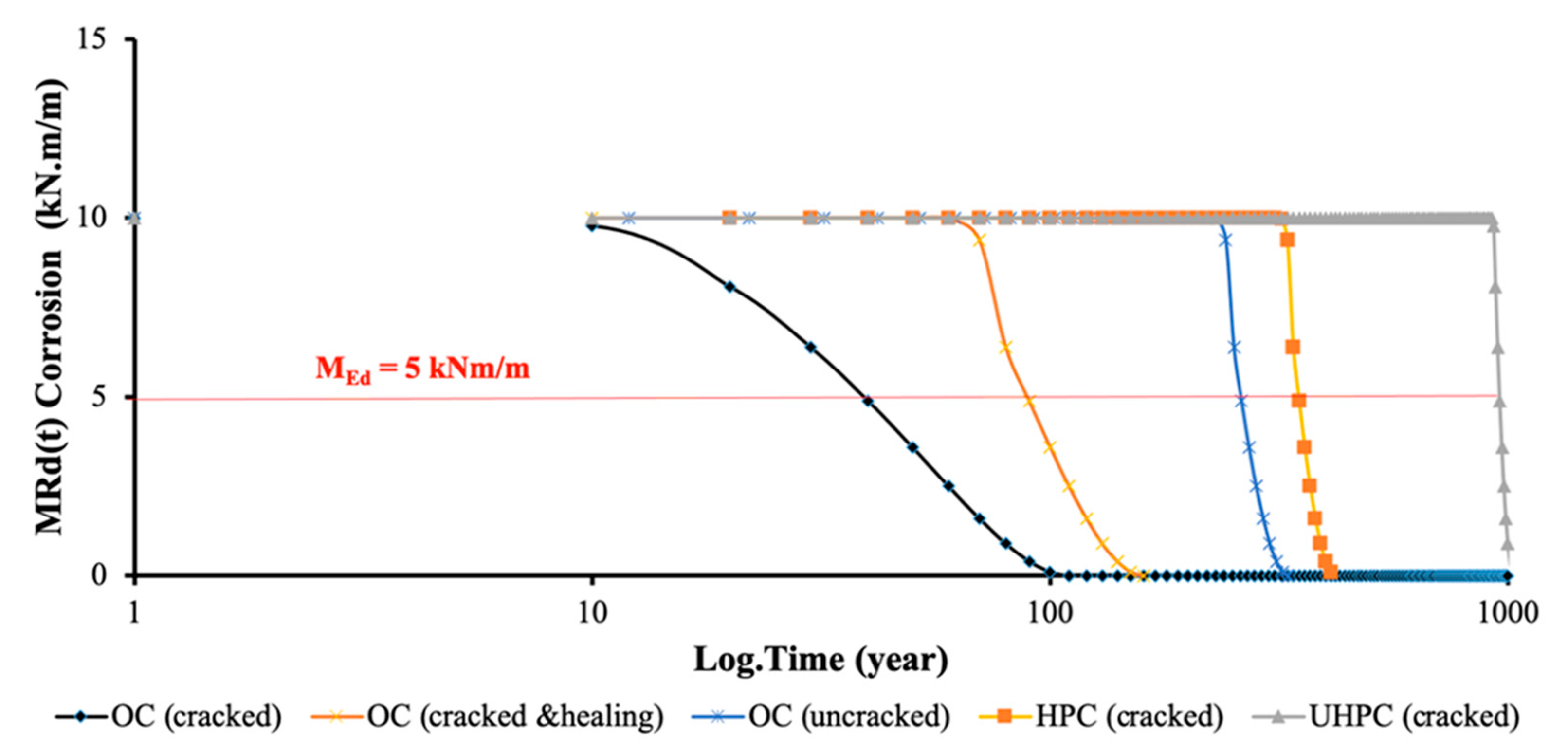
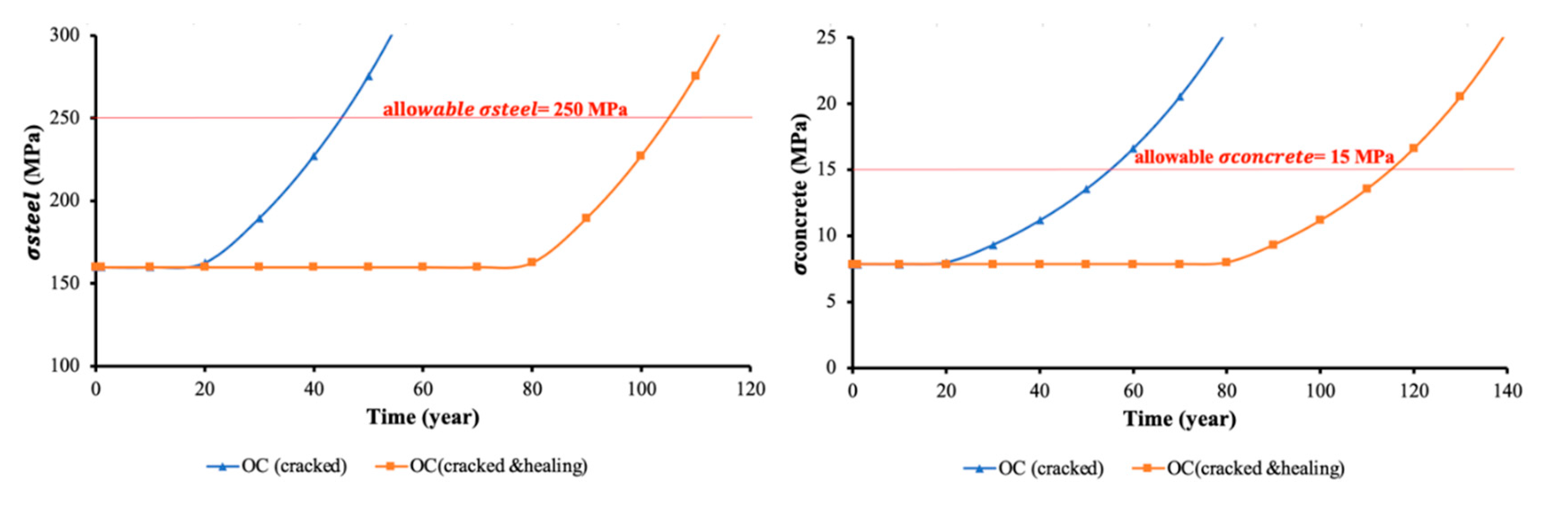
6.1. Cell 1–Ordinary Reinforced Concrete
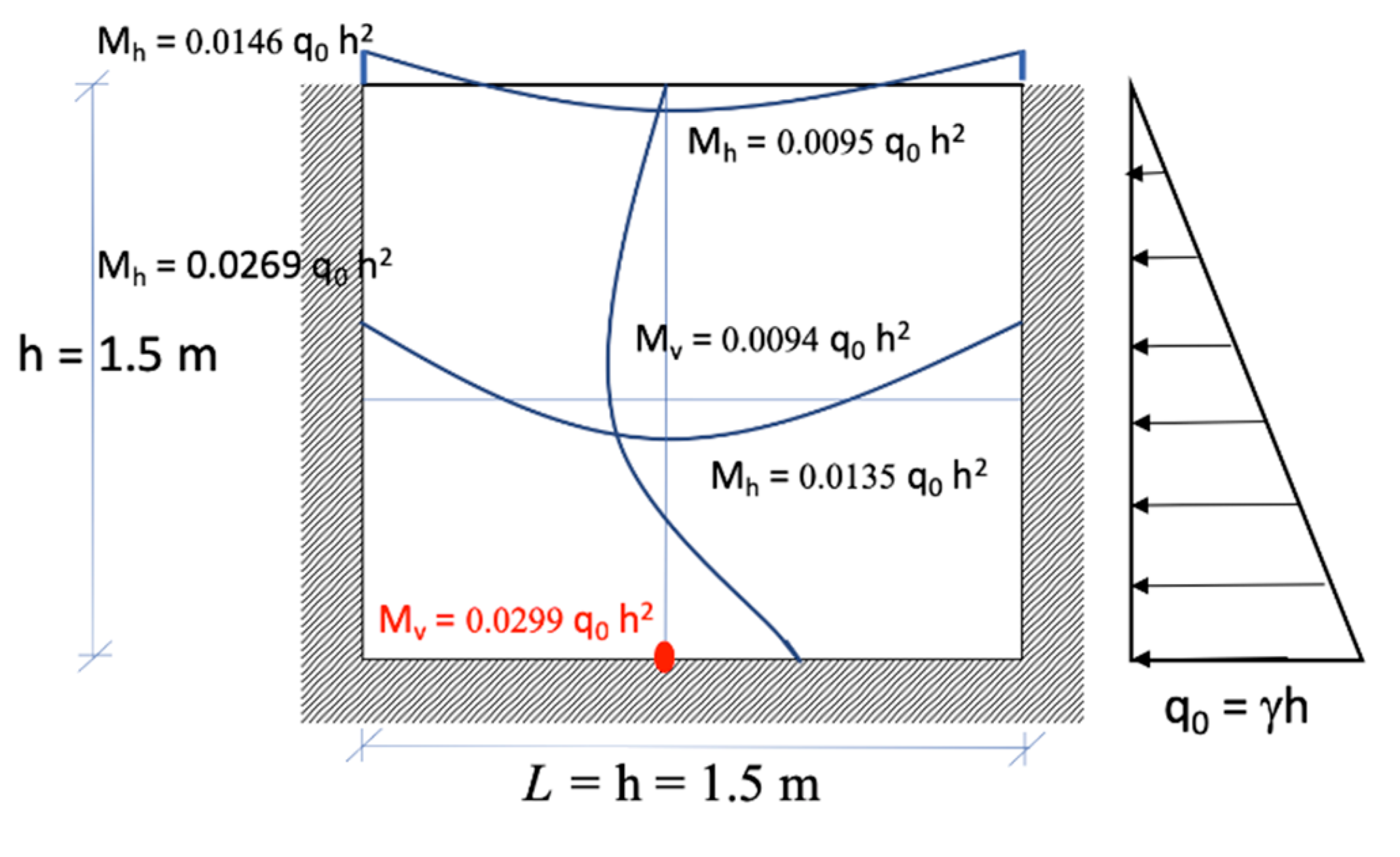
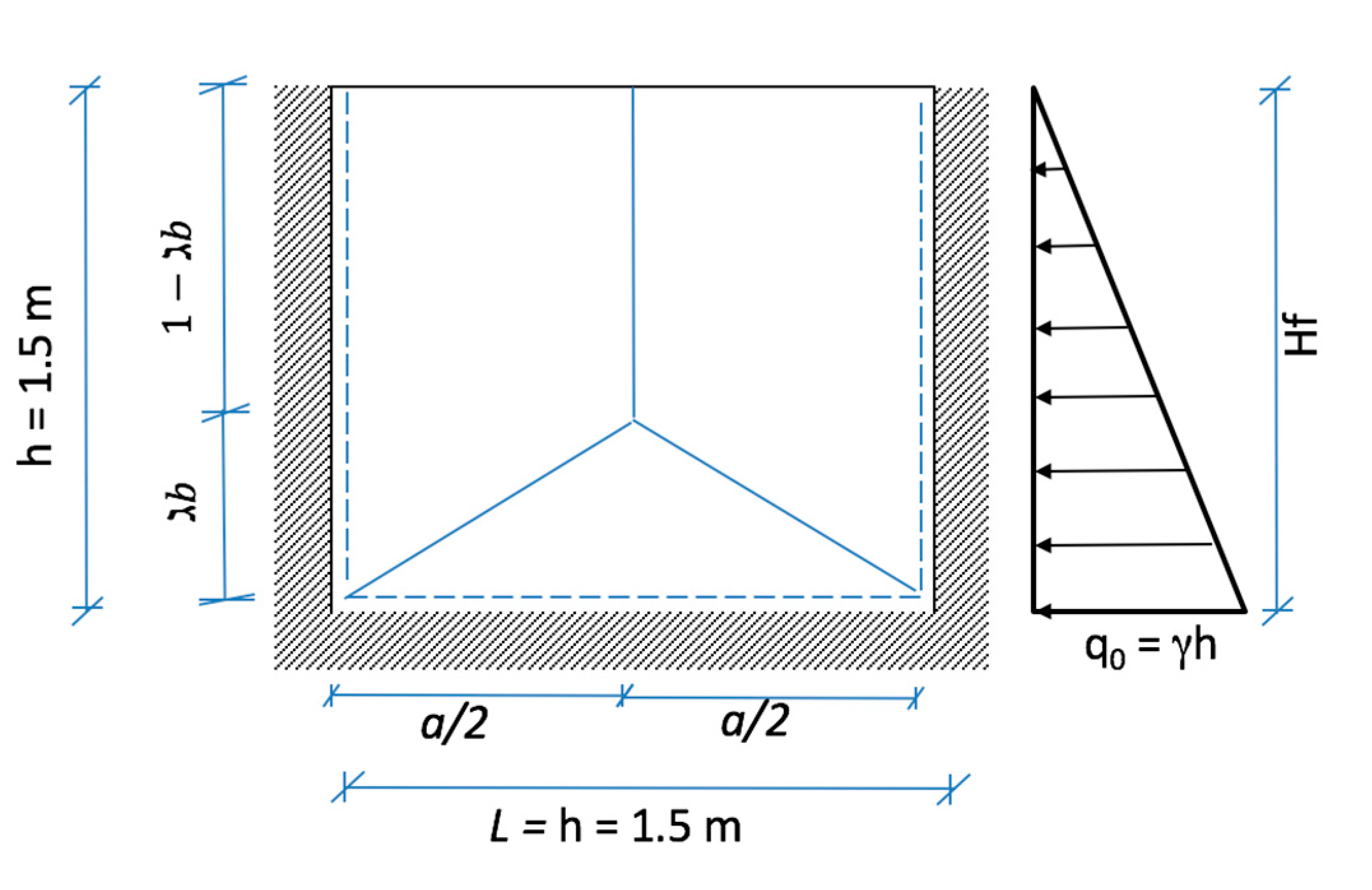
6.2. Cell 2–UHPC (Cantilever Wall Scheme)
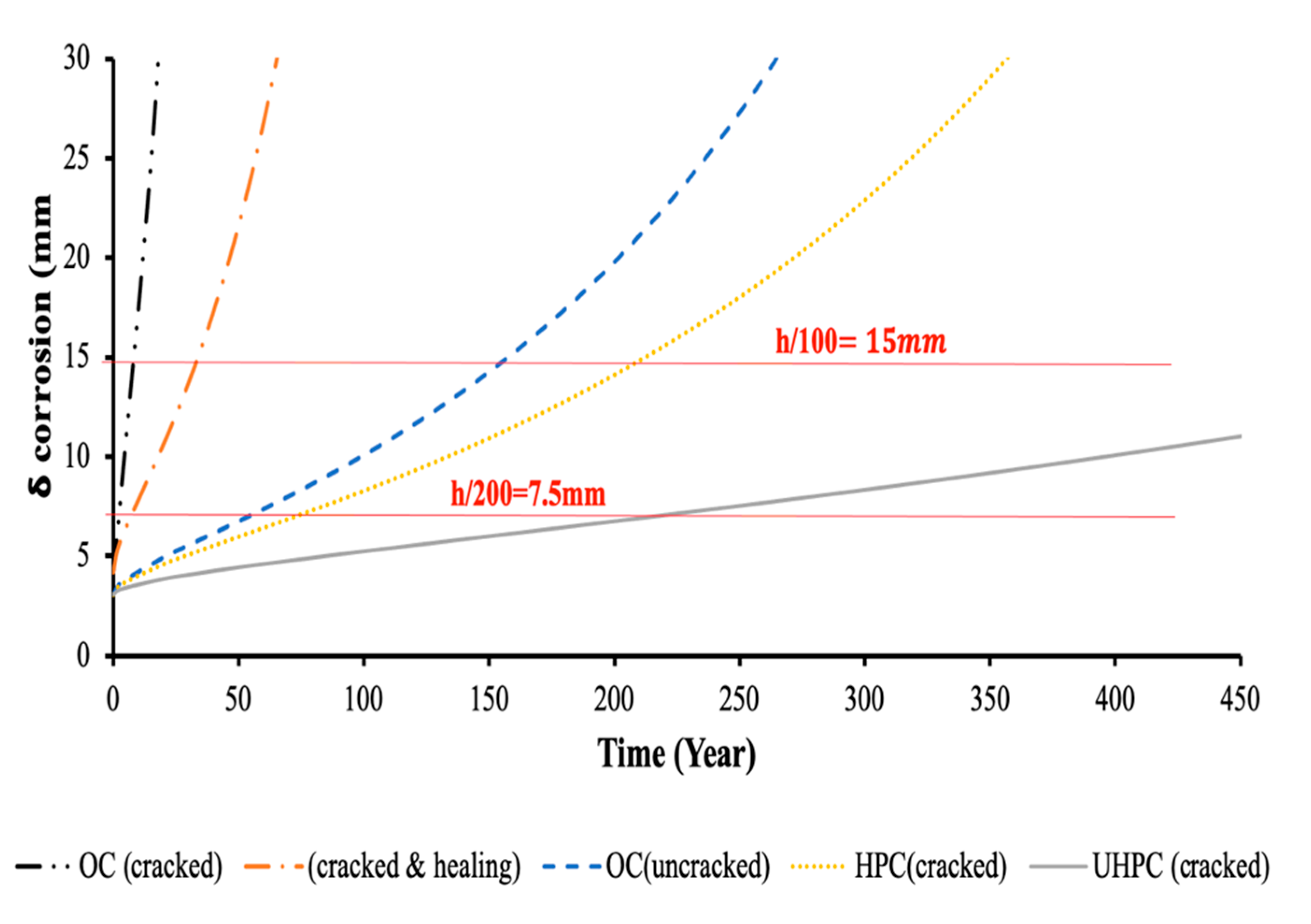
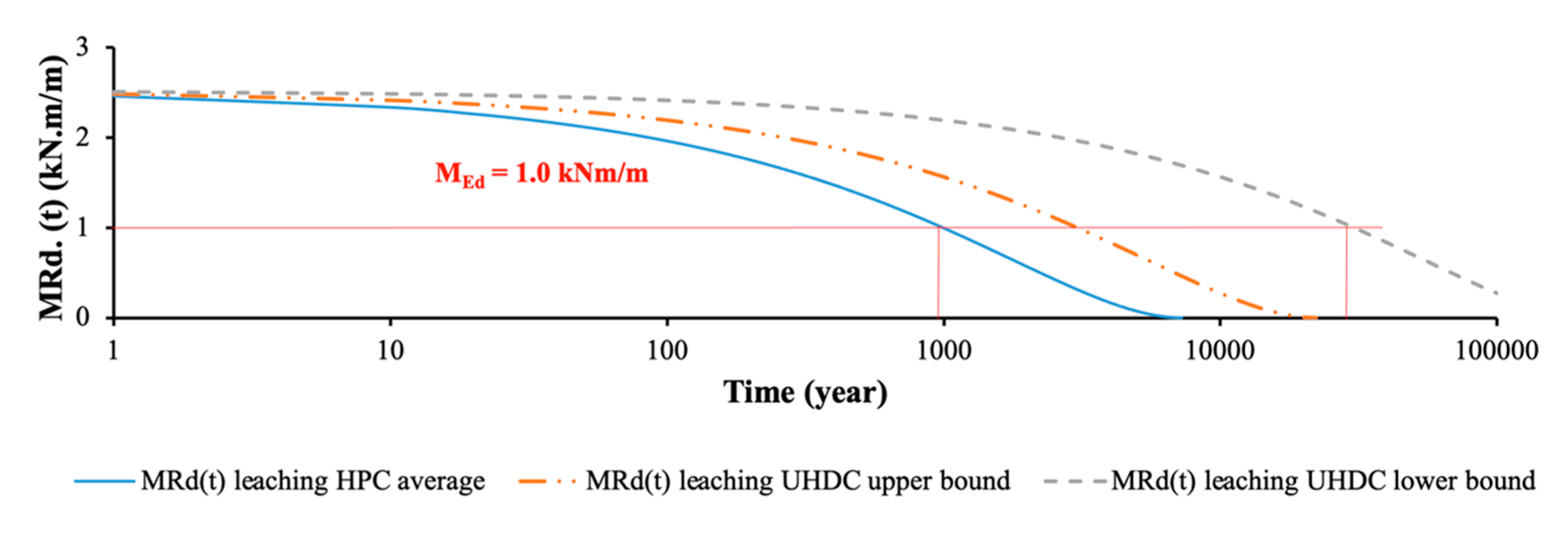
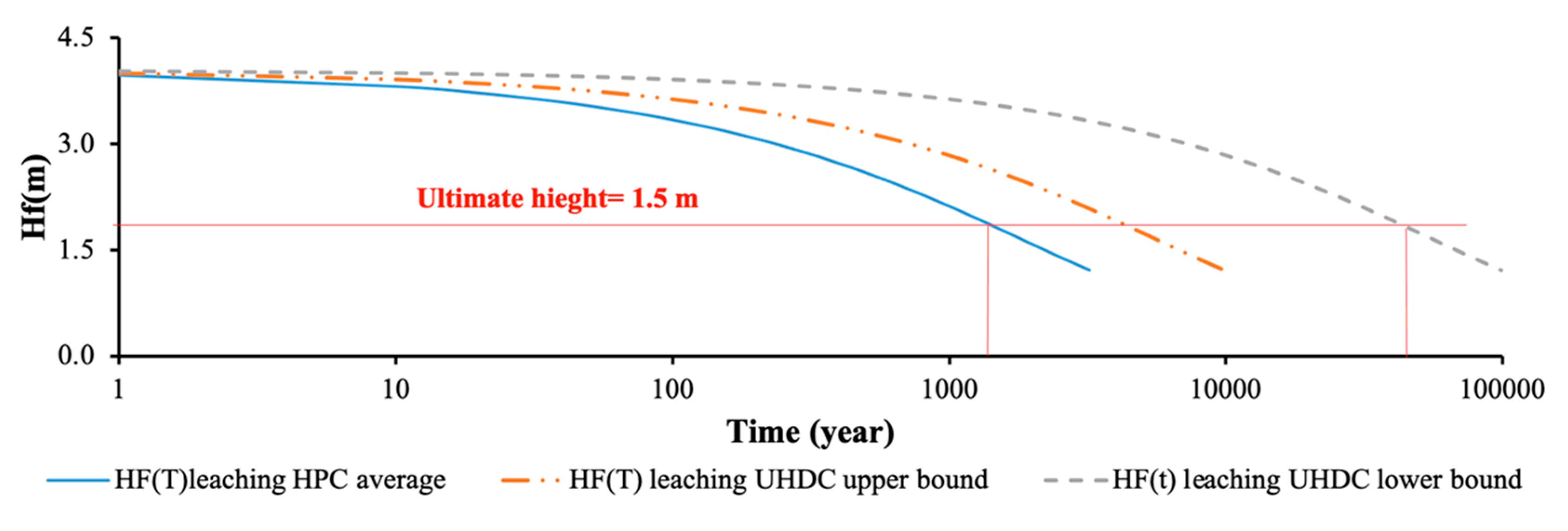
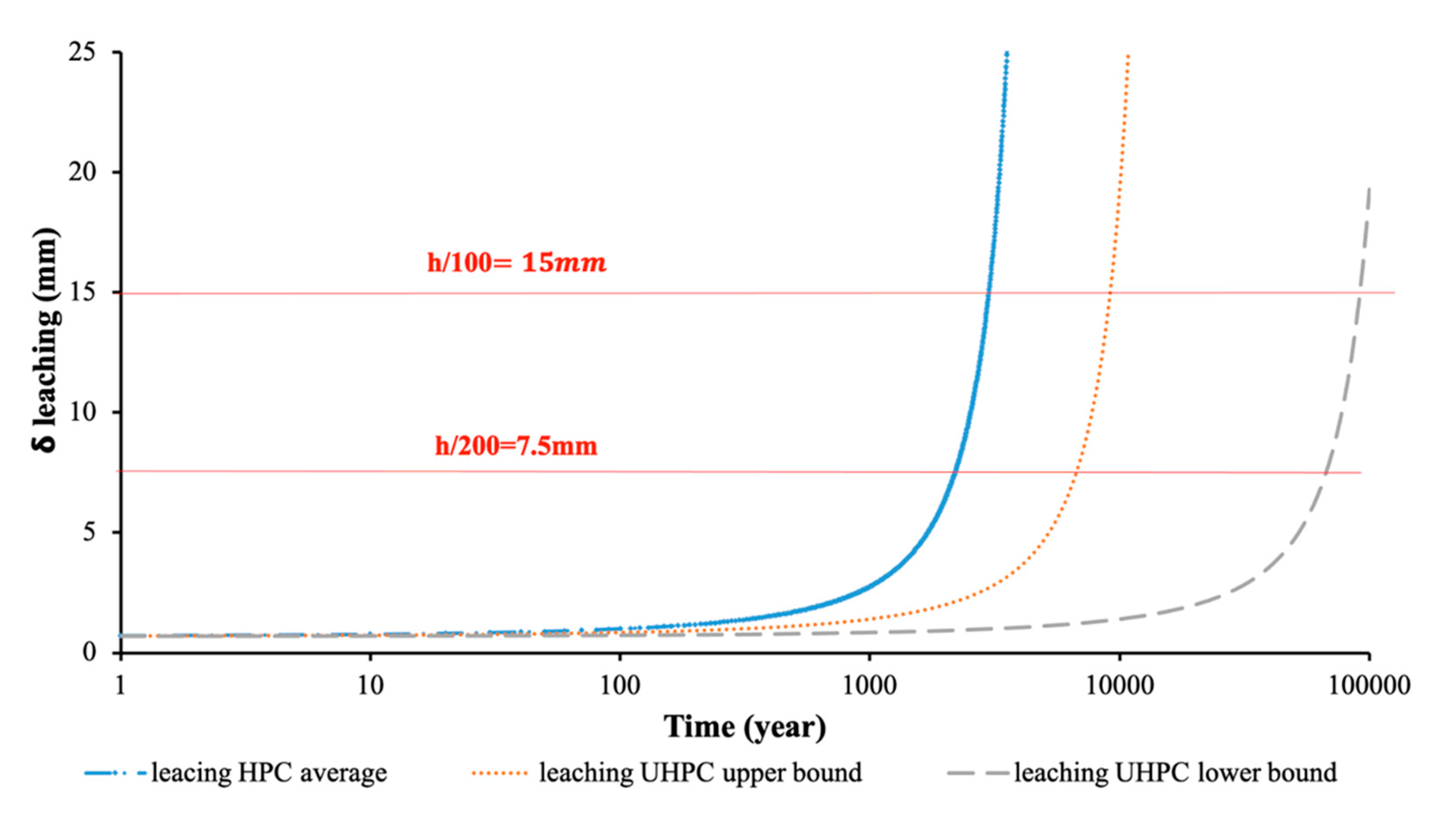
6.3. Cell 3: 30 mm Thick UHDC Slabs Supported by UHPC Cantilevers
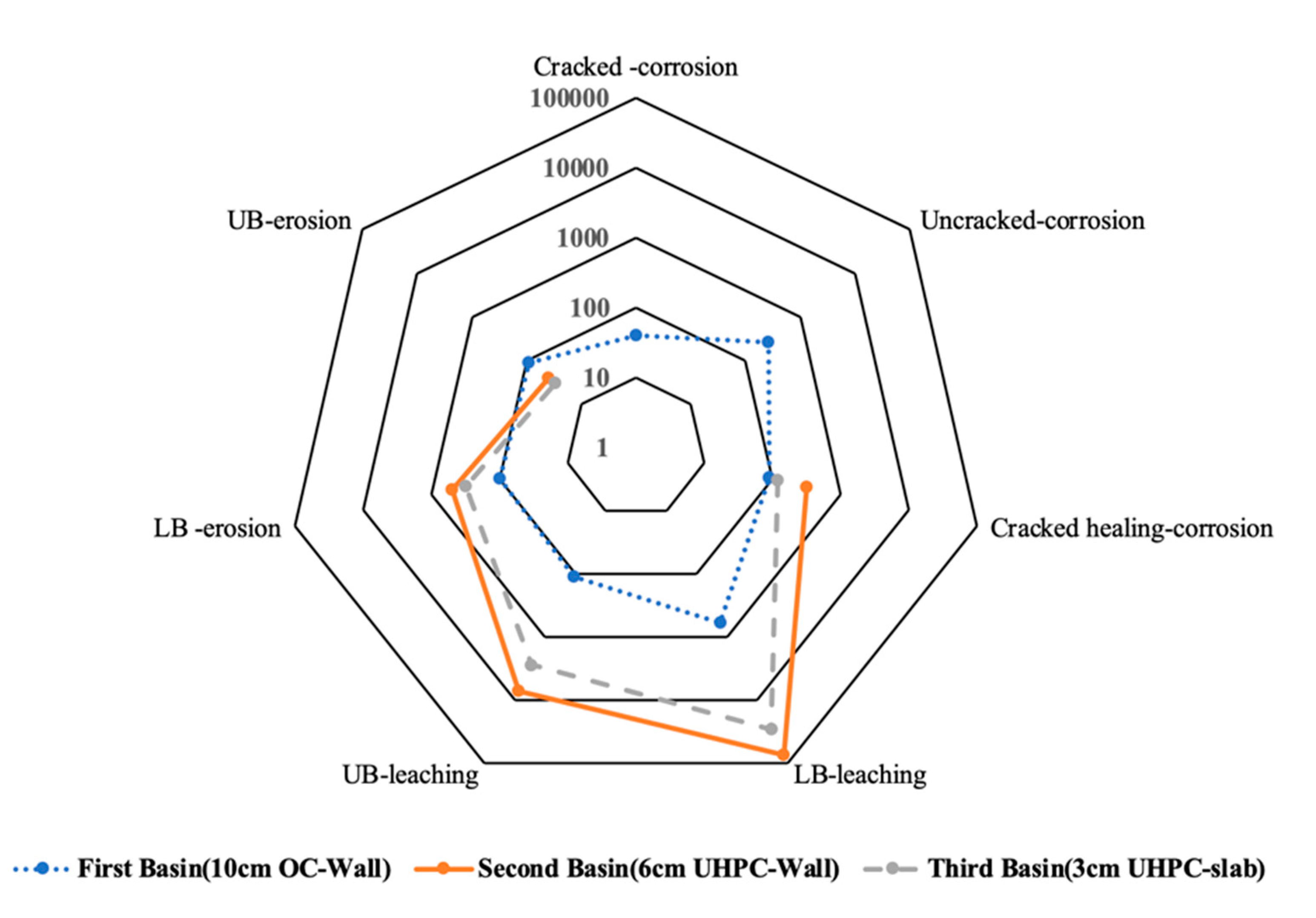
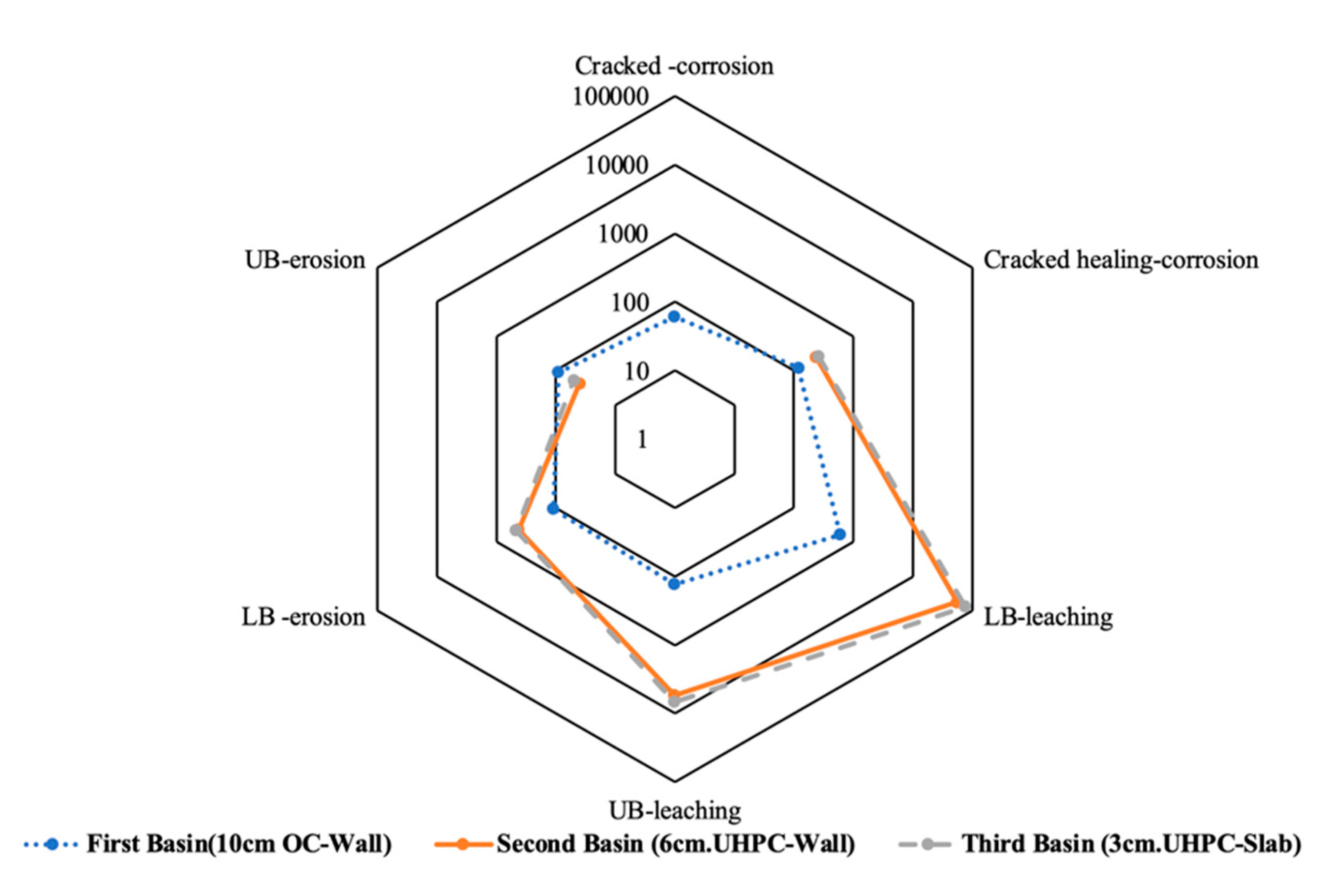
7. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schmidt, M.; Fehling, E. (Eds.) Proceedings of the First International Symposium on Undefined Ultra High Performance Concrete (UHPC); kassel university press GmbH: Kassel, Germany, 2004. [Google Scholar]
- Fehling, E.; Schmidt, M.; Stuerwald, S. (Eds.) Proceedings of the Second International Symposium on Ultra High Performance Concrete; kassel university press GmbH: Kassel, Germany, 2008. [Google Scholar]
- Schmidt, M.; Fehling, E.; Glotzbach, C.; Fröhlich, S.; Piotrowski, S. (Eds.) Proceedings of the Third International Symposium on UHPC and Nanotechnology; kassel university press GmbH: Kassel, Germeny, 2012. [Google Scholar]
- Fehling, E.; Middendorf, B.; Thiemicke, J. Proceedings of the 4th International Symposium on Ultra-High Performance Concrete and High Performance Construction Materials; kassel university press GmbH: Kassel, Germeny, 2016. [Google Scholar]
- Abbas, S.; Nehdi, M.L.; Saleem, M.A. Ultra-High Performance Concrete: Mechanical Performance, Durability, Sustainability and Implementation Challenges. Int. J. Concr. Struct. Mater. 2016, 10, 271–295. [Google Scholar] [CrossRef]
- Shi, C.; Wang, D. (Eds.) Proceedings of the 1st International Conference on UHPC Materials and Structures; RILEM Pubs: Changsha, China, 2016; p. 631. [Google Scholar]
- Shi, C.; Chen, B. (Eds.) Proceedings of the 2nd International Conference on UHPC Materials and Structures (UHPC2018-China); RILEM Pubs: Fuzhou, China, 2018; p. 832. [Google Scholar]
- Eurocode 2: Design of Concrete Structures—Part 1: General Rules and Rules for Buildings (Together with UNITED Kingdom National Application Document). Available online: http://210.42.35.72/download/834f5d1e-c5d7-4bae-bec8-507fb2cab7f3.pdf (accessed on 21 September 2020).
- Matthews, S. CONREPNET: Performance-based approach to the remediation of reinforced concrete structures: Achieving durable repaired concrete structures. J. Build. Apprais. 2007, 3, 6–20. [Google Scholar] [CrossRef]
- Li, V.; Wu, H. Conditions for Pseudo Strain-Hardening in Fiber Reinforced Brittle Matrix Composites. Appl. Mech. Rev. Aug 1992, 45, 390–398. [Google Scholar] [CrossRef]
- Li, V.C.; Stang, H.; Krenchel, H. Micromechanics of crack bridging in fibre-reinforced concrete. Mater. Struct. 1993, 26, 486–494. [Google Scholar] [CrossRef]
- Li, V.C. On Engineered Cementitious Composites (ECC) A Review of the Material and Its Applications. J. Adv. Concr. Technol. 2003, 1, 215–230. [Google Scholar] [CrossRef]
- Naaman, A.E.; Reinhardt, H.W. Proposed classification of HPFRC composites based on their tensile response. Mater. Struct. Constr. 2006, 39, 547–555. [Google Scholar] [CrossRef]
- Baril, M.A.; Sorelli, L.; Réthoré, J.; Baby, F.; Toutlemonde, F.; Ferrara, L.; Bernardi, S.; Fafard, M. Effect of casting flow defects on the crack propagation in UHPFRC thin slabs by means of stereovision Digital Image Correlation. Constr. Build. Mater. 2016, 129, 182–192. [Google Scholar] [CrossRef]
- Di Prisco, M.; Ferrara, L.; Lamperti, M.G.L. Double edge wedge splitting (DEWS): An indirect tension test to identify post-cracking behaviour of fibre reinforced cementitious composites. Mater. Struct. Constr. 2013, 46, 1893–1918. [Google Scholar] [CrossRef]
- Ferrara, L.; Ozyurt, N.; Di Prisco, M. High mechanical performance of fibre reinforced cementitious composites: The role of “casting-flow induced” fibre orientation. Mater. Struct. Constr. 2011, 44, 109–128. [Google Scholar] [CrossRef]
- Ferrara, L.; Faifer, M.; Toscani, S. A magnetic method for non destructive monitoring of fiber dispersion and orientation in steel fiber reinforced cementitious composites-part 1: Method calibration. Mater. Struct. Constr. 2012, 45, 575–589. [Google Scholar] [CrossRef]
- Ferrara, L.; Faifer, M.; Muhaxheri, M.; Toscani, S. A magnetic method for non destructive monitoring of fiber dispersion and orientation in steel fiber reinforced cementitious composites. Part 2: Correlation to tensile fracture toughness. Mater. Struct. Constr. 2012, 45, 591–598. [Google Scholar] [CrossRef]
- Ferrara, L.; Cremonesi, M.; Faifer, M.; Toscani, S.; Sorelli, L.; Baril, M.A.; Réthoré, J.; Baby, F.; Toutlemonde, F.; Bernardi, S. Structural elements made with highly flowable UHPFRC: Correlating computational fluid dynamics (CFD) predictions and non-destructive survey of fiber dispersion with failure modes. Eng. Struct. 2017, 133, 151–171. [Google Scholar] [CrossRef]
- Ferrara, L.; Albertini, I.; Gettu, R.; Krelani, V.; Moscato, S.; Pirritano, F.; Flores, M.R.; Ros, P.S.; Theeda, S.M. Self Healing of cement based materials engineered through crystalline admixtures: Experimental results from a multinational university network. Spec. Publ. 2015, 305, 13.1–13.10. [Google Scholar]
- Ferrara, L.; Ferreira, S.R.; Krelani, V.; Torre, M.D.; Silva, F.; Filho, R.D.T. Natural fibres as promoters of autogeneous healing in HPFRCCS: Results from on-going Brazil-Italy cooperation. Spec. Publ. 2015, 305, 11.1–11.10. [Google Scholar]
- Zhang, Z.; Qian, S.; Ma, H. Investigating mechanical properties and self-healing behavior of micro-cracked ECC with different volume of fly ash. Constr. Build. Mater. 2014, 52, 17–23. [Google Scholar] [CrossRef]
- Şahmaran, M.; Li, V.C. Durability of mechanically loaded engineered cementitious composites under highly alkaline environments. Cem. Concr. Compos. 2008, 30, 72–81. [Google Scholar] [CrossRef]
- Lepech, M.D.; Li, V.C. Water permeability of engineered cementitious composites. Cem. Concr. Compos. 2009, 31, 744–753. [Google Scholar] [CrossRef]
- Plagué, T.; Desmettre, C.; Charron, J.P. Influence of fiber type and fiber orientation on cracking and permeability of reinforced concrete under tensile loading. Cem. Concr. Res. 2017, 94, 59–70. [Google Scholar] [CrossRef]
- Li, V.C.; Lim, Y.M.; Chan, Y.W. Feasibility study of a passive smart self-healing cementitious composite. Compos. Part B Eng. 1998, 29, 819–827. [Google Scholar] [CrossRef]
- Özbay, E.; Šahmaran, M.; Lachemi, M.; Yücel, H.E. Self-Healing of Microcracks in High-Volume Fly-Ash-Incorporated Engineered Cementitious Composites. ACI Mater. J. 2013, 110, 33–43. [Google Scholar]
- Kim, D.; Kang, S.; Ahn, T.-H. Mechanical Characterization of High-Performance Steel-Fiber Reinforced Cement Composites with Self-Healing Effect. Materials (Basel) 2014, 7, 508–526. [Google Scholar] [CrossRef]
- Ferrara, L. Tailoring the orientation of fibres in high performance fibre reinforced cementitious composites: Part 2—Correlation to mechanical properties and design implications. Int. J. Mater. Struct. Integr. 2015, 9, 92–107. [Google Scholar] [CrossRef]
- Ferrara, L. Tailoring the orientation of fibres in high performance fibre reinforced cementitious composites: Part 1—Experimental evidence, monitoring and prediction. Int. J. Mater. Struct. Integr. 2015, 9, 72–91. [Google Scholar] [CrossRef]
- Krelani, V.; Krelani, V.; Moretti, F. Autogenous healing on the recovery of mechanical performance of High Performance Fibre Reinforced Cementitious Composites (HPFRCCs): Part 2—Correlation between healing of mechanical performance and crack sealing. Cem. Concr. Compos. 2016, 73, 299–315. [Google Scholar] [CrossRef]
- Şahmaran, M.; Yildirim, G.; Noori, R.; Ozbay, E.; Lachemi, M. Repeatability and pervasiveness of self-healing in engineered cementitious composites. ACI Mater. J. 2015, 112, 513–522. [Google Scholar] [CrossRef]
- Sahmaran, M.; Li, M.; Li, V.C. Transport properties of engineered cementitious composites under chloride exposure. ACI Mater. J. 2007, 104, 604–611. [Google Scholar] [CrossRef]
- Siad, H.; Alyousif, A.; Keskin, O.K.; Keskin, S.B.; Lachemi, M.; Sahmaran, M.; Hossain, K.M.A. Influence of limestone powder on mechanical, physical and self-healing behavior of Engineered Cementitious Composites. Constr. Build. Mater. 2015, 99, 1–10. [Google Scholar] [CrossRef]
- Yildirim, G.; Keskin, Ö.K.; Keskin, S.B.I.; Şahmaran, M.; Lachemi, M. A review of intrinsic self-healing capability of engineered cementitious composites: Recovery of transport and mechanical properties. Constr. Build. Mater. 2015, 101, 10–21. [Google Scholar] [CrossRef]
- Yildirim, G.; Alyousif, A.; Şahmaran, M.; Lachemi, M. Assessing the self-healing capability of cementitious composites under increasing sustained loading. Adv. Cem. Res. 2015, 27, 581–592. [Google Scholar] [CrossRef]
- Qian, S.; Zhou, J.; de Rooij, M.R.; Schlangen, E.; Ye, G.; van Breugel, K. Self-healing behavior of strain hardening cementitious composites incorporating local waste materials. Cem. Concr. Compos. 2009, 31, 613–621. [Google Scholar] [CrossRef]
- Yildirim, G.; Sahmaran, M.; Ahmed, H.U. Influence of Hydrated Lime Addition on the Self-Healing Capability of High-Volume Fly Ash Incorporated Cementitious Composites. J. Mater. Civ. Eng. 2015, 27, 04014187. [Google Scholar] [CrossRef]
- Yildirim, G.; Aras, G.H.; Banyhussan, Q.S.; Şahmaran, M.; Lachemi, M. Estimating the self-healing capability of cementitious composites through non-destructive electrical-based monitoring. NDT E Int. 2015, 76, 26–37. [Google Scholar] [CrossRef]
- Yildirim, G.; Sahmaran, M.; Balcikanli, M.; Ozbay, E.; Lachemi, M. Influence of cracking and healing on the gas permeability of cementitious composites. Constr. Build. Mater. 2015, 85, 217–226. [Google Scholar] [CrossRef]
- Snoeck, D.; De Belie, N. Repeated Autogenous Healing in Strain-Hardening Cementitious Composites by Using Superabsorbent Polymers. J. Mater. Civ. Eng. 2016, 28, 04015086. [Google Scholar] [CrossRef]
- Cuenca, E.; Ferrara, L. Self-healing capacity of fiber reinforced cementitious composites. State of the art and perspectives. KSCE J. Civ. Eng. 2017, 21, 2777–2789. [Google Scholar] [CrossRef]
- Yang, Y.; Lepech, M.D.; Yang, E.H.; Li, V.C. Autogenous healing of engineered cementitious composites under wet-dry cycles. Cem. Concr. Res. 2009, 39, 382–390. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, E.H.; Li, V.C. Autogenous healing of engineered cementitious composites at early age. Cem. Concr. Res. 2011, 41, 176–183. [Google Scholar] [CrossRef]
- Li, M.; Li, V.C. Cracking and healing of engineered cementitious composites under chloride environment. ACI Mater. J. 2011, 108, 333–340. [Google Scholar] [CrossRef]
- Nishiwaki, T.; Koda, M.; Yamada, M.; Mihashi, H.; Kikuta, T. Experimental Study on Self-Healing Capability of FRCC Using Different Types of Synthetic Fibers. J. Adv. Concr. Technol. 2012, 10, 195–206. [Google Scholar] [CrossRef]
- Nishiwaki, T.; Kwon, S.; Homma, D.; Yamada, M.; Mihashi, H. Self-Healing Capability of Fiber-Reinforced Cementitious Composites for Recovery of Watertightness and Mechanical Properties. Materials (Basel) 2014, 7, 2141–2154. [Google Scholar] [CrossRef]
- Wu, M.; Johannesson, B.; Geiker, M. A review: Self-healing in cementitious materials and engineered cementitious composite as a self-healing material. Constr. Build. Mater. 2012, 28, 571–583. [Google Scholar] [CrossRef]
- Ozbay, E.; Sahmaran, M.; Yucel, H.E.; Erdem, T.K.; Lachemi, M.; Li, V.C. Effect of Sustained Flexural Loading on Self-Healing of Engineered Cementitious Composites. J. Adv. Concr. Technol. 2013, 11, 167–179. [Google Scholar] [CrossRef]
- Qiu, F.-X.J.; He, S.; Wang, Q.; Su, H.; Yang, E.H.; Qiu, J.; He, S.; Wang, Q.; Su, H.; Yang, E.-H. Numerical Investigation of Factors Influencing the experimental Determination Of Concrete Fracture energy. In Proceedings of the 10th International Conference on Fracture Mechanics of Concrete and Concrete Structures Autogenous Healing of Fiber/Matrix Interface and Its Enhancement, Bayonne, France, 23–26 June 2019. [Google Scholar] [CrossRef]
- Graybeal, B. Design and Construction of Field-Cast UHPC Connections; No. FHWA-HRT-14-084; HRDI-40/10-14(750); Federal Highway Administration: Washington, DC, USA, 2014. [Google Scholar]
- Walraven, J. Fib model code for concrete structures 2010: Mastering challenges and encountering new ones. Struct. Concr. 2013, 14, 3–9. [Google Scholar] [CrossRef]
- Serna, P.; Navarro-Gregori, J.; Camacho, E. An inverse analysis method based on deflection to curvature transformation to determine the tensile properties of UHPFRC. Mater. Struct. Constr. 2015, 48, 3703–3718. [Google Scholar] [CrossRef]
- López, J.Á.; Serna, P.; Navarro-Gregori, J.; Coll, H. A simplified five-point inverse analysis method to determine the tensile properties of UHPFRC from unnotched four-point bending tests. Compos. Part B Eng. 2016, 91, 189–204. [Google Scholar] [CrossRef]
- BSI Standards Publication Concrete-Specification, Performance, Production and Conformity; Br.Stand 2013. Available online: https://www.academia.edu/40697042/BSI_Standards_Publication_Concrete_Specification_performance_production_and_conformity (accessed on 11 May 2020).
- National Addition to Eurocode 2-Design of Concrete Structures: Specific Rules for Ultra-High Performance Fibre-Reinforced Concrete (UHPFRC). Available online: https://www.diva-portal.org (accessed on 13 November 2020).
- Gowripalan, N.; Gilbert, R.I. Design Guidelines for Ductal Prestressed Concrete Beams; Design Guide; University of NSW: Sydney, Australia, 2000. [Google Scholar]
- Canadian Standards Association CSA A23.1/2 Annex S on Ultra-High Performance Concrete. Available online: https://www.concretefloors.ca/?page_id=708 (accessed on 13 November 2020).
- Schmidt, M.; Leutbecher, T.; Piotrowski, S.; Wiens, U. THE GERMAN GUIDELINE FOR ULTRA-HIGH PERFORMANCE CONCRETE. In Proceedings of the FGC-ACI-fib-RILEM Int. Symposium on Ultra-High Performance Fibre-Reinforced Concrete, Montpellier, France, 2–4 October 2017. [Google Scholar]
- Buttignol, T.E.T.; Sousa, J.L.A.O.; Bittencourt, T.N. Ultra High-Performance Fiber-Reinforced Concrete (UHPFRC): A review of material properties and design procedures. Rev. IBRACON Estrut. Mater. 2017, 10, 957–971. [Google Scholar] [CrossRef]
- BFUHP—Bétons Fibrés à Ultra Hautes Performances. Available online: https://ibeton.ch/recherrch/BFUHP/Default.asp (accessed on 13 November 2020).
- ReSHEALience. Available online: https://uhdc.eu/ (accessed on 21 September 2020).
- Biondini, F.; Bontempi, F.; Frangopol, D.M.; Malerba, P.G. Probabilistic Service Life Assessment and Maintenance Planning of Concrete Structures. J. Struct. Eng. 2006, 132, 810–825. [Google Scholar] [CrossRef]
- Biondini, F.; Bontempi, F.; Frangopol, D.M.; Malerba, P.G. Cellular Automata Approach to Durability Analysis of Concrete Structures in Aggressive Environments. J. Struct. Eng. 2004, 130, 1724–1737. [Google Scholar] [CrossRef]
- Biondini, F.; Frangopol, D.M. Life-cycle performance of deteriorating structural systems under uncertainty: Review. J. Struct. Eng. (United States) 2016, 142, F4016001. [Google Scholar] [CrossRef]
- Biondini, F.; Camnasio, E.; Palermo, A. Structure and Infrastructure Engineering Maintenance, Management, Life-Cycle Design and Performance Lifetime seismic performance of concrete bridges exposed to corrosion Lifetime seismic performance of concrete bridges exposed to corrosion. Taylor Fr. 2013, 10, 880–900. [Google Scholar] [CrossRef]
- Biondini, F.; Frangopol, D.M. Lifetime reliability-based optimization of reinforced concrete cross-sections under corrosion. Struct. Saf. 2009, 31, 483–489. [Google Scholar] [CrossRef]
- Biondini, F.; Vergani, M. Deteriorating beam finite element for nonlinear analysis of concrete structures under corrosion. Struct. Infrastruct. Eng. 2015, 11, 519–532. [Google Scholar] [CrossRef]
- Cuenca, E.; Criado, M.; Gimenez, M.; Alonso, M.C.; Ferrara, L. Durability of ultra-high performance fiber reinforced cementitious composites exposed to chemically aggressive environments: Up-grading to ultra-high durability concrete through nano-constituents. Cem. Concr. Compos. 2020. submitted. [Google Scholar]
- Cuenca, E.; Mezzena, A.; Ferrara, L. Synergy between crystalline admixtures and nano-constituents in enhancing autogenous healing capacity of cementitious composites under cracking and healing cycles in aggressive waters. Constr. Build. Mater. 2020, in press. [Google Scholar] [CrossRef]
- Cuenca, E.; D’Ambrosio, L.; Lizunov, D.; Tretjakov, A.; Volobujeva, O.; Ferrara, L. Mechanical properties and self-healing capacity of Ultra High Performance Fibre Reinforced Concrete with alumina nanofibers: Tailoring Ultra High Durability Concrete for aggressive exposure scenarios. Cem. Concr. Compos. 2020. submitted. [Google Scholar]
- Deze, E.G.; Cuenca, E.; Násner, M.A.; Iakovlev, M.; Sideria, S.; Sapalidis, A.; Borg, R.P.; Nanocellulose, L.F. Containing concretes: Evaluation of NC properties affecting UHDC & Development of mixing protocols. Mater. Today Proc. 2020, in press. [Google Scholar]
- DNVGL-ST-C502 Offshore Concrete Structures—DNV GL. Available online: https://oilgas.standards.dnvgl.com/download/dnvgl-st-c502-offshore-concrete-structures (accessed on 21 September 2020).
- Westendarp, A. ZTV-W LB 215 Aspekte zu Beton und Bauausführung. In Bundesanstalt fur Wasserbau (Hg.): Wasserbauwerke nach Neuer Norm; Bundesanstalt fur Wasserbau: Karlsruhe, Germany, 2004; pp. 19–25. [Google Scholar]
- Rilem, T.C. 178-TMC: “Testing and modelling chloride penetration in concrete”—Analysis of total chloride content in concrete. Mater. Struct. Constr. 2002, 35, 583–585. [Google Scholar] [CrossRef]
- Depth of Penetration of Water under Pressure, British Standards Institution. BS EN 12390-8:2019 Testing Hardened Concrete; Depth of Penetration of Water under Pressure, British Standards Institution—Publication Index|NBS: London, UK, 2019. [Google Scholar]
- Cuenca, E.; Tejedor, A.; Ferrara, L. A methodology to assess crack-sealing effectiveness of crystalline admixtures under repeated cracking-healing cycles. Constr. Build. Mater. 2018, 179, 619–632. [Google Scholar] [CrossRef]
- Cuenca, E.; Rigamonti, S.; Gastaldo Brac, E.M.; Ferrara, L. Crystalline admixture as healing promoter in concrete exposed to chloride-rich environments: An experimental study. ASCE J. Mater. Civ. Eng. 2020, in press. [Google Scholar] [CrossRef]
- Lo Monte, F.; Ferrara, L. Tensile behaviour identification in Ultra-High Performance Fibre Reinforced Cementitious Composites: Indirect tension tests and back-analysis of flexural test resylts. Mater. Struct. 2020, in press. [Google Scholar]
- Bamonte, P.; Al-Obaidi, S.; Animato, F.; Lo Monte, F.; Mazzantini, I.; Ferrara, L. An innovative design concept for aggressive water tanks with Ultra High Durability Concrete: Pilot material and structural validation by H2020 ReSHEALience project. Sustainability 2021. under review. [Google Scholar]
- Van Belleghem, B.; Van den Heede, P.; Van Tittelboom, K.; De Belie, N.D. Quantification of the service life extension and environmental benefit of Chloride Exposed Self-Healing Concrete. Materials (Basel) 2017, 10, 5. [Google Scholar] [CrossRef]
- Maes, M.; Snoeck, D.; De Belie, N. Chloride penetration in cracked mortar and the influence of autogenous crack healing. Constr. Build. Mater. 2016, 115, 114–124. [Google Scholar] [CrossRef]
- Darquennes, A.; Olivier, K.; Benboudjema, F.; Gagné, R. Self-healing at early-age, a way to improve the chloride resistance of blast-furnace slag cementitious materials. Constr. Build. Mater. 2016, 113, 1017–1028. [Google Scholar] [CrossRef]
- D3.2—Definition of Key Durability Parameters for Each Scenario—ReSHEALience. Available online: https://uhdc.eu/documentation/d3-2-definition-of-key-durability-parameters-for-each-scenario/ (accessed on 21 September 2020).
- Ann, K.Y.; Song, H.W. Chloride threshold level for corrosion of steel in concrete. Corros. Sci. 2007, 49, 4113–4133. [Google Scholar] [CrossRef]
- Angst, U.; Elsener, B.; Larsen, C.K.; Vennesland, Ø. Critical chloride content in reinforced concrete—A review. Cem. Concr. Res. 2009, 39, 1122–1138. [Google Scholar] [CrossRef]
- Alonso, M.C.; Sanchez, M. Analysis of the variability of chloride threshold values in the literature. Mater. Corros. 2009, 60, 631–637. [Google Scholar] [CrossRef]
- Angst, U.M.; Geiker, M.R.; Michel, A.; Gehlen, C.; Wong, H.; Isgor, O.B.; Elsener, B.; Hansson, C.M.; François, R.; Hornbostel, K.; et al. The steel–concrete interface. Mater. Struct. Constr. 2017, 50. [Google Scholar] [CrossRef]
- Shafikhani, M.; Chidiac, S.E. Quantification of concrete chloride diffusion coefficient—A critical review. Cem. Concr. Compos. 2019, 99, 225–250. [Google Scholar] [CrossRef]
- Djerbi, A.; Bonnet, S.; Khelidj, A.; Baroghel-bouny, V. Influence of traversing crack on chloride diffusion into concrete. Cem. Concr. Res. 2008, 38, 877–883. [Google Scholar] [CrossRef]
- Win, P.P.; Watanabe, M.; Machida, A. Penetration profile of chloride ion in cracked reinforced concrete. Cem. Concr. Res. 2004, 34, 1073–1079. [Google Scholar] [CrossRef]
- Konin, A.; François, R.; Arliguie, G. Penetration of chlorides in relation to the microcracking state into reinforced ordinary and high strength concrete. Mater. Struct. Constr. 1996, 31, 310–316. [Google Scholar] [CrossRef]
- Gowripalan, N.; Sirivivatnanon, V.; Lim, C.C. Chloride diffusivity of concrete cracked in flexure. Cem. Concr. Res. 2000, 30, 725–730. [Google Scholar] [CrossRef]
- Thomas, M.; Green, B.; O’Neal, E.; Perry, V.; Hayman, S.; Hossack, A. Marine performance of UHPC at Treat Island. In Proceedings of the 3rd International Symposium on UHPC and Nanotechnology for High Performance Construction Materials, Kassel, Germany, 7–9 March 2012. [Google Scholar]
- Ideker, J.H. ACI 201 ACI 201—Guide to Durable Concrete Guide to Durable Concrete. ACI Mater. J. 1991, 88, 544–582. [Google Scholar]
- Corrosion of Prestressing Steels. Available online: http://civilwares.free.fr/ACI/MCP04/2222r_01.pdf (accessed on 21 September 2020).
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary. Available online: http://dl.mycivil.ir/dozanani/ACI/ACI%20318-08%20Building%20Code%20Requirements%20for%20Structural%20Concrete%20(ACI%20318-08)%20and%20Commentary_MyCivil.ir.pdf (accessed on 21 September 2020).
- BS 8110. Available online: https://www.concretecentre.com/Codes/BS-8110.aspx (accessed on 21 September 2020).
- Critical Chloride Content in Reinforced Concrete. 2008. ISBN 9788253610764. Available online: www.coinweb.no (accessed on 21 September 2020).
- Hope, B.; Journal, A.I.-M. Chloride Corrosion Threshold in Concrete. 1987. Available online: concrete.org (accessed on 1 October 2020).
- Everett, L.; Treadaway, K. Deterioration due to Corrosion in Reinforced Concrete; Building research establishment: Watford, UK, 1980. [Google Scholar]
- Thomas, M. Chloride Thresholds in Marine Concrete; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Hussain, S.; Journal, A.A.-G.-M. Chloride Threshold for Corrosion of Reinforcement in Concrete. 1996. Available online: concrete.org (accessed on 1 October 2020).
- Page, C.L.; Havdahl, J. Electrochemical monitoring of corrosion of steel in microsilica cement pastes. Mater. Struct. 1985, 18, 41–47. [Google Scholar] [CrossRef]
- Stratfull, R.F.; Jurkovich, W.J.; Spellman, D.L. Corrosion Testing of Bridge Decks. In Proceedings of the 54th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 13–17 January 1975. [Google Scholar]
- Šavija, B.; Schlangen, E.; Pacheco, J.; Millar, S.; Eichler, T.; Wilsch, G. Chloride ingress in cracked concrete: A laser induced breakdown spectroscopy (LIBS) study. J. Adv. Concr. Technol. 2014, 12, 425–442. [Google Scholar] [CrossRef]
- Borg, R.P.; Cuenca, E.; Gastaldo Brac, E.M.; Ferrara, L. Crack sealing capacity in chloride-rich environments of mortars containing different cement substitutes and crystalline admixtures. J. Sustain. Cem. Mater. 2018, 7, 141–159. [Google Scholar] [CrossRef]
- Val, D.V.; Melchers, R.E. Reliability of Deteriorating RC Slab Bridges. J. Struct. Eng. 1997, 123, 1638–1644. [Google Scholar] [CrossRef]
- Vu, K.A.T.; Stewart, M.G. Structural reliability of concrete bridges including improved chloride-induced corrosion models. Struct. Saf. 2000, 22, 313–333. [Google Scholar] [CrossRef]
- Val, D.V.; Stewart, M.G. Life-cycle cost analysis of reinforced concrete structures in marine environments. Struct. Saf. 2003, 25, 343–362. [Google Scholar] [CrossRef]
- Marcos-Meson, V.; Michel, A.; Solgaard, A.; Fischer, G.; Edvardsen, C.; Skovhus, T.L. Corrosion resistance of steel fibre reinforced concrete—A literature review. Cem. Concr. Res. 2018, 103, 1–20. [Google Scholar] [CrossRef]
- Marcos-Meson, V.; Solgaard, A.; Fischer, G.; Edvardsen, C.; Michel, A. Pull-out behaviour of hooked-end steel fibres in cracked concrete exposed to wet-dry cycles of chlorides and carbon dioxide—Mechanical performance. Constr. Build. Mater. 2020, 240, 117764. [Google Scholar] [CrossRef]
- Homma, D.; Mihashi, H.; Nishiwaki, T. Self-Healing Capability of Fibre Reinforced Cementitious Composites. J. Adv. Concr. Technol. 2009, 7, 217–228. [Google Scholar] [CrossRef]
- Bensted, J.; Brough, A.; Composites, M.P. Chemical Degradation of Concrete. 2007. Available online: books.google.com (accessed on 1 October 2020).
- Menéndez, E.; Matschei, T.; Glasser, F.P. Sulfate attack of concrete. RILEM State Art Rep. 2013, 10, 7–74. [Google Scholar] [CrossRef]
- Santhanam, M.; Cohen, M.D.; Olek, J. Sulfate attack research—Whither now? Cem. Concr. Res. 2001, 31, 845–851. [Google Scholar] [CrossRef]
- Kurtis, K.E.; Monteiro, P.J.M.; Madanat, S.M. Empirical models to predict concrete expansion caused by sulfate attack. ACI Struct. J. 2000, 97, 156–161. [Google Scholar] [CrossRef]
- Monteiro, P.J.M.; Kurtis, K.E. Time to failure for concrete exposed to severe sulfate attack. Cem. Concr. Res. 2003, 33, 987–993. [Google Scholar] [CrossRef]
- Barcelo, L.; Gartner, E.; Barbarulo, R.; Hossack, A.; Ahani, R.; Thomas, M.; Hooton, D.; Brouard, E.; Delagrave, A.; Blair, B. A modified ASTM C1012 procedure for qualifying blended cements containing limestone and SCMs for use in sulfate-rich environments. Cem. Concr. Res. 2014, 63, 75–88. [Google Scholar] [CrossRef]
- Hossack, A.M.; Thomas, M.D.A. Evaluation of the effect of tricalcium aluminate content on the severity of sulfate attack in Portland cement and Portland limestone cement mortars. Cem. Concr. Compos. 2015, 56, 115–120. [Google Scholar] [CrossRef]
- De Belie, N.; De Coster, V.; Van Nieuwenburg, D. Use of fly ash or silica fume to increase the resistance of concrete to feed acids. Mag. Concr. Res. 1997, 49, 337–344. [Google Scholar] [CrossRef]
- Fagerlund, G. Contecvet a Validated Users Manual for Assessing the Residual Service Life of Concrete Structures Leaching of Concrete the leaching process. In Extrapolation of Deterioration; Effect on the Structural Stability; Report TVBM-3091; Division of Building Materials Lund Institute of Technology: Lund, Sweden, 2000. [Google Scholar]
- Matte, V.; Moranville, M.; Adenot, F.; Richet, C.; Torrenti, J.M. Simulated microstructure and transport properties of ultra-high performance cement-based materials. Cem. Concr. Res. 2000, 30, 1947–1954. [Google Scholar] [CrossRef]
- Maltais, Y.; Samson, E.; Marchand, J. Predicting the durability of Portland cement systems in aggressive environments—Laboratory validation. Cem. Concr. Res. 2004, 34, 1579–1589. [Google Scholar] [CrossRef]
- Alonso, C.; Castellote, M.; Llorente, I.; Andrade, C. Ground water leaching resistance of high and ultra high performance concretes in relation to the testing convection regime. Cem. Concr. Res. 2006, 36, 1583–1594. [Google Scholar] [CrossRef]
- CEN (European Committee for Standardization). EN 1992-1-1: Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Hay, R.; Ostertag, C.P. Acidification at rebar-concrete interface induced by accelerated corrosion test in aggressive chloride environment. Cem. Concr. Compos. 2020, 110, 103573. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]








| Jurisdiction | Document | Durability Parameter | Value(Recommended/Compulsory) |
|---|---|---|---|
| France [56] | NF P 18 459 | Porosity to water | ≤9% |
| XP P 18 462 | Coefficient of diffusion of chlorides at 90 days | ≤0.5 × 10−12 m2/s | |
| XP P 18 463 | Permeability to gas at 90 days | ≤9.0 × 10−19 m2 | |
| Australia [57] | “Design Guidelines for RPC Prestressed Concrete Beams” | Matrix porosity | 5% |
| Minimum cover to tendons | 20 mm | ||
| Minimum spacing between adjacent tendons | Min (1.5∙φ; 20 mm) Where φ = tendon diameter | ||
| Crack width | 1.5∙H∙(εb–0.00016) Where H = section depth εb = concrete strain | ||
| Canada [58] | CSA A23.1—“Concrete materials and methods of concrete construction” | Durability requirements | 3 levels for durability |
| Chloride ion penetrability | - | ||
| Concrete cover | - | ||
| Germany [59] | German Guideline for Ultra-High Performance Concrete” | w/c | ≤0.25 |
| Spain [60] | Spanish Guideline | EN requirements | - |
| Swiss standards [61] | BFUP (Bétons Fibers Ultra hautes Performance) | Porosity to water | 2–5% |
| Permeability to Nitrogen | 1–5 × 10−20 m2 | ||
| Freeze and thaw Residual module after 300 cycles Loss of mass after 300 cycles | 100% <10 gm/m2 | ||
| Abrasion Coefficient CNR | 1.3 | ||
| Carbonation, penetration after 15 mm | Several years | ||
| Permeability to Oxygen | <10−9 m2 | ||
| Coefficient of diffusion of chlorides | 2 × 10−14 m2/s |
| Plant | Nuova San Martino | Le Prata | Vallesecolo Gr.1 | Bagnore 4 | Chiusdino | |
|---|---|---|---|---|---|---|
| Location | Lago | Lago | Larderello | Piancastagnaio | Radicondoli | |
| Date | 06-mar-18 | 12-gen-17 | 27-mar-17 | 26-gen-17 | 07-lug-17 | |
| Typology kind of water | Blown down water | Column C2 water inlet | Column C2 water inlet | Injection water | Cooling water tower inlet | |
| T | Co | n.d. | 19.3 | 16.0 | 19.9 | n.d. |
| pH | −log [H+] | 7.07 | 7.08 | 7.99 | 6.49 | 6.9 |
| Cond | µS/cm | 4.430 | 6.460 | 1.060 | 24.200 | 7.870 |
| Alk | Mg/L Hcl | 3.0 | 11 | 4.9 | 3.1 | n.d. |
| Alk rit | Mg/L Hcl | 1.8 | n.d. | n.d. | n.d. | n.d. |
| O2 dissolved | Mg/L | 0.1 | n.d. | n.d. | 1.1 | n.d. |
| H2S | Mg/L | 0.4 | 0.2 | u.d.l | 0.3 | 1.5 |
| SO42− | Mg/L | 1.223 | 2.292 | 202 | 10.020 | 5.119 |
| SO32− | Mg/L | 77 | 980 | u.d.l | 505 | 325 |
| S2O32− | Mg/L | 26 | 229 | u.d.l | 11.2 | 46 |
| Cl− | Mg/L | 213 | 1.1 | 2.6 | 2.8 | 1.0 |
| Na+ | Mg/L | n.d. | 1.352 | 7 | 0.9 | n.d. |
| Tightness Class | Requirements for Leakage | Specific Requirements |
|---|---|---|
| 0 | Some degree of leakage acceptable, or leakage of liquids irrelevant. | Silos holding dry materials may generally be designed with this class. |
| 1 | Leakage to be limited to a small amount. Some surface staining or damp patches acceptable. | Any cracks expected to pass through the full thickness should be limited to wk1, Healing may be assumed if the expected range of strain under service condition is less than 150 × 10−6. |
| 2 | Leakage to be minimal. Appearance not to be impaired bg. | Cracks should not pass through the full width of a section, the design value of the depth of the compression zone should be at least xmin. xmin = min (50 mm or 0.2 h—h is the element thickness). |
| 3 | No leakage permitted. |
| Maximum w/c | Minimum Cement Content (kg/m3) | Minimum Compressive Strength (N/mm2) | Minimum Concrete Cover (mm) | Maximum Crack Width (mm) | ||
|---|---|---|---|---|---|---|
| XS | 0.40–0.65 | 300–400 | 25/30 to 40/50 | 25–75 | 0.1–0.4 | |
| XA | 0.45–0.65 | 275 | 400 | 25/30 to 40/50 | - | 0.1–0.3 |
| 325 | ||||||
| Constituents | XA-CA | XA-CA + ANF | XA-CA-CNC |
|---|---|---|---|
| CEM I 52,5 R | 600 | 600 | 600 |
| Slag | 500 | 500 | 500 |
| Water | 200 | 200 | 200 |
| Steel fibers Azichem Readymesh 200 ® | 120 | 120 | 120 |
| Sand 0–2 mm | 982 | 982 | 982 |
| Superplasticizer Glenium ACE 300 ® | 33 | 33 | 33 |
| Crystalline Admixture Penetron Admix ® | 4.8 | 4.8 | 4.8 |
| Alumina nanofibers NAFEN ®* | - | 0.25 | - |
| Cellulose nanofibrils Navitas ®* | - | - | 0.15 |
| Concrete Use | Chloride Content Class a | Maximum Cl− Content by Mass of Cement b % |
|---|---|---|
| Not containing steel reinforcement or other embedded metal with the exception of corrosion -resisting lifting devices | Cl 1.0 | 1.00 |
| Containing steel reinforcement or other embedded metal | Cl 0.20 | 0.20 |
| Cl 0.40 c | 0.40 | |
| Containing prestressed steel reinforcement in direct contact with concrete | Cl 0.10 | 0.10 |
| Cl 0.20 | 0.20 |
| Exposure Environment | NaCl Concentration (g/L) |
|---|---|
| Baltic Sea | 3–8 |
| Black Sea | 18.3–22.2 |
| White Sea | 26–29.7 |
| Atlantic Ocean | 33.5–37.4 |
| Pacific Ocean | 34.5–36.7 |
| Mediterranean Sea | 38.4–41.2 |
| Red Sea | 50.8–58.5 |
| Ontario Lake | 72 |
| Caspian Sea | 126.7–185 |
| Dead Sea | 192.2–260 |
| Elton Lake | 265 |
| Soluble in Water | Soluble in Acid | |
|---|---|---|
| ACI 201 [95] | (0.10 to 0.15) | - |
| ACI 222 [96] | - | 0.20 |
| ACI 318 [97] | (0.15 to 0.30) | 0.20 |
| BS 8110 [98] | - | 0.40 |
| Australian Standards [57] | - | 0.60 |
| RILEM [75] | - | 0.40 |
| Norway Standards [99] | - | 0.60 |
| Hope and Ip [100] | - | (0.10 to 0.20) |
| Everett and Treadaway [101] | - | 0.40 |
| Thomas [102] | - | 0.50 |
| Hussain, SE [103] | - | (0.18 to 1.2) |
| Page and Havdahl [104] | 0.54 | 1.00 |
| R. F. Stratfull.et al [105] | - | 0.15 |
| Uncracked | Ordinary Concrete | High-Performance Concrete | Ultra-High Performance (Fiber-Reinforced) Concrete |
|---|---|---|---|
| Non-steady Ca leaching coefficient DnsCa (m2/s) (3 to 30 months) | (2.5–1.0) × 10−10 | (1.2–0.5) × 10−10 | (5–3) × 10−11 |
| Leached layer (mm) | 2 | 0.25 | 0.10 |
| a (mm d−0.5) | 0.21–0.067 | 0.026–0.0084 | 0.011–0.0034 |
| Ke (mm d−1) | 0.022–0.002 | 0.003–0.0003 | 0.0011–0.0001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Obaidi, S.; Bamonte, P.; Luchini, M.; Mazzantini, I.; Ferrara, L. Durability-Based Design of Structures Made with Ultra-High-Performance/Ultra-High-Durability Concrete in Extremely Aggressive Scenarios: Application to a Geothermal Water Basin Case Study. Infrastructures 2020, 5, 102. https://doi.org/10.3390/infrastructures5110102
Al-Obaidi S, Bamonte P, Luchini M, Mazzantini I, Ferrara L. Durability-Based Design of Structures Made with Ultra-High-Performance/Ultra-High-Durability Concrete in Extremely Aggressive Scenarios: Application to a Geothermal Water Basin Case Study. Infrastructures. 2020; 5(11):102. https://doi.org/10.3390/infrastructures5110102
Chicago/Turabian StyleAl-Obaidi, Salam, Patrick Bamonte, Massimo Luchini, Iacopo Mazzantini, and Liberato Ferrara. 2020. "Durability-Based Design of Structures Made with Ultra-High-Performance/Ultra-High-Durability Concrete in Extremely Aggressive Scenarios: Application to a Geothermal Water Basin Case Study" Infrastructures 5, no. 11: 102. https://doi.org/10.3390/infrastructures5110102
APA StyleAl-Obaidi, S., Bamonte, P., Luchini, M., Mazzantini, I., & Ferrara, L. (2020). Durability-Based Design of Structures Made with Ultra-High-Performance/Ultra-High-Durability Concrete in Extremely Aggressive Scenarios: Application to a Geothermal Water Basin Case Study. Infrastructures, 5(11), 102. https://doi.org/10.3390/infrastructures5110102






