1. Introduction
Resilience from natural disasters has becoming a relevant issue for civil communities that rely particularly on bridges, being significantly exposed to natural disasters, such as earthquakes and thus quantitative estimations of seismic resilience are fundamental to define pre- and post-earthquake decision-making procedures. In particular, seismic risk assessment methodologies become crucial in planning adequate mitigation procedures and recovery activities to minimize the disruptions [
1]. In this regard, resilience quantifies the recovery time and procedures in order to facilitate and enhance pre-hazard and post-hazard event mitigation and emergency response strategies of transportation systems and entire communities [
2,
3]. In particular, as shown in the JOINT RESEARCH PROJECT by the European Commission [
4] resilience calculation depends on two important models: a loss model and a recovery model.
(1) A loss model is necessary to assess the reduction of functionality due to the impact of earthquakes [
5] and risk assessment of structures requires a probabilistic-based approach to consider all the possible damage and failure scenarios of each component within a bridge, as shown in [
6]. In [
7], expected direct costs were calculated as the sum of the losses associated with all the vulnerable components failure/damage states in all possible conditions while indirect losses were defined as those associated with system failures by a scenario-based approach regarding the condition states of the components. However, indirect losses have many consequences and uncertainties that need to be assessed with interdisciplinary approaches [
8,
9].
(2) Recovery is a complex process that comprises a series of event, actions or changes to enhance the capacity of an affected bridge, but also community, when faced with singular, multiple or unique shocks and stresses, places emphasis on the human role. Therefore, recovery functions are essential for evaluating resilience but influenced by many variables, time dimensions and spatial dimensions with disparities among different geographic areas, in the same community or state and showing different rates and quality of recovery. To the best of our knowledge, there are few applications to earthquakes [
10,
11]. In Europe in particular, the restoration procedures have been left to the discretion of each nation and a standardized approach would start from the existing BRIME project that focused on bridge deterioration, and the two of the standing European projects: INPREP for improving effective inter-organizational response capacity in complex environments of disasters and PANOPTIS, a decision support system for increasing the resilience of transportation infrastructure. In the US, several implementations within computational platforms were developed (i.e., [
12,
13]).
A state of the art of such procedures was proposed by [
14]. Many approaches focused on maintenance, safety, and robustness [
11,
15,
16] analyzed post-earthquake functionality, while [
17,
18,
19] proposed holistic risk management approaches. As underlined by [
20], practical approaches that may incorporate bridge resilience have becoming fundamental to assess recovery procedures. Among others, a multi-objective evolutionary algorithm was proposed and applied by [
21] with the aim to evaluate resilience of the retrofitted bridge under the multi-hazard effect of earthquake and flood-induced scour. The framework of [
22] was applied for time-variant loss and resilience assessment of Californian highway bridges under time-dependent multiple hazards.
Against this background, [
23] compared the performance of several isolated bridge configurations under soil–structure interaction (SSI) effects, by applying the performance-based earthquake engineering (PBEE) methodology to calculate repair costs without quantifying resilience. The present paper aims to contribute by performing the procedure proposed by [
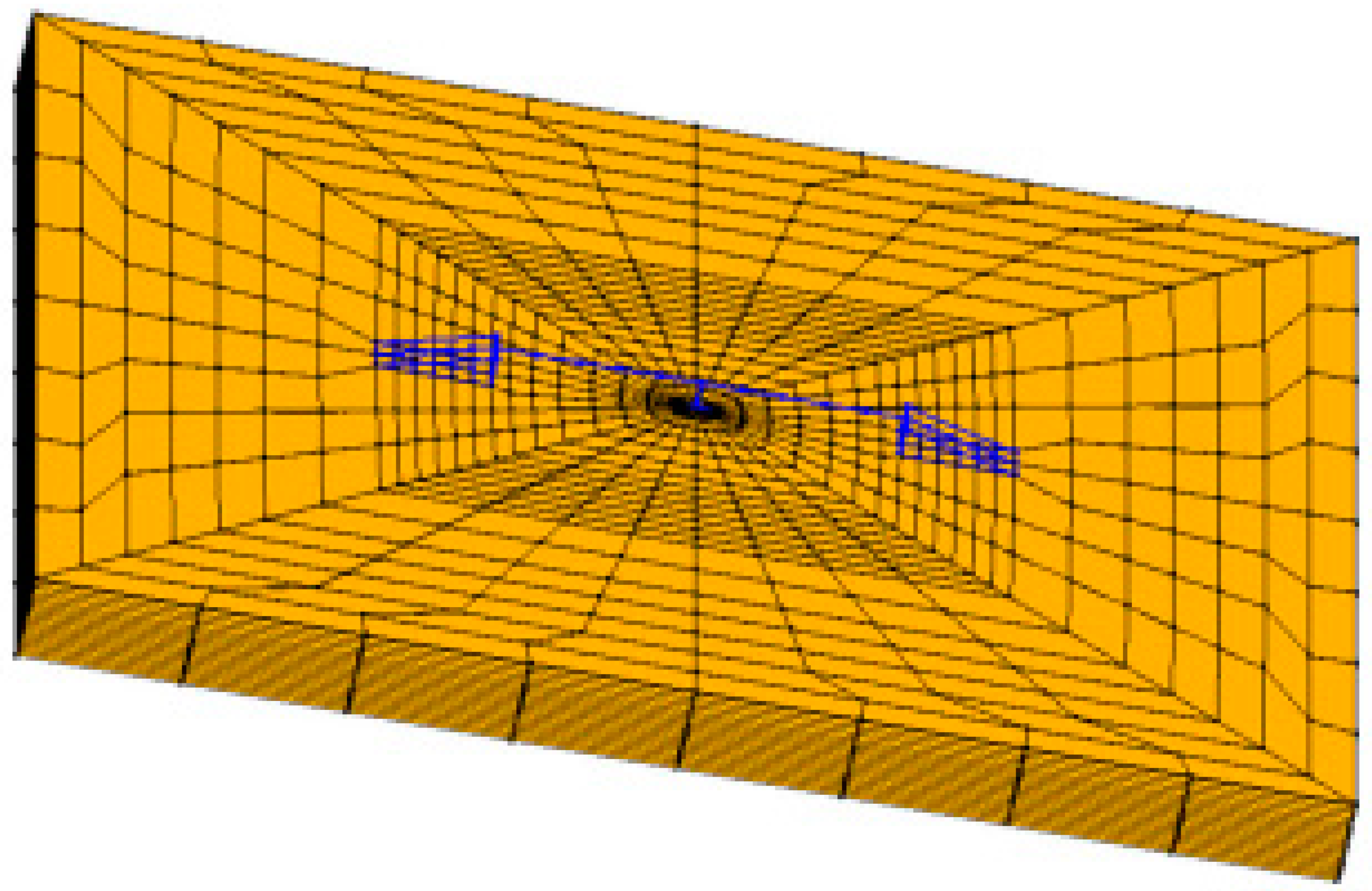
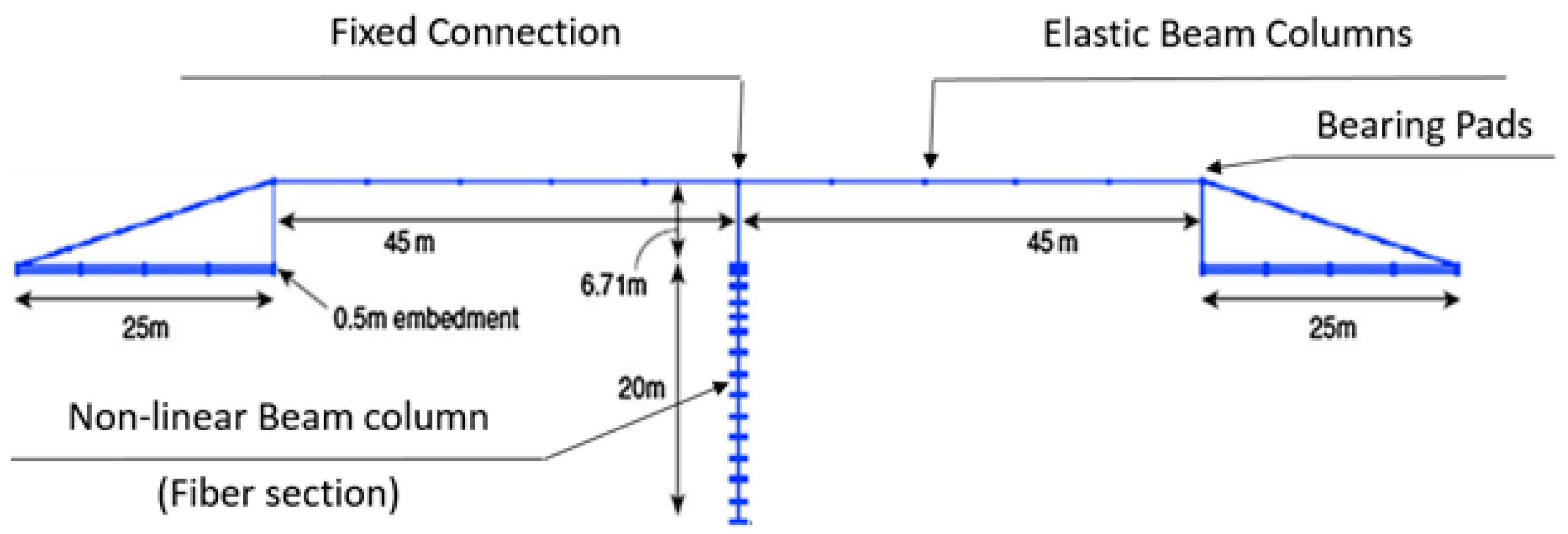
5] to study the effects of SSI on the seismic resilience of a bridge configuration. The ultimate objective is to perform a case study on a typical highway overpass by performing tridimensional numerical simulations of an integrated bridge-foundation-ground model and a performance-based assessment framework. The role of soil structure interaction (SSI) has been accounted for in order to perform a realistic risk assessment by founding the bridge on three different grounds with varying stiffness and strength (ranging from a rigid to a weak soil uniform layer). In particular, the SSI is fundamental to be considered at the design stage to consider the detrimental effects that considering the soil may influence the seismic assessment of the structural vulnerability.
Following the first attempt by [
24], the paper has several elements of novelty: (1) it aims to overcome the lack of bridge resilience assessments necessary for investments, decision-making procedures and pre- and post-hazard risk mitigations; (2) the role of SSI is here investigated with a new approach based on quantification of resilience; and (3) the presented outputs may be applied by decision-makers to choose the best investments for post-hazard event mitigations, emergency responses and recovery strategies with more realistic scenarios. In particular, resilience is a key parameter that may include issues from several disciplines, such as structural, physical, social and economic relationships. This multi-disciplinary dimension is another important novelty of the methodology proposed herein. The paper is organized into 5 sections.
Section 2 explains the numerical models.
Section 3,
Section 4 and
Section 5 the methodology that was proposed is described by considering the definition of resilience and loss and recovery models. The results are shown in
Section 6 where the discussion of the mail applications is also proposed.
4. Recovery Model
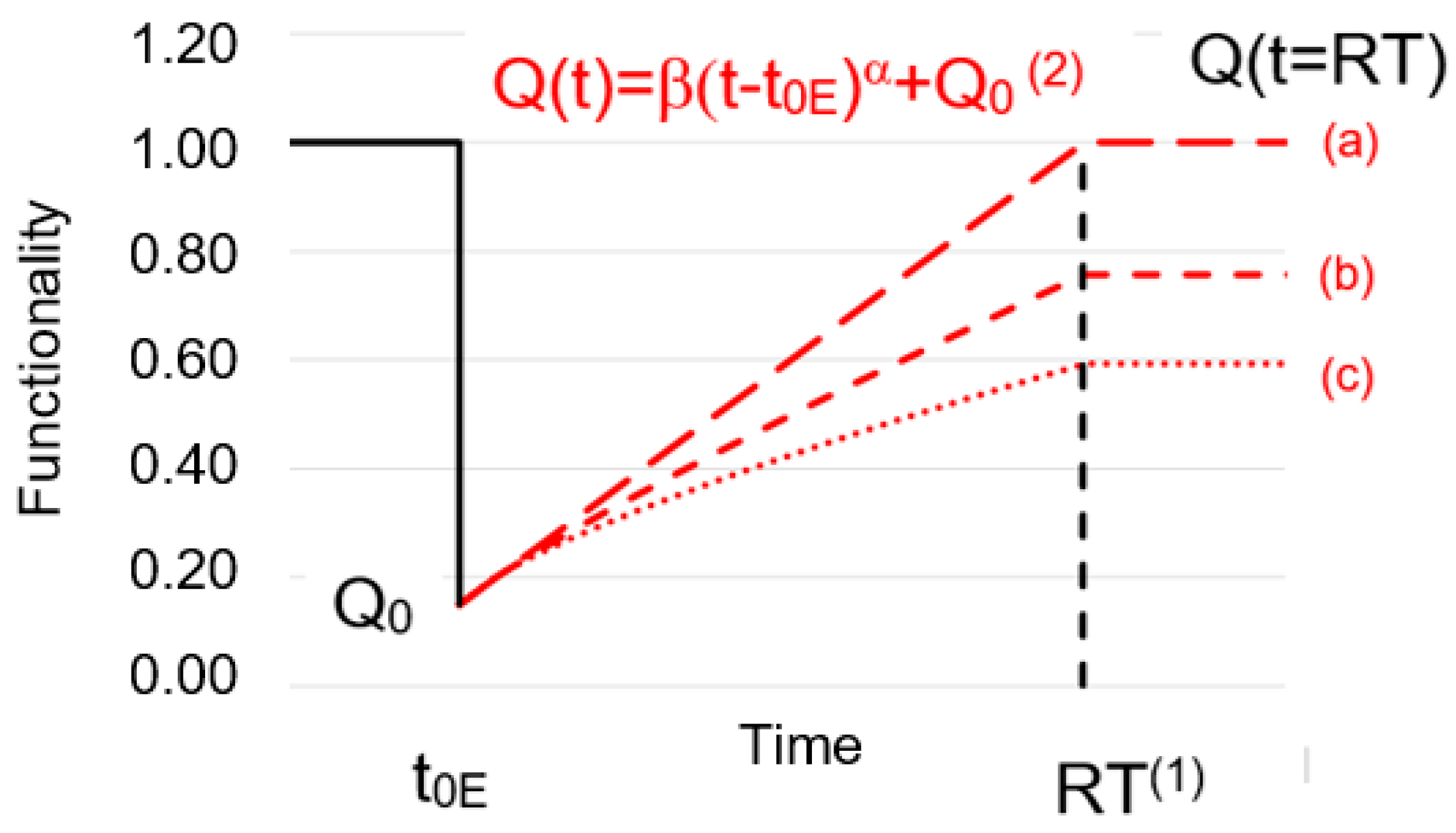
Recovery models quantify the recovery procedures to recover from the seismic event and this paper proposes a formulation to describe the recovery process with a continuous function that assesses the increase of bridge functionality (
Q) in dependence with time (
t) by a power model that is generally applied to describe log-normally distributed phenomenon. Such a formulation is useful because the unknown coefficients can be obtained from regression analyses that are statistical processes for estimating the relationships between variables. Therefore,
Q is defined as the percentage of the pre-earthquake functionality (see
Figure 6):
where
t0E is the time of occurrence of the event
E,
RT is the repair time (or recovery time) necessary to restore the functionality of the bridge and it is calculated with the PBEE methodology, as shown in the next section.
Q(
t) is the recovery function that quantifies the recovery process to return to the pre-earthquake level of functionality. Resilience is defined graphically as the normalized shaded area underneath the recovery function
Q(
t) and thus its quantification is based on the definition of
Q(
t) functions [
5].
β represents the ratio between the final functionality Q and the original value of functionality (that is assumed equal to one). This ratio can generally vary from 0 to 1 (0% to 100%). Sometimes recovery procedures allow an improvement relative to the original functionality, and this value can be higher than 1.0.
α defines the exponent of the growth and it is related to the specific strategy applied. It depends on many uncertainties and can be assessed by statistical approaches, such as optimization procedures.
Q0 is the level of functionality due to the impact of the earthquake in correspondence with the time of occurrence of the event
E (
t0E) and needs to be assessed by the estimation of direct and indirect losses (see next section), as described in [
5]. The proposed formulation (2) is based on two parameters (
α and β and a mathematical structure (power function) that can describe restoration procedures more realistically than the linear one. In particular,
α and β need to be consistent with practical experience coming from bridge multi-sectorial actors (i.e., bridge owners, transportation authorities and public administrators) to cover various bridge classes, different bridge characteristics and specific recovery procedures.
5. Loss Model
Recovery time and costs of repair were calculated by applying the Pacific Earthquake Engineering Research (PEER) centre methodology [
34,
35]; 100 input motions were selected from the PEER NGA database (
http://peer.berkeley.edu/nga/). They consist of 3D triplets, composed of 3 perpendicular acceleration time history components (2 lateral and 1 vertical) and reproduce typical California seismicity, with characteristic periods similar to the fundamental of the bridges, [
23].
The ground motion hazard was introduced for a hypothetical site with intensity data specified at three specific probabilities of exceedance in 50 years (2%, 10%, and 50%). The calculation of the losses is based on the Caltrans Comparative Bridge Costs database and consisted in a probabilistic procedure called the local linearization repair cost and time methodology (LLRCAT) developed by Mackie et al., 2011 and 2012. Repair time is expressed in crew working days (CWD) that is not the number of days that would be required for repair but depends on several factors, such as the number of crews, incentives, number of hours per day on site, etc. Repair costs are expressed in terms of RCR defined as the ratio between the cost of repair and the cost of replacement (does not include demolition) and it can range between 0% and some number higher than 100%. Repair costs are calculated on the basis of performance groups and cost functions that allow to define the loss with a probabilistic-base approach and on the bases of economic estimations [
34,
35]. The results for three different soil conditions are shown
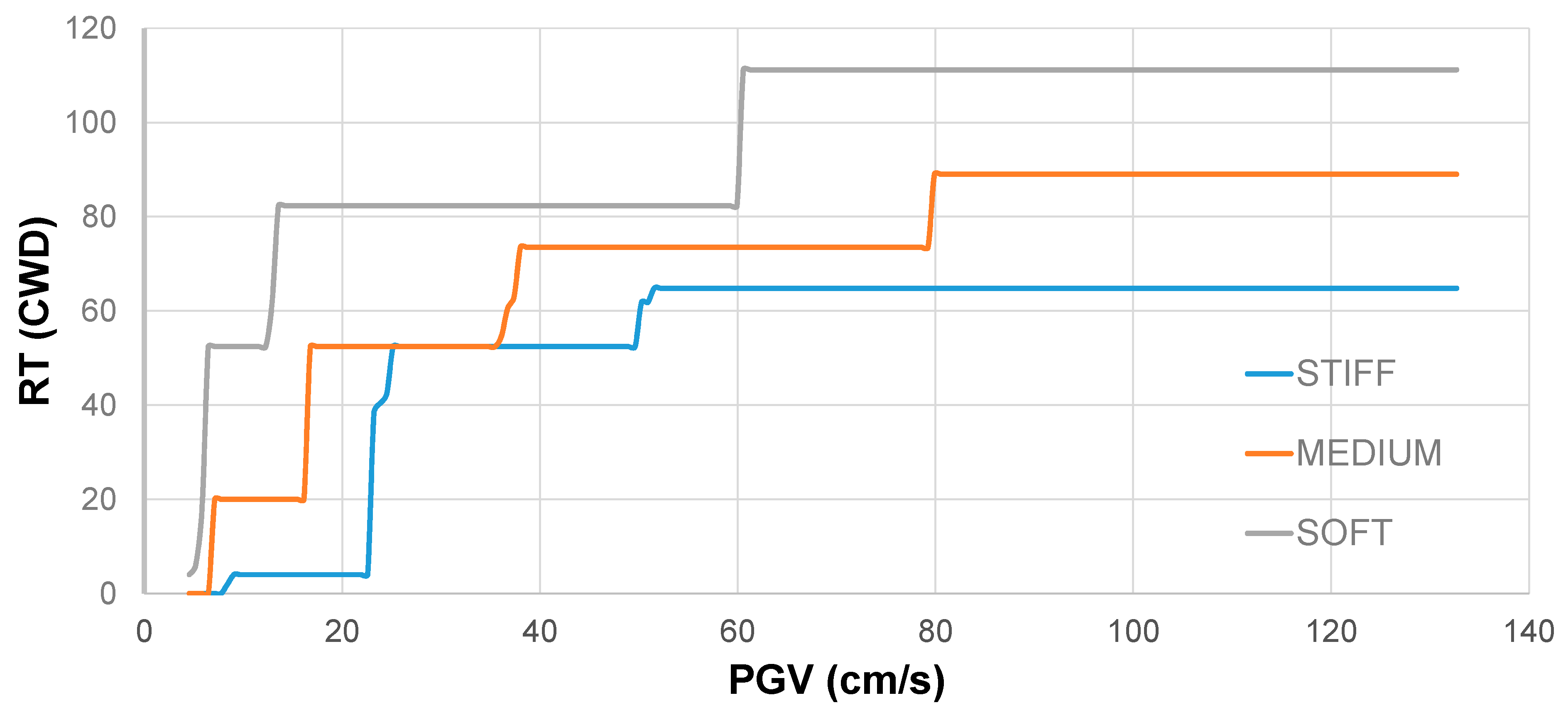
Figure 7 and
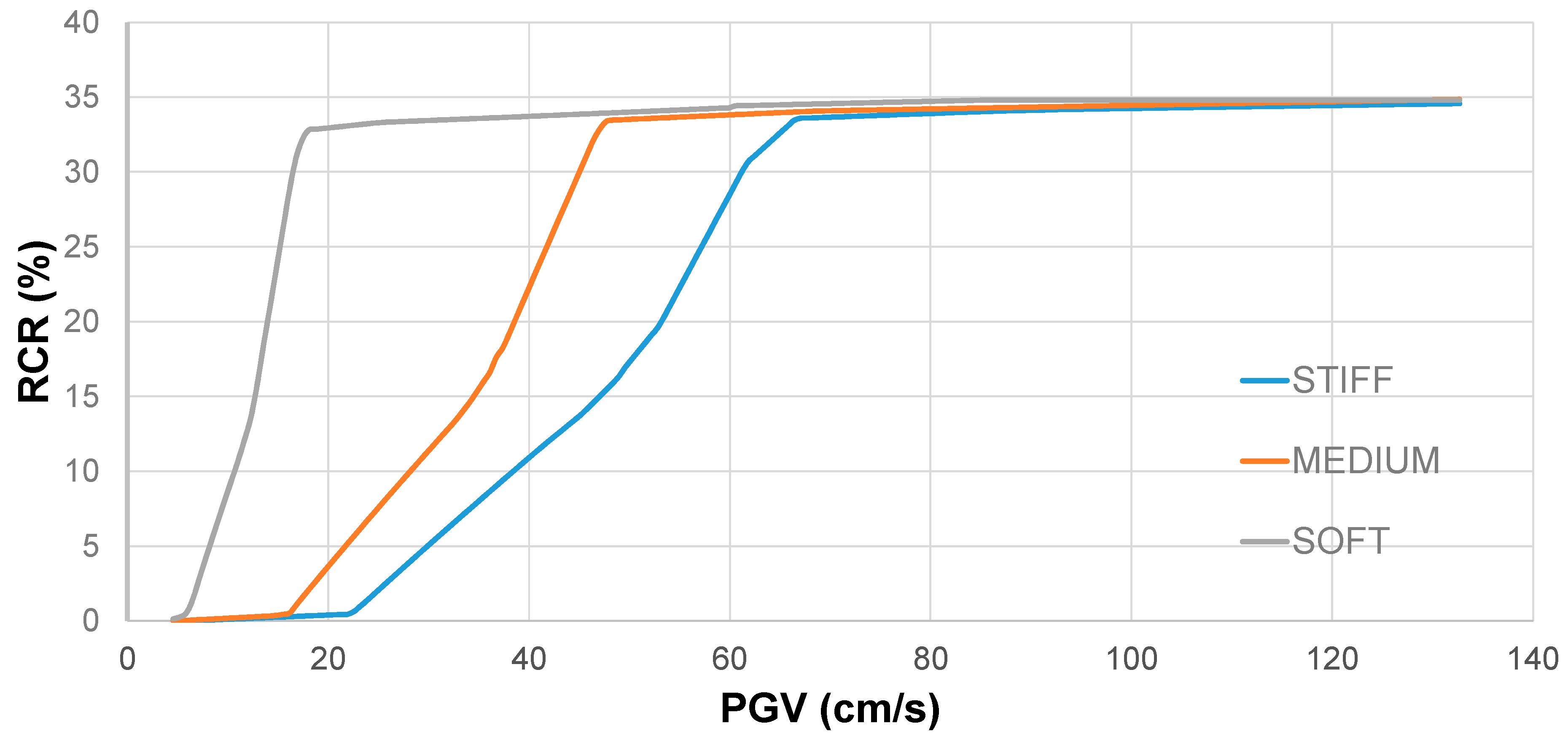
Figure 8 in terms of PGV (Peak Ground Velocity), used as the reference intensity measure.
The effects of soil deformability on the performance of the bridge and thus on the losses depend on the mutual interaction between the dynamic characteristics of the input motion and of the structure, as shown in [
24]. It is worth noting here that accounting SSI effects lead to an increase of both the losses, with a less continuous increase for RTs, due to the triggering of repair activities, as shown in [
8].
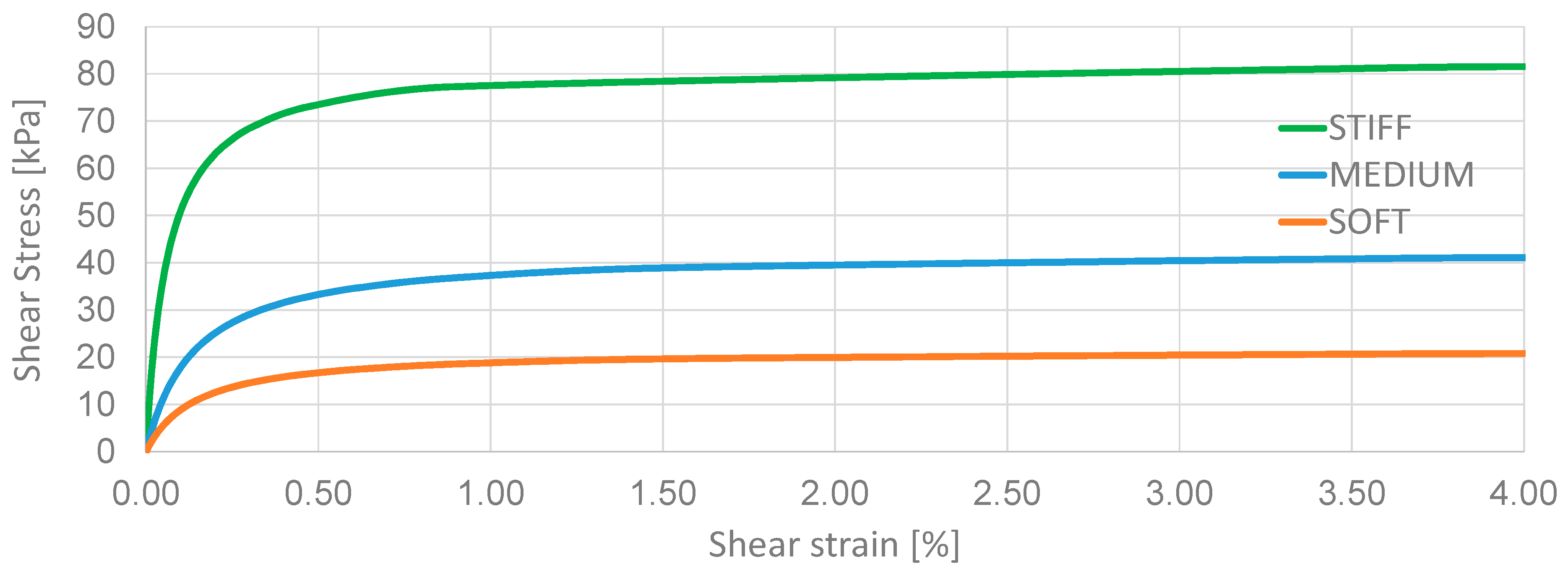
Figure 7 shows that the STIFF condition accumulates the least RT (as would be expected) before reaching a plateau (around 52.5 CWD) above which RTs do not continue to increase because the intensities of PGV are insufficient to cause more failure in the superstructure. The weaker soil cases also exhibit a cost plateau, followed by another increase at PGV (equal to 60 cm/s and 80 cm/s, respectively for SOFT and MEDIUM), due to the accumulation of damage at foundation level. The maximum values of RT are 111.1 CWD and 82.3 CWD, respectively for SOFT and MEDIUM soil.
Figure 8 shows that for MEDIUM and STIFF soil scenarios, RCRs begin to accumulate only after a certain level of PGV (approximately 15 cm/s and 20 cm/s, respectively for MEDIUM and STIFF). For the SOFT condition, there is no retardation in the increase of RCRs that is quicker than for the other soil conditions to reach a plateau above which the cost is relatively constant (for PGV bigger than 18 cm/s). For other soil conditions, RCRs increase for PGVs ranging between 15 cm/s to 45 cm/s for MEDIUM soil and between 22 cm/s to 65 cm/s for STIFF soil. After these intensities, all the soil conditions show the same (almost constant) values of RCR (33–35%).
Table 2 and
Table 3 show the results in terms of RT and RCR for the three considered soil conditions and with three specific probabilities of exceedance in 50 years (2%, 5% and 10%).
In order to apply (2) and thus quantify resilience, it is essential to calculate
Q0 as the level of functionality consequent to the impact of the earthquake at the time of occurrence of the event
E (
t0E). According with [
5],
Q0 may be defined as:
where
Q0 is the ordinate in correspondence with
t0E and is obtained by subtracting the losses (indicated in (3) with L) to the original functionality (supposed to be 100%). Note that
Q0 and
RCR are expressed in percentage, while
RT in CWD, therefore
i is a coefficient with the dimensions of [1/T]. As proposed by [
5], direct and indirect losses can be divided in the losses directly identified as the economic costs and those related to the casualties and because the extreme uncertainties related to the estimation of casualties, the losses are herein calculated by considering only the economic losses.
Direct economic costs were assumed to be described with the previous calculated RCR (
Figure 8), since they represent the total costs in terms of structural and non-structural elements, as proposed already in [
24]. Indirect economic losses can be related with the repair time RT (
Figure 7) and they consist of two typologies: prolongation time and connectivity losses, as proposed and applied in [
23]. In particular, the assessment of indirect losses is a challenging issue and implementing their calculation in a comprehensive framework may be difficult because the extreme variability of this typology of losses and the dependency of indirect losses on structures and on network conditions, do not allow a unique definition, as shown in [
8]. In addition, deducing indirect losses from repair time helps to avoid the uncertainties connected with the estimation of traffic flow before and after the critical event as proposed in some contributions (e.g., [
36]). Applying the PBEE methodology is also important in adopting a probabilistic-based approach instead of a deterministic estimation of indirect losses. Indirect losses connected with the prolongation of travel (PT) are caused by interventions on the infrastructure and the consequent detours that might be needed. Losses due to PT are important when a network is redundant and there are other alternative networks that can be used to cover the journey. The second dimension of indirect losses consists of connectivity loss (CL), principally due to the loss of economic activity that occurs when travel is not possible or the journey can become prohibitive for commercial and industrial traffic and the entire journey is not covered any more. This intangible nature of CL makes the assessment relatively challenging. In this paper indirect losses are calculated as proportional to repair time, calculated in the previous section (
Figure 7), by applying a different coefficient
i in order to represent the cases where only direct losses are considered (
i = 0) and several cases where indirect losses become more important.
6. Seismic Assessment of Soil–Structure Interaction
This section discusses the calculation of resilience by applying the (1) and (2). Several assumptions were made in the choice of the various parameters: (1) this paper applied a linear restoration function (α = 1), in absence of information about preparedness and available resources, (2) 3 values of β were considered: 0.8, 1 and 1.1 (
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8) to define the level of recover the original functionality after the earthquake (a partial, a full recovery, and an improvement, respectively).
The results of the analyses in terms of resilience are shown in
Figure 9,
Figure 10 and
Figure 11 that compare the three selected soil conditions in order to assess the role of soil deformability on the quantification of resilience of the whole system. As shown in
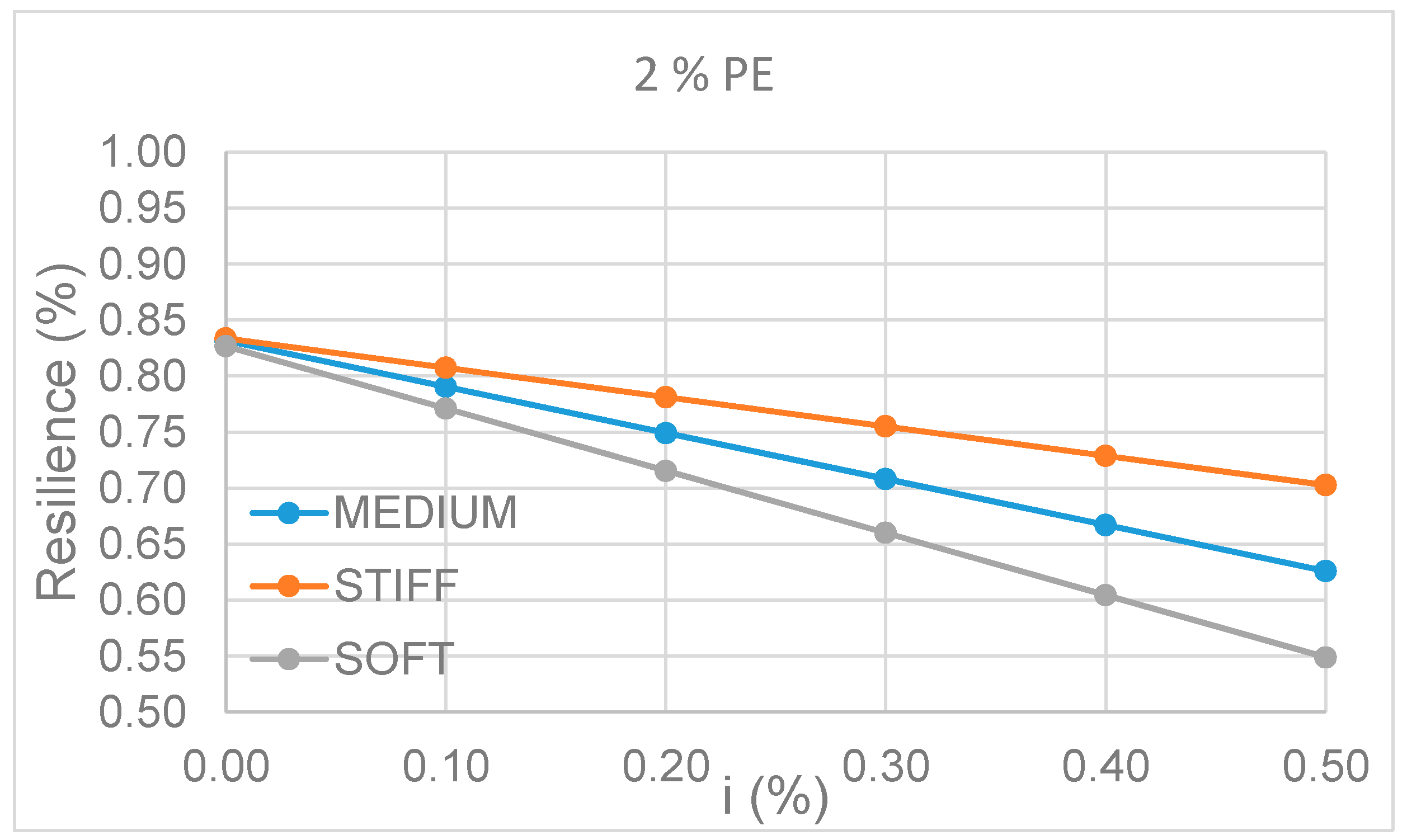
Figure 8, the results are conditioned by the increased effects of RCRs mainly at high intensities when foundation repair is triggered and significant costs accumulate. This is particularly true when the calculation includes direct losses only (i = 0) and particularly at the 2%-in-50 year exceeding probability (
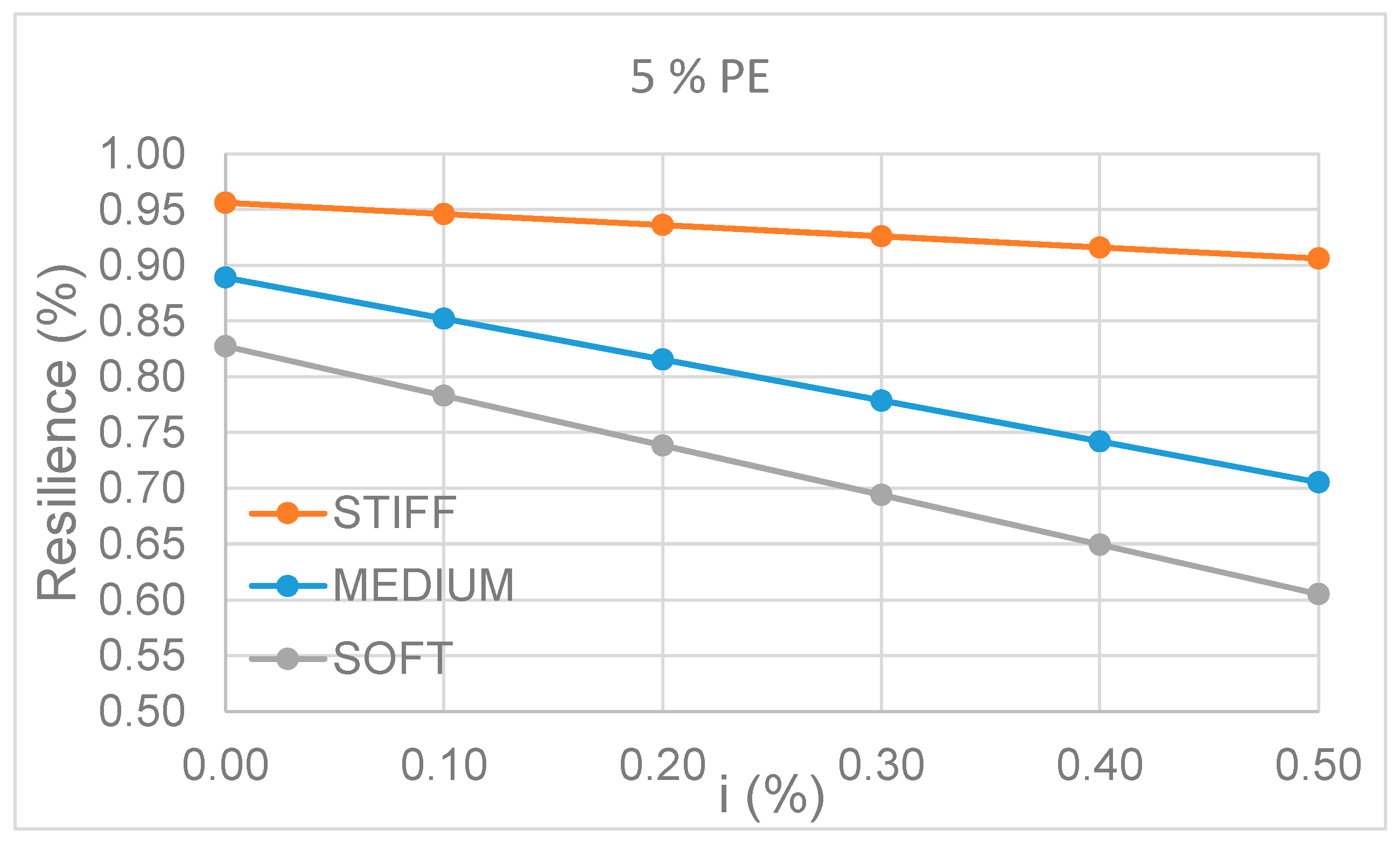
Figure 9). It is worth noticing that indirect losses reduce the values of resilience that is significantly affected by soil deformability. However, this level of seismic hazard is extremely severe. When a 5%-in-50 year level is considered (
Figure 10), it is possible to see (even more clearly) that considering SSI is detrimental to the benchmark bridge, with significant reductions of resilience occurring.
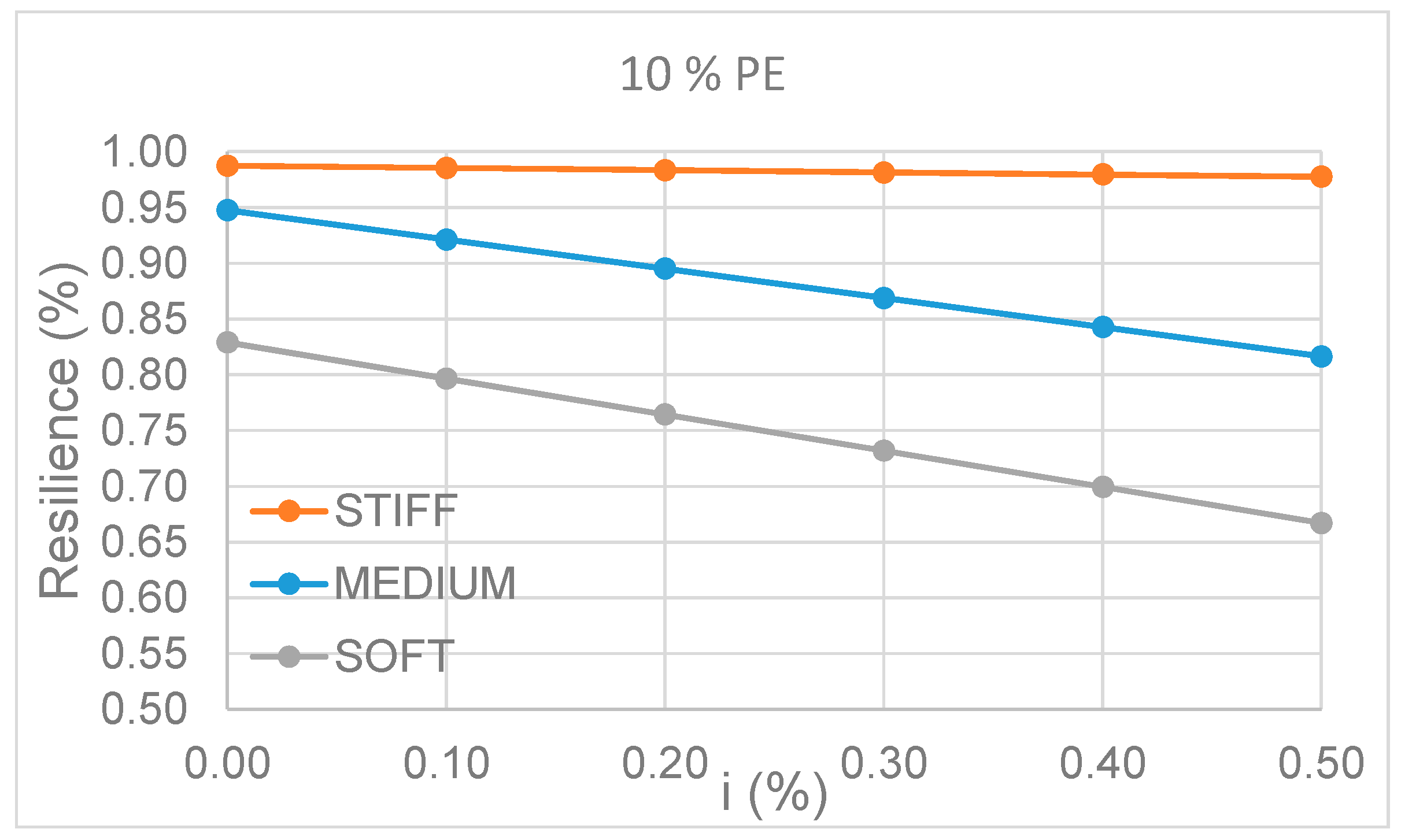
If the most frequent event (10%-in-50 year level) is considered (
Figure 11), resilience is close to unity (100%,
Table 4,
Table 5 and
Table 6) and fairly insensitive to indirect losses for STIFF condition. This means that neglecting the contribution of soil deformability may be too conservative and estimating SSI is necessary to assess realistically the values of resilience.
Figure 11 also confirms the importance of soil deformability even for lower severity of seismic condition, for example noticing the significant difference in resilience between MEDIUM and SOFT soil conditions.
Table 4,
Table 7 and
Table 8 show the results for i = 0.5 and various value of β (0.8, 1 and 1.1), in order to assess the effects on resilience of various levels of recovery the pre-earthquake functionality. It is worth noting that only STIFF soil allows high values of resilience (almost 100%), while even with improvement procedures (β = 1.1), the weak soils show small values of resilience, confirming the significant role of SSI in the assessment of resilience.
Overall, the presented framework assesses the importance of SSI by proposing easier-to-read findings and for a wider range of stakeholders than those resulted by simply considering structural performance. In this regard, the results can be of interest for multi-sectorial actors, such as bridge owners, transportation authorities and public administrators, allowing interdisciplinary applications, such as the assessment of recovery techniques and solutions and/or new easy-to-use decision-making approaches.