Predicting Operating Speeds of Passenger Cars on Single-Carriageway Road Tangents
Abstract
1. Introduction
2. Methodology
2.1. Data Collection
- Geographical region: Central Croatia, Slavonia and Baranja, Lika, Istria, and Dalmatia.
- Existing speed limits: 70, 80, and 90 km/h. It is important to note that in Croatia, the default speed limit outside urban areas is 90 km/h unless otherwise specified by a posted speed limit sign.
- Additional factors: Road design characteristics, vehicle composition, road capacity, and other relevant influencing elements.
2.1.1. Data Collected Through Field Survey
2.1.2. Data from Fixed Traffic Counters Operated by Croatian Roads Ltd.
2.2. Variable Identification
- Passenger side (3 categories: cut sections, guardrails, and flat area);
- Shoulder type (5 categories: no shoulder, extremely narrow, unpaved (earth/grass), gravel, and paved (asphalt/concrete));
- Edge line quality (4 categories: absent, poor, satisfactory, and excellent);
- Visibility (3 categories: poor, good, and excellent);
- Pavement quality;
- Lateral access density;
- Tangent length (up to measurement point);
- Tangent length (from measurement point);
- Speed limit;
- AADT;
- ASDT;
- Lane width;
- Longitudinal slope;
- Crash ratio;
- Design speed;
- Terrain type;
- Guardrail presence;
- Edge lane presence;
- Radius of previous curve;
- Radius of following curve;
- Road category;
- Overtaking allowed;
- Heavy goods vehicles share;
- Disruptive factor presence.
2.3. Data Analysis
3. Results and Discussion
3.1. Relationship Between Operating Speed and Determined Variables
- Free-flow measurement conditions: Data were collected only under free-flow conditions, with passenger cars having no immediate leading vehicle within five seconds. In this situation, higher HVS values might reflect lower overall traffic density for passenger cars, enabling them to travel faster.
- Driver behaviour adaptation: In mixed traffic, where heavy goods vehicles are common, passenger car drivers may accelerate more aggressively during overtaking opportunities, especially on long tangents with overtaking permitted, thereby raising the observed V85.
3.2. Operating Speed Prediction Model Development
3.3. Operating Speed Prediction Model Validation
4. Conclusions
- Shoulder type—gravel;
- Edge line quality—excellent;
- Edge line quality—satisfactory;
- Pavement quality—excellent;
- ASDT;
- Crash ratio;
- Edge lane presence;
- Overtaking allowed;
- Heavy goods vehicles share.
- Geographic specificity: The model is based solely on Croatian road infrastructure and driver behaviour. While it reflects national conditions accurately, extrapolation to other countries or regions should be performed cautiously and with potential local calibration. Also, it should be taken into account that the share of foreign drivers within the scope of this research is unknown.
- Environmental constraints: The analysis only included data collected under favourable weather and daylight conditions. Variables such as nighttime visibility, rain, snow, or fog were not included, potentially limiting applicability to broader scenarios.
- Data resolution limitations: Some variables, such as the crash ratio, were defined at the county level, which may obscure local safety nuances. Additionally, heavy goods vehicle share and traffic data were averaged across cross-sections, potentially smoothing out micro-level effects. Therefore, more precise data on these variables is necessary for future research.
- Variable interpretability and borderline significance: Although tangent length (from the measurement point) had a p-value slightly above 0.05, it was retained to preserve model integrity. Nonetheless, its individual explanatory impact remains modest and may benefit from further investigation into future models.
- Model structure: The use of stepwise linear regression, though effective and statistically valid, has inherent limitations in capturing nonlinearities or interaction effects among predictors. More advanced techniques, such as generalized additive models, random forests, or quantile regression, could be explored in future research, especially with larger or more granular datasets.
- This study included a sample of only 46 locations; while sufficient for traditional statistical modelling, it raises the question of how the results might evolve with a substantially larger dataset. Future research could explore the development of predictive models based on big data sources, such as those provided by platforms like Google or TomTom, which may offer extensive, high-resolution traffic and speed data across time and space. Such an approach might enable more nuanced modelling and potentially reveal patterns and interactions that are not detectable through conventional data collection methods.
- Another direction involves testing the model’s transferability to other road categories and geometric contexts. While this study focused on single-carriageway tangents, applying and calibrating the methodology to dual-carriageways and tangent–curve sequences could reveal whether different lane configurations, median treatments, or curve proximities alter the relative influence of geometric and traffic variables on operating speed.
- In addition to the limitations already noted, it is important to recognize that certain findings from this study diverge from widely reported relationships in the operating speed literature. A notable example is the effect of lane width: while many previous studies have found that wider lanes are generally associated with higher operating speeds [29,46], this analysis indicated the opposite trend, with narrower lanes linked to slightly higher speeds on the sampled tangents. This result may reflect context-specific influences such as driver expectancy, the interaction between lane width and shoulder type, or site selection bias within the dataset. It may also indicate that in certain environments, narrower lanes occur on higher-standard tangents with favourable alignment and visibility, thus supporting higher speeds despite the reduced lane width. Such findings should be interpreted cautiously and verified through further research in other settings before being generalized. This reinforces the need for broader data collection across different road classes, traffic compositions, and environmental conditions to determine whether such inverse relationships represent local anomalies or point to a need to revisit widely accepted design speed assumptions in the literature.
- Finally, incorporating human factors in a more explicit and measurable way offers potential to improve predictive accuracy. Variables that reflect drivers’ perceived likelihood of interaction with other road users, such as roadside activity, overtaking frequency, or sight-line interruptions, could be operationalized through on-field observation or video analytics. By capturing not only the infrastructural and physical attributes of the road but also how drivers interpret them, future models could better explain deviations between posted limits, design speeds, and operating speeds. Integrating these enhanced models into practical decision support tools for engineers and planners would help bridge the gap between predictive research and everyday road design practice.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Locations (Cross-Sections) General Data
| Data Collected Through Field Survey [40] | |||||||
| Road Category | Location Name | Direction | Speed Limit [km/h] | AADT [veh/day] | ASDT [veh/day] | Total Sample Size (All Vehicle Categories) [veh] | Filtered Sample Size (Passenger Cars) [veh] |
| State road | Dubrovnik | towards Dubrovnik | 90 | 18,292 | 25,757 | 8222 | 1024 |
| towards Čilipi | 90 | 18,292 | 25,757 | 6802 | 1287 | ||
| County road | Gospić | from toll | 90 | 878 | 1118 | 242 | 161 |
| towards toll | 90 | 878 | 1118 | 176 | 119 | ||
| County road | Knin | from Knin | 90 | 1216 | 1450 | 88 | 70 |
| towards Knin | 90 | 1216 | 1450 | 76 | 56 | ||
| County road | Osijek | from Osijek | 70 | 8717 | 8438 | 2433 | 933 |
| towards Osijek | 70 | 8717 | 8438 | 3526 | 1147 | ||
| State road | Pazin | from Pazin | 90 | 3391 | 3847 | 492 | 335 |
| towards Pazin | 90 | 3391 | 3847 | 488 | 338 | ||
| County road | Požega | from Požega | 90 | 1656 | 1655 | 836 | 323 |
| towards Požega | 90 | 1656 | 1655 | 928 | 429 | ||
| State road | Pula | from Pula | 90 | 2873 | 4375 | 1602 | 771 |
| towards Pula | 90 | 2873 | 4375 | 1557 | 762 | ||
| State road | Sisak | towards Sisak | 90 | 3953 | 4550 | 479 | 248 |
| towards Stružec | 90 | 3953 | 4550 | 516 | 234 | ||
| State road | Split | from Klis | 80 | 2404 | 3522 | 823 | 299 |
| towards Klis | 80 | 2404 | 3522 | 1234 | 359 | ||
| State road | Varaždin | from Varaždin | 90 | 8947 | 8773 | 1603 | 564 |
| towards Varaždin | 90 | 8947 | 8773 | 1696 | 661 | ||
| County road | Virovitica | from Novaki | 90 | 380 | 410 | 74 | 62 |
| towards Novaki | 90 | 380 | 410 | 75 | 63 | ||
| State road | Zadar | towards Zadar | 90 | 13,022 | 22,904 | 1914 | 906 |
| towards Nin | 90 | 13,022 | 22,904 | 1211 | 502 | ||
| Total: | 37,093 | 11,653 | |||||
| Data from Fixed Traffic Counters Operated by Croatian Roads Ltd. [41] | |||||||
| Road Category | Location Name | Direction | Speed Limit [km/h] | AADT [veh/day] | ASDT [veh/day] | Total Sample Size (All Vehicle Categories) [veh] | Filtered Sample Size (Passenger Cars) [veh] |
| State road | Trnovec Bartolovečki | towards Ludbreg | 90 | 8700 | 8650 | N/A | N/A |
| towards Varaždin | 90 | 8700 | 8650 | N/A | N/A | ||
| State road | Paka | towards Sveti Ivan Zelina | 90 | 4525 | 4766 | N/A | N/A |
| towards Novi Marof | 90 | 4525 | 4766 | N/A | N/A | ||
| State road | Brlenić | towards Draganić | 90 | 2673 | 2689 | N/A | N/A |
| towards Krašić | 90 | 2673 | 2689 | N/A | N/A | ||
| State road | Kašina | towards Soblinec (DC3) | 70 | 3465 | 3593 | N/A | N/A |
| towards Marija Bistrica | 70 | 3465 | 3593 | N/A | N/A | ||
| State road | Trema | towards Sveti Ivan Žabno | 90 | 2470 | 2365 | N/A | N/A |
| towards Križevci | 90 | 2470 | 2365 | N/A | N/A | ||
| State road | Virovitica bypass-North | towards Grubišno Polje | 90 | 1799 | 2109 | N/A | N/A |
| towards Terezino Polje | 90 | 1799 | 2109 | N/A | N/A | ||
| State road | Podravska Moslavina | towards Donji Miholjac | 90 | 2324 | 2506 | N/A | N/A |
| towards Slatina | 90 | 2324 | 2506 | N/A | N/A | ||
| State road | Sibinj Krmpotski | towards Senj | 90 | 4254 | 8745 | N/A | N/A |
| towards Novi Vinodolski | 90 | 4254 | 8745 | N/A | N/A | ||
| State road | Bračevci | towards Đakovo | 90 | 1565 | 1765 | N/A | N/A |
| towards Našice | 90 | 1565 | 1765 | N/A | N/A | ||
| State road | Pirovac | towards Vodice | 90 | 5026 | 10,154 | N/A | N/A |
| towards Pakoštane | 90 | 5026 | 10,154 | N/A | N/A | ||
| State road | Pakovo Selo | towards Šibenik | 70 | 2335 | 3333 | N/A | N/A |
| towards Drniš | 70 | 2335 | 3333 | N/A | N/A | ||
| Total: | N/A | N/A | |||||
Appendix B. Variables—Descriptive Statistics
| Training Set (13 Cross-Sections/36 Locations) | ||||||||
| Operating Speed Values | Symbol | Unit of Measure | Type | Mean | StDev | Min | Max | Median |
| Operating speed (V85) | V85 | [km/h] | Continuous | 103.08 | 13.76 | 74 | 128 | 101 |
| Variables | Symbol | Unit of Measure | Type | Mean | StDev | Min | Max | Median |
| Passenger side | PS | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Passenger side—Cutting | PS-C | [-] | Binary (dummy) | 0.17 | 0.38 | 0 | 1 | 0 |
| Passenger side—Guardrail | PS-G | [-] | Binary (dummy) | 0.17 | 0.38 | 0 | 1 | 0 |
| Shoulder type | ST | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Shoulder type—Narrow | ST-N | [-] | Binary (dummy) | 0.22 | 0.42 | 0 | 1 | 0 |
| Shoulder type—Gravel | ST-Grv | [-] | Binary (dummy) | 0.25 | 0.44 | 0 | 1 | 0 |
| Shoulder type—Grass | ST-Grs | [-] | Binary (dummy) | 0.31 | 0.47 | 0 | 1 | 0 |
| Shoulder type—Paved | ST-P | [-] | Binary (dummy) | 0.08 | 0.28 | 0 | 1 | 0 |
| Edge line quality | ELQ | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Edge line quality—Poor | ELQ-P | [-] | Binary (dummy) | 0.06 | 0.23 | 0 | 1 | 0 |
| Edge line quality—Satisfactory | ELQ-S | [-] | Binary (dummy) | 0.19 | 0.40 | 0 | 1 | 0 |
| Edge line quality—Excellent | ELQ-E | [-] | Binary (dummy) | 0.64 | 0.49 | 0 | 1 | 1 |
| Visibility | Vsb | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Visibility—Good | Vsb-G | [-] | Binary (dummy) | 0.33 | 0.48 | 0 | 1 | 0 |
| Visibility—Excellent | Vsb-E | [-] | Binary (dummy) | 0.64 | 0.49 | 0 | 1 | 1 |
| Pavement quality | PQ | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Pavement quality—Poor | PQ-P | [-] | Binary (dummy) | 0.06 | 0.23 | 0 | 1 | 0 |
| Pavement quality—Excellent | PQ-E | [-] | Binary (dummy) | 0.56 | 0.50 | 0 | 1 | 1 |
| Lateral access density | LAD | [-] | Continuous | 1.36 | 1.44 | 0 | 6 | 1 |
| Tangent length (up to measurement point) | TL1 | [m] | Continuous | 767.50 | 563.09 | 110 | 2500 | 635 |
| Tangent length (from measurement point) | TL2 | [m] | Continuous | 808.19 | 536.49 | 150 | 2500 | 700 |
| Speed limit | SL | [km/h] | Continuous | 86.67 | 7.17 | 70 | 90 | 90 |
| AADT | AADT | [veh/day] | Continuous | 4203.39 | 3746.35 | 878 | 18,292 | 2773 |
| ASDT | ASDT | [veh/day] | Continuous | 5403.78 | 5432.99 | 1118 | 25,757 | 3557.50 |
| Lane width | LW | [m] | Continuous | 3.08 | 0.24 | 2.75 | 3.50 | 3 |
| Longitudinal slope | LS | [%] | Continuous | −0.08 | 2.49 | −5.20 | 5.20 | 0 |
| Crash ratio | CR | [-] | Continuous | 0.004 | 0.002 | 0.002 | 0.012 | 0.003 |
| Design speed | Vp | [km/h] | Continuous | 72.78 | 15.04 | 50 | 100 | 70 |
| Terrain type | TT | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Terrain type—Flat | TT-F | [-] | Binary (dummy) | 0.47 | 0.51 | 0 | 1 | 0 |
| Terrain type—Mountainous | TT-M | [-] | Binary (dummy) | 0.06 | 0.23 | 0 | 1 | 0 |
| Guardrail presence | GP | [-] | Binary | 0.14 | 0.35 | 0 | 1 | 0 |
| Edge lane presence | ELP | [-] | Binary | 0.75 | 0.44 | 0 | 1 | 1 |
| Radius of previous curve | RpC | [m] | Continuous | 403.17 | 295.66 | 20 | 1200 | 325 |
| Radius of following curve | RfC | [m] | Continuous | 421.56 | 359.02 | 20 | 1500 | 305 |
| Road category | RC | [-] | Binary | 0.31 | 0.47 | 0 | 1 | 0 |
| Overtaking allowed (in zone) | OA | [-] | Binary | 0.81 | 0.40 | 0 | 1 | 1 |
| Heavy goods vehicle share | HVS | [%] | Continuous | 0.08 | 0.10 | 0.01 | 0.43 | 0.04 |
| Disruptive factor presence | DFP | [-] | Binary | 0.11 | 0.32 | 0 | 1 | 0 |
| Test Set (5 Cross-Sections/10 Locations) | ||||||||
| Operating Speed Values | Symbol | Unit of Measure | Type | Mean | StDev | Min | Max | Median |
| Operating speed (V85) | V85 | [km/h] | Continuous | 93.50 | 7.20 | 76 | 100 | 96.50 |
| Variables | Symbol | Unit of Measure | Type | Mean | StDev | Min | Max | Median |
| Passenger side | PS | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Passenger side—Cutting | PS-C | [-] | Binary (dummy) | 0.20 | 0.42 | 0 | 1 | 0 |
| Passenger side—Guardrail | PS-G | [-] | Binary (dummy) | 0.10 | 0.32 | 0 | 1 | 0 |
| Shoulder type | ST | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Shoulder type—Narrow | ST-N | [-] | Binary (dummy) | 0.50 | 0.53 | 0 | 1 | 0.50 |
| Shoulder type—Gravel | ST-Grv | [-] | Binary (dummy) | 0 | 0 | 0 | 0 | 0 |
| Shoulder type—Grass | ST-Grs | [-] | Binary (dummy) | 0.20 | 0.42 | 0 | 1 | 0 |
| Shoulder type—Paved | ST-P | [-] | Binary (dummy) | 0.20 | 0.42 | 0 | 1 | 0 |
| Edge line quality | ELQ | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Edge line quality—Poor | ELQ-P | [-] | Binary (dummy) | 0 | 0 | 0 | 0 | 0 |
| Edge line quality—Satisfactory | ELQ-S | [-] | Binary (dummy) | 0 | 0 | 0 | 0 | 0 |
| Edge line quality—Excellent | ELQ-E | [-] | Binary (dummy) | 0.60 | 0.52 | 0 | 1 | 1 |
| Visibility | Vsb | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Visibility—Good | Vsb-G | [-] | Binary (dummy) | 0.60 | 0.52 | 0 | 1 | 1 |
| Visibility—Excellent | Vsb-E | [-] | Binary (dummy) | 0.40 | 0.52 | 0 | 1 | 0 |
| Pavement quality | PQ | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Pavement quality—Poor | PQ-P | [-] | Binary (dummy) | 0 | 0 | 0 | 0 | 0 |
| Pavement quality—Excellent | PQ-E | [-] | Binary (dummy) | 0.50 | 0.53 | 0 | 1 | 0.50 |
| Lateral access density | LAD | [-] | Continuous | 1.50 | 1.35 | 0 | 4 | 1.50 |
| Tangent length (up to measurement point) | TL1 | [m] | Continuous | 624 | 323.63 | 200 | 1200 | 590 |
| Tangent length (from measurement point) | TL2 | [m] | Continuous | 477.50 | 375.92 | 110 | 1200 | 370 |
| Speed limit | SL | [km/h] | Continuous | 88 | 6.32 | 70 | 90 | 90 |
| AADT | AADT | [veh/day] | Continuous | 5840.80 | 5842.20 | 380 | 18,292 | 3859.50 |
| ASDT | ASDT | [veh/day] | Continuous | 8041.20 | 9089.87 | 410 | 25,757 | 4179.50 |
| Lane width | LW | [m] | Continuous | 3.05 | 0.35 | 2.50 | 3.50 | 3.25 |
| Longitudinal slope | LS | [%] | Continuous | −0.25 | 3.04 | −5.20 | 3.50 | 0 |
| Crash ratio | CR | [-] | Continuous | 0.00312 | 0.00083 | 0.00211 | 0.00483 | 0.00301 |
| Design speed | Vp | [km/h] | Continuous | 70 | 20 | 40 | 100 | 80 |
| Terrain type | TT | [-] | Categorical—Multi-level | --- | --- | --- | --- | --- |
| Terrain type—Flat | TT-F | [-] | Binary (dummy) | 0.50 | 0.53 | 0 | 1 | 0.50 |
| Terrain type—Mountainous | TT-M | [-] | Binary (dummy) | 0.20 | 0.42 | 0 | 1 | 0 |
| Guardrail presence | GP | [-] | Binary | 0 | 0 | 0 | 0 | 0 |
| Edge lane presence | ELP | [-] | Binary | 0.60 | 0.52 | 0 | 1 | 1 |
| Radius of previous curve | RpC | [m] | Continuous | 424.90 | 475.41 | 25 | 1500 | 247.50 |
| Radius of following curve | RfC | [m] | Continuous | 358.70 | 248.33 | 95 | 950 | 320 |
| Road category | RC | [-] | Binary | 0.30 | 0.48 | 0 | 1 | 0 |
| Overtaking allowed (in zone) | OA | [-] | Binary | 0.80 | 0.42 | 0 | 1 | 1 |
| Heavy goods vehicles share | HVS | [%] | Continuous | 0.047 | 0.020 | 0.018 | 0.084 | 0.048 |
| Disruptive factor presence | DFP | [-] | Binary | 0.10 | 0.32 | 0 | 1 | 0 |
Appendix C. Correlation Matrix
| PS-C | PS-G | ST-N | ST-Grv | ST-Grs | ST-P | ELQ-E | ELQ-S | ELQ-P | Vsb-E | Vsb-G | PQ-E | PQ-P | LAD | TL1 | TL2 | SL | AADT | ASDT | LW | LS | CR | Vp | TT-F | TT-M | GP | ELP | RpC | RfC | RC | OA | HVS | DFP | |
| PS-C | 1.00 | −0.20 | 0.30 | −0.09 | −0.13 | −0.13 | 0.18 | −0.22 | −0.11 | −0.44 | 0.47 | −0.05 | −0.11 | −0.22 | −0.07 | −0.04 | 0.00 | −0.03 | 0.07 | 0.00 | 0.07 | −0.17 | −0.03 | −0.42 | −0.11 | −0.18 | −0.26 | 0.09 | 0.06 | 0.03 | −0.35 | −0.20 | −0.16 |
| PS-G | −0.20 | 1.00 | 0.30 | −0.09 | −0.13 | −0.13 | −0.28 | 0.16 | 0.54 | 0.03 | 0.00 | −0.05 | −0.11 | −0.17 | −0.02 | −0.06 | −0.21 | 0.15 | 0.13 | 0.08 | 0.11 | 0.51 | 0.12 | −0.12 | 0.22 | 0.68 | 0.09 | −0.17 | −0.27 | −0.13 | 0.22 | −0.02 | 0.32 |
| ST-N | 0.30 | 0.30 | 1.00 | −0.31 | −0.35 | −0.16 | −0.15 | 0.24 | 0.16 | −0.02 | −0.09 | −0.19 | −0.13 | −0.09 | 0.03 | −0.07 | 0.06 | −0.10 | −0.10 | 0.09 | 0.02 | 0.39 | 0.13 | −0.24 | −0.13 | 0.56 | 0.15 | −0.23 | −0.12 | −0.06 | −0.08 | −0.04 | 0.02 |
| ST-Grv | −0.09 | −0.09 | −0.31 | 1.00 | −0.38 | −0.17 | 0.30 | −0.12 | −0.14 | 0.03 | 0.00 | 0.39 | −0.14 | −0.01 | −0.01 | −0.04 | −0.27 | −0.10 | 0.04 | −0.34 | −0.13 | −0.02 | −0.37 | −0.29 | −0.14 | −0.23 | 0.33 | −0.03 | 0.06 | 0.03 | −0.04 | −0.17 | 0.00 |
| ST-Grs | −0.13 | −0.13 | −0.35 | −0.38 | 1.00 | −0.20 | −0.13 | 0.13 | −0.16 | −0.13 | 0.17 | −0.01 | −0.16 | −0.13 | 0.00 | 0.00 | −0.03 | −0.17 | −0.24 | 0.15 | −0.06 | −0.12 | 0.20 | 0.34 | −0.16 | −0.27 | −0.17 | 0.06 | 0.15 | −0.05 | 0.02 | 0.39 | −0.04 |
| ST-P | −0.13 | −0.13 | −0.16 | −0.17 | −0.20 | 1.00 | 0.23 | −0.15 | −0.07 | 0.23 | −0.21 | −0.13 | −0.07 | 0.35 | 0.06 | 0.01 | 0.14 | 0.37 | 0.19 | 0.32 | −0.13 | −0.10 | 0.28 | 0.32 | −0.07 | −0.12 | 0.17 | −0.12 | −0.20 | 0.02 | −0.11 | −0.07 | −0.11 |
| ELQ-E | 0.18 | −0.28 | −0.15 | 0.30 | −0.13 | 0.23 | 1.00 | −0.65 | −0.32 | 0.04 | 0.04 | 0.49 | −0.32 | −0.01 | −0.14 | −0.12 | 0.14 | −0.06 | 0.03 | 0.08 | −0.19 | −0.15 | 0.06 | 0.02 | −0.07 | −0.37 | 0.23 | 0.22 | 0.15 | 0.12 | −0.37 | 0.10 | 0.08 |
| ELQ-S | −0.22 | 0.16 | 0.24 | −0.12 | 0.13 | −0.15 | −0.65 | 1.00 | −0.12 | 0.08 | −0.20 | −0.27 | −0.12 | 0.12 | 0.32 | 0.29 | −0.17 | 0.01 | −0.09 | 0.12 | −0.03 | 0.13 | 0.19 | 0.10 | −0.12 | 0.21 | 0.28 | −0.33 | −0.30 | −0.02 | 0.24 | 0.03 | −0.17 |
| ELQ-P | −0.11 | 0.54 | 0.16 | −0.14 | −0.16 | −0.07 | −0.32 | −0.12 | 1.00 | −0.07 | 0.09 | −0.03 | −0.06 | −0.06 | −0.25 | −0.24 | 0.11 | 0.35 | 0.36 | 0.04 | 0.35 | 0.38 | 0.04 | −0.23 | 0.47 | 0.60 | −0.14 | −0.11 | −0.12 | 0.10 | 0.12 | −0.05 | 0.30 |
| Vsb-E | −0.44 | 0.03 | −0.02 | 0.03 | −0.13 | 0.23 | 0.04 | 0.08 | −0.07 | 1.00 | −0.94 | −0.09 | 0.18 | 0.03 | 0.43 | 0.21 | −0.03 | −0.09 | −0.14 | 0.08 | −0.31 | 0.20 | 0.10 | 0.48 | −0.07 | 0.13 | 0.37 | −0.01 | 0.13 | −0.25 | 0.07 | 0.31 | 0.08 |
| Vsb-G | 0.47 | 0.00 | −0.09 | 0.00 | 0.17 | −0.21 | 0.04 | −0.20 | 0.09 | −0.94 | 1.00 | 0.16 | −0.17 | −0.14 | −0.42 | −0.14 | 0.00 | 0.10 | 0.16 | −0.06 | 0.19 | −0.16 | −0.09 | −0.43 | 0.09 | −0.11 | −0.41 | 0.04 | −0.09 | 0.17 | −0.10 | −0.29 | −0.06 |
| PQ-E | −0.05 | −0.05 | −0.19 | 0.39 | −0.01 | −0.13 | 0.49 | −0.27 | −0.03 | −0.09 | 0.16 | 1.00 | −0.27 | −0.13 | −0.14 | −0.04 | −0.26 | 0.27 | 0.34 | 0.26 | 0.01 | −0.07 | 0.21 | −0.05 | 0.22 | −0.13 | 0.26 | −0.03 | 0.07 | −0.01 | −0.30 | −0.05 | −0.04 |
| PQ-P | −0.11 | −0.11 | −0.13 | −0.14 | −0.16 | −0.07 | −0.32 | −0.12 | −0.06 | 0.18 | −0.17 | −0.27 | 1.00 | 0.02 | 0.15 | 0.13 | 0.11 | −0.17 | −0.17 | −0.34 | 0.01 | −0.14 | −0.37 | 0.26 | −0.06 | −0.10 | −0.42 | 0.22 | 0.17 | −0.16 | 0.12 | −0.13 | −0.09 |
| LAD | −0.22 | −0.17 | −0.09 | −0.01 | −0.13 | 0.35 | −0.01 | 0.12 | −0.06 | 0.03 | −0.14 | −0.13 | 0.02 | 1.00 | −0.12 | −0.15 | 0.20 | 0.09 | 0.05 | −0.15 | 0.19 | −0.08 | −0.17 | −0.01 | −0.06 | −0.10 | 0.10 | −0.06 | −0.13 | 0.38 | −0.02 | −0.12 | −0.09 |
| TL1 | −0.07 | −0.02 | 0.03 | −0.01 | 0.00 | 0.06 | −0.14 | 0.32 | −0.25 | 0.43 | −0.42 | −0.14 | 0.15 | −0.12 | 1.00 | 0.49 | −0.30 | 0.02 | −0.11 | 0.10 | −0.17 | −0.21 | 0.14 | 0.35 | −0.27 | −0.11 | −0.07 | −0.02 | 0.06 | 0.01 | 0.17 | −0.05 | −0.09 |
| TL2 | −0.04 | −0.06 | −0.07 | −0.04 | 0.00 | 0.01 | −0.12 | 0.29 | −0.24 | 0.21 | −0.14 | −0.04 | 0.13 | −0.15 | 0.49 | 1.00 | −0.30 | 0.01 | −0.13 | 0.09 | 0.03 | −0.25 | 0.14 | 0.37 | −0.26 | 0.04 | −0.06 | 0.07 | −0.07 | −0.05 | 0.22 | −0.06 | −0.07 |
| SL | 0.00 | −0.21 | 0.06 | −0.27 | −0.03 | 0.14 | 0.14 | −0.17 | 0.11 | −0.03 | 0.00 | −0.26 | 0.11 | 0.20 | −0.30 | −0.30 | 1.00 | −0.06 | 0.03 | 0.00 | −0.01 | 0.11 | −0.02 | 0.13 | 0.11 | −0.04 | −0.09 | 0.30 | 0.27 | 0.14 | −0.13 | 0.24 | 0.04 |
| AADT | −0.03 | 0.15 | −0.10 | −0.10 | −0.17 | 0.37 | −0.06 | 0.01 | 0.35 | −0.09 | 0.10 | 0.27 | −0.17 | 0.09 | 0.02 | 0.01 | −0.06 | 1.00 | 0.94 | 0.52 | 0.09 | −0.20 | 0.46 | 0.16 | 0.46 | 0.20 | −0.06 | −0.05 | −0.01 | 0.31 | 0.00 | −0.29 | 0.17 |
| ASDT | 0.07 | 0.13 | −0.10 | 0.04 | −0.24 | 0.19 | 0.03 | −0.09 | 0.36 | −0.14 | 0.16 | 0.34 | −0.17 | 0.05 | −0.11 | −0.13 | 0.03 | 0.94 | 1.00 | 0.44 | 0.06 | −0.13 | 0.36 | 0.02 | 0.54 | 0.17 | −0.05 | 0.07 | 0.13 | 0.34 | −0.05 | −0.29 | 0.18 |
| LW | 0.00 | 0.08 | 0.09 | −0.34 | 0.15 | 0.32 | 0.08 | 0.12 | 0.04 | 0.08 | −0.06 | 0.26 | −0.34 | −0.15 | 0.10 | 0.09 | 0.00 | 0.52 | 0.44 | 1.00 | −0.09 | −0.01 | 0.99 | 0.31 | 0.17 | 0.11 | 0.27 | 0.13 | 0.11 | −0.11 | −0.42 | 0.32 | −0.13 |
| LS | 0.07 | 0.11 | 0.02 | −0.13 | −0.06 | −0.13 | −0.19 | −0.03 | 0.35 | −0.31 | 0.19 | 0.01 | 0.01 | 0.19 | −0.17 | 0.03 | −0.01 | 0.09 | 0.06 | −0.09 | 1.00 | −0.07 | −0.10 | −0.13 | 0.21 | 0.18 | −0.21 | 0.05 | −0.21 | −0.02 | −0.02 | 0.01 | 0.07 |
| CR | −0.17 | 0.51 | 0.39 | −0.02 | −0.12 | −0.10 | −0.15 | 0.13 | 0.38 | 0.20 | −0.16 | −0.07 | −0.14 | −0.08 | −0.21 | −0.25 | 0.11 | −0.20 | −0.13 | −0.01 | −0.07 | 1.00 | 0.03 | −0.11 | −0.07 | 0.54 | 0.24 | −0.10 | −0.07 | −0.22 | 0.09 | 0.06 | −0.14 |
| Vp | −0.03 | 0.12 | 0.13 | −0.37 | 0.20 | 0.28 | 0.06 | 0.19 | 0.04 | 0.10 | −0.09 | 0.21 | −0.37 | −0.17 | 0.14 | 0.14 | −0.02 | 0.46 | 0.36 | 0.99 | −0.10 | 0.03 | 1.00 | 0.35 | 0.12 | 0.14 | 0.28 | 0.12 | 0.09 | −0.08 | −0.38 | 0.36 | −0.13 |
| TT-F | −0.42 | −0.12 | −0.24 | −0.29 | 0.34 | 0.32 | 0.02 | 0.10 | −0.23 | 0.48 | −0.43 | −0.05 | 0.26 | −0.01 | 0.35 | 0.37 | 0.13 | 0.16 | 0.02 | 0.31 | −0.13 | −0.11 | 0.35 | 1.00 | −0.23 | −0.06 | 0.03 | 0.17 | 0.14 | −0.14 | 0.04 | 0.40 | 0.02 |
| TT-M | −0.11 | 0.22 | −0.13 | −0.14 | −0.16 | −0.07 | −0.07 | −0.12 | 0.47 | −0.07 | 0.09 | 0.22 | −0.06 | −0.06 | −0.27 | −0.26 | 0.11 | 0.46 | 0.54 | 0.17 | 0.21 | −0.07 | 0.12 | −0.23 | 1.00 | 0.25 | −0.14 | −0.04 | −0.12 | 0.10 | 0.12 | −0.11 | 0.30 |
| GP | −0.18 | 0.68 | 0.56 | −0.23 | −0.27 | −0.12 | −0.37 | 0.21 | 0.60 | 0.13 | −0.11 | −0.13 | −0.10 | −0.10 | −0.11 | 0.04 | −0.04 | 0.20 | 0.17 | 0.11 | 0.18 | 0.54 | 0.14 | −0.06 | 0.25 | 1.00 | 0.05 | −0.17 | −0.24 | −0.09 | 0.20 | 0.02 | 0.37 |
| ELP | −0.26 | 0.09 | 0.15 | 0.33 | −0.17 | 0.17 | 0.23 | 0.28 | −0.14 | 0.37 | −0.41 | 0.26 | −0.42 | 0.10 | −0.07 | −0.06 | −0.09 | −0.06 | −0.05 | 0.27 | −0.21 | 0.24 | 0.28 | 0.03 | −0.14 | 0.05 | 1.00 | −0.28 | −0.27 | −0.31 | −0.28 | 0.28 | 0.00 |
| RpC | 0.09 | −0.17 | −0.23 | −0.03 | 0.06 | −0.12 | 0.22 | −0.33 | −0.11 | −0.01 | 0.04 | −0.03 | 0.22 | −0.06 | −0.02 | 0.07 | 0.30 | −0.05 | 0.07 | 0.13 | 0.05 | −0.10 | 0.12 | 0.17 | −0.04 | −0.17 | −0.28 | 1.00 | 0.43 | 0.11 | −0.21 | 0.34 | −0.13 |
| RfC | 0.06 | −0.27 | −0.12 | 0.06 | 0.15 | −0.20 | 0.15 | −0.30 | −0.12 | 0.13 | −0.09 | 0.07 | 0.17 | −0.13 | 0.06 | −0.07 | 0.27 | −0.01 | 0.13 | 0.11 | −0.21 | −0.07 | 0.09 | 0.14 | −0.12 | −0.24 | −0.27 | 0.43 | 1.00 | 0.09 | −0.06 | 0.24 | −0.09 |
| RC | 0.03 | −0.13 | −0.06 | 0.03 | −0.05 | 0.02 | 0.12 | −0.02 | 0.10 | −0.25 | 0.17 | −0.01 | −0.16 | 0.38 | 0.01 | −0.05 | 0.14 | 0.31 | 0.34 | −0.11 | −0.02 | −0.22 | −0.08 | −0.14 | 0.10 | −0.09 | −0.31 | 0.11 | 0.09 | 1.00 | 0.02 | −0.29 | 0.15 |
| OA | −0.35 | 0.22 | −0.08 | −0.04 | 0.02 | −0.11 | −0.37 | 0.24 | 0.12 | 0.07 | −0.10 | −0.30 | 0.12 | −0.02 | 0.17 | 0.22 | −0.13 | 0.00 | −0.05 | −0.42 | −0.02 | 0.09 | −0.38 | 0.04 | 0.12 | 0.20 | −0.28 | −0.21 | −0.06 | 0.02 | 1.00 | −0.37 | 0.17 |
| HVS | −0.20 | −0.02 | −0.04 | −0.17 | 0.39 | −0.07 | 0.10 | 0.03 | −0.05 | 0.31 | −0.29 | −0.05 | −0.13 | −0.12 | −0.05 | −0.06 | 0.24 | −0.29 | −0.29 | 0.32 | 0.01 | 0.06 | 0.36 | 0.40 | −0.11 | 0.02 | 0.28 | 0.34 | 0.24 | −0.29 | −0.37 | 1.00 | 0.15 |
| DFP | −0.16 | 0.32 | 0.02 | 0.00 | −0.04 | −0.11 | 0.08 | −0.17 | 0.30 | 0.08 | −0.06 | −0.04 | −0.09 | −0.09 | −0.09 | −0.07 | 0.04 | 0.17 | 0.18 | −0.13 | 0.07 | −0.14 | −0.13 | 0.02 | 0.30 | 0.37 | 0.00 | −0.13 | −0.09 | 0.15 | 0.17 | 0.15 | 1.00 |
References
- World Health Organization. Global Status Report on Road Safety 2023; World Health Organization: Geneva, Switzerland, 2023. [Google Scholar]
- Ministry of the Interior, Republic of Croatia. National Road Safety Plan of the Republic of Croatia for the Period 2021–2030; Ministry of the Interior: Zagreb, Croatia, 2021.
- International Transport Forum (ITF). Road Safety Annual Report 2018; OECD Publishing: Paris, France, 2018; Available online: https://www.oecd.org/en/publications/road-safety-annual-report-2018_1c884dcb-en.html (accessed on 10 July 2025).
- SWOV Institute for Road Safety Research. Speed and Speed Management; SWOV: The Hague, The Netherlands, 2021. [Google Scholar]
- Taylor, M.; Baruya, A.; Kennedy, J.V. The Relationship Between Speed and Accidents on Rural Single Carriageway Roads; TRL Report TRL511; Transport Research Laboratory: Crowthorne, UK, 2002. [Google Scholar]
- Aarts, L.; van Schagen, I. Driving Speed and the Risk of Road Crashes: A Review. Accid. Anal. Prev. 2006, 38, 215–224. [Google Scholar] [CrossRef]
- Kloeden, C.N.; Ponte, G.; McLean, A.J. Travelling Speed and the Risk of Crash Involvement on Rural Roads; Road Accident Research Unit, Adelaide University: Adelaide, Australia, 2001. [Google Scholar]
- National Highway Traffic Safety Administration (NHTSA). Traffic Safety Facts: Speeding; NHTSA: Washington, DC, USA, 2022.
- Insurance Institute for Highway Safety (IIHS). Speed and Fatality Statistics; IIHS: Arlington, VA, USA, 2022. [Google Scholar]
- National Highway Traffic Safety Administration (NHTSA). Crash Data Analysis; NHTSA: Washington, DC, USA, 2022.
- World Health Organization (WHO). Speed and Road Safety; WHO: Geneva, Switzerland, 2021. [Google Scholar]
- PIARC. Setting Credible Speed Limits; World Road Association (PIARC): Paris, France, 2020. [Google Scholar]
- Fitzpatrick, K.; Carlson, P.; Brewer, M.; Wooldridge, M. Design Speed, Operating Speed, and Posted Speed Practices; Transportation Research Board: Washington, DC, USA, 2003. [Google Scholar]
- Transport for New South Wales (Transport NSW). Annual Report 2010; Transport NSW: Sydney, Australia, 2010. Available online: https://www.transport.nsw.gov.au/system/files/media/documents/2023/2010-annual-report-overview.pdf (accessed on 10 July 2025).
- European Automobile Manufacturers Association. Road Safety: Safe Vehicles, Safe Drivers, Safe Roads; European Automobile Manufacturers Association: Brussels, Belgium, 2019; Available online: https://www.roadsafetyfacts.eu/themes/ACEA-Road-Safety-Facts/img/ACEA_Road_Safety.pdf (accessed on 10 July 2025).
- Tabish, S.A. Road Traffic & Safety: Risk Factors & Recommendations; Nova Science Publishers Inc.: Hauppauge, NY, USA, 2017. [Google Scholar]
- European Transport Safety Council. Reducing Speeding in Europe. PIN Flash Report 36; European Transport Safety Council: Brussels, Belgium, 2019; Available online: https://etsc.eu/wp-content/uploads/PIN-flash-report-36-Final.pdf (accessed on 10 July 2025).
- Eluru, N.; Bhat, C.R. A Joint Econometric Analysis of Seat Belt Use and Crash-Related Injury Severity. Accid. Anal. Prev. 2007, 39, 1037–1049. [Google Scholar] [CrossRef]
- Maji, A.; Singh, D.; Agrawal, N.; Zaman, M. Operating Speed Prediction Models for Tangent Sections of Two-Lane Rural Highways in Oklahoma State. Transp. Lett. 2020, 12, 130–137. [Google Scholar] [CrossRef]
- Wang, B.; Hallmark, S.; Savolainen, P.; Dong, J. Examining Vehicle Operating Speeds on Rural Two-Lane Curves Using Naturalistic Driving Data. Accid. Anal. Prev. 2018, 118, 236–243. [Google Scholar] [CrossRef]
- Abdul-Mawjoud, A.A.; Sofia, G.G. Development of Models for Predicting Speed on Horizontal Curves for Two-Lane Rural Highways. Arab. J. Sci. Eng. 2008, 33, 365–377. [Google Scholar]
- Echaveguren, T.; Díaz, Á.; Vargas-Tejeda, S. Operating Speed Models for Horizontal Reverse Curves. Proc. Inst. Civ. Eng. Transp. 2015, 168, 510–522. [Google Scholar] [CrossRef]
- Shallam, R.D.K.; Ahmed, M.A. Operating Speed Models on Horizontal Curves for Two-Lane Highways. Transp. Res. Procedia 2016, 17, 445–451. [Google Scholar] [CrossRef]
- Malaghan, V.; Pawar, D.S.; Dia, H. Modeling Operating Speed Using Continuous Speed Profiles on Two-Lane Rural Highways in India. J. Transp. Eng. Part A Syst. 2020, 146, 04020124. [Google Scholar] [CrossRef]
- Jiang, Z.; Jadaan, K.; Ouyang, Y. Speed Harmonization—Design Speed vs. Operating Speed; Civil Engineering Studies, Illinois Center for Transportation Series No. 16-021; Illinois Center for Transportation: Rantoul, IL, USA, 2016; Available online: https://apps.ict.illinois.edu/projects/getfile.asp?id=5056 (accessed on 10 March 2025).
- Pérez Zuriaga, A.M.; García García, A.; Camacho Torregrosa, F.J.; D’Attoma, P. Modeling Operating Speed and Deceleration on Two-Lane Rural Roads with Global Positioning System Data. Transp. Res. Rec. 2010, 2171, 11–20. [Google Scholar] [CrossRef]
- Praticò, F.; Giunta, M. Modeling Operating Speed of Two Lane Rural Roads. Procedia-Soc. Behav. Sci. 2012, 53, 665–672. [Google Scholar] [CrossRef]
- Cvitanić, D.; Maljković, B. Operating speed models of two-lane rural state roads developed on continuous speed data. Teh. Vjesn. 2017, 24, 1915–1921. [Google Scholar] [CrossRef]
- Fitzpatrick, K.; Miaou, S.P.; Brewer, M.; Carlson, P.; Wooldridge, M.D. Exploration of the Relationship between Operating Speed and Roadway Features on Tangent Sections. J. Transp. Eng. 2005, 131, 261–269. [Google Scholar] [CrossRef]
- Bella, F.; Calvi, A.; D’Amico, F. Predictive Speed Models for Two-Lane Rural Roads Using GPS Equipment. Int. J. Mob. Netw. Des. Innov. 2014, 5, 187–194. [Google Scholar] [CrossRef]
- Del Serrone, G.; Cantisani, G. Speed Prediction Models for Tangent Segments Between Horizontal Curves Using Floating Car Data. Vehicles 2025, 7, 68. [Google Scholar] [CrossRef]
- Marchionna, A.; Perco, P. Operating speed-profile prediction model for two-lane rural roads in the Italian context. Adv. Transp. Stud. 2008, 14, 57–68. [Google Scholar]
- Federal Highway Administration (FHWA). Safety Performance Functions: Development and Application; U.S. Department of Transportation: Washington, DC, USA, 2015. Available online: https://www.fhwa.dot.gov/publications/research/safety/15030/006.cfm#073 (accessed on 10 July 2025).
- Özkan, T.; Lajunen, T.; El Chliaoutakis, J.; Parker, D.; Summala, H. Cross-Cultural Differences in Driving Behaviours: A Comparison of Six Countries. Transp. Res. Part F Traffic Psychol. Behav. 2006, 9, 227–242. [Google Scholar] [CrossRef]
- Eboli, L.; Guido, G.; Mazzulla, G.; Pungillo, G. Experimental Relationships between Operating Speeds of Successive Road Design Elements in Two-Lane Rural Highways. Transport 2017, 32, 138–145. [Google Scholar] [CrossRef]
- Abbondati, F.; Capaldo, F.S.; Lamberti, R. Predicting Driver Speed Behavior on Tangent Sections of Low-Volume Roads. Int. J. Civ. Eng. Technol. 2017, 8, 1047–1060. [Google Scholar]
- Dell’Acqua, G.; Esposito, T.; Lamberti, R.; Abate, D. Operating Speed Model on Tangents of Two-Lane Rural Highways. In Proceedings of the 4th International SIIV Congress–Palermo (Italy), Palermo, Italy, 12–14 September 2007; p. 2848. [Google Scholar]
- Crisman, B. Operating Speed Prediction Model for Two-Lane Rural Roads. In Proceedings of the 3rd International Symposium on Highway Geometric Design, Chicago, IL, USA, 29 June–1 July 2005. [Google Scholar]
- Cvitanić, D.; Maljković, B. Operating Speed Models on Tangent Sections of Two-Lane Rural Roads. In Proceedings of the International Conference on Road and Rail Infrastructure (CETRA 2016), Šibenik, Croatia, 23–25 May 2016; pp. 855–860. [Google Scholar]
- Vertlberg, J.L.; Jakovljević, M.; Abramović, B.; Ševrović, M. Determining Factors Influencing Operating Speeds on Road Tangents. Appl. Sci. 2025, 15, 7549. [Google Scholar] [CrossRef]
- PROMETIS. Vehicle Speeds on Croatian Roads in 2021; PROMETIS Ltd.: Zagreb, Croatia, 2022. [Google Scholar]
- Croatian Roads Ltd. Traffic Counting on the Roads of the Republic of Croatia, 2023; Croatian Roads Ltd.: Zagreb, Croatia, 2023; Available online: https://hrvatske-ceste.hr/uploads/documents/attachment_file/file/1804/Brojenje_prometa_na_cestama_Republike_Hrvatske_godine_2023.pdf (accessed on 10 July 2025).
- Ministry of the Sea, Transport and Infrastructure. Ordinance on Basic Conditions That Public Roads Outside Settlements and Their Elements Must Meet from the Point of View of Traffic Safety (OG 110/2001 and 90/2022); Ministry of the Sea, Transport and Infrastructure: Zagreb, Croatia, 2022.
- Martinelli, V.; Ventura, R.; Bonera, M.; Barabino, B.; Maternini, G. Estimating Operating Speed for County Road Segments—Evidence from Italy. Int. J. Transp. Sci. Technol. 2022, 12, 560–577. [Google Scholar] [CrossRef]
- Paliotto, A.; Meocci, M. Development of a Network-Level Road Safety Assessment Procedure Based on Human Factors Principles. Infrastructures 2024, 9, 35. [Google Scholar] [CrossRef]
- Lamm, R.; Psarianos, B.; Mailaender, T. Highway Design and Traffic Safety Engineering Handbook; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]





| Variable | Type | Normal Distribution | Test Used |
|---|---|---|---|
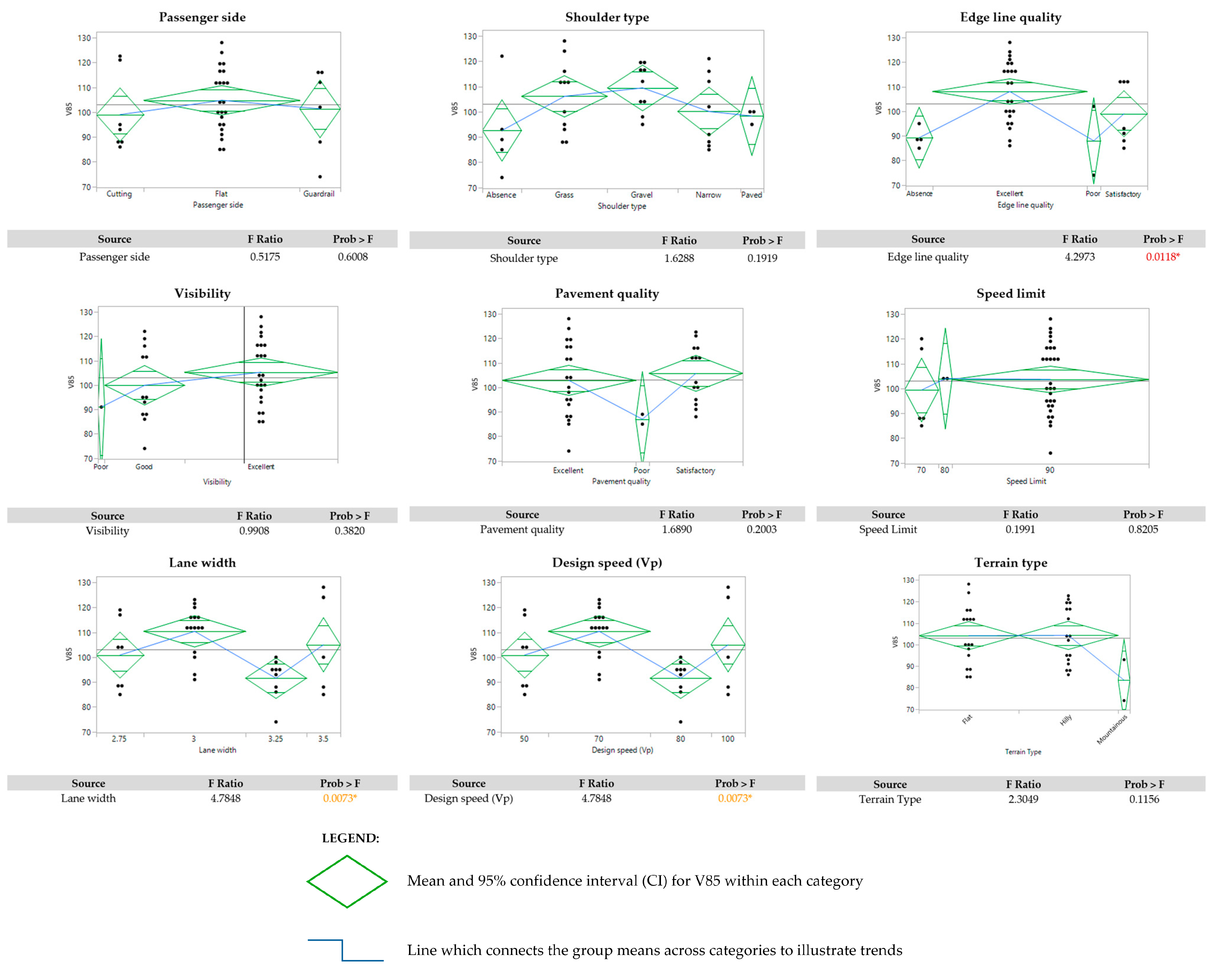
| Passenger side | Categorical—Multi-level | --- | ANOVA |
| Shoulder type | Categorical—Multi-level | --- | ANOVA |
| Edge line quality | Categorical—Multi-level | --- | ANOVA |
| Visibility | Categorical—Multi-level | --- | ANOVA |
| Pavement quality | Categorical—Multi-level | --- | ANOVA |
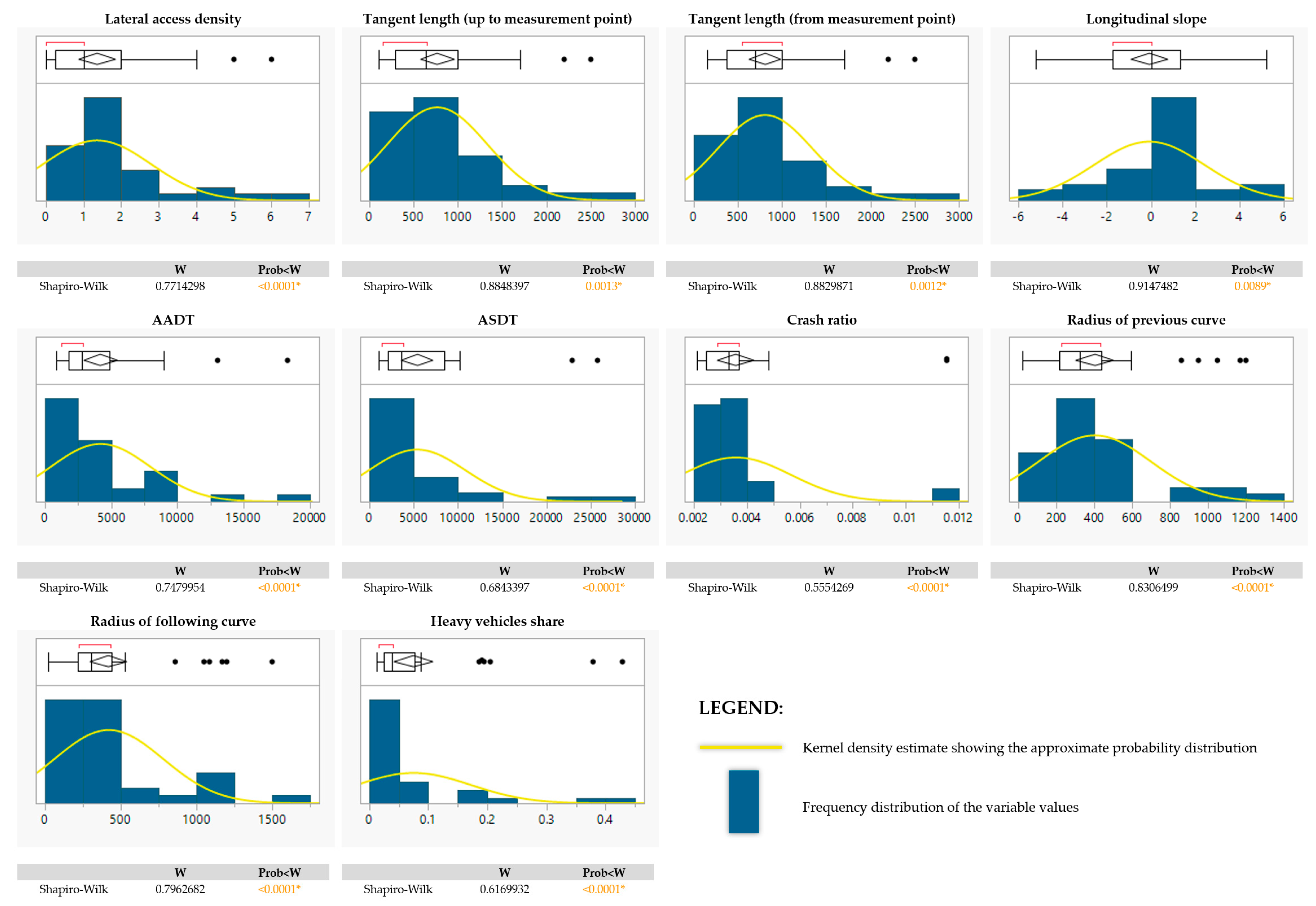
| Lateral access density | Continuous | NO | Spearman |
| Tangent length (up to measurement point) | Continuous | NO | Spearman |
| Tangent length (from measurement point) | Continuous | NO | Spearman |
| Speed limit | Categorical—Multi-level | --- | ANOVA |
| AADT | Continuous | NO | Spearman |
| ASDT | Continuous | NO | Spearman |
| Lane width | Categorical—Multi-level | --- | ANOVA |
| Longitudinal slope | Continuous | NO | Spearman |
| Crash ratio | Continuous | NO | Spearman |
| Design speed | Categorical—Multi-level | --- | ANOVA |
| Terrain type | Categorical—Multi-level | --- | ANOVA |
| Guardrail presence | Binary | --- | t-test |
| Edge lane presence | Binary | --- | t-test |
| Radius of previous curve | Continuous | NO | Spearman |
| Radius of following curve | Continuous | NO | Spearman |
| Road category | Binary | --- | t-test |
| Overtaking allowed | Binary | --- | t-test |
| Heavy goods vehicles share | Continuous | NO | Spearman |
| Disruptive factor presence | Binary | --- | t-test |
| Continuous Variables | Spearman’s ρ | Significance Level (p-Value) |
|---|---|---|
| Lateral access density | −0.1119 | 0.5159 |
| Tangent length (up to measurement point) | 0.2278 | 0.1816 |
| Tangent length (from measurement point) | 0.1878 | 0.2728 |
| AADT | −0.5669 | 0.0003 * |
| ASDT | −0.4713 | 0.0037 * |
| Longitudinal slope | −0.1246 | 0.4689 |
| Crash ratio | 0.3065 | 0.0690 |
| Radius of previous curve | 0.3099 | 0.0659 |
| Radius of following curve | 0.3313 | 0.0484 * |
| Heavy goods vehicle share | 0.2645 | 0.1190 |
| Variable | Estimate | Std Error | p-Value | Lower 95% | Upper 95% | VIF |
|---|---|---|---|---|---|---|
| Intercept | 78.46 | 4.18 | <0.0001 | 69.86 | 87.06 | --- |
| Shoulder type—Gravel | 12.32 | 2.43 | <0.0001 | 7.32 | 17.32 | 1.46 |
| Edge line quality—Excellent | 26.99 | 3.22 | <0.0001 | 20.36 | 33.61 | 3.14 |
| Edge line quality—Satisfactory | 16.24 | 3.79 | 0.0002 | 8.46 | 24.02 | 2.95 |
| Pavement quality—Excellent | −5.25 | 2.32 | 0.0325 | −10.02 | −0.47 | 1.75 |
| ASDT | −0.0007 | 0.00 | 0.0016 | −0.00104 | −0.00027 | 1.32 |
| Crash ratio | 1795.02 | 467.25 | 0.0007 | 834.57 | 2755.47 | 1.20 |
| Edge lane presence | −14.63 | 3.10 | <0.0001 | −21.00 | −8.26 | 2.36 |
| Overtaking allowed | 7.59 | 2.70 | 0.0093 | 2.04 | 13.14 | 1.50 |
| Heavy goods vehicle share | 80.11 | 11.08 | <0.0001 | 57.34 | 102.88 | 1.47 |
| R2 | 0.89 | |||||
| R2Adj | 0.86 | |||||
| RMSE | 5.24 | |||||
| Mean of response | 103.08 | |||||
| SSE | 713.20 | |||||
| DFE | 26 | |||||
| Cp | 10 | |||||
| Observations | 36 | |||||
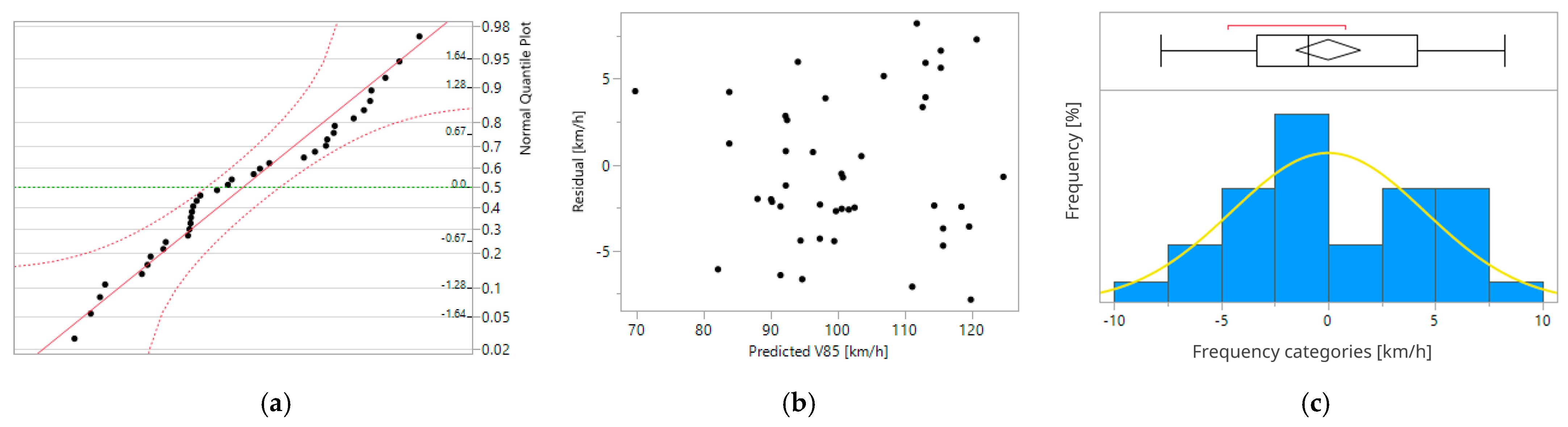
| W | p-Value | |
|---|---|---|
| Shapiro–Wilk | 0.95 | 0.12 |
| Source | Sum of Squares | Mean Square | F Ratio |
|---|---|---|---|
| Model | 2630.03 | 292.23 | 0.77 |
| Error | 9931.24 | 381.97 | Prob > F |
| C. Total | 12,561.28 | 0.65 |
| Data Collected from | Location Name | Direction | V85-Test [km/h] | V85-Predicted [km/h] | Absolute Difference [km/h] | Absolute Deviation [%] |
|---|---|---|---|---|---|---|
| Field survey | Dubrovnik | towards Dubrovnik | 76 | 80.99 | 4.99 | 6.56% |
| Field survey | Varaždin | from Varaždin | 99 | 101.23 | 2.23 | 2.25% |
| Field survey | Virovitica | from Novaki | 97 | 96.24 | 0.76 | 0.78% |
| Field survey | Virovitica | towards Novaki | 97 | 96.24 | 0.76 | 0.78% |
| Field survey | Zadar | towards Zadar | 96 | 97.24 | 1.24 | 1.29% |
| Fixed traffic counter | Paka | towards Novi Marof | 90 | 94.20 | 4.20 | 4.67% |
| Fixed traffic counter | Brlenić | towards Draganić | 95 | 92.28 | 2.72 | 2.86% |
| Fixed traffic counter | Kašina | towards Soblinec (DC3) | 88 | 89.85 | 1.85 | 2.11% |
| Fixed traffic counter | Trema | towards Sveti Ivan Žabno | 100 | 100.63 | 0.63 | 0.63% |
| Fixed traffic counter | Sibinj Krmpotski | towards Senj | 97 | 99.32 | 2.32 | 2.39% |
| Average absolute deviation | 2.43% | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vertlberg, J.L.; Jakovljević, M.; Abramović, B.; Ševrović, M. Predicting Operating Speeds of Passenger Cars on Single-Carriageway Road Tangents. Infrastructures 2025, 10, 221. https://doi.org/10.3390/infrastructures10080221
Vertlberg JL, Jakovljević M, Abramović B, Ševrović M. Predicting Operating Speeds of Passenger Cars on Single-Carriageway Road Tangents. Infrastructures. 2025; 10(8):221. https://doi.org/10.3390/infrastructures10080221
Chicago/Turabian StyleVertlberg, Juraj Leonard, Marijan Jakovljević, Borna Abramović, and Marko Ševrović. 2025. "Predicting Operating Speeds of Passenger Cars on Single-Carriageway Road Tangents" Infrastructures 10, no. 8: 221. https://doi.org/10.3390/infrastructures10080221
APA StyleVertlberg, J. L., Jakovljević, M., Abramović, B., & Ševrović, M. (2025). Predicting Operating Speeds of Passenger Cars on Single-Carriageway Road Tangents. Infrastructures, 10(8), 221. https://doi.org/10.3390/infrastructures10080221








