Developing Statistical and Multilayer Perceptron Neural Network Models for a Concrete Dam Dynamic Behaviour Interpretation †
Abstract
1. Introduction
2. Materials and Methods
2.1. Interpretation of Structural Behaviour Based on HST and HTT Approaches
- —The observed value of the variable under analysis in observation , which depends on hydrostatic pressure, temperature, and the point in time when the observation is made;
- —Components of the variable that correspond to the elastic effect of the reservoir water level, the elastic effect of seasonal temperature variations, and the effect of time in the observation;
- —A constant that corresponds to the difference between observed and calculated values at the beginning of the calibration period;
- —The residual of the observation, given by the difference between the estimated value and the observed value.
2.2. The Multiple Linear Regression Model
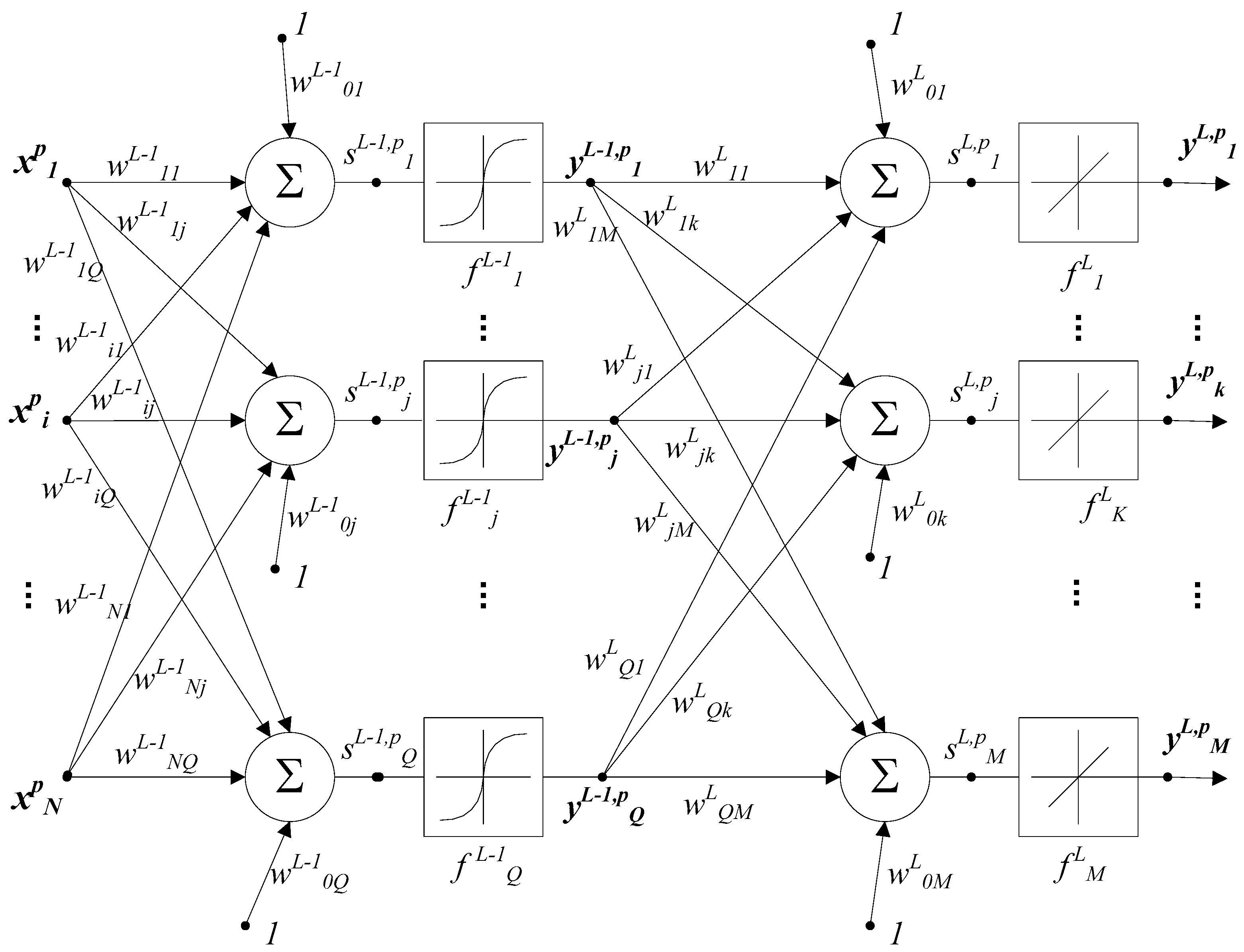
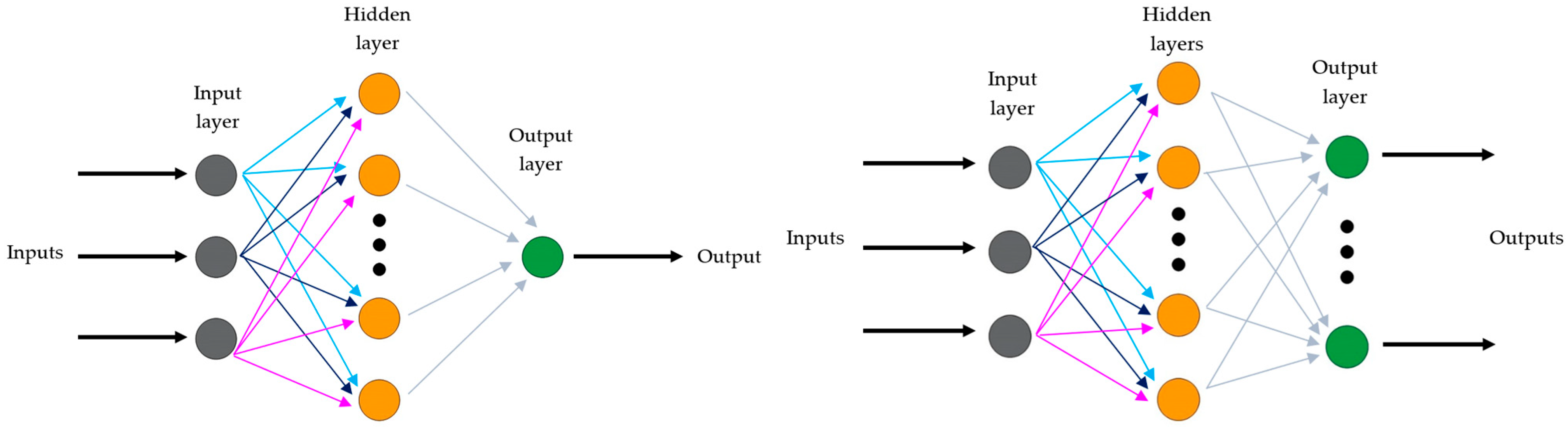
2.3. The Multilayer Perceptron Neural Network Model
- — input network , from pattern ;
- —number of patterns;
- —output layer;
- —hidden layer;
- N—number of inputs in input layer;
- —number of processing elements in the hidden layer;
- —number of processing elements in the output layer;
- —synoptic weight between input network from layer at processing element j;
- —activation value at processing element from layer , from pattern ;
- —activation function at processing element from layer ;
- —output unit i, from layer , from pattern .
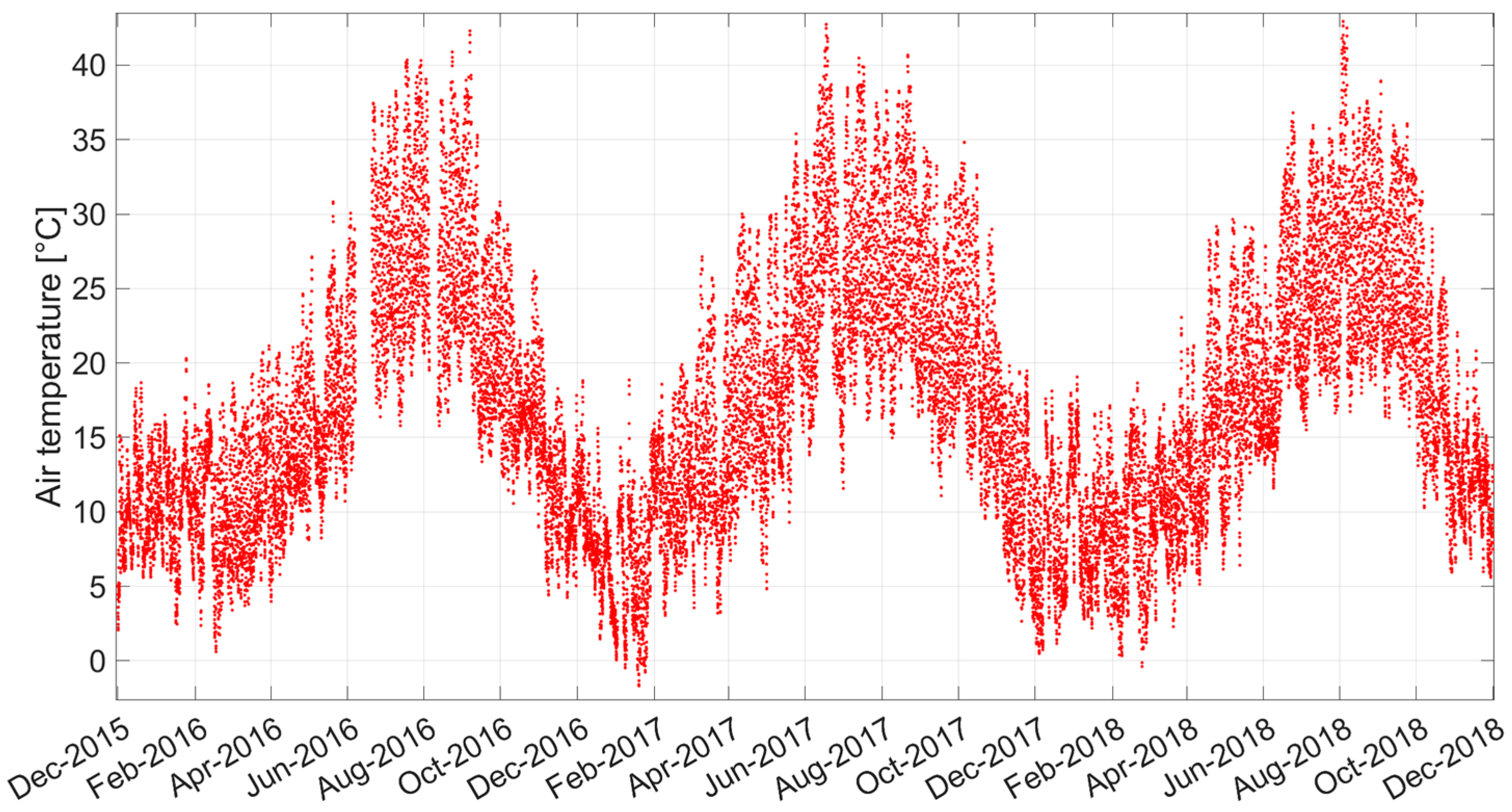
3. Case Study
4. Results and Discussion
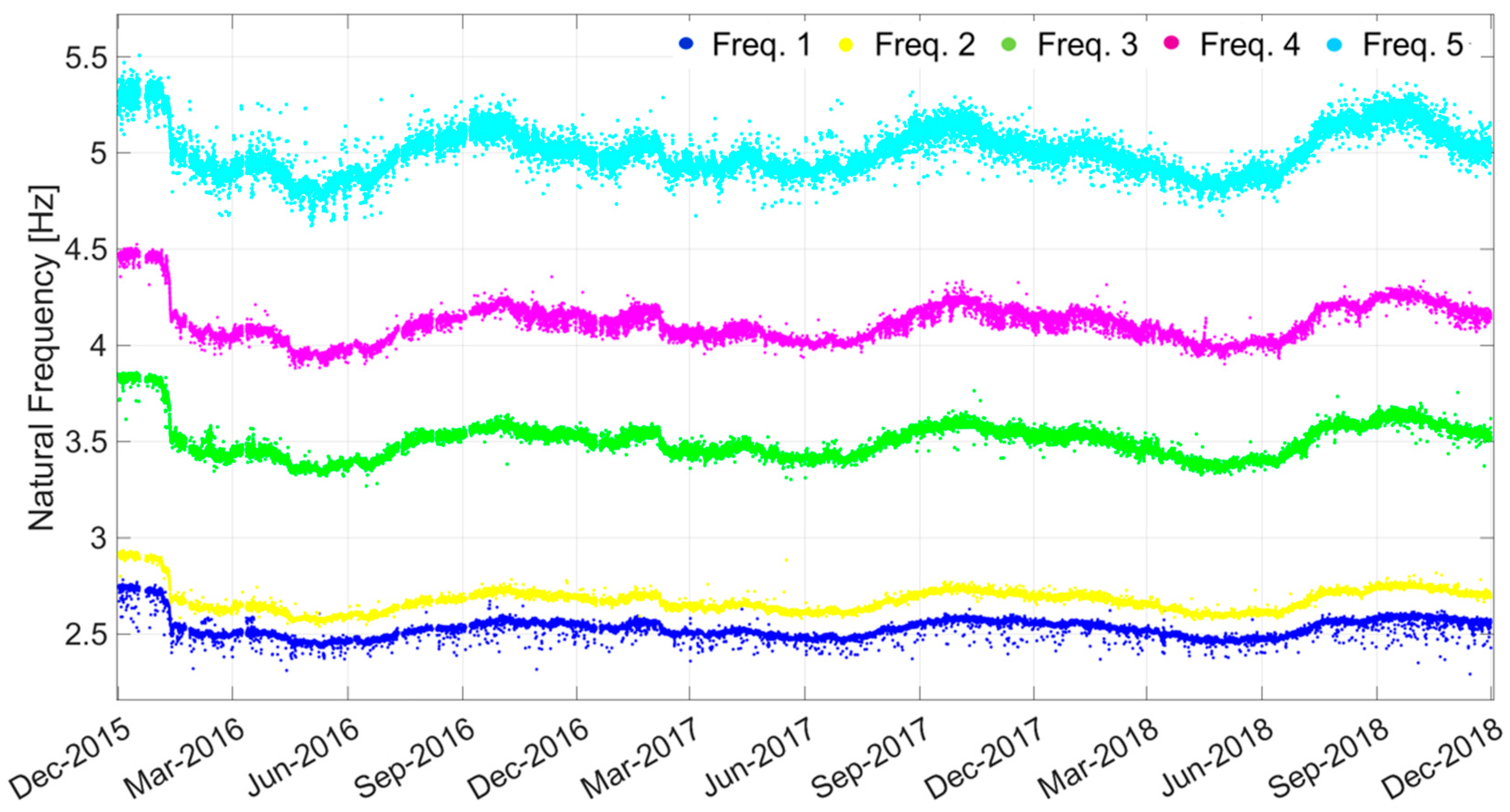
4.1. Multiple Linear Regression Models for the Characterisation of the Natural Frequency Pattern
4.2. Multilayer Perceptron Neural Network Models
5. Conclusions and Final Remarks
- Overall performance: Both methods performed well in predicting data, suggesting that both approaches are suitable for the problem at hand.
- Prediction accuracy: The neural network models slightly outperformed the regression model in terms of prediction accuracy. This suggests that the neural network was better able to capture the relationship between input features and the target variable compared to the regression model.
- Model flexibility: The neural network models can capture complex relationships between input features and the target variable, explaining its better performance on a dataset.
- A neural network with multiple outputs offers the advantage of capturing relationships among different target variables within a single model. This approach can reduce training time and help maintain consistency in predictions, especially when the outputs are correlated and sufficient data is available for all targets. However, networks with multiple outputs can be more challenging to train because the model must balance the learning process across all outputs. Poor quality of the observed behaviour in one output may negatively affect others. In contrast, single-output networks are simpler to design and optimise since they focus on one target at a time, but they require separate models for each variable and do not exploit potential correlations between outputs.
- Model interpretation: The linear regression model is easier to interpret than the neural network, as relationships between input features and the target variable are linear and easily interpreted. Additionally, the neural network might be considered as a black-box model by some users, making it more challenging to understand its behaviour.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ICOLD. Dam Safety. Guidelines. In Bulletin Number 59; International Commission on Large Dams: France, Paris, 1987. [Google Scholar]
- ICOLD. Automated dam monitoring systems. Guidelines and case histories. In Bulletin Number 118; International Commission on Large Dams: France, Paris, 2000. [Google Scholar]
- Bossoney, C. Knowledge-based modelling of dam behaviour with neural networks. In Research and Development in the Field of Dams; Swiss National Committee on Large Dams: Crans-Montana, Switzerland, 1995; pp. 201–217. [Google Scholar]
- Hattingh, O.C. Surveillance of Gariep Dam using neural networks. In Proceedings of the International Symposium on New Trends and Guidelines on Dam Safety, Barcelona, Spain, 17–19 June 1998. [Google Scholar]
- Willm, G.; Beaujoint, N. Les méthodes de surveillance des barrages au service de la production hydraulique d’Electricité de France-Problèmes ancients et solutions nouvelles. In Proceedings of the 9th ICOLD Congress, Istanbul, Turkey, 4–8 September 1967; pp. 529–550. (In French). [Google Scholar]
- Hariri-Ardebili, M.A.; Salazar, F.; Pourkamali-Anaraki, F.; Mazzà, G.; Mata, J. Soft Computing and Machine Learning in Dam Engineering. Water 2023, 15, 917. [Google Scholar] [CrossRef]
- Tardieu, B.; Bourdarot, E.; Robbe, E.; Sasaki, T.; Kondo, M. Framework, results and lessons learned from the CFBR-JCOLD cooperation on concrete dams. In Validation of Dynamic Analyses of Dams and Their Equipment; Fry, M., Ed.; CRC Press: Boca Raton, FL, USA, 2018; 2018 CIGB/COLD; ISBN 978-1-138-59017-5457. [Google Scholar]
- Bourdarot, E.; Kashiwayanagi, M.; Sasaki, T. Dynamic analysis, experimental and in-situ results, calibration and validation for concrete dams. In Validation of Dynamic Analyses of Dams and Their Equipment; Fry, M., Ed.; CRC Press: Boca Raton, FL, USA, 2018; 2018 CIGB/COLD; ISBN 978-1-138-59017-5457. [Google Scholar]
- Gomes, J.; Lemos, J. Characterization of the dynamic behaviour of an arch dam by means of forced vibration tests. In Validation of Dynamic Analyses of Dams and Their Equipment; Fry, M., Ed.; CRC Press: Boca Raton, FL, USA, 2018; 2018 CIGB/COLD; ISBN 978-1-138-59017-5457. [Google Scholar]
- Yang, X.; Xiang, Y.; Shen, G.; Sun, M. A Combination Model for Displacement Interval Prediction of Concrete Dams Based on Residual Estimation. Sustainability 2022, 14, 16025. [Google Scholar] [CrossRef]
- Fang, C.; Jiao, Y.; Wang, X.; Lu, T.; Gu, H. A Dam Displacement Prediction Method Based on a Model Combining Random Forest, a Convolutional Neural Network, and a Residual Attention Informer. Water 2024, 16, 3687. [Google Scholar] [CrossRef]
- Mata, J.; Salazar, F.; Barateiro, J.; Antunes, A. Validation of Machine Learning Models for Structural Dam Behaviour Interpretation and Prediction. Water 2021, 13, 2717. [Google Scholar] [CrossRef]
- Silva-Cancino, N.; Salazar, F.; Irazábal, J.; Mata, J. Adaptive Warning Thresholds for Dam Safety: A KDE-Based Approach. Infrastructures 2025, 10, 158. [Google Scholar] [CrossRef]
- Zhou, T.; Niu, X.; Ma, N.; Sun, F.; Gong, S. Deep Learning- and Multi-Point Analysis-Based Systematic Deformation Warning for Arch Dams. Infrastructures 2025, 10, 170. [Google Scholar] [CrossRef]
- Mata, J.; Miranda, F.; Antunes, A.; Romão, X.; Pedro Santos, J. Characterization of Relative Movements between Blocks Observed in a Concrete Dam and Definition of Thresholds for Novelty Identification Based on Machine Learning Models. Water 2023, 15, 297. [Google Scholar] [CrossRef]
- Zhang, H.; Song, Z.; Peng, P.; Sun, Y.; Ding, Z.; Zhang, X. Research on seepage field of concrete dam foundation based on artificial neural network. Alex. Eng. J. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Irazábal, J.; Salazar, F.; Silva-Cancino, N.; Vicente, D.J. Detection of outliers in dam monitoring time series with autoencoders. J. Civ. Struct. Heal. Monit. 2025, 15, 1771–1792. [Google Scholar] [CrossRef]
- Rico, J.; Barateiro, J.; Mata, J.; Antunes, A.; Cardoso, E. Applying Advanced Data Analytics and Machine Learning to Enhance the Safety Control of Dams. In Machine Learning Paradigms. Learning and Analytics in Intelligent Systems; Tsihrintzis, G., Virvou, M., Sakkopoulos, E., Jain, L., Eds.; Springer: Cham, Switzerland, 2019; Volume 1. [Google Scholar] [CrossRef]
- Fang, X.; Li, H.; Zhang, S.; Wang, X.; Wang, C.; Luo, X. A combined finite element and deep learning network for structural dynamic response estimation on concrete gravity dam subjected to blast loads. Def. Technol. 2023, 24, 298–313. [Google Scholar] [CrossRef]
- Wei, H.; Liu, X.; Wang, F.; Ai, X. An integrated deep learning model for predicting concrete dam deformation with multi-point spatiotemporal correlation. Meas. J. 2025, 256 Pt E, 118546. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, W.; Li, Y.; Wen, L. A deep learning prediction model of DenseNet-LSTM for concrete gravity dam deformation based on feature selection. Eng. Struct. 2023, 295, 116827. [Google Scholar] [CrossRef]
- Xu, B.; Zhu, Z.; Qiu, X.; Wang, S.; Chen, Z.; Zhang, H.; Lu, J. Real measurement data-driven correlated hysteresis monitoring model for concrete arch dam displacements. Expert Syst. Appl. 2024, 238 Pt A, 121752. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Gao, Z.; Shu, X.; Zhang, K.; Xie, L.; Zhang, Z. A new dam structural response estimation paradigm powered by deep learning and transfer learning techniques. Struct. Health Monit. 2021, 21, 770–787. [Google Scholar] [CrossRef]
- Léger, P.; Leclerc, M. Hydrostatic, temperature, time-displacement model for concrete dams. J. Eng. Mech. 2007, 133, 267–277. [Google Scholar] [CrossRef]
- Mata, J.; Gomes, J.; Pereira, S.; Magalhães, F.; Cunha, A. Analysis and interpretation of observed dynamic behaviour of a large concrete dam aided by soft computing and machine learning techniques. Eng. Struct. J. 2023, 296, 116940. [Google Scholar] [CrossRef]
- Johnson, A.; Wichern, W. Applied Multivariate Statistical Analysis, 6th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2007; ISBN 978-0-13-187715-3. [Google Scholar]
- Banoula, M. An Overview on Multilayer Perceptron (MLP). AI & Machine Learning. Internet. 2023. Available online: https://www.simplilearn.com/tutorials/deep-learning-tutorial/multilayer-perceptron (accessed on 24 May 2024).
- Pereira, S.; Magalhães, F.; Gomes, J.; Cunha, Á.; Lemos, J. Dynamic monitoring of a concrete arch dam during the first filling of the reservoir. Eng. Struct. 2018, 174, 548–560. [Google Scholar] [CrossRef]
- MathWorks. Train Neural Network Regression Model. 2021. Available online: https://de.mathworks.com/help/stats/fitrnet.html (accessed on 28 March 2024).
- Sejas, A.; Pereira, S.; Mata, J.; Cunha, Á. Dynamic behaviour of a concrete dam: Development of statistical and machine learning models for interpretation of monitoring data. In Proceedings of the Fifth International Dam World Conference, Lisbon, Portugal, 13–17 April 2025. [Google Scholar]





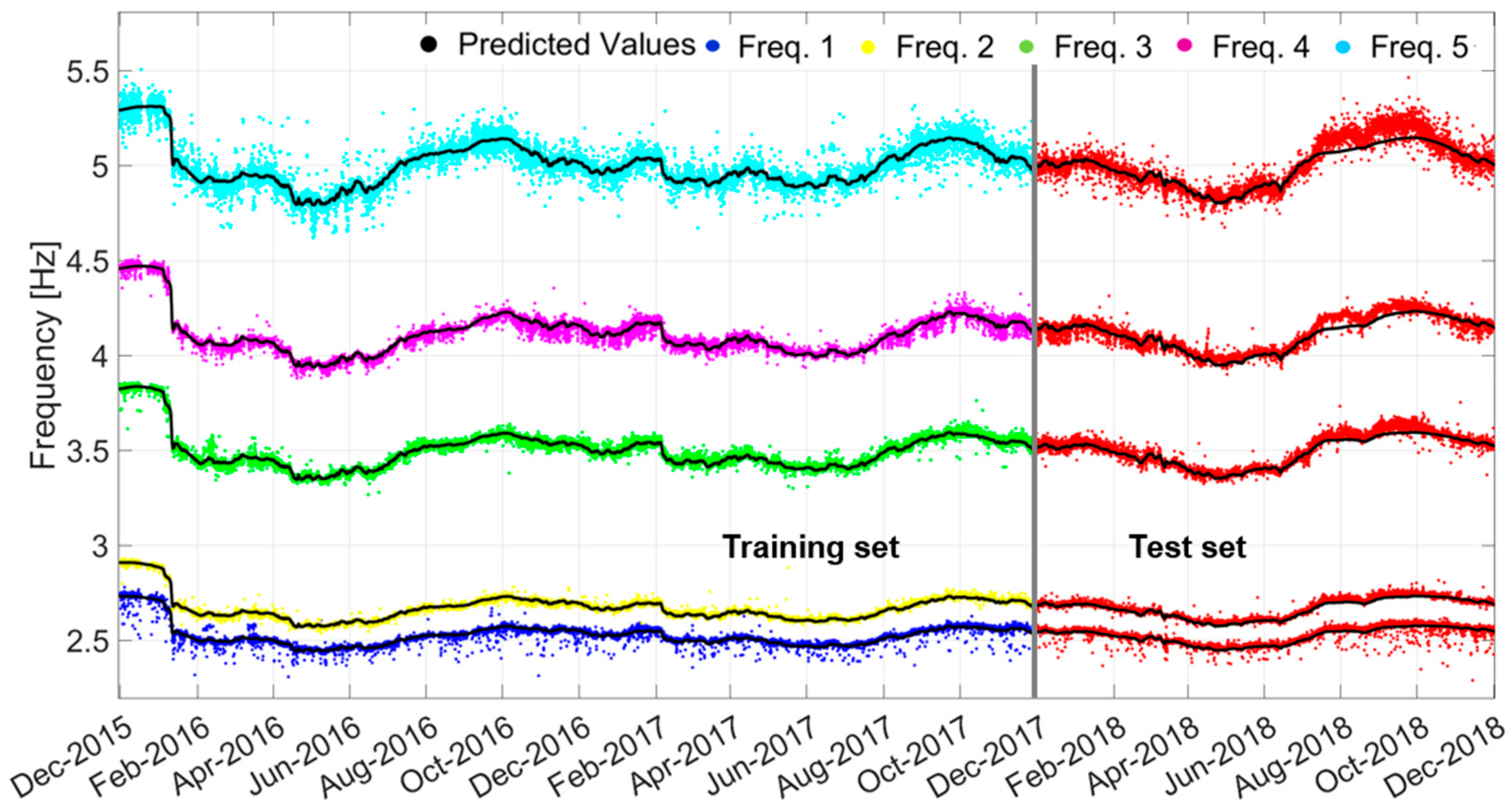
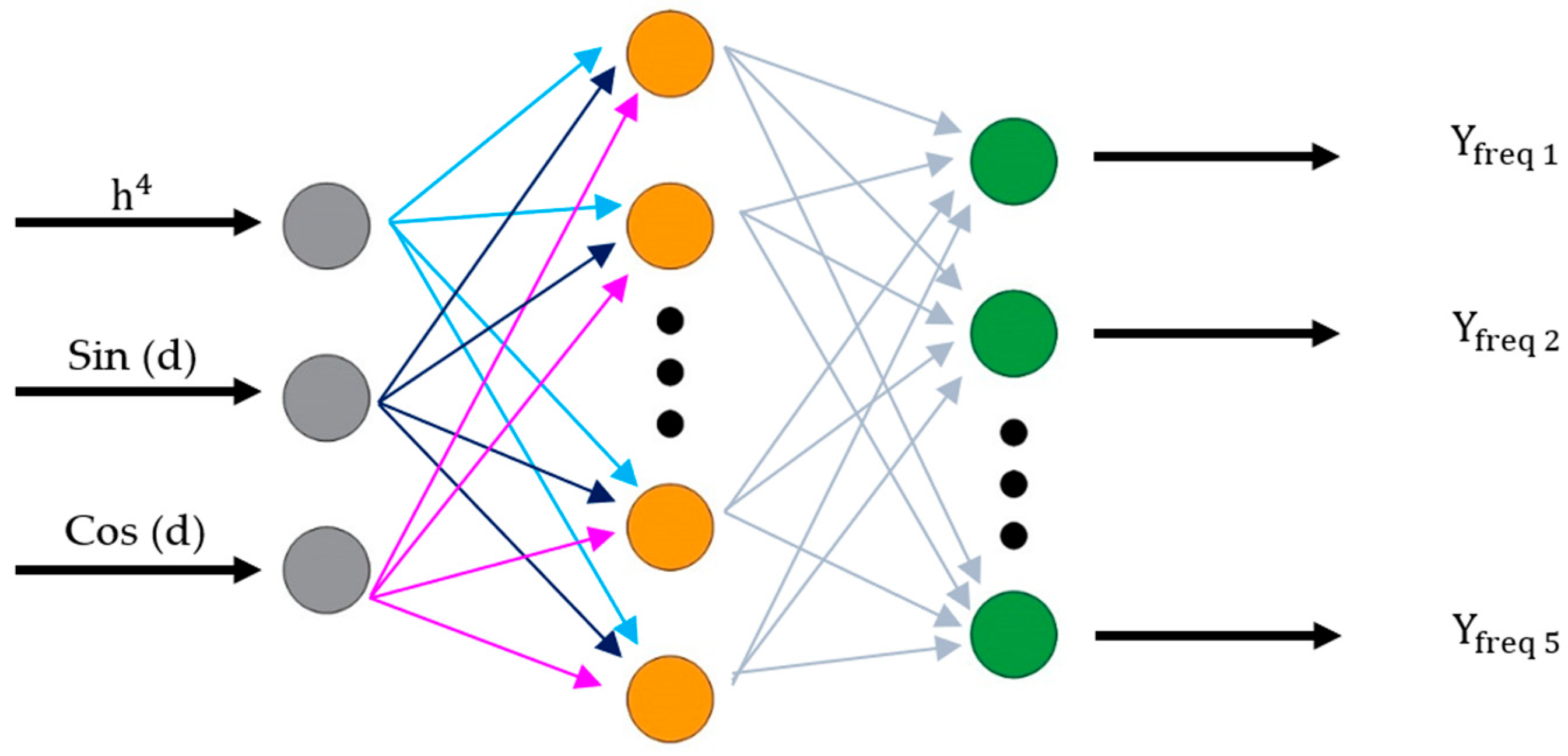
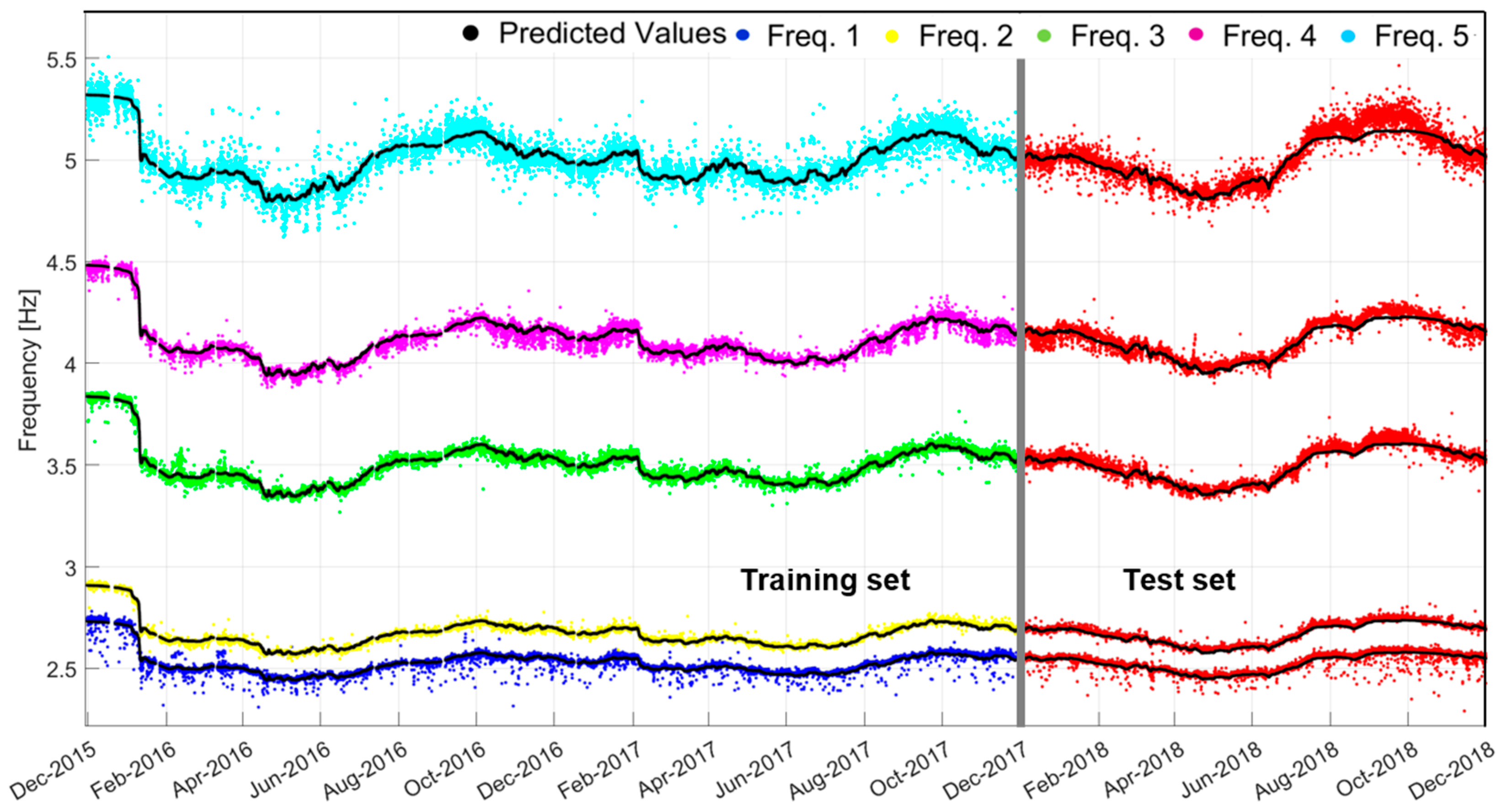
| Vibration Mode | β0 | β1 | β2 | β3 |
|---|---|---|---|---|
| Mode 1 | 2.9543 | −2.2235 × 10−9 | −0.01009 | −0.004045 |
| Mode 2 | 3.1742 | −2.6178 × 10−9 | −0.14286 | −0.008275 |
| Mode 3 | 4.2382 | −3.8372 × 10−9 | −0.26121 | −0.018613 |
| Mode 4 | 4.8933 | −4.0449 × 10−9 | −0.02773 | −0.008189 |
| Mode 5 | 5.7554 | −3.9158 × 10−9 | −0.05067 | −0.034902 |
| Model | Indicator | Set | Freq. 1 | Freq. 2 | Freq. 3 | Freq. 4 | Freq. 5 |
|---|---|---|---|---|---|---|---|
| R2 [%] | Training | 92.4 | 96.9 | 95.3 | 93.5 | 81.6 | |
| Test | 83.4 | 91.8 | 89.6 | 84.6 | 78.5 | ||
| MLR | [Hz] | Training | 0.0162 | 0.0116 | 0.0212 | 0.0277 | 0.0498 |
| Test | 0.0163 | 0.0116 | 0.0247 | 0.0313 | 0.0550 |
| Model | Indicator | Set | Freq. 1 | Freq. 2 | Freq. 3 | Freq. 4 | Freq. 5 |
|---|---|---|---|---|---|---|---|
| R2 [%] | Training | 93.3 | 98.1 | 97.1 | 97.9 | 90.1 | |
| Test | 89.4 | 96.3 | 95.0 | 93.4 | 89.3 | ||
| MLP-NN(i) | [Hz] | Training | 0.0152 | 0.0091 | 0.0165 | 0.0202 | 0.0386 |
| i = 1, …, 5 | Test | 0.0154 | 0.0086 | 0.0177 | 0.0224 | 0.0368 | |
| Number ofneurons in hidden layers | [2 5] | [2 8] | [2 5] | [2 5] | [3 5] |
| Model | Indicator | Set | Freq. 1 | Freq. 2 | Freq. 3 | Freq. 4 | Freq. 5 |
|---|---|---|---|---|---|---|---|
| R2 [%] | Training | 93.4 | 98.5 | 97.4 | 96.8 | 89.3 | |
| Test | 83.3 | 92.3 | 92.5 | 90.0 | 88.6 | ||
| MLP-NN(1,2,3,4,5) | [Hz] | Training | 0.015 | 0.008 | 0.016 | 0.02 | 0.038 |
| Test | 0.017 | 0.011 | 0.021 | 0.025 | 0.041 | ||
| Number of neurons in hidden layer | [10] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzmán Sejas, A.M.; Pereira, S.; Mata, J.; Cunha, Á. Developing Statistical and Multilayer Perceptron Neural Network Models for a Concrete Dam Dynamic Behaviour Interpretation. Infrastructures 2025, 10, 301. https://doi.org/10.3390/infrastructures10110301
Guzmán Sejas AM, Pereira S, Mata J, Cunha Á. Developing Statistical and Multilayer Perceptron Neural Network Models for a Concrete Dam Dynamic Behaviour Interpretation. Infrastructures. 2025; 10(11):301. https://doi.org/10.3390/infrastructures10110301
Chicago/Turabian StyleGuzmán Sejas, Andrés Mauricio, Sérgio Pereira, Juan Mata, and Álvaro Cunha. 2025. "Developing Statistical and Multilayer Perceptron Neural Network Models for a Concrete Dam Dynamic Behaviour Interpretation" Infrastructures 10, no. 11: 301. https://doi.org/10.3390/infrastructures10110301
APA StyleGuzmán Sejas, A. M., Pereira, S., Mata, J., & Cunha, Á. (2025). Developing Statistical and Multilayer Perceptron Neural Network Models for a Concrete Dam Dynamic Behaviour Interpretation. Infrastructures, 10(11), 301. https://doi.org/10.3390/infrastructures10110301









