Towards Self-Assembling 3D-Printed Shapes Through Βiomimetic Μechanical Interlocking
Abstract
1. Introduction
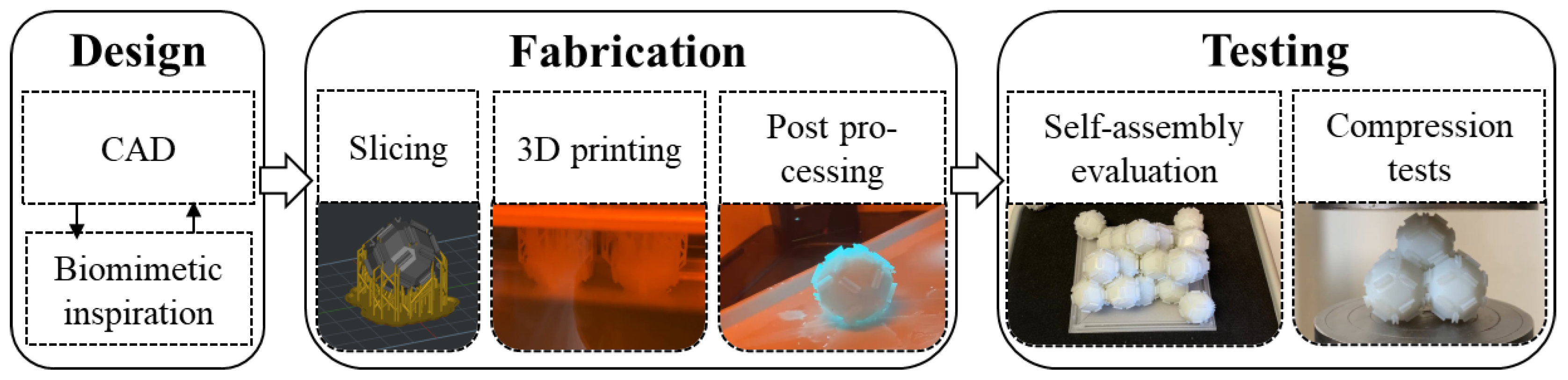
2. Materials and Methods
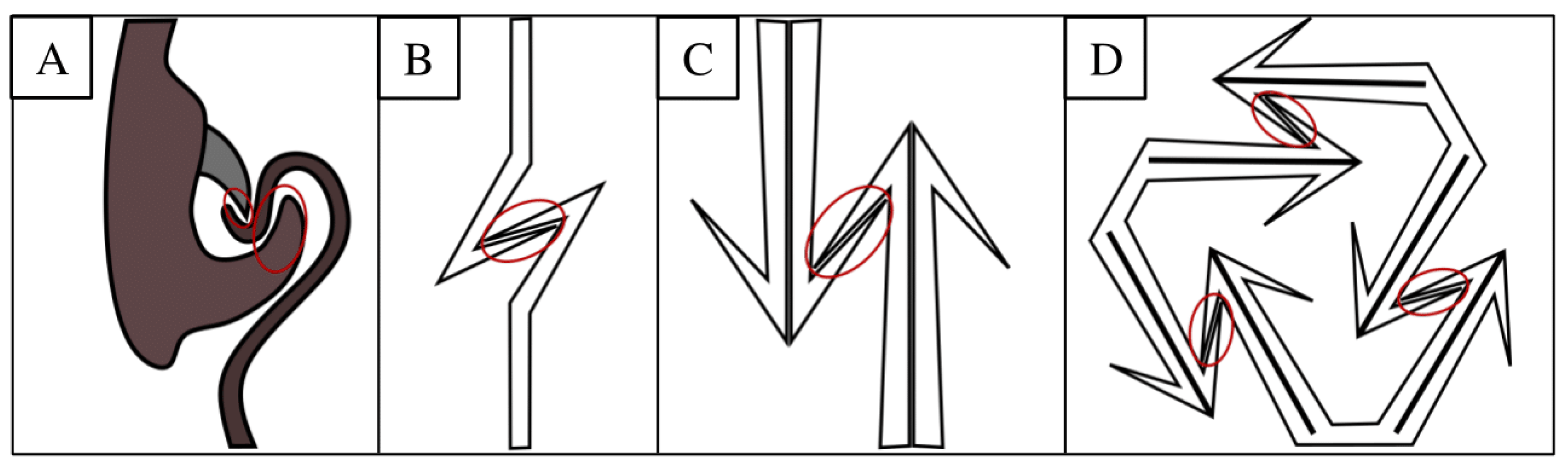
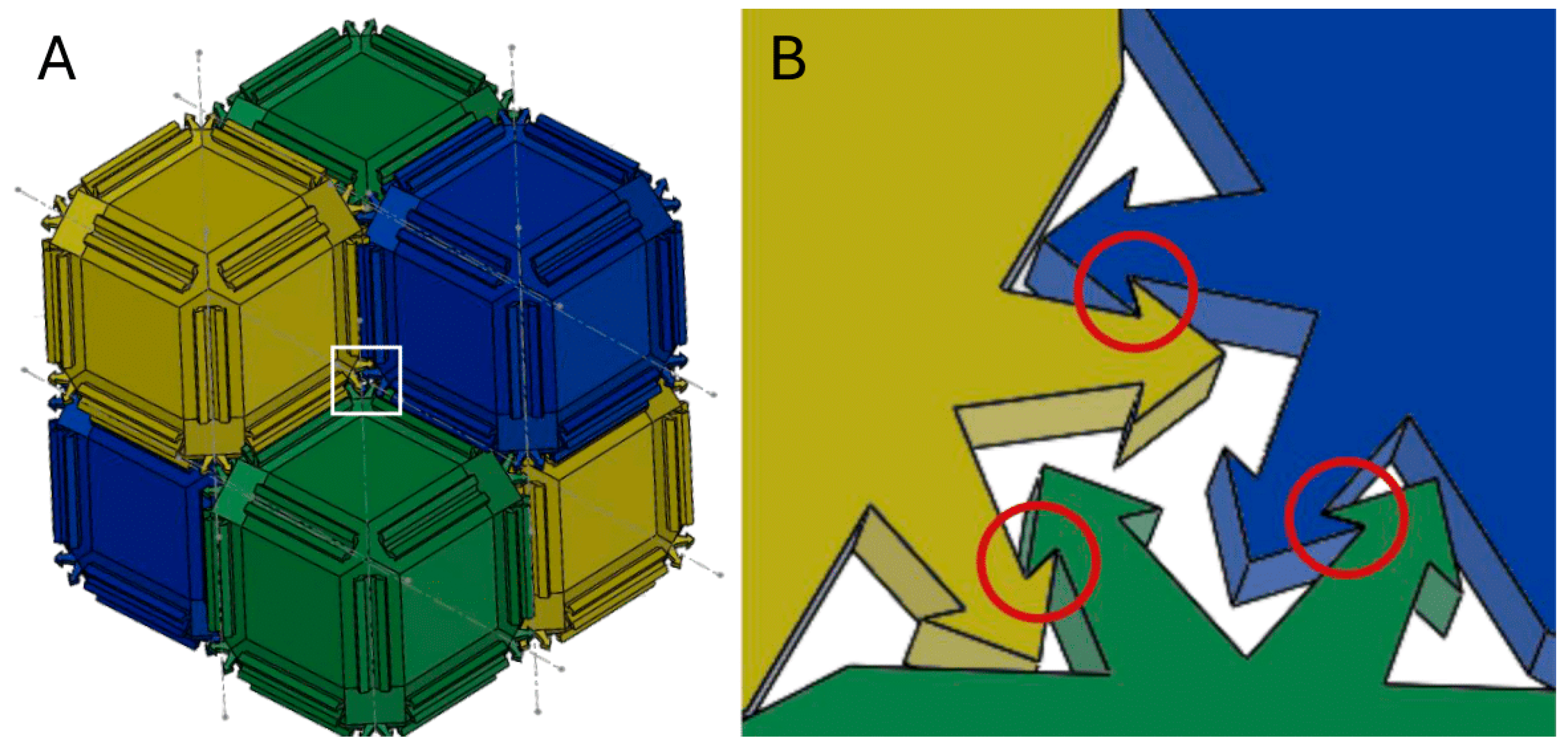
2.1. Design
2.2. Fabrication
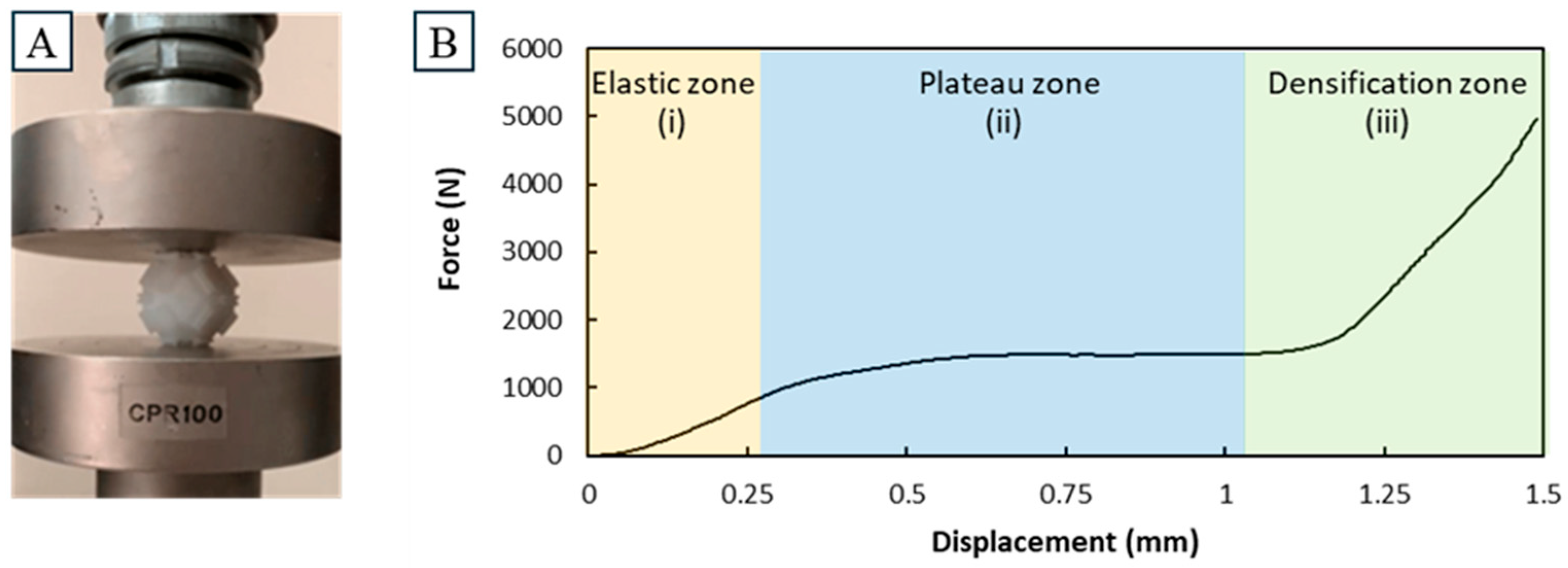
2.3. Compression Tests
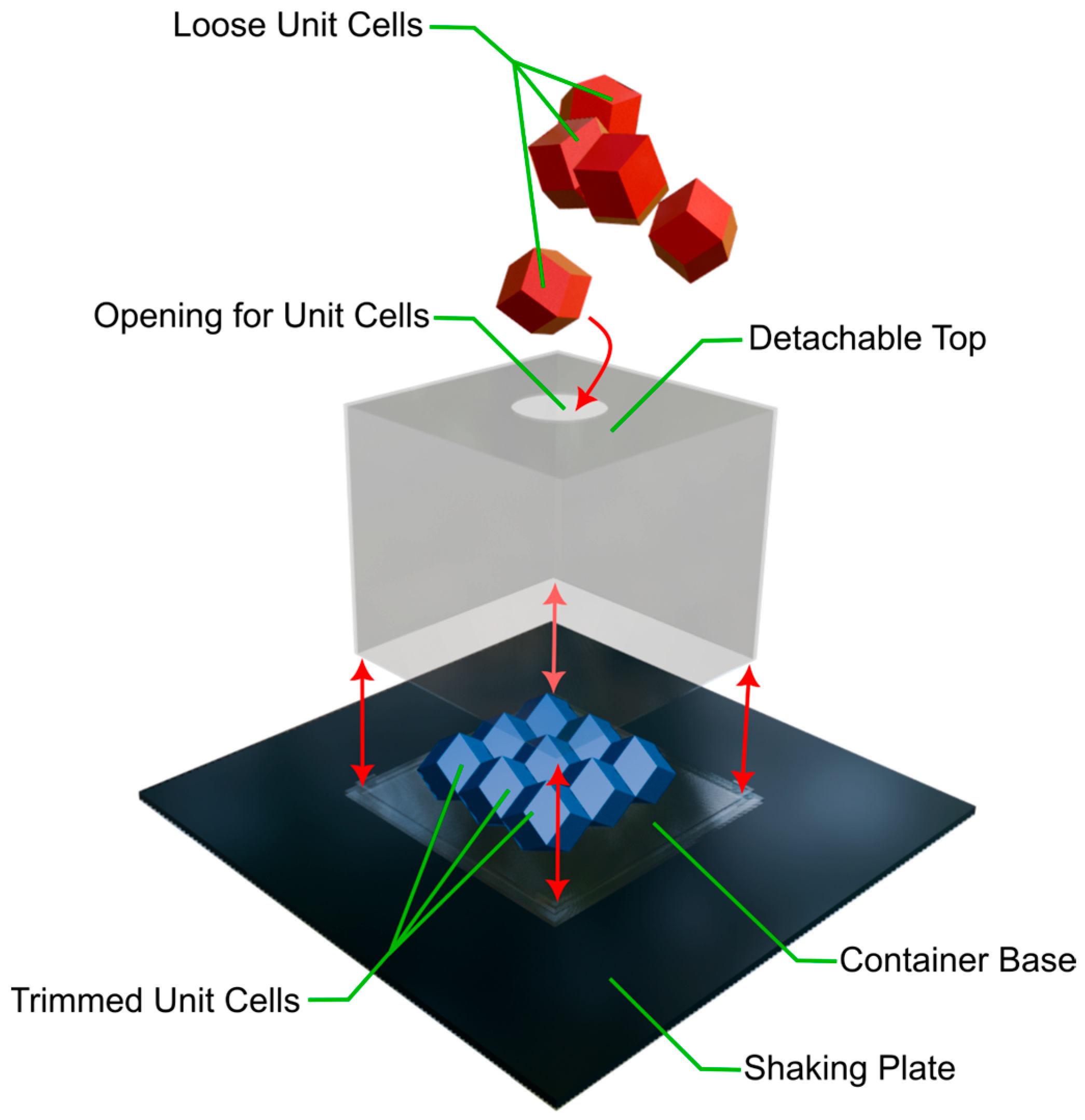
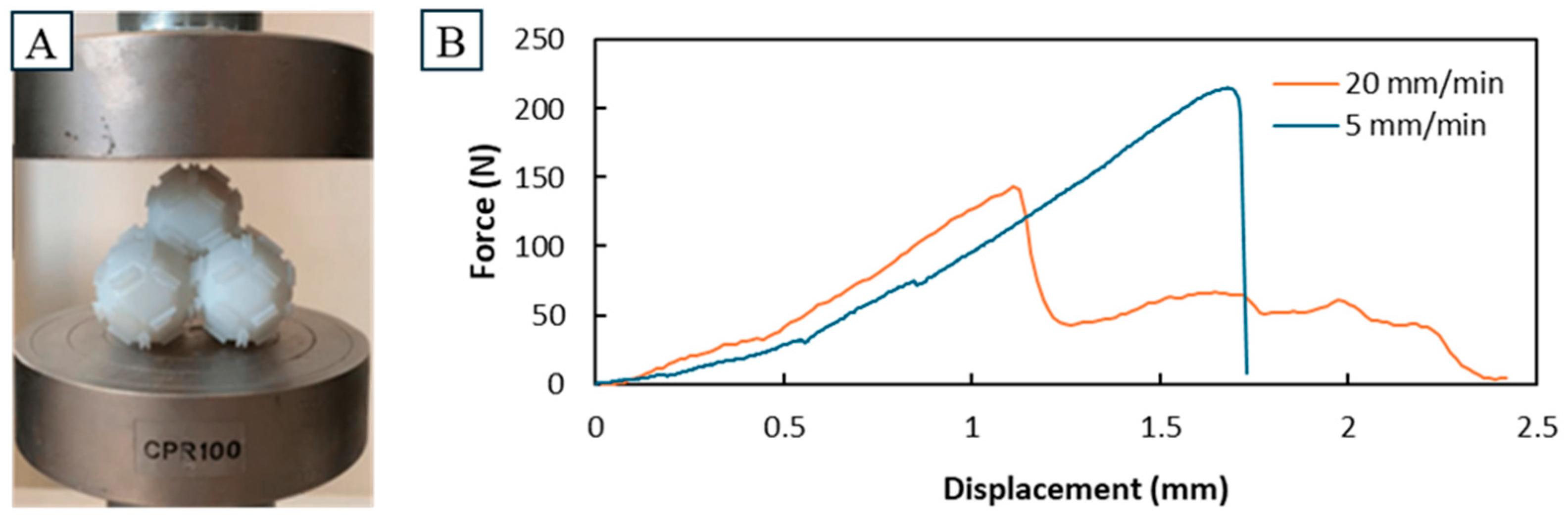
2.4. Self-Assembly Tests
3. Results
3.1. Interlocking Mechanism
3.2. Compression Results
3.3. Self-Assembly Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Falahati, H.; Haji-Akbari, A. Thermodynamically driven assemblies and liquid–liquid phase separations in biology. Soft Matter 2019, 15, 1135–1154. [Google Scholar] [CrossRef] [PubMed]
- Whitesides, G.M.; Mathias, J.P.; Seto, C.T. Molecular self-assembly and nanochemistry: A chemical strategy for the synthesis of nanostructures. Science 1991, 254, 1312–1319. [Google Scholar] [CrossRef] [PubMed]
- Amadi, E.V.; Venkataraman, A.; Papadopoulos, C. Nanoscale self-assembly: Concepts, applications and challenges. Nanotechnology 2022, 33, 132001. [Google Scholar] [CrossRef]
- Yang, S.; Jiang, L. Biomimetic self-assembly of subcellular structures. Chem. Commun. 2020, 56, 8342–8354. [Google Scholar] [CrossRef]
- Whitesides, G.M.; Grzybowski, B. Self-assembly at all scales. Science 2002, 295, 2418–2421. [Google Scholar] [CrossRef] [PubMed]
- Breen, T.; Tien, J.; Oliver, S.J.; Hadzic, T.; Whitesides, G.M. Design and self-assembly of open, regular, 3D mesostructures. Science 1999, 284, 948–951. [Google Scholar] [CrossRef]
- Whitesides, G.M.; Boncheva, M. Beyond molecules: Self-assembly of mesoscopic and macroscopic components. Proc. Natl. Acad. Sci. USA 2002, 99, 4769–4774. [Google Scholar] [CrossRef]
- Groß, R.; Dorigo, M. Self-assembly at the macroscopic scale. Proc. IEEE 2008, 96, 1490–1508. [Google Scholar] [CrossRef]
- Kim, Y.; Yuk, H.; Zhao, R.; Chester, S.A.; Zhao, X. Printing ferromagnetic domains for untethered fast-transforming soft materials. Nature 2018, 558, 274–279. [Google Scholar] [CrossRef]
- Rubenstein, M.; Cornejo, A.; Nagpal, R. Programmable self-assembly in a thousand-robot swarm. Science 2014, 345, 795–799. [Google Scholar] [CrossRef]
- Chung, B.J.; Vaidya, A. Non-equilibrium pattern selection in particle sedimentation. Appl. Math. Comput. 2011, 218, 3451–3465. [Google Scholar] [CrossRef]
- Frenkel, D. Order through entropy. Nat. Mater. 2014, 14, 9–12. [Google Scholar] [CrossRef] [PubMed]
- Gracias, D.H.; Tien, J.; Breen, T.L.; Hsu, C.; Whitesides, G.M. Forming electrical networks in three dimensions by self-assembly. Science 2000, 289, 1170–1172. [Google Scholar] [CrossRef]
- Terfort, A.; Bowden, N.; Whitesides, G.M. Three-dimensional self-assembly of millimetre-scale components. Nature 1997, 386, 162–164. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure. VDI 6220: Biomimetics—Conceptions and Strategy, Differences Between Biomimetic and Conventional Methods/Products; Verlag des Vereins Deutscher Ingenieure: Düsseldorf, Germany, 2012. [Google Scholar]
- Eraghi, S.; Toofani, A.; Khaheshi, A.; Khorsandi, M.; Darvizeh, A.; Gorb, S.; Rajabi, H. Wing coupling in bees and wasps: From the underlying science to bioinspired engineering. Adv. Sci. 2021, 8, e2004383. [Google Scholar] [CrossRef] [PubMed]
- Jemghili, R.; Ait Taleb, A.; Khalifa, M. A bibliometric indicators analysis of additive manufacturing research trends from 2010 to 2020. Rapid Prototyp. J. 2021, 27, 1432–1454. [Google Scholar] [CrossRef]
- Obi, M.U.; Pradel, P.; Sinclair, M.; Bibb, R. A bibliometric analysis of research in design for additive manufacturing. Rapid Prototyp. J. 2022, 28, 967–987. [Google Scholar] [CrossRef]
- Mhmood, T.R.; Al-Karkhi, N.K. A review of the stereolithography 3D printing process and the effect of parameters on quality. Al-Khwarizmi Eng. J. 2023, 19, 82–94. [Google Scholar] [CrossRef]
- Drechslerová, V.; Neuhäuserová, M.; Falta, J.; Šleichrt, J.; Kytýř, D. Stereolithography for manufacturing of advanced porous solids. Acta Polytech. CTU Proc. 2023, 41, 1–7. [Google Scholar] [CrossRef]
- Schmidleithner, C.; Kalaskar, D.M. Stereolithography. In 3D Printing; IntechOpen: London, UK, 2018. [Google Scholar]
- Doualle, T.; Gallais, L.; André, J.C. Light–matter complex interactions in stereolithographies. Appl. Sci. 2023, 13, 6844. [Google Scholar] [CrossRef]
- Jin, Y.; Ji, S.; Li, X.; Yu, J. A scientometric review of hotspots and emerging trends in additive manufacturing. J. Manuf. Technol. Manag. 2017, 28, 18–38. [Google Scholar] [CrossRef]
- Hamilton, A.; Xu, Y.; Kartal, M.E.; Kumar, S.; Gadegaard, N.; Mulvihill, D.M. Optimisation of interlocking microstructured adhesive joints via finite element modelling, design of experiments and 3D printing. Int. J. Adhes. Adhes. 2023, 120, 103292. [Google Scholar] [CrossRef]
- Song, P.; Fu, Z.; Liu, L.; Fu, C.W. Printing 3D objects with interlocking parts. Comput. Aided Geom. Des. 2015, 35, 137–148. [Google Scholar] [CrossRef]
- Alemanno, G.; Cignoni, P.; Pietroni, N.; Ponchio, F.; Scopigno, R. Interlocking pieces for printing tangible cultural heritage replicas. In Proceedings of the GCH Conference, Darmstadt, Germany, 6–8 October 2014; pp. 145–154. [Google Scholar]
- Gloyer, P.; Schek, L.N.; Flöttmann, H.L.; Wüst, P.; Völlmecke, C. Extrusion-based additive manufacturing-driven design and testing of the snapping interlocking metasurface mechanism ShroomLock. Inventions 2023, 8, 137. [Google Scholar] [CrossRef]
- Damasceno, P.; Engel, M.; Glotzer, S. Predictive self-assembly of polyhedra into complex structures. Science 2012, 337, 453–457. [Google Scholar] [CrossRef]
- Weissenbek, E.; Böhm, H.; Rammerstorfer, F. Micromechanical investigations of arrangement effects in particle reinforced metal matrix composites. Comput. Mater. Sci. 1994, 3, 263–278. [Google Scholar] [CrossRef]
- Ma, Y.; Wan, C.; Gorb, S.; Rajabi, H. Biomechanics of fore wing to hind wing coupling in the southern green stink bug Nezara viridula (Pentatomidae). Acta Biomater. 2016, 100, 10–17. [Google Scholar] [CrossRef]
- Sun, J.; Liu, C.; Bhushan, B.; Wu, W.; Tong, J. Effect of microtrichia on the interlocking mechanism in the Asian ladybeetle, Harmonia axyridis (Coleoptera: Coccinellidae). Beilstein J. Nanotechnol. 2018, 9, 812–823. [Google Scholar] [CrossRef]
- Breed, R.; Ball, E. The interlocking mechanisms which are found in connection with the elytra of Coleoptera. Biol. Bull. 1908, 15, 289–303. [Google Scholar] [CrossRef]




| Initial Exposure | Exposure Time | Rising Height | Motor Speed | Light-Off Delay |
|---|---|---|---|---|
| 30 s | 2.8 s | 8 mm | 5 mm/s | 6 s |
| Test | Time (min) | Speed (rpm) |
|---|---|---|
| 300 | 6 | 300 |
| 350 | 6 | 350 |
| 400 | 6 | 400 |
| Mix | 2/2/2 | 400/350/300 |
| Control | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marte, T.; Koltsakidis, S.; Profitiliotis, T.; Tzimtzimis, E.; Tzetzis, D. Towards Self-Assembling 3D-Printed Shapes Through Βiomimetic Μechanical Interlocking. Biomimetics 2025, 10, 400. https://doi.org/10.3390/biomimetics10060400
Marte T, Koltsakidis S, Profitiliotis T, Tzimtzimis E, Tzetzis D. Towards Self-Assembling 3D-Printed Shapes Through Βiomimetic Μechanical Interlocking. Biomimetics. 2025; 10(6):400. https://doi.org/10.3390/biomimetics10060400
Chicago/Turabian StyleMarte, Tino, Savvas Koltsakidis, Thomas Profitiliotis, Emmanouil Tzimtzimis, and Dimitrios Tzetzis. 2025. "Towards Self-Assembling 3D-Printed Shapes Through Βiomimetic Μechanical Interlocking" Biomimetics 10, no. 6: 400. https://doi.org/10.3390/biomimetics10060400
APA StyleMarte, T., Koltsakidis, S., Profitiliotis, T., Tzimtzimis, E., & Tzetzis, D. (2025). Towards Self-Assembling 3D-Printed Shapes Through Βiomimetic Μechanical Interlocking. Biomimetics, 10(6), 400. https://doi.org/10.3390/biomimetics10060400









