Biomimetic Lattice Structures Design and Manufacturing for High Stress, Deformation, and Energy Absorption Performance
Abstract
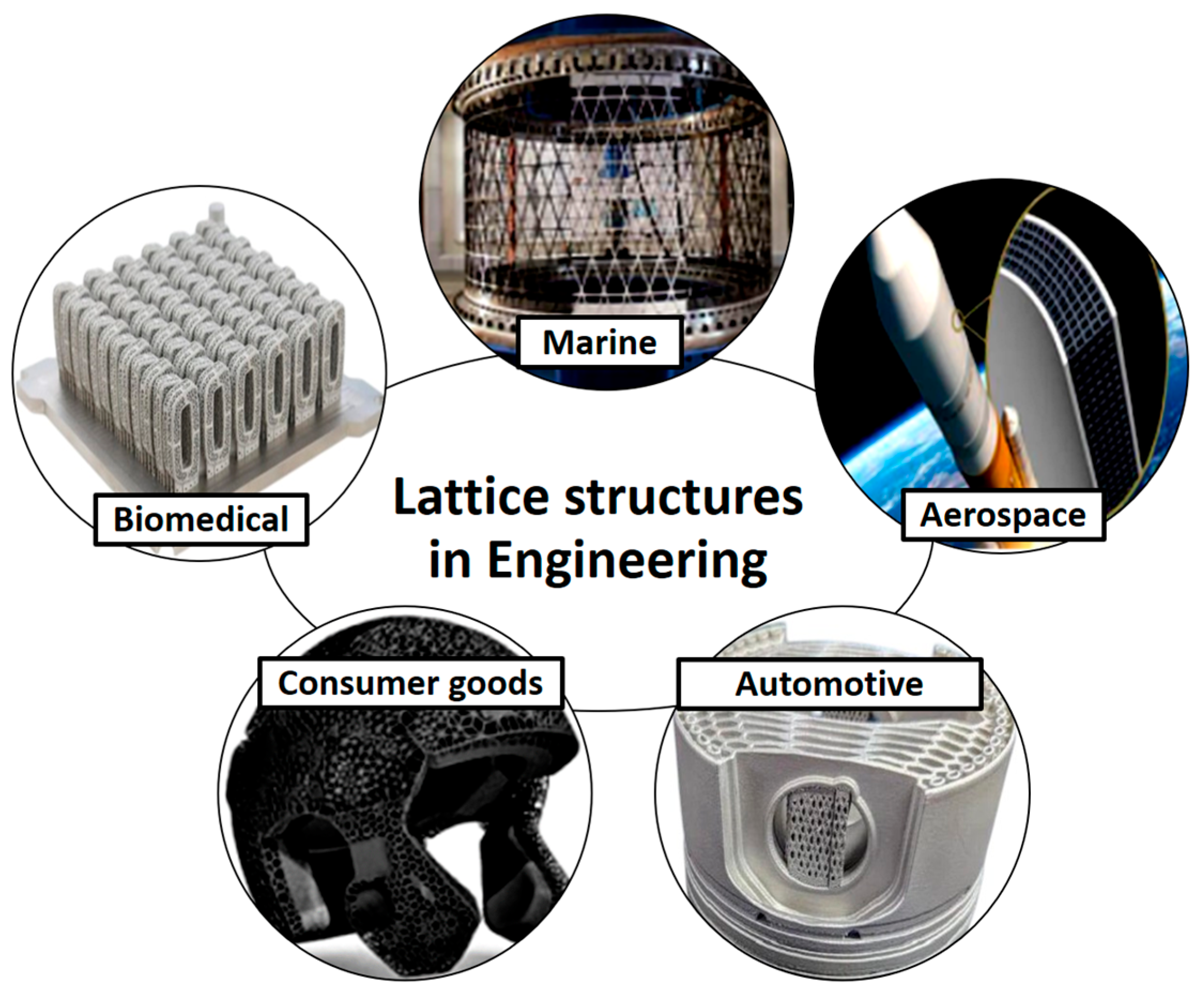
1. Introduction
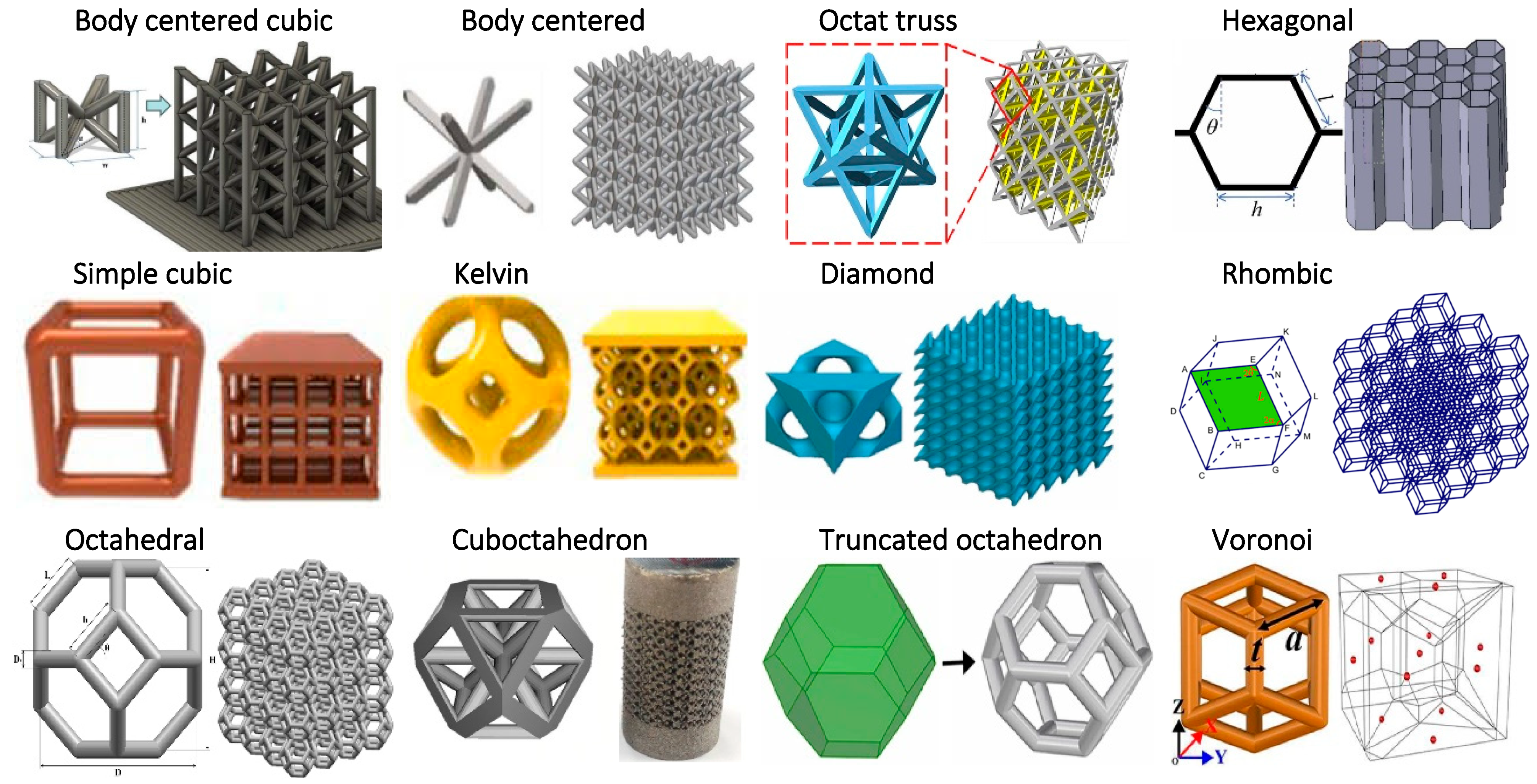
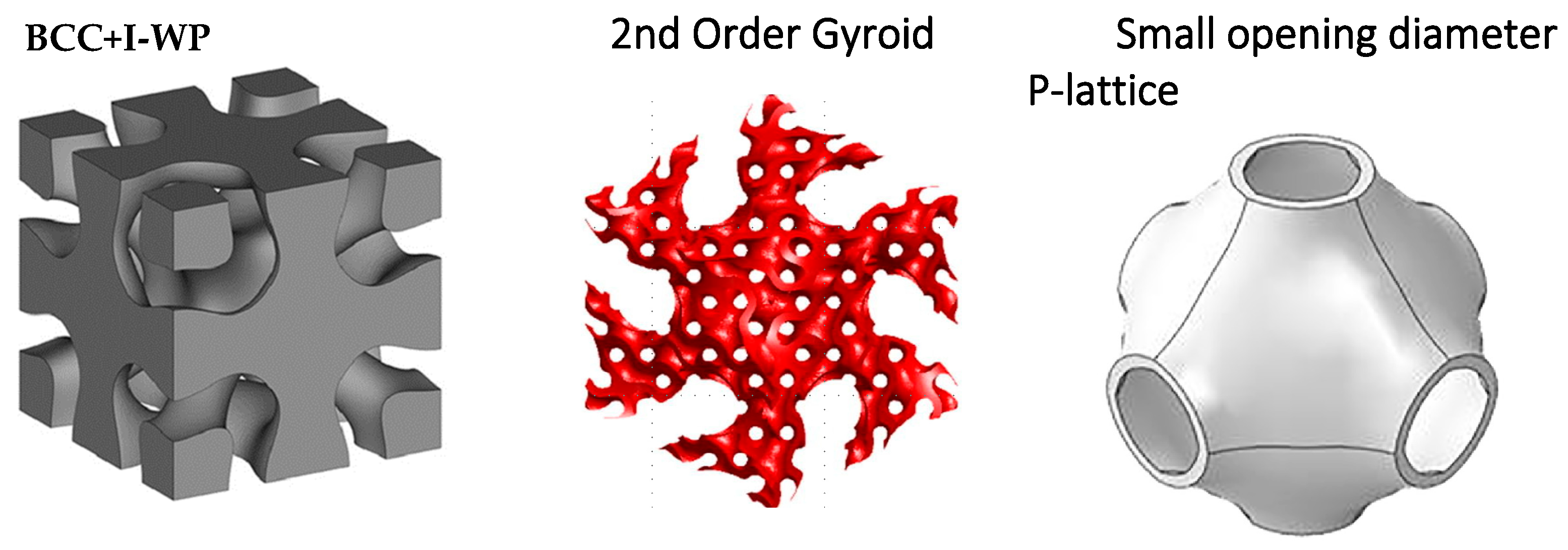
2. Current Design, Classification, and Manufacturing Methods of Lattice Structures
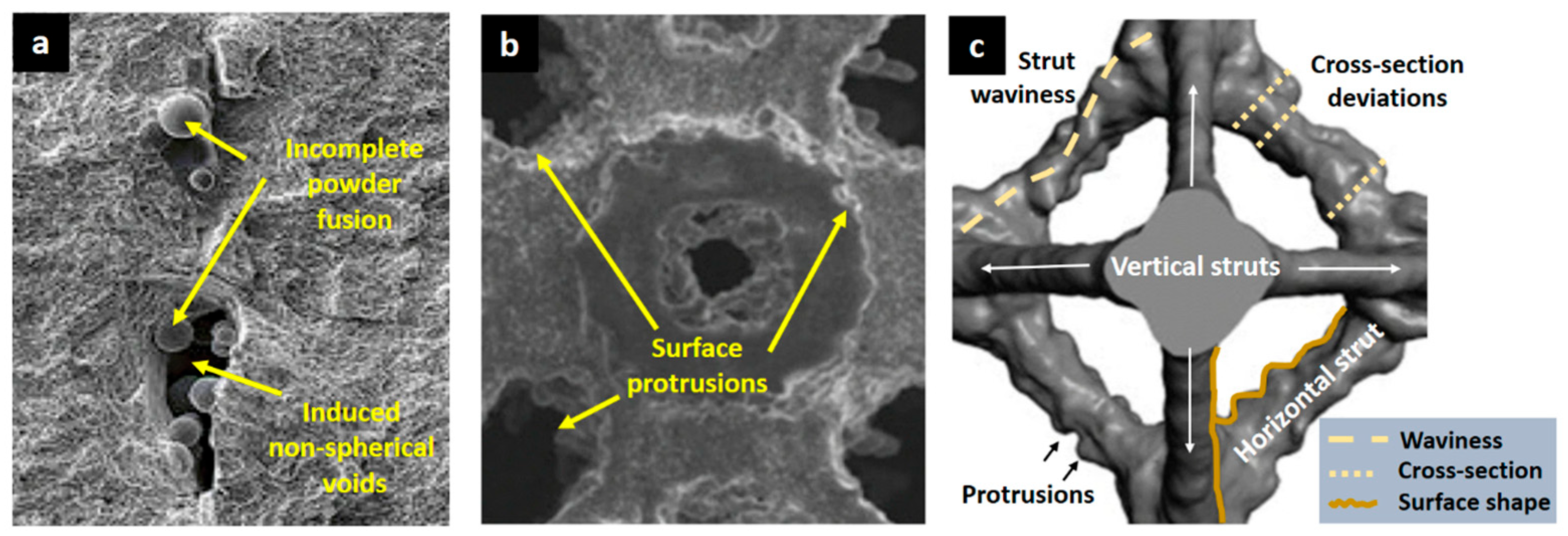
3. Manufacturing Defects in LPBF-Fabricated Lattice Structures: Causes, Measurement Techniques, and Mitigation Strategies
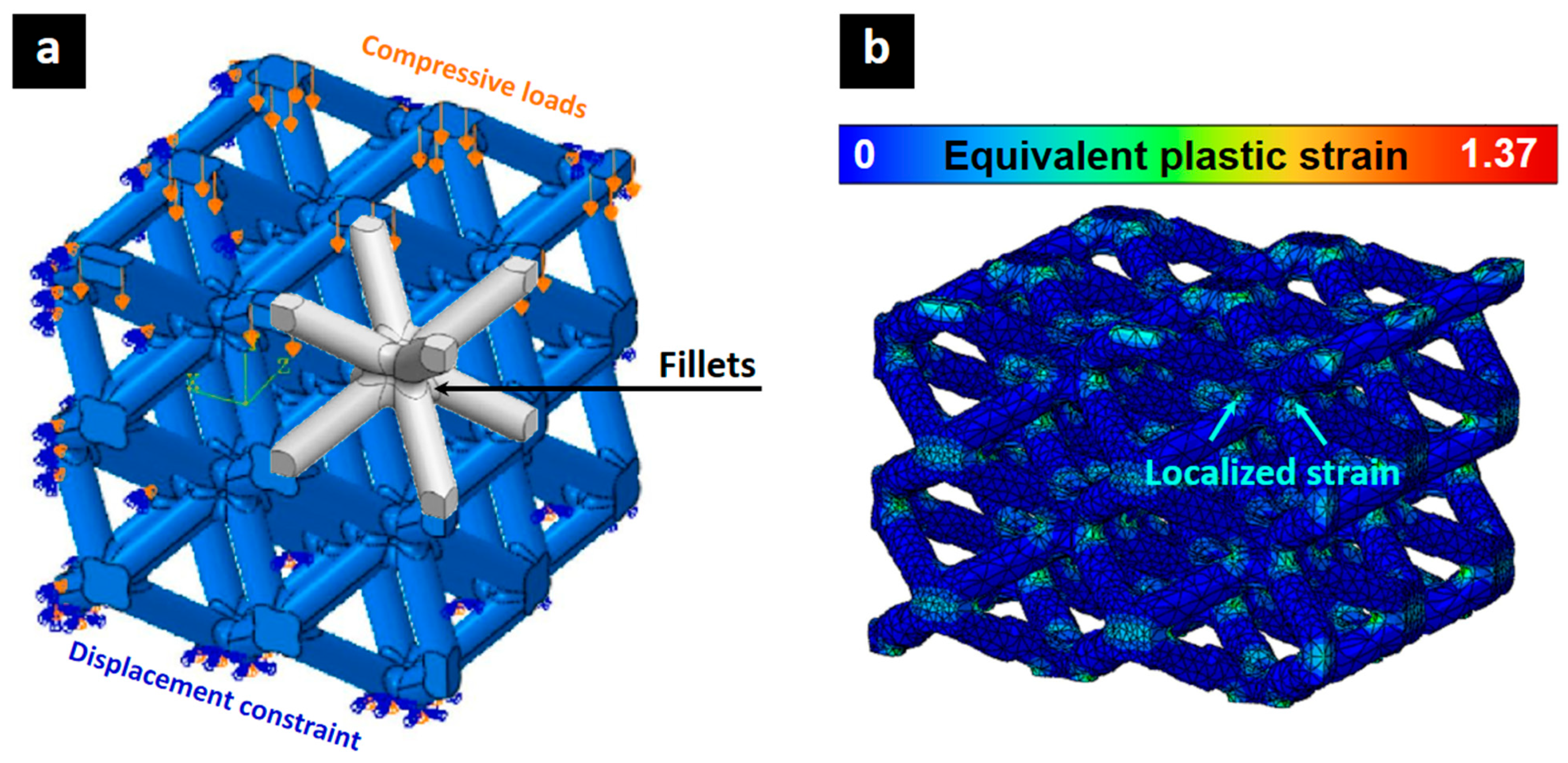
4. Performance Analysis of Lattice Structures
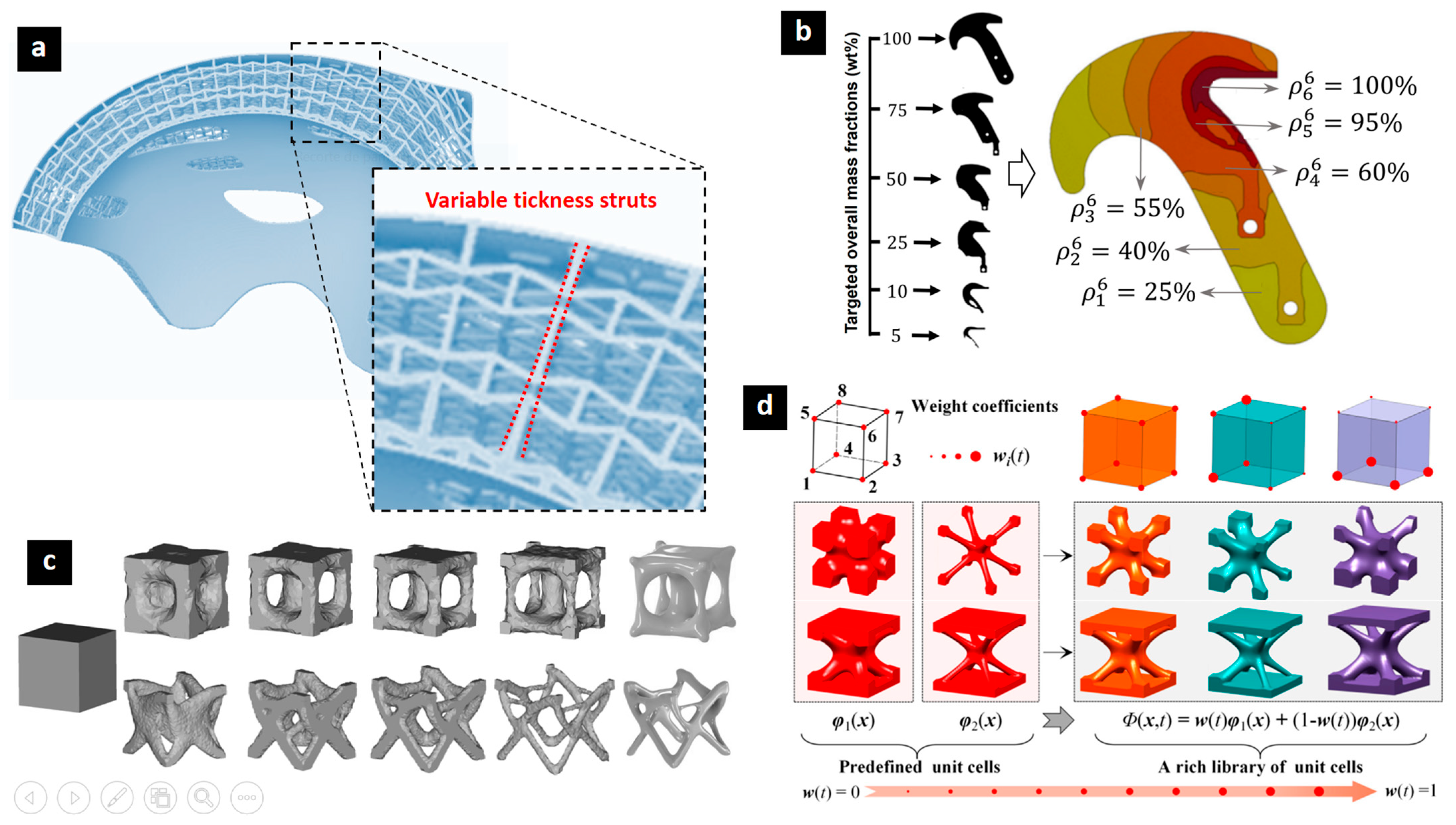
5. Optimization Strategies for Lattice Structures: Computational Methods, Bio-Inspired Approaches, and Advanced Manufacturing Integration
6. Challenges in the Design and Performance of Biomimetic Lattice Structures
7. Open Challenges in Predictive Modeling, Additive Manufacturing, and Multi-Scale Validation of Biomimetic Lattice Structures
7.1. Predictive Modeling and Simulation
7.2. Optimization of Additive Manufacturing Techniques
7.3. Multi-Scale Experimental Validation
7.4. Integration of Smart Materials and Scalability Weakness
8. Conclusions
9. Future Research
Funding
Conflicts of Interest
References
- Yin, H.; Zhang, W.; Zhu, L.; Meng, F.; Liu, J.; Wen, G. Review on Lattice Structures for Energy Absorption Properties. Compos. Struct. 2023, 304, 116397. [Google Scholar] [CrossRef]
- Garrido, C.; Pincheira, G.; Valle, R.; Fernández, J.; Tuninetti, V. Plastic Deformation Behavior and Energy Absorption Performance of a Composite Metamaterial Based on Asymmetric Auxetic Lattices. Compos. Struct. 2024, 346, 118410. [Google Scholar] [CrossRef]
- Bustos, F.; Hinojosa, J.; Olivos, A. Numerical Characterization and Experimental Validation of Steel Plate Shear Yielding Damper. Structures 2025, 72, 108215. [Google Scholar] [CrossRef]
- Ríos, I.; Martínez, A.; Saggionetto, E.; Mertens, A.; Duchêne, L.; Habraken, A.M.; Tuninetti, V. Numerical Modeling of the Compressive Behavior of 316L Body-Centered Cubic Lattice Structures. Mater. Res. Proc. 2024, 41, 224–233. [Google Scholar] [CrossRef]
- Valle, R.; Pincheira, G.; Tuninetti, V.; Garrido, C.; Treviño, C.; Morales, J. Evaluation of the Orthotropic Behavior in an Auxetic Structure Based on a Novel Design Parameter of a Square Cell with Re-Entrant Struts. Polymers 2022, 14, 4325. [Google Scholar] [CrossRef]
- Valle, R.; Pincheira, G.; Tuninetti, V.; Fernandez, E.; Uribe-Lam, E. Design and Characterization of Asymmetric Cell Structure of Auxetic Material for Predictable Directional Mechanical Response. Materials 2022, 15, 1841. [Google Scholar] [CrossRef]
- Hindi, S.S.Z.; Abohassan, R.A. Cellulose Triacetate Synthesis from Cellulosic Wastes by Heterogeneous Reactions. BioResources 2015, 10, 5030–5048. [Google Scholar] [CrossRef]
- Liao, C.; Tian, Y.; Xu, W.; Zhang, J.; Sun, Z.; Liu, Z. Cushioning Performance of the Biomimetic Cobweb Cushioning Silicone Pad. Biomimetics 2023, 8, 276. [Google Scholar] [CrossRef]
- Dara, A.; Bahubalendruni, M.V.A.R.; Johnney Mertens, A.; Balamurali, G. Numerical and Experimental Investigations of Novel Nature Inspired Open Lattice Cellular Structures for Enhanced Stiffness and Specific Energy Absorption. Mater. Today Commun. 2022, 31, 103286. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Ataollahi, S. A Review on Additive Manufacturing of Lattice Structures in Tissue Engineering. Bioprinting 2023, 35, e00304. [Google Scholar] [CrossRef]
- Bernard, A.R.; ElSayed, M.S.A. Design, Manufacturing, and Analysis of Periodic Three-Dimensional Cellular Materials for Energy Absorption Applications: A Critical Review. Materials 2024, 17, 2181. [Google Scholar] [CrossRef] [PubMed]
- Avalle, M. A Generic Model to Assess the Efficiency Analysis of Cellular Foams. Materials 2024, 17, 746. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Zuo, Y.; Chang, Z. Evaluation of Energy Absorption Capabilities of Polyethylene Foam under Impact Deformation. Materials 2021, 14, 3613. [Google Scholar] [CrossRef]
- Lin, W.; Sundén, B.; Yuan, J. A Performance Analysis of Porous Graphite Foam Heat Exchangers in Vehicles. Appl. Therm. Eng. 2013, 50, 1201–1210. [Google Scholar] [CrossRef]
- Zheng, H.; Li, Y.; He, D.; Wen, P.; Yan, S. High-Performance Flexible Piezoelectric Sensors Based on Honeycomb Graphene Macro-Film Exploiting Auxetic Mechanical Property. Sens. Actuators A Phys. 2024, 372, 115374. [Google Scholar] [CrossRef]
- Kaur, I.; Aider, Y.; Nithyanandam, K.; Singh, P. Thermal-Hydraulic Performance of Additively Manufactured Lattices for Gas Turbine Blade Trailing Edge Cooling. Appl. Therm. Eng. 2022, 211, 118461. [Google Scholar] [CrossRef]
- Dhote, G.M.; Selvaraj, K.; Jain, A.; Rajendran, S. Nature Inspires Biomimetic Robots to Build Lattice Structures of Unprecedented Strength. Int. J. Adv. Manuf. Technol. 2024. [Google Scholar] [CrossRef]
- Großmann, A.; Gosmann, J.; Mittelstedt, C. Lightweight Lattice Structures in Selective Laser Melting: Design, Fabrication and Mechanical Properties. Mater. Sci. Eng. A 2019, 766, 138356. [Google Scholar] [CrossRef]
- Khan, N.; Riccio, A. A Systematic Review of Design for Additive Manufacturing of Aerospace Lattice Structures: Current Trends and Future Directions. Prog. Aerosp. Sci. 2024, 149, 101021. [Google Scholar] [CrossRef]
- Aslan, B.; Yıldız, A.R. Optimum Design of Automobile Components Using Lattice Structures for Additive Manufacturing. Mater. Test. 2020, 62, 633–639. [Google Scholar] [CrossRef]
- Armanfar, A.; Alper Tasmektepligil, A.; Kilic, R.T.; Demir, S.; Cam, S.; Karafi, Y.; El Majd, B.A.; Gunpinar, E. Embedding Lattice Structures into Ship Hulls for Structural Optimization and Additive Manufacturing. Ocean Eng. 2024, 301, 117601. [Google Scholar] [CrossRef]
- Nogueira, P.; Lopes, P.; Oliveira, L.; Alves, J.L.; Magrinho, J.P.G.; de Deus, A.M.; Vaz, M.F.; Silva, M.B. Evaluation of Lattice Structures for Medical Implants: A Study on the Mechanical Properties of Various Unit Cell Types. Metals 2024, 14, 780. [Google Scholar] [CrossRef]
- Zechmeister, C.; Gil Pérez, M.; Dambrosio, N.; Knippers, J.; Menges, A. Extension of Computational Co-Design Methods for Modular, Prefabricated Composite Building Components Using Bio-Based Material Systems. Sustainability 2023, 15, 12189. [Google Scholar] [CrossRef]
- Mahmoud, D.; Elbestawi, M.A. Lattice Structures and Functionally Graded Materials Applications in Additive Manufacturing of Orthopedic Implants: A Review. J. Manuf. Mater. Process. 2017, 1, 13. [Google Scholar] [CrossRef]
- Tuninetti, V.; Forcael, D.; Valenzuela, M.; Martínez, A.; Ávila, A.; Medina, C.; Pincheira, G.; Salas, A.; Oñate, A.; Duchêne, L. Assessing Feed-Forward Backpropagation Artificial Neural Networks for Strain-Rate-Sensitive Mechanical Modeling. Materials 2024, 17, 317. [Google Scholar] [CrossRef]
- Tuninetti, V.; Sepúlveda, H.; Beecher, C.; Rojas-Ulloa, C.; Oñate, A.; Medina, C.; Valenzuela, M. A Combined Experimental and Numerical Calibration Approach for Modeling the Performance of Aerospace-Grade Titanium Alloy Products. Aerospace 2024, 11, 285. [Google Scholar] [CrossRef]
- Tuninetti, V.; Fuentes, G.; Oñate, A.; Narayan, S.; Celentano, D.; García-Herrera, C.; Menacer, B.; Pincheira, G.; Garrido, C.; Valle, R. Computational Shape Design Optimization of Femoral Implants: Towards Efficient Forging Manufacturing. Appl. Sci. 2024, 14, 8289. [Google Scholar] [CrossRef]
- Feng, J.; Liu, B.; Lin, Z.; Fu, J. Isotropic Octet-Truss Lattice Structure Design and Anisotropy Control Strategies for Implant Application. Mater. Des. 2021, 203, 109595. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Leary, M.; Tang, H.P.; Song, T.; Qian, M. Selective Electron Beam Manufactured Ti-6Al-4V Lattice Structures for Orthopedic Implant Applications: Current Status and Outstanding Challenges. Curr. Opin. Solid State Mater. Sci. 2018, 22, 75–99. [Google Scholar] [CrossRef]
- Rilling, S.; Ríos, I.; Gómez, Á.; Valenzuela, M.; Oñate, A.; Tuninetti, V. Optimized Infill Density through Topological Optimization Increases Strength of Additively Manufactured Porous Polylactic Acid. Int. J. Adv. Manuf. Technol. 2023, 129, 3739–3750. [Google Scholar] [CrossRef]
- Cheung, K.C.; Gershenfeld, N. Reversibly Assembled Cellular Composite Materials. Science 2013, 341, 1219–1221. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z. Biomimetic Design and Topology Optimization of Discontinuous Carbon Fiber-Reinforced Composite Lattice Structures. Biomimetics 2023, 8, 148. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Wang, J. Porous Material Energy Absorbing Structure Based on Spider Web Biomimetic Structure. Manuf. Rev. 2024, 11, 12. [Google Scholar] [CrossRef]
- Wang, S.; Shi, Z.; Liu, L.; Huang, Z.; Li, Z.; Liu, J.; Hao, Y. Honeycomb Structure Is Promising for the Repair of Human Bone Defects. Mater. Des. 2021, 207, 109832. [Google Scholar] [CrossRef]
- Xu, L.; Ruan, Q.; Shen, Q.; Xi, L.; Gao, J.; Li, Y. Optimization Design of Lattice Structures in Internal Cooling Channel with Variable Aspect Ratio of Gas Turbine Blade. Energies 2021, 14, 3954. [Google Scholar] [CrossRef]
- Li, X.; Zhao, M.; Yu, X.; Wei Chua, J.; Yang, Y.; Lim, K.M.; Zhai, W. Multifunctional and Customizable Lattice Structures for Simultaneous Sound Insulation and Structural Applications. Mater. Des. 2023, 234, 112354. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, A.; Liu, Z.; Du, P.; Guo, Y. The Sound Absorption Performance of Laser-Sintered Composite Biomimetic Wood Porous Structures. Polymers 2024, 16, 3290. [Google Scholar] [CrossRef]
- Miao, X.; Hu, J.; Xu, Y.; Su, J.; Jing, Y. Review on Mechanical Properties of Metal Lattice Structures. Compos. Struct. 2024, 342, 118267. [Google Scholar] [CrossRef]
- McDonnell, B.; Errico, V.; Posa, P.; Angelastro, A.; Furman, A.; O’Hara, E.; Campanelli, S.L.; Harrison, N. Bi-Metallic Lattice Structures Manufactured via an Intralayer Multi-Material Powder Bed Fusion Method. Addit. Manuf. 2024, 89, 104301. [Google Scholar] [CrossRef]
- Yin, H.; Meng, F.; Zhu, L.; Wen, G. Optimization Design of a Novel Hybrid Hierarchical Cellular Structure for Crashworthiness. Compos. Struct. 2023, 303, 116335. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Y.; Li, Z.; Ye, G.; Zhang, C.; Wang, T.; Wang, L. Comparison of Out-of-Plane Compression Performance of Cellular Structures with Different Configuration: Hexagon, Re-Entrant, Chirality. Structures 2025, 73, 108396. [Google Scholar] [CrossRef]
- Ghannadpour, S.A.M.; Mahmoudi, M.; Hossein Nedjad, K. Structural Behavior of 3D-Printed Sandwich Beams with Strut-Based Lattice Core: Experimental and Numerical Study. Compos. Struct. 2022, 281, 115113. [Google Scholar] [CrossRef]
- Nazir, A.; Hussain, S.; Ali, H.M.; Waqar, S. Design and Mechanical Performance of Nature-Inspired Novel Hybrid Triply Periodic Minimal Surface Lattice Structures Fabricated Using Material Extrusion. Mater. Today Commun. 2024, 38, 108349. [Google Scholar] [CrossRef]
- Babaee, S.; Jahromi, B.H.; Ajdari, A.; Nayeb-Hashemi, H.; Vaziri, A. Mechanical Properties of Open-Cell Rhombic Dodecahedron Cellular Structures. Acta Mater. 2012, 60, 2873–2885. [Google Scholar] [CrossRef]
- Chen, L.-Y.; Liang, S.-X.; Liu, Y.; Zhang, L.-C. Additive Manufacturing of Metallic Lattice Structures: Unconstrained Design, Accurate Fabrication, Fascinated Performances, and Challenges. Mater. Sci. Eng. R Rep. 2021, 146, 100648. [Google Scholar] [CrossRef]
- Chen, J.K.; Wu, M.W.; Cheng, T.L.; Chiang, P.H. Continuous Compression Behaviors of Selective Laser Melting Ti-6Al-4V Alloy with Cuboctahedron Cellular Structures. Mater. Sci. Eng. C 2019, 100, 781–788. [Google Scholar] [CrossRef]
- Guo, S.; Teng, Z.; Kitazono, K. Excellent Compression Strength and Energy Absorption of Additively Manufactured Porous Titanium with Trapezo-Rhombic Dodecahedron Cell. Mater. Today Commun. 2022, 33, 104842. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, R.; Li, B.; Zhang, G.; Yang, D.; Yue, X.; Guo, X.; Tang, H.; Zhang, F. A Gradient Disordered Cellular Porous Ti-6Al-4V Alloy Fabricated by Powder Bed Fusion with High Energy Absorption and Low Anisotropy. Thin-Walled Struct. 2025, 210, 113012. [Google Scholar] [CrossRef]
- Rahimi, S.; Asghari, M. Design and Evaluation of Two Proposed Hybrid FCC-BCC Lattice Structures for Enhanced Mechanical Performance. Heliyon 2025, 11, e40911. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, X.; Yang, G.; Song, B.; Sha, H. Design and Mechanical Performance Analysis of T-BCC Lattice Structures. J. Mater. Res. Technol. 2024, 32, 1538–1551. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, X.; Yan, K.; Zhao, Y.; Cui, J. An Improved BCC Lattice Structure for Vibration Isolation in Extreme Environment. Adv. Mech. Eng. 2024, 16, 1–15. [Google Scholar] [CrossRef]
- Kokil-Shah, S.; Sur, A.; Shah, M.; Darvekar, S.K. Performance Prediction of Different BCC Lattice Structures under Static Loading: An Experimental Approach. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 581. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, D.Z.; Li, Z.; Zhang, T.; Zhou, H.; Ren, Z. Design, Mechanical Properties, and Optimization of BCC Lattice Structures with Taper Struts. Compos. Struct. 2022, 295, 115830. [Google Scholar] [CrossRef]
- Liu, C.; Ni, R.; Ji, K.; Zhao, A.; Sun, X.; Wu, H. Improving Mechanical Properties of Lattice Structures Using Nonuniform Hollow Struts. Int. J. Mech. Sci. 2024, 283, 109674. [Google Scholar] [CrossRef]
- Cardeña, A.; Sancho, R.; Barba, D.; Gálvez, F. Dynamic Behaviour of Additively Manufactured Ti6Al4V BCC Lattice-Based Structures. Mater. Lett. 2024, 354, 2023–2025. [Google Scholar] [CrossRef]
- Cao, X.; Duan, S.; Liang, J.; Wen, W.; Fang, D. Mechanical Properties of an Improved 3D-Printed Rhombic Dodecahedron Stainless Steel Lattice Structure of Variable Cross Section. Int. J. Mech. Sci. 2018, 145, 53–63. [Google Scholar] [CrossRef]
- Lei, H.Y.; Li, J.R.; Xu, Z.J.; Wang, Q.H. Parametric Design of Voronoi-Based Lattice Porous Structures. Mater. Des. 2020, 191, 108607. [Google Scholar] [CrossRef]
- Zou, S.; Gong, H.; Gao, J. Additively Manufactured Multilevel Voronoi-Lattice Scaffolds with Bonelike Mechanical Properties. ACS Biomater. Sci. Eng. 2022, 8, 3022–3037. [Google Scholar] [CrossRef]
- Han, C.; Wang, Y.; Wang, Z.; Dong, Z.; Li, K.; Song, C.; Cai, C.; Yan, X.; Yang, Y.; Wang, D. Enhancing Mechanical Properties of Additively Manufactured Voronoi-Based Architected Metamaterials via a Lattice-Inspired Design Strategy. Int. J. Mach. Tools Manuf. 2024, 202, 104199. [Google Scholar] [CrossRef]
- Bregoli, C.; Fiocchi, J.; Mehrpouya, M.; Vergani, L.M.; Tuissi, A.; Biffi, C.A. Mechanical Response of LPBFed TI64 Thickness Graded Voronoi Lattice Structures. Materialia 2024, 38, 102234. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Liu, M.; Huang, H.; Xu, S.; Xia, Y.; Qian, G.; Wu, W. Mechanical Behaviors of SLM Additive Manufactured Octet-Truss and Truncated-Octahedron Lattice Structures with Uniform and Taper Beams. Int. J. Mech. Sci. 2019, 163, 105091. [Google Scholar] [CrossRef]
- Saremian, R.; Badrossamay, M.; Foroozmehr, E.; Kadkhodaei, M.; Forooghi, F. Experimental and Numerical Investigation on Lattice Structures Fabricated by Selective Laser Melting Process under Quasi-Static and Dynamic Loadings. Int. J. Adv. Manuf. Technol. 2021, 112, 2815–2836. [Google Scholar] [CrossRef]
- Di Caprio, F.; Franchitti, S.; Borrelli, R.; Bellini, C.; Di Cocco, V.; Sorrentino, L. Ti-6Al-4V Octet-Truss Lattice Structures under Bending Load Conditions: Numerical and Experimental Results. Metals 2022, 12, 410. [Google Scholar] [CrossRef]
- Arsentev, M.; Topalov, E.; Balabanov, S.; Sysoev, E.; Shulga, I.; Akhmatnabiev, M.; Sychov, M.; Skorb, E.; Nosonovsky, M. Crystal-Inspired Cellular Metamaterials and Triply Periodic Minimal Surfaces. Biomimetics 2024, 9, 285. [Google Scholar] [CrossRef]
- Khanna, P.; Sood, S.; Mishra, P.; Bharadwaj, V.; Aggarwal, A.; Singh, S.J. Analysis of Compression and Energy Absorption Behaviour of SLM Printed AlSi10Mg Triply Periodic Minimal Surface Lattice Structures. Structures 2024, 64, 106580. [Google Scholar] [CrossRef]
- Araghi, M.; Nayebi, A.; Rokhgireh, H. Laser Powder Bed Fusion Manufactured TPMS Cellular Structures: Failure Modeling by Using Initial Damage Concept and Continuum Damage Mechanics Model. Structures 2024, 68, 107272. [Google Scholar] [CrossRef]
- Novak, N.; Borovinšek, M.; Al-Ketan, O.; Ren, Z.; Vesenjak, M. Impact and Blast Resistance of Uniform and Graded Sandwich Panels with TPMS Cellular Structures. Compos. Struct. 2022, 300, 116174. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, Z.; Wang, M.Y.; Feih, S. Hierarchical Sheet Triply Periodic Minimal Surface Lattices: Design, Geometric and Mechanical Performance. Mater. Des. 2021, 209, 109931. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Zhang, D.Z.; Zhai, W. TPMS-Based Interpenetrating Lattice Structures: Design, Mechanical Properties and Multiscale Optimization. Int. J. Mech. Sci. 2023, 244, 108092. [Google Scholar] [CrossRef]
- Guo, X.; Ding, J.; Li, X.; Qu, S.; Song, X.; Fuh, J.Y.H.; Lu, W.F.; Zhai, W. Enhancement in the Mechanical Behaviour of a Schwarz Primitive Periodic Minimal Surface Lattice Structure Design. Int. J. Mech. Sci. 2022, 216, 106977. [Google Scholar] [CrossRef]
- Bustos, F.; Hinojosa, J.; Tuninetti, V. Computational Comparison of Performance of Different Steel Plate Shear Yielding Dampers. Buildings 2023, 13, 793. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Rawson, S.D.; Puga, H.; Meireles, J.; Withers, P.J. Additive Manufacturing Assisted Investment Casting: A Low-Cost Method to Fabricate Periodic Metallic Cellular Lattices. Addit. Manuf. 2020, 33, 101085. [Google Scholar] [CrossRef]
- Luukkonen, T.; Yliniemi, J.; Sreenivasan, H.; Ohenoja, K.; Finnilä, M.; Franchin, G.; Colombo, P. Ag- or Cu-Modified Geopolymer Filters for Water Treatment Manufactured by 3D Printing, Direct Foaming, or Granulation. Sci. Rep. 2020, 10, 7233. [Google Scholar] [CrossRef] [PubMed]
- Kang, K.-J. Wire-Woven Cellular Metals: The Present and Future. Prog. Mater. Sci. 2015, 69, 213–307. [Google Scholar] [CrossRef]
- Li, Y.; Yang, C.; Zhao, H.; Qu, S.; Li, X.; Li, Y. New Developments of Ti-Based Alloys for Biomedical Applications. Materials 2014, 7, 1709–1800. [Google Scholar] [CrossRef]
- Richard, C.T.; Kwok, T.H. Analysis and Design of Lattice Structures for Rapid-Investment Casting. Materials 2021, 14, 4867. [Google Scholar] [CrossRef]
- Dong, G.; Tang, Y.; Zhao, Y.F. A Survey of Modeling of Lattice Structures Fabricated by Additive Manufacturing. J. Mech. Des. 2017, 139, 100906. [Google Scholar] [CrossRef]
- Echeta, I.; Feng, X.; Dutton, B.; Leach, R.; Piano, S. Review of Defects in Lattice Structures Manufactured by Powder Bed Fusion. Int. J. Adv. Manuf. Technol. 2020, 106, 2649–2668. [Google Scholar] [CrossRef]
- Melancon, D.; Bagheri, Z.S.; Johnston, R.B.; Liu, L.; Tanzer, M.; Pasini, D. Mechanical Characterization of Structurally Porous Biomaterials Built via Additive Manufacturing: Experiments, Predictive Models, and Design Maps for Load-Bearing Bone Replacement Implants. Acta Biomater. 2017, 63, 350–368. [Google Scholar] [CrossRef]
- Decker, T.; Kedziora, S. Optimizing the Thickness of Functionally Graded Lattice Structures for High-Performance Energy Absorption: A Case Study Based on a Bicycle Helmet. Appl. Sci. 2024, 14, 2788. [Google Scholar] [CrossRef]
- Jardin, R.T.; Tuninetti, V.; Tchuindjang, J.T.; Duchêne, L.; Hashemi, N.; Tran, H.S.; Carrus, R.; Mertens, A.; Habraken, A.M. Optimizing Laser Power of Directed Energy Deposition Process for Homogeneous AISI M4 Steel Microstructure. Opt. Laser Technol. 2023, 163, 109426. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, Z.; Yang, X.; Jiao, H.; Huang, W. Effect of Scanning Strategies on the Microstructure and Mechanical Properties of Ti-22Al-25Nb Alloy Fabricated through Selective Laser Melting. Metals 2023, 13, 634. [Google Scholar] [CrossRef]
- Kim, M.; Han, S.J.; Kang, H.S.; Bang, G.B.; Lee, T.W.; Kim, G.H.; Kim, W.R.; Sung, S.; Kwon, O.; Kim, H.G. Optimization of Hatch Spacing for Improved Build Rate and High Density Preservation in Laser Powder Bed Fusion of Pure Titanium. J. Mater. Res. Technol. 2024, 33, 9853–9861. [Google Scholar] [CrossRef]
- Van Hooreweder, B.; Apers, Y.; Lietaert, K.; Kruth, J.-P. Improving the Fatigue Performance of Porous Metallic Biomaterials Produced by Selective Laser Melting. Acta Biomater. 2017, 47, 193–202. [Google Scholar] [CrossRef]
- Melle, D.; Pessard, E.; Morel, F.; Bellett, D.; Adamski, F.; Billardon, R. Effect of Chemical Etching Time on the Fatigue Behavior of Ti-6Al-4V Produced by Laser Powder Bed Fusion. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 4498–4515. [Google Scholar] [CrossRef]
- Adelmann, B.; Hellmann, R. Mechanical Properties of LPBF-Built Titanium Lattice Structures—A Comparative Study of As-Built and Hot Isostatic Pressed Structures for Medical Implants. Metals 2022, 12, 2072. [Google Scholar] [CrossRef]
- Liu, F.; Chen, M.; Liu, S.; Xiang, Z.; Huang, S.; Lim, E.G.; Zhang, S. Stress-Driven Generative Design and Numerical Assessment of Customized Additive Manufactured Lattice Structures. Mater. Des. 2024, 241, 112956. [Google Scholar] [CrossRef]
- Ríos, I.; Garrido, C.; Pincheira, G.; Tuninetti, V. Challenges of Compression Test Simulations of a Resin-Filled Auxetic Polylactic Acid Structure. In Recent Advances on the Mechanical Behaviour of Materials; Saavedra Flores, E.I., Astroza, R., Das, R., Eds.; Springer: Cham, Switzerland, 2024; pp. 57–67. [Google Scholar]
- Wu, B.; Chen, Q.; Liu, F.; Chen, M.; Lu, Y.; Jiang, D.; Yi, Y. Study on Dynamic Mechanics of Node-Enhanced Graded Lattice Structure and Application Optimization in Automobile Energy Absorbing Box. Materials 2023, 16, 6893. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, J.; Wang, W. Compression and Deformation Behaviors of Hierarchical Circular-Cell Lattice Structure with Enhanced Mechanical Properties and Energy Absorption Capacity. Aerospace 2022, 9, 786. [Google Scholar] [CrossRef]
- Top, N.; Şahin, İ.; Gökçe, H. The Mechanical Properties of Functionally Graded Lattice Structures Derived Using Computer-Aided Design for Additive Manufacturing. Appl. Sci. 2023, 13, 11667. [Google Scholar] [CrossRef]
- Park, S.J.; Lee, J.H.; Yang, J.; Moon, S.K.; Son, Y.; Park, J. Enhanced Energy Absorption of Additive-Manufactured Ti-6Al-4V Parts via Hybrid Lattice Structures. Micromachines 2023, 14, 1982. [Google Scholar] [CrossRef]
- Al Nashar, M.; Sutradhar, A. Design of Hierarchical Architected Lattices for Enhanced Energy Absorption. Materials 2021, 14, 5384. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, F.; Li, L.; Wu, J. Bio-Inspired Curved-Elliptical Lattice Structures for Enhanced Mechanical Performance and Deformation Stability. Materials 2024, 17, 4191. [Google Scholar] [CrossRef]
- He, Q.; Feng, J.; Zhou, H. A Numerical Study on the In-Plane Dynamic Crushing of Self-Similar Hierarchical Honeycombs. Mech. Mater. 2019, 138, 103151. [Google Scholar] [CrossRef]
- Zhang, W.; Yin, S.; Yu, T.X.; Xu, J. Crushing Resistance and Energy Absorption of Pomelo Peel Inspired Hierarchical Honeycomb. Int. J. Impact Eng. 2019, 125, 163–172. [Google Scholar] [CrossRef]
- Lu, Q.; Qi, D.; Li, Y.; Xiao, D.; Wu, W. Impact Energy Absorption Performances of Ordinary and Hierarchical Chiral Structures. Thin-Walled Struct. 2019, 140, 495–505. [Google Scholar] [CrossRef]
- Habib, F.N.; Iovenitti, P.; Masood, S.H.; Nikzad, M. Fabrication of Polymeric Lattice Structures for Optimum Energy Absorption Using Multi Jet Fusion Technology. Mater. Des. 2018, 155, 86–98. [Google Scholar] [CrossRef]
- Yin, H.; Huang, X.; Scarpa, F.; Wen, G.; Chen, Y.; Zhang, C. In-Plane Crashworthiness of Bio-Inspired Hierarchical Honeycombs. Compos. Struct. 2018, 192, 516–527. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, X.; Shi, Z.; Xue, J.; Han, F. Compressive and Energy Absorption Properties of Pyramidal Lattice Structures by Various Preparation Methods. Materials 2021, 14, 6484. [Google Scholar] [CrossRef]
- Sari, A.; Askar, S.; Rodriguez-Benites, C.; Rajabovich, T.Y. Machine Learning-Aided Examination of Energy Absorption and Mechanical Properties in Steel Lattice Structures. Trans. Indian Inst. Met. 2025, 78, 74. [Google Scholar] [CrossRef]
- Rahman, H.; Yarali, E.; Zolfagharian, A.; Serjouei, A.; Bodaghi, M. Energy Absorption and Mechanical Performance of Functionally Graded Soft–Hard Lattice Structures. Materials 2021, 14, 1366. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, D.; Zhao, R.; Wang, X.; Wang, L.; Zhang, L.C. High Mechanical Performance of Lattice Structures Fabricated by Additive Manufacturing. Metals 2024, 14, 1165. [Google Scholar] [CrossRef]
- Almesmari, A.; Alagha, A.N.; Naji, M.M.; Sheikh-Ahmad, J.; Jarrar, F. Recent Advancements in Design Optimization of Lattice-Structured Materials. Adv. Eng. Mater. 2023, 25, 2201780. [Google Scholar] [CrossRef]
- Zheng, M.; Ghabraie, K.; Yang, Y.; Elambasseril, J.; Xu, W.; Wang, Y. Quantitative Surface Characterisation and Stress Concentration of Additively Manufactured NiTi Lattice Struts. Int. J. Adv. Manuf. Technol. 2024, 130, 4861–4882. [Google Scholar] [CrossRef]
- McDonnell, B.; O’Hara, E.M.; Harrison, N.M. Simulation-Driven-Design of Metal Lattice Structures for a Target Stress–Strain Curve. Mater. Des. 2024, 237, 112543. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, R.; Tao, C.; Wang, Y.; Liang, X. Mechanical Performance of a Node-Reinforced Body-Centered Cubic Lattice Structure: An Equal-Strength Concept Design. Aerospace 2024, 11, 4. [Google Scholar] [CrossRef]
- Dara, A.; Mertens, A.J.; Gunji, B.; Bahubalendruni, M.V.A.R. Quasi-Static and Dynamic Response of Open Lattice Structures for Enhanced Plateau Stresses: Simulation and Experiment Validation. Mater. Today Commun. 2025, 44, 111953. [Google Scholar] [CrossRef]
- Yang, C.; Shahverdi Moghaddam, H.; Keshavanarayana, S.R.; Horner, A.L. An Analytical Approach to Characterize Uniaxial In-Plane Responses of Commercial Hexagonal Honeycomb Core under Large Deformations. Compos. Struct. 2019, 211, 100–111. [Google Scholar] [CrossRef]
- Araghi, M.; Rokhgireh, H.; Nayebi, A. Experimental and FEM Investigation of BCC Lattice Structure under Compression Test by Using Continuum Damage Mechanics with Micro-Defect Closure Effect. Mater. Des. 2023, 232, 112125. [Google Scholar] [CrossRef]
- Doodi, R.; Gunji, B.M. An Experimental and Numerical Investigation on the Performance of Novel Hybrid Bio-Inspired 3D Printed Lattice Structures for Stiffness and Energy Absorption Applications. Mech. Adv. Mater. Struct. 2024, 31, 3970–3979. [Google Scholar] [CrossRef]
- Bruggeman, K.; Klingbeil, N.; Palazotto, A. Residual Stress Generation in Additive Manufacturing of Complex Lattice Geometries. J. Mater. Eng. Perform. 2024, 33, 4088–4105. [Google Scholar] [CrossRef]
- Onyibo, E.C.; Gazioglu, A.; Ahmed, A.A.M.; Ameer, A.A.A.; Abdelrahman, M.E.B.; Oladipupo, O.A.; Sarkon, G.K.; Sahmani, S.; Safaei, B. Experimental and Numerical Investigations on Uniaxial-Stress Ductility Failure of Additive Manufactured Lattice Structures Based on Frequency Fatigue Technique. Acta Mech. 2025, 236, 37–57. [Google Scholar] [CrossRef]
- Ge, J.; Song, Y.; Chen, Z.; Zhuo, Y.; Wei, T.; Ge, C.; Cheng, Y.; Liu, M.; Jia, Q. Effect of Geometrical Parameters on the Mechanical Performance of Bamboo-Inspired Gradient Hollow-Strut Octet Lattice Structure Fabricated by Additive Manufacturing. Micromachines 2024, 15, 583. [Google Scholar] [CrossRef]
- Lee, G.; Jeong, S.G.; Kwon, J.; Ahn, S.Y.; SaGong, M.J.; Lee, K.-A.; Kim, H.S. Shear Deformation Behavior of Additively Manufactured 316L Stainless Steel Lattice Structures. Addit. Manuf. 2024, 93, 104425. [Google Scholar] [CrossRef]
- Patel, B.H.; Pandey, P.M. Design, Manufacturing, and Deformation Behavior of Novel Bio-Inspired Lattice Structures with Arc-Shaped Strut Configurations. Rapid Prototyp. J. 2024. ahead of print. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Tsongas, K.; Tzetzis, D. Finite Element Analysis of Orthopedic Hip Implant with Functionally Graded Bioinspired Lattice Structures. Biomimetics 2020, 5, 44. [Google Scholar] [CrossRef]
- Sienkiewicz, J.; Płatek, P.; Jiang, F.; Sun, X.; Rusinek, A. Investigations on the Mechanical Response of Gradient Lattice Structures Manufactured via Slm. Metals 2020, 10, 213. [Google Scholar] [CrossRef]
- Chen, L.; Che, J.; Liang, S.; Wang, Y. Multiscale Topology Optimization of Gradient Lattice Structure Based on Volume Parametric Modeling. Compos. Struct. 2024, 328, 117746. [Google Scholar] [CrossRef]
- Pan, C.; Han, Y.; Lu, J. Design and Optimization of Lattice Structures: A Review. Appl. Sci. 2020, 10, 6374. [Google Scholar] [CrossRef]
- Paudel, A.C.; Doranga, S.; Li, Y.; Khanal, M. System Identification and Dynamic Analysis of the Propulsion Shaft Systems Using Response Surface Optimization Technique. Appl. Mech. 2024, 5, 305–321. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, H.; Shi, W.; Zeng, F.; Zeng, H.; Chen, G. Vibration Tests of 3D Printed Satellite Structure Made of Lattice Sandwich Panels. AIAA J. 2018, 56, 4213–4217. [Google Scholar] [CrossRef]
- Gongora, A.E.; Friedman, C.; Newton, D.K.; Yee, T.D.; Doorenbos, Z.; Giera, B.; Duoss, E.B.; Han, T.Y.J.; Sullivan, K.; Rodriguez, J.N. Accelerating the Design of Lattice Structures Using Machine Learning. Sci. Rep. 2024, 14, 13703. [Google Scholar] [CrossRef]
- Liu, W.; Xu, G.; Fan, W.; Lyu, M.; Xia, Z. Machine-Learning-Based Characterization and Inverse Design of Metamaterials. Materials 2024, 17, 3512. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Yan, X.; Zhou, N.; Pang, B.; Peng, B.; Zeng, Z. Machine Learning Accelerated Design of Lattice Metamaterials for Customizable Energy Absorption. Thin-Walled Struct. 2025, 208, 112845. [Google Scholar] [CrossRef]
- Lee, S.; Zhang, Z.; Gu, G.X. Deep Learning Accelerated Design of Mechanically Efficient Architected Materials. ACS Appl. Mater. Interfaces 2023, 15, 22543–22552. [Google Scholar] [CrossRef]
- Garland, A.P.; White, B.C.; Jensen, S.C.; Boyce, B.L. Pragmatic Generative Optimization of Novel Structural Lattice Metamaterials with Machine Learning. Mater. Des. 2021, 203, 109632. [Google Scholar] [CrossRef]
- Challapalli, A.; Li, G. Machine Learning Assisted Design of New Lattice Core for Sandwich Structures with Superior Load Carrying Capacity. Sci. Rep. 2021, 11, 18552. [Google Scholar] [CrossRef]
- Teimouri, A.; Challapalli, A.; Konlan, J.; Li, G. Machine Learning Assisted Design and Optimization of Plate-Lattice Structures with Superior Specific Recovery Force. Giant 2024, 18, 100282. [Google Scholar] [CrossRef]
- Wu, C.; Luo, J.; Zhong, J.; Xu, Y.; Wan, B.; Huang, W.; Fang, J.; Steven, G.P.; Sun, G.; Li, Q. Topology Optimisation for Design and Additive Manufacturing of Functionally Graded Lattice Structures Using Derivative-Aware Machine Learning Algorithms. Addit. Manuf. 2023, 78, 103833. [Google Scholar] [CrossRef]
- Oñate, A.; Sanhueza, J.P.; Zegpi, D.; Tuninetti, V.; Ramirez, J.; Medina, C.; Melendrez, M.; Rojas, D. Supervised Machine Learning-Based Multi-Class Phase Prediction in High-Entropy Alloys Using Robust Databases. J. Alloys Compd. 2023, 962, 171224. [Google Scholar] [CrossRef]
- Doodi, R.; Gunji, B.M. Prediction and Experimental Validation Approach to Improve Performance of Novel Hybrid Bio-Inspired 3D Printed Lattice Structures Using Artificial Neural Networks. Sci. Rep. 2023, 13, 7763. [Google Scholar] [CrossRef]
- Wan, X.; Xiao, Z.; Tian, Y.; Chen, M.; Liu, F.; Wang, D.; Liu, Y.; Bartolo, P.J.D.S.; Yan, C.; Shi, Y.; et al. Recent Advances in 4D Printing of Advanced Materials and Structures for Functional Applications. Adv. Mater. 2024, 36, 2312263. [Google Scholar] [CrossRef]
- Teimouri, M.; Mahbod, M.; Asgari, M. Topology-Optimized Hybrid Solid-Lattice Structures for Efficient Mechanical Performance. Structures 2021, 29, 549–560. [Google Scholar] [CrossRef]
- Jared, B.H.; Aguilo, M.A.; Beghini, L.L.; Boyce, B.L.; Clark, B.W.; Cook, A.; Kaehr, B.J.; Robbins, J. Additive Manufacturing: Toward Holistic Design. Scr. Mater. 2017, 135, 141–147. [Google Scholar] [CrossRef]
- Cibrario, L.; Gastaldi, C.; Delprete, C.; Cozza, I.F. Mechanical Design of Lattice Metamaterials: A Multiscale Homogenization-Based Operational Procedure. Mater. Des. 2025, 251, 113614. [Google Scholar] [CrossRef]
- Costa, M.R.; Sohouli, A.; Suleman, A. Multi-Scale and Multi-Material Topology Optimization of Gradient Lattice Structures Using Surrogate Models. Compos. Struct. 2022, 289, 115402. [Google Scholar] [CrossRef]
- Ntintakis, I.; Stavroulakis, G.E. Infill Microstructures for Additive Manufacturing. Appl. Sci. 2022, 12, 7386. [Google Scholar] [CrossRef]
- Fu, J.; Shu, Z.; Gao, L.; Zhou, X. A Hybrid Level Set Method for the Topology Optimization of Functionally Graded Structures. Materials 2022, 15, 4483. [Google Scholar] [CrossRef]
- Vigliotti, A.; Pasini, D. Structural Optimization of Lattice Materials. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; Volume 54822, pp. 925–934. [Google Scholar]
- Lee, D.; Chen, W.; Wang, L.; Chan, Y.C.; Chen, W. Data-Driven Design for Metamaterials and Multiscale Systems: A Review. Adv. Mater. 2024, 36, 2305254. [Google Scholar] [CrossRef]
- Zargarian, A.; Esfahanian, M.; Kadkhodapour, J.; Ziaei-Rad, S.; Zamani, D. On the Fatigue Behavior of Additive Manufactured Lattice Structures. Theor. Appl. Fract. Mech. 2019, 100, 225–232. [Google Scholar] [CrossRef]
- Zhu, Y.; Deng, J.; Xiong, W.; You, T.; Zhou, W. Koch Hierarchical Honeycomb: A Fractal-Based Design for Enhanced Mechanical Performance and Energy Absorption. Materials 2023, 16, 3670. [Google Scholar] [CrossRef]
- McCracken, A.; Sadeghian, P. Corrugated Cardboard Core Sandwich Beams with Bio-Based Flax Fiber Composite Skins. J. Build. Eng. 2018, 20, 114–122. [Google Scholar] [CrossRef]
- Oliveira, P.R.; May, M.; Panzera, T.H.; Hiermaier, S. Bio-Based/Green Sandwich Structures: A Review. Thin-Walled Struct. 2022, 177, 109426. [Google Scholar] [CrossRef]
- Wang, Z.; Jing, L.; Ning, J.; Zhao, L. The Structural Response of Clamped Sandwich Beams Subjected to Impact Loading. Compos. Struct. 2011, 93, 1300–1308. [Google Scholar] [CrossRef]
- Choudhry, N.K.; Bankar, S.R.; Panda, B.; Singh, H. Experimental and Numerical Analysis of the Bending Behavior of 3D Printed Modified Auxetic Sandwich Structures. Mater. Today Proc. 2022, 56, 1356–1363. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, G.; You, Z. Large Deformation and Energy Absorption of Additively Manufactured Auxetic Materials and Structures: A Review. Compos. Part B Eng. 2020, 201, 108340. [Google Scholar] [CrossRef]
- Singh, P.; Sheikh, J.; Behera, B.K. Metal-Faced Sandwich Composite Panels: A Review. Thin-Walled Struct. 2024, 195, 111376. [Google Scholar] [CrossRef]
- Smardzewski, J.; Wojciechowski, K.W. Response of Wood-Based Sandwich Beams with Three-Dimensional Lattice Core. Compos. Struct. 2019, 216, 340–349. [Google Scholar] [CrossRef]
- Amendola, A.; Fraternali, F. Incremental Auxetic Response of Composite Lattices under Isotropic Prestress. Compos. Struct. 2018, 191, 145–153. [Google Scholar] [CrossRef]
- Yang, D.U.; Lee, S.; Huang, F.Y. Geometric Effects on Micropolar Elastic Honeycomb Structure with Negative Poisson’s Ratio Using the Finite Element Method. Finite Elem. Anal. Des. 2003, 39, 187–205. [Google Scholar] [CrossRef]
- Zhang, B.; Lian, Y.; Li, M.J.; Wang, C.; Gao, R. Mechanical Characterization of Lattice Structures Fabricated by Selective Laser Melting via an Image-Based Finite Cell Method with a Damage Model. Mater. Des. 2024, 244, 113168. [Google Scholar] [CrossRef]
- Rojas-Ulloa, C.; Tuninetti, V.; Sepúlveda, H.; Betaieb, E.; Pincheira, G.; Gilles, G.; Duchêne, L.; Habraken, A.M. Accurate Numerical Prediction of Ductile Fracture and Micromechanical Damage Evolution for Ti6Al4V Alloy. Comput. Mech. 2023, 73, 177–198. [Google Scholar] [CrossRef]
- Oñate, Á.; Torres, E.; Olave, D.; Ramírez, J.; Medina, C.; Sanhueza, J.P.; Melendrez, M.; Tuninetti, V.; Rojas, D. Exploring the Impact of Cooling Rate on Microstructural Features, Mechanical Properties, and Corrosion Resistance of a Novel Nb-Stabilized Super Duplex Stainless Steel in Shielded Metal Arc Welding. Crystals 2023, 13, 1192. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Jiang, S.; Zhong, C.; Zhao, C.; Jiao, Y.; Shen, J.; Chen, H.; Ye, M.; Zhou, J.; et al. The Design of Strut/TPMS-Based Pore Geometries in Bioceramic Scaffolds Guiding Osteogenesis and Angiogenesis in Bone Regeneration. Mater. Today Bio 2023, 20, 100667. [Google Scholar] [CrossRef]
- Albertini, F.; Dirrenberger, J.; Sollogoub, C.; Maconachie, T.; Leary, M.; Molotnikov, A. Experimental and Computational Analysis of the Mechanical Properties of Composite Auxetic Lattice Structures. Addit. Manuf. 2021, 47, 102351. [Google Scholar] [CrossRef]
- Utzeri, M.; Sasso, M.; Deshpande, V.S.; Kumar, S. Multiscale Experiments and Predictive Modeling for Failure Mitigation in Additive Manufacturing of Lattices. Adv. Mater. Technol. 2024, 9, 2400457. [Google Scholar] [CrossRef]
- Bai, J.; Li, M.; Shen, J. Prediction of Mechanical Properties of Lattice Structures: An Application of Artificial Neural Networks Algorithms. Materials 2024, 17, 4222. [Google Scholar] [CrossRef]
- Boursier Niutta, C.; Ciardiello, R.; Berto, F.; Paolino, D.S.; Tridello, A. On the Influence of Additive Manufacturing Defects on the Energy Absorption Capability of a Lattice Structure. Procedia Struct. Integr. 2022, 42, 1449–1457. [Google Scholar] [CrossRef]
- Gallo, C.; Duchêne, L.; Quy Duc Pham, T.; Jardin, R.; Tuninetti, V.; Habraken, A.-M. Impact of Boundary Parameters Accuracy on Modeling of Directed Energy Deposition Thermal Field. Metals 2024, 14, 173. [Google Scholar] [CrossRef]
- Jardin, R.T.; Tuninetti, V.; Tchuindjang, J.T.; Hashemi, N.; Carrus, R.; Mertens, A.; Duchêne, L.; Tran, H.S.; Habraken, A.M. Sensitivity Analysis in the Modelling of a High Speed Steel Thin-Wall Produced by Directed Energy Deposition. Metals 2020, 10, 1554. [Google Scholar] [CrossRef]
- Niinomi, M. Recent Research and Development in Titanium Alloys for Biomedical Applications and Healthcare Goods. Sci. Technol. Adv. Mater. 2003, 4, 445–454. [Google Scholar] [CrossRef]
- Parga Montemayor, R.D.; Reyes Osorio, L.A.; Lopez-Pavon, L.; Garcia-Salazar, O.; Moreno-Cortez, I.E.; Kim, H.Y. Modeling of Superelastic Auxetic Structures of Ti–Zr Base Alloy. Finite Elem. Anal. Des. 2022, 201, 103705. [Google Scholar] [CrossRef]
- Valle, R.; Pincheira, G.; Tuninetti, V. Design of an Auxetic Cellular Structure with Different Elastic Properties in Its Three Orthogonal Directions. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1341–1350. [Google Scholar] [CrossRef]
- He, L.; Wang, P.; Yang, J.; Fan, K.; Zhang, H.; Zhang, L.; Jiang, M.; Chen, X.; Chen, Z.; Chen, M.; et al. Smart Lattice Structures with Self-Sensing Functionalities via Hybrid Additive Manufacturing Technology. Micromachines 2024, 15, 2. [Google Scholar] [CrossRef]
- Vasconcelos, A.R.C.; de Matos, R.A.; Silveira, M.V.; Mesquita, E. Applications of Smart and Self-Sensing Materials for Structural Health Monitoring in Civil Engineering: A Systematic Review. Buildings 2024, 14, 2345. [Google Scholar] [CrossRef]
- Piacquadio, S.; Soika, J.; Schirp, M.; Schröder, K.U.; Filippeschi, S. On the Effective Thermophysical Properties of Phase Change Materials Embedded in Metallic Lattice Structures with Generic Topological Parameters. Thermo 2023, 3, 566–592. [Google Scholar] [CrossRef]
- Ahmed Qureshi, Z.; Addin Burhan Al-Omari, S.; Elnajjar, E.; Al-Ketan, O.; Abu Al-Rub, R. Architected Lattices Embedded with Phase Change Materials for Thermal Management of High-Power Electronics: A Numerical Study. Appl. Therm. Eng. 2023, 219, 119420. [Google Scholar] [CrossRef]
- Shen, S. Numerical Simulation and ANN Prediction of Phase Change Material Embedded within 3D Printing Lattice Structures. Case Stud. Therm. Eng. 2024, 53, 103818. [Google Scholar] [CrossRef]
- Qureshi, Z.A.; Al Omari, S.A.B.; Elnajjar, E.; Mahmoud, F.; Al-Ketan, O.; Al-Rub, R.A. Thermal Characterization of 3D-Printed Lattices Based on Triply Periodic Minimal Surfaces Embedded with Organic Phase Change Material. Case Stud. Therm. Eng. 2021, 27, 101315. [Google Scholar] [CrossRef]






| Manufacturing Method | Description | Advantages | Disadvantages |
|---|---|---|---|
| Conventional/subtractive | Material removal processes such as machining, drilling, and etching are used to create lattice structures from a solid block [3,72]. | Suitable for specific lattice types, high precision achievable, and established processes. | Limited complexity, material waste, challenging for intricate internal features, and scalability issues. |
| Additive manufacturing | Layer-by-layer deposition of material to build 3D structures. Includes techniques such as SLM, EBM, FDM, and SLA [46]. | Complex geometries achievable, minimal material waste, design flexibility, and rapid prototyping. | Limited material selection compared to conventional methods, potential for manufacturing defects (porosity, anisotropy), and post-processing may be required. |
| Hybrid additive manufacturing | Combines additive manufacturing with conventional techniques. For example, a lattice structure may be 3D printed and then machined for enhanced surface finish or precision. | Combines advantages of both methods, enables complex designs with enhanced functionalities, improved surface finish and precision. | More complex process, requires integration of different manufacturing systems, and higher cost compared to individual methods. |
| Alternative methods | Additive manufacturing-assisted investment casting: a fused filament fabricated pattern is infiltrated with plaster to create a mold [73]. | Intricate geometries, design flexibility, wider material selection for patterns, reduced lead times and tooling costs, and improved accuracy and surface finish. | Potential issues include porosity and structural heterogeneity, size limits based on casting capabilities, and combined AM/casting costs. |
| Direct foaming: Gas bubbles are introduced into a molten metal (or other material) to create a foamed structure. This can be achieved through various methods, including gas injection or the addition of blowing agents that decompose and release gas [74]. | Complex shapes and open-cell structures, relatively low cost compared to some other lattice fabrication methods, and can be applied to a variety of materials. | Difficult pore control (size, distribution, heterogeneity), limited architectural control (vs. 3D printing), viscosity hindering bubble rise/creating defects, and potential casting defects (porosity). | |
| Wire-woven methods: metallic wires are woven into a lattice structure [75]. | Complex geometries, good pore control, and potentially high-strength/stiffness (depending on material and weave). | Lower production efficiency (especially for complex 3D shapes), limited scalability, and difficulties with complex 3D architectures and material integration. | |
| Interlocking assembly: fibers or elements are interlocked to form a lattice [32]. | Can be relatively simple and low-cost, depending on the materials and interlocking mechanism used. Suitable for large-scale structures. | Fine structures are unavailable; limited to simpler geometries. | |
| Powder metallurgy: metallic powder is mixed with binders, compacted, then sintered at high temperatures [76]. | Complex shape creation, good porosity control, material flexibility, and reduced waste through near-net-shape manufacturing. | Expensive for large production runs; limited in size due to equipment constraints; some materials are difficult to process; and post-processing may be required for tolerances and surface finish. |
| Study | Focus Area | Key Findings | Lattice Shape | Relative Density (ρ/ρs)* | Relative Strength (σ/σs)* | Corrected Relative Energy Absorption (E/Es)* | Relative Stiffness (E/Es)* |
|---|---|---|---|---|---|---|---|
| [96] | Deformation modes in lattice structures | Identified quasi-static, transition, and dynamic deformation modes | Hierarchical honeycomb | 0.15 | 0.058 | 0.027 | 0.023 |
| [97] | Hierarchical honeycomb for improved SEA | SEA and equivalent stress higher than traditional honeycomb | Pomelo peel-inspired honeycomb | 0.20 | 0.089 | 0.032 | 0.040 |
| [98] | Hierarchical chiral structures’ energy absorption | Anti-tetrachiral structure superior to hexachiral | Hierarchical chiral structure | 0.18 | 0.076 | 0.030 | 0.032 |
| [99] | Polymeric lattice structures for energy absorption | Crushing response and energy absorption characteristics analyzed | Polymeric lattice | 0.22 | 0.103 | 0.034 | 0.048 |
| [100] | Bio-inspired hierarchical honeycombs | Crashworthiness enhanced via hierarchical structure | Triangular hierarchical honeycomb | 0.17 | 0.070 | 0.029 | 0.029 |
| [101] | Compressive properties of pyramidal lattice | Preparation method affected stress fluctuations | Pyramidal lattice | 0.19 | 0.083 | 0.031 | 0.036 |
| [102] | ML predictions of SEA and MCF in lattice structures | SEA and MCF successfully predicted using ML | Polycrystalline-like lattice | 0.21 | 0.096 | 0.033 | 0.044 |
| [103] | Functionally graded lattice structures’ energy absorption | Elastic–plastic modeling and stiffness evaluation | Functionally graded soft-hard lattice | 0.16 | 0.064 | 0.028 | 0.026 |
| [104] | High-performance AM lattice structures | AM enhanced mechanical properties of lattice structures | Octet-truss lattice | 0.23 | 0.110 | 0.035 | 0.053 |
| [106] | Surface and stress analysis of NiTi lattice struts | Strut diameters and inclination angles influenced stress concentrations | NiTi lattice struts | 0.14 | 0.052 | 0.026 | 0.020 |
| [107] | Simulation-driven design of metal lattice structures | Simulation-driven unit cell optimization improved performance | Metal lattice with unit cell optimization | 0.20 | 0.089 | 0.032 | 0.040 |
| [108] | Equal-strength BCC lattice mechanical performance | Failure location shifted from nodes to strut center, improving performance | ES-BCC | 0.18 | 0.076 | 0.030 | 0.032 |
| [115] | Gradient hollow-strut octet lattice properties | Geometrical parameters optimized via FEA | Gradient hollow-strut octet lattice | 0.19 | 0.083 | 0.031 | 0.036 |
| [113] | Residual stress in AM lattice geometries | Lattice geometry significantly affects residual stress distribution | Plate and cube-shaped lattice | 0.15 | 0.058 | 0.027 | 0.023 |
| [114] | Ductility failure analysis in AM lattice structures | AM lattices showed good dynamic behavior and high frequency resonance | Octet lattice structure | 0.22 | 0.103 | 0.034 | 0.048 |
| [116] | Shear behavior of 316L AM lattice structures | Stiffness under shear loading did not follow Maxwell’s equations | BCC lattice under shear loading | 0.16 | 0.064 | 0.028 | 0.026 |
| [95] | Curved-elliptical lattice structures for stability | Curved-elliptical structures exhibited strong mechanical performance | Curved-elliptical lattice | 0.21 | 0.096 | 0.033 | 0.044 |
| [117] | Arc-shaped strut lattice deformation analysis | TPU arc-strut lattices optimized for energy absorption | Arc-shaped strut lattice | 0.19 | 0.083 | 0.031 | 0.036 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuninetti, V.; Narayan, S.; Ríos, I.; Menacer, B.; Valle, R.; Al-lehaibi, M.; Kaisan, M.U.; Samuel, J.; Oñate, A.; Pincheira, G.; et al. Biomimetic Lattice Structures Design and Manufacturing for High Stress, Deformation, and Energy Absorption Performance. Biomimetics 2025, 10, 458. https://doi.org/10.3390/biomimetics10070458
Tuninetti V, Narayan S, Ríos I, Menacer B, Valle R, Al-lehaibi M, Kaisan MU, Samuel J, Oñate A, Pincheira G, et al. Biomimetic Lattice Structures Design and Manufacturing for High Stress, Deformation, and Energy Absorption Performance. Biomimetics. 2025; 10(7):458. https://doi.org/10.3390/biomimetics10070458
Chicago/Turabian StyleTuninetti, Víctor, Sunny Narayan, Ignacio Ríos, Brahim Menacer, Rodrigo Valle, Moaz Al-lehaibi, Muhammad Usman Kaisan, Joseph Samuel, Angelo Oñate, Gonzalo Pincheira, and et al. 2025. "Biomimetic Lattice Structures Design and Manufacturing for High Stress, Deformation, and Energy Absorption Performance" Biomimetics 10, no. 7: 458. https://doi.org/10.3390/biomimetics10070458
APA StyleTuninetti, V., Narayan, S., Ríos, I., Menacer, B., Valle, R., Al-lehaibi, M., Kaisan, M. U., Samuel, J., Oñate, A., Pincheira, G., Mertens, A., Duchêne, L., & Garrido, C. (2025). Biomimetic Lattice Structures Design and Manufacturing for High Stress, Deformation, and Energy Absorption Performance. Biomimetics, 10(7), 458. https://doi.org/10.3390/biomimetics10070458







