Microstructure, Critical Behavior and Magnetocaloric Properties of Melt-Spun Ni_51.82Mn_32.37In_15.81

Abstract

Heusler alloy with an atomic composition of Ni_51.82Mn_32.37In_15.81 was prepared by melt spinning from arc-melted ingots. X-ray diffraction, scanning electron microscopy and magnetic measurements were used to study the structural, microstructural and magnetic properties. The crystal structure consists of a mixture of $B2$ austenite (~50%) and $14M$ martensite (~50%). The alloy undergoes a second order magnetic transition at a Curie temperature of $T_c^A=194.2$K. The hysteresis loop reveals the occurrence of exchange bias phenomenon at room temperature. The critical exponents $\beta$, $\gamma$ and $\delta$ were estimated using modified Arrott plots, Kouvel–Fisher curves and critical isothermal analysis. The respective values are $\beta =0.500\pm 0.015$, $\gamma =1.282\pm 0.055$ and $\delta =3.003\pm 0.002$. The critical behaviour in ribbons is governed by the mean field model with a dominated long-range order of ferromagnetic interactions. The maximum entropy change, $∆S_M^{max}$, for an applied magnetic field of 5 T reaches an absolute value of 0.92 J/kg·K. The experimental results of entropy changes are in good agreement with those calculated using Landau theory.

1. Introduction

Since structural and magnetic transformations have been reported in Ni-Mn-Z (Z = Ga, Sn, In) alloys [1], many studies on austenitic and martensitic states have been investigated [2,3,4,5,6,7,8,9]. Upon cooling, these alloys undergo a first order martensitic transition from a high temperature cubic austenite phase ($\mathrm{Ast}$), displaying long ferromagnetic ($\mathrm{FM}$) order, to a low temperature modulated or non-modulated martensite phase ($\mathrm{Mst}$) with complex magnetic behavior. The magnetization is smaller in the $\mathrm{Mst}$ phase than in the $\mathrm{Ast}$. Additionally, the magnetic coupling is $\mathrm{FM}$ in the high temperature phase and is short range antiferromagnetic ($\mathrm{AFM}$) for Mn-rich compounds [10,11]. Moreover, the magnetic properties are dominated by Mn-Mn coupling in stoichiometric compositions of Ni₂MnZ. However, $\mathrm{FM}-\mathrm{AFM}$ interactions were found in off-stoichiometric alloys, in which Mn atoms occupying Z sites coupled antiferromagnetically to Mn atoms in their own regular sites.

Due to their good magneto-functional performances, these magnetic materials have attracted much attention owing to their potential application in magnetic refrigeration, spintronics and actuation [12,13]. These technological applications are related to the strong correlation between the magnetism and the structural transition such as the magnetocaloric effect ($\mathrm{MCE}$), magnetostructural resistance, shape memory, exchange bias behaviour ($\mathrm{EB}$), etc. [7,14,15,16,17,18,19,20,21]. Thus, any change in the chemical composition, sample preparation, type of crystal structure homogeneity, heat treatment, application of an external magnetic field or stress can affect the phase transitions. $\mathrm{MCE}$ is strongly dependent on the type of magnetic transition. For example, most Heusler alloys have a second-order magnetic transition ($\mathrm{SOMT}$), from $\mathrm{FM}$ to paramagnetic state ($\mathrm{PM}$) around the Curie temperature ($T_c$), resulting in a negative magnetic entropy change known as direct $\mathrm{MCE}$, and a first-order magnetic transition resulting in a positive magnetic entropy change, known as inverse magnetocaloric effect ($\mathrm{IMCE}$) near the martensitic transition [22,23].

Many studies have been conducted on polycrystalline Ni–Mn–In ingots prepared by arc melting and succeeding heat treatment at high temperature for homogenization. The crystal structure and physical properties can be affected considerably by a small change in composition and/or sample preparation as the magnetic interactions and their strength can be modified by the substitution of Mn atoms for Ni and In atoms. For example, a mixture of austenite and martensite phases was observed in bulk Ni₅₀Mn_50-xIn_x (x = 14.8, 15.05 and 15.2), while a single austenite phase (space group $Fm\overline{3}m$) was observed for x = 14.5, and an orthorhombic martensite (space group $Pmm2$) for x = 15 [24]. In addition, the crystal structure of the arc-melted Ni₅₀Mn₃₅In₁₅ consisted of a mixture of austenite and orthorhombic martensite having different magnetic transition temperatures of about $T_c^A$ = 310 K and $T_c^M$ = 200 K, respectively. For the as-quenched Ni_51.1Mn_31.2In_17.7, the disordered $B2$ structure, which is observed at room temperature, transformed into an ordered $L{2}_1$ structure after a short annealing time [25]. It is important to mention that the arc melting process may cause different problems that negatively affect the functional properties of the alloys [26]. Hence, the melt-spinning process can be considered as an alternative way of produce ribbons in a metastable state with homogeneous chemical composition avoiding annealing at high temperature [27]. Furthermore, it is possible to obtain a nearly single-phase [8,28] and highly textured microstructure owing to the high cooling rate (~10⁶ K/s), which leads to a change in the atomic order. Consequently, this fact is of great interest to investigate. Additionally, the ribbon’s shape could be used mainly as sensors and actuators, and in magnetocaloric devices.

The current work was carried out to investigate the effect of the melt-spinning process on the structure, morphology and magnetic properties of melt-spun Ni₅₀Mn₃₅In₁₅ ribbons. Structure, morphology and magnetic properties were studied using X-ray diffraction, scanning electron microscopy (SEM) coupled with energy-dispersive X-ray spectroscopy (EDS), and magnetic measurements. In order to distinguish the nature of the magnetic interaction around the magnetic transition, the critical behavior around the Curie temperature was investigated through isothermal magnetization data, $M\left(H\right)$, using several techniques [29] of the conventional critical exponents for the mean field model ($\mathrm{MF}$) $\beta =0.5$ and $\gamma =1$, 3D Heisenberg model $\beta =0.365$ and $\gamma =1.336$, 3D Ising model $\beta =0.325$ and $\gamma =1.241$, and for tricritical mean field model $\beta =0.25$ and $\gamma =1$. Thus, the Curie temperature and the critical exponents were estimated.

2. Materials and Methods

Polycrystalline ribbons with nominal composition of Ni_51.82Mn_32.37In_15.81 were prepared by melt-spinning at high wheel speed of 40 m/s from arc-melted pure elements. An ingot of about 5 g was prepared from high purity (>99.98%) Ni, Mn and In elements (Sigma Aldrich, Saint Louis, MO, USA) by arc melting in a MAM-1 Buhler (Edmund Bühler GmbH, Bodelshausen, Germany) compact arc melter, in a water-cooled copper crucible, under argon atmosphere. The ingot was melted several times to ensure good homogeneity. The ribbons were obtained in a MSP10 melt-spinning system (Edmund Bühler GmbH, Bodelshausen, Germany), under argon atmosphere (400 mbar), onto a polished surface of copper wheel rotating at a linear speed of 40 m/s, with a nozzle wheel distance of 3 mm, an orifice diameter of 0.5 mm and an injection pressure of 500 mbar.

Magnetization measurements versus temperature were carried out using BS1 magnetometer developed at Néel Institute. The hysteresis loop, at room temperature, was measured with a Lake Shore 7400 VSM vibrating sample magnetometer (Lake Shore Cryotonics, Westerwille, OH, USA). Ribbons’ morphology was investigated using a scanning electron microscope (SEM, TESCAN, Brno, Czech Republic) operating at 30 kV and equipped with the energy dispersive X-ray spectrometer (EDS, TESCAN, Brno, Czech Republic). The alloy structure was followed by X-ray diffraction (XRD) on a D8 Advance diffractometer (Bruker, Billerica, MA, USA) in a (θ−2θ) Bragg Brentano geometry using Cu−Kα radiation (λ_Cu = 0.154056 nm). The XRD analysis was carried out using the Maud program [30], which is based on the Rietveld method.

3. Results and Discussion

3.1. Structure and Morphology

Figure 1 displays secondary electron SEM micrographs showing the fracture cross section microstructure, wheel surface microstructure and free surface microstructure of Ni_51.82Mn_32.37In_15.81 as-spun ribbons. One observes that the grains are highly ordered columnar-like microstructures with their longer axis being perpendicular to the ribbon sides (Figure 1c). The wheel surface shows typical elongated thin plates corresponding to martensite variants (Figure 1a), and the free surface displays granular microstructure with different grain sizes and shapes (Figure 1b). EDS element-mapping over one defined region indicates that the three elements (Ni, Mn, and In) are homogeneously distributed (Figure 1d). From EDS analysis over many points an average elemental composition Ni_51.82Mn_32.37In_15.81 is obtained. Therefore, the electron-to-atom ratio ($e/a$) calculated from the outer shell of each element is 7.922.

Figure 1. Typical SEM micrographs of wheel surface (a), free surface (b), fracture cross-section (c), and (d) EDS element-mapping of Ni_51.82Mn_32.37In_15.81 ribbons.

Rietveld refinement of the XRD pattern of the melt-spun ribbons (Figure 2) reveals the coexistence of a seven-layered monoclinic $14M$ structure, $P2/m$ space group, with lattice parameters $a=\left(4.3381\pm 0.0002\right)\mathrm{\AA }$, $b=\left(5.5642\pm 0.0002\right)\mathrm{\AA }$ and $c=\left(29.235\pm 0.0005\right)\mathrm{\AA }$ and $\beta =92.92°$, and a cubic $B2$ austenite structure, space group$Pm\overline{3}m$, and a lattice parameter of $a=\left(2.9684\pm 0.0002\right)\mathrm{\AA }$. The relative deviations of the lattice parameters shown by: $∆a=\frac{\left(a-a_0\right)}{a_0},∆b=\frac{\left(b-b_0\right)}{b_0},and∆c=\frac{\left(c-c_0\right)}{c_0}$ where a₀, b₀ and c₀ are the lattice parameters of a perfect crystal, reaching as much as Δa = 0.88%, Δb = −3.6% and Δc = 0.81% for the 14M structure, and $∆a=-1.6\%$ for the B2 austenite. In addition, the weight fractions of both the 14M martensite and B2 austenite structures are equal to 50%, and their crystallite sizes are of about 65 nm and 96 nm, respectively. The nanocrystalline state of the obtained ribbons can be attributed to the atomic disorder, which is induced by the rapid solidification of the melt-spun ribbons.

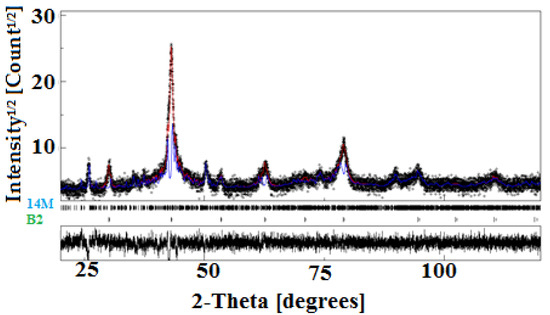
Figure 2. Rietveld refinement of the XRD pattern of melt-spun ribbons.

Krenke et al. reported that bulk Ni_0.5Mn_0.5-xIn_x ($x=0.05-0.25$) alloys displayed an austenite structure with x ranging from $0.16$ to $0.25$, and a martensite structure for $0.05\le x\le 0.155$ [2]. Çakir et al. reported that bulk Ni₅₀Mn_50-xIn_x exhibited modulated $7M$ and austenite structures for x = 14.4 [31]. Sánchez Llamazares et al. found that Ni_51.1Mn_31.2In_17.7 ribbons presented a $B2$ structure [25]. The obtained result differs from those reported above, since the elaboration technics affect the alloy composition and physical properties. Furthermore, the martensitic transformation temperature can be twined by electron-to-atom ratio, Mn nearest neighbor interatomic distances, atomic order degree and crystallite size [32,33]. From differential calorimetry scans (not shown here), no structural transformation was detected in these ribbons since the modulated martensite has a lower symmetry than the austenite, and the $B2$ structure is considered as disordered compared to the $L{2}_1$ structure. Such structural complexity can affect other physical properties, especially the magnetic results.

3.2. Magnetic Properties

Figure 3a displays magnetization evolution versus temperature $M\left(T\right)$, in the temperature range 5–330 K, upon cooling under an applied magnetic field of 500 Oe. The melt-spun ribbons exhibit a paramagnetic to ferromagnetic transition at the Curie temperature of austenite, Tc (As) = 194.2 K, which is defined as the minimum peak position of dM/dT curve (Figure 3b).

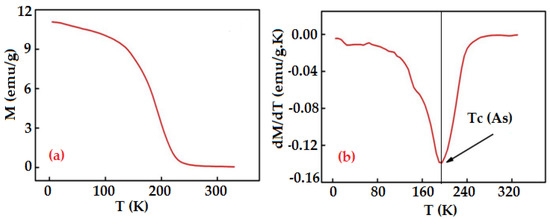
Figure 3. Temperature dependence of the magnetization measured at 500 Oe (a), and the derivative dM/dT curve showing the magnetic transition temperature (Tc (As)) (b).

The isothermal magnetization curves as a function of the applied magnetic field, $M\left(H\right)$, are shown in Figure 4. All the curves do not saturate even at 5 T and show a typical $\mathrm{FM}$ character when $T<194.2K$and $PM$ behavior when $T>194.2K$. According to Banerjee’s criteria [34], the second order $\mathrm{FM}-\mathrm{PM}$ phase transition (SOMT) is characterised by a positive slope in Arrott curves, $M^2$ versus ${\mu }_{0}H/M$. Thus, the studied ribbons undergo SOMT phase transition since they show a positive slope (Figure 5). In the low-field region, $M^2=f\left({\mu }_{0}H/M\right)$ curves have two parts in the opposite directions indicating the $\mathrm{FM}-\mathrm{PM}$ separation. However, in the vicinity of $T_c$, a linear $M^2=f\left({\mu }_{0}H/M\right)$ line passing through the coordinate origin is observed. Hence, the $T_c$ value deduced from the Arrott plots is very close to that obtained from $M\left(T\right)$. This feature supports evidence of the long-rang $\mathrm{FM}$-order character of the sample.

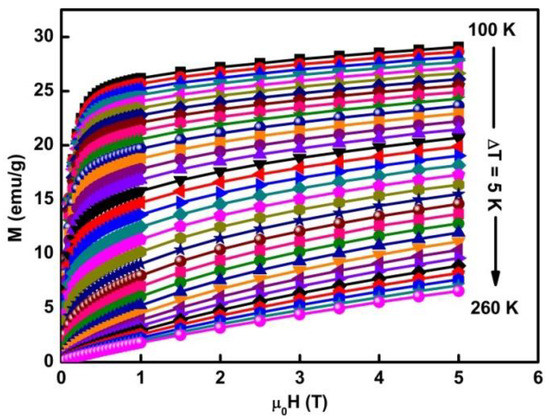
Figure 4. Isothermal magnetization around $T_c^A$ at different temperatures from 100 to 260 K (increments of 5 K).

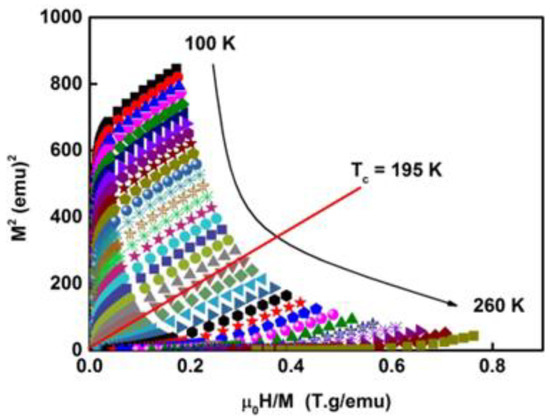
Figure 5. Standard Arrott plot isotherms $M^{2}vs.{\mu }_{0}H/M$. From 100 to 260 K (increments of 5 K).

Figure 6 displays the enlargement of the low magnetic field region of the hysteresis loop measured, at room temperature, under an applied magnetic field of 2 T. The inset shows the hysteresis cycle. This later exhibits a nearly straight line typical of a paramagnetic-type comportment due to the increase of atomic disorder, which is a characteristic of the melt-spinning process. Furthermore, the hysteresis loop shows a positive horizontal shift and a negative vertical shift. The horizontal H-axis shift can be related to the development of a magnetically non-homogeneous AF/FM matrix where the interfacial pinning of FM spins by the AF component gives rise to an exchange bias (EB) behavior at room temperature. The exchange bias phenomenon is associated with the exchange anisotropy created at the interface between AFM and FM regions and can be ascribed to the formation of an FM unidirectional anisotropy (texture) at the interface between different magnetic phases during the formation of the ribbons. This result is different from those reported earlier for a similar composition where the EB was observed at lower temperature of martensitic state in bulk Ni₅₀Mn₃₅In₁₅ alloy [31]. The obtained result confirms the fact that the processing conditions, crystal structure and microstructure affect considerably the magnetic properties leading to the observation of EB in the Ni_51.82Mn_32.37In_15.81 ribbons at room temperature. The values of EB and the coercivity field are calculated using $H_E=-\left(H_1+H_2\right)⁄2$ and $H_c=\left|H_1-H_2\right|⁄2$, respectively, where $H_1$ and $H_2$ are the left and the right field values at zero magnetization. Hence, the coercivity and EB values are 48.54 Oe and 100 Oe, respectively.

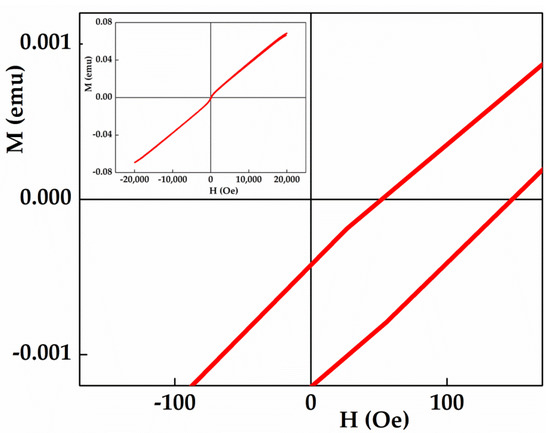
Figure 6. Enlargement of the low magnetic field region of the hysteresis loop measured at room temperature. The inset shows the corresponding hysteresis cycle.

The vertical shift observed in the magnetization curve may be attributed to the strong AFM interactions in the martensite structure and/or to the short-range AFM magnetic coupling in the Mn-rich areas. Indeed, the rapid solidification leads to structural heterogeneities owing to the temperature difference between the free and wheel surfaces of the ribbons. It is obvious that a small change in the composition or in the elaboration conditions affects the physical properties of the Heusler alloys as shown in Table 1 [2,35,36].

Table 1. Comparison of the obtained physical properties of Ni_51.82Mn_32.37In_15.81 ribbons with earlier reports.

Sample	Method	e/a	Phase	a, b, c (Å)	Tc (K)	±ΔS (J/kg.K)	Hc (Oe)	Ref.
Ni51.82Mn32.37In15.81	Melt spinning	7.922	cubic B2 14 M	a = 2.968 a = 4.327 b = 5.567 c = 29.035	194.2	0.92 (5 T)	48.54 (2 T)	This work
Ni50Mn35In15	Arc melting and annealing at 1073K for 2h	7.902	10 M	a = 4.391 b = 5.882 c = 21.184				[2]
Ni51Mn33.4In15.6	Arc melting and annealing at 1173K for 48 h		cubic L21	a = 6.008	309.5	15 (5 T)		[35]
Ni52Mn32.5In15.5	Arc melting and annealing at 1173K for 48 h		cubic L21 orthorhombic	a = 6.010 a = 17.961 b = 10.766 c = 4.608	182			[31]

3.3. Critical Behavior

The critical exponents $\beta$, $\gamma$ and $\delta$ characterize the samples that underwent SOMT. The exponent β, which is linked to the evolution of the spontaneous magnetization with respect to the temperature (Ms ∝${\left(T-T_C\right)}^{\beta }$), describes the growth of the ordered moment below Tc; γ is related to the temperature dependence of the initial magnetic susceptibility (${\chi }_0^{-1}\propto {\left(T-T_C\right)}^{\gamma }$. It defines the divergence of χ₀ at T_c, and δ is associated with the critical isothermal magnetization. It describes the curvature of the isothermal magnetization curves $M\left(H\right)$ at $T_C$. For further confirmation of the long-range nature of $\mathrm{FM}$ interactions that characterize the sample, the modified Arrott plots ($\mathrm{MAPs}$) [37] are presented for the mean field model, 3D-Heisenberg model, 3D-Ising model and tricritical mean field model in Figure 7.

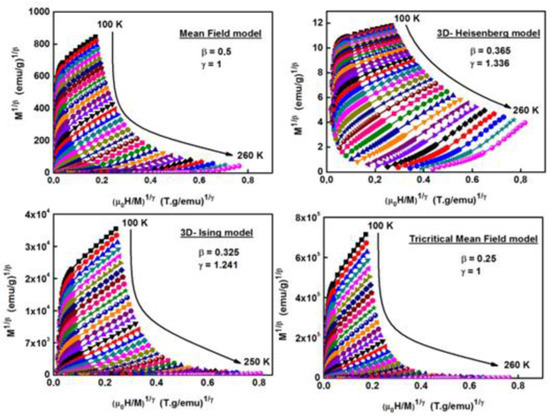
Figure 7. Modified Arrott plots: isotherms of $M^{1/\beta }vs.{\left(H/M\right)}^{1/\gamma }$ with the mean field model, 3D-Heisenberg model, 3D-Ising model and tricritical mean field model. From 100 to 260 K (increments of 5 K).

These models are used to plot the calculated relative slope $RS$ using the linear fit from the high field region of each curve. The relative slope, which is given by $RS=S\left(T\right)/S\left(T_{Cr}\right)$ (Figure 8), is identified as the ratio between the slope at each temperature, S(T), and the slope at the critical temperature, S(T_Cr). Generally, for a given conventional model, $RS$ is much closer to the unit. Accordingly, the critical behaviour of the ribbons can be well-described by the mean field, $\mathrm{MF}$, with a dominated long-range order of ferromagnetic interactions. Similar critical behaviour was reported for the Ni₄₃Mn₄₆Sn₈In₃ Heusler alloy prepared by arc melting and annealing at 1323 K for 48 h. The small deviations in critical exponents β and γ from those expected for the mean field model were related to the coexistence of FM and AFM interactions in the alloy [38]. It is obvious that preparation conditions and, consequently, the alloy’s microstructure influences their critical behavior considerably.

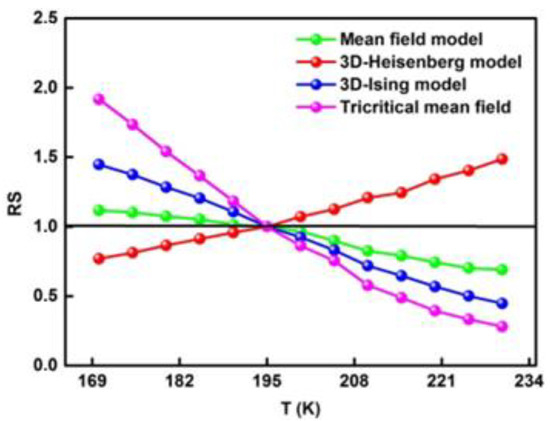
Figure 8. Relative slope (RS) as function of temperature defined as $RS=S\left(T\right)/S\left(T_{cr}\right)$ using different models.

The first estimation of $\beta$ and $\gamma$ values as well as $T_c$ are provided through the non-linear fit of the spontaneous magnetization $M_s\left(T,0\right)$ and the inverse of the initial susceptibility ${\chi }_0^{-1}\left(T,0\right)$ curves using Equations (1) and (2), respectively:

$$M_S\left(T\right)=M_0{\left(-\epsilon \right)}^{\beta };\epsilon <0,T<T_c$$

(1)

$${\chi }_0^{-1}\left(T\right)=\left(\frac{h_0}{M_0}\right){\epsilon }^{\gamma };\epsilon >0,T>T_c$$

(2)

$$M=D{H}^{1/\delta };\epsilon =0,T=T_c$$

(3)

where $\epsilon =\left(T-T_c\right)/T_c$ is the reduced temperature, $M_0$, $h_0$ and $D$ are the critical amplitudes. The values of $\beta$, $\gamma$ and $T_c$ are shown in Figure 9, in which $\beta =0.500\pm 0.015$, $\gamma =1.282\pm 0.055$ and $T_c=\left(198.456\pm 1.077\right)K$ are close to the $MF$ model and the estimated $T_c$ is closer to the obtained value from the $M\left(T\right)$ curve.

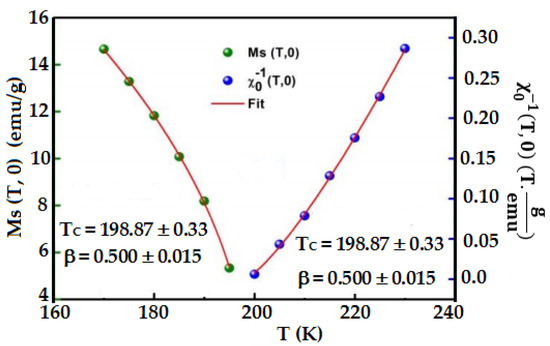
Figure 9. Temperature dependence of spontaneous magnetization $M_S\left(T,0\right)$ and the inverse of initial susceptibility ${\chi }_0^{-1}\left(T,0\right)$.

Straight-lined Kouvel–Fisher plots [39,40] ($K-F$) of $M_S\left(T\right){\left(d{M}_S\left(T\right)/dT\right)}^{-1}$ and ${\chi }_0^{-1}\left(T\right){\left(d{\chi }_0^{-1}\left(T\right)/dT\right)}^{-1}vs.T$, with slopes $1/\beta$ and $1/\gamma$, show the most precise values of the critical exponents and $T_c$. This was later determined by an extrapolation to the T-axis (Figure 10). One observes that the accurate values are close to those obtained from the $MAPs$. The value of the third exponent $\delta$ can be determined directly from the critical isotherm ($CI$) curve $M=f\left({\mu }_{0}H,T_c\right)$ (Figure 11). The inset in Figure 11 displays the log–log plot, where the linear fit using Equation (3) leads to a value of $\delta =3.003\pm 0.002$. The accuracy of the gained exponent values $\beta$ and $\gamma$ are interrelated to the third exponent $\delta$ via Widom scaling relation ($\delta =1+\left(\gamma /\beta \right)$) [41]. The calculated $\delta =3.353\pm 0.027$ is slightly large than that determined experimentally from the critical isotherm $\delta =3.003\pm 0.002$. The difference may be attributed to the coexistence of 14M and B2 structures leading to the coexistence of FM and AFM interactions in the prepared Heusler alloy. Consequently, the temperature dependence of the initial magnetic susceptibility can be affected. Critical exponents often show a deviation from the values of theoretical models. This appears as if a magnetic system is governed by various competing coupling and/or disorders [42,43].

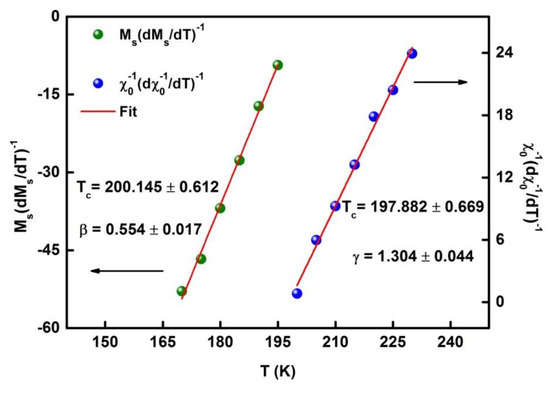
Figure 10. Kouvel–Fisher plots for the spontaneous magnetization and the inverse of initial susceptibility.

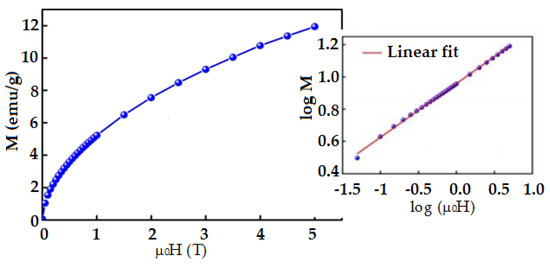
Figure 11. Critical isotherms of $M\left({\mu }_{0}H,T_c^A\right)$. The inset shows the logarithmic scale.

The reliability of the obtained critical exponents and $T_c$ values can be confirmed by the scaling hypothesis [44], which presents two distinct branches below and above $T_c$; confirming that the estimated critical exponents and $T_c$ are reasonably accurate (Figure 12). As summarized in Table 2, the estimated values match well the mean field model [29,30,45].

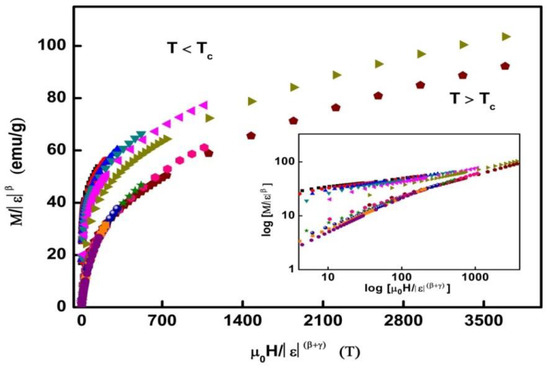
Figure 12. Scaling plots (following the procedure described in ref. [28] where the points correspond to regular analytical functions) indicating universal curves above and below $T_c^A$. The inset shows the same plot in log–log scale.

Table 2. Comparison of estimated critical exponents of Ni_51.82Mn_32.37In_15.81 ribbons with other reports and the various theoretical models.

Material	Technique	$\mathit{\beta }$	$\mathit{\gamma }$	$\mathit{\delta }$	Ref.
Ni51.82Mn32.37In15.81	MAPs	0.500 ± 0.015	1.282 ± 0.055	----	This work
	K-F	0.554 ± 0.017	1.304 ± 0.044	3.353 ± 0.027
	CI	----	----	3.003 ± 0.002
Ni50Mn35In14Si1	MAPs	0.510	0.987	2.935	[44]
	CI	----	----	2.950
	MAPs	0.550	0.944	2.716
	CI	----	----	2.670
Ni50Mn35Sn15	MAPs	0.50 ± 0.03	0.92 ± 0.03	----	[30]
	K-F	0.45 ± 0.01	0.88 ± 0.03	2.92
	CI			3.02 ± 0.02
Mean field model		0.5	1.0	3.0	[29]
3D Heisenberg model		0.365	1.336	4.80	[29]
3D Ising model		0.325	1.241	4.82	[29]
Tricritical mean field		0.25	1.0	5.0	[29]

3.4. Magnetocaloric Effect

The MCE can be evaluated by calculating the magnetic entropy change ($∆S_M$). This is calculated by using the thermodynamic Maxwell relation as follows:

$$∆S_M\left(T,∆H\right)=S_M(T,H_2)-S_M\left(T,H_1\right)={{\displaystyle \int }}_{H1}^{H2}{\left(\frac{\partial M}{\partial T}\right)}_{T}dH$$

(4)

where $H_1$ and $H_2$ are the applied fields and $∆H=H_2-H_1$, $H_1\le H_2$.

Numerically, $∆S_M$ can be deduced by the integration of the magnetic isotherm plots at small discrete magnetic field and temperature intervals, and can be approximated as follows:

$$∆S_M\left(T,M\right)={{\displaystyle \sum }}_i\frac{M_{i+1}\left(T_{i+1},H_{i+1}\right)-M_i\left(T_i,H_i\right)}{T_{i+1}-T_i}∆H$$

(5)

where $M_i$ and $M_{i+1}$ are the experimental data of the magnetization at temperatures $T_i$ and $T_{i+1}$, respectively, under a magnetic field $H_i$. Figure 13 displays the $-∆S_M$ versus $T$ plots for different applied magnetic fields ranging from 1 to 5 T. One observes that the magnetic entropy’s peak ($-∆S_M^{max}$) rises continuously with increasing the field from 0.11 to 0.92 J/kg.K for 1 T and 5 T, respectively (inset in Figure 13). This value is lower than that obtained for the melt-spun Ni₅₀Mn₃₅Sn₁₅ ribbons [28] and bulk Ni₅₁Mn_33.4In_15.6 alloy [35]. The much lower magnetic entropy change compared to that of the polycrystalline Ni₅₁Mn_33.4In_15.6 sample prepared by arc melting, followed by annealing at 1173 K for 48 h and quenching in ice water [35], can be associated with the modifications in the magnetic order of the sample, which is related to the preparation conditions and crystal structure. This later consists of a single cubic cell (space group Fm3m, and a = 6.008(2) Å) for the bulk Ni₅₁Mn_33.4In_15.6, and a mixture of 14 M martensite (50%) and cubic B2 austenite structure (50%), (space group $Pm\overline{3}m$, and a = 2.9684Å) for the ribbons.

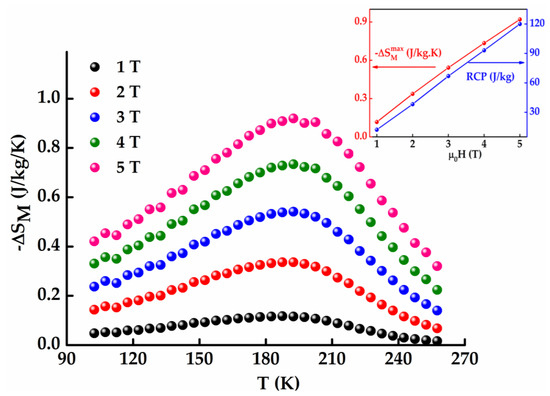
Figure 13. $-∆S_M\left(T\right)$ curves for Ni_51.82Mn_32.37In_15.81 ribbons under applied fields of 1−5 T. The inset shows magnetic field dependence of $-∆S_M^{max}$.

The theoretical model proposed by Amaral et al. takes into account the contribution of the magneto-elastic electron’s interactions [46]. The model is based on Landau theory in the vicinity of $T_c$ [47]. In this model, free energy ($G$) is developed as a function of magnetization ($M$) as follows:

$$G\left(M,T\right)=G_0+\frac{a\left(T\right)}{2}{M}^2+\frac{b\left(T\right)}{4}{M}^4+\frac{c\left(T\right)}{6}{M}^6+\cdots \cdots -HM$$

(6)

Considering the equilibrium condition, $\partial G/\partial M=0$, the total magnetization around $T_c$ can be described as follows:

$$H=a\left(T\right)M+b\left(T\right)M^3+c\left(T\right)M^5$$

(7)

By using Equation (7), the polynomial fit of the experimental $M\left(H\right)$ data can be used to determine Landau’s coefficient $a\left(T\right)$, $b\left(T\right)$ and $c\left(T\right)$. One notes that the $a\left(T\right)$ value is always positive and presents a minimum around $T_c$, and the $b\left(T\right)$ value can be negative, zero or positive. Additionally, $b\left(T_c\right)=0$ confirms that the transition belongs to the second order character. The $c\left(T\right)$ value is always negative. Accordingly, the calculated values are in good agreement with the Landau model.

The magnetic entropy change can be modelled theoretically by using the derivative of the free energy with respect to the temperature according to the subsequent equation:

$$-∆S_M\left(T,H\right)={\left(\frac{dG}{dT}\right)}_{{\mu }_{0}H}=\frac{a^{\prime }\left(T\right)}{2}{M}^2+\frac{b^{\prime }\left(T\right)}{4}{M}^4+\frac{c^{\prime }\left(T\right)}{6}{M}^6$$

(8)

where $a’\left(T\right)$, $b’\left(T\right)$ and $c’\left(T\right)$ are the derivative of Landau’s coefficient with respect to temperature. The plots of the numeric calculation of $-∆S_M$ are in good concordance with experimental results as illustrated in Figure 14. One observes that in the $\mathrm{PM}$ region ($T>T_c$), ${\left(-∆S_M\right)}_{exp}$ and ${\left(-∆S_M\right)}_{theo}$ are well superposed, suggesting that the calculated Landau’s coefficients are accurate. The small deviations around the maximum of the magnetic entropy curves can be related to the numerical derivatives that are introduced in the calculation, which may present a source of errors close to the transition temperature. In addition, these deviations may be attributed to the existence of inhomogeneous magnetism that could be associated with the coexistence of FM and AFM interactions in this Heusler alloy.

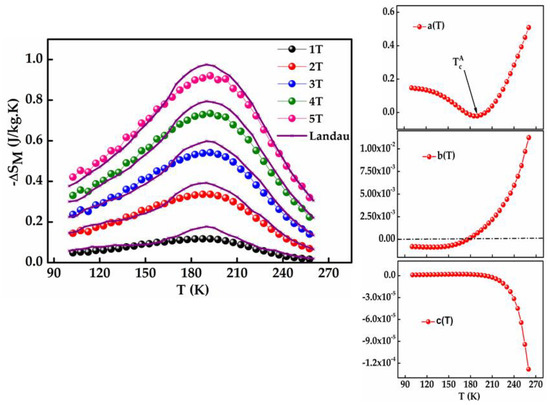
Figure 14. Superposition of experimental and calculated $-∆S_M\left(T\right)$ curves for Ni_51.82Mn_32.37In_15.81 ribbons under applied fields of 1−5 T (left), and the corresponding Landau coefficient a(T), b(T) and c(T) (right).

4. Conclusions

Heusler Ni_51.82Mn_32.37In_15.81 ribbons were prepared by melt-spinning from arc-melted ingots. The crystal structure consisted of a mixture of B2 austenite (~50%) and 14M martensite (~50%). The SOMT occurred at a Curie temperature of $T_C^A=194.2K$. The occurrence of the exchange bias, at room temperature, can be related to the experimental conditions. The exchange bias can be ascribed to the coupling of AFM and FM at the interfaces. According to the critical exponent values (β = 0.500 ± 0.015, γ = 1.282 ± 0.055 and δ = 3.003 ± 0.002), the critical behavior is governed by the mean field model with a dominated long-range order of ferromagnetic interactions. The maximum entropy change reached an absolute value of 0.92 J/kg·K for an applied magnetic field of 5 T. The experimental results from the magnetic entropy changes are in good agreement with those calculated using the Landau theory.