Trend Analysis of Different Climate Parameters and Watering Requirements for Hazelnut in Central Italy Related to Climate Change
Abstract
1. Introduction
2. Materials and Methods
2.1. Climate Description and Climatic Data Collection from the Umbria Region
2.2. Estimation of Chilling Accumulation
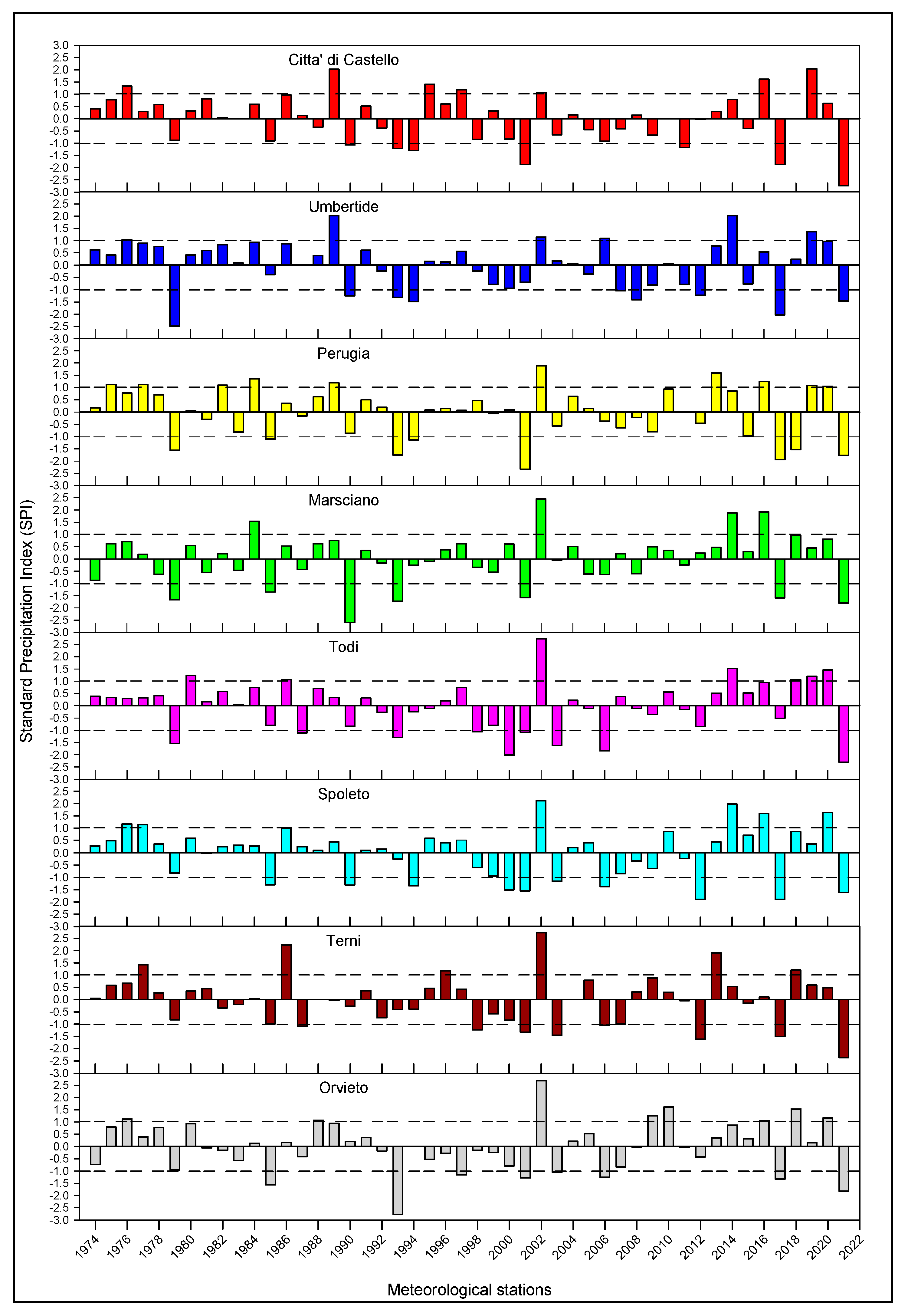
2.3. Standard Precipitation Index (SPI)
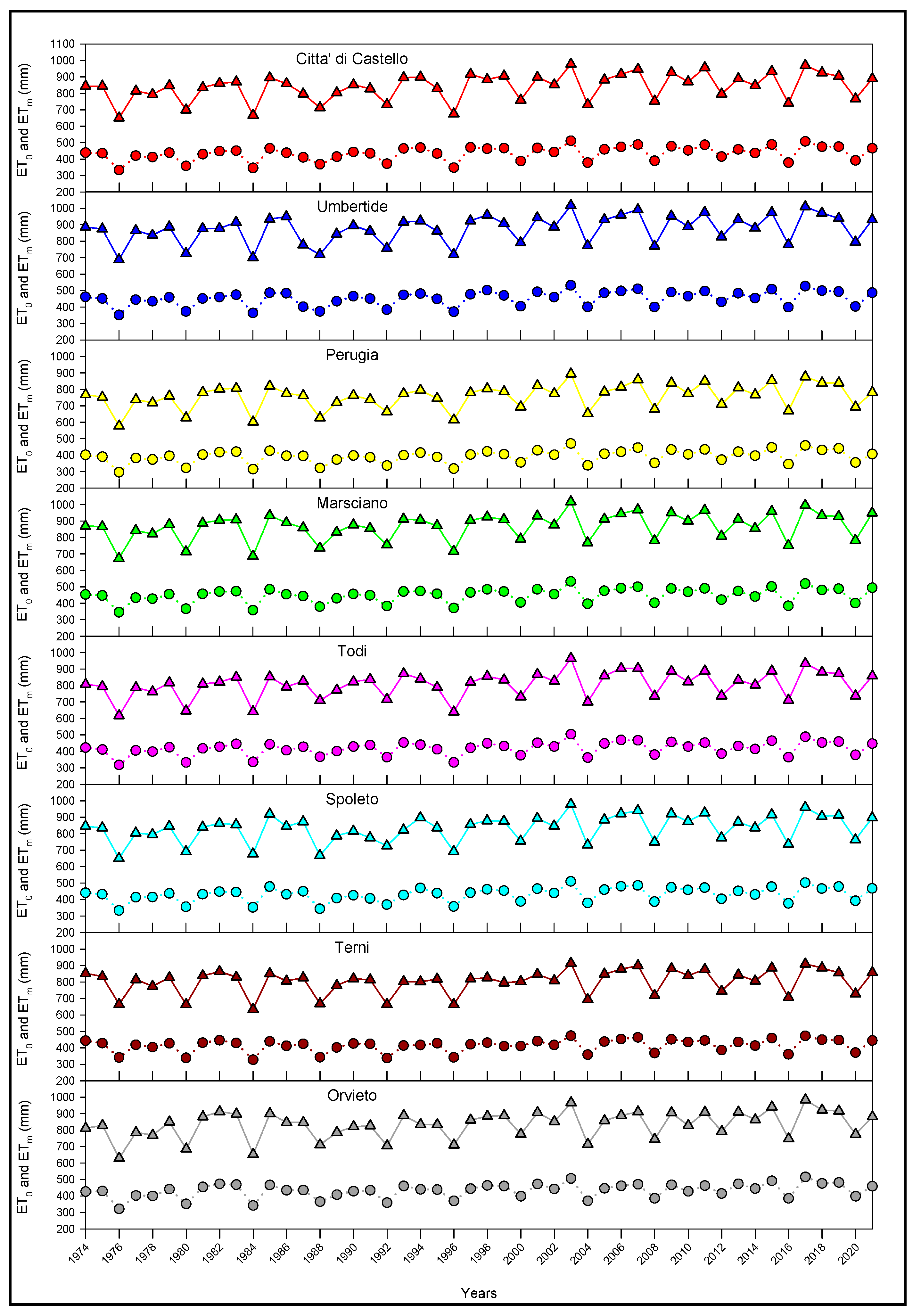
2.4. Estimation of Water Requirement Using the Soil Water Balance
2.5. Statistical Analysis of Trends
3. Results
3.1. Analysis of the Precipitation and Temperature on the Umbria Region
3.2. Estimation of Chilling Accumulation (CU)
3.3. Estimation of 4-Month SPI
3.4. Estimation of Reference Evapotranspiration (ET0), Crop Evapotranspiration (ETm), and Water Balance
3.5. Statistical Analysis of the Trends
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Freitas, T.R.; Santos, J.A.; Silva, A.P.; Fraga, H. Influence of climate change on chestnut trees: A review. Plants 2021, 10, 1463. [Google Scholar] [CrossRef]
- Pathak, T.B.; Maskey, M.L.; Dahlberg, J.A.; Kearns, F.; Bali, K.M.; Zaccaria, D. Climate change trends and impacts on California agriculture: A detailed review. Agronomy 2018, 8, 25. [Google Scholar] [CrossRef]
- Pantelidis, G.; Mavromatis, T.; Drogoudi, P. Consecutive wet days may impede fruit quality of peach and nectarine and cause fruit drop. Sci. Hortic. 2021, 282, 110011. [Google Scholar] [CrossRef]
- Valdes-Abellan, J.; Pardo, M.A.; Tenza-Abril, A.J. Observed precipitation trend changes in the western Mediterranean region. Int. J. Climatol. 2017, 37, 1285–1296. [Google Scholar] [CrossRef]
- Cramer, W.; Guiot, J.; Fader, M.; Garrabou, J.; Gattuso, J.-P.; Iglesias, A.; Lange, M.A.; Lionello, P.; Llasat, M.C.; Paz, S.; et al. Climate change and interconnected risks to sustainable development in the Mediterranean. Nat. Clim. Chang. 2018, 8, 972–980. [Google Scholar] [CrossRef]
- An, N.; Turp, M.T.; Türkeş, M.; Kurnaz, M.L. Mid-term impact of climate change on hazelnut yield. Agriculture 2020, 10, 159. [Google Scholar] [CrossRef]
- Rodríguez, A.; Pérez-López, D.; Centeno, A.; Ruiz-Ramos, M. Viability of temperate fruit tree varieties in Spain under climate change according to chilling accumulation. Agric. Syst. 2021, 186, 102961. [Google Scholar] [CrossRef]
- Di Lena, B.; Curci, G.; Vergni, L.; Farinelli, D. Climatic Suitability of Different Areas in Abruzzo, Central Italy, for the Cultivation of Hazelnut. Horticulturae 2022, 8, 580. [Google Scholar] [CrossRef]
- Luciani, E.; Palliotti, A.; Frioni, T.; Tombesi, S.; Villa, F.; Zadra, C.; Farinelli, D. Kaolin treatments on Tonda Giffoni hazelnut (Corylus avellana L.) for the control of heat stress damages. Sci. Hortic. 2020, 263, 109097. [Google Scholar] [CrossRef]
- Tercan, E.; Dengiz, O.; Özkan, B.; Dereli, M.A.; Öztekin, Y.B. Geographic information system–assisted site quality assessment for hazelnut cultivation using multi-criteria decision analysis in the Black Sea region, Turkey. Environ. Sci. Pollut. Res. 2022, 29, 35908–35933. [Google Scholar] [CrossRef]
- FAOSTAT Crops and Livestock Products. 2021. Available online: https://www.fao.org/faostat/en/#data (accessed on 10 February 2023).
- Vinci, A.; Brigante, R.; Traini, C.; Farinelli, D. Geometrical Characterization of Hazelnut Trees in an Intensive Orchard by an Unmanned Aerial Vehicle (UAV) for Precision Agriculture Applications. Remote. Sens. 2023, 15, 541. [Google Scholar] [CrossRef]
- Silvestri, C.; Bacchetta, L.; Bellincontro, A.; Cristofori, V. Advances in cultivar choice, hazelnut orchard management, and nut storage to enhance product quality and safety: An overview. J. Sci. Food Agric. 2021, 101, 27–43. [Google Scholar] [CrossRef] [PubMed]
- Piano Corilicolo Nazionale. 2022. Available online: https://www.politicheagricole.it/flex/cm/pages/ServeBLOB.php/L/IT/IDPagina/3282 (accessed on 10 March 2023).
- Bregaglio, S.; Orlando, F.; Forni, E.; De Gregorio, T.; Falzoi, S.; Boni, C.; Pisetta, M.; Confalonieri, R. Development and evaluation of new modelling solutions to simulate hazelnut (Corylus avellana L.) growth and development. Ecol. Model. 2016, 329, 86–99. [Google Scholar] [CrossRef]
- Portarena, S.; Gavrichkova, O.; Brugnoli, E.; Battistelli, A.; Proietti, S.; Moscatello, S.; Famiani, F.; Tombesi, S.; Zadra, C.; Farinelli, D. Carbon allocation strategies and water uptake in young grafted and own-rooted hazelnut (Corylus avellana L.) cultivars. Tree Physiol. 2022, 42, 939–957. [Google Scholar] [CrossRef] [PubMed]
- Cincera, I.; Frioni, T.; Ughini, V.; Poni, S.; Farinelli, D.; Tombesi, S. Intra-specific variability of stomatal sensitivity to vapour pressure deficit in Corylus avellana L.: A candidate factor influencing different adaptability to different climates? J. Plant Physiol. 2019, 232, 241–247. [Google Scholar] [CrossRef]
- Streit, M.; Gehlenborg, N. Points of view: Bar charts and box plots. Nat. Methods 2014, 11, 117. [Google Scholar] [CrossRef]
- Luciani, E.; Palliotti, A.; Tombesi, S.; Gardi, T.; Micheli, M.; Berrios, J.G.; Farinelli, D. Mitigation of multiple summer stresses on hazelnut (Corylus avellana L.): Effects of the new arbuscular mycorrhiza Glomus iranicum tenuihypharum sp. nova. Sci. Hortic. 2019, 257, 108659. [Google Scholar] [CrossRef]
- Jha, P.K.; Materia, S.; Zizzi, G.; Costa-Saura, J.M.; Trabucco, A.; Evans, J.; Bregaglio, S. Climate change impacts on phenology and yield of hazelnut in Australia. Agric. Syst. 2021, 186, 102982. [Google Scholar] [CrossRef]
- Branquinho, S.; João, R.; Teixeira, J.L. Climate change adaptation measures in the irrigation of a super-intensive olive orchard in the south of Portugal. Agronomy 2021, 11, 1658. [Google Scholar] [CrossRef]
- Ucar, Y.; Kocięcka, J.; Liberacki, D.; Rolbiecki, R. Analysis of Crop Water Requirements for Apple Using Dependable Precipitation. Atmosphere 2023, 14, 99. [Google Scholar] [CrossRef]
- Vergni, L.; Todisco, F. Spatio-temporal variability of precipitation, temperature and agricultural drought indices in Central Italy. Agric. For. Meteorol. 2011, 151, 301–313. [Google Scholar] [CrossRef]
- Khavari, M.; Fatahi, R.; Zamani, Z. Salicylic acid and kaolin effects on pomological, physiological, and phytochemical characters of hazelnut (Corylus avellana) at warm summer condition. Sci. Rep. 2021, 11, 4568. [Google Scholar] [CrossRef] [PubMed]
- Cabo, S.; Aires, A.; Carvalho, R.; Vilela, A.; Pascual-Seva, N.; Silva, A.P.; Gonçalves, B. Kaolin, Ascophyllum nodosum and salicylic acid mitigate effects of summer stress improving hazelnut quality. J. Sci. Food Agric. 2021, 101, 459–475. [Google Scholar] [CrossRef]
- Fratianni, S.; Acquaotta, F. The Climate of Italy. In Landscapes and Landforms of Italy. World Geomorphological Landscapes; Soldati, M., Marchetti, M., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Curci, G.; Guijarro, J.A.; Di Antonio, L.; Di Bacco, M.; Di Lena, B.; Scorzini, A.R. Building a local climate reference dataset:Application to the Abruzzo region (Central Italy), 1930–2019. Int J Climatol. 2021, 41, 4414–4436. [Google Scholar] [CrossRef]
- SigmaPlot, version 13; Systat Software, Inc.: San Jose, CA, USA, 2016.
- Farinelli, D.; Portarena, S.; Da Silva, D.F.; Traini, C.; Da Silva, G.M.; Da Silva, E.C.; da Veiga, J.F.; Pollegioni, P.; Villa, F. Variability of Fruit Quality among 103 Acerola (Malpighia emarginata DC) Phenotypes from the Subtropical Region of Brazil. Agriculture 2021, 11, 1078. [Google Scholar] [CrossRef]
- Farinelli, D.; Boco, M.; Tombesi, A. Influence of canopy density on fruit growth and flower formation. Acta Hortic. 2005, 686, 247–252. [Google Scholar] [CrossRef]
- Vergni, L.; Vinci, A.; Todisco, F. Effectiveness of the new standardized deficit distance index and other meteorological indices in the assessment of agricultural drought impacts in central Italy. J. Hydr. 2021, 603, 126986. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; p. 300. Available online: https://www.fao.org/3/X0490E/x0490e00.htm#Contents (accessed on 10 January 2023).
- Gucci, R. Irrigazione. In Collana Divulgativa; dell’Accademia Nazionale dell’olivo e dell’olio: Spoleto, Italy, 2012; Volume IX, ISSN 2281-4930. [Google Scholar]
- Vinci, A.; Traini, C.; Farinelli, D.; Brigante, R. Assessment of the geometrical characteristics of hazelnut intensive orchard by an Unmanned Aerial Vehicle (UAV). In Proceedings of the 2022 IEEE Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Perugia, Italy, 3–5 November 2022; pp. 218–222. [Google Scholar] [CrossRef]
- Vinci, A.; Traini, C.; Portarena, S.; Farinelli, D. Assessment of the Midseason Crop Coefficient for the Evaluation of the Water Demand of Young, Grafted Hazelnut Trees in High-Density Orchards. Water 2023, 15, 1683. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Todisco, F.; Vergni, L. Climatic changes in Central Italy and their potential effects on corn water consumption. Agric. For. Meteorol. 2008, 148, 1–11. [Google Scholar] [CrossRef]
- Valentini, N.; Moraglio, S.T.; Rolle, L.; Tavella, L.; Botta, R. Nut and kernel growth and shell hardening in eighteen hazelnut cultivars (Corylus avellana L.). Hortic. Sci. 2015, 42, 149–158. [Google Scholar] [CrossRef]
- Tombesi, A.; Rosati, A. Hazelnut response to water levels in relation to productive cycle. Acta Hortic. 1997, 445, 269–278. [Google Scholar] [CrossRef]
- Mannocchi, F.; Vinci, A. Risparmio Idrico e Pianificazione dell’uso Della Risorsa a Scopo Irriguo, 1st ed.; Nuova Bios: Castrolibero, Italy, 2009. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods; Griffin & Co: London, UK, 1975; ISBN 0-85264-199-0. [Google Scholar]
- Ahmadi, H.; Baaghideh, M. Assessment of anomalies and effects of climate change on reference evapotranspiration and water requirement in pistachio cultivation areas in Iran. Arab. J. Geosci. 2020, 13, 332. [Google Scholar] [CrossRef]
- Watson-Hernández, F.; Serrano-Núñez, V.; Gómez-Calderón, N.; Pereira da Silva, R. Quantification and Evaluation of Water Requirements of Oil Palm Cultivation for Different Climate Change Scenarios in the Central Pacific of Costa Rica Using APSIM. Agronomy 2022, 13, 19. [Google Scholar] [CrossRef]
- Mehlenbacher, S.A. Chilling requirements of hazelnut cultivars. Sci. Hortic. 1991, 47, 271–282. [Google Scholar] [CrossRef]
- Mehlenbacher, S.A. Hazelnuts (Corylus). Acta Hortic. 1991, 290, 791–838. [Google Scholar] [CrossRef]
- Črepinšek, Z.; Štampar, F.; Kajfež-Bogataj, L.; Solar, A. The response of Corylus avellana L. phenology to rising temperature in north-eastern Slovenia. Int. J. Biometeorol. 2012, 56, 681–694. [Google Scholar] [CrossRef]
- Kireva, R.; Mihov, M. Reduction of losses from drought by optimizing the use of water resources for irrigation of agricultural crops. Mech. Agric. Conserv. Resour. 2019, 65, 190–192. [Google Scholar]
- Stachowski, P.; Jagosz, B.; Rolbiecki, S.; Rolbiecki, R. Predictive capacity of precipitation data to estimate the water needs of fruit plants in water deficit areas. Atmosphere 2021, 12, 550. [Google Scholar] [CrossRef]
- Kahlown, M.A.; Ashraf, M. Effect of shallow groundwater table on crop water requirements and crop yields. Agric. Water Manag. 2005, 76, 24–35. [Google Scholar] [CrossRef]
- Farinelli, D.; Luciani, E.; Villa, F.; Manzo, A.; Tombesi, S. First selection of non-suckering rootstocks for hazelnut cultivars. Acta Hortic. 2022, 1346, 699–708. [Google Scholar] [CrossRef]
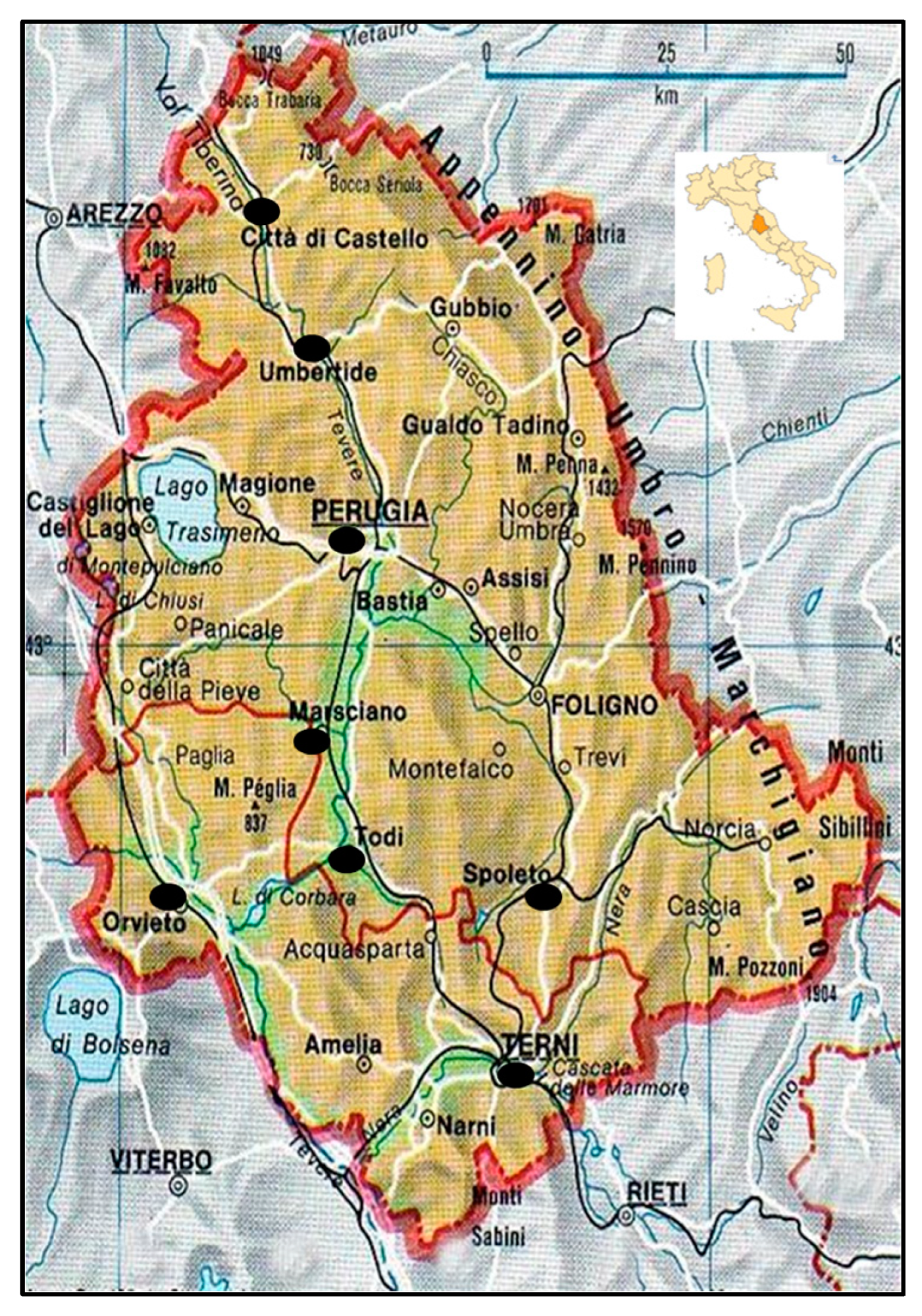
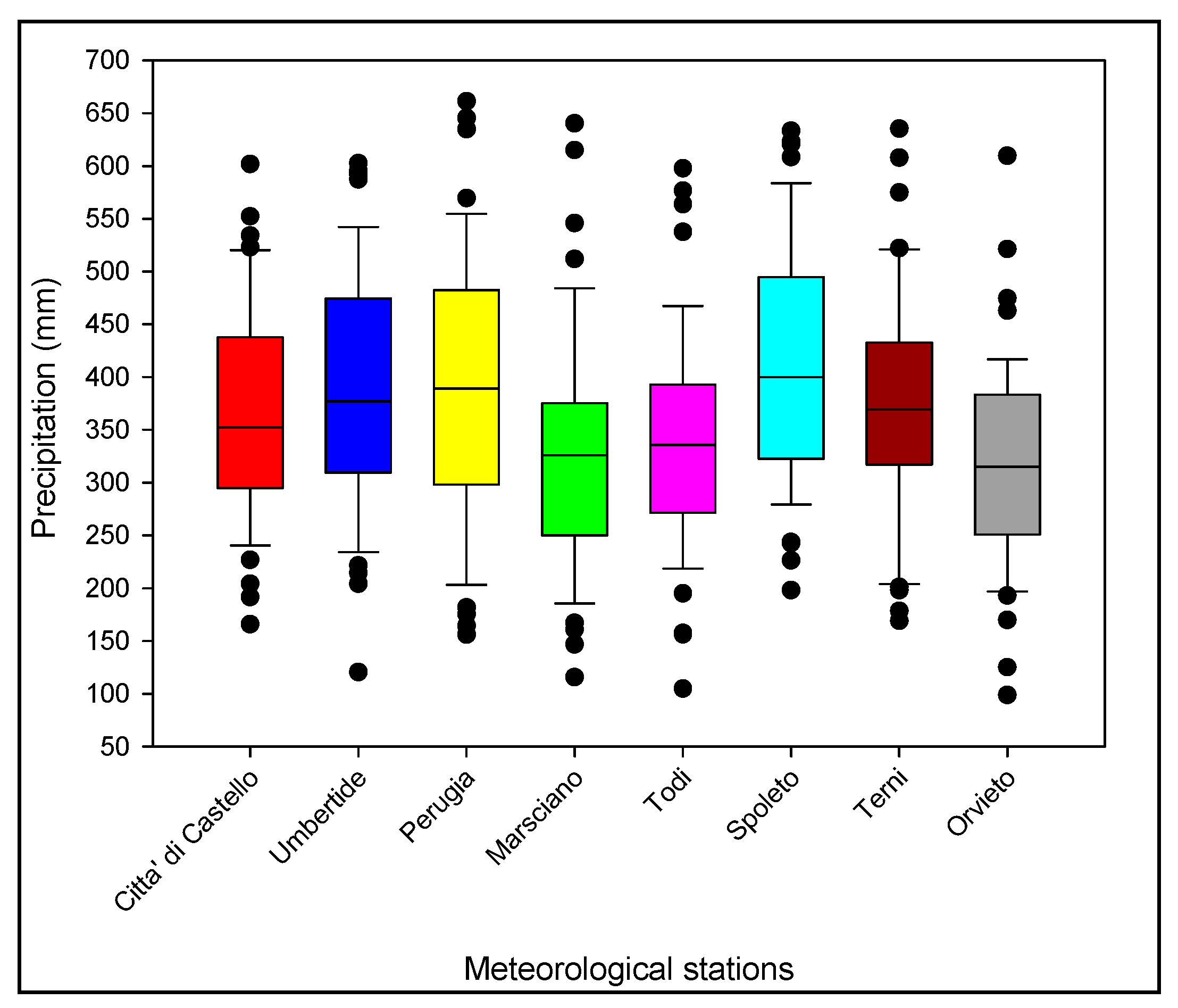
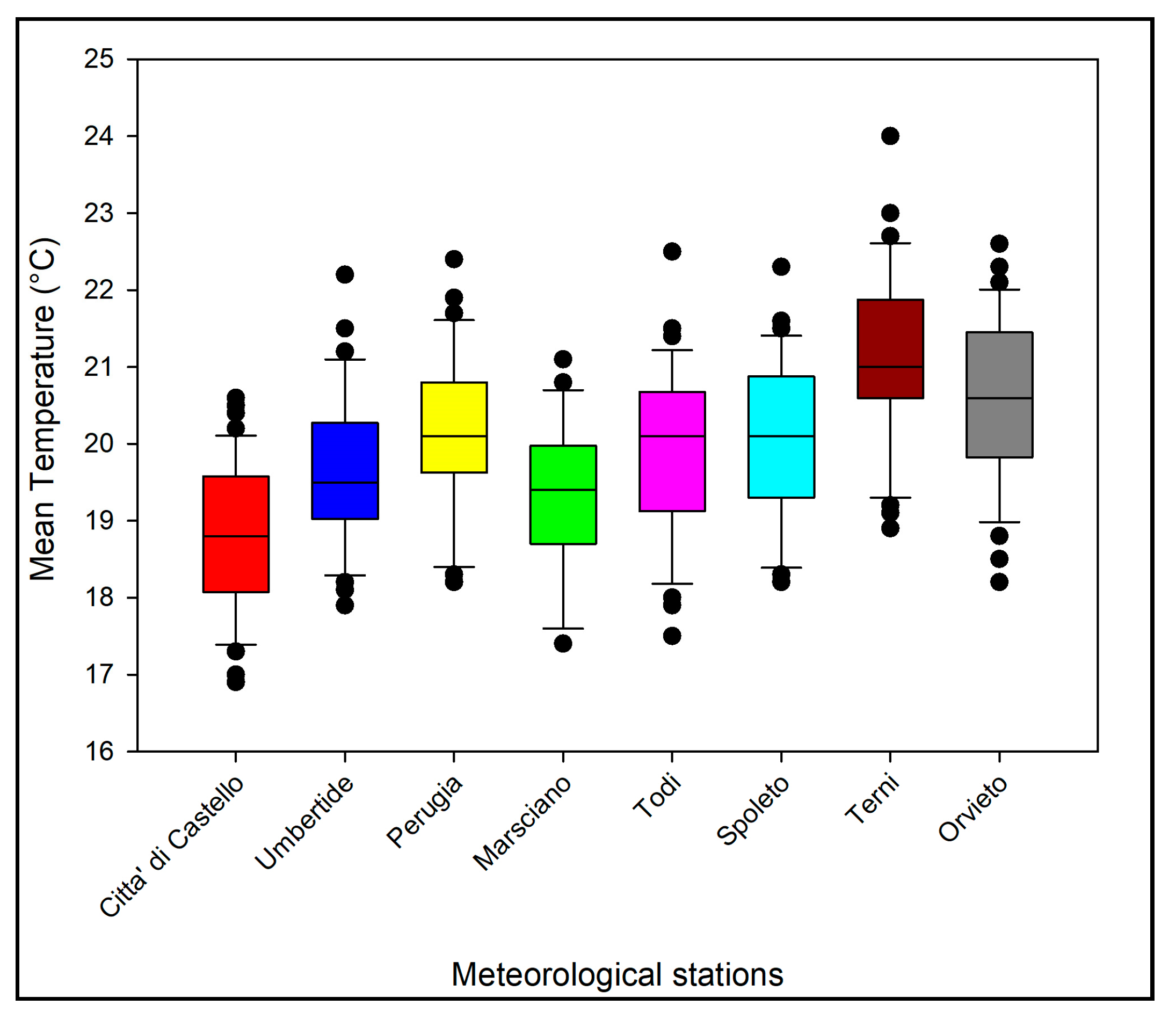
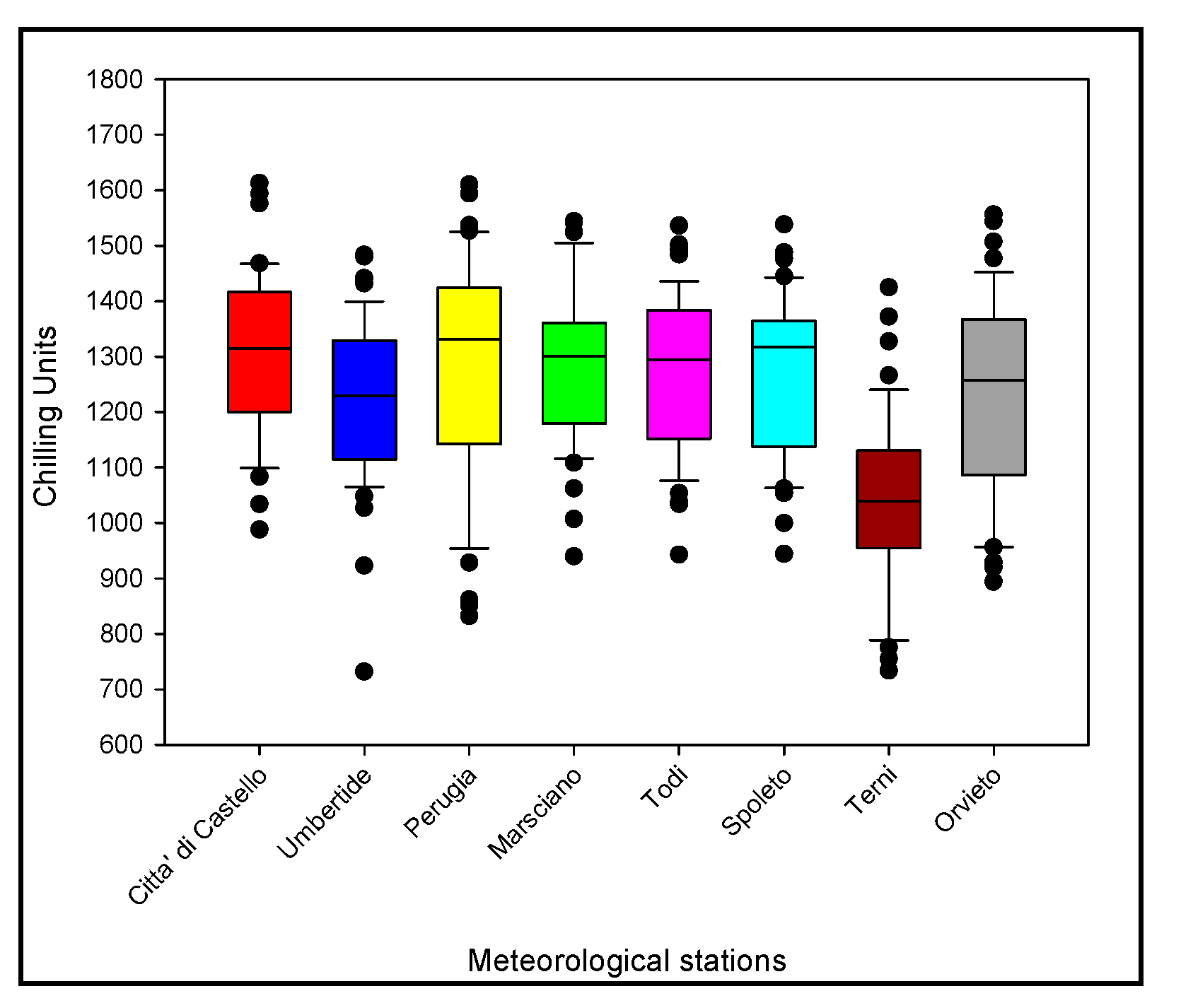


| Meteorological Station Name | Latitude World Geodetic System 84 (WGS 84) | Longitude World Geodetic System 84 (WGS 84) | Altitude (m a.s.l.) |
|---|---|---|---|
| Città di Castello | 43.46138889 | 12.25138889 | 304 |
| Marsciano | 42.94777778 | 12.28361111 | 244 |
| Orvieto | 42.71803 | 12.10773 | 315 |
| Perugia | 43.101242 | 12.395929 | 439 |
| Spoleto | 42.75583333 | 12.73861111 | 357 |
| Terni | 42.55972222 | 12.65027778 | 130 |
| Todi | 42.78611111 | 12.40916667 | 331 |
| Umbertide | 43.31166667 | 12.34722222 | 304 |
| Category | SPI |
|---|---|
| Wet | SPI ≥ 1.0 |
| Normal | −1.0 ≤ SPI < 1.0 |
| Dry | SPI ≤ −1.0 |
| Station Name Parameter | Città di Castello | Marsciano | Orvieto | Perugia | Spoleto | Terni | Todi | Umbertide | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Temperature | Zm | 5.022 | 5.591 | 5.306 | 5.288 | 5.395 | 5.146 | 5.573 | 4.951 | ||||||||
| p-value | 0.000 | *** | 0.000 | *** | 0.000 | *** | 0.000 | *** | 0.000 | *** | 0.000 | *** | 0.000 | *** | 0.000 | *** | |
| b | 0.049 | 0.052 | 0.058 | 0.053 | 0.053 | 0.051 | 0.054 | 0.047 | |||||||||
| Chilling Units | Zm | −3.962 | *** | −4.586 | *** | −2.669 | ** | −1.862 | ns | −2.302 | * | −0.853 | ns | −2.229 | * | −2.770 | ** |
| p-value | 0.000 | 0.000 | 0.008 | 0.063 | 0.021 | 0.394 | 0.026 | 0.006 | |||||||||
| b | −5.500 | −6.357 | −5.118 | −4.308 | −3.138 | −1.571 | −3.733 | −4.293 | |||||||||
| ET0 | Zm | 2.995 | 2.871 | 2.924 | 2.675 | 2.711 | 1.893 | 2.871 | 2.853 | ||||||||
| p-value | 0.003 | ** | 0.004 | ** | 0.003 | ** | 0.007 | ** | 0.007 | ** | 0.058 | ns | 0.004 | ** | 0.004 | ** | |
| b | 2.244 | 2.083 | 2.161 | 1.937 | 2.118 | 1.249 | 1.955 | 2.192 | |||||||||
| ETm | Zm | 3.049 | 3.031 | 2.871 | 2.800 | 2.711 | 1.982 | 2.835 | 2.835 | ||||||||
| p-value | 0.002 | ** | 0.002 | ** | 0.004 | ** | 0.005 | ** | 0.007 | ** | 0.047 | * | 0.005 | ** | 0.005 | ** | |
| b | 1.196 | 1.130 | 1.129 | 0.972 | 1.099 | 0.612 | 1.007 | 1.128 | |||||||||
| Water requirements | Zm | 1.785 | 0.571 | 1.553 | 1.670 | 1.489 | 1.398 | 1.018 | 2.332 | ||||||||
| Loam soil | p-value | 0.074 | ns | 0.568 | ns | 0.120 | ns | 0.095 | ns | 0.136 | ns | 0.162 | ns | 0.309 | ns | 0.020 | * |
| June–August | b | 0.733 | 0.116 | 0.602 | 0.680 | 0.733 | 0.374 | 0.433 | 0.952 | ||||||||
| Water requirements | Zm | 1.893 | 0.269 | 1.763 | 1.603 | 1.910 | 1.144 | 1.478 | 2.395 | ||||||||
| Loam soil | p-value | 0.058 | ns | 0.788 | ns | 0.078 | ns | 0.109 | ns | 0.056 | ns | 0.253 | ns | 0.139 | ns | 0.017 | * |
| July–August | b | 0.529 | 0.000 | 0.340 | 0.476 | 0.508 | 0.000 | 0.280 | 0.635 | ||||||||
| Water requirements | Zm | 1.434 | 0.428 | 1.498 | 1.445 | 1.007 | 1.463 | 1.025 | 1.810 | ||||||||
| Silty clay soil | p-value | 0.151 | 0.669 | 0.134 | 0.148 | 0.314 | 0.143 | 0.305 | 0.070 | ||||||||
| June–August | b | 0.748 | ns | 0.193 | ns | 0.692 | ns | 0.644 | ns | 0.515 | ns | 0.486 | ns | 0.483 | ns | 0.786 | ns |
| Water requirements | Zm | 2.039 | −0.223 | 2.158 | 1.118 | 1.228 | 1.329 | 2.006 | 1.969 | ||||||||
| Silty clay soil | p-value | 0.041 | * | 0.823 | ns | 0.031 | * | 0.263 | ns | 0.220 | ns | 0.184 | ns | 0.045 | * | 0.049 | * |
| July–August | b | 0.594 | 0.000 | 0.507 | 0.368 | 0.322 | 0.233 | 0.483 | 0.527 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vinci, A.; Di Lena, B.; Portarena, S.; Farinelli, D. Trend Analysis of Different Climate Parameters and Watering Requirements for Hazelnut in Central Italy Related to Climate Change. Horticulturae 2023, 9, 593. https://doi.org/10.3390/horticulturae9050593
Vinci A, Di Lena B, Portarena S, Farinelli D. Trend Analysis of Different Climate Parameters and Watering Requirements for Hazelnut in Central Italy Related to Climate Change. Horticulturae. 2023; 9(5):593. https://doi.org/10.3390/horticulturae9050593
Chicago/Turabian StyleVinci, Alessandra, Bruno Di Lena, Silvia Portarena, and Daniela Farinelli. 2023. "Trend Analysis of Different Climate Parameters and Watering Requirements for Hazelnut in Central Italy Related to Climate Change" Horticulturae 9, no. 5: 593. https://doi.org/10.3390/horticulturae9050593
APA StyleVinci, A., Di Lena, B., Portarena, S., & Farinelli, D. (2023). Trend Analysis of Different Climate Parameters and Watering Requirements for Hazelnut in Central Italy Related to Climate Change. Horticulturae, 9(5), 593. https://doi.org/10.3390/horticulturae9050593







