Abstract
Efficient marketing of winegrapes involves negotiating with potential buyers long before the harvest, when little is known about the expected vintage. Grapevine physiology is affected by weather conditions as well as by soil properties and such information can be applied to build yield prediction models. In this study, Partial Least Squares Regression (PLSR), Cubist (CUB) and Random Forest (RF) algorithms were used to predict yield from imputed weather station data and soil sample analysis reports. Models using only soil variables had the worst general results (R2 = 0.15, RMSE = 4.16 Mg ha−1, MAE = 3.20 Mg ha−1), while the use of only weather variables yielded the best performance (R2 = 0.52, RMSE = 2.99 Mg ha−1, MAE = 2.43 Mg ha−1). Models built with CUB and RF algorithms showed signs of overfitting, yet RF models achieved the best average results (R2 = 0.58, RMSE = 2.85 Mg ha−1, MAE = 2.24 Mg ha−1) using only weather variables as predictors. Weather data imputation affected RF and CUB models more intensely while PLSR remained fairly insensitive. Plant age, yield level group, vineyard plot, May temperatures, soil pH and exchangeable concentrations of Zn, Cu, K and Mn were identified as important predictors. This exploratory work offers insights for future research on grape yield predictive modeling and grouping strategies to obtain more assertive results, thus contributing to a more efficient grapevine production chain in southern Brazil and worldwide.
1. Introduction
In 2021, 7.3 million hectares of land were occupied by vineyards worldwide. Total grape production reached 77.8 Mt with over 57% destined to the wine industry. World wine production in 2021 was estimated in 26 GL, excluding juices and musts [1,2]. In Brazil over 75 thousand hectares of vineyards were harvested in 2022 [3] and the socioeconomic importance of viticulture is highlighted by a national wine market of BRL 20.3 billion (~USD 4 billion), which employed around 200 thousand people in 2019 [4]. Despite being the second largest market in South America after Argentina [2], 86 of every 100 bottles consumed by Brazilians in 2019 were imported [4], revealing the enormous growth potential for national wineries.
Efficient marketing of wine grapes involves negotiating with potential buyers long before the harvest, when little is known about the expected vintage. In addition, grape fertilizing practices also rely on yield expectations for the definition of application doses [5]. To anticipate yields, one must inevitably rely on some conceptual or numerical model of how crops respond to surrounding conditions. The use of predictive models in fruit growing can improve the effectiveness of decision-making processes and, as a result, there has been substantial industry and academic interest in building predictive models for grapevines [6,7,8,9,10].
Soil chemical properties and nutrient levels have a decisive impact on vineyards’ production [11,12,13]. Grapevine mineral nutrition is one of the most important factors in fruit production, especially in high-density orchards [14], as minerals are responsible for several functions in plants, such as tissue constitution, enzymatic activation, osmotic regulation of membranes and intermediation of energetic processes [15,16]. Unbalanced grapevine nutrition can compromise yields and the quality of grapes, affecting their appearance, color, flavor, size, aroma, post-harvest storage capacity and tolerance to pests and diseases [17,18], which is later reflected in the characteristics of the resulting must and wines [19,20,21]. Farmers generally rely on soil analysis to assess properties such as texture and organic matter content, pH and exchangeable nutrient levels in order to guide fertilizing management [22,23] but this type of data can be of limited availability due to cost constraints. Recent advances in soil sensing, however, may lead to more affordable, applicable and shareable soil information that can help circumvent current limitations in the near future [24,25,26,27,28].
Aside from nutrition, plant productivity is strongly driven by environmental factors. Meteorological conditions play a predominant role in grapevine physiology [29], influencing its growth, phenological development, yield and must properties [12,13,30], thus affecting wine quality [31]. Sunlight exposure is a key component of development, as solar radiation is captured by the plants and transformed into biomass [32]. Incoming solar energy is also converted to temperature with direct effects on grapevine production. High temperatures affect photosynthesis, transpiration and grape berry composition [33], whereas low temperatures contribute to the accumulation of chill units and have effects on bud dormancy [34,35]. Water availability is arguably the most important environmental factor limiting crop growth and productivity. Despite the growth of irrigated viticulture worldwide, precipitation remains of paramount importance, making grapevines susceptible to altered water regimes and, while grapevine drought tolerance mechanisms are not fully understood [36], high precipitation is known to increase the risk of downy mildew (Plasmopora viticola) occurrence [37]. Fungal spores can be dispersed by wind, spreading infestation and compromising vineyard health [38]. High wind speed, in turn, can reduce grape berry susceptibility to sunburn [39]. Along with humidity and temperature, wind can be used to estimate grapevine canopy evapotranspiration, which reflects water usage by plants [40]. The sheer importance of weather factors to grapevine production raises concerns over climate change impacts on wine-growing regions [31,41,42,43,44,45,46].
Climate data is now abundant, relatively cheap and can be found in different resolutions, as weather stations across the world continuously record and monitor various parameters for climate classification, planning, modeling and management purposes [47]. However, measuring instruments are subject to recording errors, malfunctioning, maintenance, network transmission and storage failures among other events that can generate data gaps and result in incomplete datasets [48,49,50]. Data missingness adversely impacts the analysis carried out afterwards and may lead to erroneous findings, false conclusions and inaccurate predictions [51].
The choice of the best strategy to handle missing data is not straightforward but most studies conclude that imputation is more advisable than removing data in order to reduce the risk of introducing bias in datasets and subsequent analyses [50,52,53]. Consequently, data imputation is an important preprocessing task in modeling. The simplest imputation methods consist in replacing the missing values with some measure of central tendency calculated from the non-missing values, such as the mean, mode or median or by randomly selecting values within the entire data or subset (e.g., hot deck imputation) [50,54]. Despite the simplicity, these methods can reduce overall data variance and are bound to the non-missing data range. Climatic data properties such as autocorrelation between time lags, seasonality, periodic trends and cycles can be useful for the development of imputation strategies [47,55]. In addition to leveraging univariate patterns, multivariate approaches can be applied to estimate missing data by means of predictive modeling, where non-missing variables are used as predictors. As a result, different statistical and machine learning methods have long been used to address the data missingness issue in different knowledge domains [51,56,57], including climate data [47,49,50,58,59]. In advanced multiple imputation schemes, the process of generating replacement values for missing data is repeated many times, resulting in m complete datasets that are further analyzed. The literature recommends the number of imputed datasets (m) ought to be between 5 and 10 [60]. These datasets are then used in subsequent analysis and the outcomes are pooled in order to obtain robust results, reducing uncertainty and bias [50,60,61].
Machine learning (ML) is a segment of artificial intelligence that has thrived in the recent context of big data technologies and high-performance computing [62]. ML represents an alternative to statistical models where deterministic processes take precedence over probability or likelihood measures in accomplishing estimation tasks [63]. As such, forecasting models can be built based on nonparametric and semi-parametric structures with validation relying on prediction accuracy. These empirical models are data-driven and do not require deep knowledge of the biophysical mechanisms that produced the data nor a predefined structure of the model, making such techniques inexpensive and relatively easy to apply [10]. Moreover, some ML algorithms can work with a large number of predictors from both categorical and numerical data types all at once, requiring little data preprocessing. These features have led to a prominent adoption of ML methods in agriculture [62] and crop yield prediction [63,64]. Previous studies attempted to model grape yields in wine-growing regions [6,7,10], but to date there have not been such attempts focusing on the well-established viticulture region of southern Brazil. Furthermore, studies have generally not evaluated the effect of imputing missing data on the predictive modeling of grape yields.
The aims of this study were to assess the suitability of different machine learning algorithms in grape yield forecasting; evaluate the effects of data imputations on model performance; and investigate the importance of soil analysis and weather station data in grape yield predictions.
2. Materials and Methods
2.1. Study Region and Grapevine Data
The study area lies in Santana do Livramento (latitude 30°53′27” S, longitude 55°31′58” W), located in the Campanha Gaúcha region of Rio Grande do Sul state, in southern Brazil (Figure 1). It is a traditional winegrape region with a humid subtropical climate with hot summers and no dry seasons (Köppen-Geiger classification Cfa) [65]. Data was obtained from a commercial vineyard grown on sandy textured Alisol [66]. Grapevines were grafted onto SO4 (Selection Oppenheim 4) rootstocks and grown in an espalier system.
Figure 1.
Santana do Livramento location (yellow) in Rio Grande do Sul state (red), southern Brazil.
Yield records (n = 534) ranged from 0.11 to 26.13 ton ha−1, with a mean of 9.10 ± 4.81 Mg ha−1, comprising 14 harvests (1999:2007, 2009, 2011, 2013, 2018, 2019) of 27 cultivars, aging from 2 to 40 years (Alicante Bouschet, Ancelota, Arinarnoa, Cabernet Franc, Cabernet Sauvignon, Chardonnay, Chenin Blanc, Ekigaina, Flora, French Colombard, Gamay Beaujolais, Gewurztraminer, Marselan, Merlot, Moscato Blanco, Moscato d’Amburgo, Napa Gamay, Petite Sirah, Pinot Noir, Pinot Saint Georges, Pinotage, Riesling Italico, Riesling Renano, Saint Emilion, Sauvignon Blanc, Semillon and Tannat).
Yield observations were sorted by harvest. In each harvest, yield distribution was divided into three groups (“high”, “medium” and “low” yield) using Jenks Natural breaks optimization [67], implemented via the BAMM tools [68] package in R. Jenks Natural breaks method is borrowed from the field of cartography and seeks to minimize the variance within categories while maximizing the variance between categories. Observations were then assigned to each group based on the yield recorded at a given harvest and the respective defined breaks. After classification, the data was grouped by cultivar and the frequency in which they were classified as “high”, “medium” or “low” was calculated. This information was used along with the general yield distribution and the number of observations by cultivar to determine the final yield class of each cultivar. Clustering results (Figure 2) were validated by expert knowledge provided by the agronomist responsible for the studied vineyard.
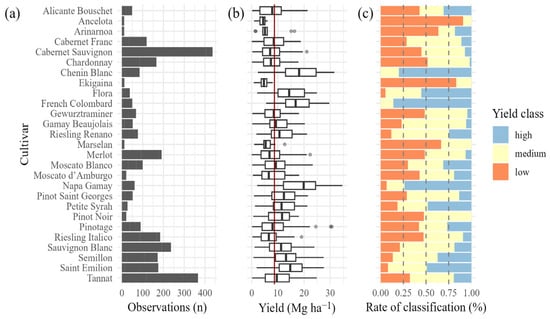
Figure 2.
Number of observations (a), yield distribution (b) and Jenks Natural breaks classification frequency (c) by cultivar. Vertical red line represent cultivar average yield and gray bullets represent outliers.
2.2. Soil Data
Soil data consisted of routine laboratory analysis results obtained from soil top layer samples (0–20 cm) collected under canopy projection and contained information on soil exchange capacity (potential and effective), acidity (potential, pH and SMP index), base and aluminum saturation, clay and organic matter contents, as well as exchangeable concentrations of aluminum (Al), phosphorus (P), potassium (K), calcium (Ca), magnesium (Mg), sulfur (S), copper (Cu), zinc (Zn), boron (B) and manganese (Mn) (Table 1 and Figure 3). Soil analyses followed methodologies recommended by [69,70].

Table 1.
Grapevine, soil and weather data used in yield forecasting models, grouped by predictor set.
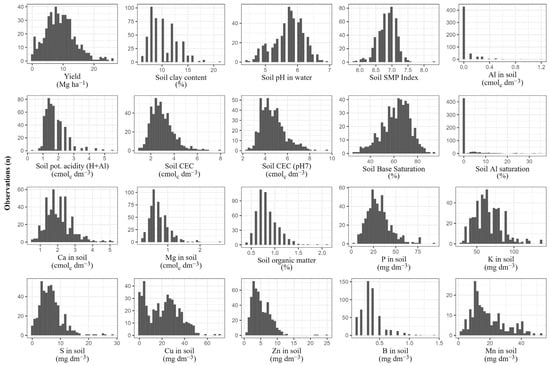
Figure 3.
Distribution of yield and soil-related variables used in grapevine prediction models.
2.3. Weather Data
Data from the Santana do Livramento ground meteorological station, the closest to the vineyards, was retrieved from the Brazilian National Institute of Meteorology database (https://bdmep.inmet.gov.br/, accessed on 26 July 2023) for the period between 1990 and 2020. Due to the homogeneity of the climate and relief of the study region, data from the nearby weather station of Bagé (~160km apart) was also retrieved in order to provide auxiliary information and aid missing data imputation [60]. Monthly average values of potential and real evaporation, evapotranspiration, sunlight exposure, cloudiness, temperatures (maximum, average and minimum), relative humidity and average wind speed were available, as well as the total number of rainy days and precipitation volumes (Table 1).
2.4. Data Imputation
In this study, missing data from the Santana do Livramento weather station was partially missing within the period covered by soil sampling data (Figure 4) and was imputed using either uni- or multivariate methods, depending on the gap size. Gaps equal to or shorter than nine consecutive observations (i.e., 9 months or 75%) were imputed using a univariate approach, which consisted of splitting the times series into seasons and performing imputation separately for each of the resulting subsets using interpolation. In this study, the univariate imputation of meteorological data was performed using the imputeTS package [71] with a 12-month season.
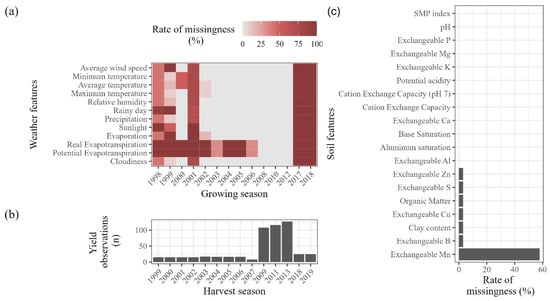
Figure 4.
Rate of missingness in Santana do Livramento weather station data, by variable and growing season (a). Number of yield observations by harvest (b). Rate of missing observations by variable in soil dataset (c).
Univariate methods may fail to provide reasonable imputations for a variable when periods of missing values are large [51], so for gaps larger than 9 months Multivariate Imputation by Chained Equations, or MICE [61] was used. MICE turns the imputation problem into a series of estimations, where each variable has its own imputation model built using the other remaining variables of the dataset. First, only the complete data is used to estimate values for the variable with the smallest number of missing observations. Next, the recently imputed variable is used along with the originally complete data to estimate the variable with the second smallest number of missing observations and so on. The first iteration is finished when all missing values are estimated once. In the second iteration, the order of imputation remains but the imputed values are now updatedconsidering all estimates generated in the previous steps. This process is repeated through a number of iterations to achieve a stable imputation. A single imputed dataset is obtained in the last iteration [72]. To attain robust results, it is recommended that many imputed datasets (m) are used for the desired analysis so that the pooled results can be evaluated [53]. The MICE algorithm was implemented using the mice [61] package to generate five different imputed datasets after 50 iterations each, produced with random forest models containing 500 trees.
In addition to weather station data, some of the soil analysis reports also hosted missing values, particularly regarding soil micronutrients (Figure 4). Since no seasonality can be attributed to these soil features and given the fact that the missingness mechanism did not seem to be random, a more simple approach was chosen and median imputation was performed to fill soil data gaps.
2.5. Modeling
The underlying assumption of this study is that weather and soil data hold information that is useful to forecast yields and, to investigate its contribution to estimates, models were built using different sets of predictors (p), namely “Soil” (p = 24: four categorical, 20 numeric), “Weather” (p = 149: four categorical, 145 numeric) and “Weather + Soil” (p = 168: four categorical, 164 numeric) (Table 1). In order to handle the high number of predictors and the possible non-linear relationships between variables, three algorithms—Partial Least Squares Regression (PLSR) [73], Cubist (CUB) [74,75] and Random Forest (RF) [76]—were used to predict grape yields. PLSR seeks to produce uncorrelated predictors by resorting to orthogonal projections. As such, predictors are expected to be numeric, therefore, categorical variables in the dataset were one-hot encoded prior to running this algorithm while numeric ones were centered and scaled. Moreover, the “plot” variable, which refers to a vineyard parcel, was removed since it contains 135 possible values and can be considered high cardinality data, yielding too many new variables after one-hot encoding. To evaluate model performance, the coefficient of determination (R2) (Equation (1)) was used as a measure of variance explained by the predictors while Root Mean Squared Error (RMSE) (Equation (2)) and Mean Absolute Error (MAE) (Equation (3)) were used as a measure of spread in predictions [77].
All models were fit using the caret package [78] (“pls”, “ranger” and “cubist” engines) on a training set (n = 399, 75%) with 10-fold cross-validation and five repetitions. Model tuning was performed using grids methods, optimized to reduce Root Mean Squared Error. For PLSR tuning, the number of principal components ranged from 1 to 20. In CUB, 100 committees were used and five different numbers of neighbors were tested (1, 3, 5, 7 and 9). The number of random variables (mtry) used in each RF tree depended on the dataset used for predictions. For “Weather” and “Weather + Soil”, four values were tested (50, 65, 80 and 95), whereas the “Soil” dataset was tuned using five values (9, 12, 15, 18 and 21). The same minimum node sizes were tested for all datasets (3, 5, 7 and 10). All RF models were built using 100 trees. Model best fit parameters were applied in the validation model and performance was assessed on a hold-out test set (n = 135, 25%). Data handling, imputing and modeling were performed in R language [79] using RStudio IDE [80].
where ŷ = predicted value; ȳ = mean observed value; y = observed values; N = number of samples with i = 1, 2…
3. Results
3.1. Model Performance and Imputation Effects
Model outcomes indicate that the choice of predictors had a considerable impact on grape yield forecasting. Regardless of the algorithm used, models built with the “Soil” dataset had the worst average results (R2 = 0.15, RMSE = 4.16 Mg ha−1, MAE = 3.20 Mg ha−1), while the use of only the “Weather” dataset yielded the best performance (R2 = 0.52, RMSE = 2.99 Mg ha−1, MAE = 2.43 Mg ha−1). The combination of soil and weather predictors had slightly worse results than weather variables alone (R2 = 0.50, RMSE = 3.05 Mg ha−1, MAE = 2.43 Mg ha−1), probably as a consequence of the higher number of variables with low predictive power. On the other hand, as the number of predictors increased, the difference between the three algorithms (i.e., the spread) decreased, suggesting a trade-off between higher precision and lower accuracy (Figure 5 and Table 2).
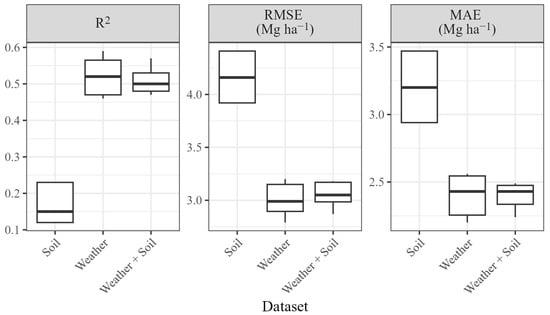
Figure 5.
Coefficient of determination (R2), Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) of all combined algorithms by dataset.

Table 2.
Average coefficient of determination (R2), Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) values for Partial Least Squares Regression (PLSR), Cubist (CUB) and Random Forest (RF) algorithms by predictor dataset.
In general, the RF model had the highest R2 and the lowest RMSE and MAE, followed by CUB and PLSR, regardless of the predictors used (Table 3). However, CUB and RF were the two algorithms most affected by overfitting, presenting very sharp changes in metrics when training and test sets are compared, especially when soil-related predictors were used. In addition, CUB and RF were also the most affected by different imputation sets and, once more, the presence of soil-related predictors contributed to higher variance in model metrics (Figure 6).

Table 3.
Grape yield prediction coefficient of determination (R2), Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) by algorithm, predictor dataset and imputation set. Best fit refers to optimized tuning parameters for Partial Least Squares Regressions (PLSR: number of principal components), Cubist (CUB: number of neighbors) and Random Forest (RF: random predictors subset/minimum node size).
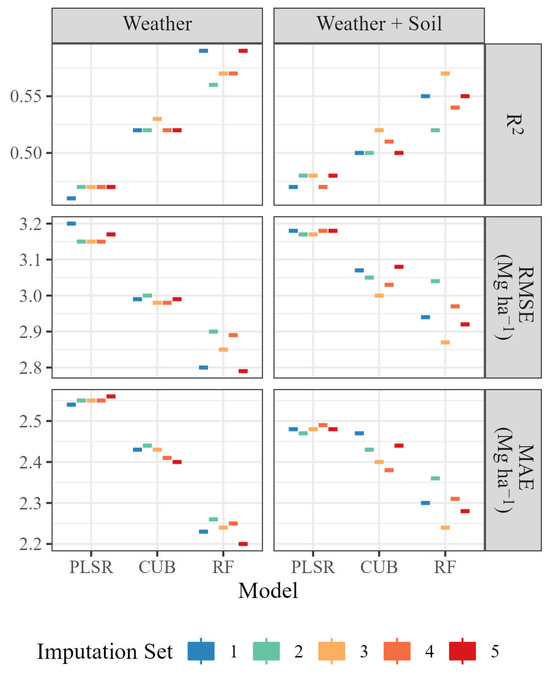
Figure 6.
Impact of weather data imputation on coefficient of determination (R2), Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) of grapevine yield predictions using Partial Least Squares Regression (PLSR), Cubist (CUB) and Random Forest (RF) algorithms with different sets of predictors.
The impact of imputation sets on model performance arises from changes in predictor distribution and range after filling in the missing values, therefore, the importance of predictors can also be indirectly assessed by investigating the differences between the imputed datasets. Imputation sets were fairly uniform and shaped similarly to the original observed data for most predictors except the mean wind speed and, to some extent, potential evapotranspiration. The number of rainy days, precipitation and relative humidity had at least one imputation set whose distribution appeared different from the others (Figure 7).
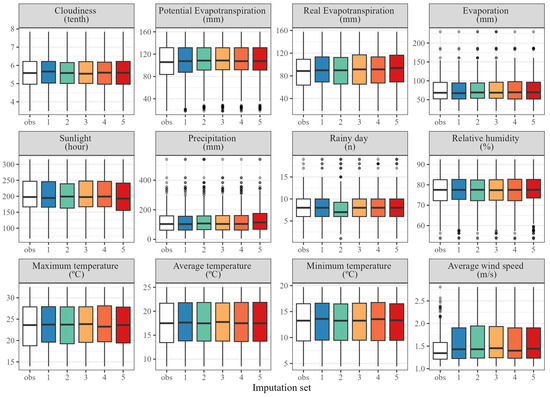
Figure 7.
Distributions of weather variables in observed data (obs, in white) and the five different complete datasets produced after multivariate chained equation (MICE) imputations (1–5, coloured). Gray bullets represent outliers.
3.2. Variable Importance
The assessments of variable importance can enable insights about the nature of the most important predictors and point to the direction for data acquisition and prediction improvements. Across all algorithms and all predictor datasets, plant age and yield class were the most important variables. May temperatures, especially the minimum, were the most important weather-related variable. Soil pH and concentrations of Zn and Cu were the most important soil-related predictors, followed by soil K and Mn. In addition, plot and cultivar were important predictors in CUB and RF models. The importance of other predictors varied among dataset x model combinations (Figure 8).
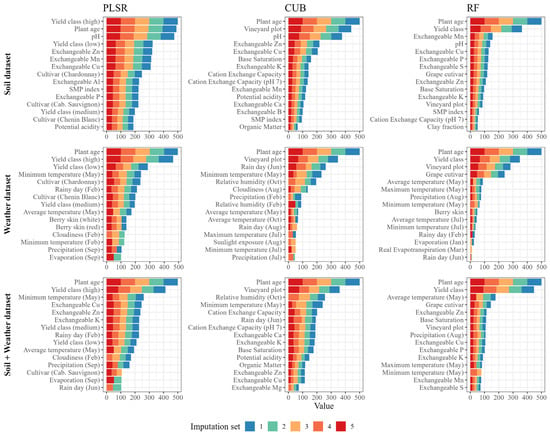
Figure 8.
The 15 most important variables by algorithm, predictor and imputation set. For each imputation set, variable importance is given on a 0 to 100 scale and x-axis values are the sum of the importance in m imputation sets. Soil dataset was only imputed using a median method, hence the results are the same for all imputation sets.
4. Discussion
The effects of data imputation on model performance vary according to the algorithm used. The different sensitivities between PLSR, CUB and RF arise due to how each of these algorithms work. The PLSR acts as a supervised Principal Component Regression (PCR) producing new features (PCs) which are linear combinations of the original predictors that maximize the explained variance in the response [73]. Therefore, changes in particular variables due to imputation may have their effects diluted or even ignored given this optimization constraint.
Building on Quinlan’s original M5 model [74,75], its modern version called Cubist (CUB) is a rule-based algorithm that makes predictions by building regression models on its terminal nodes [81]. This algorithm works by creating a split in the dataset and fitting a regression with every predictor available. In the next node, data is split again and a new regression is fit using the new subset of predictors. Moreover, CUB includes an ensemble method for predictions called committees and a nearest-neighbor adjustment that occurs after the model predictions [81]. In committee ensembles, the outcome values are modified for each iteration in an effort to reduce over- and under-predictions, whereas the final result is obtained by averaging over the committee model estimates. After model prediction, it is possible to conduct a post-model K-nearest neighbor adjustment where the closest observations in the training set (along with their original predictions) are used to correct prediction errors and trends in the dependent variable [74,81]. In the current study, the number of committees and neighbors used was high and, while effective in improving performance metrics, it is likely that it caused overfitting in the training set, hampering predictive ability during the validation stage.
Random Forest is an ensemble of decision trees that do not build regression models on terminal nodes, but rather use average values and, as a consequence, may be more sensitive to variations caused by imputation, given the changes in imputed data distributions. The number of variables randomly sampled as candidates at each split (mtry) is a tuning parameter that impacts the likelihood of selecting important features that are actually related to the outcome variable for most of the splits that are made. Too large mtry values can reduce randomness in the model, diminishing the benefits of building multiple independent decision trees. Minimum node size, in turn, defines how deep a tree can grow, that is, the minimum number of observations a node requires to proceed with a split. Our results present clear signs of overfitting, suggesting that the combination of large mtry values and small node size (Table 3) is detrimental to modeling and should be reconsidered. Nevertheless, the pooled results of RF yielded the best predictive performance, indicating that some of the overfitting issues were addressed by the averaging effect of multiple trees (a.k.a. the law of large numbers) [76], although higher values should also be tested.
Our results corroborate with the well-established importance of meteorological variables in resulting grape yield [12,13,30]. However, our models highlighted end-of-cycle temperatures (May) as being important predictors, as opposed to the most commonly reported temperatures at bud break, flowering, fruit-set and berry development stages [8,10,31,82,83]. Post-harvest temperature might contribute to greater carbohydrate accumulation in plant tissues, which are translocated in the next cycle to the leaves and branches at the beginning of vegetative growth [84].
Relative humidity and precipitation were previously reported as relevant predictors for grape yield models [10,46] but did not show consistent predictive power in the present study. This may arise from the inherit difficulty in capturing rain records. Since rain and humidity can be very heterogeneous across landscape, even nearby stations may not represent the water regime faithfully, let alone in imputed datasets [58], an issue of known concern [58,85]. Imputation of time series and its impact on modeling results is still an active field of research [47,51,53,56] and further studies need to be carried out to avoid erroneous conclusions and inaccurate predictions.
Despite the undeniable importance of plant nutrition to obtain proper grapevine yields, the predictive power of soil variables was considerably low. Grape root systems can grow over a meter deep, therefore, the dynamics of nutrient uptake are not fully captured by top layer soil samples [18]. Moreover, adult grapevines reach nutritional stability and are able to mobilize reserves [86], hindering the relationship between soil nutrient concentrations and yield parameters. This is also reflected in the ubiquitous presence of plant age as the most important yield predictor.
Soil pH plays a key role in plant development due to its effects on nutrient availability and toxicity [87] and such importance is promptly captured by all three models. The importance of soil Cu and Zn as yield predictors can, however, be related to phytosanitary control, since they are components of fungicides largely used against crop diseases, ensuring higher yields but also leading to their accumulation in vineyard soils [88,89,90]. Grape berries are great sinks of K [91] and clusters can account for over 60% of the total content in the above-ground organs [92], so it is sound that soil K figures as an important yield predictor, which is supported by recent modeling attempts [10]. Grapevines are particularly susceptible to Mn deficiency and shortage of supply can lead to small and poor quality yields [93]. In addition, recent studies suggest that Mn plays a role in enhancing plant resistance to water stress [94], so despite being a micronutrient, Mn soil concentrations seem to play key role in grape production. It is worth noting that Mn was the single most imputed variable in soil-related datasets (Figure 4) and, while having artificially reduced variance, it figured as a relevant predictor when soil variables were considered.
Categorical variables were also important to model estimates. The high importance of vineyard plot information suggests spatial dependency, consistent with recent studies on the effects of intra-vineyard variability and soil heterogeneity on vine performance, dry matter and nutrient partitioning [95], where, based on the Normalized Difference Vegetation Index NDVI, authors divided the vineyard into high, medium and low vigor zones. The availability of georeferenced data can improve yield response estimates by enabling the use of covariates in modeling [96] and imputations [97] but such information was unavailable in the current study. Instead, the cultivars were grouped into low, medium or high yield levels based on numerical clustering, historical yield levels (Figure 2) and expert knowledge. This feature engineering improved model performance by better partitioning the variability while retaining agronomic sense. Similarly, other groupings (or clusterings) could enhance the predictive ability of models. Research has shown the importance of phenological stage grouping for modeling [6,10,98]. Moreover, advances in fruit tree fertilizing indicate different nutrition profiles for each cultivar [12,99,100] or site-specific conditions [101] and, while requiring further elucidation, have the potential to leverage soil data predictive power.
The present study showed that the combined use of databases and robust machine learning methods has the potential to estimate grapevine productivity, helping decision makers to be more assertive not only during commercialization stage but also in fertilizer recommendations and phytosanitary management of vineyards. The herein adopted strategies can be extended for other relevant applications in orchards worldwide, estimating the performance of fruit trees under specific conditions (culture, site, management, etc.), while keeping in mind multiple factors such as increased yield and economic viability, higher visual and bromatological quality of fruits, plant nutrition for proper development, rational use of fertilizers and adaptation within a climate change scenario.
5. Conclusions
In this study, Partial Least Square (PLSR), Cubist (CUB) and Random Forest (RF) algorithms were used to predict grape yields from weather and soil data separately and in conjunction. Overall, the results were best when using only weather predictors, followed by weather and soil data combined and, lastly, soil data alone. Weather data from ground meteorological stations contained observations with missing values and these were imputed by uni- or multivariate methods. The RF and CUB algorithms were the most affected by weather data imputations, while PLSR remained fairly insensitive. Parameter tuning optimized to reduce Root Mean Squared Error led to overfitting in CUB- and RF-based models and (hyper)parameter values should be reconsidered to improve performance. Nevertheless, RF achieved the best metrics, followed closely by CUB, while PLSR yielded the poorest yet most stable results. Plant age, May temperatures, soil pH and concentrations of Zn, Cu, K and Mn were identified as important predictors, even though 57% of soil Mn observations were missing and were imputed using a median method. Yield level groups had high importance in predictions, indicating that clustering can be a useful strategy, whereas the importance of vineyard plots suggests spatial dependencies that can be further explored by using georeferenced data. This exploratory work offers insights for future research on grape yield predictive modeling and highlights the importance of high resolution data and grouping strategies to obtain more assertive results, thus contributing to a more efficient grapevine production chain in southern Brazil and worldwide.
Author Contributions
Conceptualization, G.B., J.J.C., J.M.M.-B. and C.B.A.; methodology, J.M.M.-B. and C.B.A.; software, J.M.M.-B. and C.B.A.; J.M.M.-B. and C.B.A.; formal analysis, C.B.A.; investigation, J.M.M.-B. and C.B.A.; resources, G.B and J.J.C.; data curation, C.B.A.; writing—original draft preparation, J.M.M.-B. and C.B.A.; writing—review and editing, G.B., J.J.C. and J.M.M.-B.; visualization, G.B., J.J.C., J.M.M.-B. and C.B.A.; supervision, G.B., J.J.C. and J.M.M.-B.; project administration, G.B. and J.J.C.; funding acquisition, G.B. and J.J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Council for Scientific and Technological Development (CNPq—process: 302023/2019-4) and the Foundation for Support of Research Rio Grande do Sul—Brazil (FAPERGS—process: 21/2551-0002232-9).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to company data privacy.
Acknowledgments
We would like to thank the professionals involved in data collection, as well as the winery administration that generously shared its data so that the present study could be carried out. We also thank the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brazil (CAPES) and the National Council for Scientific and Technological Development (CNPq).
Conflicts of Interest
The authors declare no conflict of interest.
References
- OIV. Statistical Report on World Vitiviniculture; International Organisation of Vine and Wine: Dijon, France, 2019; p. 23. [Google Scholar]
- OIV. State of the World Vine and Wine Sector; International Organisation of Vine and Wine: Dijon, France, 2022; p. 20. [Google Scholar]
- IBGE. Levantamento Sistemático da Produção Agropecuária; IBGE: Rio de Janeiro, Brazil, 2022. [Google Scholar]
- De Mello, L.M.R.; Machado, C.A.E. Vitivinicultura Brasileira: Panorama 2019; Comunicado Técnico, 214; Embrapa Uva e Vinho: Bento Gonçalves, Brazil, 2020; pp. 1–21. [Google Scholar]
- CQFS-RS/SC. Manual de Calagem e Adubação para os Estados do Rio Grande do Sul e Santa Catarina; Comissão de Química e Fertilidade do Solo/Núcleo Regional Sul-Sociedade Brasileira de Ciência do Solos: Passo Fundo, Brazil, 2016; ISBN 978-85-66301-80-9. [Google Scholar]
- Arab, S.T.; Noguchi, R.; Matsushita, S.; Ahamed, T. Prediction of Grape Yields from Time-Series Vegetation Indices Using Satellite Remote Sensing and a Machine-Learning Approach. Remote Sens. Appl. Soc. Environ. 2021, 22, 100485. [Google Scholar] [CrossRef]
- Barriguinha, A.; Jardim, B.; De Castro Neto, M.; Gil, A. Using NDVI, Climate Data and Machine Learning to Estimate Yield in the Douro Wine Region. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103069. [Google Scholar] [CrossRef]
- Cunha, M.; Ribeiro, H.; Abreu, I. Pollen-Based Predictive Modelling of Wine Production: Application to an Arid Region. Eur. J. Agron. 2016, 73, 42–54. [Google Scholar] [CrossRef]
- Kadbhane, S.J.; Manekar, V.L. Development of Agro-Climatic Grape Yield Model with Future Prospective. Ital. J. Agrometeorol. 2021, 2021, 89–103. [Google Scholar] [CrossRef]
- Sirsat, M.S.; Mendes-Moreira, J.; Ferreira, C.; Cunha, M. Machine Learning Predictive Model of Grapevine Yield Based on Agroclimatic Patterns. Eng. Agric. Environ. Food 2019, 12, 443–450. [Google Scholar] [CrossRef]
- Krzyszczak, J.; Brodowska, M.; Bednarek, W.; Dresler, S.; Tkaczyk, P.; Krzyszczak, J.; Baranowski, P. Content of Certain Macro- and Microelements in Orchard Soils in Relation to Agronomic Categories and Reaction of These Soils. J. Elem. 2018, 23, 1361–1372. [Google Scholar] [CrossRef]
- Stefanello, L.; Schwalbert, R.; Schwalbert, R.; Tassinari, A.; Garlet, L.; De Conti, L.; Ciotta, M.; Ceretta, C.; Ciampitti, I.; Brunetto, G. Phosphorus Critical Levels in Soil and Grapevine Leaves for South Brazil Vineyards: A Bayesian Approach. Eur. J. Agron. 2023, 144, 126752. [Google Scholar] [CrossRef]
- Stefanello, L.O.; Schwalbert, R.; Schwalbert, R.A.; Drescher, G.L.; De Conti, L.; Pott, L.P.; Tassinari, A.; Kulmann, M.S.d.S.; da Silva, I.C.B.; Brunetto, G. Ideal Nitrogen Concentration in Leaves for the Production of High-Quality Grapes Cv ‘Alicante Bouschet’ (Vitis vinifera L.) Subjected to Modes of Application and Nitrogen Doses. Eur. J. Agron. 2021, 123, 126200. [Google Scholar] [CrossRef]
- Ebert, G. Fertilizing for High Yield and Quality: Pome and Stone Fruits of the Temperate Zone; IPI Bulletin; International Potash Institute: Horgen, Switzerland, 2009; p. 74. [Google Scholar]
- Faust, M. Physiology of Temperate Zone Fruit Trees; Wiley-Interscience: New York, NY, USA, 1989. [Google Scholar]
- Marschner, P. Marschner’s Mineral Nutrition of Higher Plants; Academic Press: San Diego, CA, USA, 2012; ISBN 978-0-12-384905-2. [Google Scholar]
- Brunetto, G.; Melo, G.W.B.D.; Toselli, M.; Quartieri, M.; Tagliavini, M. The Role of Mineral Nutrition on Yields and Fruit Quality in Grapevine, Pear and Apple. Rev. Bras. Frutic. 2015, 37, 1089–1104. [Google Scholar] [CrossRef]
- Rozane, D.E.; Parent, L.E.; Natale, W. Evolution of the Predictive Criteria for the Tropical Fruit Tree Nutritional Status. Científica 2015, 44, 102. [Google Scholar] [CrossRef]
- Brunetto, G.; Ceretta, C.A.; Kaminski, J.; de Melo, G.W.B.; Lourenzi, C.R.; Furlanetto, V.; Moraes, A. Aplicação de Nitrogênio Em Videiras Na Campanha Gaúcha: Produtividade e Características Químicas Do Mosto Da Uva. Ciência Rural. 2007, 37, 389–393. [Google Scholar] [CrossRef]
- Considine, M.J.; Foyer, C.H. Metabolic Responses to Sulfur Dioxide in Grapevine (Vitis vinifera L.): Photosynthetic Tissues and Berries. Front. Plant Sci. 2015, 6, 60. [Google Scholar] [CrossRef] [PubMed]
- Skinner, P.W.; Ishii, R.; O’Mahony, M.; Matthews, M.A. Sensory Attributes of Wines Made from Vines of Differing Phosphorus Status. Oeno One 2019, 53, 205–219. [Google Scholar] [CrossRef]
- Brunetto, G.; Ricachenevsky, F.K.; Stefanello, L.O.; de Paula, B.V.; de Souza Kulmann, M.S.; Tassinari, A.; de Melo, G.W.B.; Natale, W.; Rozane, D.E.; Ciotta, M.N.; et al. Chapter 47—Diagnosis and Management of Nutrient Constraints in Grape. In Fruit Crops; Srivastava, A.K., Hu, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 693–710. ISBN 978-0-12-818732-6. [Google Scholar]
- Rozane, D.E.; de Paula, B.V.; de Melo, G.W.B.; Dos Santos, E.M.H.; Trentin, E.; Marchezan, C.; da Silva, L.O.S.; Tassinari, A.; Dotto, L.; de Oliveira, F.N.; et al. Compositional Nutrient Diagnosis (CND) Applied to Grapevines Grown in Subtropical Climate Region. Horticulturae 2020, 6, 56. [Google Scholar] [CrossRef]
- Tavares, T.R.; Molin, J.P.; Nunes, L.C.; Alves, E.E.N.; Krug, F.J.; De Carvalho, H.W.P. Spectral Data of Tropical Soils Using Dry-Chemistry Techniques (VNIR, XRF, and LIBS): A Dataset for Soil Fertility Prediction. Data Brief 2022, 41, 108004. [Google Scholar] [CrossRef] [PubMed]
- Tavares, T.R.; De Almeida, E.; Junior, C.R.P.; Guerrero, A.; Fiorio, P.R.; De Carvalho, H.W.P. Analysis of Total Soil Nutrient Content with X-ray Fluorescence Spectroscopy (XRF): Assessing Different Predictive Modeling Strategies and Auxiliary Variables. AgriEngineering 2023, 5, 680–697. [Google Scholar] [CrossRef]
- Poppiel, R.R.; Paiva, A.F.D.S.; Demattê, J.A.M. Bridging the Gap between Soil Spectroscopy and Traditional Laboratory: Insights for Routine Implementation. Geoderma 2022, 425, 116029. [Google Scholar] [CrossRef]
- Nadporozhskaya, M.; Kovsh, N.; Paolesse, R.; Lvova, L. Recent Advances in Chemical Sensors for Soil Analysis: A Review. Chemosensors 2022, 10, 35. [Google Scholar] [CrossRef]
- De Mello, D.C.; Barros Souza, A.; Mello, F.A.O.; Marques, K.P.P.; Poppiel, R.R.; Belinasso, H.; Di Raimo, L.D.L.; Francelino, M.R.; Fernandes-Filho, E.I.; Veloso, G.V.; et al. Sensor-Based Field Methods for Pedology and Soil Surveys: Protocol Suggestions for Brazilian Tropical Soils. Geoderma Reg. 2023, 33, e00651. [Google Scholar] [CrossRef]
- Keller, M. Managing Grapevines to Optimise Fruit Development in a Challenging Environment: A Climate Change Primer for Viticulturists. Aust. J. Grape Wine Res. 2010, 16, 56–69. [Google Scholar] [CrossRef]
- Ciotta, M.N.; Ceretta, C.A.; Ferreira, P.A.; Stefanello, L.O.; da Rosa Couto, R.; Tassianri, A.; Marchezan, C.; Girotto, E.; Conti, L.D.; Lourenzi, C.R.; et al. Phosphorus Fertilization for Young Grapevines of Chardonnay and Pinot Noir in Sandy Soil. IDESIA 2018, 36, 27–34. [Google Scholar] [CrossRef]
- Fraga, H.; de Cortázar Atauri, I.G.; Malheiro, A.C.; Santos, J.A. Modelling Climate Change Impacts on Viticultural Yield, Phenology and Stress Conditions in Europe. Glob. Chang. Biol. 2016, 22, 3774–3788. [Google Scholar] [CrossRef] [PubMed]
- Campillo, C.; Fortes, R.; Henar Prieto, M.D. Solar Radiation Effect on Crop Production. In Solar Radiation; Babatunde, E.B., Ed.; IntechOpen: London, UK, 2012; ISBN 978-953-51-6163-9. [Google Scholar]
- Venios, X.; Korkas, E.; Nisiotou, A.; Banilas, G. Grapevine Responses to Heat Stress and Global Warming. Plants 2020, 9, 1754. [Google Scholar] [CrossRef] [PubMed]
- Anzanello, R. Evolution of the Grapevine Bud Dormancy under Different Thermal Regimes. Semin. Cienc. Agrar. 2019, 40, 3419. [Google Scholar] [CrossRef]
- North, M.; Workmaster, B.A.; Atucha, A. Effects of Chill Unit Accumulation and Temperature on Woody Plant Deacclimation Kinetics. Physiol. Plant. 2022, 174, e13717. [Google Scholar] [CrossRef] [PubMed]
- Gambetta, G.A.; Herrera, J.C.; Dayer, S.; Feng, Q.; Hochberg, U.; Castellarin, S.D. The Physiology of Drought Stress in Grapevine: Towards an Integrative Definition of Drought Tolerance. J. Exp. Bot. 2020, 71, 4658–4676. [Google Scholar] [CrossRef]
- Chen, M.; Brun, F.; Raynal, M.; Makowski, D. Forecasting Severe Grape Downy Mildew Attacks Using Machine Learning. PLoS ONE 2020, 15, e0230254. [Google Scholar] [CrossRef]
- Mezei, I.; Lukić, M.; Berbakov, L.; Pavković, B.; Radovanović, B. Grapevine Downy Mildew Warning System Based on NB-IoT and Energy Harvesting Technology. Electronics 2022, 11, 356. [Google Scholar] [CrossRef]
- Müller, K.; Keller, M.; Stoll, M.; Friedel, M. Wind Speed, Sun Exposure and Water Status Alter Sunburn Susceptibility of Grape Berries. Front. Plant Sci. 2023, 14, 1145274. [Google Scholar] [CrossRef]
- Jenkins, M.; Mannsfeld, A.; Nikzad, S.; Lambert, J.-J.; Miller, K.; Burns, M.; Earles, J.M.; Block, D.E. Novel Algorithms for High-Resolution Prediction of Canopy Evapotranspiration in Grapevine. OENO One 2023, 57, 315–326. [Google Scholar] [CrossRef]
- Bonfante, A.; Alfieri, S.M.; Albrizio, R.; Basile, A.; De Mascellis, R.; Gambuti, A.; Giorio, P.; Langella, G.; Manna, P.; Monaco, E.; et al. Evaluation of the Effects of Future Climate Change on Grape Quality through a Physically Based Model Application: A Case Study for the Aglianico Grapevine in Campania Region, Italy. Agric. Syst. 2017, 152, 100–109. [Google Scholar] [CrossRef]
- Droulia, F.; Charalampopoulos, I. Future Climate Change Impacts on European Viticulture: A Review on Recent Scientific Advances. Atmosphere 2021, 12, 495. [Google Scholar] [CrossRef]
- Fraga, H.; Molitor, D.; Leolini, L.; Santos, J.A. What Is the Impact of Heatwaves on European Viticulture? A Modelling Assessment. Appl. Sci. 2020, 10, 3030. [Google Scholar] [CrossRef]
- Holland, T.; Smit, B. Climate Change and the Wine Industry: Current Research Themes and New Directions. J. Wine Res. 2010, 21, 125–136. [Google Scholar] [CrossRef]
- Moriondo, M.; Ferrise, R.; Trombi, G.; Brilli, L.; Dibari, C.; Bindi, M. Modelling Olive Trees and Grapevines in a Changing Climate. Environ. Model. Softw. 2015, 72, 387–401. [Google Scholar] [CrossRef]
- Fraga, H.; Santos, J.A. Daily Prediction of Seasonal Grapevine Production in the Douro Wine Region Based on Favourable Meteorological Conditions: Predicting Winery Grape Production in the Douro. Aust. J. Grape Wine Res. 2017, 23, 296–304. [Google Scholar] [CrossRef]
- Afrifa-Yamoah, E.; Mueller, U.A.; Taylor, S.M.; Fisher, A.J. Missing Data Imputation of High-Resolution Temporal Climate Time Series Data. Meteorol. Appl. 2020, 27, 1873. [Google Scholar] [CrossRef]
- Yozgatligil, C.; Aslan, S.; Iyigun, C.; Batmaz, I. Comparison of Missing Value Imputation Methods in Time Series: The Case of Turkish Meteorological Data. Theor. Appl. Climatol. 2013, 112, 143–167. [Google Scholar] [CrossRef]
- Parra-Plazas, J.; Gaona-Garcia, P.; Plazas-Nossa, L. Time Series Outlier Removal and Imputing Methods Based on Colombian Weather Stations Data. Environ. Sci. Pollut. Res. 2023, 30, 72319–72335. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Ren, X.; Zhao, G. Machine-Learning-Based Imputation Method for Filling Missing Values in Ground Meteorological Observation Data. Algorithms 2023, 16, 422. [Google Scholar] [CrossRef]
- Chaudhry, A.; Li, W.; Basri, A.; Patenaude, F. A Method for Improving Imputation and Prediction Accuracy of Highly Seasonal Univariate Data with Large Periods of Missingness. Wirel. Commun. Mob. Comput. 2019, 2019, 4039758. [Google Scholar] [CrossRef]
- Little, R.; Rubin, D. Statistical Analysis with Missing Data, 3rd ed.; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2019; ISBN 978-1-119-48226-0. [Google Scholar]
- Mera-Gaona, M.; Neumann, U.; Vargas-Canas, R.; López, D.M. Evaluating the Impact of Multivariate Imputation by MICE in Feature Selection. PLoS ONE 2021, 16, e0254720. [Google Scholar] [CrossRef]
- Andridge, R.R.; Little, R.J.A. A Review of Hot Deck Imputation for Survey Non-Response. Int. Stat. Rev. 2010, 78, 40–64. [Google Scholar] [CrossRef] [PubMed]
- Moritz, S.; Sardá, A.; Bartz-Beielstein, T.; Zaefferer, M.; Stork, J. Comparison of Different Methods for Univariate Time Series Imputation in R. arXiv 2015, arXiv:1510.03924. [Google Scholar]
- Ahn, H.; Sun, K.; Kim, K.P. Comparison of Missing Data Imputation Methods in Time Series Forecasting. Comput. Mater. Contin. 2021, 70, 767–779. [Google Scholar] [CrossRef]
- Lin, W.C.; Tsai, C.F. Missing Value Imputation: A Review and Analysis of the Literature (2006–2017). Artif. Intell. Rev. 2020, 53, 1487–1509. [Google Scholar] [CrossRef]
- Kannegowda, N.; Udayar Pillai, S.; Kommireddi, C.V.N.K. Fousiya Comparative Assessment of Univariate and Multivariate Imputation Models for Varying Lengths of Missing Rainfall Data in a Humid Tropical Region: A Case Study of Kozhikode, Kerala, India. Acta Geophys. 2023. [Google Scholar] [CrossRef]
- Lara-Estrada, L.; Rasche, L.; Sucar, L.; Schneider, U. Inferring Missing Climate Data for Agricultural Planning Using Bayesian Networks. Land 2018, 7, 4. [Google Scholar] [CrossRef]
- Azur, M.J.; Stuart, E.A.; Frangakis, C.; Leaf, P.J. Multiple Imputation by Chained Equations: What Is It and How Does It Work? Multiple Imputation by Chained Equations. Int. J. Methods Psychiatr. Res. 2011, 20, 40–49. [Google Scholar] [CrossRef]
- Buuren, S.V.; Groothuis-Oudshoorn, K. Mice: Multivariate Imputation by Chained Equations in R. J. Stat. Soft. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Liakos, K.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed]
- Elavarasan, D.; Vincent, D.R.; Sharma, V.; Zomaya, A.Y.; Srinivasan, K. Forecasting Yield by Integrating Agrarian Factors and Machine Learning Models: A Survey. Comput. Electron. Agric. 2018, 155, 257–282. [Google Scholar] [CrossRef]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine Learning Approaches for Crop Yield Prediction and Nitrogen Status Estimation in Precision Agriculture: A Review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; de Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s Climate Classification Map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef] [PubMed]
- Soil Survey Staff. Keys to Soil Taxonomy, 12th ed.; USDA-Natural Resources Conservation Service: Washington, DC, USA, 2014. [Google Scholar]
- Jenks, G.F. The Data Model Concept in Statistical Mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Rabosky, D.L.; Grundler, M.; Anderson, C.; Title, P.; Shi, J.J.; Brown, J.W.; Huang, H.; Larson, J.G. BAMM Tools: An R Package for the Analysis of Evolutionary Dynamics on Phylogenetic Trees. Methods Ecol. Evol. 2014, 5, 701–707. [Google Scholar] [CrossRef]
- Tedesco, J.M.; Gianello, C.; Bissani, C.A.; Bohnem, H.; Volkweiss, S.J. Análise de Solo, Plantas e Outros Materiais, 2nd ed.; Universidade Federal do Rio Grande do Sul: Porto Alegre, Brazil, 1995. [Google Scholar]
- Teixeira, P.C.; Donagemma, G.K.; Fontana, A.; Teixeira, W.G. Manual de Métodos de Análise de Solo, 3rd ed.; Embrapa: Brasília, Brazil, 2017; ISBN 978-85-7035-771-7. [Google Scholar]
- Moritz, S.; Bartz-Beielstein, T. imputeTS: Time Series Missing Value Imputation in R. R J. 2017, 9, 207. [Google Scholar] [CrossRef]
- Wulff, J.; Ejlskov, L. Multiple Imputation by Chained Equations in Praxis: Guidelines and Review. Electron. J. Bus. Res. Methods 2017, 15, 2017–2058. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-Regression: A Basic Tool of Chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Quinlan, J.R. Combining Instance-Based and Model-Based Learning. In Proceedings of the Tenth International Conference on International Conference on Machine Learning, Amherst, MA, USA, 27–29 July 1993; pp. 236–243, ISBN 978-1-55860-307-3. [Google Scholar]
- Quinlan, J.R. Learning with Continuous Classes; World Scientific: Sinagpore, 1992; Volume 92, pp. 343–348. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)?—Arguments against Avoiding RMSE in the Literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Soft. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- RStudio Team. RStudio: Integrated Development for R; PBC: Boston, MA, USA, 2023. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-6848-6. [Google Scholar]
- Reis Pereira, M.; Ribeiro, H.; Abreu, I.; Eiras-Dias, J.; Mota, T.; Cunha, M. Predicting the Flowering Date of Portuguese Grapevine Varieties Using Temperature-Based Phenological Models: A Multi-Site Approach. J. Agric. Sci. 2018, 156, 865–876. [Google Scholar] [CrossRef]
- Santos, J.A.; Grätsch, S.D.; Karremann, M.K.; Jones, G.V.; Pinto, J.G. Ensemble Projections for Wine Production in the Douro Valley of Portugal. Clim. Chang. 2013, 117, 211–225. [Google Scholar] [CrossRef]
- Rafael, A.; Souza, P.V.D.D. Conteúdo de Reservas, Vigor Vegetativo e Rendimento de Videiras Submetidas a Duas Safras Por Ciclo Vegetativo. Sem. Ci. Agr. 2015, 36, 719. [Google Scholar] [CrossRef][Green Version]
- Aieb, A.; Madani, K.; Scarpa, M.; Bonacorso, B.; Lefsih, K. A New Approach for Processing Climate Missing Databases Applied to Daily Rainfall Data in Soummam Watershed, Algeria. Heliyon 2019, 5, e01247. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, B.P. Seasonal Vine Nutrient Dynamics and Distribution of Shiraz Grapevines. OENO One 2019, 53, 363–372. [Google Scholar] [CrossRef]
- Sparks, D.L. Environmental Soil Chemistry, 2nd ed.; Academic Press: San Diego, CA, USA, 2003; ISBN 978-0-12-656446-4. [Google Scholar]
- Brunetto, G.; Ferreira, P.A.A.; Melo, G.W.; Ceretta, C.A.; Toselli, M. Heavy Metals in Vineyards and Orchard Soils. Rev. Bras. De Frutic. 2017, 39, 1–12. [Google Scholar] [CrossRef]
- Brunetto, G.; de Melo, G.W.B.; Terzano, R.; Del Buono, D.; Astolfi, S.; Tomasi, N.; Pii, Y.; Mimmo, T.; Cesco, S. Copper Accumulation in Vineyard Soils: Rhizosphere Processes and Agronomic Practices to Limit Its Toxicity. Chemosphere 2016, 162, 293–307. [Google Scholar] [CrossRef]
- Brunetto, G.; Miotto, A.; Ceretta, C.A.; Schmitt, D.E.; Heinzen, J.; de Moraes, M.P.; Canton, L.; Tiecher, T.L.; Comin, J.J.; Girotto, E. Mobility of Copper and Zinc Fractions in Fungicide-Amended Vineyard Sandy Soils. Arch. Agron. Soil Sci. 2014, 60, 609–624. [Google Scholar] [CrossRef]
- Rogiers, S.Y.; Coetzee, Z.A.; Walker, R.R.; Deloire, A.; Tyerman, S.D. Potassium in the Grape (Vitis vinifera L.) Berry: Transport and Function. Front. Plant Sci. 2017, 8, 01629. [Google Scholar] [CrossRef] [PubMed]
- Mpelasoka, B.S.; Schachtman, D.P.; Treeby, M.T.; Thomas, M.R. A Review of Potassium Nutrition in Grapevines with Special Emphasis on Berry Accumulation. Aust. J. Grape Wine Res. 2003, 9, 154–168. [Google Scholar] [CrossRef]
- Alloway, B.J. Micronutrients and Crop Production: An Introduction. In Micronutrient Deficiencies in Global Crop Production; Alloway, B.J., Ed.; Springer: Dordrecht, The Netherlands, 2008; pp. 1–39. ISBN 978-1-4020-6860-7. [Google Scholar]
- Ghorbani, P.; Eshghi, S.; Ershadi, A.; Shekafandeh, A.; Razzaghi, F. The Possible Role of Foliar Application of Manganese Sulfate on Mitigating Adverse Effects of Water Stress in Grapevine. Commun. Soil Sci. Plant Anal. 2019, 50, 1550–1562. [Google Scholar] [CrossRef]
- Gatti, M.; Garavani, A.; Squeri, C.; Diti, I.; De Monte, A.; Scotti, C.; Poni, S. Effects of Intra-Vineyard Variability and Soil Heterogeneity on Vine Performance, Dry Matter and Nutrient Partitioning. Precis. Agric 2022, 23, 150–177. [Google Scholar] [CrossRef]
- Paccioretti, P.; Bruno, C.; Gianinni Kurina, F.; Córdoba, M.; Bullock, D.S.; Balzarini, M. Statistical Models of Yield in On-farm Precision Experimentation. Agron. J. 2021, 113, 4916–4929. [Google Scholar] [CrossRef]
- Grund, S.; Lüdtke, O.; Robitzsch, A. Multiple Imputation of Missing Data in Multilevel Models with the R Package Mdmb: A Flexible Sequential Modeling Approach. Behav. Res. Methods 2021, 53, 2631–2649. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Lagos, J.E.; González-Araya, M.C.; Ortega Blu, R.; Acosta Espejo, L.G. A New Method Based on Machine Learning to Forecast Fruit Yield Using Spectrometric Data: Analysis in a Fruit Supply Chain Context. Precis. Agric 2023, 24, 326–352. [Google Scholar] [CrossRef]
- Melo, G.W.; Rozane, D.E.; Brunetto, G.; Lattuada, D.S.; Brasileira, E.; Agropecua, D.P.; Gonçalves, B.; Grande, R. Discriminant Analysis in the Selection of Groups of Peach Cultivars. Acta Hortic. 2018, 1217, 335–342. [Google Scholar] [CrossRef]
- Parent, S.É.; Parent, L.E.; Rozane, D.E.; Natale, W. Plant Ionome Diagnosis Using Sound Balances: Case Study with Mango (Mangifera indica). Front. Plant Sci. 2013, 4, 00449. [Google Scholar] [CrossRef]
- Andrade, C.B.; Comin, J.J.; Moura-Bueno, J.M.; Brunetto, G. Obtaining Reference Values for Nutrients in Vineyard Soils through Boundary Line Approach Using Bayesian Segmented Quantile Regression on Commercial Farm Data. Eur. J. Agron. 2023, 150, 126928. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).