Effect of Dissolved Carbon Dioxide on Cavitation in a Circular Orifice
Abstract
1. Introduction
1.1. Experimental Studies on Orifice Cavitation
1.2. Numerical Studies on Orifice Cavitation and the Effect of Dissolved Gases on Cavitation
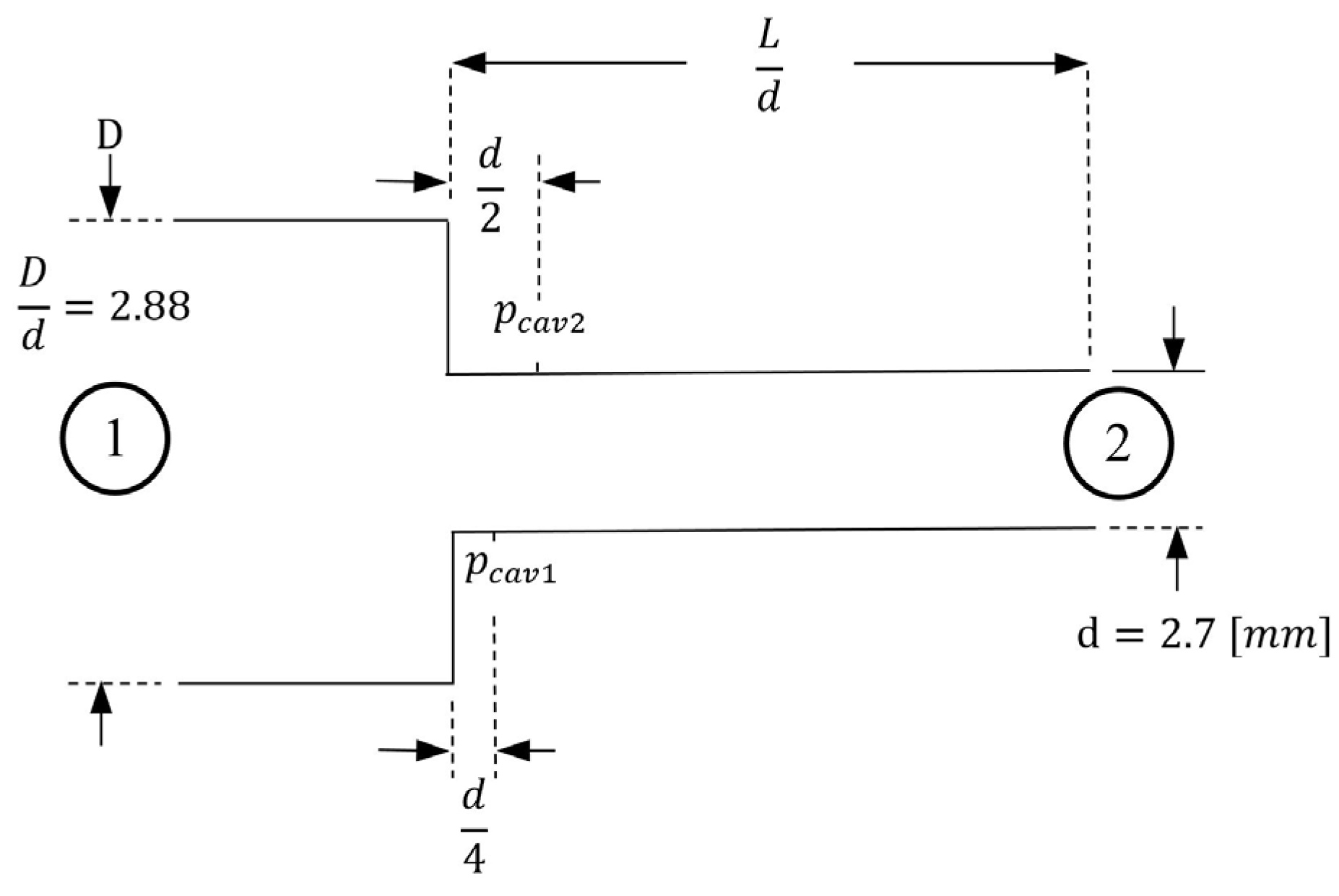
2. Basic Definitions for Orifice Flows
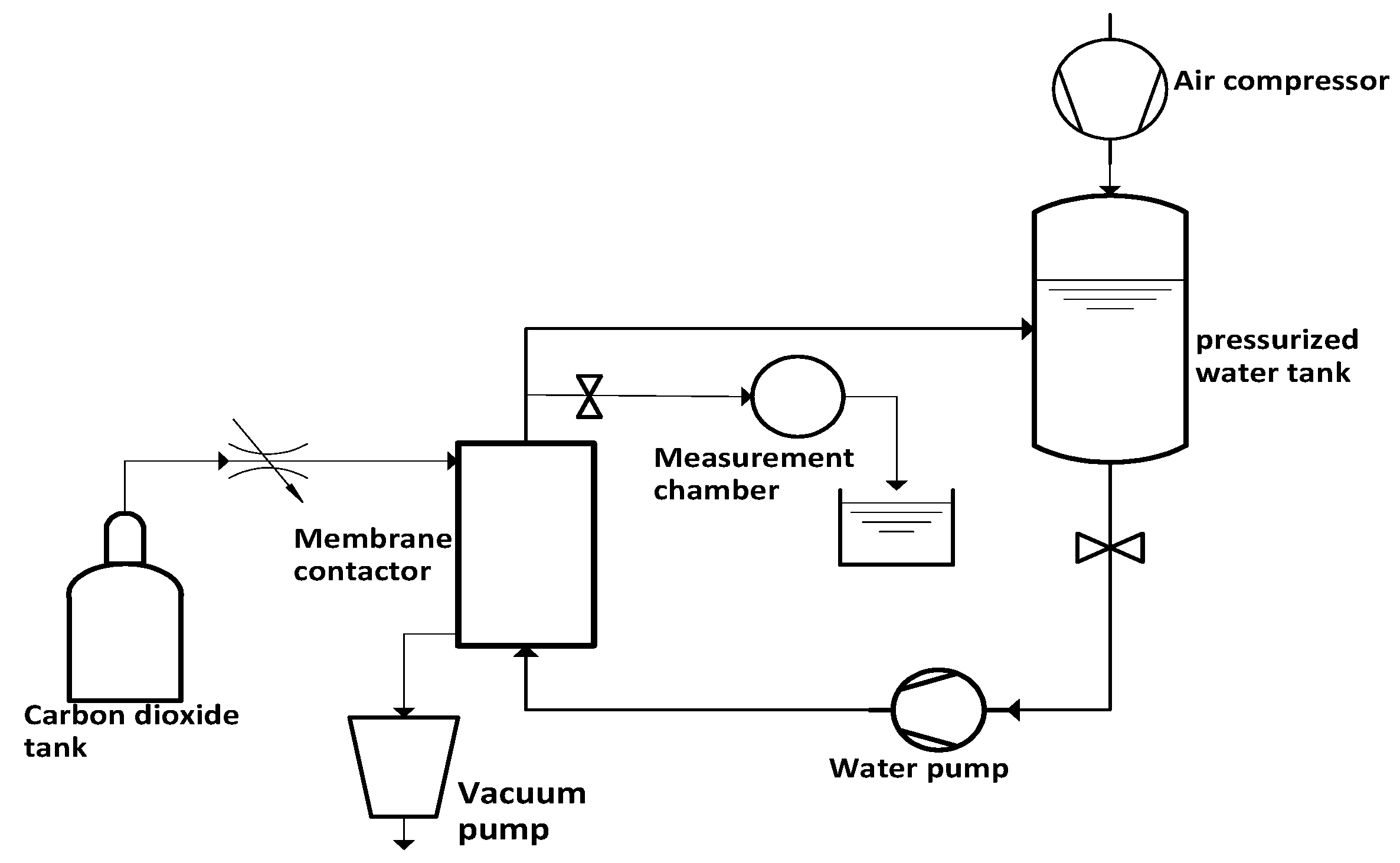
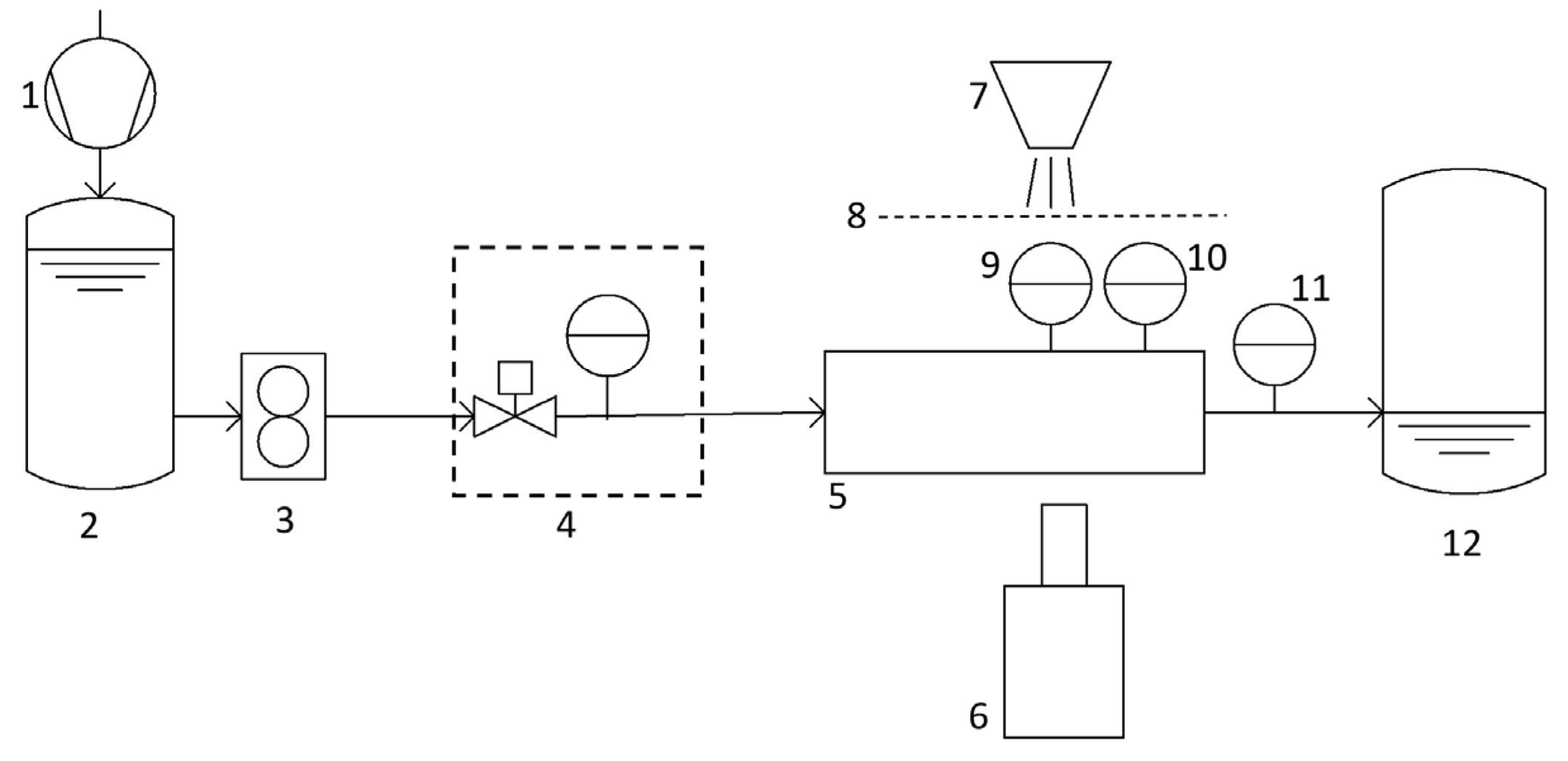
3. Experimental Test Setup
3.1. Water-Preparation Cycle
3.2. Cavitating Orifice Flow–Flow Measurements
3.3. Cavitating Orifice Flow–Flow Visualization
4. Numerical Analysis Model
5. Results
5.1. Experimental Results
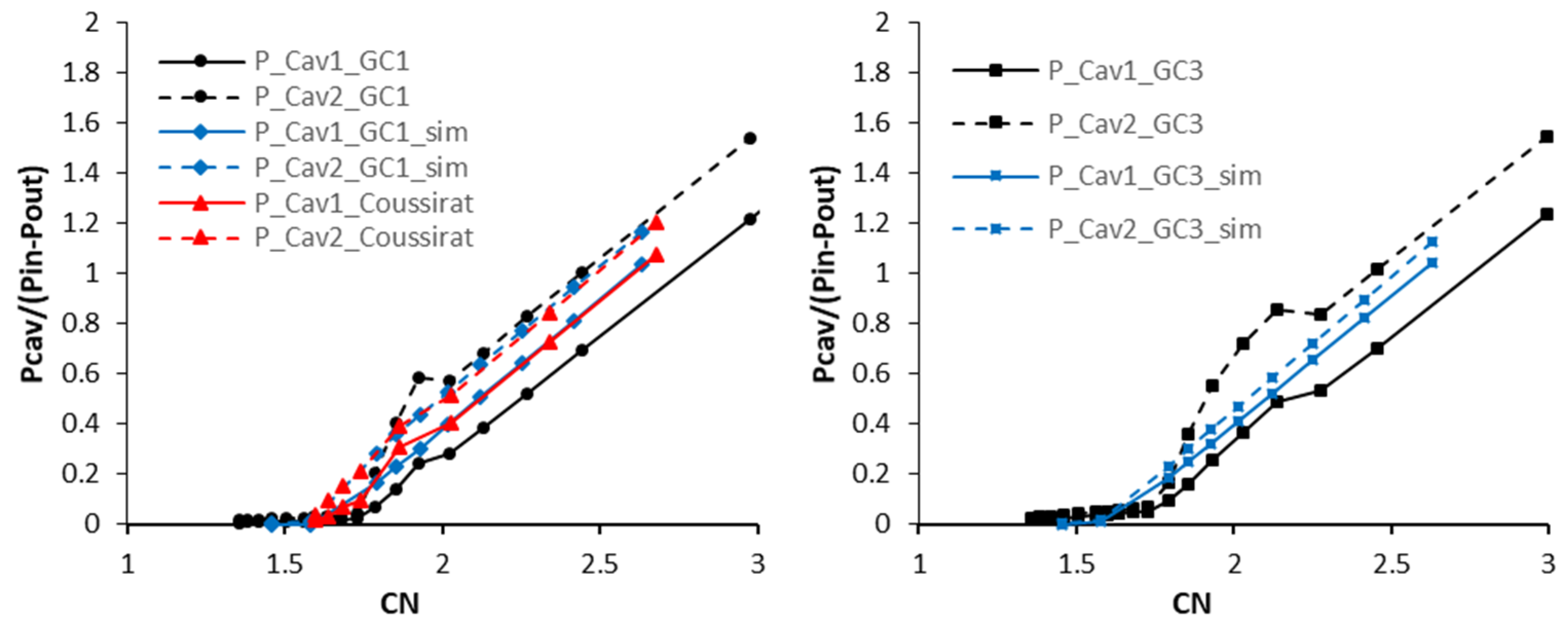
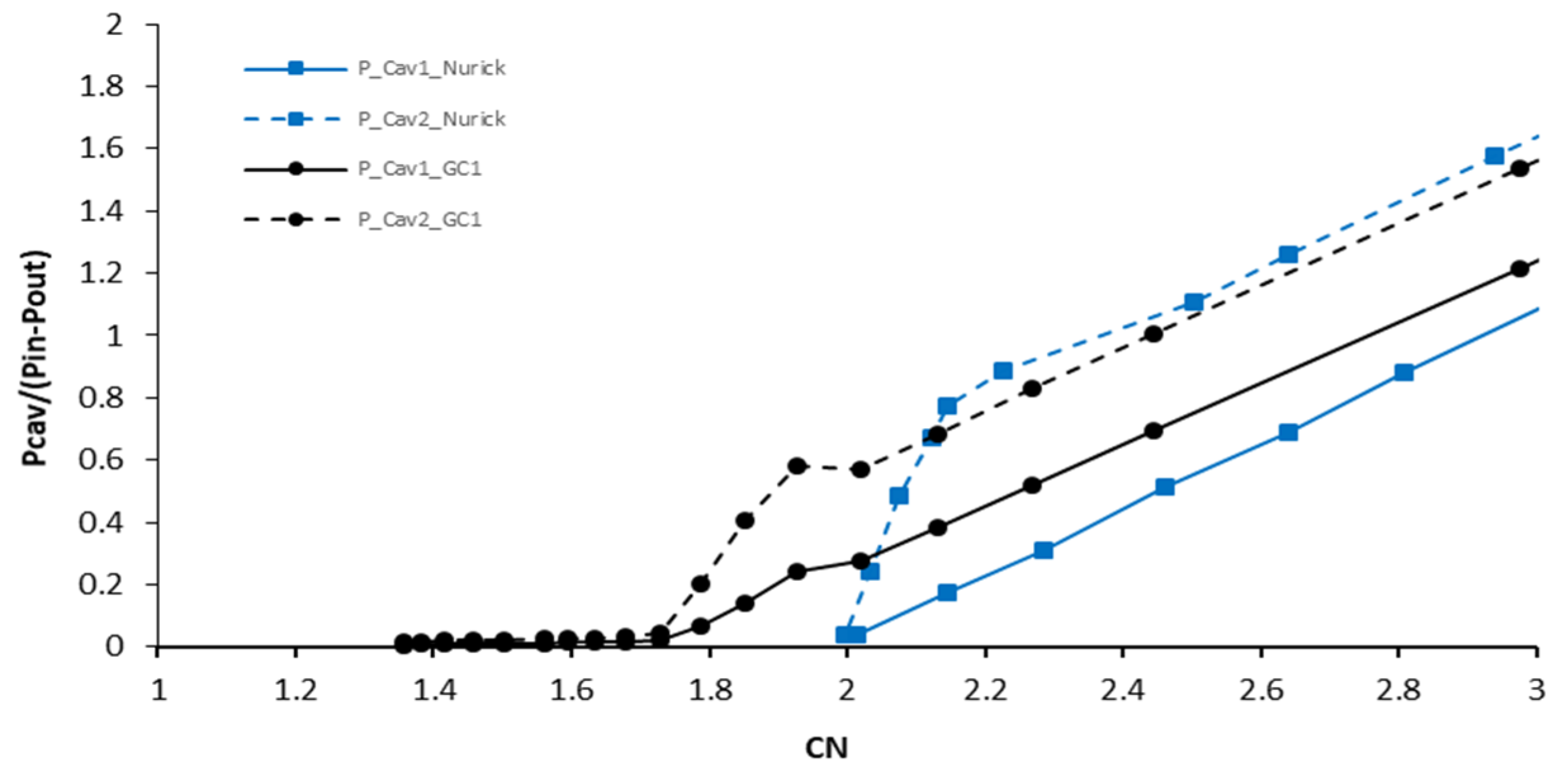
5.1.1. Comparison of Measured Cavity Pressures with Results from Nurick Experiments
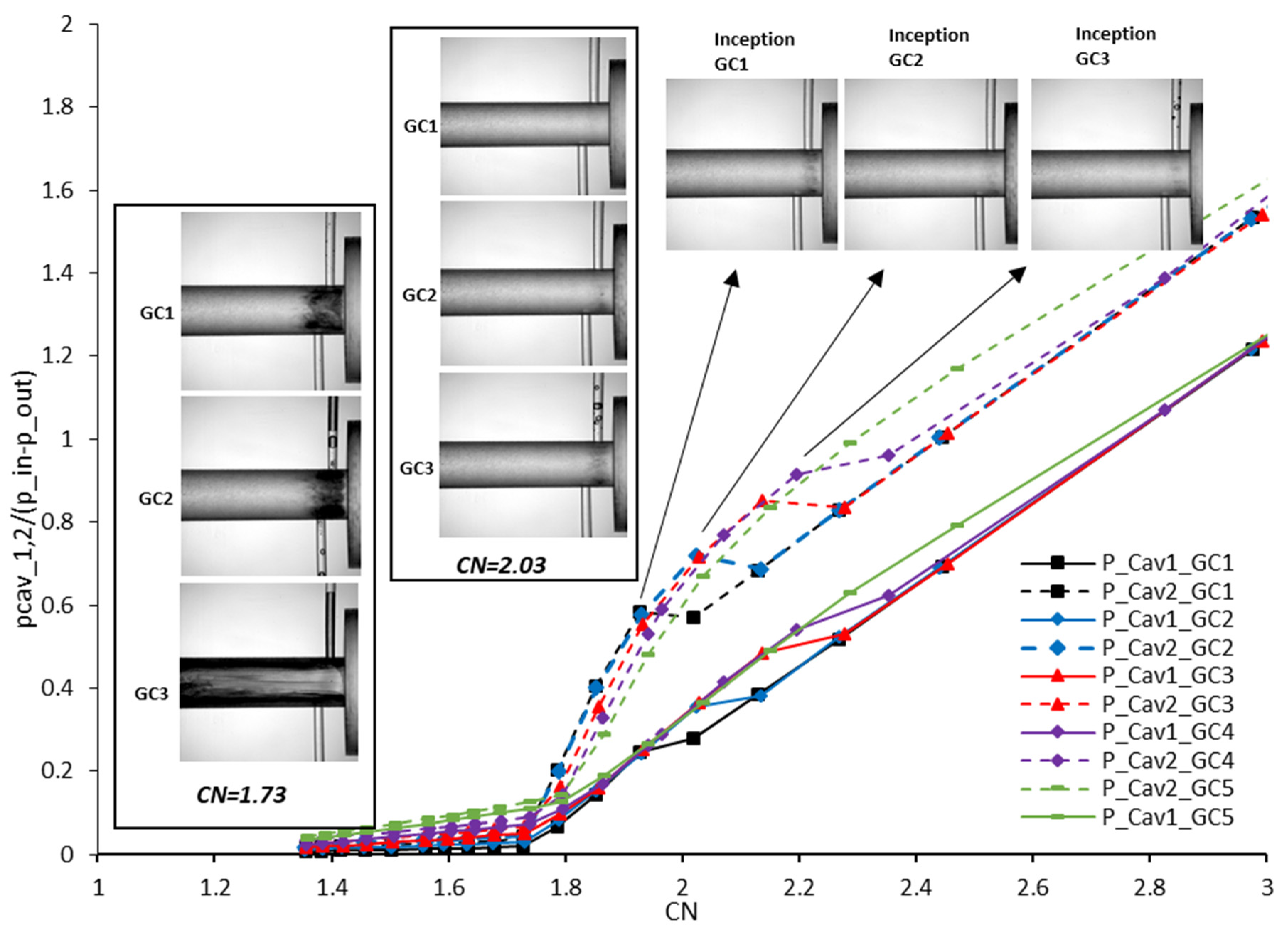
5.1.2. Influence of Dissolved Gas on Cavitation Inception



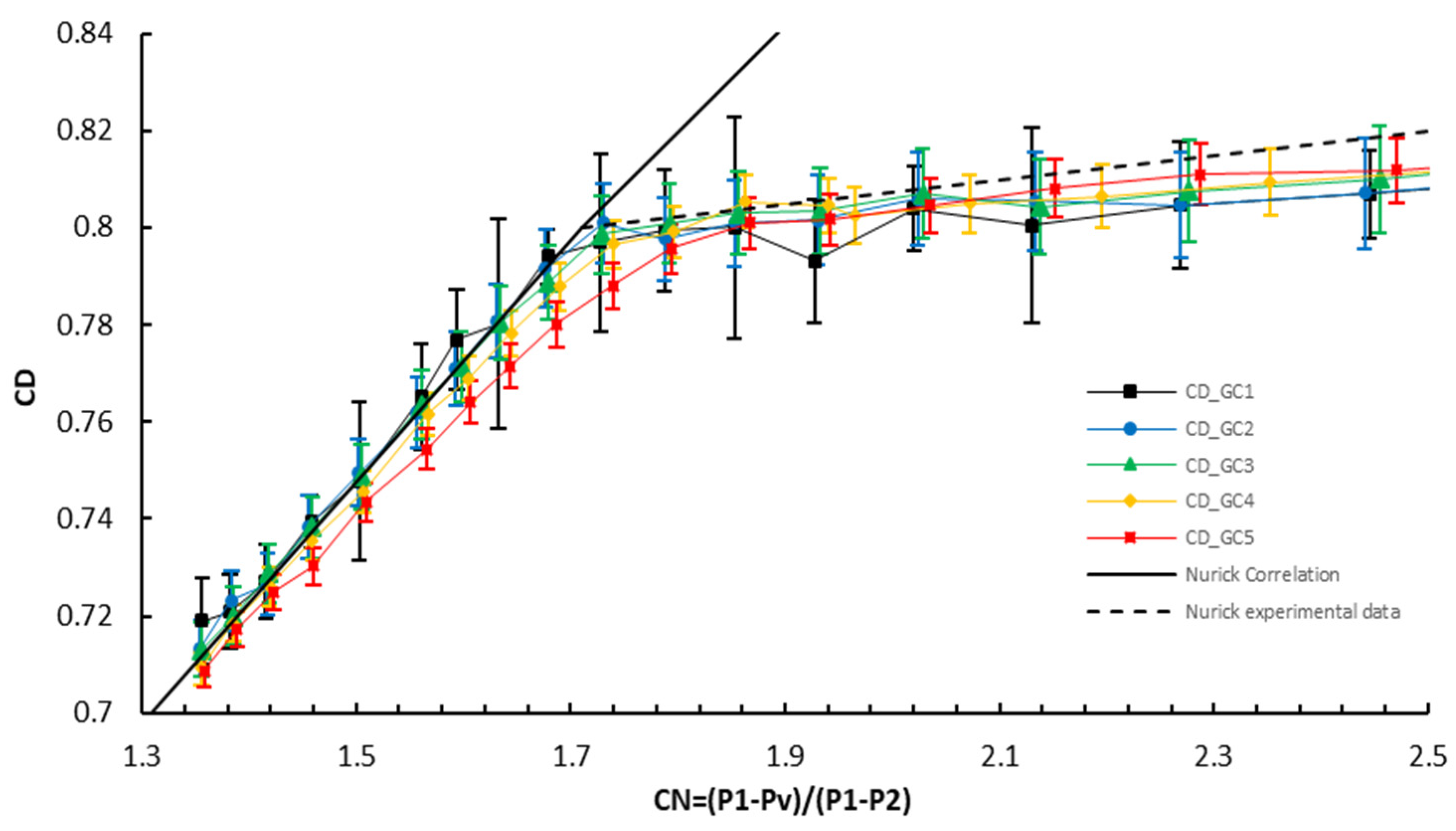
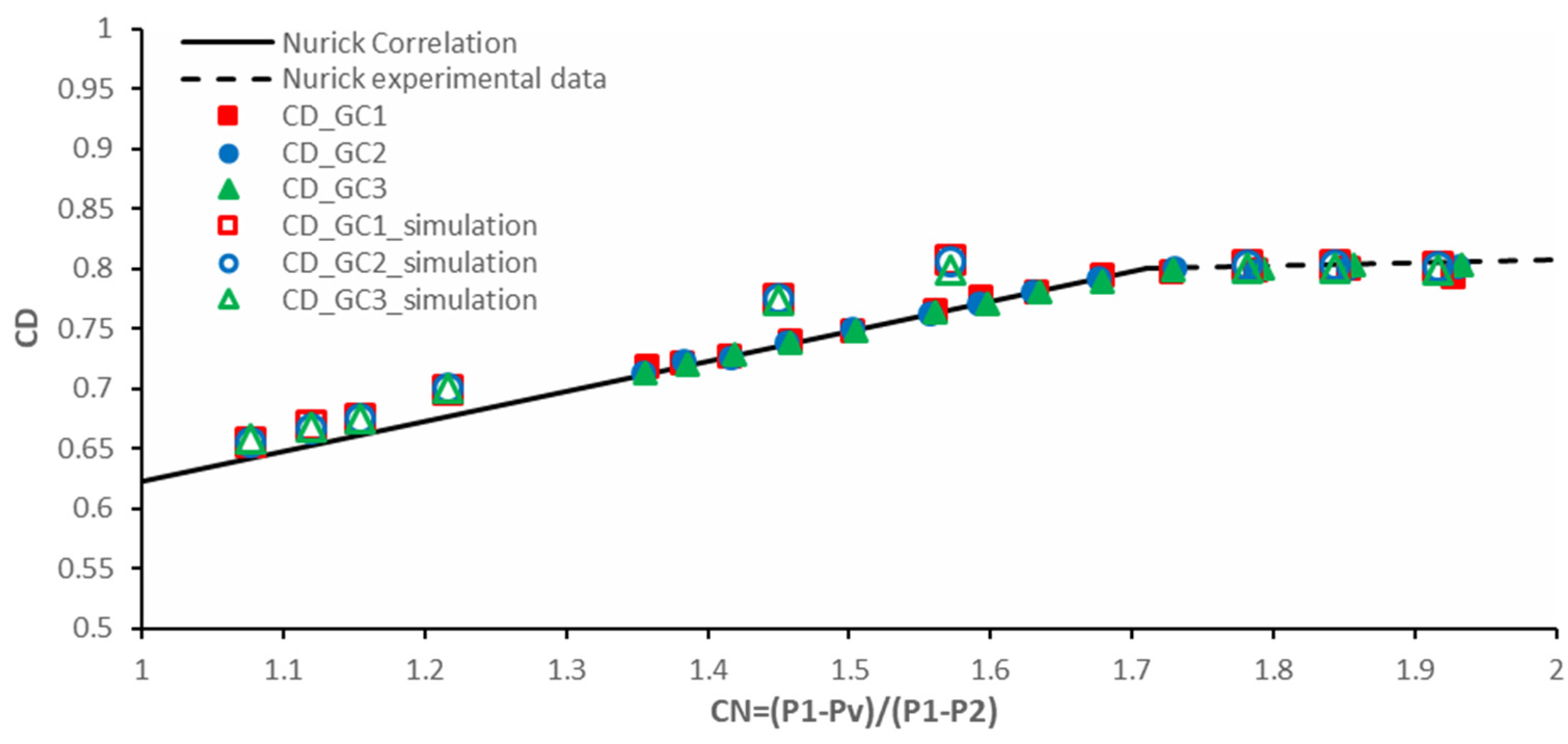
5.1.3. Measurements of the Discharge Coefficient
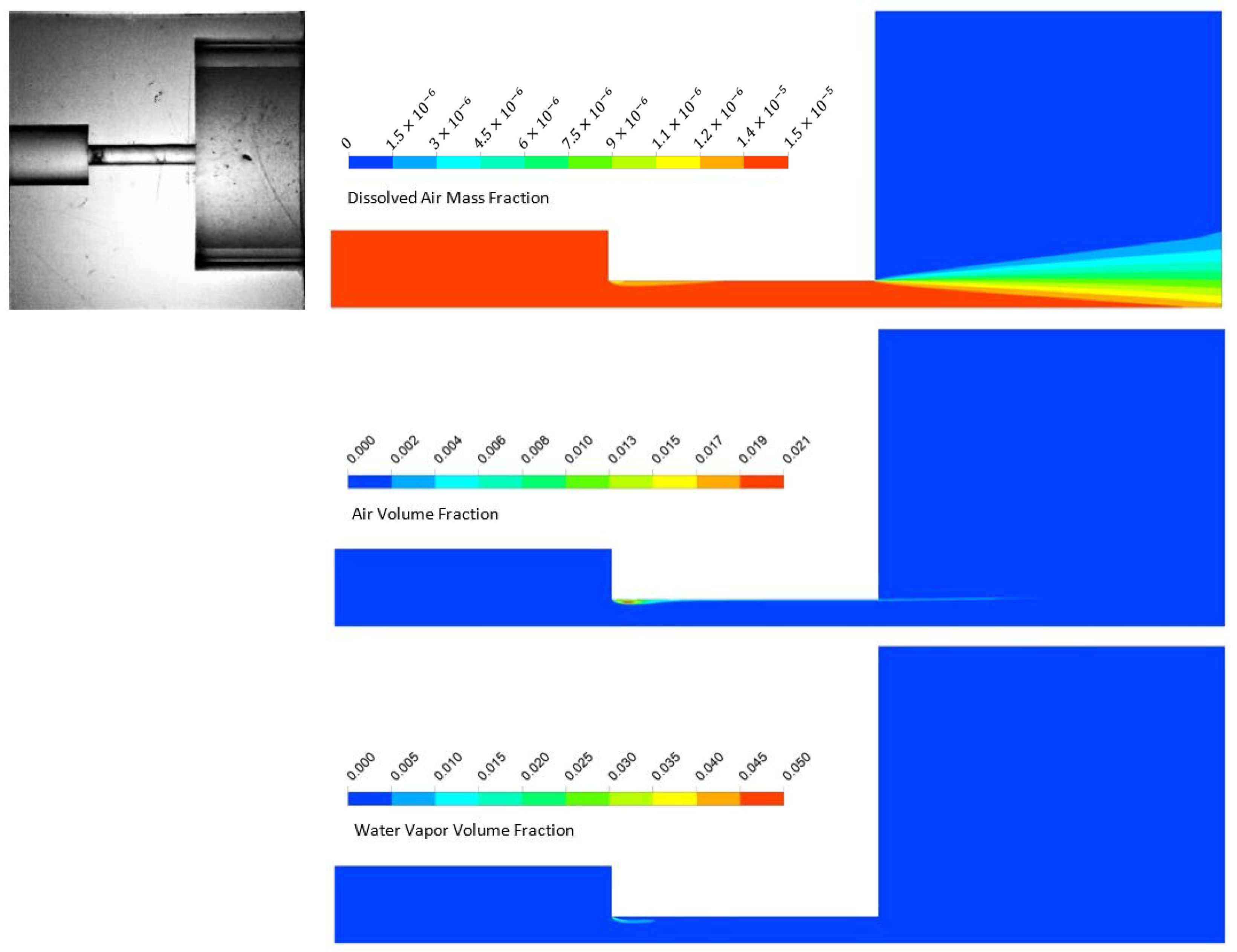
5.2. Numerical Analysis Results


6. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Brennen, C. Cavitation and Bubble Dynamics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Brennen, C. Fundamentals of Multiphase Flow; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Franc, J.-P.; Michel, J.-M. Fundamentals of Cavitation. In Fluid Mechanics and Its Applications; Moreau, R., Ed.; Springer Science & Business Media: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Perk, O.Y.; Şeşen, M.; Gozuacik, D.; Koşar, A. Kidney stone erosion by micro scale hydrodynamic cavitation and consequent kidney stone treatment. Ann. Biomed. Eng. 2012, 40, 1895–1902. [Google Scholar] [CrossRef]
- Zijlstra, A.G. Acoustic Surface Cavitation. Ph.D. Dissertation, University of Twente, Enschede, The Netherlands, 2011. [Google Scholar]
- Vasile, E.; Ciocanea, A.; Ionescu, V.; Lepadatu, I.; Diac, C.; Stamatin, S.N. Making precious metals cheap: A sonoelectrochemical–Hydrodynamic cavitation method to recycle platinum group metals from spent automotive catalysts. Ultrason. Sonochem. 2021, 72, 105404. [Google Scholar] [CrossRef]
- Kim, M.; Kim, D.; Cho, J.M.; Nam, K.; Lee, H.; Nayak, M.; Han, J.; Oh, H.-M.; Chang, Y.K. Hydrodynamic cavitation for bacterial disinfection and medium recycling for sustainable Ettlia sp. Cultivation. J. Environ. Chem. Eng. 2021, 9, 105411. [Google Scholar] [CrossRef]
- Kosel, J.; Šuštaršič, M.; Petkovšek, M.; Zupanc, M.; Sežun, M.; Dular, M. Application of (super) cavitation for the recycling of process waters in paper producing industry. Ultrason. Sonochemistry 2020, 64, 105002. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Hou, R.; Zhang, W.; Liu, J. Hydrodynamic cavitation as an efficient water treatment method for various sewage: A review. Water Sci. Technol. 2022, 86, 302–320. [Google Scholar] [CrossRef]
- Gogate, P.R.; Pandit, A.B. Cavitation generation and usage without ultrasound: Hydrodynamic cavitation. Theor. Exp. Sonochem. Involv. Inorg. Syst. 2011, 69–106. [Google Scholar] [CrossRef]
- Li, B.; Gu, Y.; Chen, M. An experimental study on the cavitation of water with dissolved gases. Exp. Fluids 2017, 58, 164. [Google Scholar] [CrossRef]
- Mehring, C. Liquid-Fuel Ejector Pump under Multiphase-Flow Conditions. In Proceedings of the 25th European Conference on Liquid Atomization and Spray Systems, Chania, Greece, 1–4 September 2013. [Google Scholar]
- Zheng, H.; Zheng, Y.; Zhu, J. Recent developments in hydrodynamic cavitation reactors: Cavitation mechanism, reactor design, and applications. Engineering 2022, 19, 180–198. [Google Scholar] [CrossRef]
- Nurick, W.H. Orifice cavitation and its effect on spray mixing. J. Flusids Eng. 1976, 98, 681–687. [Google Scholar] [CrossRef]
- Arakeri, V.H. Cavitation inception. Proc. Indian Acad. Sci. Sect. C Eng. Sci. 1979, 2, 149–177. [Google Scholar] [CrossRef]
- Nurick, W.H.; Ohanian, T.; Talley, D.G.; Strakey, P.A. Impact of L/D on 90 Degree Sharp-Edge Orifice Flow with Manifold Passage Cross Flow (Preprint). J. Artic. 2007, 30, 2. [Google Scholar]
- Yan, Y.; Thorpe, R.B. Flow regime transitions due to cavitation in the flow through an orifice. Int. J. Multiph. Flow 1990, 16, 1023–1045. [Google Scholar] [CrossRef]
- Mishra, C.; Peles, Y. Cavitation in flow through a micro-orifice inside a silicon microchannel. Phys. Fluids 2005, 17, 013601. [Google Scholar] [CrossRef]
- Zhang, H.; Zuo, Z.; Liu, S. Influence of Dissolved Gas Content on Venturi Cavitation at Thermally Sensitive Conditions. In Proceedings of the 10th International Symposium on Cavitation (CAV2018), Baltimore, MD, USA, 14–16 May 2018; pp. 546–550. [Google Scholar]
- Rooze, J. Cavitation in Gas-Saturated Liquids. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2012. [Google Scholar]
- Freudigmann, H.A.; Dörr, A.; Iben, U.; Pelz, P.F. Modeling of cavitation-induced air release phenomena in micro-orifice flows. J. Fluids Eng. 2017, 139, 111301. [Google Scholar] [CrossRef]
- Kowalski, K.; Pollak, S.; Skoda, R.; Hussong, J. Experimental study on cavitation-induced air release in orifice flows. ASME J. Fluids Eng. 2018, 140, 061201. [Google Scholar] [CrossRef]
- Duke, D.; Kastengren, A.L.; Tilocco, F.Z.; Swantek, A.B.; Powell, C.F. X-ray radiography measurements of cavitating nozzle flow. At. Sprays 2013, 23. [Google Scholar] [CrossRef]
- Duke, D.J.; Swantek, A.B.; Kastengren, A.L.; Powell, C.F. X-ray diagnostics for cavitating nozzle flow. J. Phys. Conf. Ser. 2015, 656, 012110. [Google Scholar] [CrossRef]
- Duke, D.J.; Matusik, K.E.; Kastengren, A.L.; Swantek, A.B.; Sovis, N.; Payri, R.; Viera, J.P.; Powell, C.F. X-ray radiography of cavitation in a beryllium alloy nozzle. Int. J. Engine Res. 2017, 18, 39–50. [Google Scholar] [CrossRef]
- Sou, A.; Biçer, B.; Tomiyama, A. Numerical simulation of incipient cavitation flow in a nozzle of fuel injector. Comput. Fluids 2014, 103, 42–48. [Google Scholar] [CrossRef]
- Schnerr, G.H.; Sauer, J. Physical and Numerical Modeling of Unsteady Cavitation Dynamics. In Proceedings of the Fourth International Conference on Multiphase Flow (Vol. 1), New Orleans, LO, USA, 27 May–1 June 2001. [Google Scholar]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T.R. A preconditioned Navier–Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A Two-Phase Flow Model for Predicting Cavitation Dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004; p. 152. [Google Scholar]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical basis and validation of the full cavitation model. ASME J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Battistoni, M.; Som, S.; Longman, D.E. Comparison of mixture and multifluid models for in-nozzle cavitation prediction. J. Eng. Gas Turbines Power 2014, 136, 061506. [Google Scholar] [CrossRef]
- Li, W.; Yu, Z. Cavitation models with thermodynamic effect for organic fluid cavitating flows in organic Rankine cycle systems: A review. Therm. Sci. Eng. Prog. 2021, 26, 101079. [Google Scholar] [CrossRef]
- Battistoni, M.; Duke, D.; Swantek, A.B.; Tilocco, F.Z.; Powell, C.F.; Som, S. Effects of noncondensable gas on cavitating nozzles. At. Sprays 2015, 25. [Google Scholar] [CrossRef]
- Yang, S.; Habchi, C. Real-fluid phase transition in cavitation modeling considering dissolved non-condensable gas. Phys. Fluids 2020, 32, 032102. [Google Scholar] [CrossRef]
- Amini, A.; Reclari, M.; Sano, T.; Farhat, M. Effect of Gas Content on Tip Vortex Cavitation. In Proceedings of the 10th International Symposium on Cavitation (CAV2018), Baltimore, MD, USA, 14–16 May 2018. [Google Scholar]
- Mukherjee, S.; Gomez, H. Effect of dissolved gas on the tensile strength of water. Phys. Fluids 2022, 34, 126112. [Google Scholar] [CrossRef]
- Iben, U.; Makhnov, A.; Schmidt, A. Numerical study of the effects of dissolved gas release in cavitating flow. AIP Conf. Proc. 2018, 2027, 030128. [Google Scholar]
- Iben, U.; Makhnov, A.; Schmidt, A. Numerical study of dissolved gas release induced by cavitation in a high speed channel flow. J. Phys. Conf. Ser. 2019, 1400, 077037. [Google Scholar] [CrossRef]
- Malekshah, E.H.; Wróblewski, W. Merging theory-based cavitation model adaptable with non-condensable gas effects in prediction of compressible three-phase cavitating flow. Int. J. Heat Mass Transf. 2022, 196, 123279. [Google Scholar] [CrossRef]
- Richards, K.; Senecal, P.; Pomraning, E. Converge 2.1.0 Theory Manual; Convergent Science Inc.: Middleton, WI, USA, 2013. [Google Scholar]
- Bohbot, J.; Gillet, N.; Benkenida, A. IFP-C3D: An unstructured parallel solver for reactive compressible gas flow with spray. Oil Gas Sci. Technol.-Rev. De L’ifp 2009, 64, 309–335. [Google Scholar] [CrossRef]
- Darbandi, M.; Sadegh, H.; Schneider, G.E. Simulating Orifice Cavitation Using the Full Cavitation Model. In Proceedings of the 17th Annual Conference of the CFD Society of Canada, Ottawa, ON, Canada, 3–5 May 2009. [Google Scholar]
- Darbandi, M.; Sadeghi, H. Numerical simulation of orifice cavitating flows using two-fluid and three-fluid cavitation models. Numer. Heat Transf. Part A Appl. 2010, 58, 505–526. [Google Scholar] [CrossRef]
- Lifante, C.; Frank, T. Investigation of Higher Order Pressure Fluctuations and Its Influence on Ship Stern, Taking into Account Cavitation at Propeller Blades; TR-08-04; ANSYS Germany GmbH: Berlin, Germany, 2008. [Google Scholar]
- Yang, H.Q.; Singhal, A.K.; Megahed, M. Industrial two-phase flow CFD—The Full Cavitation Model. Von Karman Inst. Fluid Dyn. Lect. Ser. 2005, 4. [Google Scholar]
- Coussirat, M.; Moll, F.; Cappa, F.; Fontanals, A. Study of Available Turbulence and Cavitation Models to Reproduce Flow Patterns in Confined Flows. ASME. J. Fluids Eng. 2016, 138, 091304. [Google Scholar] [CrossRef]
- Stanley, C.; Barber, T.; Milton, B.; Rosengarten, G. Periodic cavitation shedding in a cylindrical orifice. Exp. Fluids 2011, 51, 1189–1200. [Google Scholar] [CrossRef]
- Mauger, C.; Méès, L.; Michard, M.; Azouzi, A.; Valette, S. Shadowgraph, Schlieren and interferometry in a 2D cavitating channel flow. Exp. Fluids 2012, 53, 1895–1913. [Google Scholar] [CrossRef]
- Saurabh, A. Cavitation in Injectors: A Brief Review of the Diagnostics of Liquid-Vapour Flow Within Injector Nozzles. Simulations and Optical Diagnostics for Internal Combustion Engines. Curr. Status Way Forw. 2020, 85–93. [Google Scholar] [CrossRef]
- Menter, F. Zonal Two Equation kw Turbulence Models for Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; p. 2906. [Google Scholar]
- Peterson, F.B. Discussion: “Orifice Cavitation and Its Effect on Spray Mixing” (Nurick, W.H., 1976, ASME J. Fluids Eng., 98, pp. 681–687). ASME. J. Fluids Eng. 1977, 99, 426. [Google Scholar] [CrossRef][Green Version]
- Winklhofer, E.; Kull, E.; Kelz, E.; Morozov, A. Comprehensive Hydraulic and Flow Field Documentation in Model Throttle Experiments under Cavitation Conditions. In Proceedings of the ILASS-Europe Conference, Zurich, Switzerland, 2–6 September 2001; pp. 574–579. [Google Scholar]
- Martynov, S.; Mason, D.; Heikal, M.R.; Sazhin, S.S.; Gorokhovski, M. Modelling of Cavitation Flow in a Nozzle and Its Effect on Spray Development. In Proceedings of the International Heat Transfer Conference 13, Sydney, Australia, 13–18 August 2006; Begel House Inc.: New York, NY, USA, 2006. [Google Scholar]
- IEC 60770; Transmitters for Use in Industrial-Process Control Systems—Part 1: Methods for Performance Evaluation. International Electrotechnical Commission: Geneva, Switzerland, 2010.
- Battino, R.; Clever, H.L. The solubility of gases in liquids. Chem. Rev. 1966, 66, 395–463. [Google Scholar] [CrossRef]
- Manninen, M.; Taivassalo, V.; Kallio, S. On the Mixture Model for Multiphase Flow; Technical Research Center of Finland, VIT Publications 288: Espoo, Finland, 1996. [Google Scholar]
- Joseph, D.D. Cavitation and the state of stress in a flowing liquid. J. Fluid Mech. 1998, 366, 367–378. [Google Scholar] [CrossRef]
- Martynov, S.B.; Mason, D.J.; Heikal, M.R. Effect of Viscous Stress on Cavitation Flow in Nozzles. J. Fluids Eng. 2006, 9, 2006. [Google Scholar]





| Gas Type | Mass Concentration [ppm] | ||||
|---|---|---|---|---|---|
| GC1 | GC2 | GC3 | GC4 | GC5 | |
| Carbon dioxide | 0 | 318 | 707 | 1060 | 1493 |
| Oxygen | 0.85 | 1.09 | 0.42 | 1.02 | 0.52 |
| Nitrogen | 2.03 | 2.41 | 1.30 | 2.28 | 1.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safaei, S.; Mehring, C. Effect of Dissolved Carbon Dioxide on Cavitation in a Circular Orifice. Fluids 2024, 9, 41. https://doi.org/10.3390/fluids9020041
Safaei S, Mehring C. Effect of Dissolved Carbon Dioxide on Cavitation in a Circular Orifice. Fluids. 2024; 9(2):41. https://doi.org/10.3390/fluids9020041
Chicago/Turabian StyleSafaei, Sina, and Carsten Mehring. 2024. "Effect of Dissolved Carbon Dioxide on Cavitation in a Circular Orifice" Fluids 9, no. 2: 41. https://doi.org/10.3390/fluids9020041
APA StyleSafaei, S., & Mehring, C. (2024). Effect of Dissolved Carbon Dioxide on Cavitation in a Circular Orifice. Fluids, 9(2), 41. https://doi.org/10.3390/fluids9020041






