Application of Central-Weighted Essentially Non-Oscillatory Finite-Volume Interface-Capturing Schemes for Modeling Cavitation Induced by an Underwater Explosion
Abstract
1. Introduction
2. The Five-Equation Diffuse Interface Model
Cut-Off Methods
3. Numerical Model
3.1. Finite-Volume Framework
3.2. CWENO Scheme
3.3. Fluxes and Time Advancement
4. Test Cases
- 2D underwater explosion near a free surface.
- 2D cylindrical underwater explosion near a planar rigid wall.
- 3D underwater explosion in an enclosed, rigid cylindrical wall.
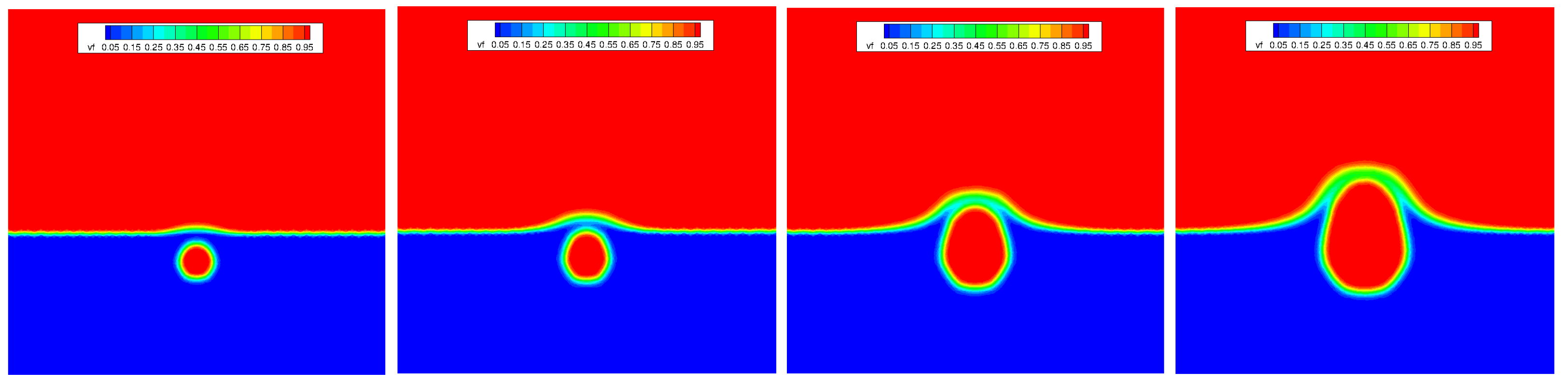
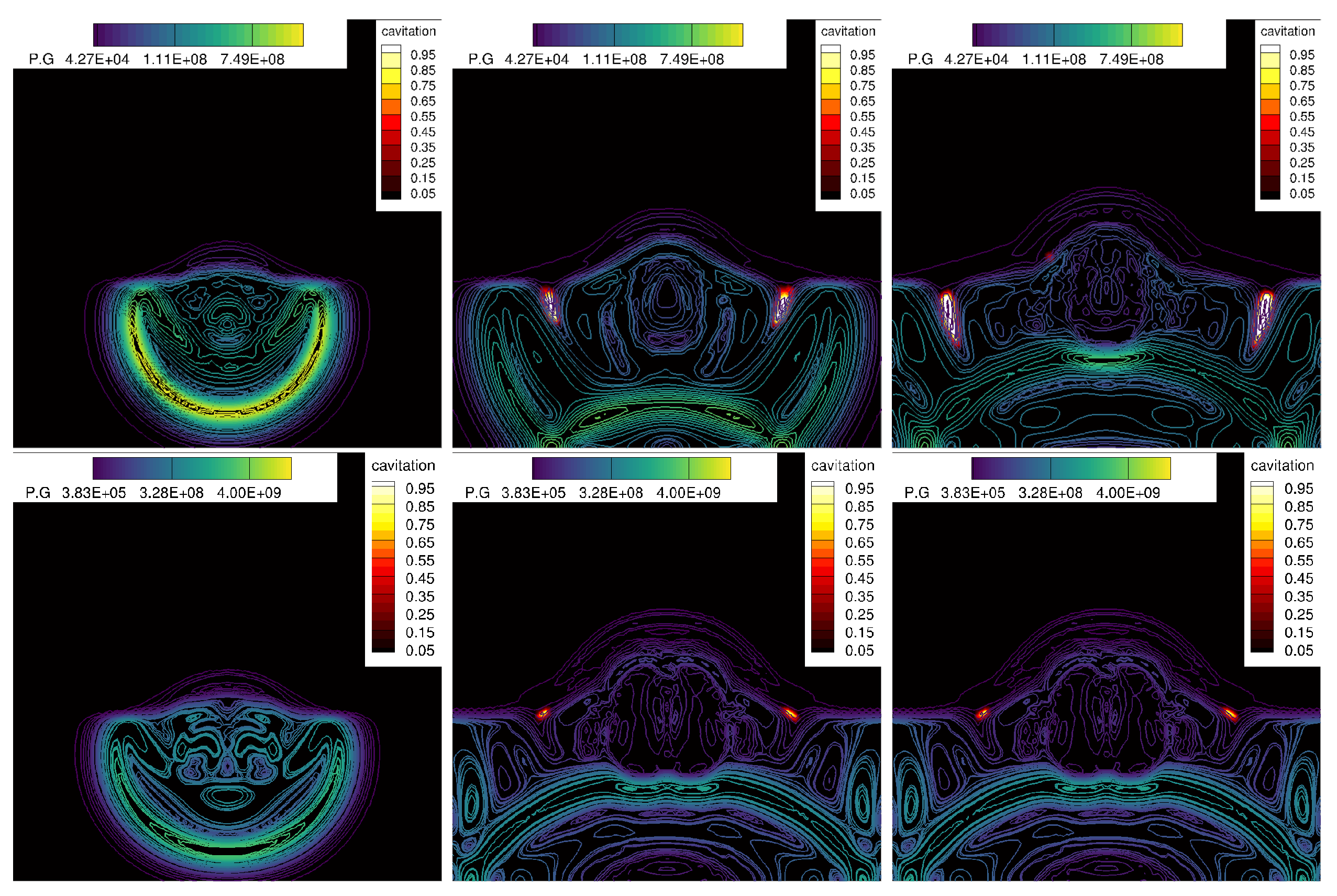
- 2D underwater explosion of two bubbles placed horizontally near a free surface.
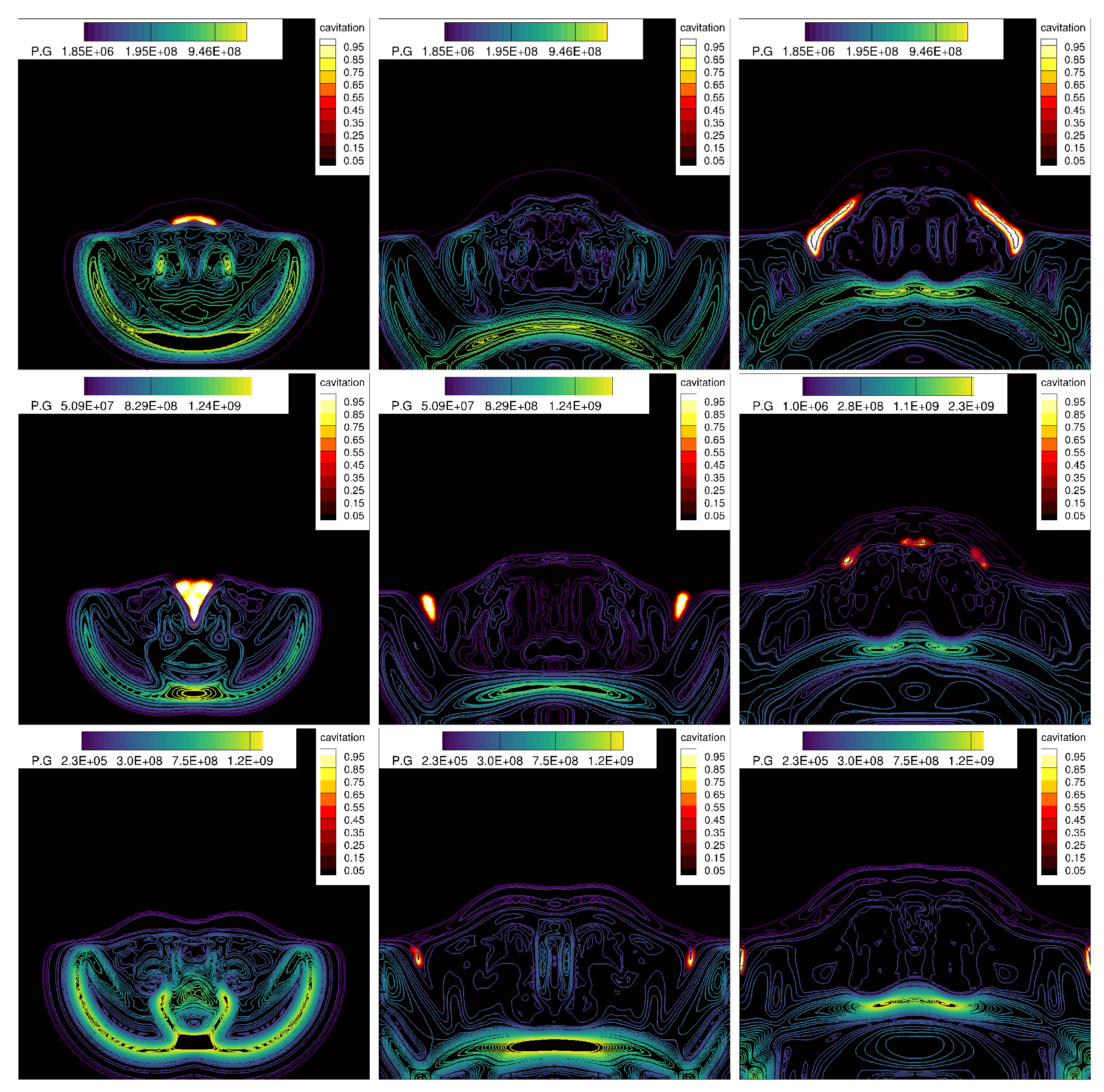
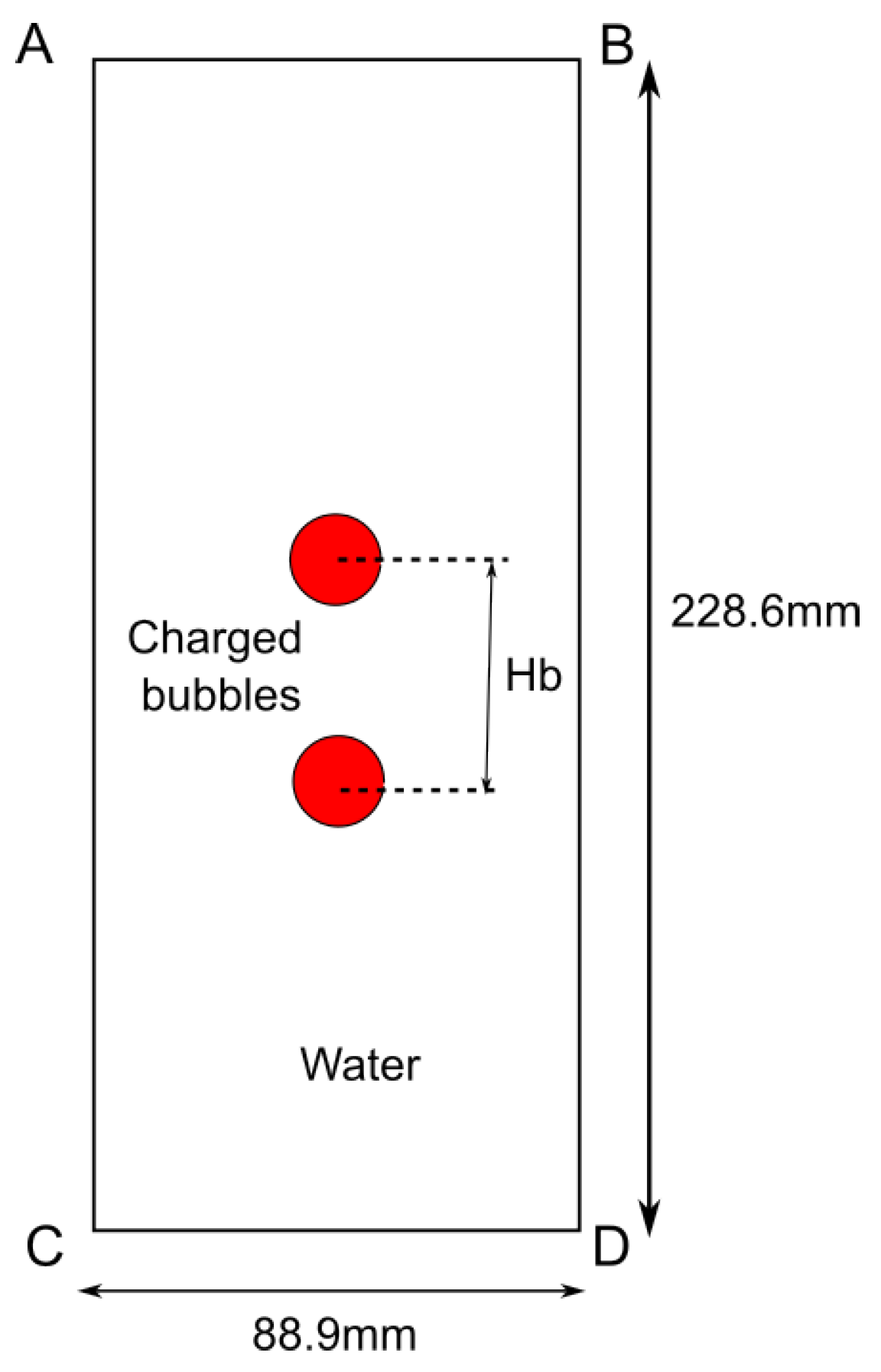
- 3D underwater of two bubbles placed vertically in an enclosed region.
| Test Cases | Materials | u | v | p | |||
|---|---|---|---|---|---|---|---|
| Test 4.1 | Air | 1.225 | 0 | 0 | 2.0 | 0 | |
| Explosive | 1250 | 0 | 0 | 2.0 | 1 | ||
| Water | 1000 | 0 | 0 | 7.15 | 0 | ||
| Test 4.2 | Explosive | 1270 | 0 | 0 | 2.0 | 1 | |
| Water | 1000 | 0 | 0 | 7.15 | 0 | ||
| Test 4.3 | Explosive | 1770 | 0 | 0 | 2.0 | 1 | |
| Water | 1000 | 0 | 0 | 7.15 | 0 | ||
| Test 4.4 | Air | 1.225 | 0 | 0 | 2.0 | 0 | |
| Explosive | 1250 | 0 | 0 | 2.0 | 1 | ||
| Water | 1000 | 0 | 0 | 7.15 | 0 | ||
| Test 4.5 | Explosive | 1770 | 0 | 0 | 2.0 | 1 | |
| Water | 1000 | 0 | 0 | 7.15 | 0 |
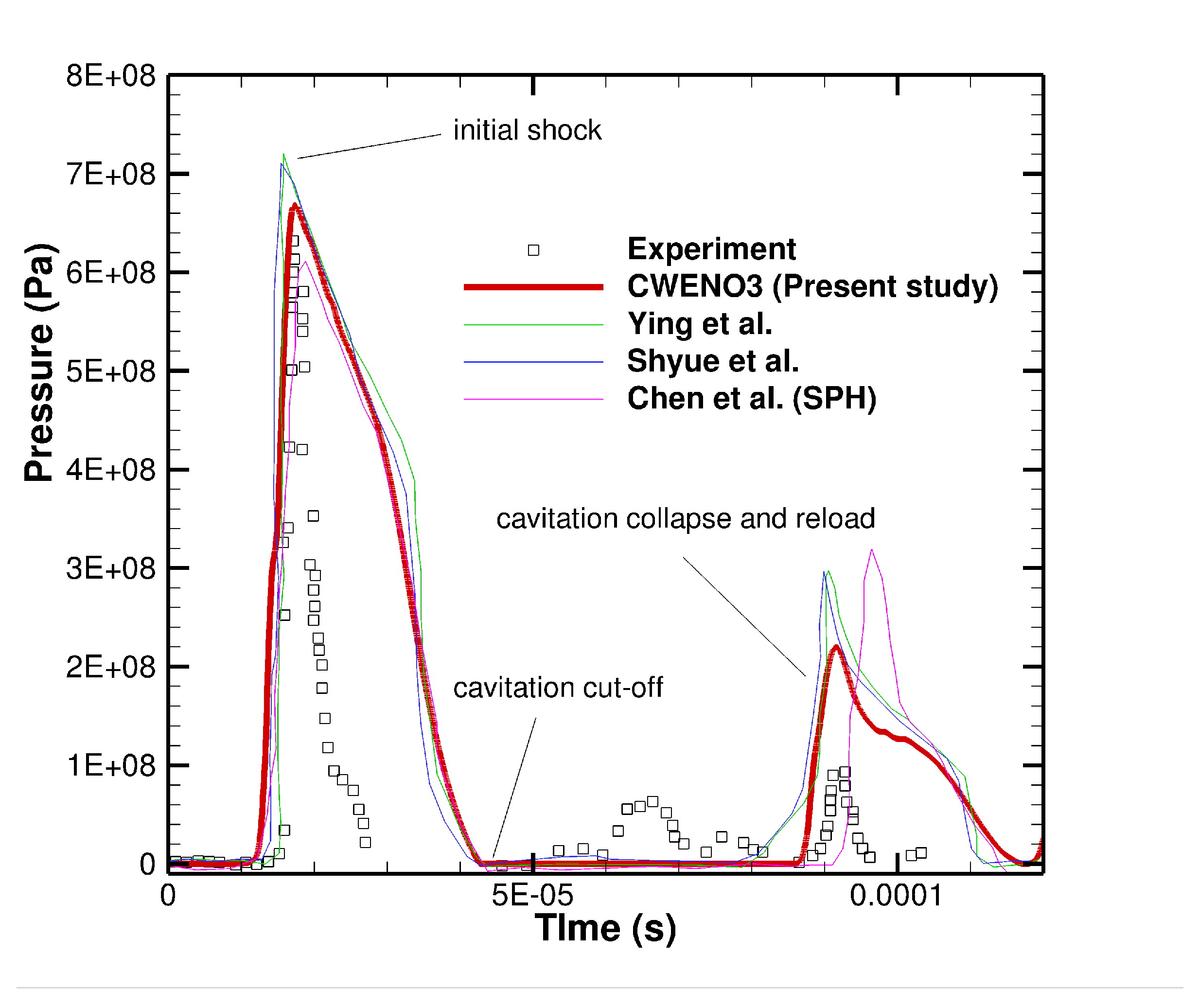
4.1. 2D Underwater Explosion near a Free Surface
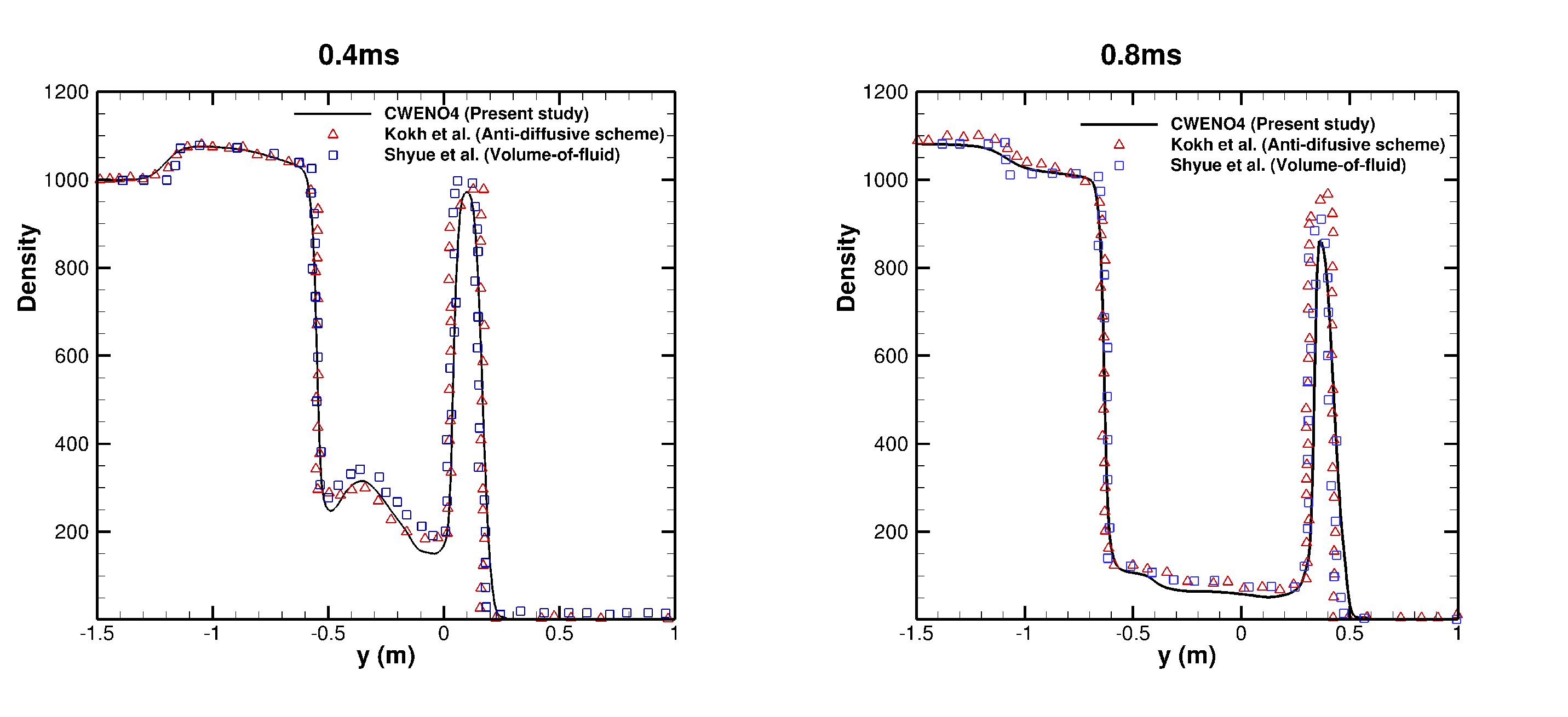
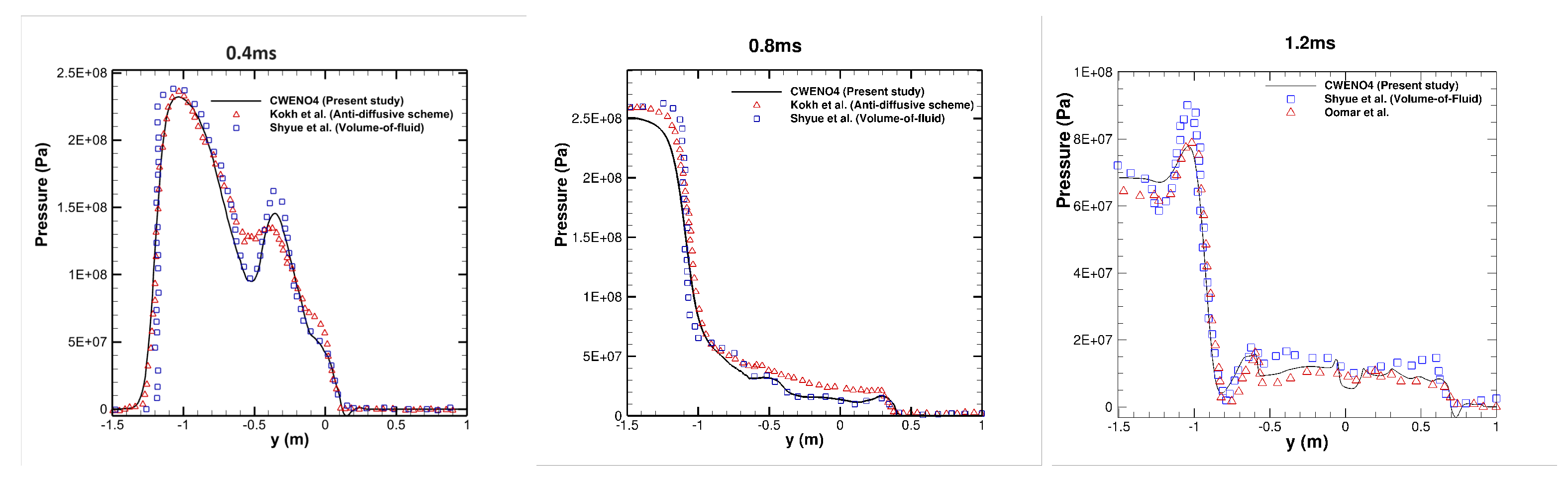

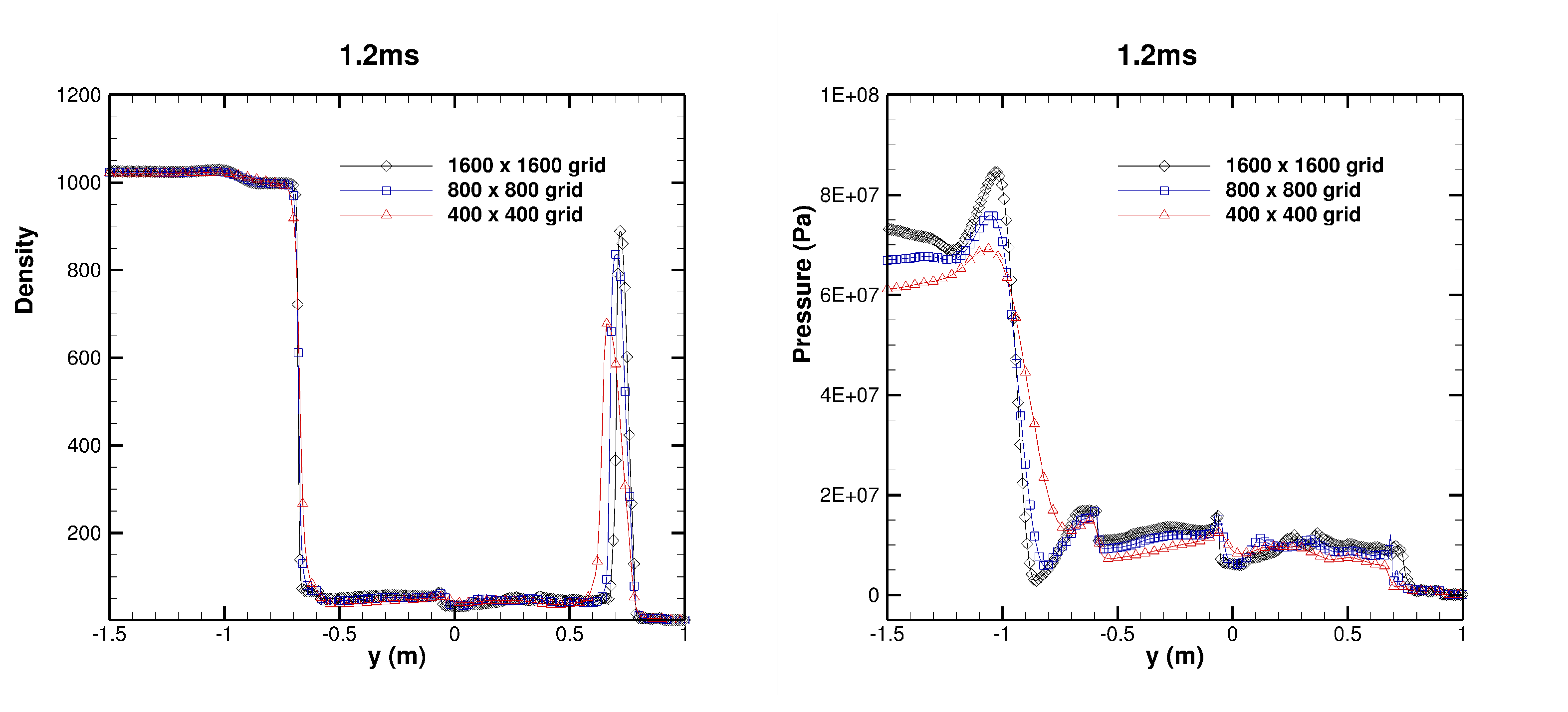
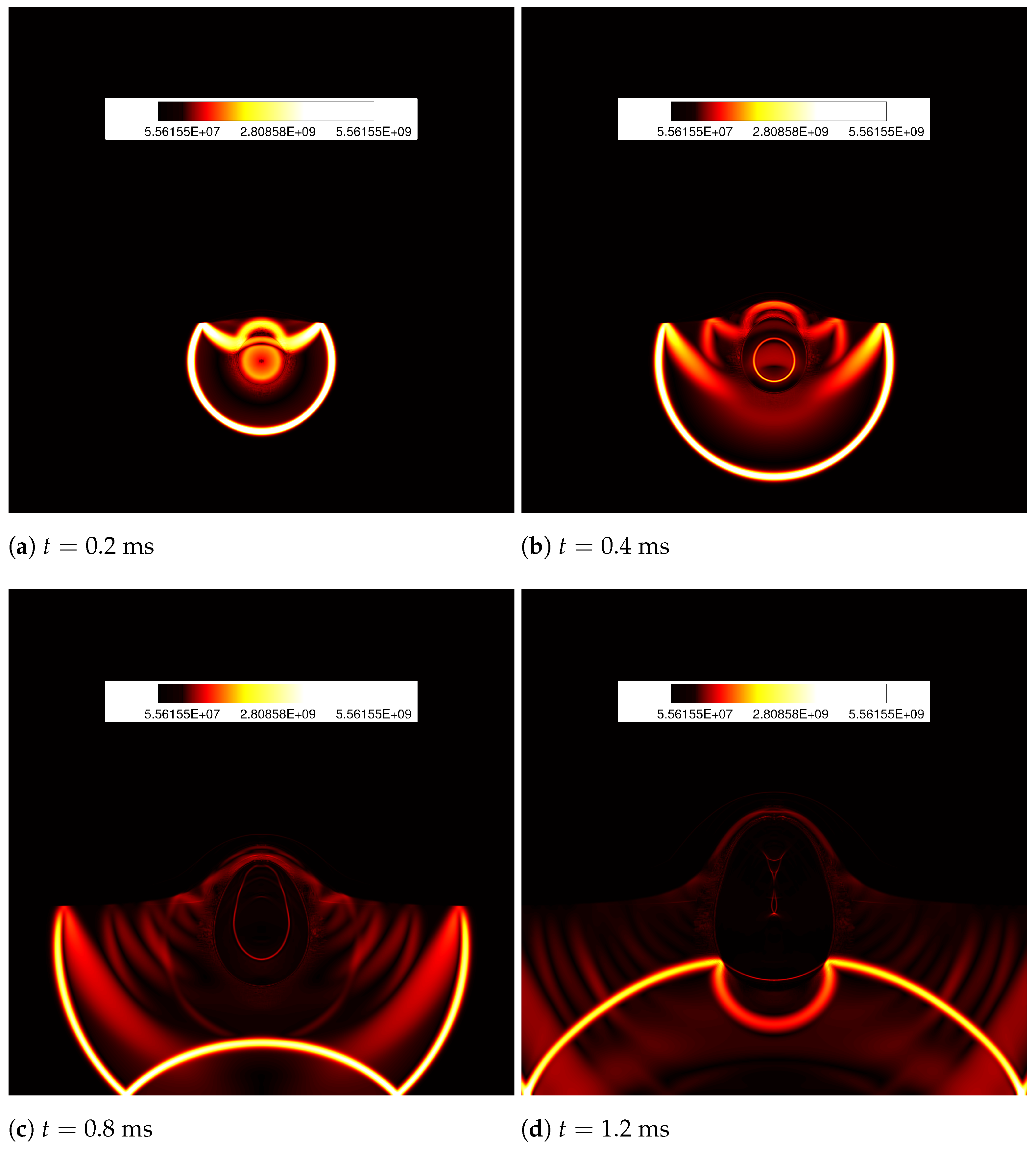
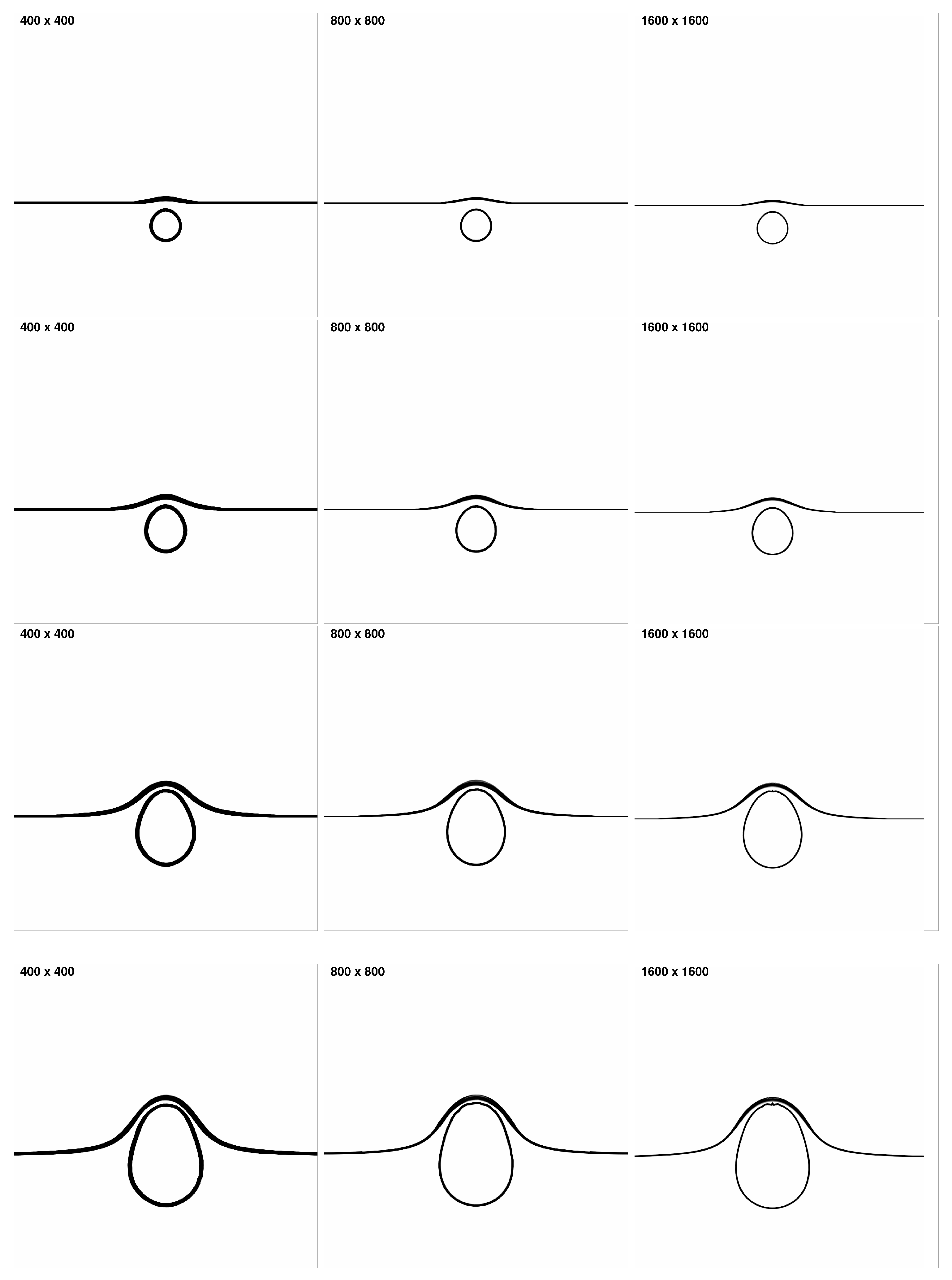
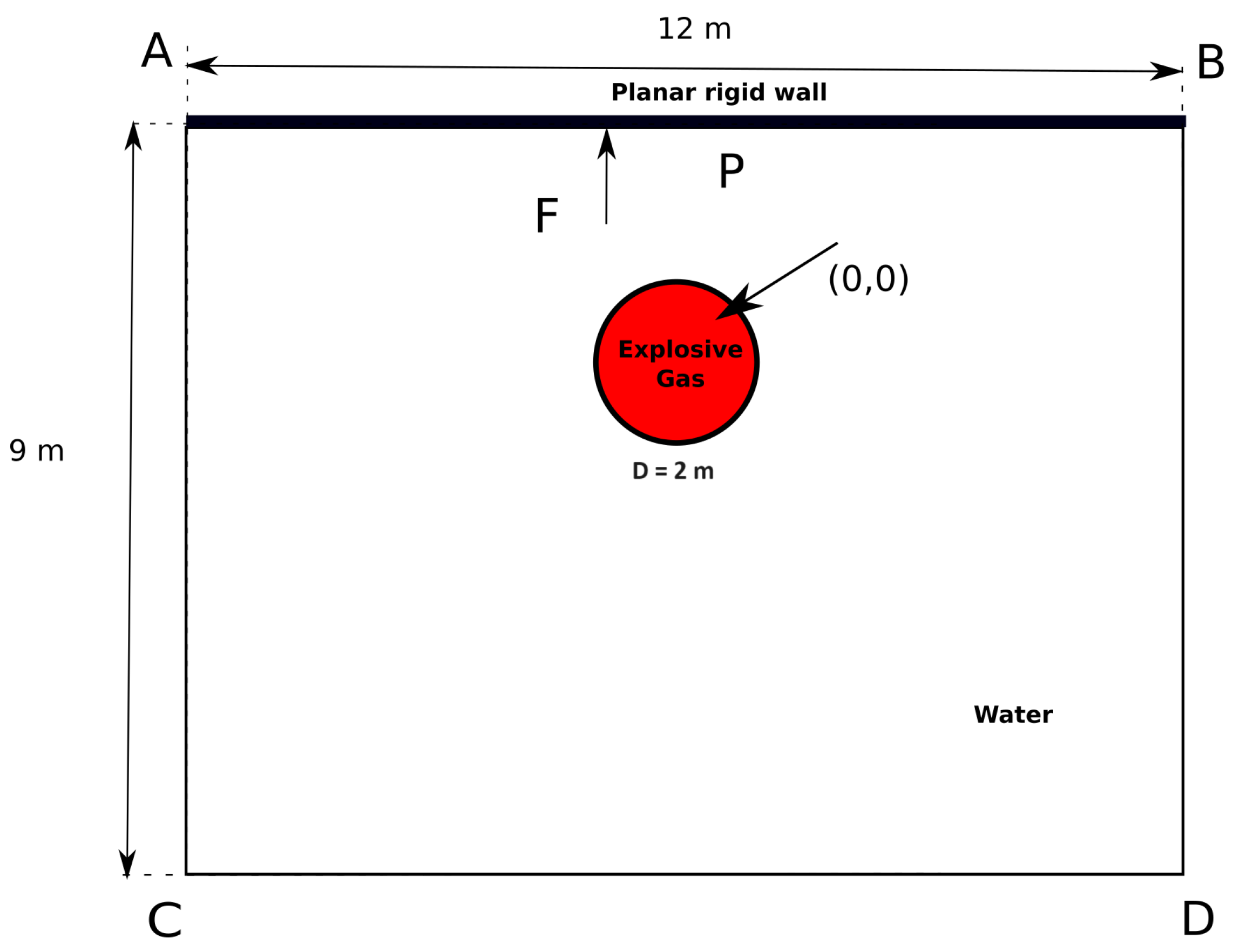
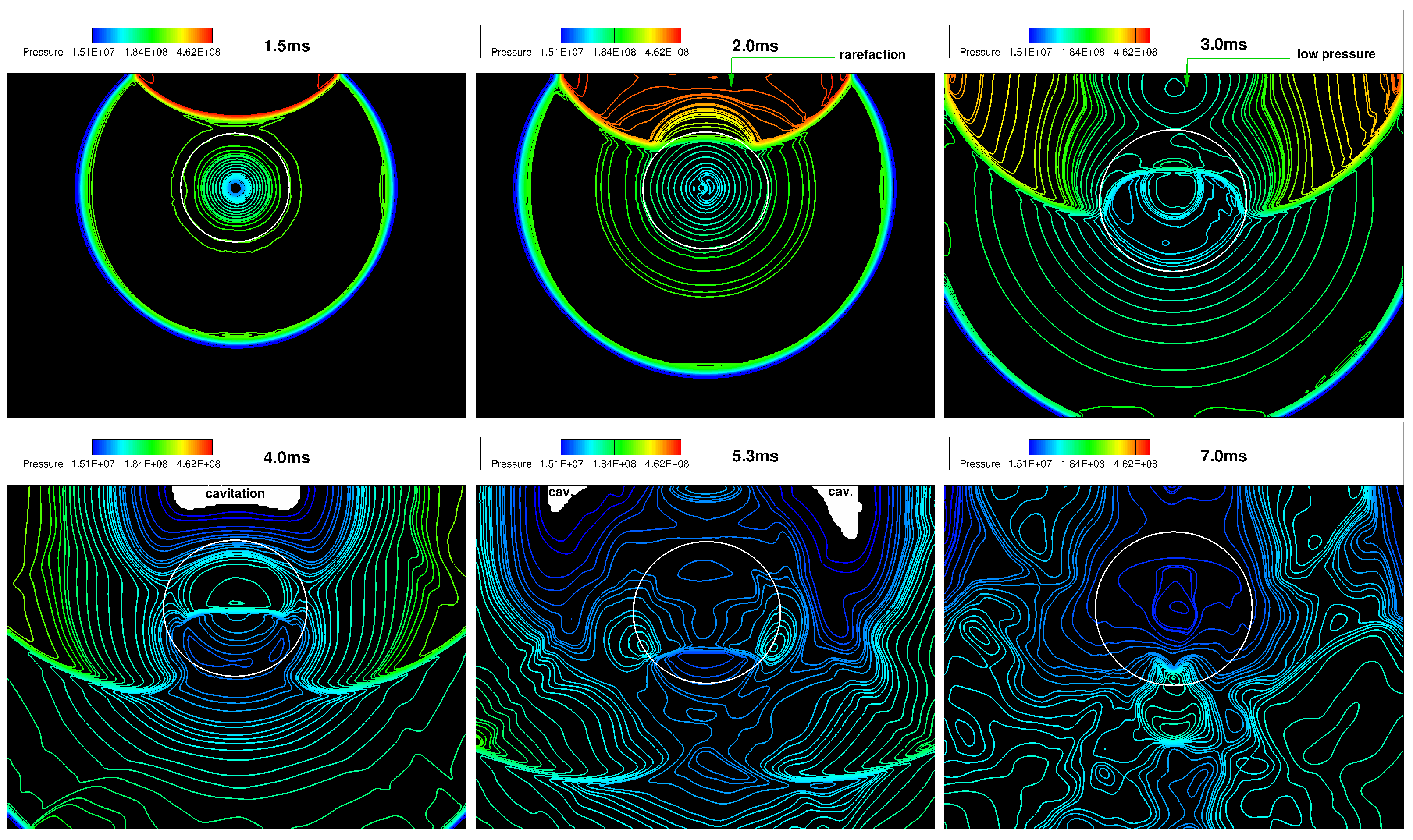
4.2. 2D Cylindrical Underwater Explosion near a Planar Rigid Wall
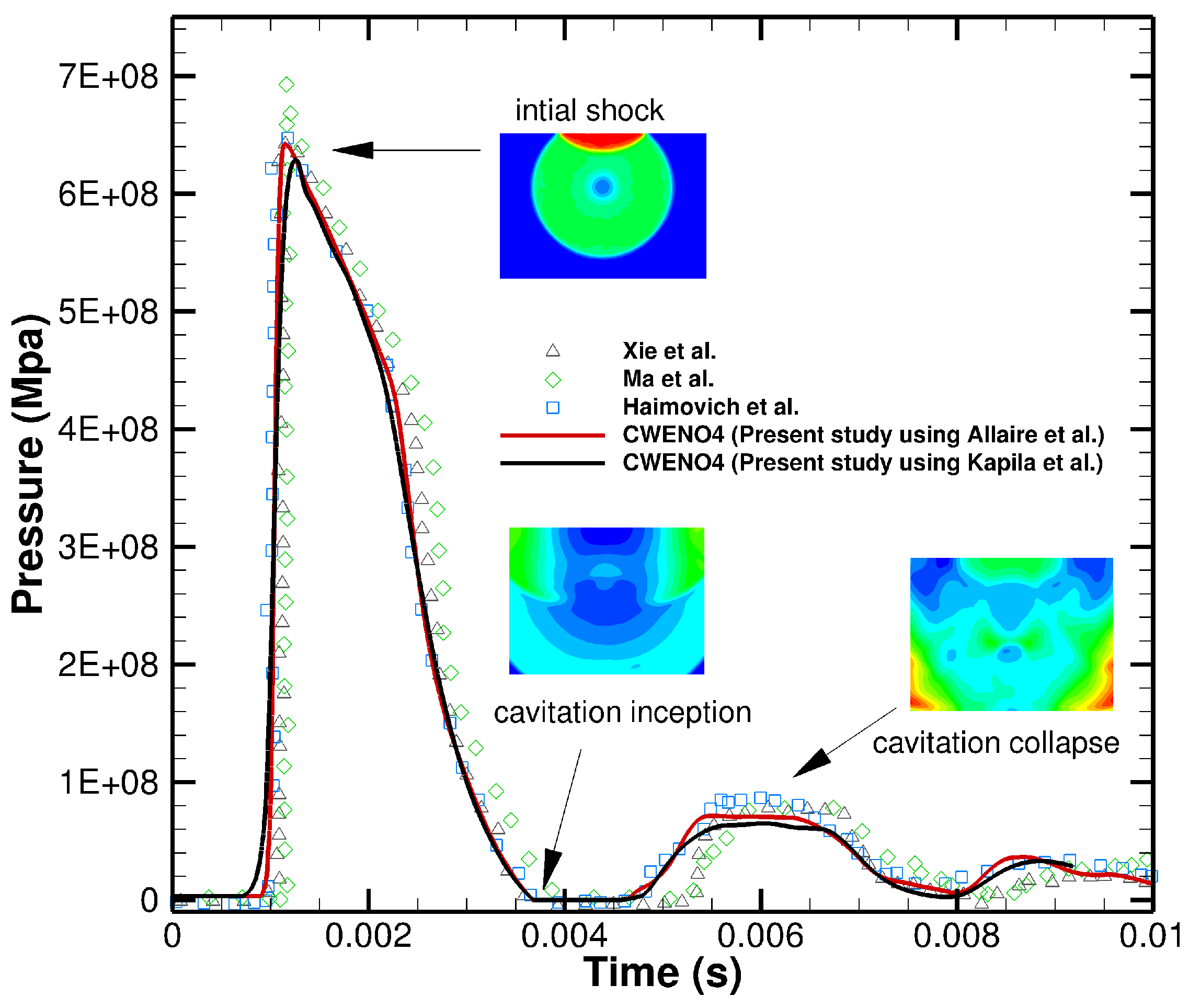
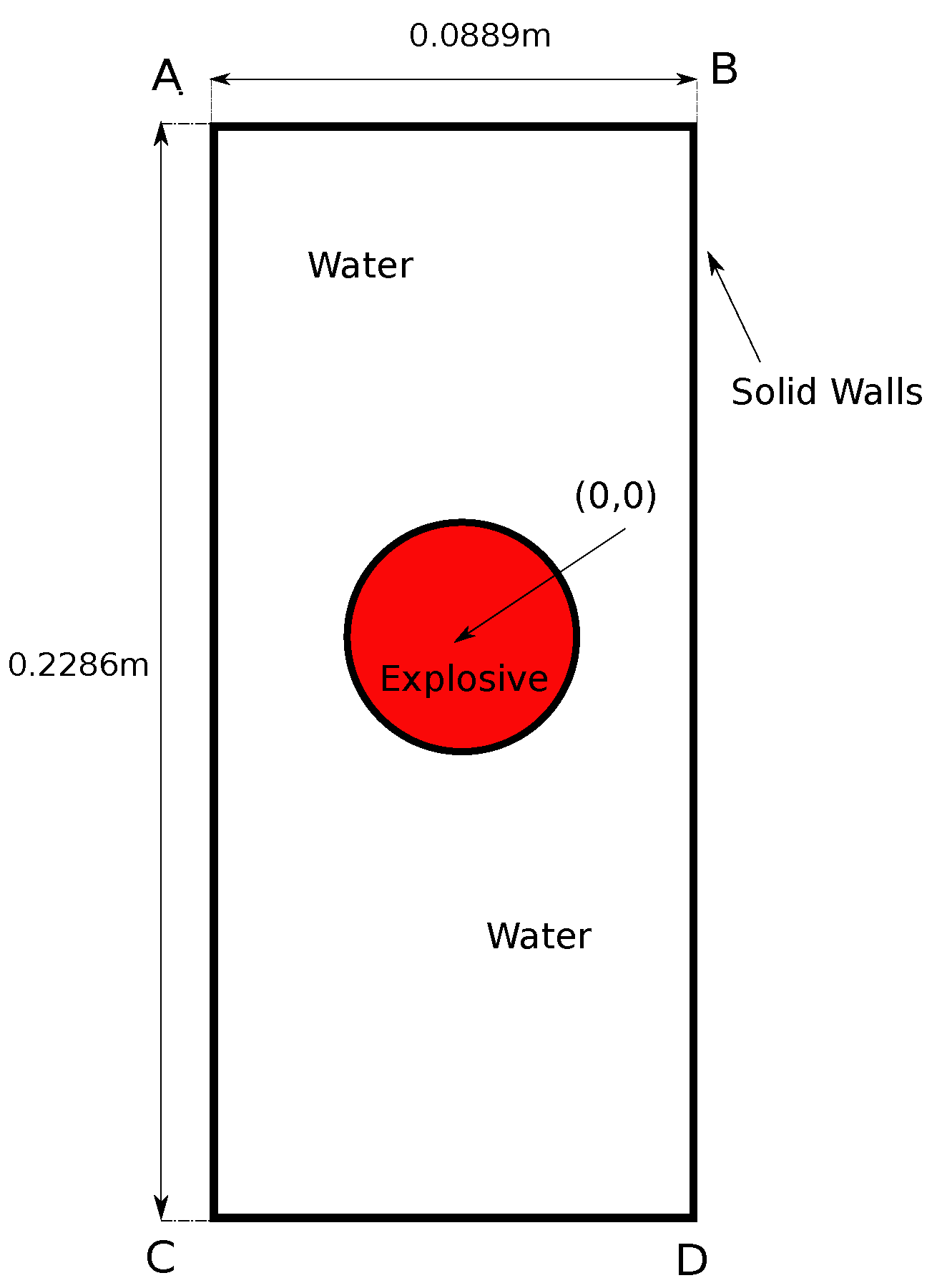
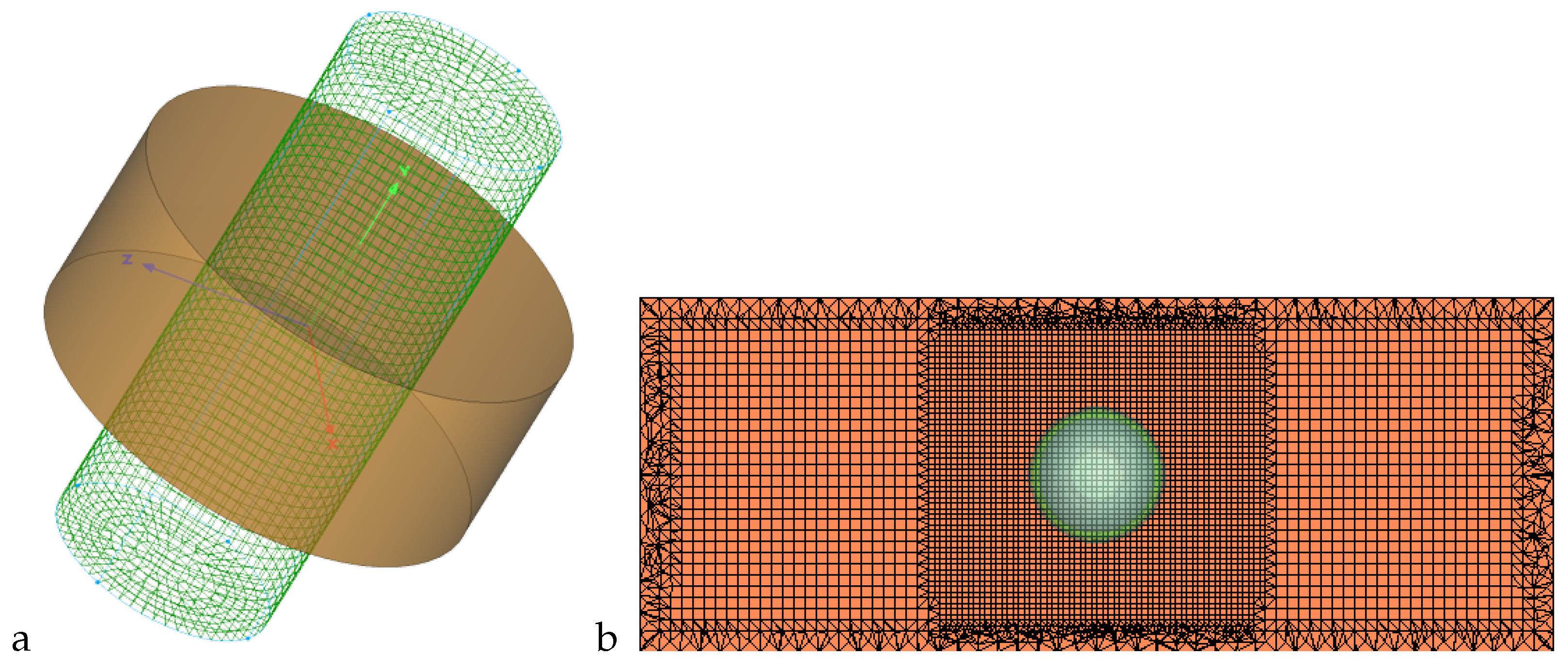
4.3. 3D Underwater Explosion in an Enclosed, Rigid Cylindrical Wall
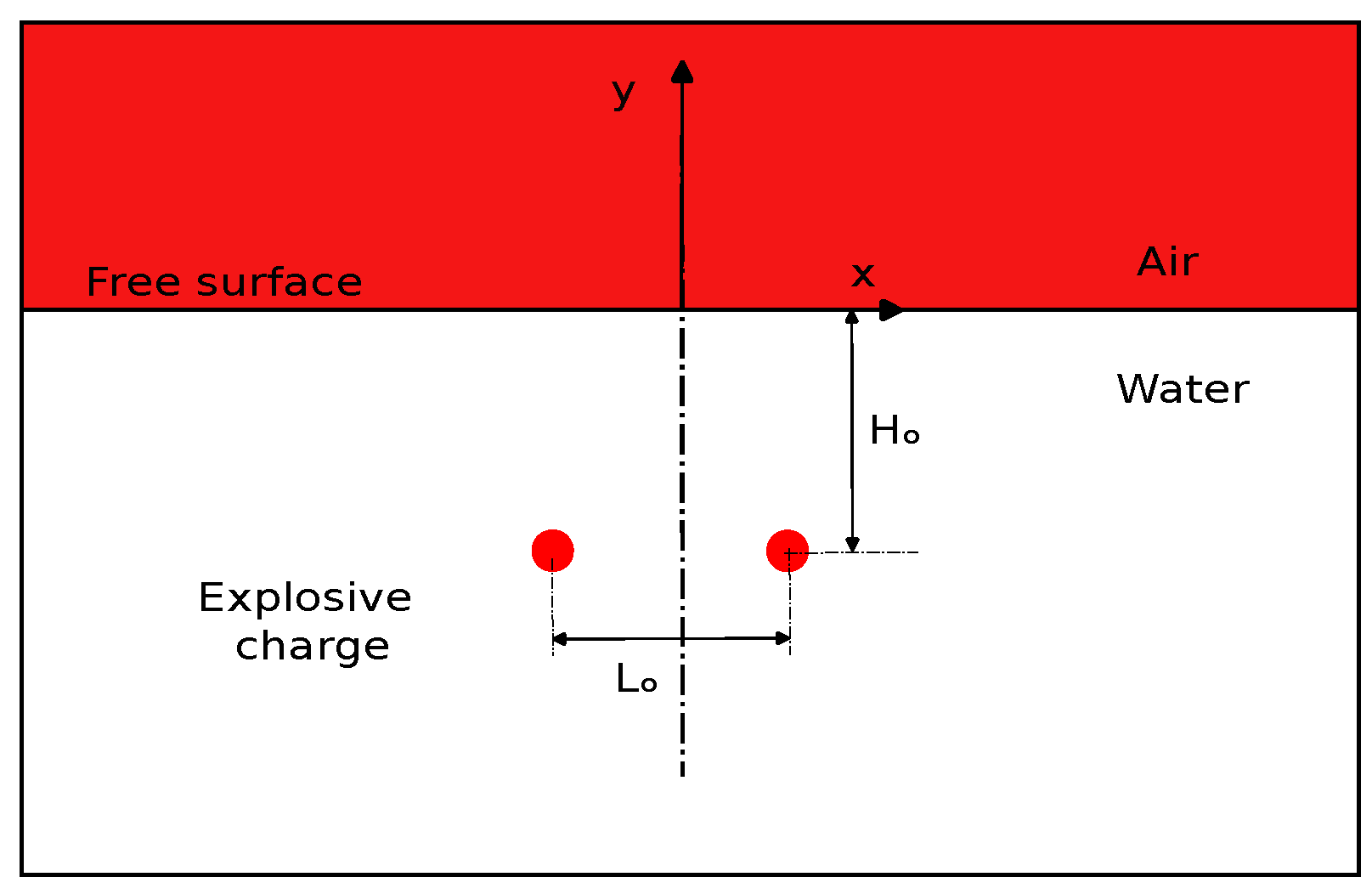
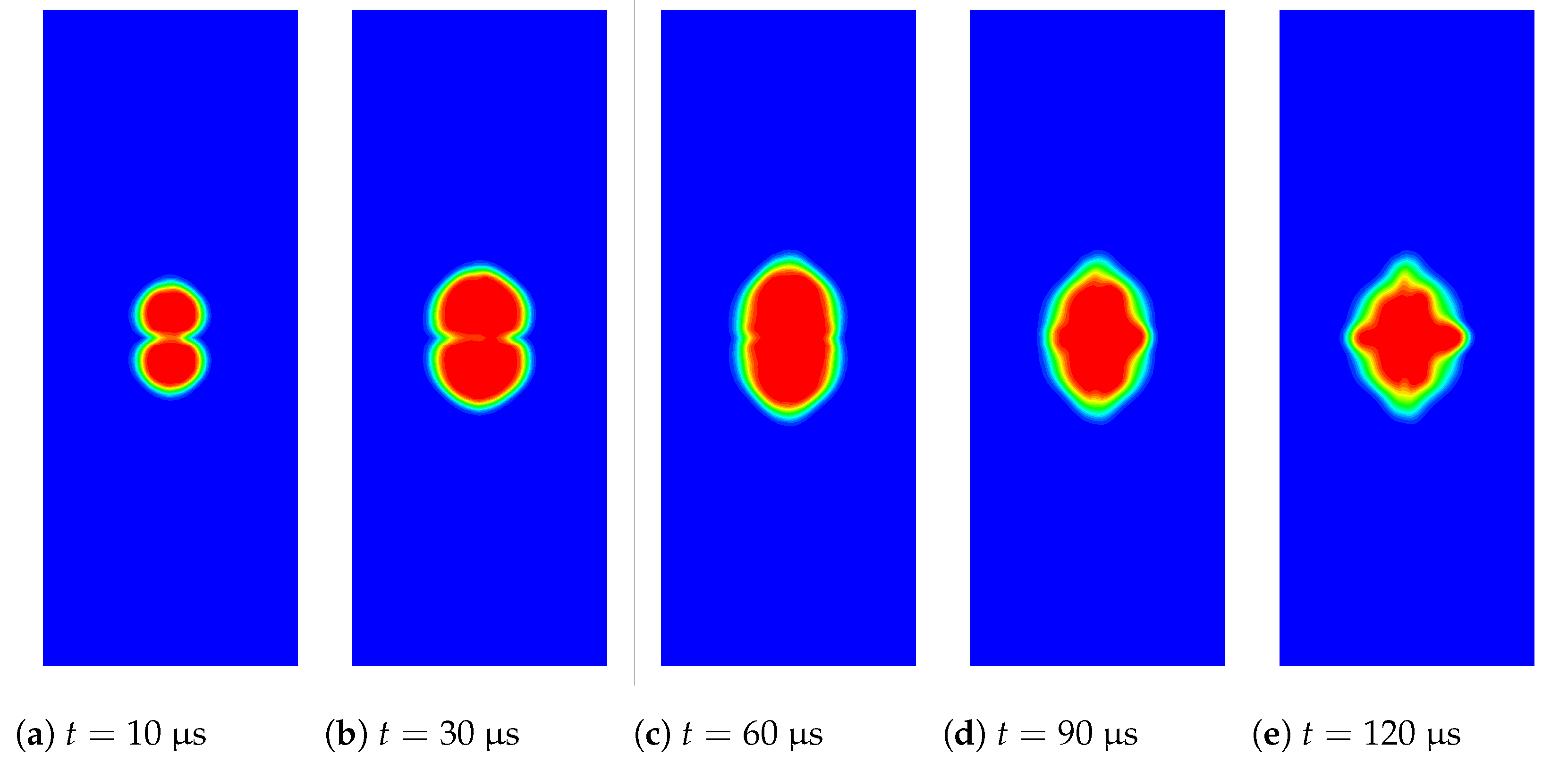
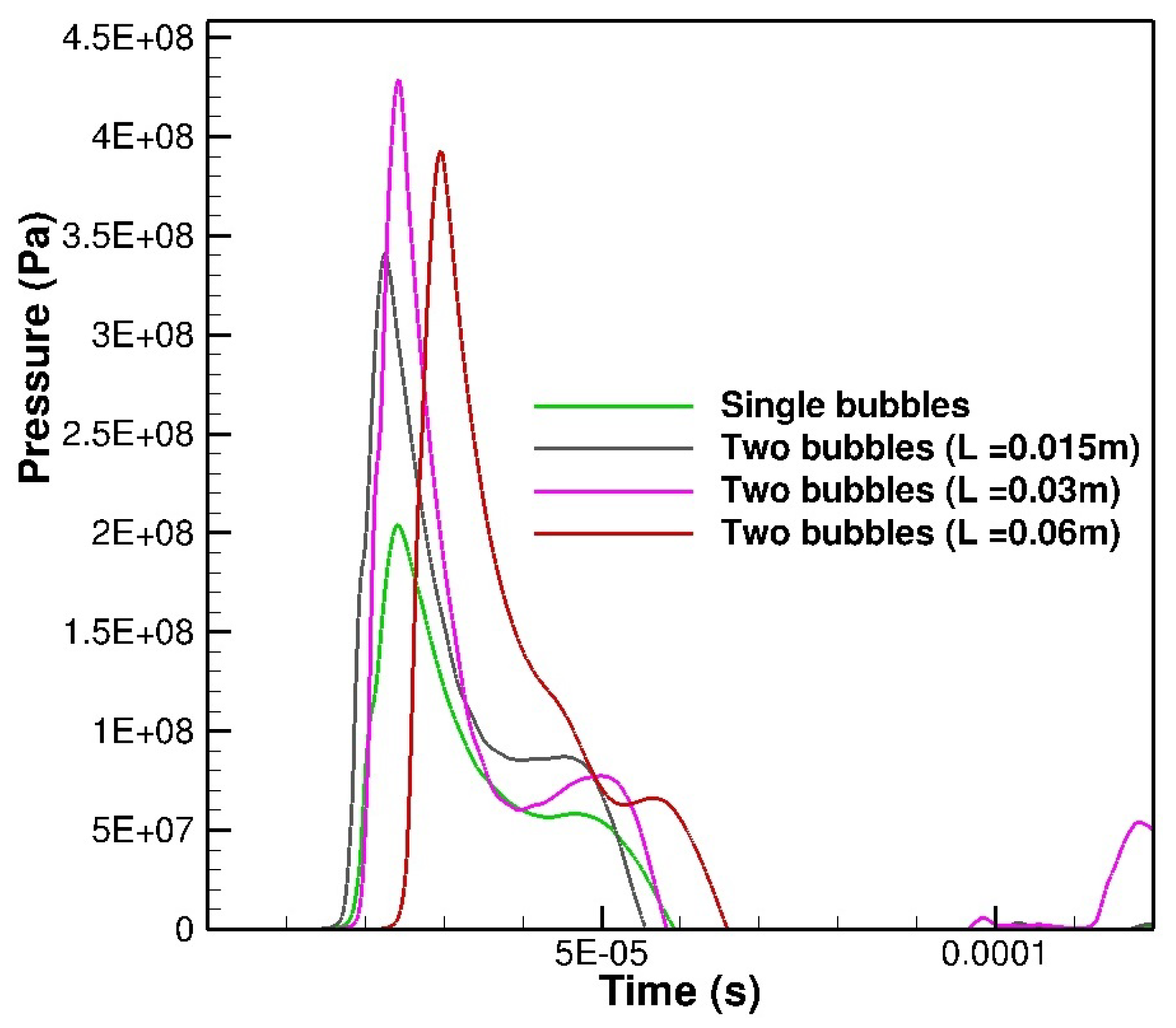
4.4. 2D Underwater Explosion of Two Bubbles Placed Horizontally near a Free Surface
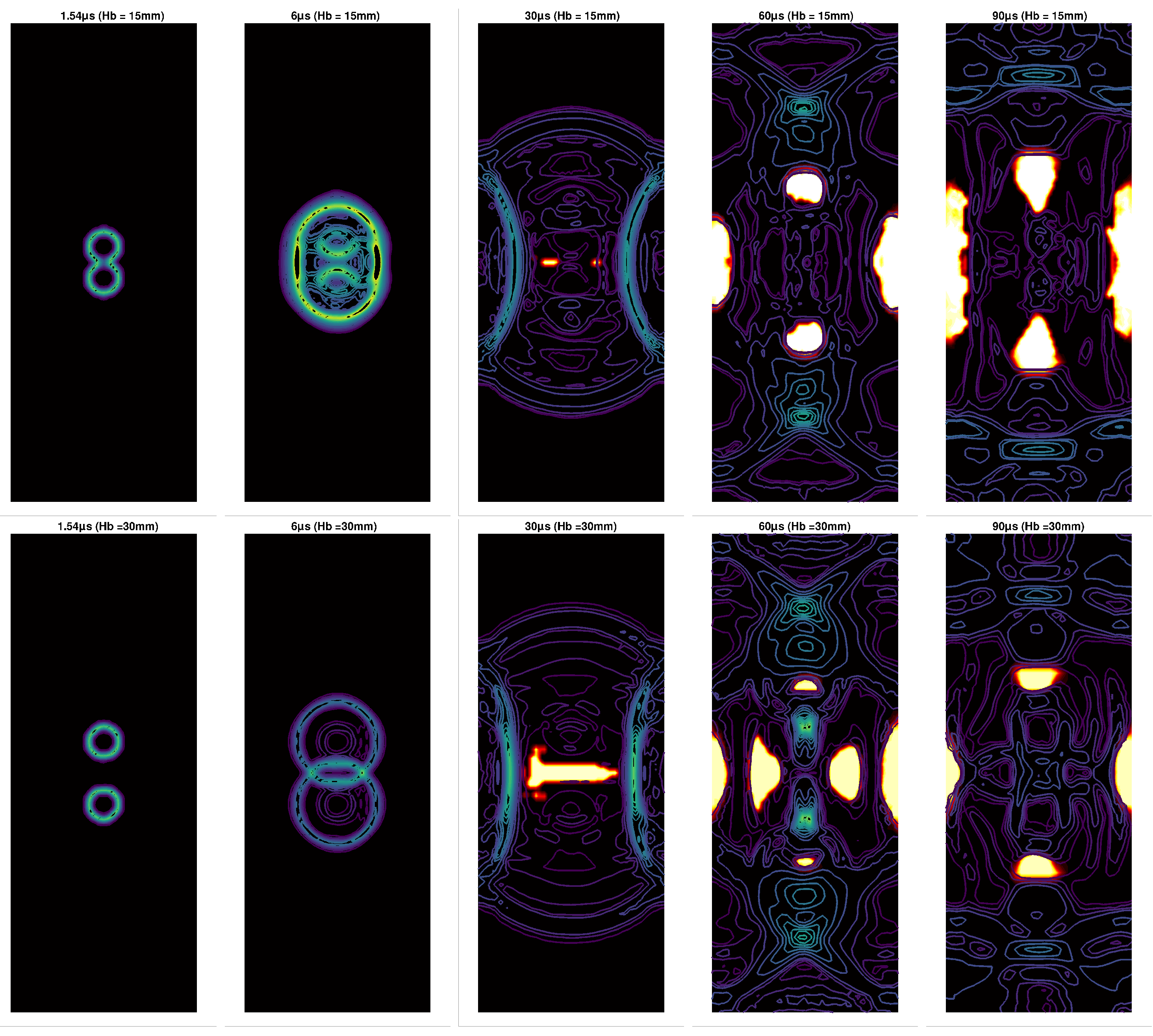
4.5. 3D Underwater of Two Bubbles Placed Vertically in an Enclosed Region
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UNDEX | Underwater Explosion |
| DIM | Diffuse Interface Models |
| UCNS3D | Unstructured Compressible Navier–Stokes 3D |
| CWENO | Central-Weighted Essentially Non-Oscillatory |
| FV | Finite Volume |
References
- Petitpas, F.; Massoni, J.; Saurel, R.; Lapebie, E.; Munier, L. Diffuse interface model for high speed cavitating underwater systems. Int. J. Multiph. Flow 2009, 35, 747–759. [Google Scholar] [CrossRef]
- Petitpas, F.; Saurel, R.; Ahn, B.K.; Ko, S. Modelling cavitating flow around underwater missiles. Int. J. Nav. Archit. Ocean. Eng. 2011, 3, 263–273. [Google Scholar] [CrossRef]
- Kwack, Y.K.; Ko, S.H. Numerical analysis for supercavitating flows around axisymmetric cavitators. Int. J. Nav. Archit. Ocean. Eng. 2013, 5, 325–332. [Google Scholar] [CrossRef]
- Wenfeng, X. A Numerical Simulation of Underwater Shock-Cavitation-Structure Interaction. Ph.D. Thesis, National University of Singapore, Singapore, 2005; pp. 1–207. [Google Scholar]
- Daramizadeh, A.; Ansari, M.R. Numerical simulation of underwater explosion near air-water free surface using a five-equation reduced model. Ocean. Eng. 2015, 110, 25–35. [Google Scholar] [CrossRef]
- Xie, W.F.; Liu, T.G.; Khoo, B.C. The simulation of cavitating flows induced by underwater shock and free surface interaction. Appl. Numer. Math. 2007, 57, 734–745. [Google Scholar] [CrossRef]
- Saurel, R.; Lemetayer, O. A multiphase model for compressible flows with interfaces, shocks, detonation waves and cavitation. J. Fluid Mech. 2001, 431, 239–271. [Google Scholar] [CrossRef]
- Ghidaglia, J.M.; Mrabet, A.A. A regularized stiffened-gas equation of state. J. Appl. Anal. Comput. 2018, 8, 675–689. [Google Scholar] [CrossRef]
- Shyue, K.M. An Anti-Diffusion based Eulerian Interface-Sharpening Algorithm for Compressible Two-Phase Flow with Cavitation. In Proceedings of the 8th International Symposium on Cavitation, Singapore, 13–16 August 2012; Volume 268, pp. 7–12. [Google Scholar] [CrossRef]
- Maltsev, V.; Skote, M.; Tsoutsanis, P. High-order methods for diffuse-interface models in compressible multi-medium flows: A review. Phys. Fluids 2022, 34, 021301. [Google Scholar] [CrossRef]
- Pelanti, M.; Shyue, K.M. A mixture-energy-consistent six-equation two-phase numerical model for fluids with interfaces, cavitation and evaporation waves. J. Comput. Phys. 2014, 259, 331–357. [Google Scholar] [CrossRef]
- Pelanti, M.; Shyue, K.M. A numerical model for multiphase liquid–vapour–gas flows with interfaces and cavitation. Int. J. Multiph. Flow 2019, 113, 208–230. [Google Scholar] [CrossRef]
- Baer, M.; Nunziato, J. A two-phase mixture theory for the deflagration-to-detonation transition (ddt) in reactive granular materials. Int. J. Multiph. Flow 1986, 12, 861–889. [Google Scholar] [CrossRef]
- Saurel, R.; Petitpas, F.; Abgrall, R. Modelling phase transition in metastable liquids: Application to cavitating and flashing flows. J. Fluid Mech. 2008, 607, 313–350. [Google Scholar] [CrossRef]
- Jun, Y.; Jian-qiang, P.; Hai-kun, W.; Hai-bin, M. Application of Compressible Multi-component Flow in Underwater Explosion Problems. Procedia Eng. 2015, 126, 339–343. [Google Scholar] [CrossRef]
- Chiapolino, A.; Saurel, R.; Nkonga, B. Sharpening diffuse interfaces with compressible fluids on unstructured meshes. J. Comput. Phys. 2017, 340, 389–417. [Google Scholar] [CrossRef]
- LeMartelot, S.; Nkonga, B.; Saurel, R. Liquid and liquid–gas flows at all speeds. J. Comput. Phys. 2013, 255, 53–82. [Google Scholar] [CrossRef]
- Zein, A. Numerical Methods for Multiphase Mixture Conservation Laws with Phase Transition. Ph.D. Thesis, Otto von Guericke University Magdeburg, Magdeburg, Germany, 2010. [Google Scholar]
- Ma, Z.H.; Causon, D.M.; Qian, L.; Gu, H.B.; Mingham, C.G.; Martínez Ferrer, P. A GPU based compressible multiphase hydrocode for modelling violent hydrodynamic impact problems. Comput. Fluids 2015, 120, 1–23. [Google Scholar] [CrossRef]
- Kapila, A.K.; Menikoff, R.; Bdzil, J.B.; Son, S.F.; Stewart, D.S. Two-phase modeling of deflagration-to-detonation transition in granular materials: Reduced equations. Phys. Fluids 2001, 13, 3002–3024. [Google Scholar] [CrossRef]
- Allaire, G.; Clerc, S.; Kokh, S. A five-equation model for the simulation of interfaces between compressible fluids. J. Comput. Phys. 2002, 181, 577–616. [Google Scholar] [CrossRef]
- Antoniadis, A.; Drikakis, D.; Farmakis, P.; Fu, L.; Kokkinakis, I.; Nogueira, X.; Silva, P.; Skote, M.; Titarev, V.; Tsoutsanis, P. UCNS3D: An open-source high-order finite-volume unstructured CFD solver. Comput. Phys. Commun. 2022, 279, 108453. [Google Scholar] [CrossRef]
- Tsoutsanis, P.; Dumbser, M. Arbitrary high order central non-oscillatory schemes on mixed-element unstructured meshes. Comput. Fluids 2021, 225, 104961. [Google Scholar] [CrossRef]
- Murrone, A.; Guillard, H. A five equation reduced model for compressible two phase flow problems. J. Comput. Phys. 2005, 202, 664–698. [Google Scholar] [CrossRef]
- Wackers, J.; Koren, B. A fully conservative model for compressible two-fluid flow. Int. J. Numer. Methods Fluids 2005, 47, 1337–1343. [Google Scholar] [CrossRef]
- Schmidmayer, K.; Bryngelson, S.H.; Colonius, T. An assessment of multicomponent flow models and interface capturing schemes for spherical bubble dynamics. J. Comput. Phys. 2020, 402, 109080. [Google Scholar] [CrossRef]
- Zhang, J. A simple and effective five-equation two-phase numerical model for liquid-vapour phase transition in cavitating flows. Int. J. Multiph. Flow 2020, 132, 103417. [Google Scholar] [CrossRef]
- Harlow, F.H.; Amsden, A.A. Numerical calculation of almost incompressible flow. J. Comput. Phys. 1968, 3, 80–93. [Google Scholar] [CrossRef]
- Johnsen, E.; Colonius, T. Implementation of WENO schemes in compressible multicomponent flow problems. J. Comput. Phys. 2006, 219, 715–732. [Google Scholar] [CrossRef]
- Harlow, F.H.; Amsden, A.A. A numerical fluid dynamics calculation method for all flow speeds. J. Comput. Phys. 1971, 8, 197–213. [Google Scholar] [CrossRef]
- Saurel, R.; Abgrall, R. Simple method for compressible multifluid flows. Siam J. Sci. Comput. 1999, 21, 1115–1145. [Google Scholar] [CrossRef]
- Quirk, J.J.; Karni, S. On the dynamics of a shock-bubble interaction. J. Fluid Mech. 1996, 318, 129–163. [Google Scholar] [CrossRef]
- Tsoutsanis, P.; Adebayo, E.; Merino, A.; Arjona, A.; Skote, M. CWENO Finite-Volume Interface Capturing Schemes for Multicomponent Flows Using Unstructured Meshes. J. Sci. Comput. 2021, 89, 64. [Google Scholar] [CrossRef]
- Liu, T.; Khoo, B.; Xie, W. Isentropic one-fluid modelling of unsteady cavitating flow. J. Comput. Phys. 2004, 201, 80–108. [Google Scholar] [CrossRef]
- Ansari, M.; Daramizadeh, A. Numerical simulation of compressible two-phase flow using a diffuse interface method. Int. J. Heat Fluid Flow 2013, 42, 209–223. [Google Scholar] [CrossRef]
- Tsoutsanis, P.; Titarev, V.; Drikakis, D. WENO schemes on arbitrary mixed-element unstructured meshes in three space dimensions. J. Comput. Phys. 2011, 230, 1585–1601. [Google Scholar] [CrossRef]
- Tsoutsanis, P.; Pavan Kumar, M.; Farmakis, P. A relaxed a posteriori MOOD algorithm for multicomponent compressible flows using high-order finite-volume methods on unstructured meshes. Appl. Math. Comput. 2023, 437, 127544. [Google Scholar] [CrossRef]
- Tsoutsanis, P.; Farmakis, P. A posteriori mood limiting approach for multicomponent flows on unstructured meshes. In Proceedings of the World Congress in Computational Mechanics and ECCOMAS Congress, Oslo, Norway, 5–9 June 2022. [Google Scholar] [CrossRef]
- Tsoutsanis, P. Stencil selection algorithms for WENO schemes on unstructured meshes. J. Comput. Phys. 2023, 475, 100037. [Google Scholar] [CrossRef]
- Toro, E.; Spruce, M.; Speares, W. Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 1994, 4, 25–34. [Google Scholar] [CrossRef]
- Tsoutsanis, P.; Antoniadis, A.; Jenkins, K. Improvement of the computational performance of a parallel unstructured WENO finite volume CFD code for Implicit Large Eddy Simulation. Comput. Fluids 2018, 173, 157–170. [Google Scholar] [CrossRef]
- Petrov, N.V.; Schmidt, A.A. Multiphase phenomena in underwater explosion. Exp. Therm. Fluid Sci. 2015, 60, 367–373. [Google Scholar] [CrossRef]
- Haimovich, O.; Frankel, S.H. Numerical simulations of compressible multicomponent and multiphase flow using a high-order targeted ENO (TENO) finite-volume method. Comput. Fluids 2017, 146, 105–116. [Google Scholar] [CrossRef]
- Yeom, G.S.; Chang, K.S. A modified HLLC-type Riemann solver for the compressible six-equation two-fluid model. Comput. Fluids 2013, 76, 86–104. [Google Scholar] [CrossRef]
- Shukla, R.K.; Pantano, C.; Freund, J.B. An interface capturing method for the simulation of multi-phase compressible flows. J. Comput. Phys. 2010, 229, 7411–7439. [Google Scholar] [CrossRef]
- Shukla, R.K. Nonlinear preconditioning for efficient and accurate interface capturing in simulation of multicomponent compressible flows. J. Comput. Phys. 2014, 276, 508–540. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Wang, C.; Zhang, A.M.; Silberschmidt, V.V.; Wang, L.K. SPH-BEM simulation of underwater explosion and bubble dynamics near rigid wall. Sci. China Technol. Sci. 2019, 62, 1082–1093. [Google Scholar] [CrossRef]
- Kleine, H.; Tepper, S.; Takehara, K.; Etoh, T.; Hiraki, K. Cavitation induced by low-speed underwater impact. Shockwaves 2009, 2, 895–900. [Google Scholar] [CrossRef]
- Kokh, S.; Lagoutière, F. An anti-diffusive numerical scheme for the simulation of interfaces between compressible fluids by means of a five-equation model. J. Comput. Phys. 2010, 229, 2773–2809. [Google Scholar] [CrossRef]
- Oomar, M.; Malan, A.; Jones, B.; Horwitz, R.; Langdon, G. An all-Mach number HLLC based scheme for Multi-phase Flow with Surface Tension. Appl. Sci. 2021, 11, 3413. [Google Scholar] [CrossRef]
- Deng, X.; Inaba, S.; Xie, B.; Shyue, K.M.; Xiao, F. High fidelity discontinuity-resolving reconstruction for compressible multiphase flows with moving interfaces. J. Comput. Phys. 2018, 371, 945–966. [Google Scholar] [CrossRef]
- Shyue, K.M. A wave-propagation based volume tracking method for compressible multicomponent flow in two space dimensions. J. Comput. Phys. 2006, 215, 219–244. [Google Scholar] [CrossRef]
- Xie, W.F.; Young, Y.L.; Liu, T.G.; Khoo, B.C. Dynamic response of deformable structures subjected to shock load and cavitation reload. Comput. Mech. 2007, 40, 667–681. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, Y.; Wang, Z.; Yao, X. The Influence of Various Structure Surface Boundary Conditions on Pressure Characteristics of Underwater Explosion. Comput. Model. Eng. Sci. 2021, 126, 1093–1123. [Google Scholar] [CrossRef]
- Xie, W.; Liu, T.; Khoo, B. Application of a one-fluid model for large scale homogeneous unsteady cavitation: The modified Schmidt model. Comput. Fluids 2006, 35, 1177–1192. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Wang, C.; Wang, L.K.; Zhang, A.M.; Silberschmidt, V.V. Underwater explosion of cylindrical charge near plates: Analysis of pressure characteristics and cavitation effects. Int. J. Impact Eng. 2018, 121, 91–105. [Google Scholar] [CrossRef]
- Hong, Y.; Wang, B.; Liu, H. Numerical simulation of compressible multiphase hydrodynamic problems using reduced five-equation model on body-fitted grids. Comput. Fluids 2022, 233, 105243. [Google Scholar] [CrossRef]
- Jafarian, A.; Pishevar, A. An exact multiphase Riemann solver for compressible cavitating flows. Int. J. Multiph. Flow 2017, 88, 152–166. [Google Scholar] [CrossRef]
- Wardlaw, A.B.; Luton, J.A. Fluid-structure interaction mechanisms for close-in explosions. Shock Vib. 2000, 7, 265–275. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, X.; Qin, Y. Investigation on influence factors about damage characteristics of ice sheet subjected to explosion loads: Underwater explosion and air contact explosion. Ocean. Eng. 2022, 260, 111828. [Google Scholar] [CrossRef]
- Chen, J.Y.; Peng, C.; Lien, F.S.; Yee, E.; Zhao, X.H. Simulations for the explosion in a water-filled tube including cavitation using the SPH method. Comput. Part. Mech. 2019, 6, 515–527. [Google Scholar] [CrossRef]
- Schmidt, D.; Rutland, C.; Corradini, M. A fully compressible, two-dimensional model of small, high-speed, cavitating nozzles. At. Sprays 1999, 9, 255–276. [Google Scholar] [CrossRef]
- Yu, J.; Liu, J.h.; Wang, H.k.; Wang, J.; Zhou, Z.t.; Mao, H.b. Application of two-phase transition model in underwater explosion cavitation based on compressible multiphase flows. Aip Adv. 2022, 12, 025209. [Google Scholar] [CrossRef]
- Cheng, J.; Shu, C.W. High Order Schemes for CFD: A Review. Chin. J. Comput. Phys. 2009, 26, 633. Available online: http://www.cjcp.org.cn/EN/abstract/article_825.shtml (accessed on 23 January 2024).
- Yingtang, D.; Lanhao, Z.; Jia, M.; Eldad, A. A resolved CFD-DEM-IBM algorithm for water entry problems. Ocean. Eng. 2021, 240, 110014. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adebayo, E.M.; Tsoutsanis, P.; Jenkins, K.W. Application of Central-Weighted Essentially Non-Oscillatory Finite-Volume Interface-Capturing Schemes for Modeling Cavitation Induced by an Underwater Explosion. Fluids 2024, 9, 33. https://doi.org/10.3390/fluids9020033
Adebayo EM, Tsoutsanis P, Jenkins KW. Application of Central-Weighted Essentially Non-Oscillatory Finite-Volume Interface-Capturing Schemes for Modeling Cavitation Induced by an Underwater Explosion. Fluids. 2024; 9(2):33. https://doi.org/10.3390/fluids9020033
Chicago/Turabian StyleAdebayo, Ebenezer Mayowa, Panagiotis Tsoutsanis, and Karl W. Jenkins. 2024. "Application of Central-Weighted Essentially Non-Oscillatory Finite-Volume Interface-Capturing Schemes for Modeling Cavitation Induced by an Underwater Explosion" Fluids 9, no. 2: 33. https://doi.org/10.3390/fluids9020033
APA StyleAdebayo, E. M., Tsoutsanis, P., & Jenkins, K. W. (2024). Application of Central-Weighted Essentially Non-Oscillatory Finite-Volume Interface-Capturing Schemes for Modeling Cavitation Induced by an Underwater Explosion. Fluids, 9(2), 33. https://doi.org/10.3390/fluids9020033