Interpreting Image Patterns for Agricultural Sprays Using Statistics and Machine Learning Techniques

Abstract

The atomization of liquid spray solutions through nozzles is a mechanism for delivering many pesticides to the target. The smallest drop sizes (<150 μm) are known as driftable fines and have a propensity for wind-induced convection. Many agricultural applications include oil-in-water formulations. The experimental metrics obtained from spray images of these formulations include the distance from the nozzle origin to the drop centroid once a drop has formed; the hole location and surface area for holes that form in the liquid sheet (all hole areas approximated as polygons); the angles formed between polygon segments (whose vertices are represented as boundary points); and the ligament dimensions that form from intersecting holes, such as the ligament aspect ratio (R/L), ligament length (L), and ligament radius (width), along with the number of drops a ligament breaks up into. These metrics were used in a principal component regression (PCR) analysis, and the results illustrated that 99% of the variability in the response variable (DT10) was addressed by 10 principal components. Angles formed by the colliding holes, hole distance from the nozzle, drop distance, hole number, ligament number, and drop number were negatively correlated to the atomization driftable fine fraction, while hole area, ligament distance, ligament area, and boundary area were positively correlated. Thus, to decrease/minimize driftable fines, one needs to increase the negatively correlated metrics.

1. Introduction

Foliar adherence and drift propensity are important considerations for pesticide formulations. Two of the most important factors influencing the spray properties of an agricultural formulation are nozzle selection and adjuvant additions. Both factors have been well studied using a variety of experimental and computational techniques [1,2,3,4,5,6,7,8,9]. However, the spraying phenomenon largely remains an enigma and persists as an obstacle in the product formulation process. Flat fan spray nozzles operate by discharging a liquid sheet, which subsequently breaks up into droplets. In agricultural settings, droplets that are too small can become entrained in ambient air currents and be carried off target, while larger droplets often reduce pesticide coverage and efficacy.

Three distinct mechanisms of sheet breakup are observed based on the properties of the formulation being sprayed, the nozzle geometry, and process conditions. Mechanisms leading to sheet rupture include wave growth, rim breakup, and collisions of growing holes within the sheet in multiphase systems [10]. Many agricultural chemicals are dissolved in an oil phase and subsequently formulated as an emulsifiable concentrate that spontaneously forms an oil-in-water emulsion when mixed with water. Spray patterns of an oil-in-water emulsion (and breakup mechanisms) are very different from those of pure water in terms of the droplet breakup mechanism (e.g., flapping sheet vs. hole growth), as are the resulting droplet size distribution and mechanisms [10,11]. It is hypothesized that the oil drops in the multiphase system create nucleation sites for hole formation as the oil penetrates the water/air interface. An oil-in-water spray pattern can be segregated into three regimes: (i) continuous sheet nucleation, (ii) hole growth and collision, and (iii) ligament formation and breakup into drops [11,12,13].

High-speed imaging of the spray trajectory is one technique that has been used to study spray phenomena [14,15,16,17]. Typically, these efforts have attempted to serve as a proxy technology for establishing the droplet size distribution. Our proposed technique departs from previous efforts in both scope and approach. Rather than attempt to provide a numerical descriptor (e.g., droplet size, etc.), our objective is to empirically provide a navigable landscape with which to explore the potential formulation space (for a specific nozzle/pressure) visually and iteratively. By establishing a set of known reference formulations (e.g., solution controls as well as various commercial formulations) in the exploration landscape and projecting any new putative formulation onto this landscape, it is then possible to qualitatively establish where the new product formulation stands with respect to known formulations. The overall result of any iterative modifications can then be readily visualized.

2. Materials and Methods

High-speed videos were taken of atomization sprays, from which characteristic metrics were defined and explored [14,15]. Physical and empirical metrics were defined, and algorithms were written (Matlab v. 2019a or C++) such that the video images could be distinguished from each other based on the differences in image analysis (IA) metrics. Videos of 21 different oil-in-water formulations being sprayed through a conventional flat fan nozzle (XR8002, TeeJet, Glendale Heights, IL, USA) were taken at two different pressures (40 and 10 psi) and oil-phase concentrations (2.5 and 5.0%). Thus, the two-phase fluid being sprayed was mostly water with a small fraction (2.5–5%) of oil, which is representative of typical agricultural sprays. A HELOS Sympatec laser diffraction system (Sympatec GmbH, Clausthal-Zellerfeld, Germany) was used to measure the resulting droplet size distribution upon atomization. The laser was aligned at the center of the spray, located below the continuous sheet at 330 mm below the nozzle (thus, the sheet was fully broken up into droplets). The XR8002 flat fan nozzle is a conventional nozzle with a spray angle of 80°. Further details of the experimental system can be found elsewhere [12].

2.1. Numerical Descriptors

The image analysis toolbox of Matlab v. 2019 was used to program customized functions for determining physical metrics from a series of steady-state images logged by a high-speed video camera, as shown in

Table 1. Physical IA metrics (automated) that are characterized for each frame in a video.

Feature (Metric)	Variable Name	Detailed Description
Control volume	Bdr_area	Area of the continuous liquid sheet before being disrupted by hole formation
Breakup length	Bdr_dis	Farthest location from the origin of the control volume
Hole location	hole_dis	Spatial location and size of holes that form inside and outside of the continuous liquid sheet
Hole surface area	hole_area	Area of holes within the continuous sheet
Polygon representation for all holes	Poly	Approximation of hole surface area (as collide holes) as a polygon (vertices ≤ 12) that is optimally fit to each hole
Boundary points characterizing each hole	BP	Vertices of a polygon (≤12 vertices) that are optimally fit to each hole
Angles formed as holes collide	Angle	Angles formed as holes collide with other holes, forming liquid ligaments
Ligament aspect ratio	R/L	Aspect ratios (R/L) for liquid bridges (ligaments) formed from the collision of multiple holes as the holes grow
Ligament length	L	Length of the liquid bridges that form upon the collision of multiple holes
Ligament width	W = 2R	Width of the liquid bridges that form upon the collision of multiple holes
Ligament area	Liga_area	Area of a ligament
Ligament distance from origin	liga_dis	Distance from the flat fan nozzle (origin) to the centroid of the ligament
Droplet distance	Drop_dis	Distance from the flat fan nozzle (origin) to the drop centroid
Droplet area	Drop_area	Area of the drop
Droplet radius	Drop_radius	Radius of the drop (assumed to be spherical)
Number of holes in continuous sheet	Hole_n	Number of holes in the image
# ligaments	Liga_n	Number of ligaments in the image
# drops	Drop_n	Number of drops in the image

. Each metric quantified a physical or geometrical feature(s) that characterizes the spray pattern (e.g., destabilization and breakup into drops of a continuous liquid sheet emanating from an agricultural flat fan nozzle). The nozzle in the images had a known size (as measured by a micrometer) and was used as the reference for all measurements taken from the image. The diameter of the ligament was assumed to be cylindrical, with the diameter given by the measured ligament width. Holes within the sheet were approximated as polygons. The detected features were the average angle of the polygons representing holes (angle); average distance from holes’ centroids to the nozzle (hole_dis); average area of holes (hole_area); average distance from ligaments’ centroids to the nozzle (liga_dis); average area of ligaments (liga_area); aspect ratio (average radius over length of ligaments, R/L); average distance from droplets’ centroids to the nozzle (drop_dis); average area of droplets (drop_area); average radius of droplets (drop_radius); average distance from continuous water sheets’ centroid to the nozzle (bdr_dis); average area of continuous water sheets (bdr_area); and average number of holes, ligaments, and droplets (hole_n, liga_n, and drop_n, respectively). The physical and empirical image analysis (IA) metrics presented in Table 1 were used in statistical analysis to uncover possible relationships to the droplet size distribution, specifically focusing on the driftable fine fraction (e.g., drop sizes < 150 μm in size).

2.2. Visual Navigable Landscape (Empirical)

As a proof of concept, a set of experiments was performed (distinct formulations and nozzle configurations) to generate high-speed videos for several spray events. At any given time point (i.e., a single video frame), the phenomenologically chaotic arrangement exhibited by the spray pattern can be characterized numerically using image texture features (e.g., entropy, fractal number, and statistical regularity; see Figure 1). Essentially, this technique strives to ascribe a descriptor of the image pattern that is numerically consistent within images of the same category (i.e., class) yet distinct from images of different categories [18]. For the most part, these computations are irreversible and noninterpretable, but they offer the ability to numerically categorize distinct, seemingly intractable image patterns, as shown in Table 2. The 21 videos resulted in 3281 images.

Ideally, a dynamic texture approach [18,19,20] would best describe the given system; however, here, we chose a simpler approximation scheme for the proof of concept. For each video, we randomly selected approximately 150 single frames, labeled each image with the corresponding formulation/nozzle combination (i.e., class), and then learned the best combination of image features to numerically categorize each image into its appropriate class. It is important to note that the more powerful dynamic texture approach extracts numeric features representing temporal changes in texture throughout the course of the video, whereas the current approach simply uses the texture at a static point in time. Therefore, any successful proof of concept for the single frame approach would support the assumption that the dynamic texture approach would offer better performance.

To account for experimental variability in the video capture (e.g., camera placement, lighting differences, nozzle geometry, etc.), each image frame was standardized so that the center of each nozzle lip was cropped and registered (e.g., aligned) with respect to all other frames. In addition, the background pixel intensities were suppressed. All image manipulation was performed using the CImg 1.5.1 C++ image handling libraries. The continuous sheet was characterized by the area (pixels), the farthest distance of the sheet from the nozzle before breakup, and by a centroid in relation to the origin (e.g., nozzle tip), as shown in Figure 1. Approximately 150 frames from each of the 21 video experiments (a subset of the 80 videos analyzed) were extracted for analysis. Different spray formulations and additives, such as solid particles, were investigated. Some of these 21 experiments were replicates, resulting in 17 unique classes.

Table 2. Representative empirical IA feature metrics determined for each frame in a video.

Empirical Feature (Metric)	Description
Run Length	Characterizes textures via patterns of sequence segments of similar pixel intensities (Tang, 1998 [21])
Haralick	Characterizes images via estimation of pixel entropy, pixel differences, etc. (Haralick et al., 1973 [22])
Simple statistics	Characterizes images via statistical values of pixels and their neighborhoods (e.g., average, variance, skew, kurtosis, etc.)
Lacunarity	Fractal-type descriptors for quantifying spatial complexity (Plotnick et al., 1996 [23]; Vernon-Carter et al., 2009 [24])

Table 2. Representative empirical IA feature metrics determined for each frame in a video.

Empirical Feature (Metric)	Description
Run Length	Characterizes textures via patterns of sequence segments of similar pixel intensities (Tang, 1998 [21])
Haralick	Characterizes images via estimation of pixel entropy, pixel differences, etc. (Haralick et al., 1973 [22])
Simple statistics	Characterizes images via statistical values of pixels and their neighborhoods (e.g., average, variance, skew, kurtosis, etc.)
Lacunarity	Fractal-type descriptors for quantifying spatial complexity (Plotnick et al., 1996 [23]; Vernon-Carter et al., 2009 [24])

2.3. Experimental

The experimental setup consisted of an enclosed spray chamber, a nozzle system, a Sympatec laser, an LED lighting system, tripod supports, and a high-speed video camera. Other metrics obtained by image analysis are presented in Figure 2. Another method to quantify sheet breakup involves representing holes that form within the liquid sheet using a polygon approximation method for these holes or “blobs” (Figure 2). This simplified approach reduces the number of vertices needed to describe the hole and allows the polygon area and side lengths of a hole to be computed. Details of the experimental setup used in the paper can be found elsewhere [12]. Figure 3 illustrates the flowchart used to represent the image processing procedure.

2.4. Theoretical

Perforations in the liquid spray sheet lead to hole formation. These holes expand and collide, which leads to the formation of ligaments (Figure 4). These ligaments subsequently stretch and ultimately succumb to finite-amplitude disturbances and break up into drops. It is the breakup of multiple ligaments that leads to the atomization drop size distribution for the oil-in-water breakup mechanism [10]. Liquid ligaments are treated as liquid cylinders whose endpoints are either free or constrained (pinned). Details of this linear stability analysis can be found elsewhere [25]. IA metrics for ligaments include ligament length, radius, and the distance from the nozzle (origin), where they are located. The stability of the ligament is governed by the aspect ratio (R/L); thus, we can compare the observed ligament stability from IA metrics with theoretical calculations for the onset of ligament breakup [25].

3. Results

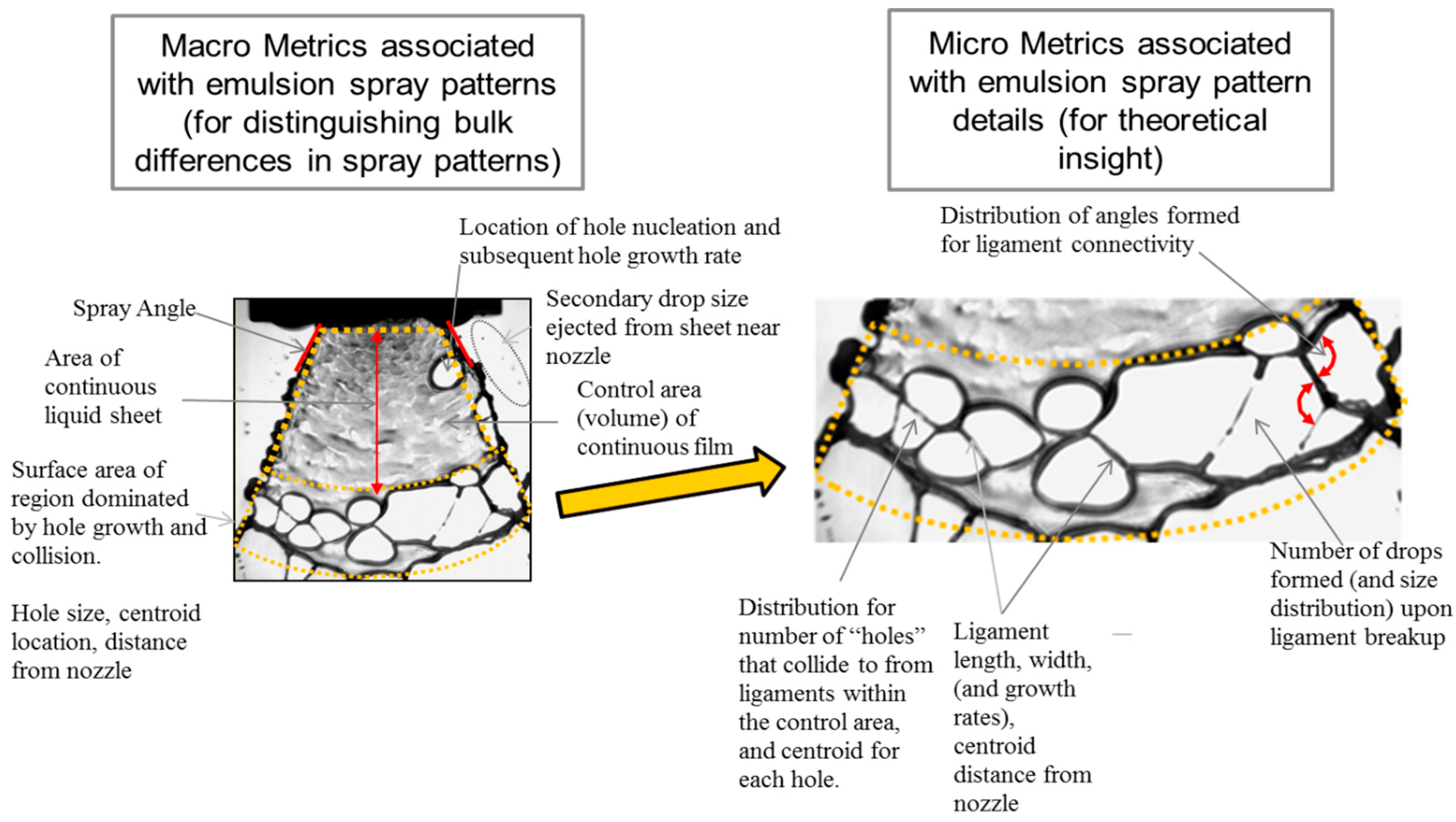
3.1. Visual Navigable Landscape (Empirical)

For each image, dozens of numerical image features were extracted ([21,24,26,27]. Using the class labels (e.g., formulation type), the image features were subjected to a feature selection algorithm that selects a small subset of features that are most correlated with the class label structure [28,29]. The 10 most correlated features were linearly combined (i.e., weighted and summed; principal components) and then used to classify each sample image. 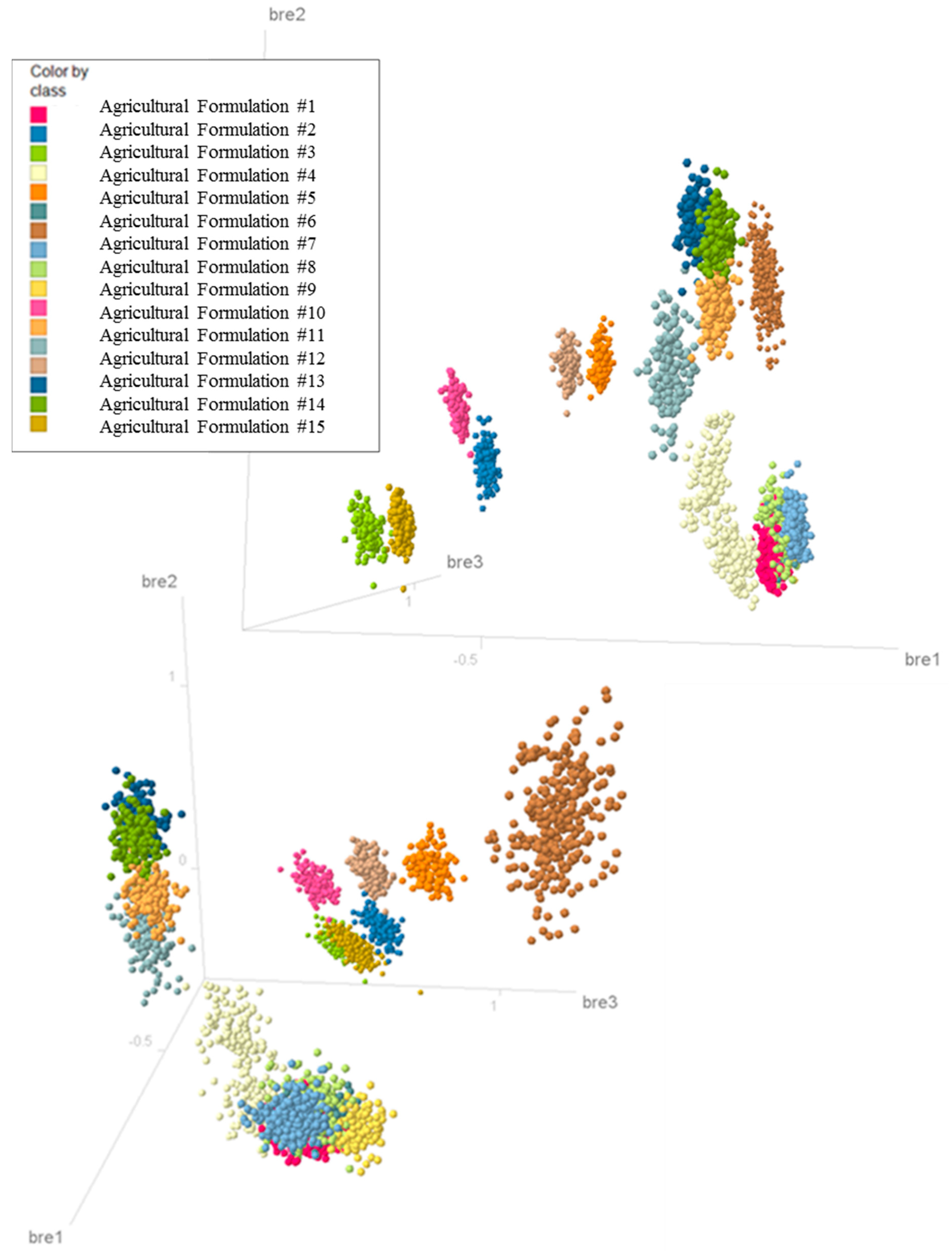This was performed so that three distinct linear combinations were computed that best separate the classes into three dimensions [30], thus allowing the images to be “projected” into a 3D graphical visualization. The resulting projection for the 21-video subset using different formulations is depicted in Figure 5, with bre1, bre2, and bre3 representing the three principal components used. Separation between the class label structures (e.g., different formulation types) indicates that image analysis (IA) metrics could distinguish between atomization (breakup) patterns for all the formulations investigated in the navigable landscape exercise. Thus, metrics generated from images of spray patterns can be used as dependent parameters in data mining and statistical techniques and in offering insight/quantification for mechanistic modeling of sheet atomization.

3.2. Physical Image Analysis (IA) Metrics

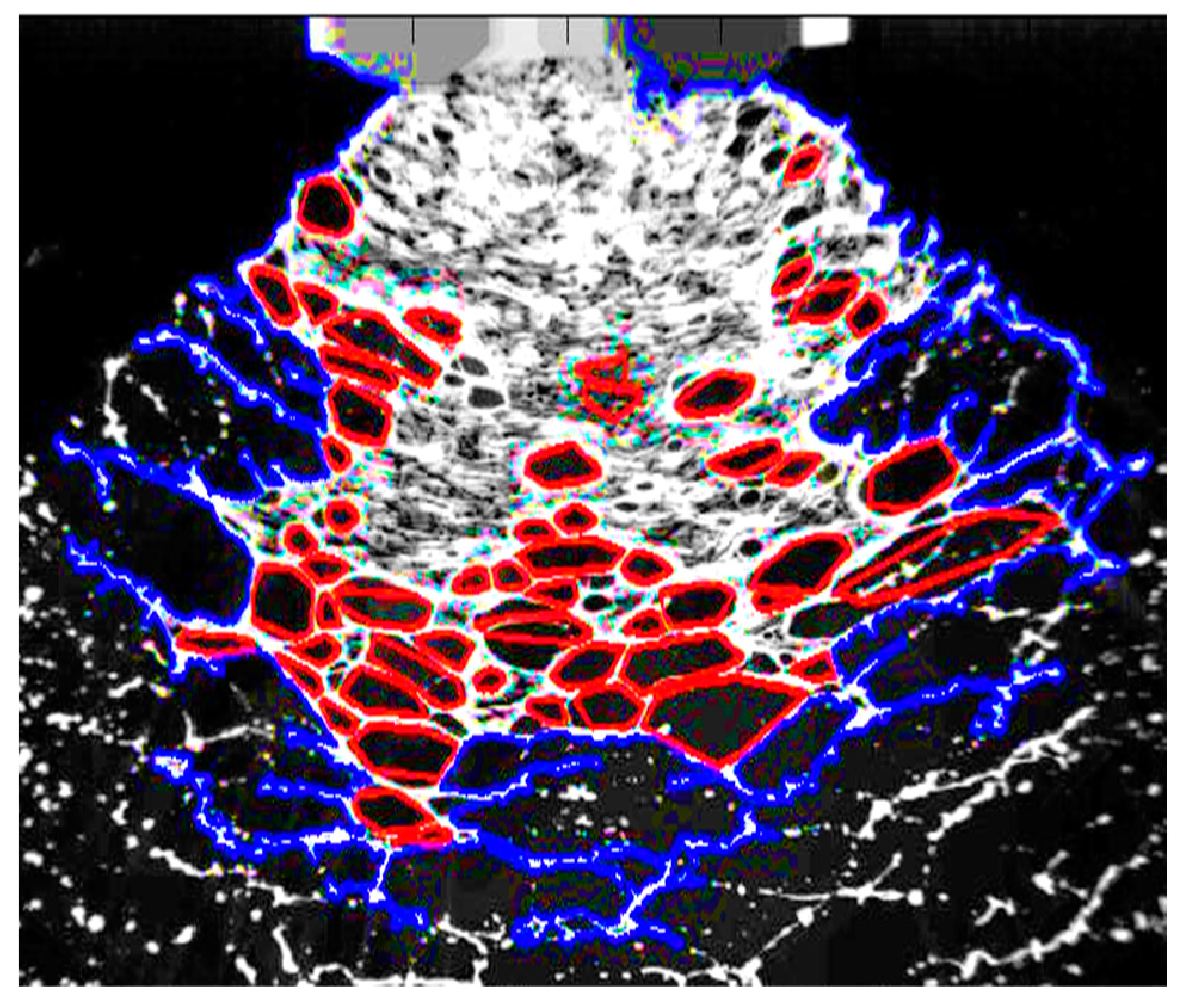
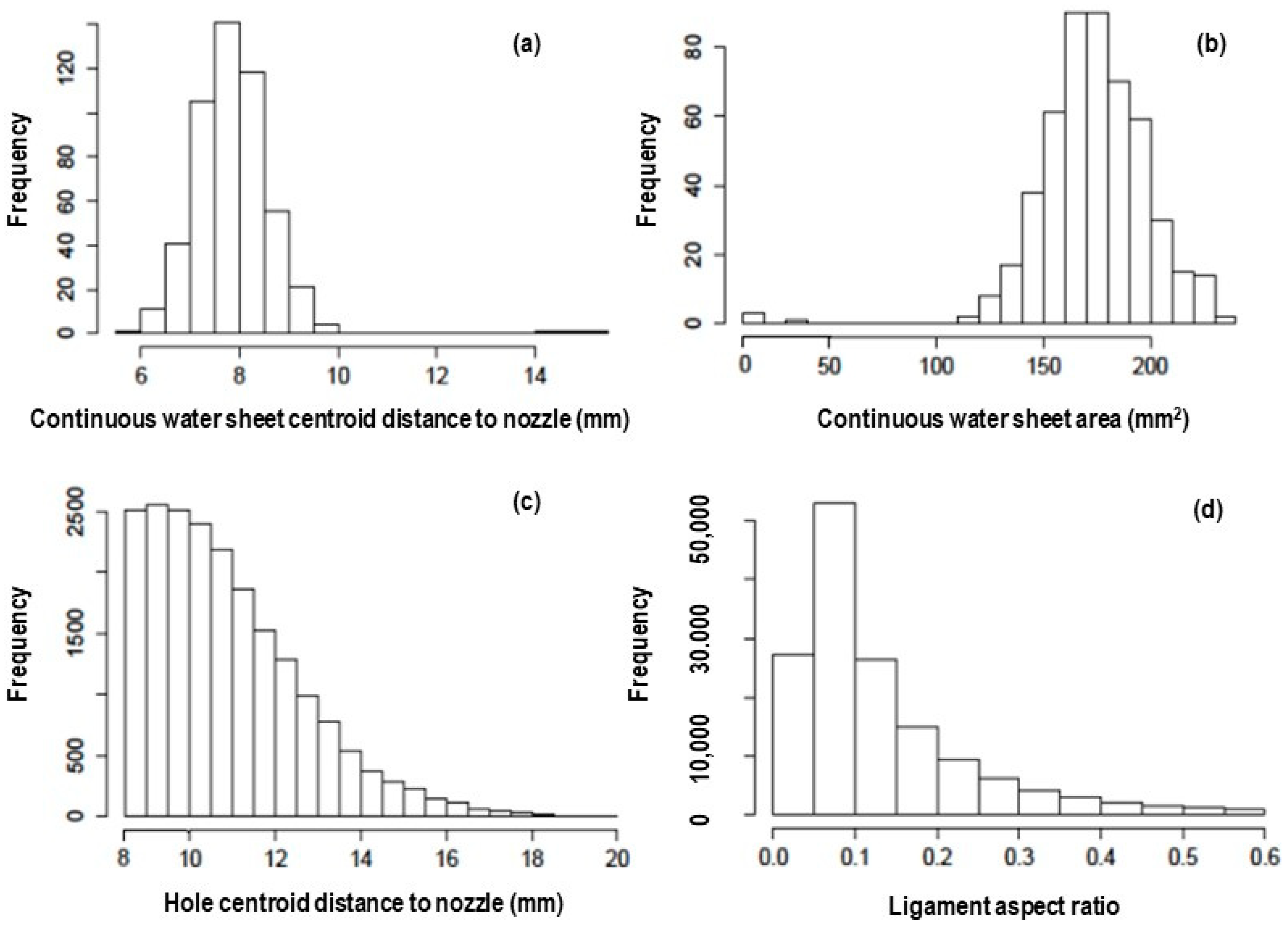
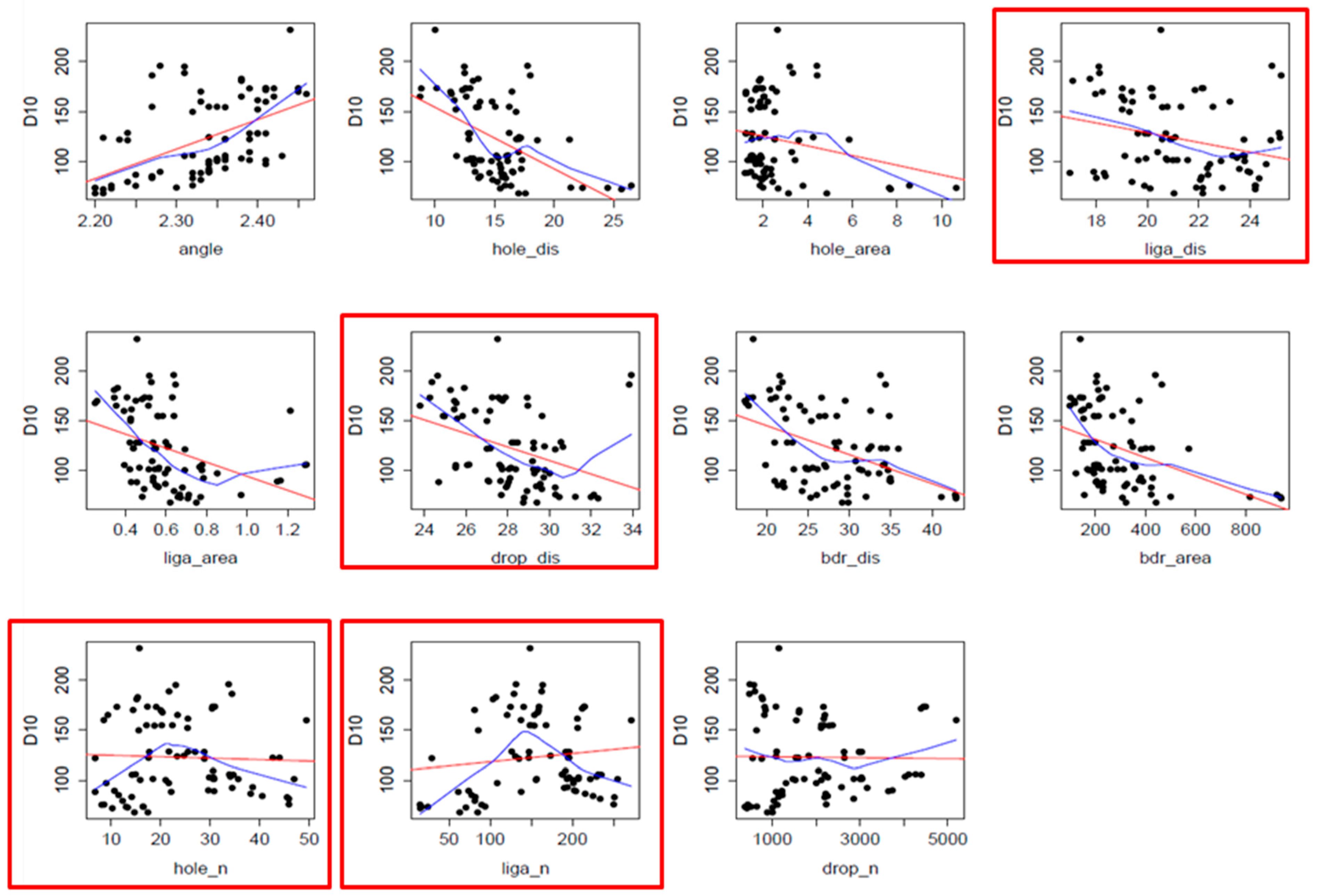
Histograms for metric measurements for a single atomization video for a two-phase system (1% oil) using an AIXR 110° nozzle are provided in Figure 6. The metrics included the centroid of the drops following atomization, liquid ligaments, and holes within each video frame, along with the area and the centroid of the continuous sheet of liquid before succumbing to the instability responsible for sheet breakup. Lastly, the aspect ratio (R/L) for each of the many ligaments found in an image was measured and tabulated as a histogram (bottom right in Figure 6).

The breakup of a cylinder ligament is not instantaneous. In Altieri, Cryer, and Acharya [10], it was assumed mathematically that the Plateau–Rayleigh instability immediately destroyed the liquid ligaments that were formed. The presence of fluid webs seen in the images is evidence that this did not happen and can be attributed to two factors: (1) the rate of growth of the cylinder instability and (2) ligament stabilization by “pinning” cylinder ends. Constraining the ends of the ligament (approximated as a cylinder) to have fixed contact lines stabilizes the ligament (based on the linear stability theory [11]) when contrasted against a liquid cylinder with “natural” endpoints (Figure 7). Not only does the pinned growth rate decrease from the corresponding free case but the R/L value for the maximum growth rate also shifts. Thus, cylinders of fluid can grow longer before becoming unstable, and it takes longer for the disturbance to grow along the cylinder interface, which ultimately leads to cylinder breakup and drop formation.

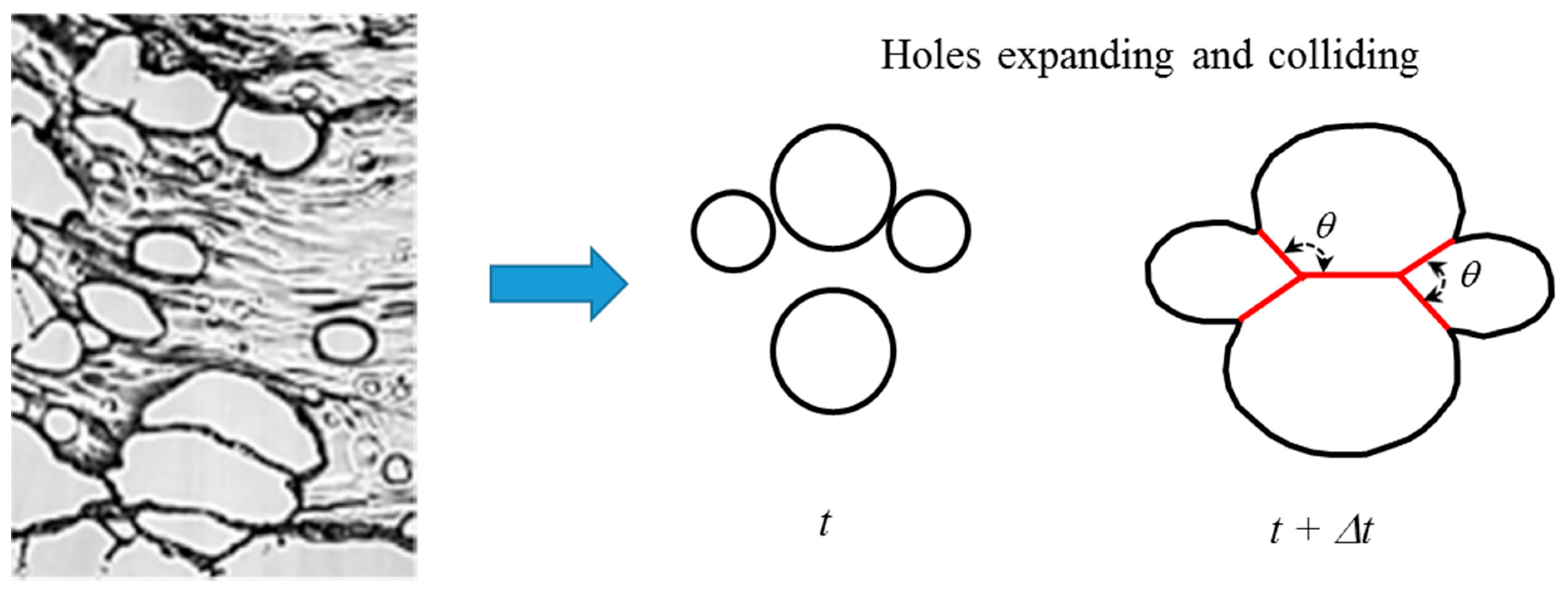
Holes that formed within the continuous liquid sheet were approximated as polygons with up to 12 edges. The angles that formed between the polygon edges were interpreted as representing the number of distinct holes that collided (Figure 7). The angle between the polygon edges decreased as more holes collided. Thus, the representative histogram describing polygon angles for a hole is related to the number of colliding holes.

3.3. Statistical Analysis

Exploratory Data Analysis: On Physical Metrics

A data set with 14 detected features from the videos and five variables were determined after running our algorithm on this spray data. The 14 detected features were as follows: average angle of the polygons representing holes (angle); average distance from holes’ centroids to the nozzle (hole_dis); average area of holes (hole_area); average distance from ligaments’ centroids to the nozzle (liga_dis); average area of ligaments (liga_area); aspect ratio (average radius over length of ligaments, R/L); average distance from droplets’ centroids to the nozzle (drop_dis); average area of droplets (drop_area); average radius of droplets (drop_radius); average distance from continuous water sheets’ centroid to the nozzle (bdr_dis); average area of continuous water sheets (bdr_area); and average number of holes, ligaments, and droplets (hole_n, liga_n, and drop_n, respectively).

The five dependent variables predicted were the atomization drop sizes D10, D50, D90, f74, and f150. Here, D10, D50, and D90 are actual drop diameters for percentiles of 10, 50, and 90%, respectively, while f74 and f150 are percentages of drops below a size of 74 and 150 μm, respectively. A linear regression model was used to represent this relationship and clearly identify which feature(s) are important in determining the response variable. Data fitted into a linear regression model should meet the standards of (1) keeping the normality of each variable, (2) adding some possibly related new terms, and (3) eliminating the linear correlation between predictors. A representative statistical analysis using D10 as the dependent variable is provided. The regression model checked assumptions that require the error distribution to be normal (all predictors should be normally distributed such that the prerequisites of the linear model are satisfied). However, the relationship between one predictor and the response variable may not be a linear one, and if the local regression model is far from being linear, then quadratic terms are added. Quadratic terms for liga_dis, drop_dis, hole_n, and liga_n (outlined by red boxes in Figure 8) were added and identified as liga2, drop2, hn2, and ln2, respectively. The distributions for hole_area, bdr_area, ln2, and hn2 did not follow an obvious normal distribution, but the logarithm for these original variables was normally distributed.

Table 3. Predictor explanations and their new names.

Predictor	Explanation	New Name
angle	Average angles of polygons representing holes	V1
hole_dis	Average distance from holes’ centroids to the nozzle	V2
hole_area	Average area of holes (take logarithm)	log(V3)
liga_dis	Average distance from ligaments’ centroids to the nozzle	V4
liga_area	Average area of ligaments	V5
drop_dis	Average distance from droplets’ centroids to the nozzle	V6
bdr_dis	Average distance from continuous water sheets’ centroid to the nozzle	V7
bdr_area	Average area of continuous water sheets (take logarithm)	log(V8)
hole_n	Average number of holes	V9
liga_n	Average number of ligaments	V10
drop_n	Average number of droplets	V11
liga2	Square of the average distance from ligaments’ centroids to the nozzle	V12
drop2	Square of the average distance from droplets’ centroids to the nozzle	V13
ln2	Square of the average number of ligaments (take logarithm)	log(V14)
hn2	Square of the average number of holes (take logarithm)	log(V15)

summarizes the parameters that were log transformed to meet normality constraints. A linear regression model will not be a good choice if the response variable is not normally distributed. However, we can find some transformations to convert the data into normal data via a Box–Cox transformation $\frac{y^{\lambda }-1}{\lambda }$ (equivalent to taking the logarithm while parameter λ = 0). Here, $y$ is the response variable, and λ is the transformation parameter. So, the probability density function for a sample $\left(y_1,\dots ,y_n\right)$ is $P(y_1,\dots ,y_n)=\prod _{i=1}^n\frac{{y_i}^{\lambda }-1}{\lambda }$. In this way, the Jacobian can be written as follows:

$$\left(\lambda ;y_1,\dots ,y_n\right)=\prod _{i=1}^n|d{y}_i^{\left(\lambda \right)}/dy|=\prod _{i=1}^n{y}_i^{\lambda -1}=GM{\left(y\right)}^{n\left(\lambda -1\right)}$$

Here, GM represents the geometric mean, so the normal log likelihood at its maximum is as follows:

$$\log \left(L\left(\widehat{\mu },\widehat{\sigma }\right)\right)=-\frac{n}{2}\left(\log \left(2\pi {\widehat{\sigma }}^2\right)+1\right)+n\left(\lambda -1\right)\log \left(GM\left(y\right)\right)=-\frac{n}{2}(\log \left(\frac{2\pi {\widehat{\sigma }}^2}{GM{\left(y\right)}^{2\left(\lambda -1\right)}}\right)+1)$$

Minimizing the sum of square residuals is equivalent to maximizing the sum of the normal log likelihood of deviations from $\frac{y^{\lambda }-1}{\lambda }$ as well as the log of the Jacobian of the transformation. The best prediction for each response variable selected (proper transformation) is summarized in

Table 4. Box–Cox transformation parameters and the corresponding functions.

	D10	D50	D90	f74	f150
Estimated λ	−0.2	0	−0.4	0.3	0.2
Suggested λ	0	0	−0.5	0.33	0.25
Transformation	$\mathrm{l}\mathrm{o}\mathrm{g}\left(\mathrm{D}10\right)$	$\mathrm{l}\mathrm{o}\mathrm{g}\left(\mathrm{D}50\right)$	1/$\sqrt{D90}$	$\sqrt[3]{f74}$	$\sqrt[4]{f150}$

.

3.4. Principal Component Analysis (PCA)

The newly transformed data for both the predictors and response variables (e.g., D10) followed an approximately normal distribution. The next step was to eliminate the linear correlation between predictors using the classical method of principal component analysis (PCA) because PCA creates a new set of orthogonal linear combinations of the original predictors. The advantages of PCA include the following:

• Orthogonal linear combinations compose a new feature space such that each feature is linearly uncorrelated with others.
• Principal components (PC) are listed in order. The order describes the variance in the data that each component can explain.

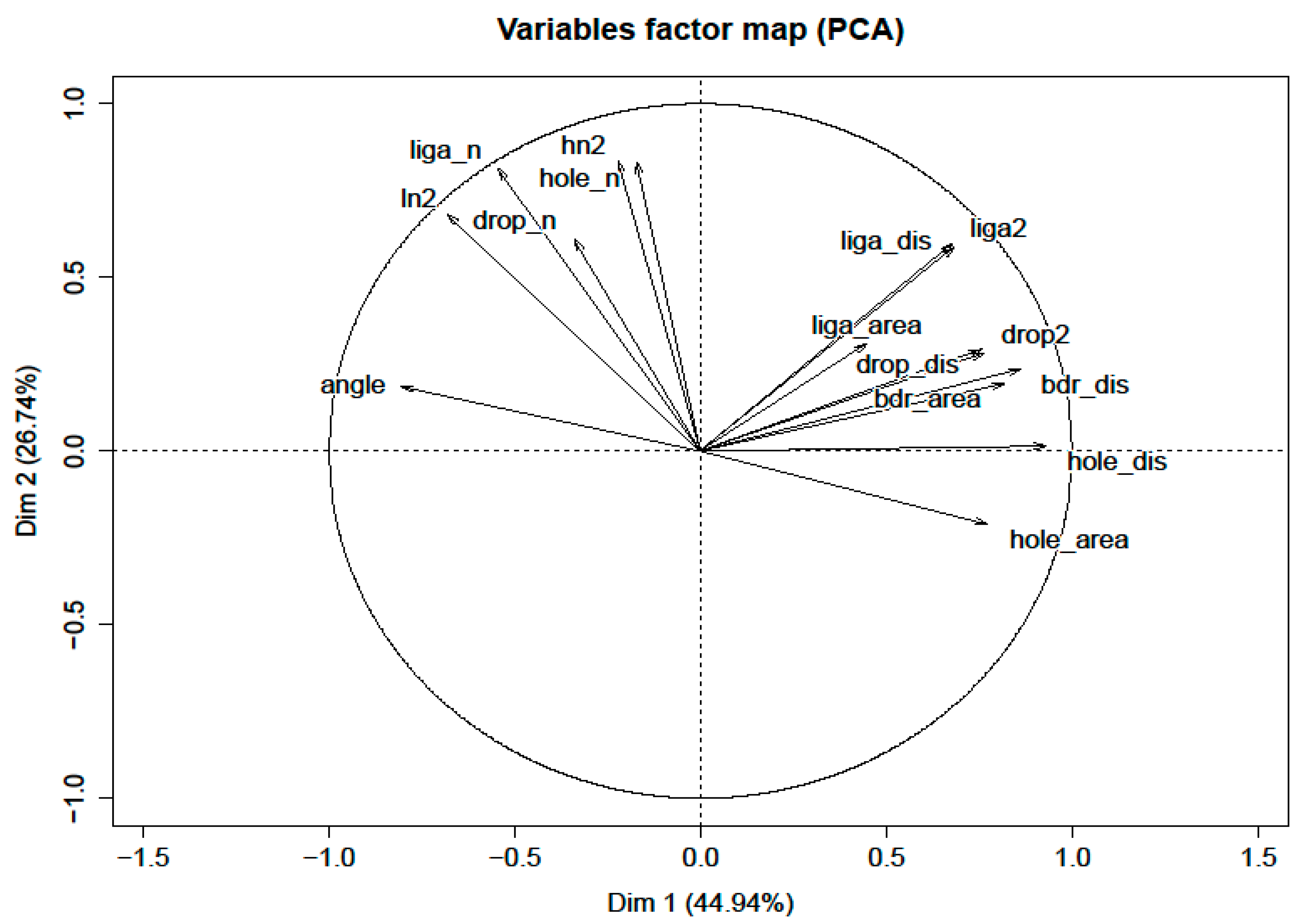
A transforming matrix was obtained while running PCA to deliver information on how the new features are composed (and these new features are easily transformed back to the original feature set). A score plot is a representative example for the first two principal components (PC), as shown in Figure 9, where the x-axis (Dim 1) and y-axis (Dim 2) represent principal components 1 and 2, respectively. PCs are orthogonal and linearly independent of each other. Figure 9 is useful to visualize the original predictor variable representation on different principal components. For example, if one takes PC1 and PC2 as the graphical axes, then one can find that the hole distance (variable) is almost horizontal (PC1) but is not related to PC2. In addition, the vector representing the variable of ligament distance (liga_dis) in Figure 9 has a length of 0.9 and forms a $\pi /4$ angle with both the x and y axes. This implies both PC1 and PC2 contain $0.9\times \mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{\pi }{4}\right)$ of liga_dis in their final representations.

Group clusters indicate the projection of each sample observation on the plane formed by PC1 and PC2. All the principal components form an orthogonal space, and each sample observation represents a point in this space. PC1 and PC2 will form a plane. After performing PCA, 15 new variables (PCs) were generated. It was found that 10 of the new PC variables could explain more than 99% of the variance in the predictors. Therefore, the first 10 PCs were kept in the analysis (e.g., PC1, PC2, …, PC10).

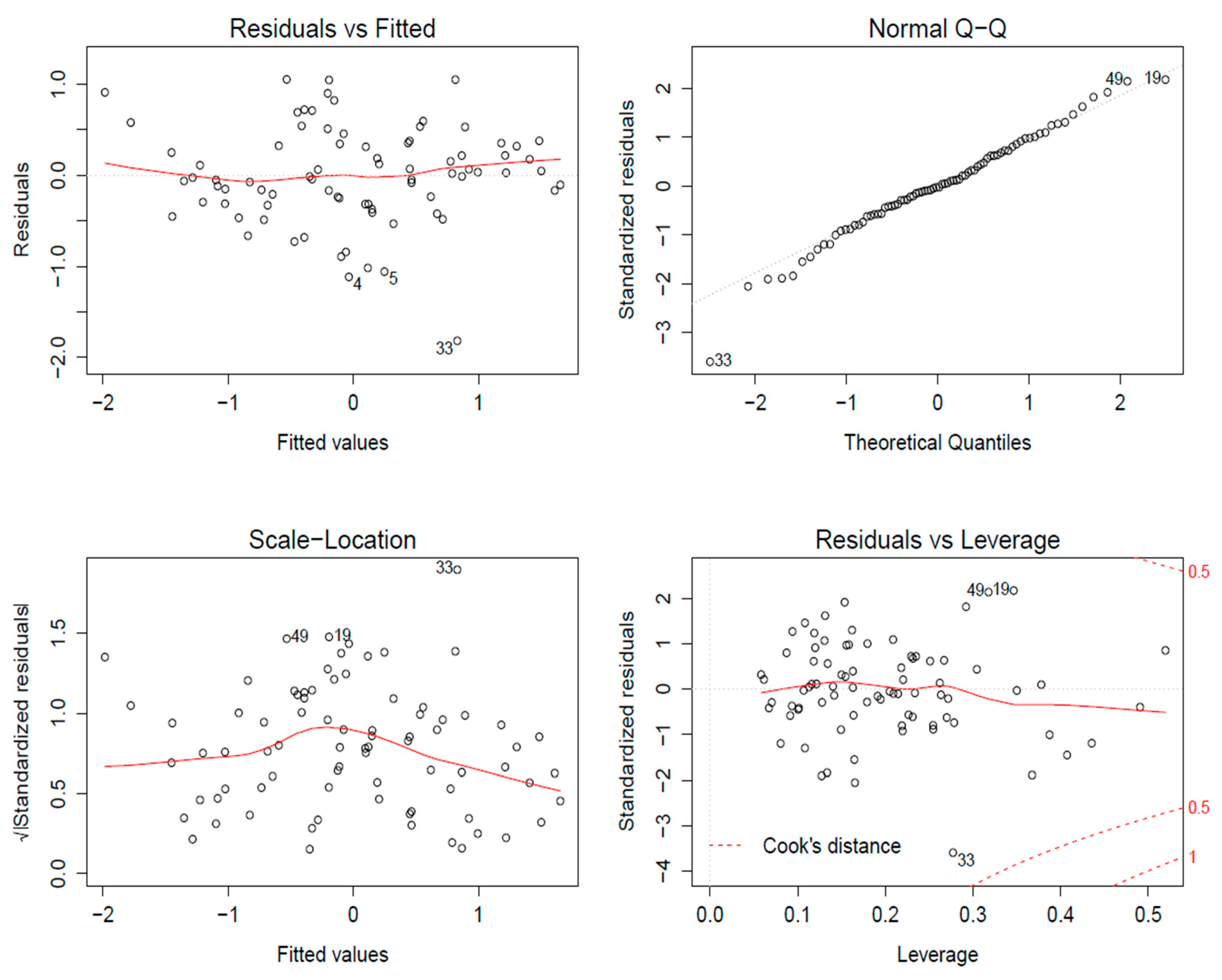
First, a full linear regression model was fitted to the data set to check whether linear regression requirements were satisfied. Figure 10 is the diagnostic plot for the full linear regression model. The diagnostic plot consisted of four parts: residual versus fitted plot, scale–location plot, normal Q–Q plot, and residual versus leverage plot and is used to evaluate whether the data and model assumptions of linear regression are satisfied. The residual versus fitted plot was relatively flat and had a magnitude of approximately absolute zero (meaning the data had an average value of 0, which implies the data followed a linear model). The normal Q–Q plot was almost a straight line, meaning that the normality condition (the error term in the linear regression model should follow a normal distribution) was true for our data set (an important assumption for building linear regression models). The scale–location plot shows the square root of the standardized residuals as a function of the fitted values. No obvious trend in this plot means the linearity of the data was satisfied. Finally, the fourth plot, the residuals versus leverage plot, shows outliers in the sample set. Outliers are defined by Cook’s distance, and usually one chooses 0.5 or 1 as the threshold. All points were located inside the (−0.5, 0.5) region, which means there were no outliers in the sample data set. The results summarized in Figure 10 imply that a linear regression model is reasonable.

A metric to balance accuracy and complexity is called AIC. Suppose there exists a full model that includes all predictors and a null model that includes no predictors. Between these two models, one can pick a set of predictors to build a linear regression model and obtain a corresponding AIC value. The model with the best AIC value is the final model that is used. A threefold cross-validation approach was used to test the robustness of this new AIC model, and the regression lines for each fold were similar, which implies that the model had similar performance on all three randomly picked subsets. Thus, one can conclude the final linear regression model is robust because it passed the cross-validation test (the finalized model is the one that used PCs), as shown in

Table 5. Formula of each response variable in principal components.

Response	Formula in PCs
D10	$\log \left(D10\right)=4.76+0.0008PC2+0.0009PC4+0.016PC5+0.019PC6+0.069PC7+0.348PC9$
D50	$\log \left(D50\right)=5.58+0.0008PC2+0.0011PC4+0.017PC5+0.019PC6+0.06PC7+0.317PC9$
D90	$\frac{1}{\sqrt{D90}}={10}^{-4}(470-0.1PC2-0.2PC3-0.2PC4-2PC5-3.7PC6-10.2PC7-72.1PC9)$
f74	$\sqrt[3]{f74}=1.37-0.001PC2-0.002PC3-0.002PC4-0.022PC5-0.024PC6-0.16PC7-0.338PC9+0.298PC10$
f150	$\sqrt[4]{f150}=2.07-0.001PC2-0.001PC4-0.019PC5-0.018PC6-0.073PC7-0.348PC9$

. Using the rotation matrix between the PCs and original features, we could translate the PC model back into original features (

Table 6. Formula of each response variable in original features.

Variable Name	$\mathbf{log}\left(\mathit{D}10\right)$	$\mathbf{log}\left(\mathit{D}50\right)$	$\frac{1}{\sqrt{\mathit{D}90}}$ $(\times {10}^{-4}$)	$\sqrt[3]{\mathit{f}74}$	$\sqrt[4]{\mathit{f}150}$	Unit	Scale
Intercept	4.76	5.58	470	1.37	2.07	1	NA
V1	−0.00219	−0.00202	0.498	−0.00652	0.00214	$\mathrm{r}\mathrm{a}\mathrm{d}$	1
V2	−0.0707	−0.063	10.5	0.174	0.0749	$\mathrm{m}\mathrm{m}$	10
log(V3)	0.278	0.253	−57.8	−0.147	−0.278	${\mathrm{m}\mathrm{m}}^2$	1
V4	0.0379	0.0345	−7.8	−0.0146	−0.0379	$\mathrm{m}\mathrm{m}$	10
V5	0.0273	0.0249	−5.68	0.0375	−0.0274	${\mathrm{m}\mathrm{m}}^2$	1
V6	−0.0179	−0.0163	3.68	0.0402	0.0179	$\mathrm{m}\mathrm{m}$	10
V7	−0.00426	−0.00736	1.63	−0.0294	0.00324	$\mathrm{m}\mathrm{m}$	10
log(V8)	0.00856	0.008	−2.34	−0.0425	−0.00791	${\mathrm{m}\mathrm{m}}^2$	10
V9	−0.015	−0.0152	2.63	0.0234	0.0175	1	10
V10	−0.00179	−0.00112	0.337	0.00221	0.00129	1	100
V11	−0.00001	−0.00002	0.00606	0.000123	0.00003	1	1000
V12	−0.00052	−0.000417	−0.0547	−0.00191	0.000627	${\mathrm{m}\mathrm{m}}^2$	100
V13	0.000153	0.000167	0.0577	0.000597	−0.00009	${\mathrm{m}\mathrm{m}}^2$	100
log(V14)	0.0792	0.0718	−15.7	0.0233	−0.0799	1	10
log(V15)	0.187	0.17	−38.8	−0.413	−0.187	1	10

“1” in the table means that we do not have any units for the corresponding predictor, such as intercept and number of holes in the picture. “Scale” means the scale of that variable; if we multiply the variable range with the coefficient, the importance of that variable is approximated.

).

3.5. Individual Factor Analysis

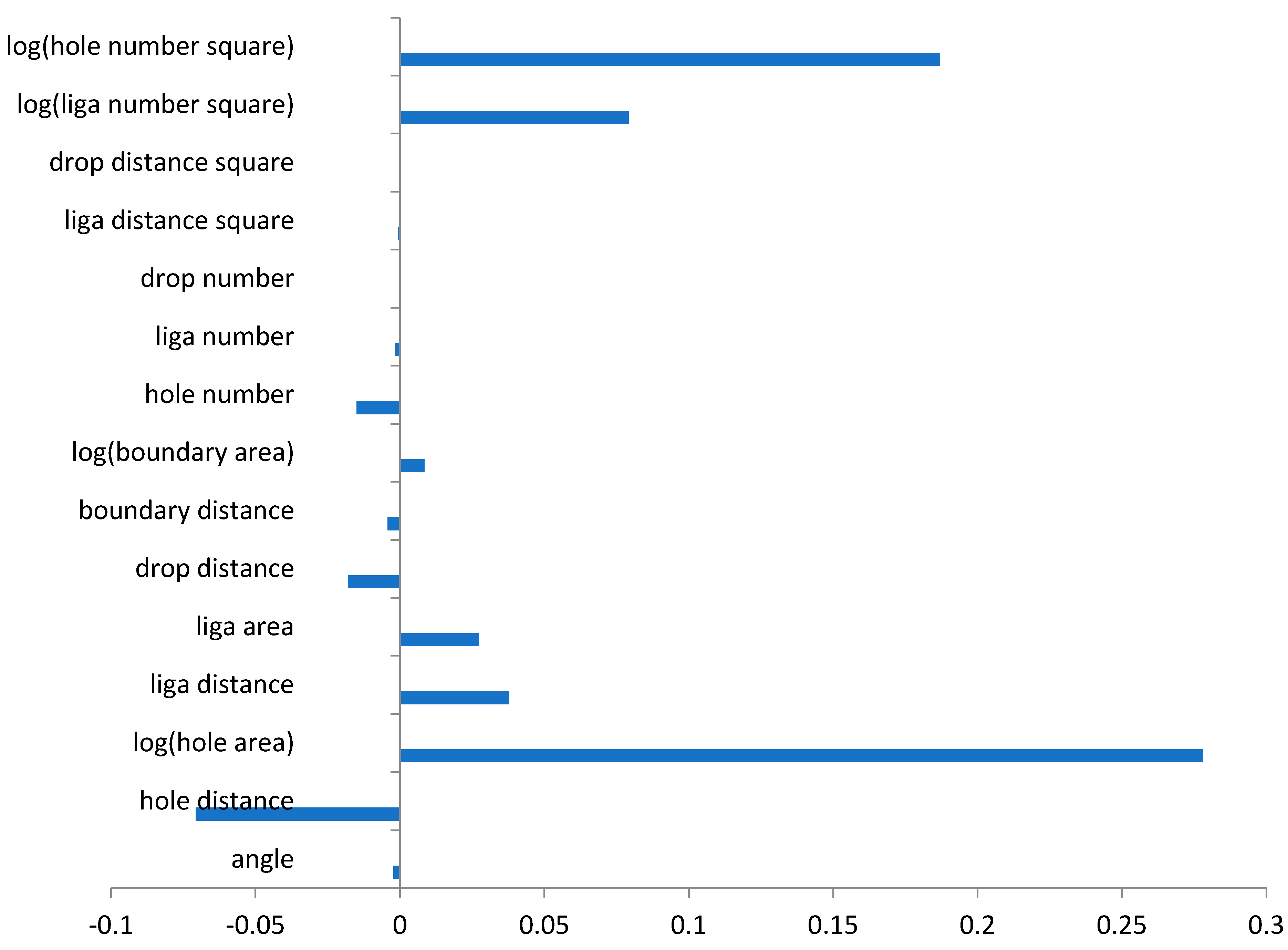
The slope of the factor plots is indicative of the relative sensitivity of the IA metric, and a positive slope indicates the response variable (e.g., log(D10)) increases as the parameter increases and vice versa (

Table 7. Correlation of primary IA metrics to driftable fine fraction (D10).

Negative Slope	Positive Slope
Angle	Hole area
Hole distance	Ligament distance
Drop distance	Ligament area
Boundary distance	Boundary area
Hole number	(Drop distance)2
Ligament number	(Ligament number)2
Drop number	(Hole number)2
(Ligament distance)2

). A short synopsis of the response variable is provided, with the drop angle of the holes that were formed being the most sensitive. As the angles formed within a hole increase, driftable fines decrease (this is related to the number of colliding holes). As more holes collide, more sides of a polygon will be needed to characterize the hole (and thus the polygon angles will decrease). Also, as the distance between the hole centroids and the nozzle increases, the driftable fines also decrease. Therefore, it is reasonable that a larger hole distance leads to a smaller response variable log(D10) (thus, we want holes to form near the nozzle, which corroborates well with the two-hole model results [11]). The angle used to approximate a hole is important and has been found to be the most sensitive parameter correlating to the prediction of driftable fines.

The current experimental observations for driftable fine reductions indicate that an upper limit for atomization drop sizes is achieved when air induction nozzles are used. This is likely attributed to the fact that the control of hole formation is lost or masked by the air being entrained into the sheet (which is an alternative way to control the number of holes that are colliding). There are several cross terms in this screening model that are sensitive, and all have an angle in the cross term. The average distance from the nozzle to the centroid of the continuous liquid sheet (Bdr_dis) analysis suggests that as this distance increases, driftable fines increase slightly. However, when one multiplies the coefficient for Bdr_dis with a scalar, then this parameter is not sensitive for DT10. Also, the number of holes in the continuous fluid sheet (Hole_n) decreases the driftable fines as this parameter increases. This is because more holes imply completeness of breakup, and smaller droplets occur; thus, the driftable fine fraction decreases. Analogous findings occur for the number of ligaments (Liga_n).

As the number of drops the sheet breaks up into increases, the number of driftable fines likewise decreases. More drops in this case means a higher fraction of smaller drops; thus, we want to keep the drop numbers to a minimum (e.g., the bigger drops). The more drops we have, the more completely the liquid sheet breaks up. The completeness of the breakup implies smaller droplet sizes.

Parameters that were found to be positively correlated were hole area, ligament distance, ligament area, and the biggest blog area. Thus, as the parameters increase in magnitude, so does the driftable fine fraction. A larger hole area is indicative of the incompleteness of the breakup procedure, so it leads to larger driftable fines. It is not intuitively clear, but the ligament distance indicates that only the short and chubby ligaments are seen a long way from the nozzle, and if this is the case, then the driftable fine fraction should decrease. An increase in ligament distance shows that ligament formation occurs, which means the breakup procedure is not complete, so an increase in drop size can be expected. A larger driftable fine fraction is implied as the ligament area increases because drops are formed when ligaments break up.

The average area of the continuous water sheet (biggest blob) is given by Bdr_area, which indicates a positive correlation to driftable fines. However, by looking at the scale and coefficient of the variable in the final model, this is not a sensitive parameter. Also, the square of the variables for ligament number and hole number should lead to a decrease in driftable fines, but the results suggest a slight increase in driftable fines. R/L, drop distance from the nozzle, and (ligament distance)² and (droplet distance)² are not sensitive parameters.

A comparison of the coefficients of each predictor in the linear regression model is given in Figure 11. The magnitude of each correlation is related to parameter sensitivity. A positive coefficient indicates that increasing the parameter increases D10 (with the converse also being true). The IA metrics found to be the most sensitive in predicting D10 were log(hole number²) and log(hole area). Details of deep learning and other software approaches are discussed in other articles [12,13].

4. Discussion

Photographs of atomization spray patterns for two-phase systems showed rich and diverse patterns that were dependent not only on the geometries/types and operating conditions of the nozzle but also on the composition of the formulation and its attributes, such as interfacial tensions between various phases, wettability, etc. Thus, metrics generated from images of spray patterns can be used as dependent parameters in data mining and statistical techniques and in offering insight/quantification for mechanistic modeling of sheet atomization. PCR analysis showed that 99% of the variability in the response variable for atomization droplet size (DT10) was addressed by 10 principal components. Sensitive parameters included the angles formed by colliding holes within the atomization sheet, hole distance from the nozzle, drop distance, hole number, ligament number, and drop number, which were negatively correlated to the atomization driftable fine fraction (drops smaller than 150 μm), while hole area, ligament distance, ligament area, and boundary area were positively correlated. Image analysis and machine learning techniques suggested the most sensitive metrics included log(hole number²) and log(hole_area), followed by hole_dis and log(ligament number²). Some variables that had a significant impact on the variance of the data were the angles that formed when holes collided and the log of hole area (log(hole_area)). Based on the coefficient and significance analysis and the analysis of variance, the variables angle, log(hole_area), drop_dis², hole_dis, and log(ligament number²) were found to be the five most important predictors that could be used to quantify the breakup of oil-in-water formulations into individual droplets,

Table 8. Variance explained in terms of attributes for magnitude for each correlation in the parameter sensitivity analysis.

Variable	Variance Explained Percentage (%)
angle	26.43
log(hole_area)	8.38
drop_dis2	4.91
hole_dis	4.01
log(ligament number2)	3.73
liga_dis2	3.63
liga_n	3.16

. PCA/PCR and linear regression were utilized to substantiate the findings in this paper.