A Comprehensive Evaluation of Turbulence Models for Predicting Heat Transfer in Turbulent Channel Flow across Various Prandtl Number Regimes
Abstract
1. Introduction
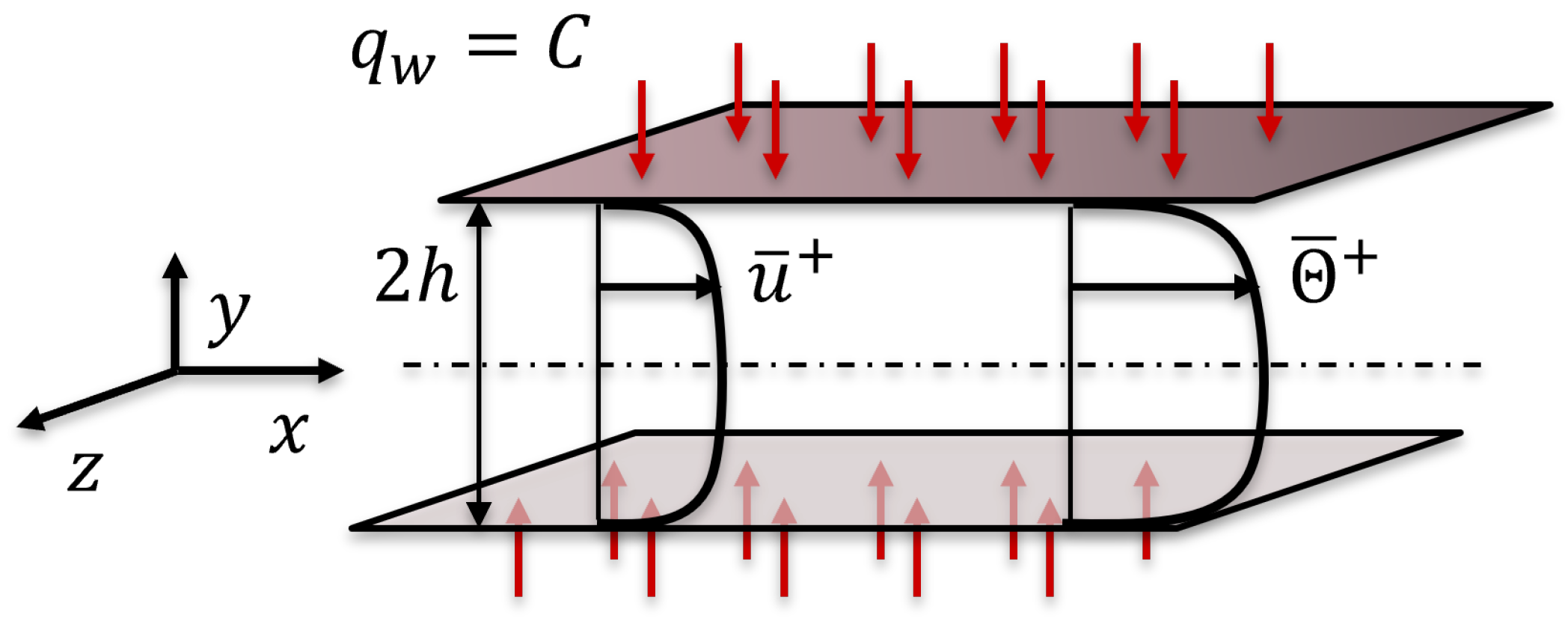
2. Governing Equations and Flow Setup
3. Model Formulations for Reynolds-Averaged Closures
3.1. Eddy Viscosity Models
3.2. Reynolds Stress Transport Models
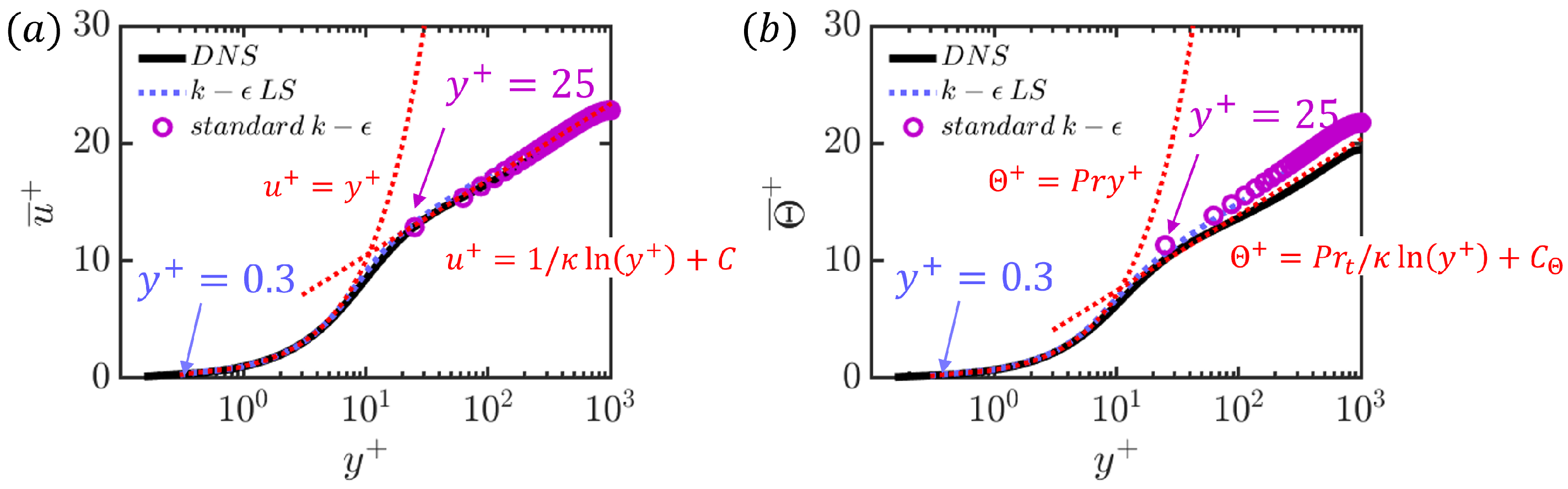
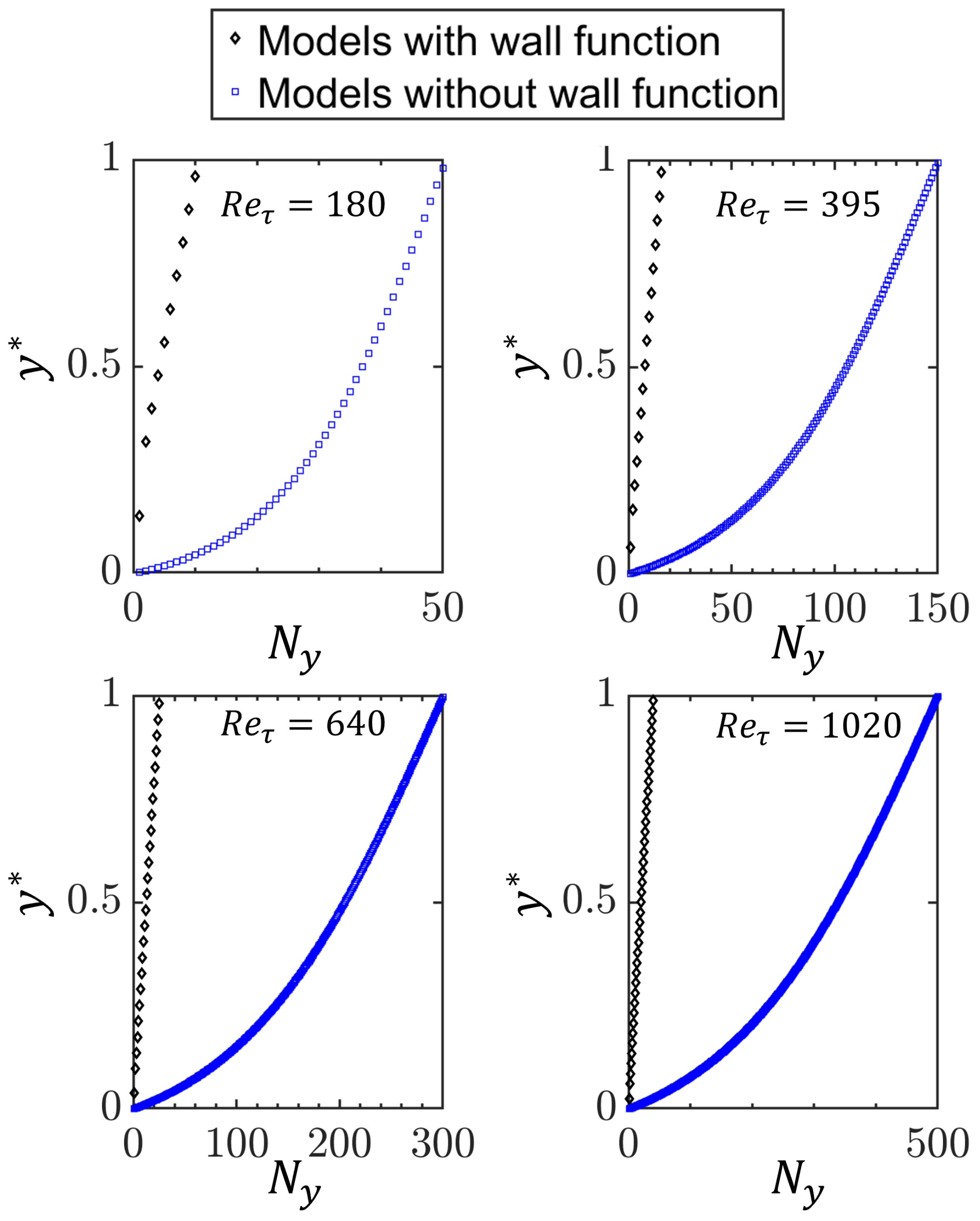
3.3. Near-Wall Treatment
3.4. A Summary of Selected Turbulence Models
4. Results and Discussion
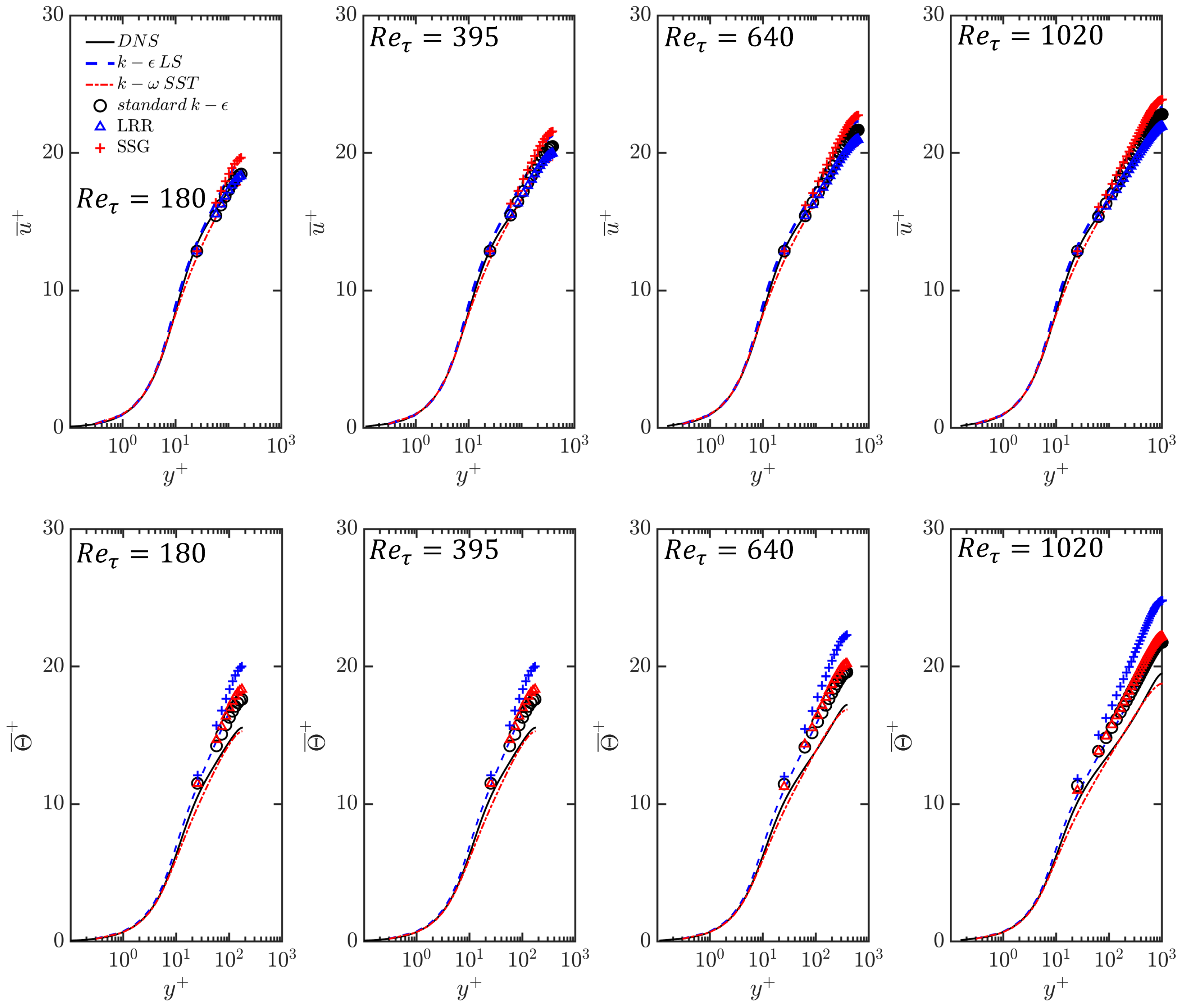
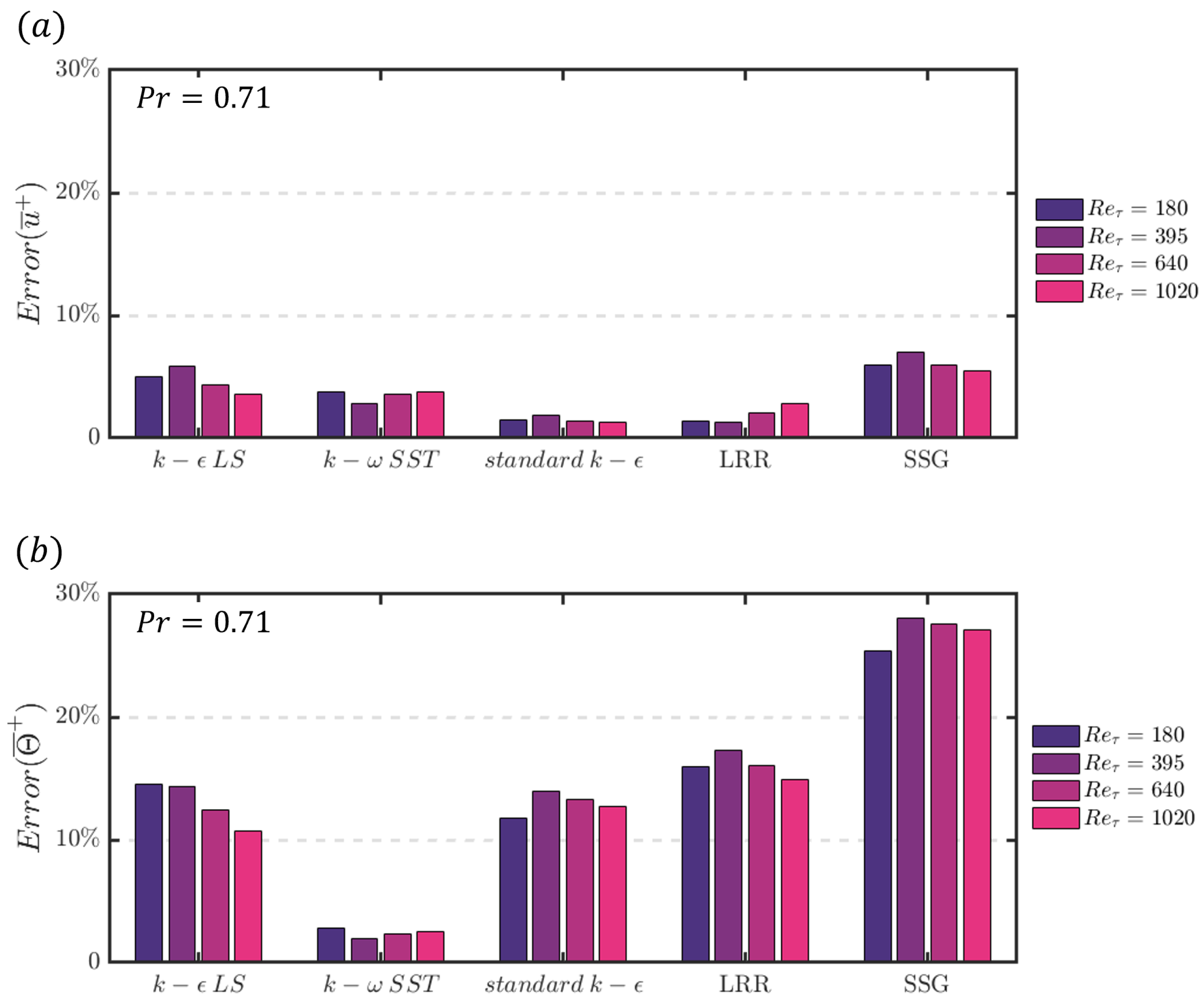
4.1. Heat Transfer Rate in Turbulent Channel Flow for Different Values of Reynolds Number
4.1.1. Mean Streamwise Velocity and Temperature Profiles
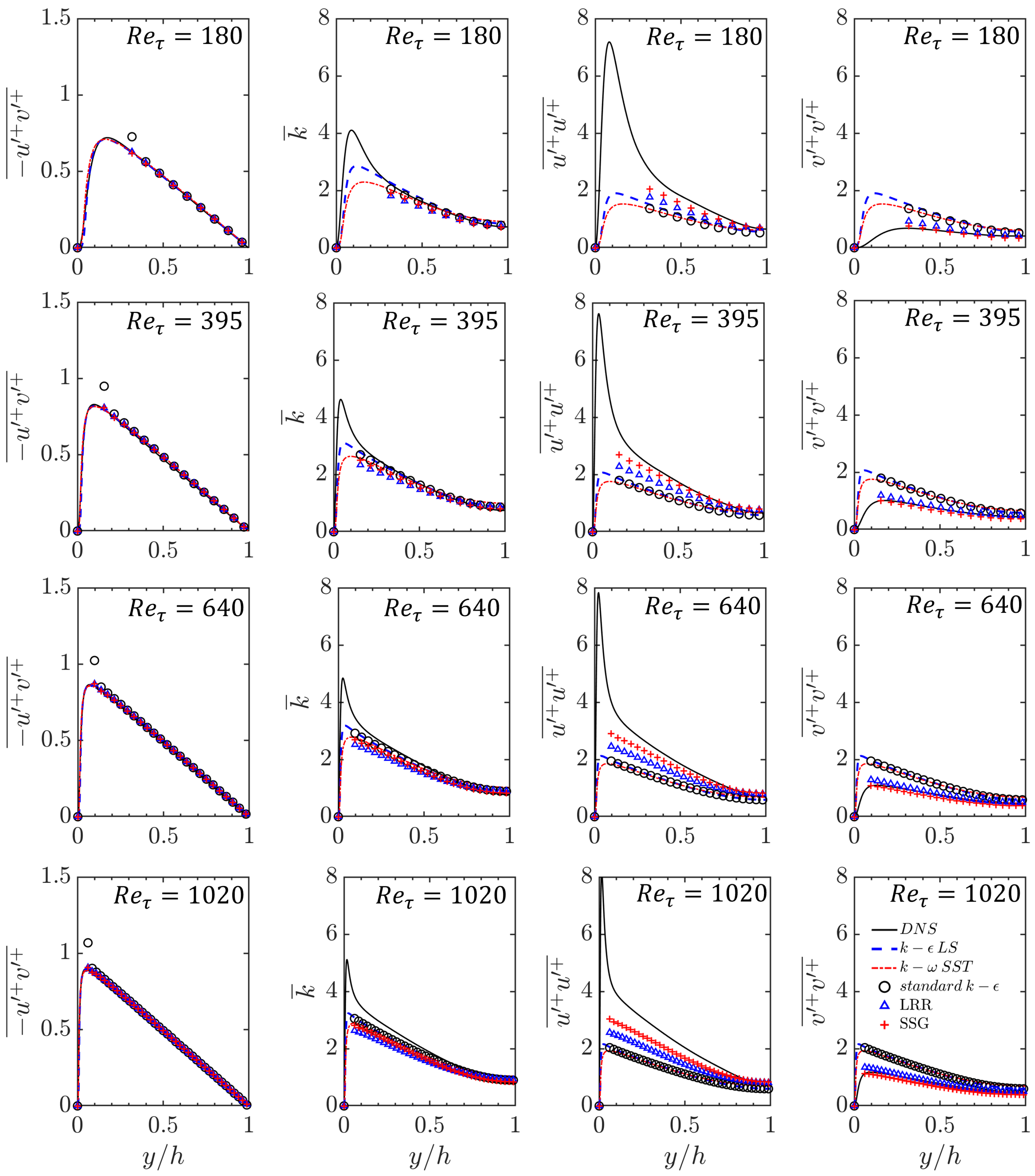
4.1.2. Reynolds Stress Prediction
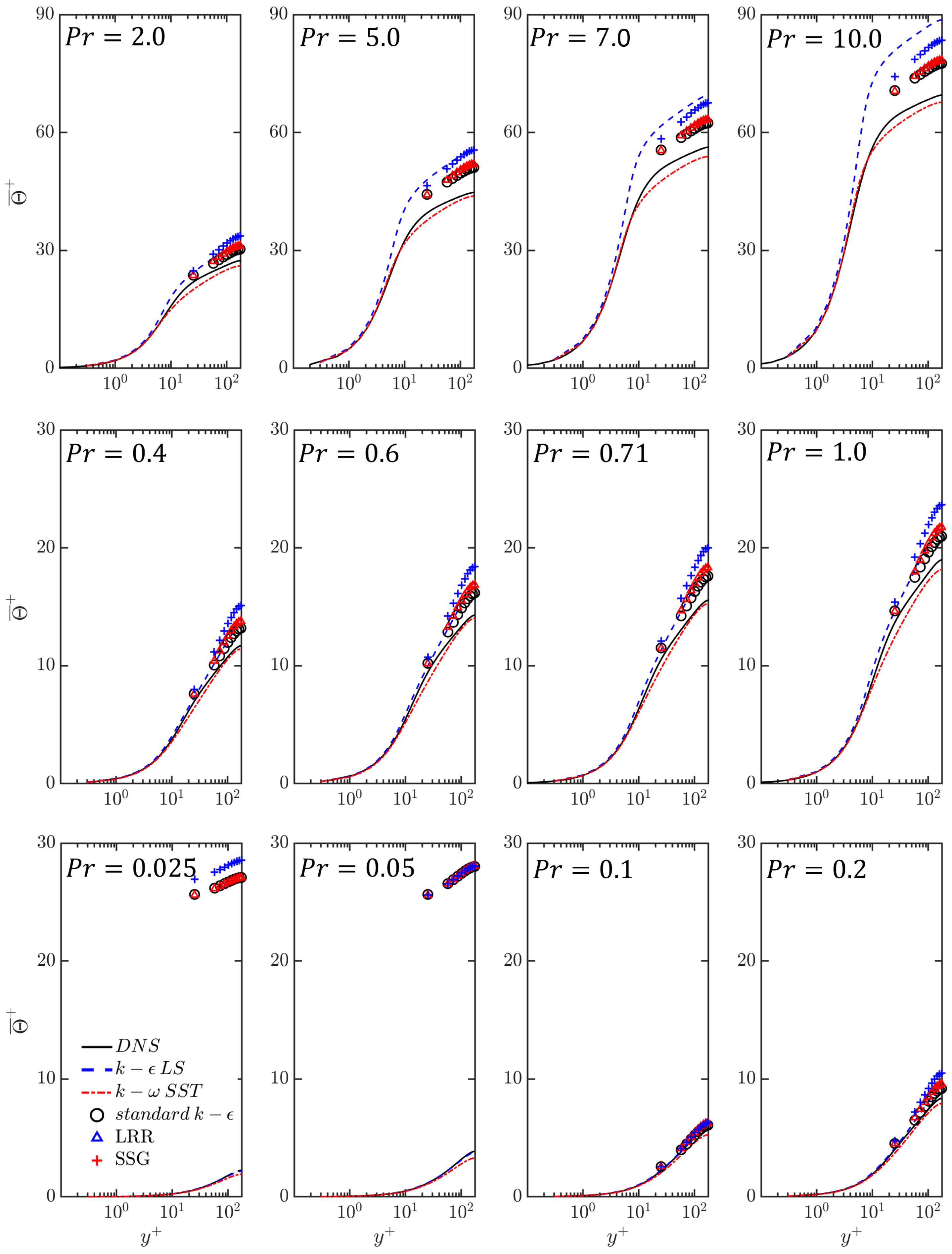
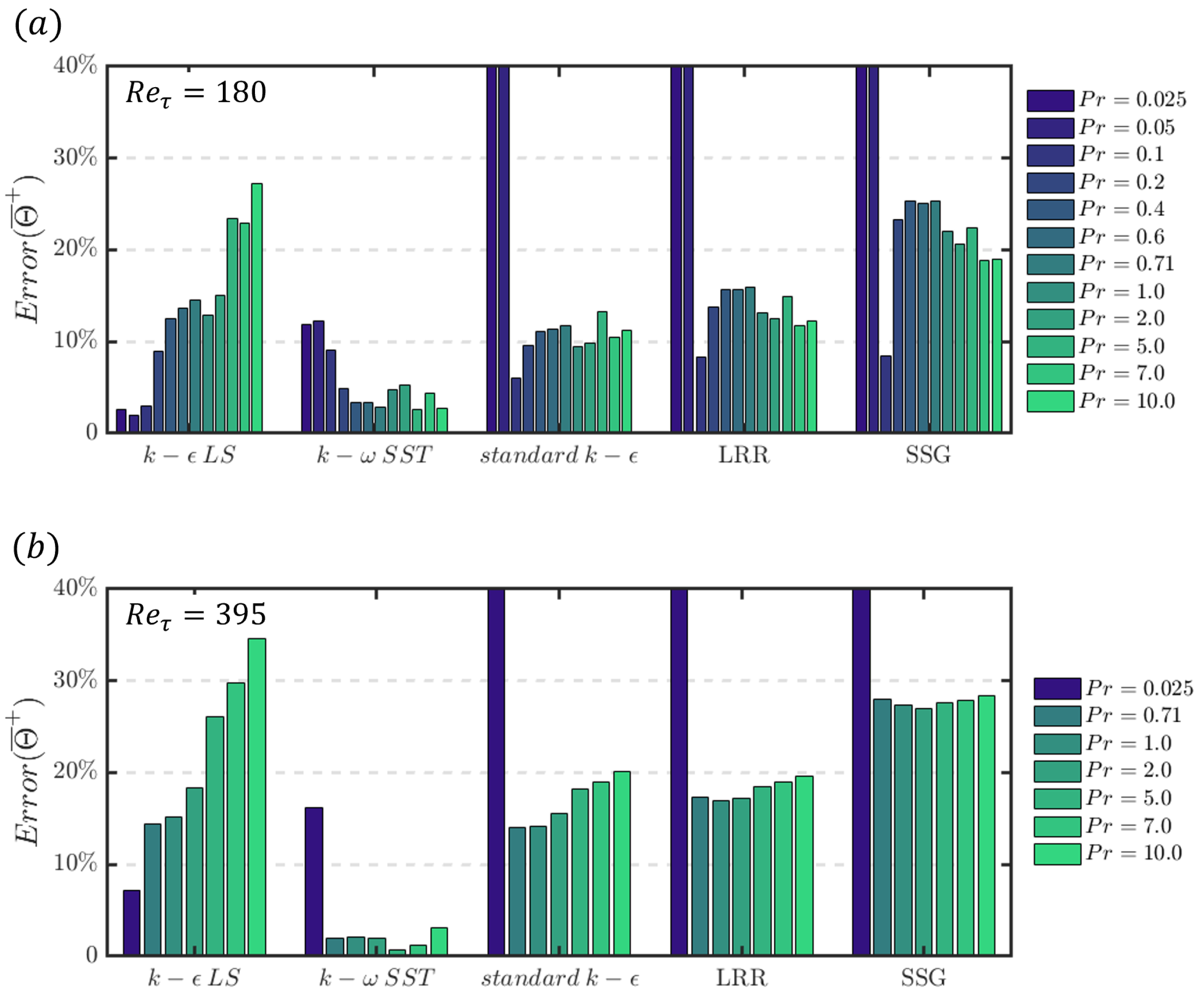
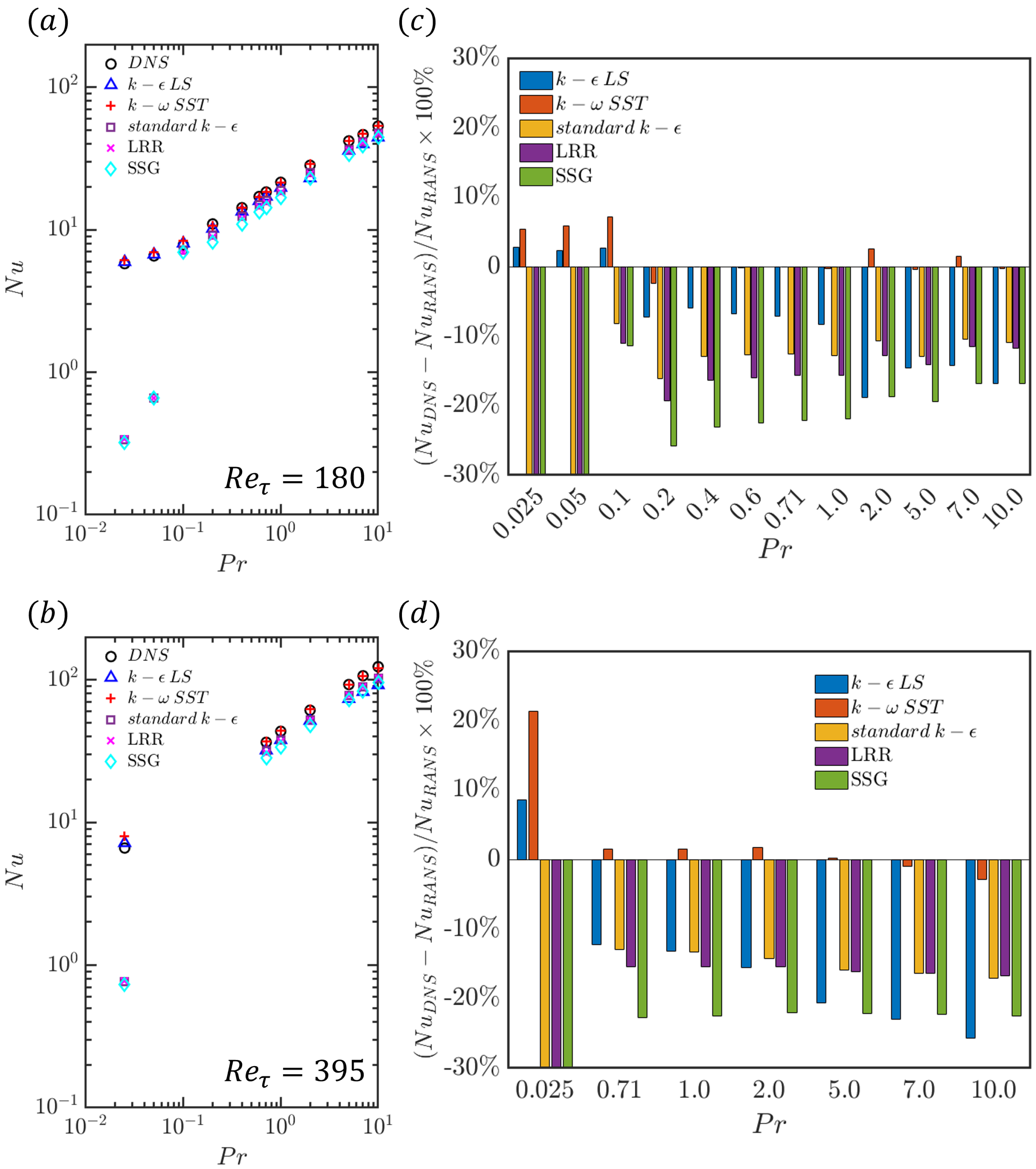
4.2. Heat Transfer Rate in Turbulent Channel Flow for Different Values of Prandtl Number
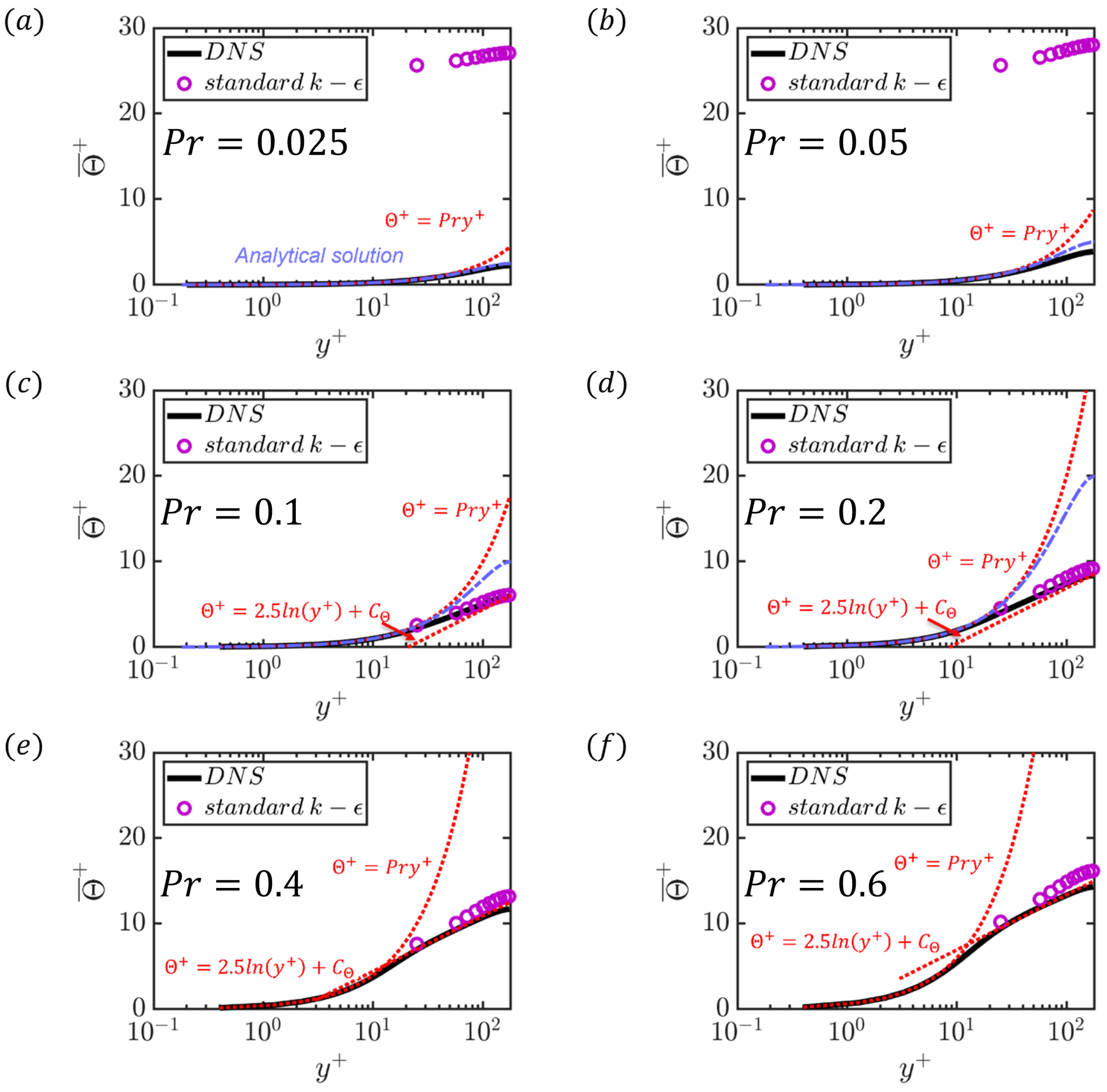
4.2.1. Mean Temperature Profiles
4.2.2. Different Regimes Based on the Ratio of Eddy Thermal Diffusivity to Molecular Thermal Diffusivity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kawamura, H.; Abe, H.; Matsuo, Y. DNS of turbulent heat transfer in channel flow with respect to Reynolds and Prandtl number effects. Int. J. Heat Fluid Flow 1999, 20, 196–207. [Google Scholar] [CrossRef]
- Johansson, A.V.; Wikström, P.M. DNS and modelling of passive scalar transport in turbulent channel flow with a focus on scalar dissipation rate modelling. Flow Turbul. Combust 2000, 63, 223–245. [Google Scholar] [CrossRef]
- Mujumdar, A.S.; Mashelkar, R.A. Advances in Transport Processes; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Kim, J.; Moin, P. Transport of passive scalars in a turbulent channel flow. In Turbulent Shear Flows 6; Springer: Berlin/Heidelberg, Germany, 1989; pp. 85–96. [Google Scholar]
- Kasagi, N.; Tomita, Y.; Kuroda, A. Direct numerical simulation of passive scalar field in a turbulent channel flow. ASME J. Heat Transf. 1992, 114, 589–606. [Google Scholar] [CrossRef]
- Kasagi, N.; Ohtsubo, Y. Direct numerical simulation of low Prandtl number thermal field in a turbulent channel flow. In Turbulent Shear Flows 8; Springer: Berlin/Heidelberg, Germany, 1993; pp. 97–119. [Google Scholar]
- Kawamura, H.; Ohsaka, K.; Abe, H.; Yamamoto, K. DNS of turbulent heat transfer in channel flow with low to medium-high Prandtl number fluid. Int. J. Heat Fluid Flow 1998, 19, 482–491. [Google Scholar] [CrossRef]
- Abe, H.; Kawamura, H.; Matsuo, Y. Surface heat-flux fluctuations in a turbulent channel flow up to Reτ = 1020 with Pr = 0.025 and 0.71. Int. J. Heat Fluid Flow 2004, 25, 404–419. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale Eddy Viscosity Model. Phys. Fluids 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Moin, P.; Squires, K.; Cabot, W.; Lee, S. A dynamic subgrid-scale Model for compressible turbulence and scalar transport. Phys. Fluids 1991, 3, 2746–2757. [Google Scholar] [CrossRef]
- Wang, W.P.; Pletcher, R.H. On the large Eddy simulation of a turbulent channel flow with significant heat transfer. Phys. Fluids 1996, 8, 3354–3366. [Google Scholar] [CrossRef]
- Wang, L.; Dong, Y.H.; Lu, X.Y. An investigation of turbulent open channel flow with heat transfer by large Eddy simulation. Comput. Fluids 2005, 34, 23–47. [Google Scholar] [CrossRef]
- Wu, H.; Wang, J.; Tao, Z. Passive heat transfer in a turbulent channel flow simulation using large Eddy simulation based on the lattice Boltzmann method framework. Int. J. Heat Fluid Flow 2011, 32, 1111–1119. [Google Scholar] [CrossRef]
- Abe, K.; Suga, K. Towards the development of a Reynolds-Averaged algebraic turbulent scalar-flux Model. Int. J. Heat Fluid Flow 2001, 22, 19–29. [Google Scholar] [CrossRef]
- Pozorski, J.; Wacławczyk, M.; Minier, J.P. Full velocity-scalar probability density function computation of heated channel flow with wall function approach. Phys. Fluids 2003, 15, 1220–1232. [Google Scholar] [CrossRef]
- Pozorski, J.; Waclawczyk, M.; Minier, J.P. Probability density function computation of heated turbulent channel flow with the bounded Langevin Model. J. Turbul. 2003, 4, 011. [Google Scholar] [CrossRef]
- Wei, T. Heat transfer regimes in fully developed plane-channel flows. Int. J. Heat Fluid Flow 2019, 131, 140–149. [Google Scholar] [CrossRef]
- Mathur, A.; Roelofs, F.; Fiore, M.; Koloszar, L. State-of-the-art turbulent heat flux modelling for low-Prandtl flows. Nucl. Eng. Des. 2023, 406, 112241. [Google Scholar] [CrossRef]
- Mollik, T.; Roy, B.; Saha, S. Turbulence modelling of channel flow and heat transfer: A comparison with DNS data. Procedia Eng. 2017, 194, 450–456. [Google Scholar] [CrossRef]
- Alcántara-Ávila, F.; Hoyas, S.; Pérez-Quiles, M.J. DNS of thermal channel flow up to Reτ = 2000 for medium to low Prandtl numbers. Int. J. Heat Mass Transf. 2018, 127, 349–361. [Google Scholar] [CrossRef]
- Lluesma-Rodríguez, F.; Álcantara-Ávila, F.; Pérez-Quiles, M.J.; Hoyas, S. A code for simulating heat transfer in turbulent channel flow. Mathematics 2021, 9, 756. [Google Scholar] [CrossRef]
- Archambeau, F.; Méchitoua, N.; Sakiz, M. Code Saturne: A finite volume code for the computation of turbulent incompressible flows-industrial applications. Int. J. Finite Vol. 2004, 1. [Google Scholar]
- Ahmed, U.; Prosser, R. Modelling flame turbulence interaction in RANS simulation of premixed turbulent combustion. Combust. Theory Model. 2016, 20, 34–57. [Google Scholar] [CrossRef]
- Klein, T.S.; Craft, T.J.; Iacovides, H. Assessment of the performance of different classes of turbulence Models in a wide range of non-equilibrium flows. Int. J. Heat Fluid Flow 2015, 51, 229–256. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Menter, F.R. Two-Equation Eddy Viscosity turbulence Models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Speziale, C.G.; Sarkar, S.; Gatski, T.B. Modelling the pressure–strain correlation of turbulence: An invariant dynamical systems approach. J. Fluid Mech. 1991, 227, 245–272. [Google Scholar] [CrossRef]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the development of a Reynolds-Stress turbulence closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Rotta, J. Statistical theory of nonhomogeneous turbulence. ii. Z. Phys. 1951, 131. [Google Scholar] [CrossRef]
- Hanjalić, K.; Launder, B.E. A Reynolds Stress Model of turbulence and its application to thin shear flows. J. Fluid Mech. 1972, 52, 609–638. [Google Scholar] [CrossRef]
- von Kármán, M.A. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. Math. Phys. Kl. 1930, 58. [Google Scholar]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-Equation Model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Arpaci, V.S.; Larsen, P.S. A thick gas Model near boundaries. AIAA J. 1969, 7, 602–606. [Google Scholar] [CrossRef]
- Launder, B.E.; Sharma, B.I. Application of the energy-dissipation Model of turbulence to the calculation of flow near a spinning disc. Lett. Heat Mass Transf. 1974, 1, 131–137. [Google Scholar] [CrossRef]
| 0.025 | 0.5 | 0.1 | 0.2 | 0.4 | 0.6 | 0.71 | 1.0 | 2.0 | 5.0 | 7.0 | 10.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| ✓ | ✓ | |||||||||||
| ✓ |
| Values of Constants | ||||||
|---|---|---|---|---|---|---|
| 0 | , | |||||
| , , , , , , |
| Diffusion sublayer | ||
| Intermediate layer | ||
| Log-law layer |
| Models | Reference | Model Type | Wall Function | Thermal Wall Function |
|---|---|---|---|---|
| standard | [32] | EVM | ✓ | ✓ |
| [34] | EVM | ✓ | ||
| [28] | RSM | ✓ | ✓ | |
| [27] | RSM | ✓ | ✓ | |
| [26] | EVM | ✓ |
| Models | Standard | ||||
|---|---|---|---|---|---|
| Time cost (wall clock time) | 8.3 h | 21.0 h | 0.76 h | 1.1 h | 1.5 h |
| Analytical Regime | Transitional Regime | Turbulent Diffusivity-Dominant Regime | |
|---|---|---|---|
| region | high region | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Ahmed, U.; Chakraborty, N. A Comprehensive Evaluation of Turbulence Models for Predicting Heat Transfer in Turbulent Channel Flow across Various Prandtl Number Regimes. Fluids 2024, 9, 42. https://doi.org/10.3390/fluids9020042
Liu L, Ahmed U, Chakraborty N. A Comprehensive Evaluation of Turbulence Models for Predicting Heat Transfer in Turbulent Channel Flow across Various Prandtl Number Regimes. Fluids. 2024; 9(2):42. https://doi.org/10.3390/fluids9020042
Chicago/Turabian StyleLiu, Liyuan, Umair Ahmed, and Nilanjan Chakraborty. 2024. "A Comprehensive Evaluation of Turbulence Models for Predicting Heat Transfer in Turbulent Channel Flow across Various Prandtl Number Regimes" Fluids 9, no. 2: 42. https://doi.org/10.3390/fluids9020042
APA StyleLiu, L., Ahmed, U., & Chakraborty, N. (2024). A Comprehensive Evaluation of Turbulence Models for Predicting Heat Transfer in Turbulent Channel Flow across Various Prandtl Number Regimes. Fluids, 9(2), 42. https://doi.org/10.3390/fluids9020042









