Abstract
This work’s goal is to numerically investigate the interactions between two gas bubbles in a fluid flow in a circular cross-section channel, both in the presence and in the absence of gravitational forces, with several Reynolds and Weber numbers. The first bubble is placed at the center of the channel, while the second is near the wall. Their positions are set in such a way that a dynamic interaction is expected to occur due to their velocity differences. A finite element numerical tool is utilized to solve the incompressible Navier–Stokes equations and simulate two-phase flow using an unfitted mesh to represent the fluid interface, akin to the front-tracking method. The results show that the velocity gradient influences bubble shapes near the wall. Moreover, lower viscosity and surface tension force account for more significant interactions, both in the bubble shape and in the trajectory. In this scenario, it can be observed that one bubble is trapped in the other’s wake, with the proximity possibly allowing the onset of coalescence. The results obtained contribute to a deeper understanding of two-phase inner flows.
1. Introduction
Two-phase bubble flows have a wide range of applications in micro-to-macroscale phenomena across multiple industrial sectors. For instance, bubble dynamics can alter the heat transfer coefficients in different channel geometries [1]. In petroleum-industry and carbon-abatement technologies, gas–liquid slug flows can be controlled to improve the efficiency of carbon dioxide injection into deep geological formations, as well as pipeline flow assurance [2]. In microelectronics, bubble flows favor the cooling of components when leveraging heat dissipation obtained from single-phase-flow solutions [3].
Bubble dynamics were investigated experimentally on the anode side of a proton-exchange membrane water electrolyzer to improve the performance and efficiency of its cells [4]. Another example of the use of bubble dynamics in oil is in the washing of Bio-Heavy oils. These oils, which are used for power generation, contain high amounts of sodium and potassium, which can lead to nozzle clogging and operational issues during combustion. CO2 bubbles can be employed to reduce the sodium and potassium contents of Bio-Heavy oils [5].
The involvement of a two-phase flow in a wide spectrum of engineering applications has motivated numerous investigations, both numerical and experimental, focusing on bubble and droplet behavior. The possibility of bubble coalescence is also an important phenomenon to consider, because it can alter the surface area in a gas–liquid system, influencing chemical reaction times.
Over many decades, several experimental investigations have been conducted into the rising behavior of bubbles, including notable works by [6,7,8], generating important correlations for bubble terminal velocity and shape that are still employed for benchmarking to this day. Conversely, the velocity and pressure fields in the surrounding fluid can be more easily obtained through numerical simulation.
Regarding numerical simulation, different geometries, bubble conditions, and interface-handling methods have been undertaken in the literature. One finds the Lattice Boltzmann method for simulating 3D rising bubble–bubble interactions and deformations subject to large density ratios in a quiescent fluid, where it turned out that the behavior of smaller bubbles is strongly affected by the larger ones [9]. In [10], a modification of the Lattice Boltzmann model based on Gunstensen’s binary color model for simulating a two-phase flow was proposed. Using the proposed methodology, the author presented tests for a variety of viscosity ratios and surface tension values and verified the methodology using experimental data for the co-axial and oblique coalescence of two bubbles. One disadvantage of the Lattice Boltzmann method is that the method struggles with high specific mass ratios, necessitating additional strategies to bypass this issue [11].
Front-capturing methods, such as the Volume of Fluid (VOF), have been employed to deal with 3D gas–liquid flow simulations involving multiple bubble configurations and uncover the effects of the bubble interval, diameter, arrangement, and shear [12]. Also, the VOF method succeeded in modeling bubble-train slug flows inside circular microchannels, thus providing a detailed understanding of the wall-to-bubble heat transfer, surface tension, and evaporation mechanisms. In parallel, conservative versions of the level-set (LS) method were used to simulate bubble pairs interacting under tilted and gravity-driven flows in vertical channels, whereby it can be concluded that the bubbles tend to group and move toward the channel’s center [13]. Approaches coupling the LS and VOF can also be used to understand the transition from isolated to confined bubbly flows in microchannels and their behavior in the presence of boiling [14]. One issue with front-capturing methods is the interface recovery, which is alleviated by the combination of the VOF method with the level set, but it is still challenging to extend to three dimensions [15].
In contrast, front-tracking methods, which rely on an explicit representation of interfaces, cope with dispersed bodies in an alternative way. Recent papers by the authors focusing on bubble flows resorted to the Arbitrary Lagrangian–Eulerian (ALE) technique to understand how single or many bubbles interact in distinct domain configurations, either in axisymmetric and 3D reference frames or confined by smooth or sinusoidally corrugated boundaries [16]. Bubbles’ rising velocity, film thicknesses, and temporal perimeter variations are among the main measured quantities. In another recent paper, a comparison between the ALE technique and the decoupled interface method utilized in this work was demonstrated [17]. The study found both methods to be accurate within the conducted tests, with a note that the decoupled version requires the refinement of the fluid mesh near the interface.
In this study, an established numerical tool for simulating three-dimensional two-phase flows was used to simulate two gas bubbles moving vertically, freely, and independently of each other inside a circular microchannel under gravity effects. The current formulation is a three-dimensional extension of the decoupled formulation presented in [17], which is based on the front-tracking method introduced by [18]. Our analysis focuses on the bubbles’ trajectories and shape variations over space and time. The gas–liquid properties are similar to those of crude oil/CO2 flows, which form steep gradients across the interfaces.
2. Methods
To simulate the bubble flows in this paper, the “one-fluid” formulation is used. In this method, a single set of the Navier–Stokes equations is used to represent both fluid phases, effectively encompassing the whole domain. The different fluid phases are differentiated by their properties, specifically specific mass and viscosity, which are allowed to vary over the domain. Thus, the set of the non-dimensional Navier–Stokes equations that govern the incompressible flow of interest is given by Equations (1) and (2):
where and are the specific mass and viscosity, respectively, as a function of the spatial coordinate , is the velocity, t is the time, p is the pressure, is the gravity force, and represents the surface tension force. T stands for transposed, which, in this case, is applied to the velocity gradient.
The equations above are also a function of non-dimensional groups, which appear during the non-dimensionalization procedure. These non-dimensional groups are the Reynolds number, the Froude number, and the Weber number, given by
where and are the specific mass and viscosity of the continuous phase, is the reference velocity (the bubble’s terminal velocity), L is the reference length (bubble diameter), is the reference surface tension of the continuous phase, and is the reference gravity acceleration, usually m/s2. Another dimensionless number that is a function of the fluid properties and surface tension is the Morton number, given by
As presented above, the Morton number can be written as a function of other dimensionless numbers, such as the Reynolds, Weber, and Froude numbers, or the Eötvös and Archimedes numbers for gravity-driven flows.
The Navier–Stokes equations described above are solved through the finite element and Galerkin methods. The non-linear convective term is treated explicitly using a first-order semi-Lagrangian method [19], which is unconditionally stable and preserves the convection operator symmetry. The surface tension and gravity forces are also added explicitly to the resulting linear system of equations. While Equation (2) allows for non-constant properties, this is not valid for an element’s interior, where one estimates the fluid properties by using an arithmetic average of its nodal values.
The finite element space used here is the so-called Taylor–Hood “mini” element, or P1P1+, in short [20]. Geometrically, it is a tetrahedron with degrees of freedom assigned to its four corners and to its center of mass. As one of the most straightforward elements implementable in code, it respects the Ladyzhenskaya–Babuska–Brezzi (LBB) condition and composes the tessellation forming the bubble and microchannel interior, that is to say, the 3D volume mesh. On the other hand, the tessellation that discretizes the interface arranges itself by the linear triangular element, that is to say, the 2D surface mesh.
Nodes at the interface (surface) mesh are not shareable with the fluid (volume) mesh so that the former mesh remains uncoupled from the latter. The coupling between them occurs when the interface mesh advects through a pure Lagrangian motion by the fluid-flow velocity, and, in turn, the surface tension calculated over its nodes distributes the curvature effects onto neighbor nodes located in the fluid mesh. An approximation of the Laplace–Beltrami operator computes the curvature at the interface mesh and assigns it to the fluid mesh, in a similar fashion to that in [21].
The fluid interface position is marked by a three-dimensional surface composed of triangular elements, which is advected by the fluid velocity fields at each time step. This surface mesh serves as an anchor for a Heaviside function that marks the dispersed phase with 1 and the continuous phase with 0, and the fluid properties change smoothly over the interface thickness, as exhibited on Figure 1. The Heaviside function adopted here follows [22], namely,
where is the distance from a given fluid mesh node to its closest interface mesh node, and is the interface thickness value.
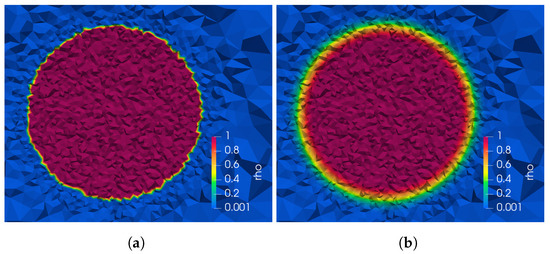
Figure 1.
Heaviside function representation is illustrated. In (a) a picture of a bubble with zero interface thickness, a gas–liquid interface with is displayed. Nodal property values are either and or and , but some elements are cut by the interface, resulting in elements with in-between properties. In (b) a picture of a bubble with an interface thickness and a gas–liquid interface with is presented. Nodal property values are smoothed in the colored band. (a) presents the minimum amount of smoothing, while in (b), significant smoothing of properties can be observed. Both approaches have trade-offs: the case portrayed in (a) ensures high accuracy in representing the interface, but it is prone to numerical instability; the case in (b) ensures numerical stability at the expense of less accuracy.
The thickness depends on the problem and is typically a multiple of the element characteristic length h. Small values, such as h, will imply a minimal interface thickness but large property gradients at the interfaces, which might destabilize the simulation. High values, such as h, generate less accurate simulations but ensure a greater degree of stability.
The uncoupled formulation utilized in this paper allows the interface thickness to be set to . In this case, since the interface mesh nodes are not aligned with the fluid mesh nodes, the interface ’cuts through’ the fluid mesh elements. In this situation, the property gradients are maximum, and the surface tension force is concentrated only on the elements that are crossed by the interface and their neighbors. On the other hand, as the interface thickness increases, the property gradients become less steep, and the surface tension force assigned to individual nodes decreases in intensity but is spread over a larger number of elements, retaining approximately the same value when evaluated as a sum over all elements.
Due to the smoothing of the property gradients, very high specific mass ratios can be simulated successfully. Accurate simulations of air bubbles rising in ethylene glycol, with a specific mass ratio of , have been achieved. Simulations representing air in ethanol, with a specific mass ratio of , and air in sugar–water, with a specific mass ratio of , have also been accomplished [23].
The fluid properties are assigned to the fluid mesh nodes based on the Heaviside function values using the following formula:
The last term on the right side of Equation (2) can be expanded to
where is the surface tension coefficient, is the Dirac-delta function related to the interface nodes, is the interface curvature, and is the unit vector normal to the interface, in this case pointing inwards (toward the bubble’s interior). Ultimately, the surface tension takes the following discrete form:
where represents the fluid mesh nodes, represents the interface mesh nodes, and is the Heaviside gradient, which discretizes the Dirac-delta function, thus achieving a distance function relative to the interface. The surface tension coefficient is made non-dimensional by the Weber number; therefore, and vanishes from Equation (8). , the interface curvature, is calculated by performing a finite element discretization of the Laplace–Beltrami operator over surfaces and applied to the interface mesh.
3. Results
In this section, the results for multiple bubbles rising in fluid with varying Reynolds and Weber numbers are presented. These results were obtained using a two-phase finite element simulation tool, and an uncoupled surface mesh separated from the fluid mesh was used to represent the interface. This numerical tool has been verified against single- and two-phase flows in various several test cases, and the results have been reported in international journals. All tests executed and presented in this section employed the fluid properties of carbon dioxide (CO2) for the gas phase and crude-oil for the liquid phase. Carbon dioxide’s specific mass is kg/m3, and its viscosity is kg/ms. The crude-oil properties can vary over a large range, depending on the oil components. It can be a lighter-than-water, low-viscosity fluid or a heavy, almost-solid substance. For this paper, the following average properties were considered: specific mass of kg/m3 and viscosity of kg/ms. The surface tension coefficient also varies with the oil type, but an average value of N/m is considered.
The simulation setup can be observed in Figure 2. A vertical circular channel is represented, with a non-dimensional diameter and length . At one end, an inflow with a uniform non-dimensional velocity is set, and at the other end, an outflow where pressure is positioned. The walls along the channel have no slip boundary conditions. Two bubbles are positioned inside the channel. The bubble at the center, labeled the free bubble, has its center positioned at , while the bubble at the side, labeled the shear bubble, has its center positioned at . Both bubbles are initially spherical in shape and have a diameter of . For reference, the center of the channel’s bottom is positioned at .
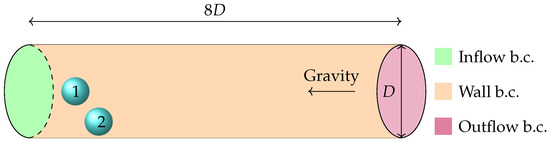
Figure 2.
Simulation setup composed of the geometry, the representation of the continuous and dispersed phases, and the boundary conditions. The channel is oriented vertically from left to right but depicted in a rotated configuration for convenience to fit within the paper sheet. As a result, the gravity field acts in the opposite direction, from right to left. At the inflow, a prescribed velocity boundary condition is assigned, . At the outflow, an homogeneous Dirichlet pressure boundary condition is assigned, . At the cylinder walls, the no-slip boundary condition is set, .
In relation to the initial positioning of the bubbles, our objective was to examine the influence of a bubble’s wake on nearby bubbles within a circular channel. The positions of the bubbles within the channel were deliberately selected so that they have different velocities, enabling one bubble to overtake the other. Additionally, the diameters were determined to ensure that, if the bubbles maintain a straight trajectory along the x-axis, they would closely approach each other at the moment of passing.
By inputting the fluid properties specified in the previous paragraph into the Morton number equation, three pairs of Reynolds and Weber numbers were selected to be simulated. The first one is and , the second one is and , and the third one is and . All three cases used . Simulations with those parameters were executed with and without gravity forces, totaling six scenarios. All simulations were conducted over 300 time steps of , resulting in non-dimensional time units, equivalent in seconds to s.
Figure 3 presents the results of the simulation executed with Weber and Reynolds and at , , , and . For the given parameters, there is very little difference between the results obtained with and without gravity forces. In the simulation executed with gravity, the bubbles travel further ahead in the channel, but the shape and position relative to one another are very similar, as can be seen in Figure 4. The bubble near the wall undergoes some deformation due to the shear forces caused by the velocity gradient. There is very little influence on the free-bubble trajectory due to the shear bubble. After the free bubble passes the shear bubble, it is carried by the flow normally.
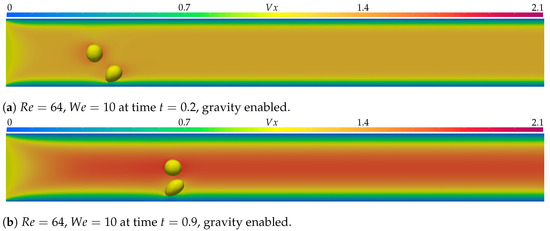
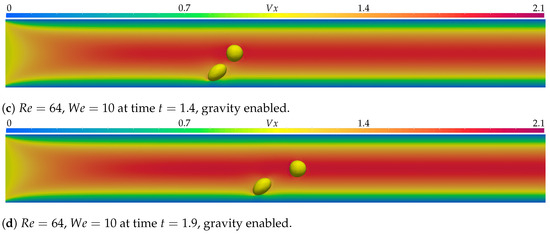
Figure 3.
In (a–d), the simulation with parameters and is displayed at times , , , and . represents the axial velocity component. Gravity forces were disabled, and the simulation was executed over 300 time steps of .
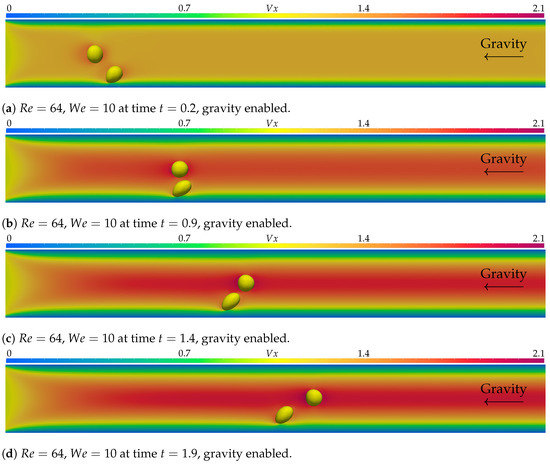
Figure 4.
In (a–d), the simulation with parameters and is displayed at times , , , and . represents the axial velocity component. Gravity forces, pointing to the left, were enabled, and the simulation was executed over 300 time steps of .
Figure 5 presents the results of the simulation executed with the Reynolds number and the Weber number , with no gravity forces, while Figure 6 shows the results with the same parameters but with gravity forces active. The times presented are , , , and . The results for the bubble simulation with no gravity forces are very similar to those of the previous simulations with and .
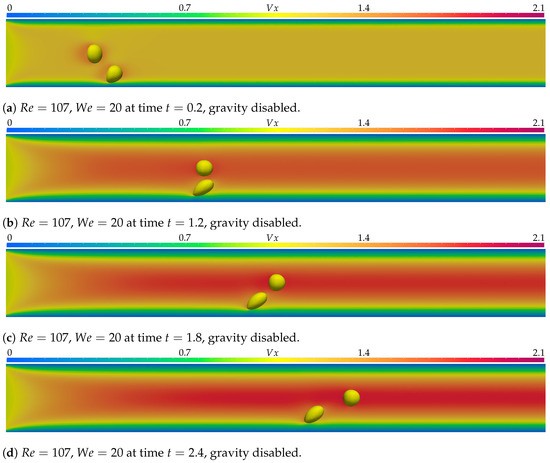
Figure 5.
In (a–d), the simulation with parameters and is displayed at times , , , and . represents the axial velocity component. Gravity forces were disabled, and the simulation was executed over 300 time steps of .
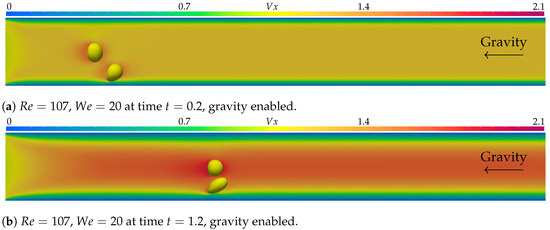
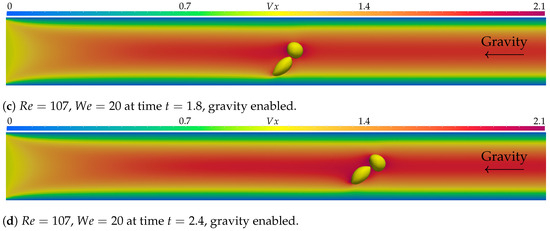
Figure 6.
In (a–d), the simulation with parameters and is displayed at times , , , and . represents the axial velocity component. Gravity forces, pointing to the left, were active, and the simulation was executed over 300 time steps of .
However, when gravity forces are active, there is some variation. The shear bubble suffers significantly more deformation and approaches the free bubble at the moment the free bubble passes it. The free bubble interacts with the shear bubble, changing shape as it moves along the flow, and the shear bubble appears to be trapped in the free bubble’s wake, increasing its velocity compared to the simulation with no gravity forces active and approaching the center of the channel. This effect can be observed in Figure 7, along with the velocity fields that originate it.
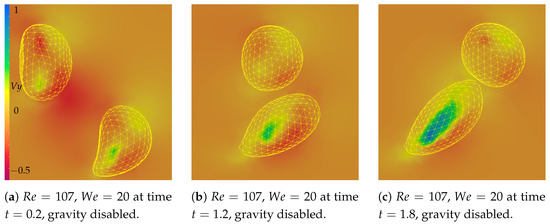
Figure 7.
Detail near the bubbles presenting the vertical velocity fields for the simulation with parameters and with gravity forces enabled at times (a) , (b) , and (c) . The bubbles are displayed in a wire frame overlaid on the velocity fields. It is possible to notice the increase in the velocity values inside the shear bubble, pushing it toward the channel center.
Figure 8 presents the results of the simulation executed with the Reynolds number and the Weber number , with no gravity forces, while Figure 9 shows the results with the same parameters but with gravity forces active. The times presented are , , , and . The simulation with no gravity presents similar results to those of other simulations without gravity, with slightly more deformation for both bubbles due to lower viscosity and lower surface tension forces. The simulation executed with gravity forces turned on offers some interesting results. The shear bubble undergoes the most deformation, being stretched toward the center, moving into the free bubble’s trajectory, and causing a contact. The current two-phase bubble-merging model was disabled for all simulations, since coalescence is not the aim of the present research, but it can be argued that it could occur under these conditions.
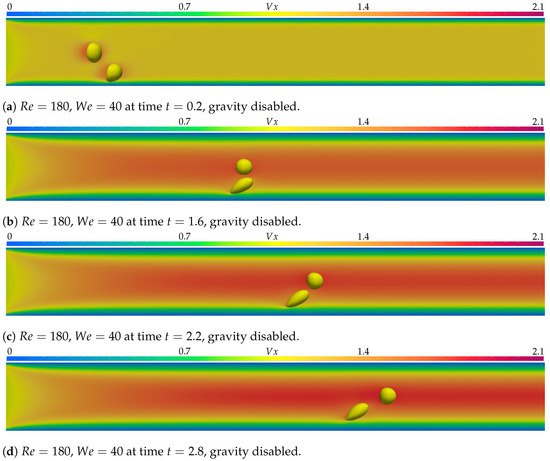
Figure 8.
In (a–d), the simulation with parameters and is displayed at times , , , and . represents the axial velocity component. Gravity forces were disabled, and the simulation was executed over 300 time steps of .
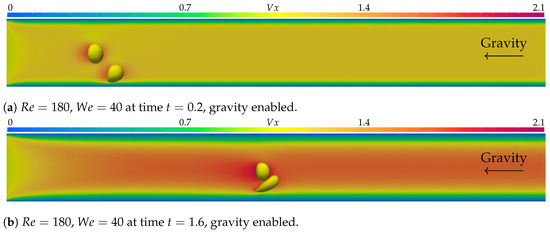
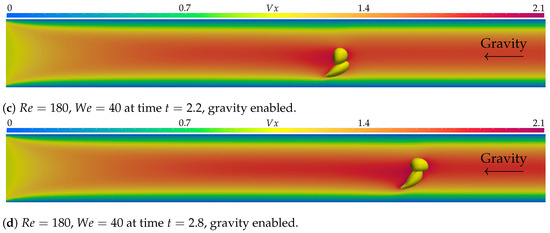
Figure 9.
In (a–d), the simulation with parameters and is displayed at times , , , and . represents the axial velocity component. Gravity forces, pointing to the left, were active, and the simulation was executed over 300 time steps of . Bubble coalescence may occur under these conditions.
Figure 10 presents the change in the z-coordinate for both bubbles in all six simulations. In all simulations, some influence can be seen in the plot, but the impact in scenarios with and is not as significant. The remaining simulations, with , show some relevant influence on both bubbles’ trajectories, especially the simulations with gravity forces.
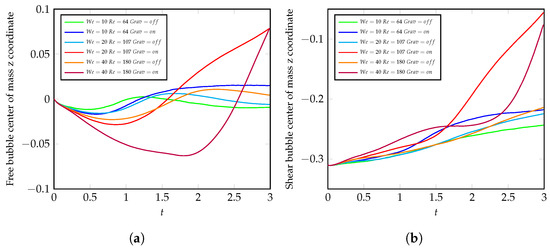
Figure 10.
In this figure, the change in the z-coordinate of the center-of-mass position is depicted for (a) the free bubble and (b) the shear bubble as a measure of the influence of the bubbles on each other’s trajectory. It can be noticed, especially in the simulations with Reynolds number and Weber number , that the shear bubble moves toward the channel’s center, and the free bubble is displaced by it.
In Figure 11, the x-direction velocity component for both bubbles is presented. It can be inferred from the plot that the free bubble is slowed down by the shear bubble’s presence, up until the point where the free bubble overtakes it. It is also evidenced that the shear bubble accelerates after the free bubble’s passage, especially in the simulations where gravity effects are enabled.
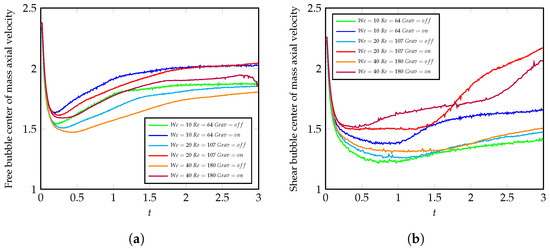
Figure 11.
This figure presents the velocity in the x-direction of (a) the free bubble and (b) the shear bubble. The moment the free bubble overtakes the shear bubble happens at , , and in the simulations with Weber numbers , , and .
4. Conclusions
In this study, we investigated the behavior of two bubbles transported by a fluid flow within a circular channel using numerical simulations to assess their dynamics. We employed a decoupled mesh method to accurately represent the interface between the two phases, akin to a front-tracking approach. Six different scenarios with varying flow parameters were simulated. The observed deformation of gas bubbles can be attributed to both their position inside the channel and the drag forces acting on the bubble. There is a velocity gradient in the channel radius direction, from the maximum velocity at the center of the channel to zero velocity at the walls. The bubbles are advected by the channel velocity fields, and this gradient provokes a shearing effect, which is most evident on the bubble near the wall due to the steeper velocity gradient in that region. The bubbles also suffer from the drag forces affecting them, especially at higher Weber numbers, where the surface tension, which works to keep the bubbles in a spherical shape, is not as strong. These deformations have the potential to culminate in bubble breakup. In cases of higher viscosity and surface tension, the mutual influence between bubbles is reduced, and their shape is preserved. Conversely, in less viscous flows, we observed an instance where one bubble entraps the other in its wake, increasing its velocity.
Our findings also indicate a trend where the shear bubbles migrate toward the center of the channel. The reason for this can be vertical velocities induced by the passing of the free bubble. As the free bubble approaches, it generates velocity away from its apex, which pushes the shear bubble. After passing, it drags the shear bubble upwards. This effect appears more significant in the example with , , and gravity forces enabled.
These findings can guide engineers to make informed decisions when designing more efficient microchannel heat sinks and CO2 injection solutions.
Author Contributions
D.B.V.S.: Conceptualization, Methodology, Software, Investigation, Writing—Original Draft, Writing—Review and Editing. G.P.O.: Writing—Review and Editing, Supervision, Funding Acquisition. N.M.: Conceptualization, Methodology. P.V.: Supervision, Funding Acquisition. G.R.A.: Conceptualization, Methodology, Resources, Writing—Review and Editing, Supervision. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the following institutions for funding this research: the Brazilian Higher Education Agency (CAPES), the Research Support Foundation of the State of Rio de Janeiro (FAPERJ), the National Council for Scientific and Technological Development (CNPq/Grant No. 405654/2022-7), and the Royal Society-Newton Advanced Fellowship (NAF\R2\202165) as part of the Newton Fund in partnership with CONFAP and CNPq.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Khodadadi, S.; Taleghani, M.H.; Domiri Ganji, D.; Gorji-Bandpy, M. Heat transfer enhancement via bubble dynamics along an inclined wall. Int. Commun. Heat Mass Transf. 2023, 145, 106829. [Google Scholar] [CrossRef]
- Bandara, U.C.; Tartakovsky, A.M.; Palmer, B.J. Pore-scale study of capillary trapping mechanism during CO2 injection in geological formations. Int. J. Greenh. Gas Control. 2011, 5, 1566–1577. [Google Scholar] [CrossRef]
- Gros, E.; Anjos, G.; Thome, J. Moving mesh method for direct numerical simulation of two-phase flow with phase change. Appl. Math. Comput. 2018, 339, 636–650. [Google Scholar] [CrossRef]
- Li, Y.; Yang, G.; Yu, S.; Mo, J.; Li, K.; Xie, Z.; Ding, L.; Wang, W.; Zhang, F.Y. High-speed characterization of two-phase flow and bubble dynamics in titanium felt porous media for hydrogen production. Electrochim. Acta 2021, 370, 137751. [Google Scholar] [CrossRef]
- Kim, Y.; Oh, J.I.; Zhang, M.; Lee, J.; Park, Y.K.; Ho Lee, K.; Kwon, E.E. Reduction of Na and K contents in bio-heavy oil using micro-/nano-sized CO2 bubbles. J. CO2 Util. 2019, 34, 430–436. [Google Scholar] [CrossRef]
- Bhaga, D.; Weber, M.E. Bubbles in viscous liquids: Shapes, wakes and velocities. J. Fluid Mech. 1981, 105, 61. [Google Scholar] [CrossRef]
- White, E.; Beardmore, R. The velocity of rise of single cylindrical air bubbles through liquids contained in vertical tubes. Chem. Eng. Sci. 1962, 17, 351–361. [Google Scholar] [CrossRef]
- Hnat, J.G. Spherical cap bubbles and skirt formation. Phys. Fluids 1976, 19, 182. [Google Scholar] [CrossRef]
- Cheng, M.; Hua, J.; Lou, J. Simulation of bubble–bubble interaction using a lattice Boltzmann method. Comput. Fluids 2010, 39, 260–270. [Google Scholar] [CrossRef]
- Anwar, S. Lattice Boltzmann modeling of buoyant rise of single and multiple bubbles. Comput. Fluids 2013, 88, 430–439. [Google Scholar] [CrossRef]
- Mitchell, T.; Leonardi, C.; Fakhari, A. Development of a three-dimensional phase-field lattice Boltzmann method for the study of immiscible fluids at high density ratios. Int. J. Multiph. Flow 2018, 107, 1–15. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, C.; Wang, X.; Fu, T.; Ma, Y.; Li, H. Three-dimensional numerical simulation of coalescence and interactions of multiple horizontal bubbles rising in shear-thinning fluids. AIChE J. 2015, 61, 3528–3546. [Google Scholar] [CrossRef]
- Balcázar, N.; Lehmkuhl, O.; Jofre, L.; Oliva, A. Level-set simulations of buoyancy-driven motion of single and multiple bubbles. Int. J. Heat Fluid Flow 2015, 56, 91–107. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, W.; Palm, B. Numerical study of the interactions and merge of multiple bubbles during convective boiling in micro channels. Int. Commun. Heat Mass Transf. 2017, 80, 10–17. [Google Scholar] [CrossRef]
- Sattari, A.; Hanafizadeh, P.; Hoorfar, M. Multiphase flow in microfluidics: From droplets and bubbles to the encapsulated structures. Adv. Colloid Interface Sci. 2020, 282, 102208. [Google Scholar] [CrossRef]
- Anjos, G.R. Numerical Investigation of Two-Phase Flows in Corrugated Channel with Single and Multiples Drops. Fluids 2020, 6, 13. [Google Scholar] [CrossRef]
- Anjos, G. Moving mesh methods for two-phase flow systems: Assessment, comparison and analysis. Comput. Fluids 2021, 228, 105053. [Google Scholar] [CrossRef]
- Unverdi, S.O.; Tryggvason, G. A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 1992, 100, 25–37. [Google Scholar] [CrossRef]
- Anjos, G.R.; Oliveira, G.P.; Mangiavacchi, N.; Thome, J.R. One- and two-step semi-Lagrangian integrators for arbitrary Lagrangian–Eulerian-finite element two-phase flow simulations. Int. J. Numer. Methods Fluids 2022, 94, 632–654. [Google Scholar] [CrossRef]
- Arnold, D.N.; Brezzi, F.; Fortin, M. A Stable Finite Element For The Stokes Equations. Estrato Calc. 1984, XXI, 337–344. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A Continuum Method for Modelling Surface Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A Level Set Approach for Computing Solutions to Incompressible Two-Phase Flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Anjos, G.; Mangiavacchi, N.; Borhani, N.; Thome, J.R. 3D ALE Finite-Element Method for Two-Phase Flows with Phase Change. Heat Transf. Eng. 2014, 35, 537–547. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).