Abstract
Mosquitoes’ self-generated air movements around their antennae, especially at the wing-beat frequency, are crucial for both obstacle avoidance and mating communication. However, the characteristics of these air movements are not well clarified. In this study, the air movements induced by wing tones (sound generated by flapping wings in flight) around the antennae of a mosquito-like model (Culex quinquefasciatus, male) are investigated using the acoustic analogy method. Both the self-generated wing tone and the wing tone reflected from the ground are calculated. Given that the tiny changes in direction and magnitude of air movements can be detected by the mosquito’s antennae, a novel method is introduced to intuitively characterize the air movements induced by the wing tone. The air movements are decomposed into two basic modes (oscillation and revolution). Our results show that, without considering the scattering on the mosquito’s body, the self-generated sound wave of the wing-beat frequency around the antennae mainly induces air oscillation, with the velocity amplitude exceeding the mosquito’s hearing threshold of the male wingbeat frequency by two orders of magnitude. Moreover, when the model is positioned at a distance from the ground greater than approximately two wing lengths, the reflected sound wave at the male wingbeat frequency attenuates below the hearing threshold. That is, the role of reflected wing tone in the mosquito’s obstacle avoidance mechanism appears negligible. Our findings and method may provide insight into how mosquitoes avoid obstacles when their vision is unavailable and inspire the development of collision avoidance systems in micro-aerial vehicles.
1. Introduction
Insects possess diverse sensory organs that are highly sensitive to light, odor, heat, and sound. This enables them to perform certain biological activities even in the absence of a particular sensory signal. A behavioral experiment [1] has suggested that mosquitoes could perceive and avoid obstacles even when their vision is unavailable, but this has not been shown yet. This absence of visual cues suggests the presence of another source of close-range information [2].
The ‘ears’ of mosquitoes are among the most likely organs assisting them in obstacle avoidance under low-light conditions. Among all tested insects, mosquitoes possess the most sensitive auditory system [3]. This auditory system primarily comprises the antennal flagellum and Johnston’s organ (JO) located at the base of the flagellum. When unsteady air movements (including convective flow and sound waves) occur around the antennal flagellum, the flagellum undergoes slight vibrations. Then, it compresses and stretches the auditory neurons within the JO, generating auditory signals. Thus, the self-generated convective velocity (also termed as flow velocity [2], which represents the incompressible part) and sound particle velocity (i.e., wing tone, which is compressible) may play a crucial role in obstacle avoidance [2]. It is important to note that this role is not necessarily beneficial and could pose challenges that need to be addressed.
By using the overset-grid method to solve the incompressible Navier-Stokes equation, Nakata et al. [2] investigated the changes in convective velocity around the antennae as the mosquito (Culex quinquefasciatus, male) approaches the ground plane. As the distance between the mosquito and ground decreases from to , the magnitude of convective velocity at the wing-beat frequency around the mosquito’s antennae increases almost linearly from the mosquito’s hearing threshold at the male wingbeat frequency (i.e., ) to . Unlike ground effect [2,4] typically referred to in the aerodynamic literature (i.e., changes in aerodynamic forces due to the proximity of a ground plane), this change in convective velocity can be comfortably perceived by mosquitoes at a considerably large distance (approximately 20.2 wing lengths) from the ground. Therefore, convective velocity may be a crucial source of close-range information. However, we cannot rule out the possibility that the JO could detect the reflected particle velocity component of self-generated wing tones [2]. In addition, the interference of the self-generated wing tones in the mosquito’s detection of convective velocity might not be neglected, especially at the wing-beat frequency.
Indeed, mosquitoes are unusual in using a pair of wings for two purposes at the same time: to fly and to communicate with each other [3]. During courtship, male and female mosquitoes frequently modulate their wing kinematics to engage in wing-tone-based ‘communication’ [3]. It is interesting to find that male mosquitoes are not sensitive to female wing tones unless their own antennae receive the self-generated wing tone at the wing-beat frequency [3,5,6,7,8]. Therefore, the air movements induced around the mosquito’s antennae by the self-generated sound wave of the wing-beat frequency are also important for mating communication. Recently, there has been increasing research attention on the sound generated by the flapping wing [9,10,11,12,13,14]. However, to the best of our knowledge, most studies focus on the mechanisms of wing-tone generation, sound generation efficiency, sound field directivity, etc. Despite the crucial role of self-generated wing tones in insects for mating communication, the characteristics of the air movements induced by wing tones around the insects’ antennae have not received sufficient attention.
In this study, numerical methods have been used to investigate air movements, induced by the sound wave at the wing-beat frequency, around the antennae of a mosquito-like model (Culex quinquefasciatus, male). Both the self-generated wing tone and the wing tone reflected from the ground have been calculated, without considering the scattering on the mosquito’s body. The flow field around the wing is simulated by solving the incompressible Navier-Stokes equation. Since the convective velocity around the antennae is sufficiently low when the model is away from the ground [2], the wing tone can be predicted by the Ffowcs Williams and Hawkings (FW–H) equation using data from the aerodynamic simulations [15]. Considering that the mosquito’s antennae can detect tiny changes in both the direction and magnitude of air movements [3,16], a novel method is introduced to intuitively characterize the air movements induced by the wing tone. The air movements are decomposed into two basic modes (oscillation and revolution). In addition, the effect of wing kinematics on the air movements around the antennae induced by the wing tone has been examined.
2. Methods
2.1. Mosquito Wing Geometry and Flapping Kinematics
Figure 1 shows the wing kinematics and spatial position of the antennae. In this study, the wing geometry and kinematics of the mosquito published by Bomphrey et al. [17] are used. The wing length is , the wing aspect ratio is given by 4.2, where represents the chord length, and the wing-beat frequency is . As illustrated in Figure 1a, the kinematics of a flapping wing can be described by three Euler angles (i.e., stroke angle , deviation angle , and pitch angle ). Previous studies [18,19] suggest that, when the wings only conduct translation during the middle portion of the stroke (i.e., the pitch angle remains constant during the mid-stroke and the time profile of the pitch angle can be represented by the solid blue line in Figure 1b), the lift is not sufficient to support the weight of the mosquito. Therefore, to produce sufficient lift, the mosquitoes need to rapidly pitch up their wings during the middle portion of the stroke (i.e., the pitch angle represented by the dashed blue line in Figure 1b). In wing kinematics reported by Liu et al. [20], the wings rapidly pitch up during the middle portion of both the upstroke and the downstroke. However, in wing kinematics reported by Bomphery et al. [17], the wings mostly conduct translation during the middle portion of the downstroke. In this study, the wing tones generated by the two different flapping modes depicted in Figure 1b are compared, with the goal of examining the effect of wing kinematics on sound particle velocity around the antennae. The position of the antennae is referred to the Figure S1 published by Nakata et al. [2]. The antennal flagellum of the mosquito is represented as the straight line . The point represents the root of one of the two flagella and is assumed to be located at within the coordinate system . The Euler angles used to describe the position of antennae are set to: , . The length of the antennal flagellum is .
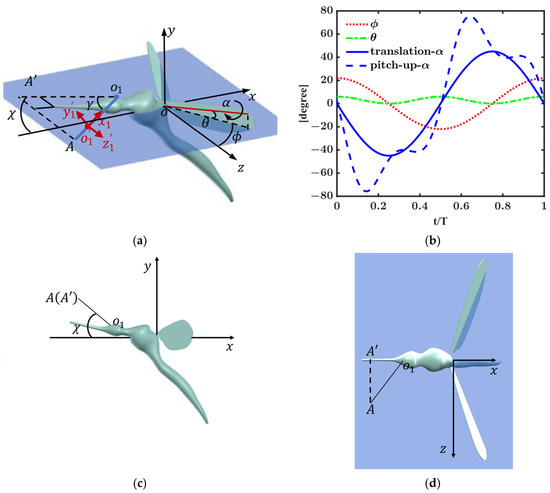
Figure 1.
(a) Wing kinematics and position of the antennae flagellum (represented by the blue solid line ). (b) Time profiles of three Euler angles (stroke angle , deviation angle and pitch angle ) describing the wing flapping motion of the mosquito. is wing-beat period. Kinematics data are adopted from Bomphery et al. [17] except for the pitch angle. (c,d) are side and top views of the mosquito-like model.
2.2. Aerodynamics Simulation
Simulation of the aerodynamics is performed by solving the incompressible Navie–Stokes equations using the overPimpleDyMFoam solver in OpenFOAM v2206, which is an open-source CFD software and has been used extensively for simulating the aerodynamics of flapping wings [21,22,23]. The incompressible Navier–Stokes equations are given by:
where is the convective velocity vector, is the pressure, and and are the density and kinematic viscosity of air, respectively.
The simulation is performed for the left wing, using a symmetric boundary condition set at the plane. The flow field for the right wing is obtained by mirroring the flow field of the left wing across the symmetry plane. Second-order accurate backward and central difference schemes are employed for temporal and spatial discretization, respectively [23]. The flow domain size is . Calculation of the wing tone is based on results from the fourth wing-beat cycle. Details of the grid convergence study and CFD solver validation are presented in Appendixe A and Appendixe B, respectively.
2.3. Prediction of Sound Particle Velocity Induced by Wing Tone
Because of the shallow stroke amplitude, the wake generated by the wing flapping of a mosquito is more focused than the wake of other flying animals [2]. As shown in Figure 1E,F published by Nakata et al. [2], the amplitude of the convective velocity around the antennae falls below the mosquito’s hearing threshold at the male wingbeat frequency (i.e., ) when the distance between the mosquito and ground is greater than . Therefore, the convective velocity around the antennae is sufficiently low to be neglected when the mosquito is far away from the ground. The FW–H equation provides a good model for the prediction of the sound for the present case [15]. The validation of the accuracy of the FW–H equation in the near field (outside the wake) can be found in the work by Cianferra et al. [24]. They calculated the sound generated by the turbulent flow around a sphere and compared the pressure signals provided by the FW-H equation with those provided by large eddy simulation (LES) for three probes with coordinates , , and , where is the diameter of the sphere. As shown in Figure 6, published by Cianferra et al. [24], the results provided by the two methods agree quite well. Similar comparations also can be found in other studies [25,26].
In this study, an integral formulation of the FW–H equation proposed by Brentner and Farassat [27] is used. For a zero-thickness body, the sound pressure at a point is given by:
and
is the sound pressure, is the sound speed, the dot over the variable represents the time derivative, is the unit vector normal to the wall (i.e., the surface of the wing), is the distance between the sound source and observer, is the surface velocity, is the unit vector from the sound source to the observer, and ‘ret’ denotes the evaluation at the retarded time (i.e., the source time ). It should be noted that the scattering of wing tone on the mosquito’s body is not considered in this study.
During hovering flight, the wing tone is periodic and can be regarded as the superposition of harmonic sequences [7,28,29]. At the position , the sound particle velocity at angular frequency can be determined by [15]:
Figure 2 shows the attenuation of the radial sound particle velocity of the wing-beat frequency along the negative x-axis direction depicted in Figure 1a. The radial sound particle velocity is the projection of the sound particle velocity on the negative x-axis direction. The results of the present work agree well with previous simulation [28] and experimental [30] data.
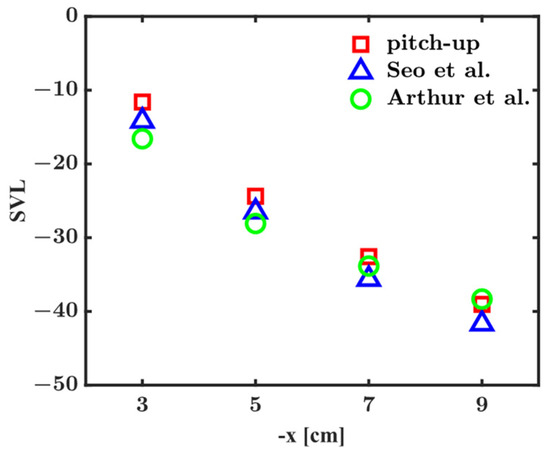
Figure 2.
Attenuation of radial sound particle velocity of the wing-beat frequency along the negative x-axis. ‘SVL’ is sound particle velocity level. Triangles represent simulation data from Seo et al. [28] for Culex quinquefasciatus, male. Circles are experimental data from Arthur et al. [30] for tethered Ades aegypti, male.
2.4. Characterization of Air Movements around the Antennae
Previous studies have tended to focus on the sound pressure [28,29] or the magnitude of particle velocity [2,7]. However, unlike eardrums that sense sound pressure, the mosquito’s antennae can detect tiny changes in both the magnitude and direction of air movements [2]. Specifically, the JO is thought to be able to detect a signal regardless of its direction with respect to the flagellum [7,16]. Based on the biological characteristics of antennae, we introduce a method to characterize air movements around the antennae. The air movements are decomposed into two basic modes: oscillation along a fixed direction and revolution with a constant angular velocity. This method provides a more intuitive representation of the characteristics (including amplitude and direction) of air movements around the antennae.
As shown in Figure 1a, denotes a coordinate system fixed on the body of the mosquito-like model. When the antennal flagellum is at rest, is located on the antennal flagellum, with the axis parallel to the antennal flagellum. We define the projection of the sound particle velocity onto the axes and as:
where and are amplitudes, and is the phase difference between the velocity components and . Since the tiny hairs (also known as fibrillae [3]) perpendicular to the flagellum are not considered in this study, the velocity component parallel to the antennal flagellum has been neglected (consistent with assumptions made in a previous mathematical model of mosquito antennae [31]).
Furthermore, the projection of sound particle velocity onto the plane can be rearranged as:
where and represent the unit vectors in the directions of axes and , respectively; the velocity components and are given by:
According to Equations (8) and (9), the fluctuation amplitudes of the velocity components and can be defined by:
The velocity is now represented by another two velocity components, and . Figure 3a,b show the modes of air movements corresponding to the velocity components and , respectively. According to Equation (8), in the coordinate system , the direction of remains constant over time. Thus, as depicted in Figure 3a, represents that the air particles (rectangle) propel the cross-section of antennae (solid circle) back and forth along a fixed direction. Conversely, according to Equation (9) the magnitude of remains constant, while the velocity vector rotates with a constant angular velocity . Therefore, as shown in Figure 3b, represents that the air particles propel the antennal cross-section in a revolving motion.
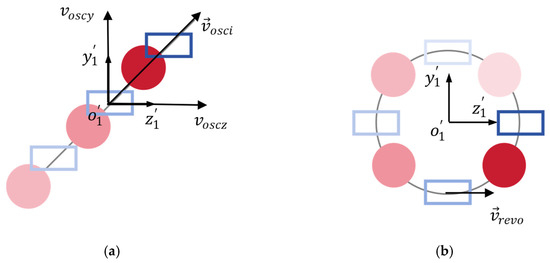
Figure 3.
Modes of air movements corresponding to the velocity components and , respectively. (a) : oscillation along a fixed direction. (b) : revolution with a constant angular velocity. Rectangles represent the trajectory of the air particles, while circles represent the trajectory of the cross-section of the mosquito’s antennae.
3. Results and Discussion
3.1. Aerodynamics
Figure 4 shows the flow fields and lift generated when the wing conducts the two flapping modes depicted in Figure 1b. Figure 4a presents the flow fields generated during the middle portion of the downstroke (). Contour plots of pressure are shown on the wing surfaces, while the contour plots of spanwise component of vorticity are provided at different spanwise sections. As shown on the left of Figure 4a, when the wing only conducts translation during the middle portion of the stroke, vortices are simultaneously shed from the leading and trailing edge, and there is a region of low pressure directly beneath the leading-edge vortex. A similar flow-field structure can be found in Figure 2 published by Eldredge et al. [32]. It should be noted that the leading-edge vortex actually does not develop fully because the mosquito’s stroke amplitude (approximately ) is much lower than that of other insects (around or larger) [20]. Consequently, the negative pressure induced by the leading-edge vortex is quite weak. On the contrary, as depicted on the right side of Figure 4a, the low-pressure region almost covers the front half of the wing when the wing rapidly pitches up during the middle portion of the stroke. Comparing the lift generated under the two wing-flapping modes (i.e., Figure 4b), we will find a significant enhancement in lift during the middle portion of the stroke when the wing rapidly pitches up. The lift peak during the middle portion of the stroke, generated when the wing rapidly pitches up, is almost 3.3 times that generated when the wing only conduct translation. A similar lift enhancement (or termed ‘fast-pitching-up rotation’ mechanism) has been reported by Liu et al. [18] This mechanism clarifies the answer to the question of why, in the lift time profiles reported by Bomphery et al. [17] and Nakata et al. [2], the lift peak during the upstroke is higher than that during the downstroke. Indeed, in their studies, the wing performs a more rapid pitch-up during the upstroke compared to the downstroke.
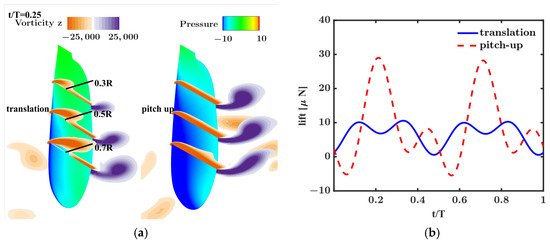
Figure 4.
(a) Spanwise vorticity counters at different sections and pressure counters on the wing surface during the middle portion of the downstroke (i.e., ). (b) Lift produced by one wing in one wing-beat cycle.
3.2. Sound Particle Velocity Induced by the Self-Generated Wing Tone
The self-generated wing tone is predicted by Equation (3). Figure 5 shows the distribution of amplitudes of sound particle velocity (i.e., the velocity magnitudes , , and as defined in Equation (10)) at the wing-beat frequency along the antennal flagellum . Variables and represent the velocity amplitudes of air particles oscillating along the and axes, as depicted in Figure 3a. The ratio between the velocity magnitudes and determines the oscillation direction of air particles. The variable represents the velocity amplitude of air particles revolving counterclockwise, as depicted in Figure 3b. Figure 5a shows the velocity amplitudes generated when the wing only conducts translation during the middle portion of the stroke. The velocity amplitudes are almost uniformly distributed along the antennae. The average velocity amplitudes of air oscillation and revolution are, respectively, , , and . Therefore, the oscillation along the axis dominates the air movements of the wing-beat frequency around the antennae. The maximum amplitude of oscillation velocity is located at the middle portion of the antennal flagellum. As shown in Figure 5b, when the wing rapidly pitches up during the middle portion of the stroke, the direction of air oscillation remains almost aligned with the axis. However, along the antennal direction (i.e., ), the velocity amplitude of air oscillation decreases almost linearly from to . In addition, the velocity amplitude of air revolution (i.e., ) generated when the wing rapidly pitches up is almost 3.2 times that generated when the wing only conducts translation. These alterations in air movements around the antennae caused by modulating the wing kinematics may be crucial in the mating communication among mosquitoes. More importantly, the intensity of acoustic particle velocity at the wing-beat frequency (approximately ) is considerably larger than the corresponding hearing threshold (approximately ) of the mosquito (Culex quinquefasciatus, male). According to the study by Nakata et al. [2], as the distance between the mosquito and the ground decreases from to , the magnitude of convective velocity at the wing-beat frequency around the mosquito’s antennae increases from about to . Therefore, the wing tone seems strong enough to mask the changes in convective velocity magnitude of the wing-beat frequency when the mosquito-like model approaches the ground.
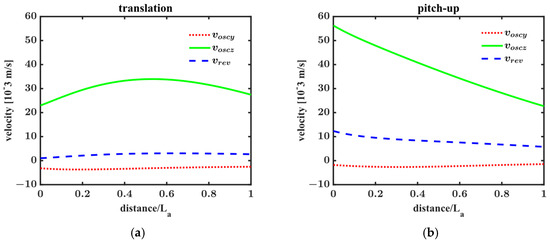
Figure 5.
Amplitudes of sound particle velocity at the wing-beat frequency along the antennal flagellum. (a) Amplitudes when a pair of wings only conduct translation during the middle portion of the stroke. (b) Amplitudes when a pair of wings rapidly pitch up during the middle portion of the stroke. The horizontal axis represents the distance between the point on the antennal flagellum and antennal root . is the length of the antennal flagellum.
3.3. Sound Particle Velocity Induced by the Reflected Wing Tone
As mosquitoes approach the ground, the air movements induced by the reflected wing tone might also be detected by the antennae. In this study, the reflected wing tone is generated by mirrored virtual sound sources. The mirrored virtual sound sources are symmetrical to the sound sources distributed on the flapping wing with respect to the ground. The ground is located beneath the flapping wing model and is parallel to the plane shown in Figure 1a. Figure 6 shows the averaged amplitudes of the reflected sound particle velocity at the wing-beat frequency as a function of the distance between the flapping-wing model and the ground plane. The variables , , and represent the averaged velocity amplitude along the antennal flagellum ; the black dashed line represents the hearing threshold of the mosquito (Culex quinquefasciatus, male) at the male wingbeat frequency. As shown in Figure 6a,b, the reflected sound particle velocity decreases rapidly with the increasing distance between the flapping wing model and the ground plane. Specifically, when the distance is greater than (approximately two wing lengths), the amplitudes of reflected sound particle velocity attenuate below the hearing threshold. This indicates that the antennae can detect the reflected wing tone at the wing-beat frequency only when the flapping-wing model is extremely close to the ground. Therefore, the role of reflected wing tone in the mosquito’s obstacle avoidance may be negligible.
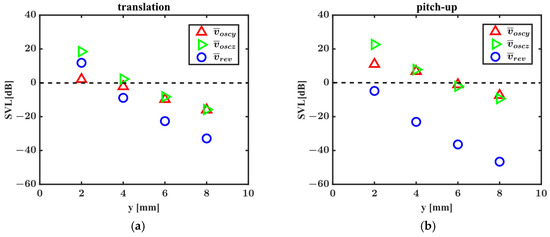
Figure 6.
Averaged amplitudes of reflected sound particle velocity at the wing-beat frequency as a function of distance between the flapping-wing model and the ground plane. (a) Averaged amplitudes when a pair of wings only conduct translation during the middle portion of the stroke. (b) Averaged amplitudes when a pair of wings rapidly pitch up during the middle portion of the stroke.
4. Conclusions
In this study, the air movements induced by the sound wave of the wing-beat frequency around the antennae of a mosquito-like model (Culex quinquefasciatus, male) are investigated using the acoustic analogy method. Based on the biological characteristics of antennae, we introduce a method to intuitively characterize the air movements induced by the wing tone around the antennae. The air movements are decomposed into two basic modes: oscillation along a fixed direction and revolution with constant angular velocity. We find that, without considering the scattering on the mosquito’s body, the self-generated sound wave of the wing-beat frequency around the antennae mainly induces air oscillation, with the velocity amplitude exceeding the mosquito’s hearing threshold at the standard male wing-beat frequency by two orders of magnitude. This indicates that while the sound wave of the wing-beat frequency is essential for the mosquito to hear potential mates, it might become a considerable background noise for mosquitoes to perceive the changes in convective velocity when approaching the ground.
In addition, the reflection of the wing tone on the ground is also examined. Results indicate that the reflected sound wave at the wing-beat frequency can be detected only when the flapping wing model is extremely close to the ground, approximately two wing lengths away. Thus, the role of reflected wing tone in the mosquito’s obstacle avoidance mechanism appears negligible; convective velocity may be the only source of useful close-range information. However, it should be noted that as convective velocity grows to a level close to that of the self-generated sound particle velocity (i.e., when mosquitoes are close to the ground), nonlinear interactions between convective flow and sound waves might become important. This could render the previously used prediction methods for the convective velocity and wing tone ineffective.
Author Contributions
Conceptualization, Y.W.; methodology, Y.W. and Z.Z.; validation, Y.W.; formal analysis, Y.W.; investigation, Y.W.; Software, Y.W. and Z.X.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W., Z.X. and Z.Z.; visualization, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Grid Convergence
To check grid convergence of the simulation results, simulations for the wing kinematics shown in Figure 1b are performed on different computational grids. Figure A1 shows the grid used in the CFD simulation. The size of the computational domain is , where is chord length. As shown in Figure A1b, the wing geometry reported by Bomphery et al. [17] is used in this study. The total number of Cartesian cells of the coarse grid is approximately 1.5 million and the minimum cell size for the background grid is . For the fine resolution grid, the minimum size for the background grid is , and approximately 4.6 million Cartesian cells are used. The simulation results on these two grids are compared in Figure A2 and Figure A3. The time profile of the lift is compared in Figure A2. The result on the coarse grid agrees well with the one on the fine grid. The difference between the results on the two different grids is found to be less than 5%. Figure A3 shows the comparation of the flow fields. The vortex structures are almost identical for both grids. Based on this, the coarse grid is used for all other flow simulations in this study.
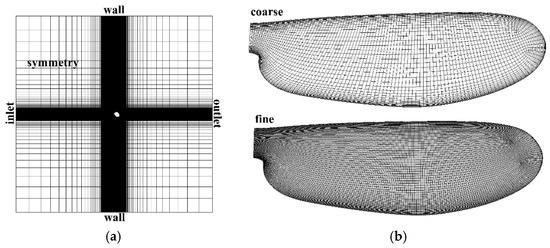
Figure A1.
(a) Background grid and (b) wing grid used in CFD simulations.
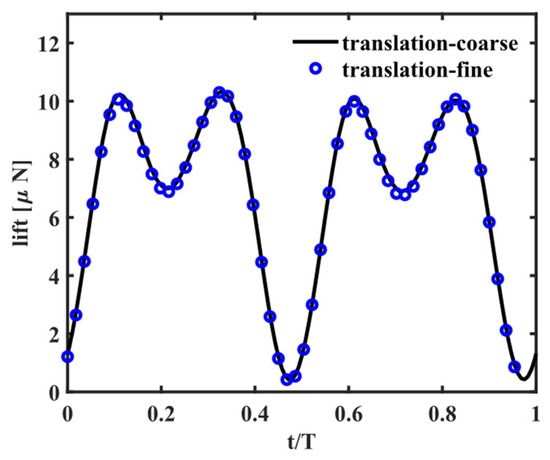
Figure A2.
Time profiles of the lift force simulated with coarse and fine grids.
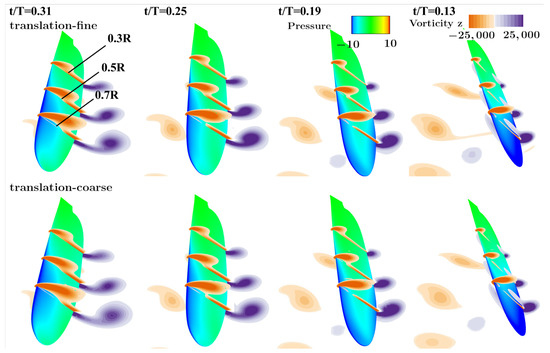
Figure A3.
Spanwise vorticity counters at different sections and pressure counters on the wing surface.
Appendix B. Validation of the CFD Solver
The CFD solver used in this research is validated by reperforming case 11 as published by Trizila et al. [33]. This benchmark case uses a flapping-wing model similar to the one used in this study, with a similar Reynolds number . The comparation of lift coefficients is shown in Figure A4. The maximum difference between the two results is less than 6%.
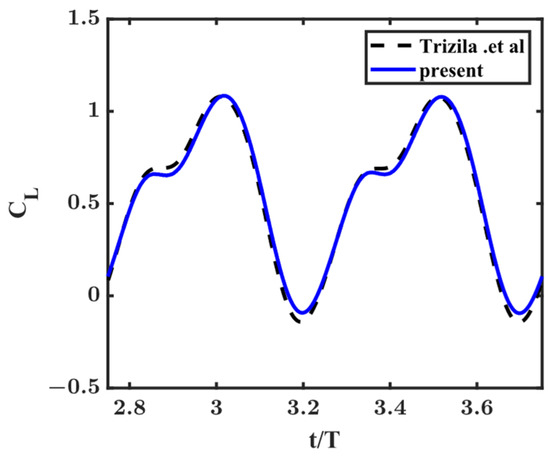
Figure A4.
Validation of the CFD solver. The black dashed line is data from Trizila et al. [33].
In addition, as shown in Figure A5, we compare the lifts obtained from the mosquito-like model depicted in Figure 1 with the lift provided by Bomphery et al. [17]. In the wing kinematics reported by Bomphery et al. [17], the wing mostly conducts translation during the middle portion of the downstroke and rapidly pitches up during the middle portion of the upstroke. Therefore, we will find that, during the downstroke (i.e., ), the lift provided by Bomphery et al. [17] (i.e., the green solid line) is similar to the lift generated when the wing of the mosquito-like model only conducts translation during the middle portion of the stroke (i.e., the blue solid line). During the upstroke (i.e., ), the lift provided by Bomphery et al. [17] is similar to the lift generated when the wing of the mosquito-like model rapidly pitches up during the middle portion of the stroke (i.e., the red dashed line).
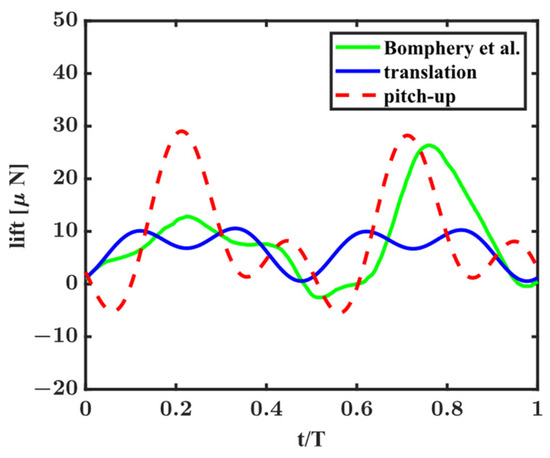
Figure A5.
Comparison between the lifts obtained from the mosquito-like model depicted in Figure 1 with the lift provided by Bomphery et al. [17].
References
- Hawkes, F.; Gibson, G. Seeing is believing: The nocturnal malarial mosquito Anopheles coluzzii responds to visual host-cues when odour indicates a host is nearby. Parasit. Vectors 2016, 9, 1–13. [Google Scholar] [CrossRef]
- Nakata, T.; Phillips, N.; Simões, P.; Russell, I.J.; Cheney, J.A.; Walker, S.M.; Bomphrey, R.J. Aerodynamic imaging by mosquitoes inspires a surface detector for autonomous flying vehicles. Science 2020, 368, 634–637. [Google Scholar] [CrossRef]
- Feugère, L.; Simões, P.; Russell, I.J.; Gibson, G. The role of hearing in mosquito behaviour. In Sensory Ecology of Disease Vectors; Ignell, R., Lazzari, C.R., Lorenzo, M.G., Hill, S.R., Eds.; Wageningen Academic Publishers: Wageningen, The Netherlands, 2022; pp. 683–708. [Google Scholar]
- Meng, X.; Han, Y.; Chen, Z.; Ghaffar, A.; Chen, G. Aerodynamic effects of ceiling and ground vicinity on flapping wings. Appl. Sci. 2022, 12, 4012. [Google Scholar] [CrossRef]
- Su, M.P.; Andrés, M.; Boyd-Gibbins, N.; Somers, J.; Albert, J.T. Sex and species specific hearing mechanisms in mosquito flagellar ears. Nat. Commun. 2018, 9, 3911. [Google Scholar] [CrossRef]
- Simões, P.M.; Ingham, R.A.; Gibson, G.; Russell, I.J. A role for acoustic distortion in novel rapid frequency modulation behaviour in free-flying male mosquitoes. J. Exp. Biol. 2016, 219, 2039–2047. [Google Scholar] [CrossRef]
- Nakata, T.; Simões, P.; Walker, S.M.; Russell, I.J.; Bomphrey, R.J. Auditory sensory range of male mosquitoes for the detection of female flight sound. J. R. Soc. Interface 2022, 19, 20220285. [Google Scholar] [CrossRef]
- Warren, B.; Gibson, G.; Russell, I.J. Sex Recognition through midflight mating duets in Culex mosquitoes is mediated by acoustic distortion. Curr. Biol. 2009, 19, 485–491. [Google Scholar] [CrossRef]
- Bae, Y.; Moon, Y.J. Aerodynamic sound generation of flapping wing. J. Acoust. Soc. Am. 2008, 124, 72–81. [Google Scholar] [CrossRef]
- Geng, B.; Xue, Q.; Zheng, X.; Liu, G.; Ren, Y.; Dong, H. The effect of wing flexibility on sound generation of flapping wings. Bioinspir. Biomim. 2017, 13, 016010. [Google Scholar] [CrossRef]
- Wang, L.; Tian, F.B. Numerical study of sound generation by three-dimensional flexible flapping wings during hovering flight. J. Fluids. Struct. 2020, 99, 103–165. [Google Scholar] [CrossRef]
- Debiasi, M.; Lu, Z.; Nguyen, Q.V.; Chan, W.L. Low-noise flapping wings with tensed membrane. AIAA J. 2020, 58, 2388–2397. [Google Scholar] [CrossRef]
- Nedunchezian, K.; Kang, C.K.; Aono, H. Effects of flapping wing kinematics on the aeroacoustics of hovering flight. J. Sound Vib. 2019, 442, 366–383. [Google Scholar] [CrossRef]
- Inada, Y.; Aono, H.; Liu, H.; Aoyama, T. Numerical analysis of sound generation of insect flapping wings. Theor. Appl. Mech. Jpn. 2009, 57, 437–447. [Google Scholar]
- Glegg, S.; Devenport, W. Aeroacoustics of Low Mach Number Flows: Fundamentals, Analysis, and Measurement; Academic Press: London, UK, 2017; p. 50. [Google Scholar]
- Lapshin, D.N.; Vorontsov, D.D. Directional and frequency characteristics of auditory neurons in Culex male mosquitoes. J. Exp. Biol. 2019, 222, jeb208785. [Google Scholar] [CrossRef]
- Bomphrey, R.J.; Nakata, T.; Phillips, N.; Walker, S.M.J.N. Smart wing rotation and trailing-edge vortices enable high frequency mosquito flight. Nature 2017, 544, 92–95. [Google Scholar] [CrossRef]
- Liu, L.; Sun, M. Dynamic flight stability of hovering mosquitoes. J. Theor. Biol. 2019, 464, 149–158. [Google Scholar] [CrossRef]
- Zhang, J.-D.; Huang, W.-X. On the role of vortical structures in aerodynamic performance of a hovering mosquito. Phys. Fluids 2019, 31, 051906. [Google Scholar] [CrossRef]
- Liu, L.G.; Du, G.; Sun, M. Aerodynamic-force production mechanisms in hovering mosquitoes. J. Fluid Mech. 2020, 898, A19. [Google Scholar] [CrossRef]
- Calado, A.; Poletti, R.; Koloszar, L.K.; Mendez, M.A. A robust data-driven model for flapping aerodynamics under different hovering kinematics. Phys. Fluids 2023, 35, 047122. [Google Scholar] [CrossRef]
- Wu, Y.K.; Sun, M.; Liu, Y.P. The wing− wing interaction mechanism of bristled wing pair in fling motion. Phys. Fluids 2022, 34, 071903. [Google Scholar] [CrossRef]
- Verma, S.; Hemmati, A. Characterization of bifurcated dual vortex streets in the wake of an oscillating foil. J. Fluid Mech. 2022, 945, A7. [Google Scholar] [CrossRef]
- Cianferra, M.; Armenio, V.; Ianniello, S. Hydroacoustic noise from different geometries. Int. J. Heat Fluid Flow 2018, 70, 348–362. [Google Scholar] [CrossRef]
- Cianferra, M.; Ianniello, S.; Armenio, V. Assessment of methodologies for the solution of the Ffowcs Williams and Hawkings equation using LES of incompressible single-phase flow around a finite-size square cylinder. J. Sound Vib. 2019, 453, 1–24. [Google Scholar] [CrossRef]
- Ricciardi, T.R.; Wolf, W.R.; Spalart, P.R. On the application of incomplete Ffowcs Williams and Hawkings surfaces for aeroacoustic predictions. AIAA J. 2022, 60, 1971–1977. [Google Scholar] [CrossRef]
- Brentner, K.S.; Farassat, F. Analytical comparison of the acoustic analogy and Kirchhoff formulation for moving surfaces. AIAA J. 1998, 36, 1379–1386. [Google Scholar] [CrossRef]
- Seo, J.H.; Hedrick, T.L.; Mittal, R. Mechanism and scaling of wing tone generation in mosquitoes. Bioinspir. Biomim. 2019, 15, 016008. [Google Scholar] [CrossRef]
- Seo, J.H.; Hedrick, T.L.; Mittal, R. Mosquitoes buzz and fruit flies don’ta comparative aeroacoustic analysis of wing-tone generation. Bioinspir. Biomim. 2021, 16, 046019. [Google Scholar] [CrossRef]
- Arthur, B.J.; Emr, K.S.; Wyttenbach, R.A.; Hoy, R.R. Mosquito (Aedes aegypti) flight tones: Frequency, harmonicity, spherical spreading, and phase relationships. J. Acoust. Soc. Am. 2014, 135, 933–941. [Google Scholar] [CrossRef]
- Avitabile, D.; Homer, M.; Champneys, A.R.; Jackson, J.C.; Robert, D. Mathematical modelling of the active hearing process in mosquitoes. J. R. Soc. Interface 2010, 7, 105–122. [Google Scholar] [CrossRef][Green Version]
- Eldredge, J.D.; Jones, A.R. Leading-edge vortices: Mechanics and modeling. Annu. Rev. Fluid Mech. 2019, 51, 75–104. [Google Scholar] [CrossRef]
- Trizila, P.; Kang, C.K.; Aono, H.; Shyy, W.; Visbal, M. Low-Reynolds-number aerodynamics of a flapping rigid flat plate. AIAA J. 2011, 49, 806–823. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).